En este módulo, se presentan los conceptos de la regresión lineal.
La regresión lineal es una técnica estadística que se usa para encontrar la relación entre las variables. En el contexto del AA, la regresión lineal encuentra la relación entre los atributos y una etiqueta.
Por ejemplo, supongamos que queremos predecir la eficiencia del combustible de un automóvil en millas por galón en función de su peso, y tenemos el siguiente conjunto de datos:
| Libras en miles (característica) | Millas por galón (etiqueta) |
|---|---|
| 3.5 | 18 |
| 3.69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| 4.34 | 15 |
| 4.42 | 14 |
| 2.37 | 24 |
Si graficáramos estos puntos, obtendríamos el siguiente gráfico:
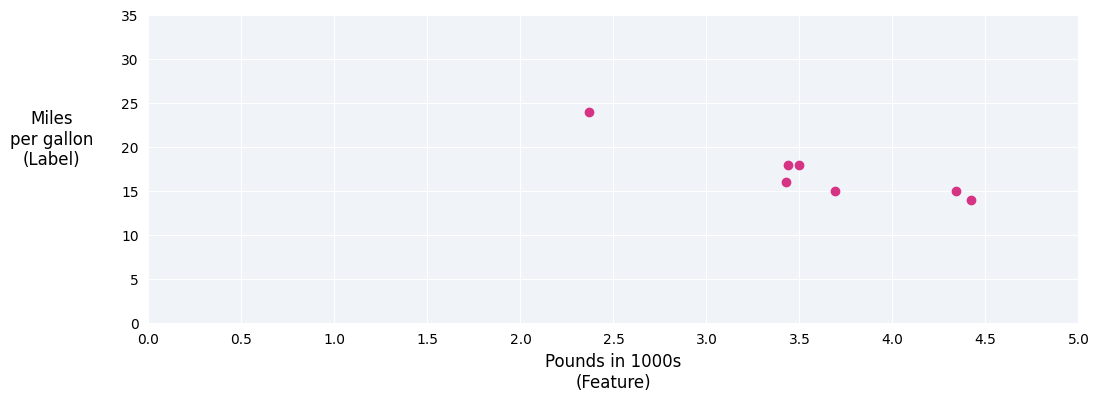
Figura 1. Peso del automóvil (en libras) en comparación con la clasificación de millas por galón. A medida que un automóvil se vuelve más pesado, su clasificación de millas por galón generalmente disminuye.
Podríamos crear nuestro propio modelo trazando una línea de mejor ajuste a través de los puntos:

Figura 2. Una línea de mejor ajuste trazada a través de los datos de la figura anterior.
Ecuación de regresión lineal
En términos algebraicos, el modelo se definiría como $ y = mx + b $, donde
- $ y $ son las millas por galón, el valor que queremos predecir.
- $ m $ es la pendiente de la recta.
- $ x $ son libras, nuestro valor de entrada.
- $ b $ es la intersección en Y.
En AA, escribimos la ecuación para un modelo de regresión lineal de la siguiente manera:
Donde:
- $ y' $ es la etiqueta predicha, es decir, el resultado.
- $ b $ es el sesgo del modelo. El sesgo es el mismo concepto que la intersección Y en la ecuación algebraica de una línea. En AA, el sesgo a veces se denomina $ w_0 $. El sesgo es un parámetro del modelo y se calcula durante el entrenamiento.
- $ w_1 $ es el peso del atributo. El peso es el mismo concepto que la pendiente $ m $ en la ecuación algebraica de una línea. El peso es un parámetro del modelo y se calcula durante el entrenamiento.
- $ x_1 $ es un atributo, la entrada.
Durante el entrenamiento, el modelo calcula el peso y el sesgo que producen el mejor modelo.
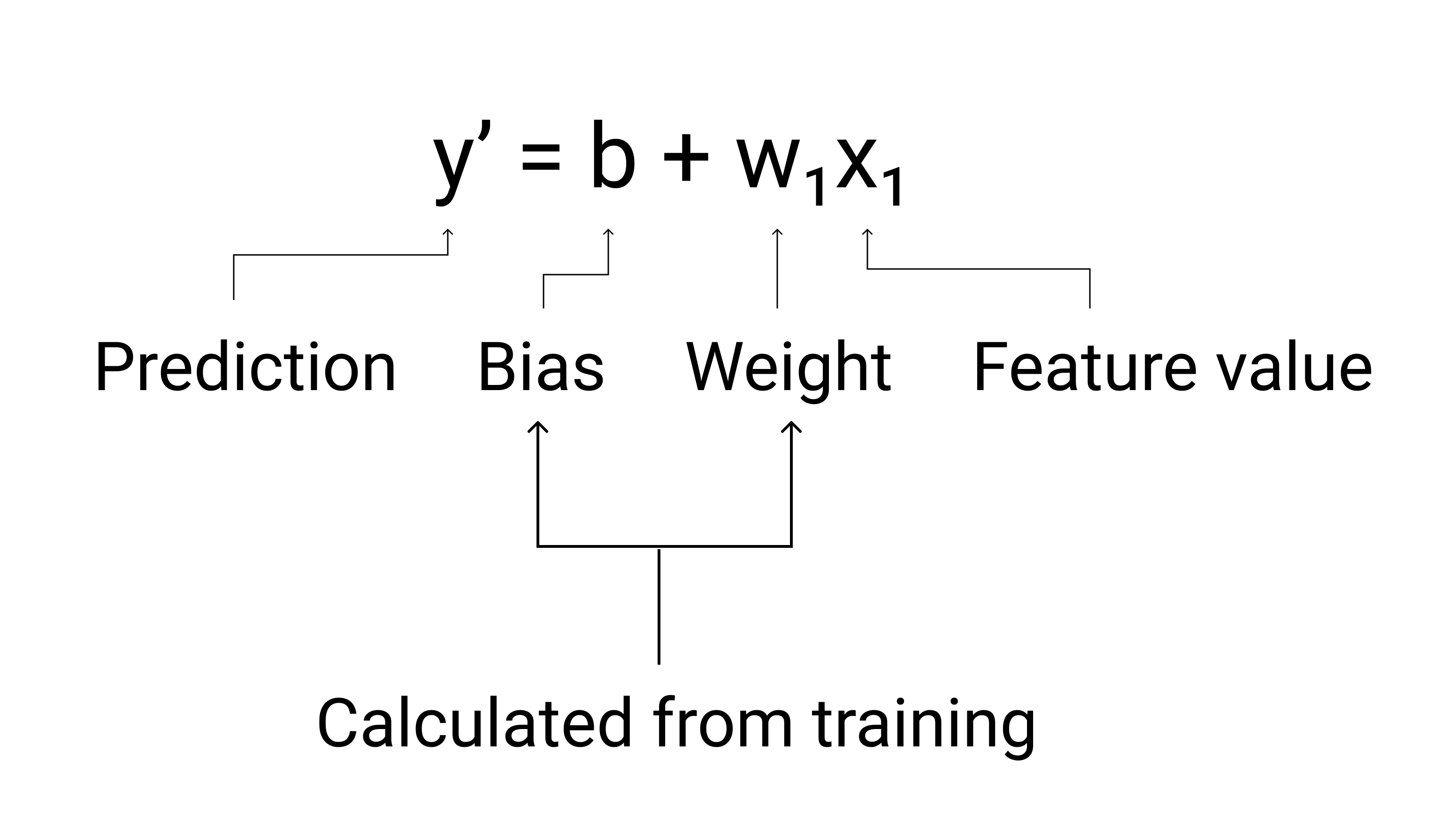
Figura 3. Representación matemática de un modelo lineal.
En nuestro ejemplo, calcularíamos el peso y la desviación a partir de la línea que trazamos. El sesgo es 34 (donde la línea se cruza con el eje Y) y el peso es -4.6 (la pendiente de la línea). El modelo se definiría como $ y' = 34 + (-4.6)(x_1)$ y podríamos usarlo para hacer predicciones. Por ejemplo, con este modelo, se predeciría que un automóvil de 1,814 kg tendría una eficiencia de combustible de 6.6 km/l.
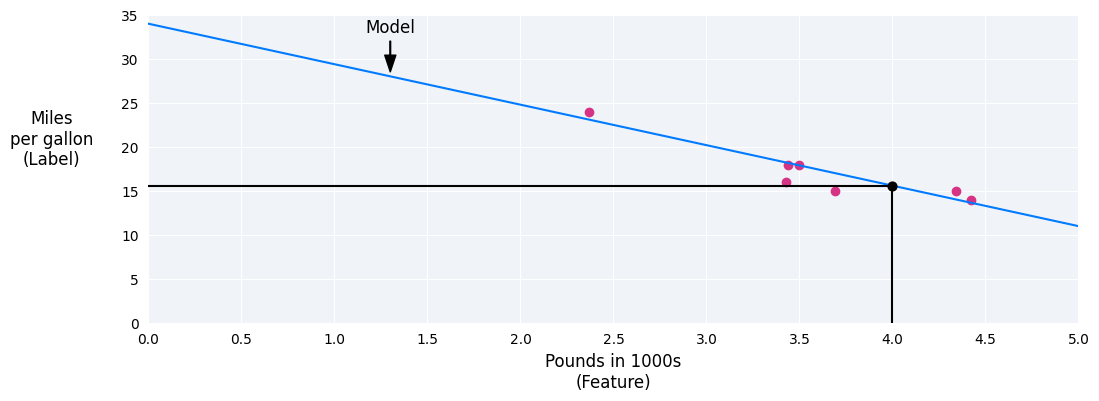
Figura 4. Con el modelo, se predice que un automóvil de 1,814 kg tiene una eficiencia de combustible de 6.6 km/l.
Modelos con múltiples características
Aunque el ejemplo de esta sección usa solo un atributo (el peso del automóvil), un modelo más sofisticado podría usar múltiples atributos, cada uno con un peso distinto ($ w_1 $, $ w_2 $, etc.). Por ejemplo, un modelo que se basa en cinco atributos se escribiría de la siguiente manera:
$ y' = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 $
Por ejemplo, un modelo que predice el consumo de combustible podría usar también atributos como los siguientes:
- Cilindrada del motor
- Aceleración
- Cantidad de cilindros
- Potencia
Este modelo se escribiría de la siguiente manera:

Figura 5. Un modelo con cinco atributos para predecir la calificación de millas por galón de un automóvil.
Si graficamos algunas de estas funciones adicionales, podemos ver que también tienen una relación lineal con la etiqueta, millas por galón:
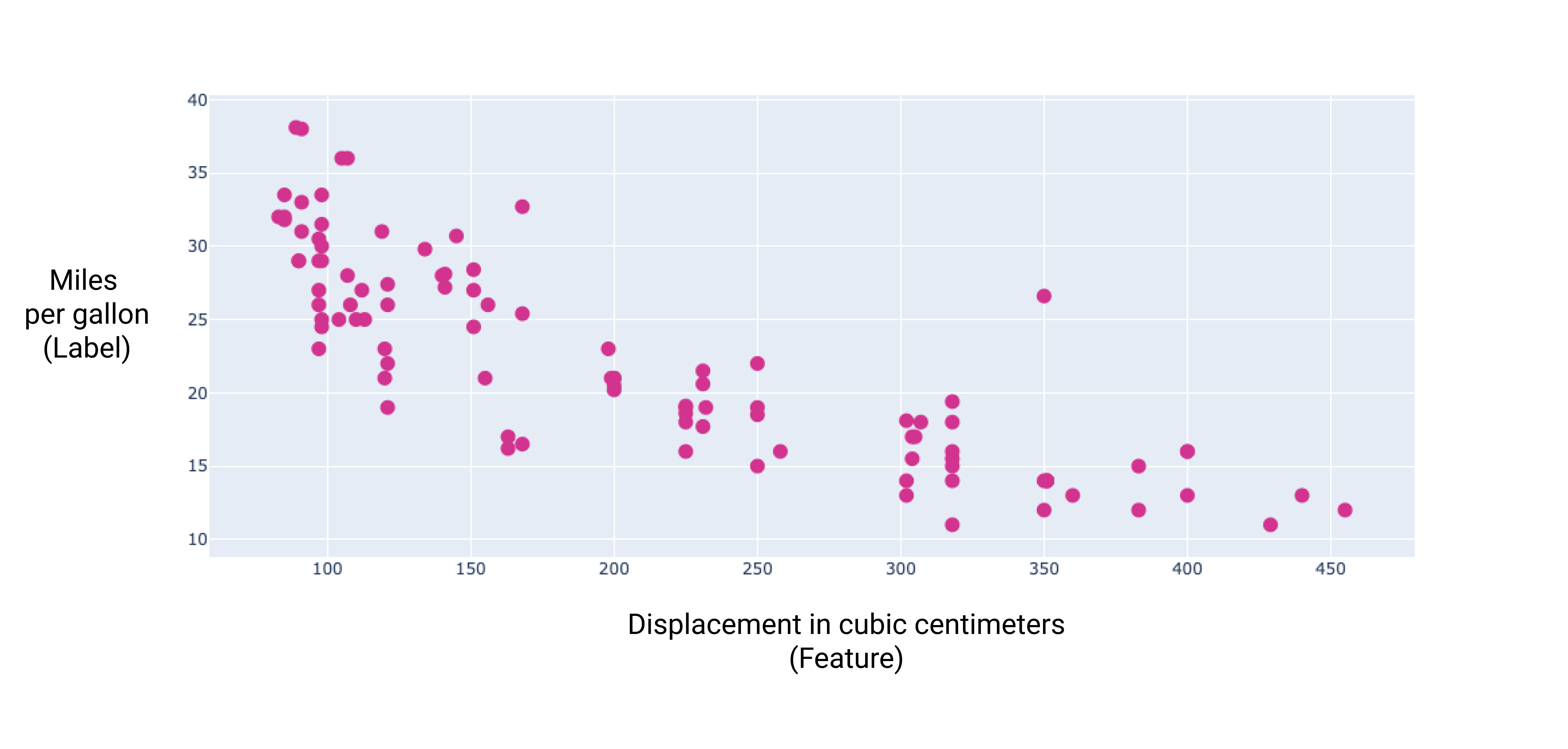
Figura 6. El desplazamiento de un automóvil en centímetros cúbicos y su clasificación de millas por galón A medida que el motor de un automóvil se hace más grande, su clasificación de millas por galón generalmente disminuye.
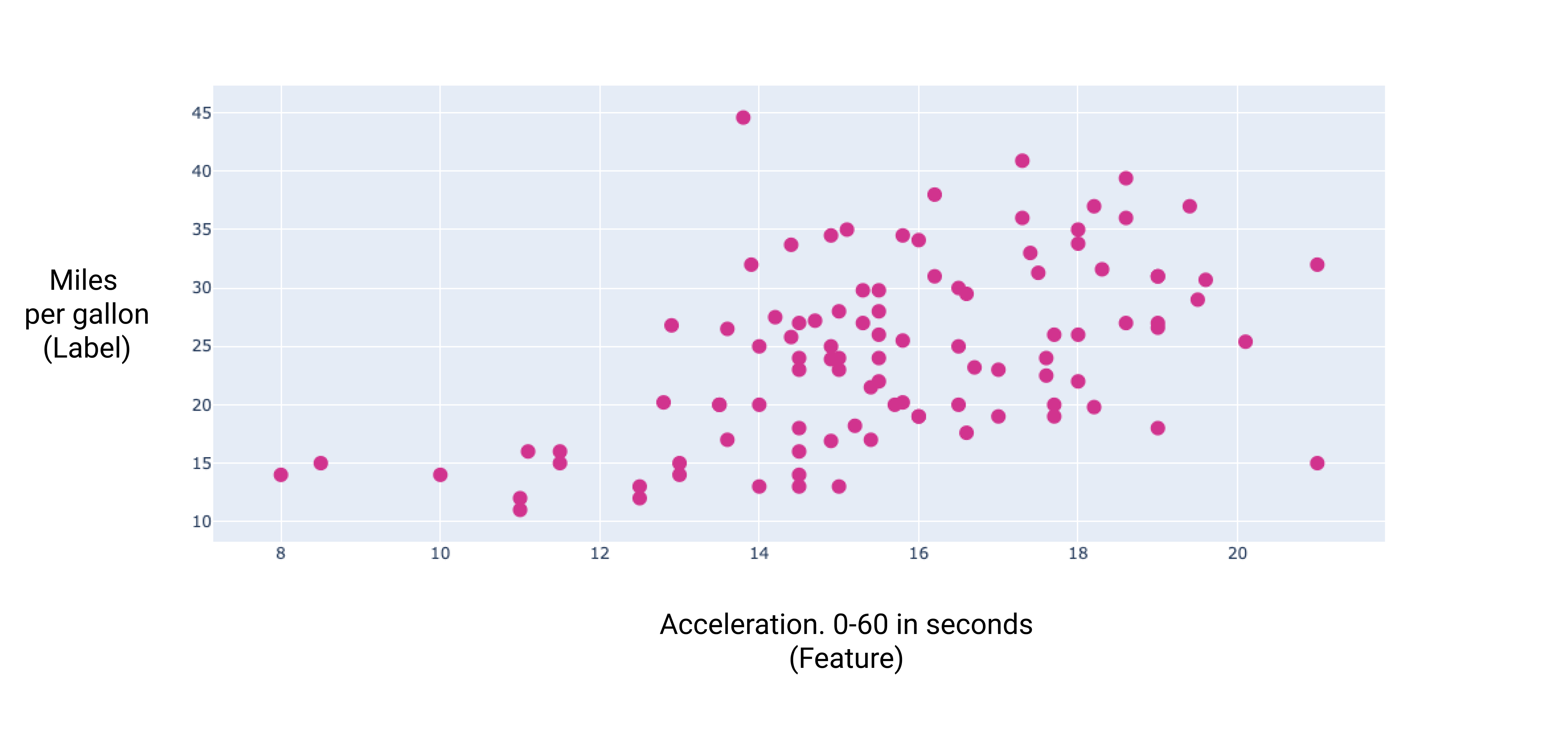
Figura 7. La aceleración de un automóvil y su clasificación de millas por galón. A medida que la aceleración de un automóvil tarda más, la clasificación de millas por galón generalmente aumenta.
