Page Summary
-
Hyperparameters, such as learning rate, batch size, and epochs, are external configurations that influence the training process of a machine learning model.
-
The learning rate determines the step size during model training, impacting the speed and stability of convergence.
-
Batch size dictates the number of training examples processed before updating model parameters, influencing training speed and noise.
-
Epochs represent the number of times the entire training dataset is used during training, affecting model performance and training time.
-
Choosing appropriate hyperparameters is crucial for optimizing model training and achieving desired results.
Hyperparameters are variables that control different aspects of training. Three common hyperparameters are:
In contrast, parameters are the variables, like the weights and bias, that are part of the model itself. In other words, hyperparameters are values that you control; parameters are values that the model calculates during training.
Learning rate
Learning rate is a floating point number you set that influences how quickly the model converges. If the learning rate is too low, the model can take a long time to converge. However, if the learning rate is too high, the model never converges, but instead bounces around the weights and bias that minimize the loss. The goal is to pick a learning rate that's not too high nor too low so that the model converges quickly.
The learning rate determines the magnitude of the changes to make to the weights and bias during each step of the gradient descent process. The model multiplies the gradient by the learning rate to determine the model's parameters (weight and bias values) for the next iteration. In the third step of gradient descent, the "small amount" to move in the direction of negative slope refers to the learning rate.
The difference between the old model parameters and the new model parameters is proportional to the slope of the loss function. For example, if the slope is large, the model takes a large step. If small, it takes a small step. For example, if the gradient's magnitude is 2.5 and the learning rate is 0.01, then the model will change the parameter by 0.025.
The ideal learning rate helps the model to converge within a reasonable number of iterations. In Figure 20, the loss curve shows the model significantly improving during the first 20 iterations before beginning to converge:

Figure 20. Loss graph showing a model trained with a learning rate that converges quickly.
In contrast, a learning rate that's too small can take too many iterations to converge. In Figure 21, the loss curve shows the model making only minor improvements after each iteration:
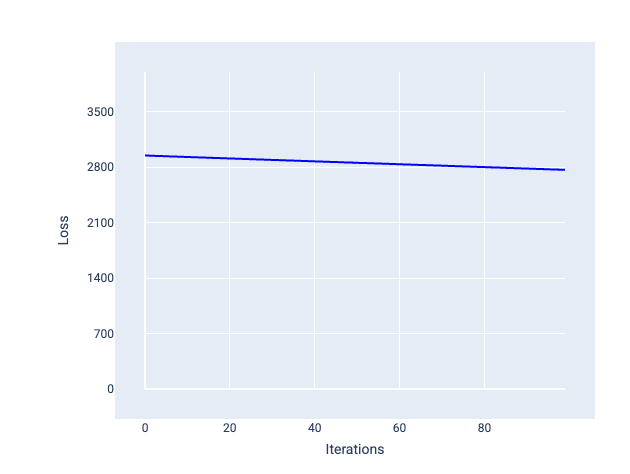
Figure 21. Loss graph showing a model trained with a small learning rate.
A learning rate that's too large never converges because each iteration either causes the loss to bounce around or continually increase. In Figure 22, the loss curve shows the model decreasing and then increasing loss after each iteration, and in Figure 23 the loss increases at later iterations:
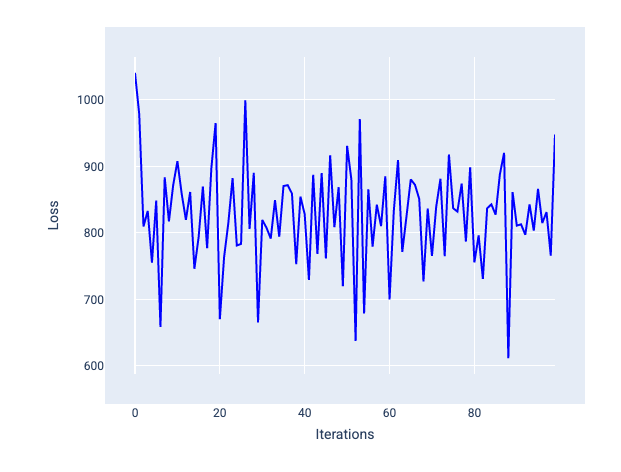
Figure 22. Loss graph showing a model trained with a learning rate that's too big, where the loss curve fluctuates wildly, going up and down as the iterations increase.
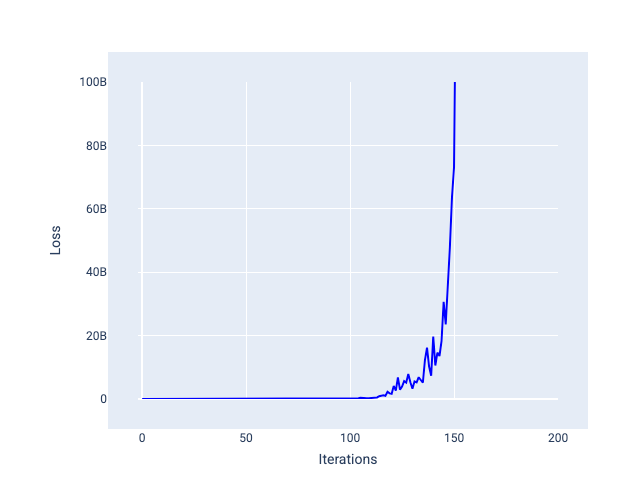
Figure 23. Loss graph showing a model trained with a learning rate that's too big, where the loss curve drastically increases in later iterations.
Exercise: Check your understanding
Batch size
Batch size is a hyperparameter that refers to the number of examples the model processes before updating its weights and bias. You might think that the model should calculate the loss for every example in the dataset before updating the weights and bias. However, when a dataset contains hundreds of thousands or even millions of examples, using the full batch isn't practical.
Two common techniques to get the right gradient on average without needing to look at every example in the dataset before updating the weights and bias are stochastic gradient descent and mini-batch stochastic gradient descent:
Stochastic gradient descent (SGD): Stochastic gradient descent uses only a single example (a batch size of one) per iteration. Given enough iterations, SGD works but is very noisy. "Noise" refers to variations during training that cause the loss to increase rather than decrease during an iteration. The term "stochastic" indicates that the one example comprising each batch is chosen at random.
Notice in the following image how loss slightly fluctuates as the model updates its weights and bias using SGD, which can lead to noise in the loss graph:
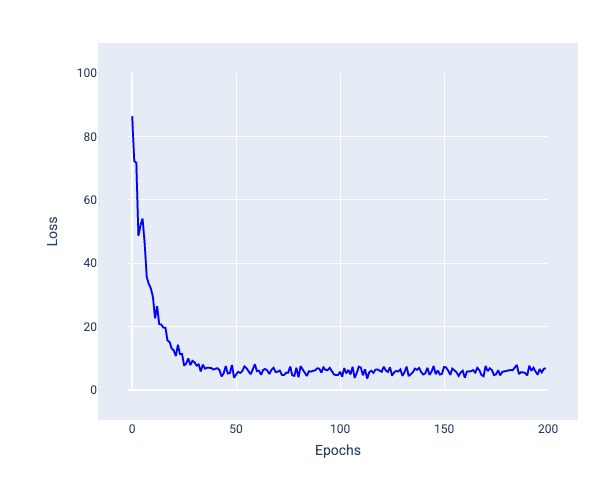
Figure 24. Model trained with stochastic gradient descent (SGD) showing noise in the loss curve.
Note that using stochastic gradient descent can produce noise throughout the entire loss curve, not just near convergence.
Mini-batch stochastic gradient descent (mini-batch SGD): Mini-batch stochastic gradient descent is a compromise between full-batch and SGD. For $ N $ number of data points, the batch size can be any number greater than 1 and less than $ N $. The model chooses the examples included in each batch at random, averages their gradients, and then updates the weights and bias once per iteration.
Determining the number of examples for each batch depends on the dataset and the available compute resources. In general, small batch sizes behaves like SGD, and larger batch sizes behaves like full-batch gradient descent.
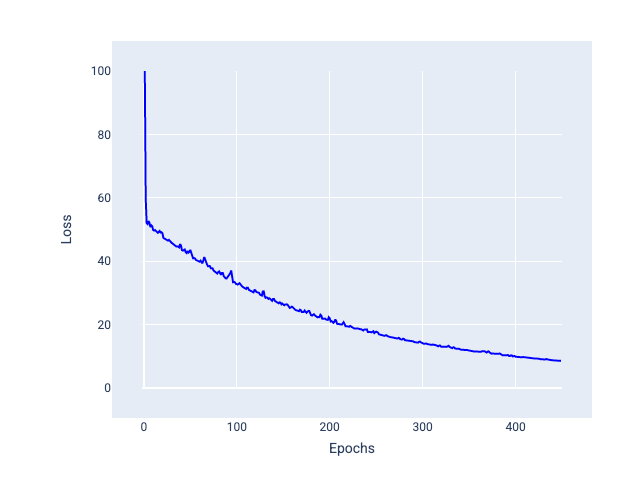
Figure 25. Model trained with mini-batch SGD.
When training a model, you might think that noise is an undesirable characteristic that should be eliminated. However, a certain amount of noise can be a good thing. In later modules, you'll learn how noise can help a model generalize better and find the optimal weights and bias in a neural network.
Epochs
During training, an epoch means that the model has processed every example in the training set once. For example, given a training set with 1,000 examples and a mini-batch size of 100 examples, it will take the model 10 iterations to complete one epoch.
Training typically requires many epochs. That is, the system needs to process every example in the training set multiple times.
The number of epochs is a hyperparameter you set before the model begins training. In many cases, you'll need to experiment with how many epochs it takes for the model to converge. In general, more epochs produces a better model, but also takes more time to train.
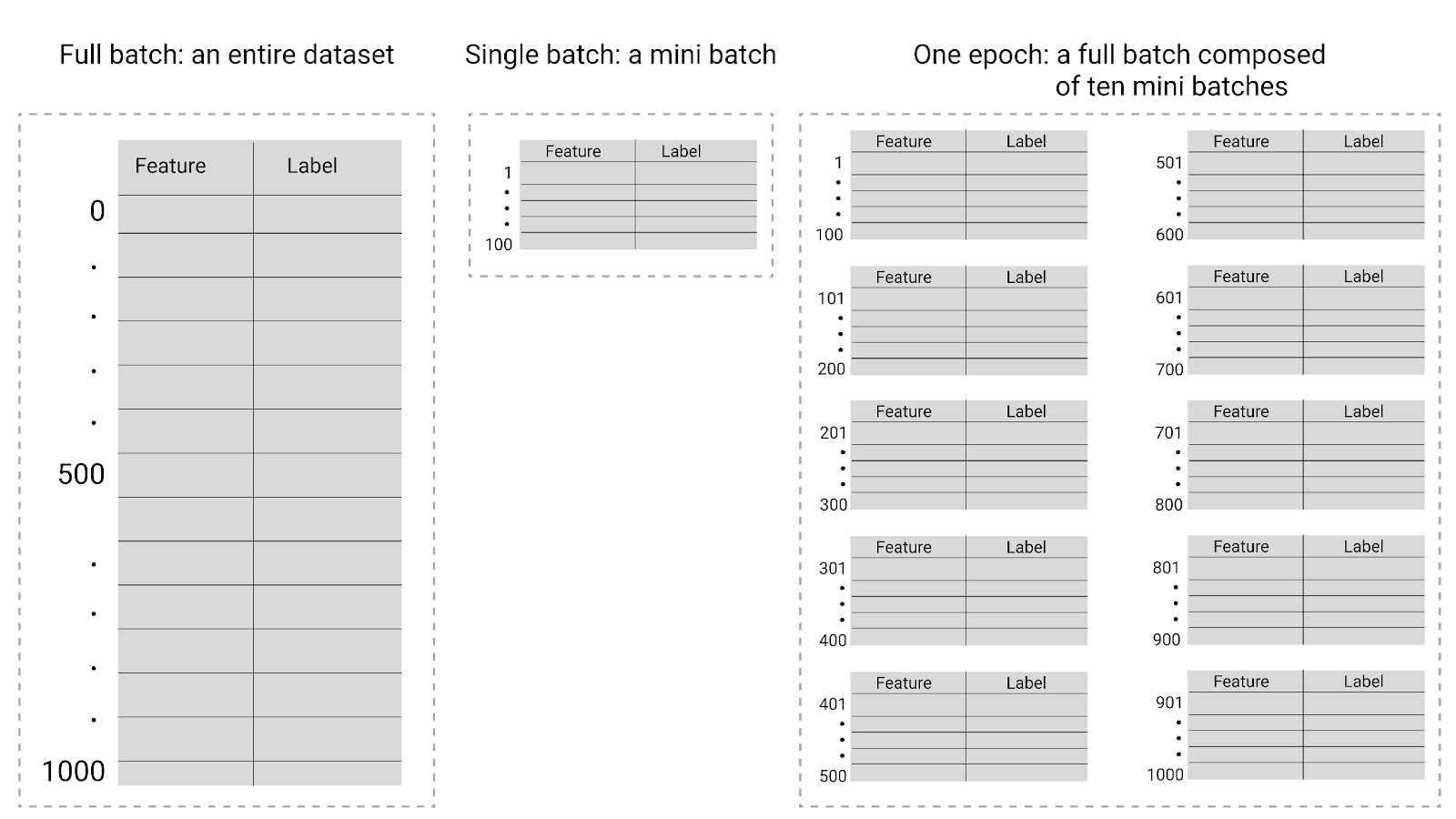
Figure 26. Full batch versus mini batch.
The following table describes how batch size and epochs relate to the number of times a model updates its parameters.
| Batch type | When weights and bias updates occur |
|---|---|
| Full batch | After the model looks at all the examples in the dataset. For instance, if a dataset contains 1,000 examples and the model trains for 20 epochs, the model updates the weights and bias 20 times, once per epoch. |
| Stochastic gradient descent | After the model looks at a single example from the dataset. For instance, if a dataset contains 1,000 examples and trains for 20 epochs, the model updates the weights and bias 20,000 times. |
| Mini-batch stochastic gradient descent | After the model looks at the examples in each batch. For instance, if a dataset contains 1,000 examples, and the batch size is 100, and the model trains for 20 epochs, the model updates the weights and bias 200 times. |