Page Summary
-
Data normalization is crucial for enhancing machine learning model performance by scaling features to a similar range.
-
Linear scaling, Z-score scaling, and log scaling are common normalization techniques, each suitable for different data distributions.
-
Clipping helps manage outliers by limiting extreme values within a defined range, improving model robustness.
-
Selecting the appropriate normalization method depends on the specific dataset and feature characteristics, often requiring experimentation for optimal results.
-
Applying normalization consistently during both training and prediction stages ensures accurate and reliable model outcomes.
After examining your data through statistical and visualization techniques, you should transform your data in ways that will help your model train more effectively. The goal of normalization is to transform features to be on a similar scale. For example, consider the following two features:
- Feature
Xspans the range 154 to 24,917,482. - Feature
Yspans the range 5 to 22.
These two features span very different ranges. Normalization might manipulate
X and Y so that they span a similar range, perhaps 0 to 1.
Normalization provides the following benefits:
- Helps models converge more quickly during training. When different features have different ranges, gradient descent can "bounce" and slow convergence. That said, more advanced optimizers like Adagrad and Adam protect against this problem by changing the effective learning rate over time.
- Helps models infer better predictions. When different features have different ranges, the resulting model might make somewhat less useful predictions.
- Helps avoid the "NaN trap" when feature values are very high.
NaN is an abbreviation for
not a number. When a value in a model exceeds the
floating-point precision limit, the system sets the value to
NaNinstead of a number. When one number in the model becomes a NaN, other numbers in the model also eventually become a NaN. - Helps the model learn appropriate weights for each feature. Without feature scaling, the model pays too much attention to features with wide ranges and not enough attention to features with narrow ranges.
We recommend normalizing numeric features covering distinctly
different ranges (for example, age and income).
We also recommend normalizing a single numeric feature that covers a wide range,
such as city population.
Consider the following two features:
- Feature
A's lowest value is -0.5 and highest is +0.5. - Feature
B's lowest value is -5.0 and highest is +5.0.
Feature A and Feature B have relatively narrow spans. However, Feature B's
span is 10 times wider than Feature A's span. Therefore:
- At the start of training, the model assumes that Feature
Bis ten times more "important" than FeatureA. - Training will take longer than it should.
- The resulting model may be suboptimal.
The overall damage due to not normalizing will be relatively small; however, we still recommend normalizing Feature A and Feature B to the same scale, perhaps -1.0 to +1.0.
Now consider two features with a greater disparity of ranges:
- Feature
C's lowest value is -1 and highest is +1. - Feature
D's lowest value is +5000 and highest is +1,000,000,000.
If you don't normalize Feature C and Feature D, your model will likely
be suboptimal. Furthermore, training will take much longer to
converge or even fail to converge entirely!
This section covers three popular normalization methods:
- linear scaling
- Z-score scaling
- log scaling
This section additionally covers clipping. Although not a true normalization technique, clipping does tame unruly numerical features into ranges that produce better models.
Linear scaling
Linear scaling (more commonly shortened to just scaling) means converting floating-point values from their natural range into a standard range—usually 0 to 1 or -1 to +1.
Linear scaling is a good choice when all of the following conditions are met:
- The lower and upper bounds of your data don't change much over time.
- The feature contains few or no outliers, and those outliers aren't extreme.
- The feature is approximately uniformly distributed across its range. That is, a histogram would show roughly even bars for most values.
Suppose human age is a feature. Linear scaling is a good normalization
technique for age because:
- The approximate lower and upper bounds are 0 to 100.
agecontains a relatively small percentage of outliers. Only about 0.3% of the population is over 100.- Although certain ages are somewhat better represented than others, a large dataset should contain sufficient examples of all ages.
Exercise: Check your understanding
Suppose your model has a feature namednet_worth that holds the net
worth of different people. Would linear scaling be a good normalization
technique for net_worth? Why or why not?
Z-score scaling
A Z-score is the number of standard deviations a value is from the mean. For example, a value that is 2 standard deviations greater than the mean has a Z-score of +2.0. A value that is 1.5 standard deviations less than the mean has a Z-score of -1.5.
Representing a feature with Z-score scaling means storing that feature's Z-score in the feature vector. For example, the following figure shows two histograms:
- On the left, a classic normal distribution.
- On the right, the same distribution normalized by Z-score scaling.

Z-score scaling is also a good choice for data like that shown in the following figure, which has only a vaguely normal distribution.

Z-score is a good choice when the data follows a normal distribution or a distribution somewhat like a normal distribution.
Note that some distributions might be normal within the bulk of their
range, but still contain extreme outliers. For example, nearly all of the
points in a net_worth feature might fit neatly into 3 standard deviations,
but a few examples of this feature could be hundreds of standard deviations
away from the mean. In these situations, you can combine Z-score scaling with
another form of normalization (usually clipping) to handle this situation.
Exercise: Check your understanding
Suppose your model trains on a feature namedheight that holds the adult
heights of ten million women. Would Z-score scaling be a good normalization
technique for height? Why or why not?
Log scaling
Log scaling computes the logarithm of the raw value. In theory, the logarithm could be any base; in practice, log scaling usually calculates the natural logarithm (ln).
Log scaling is helpful when the data conforms to a power law distribution. Casually speaking, a power law distribution looks as follows:
- Low values of
Xhave very high values ofY. - As the values of
Xincrease, the values ofYquickly decrease. Consequently, high values ofXhave very low values ofY.
Movie ratings are a good example of a power law distribution. In the following figure, notice:
- A few movies have lots of user ratings. (Low values of
Xhave high values ofY.) - Most movies have very few user ratings. (High values of
Xhave low values ofY.)
Log scaling changes the distribution, which helps train a model that will make better predictions.

As a second example, book sales conform to a power law distribution because:
- Most published books sell a tiny number of copies, maybe one or two hundred.
- Some books sell a moderate number of copies, in the thousands.
- Only a few bestsellers will sell more than a million copies.
Suppose you are training a linear model to find the relationship of, say, book covers to book sales. A linear model training on raw values would have to find something about book covers on books that sell a million copies that is 10,000 more powerful than book covers that sell only 100 copies. However, log scaling all the sales figures makes the task far more feasible. For example, the log of 100 is:
~4.6 = ln(100)
while the log of 1,000,000 is:
~13.8 = ln(1,000,000)
So, the log of 1,000,000 is only about three times larger than the log of 100. You probably could imagine a bestseller book cover being about three times more powerful (in some way) than a tiny-selling book cover.
Clipping
Clipping is a technique to minimize the influence of extreme outliers. In brief, clipping usually caps (reduces) the value of outliers to a specific maximum value. Clipping is a strange idea, and yet, it can be very effective.
For example, imagine a dataset containing a feature named roomsPerPerson,
which represents the number of rooms (total rooms divided
by number of occupants) for various houses. The following plot shows that over
99% of the feature values conform to a normal distribution (roughly, a mean of
1.8 and a standard deviation of 0.7). However, the feature contains
a few outliers, some of them extreme:

How can you minimize the influence of those extreme outliers? Well, the
histogram is not an even distribution, a normal distribution, or a power law
distribution. What if you simply cap or clip the maximum value of
roomsPerPerson at an arbitrary value, say 4.0?

Clipping the feature value at 4.0 doesn't mean that your model ignores all values greater than 4.0. Rather, it means that all values that were greater than 4.0 now become 4.0. This explains the peculiar hill at 4.0. Despite that hill, the scaled feature set is now more useful than the original data.
Wait a second! Can you really reduce every outlier value to some arbitrary upper threshold? When training a model, yes.
You can also clip values after applying other forms of normalization. For example, suppose you use Z-score scaling, but a few outliers have absolute values far greater than 3. In this case, you could:
- Clip Z-scores greater than 3 to become exactly 3.
- Clip Z-scores less than -3 to become exactly -3.
Clipping prevents your model from overindexing on unimportant data. However, some outliers are actually important, so clip values carefully.
Summary of normalization techniques
| Normalization technique | Formula | When to use |
|---|---|---|
| Linear scaling | $$ x' = \frac{x - x_{min}}{x_{max} - x_{min}} $$ | When the feature is mostly uniformly distributed across range. Flat-shaped |
| Z-score scaling | $$ x' = \frac{x - μ}{σ}$$ | When the feature is normally distributed (peak close to mean). Bell-shaped |
| Log scaling | $$ x' = log(x)$$ | When the feature distribution is heavy skewed on at least either side of tail. Heavy Tail-shaped |
| Clipping | If $x > max$, set $x' = max$ If $x < min$, set $x' = min$ |
When the feature contains extreme outliers. |
Exercise: Test your knowledge
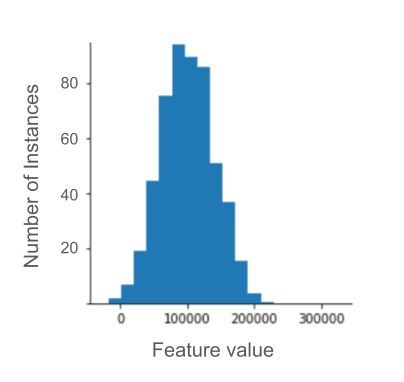
Suppose you are developing a model that predicts a data center's
productivity based on the temperature measured inside the data center.
Almost all of the temperature values in your dataset fall
between 15 and 30 (Celsius), with the following exceptions:
- Once or twice per year, on extremely hot days, a few values between
31 and 45 are recorded in
temperature. - Every 1,000th point in
temperatureis set to 1,000 rather than the actual temperature.
Which would be a reasonable normalization technique for
temperature?
The values of 1,000 are mistakes, and should be deleted rather than clipped.
The values between 31 and 45 are legitimate data points. Clipping would probably be a good idea for these values, assuming the dataset doesn't contain enough examples in this temperature range to train the model to make good predictions. However, during inference, note that the clipped model would therefore make the same prediction for a temperature of 45 as for a temperature of 35.