En este glosario, se definen términos relacionados con la inteligencia artificial.
A
ablación
Técnica para evaluar la importancia de un atributo o componente quitándolo temporalmente de un modelo. Luego, vuelves a entrenar el modelo sin ese atributo o componente y, si el modelo reentrenado tiene un rendimiento significativamente peor, es probable que el atributo o componente quitado fuera importante.
Por ejemplo, supongamos que entrenas un modelo de clasificación con 10 atributos y logras una precisión del 88% en el conjunto de prueba. Para verificar la importancia del primer atributo, puedes volver a entrenar el modelo usando solo los otros nueve atributos. Si el modelo reentrenado tiene un rendimiento significativamente peor (por ejemplo, un 55% de precisión), es probable que el atributo quitado fuera importante. Por el contrario, si el modelo reentrenado tiene un rendimiento igual de bueno, es probable que ese atributo no fuera tan importante.
La ablación también puede ayudar a determinar la importancia de lo siguiente:
- Componentes más grandes, como un subsistema completo de un sistema de AA más grande
- Procesos o técnicas, como un paso de preprocesamiento de datos
En ambos casos, observarías cómo cambia (o no cambia) el rendimiento del sistema después de quitar el componente.
Pruebas A/B
Es una forma estadística de comparar dos (o más) técnicas: la A y la B. Por lo general, la A es una técnica existente y la B es una técnica nueva. Las pruebas A/B no solo determinan qué técnica tiene mejor rendimiento, sino también si la diferencia es estadísticamente significativa.
Las pruebas A/B suelen comparar una sola métrica en dos técnicas. Por ejemplo, ¿cómo se compara la precisión del modelo para dos técnicas? Sin embargo, las pruebas A/B también pueden comparar cualquier cantidad finita de métricas.
chip acelerador
Es una categoría de componentes de hardware especializados diseñados para realizar cálculos clave necesarios para los algoritmos de aprendizaje profundo.
Los chips aceleradores (o simplemente aceleradores) pueden aumentar significativamente la velocidad y la eficiencia de las tareas de entrenamiento y de inferencia en comparación con una CPU de uso general. Son ideales para entrenar redes neuronales y realizar tareas similares que requieren un uso intensivo del procesamiento.
Estos son algunos ejemplos de chips aceleradores:
- Las unidades de procesamiento tensorial (TPUs) de Google con hardware dedicado para el aprendizaje profundo.
- Las GPU de NVIDIA, aunque se diseñaron inicialmente para el procesamiento de gráficos, están diseñadas para permitir el procesamiento paralelo, lo que puede aumentar significativamente la velocidad de procesamiento.
exactitud
Es la cantidad de predicciones de clasificación correctas dividida por la cantidad total de predicciones. Es decir:
Por ejemplo, un modelo que realizó 40 predicciones correctas y 10 incorrectas tendría una precisión de:
La clasificación binaria proporciona nombres específicos para las diferentes categorías de predicciones correctas y predicciones incorrectas. Por lo tanto, la fórmula de exactitud para la clasificación binaria es la siguiente:
Donde:
- TP es la cantidad de verdaderos positivos (predicciones correctas).
- TN es la cantidad de verdaderos negativos (predicciones correctas).
- FP es la cantidad de falsos positivos (predicciones incorrectas).
- FN es la cantidad de falsos negativos (predicciones incorrectas).
Compara y contrasta la exactitud con la precisión y la recuperación.
Consulta Clasificación: Precisión, recuperación, exactitud y métricas relacionadas en el Curso intensivo de aprendizaje automático para obtener más información.
acción
En el aprendizaje por refuerzo, es el mecanismo por el cual el agente realiza la transición entre los estados del entorno. El agente elige la acción con una política.
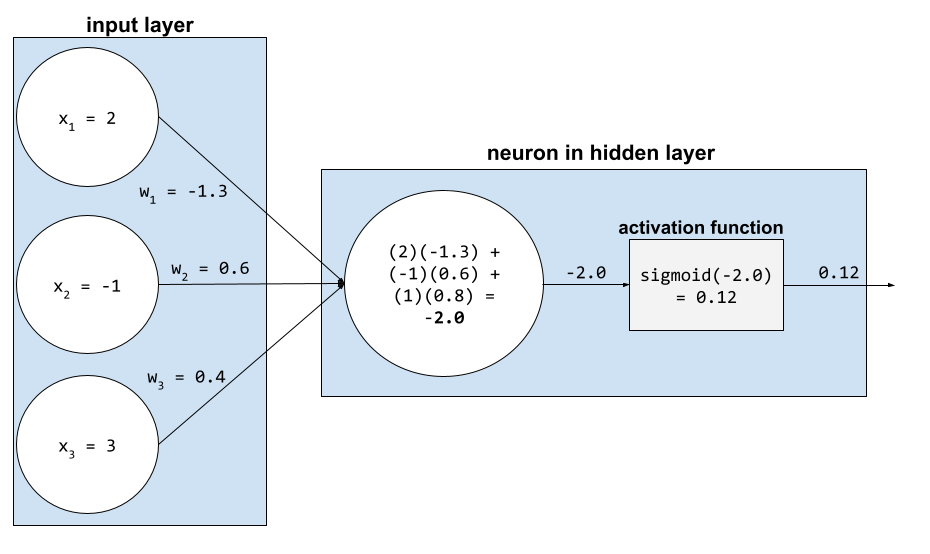
función de activación
Es una función que permite que las redes neuronales aprendan relaciones no lineales (complejas) entre las características y la etiqueta.
Entre las funciones de activación populares, se incluyen las siguientes:
Los diagramas de las funciones de activación nunca son líneas rectas únicas. Por ejemplo, el gráfico de la función de activación ReLU consta de dos líneas rectas:

El gráfico de la función de activación sigmoidea se ve de la siguiente manera:

Consulta Redes neuronales: Funciones de activación en el Curso intensivo de aprendizaje automático para obtener más información.
aprendizaje activo
Un enfoque de entrenamiento en el que el algoritmo elige algunos de los datos sobre los cuales aprende. El aprendizaje activo es especialmente útil cuando los ejemplos etiquetados son pocos o difíciles de obtener. En lugar de buscar a ciegas un rango diverso de ejemplos etiquetados, un algoritmo de aprendizaje activo busca selectivamente el rango particular de ejemplos que necesita para aprender.
AdaGrad
Algoritmo de descenso de gradientes que reajusta los gradientes de cada parámetro y le asigna una tasa de aprendizaje independiente a cada uno. Para obtener una explicación completa, consulta Adaptive Subgradient Methods for Online Learning and Stochastic Optimization.
adaptación
Sinónimo de ajuste o ajuste fino.
agente
Software que puede razonar sobre las entradas multimodales del usuario para planificar y ejecutar acciones en nombre del usuario.
En el aprendizaje por refuerzo, un agente es la entidad que usa una política para maximizar el retorno esperado que se obtiene de la transición entre los estados del entorno.
agéntico/agéntica
Forma adjetiva de agente. El término "agéntico" se refiere a las cualidades que poseen los agentes (como la autonomía).
flujo de trabajo de agentes
Es un proceso dinámico en el que un agente planifica y ejecuta acciones de forma autónoma para lograr un objetivo. El proceso puede implicar razonamiento, invocar herramientas externas y corregir su plan por sí mismo.
agrupamiento aglomerado
Consulta agrupamiento en clústeres jerárquico.
Margen de error de la IA
Es el resultado de un sistema de IA generativa que prioriza la cantidad por sobre la calidad. Por ejemplo, una página web con pendiente de IA está repleta de contenido de baja calidad, generado por IA y producido de forma económica.
Detección de anomalías
Proceso de identificación de valores atípicos. Por ejemplo, si la media de un determinado atributo es 100 con una desviación estándar de 10, la detección de anomalías debería marcar un valor de 200 como sospechoso.
AR
Abreviatura de realidad aumentada.
Área bajo la curva de PR
Consulta PR AUC (área bajo la curva de PR).
área bajo la curva ROC
Consulta AUC (área bajo la curva ROC).
Inteligencia artificial general
Un mecanismo no humano que demuestra una amplia variedad de capacidades de resolución de problemas, creatividad y adaptabilidad. Por ejemplo, un programa que demuestre inteligencia general artificial podría traducir texto, componer sinfonías y destacarse en juegos que aún no se han inventado.
inteligencia artificial
Es un programa o modelo no humano que puede resolver tareas sofisticadas. Por ejemplo, los programas o modelos que traducen textos o que identifican enfermedades a partir de imágenes radiológicas son muestras de inteligencia artificial.
Técnicamente, el aprendizaje automático es un subcampo de la inteligencia artificial. Sin embargo, en los últimos años, algunas organizaciones comenzaron a utilizar los términos inteligencia artificial y aprendizaje automático de manera indistinta.
Attention,
Es un mecanismo que se usa en una red neuronal y que indica la importancia de una palabra o parte de una palabra en particular. La atención comprime la cantidad de información que necesita un modelo para predecir el siguiente token o palabra. Un mecanismo de atención típico puede consistir en una suma ponderada sobre un conjunto de entradas, en la que otra parte de la red neuronal calcula el peso de cada entrada.
Consulta también autoatención y autoatención de múltiples cabezales, que son los componentes básicos de los Transformers.
Consulta LLMs: ¿Qué es un modelo de lenguaje grande? en el Curso intensivo de aprendizaje automático para obtener más información sobre la autoatención.
atributo
Sinónimo de atributo.
En la equidad del aprendizaje automático, los atributos suelen hacer referencia a características relacionadas con las personas.
muestreo de atributos
Es una táctica para entrenar un bosque de decisión en el que cada árbol de decisión considera solo un subconjunto aleatorio de posibles atributos cuando aprende la condición. En general, se muestrea un subconjunto diferente de atributos para cada nodo. En cambio, cuando se entrena un árbol de decisión sin muestreo de atributos, se consideran todos los atributos posibles para cada nodo.
AUC (área bajo la curva ROC)
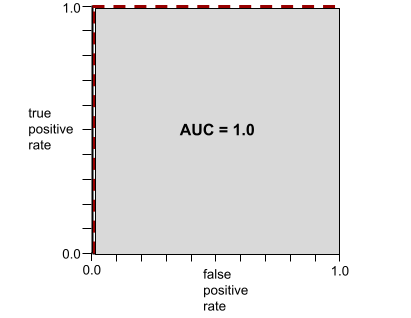
Es un número entre 0.0 y 1.0 que representa la capacidad de un modelo de clasificación binaria para separar las clases positivas de las clases negativas. Cuanto más cerca esté el AUC de 1.0, mejor será la capacidad del modelo para separar las clases entre sí.
Por ejemplo, la siguiente ilustración muestra un modelo de clasificación que separa perfectamente las clases positivas (óvalos verdes) de las clases negativas (rectángulos morados). Este modelo irrealmente perfecto tiene un AUC de 1.0:

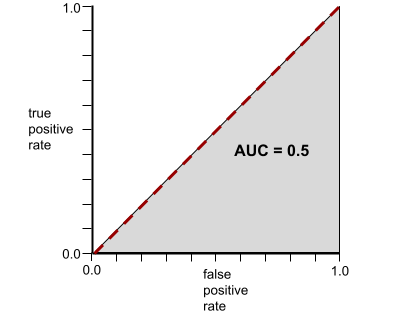
Por el contrario, la siguiente ilustración muestra los resultados de un modelo de clasificación que generó resultados aleatorios. Este modelo tiene un AUC de 0.5:

Sí, el modelo anterior tiene un AUC de 0.5, no de 0.0.
La mayoría de los modelos se encuentran en algún punto intermedio entre los dos extremos. Por ejemplo, el siguiente modelo separa los positivos de los negativos en cierta medida y, por lo tanto, tiene un AUC entre 0.5 y 1.0:

El AUC ignora cualquier valor que establezcas para el umbral de clasificación. En cambio, el AUC considera todos los umbrales de clasificación posibles.
Para obtener más información, consulta Clasificación: ROC y AUC en el Curso intensivo de aprendizaje automático.
realidad aumentada
Es una tecnología que superpone una imagen generada por computadora en la vista del mundo real de un usuario, lo que proporciona una vista compuesta.
codificador automático
Es un sistema que aprende a extraer la información más importante de la entrada. Los autoencoders son una combinación de un codificador y un decodificador. Los autoencoders se basan en el siguiente proceso de dos pasos:
- El codificador asigna la entrada a un formato (intermedio) de menor dimensión (por lo general, con pérdida).
- El decodificador crea una versión con pérdida de la entrada original asignando el formato de menor dimensión al formato de entrada original de mayor dimensión.
Los codificadores automáticos se entrenan de extremo a extremo haciendo que el decodificador intente reconstruir la entrada original a partir del formato intermedio del codificador de la manera más precisa posible. Dado que el formato intermedio es más pequeño (de menor dimensión) que el formato original, el codificador automático se ve obligado a aprender qué información de la entrada es esencial, y la salida no será perfectamente idéntica a la entrada.
Por ejemplo:
- Si los datos de entrada son gráficos, la copia no exacta sería similar al gráfico original, pero con algunas modificaciones. Quizás la copia no exacta quite ruido del gráfico original o complete algunos píxeles faltantes.
- Si los datos de entrada son texto, un codificador automático generaría texto nuevo que imita (pero no es idéntico a) el texto original.
Consulta también codificadores automáticos variacionales.
evaluación automática
Usar software para juzgar la calidad del resultado de un modelo
Cuando el resultado del modelo es relativamente sencillo, una secuencia de comandos o un programa pueden comparar el resultado del modelo con una respuesta ideal. A veces, este tipo de evaluación automática se denomina evaluación programática. Las métricas como ROUGE o BLEU suelen ser útiles para la evaluación programática.
Cuando el resultado del modelo es complejo o no tiene una respuesta correcta, a veces, un programa de AA independiente llamado calificador automático realiza la evaluación automática.
Compara esto con la evaluación humana.
sesgo de automatización
Cuando una persona que toma decisiones favorece las recomendaciones hechas por un sistema automático de decisión por sobre la información obtenida sin automatización, incluso cuando el sistema de decisión automatizado comete un error.
Consulta Equidad: Tipos de sesgo en el Curso intensivo de aprendizaje automático para obtener más información.
AutoML
Cualquier proceso automatizado para compilar modelos de aprendizaje automático. AutoML puede realizar automáticamente tareas como las siguientes:
- Busca el modelo más adecuado.
- Ajusta los hiperparámetros.
- Prepara los datos (incluida la ingeniería de atributos).
- Implementa el modelo resultante.
AutoML es útil para los científicos de datos porque les permite ahorrar tiempo y esfuerzo en el desarrollo de canalizaciones de aprendizaje automático, y mejorar la precisión de las predicciones. También es útil para los no expertos, ya que les permite acceder a tareas complicadas de aprendizaje automático.
Consulta Aprendizaje automático automatizado (AutoML) en el Curso intensivo de aprendizaje automático para obtener más información.
Evaluación del evaluador automático
Es un mecanismo híbrido para juzgar la calidad del resultado de un modelo de IA generativa que combina la evaluación humana con la evaluación automática. Un evaluador automático es un modelo de AA entrenado con datos creados por la evaluación humana. Lo ideal es que un autor aprenda a imitar a un evaluador humano.Hay autorraters prediseñados disponibles, pero los mejores se ajustan específicamente para la tarea que evalúas.
Modelo autorregresivo
Un modelo que infiere una predicción en función de sus propias predicciones anteriores. Por ejemplo, los modelos de lenguaje autorregresivos predicen el siguiente token en función de los tokens predichos anteriormente. Todos los modelos de lenguaje grandes basados en Transformer son de regresión automática.
En cambio, los modelos de imágenes basados en GAN no suelen ser autorregresivos, ya que generan una imagen en un solo pase hacia adelante y no de forma iterativa en pasos. Sin embargo, ciertos modelos de generación de imágenes son autorregresivos porque generan una imagen en pasos.
Pérdida auxiliar
Una función de pérdida (que se usa junto con la función de pérdida principal del modelo de red neuronal) que ayuda a acelerar el entrenamiento durante las primeras iteraciones cuando los pesos se inicializan de forma aleatoria.
Las funciones de pérdida auxiliares envían gradientes efectivos a las capas anteriores. Esto facilita la convergencia durante el entrenamiento, ya que combate el problema de desvanecimiento del gradiente.
Precisión promedio en k
Es una métrica para resumir el rendimiento de un modelo en una sola instrucción que genera resultados clasificados, como una lista numerada de recomendaciones de libros. La precisión promedio en k es, bueno, el promedio de los valores de precisión en k para cada resultado relevante. Por lo tanto, la fórmula para la precisión promedio en k es la siguiente:
\[{\text{average precision at k}} = \frac{1}{n} \sum_{i=1}^n {\text{precision at k for each relevant item} } \]
Donde:
- \(n\) es la cantidad de elementos pertinentes en la lista.
Compara esto con la recuperación en k.
Condición alineada con el eje
En un árbol de decisión, una condición que involucra solo una característica. Por ejemplo, si area es una característica, la siguiente es una condición alineada con el eje:
area > 200
Compara esto con la condición oblicua.
B
propagación inversa
Es el algoritmo que implementa el descenso de gradientes en las redes neuronales.
El entrenamiento de una red neuronal implica muchas iteraciones del siguiente ciclo de dos pasos:
- Durante el pase hacia adelante, el sistema procesa un lote de ejemplos para generar predicciones. El sistema compara cada predicción con cada valor de la etiqueta. La diferencia entre la predicción y el valor de la etiqueta es la pérdida para ese ejemplo. El sistema agrega las pérdidas de todos los ejemplos para calcular la pérdida total del lote actual.
- Durante el pase hacia atrás (retropropagación), el sistema reduce la pérdida ajustando los pesos de todas las neuronas en todas las capas ocultas.
Las redes neuronales suelen contener muchas neuronas en muchas capas ocultas. Cada una de esas neuronas contribuye a la pérdida general de diferentes maneras. La retropropagación determina si se deben aumentar o disminuir los pesos aplicados a neuronas específicas.
La tasa de aprendizaje es un multiplicador que controla el grado en que cada pase hacia atrás aumenta o disminuye cada peso. Una tasa de aprendizaje grande aumentará o disminuirá cada peso más que una tasa de aprendizaje pequeña.
En términos de cálculo, la retropropagación implementa la regla de la cadena del cálculo. Es decir, la retropropagación calcula la derivada parcial del error con respecto a cada parámetro.
Hace años, los profesionales del AA tenían que escribir código para implementar la retropropagación. Las APIs de AA modernas, como Keras, ahora implementan la retropropagación por ti. ¡Vaya!
Consulta Redes neuronales en el Curso intensivo de aprendizaje automático para obtener más información.
Bagging
Es un método para entrenar un ensamble en el que cada modelo constituyente se entrena con un subconjunto aleatorio de ejemplos de entrenamiento muestreados con reemplazo. Por ejemplo, un bosque aleatorio es una colección de árboles de decisión entrenados con bagging.
El término bagging es la abreviatura de bootstrap aggregating.
Consulta Bosques aleatorios en el curso de Bosques de decisión para obtener más información.
Bolsa de palabras
Representación de las palabras de una frase o pasaje, sin importar el orden. Por ejemplo, una bolsa de palabras representa las tres frases siguientes de forma idéntica:
- el perro salta
- salta el perro
- perro salta el
Cada palabra se asigna a un índice en un vector disperso, donde el vector tiene un índice para cada palabra del vocabulario. Por ejemplo, la frase el perro salta se asigna a un vector de atributos con valores distintos de cero en los tres índices correspondientes a las palabras el, perro y salta. El valor distinto de cero puede ser cualquiera de los siguientes:
- Un 1 para indicar la presencia de una palabra
- Es el recuento de la cantidad de veces que una palabra aparece en la bolsa. (por ejemplo, si la frase fuera el perro negro es un perro con pelaje negro, entonces tanto negro como perro se representarían con un 2, mientras que las demás palabras con un 1)
- Algún otro valor como, por ejemplo, el logaritmo del recuento de la cantidad de veces que una palabra aparece en la bolsa
modelo de referencia
Un modelo que se usa como punto de referencia para comparar el rendimiento de otro modelo (por lo general, uno más complejo). Por ejemplo, un modelo de regresión logística podría servir como un buen modelo de referencia para un modelo profundo.
Para un problema en particular, el modelo de referencia ayuda a los desarrolladores a cuantificar el rendimiento mínimo esperado que debe alcanzar un modelo nuevo para que sea útil.
modelo base
Un modelo previamente entrenado que puede servir como punto de partida para el ajuste para abordar tareas o aplicaciones específicas
Consulta también modelo previamente entrenado y modelo fundamental.
lote
Es el conjunto de ejemplos que se usan en una iteración de entrenamiento. El tamaño del lote determina la cantidad de ejemplos en un lote.
Consulta época para obtener una explicación de cómo se relaciona un lote con una época.
Consulta Regresión lineal: Hiperparámetros en el Curso intensivo de aprendizaje automático para obtener más información.
Inferencia por lotes
Proceso de inferencia de predicciones en varios ejemplos sin etiquetar divididos en subconjuntos más pequeños ("lotes").
La inferencia por lotes puede aprovechar las funciones de paralelización de los chips aceleradores. Es decir, varios aceleradores pueden inferir predicciones de forma simultánea en diferentes lotes de ejemplos sin etiquetar, lo que aumenta drásticamente la cantidad de inferencias por segundo.
Para obtener más información, consulta Sistemas de AA en producción: inferencia estática versus dinámica en el Curso intensivo de aprendizaje automático.
normalización por lotes
Normalizar la entrada o la salida de las funciones de activación en una capa oculta La normalización por lotes puede proporcionar los siguientes beneficios:
- Hacer las redes neuronales más estables protegiéndolas de valores atípicos de pesos
- Permitir tasas de aprendizaje más altas, lo que puede acelerar el entrenamiento
- Reducir el sobreajuste
tamaño del lote
Cantidad de ejemplos en un lote. Por ejemplo, si el tamaño del lote es 100, el modelo procesa 100 ejemplos por iteración.
A continuación, se indican algunas estrategias populares para determinar el tamaño del lote:
- Descenso de gradientes estocástico (SGD), en el que el tamaño del lote es 1.
- Lote completo, en el que el tamaño del lote es la cantidad de ejemplos en todo el conjunto de entrenamiento. Por ejemplo, si el conjunto de entrenamiento contiene un millón de ejemplos, el tamaño del lote sería de un millón de ejemplos. Por lo general, el procesamiento por lotes completo es una estrategia ineficiente.
- Minilote, en el que el tamaño del lote suele ser entre 10 y 1,000. Por lo general, el minilote es la estrategia más eficiente.
Consulte los siguientes artículos para obtener más información:
- Sistemas de AA de producción: inferencia estática frente a inferencia dinámica en el Curso intensivo de aprendizaje automático.
- Guía de ajuste del aprendizaje profundo.
Red neuronal bayesiana
Una red neuronal probabilística que representa la incertidumbre entre pesos y resultados. Un modelo de regresión de red neuronal estándar suele predecir un valor escalar; por ejemplo, un modelo estándar predice el precio de una casa en 853,000. En contraste, una red neuronal Bayesiana predice una distribución de valores, por ejemplo, un modelo Bayesiano predice el precio de una casa en 853,000 con una desviación estándar de 67,200.
Las redes neuronales Bayesianas se basan en el Teorema de Bayes para calcular la incertidumbre entre pesos y predicciones. Una red neuronal bayesiana puede ser útil en los casos en que se precisa calcular el grado de incertidumbre, como en modelos relacionados con la industria farmacéutica. Las redes neuronales Bayesianas también pueden ayudar a reducir el sobreajuste.
Optimización bayesiana
Técnica de modelo de regresión probabilístico para optimizar funciones objetivo costosas desde el punto de vista computacional. En cambio, se optimiza un sustituto que cuantifica la incertidumbre con una técnica de aprendizaje bayesiano. Dado que la optimización bayesiana es muy costosa, se suele usar para optimizar tareas costosas de evaluar que tienen una pequeña cantidad de parámetros, como la selección de hiperparámetros.
Ecuación de Bellman
En el aprendizaje por refuerzo, la función Q óptima satisface la siguiente identidad:
\[Q(s, a) = r(s, a) + \gamma \mathbb{E}_{s'|s,a} \max_{a'} Q(s', a')\]
Los algoritmos de aprendizaje por refuerzo aplican esta identidad para crear el aprendizaje Q con la siguiente regla de actualización:
\[Q(s,a) \gets Q(s,a) + \alpha \left[r(s,a) + \gamma \displaystyle\max_{\substack{a_1}} Q(s',a') - Q(s,a) \right] \]
Más allá del aprendizaje por refuerzo, la ecuación de Bellman tiene aplicaciones en la programación dinámica. Consulta la entrada de Wikipedia sobre la ecuación de Bellman.
BERT (Bidirectional Encoder Representations from Transformers)
Es una arquitectura de modelo para la representación de texto. Un modelo BERT entrenado puede actuar como parte de un modelo más grande para la clasificación de texto o para otras tareas de AA.
BERT tiene las siguientes características:
- Utiliza la arquitectura Transformer y, por lo tanto, se basa en la autoatención.
- Usa la parte del codificador del Transformer. El trabajo del codificador es producir buenas representaciones de texto, en lugar de realizar una tarea específica como la clasificación.
- Es bidireccional.
- Utiliza el enmascaramiento para el entrenamiento no supervisado.
Las variantes de BERT incluyen las siguientes:
Consulta Open Sourcing BERT: State-of-the-Art Pre-training for Natural Language Processing para obtener una descripción general de BERT.
sesgo (ética/equidad)
1. Estereotipo, prejuicio o preferencia de cosas, personas o grupos por sobre otros. Estos sesgos pueden afectar la recopilación y la interpretación de datos, el diseño de un sistema y cómo los usuarios interactúan con él. Algunos tipos de este sesgo incluyen:
- sesgo de automatización
- sesgo de confirmación
- Sesgo del experimentador
- sesgo de correspondencia
- Sesgo implícito
- Sesgo endogrupal
- Sesgo de homogeneidad de los demás
2. Error sistemático debido a un procedimiento de muestreo o de realización de un informe. Algunos tipos de este sesgo incluyen:
- Sesgo de cobertura
- Sesgo de no respuesta
- Sesgo de participación
- Sesgo de reporte
- Sesgo de muestreo
- Sesgo de selección
No se debe confundir con el término de sesgo en los modelos de aprendizaje automático ni con el sesgo de predicción.
Consulta Equidad: Tipos de sesgo en el Curso intensivo de aprendizaje automático para obtener más información.
ordenada al origen (matemática) o término de sesgo
Una intersección o desplazamiento de un origen. El sesgo es un parámetro en los modelos de aprendizaje automático, que se simboliza con cualquiera de los siguientes elementos:
- b
- w0
Por ejemplo, la ordenada al origen es la b en la siguiente fórmula:
En una línea bidimensional simple, el sesgo solo significa "intersección con el eje Y". Por ejemplo, la ordenada al origen de la línea en la siguiente ilustración es 2.
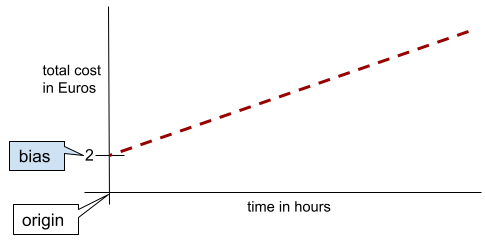
El sesgo existe porque no todos los modelos comienzan desde el origen (0,0). Por ejemplo, supongamos que la entrada a un parque de diversiones cuesta EUR 2 y se cobran EUR 0.5 adicionales por cada hora que se quede un cliente. Por lo tanto, un modelo que asigna el costo total tiene un sesgo de 2 porque el costo más bajo es de 2 euros.
El sesgo no se debe confundir con el sesgo en ética y equidad ni con el sesgo de predicción.
Consulta Regresión lineal en el Curso intensivo de aprendizaje automático para obtener más información.
bidireccional
Término que se usa para describir un sistema que evalúa el texto que precede y sigue a una sección de texto objetivo. En cambio, un sistema unidireccional solo evalúa el texto que precede a una sección de texto objetivo.
Por ejemplo, considera un modelo de lenguaje enmascarado que debe determinar las probabilidades de la palabra o las palabras que representan el subrayado en la siguiente pregunta:
¿Qué te _____?
Un modelo de lenguaje unidireccional tendría que basar sus probabilidades solo en el contexto proporcionado por las palabras "¿Cuál", "es" y "la". En cambio, un modelo de lenguaje bidireccional también podría obtener contexto de "con" y "tú", lo que podría ayudarlo a generar mejores predicciones.
modelo de lenguaje bidireccional
Un modelo de lenguaje que determina la probabilidad de que un token determinado esté presente en una ubicación específica de un fragmento de texto según el texto anterior y siguiente.
bigrama
Un n-grama en el que N=2.
Clasificación binaria
Es un tipo de tarea de clasificación que predice una de dos clases mutuamente exclusivas:
- la clase positiva
- la clase negativa
Por ejemplo, los siguientes dos modelos de aprendizaje automático realizan una clasificación binaria:
- Un modelo que determina si los mensajes de correo electrónico son spam (la clase positiva) o no son spam (la clase negativa).
- Un modelo que evalúa síntomas médicos para determinar si una persona tiene una enfermedad en particular (la clase positiva) o no la tiene (la clase negativa).
Compara esto con la clasificación de clases múltiples.
Consulta también regresión logística y umbral de clasificación.
Para obtener más información, consulta Clasificación en el Curso intensivo de aprendizaje automático.
condición binaria
En un árbol de decisión, una condición que tiene solo dos resultados posibles, por lo general, sí o no. Por ejemplo, la siguiente es una condición binaria:
temperature >= 100
Compara esto con la condición no binaria.
Consulta Tipos de condiciones en el curso de Bosques de decisión para obtener más información.
discretización
Sinónimo de agrupamiento.
Modelo de caja negra
Un modelo cuyo "razonamiento" es imposible o difícil de entender para los humanos. Es decir, si bien las personas pueden ver cómo las instrucciones afectan las respuestas, no pueden determinar con exactitud cómo un modelo de caja negra determina la respuesta. En otras palabras, un modelo de caja negra carece de interpretabilidad.
La mayoría de los modelos profundos y los modelos de lenguaje grandes son cajas negras.
BLEU (Bilingual Evaluation Understudy)
Es una métrica entre 0.0 y 1.0 para evaluar las traducciones automáticas, por ejemplo, del español al japonés.
Para calcular una puntuación, BLEU suele comparar la traducción de un modelo de AA (texto generado) con la traducción de un experto humano (texto de referencia). El grado en que coinciden los n-gramas en el texto generado y el texto de referencia determina la puntuación BLEU.
El documento original sobre esta métrica es BLEU: a Method for Automatic Evaluation of Machine Translation.
Consulta también BLEURT.
BLEURT (Bilingual Evaluation Understudy from Transformers)
Es una métrica para evaluar las traducciones automáticas de un idioma a otro, en especial, hacia y desde el inglés.
En el caso de las traducciones hacia y desde el inglés, BLEURT se alinea más estrechamente con las calificaciones humanas que BLEU. A diferencia de BLEU, BLEURT enfatiza las similitudes semánticas (de significado) y puede adaptarse al parafraseo.
BLEURT se basa en un modelo de lenguaje grande entrenado previamente (BERT, para ser exactos) que luego se ajusta con texto de traductores humanos.
El documento original sobre esta métrica es BLEURT: Learning Robust Metrics for Text Generation.
Preguntas booleanas (BoolQ)
Es un conjunto de datos para evaluar la competencia de un LLM a la hora de responder preguntas de sí o no. Cada uno de los desafíos del conjunto de datos tiene tres componentes:
- Una consulta
- Es un pasaje que implica la respuesta a la búsqueda.
- La respuesta correcta, que es sí o no.
Por ejemplo:
- Pregunta: ¿Hay centrales nucleares en Michigan?
- Pasaje: …tres centrales nucleares suministran a Michigan alrededor del 30% de su electricidad.
- Respuesta correcta: Sí
Los investigadores recopilaron las preguntas de las búsquedas agregadas y anonimizadas de la Búsqueda de Google y, luego, usaron las páginas de Wikipedia para fundamentar la información.
Para obtener más información, consulta BoolQ: Exploring the Surprising Difficulty of Natural Yes/No Questions.
BoolQ es un componente del conjunto de SuperGLUE.
BoolQ
Abreviatura de Preguntas booleanas.
potenciación
Técnica de aprendizaje automático que combina de forma iterativa un conjunto de modelos de clasificación simples y no muy precisos (también conocidos como "clasificadores débiles") en un modelo de clasificación con alta precisión (un "clasificador fuerte") mediante un incremento de ponderación para los ejemplos que el modelo actualmente clasifica de forma errónea.
Consulta ¿Qué son los árboles de decisión potenciados por gradiente? en el curso de Bosques de decisión para obtener más información.
cuadro de límite
En una imagen, las coordenadas (x, y) de un rectángulo alrededor de un área de interés, como el perro en la siguiente imagen.

transmisión
En una operación matemática de matrices, expansión de la forma de un operando a dimensiones compatibles para esa operación. Por ejemplo, el álgebra lineal requiere que los dos operandos en una operación de suma de matrices tengan las mismas dimensiones. En consecuencia, no se puede agregar una matriz de forma (m, n) a un vector de longitud n. La transmisión permite esta operación expandiendo virtualmente el vector de longitud n en una matriz de forma (m, n) replicando los mismos valores en cada columna.
Para obtener más detalles, consulta la siguiente descripción de la emisión en NumPy.
Agrupamiento
Conversión de un solo atributo en varios atributos binarios denominados agrupamientos o discretizaciones, que en general se basan en un rango de valores. Por lo general, el atributo segmentado es un atributo continuo.
Por ejemplo, en lugar de representar la temperatura como un solo atributo de punto flotante continuo, podrías dividir los rangos de temperatura en discretos discretos, como los siguientes:
- Las temperaturas inferiores o iguales a 10 grados Celsius se incluirían en el intervalo “frío”.
- El intervalo de 11 a 24 grados Celsius sería el intervalo "templado".
- Los valores mayores o iguales a 25 grados Celsius se incluirían en el bucket "cálido".
El modelo tratará cada valor del mismo bucket de forma idéntica. Por ejemplo, los valores 13 y 22 se encuentran en el bucket de temperatura, por lo que el modelo trata ambos valores de forma idéntica.
Consulta Datos numéricos: discretización en el Curso intensivo de aprendizaje automático para obtener más información.
C
capa de calibración
Ajuste posterior a la predicción, generalmente para dar cuenta del sesgo de predicción. Las predicciones ajustadas y las probabilidades deben coincidir con la distribución del conjunto de etiquetas observado.
generación de candidatos
Es el conjunto inicial de recomendaciones que elige un sistema de recomendación. Por ejemplo, considera una librería que ofrece 100,000 títulos. La fase de generación de candidatos crea una lista mucho menor de libros adecuados para un usuario específico, digamos 500. Pero incluso 500 libros son demasiados para recomendar a un usuario. Las fases posteriores y más costosas de un sistema de recomendación (como la puntuación y la reclasificación) reducen esos 500 a un conjunto de recomendaciones mucho más pequeño y útil.
Para obtener más información, consulta la descripción general de la generación de candidatos en el curso de Sistemas de recomendación.
muestreo de candidatos
Es una optimización del entrenamiento que calcula una probabilidad para todas las etiquetas positivas, por ejemplo, con softmax, pero solo para una muestra aleatoria de etiquetas negativas. Por ejemplo, dado un ejemplo etiquetado como beagle y perro, el muestreo de candidatos calcula las probabilidades predichas y los términos de pérdida correspondientes para lo siguiente:
- beagle
- perro
- un subconjunto aleatorio de las clases negativas restantes (por ejemplo, gato, golosina, cerca)
La idea es que las clases negativas pueden aprender de un refuerzo negativo menos frecuente, siempre y cuando las clases positivas siempre reciban el refuerzo positivo apropiado, y esto se observa empíricamente.
El muestreo de candidatos es más eficiente en términos de procesamiento que los algoritmos de entrenamiento que calculan predicciones para todas las clases negativas, en especial cuando la cantidad de clases negativas es muy grande.
datos categóricos
Atributos que tienen un conjunto específico de valores posibles. Por ejemplo, considera un atributo categórico llamado traffic-light-state, que solo puede tener uno de los siguientes tres valores posibles:
redyellowgreen
Si se representa traffic-light-state como un atributo categórico, un modelo puede aprender los diferentes impactos de red, green y yellow en el comportamiento del conductor.
En ocasiones, los atributos categóricos se denominan atributos discretos.
Compara esto con los datos numéricos.
Consulta Cómo trabajar con datos categóricos en el Curso intensivo de aprendizaje automático para obtener más información.
modelo de lenguaje causal
Sinónimo de modelo de lenguaje unidireccional.
Consulta modelo de lenguaje bidireccional para comparar diferentes enfoques direccionales en el modelado del lenguaje.
CB
Abreviatura de CommitmentBank.
centroid
Es el centro de un clúster determinado por un algoritmo de k-means o k-median. Por ejemplo, si k es 3, entonces el algoritmo k-means o k-median encuentra 3 centroides.
Consulta Algoritmos de agrupamiento en el curso de Clustering para obtener más información.
agrupamiento en clústeres basado en centroides
Categoría de algoritmos de agrupamiento en clústeres que organiza los datos en clústeres no jerárquicos. k-means es el algoritmo de agrupamiento en clústeres basado en centroides más utilizado.
Compara esto con los algoritmos de agrupamiento en clústeres jerárquico.
Consulta Algoritmos de agrupamiento en el curso de Clustering para obtener más información.
Cadena de pensamientos
Una técnica de ingeniería de instrucciones que alienta a un modelo de lenguaje grande (LLM) a explicar su razonamiento paso a paso. Por ejemplo, considera la siguiente instrucción, y presta especial atención a la segunda oración:
¿Cuántas fuerzas G experimentaría un conductor en un automóvil que va de 0 a 60 millas por hora en 7 segundos? En la respuesta, muestra todos los cálculos pertinentes.
Es probable que la respuesta del LLM haga lo siguiente:
- Muestra una secuencia de fórmulas físicas, reemplazando los valores 0, 60 y 7 en los lugares correspondientes.
- Explica por qué eligió esas fórmulas y qué significan las distintas variables.
La instrucción de cadena de pensamientos obliga al LLM a realizar todos los cálculos, lo que podría generar una respuesta más correcta. Además, las instrucciones de encadenamiento de pensamiento permiten que el usuario examine los pasos del LLM para determinar si la respuesta tiene sentido.
Puntuación F de n-gramas de caracteres (ChrF)
Es una métrica para evaluar los modelos de traducción automática. La puntuación F de n-gramas de caracteres determina el grado en que los n-gramas en el texto de referencia se superponen con los n-gramas en el texto generado de un modelo de AA.
La puntuación F de n-gramas de caracteres es similar a las métricas de las familias ROUGE y BLEU, excepto que:
- La puntuación F de n-gramas de caracteres opera en n-gramas de caracteres.
- ROUGE y BLEU operan en N-gramas de palabras o tokens.
chat
Contenido de un diálogo bidireccional con un sistema de AA, por lo general, un modelo de lenguaje grande. La interacción anterior en un chat (lo que escribiste y cómo respondió el modelo de lenguaje grande) se convierte en el contexto para las partes posteriores del chat.
Un chatbot es una aplicación de un modelo de lenguaje grande.
punto de control
Son los datos que capturan el estado de los parámetros de un modelo durante el entrenamiento o después de que este se completa. Por ejemplo, durante el entrenamiento, puedes hacer lo siguiente:
- Detener el entrenamiento, tal vez de forma intencional o como resultado de ciertos errores
- Captura el punto de control.
- Más adelante, vuelve a cargar el punto de control, posiblemente en hardware diferente.
- Reinicia el entrenamiento.
Elección de alternativas plausibles (COPA)
Es un conjunto de datos para evaluar qué tan bien un LLM puede identificar la mejor de dos respuestas alternativas a una premisa. Cada uno de los desafíos del conjunto de datos consta de tres componentes:
- Una premisa, que suele ser una afirmación seguida de una pregunta
- Dos respuestas posibles a la pregunta planteada en la premisa, una de las cuales es correcta y la otra incorrecta
- La respuesta correcta
Por ejemplo:
- Premisa: El hombre se rompió el dedo del pie. ¿Cuál fue la CAUSA de este problema?
- Respuestas posibles:
- Se le hizo un agujero en el calcetín.
- Se le cayó un martillo en el pie.
- Respuesta correcta: 2
COPA es un componente del conjunto de SuperGLUE.
clase
Es una categoría a la que puede pertenecer una etiqueta. Por ejemplo:
- En un modelo de clasificación binaria que detecta spam, las dos clases podrían ser spam y no es spam.
- En un modelo de clasificación de varias clases que identifica razas de perros, las clases podrían ser caniche, beagle, pug, etcétera.
Un modelo de clasificación predice una clase. Por el contrario, un modelo de regresión predice un número en lugar de una clase.
Para obtener más información, consulta Clasificación en el Curso intensivo de aprendizaje automático.
conjunto de datos equilibrado por clase
Un conjunto de datos que contiene etiquetas categóricas en el que la cantidad de instancias de cada categoría es aproximadamente igual. Por ejemplo, considera un conjunto de datos botánicos cuya etiqueta binaria puede ser planta nativa o planta no nativa:
- Un conjunto de datos con 515 plantas nativas y 485 plantas no nativas es un conjunto de datos equilibrado por clase.
- Un conjunto de datos con 875 plantas nativas y 125 plantas no nativas es un conjunto de datos con desequilibrio de clases.
No existe una línea divisoria formal entre los conjuntos de datos con equilibrio de clases y los conjuntos de datos con desequilibrio de clases. La distinción solo se vuelve importante cuando un modelo entrenado en un conjunto de datos con un gran desequilibrio de clases no puede converger. Consulta Conjuntos de datos: conjuntos de datos desequilibrados en el Curso intensivo de aprendizaje automático para obtener más información.
modelo de clasificación
Un modelo cuya predicción es una clase. Por ejemplo, todos los siguientes son modelos de clasificación:
- Un modelo que predice el idioma de una oración de entrada (¿francés? ¿Español? ¿Italiano?
- Un modelo que predice especies de árboles (¿arce? ¿Roble? ¿Baobab?).
- Un modelo que predice la clase positiva o negativa para una afección médica en particular.
Por el contrario, los modelos de regresión predicen números en lugar de clases.
Estos son dos tipos comunes de modelos de clasificación:
umbral de clasificación
En una clasificación binaria, es un número entre 0 y 1 que convierte el resultado sin procesar de un modelo de regresión logística en una predicción de la clase positiva o la clase negativa. Ten en cuenta que el umbral de clasificación es un valor que elige un humano, no un valor que se elige durante el entrenamiento del modelo.
Un modelo de regresión logística genera un valor sin procesar entre 0 y 1. Luego:
- Si este valor sin procesar es mayor que el umbral de clasificación, se predice la clase positiva.
- Si este valor sin procesar es menor que el umbral de clasificación, se predice la clase negativa.
Por ejemplo, supongamos que el umbral de clasificación es 0.8. Si el valor sin procesar es 0.9, el modelo predice la clase positiva. Si el valor sin procesar es 0.7, el modelo predice la clase negativa.
La elección del umbral de clasificación influye en gran medida en la cantidad de falsos positivos y falsos negativos.
Para obtener más información, consulta Umbrales y la matriz de confusión en el Curso intensivo de aprendizaje automático.
clasificador
Término informal para un modelo de clasificación.
conjunto de datos con desequilibrio de clases
Un conjunto de datos para una clasificación en la que la cantidad total de etiquetas de cada clase difiere significativamente. Por ejemplo, considera un conjunto de datos de clasificación binaria cuyas dos etiquetas se dividen de la siguiente manera:
- 1,000,000 de etiquetas negativas
- 10 etiquetas positivas
La proporción de etiquetas negativas y positivas es de 100,000 a 1, por lo que se trata de un conjunto de datos con desequilibrio de clases.
En cambio, el siguiente conjunto de datos está equilibrado en cuanto a las clases porque la proporción de etiquetas negativas y positivas es relativamente cercana a 1:
- 517 etiquetas negativas
- 483 etiquetas positivas
Los conjuntos de datos de varias clases también pueden tener un desequilibrio de clases. Por ejemplo, el siguiente conjunto de datos de clasificación de varias clases también está desequilibrado en cuanto a las clases, ya que una etiqueta tiene muchos más ejemplos que las otras dos:
- 1,000,000 de etiquetas con la clase "verde"
- 200 etiquetas con la clase "púrpura"
- 350 etiquetas con la clase "naranja"
El entrenamiento de conjuntos de datos con desequilibrio de clases puede presentar desafíos especiales. Consulta Conjuntos de datos desequilibrados en el Curso intensivo de aprendizaje automático para obtener más detalles.
Consulta también entropía, clase mayoritaria y clase minoritaria.
recorte
Técnica para manejar valores atípicos realizando una o ambas de las siguientes acciones:
- Se reducen los valores de características que superan un umbral máximo hasta ese umbral.
- Se incrementan hasta un umbral mínimo aquellos valores de atributo que sean menores.
Por ejemplo, supongamos que menos del 0.5% de los valores de un atributo en particular se encuentran fuera del rango de 40 a 60. En ese caso, puedes hacer lo siguiente:
- Recorta todos los valores superiores a 60 (el umbral máximo) para que sean exactamente 60.
- Hacer un recorte de todos los valores menores que 40 (el umbral mínimo) para que sean exactamente 40
Los valores atípicos pueden dañar los modelos y, a veces, provocar un desbordamiento de los pesos durante el entrenamiento. Algunos valores atípicos también pueden afectar significativamente las métricas, como la precisión. El recorte es una técnica común para limitar el daño.
El recorte de gradientes fuerza los valores del gradiente dentro de un rango designado durante el entrenamiento.
Consulta Datos numéricos: Normalización en el Curso intensivo de aprendizaje automático para obtener más información.
Cloud TPU
Es un acelerador de hardware especializado diseñado para acelerar las cargas de trabajo de aprendizaje automático en Google Cloud.
agrupamiento en clústeres
Agrupar ejemplos relacionados, en especial durante el aprendizaje no supervisado Una vez que todos los ejemplos están agrupados, una persona puede, de forma opcional, asignar un significado a cada clúster.
Existen muchos algoritmos de agrupamiento en clústeres. Por ejemplo, el algoritmo k-means agrupa los ejemplos según su proximidad a un centroide, como se muestra en el siguiente diagrama:

Un investigador humano podría luego revisar los clústeres y, por ejemplo, etiquetar el grupo 1 como "árboles enanos" y el grupo 2 como "árboles grandes".
Otro ejemplo podría ser un algoritmo de agrupamiento basado en la distancia del ejemplo desde un punto central, como se ilustra a continuación:

Consulta el curso sobre clustering para obtener más información.
coadaptación
Es un comportamiento no deseado en el que las neuronas predicen patrones en los datos de entrenamiento basándose casi exclusivamente en salidas de otras neuronas específicas en lugar de basarse en el comportamiento de la red como un todo. Cuando los patrones que causan la coadaptación no están presentes en los datos de validación, la coadaptación provoca un sobreajuste. La regularización de retirados reduce la coadaptación ya que asegura que las neuronas no puedan basarse solo en otras neuronas específicas.
filtrado colaborativo
Realizar predicciones sobre los intereses de un usuario en función de los intereses de muchos otros usuarios El filtrado colaborativo se usa con frecuencia en los sistemas de recomendación.
Para obtener más información, consulta Filtrado colaborativo en el curso de Sistemas de recomendación.
CommitmentBank (CB)
Es un conjunto de datos para evaluar la competencia de un LLM a la hora de determinar si el autor de un pasaje cree en una cláusula objetivo dentro de ese pasaje. Cada entrada del conjunto de datos contiene lo siguiente:
- Un pasaje
- Una cláusula de destino dentro de ese pasaje
- Es un valor booleano que indica si el autor del pasaje cree que la cláusula objetivo
Por ejemplo:
- Pasaje: Qué divertido escuchar la risa de Artemisa. Es una niña muy seria. No sabía que tenía sentido del humor.
- Cláusula objetivo: Tenía sentido del humor.
- Booleano: Verdadero, lo que significa que el autor cree que la cláusula objetivo
CommitmentBank es un componente del conjunto de SuperGLUE.
Modelo compacto
Cualquier modelo pequeño diseñado para ejecutarse en dispositivos pequeños con recursos de procesamiento limitados. Por ejemplo, los modelos compactos se pueden ejecutar en teléfonos celulares, tablets o sistemas integrados.
procesamiento
(Sustantivo) Recursos de procesamiento que usa un modelo o sistema, como la potencia de procesamiento, la memoria y el almacenamiento.
Consulta chips aceleradores.
Desviación de conceptos
Un cambio en la relación entre los atributos y la etiqueta Con el tiempo, la desviación del concepto reduce la calidad de un modelo.
Durante el entrenamiento, el modelo aprende la relación entre los atributos y sus etiquetas en el conjunto de entrenamiento. Si las etiquetas del conjunto de entrenamiento son buenos sustitutos del mundo real, el modelo debería hacer buenas predicciones del mundo real. Sin embargo, debido a la desviación de conceptos, las predicciones del modelo tienden a degradarse con el tiempo.
Por ejemplo, considera un modelo de clasificación binaria que predice si un determinado modelo de automóvil es "eficiente en el consumo de combustible" o no. Es decir, las características podrían ser las siguientes:
- Peso del automóvil
- Compresión del motor
- Tipo de transmisión
mientras que la etiqueta puede ser una de las siguientes:
- eficiente en el consumo de combustible
- No es eficiente en el consumo de combustible
Sin embargo, el concepto de "automóvil eficiente en el consumo de combustible" cambia constantemente. Un modelo de automóvil etiquetado como eficiente en el consumo de combustible en 1994 casi con certeza se etiquetaría como no eficiente en el consumo de combustible en 2024. Un modelo que sufre de desviación del concepto tiende a hacer predicciones cada vez menos útiles con el tiempo.
Compara y contrasta con la no estacionariedad.
de transición
En un árbol de decisión, cualquier nodo que realice una prueba. Por ejemplo, el siguiente árbol de decisión contiene dos condiciones:
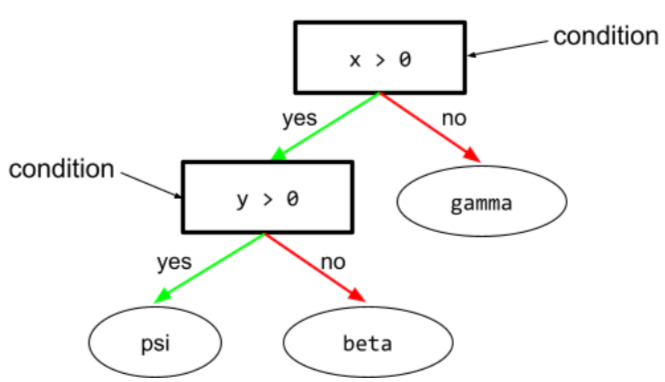
Una condición también se denomina división o prueba.
Condición de contraste con hoja.
Consulta lo siguiente:
Consulta Tipos de condiciones en el curso de Bosques de decisión para obtener más información.
confabulación
Sinónimo de alucinación.
Es probable que confabulación sea un término más preciso desde el punto de vista técnico que alucinación. Sin embargo, la alucinación se popularizó primero.
configuración
Proceso de asignación de los valores iniciales de las propiedades que se usan para entrenar un modelo, lo que incluye lo siguiente:
- las capas de composición del modelo
- La ubicación de los datos
- Hiperparámetros, como los siguientes:
En los proyectos de aprendizaje automático, la configuración se puede realizar a través de un archivo de configuración especial o con bibliotecas de configuración, como las siguientes:
sesgo de confirmación
Tendencia a buscar, interpretar, favorecer y recordar información de una manera que confirme las creencias o hipótesis preexistentes propias. Los desarrolladores de aprendizaje automático pueden recopilar o etiquetar inadvertidamente los datos de formas que influyan en un resultado que respalde sus creencias. El sesgo de confirmación es una forma de sesgo implícito.
El sesgo de investigación es una forma de sesgo de confirmación en el cual un investigador continúa entrenando modelos hasta confirmar una hipótesis preexistente.
matriz de confusión
Es una tabla de NxN que resume la cantidad de predicciones correctas e incorrectas que realizó un modelo de clasificación. Por ejemplo, considera la siguiente matriz de confusión para un modelo de clasificación binaria:
| Tumor (previsto) | Sin tumor (predicción) | |
|---|---|---|
| Tumor (verdad fundamental) | 18 (TP) | 1 (FN) |
| No tumor (verdad fundamental) | 6 (FP) | 452 (TN) |
En la matriz de confusión anterior, se muestra lo siguiente:
- De las 19 predicciones en las que la verdad fundamental era Tumor, el modelo clasificó correctamente 18 y clasificó incorrectamente 1.
- De las 458 predicciones en las que la verdad fundamental era Non-Tumor, el modelo clasificó correctamente 452 y clasificó incorrectamente 6.
La matriz de confusión para un problema de clasificación de varias clases puede ayudarte a identificar patrones de errores. Por ejemplo, considera la siguiente matriz de confusión para un modelo de clasificación multiclase de 3 clases que categoriza tres tipos diferentes de iris (Virginica, Versicolor y Setosa). Cuando la verdad fundamental era Virginica, la matriz de confusión muestra que el modelo era mucho más propenso a predecir erróneamente Versicolor que Setosa:
| Setosa (previsto) | Versicolor (previsto) | Virginica (previsto) | |
|---|---|---|---|
| Setosa (verdad fundamental) | 88 | 12 | 0 |
| Versicolor (verdad fundamental) | 6 | 141 | 7 |
| Virginica (verdad fundamental) | 2 | 27 | 109 |
Como otro ejemplo, una matriz de confusión podría revelar que un modelo entrenado para reconocer dígitos escritos a mano tiende a predecir de manera incorrecta 9 en lugar de 4, o 1 en lugar de 7.
Las matrices de confusión contienen suficiente información para calcular una variedad de métricas de rendimiento, incluidas la precisión y la recuperación.
Análisis sintáctico de circunscripciones
Dividir una oración en estructuras gramaticales más pequeñas ("constituyentes") Una parte posterior del sistema de AA, como un modelo de comprensión del lenguaje natural, puede analizar los componentes con mayor facilidad que la oración original. Por ejemplo, considera la siguiente oración:
Mi amigo adoptó dos gatos.
Un analizador sintáctico de constituyentes puede dividir esta oración en los siguientes dos constituyentes:
- Mi amigo es una frase nominal.
- Adoptó dos gatos es una frase verbal.
Estos componentes se pueden subdividir aún más en componentes más pequeños. Por ejemplo, la frase verbal
adoptó dos gatos
se podría subdividir aún más en los siguientes elementos:
- Adoptado es un verbo.
- Dos gatos es otra frase nominal.
embedding de lenguaje contextualizado
Un embedding que se acerca a "comprender" palabras y frases de formas en que pueden hacerlo los hablantes humanos fluidos. Las incorporaciones de lenguaje contextualizadas pueden comprender la sintaxis, la semántica y el contexto complejos.
Por ejemplo, considera las incorporaciones de la palabra en inglés cow (vaca). Las incorporaciones más antiguas, como word2vec, pueden representar palabras en inglés de modo que la distancia en el espacio de incorporación de vaca a toro sea similar a la distancia de oveja (oveja hembra) a carnero (oveja macho) o de mujer a hombre. Las incorporaciones de lenguaje contextualizadas pueden ir un paso más allá y reconocer que los angloparlantes a veces usan la palabra cow de manera informal para referirse a una vaca o a un toro.
ventana de contexto
Es la cantidad de tokens que un modelo puede procesar en una instrucción determinada. Cuanto más grande sea la ventana de contexto, más información podrá usar el modelo para proporcionar respuestas coherentes y uniformes a la instrucción.
atributo continuo
Un atributo de punto flotante con un rango infinito de valores posibles, como la temperatura o el peso.
Compara esto con atributo discreto.
muestreo de conveniencia
Uso de un conjunto de datos no recopilados científicamente con el objetivo de realizar experimentos rápidos. Posteriormente, es fundamental cambiar a un conjunto de datos recopilados científicamente.
convergencia
Es un estado que se alcanza cuando los valores de la pérdida cambian muy poco o nada con cada iteración. Por ejemplo, la siguiente curva de pérdida sugiere convergencia alrededor de las 700 iteraciones:
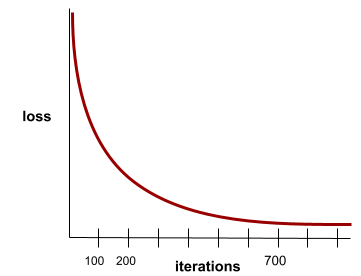
Un modelo converge cuando el entrenamiento adicional no lo mejora.
En el aprendizaje profundo, los valores de pérdida a veces se mantienen constantes o casi constantes durante muchas iteraciones antes de descender finalmente. Durante un período prolongado de valores de pérdida constantes, es posible que, temporalmente, tengas una falsa sensación de convergencia.
Consulta también interrupción anticipada.
Consulta Curvas de pérdida y convergencia del modelo en el Curso intensivo de aprendizaje automático para obtener más información.
Programación conversacional
Es un diálogo iterativo entre tú y un modelo de IA generativa con el propósito de crear software. Emite una instrucción que describe algún software. Luego, el modelo usa esa descripción para generar código. Luego, emites una nueva instrucción para abordar las fallas de la instrucción anterior o del código generado, y el modelo genera código actualizado. Ambos siguen intercambiando ideas hasta que el software generado es lo suficientemente bueno.
El codificado de conversaciones es, en esencia, el significado original de vibe coding.
Compara esto con la codificación especificacional.
función convexa
Función en la que la región por encima del gráfico de la función es un conjunto convexo. La función convexa prototípica tiene una forma similar a la letra U. Por ejemplo, las siguientes son todas funciones convexas:
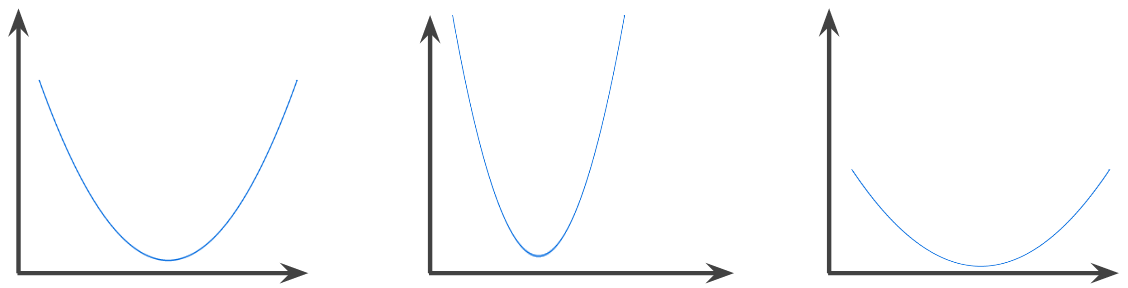
En contraste, la siguiente función no es convexa. Observa cómo la región sobre el gráfico no es un conjunto convexo:

Una función estrictamente convexa tiene exactamente un punto mínimo local, que también es el punto mínimo global. Las funciones clásicas con forma de U son funciones estrictamente convexas. Sin embargo, algunas funciones convexas (por ejemplo, las líneas rectas) no lo son.
Consulta Convergencia y funciones convexas en el Curso intensivo de aprendizaje automático para obtener más información.
optimización de función convexa
Proceso de uso de técnicas matemáticas, como el descenso de gradientes, para encontrar el mínimo de una función convexa. Gran parte de la investigación sobre el aprendizaje automático se ha centrado en formular distintos problemas como problemas de optimización convexa y en solucionar esas cuestiones de manera más eficaz.
Para obtener más información, consulta Convex Optimization de Boyd y Vandenberghe.
conjunto convexo
Es un subconjunto del espacio euclidiano tal que una línea trazada entre dos puntos cualesquiera del subconjunto permanece completamente dentro de él. Por ejemplo, las siguientes dos formas son conjuntos convexos:

En contraste, las siguientes dos formas no son conjuntos convexos:

convolución
En matemáticas, la convolución es (informalmente) una manera de mezclar dos funciones que mide cuanta superposición hay entre las dos funciones En el aprendizaje automático, una convolución mezcla el filtro convolucional y la matriz de entrada para entrenar pesos.
En el aprendizaje automático, el término "convolución" suele ser una forma abreviada de referirse a la operación convolucional o a la capa convolucional.
Sin convoluciones, un algoritmo de aprendizaje automático tendría que aprender un peso separado para cada celda en un tensor grande. Por ejemplo, un algoritmo de aprendizaje automático que se entrena con imágenes de 2,000 x 2,000 se vería obligado a encontrar 4 millones de pesos separados. Gracias a las convoluciones, un algoritmo de aprendizaje automático solo tiene que encontrar pesos para cada celda en el filtro convolucional, lo que reduce drásticamente la memoria necesaria para entrenar el modelo. Cuando se aplica el filtro convolucional, simplemente se replica en todas las celdas de modo que cada una se multiplique por el filtro.
filtro convolucional
Uno de los dos actores en una operación convolucional (El otro actor es una porción de una matriz de entrada). Un filtro convolucional es una matriz que tiene el mismo rango que la de entrada, pero una forma más pequeña. Por ejemplo, en una matriz de entrada 28 x 28, el filtro podría ser cualquier matriz 2D más pequeña que 28 x 28.
En la manipulación fotográfica, todas las celdas de un filtro convolucional suelen establecerse en un patrón constante de unos y ceros. En el aprendizaje automático, los filtros convolucionales suelen inicializarse con números aleatorios y, luego, la red entrena los valores ideales.
capa convolucional
Capa de una red neuronal profunda en la que un filtro convolucional pasa a lo largo de una matriz de entrada. Por ejemplo, considera el siguiente filtro convolucional de 3 x 3:
![Una matriz de 3x3 con los siguientes valores: [[0,1,0], [1,0,1], [0,1,0]]](https://developers.google.com/static/machine-learning/glossary/images/ConvolutionalFilter33.svg?hl=es-419)
En la siguiente animación, se muestra una capa convolucional que consta de 9 operaciones convolucionales que involucran la matriz de entrada de 5 x 5. Observa que cada operación convolucional funciona en una porción diferente de 3x3 de la matriz de entrada. La matriz resultante de 3 x 3 (a la derecha) consta de los resultados de las 9 operaciones convolucionales:
![Animación que muestra dos matrices. La primera matriz es la matriz de 5 x 5: [[128,97,53,201,198], [35,22,25,200,195], [37,24,28,197,182], [33,28,92,195,179], [31,40,100,192,177]].
La segunda matriz es la matriz de 3 x 3:
[[181,303,618], [115,338,605], [169,351,560]].
La segunda matriz se calcula aplicando el filtro convolucional [[0, 1, 0], [1, 0, 1], [0, 1, 0]] a diferentes subconjuntos de 3 x 3 de la matriz de 5 x 5.](https://developers.google.com/static/machine-learning/glossary/images/AnimatedConvolution.gif?hl=es-419)
red neuronal convolucional
Una red neuronal en la que al menos una capa es una capa convolucional. Una red neuronal convolucional típica consta de alguna combinación de las siguientes capas:
Las redes neuronales convolucionales han tenido un gran éxito en ciertos tipos de problemas, como el reconocimiento de imágenes.
operación convolucional
La siguiente operación matemática de dos pasos:
- Multiplicación por elementos del filtro convolucional y una porción de una matriz de entrada (La porción de la matriz de entrada tiene el mismo rango y tamaño que el filtro convolucional).
- Suma de todos los valores en la matriz de producto resultante
Por ejemplo, considera la siguiente matriz de entrada de 5 x 5:
![La matriz de 5 x 5: [[128,97,53,201,198], [35,22,25,200,195],
[37,24,28,197,182], [33,28,92,195,179], [31,40,100,192,177]].](https://developers.google.com/static/machine-learning/glossary/images/ConvolutionalLayerInputMatrix.svg?hl=es-419)
Ahora, imagina el siguiente filtro convolucional de 2x2:
![La matriz de 2x2: [[1, 0], [0, 1]]](https://developers.google.com/static/machine-learning/glossary/images/ConvolutionalLayerFilter.svg?hl=es-419)
Cada operación convolucional involucra una sola porción de 2 x 2 de la matriz de entrada. Por ejemplo, supongamos que usamos la división de 2 x 2 en la parte superior izquierda de la matriz de entrada. Por lo tanto, la operación de convolución en este segmento se ve de la siguiente manera:
![Aplicación del filtro convolucional [[1, 0], [0, 1]] a la sección superior izquierda de 2 x 2 de la matriz de entrada, que es [[128,97], [35,22]].
El filtro convolucional deja intactos los valores 128 y 22, pero establece en cero los valores 97 y 35. Por lo tanto, la operación de convolución arroja el valor 150 (128 + 22).](https://developers.google.com/static/machine-learning/glossary/images/ConvolutionalLayerOperation.svg?hl=es-419)
Una capa convolucional consiste en una serie de operaciones convolucionales que actúan en porciones diferentes de la matriz de entrada.
COPA
Abreviatura de Choice of Plausible Alternatives.
costo
Sinónimo de pérdida.
coentrenamiento
Un enfoque de aprendizaje semisupervisado, que es especialmente útil cuando se cumplen todas las condiciones siguientes:
- La proporción de ejemplos sin etiquetar en relación con los ejemplos etiquetados en el conjunto de datos es alta.
- Este es un problema de clasificación (binaria o multiclase).
- El conjunto de datos contiene dos conjuntos diferentes de variables predictivas que son independientes entre sí y complementarias.
El entrenamiento conjunto amplifica los indicadores independientes para generar un indicador más potente. Por ejemplo, considera un modelo de clasificación que categoriza los autos usados individuales como Buenos o Malos. Un conjunto de atributos predictivos podría enfocarse en características agregadas, como el año, la marca y el modelo del automóvil; otro conjunto de atributos predictivos podría enfocarse en el historial de conducción del propietario anterior y el historial de mantenimiento del automóvil.
El documento fundamental sobre el coentrenamiento es Combining Labeled and Unlabeled Data with Co-Training de Blum y Mitchell.
Equidad contrafáctica
Es una métrica de equidad que verifica si un modelo de clasificación produce el mismo resultado para una persona que para otra idéntica a la primera, excepto en lo que respecta a uno o más atributos sensibles. Evaluar un modelo de clasificación para la equidad contrafáctica es un método para identificar posibles fuentes de sesgo en un modelo.
Consulta cualquiera de los siguientes artículos para obtener más información:
- Equidad: Equidad contrafáctica en el Curso intensivo de aprendizaje automático.
- When Worlds Collide: Integrating Different Counterfactual Assumptions in Fairness (Cuando los mundos chocan: Integración de diferentes suposiciones contrafácticas en la equidad)
sesgo de cobertura
Consulta sesgo de selección.
crash blossom
Oración o frase con un significado ambiguo. Un crash blossom presenta un problema importante para la comprensión del lenguaje natural. Por ejemplo, el titular La cinta roja que sostiene un rascacielos es un crash blossom porque un modelo CLN podría interpretar el titular en sentido literal o figurado.
crítico
Sinónimo de Deep Q-Network.
entropía cruzada
Es una generalización de la pérdida de registro para problemas de clasificación de clases múltiples. La entropía cruzada cuantifica la diferencia entre dos distribuciones de probabilidad. Consulta también perplejidad.
validación cruzada
Es un mecanismo para estimar qué tan bien un modelo generalizará nuevos datos probando el modelo con uno o más subconjuntos de datos no superpuestos retenidos del conjunto de entrenamiento.
Función de distribución acumulativa (FDA)
Es una función que define la frecuencia de las muestras menores o iguales a un valor objetivo. Por ejemplo, considera una distribución normal de valores continuos. Una CDF indica que, aproximadamente, el 50% de las muestras debe ser menor o igual que la media, y que, aproximadamente, el 84% de las muestras debe ser menor o igual que una desviación estándar por encima de la media.
D
análisis de datos
El proceso de obtener una comprensión de los datos mediante la consideración de muestras, mediciones y visualizaciones. El análisis de datos puede ser particularmente útil cuando se recibe por primera vez un conjunto de datos, antes de crear el primer modelo. También es crucial para comprender los experimentos y problemas de depuración del sistema.
magnificación de datos
Se incrementa de forma artificial el rango y la cantidad de ejemplos de entrenamiento a través de transformaciones sobre los ejemplos existentes para crear ejemplos adicionales. Por ejemplo, supongamos que uno de tus atributos son las imágenes, pero tu conjunto de datos no contiene suficientes ejemplos de imágenes para que el modelo aprenda asociaciones útiles. Lo ideal sería agregar suficientes imágenes etiquetadas al conjunto de datos para permitir que el modelo se entrene adecuadamente. De no ser posible, la magnificación de datos puede rotar, estirar y reflejar cada imagen para producir variantes de la imagen original, lo que producirá, posiblemente, suficientes datos etiquetados para permitir un excelente entrenamiento.
DataFrame
Un tipo de datos pandas popular para representar conjuntos de datos en la memoria.
Un DataFrame es similar a una tabla o una hoja de cálculo. Cada columna de un DataFrame tiene un nombre (un encabezado) y cada fila se identifica con un número único.
Cada columna de un DataFrame se estructura como un array 2D, excepto que a cada columna se le puede asignar su propio tipo de datos.
Consulta también la página de referencia oficial de pandas.DataFrame.
Paralelismo de datos
Es una forma de escalar el entrenamiento o la inferencia que replica un modelo completo en varios dispositivos y, luego, pasa un subconjunto de los datos de entrada a cada dispositivo. El paralelismo de datos puede permitir el entrenamiento y la inferencia en tamaños de lote muy grandes. Sin embargo, requiere que el modelo sea lo suficientemente pequeño como para caber en todos los dispositivos.
Por lo general, el paralelismo de datos acelera el entrenamiento y la inferencia.
Consulta también paralelismo de modelos.
API de Dataset (tf.data)
Una API de TensorFlow de alto nivel para leer datos y transformarlos en un formato que requiere un algoritmo de aprendizaje automático.
Un objeto tf.data.Dataset representa una secuencia de elementos, en la que cada uno de ellos contiene uno o más tensores. Un objeto tf.data.Iterator proporciona acceso a los elementos de un Dataset.
conjunto de datos (data set o dataset)
Es una colección de datos sin procesar, que se suelen organizar (aunque no exclusivamente) en uno de los siguientes formatos:
- una hoja de cálculo
- Un archivo en formato CSV (valores separados por comas)
Límite de decisión
Es el separador entre las clases que aprende un modelo en problemas de clasificación binaria o de clases múltiples. Por ejemplo, en la siguiente imagen, que representa un problema de clasificación binaria, el límite de decisión es la frontera entre la clase anaranjada y la azul:

bosque de decisión
Es un modelo creado a partir de varios árboles de decisión. Un bosque de decisión realiza una predicción agregando las predicciones de sus árboles de decisión. Los tipos populares de bosques de decisión incluyen los bosques aleatorios y los árboles potenciados con gradientes.
Consulta la sección Bosques de decisión del curso sobre bosques de decisión para obtener más información.
umbral de decisión
Sinónimo de umbral de clasificación.
árbol de decisión
Es un modelo de aprendizaje supervisado compuesto por un conjunto de condiciones y hojas organizadas de forma jerárquica. Por ejemplo, el siguiente es un árbol de decisión:
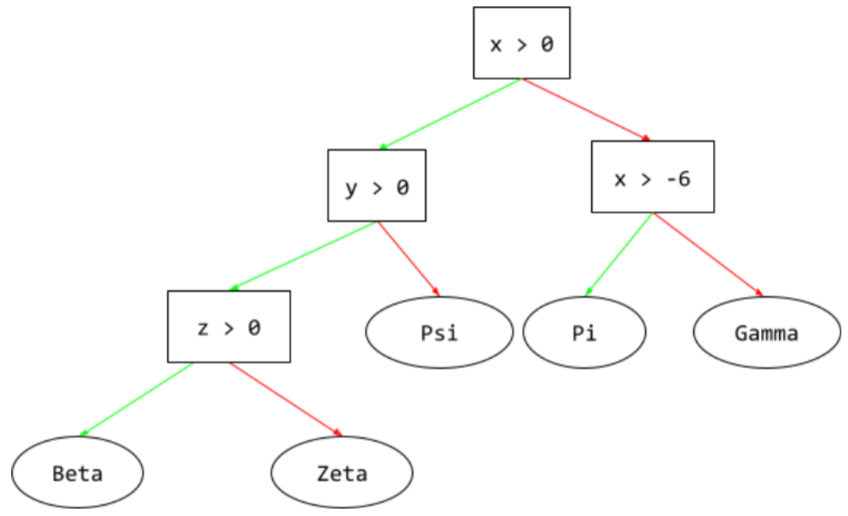
decodificador
En general, cualquier sistema de AA que convierta una representación interna, densa o procesada en una representación externa, dispersa o más sin procesar.
Los decodificadores suelen ser un componente de un modelo más grande, en el que se combinan con un codificador.
En las tareas de secuencia a secuencia, un decodificador comienza con el estado interno generado por el codificador para predecir la siguiente secuencia.
Consulta Transformer para obtener la definición de un decodificador dentro de la arquitectura de Transformer.
Consulta Modelos de lenguaje grandes en el Curso intensivo de aprendizaje automático para obtener más información.
modelo profundo
Una red neuronal que contiene más de una capa oculta.
Un modelo profundo también se denomina red neuronal profunda.
Compara esto con el modelo amplio.
diseño de red neuronal profunda
Sinónimo de modelo profundo.
Red de Deep Q (DQN)
En el aprendizaje Q, una red neuronal profunda predice funciones Q.
Crítico es un sinónimo de Deep Q-Network.
Paridad demográfica
Es una métrica de equidad que se cumple si los resultados de la clasificación de un modelo no dependen de un atributo sensible determinado.
Por ejemplo, si tanto los liliputienses como los brobdingnagianos solicitan ingresar a la Universidad de Glubbdubdrib, se logra la paridad demográfica si el porcentaje de liliputienses admitidos es el mismo que el porcentaje de brobdingnagianos admitidos, independientemente de si un grupo está, en promedio, más calificado que el otro.
Esto contrasta con la igualdad de probabilidades y la igualdad de oportunidades, que permiten que los resultados de la clasificación en conjunto dependan de atributos sensibles, pero no permiten que los resultados de la clasificación para ciertas etiquetas de verdad fundamental especificadas dependan de atributos sensibles. Consulta "Cómo combatir la discriminación con un aprendizaje automático más inteligente" para ver una visualización que explora las compensaciones cuando se optimiza la paridad demográfica.
Consulta Equidad: paridad demográfica en el Curso intensivo de aprendizaje automático para obtener más información.
Reducción de ruido
Un enfoque común del aprendizaje autosupervisado en el que se hace lo siguiente:
El eliminación de ruido permite el aprendizaje a partir de ejemplos sin etiquetar. El conjunto de datos original sirve como objetivo o etiqueta, y los datos ruidosos como entrada.
Algunos modelos de lenguaje enmascarados usan la eliminación de ruido de la siguiente manera:
- Se agrega ruido de forma artificial a una oración sin etiquetar enmascarando algunos de los tokens.
- El modelo intenta predecir los tokens originales.
atributo denso
Es una característica en la que la mayoría o todos los valores son distintos de cero, por lo general, un tensor de valores de punto flotante. Por ejemplo, el siguiente tensor de 10 elementos es denso porque 9 de sus valores no son cero:
| 8 | 3 | 7 | 5 | 2 | 4 | 0 | 4 | 9 | 6 |
Compara esto con el atributo disperso.
capa densa
Sinónimo de capa completamente conectada.
depth
La suma de los siguientes elementos en una red neuronal:
- La cantidad de capas ocultas
- La cantidad de capas de salida, que suele ser 1
- La cantidad de capas de incorporación
Por ejemplo, una red neuronal con cinco capas ocultas y una capa de salida tiene una profundidad de 6.
Ten en cuenta que la capa de entrada no influye en la profundidad.
Red neuronal convolucional separable en profundidad (sepCNN)
Es una arquitectura de red neuronal convolucional basada en Inception, pero en la que los módulos de Inception se reemplazan por convoluciones separables en profundidad. También se conoce como Xception.
Una convolución separable por profundidad (también abreviada como convolución separable) factoriza una convolución 3D estándar en dos operaciones de convolución separadas que son más eficientes desde el punto de vista computacional: primero, una convolución por profundidad, con una profundidad de 1 (n × n × 1) y, luego, una convolución punto a punto, con una longitud y un ancho de 1 (1 × 1 × n).
Para obtener más información, consulta Xception: Deep Learning with Depthwise Separable Convolutions (Xception: Aprendizaje profundo con convoluciones separables por profundidad).
etiqueta derivada
Sinónimo de etiqueta de proxy.
dispositivo
Término sobrecargado con las siguientes dos definiciones posibles:
- Categoría de hardware que puede ejecutar una sesión de TensorFlow y que incluye CPU, GPU y TPU.
- Cuando se entrena un modelo de AA en chips aceleradores (GPUs o TPU), es la parte del sistema que realmente manipula los tensores y las incorporaciones. El dispositivo funciona con chips aceleradores. En cambio, el host suele ejecutarse en una CPU.
privacidad diferencial
En el aprendizaje automático, es un enfoque de anonimización para proteger cualquier dato sensible (por ejemplo, la información personal de un individuo) incluido en el conjunto de entrenamiento de un modelo para que no se exponga. Este enfoque garantiza que el modelo no aprenda ni recuerde mucho sobre una persona específica. Esto se logra mediante el muestreo y la adición de ruido durante el entrenamiento del modelo para ocultar los datos individuales, lo que mitiga el riesgo de exponer datos de entrenamiento sensibles.
La privacidad diferencial también se usa fuera del aprendizaje automático. Por ejemplo, los científicos de datos a veces usan la privacidad diferencial para proteger la privacidad individual cuando calculan estadísticas de uso del producto para diferentes datos demográficos.
reducción de dimensiones
Disminución de la cantidad de dimensiones que se usan para representar un atributo particular en un vector de atributos, generalmente mediante la conversión en un vector de incorporación.
dimensiones
Término sobrecargado con alguna de las siguientes definiciones:
Es la cantidad de niveles de coordenadas en un Tensor. Por ejemplo:
- Un escalar tiene cero dimensiones; por ejemplo,
["Hello"]. - Un vector tiene una dimensión; por ejemplo,
[3, 5, 7, 11]. - Una matriz tiene dos dimensiones; por ejemplo,
[[2, 4, 18], [5, 7, 14]]. Se puede especificar de forma única una celda en particular en un vector unidimensional con una coordenada; se necesitan dos coordenadas para especificar de forma única una celda particular en una matriz bidimensional.
- Un escalar tiene cero dimensiones; por ejemplo,
Es la cantidad de entradas en un vector de atributos.
Es la cantidad de elementos en una capa de incorporación.
Instrucción directa
Sinónimo de instrucción sin ejemplos.
atributo discreto
Un atributo con un conjunto finito de valores posibles. Por ejemplo, un atributo cuyos valores solo pueden ser animal, vegetal o mineral es un atributo discreto (o categórico).
Compara esto con el atributo continuo.
modelo discriminativo
Un modelo que predice etiquetas a partir de un conjunto de uno o más atributos. Más formalmente, los modelos discriminativos definen la probabilidad condicional de un resultado dados ciertos atributos y pesos, es decir:
p(output | features, weights)
Por ejemplo, un modelo que predice si un correo electrónico es spam o no a partir de atributos y pesos es un modelo discriminativo.
La gran mayoría de los modelos de aprendizaje supervisado, incluidos los modelos de clasificación y regresión, son modelos discriminativos.
Compara esto con el modelo generativo.
discriminador
Sistema que determina si los ejemplos son reales o falsos.
De manera alternativa, el subsistema dentro de una red neuronal adversarial generativa que determina si los ejemplos creados por el generador son reales o falsos.
Consulta El discriminador en el curso de las GAN para obtener más información.
Impacto dispar
Tomar decisiones sobre personas que afectan de manera desproporcionada a diferentes subgrupos de la población Por lo general, se refiere a situaciones en las que un proceso algorítmico de toma de decisiones perjudica o beneficia a algunos subgrupos más que a otros.
Por ejemplo, supongamos que un algoritmo que determina la elegibilidad de un liliputiense para un préstamo de una casa en miniatura es más propenso a clasificarlo como "no apto" si su dirección postal contiene un determinado código postal. Si es más probable que los liliputienses big-endian tengan direcciones postales con este código postal que los liliputienses little-endian, este algoritmo puede generar un impacto dispar.
Se diferencia del trato dispar, que se enfoca en las disparidades que se producen cuando las características de los subgrupos son entradas explícitas en un proceso algorítmico de toma de decisiones.
Trato dispar
Incorporar los atributos sensibles de los sujetos en un proceso de toma de decisiones algorítmico de modo que los diferentes subgrupos de personas reciban un trato diferente
Por ejemplo, considera un algoritmo que determina la elegibilidad de los liliputienses para un préstamo de vivienda en miniatura según los datos que proporcionan en su solicitud de préstamo. Si el algoritmo usa la afiliación de Lilliputian como Big-Endian o Little-Endian como entrada, está aplicando un trato dispar a lo largo de esa dimensión.
Esto contrasta con el impacto dispar, que se enfoca en las disparidades en los impactos sociales de las decisiones algorítmicas en subgrupos, independientemente de si esos subgrupos son entradas para el modelo.
destilación
Proceso de reducir el tamaño de un modelo (conocido como profesor) en un modelo más pequeño (conocido como estudiante) que emula las predicciones del modelo original con la mayor fidelidad posible. La destilación es útil porque el modelo más pequeño tiene dos beneficios clave en comparación con el modelo más grande (el profesor):
- Tiempo de inferencia más rápido
- Menor uso de memoria y energía
Sin embargo, las predicciones del estudiante no suelen ser tan buenas como las del profesor.
La destilación entrena al modelo estudiante para minimizar una función de pérdida basada en la diferencia entre los resultados de las predicciones de los modelos estudiante y profesor.
Compara y contrasta la destilación con los siguientes términos:
Consulta LLMs: Ajuste, destilación y diseño de instrucciones en el Curso intensivo de aprendizaje automático para obtener más información.
distribución
La frecuencia y el rango de los diferentes valores para un atributo o una etiqueta determinados Una distribución captura la probabilidad de que se dé un valor en particular.
En la siguiente imagen, se muestran histogramas de dos distribuciones diferentes:
- A la izquierda, se muestra una distribución de ley de potencias de la riqueza en comparación con la cantidad de personas que poseen esa riqueza.
- A la derecha, se muestra una distribución normal de la altura en comparación con la cantidad de personas que tienen esa altura.

Comprender la distribución de cada atributo y etiqueta puede ayudarte a determinar cómo normalizar los valores y detectar valores atípicos.
La frase fuera de la distribución hace referencia a un valor que no aparece en el conjunto de datos o que es muy poco frecuente. Por ejemplo, una imagen del planeta Saturno se consideraría fuera de la distribución para un conjunto de datos que consta de imágenes de gatos.
agrupamiento en clústeres divisivo
Consulta agrupamiento en clústeres jerárquico.
Reducción de muestreo
Término sobrecargado que significa una de las siguientes opciones:
- Reducir la cantidad de información en un atributo para entrenar un modelo de manera más eficiente. Por ejemplo, antes de entrenar un modelo de reconocimiento de imágenes, se reduce el muestreo llevando las imágenes de alta resolución a un formato de resolución más baja.
- Entrenar con un porcentaje desproporcionadamente bajo de ejemplos de clases sobrerepresentadas para mejorar el entrenamiento del modelo en clases subrepresentadas. Por ejemplo, en un conjunto de datos con desequilibrio de clases, los modelos tienden a aprender mucho sobre la clase mayoritaria y no lo suficiente sobre la clase minoritaria. La reducción de muestreo ayuda a equilibrar la cantidad de entrenamiento en las clases mayoritarias y minoritarias.
Consulta Conjuntos de datos: Conjuntos de datos desequilibrados en el Curso intensivo de aprendizaje automático para obtener más información.
DQN
Abreviatura de Deep Q-Network.
Regularización de retirados
Es una forma de regularización útil para entrenar redes neuronales. La regularización de retirados quita una selección aleatoria de un número fijo de unidades de una capa de la red para un solo paso de gradiente. Cuantas más unidades se descarten, más sólida será la regularización. Esto es análogo a entrenar la red para emular un conjunto exponencialmente grande de redes más pequeñas. Para obtener más información, consulta Dropout: A Simple Way to Prevent Neural Networks from Overfitting.
dinámico
Algo que se hace con frecuencia o de forma continua. En el aprendizaje automático, los términos dinámico y en línea son sinónimos. A continuación, se muestran algunos usos comunes de dinámico y en línea en el aprendizaje automático:
- Un modelo dinámico (o modelo en línea) es un modelo que se vuelve a entrenar con frecuencia o de forma continua.
- El entrenamiento dinámico (o entrenamiento en línea) es el proceso de entrenamiento frecuente o continuo.
- La inferencia dinámica (o inferencia en línea) es el proceso de generar predicciones a pedido.
modelo dinámico
Un modelo que se vuelve a entrenar con frecuencia (quizás incluso de forma continua). Un modelo dinámico es un "aprendiz permanente" que se adapta constantemente a los datos en evolución. Un modelo dinámico también se conoce como modelo en línea.
Compara esto con el modelo estático.
E
ejecución inmediata
Entorno de programación de TensorFlow en el que las operaciones se ejecutan de inmediato. Por el contrario, las operaciones llamadas en la ejecución por grafos no se ejecutan hasta que no se evalúen explícitamente. La ejecución inmediata es una interfaz imperativa, al igual que el código en la mayoría de los lenguajes de programación. Los programas de ejecución inmediata son generalmente mucho más fáciles de depurar que los programas de ejecución por grafos.
Interrupción anticipada
Es un método de regularización que implica finalizar el entrenamiento antes de que la pérdida de entrenamiento deje de disminuir. En la interrupción anticipada, detienes intencionalmente el entrenamiento del modelo cuando la pérdida en un conjunto de datos de validación comienza a aumentar, es decir, cuando empeora el rendimiento de la generalización.
Compara esto con la salida anticipada.
Distancia de movimiento de tierra (EMD)
Es una medida de la similitud relativa de dos distribuciones. Cuanto menor sea la distancia de movimiento de tierra, más similares serán las distribuciones.
Distancia de edición
Es una medición de la similitud entre dos cadenas de texto. En el aprendizaje automático, la distancia de edición es útil por los siguientes motivos:
- La distancia de edición es fácil de calcular.
- La distancia de edición puede comparar dos cadenas que se sabe que son similares entre sí.
- La distancia de edición puede determinar el grado en que diferentes cadenas son similares a una cadena determinada.
Existen varias definiciones de distancia de edición, cada una con diferentes operaciones de cadenas. Consulta Distancia de Levenshtein para ver un ejemplo.
Notación de Einsum
Es una notación eficiente para describir cómo se deben combinar dos tensores. Los tensores se combinan multiplicando los elementos de un tensor por los elementos del otro tensor y, luego, sumando los productos. La notación de Einsum usa símbolos para identificar los ejes de cada tensor, y esos mismos símbolos se reorganizan para especificar la forma del nuevo tensor resultante.
NumPy proporciona una implementación común de Einsum.
Capa de embedding
Es una capa oculta especial que se entrena en un atributo categórico de alta dimensión para aprender gradualmente un vector de incorporación de menor dimensión. Una capa de incorporación permite que una red neuronal se entrene de manera mucho más eficiente que si solo se entrenara con el atributo categórico de alta dimensión.
Por ejemplo, actualmente, la Tierra admite alrededor de 73,000 especies de árboles. Supongamos que la especie de árbol es un atributo en tu modelo, por lo que la capa de entrada del modelo incluye un vector de un solo 1 de 73,000 elementos de longitud.
Por ejemplo, tal vez baobab se representaría de la siguiente manera:

Un array de 73,000 elementos es muy largo. Si no agregas una capa de incorporación al modelo, el entrenamiento consumirá mucho tiempo debido a la multiplicación de 72,999 ceros. Quizás elijas que la capa de embedding conste de 12 dimensiones. En consecuencia, la capa de incorporación aprenderá gradualmente un nuevo vector de incorporación para cada especie de árbol.
En ciertas situaciones, el hashing es una alternativa razonable a una capa de incorporación.
Consulta Incorporaciones en el Curso intensivo de aprendizaje automático para obtener más información.
espacio de embedding
Es el espacio vectorial de d dimensiones al que se asignan los atributos de un espacio vectorial de mayor dimensión. El espacio de embedding se entrena para capturar la estructura que es significativa para la aplicación prevista.
El producto escalar de dos incorporaciones es la medida de su similitud.
vector de embedding
En términos generales, es un array de números de punto flotante que se toman de cualquier capa oculta que describa las entradas de esa capa oculta. A menudo, un vector de incorporación es el array de números de punto flotante entrenado en una capa de incorporación. Por ejemplo, supongamos que una capa de embedding debe aprender un vector de embedding para cada una de las 73,000 especies de árboles de la Tierra. Quizás el siguiente array sea el vector de embedding de un árbol baobab:

Un vector de embedding no es un conjunto de números aleatorios. Una capa de embedding determina estos valores a través del entrenamiento, de manera similar a la forma en que una red neuronal aprende otros pesos durante el entrenamiento. Cada elemento del array es una calificación según alguna característica de una especie de árbol. ¿Qué elemento representa la característica de qué especie de árbol? Eso es muy difícil de determinar para los humanos.
La parte matemáticamente notable de un vector de incorporación es que los elementos similares tienen conjuntos similares de números de punto flotante. Por ejemplo, las especies de árboles similares tienen un conjunto más parecido de números de punto flotante que las especies de árboles diferentes. Las secuoyas y las secuoyas rojas son especies de árboles relacionadas, por lo que tendrán un conjunto más similar de números de punto flotante que las secuoyas y las palmeras de coco. Los números en el vector de embedding cambiarán cada vez que vuelvas a entrenar el modelo, incluso si lo vuelves a entrenar con la misma entrada.
función de distribución acumulativa empírica (eCDF o EDF)
Es una función de distribución acumulativa basada en mediciones empíricas de un conjunto de datos real. El valor de la función en cualquier punto a lo largo del eje X es la fracción de observaciones en el conjunto de datos que son menores o iguales que el valor especificado.
minimización del riesgo empírico (ERM)
Elegir la función que minimiza la pérdida en el conjunto de entrenamiento Compara esto con la minimización del riesgo estructural.
codificador
En general, cualquier sistema de AA que convierta una representación sin procesar, dispersa o externa en una representación más procesada, densa o interna.
Los codificadores suelen ser un componente de un modelo más grande, en el que se combinan con un decodificador. Algunos Transformers combinan codificadores con decodificadores, aunque otros Transformers usan solo el codificador o solo el decodificador.
Algunos sistemas usan el resultado del codificador como entrada para una red de clasificación o regresión.
En las tareas de secuencia a secuencia, un codificador toma una secuencia de entrada y devuelve un estado interno (un vector). Luego, el decodificador usa ese estado interno para predecir la siguiente secuencia.
Consulta Transformer para obtener la definición de un codificador en la arquitectura de Transformer.
Para obtener más información, consulta LLMs: ¿Qué es un modelo de lenguaje grande? en el Curso intensivo de aprendizaje automático.
extremos
Es una ubicación con dirección de red (por lo general, una URL) a la que se puede acceder a un servicio.
automatizado
Es una colección de modelos entrenados de forma independiente cuyas predicciones se promedian o agregan. En muchos casos, un conjunto produce mejores predicciones que un solo modelo. Por ejemplo, un bosque aleatorio es un ensamble creado a partir de varios árboles de decisión. Ten en cuenta que no todos los bosques de decisión son conjuntos.
Consulta Bosque aleatorio en el Curso intensivo de aprendizaje automático para obtener más información.
entropía
En la teoría de la información, es una descripción de qué tan impredecible es una distribución de probabilidad. Como alternativa, la entropía también se define como la cantidad de información que contiene cada ejemplo. Una distribución tiene la entropía más alta posible cuando todos los valores de una variable aleatoria son igualmente probables.
La entropía de un conjunto con dos valores posibles "0" y "1" (por ejemplo, las etiquetas en un problema de clasificación binaria) tiene la siguiente fórmula:
H = -p log p - q log q = -p log p - (1-p) * log (1-p)
Donde:
- H es la entropía.
- p es la fracción de ejemplos de "1".
- q es la fracción de ejemplos "0". Ten en cuenta que q = (1 - p).
- log suele ser log2. En este caso, la unidad de entropía es un bit.
Por ejemplo, supongamos lo siguiente:
- 100 ejemplos contienen el valor "1".
- 300 ejemplos contienen el valor "0".
Por lo tanto, el valor de la entropía es el siguiente:
- p = 0.25
- q = 0.75
- H = (-0.25)log2(0.25) - (0.75)log2(0.75) = 0.81 bits por ejemplo
Un conjunto perfectamente equilibrado (por ejemplo, 200 "0" y 200 "1") tendría una entropía de 1.0 bits por ejemplo. A medida que un conjunto se vuelve más desequilibrado, su entropía se acerca a 0.0.
En los árboles de decisión, la entropía ayuda a formular la ganancia de información para ayudar al divisor a seleccionar las condiciones durante el crecimiento de un árbol de decisión de clasificación.
Compara la entropía con lo siguiente:
- impureza de Gini
- Función de pérdida de entropía cruzada
A menudo, la entropía se denomina entropía de Shannon.
Consulta Divisor exacto para la clasificación binaria con características numéricas en el curso de Bosques de decisión para obtener más información.
entorno
En el aprendizaje por refuerzo, el mundo contiene al agente y le permite observar el estado de ese mundo. Por ejemplo, el mundo representado puede ser un juego como el ajedrez o un mundo físico como un laberinto. Cuando el agente aplica una acción al entorno, este cambia de estado.
episodio
En el aprendizaje por refuerzo, cada uno de los intentos repetidos del agente para aprender un entorno.
época
Un recorrido de entrenamiento completo por todo el conjunto de entrenamiento, de manera que cada ejemplo se haya procesado una vez.
Un ciclo representa N/tamaño del lote iteraciones de entrenamiento, donde N es la cantidad total de ejemplos.
Por ejemplo, supongamos lo siguiente:
- El conjunto de datos consta de 1,000 ejemplos.
- El tamaño del lote es de 50 ejemplos.
Por lo tanto, una sola época requiere 20 iteraciones:
1 epoch = (N/batch size) = (1,000 / 50) = 20 iterations
Consulta Regresión lineal: Hiperparámetros en el Curso intensivo de aprendizaje automático para obtener más información.
Política de ε-greedy
En el aprendizaje por refuerzo, una política que sigue una política aleatoria con una probabilidad de epsilon o una política voraz en otros casos. Por ejemplo, si epsilon es 0.9, la política sigue una política aleatoria el 90% del tiempo y una política voraz el 10% del tiempo.
En episodios sucesivos, el algoritmo reduce el valor de epsilon para pasar de seguir una política aleatoria a seguir una política voraz. Al cambiar la política, el agente primero explora el entorno de forma aleatoria y, luego, explota de forma codiciosa los resultados de la exploración aleatoria.
Igualdad de oportunidades
Es una métrica de equidad para evaluar si un modelo predice el resultado deseado con la misma precisión para todos los valores de un atributo sensible. En otras palabras, si el resultado deseable para un modelo es la clase positiva, el objetivo sería que la tasa de verdaderos positivos sea la misma para todos los grupos.
La igualdad de oportunidades se relaciona con la igualdad de probabilidades, que requiere que tanto las tasas de verdaderos positivos como las tasas de falsos positivos sean las mismas para todos los grupos.
Supongamos que la Universidad de Glubbdubdrib admite tanto a liliputienses como a brobdingnagianos en un programa riguroso de matemáticas. Las escuelas secundarias de Lilliput ofrecen un plan de estudios sólido de clases de matemáticas, y la gran mayoría de los estudiantes están calificados para el programa universitario. Las escuelas secundarias de Brobdingnag no ofrecen clases de matemáticas, por lo que muchos menos estudiantes están calificados. La igualdad de oportunidades se satisface para la etiqueta preferida de "admitido" con respecto a la nacionalidad (liliputiense o brobdingnagiana) si los estudiantes calificados tienen la misma probabilidad de ser admitidos, independientemente de si son liliputienses o brobdingnagianos.
Por ejemplo, supongamos que 100 liliputienses y 100 brobdingnagianos solicitan ingresar a la Universidad de Glubbdubdrib, y las decisiones de admisión se toman de la siguiente manera:
Tabla 1: Solicitantes de Lilliputian (el 90% cumple con los requisitos)
| Calificado | No cumple con los requisitos | |
|---|---|---|
| Admitida | 45 | 3 |
| Rechazado | 45 | 7 |
| Total | 90 | 10 |
|
Porcentaje de estudiantes calificados admitidos: 45/90 = 50% Porcentaje de estudiantes no calificados rechazados: 7/10 = 70% Porcentaje total de estudiantes de Lilliput admitidos: (45 + 3)/100 = 48% |
||
Tabla 2: Solicitantes brobdingnagianos (el 10% está calificado):
| Calificado | No cumple con los requisitos | |
|---|---|---|
| Admitida | 5 | 9 |
| Rechazado | 5 | 81 |
| Total | 10 | 90 |
|
Porcentaje de estudiantes calificados admitidos: 5/10 = 50% Porcentaje de estudiantes no calificados rechazados: 81/90 = 90% Porcentaje total de estudiantes de Brobdingnag admitidos: (5 + 9)/100 = 14% |
||
Los ejemplos anteriores satisfacen la igualdad de oportunidades para la aceptación de estudiantes calificados, ya que tanto los liliputienses como los brobdingnagianos calificados tienen un 50% de probabilidades de ser admitidos.
Si bien se satisface la igualdad de oportunidades, no se satisfacen las siguientes dos métricas de equidad:
- Paridad demográfica: Los liliputienses y los brobdingnagianos son admitidos en la universidad en diferentes proporciones: el 48% de los estudiantes liliputienses son admitidos, pero solo el 14% de los estudiantes brobdingnagianos.
- Probabilidades ecualizadas: Si bien los estudiantes calificados de Liliput y Brobdingnag tienen la misma probabilidad de ser admitidos, no se cumple la restricción adicional de que los estudiantes no calificados de Liliput y Brobdingnag tengan la misma probabilidad de ser rechazados. Los liliputienses no calificados tienen una tasa de rechazo del 70%, mientras que los brobdingnagianos no calificados tienen una tasa de rechazo del 90%.
Consulta Equidad: Igualdad de oportunidades en el Curso intensivo de aprendizaje automático para obtener más información.
Probabilidades ecualizadas
Es una métrica de equidad para evaluar si un modelo predice resultados con la misma precisión para todos los valores de un atributo sensible con respecto a la clase positiva y la clase negativa, no solo una clase o la otra de forma exclusiva. En otras palabras, tanto la tasa de verdaderos positivos como la tasa de falsos negativos deben ser iguales para todos los grupos.
La métrica de probabilidades igualadas se relaciona con la igualdad de oportunidades, que solo se enfoca en las tasas de error para una sola clase (positiva o negativa).
Por ejemplo, supongamos que la Universidad de Glubbdubdrib admite tanto a liliputienses como a brobdingnagianos en un riguroso programa de matemáticas. Las escuelas secundarias de Lilliput ofrecen un plan de estudios sólido de clases de matemáticas, y la gran mayoría de los estudiantes están calificados para el programa universitario. Las escuelas secundarias de Brobdingnag no ofrecen clases de matemáticas, por lo que muchos menos estudiantes están calificados. La condición de probabilidades iguales se cumple siempre que, independientemente de si un solicitante es liliputiense o brobdingnagiano, si está calificado, es igualmente probable que se lo admita en el programa y, si no está calificado, es igualmente probable que se lo rechace.
Supongamos que 100 liliputienses y 100 brobdingnagianos solicitan ingresar a la Universidad de Glubbdubdrib, y las decisiones de admisión se toman de la siguiente manera:
Tabla 3: Solicitantes de Lilliputian (el 90% cumple con los requisitos)
| Calificado | No cumple con los requisitos | |
|---|---|---|
| Admitida | 45 | 2 |
| Rechazado | 45 | 8 |
| Total | 90 | 10 |
|
Porcentaje de estudiantes calificados admitidos: 45/90 = 50% Porcentaje de estudiantes no calificados rechazados: 8/10 = 80% Porcentaje total de estudiantes de Lilliput admitidos: (45 + 2)/100 = 47% |
||
Tabla 4. Solicitantes brobdingnagianos (el 10% está calificado):
| Calificado | No cumple con los requisitos | |
|---|---|---|
| Admitida | 5 | 18 |
| Rechazado | 5 | 72 |
| Total | 10 | 90 |
|
Porcentaje de estudiantes calificados admitidos: 5/10 = 50% Porcentaje de estudiantes no calificados rechazados: 72/90 = 80% Porcentaje total de estudiantes de Brobdingnag admitidos: (5 + 18)/100 = 23% |
||
Se cumple la igualdad de probabilidades porque los estudiantes calificados de Liliput y Brobdingnag tienen un 50% de probabilidades de ser admitidos, y los estudiantes no calificados de Liliput y Brobdingnag tienen un 80% de probabilidades de ser rechazados.
La igualdad de probabilidades se define formalmente en "Equality of Opportunity in Supervised Learning" de la siguiente manera: "El predictor Ŷ satisface la igualdad de probabilidades con respecto al atributo protegido A y el resultado Y si Ŷ y A son independientes, condicionales a Y".
Estimador
Es una API de TensorFlow obsoleta. Usa tf.keras en lugar de los Estimadores.
evals
Se usa principalmente como abreviatura de evaluaciones de LLM. En términos más generales, evals es la abreviatura de cualquier forma de evaluación.
sin conexión
Proceso para medir la calidad de un modelo o comparar diferentes modelos entre sí.
Para evaluar un modelo de aprendizaje automático supervisado, por lo general, lo comparas con un conjunto de validación y un conjunto de prueba. Evaluar un LLM suele implicar evaluaciones más amplias de calidad y seguridad.
concordancia exacta
Es una métrica de todo o nada en la que el resultado del modelo coincide con la verdad fundamental o el texto de referencia de forma exacta, o no coincide. Por ejemplo, si la verdad fundamental es naranja, el único resultado del modelo que satisface la concordancia exacta es naranja.
La concordancia exacta también puede evaluar modelos cuya salida es una secuencia (una lista de elementos clasificados). En general, la coincidencia exacta requiere que la lista clasificada generada coincida exactamente con la verdad fundamental, es decir, cada elemento de ambas listas debe estar en el mismo orden. Dicho esto, si la verdad fundamental consta de varias secuencias correctas, la concordancia exacta solo requiere que la salida del modelo coincida con una de las secuencias correctas.
ejemplo
Son los valores de una fila de atributos y, posiblemente, una etiqueta. Los ejemplos de aprendizaje supervisado se dividen en dos categorías generales:
- Un ejemplo etiquetado consta de uno o más atributos y una etiqueta. Durante el entrenamiento, se usan ejemplos etiquetados.
- Un ejemplo sin etiquetar consta de uno o más atributos, pero no tiene etiqueta. Los ejemplos sin etiqueta se usan durante la inferencia.
Por ejemplo, supongamos que estás entrenando un modelo para determinar la influencia de las condiciones climáticas en las calificaciones de los estudiantes. Estos son tres ejemplos etiquetados:
| Funciones | Etiqueta | ||
|---|---|---|---|
| Temperatura | Humedad | Presionar | Puntuación de la prueba |
| 15 | 47 | 998 | Bueno |
| 19 | 34 | 1020 | Excelente |
| 18 | 92 | 1012 | Deficiente |
Estos son tres ejemplos sin etiquetas:
| Temperatura | Humedad | Presionar | |
|---|---|---|---|
| 12 | 62 | 1014 | |
| 21 | 47 | 1017 | |
| 19 | 41 | 1021 |
Por lo general, la fila de un conjunto de datos es la fuente sin procesar de un ejemplo. Es decir, un ejemplo suele consistir en un subconjunto de las columnas del conjunto de datos. Además, los atributos de un ejemplo también pueden incluir atributos sintéticos, como combinaciones de atributos.
Consulta Aprendizaje supervisado en el curso Introducción al aprendizaje automático para obtener más información.
Repetición de la experiencia
En el aprendizaje por refuerzo, es una técnica de DQN que se usa para reducir las correlaciones temporales en los datos de entrenamiento. El agente almacena las transiciones de estado en un búfer de reproducción y, luego, muestrea las transiciones del búfer de reproducción para crear datos de entrenamiento.
sesgo del experimentador
Consulta sesgo de confirmación.
Problema de gradiente explosivo
Es la tendencia de los gradientes en las redes neuronales profundas (en especial, las redes neuronales recurrentes) a volverse sorprendentemente pronunciados (altos). Los gradientes pronunciados suelen provocar actualizaciones muy grandes en los pesos de cada nodo en una red neuronal profunda.
Los modelos que sufren el problema del gradiente explosivo se vuelven difíciles o imposibles de entrenar. El ajuste de gradientes puede mitigar este problema.
Compara esto con el problema de desvanecimiento de gradiente.
Resumen extremo (xsum)
Es un conjunto de datos para evaluar la capacidad de un LLM de resumir un solo documento. Cada entrada del conjunto de datos consta de lo siguiente:
- Documento creado por la British Broadcasting Corporation (BBC).
- Un resumen de una oración de ese documento.
Para obtener más información, consulta Don't Give Me the Details, Just the Summary! Topic-Aware Convolutional Neural Networks for Extreme Summarization.
F
F1
Es una métrica de clasificación binaria "acumulada" que se basa tanto en la precisión como en la recuperación. Esta es la fórmula:
Facticidad
En el mundo del AA, una propiedad que describe un modelo cuya salida se basa en la realidad. La facticidad es un concepto, no una métrica. Por ejemplo, supongamos que envías la siguiente instrucción a un modelo de lenguaje grande:
¿Cuál es la fórmula química de la sal de mesa?
Un modelo que optimice la facticidad respondería de la siguiente manera:
NaCl
Es tentador suponer que todos los modelos deben basarse en la facticidad. Sin embargo, algunas instrucciones, como las siguientes, deberían hacer que un modelo de IA generativa optimice la creatividad en lugar de la factualidad.
Cuéntame un limerick sobre un astronauta y una oruga.
Es poco probable que la limerick resultante se base en la realidad.
Compara esto con la fundamentación.
restricción de equidad
Aplicar una restricción a un algoritmo para garantizar que se satisfagan una o más definiciones de equidad Estos son algunos ejemplos de restricciones de equidad:- Procesar posteriormente el resultado de tu modelo
- Modificar la función de pérdida para incorporar una penalización por incumplir una métrica de equidad
- Agregar directamente una restricción matemática a un problema de optimización
métrica de equidad
Una definición matemática de "equidad" que se pueda medir Algunas métricas de equidad de uso común son las siguientes:
Muchas métricas de equidad son mutuamente excluyentes. Consulta la incompatibilidad de métricas de equidad.
falso negativo (FN)
Ejemplo en el que el modelo predice de manera incorrecta la clase negativa. Por ejemplo, el modelo predice que un mensaje de correo electrónico en particular no es spam (la clase negativa), pero ese mensaje de correo electrónico en realidad sí es spam.
tasa de falsos negativos
Proporción de ejemplos positivos reales para los que el modelo predijo erróneamente la clase negativa. La siguiente fórmula calcula la tasa de falsos negativos:
Para obtener más información, consulta Umbrales y la matriz de confusión en el Curso intensivo de aprendizaje automático.
Falso positivo (FP)
Ejemplo en el que el modelo predice de manera incorrecta la clase positiva. Por ejemplo, el modelo predice que un mensaje de correo electrónico en particular es spam (la clase positiva), pero ese mensaje de correo electrónico en realidad no es spam.
Para obtener más información, consulta Umbrales y la matriz de confusión en el Curso intensivo de aprendizaje automático.
tasa de falsos positivos (FPR)
Proporción de ejemplos negativos reales para los que el modelo predijo erróneamente la clase positiva. La siguiente fórmula calcula la tasa de falsos positivos:
La tasa de falsos positivos es el eje X en una curva ROC.
Para obtener más información, consulta Clasificación: ROC y AUC en el Curso intensivo de aprendizaje automático.
Decaimiento rápido
Técnica de entrenamiento para mejorar el rendimiento de los LLM La disminución rápida implica reducir rápidamente la tasa de aprendizaje durante el entrenamiento. Esta estrategia ayuda a evitar que el modelo se sobreajuste a los datos de entrenamiento y mejora la generalización.
función
Es una variable de entrada para un modelo de aprendizaje automático. Un ejemplo consta de una o más características. Por ejemplo, supongamos que estás entrenando un modelo para determinar la influencia de las condiciones climáticas en las calificaciones de los estudiantes. En la siguiente tabla, se muestran tres ejemplos, cada uno de los cuales contiene tres características y una etiqueta:
| Funciones | Etiqueta | ||
|---|---|---|---|
| Temperatura | Humedad | Presionar | Puntuación de la prueba |
| 15 | 47 | 998 | 92 |
| 19 | 34 | 1020 | 84 |
| 18 | 92 | 1012 | 87 |
Compara esto con la etiqueta.
Consulta Aprendizaje supervisado en el curso Introducción al aprendizaje automático para obtener más información.
combinación de atributos
Un atributo sintético que se forma al "combinar" atributos categóricos o agrupados en buckets
Por ejemplo, considera un modelo de "previsión del estado de ánimo" que representa la temperatura en uno de los siguientes cuatro intervalos:
freezingchillytemperatewarm
Y representa la velocidad del viento en uno de los siguientes tres buckets:
stilllightwindy
Sin combinaciones de atributos, el modelo lineal se entrena de forma independiente en cada uno de los siete segmentos anteriores. Por lo tanto, el modelo se entrena en, por ejemplo, freezing de forma independiente del entrenamiento en, por ejemplo, windy.
Como alternativa, podrías crear una combinación de atributos de temperatura y velocidad del viento. Esta variable sintética tendría los siguientes 12 valores posibles:
freezing-stillfreezing-lightfreezing-windychilly-stillchilly-lightchilly-windytemperate-stilltemperate-lighttemperate-windywarm-stillwarm-lightwarm-windy
Gracias a las combinaciones de atributos, el modelo puede aprender las diferencias de humor entre un día freezing-windy y un día freezing-still.
Si creas un atributo sintético a partir de dos atributos que tienen muchos discretizaciones diferentes, la combinación de atributos resultante tendrá una gran cantidad de combinaciones posibles. Por ejemplo, si un atributo tiene 1,000 discretizaciones y el otro tiene 2,000, la discretización resultante tendrá 2,000,000 de discretizaciones.
Formalmente, un cruce es un producto cartesiano.
Las combinaciones de atributos se usan principalmente con modelos lineales y rara vez con redes neuronales.
Consulta Datos categóricos: combinaciones de atributos en el Curso intensivo de aprendizaje automático para obtener más información.
ingeniería de atributos.
Un proceso que incluye los siguientes pasos:
- Determinar qué atributos podrían ser útiles para entrenar un modelo
- Convertir los datos sin procesar del conjunto de datos en versiones eficientes de esos atributos
Por ejemplo, podrías determinar que temperature podría ser una función útil. Luego, puedes experimentar con el agrupamiento para optimizar lo que el modelo puede aprender de diferentes rangos de temperature.
En algunas ocasiones, la ingeniería de atributos se denomina extracción de características o featurización.
Para obtener más información, consulta Datos numéricos: Cómo un modelo ingiere datos con vectores de características en el Curso intensivo de aprendizaje automático.
extracción de atributos
Término sobrecargado con alguna de las siguientes definiciones:
- Recuperar representaciones de atributos intermedios calculadas por un modelo no supervisado o previamente entrenado (por ejemplo, valores de la capa oculta en una red neuronal) para usarlos en otro modelo como entrada
- Sinónimo de ingeniería de atributos.
Importancia de los atributos
Sinónimo de importancia de las variables.
conjunto de atributos
Es el grupo de atributos con el que se entrena el modelo de aprendizaje automático. Por ejemplo, un conjunto de atributos simple para un modelo que predice los precios de las viviendas podría constar del código postal, el tamaño de la propiedad y el estado de la propiedad.
especificación de atributos
Describe la información necesaria para extraer datos de atributos del búfer de protocolo tf.Example. Dado que el búfer de protocolo tf.Example es solo un contenedor de datos, debes especificar lo siguiente:
- Los datos que se extraerán (es decir, las claves de los atributos)
- El tipo de datos (por ejemplo, float o int)
- La longitud (fija o variable)
vector de atributos
Es el array de valores de atributo que componen un ejemplo. El vector de atributos se ingresa durante el entrenamiento y la inferencia. Por ejemplo, el vector de atributos para un modelo con dos atributos discretos podría ser el siguiente:
[0.92, 0.56]
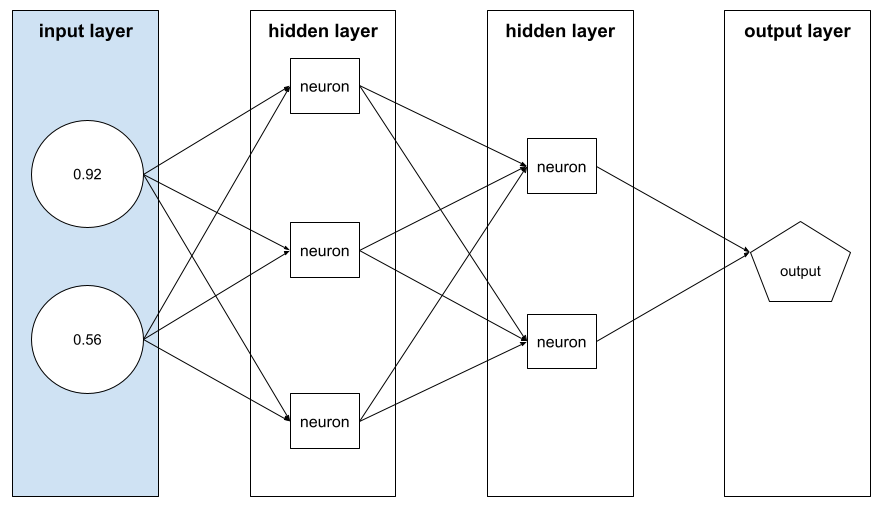
Cada ejemplo proporciona valores diferentes para el vector de atributos, por lo que el vector de atributos para el siguiente ejemplo podría ser similar al siguiente:
[0.73, 0.49]
La ingeniería de atributos determina cómo representar los atributos en el vector de atributos. Por ejemplo, un atributo categórico binario con cinco valores posibles se podría representar con codificación one-hot. En este caso, la porción del vector de características para un ejemplo en particular constaría de cuatro ceros y un solo 1.0 en la tercera posición, como se muestra a continuación:
[0.0, 0.0, 1.0, 0.0, 0.0]
Como otro ejemplo, supongamos que tu modelo consta de tres atributos:
- Un atributo categórico binario con cinco valores posibles representados con codificación one-hot; por ejemplo:
[0.0, 1.0, 0.0, 0.0, 0.0] - Otro atributo categórico binario con tres valores posibles representados con codificación one-hot; por ejemplo:
[0.0, 0.0, 1.0] - Es una característica de punto flotante, por ejemplo,
8.3.
En este caso, el vector de atributos para cada ejemplo se representaría con nueve valores. Con los valores de ejemplo de la lista anterior, el vector de atributos sería el siguiente:
0.0 1.0 0.0 0.0 0.0 0.0 0.0 1.0 8.3
Para obtener más información, consulta Datos numéricos: Cómo un modelo ingiere datos con vectores de características en el Curso intensivo de aprendizaje automático.
featurización
Proceso de extracción de atributos de una fuente de entrada, como un documento o un video, y de asignación de esos atributos a un vector de atributos.
Algunos expertos en AA usan la featurización como sinónimo de ingeniería de atributos o extracción de atributos.
aprendizaje federado
Un enfoque de aprendizaje automático distribuido que entrena modelos de aprendizaje automático usando ejemplos descentralizados que residen en dispositivos como smartphones. En el aprendizaje federado, un subconjunto de dispositivos descarga el modelo actual desde un servidor central de coordinación. Los dispositivos usan los ejemplos almacenados en ellos para mejorar el modelo. Luego, los dispositivos suben las mejoras del modelo (pero no los ejemplos de entrenamiento) al servidor de coordinación, donde se agregan con otras actualizaciones para generar un modelo global mejorado. Después de la agregación, ya no se necesitan las actualizaciones del modelo que calculan los dispositivos y se pueden descartar.
Dado que los ejemplos de entrenamiento nunca se suben, el aprendizaje federado sigue los principios de privacidad de la recopilación de datos enfocada y la minimización de datos.
Consulta el cómic sobre el aprendizaje federado (sí, un cómic) para obtener más detalles.
ciclo de retroalimentación
En el aprendizaje automático, situación en la que las predicciones de un modelo influyen en los datos de entrenamiento del mismo modelo o de otro. Por ejemplo, un modelo que recomienda películas influirá en las películas que miran las personas, lo que, a su vez, influirá en los modelos posteriores de recomendación de películas.
Para obtener más información, consulta Sistemas de AA en producción: Preguntas que debes hacer en el Curso intensivo de aprendizaje automático.
red neuronal prealimentada (FFN)
Red neuronal sin conexiones cíclicas o recurrentes. Por ejemplo, las redes neuronales profundas tradicionales son redes neuronales prealimentadas. Compara esto con las redes neuronales recurrentes, que son cíclicas.
aprendizaje en pocos intentos
Es un enfoque de aprendizaje automático que se suele usar para la clasificación de objetos y que está diseñado para entrenar modelos de clasificación eficaces con solo una pequeña cantidad de ejemplos de entrenamiento.
Consulta también aprendizaje en un intento y aprendizaje sin ejemplos.
Instrucción con varios ejemplos
Un prompt que contiene más de un ejemplo (algunos) que demuestran cómo debe responder el modelo de lenguaje extenso. Por ejemplo, la siguiente instrucción extensa contiene dos ejemplos que muestran a un modelo de lenguaje grande cómo responder una búsqueda.
| Partes de una instrucción | Notas |
|---|---|
| ¿Cuál es la moneda oficial del país especificado? | La pregunta que quieres que responda el LLM. |
| Francia: EUR | Veamos un ejemplo. |
| Reino Unido: GBP | Otro ejemplo. |
| India: | Es la búsqueda real. |
En general, las instrucciones con pocos ejemplos producen resultados más deseables que las instrucciones sin ejemplos y las instrucciones con un solo ejemplo. Sin embargo, las instrucciones con varios ejemplos requieren una instrucción más extensa.
La instrucción con ejemplos limitados es una forma de aprendizaje en pocos intentos que se aplica al aprendizaje basado en instrucciones.
Consulta Ingeniería de instrucciones en el Curso intensivo de aprendizaje automático para obtener más información.
Violín tradicional
Una biblioteca de configuración que prioriza Python y establece los valores de las funciones y las clases sin código ni infraestructura invasivos. En el caso de Pax, y otras bases de código de AA, estas funciones y clases representan modelos y hiperparámetros de entrenamiento.
Fiddle supone que las bases de código de aprendizaje automático suelen dividirse en los siguientes elementos:
- Código de la biblioteca, que define las capas y los optimizadores
- Código "pegamento" del conjunto de datos, que llama a las bibliotecas y conecta todo.
Fiddle captura la estructura de llamadas del código de vinculación en una forma mutable y sin evaluar.
Ajuste
Es un segundo paso de entrenamiento específico para la tarea que se realiza en un modelo previamente entrenado para ajustar sus parámetros para un caso de uso específico. Por ejemplo, la secuencia de entrenamiento completa para algunos modelos de lenguaje grandes es la siguiente:
- Preentrenamiento: Entrena un modelo de lenguaje grande con un vasto conjunto de datos generales, como todas las páginas de Wikipedia en inglés.
- Ajuste: Entrena el modelo previamente entrenado para realizar una tarea específica, como responder preguntas médicas. Por lo general, el ajuste implica cientos o miles de ejemplos enfocados en la tarea específica.
Como otro ejemplo, la secuencia de entrenamiento completa para un modelo de imágenes grande es la siguiente:
- Entrenamiento previo: Entrena un modelo de imágenes grande en un vasto conjunto de datos de imágenes generales, como todas las imágenes de Wikimedia Commons.
- Ajuste: Entrena el modelo previamente entrenado para realizar una tarea específica, como generar imágenes de orcas.
El ajuste puede implicar cualquier combinación de las siguientes estrategias:
- Modifica todos los parámetros existentes del modelo entrenado previamente. A veces, esto se denomina ajuste fino completo.
- Modificar solo algunos de los parámetros existentes del modelo entrenado previamente (por lo general, las capas más cercanas a la capa de salida), mientras se mantienen sin cambios otros parámetros existentes (por lo general, las capas más cercanas a la capa de entrada). Consulta ajuste eficiente de parámetros.
- Se agregan más capas, por lo general, sobre las capas existentes más cercanas a la capa de salida.
El ajuste es una forma de aprendizaje por transferencia. Por lo tanto, el ajuste puede usar una función de pérdida o un tipo de modelo diferente de los que se usan para entrenar el modelo previamente entrenado. Por ejemplo, podrías ajustar un modelo de imágenes grandes previamente entrenado para producir un modelo de regresión que devuelva la cantidad de aves en una imagen de entrada.
Compara y contrasta el ajuste fino con los siguientes términos:
Consulta Ajuste fino en el Curso intensivo de aprendizaje automático para obtener más información.
Modelo de flash
Una familia de modelos Gemini relativamente pequeños y optimizados para la velocidad y la baja latencia. Los modelos Flash están diseñados para una amplia variedad de aplicaciones en las que las respuestas rápidas y la alta capacidad de procesamiento son fundamentales.
Lino
Una biblioteca de código abierto y alto rendimiento para el aprendizaje profundo compilada en JAX. Flax proporciona funciones para entrenar redes neuronales, así como métodos para evaluar su rendimiento.
Flaxformer
Una biblioteca de Transformer de código abierto, compilada en Flax, diseñada principalmente para la investigación multimodal y el procesamiento del lenguaje natural.
Puerta de olvido
Es la parte de una celda de memoria a largo plazo y a corto plazo que regula el flujo de información a través de la celda. Las puertas de olvido mantienen el contexto, ya que deciden qué información descartar del estado de la celda.
modelo de base
Un modelo previamente entrenado muy grande entrenado con un conjunto de entrenamiento enorme y diverso. Un modelo de base puede hacer lo siguiente:
- Responder bien a una amplia variedad de solicitudes
- Sirven como modelo base para ajustes adicionales o cualquier otra personalización.
En otras palabras, un modelo de base ya es muy capaz en un sentido general, pero se puede personalizar aún más para que sea más útil para una tarea específica.
fracción de éxitos
Es una métrica para evaluar el texto generado de un modelo de AA. La fracción de éxitos es la cantidad de resultados de texto generados "correctos" dividida por la cantidad total de resultados de texto generados. Por ejemplo, si un modelo de lenguaje grande generó 10 bloques de código, de los cuales cinco fueron exitosos, la fracción de éxitos sería del 50%.
Si bien la fracción de éxitos es útil en general en todas las estadísticas, en el AA, esta métrica es principalmente útil para medir tareas verificables, como la generación de código o los problemas matemáticos.
softmax completo
Sinónimo de softmax.
Compara esto con el muestreo de candidatos.
Para obtener más información, consulta Redes neuronales: clasificación de clases múltiples en el Curso intensivo de aprendizaje automático.
capa completamente conectada
Una capa oculta en la que cada nodo está conectado a todos los nodos de la capa oculta subsiguiente.
Una capa completamente conectada también se conoce como una capa densa.
transformación de funciones
Es una función que toma otra función como entrada y devuelve una función transformada como salida. JAX usa transformaciones de funciones.
G
GAN
Abreviatura de red generativa adversaria.
Gemini
El ecosistema que comprende la IA más avanzada de Google. Los elementos de este ecosistema incluyen lo siguiente:
- Varios modelos de Gemini
- Es la interfaz conversacional interactiva para un modelo de Gemini. Los usuarios escriben instrucciones y Gemini responde a ellas.
- Varias APIs de Gemini
- Varios productos empresariales basados en modelos de Gemini, por ejemplo, Gemini para Google Cloud.
Modelos de Gemini
Modelos multimodales de última generación basados en Transformer de Google. Los modelos de Gemini están diseñados específicamente para integrarse con agentes.
Los usuarios pueden interactuar con los modelos de Gemini de diversas maneras, como a través de una interfaz de diálogo interactiva y de SDKs.
Gemma
Una familia de modelos abiertos y ligeros creados a partir de la misma investigación y tecnología que se utilizaron para crear los modelos de Gemini. Hay varios modelos de Gemma disponibles, cada uno con diferentes funciones, como visión, código y seguimiento de instrucciones. Consulta Gemma para obtener más información.
IA generativa o IAgenerativa
Abreviatura de IA generativa.
generalización
Es la capacidad de un modelo para realizar predicciones correctas sobre datos nuevos nunca antes vistos. Un modelo que puede generalizar es lo contrario de un modelo que tiene sobreajuste.
Consulta Generalización en el Curso intensivo de aprendizaje automático para obtener más información.
Curva de generalización
Un gráfico de la pérdida de entrenamiento y la pérdida de validación como una función de la cantidad de iteraciones.
Una curva de generalización puede ayudarte a detectar un posible sobreajuste. Por ejemplo, la siguiente curva de generalización sugiere sobreajuste porque la pérdida de validación se vuelve, en última instancia, significativamente mayor que la pérdida de entrenamiento.
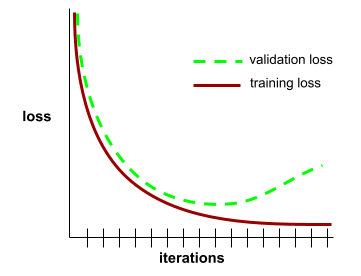
Consulta Generalización en el Curso intensivo de aprendizaje automático para obtener más información.
modelo lineal generalizado
Es una generalización de los modelos de regresión de mínimos cuadrados, que se basan en el ruido gaussiano, para otros tipos de modelos basados en otros tipos de ruido, como el ruido de Poisson o el ruido categórico. Entre los ejemplos de modelos lineales generalizados, se incluyen los siguientes:
- Regresión logística
- regresión de clases múltiples
- Regresión de mínimos cuadrados
Los parámetros de un modelo lineal generalizado se pueden encontrar a través de la optimización convexa.
Los modelos lineales generalizados tienen las siguientes propiedades:
- La predicción promedio del modelo óptimo de regresión de mínimos cuadrados es igual a la etiqueta promedio de los datos de entrenamiento.
- La probabilidad promedio predicha por el modelo óptimo de regresión logística es igual a la etiqueta promedio de los datos de entrenamiento.
La potencia de un modelo lineal generalizado está limitada por sus atributos. A diferencia de un modelo profundo, un modelo lineal generalizado no puede "aprender atributos nuevos".
Texto generado
En general, es el texto que genera un modelo de AA. Cuando se evalúan modelos de lenguaje grandes, algunas métricas comparan el texto generado con el texto de referencia. Por ejemplo, supongamos que intentas determinar la eficacia con la que un modelo de AA traduce del francés al neerlandés. En este caso, ocurre lo siguiente:
- El texto generado es la traducción al neerlandés que genera el modelo de AA.
- El texto de referencia es la traducción al neerlandés que crea un traductor humano (o un software).
Ten en cuenta que algunas estrategias de evaluación no incluyen texto de referencia.
red generativa adversaria (GAN)
Un sistema para crear datos nuevos en el que un generador crea datos y un discriminador determina si los datos creados son válidos o no.
Consulta el curso sobre redes adversarias generativas para obtener más información.
IA generativa
Es un campo transformador emergente sin una definición formal. Dicho esto, la mayoría de los expertos coinciden en que los modelos de IA generativa pueden crear ("generar") contenido que cumpla con todos los siguientes requisitos:
- emergencia compleja,
- coherente
- original
Estos son algunos ejemplos de IA generativa:
- Modelos de lenguaje grandes, que pueden generar texto original sofisticado y responder preguntas
- Modelo de generación de imágenes, que puede producir imágenes únicas.
- Modelos de generación de audio y música, que pueden componer música original o generar voz realista.
- Modelos de generación de video, que pueden generar videos originales.
Algunas tecnologías anteriores, como las LSTM y las RNN, también pueden generar contenido original y coherente. Algunos expertos consideran que estas tecnologías anteriores son IA generativa, mientras que otros creen que la verdadera IA generativa requiere resultados más complejos de los que pueden producir esas tecnologías anteriores.
Compara esto con el AA predictivo.
modelo generativo
Dicho en forma simple, un modelo que realiza una de las siguientes tareas:
- Crea (genera) nuevos ejemplos para el conjunto de datos de entrenamiento. Por ejemplo, un modelo generativo podría crear poesía luego de entrenar con un conjunto de datos de poemas. La parte del generador de una red generativa adversaria entra en esta categoría.
- Determina la probabilidad de que un nuevo ejemplo provenga del conjunto de entrenamiento o se haya creado con el mismo mecanismo que creó al conjunto de entrenamiento. Por ejemplo, luego de entrenar con un conjunto de datos formado por oraciones en inglés, un modelo generativo podría determinar la probabilidad de que una nueva entrada sea una oración válida en inglés.
Un modelo generativo puede, en teoría, discernir la distribución de ejemplos o atributos particulares en un conjunto de datos. Es decir:
p(examples)
Los modelos de aprendizaje no supervisado son generativos.
Compara esto con los modelos discriminativos.
generador
Es el subsistema dentro de una red generativa adversaria que crea nuevos ejemplos.
Compara esto con el modelo discriminativo.
Impureza de Gini
Es una métrica similar a la entropía. Los divisores usan valores derivados de la impureza de Gini o la entropía para componer condiciones para los árboles de decisión de clasificación. La ganancia de información se deriva de la entropía. No existe un término equivalente aceptado universalmente para la métrica derivada de la impureza de Gini. Sin embargo, esta métrica sin nombre es tan importante como la ganancia de información.
La impureza de Gini también se denomina índice de Gini o, simplemente, Gini.
conjunto de datos de referencia
Es un conjunto de datos seleccionados manualmente que capturan la verdad fundamental. Los equipos pueden usar uno o más conjuntos de datos de referencia para evaluar la calidad de un modelo.
Algunos conjuntos de datos de referencia capturan diferentes subdominios de la verdad fundamental. Por ejemplo, un conjunto de datos de referencia para la clasificación de imágenes podría capturar las condiciones de iluminación y la resolución de la imagen.
Respuesta dorada
Una respuesta que se sabe que es buena. Por ejemplo, dada la siguiente instrucción:
2 + 2
La respuesta ideal es la siguiente:
4
Google AI Studio
Es una herramienta de Google que proporciona una interfaz fácil de usar para experimentar con los modelos de lenguaje grandes de Google y crear aplicaciones con ellos. Consulta la página principal de Google AI Studio para obtener más detalles.
GPT (transformador generativo previamente entrenado)
Una familia de modelos de lenguaje grandes basados en Transformer desarrollados por OpenAI.
Las variantes de GPT se pueden aplicar a múltiples modalidades, incluidas las siguientes:
- Generación de imágenes (por ejemplo, ImageGPT)
- Generación de texto a imagen (por ejemplo, DALL-E)
gradient
Vector de las derivadas parciales con respecto a todas las variables independientes. En el aprendizaje automático, el gradiente es el vector de las derivadas parciales de la función del modelo. El gradiente apunta en la dirección del aumento más empinado.
Acumulación de gradientes
Una técnica de propagación hacia atrás que actualiza los parámetros solo una vez por época en lugar de una vez por iteración. Después de procesar cada minilote, la acumulación de gradientes simplemente actualiza un total acumulado de gradientes. Luego, después de procesar el último lote pequeño de la época, el sistema finalmente actualiza los parámetros en función del total de todos los cambios en el gradiente.
La acumulación de gradientes es útil cuando el tamaño del lote es muy grande en comparación con la cantidad de memoria disponible para el entrenamiento. Cuando la memoria es un problema, la tendencia natural es reducir el tamaño del lote. Sin embargo, reducir el tamaño del lote en la retropropagación normal aumenta la cantidad de actualizaciones de parámetros. La acumulación de gradientes permite que el modelo evite problemas de memoria y, al mismo tiempo, se entrene de manera eficiente.
Árboles de decisión impulsados por gradientes (GBT)
Es un tipo de bosque de decisión en el que se cumplen las siguientes condiciones:
- El entrenamiento se basa en la potenciación del gradiente.
- El modelo débil es un árbol de decisión.
Para obtener más información, consulta Árboles de decisión potenciados por gradiente en el curso de Bosques de decisión.
potenciación del gradiente
Es un algoritmo de entrenamiento en el que se entrenan modelos débiles para mejorar de forma iterativa la calidad (reducir la pérdida) de un modelo sólido. Por ejemplo, un modelo débil podría ser un modelo lineal o un modelo de árbol de decisión pequeño. El modelo sólido se convierte en la suma de todos los modelos débiles entrenados anteriormente.
En la forma más simple del boosting de gradientes, en cada iteración, se entrena un modelo débil para predecir el gradiente de pérdida del modelo fuerte. Luego, el resultado del modelo sólido se actualiza restando el gradiente predicho, de manera similar al descenso del gradiente.
Donde:
- $F_{0}$ es el modelo inicial sólido.
- $F_{i+1}$ es el siguiente modelo sólido.
- $F_{i}$ es el modelo sólido actual.
- $\xi$ es un valor entre 0.0 y 1.0 llamado reducción, que es análogo a la tasa de aprendizaje en el descenso del gradiente.
- $f_{i}$ es el modelo débil entrenado para predecir el gradiente de pérdida de $F_{i}$.
Las variaciones modernas del aumento de gradiente también incluyen la segunda derivada (hessiana) de la pérdida en su cálculo.
Los árboles de decisión se suelen usar como modelos débiles en el boosting de gradiente. Consulta árboles de decisión potenciados por gradientes.
Recorte de gradientes
Es un mecanismo que se usa comúnmente para mitigar el problema de gradientes explosivos limitando (recortando) artificialmente el valor máximo de los gradientes cuando se usa el descenso de gradientes para entrenar un modelo.
descenso de gradientes
Técnica matemática para minimizar la pérdida. El descenso de gradientes ajusta de forma iterativa los pesos y los sesgos, y encuentra gradualmente la mejor combinación para minimizar la pérdida.
El descenso del gradiente es más antiguo (mucho más antiguo) que el aprendizaje automático.
Para obtener más información, consulta Regresión lineal: Descenso del gradiente en el Curso intensivo de aprendizaje automático.
gráfico
En TensorFlow, es una especificación de cálculo. Los nodos del grafo representan operaciones. Las conexiones están orientadas y representan el paso del resultado de una operación (un Tensor) como un operando para otra operación. Para visualizar un grafo, usa TensorBoard.
ejecución por grafos
Entorno de programación de TensorFlow en el cual el programa primero construye un grafo y luego ejecuta todo el grafo o una parte de este. La ejecución por grafos es el modo de ejecución predeterminado en TensorFlow 1.x.
Compara esto con la ejecución inmediata.
Política greedy
En el aprendizaje por refuerzo, una política que siempre elige la acción con el retorno esperado más alto.
fundamentación
Es una propiedad de un modelo cuyo resultado se basa en material de origen específico. Por ejemplo, supongamos que proporcionas un libro de texto de física completo como entrada ("contexto") a un modelo de lenguaje grande. Luego, le haces una pregunta de física a ese modelo de lenguaje grande. Si la respuesta del modelo refleja información de ese libro de texto, entonces el modelo está fundamentado en ese libro de texto.Ten en cuenta que un modelo fundamentado no siempre es un modelo fáctico. Por ejemplo, el libro de texto de física de entrada podría contener errores.
Verdad fundamental
Realidad.
Lo que realmente sucedió
Por ejemplo, considera un modelo de clasificación binaria que predice si un estudiante de primer año de universidad se graduará en un plazo de seis años. La verdad fundamental para este modelo es si el estudiante se graduó o no en un plazo de seis años.
sesgo de correspondencia
La tendencia a creer que lo que es verdadero para un individuo, lo es también para todos los miembros de ese grupo Los efectos del sesgo de correspondencia pueden agravarse si se utiliza un muestreo de conveniencia para la recopilación de datos. En una muestra no representativa, puede que se creen atributos que no reflejen la realidad.
Consulta también el sesgo de homogeneidad de los demás y el sesgo endogrupal. Además, consulta Equidad: Tipos de sesgo en el Curso intensivo de aprendizaje automático para obtener más información.
H
alucinación
Producción de resultados que parecen plausibles, pero que son incorrectos desde el punto de vista fáctico por parte de un modelo de IA generativa que pretende hacer una afirmación sobre el mundo real. Por ejemplo, un modelo de IA generativa que afirma que Barack Obama murió en 1865 está alucinando.
hash
En aprendizaje automático, mecanismo para agrupar datos categóricos, especialmente cuando hay una gran cantidad de categorías, pero la cantidad que realmente aparece en el conjunto de datos es comparativamente menor.
Por ejemplo, la Tierra es el hogar de aproximadamente 73,000 especies de árboles. Se podría representar cada una de las 73,000 especies de árboles en 73,000 agrupamientos categóricos diferentes. De forma alternativa, si solo 200 de esas especies arbóreas realmente aparecen en el conjunto de datos, se podría utilizar el hashing para dividir las especies en quizás 500 agrupamientos.
Un solo agrupamiento podría contener varias especies arbóreas. Por ejemplo, con el hashing se podrían colocar baobab y arce rojo (dos especies con genéticas diferentes) en el mismo agrupamiento. En cualquier caso, el hashing sigue siendo una buena manera de mapear grandes conjuntos de categorías en la cantidad seleccionada de agrupamientos. El hashing convierte un atributo categórico con una gran cantidad de valores posibles en una cantidad mucho menor de valores agrupándolos de forma determinista.
Consulta Datos categóricos: Vocabulario y codificación one-hot en el Curso intensivo de aprendizaje automático para obtener más información.
heurística
Es una solución simple y de rápida implementación para un problema. Por ejemplo, "Con una heurística, conseguimos un 86% de exactitud. Cuando cambiamos a una red neuronal profunda, la exactitud llegó al 98%".
Capa oculta
Capa en una red neuronal entre la capa de entrada (las características) y la capa de salida (la predicción). Cada capa oculta consta de una o más neuronas. Por ejemplo, la siguiente red neuronal contiene dos capas ocultas, la primera con tres neuronas y la segunda con dos:
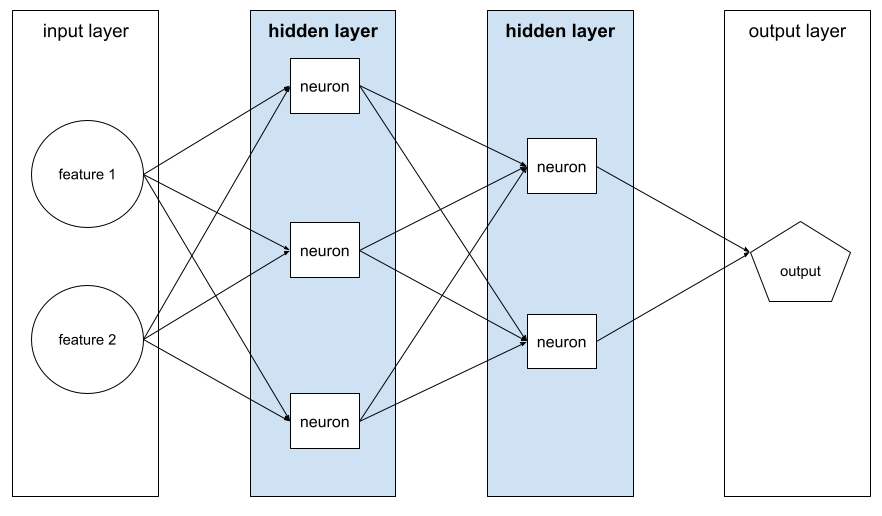
Una red neuronal profunda contiene más de una capa oculta. Por ejemplo, la ilustración anterior es una red neuronal profunda porque el modelo contiene dos capas ocultas.
Consulta Redes neuronales: Nodos y capas ocultas en el Curso intensivo de aprendizaje automático para obtener más información.
agrupamiento jerárquico
Categoría de algoritmos de agrupamiento que crean un árbol de clústeres. El agrupamiento jerárquico es muy adecuado para datos jerárquicos, como por ej., taxonomías botánicas. Existen dos tipos de algoritmos de agrupamiento jerárquico:
- El agrupamiento aglomerado asigna primero cada ejemplo a su propio clúster, luego une los clústeres más cercanos para crear un árbol de jerarquías.
- El agrupamiento en clústeres divisivo agrupa primero todos los ejemplos en un clúster y divide varias veces el clúster en un árbol jerárquico.
Compara esto con el agrupamiento en clústeres basado en centroides.
Consulta Algoritmos de agrupamiento en el curso de Clustering para obtener más información.
Ascenso de colinas
Es un algoritmo para mejorar de forma iterativa ("subir una colina") un modelo de AA hasta que el modelo deje de mejorar ("llegue a la cima de una colina"). La forma general del algoritmo es la siguiente:
- Crea un modelo inicial.
- Crea nuevos modelos candidatos haciendo pequeños ajustes en la forma en que entrenas o ajustas el modelo. Esto puede implicar trabajar con un conjunto de entrenamiento ligeramente diferente o con hiperparámetros diferentes.
- Evalúa los nuevos modelos candidatos y realiza una de las siguientes acciones:
- Si un modelo candidato supera al modelo inicial, ese modelo candidato se convierte en el nuevo modelo inicial. En este caso, repite los pasos 1, 2 y 3.
- Si ningún modelo supera al modelo inicial, significa que llegaste a la cima y debes dejar de realizar iteraciones.
Consulta el Manual de ajuste del aprendizaje profundo para obtener orientación sobre el ajuste de hiperparámetros. Consulta los módulos de datos del Curso intensivo de aprendizaje automático para obtener orientación sobre la ingeniería de atributos.
Pérdida de bisagra
Es una familia de funciones de pérdida para la clasificación diseñadas para encontrar el límite de decisión lo más distante posible de cada ejemplo de entrenamiento, para así maximizar el margen entre los ejemplos y el límite. Las KSVM usan la pérdida de bisagra (o un atributo relacionado, como la pérdida de bisagra al cuadrado). Para la clasificación binaria, la función de pérdida de bisagra se define de la siguiente manera:
donde y es la etiqueta real, ya sea -1 o +1, y y' es el resultado sin procesar del modelo de clasificación:
En consecuencia, un gráfico de la pérdida de bisagra en comparación con (y * y') se ve de la siguiente manera:

Sesgo histórico
Es un tipo de sesgo que ya existe en el mundo y que se incorporó a un conjunto de datos. Estos sesgos tienden a reflejar los estereotipos culturales, las desigualdades demográficas y los prejuicios existentes contra ciertos grupos sociales.
Por ejemplo, considera un modelo de clasificación que predice si un solicitante de préstamo incumplirá o no su préstamo, y que se entrenó con datos históricos de incumplimiento de préstamos de la década de 1980 de bancos locales en dos comunidades diferentes. Si los solicitantes anteriores de la comunidad A tenían seis veces más probabilidades de incumplir sus préstamos que los solicitantes de la comunidad B, el modelo podría aprender un sesgo histórico que lo lleve a aprobar menos préstamos en la comunidad A, incluso si las condiciones históricas que generaron las tasas de incumplimiento más altas de esa comunidad ya no son relevantes.
Consulta Equidad: Tipos de sesgo en el Curso intensivo de aprendizaje automático para obtener más información.
datos de exclusión
Ejemplos que de manera intencional no se usan (se "excluyen") durante el entrenamiento. El conjunto de datos de validación y el conjunto de datos de prueba son ejemplos de datos de exclusión. Los datos de exclusión ayudan a evaluar la capacidad del modelo para realizar generalizaciones con respecto a datos que no sean los datos con los que se entrenó. La pérdida en el conjunto de datos de exclusión proporciona una mejor estimación de la pérdida en un conjunto de datos nunca antes vistos que la pérdida en el conjunto de entrenamiento.
host
Cuando se entrena un modelo de AA en chips aceleradores (GPUs o TPUs), la parte del sistema que controla lo siguiente:
- El flujo general del código
- Es la extracción y transformación de la canalización de entrada.
Por lo general, el host se ejecuta en una CPU, no en un chip acelerador; el dispositivo manipula tensores en los chips aceleradores.
evaluación humana
Proceso en el que personas juzgan la calidad del resultado de un modelo de AA; por ejemplo, personas bilingües que juzgan la calidad de un modelo de traducción de AA. La evaluación humana es especialmente útil para juzgar modelos que no tienen una respuesta correcta.
Compara esto con la evaluación automática y la evaluación del autorrater.
con interacción humana (HITL)
Es una expresión idiomática definida de forma vaga que podría significar cualquiera de las siguientes opciones:
- Una política de visualización del resultado de la IA generativa de forma crítica o escéptica
- Es una estrategia o un sistema para garantizar que las personas ayuden a dar forma, evaluar y perfeccionar el comportamiento de un modelo. Mantener a un humano en el circuito permite que la IA se beneficie tanto de la inteligencia artificial como de la humana. Por ejemplo, un sistema en el que una IA genera código que luego revisan los ingenieros de software es un sistema con participación humana.
hiperparámetro
Son las variables que tú o un servicio de ajuste de hiperparámetros ajustan durante las ejecuciones sucesivas del entrenamiento de un modelo. Por ejemplo, la tasa de aprendizaje es un hiperparámetro. Podrías establecer la tasa de aprendizaje en 0.01 antes de una sesión de entrenamiento. Si determinas que 0.01 es demasiado alto, podrías establecer la tasa de aprendizaje en 0.003 para la próxima sesión de entrenamiento.
En cambio, los parámetros son los diversos pesos y el sesgo que el modelo aprende durante el entrenamiento.
Consulta Regresión lineal: Hiperparámetros en el Curso intensivo de aprendizaje automático para obtener más información.
hiperplano
Es un límite que separa un espacio en dos subespacios. Por ejemplo, una línea es un hiperplano en dos dimensiones y un plano es un hiperplano en tres dimensiones. En el aprendizaje automático, un hiperplano suele ser el límite que separa un espacio de alta dimensión. Las máquinas de vectores soporte de Kernel usan hiperplanos para separar las clases positivas de las negativas, frecuentemente en un espacio de dimensiones muy altas.
I
i.i.d.
Abreviatura de independiente e idénticamente distribuido.
reconocimiento de imágenes
Proceso que clasifica objetos, patrones o conceptos en una imagen. El reconocimiento de imágenes también se conoce como clasificación de imágenes.
conjunto de datos desequilibrados
Sinónimo de conjunto de datos con desequilibrio de clases.
Sesgo implícito
Hacer una asociación o una suposición, de forma automática, con base en los modelos mentales o los recuerdos de cada uno. El sesgo implícito puede afectar los siguientes aspectos:
- Cómo se recopilan y clasifican los datos
- Cómo se diseñan y desarrollan los sistemas de aprendizaje automático
Por ejemplo, cuando se crea un modelo de clasificación para identificar fotos de bodas, un ingeniero puede utilizar como atributo la presencia de un vestido blanco en la foto. Sin embargo, los vestidos blancos han sido habituales solo durante ciertas épocas y en ciertas culturas.
Consulta también sesgo de confirmación.
imputación
Es la forma abreviada de imputación de valores.
Incompatibilidad de métricas de equidad
La idea de que algunas nociones de equidad son mutuamente incompatibles y no se pueden satisfacer de manera simultánea. Como resultado, no existe una sola métrica universal para cuantificar la equidad que se pueda aplicar a todos los problemas de AA.
Si bien esto puede parecer desalentador, la incompatibilidad de las métricas de equidad no implica que los esfuerzos en pos de la equidad sean infructuosos. En cambio, sugiere que la equidad debe definirse de forma contextual para un problema de AA determinado, con el objetivo de evitar los daños específicos de sus casos de uso.
Consulta "On the (im)possibility of fairness" para obtener un análisis más detallado sobre la incompatibilidad de las métricas de equidad.
aprendizaje en contexto
Sinónimo de instrucciones con ejemplos limitados.
independiente e idénticamente distribuido (i.i.d.)
Son datos extraídos de una distribución que no cambia y en la que cada valor extraído no depende de los valores que se extrajeron anteriormente. Un i.i.d. es el gas ideal del aprendizaje automático; es una construcción matemática útil, pero casi nunca se encuentra exactamente en el mundo real. Por ejemplo, la distribución de los visitantes de una página web pueden ser datos i.i.d. en una ventana de tiempo breve, es decir, la distribución no cambia durante esa ventana breve y la visita de una persona por lo general es independiente de la visita de otra. Sin embargo, si amplías ese período, es posible que aparezcan diferencias estacionales en los visitantes de la página web.
Consulta también no estacionariedad.
equidad individual
Es una métrica de equidad que verifica si las personas similares se clasifican de manera similar. Por ejemplo, la Academia Brobdingnagian podría querer satisfacer la equidad individual garantizando que dos estudiantes con calificaciones idénticas y resultados de pruebas estandarizadas tengan la misma probabilidad de ser admitidos.
Ten en cuenta que la equidad individual depende por completo de cómo definas la "similitud" (en este caso, las calificaciones y los resultados de las pruebas), y puedes correr el riesgo de introducir nuevos problemas de equidad si tu métrica de similitud omite información importante (como el rigor del plan de estudios de un estudiante).
Consulta "Fairness Through Awareness" para obtener un análisis más detallado de la equidad individual.
Inferencia
En el aprendizaje automático tradicional, el proceso de realizar predicciones aplicando un modelo entrenado a ejemplos sin etiqueta. Consulta Aprendizaje supervisado en el curso Introducción al AA para obtener más información.
En los modelos de lenguaje grandes, la inferencia es el proceso de usar un modelo entrenado para generar una respuesta a una instrucción de entrada.
En estadística, la inferencia tiene un significado algo diferente. Consulta el artículo de Wikipedia sobre inferencia estadística para obtener más detalles.
ruta de inferencia
En un árbol de decisión, durante la inferencia, la ruta que toma un ejemplo particular desde la raíz hasta otras condiciones, que termina con una hoja. Por ejemplo, en el siguiente árbol de decisión, las flechas más gruesas muestran la ruta de inferencia para un ejemplo con los siguientes valores de atributos:
- x = 7
- y = 12
- z = -3
La ruta de inferencia en la siguiente ilustración pasa por tres condiciones antes de llegar a la hoja (Zeta).
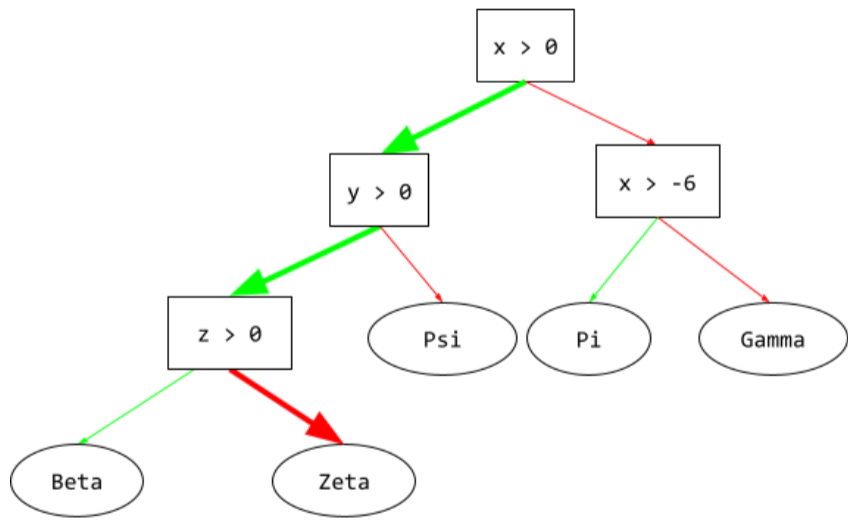
Las tres flechas gruesas muestran la ruta de inferencia.
Consulta Árboles de decisión en el curso de Bosques de decisión para obtener más información.
Ganancia de información
En los bosques de decisión, es la diferencia entre la entropía de un nodo y la suma ponderada (según la cantidad de ejemplos) de la entropía de sus nodos secundarios. La entropía de un nodo es la entropía de los ejemplos en ese nodo.
Por ejemplo, considera los siguientes valores de entropía:
- entropía del nodo principal = 0.6
- entropía de un nodo secundario con 16 ejemplos relevantes = 0.2
- entropía de otro nodo secundario con 24 ejemplos relevantes = 0.1
Por lo tanto, el 40% de los ejemplos se encuentran en un nodo secundario y el 60% en el otro. Por lo tanto:
- Suma de entropía ponderada de los nodos secundarios = (0.4 * 0.2) + (0.6 * 0.1) = 0.14
Por lo tanto, la ganancia de información es la siguiente:
- Ganancia de información = entropía del nodo principal - suma ponderada de la entropía de los nodos secundarios
- ganancia de información = 0.6 - 0.14 = 0.46
La mayoría de los divisores buscan crear condiciones que maximicen la ganancia de información.
sesgo endogrupal
Mostrar parcialidad por el propio grupo o las propias características Si quienes prueban o evalúan el modelo son amigos, familiares o colegas del desarrollador de aprendizaje automático, el sesgo endogrupal puede invalidar las pruebas del producto o el conjunto de datos.
El sesgo endogrupal es una forma de sesgo de correspondencia. Consulta también el sesgo de homogeneidad de los demás.
Consulta Equidad: Tipos de sesgo en el Curso intensivo de aprendizaje automático para obtener más información.
generador de entrada
Es un mecanismo por el cual se cargan datos en una red neuronal.
Un generador de entrada se puede considerar como un componente responsable de procesar datos sin procesar en tensores que se iteran para generar lotes para el entrenamiento, la evaluación y la inferencia.
Capa de entrada
La capa de una red neuronal que contiene el vector de atributos. Es decir, la capa de entrada proporciona ejemplos para el entrenamiento o la inferencia. Por ejemplo, la capa de entrada de la siguiente red neuronal consta de dos atributos:
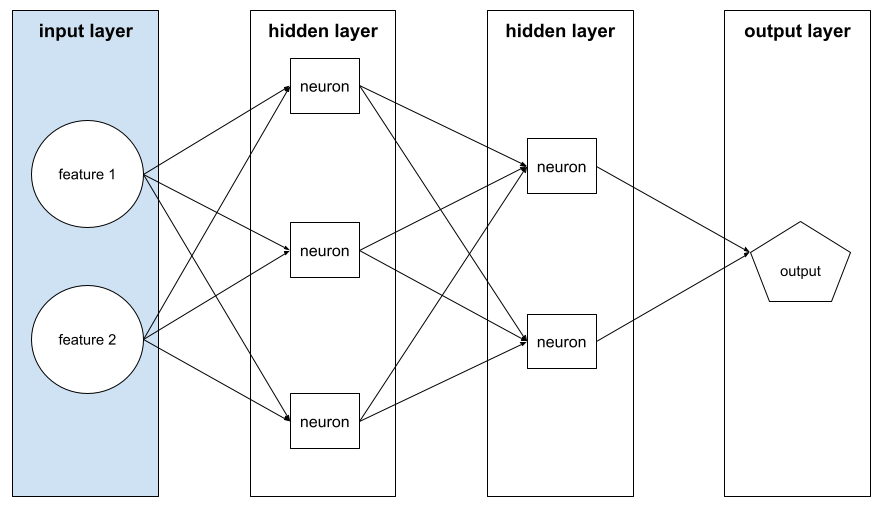
condición de conjunto
En un árbol de decisión, una condición que prueba la presencia de un elemento en un conjunto de elementos. Por ejemplo, la siguiente es una condición dentro del conjunto:
house-style in [tudor, colonial, cape]
Durante la inferencia, si el valor del atributo de estilo de la casa es tudor, colonial o cape, esta condición se evalúa como Sí. Si el valor del atributo de estilo de la casa es otro (por ejemplo, ranch), esta condición se evalúa como No.
Por lo general, las condiciones de conjunto generan árboles de decisión más eficientes que las condiciones que prueban las características codificadas como one-hot.
instancia
Sinónimo de ejemplo.
Ajuste de instrucciones
Es una forma de ajuste que mejora la capacidad de un modelo de IA generativa para seguir instrucciones. El ajuste de instrucciones implica entrenar un modelo en una serie de instrucciones, que suelen abarcar una amplia variedad de tareas. Luego, el modelo ajustado con instrucciones tiende a generar respuestas útiles a instrucciones sin ejemplos en una variedad de tareas.
Comparar y contrastar con lo siguiente:
interpretabilidad
Es la capacidad de explicar o presentar el razonamiento de un modelo de AA en términos comprensibles para los humanos.
Por ejemplo, la mayoría de los modelos de regresión lineal son altamente interpretables. (solo necesitas ver los pesos entrenados para cada función). Los bosques de decisión también son altamente interpretables. Sin embargo, algunos modelos requieren una visualización sofisticada para convertirse en interpretables.
Puedes usar la Herramienta de interpretabilidad del aprendizaje (LIT) para interpretar modelos de AA.
Acuerdo entre evaluadores
Es una medición de la frecuencia con la que los evaluadores humanos coinciden cuando realizan una tarea. Si los evaluadores no están de acuerdo, es posible que deban mejorarse las instrucciones de la tarea. En algunas ocasiones, también se denomina acuerdo entre anotadores o fiabilidad entre evaluadores. Consulta también el coeficiente kappa de Cohen, que es una de las mediciones de acuerdo entre evaluadores más populares.
Consulta Datos categóricos: Problemas comunes en el Curso intensivo de aprendizaje automático para obtener más información.
Intersección sobre unión (IoU)
Es la intersección de dos conjuntos dividida por su unión. En las tareas de detección de imágenes del aprendizaje automático, el IoU se usa para medir la precisión del cuadro de límite previsto por el modelo en relación con el cuadro de límite de la verdad fundamental. En este caso, el IoU para los dos cuadros es la proporción entre el área superpuesta y el área total, y su valor oscila entre 0 (sin superposición del cuadro de límite previsto y el cuadro de límite de verdad fundamental) y 1 (el cuadro de límite previsto y el cuadro de límite de verdad fundamental tienen exactamente las mismas coordenadas).
Por ejemplo, en la siguiente imagen:
- El cuadro delimitador predicho (las coordenadas que delimitan dónde el modelo predice que se encuentra la mesa de noche en la pintura) se muestra en color púrpura.
- El cuadro de límite de verdad fundamental (las coordenadas que delimitan dónde se encuentra realmente la mesa de noche en la pintura) se muestra en verde.
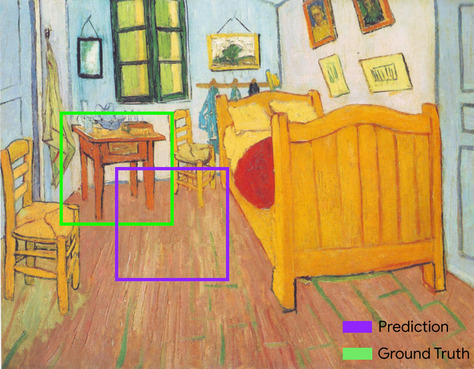
Aquí, la intersección de los cuadros de límite para la predicción y la verdad fundamental (a continuación, a la izquierda) es 1, y la unión de los cuadros de límite para la predicción y la verdad fundamental (a continuación, a la derecha) es 7, por lo que el IoU es \(\frac{1}{7}\).
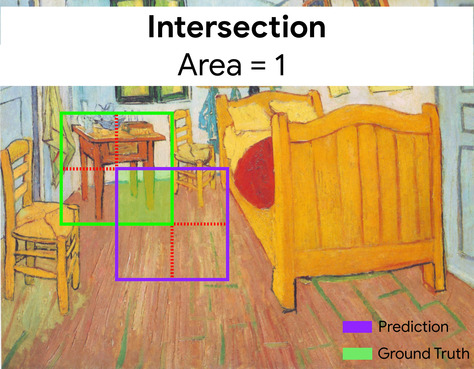
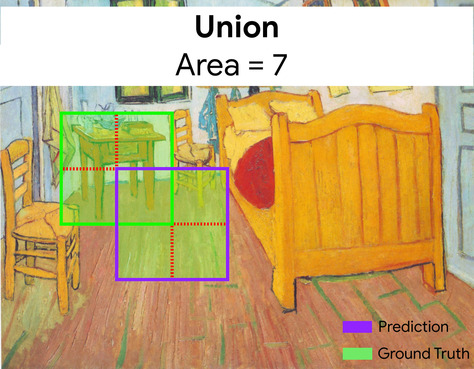
IoU
Abreviatura de intersección sobre unión.
matriz de elementos
En los sistemas de recomendación, una matriz de vectores de embedding generados por la factorización de matrices que contiene indicadores latentes sobre cada elemento. Cada fila de la matriz de elementos contiene el valor de un solo atributo latente para todos los elementos. Por ejemplo, considera un sistema de recomendación de películas. Cada columna en la matriz de elementos representa una película. Las señales latentes pueden representar géneros o pueden ser señales más complicadas de interpretar que impliquen interacciones complejas entre género, valoración, antigüedad de la película y otros factores.
La matriz de elementos tiene la misma cantidad de columnas que la matriz objetivo que se factoriza. Por ejemplo, en un modelo de recomendación de películas que evalúa 10,000 títulos de películas, la matriz de elementos tendrá 10,000 columnas.
elementos
En un sistema de recomendación, las entidades que recomienda un sistema. Por ejemplo, para una tienda de videos los elementos son videos, mientras que para una tienda de libros los elementos son libros.
iteración
Es una sola actualización de los parámetros de un modelo (los pesos y los sesgos del modelo) durante el entrenamiento. El tamaño del lote determina cuántos ejemplos procesa el modelo en una sola iteración. Por ejemplo, si el tamaño del lote es 20, el modelo procesa 20 ejemplos antes de ajustar los parámetros.
Cuando se entrena una red neuronal, una sola iteración implica los siguientes dos pases:
- Pase hacia adelante para evaluar la pérdida en un solo lote.
- Un pase hacia atrás (propagación hacia atrás) para ajustar los parámetros del modelo según la pérdida y la tasa de aprendizaje
Consulta Descenso del gradiente en el Curso intensivo de aprendizaje automático para obtener más información.
J
JAX
Una biblioteca de procesamiento de arrays que combina XLA (Accelerated Linear Algebra) y diferenciación automática para la computación numérica de alto rendimiento. JAX proporciona una API simple y potente para escribir código numérico acelerado con transformaciones componibles. JAX proporciona funciones como las siguientes:
grad(diferenciación automática)jit(compilación justo a tiempo)vmap(vectorización o procesamiento por lotes automáticos)pmap(paralelización)
JAX es un lenguaje para expresar y componer transformaciones de código numérico, análogo, pero mucho más amplio en alcance, a la biblioteca NumPy de Python. (De hecho, la biblioteca .numpy en JAX es una versión funcionalmente equivalente, pero completamente reescrita de la biblioteca NumPy de Python).
JAX es especialmente adecuado para acelerar muchas tareas de aprendizaje automático, ya que transforma los modelos y los datos en un formato adecuado para el paralelismo en las GPU y los chips aceleradores de TPU.
Flax, Optax, Pax y muchas otras bibliotecas se compilan en la infraestructura de JAX.
K
Keras
Es una API de aprendizaje automático de Python muy popular. Keras se ejecuta en varios frameworks de aprendizaje profundo, incluido TensorFlow, donde está disponible como tf.keras.
Máquinas de vectores soporte de Kernel (KSVM)
Es un algoritmo de clasificación que busca maximizar el margen entre las clases positivas y las clases negativas proyectando los vectores de datos de entrada a un espacio de dimensiones más altas. Por ejemplo, considera un problema de clasificación en el que el conjunto de datos de entrada tiene cien atributos. Para maximizar el margen entre las clases positivas y negativas, una KSVM puede asignar internamente esos atributos a un espacio de un millón de dimensiones. Las KSVM usan una función de pérdida denominada pérdida de bisagra.
puntos clave
Son las coordenadas de elementos particulares en una imagen. Por ejemplo, para un modelo de reconocimiento de imágenes que distingue las especies de flores, los puntos clave podrían ser el centro de cada pétalo, el tallo, el estambre, etcétera.
Validación cruzada de k-fold
Es un algoritmo para predecir la capacidad de un modelo de generalizar datos nuevos. La k en k-fold hace referencia a la cantidad de grupos iguales en los que divides los ejemplos de un conjunto de datos; es decir, entrenas y pruebas tu modelo k veces. En cada ronda de entrenamiento y prueba, un grupo diferente es el conjunto de prueba, y todos los grupos restantes se convierten en el conjunto de entrenamiento. Después de k rondas de entrenamiento y pruebas, calculas la media y la desviación estándar de las métricas de prueba elegidas.
Por ejemplo, supongamos que tu conjunto de datos consta de 120 ejemplos. Supongamos que decides establecer k en 4. Por lo tanto, después de mezclar los ejemplos, divide el conjunto de datos en cuatro grupos iguales de 30 ejemplos y realiza cuatro rondas de entrenamiento y prueba:
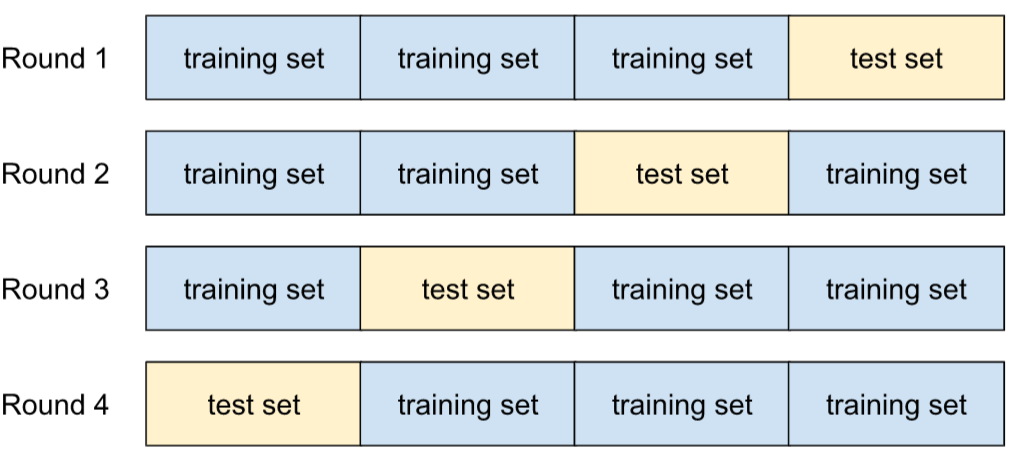
Por ejemplo, el error cuadrático medio (ECM) podría ser la métrica más significativa para un modelo de regresión lineal. Por lo tanto, calcularías la media y la desviación estándar del ECM en las cuatro rondas.
k-means
Algoritmo de agrupamiento en clústeres popular que agrupa ejemplos en el aprendizaje no supervisado. El algoritmo k-means hace básicamente lo siguiente:
- Determina de forma iterativa los mejores puntos centrales k (conocidos como centroides).
- Asigna cada ejemplo al centroide más cercano. Los ejemplos más cercanos al mismo centroide pertenecen al mismo grupo.
El algoritmo k-means selecciona las ubicaciones del centroide para minimizar el cuadrado acumulativo de las distancias desde cada ejemplo hasta su centroide más cercano.
Por ejemplo, considera el siguiente diagrama de altura y anchura de perro:

Si k=3, el algoritmo k-means determinará tres centroides. Cada ejemplo se asigna a su centroide más cercano, lo que genera tres grupos:

Imagina que un fabricante quiere determinar los tamaños ideales para los suéteres pequeños, medianos y grandes para perros. Los tres centroides identifican la altura y el ancho medios de cada perro en ese clúster. Por lo tanto, el fabricante probablemente debería basar los tamaños de los suéteres en esos tres centroides. Ten en cuenta que, por lo general, el centroide de un clúster no es un ejemplo del clúster.
Las ilustraciones anteriores muestran el algoritmo de k-means para ejemplos con solo dos atributos (altura y ancho). Ten en cuenta que k-means puede agrupar ejemplos en función de muchos atributos.
Consulta ¿Qué es el agrupamiento en clústeres de k-means? en el curso de Clustering para obtener más información.
k-median
Algoritmo de agrupamiento estrechamente relacionado con k-means. La diferencia práctica entre los dos es la siguiente:
- En k-means, los centroides se determinan minimizando la suma de los cuadrados de la distancia entre un centroide candidato y cada uno de sus ejemplos.
- En k-median, los centroides se determinan minimizando la suma de la distancia entre un centroide candidato y cada uno de sus ejemplos.
Ten en cuenta que las definiciones de distancia también son diferentes:
- k-means se basa en la distancia euclidiana del centroide a un ejemplo. (En dos dimensiones, la distancia euclidiana significa usar el teorema de Pitágoras para calcular la hipotenusa). Por ejemplo, la distancia de k-means entre (2,2) y (5,-2) sería:
- k-median se basa en la distancia Manhattan del centroide a un ejemplo. Esta distancia es la suma de los deltas absolutos en cada dimensión. Por ejemplo, la distancia k-mediana entre (2,2) y (5,-2) sería:
L
Regularización L0
Es un tipo de regularización que penaliza la cantidad total de pesos distintos de cero en un modelo. Por ejemplo, un modelo con 11 pesos distintos de cero se penalizaría más que un modelo similar con 10 pesos distintos de cero.
A veces, la regularización L0 se denomina regularización de norma L0.
Pérdida L1
Una función de pérdida que calcula el valor absoluto de la diferencia entre los valores de la etiqueta real y los valores que predice un modelo. Por ejemplo, aquí se muestra el cálculo de la pérdida L1 para un lote de cinco ejemplos:
| Valor real del ejemplo | Valor predicho del modelo | Valor absoluto del delta |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 3 |
| 4 | 6 | 2 |
| 9 | 8 | 1 |
| 8 = pérdida L1 | ||
La pérdida L1 es menos sensible a los valores atípicos que la pérdida L2.
El error absoluto medio es la pérdida promedio de L1 por ejemplo.
Consulta Regresión lineal: Pérdida en el Curso intensivo de aprendizaje automático para obtener más información.
Regularización L1
Tipo de regularización que penaliza los pesos en proporción a la suma del valor absoluto de los pesos. La regularización L1 ayuda a llevar los pesos de los atributos irrelevantes o poco relevantes a exactamente 0. Una característica con un peso de 0 se quita del modelo de manera efectiva.
Compara esto con la regularización L2.
Pérdida L2
Es una función de pérdida que calcula el cuadrado de la diferencia entre los valores de la etiqueta real y los valores que predice un modelo. Por ejemplo, aquí se muestra el cálculo de la pérdida de L2 para un lote de cinco ejemplos:
| Valor real del ejemplo | Valor predicho del modelo | Cuadrado de delta |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 9 |
| 4 | 6 | 4 |
| 9 | 8 | 1 |
| 16 = pérdida L2 | ||
Debido al componente cuadrático, la pérdida L2 amplifica la influencia de los valores atípicos. Es decir, la pérdida L2 reacciona de manera más severa a las predicciones incorrectas que la pérdida L1. Por ejemplo, la pérdida de L1 para el lote anterior sería de 8 en lugar de 16. Ten en cuenta que un solo valor atípico representa 9 de los 16.
Los modelos de regresión suelen usar la pérdida L2 como función de pérdida.
El error cuadrático medio es la pérdida promedio de L2 por ejemplo. La pérdida al cuadrado es otro nombre para la pérdida L2.
Para obtener más información, consulta Regresión logística: Pérdida y regularización en el Curso intensivo de aprendizaje automático.
Regularización L2
Tipo de regularización que penaliza los pesos en proporción a la suma de los cuadrados de los pesos. La regularización L2 ayuda a llevar los pesos de valores atípicos (aquellos con valores negativos bajos o positivos altos) más cerca del 0, pero no exactamente a ese número. Los atributos con valores muy cercanos a 0 permanecen en el modelo, pero no influyen mucho en su predicción.
La regularización L2 siempre mejora la generalización en los modelos lineales.
Compara esto con la regularización L1.
Consulta Sobreajuste: Regularización L2 en el Curso intensivo de aprendizaje automático para obtener más información.
etiqueta
En el aprendizaje automático supervisado, la parte de "respuesta" o "resultado" de un ejemplo.
Cada ejemplo etiquetado consta de uno o más atributos y una etiqueta. Por ejemplo, en un conjunto de datos de detección de spam, la etiqueta probablemente sería "es spam" o "no es spam". En un conjunto de datos de lluvia, la etiqueta podría ser la cantidad de lluvia que cayó durante un período determinado.
Consulta Aprendizaje supervisado en Introducción al aprendizaje automático para obtener más información.
ejemplo etiquetado
Es un ejemplo que contiene uno o más atributos y una etiqueta. Por ejemplo, en la siguiente tabla, se muestran tres ejemplos etiquetados de un modelo de valuación de casas, cada uno con tres atributos y una etiqueta:
| Cantidad de dormitorios | Cantidad de baños | Antigüedad de la casa | Precio de la casa (etiqueta) |
|---|---|---|---|
| 3 | 2 | 15 | USD 345,000 |
| 2 | 1 | 72 | USD 179,000 |
| 4 | 2 | 34 | USD 392,000 |
En el aprendizaje automático supervisado, los modelos se entrenan con ejemplos etiquetados y realizan predicciones sobre ejemplos sin etiqueta.
Compara el ejemplo etiquetado con los ejemplos sin etiquetar.
Consulta Aprendizaje supervisado en Introducción al aprendizaje automático para obtener más información.
Filtración de etiquetas
Es una falla en el diseño del modelo en la que un atributo es un proxy de la etiqueta. Por ejemplo, considera un modelo de clasificación binaria que predice si un cliente potencial comprará un producto en particular.
Supongamos que uno de los atributos del modelo es un valor booleano llamado SpokeToCustomerAgent. Supongamos, además, que solo se asigna un agente de atención al cliente después de que el cliente potencial haya comprado el producto. Durante el entrenamiento, el modelo aprenderá rápidamente la asociación entre SpokeToCustomerAgent y la etiqueta.
Consulta Supervisión de canalizaciones en el Curso intensivo de aprendizaje automático para obtener más información.
lambda
Sinónimo de tasa de regularización.
Lambda es un término sobrecargado. Aquí nos referimos a la definición del término dentro de la regularización.
LaMDA (Language Model for Dialogue Applications)
Un modelo de lenguaje grande basado en Transformer desarrollado por Google y entrenado con un gran conjunto de datos de diálogo que puede generar respuestas conversacionales realistas.
LaMDA: nuestra innovadora tecnología conversacional proporciona una descripción general.
puntos de referencia
Sinónimo de puntos clave.
modelo de lenguaje
Un modelo que estima la probabilidad de que un token o una secuencia de tokens aparezcan en una secuencia más larga de tokens.
Para obtener más información, consulta ¿Qué es un modelo de lenguaje? en el Curso intensivo de aprendizaje automático.
modelo de lenguaje grande
Como mínimo, un modelo de lenguaje que tenga una gran cantidad de parámetros. De manera más informal, cualquier modelo de lenguaje basado en Transformer, como Gemini o GPT.
Consulta Modelos de lenguaje grandes (LLM) en el Curso intensivo de aprendizaje automático para obtener más información.
latencia
Es el tiempo que tarda un modelo en procesar la entrada y generar una respuesta. Una respuesta de latencia alta tarda más en generarse que una respuesta de latencia baja.
Entre los factores que influyen en la latencia de los modelos de lenguaje grandes, se incluyen los siguientes:
- Longitudes de los tokens de entrada y salida
- Complejidad del modelo
- La infraestructura en la que se ejecuta el modelo
La optimización de la latencia es fundamental para crear aplicaciones responsivas y fáciles de usar.
espacio latente
Sinónimo de espacio de embedding.
oculta
Es un conjunto de neuronas en una red neuronal. A continuación, se describen tres tipos comunes de capas:
- La capa de entrada, que proporciona valores para todos los atributos.
- Una o más capas ocultas, que encuentran relaciones no lineales entre los atributos y la etiqueta
- La capa de salida, que proporciona la predicción.
Por ejemplo, en la siguiente ilustración, se muestra una red neuronal con una capa de entrada, dos capas ocultas y una capa de salida:
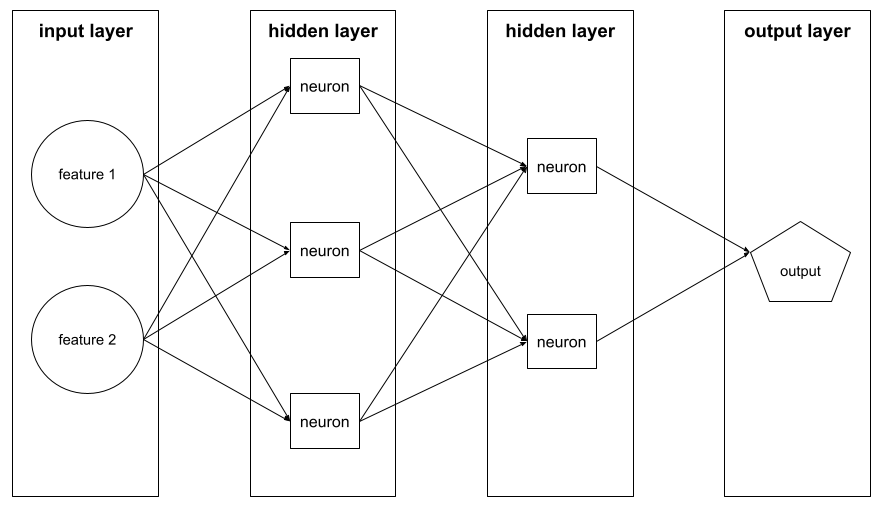
En TensorFlow, las capas también son funciones de Python que toman tensores y opciones de configuración como entrada y producen otros tensores como resultado.
API de Layers (tf.layers)
API de TensorFlow para construir una red neuronal profunda como una composición de capas. La API de Layers te permite compilar diferentes tipos de capas, como las siguientes:
tf.layers.Densepara una capa completamente conectadatf.layers.Conv2Dpara una capa convolucional
La API de Layers sigue las convenciones de la API de capas de Keras. Esto significa que, aparte de un prefijo diferente, todos los atributos de la API de Layers tienen los mismos nombres y firmas que sus contrapartes en la API de Layers de Keras.
hoja
Cualquier extremo en un árbol de decisión. A diferencia de una condición, una hoja no realiza una prueba. Más bien, una hoja es una predicción posible. Una hoja también es el nodo terminal de una ruta de inferencia.
Por ejemplo, el siguiente árbol de decisión contiene tres hojas:
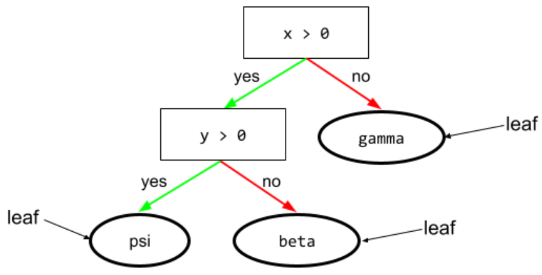
Consulta Árboles de decisión en el curso de Bosques de decisión para obtener más información.
Herramienta de interpretabilidad de aprendizaje (LIT)
Es una herramienta visual e interactiva para comprender modelos y visualizar datos.
Puedes usar LIT de código abierto para interpretar modelos o visualizar datos tabulares, de imagen y de texto.
tasa de aprendizaje
Es un número de punto flotante que le indica al algoritmo de descenso de gradientes con qué intensidad debe ajustar los pesos y las tendencias en cada iteración. Por ejemplo, una tasa de aprendizaje de 0.3 ajustaría los pesos y las tendencias tres veces más que una tasa de aprendizaje de 0.1.
La tasa de aprendizaje es un hiperparámetro fundamental. Si estableces la tasa de aprendizaje demasiado baja, el entrenamiento demorará demasiado. Si estableces la tasa de aprendizaje demasiado alta, el descenso de gradientes suele tener problemas para alcanzar la convergencia.
Consulta Regresión lineal: Hiperparámetros en el Curso intensivo de aprendizaje automático para obtener más información.
Regresión de mínimos cuadrados
Es un modelo de regresión lineal entrenado minimizando la pérdida L2.
Distancia de Levenshtein
Una métrica de distancia de edición que calcula la menor cantidad de operaciones de eliminación, inserción y sustitución necesarias para cambiar una palabra por otra. Por ejemplo, la distancia de Levenshtein entre las palabras "corazón" y "dardos" es tres porque las siguientes tres ediciones son los cambios mínimos para convertir una palabra en la otra:
- heart → deart (sustituir la "h" por la "d")
- deart → dart (se borra la letra "e")
- dart → darts (insertar "s")
Ten en cuenta que la secuencia anterior no es la única ruta de tres ediciones.
linear
Es una relación entre dos o más variables que se puede representar únicamente a través de la suma y la multiplicación.
La gráfica de una relación lineal es una línea.
Compara esto con no lineal.
modelo lineal
Un modelo que asigna un peso por atributo para realizar predicciones. (Los modelos lineales también incorporan un sesgo). Por el contrario, la relación de las características con las predicciones en los modelos profundos suele ser no lineal.
Los modelos lineales suelen ser más fáciles de entrenar y más interpretables que los modelos profundos. Sin embargo, los modelos profundos pueden aprender relaciones complejas entre los atributos.
La regresión lineal y la regresión logística son dos tipos de modelos lineales.
regresión lineal
Es un tipo de modelo de aprendizaje automático en el que se cumplen las siguientes condiciones:
- El modelo es un modelo lineal.
- La predicción es un valor de punto flotante. (Esta es la parte de la regresión de la regresión lineal).
Compara la regresión lineal con la regresión logística. Además, compara la regresión con la clasificación.
Consulta Regresión lineal en el Curso intensivo de aprendizaje automático para obtener más información.
LIT
Es la abreviatura de la Herramienta de interpretabilidad de aprendizaje (LIT), que antes se conocía como Herramienta de interpretabilidad del lenguaje.
LLM
Abreviatura de modelo de lenguaje grande.
Evaluaciones de LLM
Es un conjunto de métricas y comparativas para evaluar el rendimiento de los modelos de lenguaje grandes (LLM). A un alto nivel, las evaluaciones de LLM hacen lo siguiente:
- Ayudar a los investigadores a identificar áreas en las que los LLM necesitan mejorar
- Son útiles para comparar diferentes LLM y determinar cuál es el mejor para una tarea en particular.
- Ayudar a garantizar que los LLMs sean seguros y éticos para su uso
Consulta Modelos de lenguaje extenso (LLM) en el Curso intensivo de aprendizaje automático para obtener más información.
regresión logística
Es un tipo de modelo de regresión que predice una probabilidad. Los modelos de regresión logística tienen las siguientes características:
- La etiqueta es categórica. El término regresión logística suele referirse a la regresión logística binaria, es decir, a un modelo que calcula probabilidades para etiquetas con dos valores posibles. Una variante menos común, la regresión logística multinomial, calcula las probabilidades de las etiquetas con más de dos valores posibles.
- La función de pérdida durante el entrenamiento es la pérdida logística. (Se pueden colocar varias unidades de pérdida logarítmica en paralelo para las etiquetas con más de dos valores posibles).
- El modelo tiene una arquitectura lineal, no una red neuronal profunda. Sin embargo, el resto de esta definición también se aplica a los modelos profundos que predicen probabilidades para las etiquetas categóricas.
Por ejemplo, considera un modelo de regresión logística que calcula la probabilidad de que un correo electrónico de entrada sea spam o no spam. Durante la inferencia, supongamos que el modelo predice 0.72. Por lo tanto, el modelo estima lo siguiente:
- Hay un 72% de probabilidades de que el correo electrónico sea spam.
- Hay un 28% de probabilidades de que el correo electrónico no sea spam.
Un modelo de regresión logística usa la siguiente arquitectura de dos pasos:
- El modelo genera una predicción sin procesar (y') aplicando una función lineal de los atributos de entrada.
- El modelo usa esa predicción sin procesar como entrada para una función sigmoidea, que convierte la predicción sin procesar en un valor entre 0 y 1, sin incluir estos valores.
Al igual que cualquier modelo de regresión, un modelo de regresión logística predice un número. Sin embargo, este número suele formar parte de un modelo de clasificación binaria de la siguiente manera:
- Si el número predicho es mayor que el umbral de clasificación, el modelo de clasificación binaria predice la clase positiva.
- Si el número predicho es menor que el umbral de clasificación, el modelo de clasificación binaria predice la clase negativa.
Consulta Regresión logística en el Curso intensivo de aprendizaje automático para obtener más información.
logits
Es el vector de predicciones sin procesar (sin normalizar) que genera un modelo de clasificación y que, por lo general, se pasa a una función de normalización. Si el modelo resuelve un problema de clasificación multiclase, los logits suelen convertirse en una entrada para la función softmax. Luego, la función softmax genera un vector de probabilidades (normalizadas) con un valor para cada clase posible.
Pérdida logística
La función de pérdida que se usa en la regresión logística binaria.
Para obtener más información, consulta Regresión logística: Pérdida y regularización en el Curso intensivo de aprendizaje automático.
Logaritmo de probabilidad
Es el logaritmo de las probabilidades de algún evento.
Memoria a corto plazo de larga duración (LSTM)
Es un tipo de celda en una red neuronal recurrente que se usa para procesar secuencias de datos en aplicaciones como el reconocimiento de escritura a mano, la traducción automática y la generación de leyendas de imágenes. Las LSTM abordan el problema de la desaparición del gradiente que se produce cuando se entrenan RNN debido a largas secuencias de datos, ya que mantienen el historial en un estado de memoria interno basado en la nueva entrada y el contexto de las celdas anteriores de la RNN.
Laura
Abreviatura de Low-Rank Adaptability.
pérdida
Durante el entrenamiento de un modelo supervisado, se calcula una medida de qué tan lejos está la predicción de un modelo de su etiqueta.
Una función de pérdida calcula la pérdida.
Consulta Regresión lineal: Pérdida en el Curso intensivo de aprendizaje automático para obtener más información.
Agregador de pérdidas
Es un tipo de algoritmo de aprendizaje automático que mejora el rendimiento de un modelo combinando las predicciones de varios modelos y usando esas predicciones para generar una sola predicción. Como resultado, un agregador de pérdidas puede reducir la varianza de las predicciones y mejorar la precisión de las predicciones.
Curva de pérdida
Es un gráfico de la pérdida como una función de la cantidad de iteraciones de entrenamiento. En el siguiente gráfico, se muestra una curva de pérdida típica:
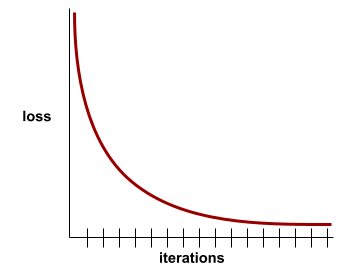
Las curvas de pérdida pueden ayudarte a determinar cuándo tu modelo está convergiendo o sobreajustándose.
Las curvas de pérdida pueden trazar todos los siguientes tipos de pérdida:
Consulta también curva de generalización.
Para obtener más información, consulta Sobreajuste: Interpretación de las curvas de pérdida en el Curso intensivo de aprendizaje automático.
función de pérdida
Durante el entrenamiento o las pruebas, una función matemática que calcula la pérdida en un lote de ejemplos. Una función de pérdida devuelve una pérdida menor para los modelos que realizan buenas predicciones que para los modelos que realizan predicciones deficientes.
Por lo general, el objetivo del entrenamiento es minimizar la pérdida que devuelve una función de pérdida.
Existen muchos tipos diferentes de funciones de pérdida. Elige la función de pérdida adecuada para el tipo de modelo que estás creando. Por ejemplo:
- La pérdida L2 (o error cuadrático medio) es la función de pérdida para la regresión lineal.
- La pérdida logística es la función de pérdida para la regresión logística.
Superficie de pérdida
Gráfico de pesos en comparación con la pérdida. El descenso de gradientes tiene como objetivo encontrar los pesos para los cuales la superficie de pérdida es el mínimo local.
Efecto de pérdida en el medio
Es la tendencia de un LLM a usar la información del principio y el final de una ventana de contexto larga de manera más eficaz que la información del medio. Es decir, dado un contexto largo, el efecto de pérdida en el medio hace que la precisión sea la siguiente:
- Relativamente alta cuando la información pertinente para formar una respuesta se encuentra cerca del comienzo o el final del contexto.
- Relativamente baja cuando la información pertinente para formar una respuesta se encuentra en el medio del contexto.
El término proviene de Lost in the Middle: How Language Models Use Long Contexts.
Adaptación de clasificación baja (LoRA)
Es una técnica eficiente en cuanto a parámetros para el ajuste que "congela" los pesos entrenados previamente del modelo (de modo que ya no se puedan modificar) y, luego, inserta un pequeño conjunto de pesos entrenables en el modelo. Este conjunto de pesos entrenables (también conocido como "matrices de actualización") es considerablemente más pequeño que el modelo base y, por lo tanto, se entrena mucho más rápido.
LoRA proporciona los siguientes beneficios:
- Mejora la calidad de las predicciones de un modelo para el dominio en el que se aplica el ajuste.
- Se ajusta con mayor rapidez que las técnicas que requieren el ajuste de todos los parámetros de un modelo.
- Reduce el costo de procesamiento de la inferencia, ya que permite la entrega simultánea de varios modelos especializados que comparten el mismo modelo base.
LSTM
Abreviatura de Long Short-Term Memory.
M
aprendizaje automático
Es un programa o sistema que entrena un modelo a partir de datos de entrada. El modelo entrenado puede hacer predicciones útiles a partir de datos nuevos (nunca vistos) extraídos de la misma distribución que la utilizada para entrenar el modelo.
El aprendizaje automático también se conoce como el campo de estudio relacionado con estos programas o sistemas.
Para obtener más información, consulta el curso Introducción al aprendizaje automático.
traducción automática
Uso de software (por lo general, un modelo de aprendizaje automático) para convertir texto de un idioma humano a otro, por ejemplo, de inglés a japonés.
clase mayoritaria
Es la etiqueta más común en un conjunto de datos con desequilibrio de clases. Por ejemplo, dado un conjunto de datos con un 99% de etiquetas negativas y un 1% de etiquetas positivas, la clase mayoritaria son las etiquetas negativas.
Compara esto con la clase minoritaria.
Consulta Conjuntos de datos: Conjuntos de datos desequilibrados en el Curso intensivo de aprendizaje automático para obtener más información.
Proceso de decisión de Markov (MDP)
Es un gráfico que representa el modelo de toma de decisiones en el que se toman decisiones (o acciones) para navegar por una secuencia de estados bajo el supuesto de que se cumple la propiedad de Markov. En el aprendizaje por refuerzo, estas transiciones entre estados devuelven una recompensa numérica.
Propiedad de Markov
Es una propiedad de ciertos entornos, en los que las transiciones de estado se determinan por completo a partir de la información implícita en el estado actual y la acción del agente.
modelo de lenguaje enmascarado
Un modelo de lenguaje que predice la probabilidad de los tokens candidatos para completar los espacios en blanco en una secuencia. Por ejemplo, un modelo de lenguaje enmascarado puede calcular las probabilidades de las palabras candidatas para reemplazar el subrayado en la siguiente oración:
El ____ en el sombrero regresó.
En la documentación, se suele usar la cadena "MASK" en lugar de un guion bajo. Por ejemplo:
El "MASK" del sombrero volvió.
La mayoría de los modelos de lenguaje enmascarados modernos son bidireccionales.
math-pass@k
Es una métrica para determinar la precisión de un LLM a la hora de resolver un problema matemático en K intentos. Por ejemplo, math-pass@2 mide la capacidad de un LLM para resolver problemas matemáticos en dos intentos. Una precisión de 0.85 en math-pass@2 indica que un LLM pudo resolver problemas matemáticos el 85% de las veces en dos intentos.
La métrica math-pass@k es idéntica a la métrica pass@k, excepto que el término math-pass@k se usa específicamente para la evaluación de matemáticas.
matplotlib
Biblioteca de código abierto Python 2D para generación de gráficos. matplotlib ayuda a visualizar diferentes aspectos del aprendizaje automático.
factorización de matrices
En matemáticas, un mecanismo para encontrar las matrices cuyo producto escalar se aproxima a una matriz objetivo.
En los sistemas de recomendación, la matriz objetivo suele contener las calificaciones de los usuarios sobre los elementos. Por ejemplo, una matriz objetivo para un sistema de recomendación de películas podría verse como la siguiente, donde los enteros positivos son calificaciones de usuarios y 0 significa que el usuario no calificó la película:
| Casablanca | The Philadelphia Story | Pantera Negra | Mujer Maravilla | Tiempos violentos | |
|---|---|---|---|---|---|
| Usuario 1 | 5.0 | 3.0 | 0.0 | 2.0 | 0.0 |
| Usuario 2 | 4.0 | 0.0 | 0.0 | 1.0 | 5.0 |
| Usuario 3 | 3.0 | 1.0 | 4.0 | 5.0 | 0.0 |
El sistema de recomendación de películas apunta a predecir las calificaciones de los usuarios para las películas que no se calificaron. Por ejemplo, ¿le gustará al Usuario 1 Pantera Negra?
Un enfoque para sistemas de recomendación es utilizar la factorización de matrices para generar las siguientes dos matrices:
- Una matriz de usuarios, formada por la cantidad de usuarios X la cantidad de dimensiones de incorporación
- Una matriz de elementos, formada por la cantidad de dimensiones de incorporación X la cantidad de elementos
Por ejemplo, el uso de la factorización de matrices en estos tres usuarios y cinco elementos podría generar la siguiente matriz de usuarios y matriz de elementos:
User Matrix Item Matrix 1.1 2.3 0.9 0.2 1.4 2.0 1.2 0.6 2.0 1.7 1.2 1.2 -0.1 2.1 2.5 0.5
El producto escalar de la matriz de usuarios y la matriz de elementos produce una matriz de recomendación que contiene no solo las calificaciones originales de los usuarios, sino también las predicciones para las películas que cada usuario no ha visto. Por ejemplo, considera la calificación del Usuario 1 de Casablanca, que fue de 5.0. El producto escalar correspondiente a esa celda en la matriz de recomendación debería ser de alrededor 5.0, y es:
(1.1 * 0.9) + (2.3 * 1.7) = 4.9Más importante aún, ¿al Usuario 1 le gustará Pantera Negra? Tomando el producto escalar correspondiente a la primera fila y la tercera columna se obtiene una calificación pronosticada de 4.3:
(1.1 * 1.4) + (2.3 * 1.2) = 4.3La factorización de matrices generalmente produce una matriz de usuarios y una matriz de elementos que, en conjunto, son significativamente más compactas que la matriz objetivo.
MBPP
Abreviatura de Mostly Basic Python Problems.
Error absoluto medio (MAE)
Es la pérdida promedio por ejemplo cuando se usa la pérdida de L1. Calcula el error absoluto medio de la siguiente manera:
- Calcula la pérdida L1 para un lote.
- Divide la pérdida de L1 entre la cantidad de ejemplos del lote.
Por ejemplo, considera el cálculo de la pérdida de L1 en el siguiente lote de cinco ejemplos:
| Valor real del ejemplo | Valor predicho del modelo | Pérdida (diferencia entre el valor real y el valor predicho) |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 3 |
| 4 | 6 | 2 |
| 9 | 8 | 1 |
| 8 = pérdida L1 | ||
Por lo tanto, la pérdida L1 es 8 y la cantidad de ejemplos es 5. Por lo tanto, el error absoluto medio es el siguiente:
Mean Absolute Error = L1 loss / Number of Examples Mean Absolute Error = 8/5 = 1.6
Compara el error absoluto medio con el error cuadrático medio y la raíz cuadrada del error cuadrático medio.
Precisión media en k (mAP@k)
Es la media estadística de todas las puntuaciones de precisión promedio en k en un conjunto de datos de validación. Un uso de la precisión media promedio en k es evaluar la calidad de las recomendaciones que genera un sistema de recomendación.
Aunque la frase "promedio medio" suena redundante, el nombre de la métrica es apropiado. Después de todo, esta métrica encuentra la media de varios valores de precisión promedio en k.
Error cuadrático medio (ECM)
Es la pérdida promedio por ejemplo cuando se usa la pérdida L2. Calcula el error cuadrático medio de la siguiente manera:
- Calcula la pérdida L2 para un lote.
- Divide la pérdida de L2 por la cantidad de ejemplos del lote.
Por ejemplo, considera la pérdida en el siguiente lote de cinco ejemplos:
| Valor real | Predicción del modelo | Pérdida | Pérdida al cuadrado |
|---|---|---|---|
| 7 | 6 | 1 | 1 |
| 5 | 4 | 1 | 1 |
| 8 | 11 | 3 | 9 |
| 4 | 6 | 2 | 4 |
| 9 | 8 | 1 | 1 |
| 16 = pérdida L2 | |||
Por lo tanto, el error cuadrático medio es el siguiente:
Mean Squared Error = L2 loss / Number of Examples Mean Squared Error = 16/5 = 3.2
El error cuadrático medio es un optimizador de entrenamiento popular, en especial para la regresión lineal.
Compara el error cuadrático medio con el error absoluto medio y la raíz cuadrada del error cuadrático medio.
TensorFlow Playground usa el error cuadrático medio para calcular los valores de pérdida.
malla
En la programación paralela de AA, es un término asociado a la asignación de los datos y el modelo a los chips de TPU, y a la definición de cómo se fragmentarán o replicarán estos valores.
Malla es un término sobrecargado que puede significar una de las siguientes opciones:
- Es un diseño físico de los chips de TPU.
- Es una construcción lógica abstracta para asignar los datos y el modelo a los chips de TPU.
En cualquier caso, una malla se especifica como una forma.
metaaprendizaje
Es un subconjunto del aprendizaje automático que descubre o mejora un algoritmo de aprendizaje. Un sistema de aprendizaje meta también puede tener como objetivo entrenar un modelo para que aprenda rápidamente una nueva tarea a partir de una pequeña cantidad de datos o de la experiencia adquirida en tareas anteriores. En general, los algoritmos de aprendizaje meta intentan lograr lo siguiente:
- Mejorar o aprender funciones diseñadas manualmente (como un inicializador o un optimizador)
- Ser más eficiente en el uso de datos y recursos de procesamiento
- Mejorar la generalización
El aprendizaje meta está relacionado con el aprendizaje en pocos intentos.
métrica
Es una estadística que te interesa.
Un objetivo es una métrica que un sistema de aprendizaje automático intenta optimizar.
API de Metrics (tf.metrics)
Es una API de TensorFlow para evaluar modelos. Por ejemplo, tf.metrics.accuracy determina con qué frecuencia las predicciones de un modelo coinciden con las etiquetas.
minilote
Es un subconjunto pequeño seleccionado al azar de un lote que se procesa en una iteración. El tamaño del lote de un minilote generalmente es entre 10 y 1,000 ejemplos.
Por ejemplo, supongamos que el conjunto de entrenamiento completo (el lote completo) consta de 1,000 ejemplos. Supongamos que estableces el tamaño del lote de cada minilote en 20. Por lo tanto, cada iteración determina la pérdida en 20 ejemplos aleatorios de los 1,000 y, luego, ajusta los pesos y los sesgos según corresponda.
Es mucho más eficiente calcular la pérdida en un minilote que en todos los ejemplos del lote completo.
Consulta Regresión lineal: Hiperparámetros en el Curso intensivo de aprendizaje automático para obtener más información.
descenso de gradientes estocástico por minilotes
Es un algoritmo de descenso de gradientes que usa minilotes. En otras palabras, el descenso de gradientes estocástico por minilotes estima el gradiente en función de un subconjunto pequeño de los datos de entrenamiento. El descenso de gradientes estocástico normal usa un minilote de tamaño 1.
Pérdida de minimax
Es una función de pérdida para las redes adversarias generativas, basada en la entropía cruzada entre la distribución de los datos generados y los datos reales.
La pérdida de Minimax se usa en el primer artículo para describir las redes adversarias generativas.
Consulta Funciones de pérdida en el curso de Redes Adversarias Generativas para obtener más información.
clase minoritaria
Es la etiqueta menos común en un conjunto de datos con desequilibrio de clases. Por ejemplo, dado un conjunto de datos con un 99% de etiquetas negativas y un 1% de etiquetas positivas, la clase minoritaria son las etiquetas positivas.
Compara esto con la clase mayoritaria.
Consulta Conjuntos de datos: Conjuntos de datos desequilibrados en el Curso intensivo de aprendizaje automático para obtener más información.
Mezcla de expertos
Es un esquema para aumentar la eficiencia de la red neuronal usando solo un subconjunto de sus parámetros (conocido como experto) para procesar un token o un ejemplo determinados. Una red de selección dirige cada token o ejemplo de entrada a los expertos adecuados.
Para obtener más detalles, consulta cualquiera de los siguientes documentos:
- Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer (Redes neuronales increíblemente grandes: la capa de mezcla de expertos con puerta dispersa)
- Mixture-of-Experts with Expert Choice Routing
AA
Abreviatura de aprendizaje automático.
MMIT
Abreviatura de ajuste de instrucciones multimodal.
MNIST
Un conjunto de datos de dominio público compilado por LeCun, Cortes y Burges que contiene 60,000 imágenes, cada imagen muestra cómo un ser humano escribió de forma manual un dígito particular del 0 al 9. Cada imagen se almacena como un array de números enteros de 28 x 28, donde cada número entero es un valor de escala de grises entre 0 y 255, ambos incluidos.
MNIST es un conjunto de datos canónico para el aprendizaje automático que a menudo se utiliza para probar nuevos enfoques de aprendizaje automático. Para obtener más información, consulta The MNIST Database of Handwritten Digits.
modality
Es una categoría de datos de alto nivel. Por ejemplo, los números, el texto, las imágenes, el video y el audio son cinco modalidades diferentes.
modelo
En general, cualquier construcción matemática que procese datos de entrada y devuelva resultados. Dicho de otra manera, un modelo es el conjunto de parámetros y la estructura necesarios para que un sistema realice predicciones. En el aprendizaje automático supervisado, un modelo toma un ejemplo como entrada y deduce una predicción como salida. Dentro del aprendizaje automático supervisado, los modelos difieren un poco. Por ejemplo:
- Un modelo de regresión lineal consta de un conjunto de pesos y un sesgo.
- Un modelo de red neuronal consta de lo siguiente:
- Un conjunto de capas ocultas, cada una de las cuales contiene una o más neuronas.
- Los pesos y el sesgo asociados a cada neurona.
- Un modelo de árbol de decisión consta de lo siguiente:
- Es la forma del árbol, es decir, el patrón en el que se conectan las condiciones y las hojas.
- Son las condiciones y las hojas.
Puedes guardar, restablecer o hacer copias de un modelo.
El aprendizaje automático no supervisado también genera modelos, por lo general, una función que puede asignar un ejemplo de entrada al clúster más adecuado.
capacidad del modelo
Es la complejidad de los problemas que un modelo puede aprender. Mientras más complejos sean los problemas que un modelo puede aprender, mayor será la capacidad del modelo. La capacidad de un modelo generalmente aumenta con la cantidad de parámetros del modelo. Para obtener una definición formal de la capacidad de un modelo de clasificación, consulta Dimensión VC.
Cascada de modelos
Es un sistema que elige el modelo ideal para una consulta de inferencia específica.
Imagina un grupo de modelos, desde muy grandes (con muchos parámetros) hasta mucho más pequeños (con muchos menos parámetros). Los modelos muy grandes consumen más recursos de procesamiento en el momento de la inferencia que los modelos más pequeños. Sin embargo, los modelos muy grandes suelen poder inferir solicitudes más complejas que los modelos más pequeños. El encadenamiento de modelos determina la complejidad de la consulta de inferencia y, luego, elige el modelo adecuado para realizar la inferencia. La principal motivación para la cascada de modelos es reducir los costos de inferencia seleccionando, en general, modelos más pequeños y solo seleccionando un modelo más grande para las búsquedas más complejas.
Imagina que un modelo pequeño se ejecuta en un teléfono y una versión más grande de ese modelo se ejecuta en un servidor remoto. La buena cascada de modelos reduce el costo y la latencia, ya que permite que el modelo más pequeño controle las solicitudes simples y solo llame al modelo remoto para controlar las solicitudes complejas.
Consulta también enrutador de modelos.
Paralelismo de modelos
Es una forma de escalar el entrenamiento o la inferencia que coloca diferentes partes de un mismo modelo en diferentes dispositivos. El paralelismo de modelos permite usar modelos que son demasiado grandes para caber en un solo dispositivo.
Para implementar el paralelismo del modelo, un sistema suele hacer lo siguiente:
- Divide el modelo en partes más pequeñas.
- Distribuye el entrenamiento de esas partes más pequeñas en varios procesadores. Cada procesador entrena su propia parte del modelo.
- Combina los resultados para crear un solo modelo.
El paralelismo de modelos ralentiza el entrenamiento.
Consulta también paralelismo de datos.
router de modelo
Es el algoritmo que determina el modelo ideal para la inferencia en la cascada de modelos. Un router de modelos suele ser un modelo de aprendizaje automático que aprende de forma gradual a elegir el mejor modelo para una entrada determinada. Sin embargo, un router de modelos a veces podría ser un algoritmo más simple que no utilice aprendizaje automático.
entrenamiento de modelos
Proceso mediante el cual se determina el mejor modelo.
MOE
Abreviatura de mezcla de expertos.
Momentum
Es un algoritmo de descenso de gradientes sofisticado en el que un paso de aprendizaje depende no solo de la derivada en el paso actual, sino también de las derivadas de los pasos que lo precedieron inmediatamente. El momento implica calcular un promedio móvil ponderado de forma exponencial de los gradientes a lo largo del tiempo, de forma análoga al momento en la física. A veces, el momento evita que el aprendizaje se atasque en mínimos locales.
Mostly Basic Python Problems (MBPP)
Es un conjunto de datos para evaluar la competencia de un LLM en la generación de código de Python. Mostly Basic Python Problems proporciona alrededor de 1,000 problemas de programación obtenidos de fuentes externas. Cada problema del conjunto de datos contiene lo siguiente:
- Una descripción de la tarea
- Código de solución
- Tres casos de prueba automatizados
MT
Abreviatura de traducción automática.
clasificación de clases múltiples
En el aprendizaje supervisado, un problema de clasificación en el que el conjunto de datos contiene más de dos clases de etiquetas. Por ejemplo, las etiquetas del conjunto de datos Iris deben ser una de las siguientes tres clases:
- Iris setosa
- Iris virginica
- Iris versicolor
Un modelo entrenado en el conjunto de datos Iris que predice el tipo de iris en ejemplos nuevos realiza una clasificación de varias clases.
En cambio, los problemas de clasificación que distinguen entre exactamente dos clases son modelos de clasificación binaria. Por ejemplo, un modelo de correo electrónico que predice si un mensaje es spam o no es spam es un modelo de clasificación binaria.
En los problemas de agrupamiento, la clasificación de clases múltiples hace referencia a más de dos clústeres.
Consulta Redes neuronales: clasificación de clases múltiples en el Curso intensivo de aprendizaje automático para obtener más información.
Regresión logística multiclase
Usa la regresión logística en problemas de clasificación multiclase.
Autoatención de varios encabezados
Es una extensión de la autoatención que aplica el mecanismo de autoatención varias veces para cada posición en la secuencia de entrada.
Transformers introdujo la autoatención de múltiples encabezados.
Ajustado con instrucciones multimodales
Un modelo ajustado según instrucciones que puede procesar entradas más allá del texto, como imágenes, video y audio.
Modelo multimodal
Modelo cuyas entradas, salidas o ambas incluyen más de una modalidad. Por ejemplo, considera un modelo que toma una imagen y una leyenda de texto (dos modalidades) como atributos y genera una puntuación que indica qué tan adecuada es la leyenda de texto para la imagen. Por lo tanto, las entradas de este modelo son multimodales y la salida es unimodal.
clasificación multinomial
Sinónimo de clasificación de clases múltiples.
Regresión multinomial
Sinónimo de regresión logística multiclase.
Comprensión de lectura de varios enunciados (MultiRC)
Es un conjunto de datos para evaluar la capacidad de un LLM de responder ejercicios de opción múltiple. Cada ejemplo del conjunto de datos contiene lo siguiente:
- Un párrafo de contexto
- Una pregunta sobre ese párrafo
- Hay varias respuestas a la pregunta. Cada respuesta se etiqueta como Verdadero o Falso. Varias respuestas pueden ser verdaderas.
Por ejemplo:
Párrafo de contexto:
Susan quería tener una fiesta de cumpleaños. Llamó a todas sus amigas. Ella tiene cinco amigos. Su mamá le dijo que Susan podía invitarlos a todos a la fiesta. Su primera amiga no pudo ir a la fiesta porque estaba enferma. Su segunda amiga se iba de la ciudad. Su tercera amiga no estaba segura de que sus padres la dejaran ir. El cuarto amigo dijo que tal vez. El quinto amigo podría ir a la fiesta sin dudas. Susan estaba un poco triste. El día de la fiesta, aparecieron los cinco amigos. Cada amigo tenía un regalo para Susana. Susan estaba feliz y les envió a sus amigos una tarjeta de agradecimiento la semana siguiente.
Pregunta: ¿Se recuperó el amigo enfermo de Susan?
Varias respuestas:
- Sí, se recuperó. (Verdadero)
- No (falso).
- Sí. (Verdadero)
- No, no se recuperó. (Falso)
- Sí, estuvo en la fiesta de Susan. (Verdadero)
MultiRC es un componente del conjunto de SuperGLUE.
Para obtener más detalles, consulta Looking Beyond the Surface: A Challenge Set for Reading Comprehension over Multiple Sentences.
Realizar varias tareas a la vez
Técnica de aprendizaje automático en la que se entrena un solo modelo para realizar varias tareas.
Los modelos de tareas múltiples se crean entrenando con datos adecuados para cada una de las diferentes tareas. Esto permite que el modelo aprenda a compartir información entre las tareas, lo que lo ayuda a aprender de forma más eficaz.
Un modelo entrenado para múltiples tareas suele tener mejores capacidades de generalización y puede ser más sólido para manejar diferentes tipos de datos.
N
Nano
Un modelo de Gemini relativamente pequeño diseñado para usarse en el dispositivo. Consulta Gemini Nano para obtener más detalles.
Trampa de NaN
Cuando un número del modelo se vuelve un NaN durante el entrenamiento, lo que causa que muchos otros números del modelo eventualmente se vuelvan un NaN.
NaN es la abreviatura de No es un Número.
procesamiento de lenguaje natural
Es el campo de la enseñanza a las computadoras para procesar lo que un usuario dijo o escribió usando reglas lingüísticas. Casi todo el procesamiento de lenguaje natural moderno se basa en el aprendizaje automático.comprensión del lenguaje natural
Es un subconjunto del procesamiento de lenguaje natural que determina las intenciones de lo que se dice o escribe. La comprensión del lenguaje natural puede ir más allá del procesamiento del lenguaje natural para tener en cuenta aspectos complejos del lenguaje, como el contexto, el sarcasmo y el sentimiento.
clase negativa
En la clasificación binaria, una clase se denomina positiva y la otra, negativa. La clase positiva es el elemento o evento que el modelo está probando, y la clase negativa es la otra posibilidad. Por ejemplo:
- La clase negativa en una prueba médica puede ser "no es un tumor".
- La clase negativa en un modelo de clasificación de correos electrónicos podría ser "no es spam".
Compara esto con la clase positiva.
Muestreo negativo
Sinónimo de muestreo de candidatos.
Búsqueda de arquitectura neuronal (NAS)
Técnica para diseñar automáticamente la arquitectura de una red neuronal. Los algoritmos de NAS pueden reducir la cantidad de tiempo y recursos necesarios para entrenar una red neuronal.
Por lo general, el NAS usa lo siguiente:
- Un espacio de búsqueda, que es un conjunto de arquitecturas posibles.
- Una función de aptitud, que es una medida de qué tan bien se desempeña una arquitectura en particular en una tarea determinada.
Los algoritmos de NAS suelen comenzar con un pequeño conjunto de arquitecturas posibles y expanden gradualmente el espacio de búsqueda a medida que el algoritmo aprende más sobre qué arquitecturas son eficaces. Por lo general, la función de aptitud se basa en el rendimiento de la arquitectura en un conjunto de entrenamiento, y el algoritmo se entrena con una técnica de aprendizaje por refuerzo.
Los algoritmos de NAS demostraron ser eficaces para encontrar arquitecturas de alto rendimiento para una variedad de tareas, como la clasificación de imágenes, la clasificación de texto y la traducción automática.
neuronal prealimentada
Un modelo que contiene al menos una capa oculta. Una red neuronal profunda es un tipo de red neuronal que contiene más de una capa oculta. Por ejemplo, en el siguiente diagrama, se muestra una red neuronal profunda que contiene dos capas ocultas.
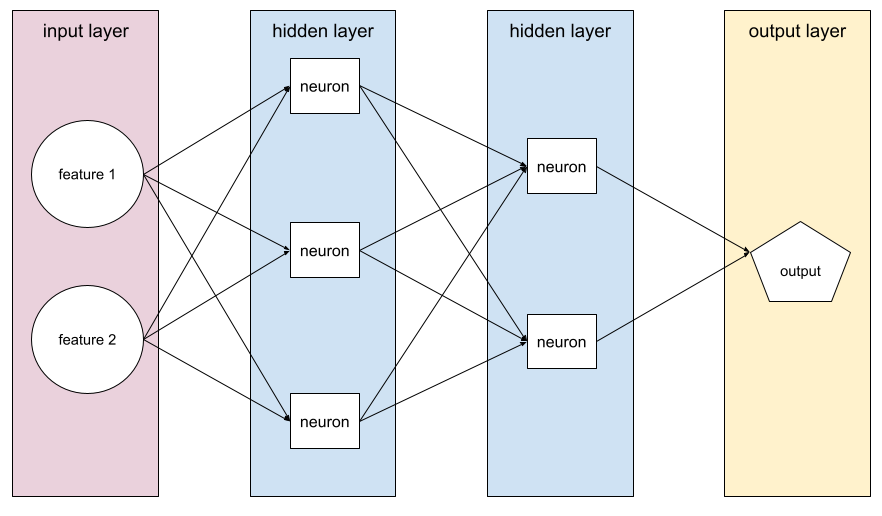
Cada neurona de una red neuronal se conecta a todos los nodos de la siguiente capa. Por ejemplo, en el diagrama anterior, observa que cada una de las tres neuronas de la primera capa oculta se conecta por separado con las dos neuronas de la segunda capa oculta.
Las redes neuronales implementadas en computadoras a veces se denominan redes neuronales artificiales para diferenciarlas de las redes neuronales que se encuentran en el cerebro y otros sistemas nerviosos.
Algunas redes neuronales pueden imitar relaciones no lineales extremadamente complejas entre diferentes atributos y la etiqueta.
Consulta también red neuronal convolucional y red neuronal recurrente.
Consulta Redes neuronales en el Curso intensivo de aprendizaje automático para obtener más información.
neurona
En el aprendizaje automático, es una unidad distinta dentro de una capa oculta de una red neuronal. Cada neurona realiza la siguiente acción de dos pasos:
- Calcula la suma ponderada de los valores de entrada multiplicados por sus pesos correspondientes.
- Pasa la suma ponderada como entrada a una función de activación.
Una neurona en la primera capa oculta acepta entradas de los valores de atributos en la capa de entrada. Una neurona en cualquier capa oculta más allá de la primera acepta entradas de las neuronas en la capa oculta precedente. Por ejemplo, una neurona en la segunda capa oculta acepta entradas de las neuronas en la primera capa oculta.
En la siguiente ilustración, se destacan dos neuronas y sus entradas.
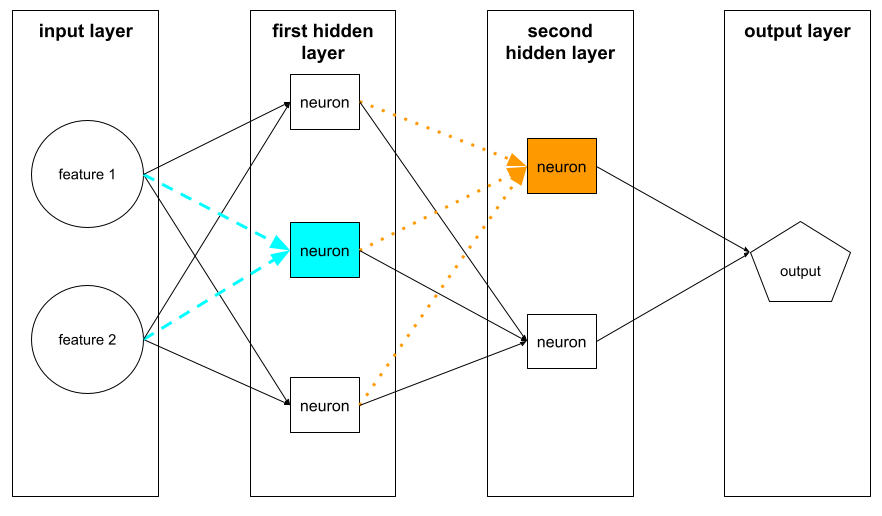
Una neurona en una red neuronal imita el comportamiento de las neuronas en el cerebro y otras partes del sistema nervioso.
N-grama
Es una secuencia ordenada de N palabras. Por ejemplo, realmente loco es un 2-grama. Ya que el orden es relevante, loco realmente es un 2-grama diferente a realmente loco.
| N | Nombres para este tipo de n-grama | Ejemplos |
|---|---|---|
| 2 | bigrama o 2-grama | ir por, por ir, asar carne, asar verduras |
| 3 | trigrama o 3-grama | comí muy poco, felices para siempre, las campanas redoblan |
| 4 | 4-grama | caminar por el parque, en el viento, el niño comía lentejas |
Muchos modelos de comprensión del lenguaje natural se basan en n-gramas para predecir la siguiente palabra que el usuario escribirá o dirá. Por ejemplo, que un usuario escribió felices para. Un modelo CLN basado en trigramas probablemente predeciría que el usuario escribirá a continuación la palabra después.
Compara los n-gramas con la bolsa de palabras, que son conjuntos desordenados de palabras.
Consulta Modelos de lenguaje grandes en el Curso intensivo de aprendizaje automático para obtener más información.
PLN
Abreviatura de procesamiento de lenguaje natural.
CLN
Abreviatura de comprensión del lenguaje natural.
nodo (árbol de decisión)
En un árbol de decisión, cualquier condición o hoja.
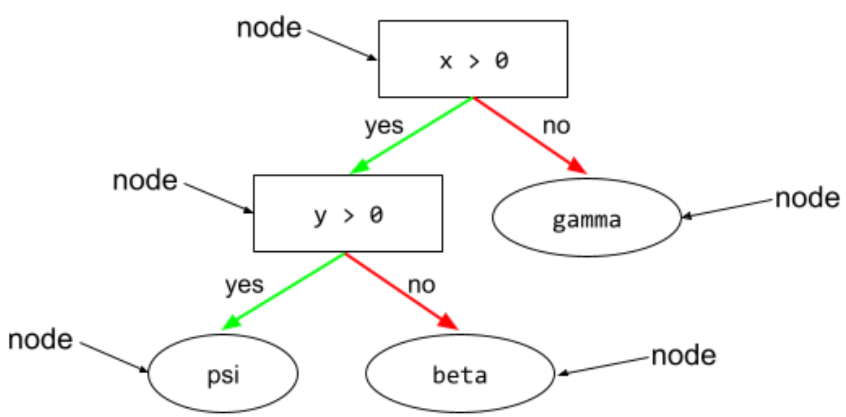
Consulta Árboles de decisión en el curso de Bosques de decisión para obtener más información.
nodo (red neuronal)
Una neurona en una capa oculta.
Consulta Redes neuronales en el Curso intensivo de aprendizaje automático para obtener más información.
nodo (grafo de TensorFlow)
Operación en un grafo de TensorFlow.
ruido
En términos generales, cualquier cosa que tape las señales en un conjunto de datos. El ruido puede introducirse en los datos de varias maneras. Por ejemplo:
- Los evaluadores humanos cometen errores durante el etiquetado.
- Los instrumentos o personas omiten o registran incorrectamente los valores de atributo.
condición no binaria
Una condición que contiene más de dos resultados posibles. Por ejemplo, la siguiente condición no binaria contiene tres resultados posibles:
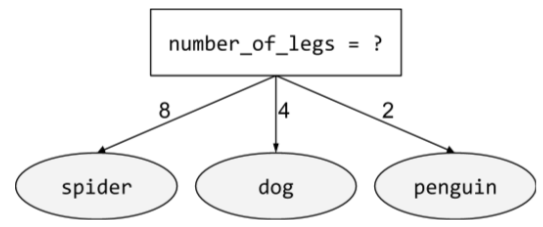
Consulta Tipos de condiciones en el curso de Bosques de decisión para obtener más información.
no lineal
Es una relación entre dos o más variables que no se puede representar solo a través de la suma y la multiplicación. Una relación lineal se puede representar como una línea, mientras que una relación no lineal no. Por ejemplo, considera dos modelos que relacionan un solo atributo con una sola etiqueta. El modelo de la izquierda es lineal y el de la derecha es no lineal:

Consulta Redes neuronales: nodos y capas ocultas en el Curso intensivo de aprendizaje automático para experimentar con diferentes tipos de funciones no lineales.
sesgo de no respuesta
Consulta sesgo de selección.
no estacionariedad
Es un atributo cuyos valores cambian en una o más dimensiones, por lo general, el tiempo. Por ejemplo, considera los siguientes ejemplos de no estacionariedad:
- La cantidad de trajes de baño que se venden en una tienda en particular varía según la temporada.
- La cantidad de una fruta en particular que se cosecha en una región específica es cero durante gran parte del año, pero es grande durante un breve período.
- Debido al cambio climático, las temperaturas medias anuales están cambiando.
Compara esto con la estacionariedad.
Sin una respuesta correcta (NORA)
Una instrucción que tiene varias respuestas correctas Por ejemplo, la siguiente instrucción no tiene una respuesta correcta:
Cuéntame un chiste divertido sobre elefantes.
Evaluar las respuestas a las instrucciones que no tienen una respuesta correcta suele ser mucho más subjetivo que evaluar las instrucciones con una respuesta correcta. Por ejemplo, evaluar un chiste sobre elefantes requiere una forma sistemática de determinar qué tan gracioso es.
NORA
Abreviatura de no hay una sola respuesta correcta.
Normalización
En términos generales, es el proceso de convertir el rango real de valores de una variable en un rango estándar de valores, como los siguientes:
- De -1 a +1
- De 0 a 1
- Puntuaciones Z (aproximadamente, de -3 a +3)
Por ejemplo, supongamos que el rango real de valores de un atributo determinado es de 800 a 2,400. Como parte de la ingeniería de atributos, podrías normalizar los valores reales en un rango estándar, como de -1 a +1.
La normalización es una tarea común en la ingeniería de funciones. Por lo general, los modelos se entrenan más rápido (y producen mejores predicciones) cuando cada atributo numérico del vector de atributos tiene aproximadamente el mismo rango.
Consulta también la normalización de la puntuación Z.
Consulta Datos numéricos: Normalización en el Curso intensivo de aprendizaje automático para obtener más información.
NotebookLM
Es una herramienta basada en Gemini que permite a los usuarios subir documentos y, luego, usar instrucciones para hacer preguntas sobre esos documentos, resumirlos u organizarlos. Por ejemplo, un autor podría subir varios cuentos y pedirle a NotebookLM que encuentre los temas comunes o que identifique cuál sería la mejor película.
detección de novedades
Proceso para determinar si un ejemplo nuevo (novedoso) proviene de la misma distribución que el conjunto de entrenamiento. En otras palabras, después del entrenamiento en el conjunto de entrenamiento, la detección de novedades determina si un ejemplo nuevo (durante la inferencia o el entrenamiento adicional) es un valor atípico.
Compara esto con la detección de valores atípicos.
datos numéricos
Atributos representados como números enteros o de valores reales. Por ejemplo, un modelo de valuación de casas probablemente representaría el tamaño de una casa (en pies cuadrados o metros cuadrados) como datos numéricos. Representar una característica como datos numéricos indica que los valores de la característica tienen una relación matemática con la etiqueta. Es decir, la cantidad de metros cuadrados de una casa probablemente tenga alguna relación matemática con su valor.
No todos los datos de números enteros deben representarse como datos numéricos. Por ejemplo, los códigos postales de algunas partes del mundo son números enteros. Sin embargo, los códigos postales enteros no deben representarse como datos numéricos en los modelos. Esto se debe a que un código postal de 20000 no es el doble (o la mitad) de potente que un código postal de 10000. Además, si bien los diferentes códigos postales sí se correlacionan con diferentes valores de bienes raíces, no podemos suponer que los valores de bienes raíces en el código postal 20000 son el doble de valiosos que los valores de bienes raíces en el código postal 10000.
Por lo tanto, los códigos postales deben representarse como datos categóricos.
En ocasiones, las funciones numéricas se denominan atributos continuos.
Para obtener más información, consulta Trabaja con datos numéricos en el Curso intensivo de aprendizaje automático.
NumPy
Biblioteca matemática de código abierto que proporciona operaciones de matrices eficaces en Python. Pandas se basa en NumPy.
O
objetivo
Es una métrica que tu algoritmo intenta optimizar.
función objetivo
Es la fórmula matemática o la métrica que un modelo intenta optimizar. Por ejemplo, la función objetivo para la regresión lineal suele ser la pérdida cuadrática media. Por lo tanto, cuando se entrena un modelo de regresión lineal, el objetivo del entrenamiento es minimizar la pérdida cuadrática media.
En algunos casos, el objetivo es maximizar la función objetivo. Por ejemplo, si la función objetivo es la precisión, el objetivo es maximizar la precisión.
Consulta también pérdida.
condición oblicua
En un árbol de decisión, una condición que involucra más de una característica. Por ejemplo, si la altura y el ancho son atributos, la siguiente es una condición oblicua:
height > width
Compara esto con la condición alineada con el eje.
Consulta Tipos de condiciones en el curso de Bosques de decisión para obtener más información.
Sin conexión
Sinónimo de estático.
inferencia sin conexión
Proceso por el que un modelo genera un lote de predicciones y, luego, las almacena en caché (las guarda). Luego, las apps pueden acceder a la predicción inferida desde la caché en lugar de volver a ejecutar el modelo.
Por ejemplo, considera un modelo que genera pronósticos del clima locales (predicciones) cada cuatro horas. Después de cada ejecución del modelo, el sistema almacena en caché todos los pronósticos del clima locales. Las apps del clima recuperan los pronósticos de la caché.
La inferencia sin conexión también se denomina inferencia estática.
Compara esto con la inferencia en línea. Para obtener más información, consulta Sistemas de AA en producción: inferencia estática versus dinámica en el Curso intensivo de aprendizaje automático.
codificación one-hot
Representa los datos categóricos como un vector en el que se cumple lo siguiente:
- Un elemento se establece en 1.
- Todos los demás elementos se establecen en 0.
La codificación one-hot se usa comúnmente para representar cadenas o identificadores que tienen un conjunto finito de valores posibles.
Por ejemplo, supongamos que un atributo categórico determinado llamado Scandinavia tiene cinco valores posibles:
- "Dinamarca"
- "Suecia"
- "Noruega"
- "Finlandia"
- "Islandia"
La codificación one-hot podría representar cada uno de los cinco valores de la siguiente manera:
| País | Vector | ||||
|---|---|---|---|---|---|
| "Dinamarca" | 1 | 0 | 0 | 0 | 0 |
| "Suecia" | 0 | 1 | 0 | 0 | 0 |
| "Noruega" | 0 | 0 | 1 | 0 | 0 |
| "Finlandia" | 0 | 0 | 0 | 1 | 0 |
| "Islandia" | 0 | 0 | 0 | 0 | 1 |
Gracias a la codificación one-hot, un modelo puede aprender diferentes conexiones en función de cada uno de los cinco países.
Representar un atributo como datos numéricos es una alternativa a la codificación one-hot. Lamentablemente, representar los países escandinavos de forma numérica no es una buena opción. Por ejemplo, considera la siguiente representación numérica:
- "Denmark" es 0.
- "Suecia" es 1.
- "Noruega" es 2.
- "Finland" es 3.
- "Islandia" es 4.
Con la codificación numérica, un modelo interpretaría los números sin procesar de forma matemática y trataría de entrenarse con esos números. Sin embargo, Islandia no tiene el doble (o la mitad) de algo que Noruega, por lo que el modelo llegaría a conclusiones extrañas.
Consulta Datos categóricos: Vocabulario y codificación one-hot en el Curso intensivo de aprendizaje automático para obtener más información.
Una respuesta correcta (ORA)
Una instrucción que tiene una sola respuesta correcta. Por ejemplo, considera la siguiente instrucción:
Verdadero o falso: Saturno es más grande que Marte.
La única respuesta correcta es verdadero.
Contrasta con no hay una respuesta correcta.
aprendizaje en un intento
Es un enfoque de aprendizaje automático que se suele usar para la clasificación de objetos y que está diseñado para aprender un modelo de clasificación eficaz a partir de un solo ejemplo de entrenamiento.
Consulta también aprendizaje en pocos intentos y aprendizaje sin ejemplos.
Instrucción con un solo ejemplo
Una instrucción que contiene un ejemplo que demuestra cómo debería responder el modelo de lenguaje grande. Por ejemplo, la siguiente instrucción contiene un ejemplo que muestra a un modelo de lenguaje grande cómo debe responder una búsqueda.
| Partes de una instrucción | Notas |
|---|---|
| ¿Cuál es la moneda oficial del país especificado? | La pregunta que quieres que responda el LLM. |
| Francia: EUR | Veamos un ejemplo. |
| India: | Es la búsqueda real. |
Compara y contrasta el one-shot prompting con los siguientes términos:
uno frente a todos
Dado un problema de clasificación con N clases, una solución que consta de N modelos de clasificación binaria independientes, es decir, un modelo de clasificación binaria para cada resultado posible. Por ejemplo, dado un modelo que clasifica ejemplos como animal, vegetal o mineral, una solución de uno frente a todos proporcionaría los siguientes tres modelos de clasificación binaria independientes:
- animal versus no animal
- vegetal o no vegetal
- mineral versus no mineral
online
Sinónimo de dinámico.
inferencia en línea
Generación de predicciones a pedido. Por ejemplo, supongamos que una app pasa una entrada a un modelo y emite una solicitud de predicción. Un sistema que usa la inferencia en línea responde a la solicitud ejecutando el modelo (y devolviendo la predicción a la app).
Compara esto con la inferencia sin conexión.
Para obtener más información, consulta Sistemas de AA en producción: inferencia estática versus dinámica en el Curso intensivo de aprendizaje automático.
operación (op)
En TensorFlow, cualquier procedimiento que crea, manipula o destruye un Tensor. Por ejemplo, una multiplicación de matrices es una operación que toma dos tensores como entrada y genera un tensor como resultado.
Optax
Biblioteca de procesamiento y optimización de gradientes para JAX. Optax facilita la investigación proporcionando componentes básicos que se pueden recombinar de formas personalizadas para optimizar modelos paramétricos, como las redes neuronales profundas. Otros objetivos incluyen los siguientes:
- Proporcionar implementaciones legibles, bien probadas y eficientes de los componentes principales
- Mejora la productividad, ya que permite combinar ingredientes de bajo nivel en optimizadores personalizados (o en otros componentes de procesamiento de gradientes).
- Acelerar la adopción de ideas nuevas facilitando la contribución de cualquier persona
optimizer
Implementación específica del algoritmo de descenso de gradientes. Entre los optimizadores populares, se incluyen los siguientes:
- AdaGrad, que significa descenso de gradientes ADAptable.
- Adam, que significa ADAptive with Momentum (adaptativo con momento).
ORA
Abreviatura de una respuesta correcta.
sesgo de homogeneidad de los demás
La tendencia a ver a los miembros externos a un grupo como más parecidos que los miembros del grupo cuando se comparan actitudes, valores, rasgos de personalidad y otras características. Endogrupal refiere a las personas con las que interactúas regularmente; los demás refiere a las personas con las que no interactúas regularmente. Si se crea un conjunto de datos pidiéndoles atributos a las personas sobre los demás, esos atributos tendrán menos matices y serán más estereotípicos que los atributos que las personas pueden indicar sobre quienes pertenecen a su mismo grupo.
Por ejemplo, una persona de Buenos Aires podría describir las casas de sus conciudadanos con gran detalle, describiendo pequeñas diferencias de estilos arquitectónicos, ventanas, puertas y tamaños. Sin embargo, la misma persona de Buenos Aires podría simplemente decir que los ciudadanos de Berlín viven todos en casas idénticas.
El sesgo de homogeneidad de los demás es un tipo de sesgo de correspondencia.
Consulta también el sesgo endogrupal.
detección de valores atípicos
Proceso de identificar valores atípicos en un conjunto de entrenamiento.
Compara esto con la detección de novedades.
los valores atípicos
Son los valores que se alejan de la mayoría de los demás valores. En el aprendizaje automático, cualquiera de los siguientes son valores atípicos:
- Son los datos de entrada cuyos valores son aproximadamente 3 desviaciones estándar de la media.
- Pesos con valores absolutos altos
- Valores predichos relativamente alejados de los valores reales
Por ejemplo, supongamos que widget-price es un atributo de un modelo determinado.
Supongamos que la media widget-price es de 7 EUR con una desviación estándar de 1 EUR. Por lo tanto, los ejemplos que contengan un widget-price de 12 o 2 euros se considerarían valores atípicos, ya que cada uno de esos precios se encuentra a cinco desviaciones estándar de la media.
Los valores atípicos suelen deberse a errores tipográficos o de entrada de datos. En otros casos, los valores atípicos no son errores. Después de todo, los valores que se encuentran a cinco desviaciones estándar de la media son poco comunes, pero no imposibles.
Los valores atípicos suelen causar problemas en el entrenamiento del modelo. El recorte es una manera de manejar los valores atípicos.
Para obtener más información, consulta Trabaja con datos numéricos en el Curso intensivo de aprendizaje automático.
Evaluación fuera de la bolsa (evaluación OOB)
Es un mecanismo para evaluar la calidad de un bosque de decisión probando cada árbol de decisión con los ejemplos que no se usaron durante el entrenamiento de ese árbol de decisión. Por ejemplo, en el siguiente diagrama, observa que el sistema entrena cada árbol de decisión con aproximadamente dos tercios de los ejemplos y, luego, realiza la evaluación con el tercio restante.

La evaluación fuera de la bolsa es una aproximación conservadora y eficiente en términos de procesamiento del mecanismo de validación cruzada. En la validación cruzada, se entrena un modelo para cada ronda de validación cruzada (por ejemplo, se entrenan 10 modelos en una validación cruzada de 10 segmentos). Con la evaluación fuera de la muestra, se entrena un solo modelo. Dado que el bagging retiene algunos datos de cada árbol durante el entrenamiento, la evaluación OOB puede usar esos datos para aproximar la validación cruzada.
Consulta Evaluación fuera de la bolsa en el curso de Bosques de decisión para obtener más información.
capa de salida
Es la capa "final" de una red neuronal. La capa de salida contiene la predicción.
En la siguiente ilustración, se muestra una pequeña red neuronal profunda con una capa de entrada, dos capas ocultas y una capa de salida:
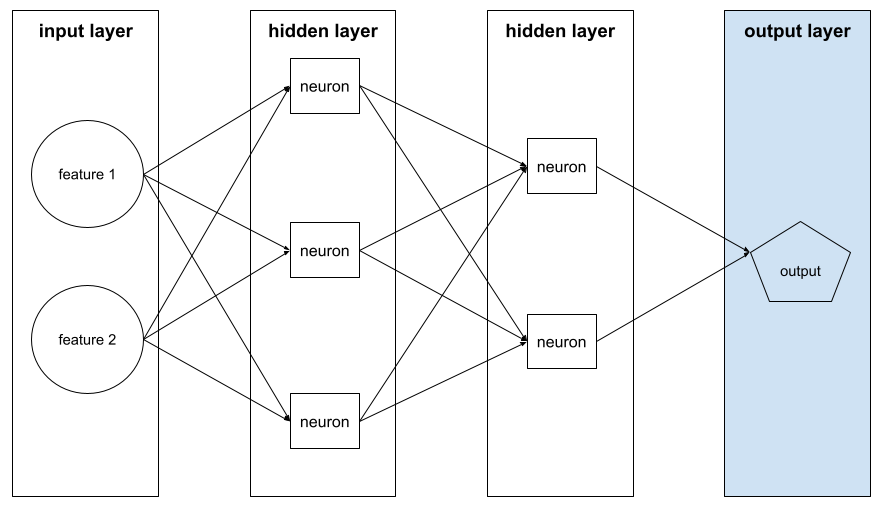
sobreajuste
Creación de un modelo que coincide de tal manera con los datos de entrenamiento que no puede realizar predicciones correctas con datos nuevos.
La regularización puede reducir el sobreajuste. Entrenar el modelo con un conjunto de datos de entrenamiento grande y diverso también puede reducir el sobreajuste.
Consulta Sobreajuste en el Curso intensivo de aprendizaje automático para obtener más información.
Sobremuestreo
Se reutilizan los ejemplos de una clase minoritaria en un conjunto de datos con desequilibrio de clases para crear un conjunto de entrenamiento más equilibrado.
Por ejemplo, considera un problema de clasificación binaria en el que la proporción de la clase mayoritaria con respecto a la clase minoritaria es de 5,000:1. Si el conjunto de datos contiene un millón de ejemplos, entonces solo contiene alrededor de 200 ejemplos de la clase minoritaria, lo que podría ser una cantidad demasiado pequeña para un entrenamiento eficaz. Para superar esta deficiencia, puedes realizar un muestreo excesivo (reutilizar) esos 200 ejemplos varias veces, lo que podría generar suficientes ejemplos para un entrenamiento útil.
Debes tener cuidado con el sobreajuste excesivo cuando realices un sobremuestreo.
Compara esto con el submuestreo.
P
Datos empaquetados
Es un enfoque para almacenar datos de manera más eficiente.
Los datos empaquetados se almacenan con un formato comprimido o de alguna otra manera que permita acceder a ellos de forma más eficiente. Los datos empaquetados minimizan la cantidad de memoria y procesamiento necesarios para acceder a ellos, lo que permite un entrenamiento más rápido y una inferencia del modelo más eficiente.
Los datos empaquetados suelen usarse con otras técnicas, como la magnificación de datos y la regularización, lo que mejora aún más el rendimiento de los modelos.
PaLM
Abreviatura de Pathways Language Model.
pandas
Es una API de análisis de datos orientada a columnas compilada sobre numpy. Muchos frameworks de aprendizaje automático, incluido TensorFlow, admiten estructuras de datos de Pandas como entradas. Para obtener más información, consulta la documentación de Pandas.
parámetro
Los pesos y los sesgos que aprende un modelo durante el entrenamiento. Por ejemplo, en un modelo de regresión lineal, los parámetros constan de la ordenada al origen (b) y todos los pesos (w1, w2, etcétera) en la siguiente fórmula:
En cambio, los hiperparámetros son los valores que tú (o un servicio de ajuste de hiperparámetros) proporcionas al modelo. Por ejemplo, la tasa de aprendizaje es un hiperparámetro.
Ajuste eficiente de parámetros
Es un conjunto de técnicas para ajustar un modelo de lenguaje entrenado previamente (PLM) grande de manera más eficiente que el ajuste completo. Por lo general, el ajuste eficiente de parámetros ajusta muchos menos parámetros que el ajuste completo, pero, aun así, produce un modelo de lenguaje extenso que funciona tan bien (o casi tan bien) como un modelo de lenguaje extenso creado a partir del ajuste completo.
Compara y contrasta el ajuste eficiente de parámetros con lo siguiente:
El ajuste eficiente de parámetros también se conoce como ajuste eficiente de parámetros.
Servidor de parámetros (PS)
Es un trabajo que mantiene un registro de los parámetros de un modelo en una configuración distribuida.
actualización de parámetros
Operación de ajustar los parámetros de un modelo durante el entrenamiento, por lo general, dentro de una sola iteración del descenso del gradiente.
derivada parcial
Es una derivada en la que todas las variables, excepto una, se consideran constantes. Por ejemplo, la derivada parcial de f(x, y) con respecto a x es la derivada de f considerada como una función de x solamente (es decir, manteniendo y constante). La derivada parcial de f con respecto a x se centra solamente en cómo cambia x e ignora todas las otras variables de la ecuación.
sesgo de participación
Sinónimo de sesgo de no respuesta. Consulta sesgo de selección.
estrategia de partición
Algoritmo por el cual las variables se dividen en servidores de parámetros.
Pase en k (pass@k)
Es una métrica para determinar la calidad del código (por ejemplo, Python) que genera un modelo de lenguaje grande. Más específicamente, la métrica de precisión en k te indica la probabilidad de que, al menos, uno de los k bloques de código generados pase todas sus pruebas de unidades.
Los modelos de lenguaje grandes suelen tener dificultades para generar código adecuado para problemas de programación complejos. Los ingenieros de software se adaptan a este problema solicitándole al modelo de lenguaje grande que genere varias (k) soluciones para el mismo problema. Luego, los ingenieros de software prueban cada una de las soluciones con pruebas de unidades. El cálculo de la aprobación en k depende del resultado de las pruebas de unidades:
- Si una o más de esas soluciones superan la prueba de unidades, el LLM aprueba ese desafío de generación de código.
- Si ninguna de las soluciones pasa la prueba de unidades, el LLM falla en ese desafío de generación de código.
La fórmula para el pase en k es la siguiente:
\[\text{pass at k} = \frac{\text{total number of passes}} {\text{total number of challenges}}\]
En general, los valores más altos de k producen puntuaciones más altas de aprobación en k; sin embargo, los valores más altos de k requieren más recursos de modelos grandes de lenguaje y pruebas de unidades.
Pathways Language Model (PaLM):
Es un modelo anterior y predecesor de los modelos de Gemini.
Pax
Es un framework de programación diseñado para entrenar modelos de redes neuronales a gran escala, tan grandes que abarcan varias porciones o pods de chips aceleradores de TPU.
Pax se basa en Flax, que se basa en JAX.
perceptrón
Sistema (de hardware o software) que toma uno o más valores de entrada, ejecuta una función sobre la suma ponderada de las entradas y calcula un valor de salida. En el aprendizaje automático, la función suele ser no lineal, como ReLU, sigmoidea o tanh. Por ejemplo, el siguiente perceptrón utiliza la función sigmoidea para procesar tres valores de entrada:
En la siguiente ilustración, el perceptrón toma tres entradas, cada una de ellas modificada por un peso antes de ingresar al perceptrón:

Los perceptrones son las neuronas en las redes neuronales.
rendimiento
Término sobrecargado con los siguientes significados:
- El significado estándar dentro de la ingeniería de software. Es decir, ¿qué tan rápidamente (o eficazmente) se ejecuta este software?
- El significado en el aprendizaje automático. Aquí, el rendimiento responde a la siguiente pregunta: ¿Qué tan correcto es este modelo? Es decir, ¿qué tan buenas son las predicciones del modelo?
Importancia de las variables por permutación
Es un tipo de importancia de la variable que evalúa el aumento en el error de predicción de un modelo después de permutar los valores del atributo. La importancia de las variables de permutación es una métrica independiente del modelo.
perplejidad
Medición de qué tan bien está logrando su tarea el modelo. Por ejemplo, supongamos que tu tarea es leer las primeras letras de una palabra que un usuario está escribiendo en el teclado de un teléfono y ofrecer una lista de posibles palabras para completar. La perplejidad, P, para esta tarea es aproximadamente la cantidad de suposiciones que debes ofrecer para que tu lista contenga la palabra real que el usuario intenta escribir.
La perplejidad está relacionada con la entropía cruzada de la siguiente manera:
canalización
Es la infraestructura que rodea a un algoritmo de aprendizaje automático. Una canalización incluye la recopilación de los datos, la colocación de los datos en archivos de datos de entrenamiento, el entrenamiento de uno o más modelos y la exportación de los modelos a producción.
Consulta Canalizaciones de AA en el curso Administración de proyectos de AA para obtener más información.
Canalización
Es una forma de paralelismo de modelos en la que el procesamiento de un modelo se divide en etapas consecutivas y cada etapa se ejecuta en un dispositivo diferente. Mientras una etapa procesa un lote, la etapa anterior puede trabajar en el siguiente lote.
Consulta también entrenamiento por etapas.
pjit
Una función de JAX que divide el código para que se ejecute en varios chips aceleradores. El usuario pasa una función a pjit, que devuelve una función que tiene la misma semántica, pero se compila en un cálculo de XLA que se ejecuta en varios dispositivos (como GPU o núcleos de TPU).
pjit permite a los usuarios fragmentar los cálculos sin volver a escribirlos con el particionador SPMD.
Desde marzo de 2023, pjit se fusionó con jit. Consulta Arrays distribuidos y paralelización automática para obtener más detalles.
PLM
Abreviatura de modelo de lenguaje previamente entrenado.
pmap
Función de JAX que ejecuta copias de una función de entrada en varios dispositivos de hardware subyacentes (CPUs, GPUs o TPUs), con diferentes valores de entrada. pmap se basa en SPMD.
.
En el aprendizaje por refuerzo, es la asignación probabilística de un agente de estados a acciones.
reducción
Reducir una matriz (o matrices) creada por una capa convolucional anterior a una matriz más pequeña. Por lo general, la reducción implica tomar el valor máximo o promedio en el área reducida. Por ejemplo, supongamos que tenemos la siguiente matriz de 3x3:
![Es la matriz de 3 x 3 [[5,3,1], [8,2,5], [9,4,3]].](https://developers.google.com/static/machine-learning/glossary/images/PoolingStart.svg?hl=es-419)
Una operación de reducción, al igual que una convolucional, divide esa matriz en porciones y luego desliza esa operación convolucional en segmentaciones. Por ejemplo, supongamos que la operación de reducción divide la matriz convolucional en porciones de 2 x 2 con una segmentación de 1 x 1. Como se ilustra en el siguiente diagrama, se realizan cuatro operaciones de pooling. Imagina que cada operación de agrupación selecciona el valor máximo de los cuatro en ese segmento:
![La matriz de entrada es de 3 x 3 con los valores: [[5,3,1], [8,2,5], [9,4,3]].
La submatriz superior izquierda de 2 x 2 de la matriz de entrada es [[5,3], [8,2]], por lo que la operación de reducción superior izquierda genera el valor 8 (que es el máximo de 5, 3, 8 y 2). La submatriz superior derecha de 2x2 de la matriz de entrada es [[3,1], [2,5]], por lo que la operación de reducción superior derecha genera el valor 5. La submatriz inferior izquierda de 2 x 2 de la matriz de entrada es [[8,2], [9,4]], por lo que la operación de reducción inferior izquierda genera el valor 9. La submatriz de 2 x 2 inferior derecha de la matriz de entrada es [[2,5], [4,3]], por lo que la operación de reducción inferior derecha genera el valor 5. En resumen, la operación de reducción genera la matriz de 2 x 2 [[8,5], [9,5]].](https://developers.google.com/static/machine-learning/glossary/images/PoolingConvolution.svg?hl=es-419)
La reducción ayuda a aplicar la invariancia traslacional en la matriz de entrada.
El pooling para las aplicaciones de visión se conoce más formalmente como pooling espacial. Las aplicaciones de series temporales suelen referirse a la agrupación como agrupación temporal. De manera menos formal, el pooling suele denominarse submuestreo o reducción de muestreo.
codificación posicional
Técnica para agregar información sobre la posición de un token en una secuencia a la incorporación del token. Los modelos Transformer utilizan la codificación posicional para comprender mejor la relación entre las diferentes partes de la secuencia.
Una implementación común de la codificación posicional usa una función sinusoidal. (Específicamente, la frecuencia y la amplitud de la función sinusoidal se determinan según la posición de la discretización en la secuencia). Esta técnica permite que un modelo Transformer aprenda a prestar atención a diferentes partes de la secuencia según su posición.
clase positiva
Es la clase para la que realizas la prueba.
Por ejemplo, la clase positiva en un modelo de cáncer podría ser "tumor". La clase positiva en un modelo de clasificación de correos electrónicos puede ser "spam".
Compara esto con la clase negativa.
posprocesamiento
Ajustar el resultado de un modelo después de que se haya ejecutado. El procesamiento posterior se puede usar para aplicar restricciones de equidad sin modificar los modelos.
Por ejemplo, se podría aplicar un posprocesamiento a un modelo de clasificación binaria estableciendo un umbral de clasificación de modo que se mantenga la igualdad de oportunidades para algún atributo verificando que la tasa de verdaderos positivos sea la misma para todos los valores de ese atributo.
modelo entrenado posteriormente
Término definido de forma imprecisa que suele hacer referencia a un modelo previamente entrenado que se sometió a algún procesamiento posterior, como uno o más de los siguientes:
PR AUC (área bajo la curva de PR)
Es el área bajo la curva de precisión-recuperación interpolada, que se obtiene trazando los puntos (recuperación, precisión) para diferentes valores del umbral de clasificación.
Praxis
Es una biblioteca de AA central y de alto rendimiento de Pax. A menudo, Praxis se denomina "biblioteca de capas".
Praxis no solo contiene las definiciones de la clase Layer, sino también la mayoría de sus componentes de asistencia, incluidos los siguientes:
- Entrada de datos
- Bibliotecas de configuración (HParam y Fiddle)
- Optimizadores
Praxis proporciona las definiciones para la clase Model.
precision
Es una métrica para los modelos de clasificación que responde la siguiente pregunta:
Cuando el modelo predijo la clase positiva, ¿qué porcentaje de las predicciones fueron correctas?
Esta es la fórmula:
Donde:
- Un verdadero positivo significa que el modelo predijo correctamente la clase positiva.
- Un falso positivo significa que el modelo predijo erróneamente la clase positiva.
Por ejemplo, supongamos que un modelo realizó 200 predicciones positivas. De estas 200 predicciones positivas, se obtuvieron los siguientes resultados:
- 150 fueron verdaderos positivos.
- 50 fueron falsos positivos.
En este caso, ocurre lo siguiente:
Compara esto con la exactitud y la recuperación.
Consulta Clasificación: Precisión, recuperación, exactitud y métricas relacionadas en el Curso intensivo de aprendizaje automático para obtener más información.
Precisión en k (precision@k)
Es una métrica para evaluar una lista de elementos clasificados (ordenados). La precisión en k identifica la fracción de los primeros k elementos de esa lista que son "relevantes". Es decir:
\[\text{precision at k} = \frac{\text{relevant items in first k items of the list}} {\text{k}}\]
El valor de k debe ser menor o igual que la longitud de la lista que se muestra. Ten en cuenta que la longitud de la lista devuelta no forma parte del cálculo.
La relevancia suele ser subjetiva. Incluso los evaluadores humanos expertos suelen no estar de acuerdo sobre qué elementos son relevantes.
Comparar con:
curva de precisión-recuperación
Curva de precisión en función de la recuperación en diferentes umbrales de clasificación.
predicción
Es el resultado de un modelo. Por ejemplo:
- La predicción de un modelo de clasificación binaria es la clase positiva o la clase negativa.
- La predicción de un modelo de clasificación de varias clases es una clase.
- La predicción de un modelo de regresión lineal es un número.
sesgo de predicción
Es un valor que indica qué tan lejos está el promedio de las predicciones del promedio de las etiquetas en el conjunto de datos.
No se debe confundir con el término de sesgo en los modelos de aprendizaje automático ni con el sesgo en la ética y la equidad.
AA predictivo
Cualquier sistema de aprendizaje automático estándar ("clásico").
El término AA predictivo no tiene una definición formal. Más bien, el término distingue una categoría de sistemas de AA no basados en la IA generativa.
Paridad predictiva
Es una métrica de equidad que verifica si, para un modelo de clasificación determinado, las tasas de precisión son equivalentes para los subgrupos en consideración.
Por ejemplo, un modelo que predice la aceptación en la universidad satisfaría la paridad predictiva para la nacionalidad si su tasa de precisión es la misma para los liliputienses y los brobdingnagianos.
A veces, la paridad predictiva también se denomina paridad de la tasa predictiva.
Consulta "Explicación de las definiciones de equidad" (sección 3.2.1) para obtener un análisis más detallado de la paridad predictiva.
Paridad de tarifas predictiva
Otro nombre para la paridad predictiva.
preprocesamiento
Procesamiento de datos antes de que se usen para entrenar un modelo El preprocesamiento puede ser tan simple como quitar palabras de un corpus de texto en inglés que no aparecen en el diccionario de inglés, o tan complejo como volver a expresar los datos de una manera que elimine la mayor cantidad posible de atributos correlacionados con los atributos sensibles. El preprocesamiento puede ayudar a satisfacer las restricciones de equidad.modelo previamente entrenado
Si bien este término podría referirse a cualquier modelo o vector de embedding entrenado, ahora se suele referir a un modelo de lenguaje grande entrenado o a otro tipo de modelo de IA generativa entrenado.
Consulta también modelo base y modelo de base.
autosupervisado
El entrenamiento inicial de un modelo en un conjunto de datos grande Algunos modelos entrenados previamente son gigantes torpes y, por lo general, deben perfeccionarse con entrenamiento adicional. Por ejemplo, los expertos en AA podrían entrenar previamente un modelo de lenguaje grande con un vasto conjunto de datos de texto, como todas las páginas en inglés de Wikipedia. Después del entrenamiento previo, el modelo resultante se puede refinar aún más con cualquiera de las siguientes técnicas:
creencia a priori
Tu conocimiento acerca de los datos antes de que empieces a entrenarlos. Por ejemplo, la regularización L2 se basa en una creencia a priori de que los pesos deben ser pequeños y estar distribuidos normalmente alrededor de cero.
Pro
Un modelo de Gemini con menos parámetros que Ultra, pero más que Nano. Consulta Gemini Pro para obtener más información.
modelo de regresión probabilística
Un modelo de regresión que usa no solo los pesos de cada atributo, sino también la incertidumbre de esos pesos. Un modelo de regresión probabilístico genera una predicción y la incertidumbre de esa predicción. Por ejemplo, un modelo de regresión probabilística podría generar una predicción de 325 con una desviación estándar de 12. Para obtener más información sobre los modelos de regresión probabilística, consulta este Colab en tensorflow.org.
función de densidad de probabilidad
Es una función que identifica la frecuencia con la que las muestras de datos tienen exactamente un valor determinado. Cuando los valores de un conjunto de datos son números de punto flotante continuos, rara vez se producen coincidencias exactas. Sin embargo, integrar una función de densidad de probabilidad desde el valor x hasta el valor y produce la frecuencia esperada de las muestras de datos entre x y y.
Por ejemplo, considera una distribución normal con una media de 200 y una desviación estándar de 30. Para determinar la frecuencia esperada de las muestras de datos que se encuentran dentro del rango de 211.4 a 218.7, puedes integrar la función de densidad de probabilidad para una distribución normal de 211.4 a 218.7.
instrucción
Cualquier texto que se ingresa como entrada en un modelo de lenguaje grande para condicionar el modelo y que se comporte de una manera determinada. Las instrucciones pueden ser tan cortas como una frase o tan largas como se desee (por ejemplo, el texto completo de una novela). Las instrucciones se clasifican en varias categorías, incluidas las que se muestran en la siguiente tabla:
| Categoría de instrucción | Ejemplo | Notas |
|---|---|---|
| Pregunta | ¿Qué tan rápido puede volar una paloma? | |
| Instrucción | Escribe un poema divertido sobre el arbitraje. | Es una instrucción que le pide al modelo de lenguaje grande que haga algo. |
| Ejemplo | Traduce el código de Markdown a HTML. Por ejemplo:
Markdown: * list item HTML: <ul> <li>list item</li> </ul> |
La primera oración de esta instrucción de ejemplo es una instrucción. El resto de la instrucción es el ejemplo. |
| Rol | Explicar por qué se usa el descenso de gradientes en el entrenamiento del aprendizaje automático a un doctor en Física | La primera parte de la oración es una instrucción; la frase "para obtener un doctorado en Física" es la parte del rol. |
| Entrada parcial para que el modelo la complete | El primer ministro del Reino Unido vive en | Una instrucción de entrada parcial puede terminar de forma abrupta (como en este ejemplo) o con un guion bajo. |
Un modelo de IA generativa puede responder a una instrucción con texto, código, imágenes, incorporaciones, videos… casi cualquier cosa.
aprendizaje basado en instrucciones
Es una capacidad de ciertos modelos que les permite adaptar su comportamiento en respuesta a entradas de texto arbitrarias (instrucciones). En un paradigma de aprendizaje basado en instrucciones típico, un modelo de lenguaje grande responde a una instrucción generando texto. Por ejemplo, supongamos que un usuario ingresa la siguiente instrucción:
Resume la tercera ley del movimiento de Newton.
Un modelo capaz de aprender a partir de instrucciones no se entrena específicamente para responder la instrucción anterior. En cambio, el modelo "conoce" muchos datos sobre física, muchas reglas generales del lenguaje y mucha información sobre lo que constituye respuestas generalmente útiles. Ese conocimiento es suficiente para proporcionar una respuesta (con suerte) útil. La retroalimentación humana adicional ("Esa respuesta fue demasiado complicada" o "¿Qué es una reacción?") permite que algunos sistemas de aprendizaje basados en instrucciones mejoren gradualmente la utilidad de sus respuestas.
Diseño de instrucciones
Sinónimo de ingeniería de instrucciones.
Ingeniería de instrucciones
El arte de crear instrucciones que produzcan las respuestas deseadas de un modelo de lenguaje grande Los humanos realizan la ingeniería de instrucciones. Escribir instrucciones bien estructuradas es una parte esencial para garantizar respuestas útiles de un modelo de lenguaje grande. La ingeniería de instrucciones depende de muchos factores, incluidos los siguientes:
- Es el conjunto de datos que se usa para entrenar previamente y, posiblemente, ajustar el modelo de lenguaje grande.
- Son el parámetro temperature y otros parámetros de decodificación que el modelo usa para generar respuestas.
Diseño de instrucciones es sinónimo de ingeniería de instrucciones.
Consulta Introducción al diseño de instrucciones para obtener más detalles sobre cómo escribir instrucciones útiles.
conjunto de instrucciones
Es un grupo de instrucciones para evaluar un modelo de lenguaje grande. Por ejemplo, la siguiente ilustración muestra un conjunto de instrucciones que consta de tres instrucciones:
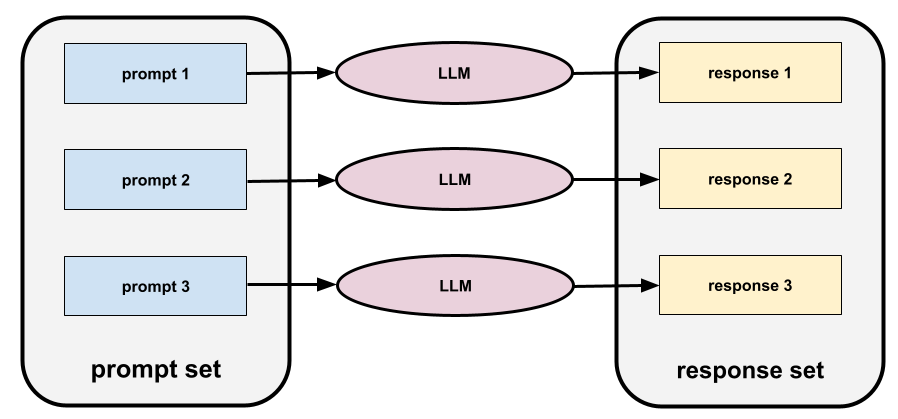
Los buenos conjuntos de instrucciones constan de una colección de instrucciones lo suficientemente "amplia" para evaluar a fondo la seguridad y la utilidad de un modelo de lenguaje grande.
Consulta también conjunto de respuestas.
Ajuste de instrucciones
Un mecanismo de ajuste eficiente de parámetros que aprende un "prefijo" que el sistema antepone a la instrucción real.
Una variación del ajuste de instrucciones, a veces denominado ajuste de prefijo, consiste en anteponer el prefijo en cada capa. En cambio, la mayoría de los ajustes de instrucciones solo agregan un prefijo a la capa de entrada.
proxy (atributos sensibles)
Es un atributo que se usa como sustituto de un atributo sensible. Por ejemplo, el código postal de una persona puede usarse como proxy de sus ingresos, raza o etnia.etiquetas de proxy
Son los datos que se usan para aproximar etiquetas que no están disponibles en el conjunto de datos de forma directa.
Por ejemplo, supongamos que debes entrenar un modelo para predecir el nivel de estrés de los empleados. Tu conjunto de datos contiene muchas variables predictivas, pero no una etiqueta llamada nivel de estrés. Sin desanimarte, eliges "accidentes laborales" como etiqueta sustituta para el nivel de estrés. Después de todo, los empleados con mucho estrés tienen más accidentes que los empleados tranquilos. ¿O sí? Quizás los accidentes laborales aumenten y disminuyan por varios motivos.
Como segundo ejemplo, supongamos que deseas que ¿Está lloviendo? sea una etiqueta booleana para tu conjunto de datos, pero este no contiene datos sobre lluvia. Si hay fotografías disponibles, podrías establecer imágenes de personas con paraguas como una etiqueta de proxy para ¿está lloviendo? ¿Es esa una buena etiqueta de proxy? Es posible, pero las personas de algunas culturas pueden ser más propensas a llevar paraguas para protegerse del sol que de la lluvia.
Las etiquetas de proxy suelen ser imperfectas. Cuando sea posible, elige etiquetas reales en lugar de etiquetas proxy. Dicho esto, cuando no haya una etiqueta real, elige la etiqueta proxy con mucho cuidado y selecciona la opción menos horrible.
Consulta Conjuntos de datos: Etiquetas en el Curso intensivo de aprendizaje automático para obtener más información.
función pura
Es una función cuyos resultados se basan solo en sus entradas y que no tiene efectos secundarios. Específicamente, una función pura no usa ni cambia ningún estado global, como el contenido de un archivo o el valor de una variable fuera de la función.
Las funciones puras se pueden usar para crear código seguro para subprocesos, lo que resulta beneficioso cuando se fragmenta el código del modelo en varios chips de acelerador.
Los métodos de transformación de funciones de JAX requieren que las funciones de entrada sean puras.
Q
Función Q
En el aprendizaje por refuerzo, es la función que predice el retorno esperado de tomar una acción en un estado y, luego, seguir una política determinada.
La función Q también se conoce como función de valor de estado-acción.
Q-learning
En el aprendizaje por refuerzo, un algoritmo que permite que un agente aprenda la función Q óptima de un proceso de decisión de Markov aplicando la ecuación de Bellman. El proceso de decisión de Markov modela un entorno.
cuantil
Cada discretización en el agrupamiento en cuantiles.
Agrupamiento en cuantiles
Distribución de los valores de un atributo en agrupamientos de forma tal que cada agrupamiento contenga la misma (o casi la misma) cantidad de ejemplos. Por ejemplo, la siguiente figura divide 44 puntos en 4 agrupamientos, cada uno de los cuales contiene 11 puntos. Para que cada grupo en la figura contenga la misma cantidad de puntos, algunos grupos abarcan un ancho diferente de valores x.

Consulta Datos numéricos: discretización en el Curso intensivo de aprendizaje automático para obtener más información.
cuantización
Término sobrecargado que se puede usar de cualquiera de las siguientes maneras:
- Implementar el agrupamiento en cuantiles en un atributo en particular
- Transformar los datos en ceros y unos para un almacenamiento, entrenamiento y generación de inferencias más rápidos Dado que los datos booleanos son más sólidos ante el ruido y los errores que otros formatos, la cuantificación puede mejorar la corrección del modelo. Las técnicas de cuantización incluyen el redondeo, el truncamiento y la discretización.
Reducir la cantidad de bits que se usan para almacenar los parámetros de un modelo Por ejemplo, supongamos que los parámetros de un modelo se almacenan como números de punto flotante de 32 bits. La cuantización convierte esos parámetros de 32 bits a 4, 8 o 16 bits. La cuantización reduce lo siguiente:
- Uso de procesamiento, memoria, disco y red
- Tiempo para inferir una predicción
- Consumo de energía
Sin embargo, a veces, la cuantización disminuye la corrección de las predicciones de un modelo.
cola
Operación de TensorFlow que implementa una estructura de datos en cola. Se suele usar en E/S.
R
RAG
Abreviatura de generación aumentada por recuperación.
bosque aleatorio
Es un ensamble de árboles de decisión en el que cada árbol de decisión se entrena con un ruido aleatorio específico, como el bagging.
Los bosques aleatorios son un tipo de bosque de decisión.
Consulta Bosque aleatorio en el curso de Bosques de decisión para obtener más información.
Política aleatoria
En el aprendizaje por refuerzo, una política que elige una acción al azar.
rango (ordinalidad)
Es la posición ordinal de una clase en un problema de aprendizaje automático que categoriza clases de la más alta a la más baja. Por ejemplo, un sistema de clasificación de conducta podría ordenar las recompensas para un perro de la más alta (un filete) a la más baja (un repollo marchitado).
rango (Tensor)
Es la cantidad de dimensiones en un Tensor. Por ejemplo, un escalar tiene rango 0, un vector tiene rango 1 y una matriz tiene rango 2.
No debe confundirse con rango (ordinalidad).
ranking
Es un tipo de aprendizaje supervisado cuyo objetivo es ordenar una lista de elementos.
evaluador
Es una persona que proporciona etiquetas para ejemplos. "Anotador" es otro nombre para calificador.
Para obtener más información, consulta Datos categóricos: Problemas comunes en el Curso intensivo de aprendizaje automático.
Conjunto de datos de comprensión de lectura con razonamiento de sentido común (ReCoRD)
Es un conjunto de datos para evaluar la capacidad de un LLM de realizar razonamientos de sentido común. Cada ejemplo del conjunto de datos contiene tres componentes:
- Un párrafo o dos de un artículo de noticias
- Es una búsqueda en la que una de las entidades identificadas de forma explícita o implícita en el pasaje está enmascarada.
- La respuesta (el nombre de la entidad que pertenece a la máscara)
Consulta ReCoRD para ver una lista extensa de ejemplos.
ReCoRD es un componente del conjunto de SuperGLUE.
RealToxicityPrompts
Es un conjunto de datos que contiene un conjunto de inicios de oraciones que podrían incluir contenido tóxico. Usa este conjunto de datos para evaluar la capacidad de un LLM de generar texto no tóxico para completar la oración. Por lo general, se usa la API de Perspective para determinar qué tan bien se desempeñó el LLM en esta tarea.
Consulta RealToxicityPrompts: Evaluating Neural Toxic Degeneration in Language Models para obtener más detalles.
recall
Es una métrica para los modelos de clasificación que responde la siguiente pregunta:
Cuando la verdad fundamental era la clase positiva, ¿qué porcentaje de predicciones identificó correctamente el modelo como la clase positiva?
Esta es la fórmula:
\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]
Donde:
- Un verdadero positivo significa que el modelo predijo correctamente la clase positiva.
- Un falso negativo significa que el modelo predijo erróneamente la clase negativa.
Por ejemplo, supongamos que tu modelo realizó 200 predicciones sobre ejemplos para los que la verdad fundamental era la clase positiva. De estas 200 predicciones, se cumplen las siguientes:
- 180 fueron verdaderos positivos.
- 20 fueron falsos negativos.
En este caso, ocurre lo siguiente:
\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]
Consulta Clasificación: Métricas de precisión, recuperación, exactitud y relacionadas para obtener más información.
Recuperación en k (recall@k)
Es una métrica para evaluar sistemas que generan una lista clasificada (ordenada) de elementos. La recuperación en k identifica la fracción de elementos pertinentes en los primeros k elementos de esa lista en relación con la cantidad total de elementos pertinentes devueltos.
\[\text{recall at k} = \frac{\text{relevant items in first k items of the list}} {\text{total number of relevant items in the list}}\]
Compara esto con la precisión en k.
Reconocimiento de la implicación textual (RTE)
Es un conjunto de datos para evaluar la capacidad de un LLM de determinar si una hipótesis se puede inferir (extraer lógicamente) de un pasaje de texto. Cada ejemplo en una evaluación de RTE consta de tres partes:
- Un pasaje, por lo general, de artículos de noticias o de Wikipedia
- Una hipótesis
- La respuesta correcta, que es una de las siguientes:
- Verdadero, lo que significa que la hipótesis puede deducirse del pasaje
- Falso, lo que significa que la hipótesis no se puede inferir del pasaje
Por ejemplo:
- Texto: El euro es la moneda de la Unión Europea.
- Hipótesis: Francia usa el euro como moneda.
- Implicación: Verdadero, porque Francia forma parte de la Unión Europea.
RTE es un componente del conjunto de SuperGLUE.
sistema de recomendación
Sistema que selecciona para cada usuario un conjunto relativamente pequeño de elementos deseables de un gran corpus. Por ejemplo, un sistema de recomendación de videos podría recomendar dos videos de un corpus de 100,000 videos, seleccionando Casablanca y The Philadelphia Story para un usuario, y Mujer Maravilla y Pantera Negra para otro. Un sistema de recomendación de video puede basar sus recomendaciones en factores tales como:
- Películas que usuarios similares han calificado o visto
- Género, directores, actores, segmento demográfico objetivo…
Para obtener más información, consulta el curso de Sistemas de recomendación.
ReCoRD
Abreviatura de Conjunto de datos de comprensión de lectura con razonamiento de sentido común.
Unidad lineal rectificada (ReLU)
Una función de activación con el siguiente comportamiento:
- Si la entrada es negativa o cero, la salida es 0.
- Si la entrada es positiva, el resultado es igual a la entrada.
Por ejemplo:
- Si la entrada es -3, la salida es 0.
- Si la entrada es +3, el resultado es 3.0.
A continuación, se muestra un gráfico de la ReLU:
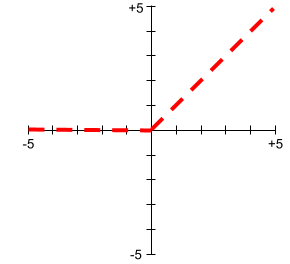
La ReLU es una función de activación muy popular. A pesar de su comportamiento simple, ReLU permite que una red neuronal aprenda relaciones no lineales entre los atributos y la etiqueta.
red neuronal recurrente
Una red neuronal que se ejecuta intencionalmente varias veces, donde partes de cada ejecución se incorporan a la siguiente ejecución. Específicamente, las capas ocultas de la ejecución anterior proporcionan parte de la entrada a la misma capa oculta en la siguiente ejecución. Las redes neuronales recurrentes son particularmente útiles para evaluar secuencias, de modo que las capas ocultas puedan aprender de las ejecuciones anteriores de la red neuronal sobre partes anteriores de la secuencia.
Por ejemplo, en la siguiente figura se muestra una red neuronal recurrente que se ejecuta cuatro veces. Observa que los valores aprendidos en las capas ocultas de la primera ejecución se convierten en parte de la entrada para las mismas capas ocultas en la segunda ejecución. De manera similar, los valores aprendidos en la capa oculta en la segunda ejecución se convierten en parte de la entrada para la misma capa oculta en la tercera ejecución. De esta manera, la red neuronal recurrente entrena y predice gradualmente el significado de toda la secuencia en lugar de solo el significado de palabras individuales.

texto de referencia
Respuesta de un experto a una instrucción. Por ejemplo, dada la siguiente instrucción:
Traduce la pregunta "¿Cómo te llamas?" del inglés al francés.
La respuesta de un experto podría ser la siguiente:
Comment vous appelez-vous?
Varias métricas (como ROUGE) miden el grado en que el texto de referencia coincide con el texto generado de un modelo de AA.
reflexión
Estrategia para mejorar la calidad de un flujo de trabajo basado en agentes examinando (reflexionando sobre) el resultado de un paso antes de pasarlo al siguiente.
A menudo, el examinador es el mismo LLM que generó la respuesta (aunque podría ser un LLM diferente). ¿Cómo podría el mismo LLM que generó una respuesta ser un juez imparcial de su propia respuesta? El "truco" consiste en poner al LLM en un estado mental crítico (reflexivo). Este proceso es análogo al de un escritor que usa una mentalidad creativa para escribir un primer borrador y, luego, cambia a una mentalidad crítica para editarlo.
Por ejemplo, imagina un flujo de trabajo de agente cuyo primer paso es crear texto para tazas de café. La instrucción para este paso podría ser la siguiente:
Eres creativo. Genera un texto original y humorístico de menos de 50 caracteres adecuado para una taza de café.
Ahora, imagina la siguiente instrucción reflexiva:
Eres bebedor de café. ¿Considerarías humorística la respuesta anterior?
Luego, el flujo de trabajo podría pasar solo el texto que recibe una puntuación de reflexión alta a la siguiente etapa.
modelo de regresión
De manera informal, un modelo que genera una predicción numérica. (En cambio, un modelo de clasificación genera una predicción de clase). Por ejemplo, todos los siguientes son modelos de regresión:
- Un modelo que predice el valor de una casa determinada en euros, por ejemplo, 423,000.
- Un modelo que predice la esperanza de vida de un árbol determinado en años, por ejemplo, 23.2.
- Un modelo que predice la cantidad de lluvia en pulgadas que caerá en una ciudad determinada durante las próximas seis horas, por ejemplo, 0.18.
Estos son dos tipos comunes de modelos de regresión:
- Regresión lineal, que encuentra la línea que mejor se ajusta a los valores de la etiqueta para los atributos.
- La regresión logística, que genera una probabilidad entre 0.0 y 1.0 que un sistema suele asignar a una predicción de clase.
No todos los modelos que generan predicciones numéricas son modelos de regresión. En algunos casos, una predicción numérica es en realidad un modelo de clasificación que tiene nombres de clase numéricos. Por ejemplo, un modelo que predice un código postal numérico es un modelo de clasificación, no un modelo de regresión.
regularización
Cualquier mecanismo que reduzca el sobreajuste Entre los tipos populares de regularización, se incluyen los siguientes:
- Regularización L1
- Regularización de L2
- Regularización de retirados
- Interrupción anticipada (este no es un método de regularización formal, pero puede limitar el sobreajuste de manera eficaz)
La regularización también se puede definir como la penalización de la complejidad de un modelo.
Consulta Sobreajuste: complejidad del modelo en el Curso intensivo de aprendizaje automático para obtener más información.
tasa de regularización
Es un número que especifica la importancia relativa de la regularización durante el entrenamiento. Aumentar la tasa de regularización reduce el sobreajuste, pero puede disminuir la capacidad predictiva del modelo. Por el contrario, reducir u omitir la tasa de regularización aumenta el sobreajuste.
Consulta Sobreajuste: Regularización L2 en el Curso intensivo de aprendizaje automático para obtener más información.
aprendizaje por refuerzo (RL)
Es una familia de algoritmos que aprenden una política óptima, cuyo objetivo es maximizar el retorno cuando interactúan con un entorno. Por ejemplo, la máxima recompensa para la mayoría de los juegos es la victoria. Los sistemas de aprendizaje por refuerzo pueden convertirse en expertos en juegos complejos evaluando secuencias de movimientos de juego anteriores que finalmente llevaron a victorias y secuencias que finalmente llevaron a derrotas.
Aprendizaje por refuerzo con retroalimentación humana (RLHF)
Usar la retroalimentación de evaluadores humanos para mejorar la calidad de las respuestas de un modelo Por ejemplo, un mecanismo de RLHF puede pedirles a los usuarios que califiquen la calidad de la respuesta de un modelo con un emoji 👍 o 👎. Luego, el sistema puede ajustar sus respuestas futuras en función de esos comentarios.
ReLU
Abreviatura de unidad lineal rectificada.
búfer de reproducción
En los algoritmos similares a DQN, es la memoria que usa el agente para almacenar las transiciones de estado y usarlas en el replay de experiencia.
de Cloud SQL
Una copia (o parte de) un conjunto de entrenamiento o un modelo, que suele almacenarse en otra máquina. Por ejemplo, un sistema podría usar la siguiente estrategia para implementar el paralelismo de datos:
- Coloca réplicas de un modelo existente en varias máquinas.
- Envía diferentes subconjuntos del conjunto de entrenamiento a cada réplica.
- Agrega las actualizaciones del parámetro.
Una réplica también puede hacer referencia a otra copia de un servidor de inferencia. Aumentar la cantidad de réplicas incrementa la cantidad de solicitudes que el sistema puede atender de forma simultánea, pero también aumenta los costos de entrega.
sesgo de reporte
El hecho de que la frecuencia con la que las personas escriben sobre acciones, resultados o propiedades no es un reflejo fiel de las frecuencias reales o del grado en que una propiedad es típica de una clase de individuos. El sesgo de reporte puede influenciar la composición de los datos sobre los que los sistemas de aprendizaje automático aprenden.
Por ejemplo, en los libros, la palabra reír es más frecuente que la que se respirar. Un modelo de aprendizaje automático que estima la frecuencia relativa de la risa y la respiración a partir de un corpus de libros probablemente determinaría que la risa es más común que la respiración.
Consulta Equidad: Tipos de sesgo en el Curso intensivo de aprendizaje automático para obtener más información.
representación de vectores
Proceso de asignar datos a atributos útiles.
reclasificación
La etapa final de un sistema de recomendación, durante la cual los elementos calificados se pueden volver a calificar de acuerdo con algún otro algoritmo (por lo general, no de AA). La reclasificación evalúa la lista de elementos generados por la fase de puntuación, realizando acciones tales como:
- Eliminar los elementos que el usuario ya compró
- Aumentar la puntuación de elementos más recientes
Para obtener más información, consulta Reordenamiento de resultados en el curso de Sistemas de recomendación.
respuesta
El texto, las imágenes, el audio o el video que infiere un modelo de IA generativa. En otras palabras, una instrucción es la entrada para un modelo de IA generativa, y la respuesta es la salida.
conjunto de respuestas
Es la colección de respuestas que un modelo de lenguaje grande devuelve a un conjunto de instrucciones de entrada.
Generación mejorada por recuperación (RAG)
Técnica para mejorar la calidad del resultado del modelo de lenguaje grande (LLM) fundamentándolo con fuentes de conocimiento recuperadas después del entrenamiento del modelo. La RAG mejora la precisión de las respuestas de los LLM, ya que les proporciona acceso a información recuperada de bases de conocimiento o documentos confiables.
Entre las motivaciones comunes para usar la generación mejorada por recuperación, se incluyen las siguientes:
- Aumentar la exactitud fáctica de las respuestas generadas por un modelo
- Darle acceso al modelo a conocimientos con los que no se entrenó
- Cambiar el conocimiento que usa el modelo
- Permite que el modelo cite fuentes.
Por ejemplo, supongamos que una app de química usa la API de PaLM para generar resúmenes relacionados con las búsquedas de los usuarios. Cuando el backend de la app recibe una búsqueda, hace lo siguiente:
- Busca (o "recupera") datos relevantes para la búsqueda del usuario.
- Agrega ("aumenta") los datos químicos pertinentes a la búsqueda del usuario.
- Indica al LLM que cree un resumen basado en los datos adjuntos.
devolución
En el aprendizaje por refuerzo, dada una política y un estado determinados, el retorno es la suma de todas las recompensas que el agente espera recibir cuando sigue la política desde el estado hasta el final del episodio. El agente tiene en cuenta la naturaleza retrasada de las recompensas esperadas descontando las recompensas según las transiciones de estado necesarias para obtener la recompensa.
Por lo tanto, si el factor de descuento es \(\gamma\), y \(r_0, \ldots, r_{N}\)denota las recompensas hasta el final del episodio, el cálculo del retorno es el siguiente:
una recompensa
En el aprendizaje por refuerzo, el resultado numérico de realizar una acción en un estado, según lo define el entorno.
Regularización de cresta
Sinónimo de regularización L2. El término regularización de cresta se usa con más frecuencia en contextos de estadística pura, mientras que regularización L2 se usa con más frecuencia en el aprendizaje automático.
RNN
Abreviatura de redes neuronales recurrentes.
Curva ROC (característica operativa del receptor)
Es un gráfico de la tasa de verdaderos positivos en comparación con la tasa de falsos positivos para diferentes umbrales de clasificación en la clasificación binaria.
La forma de una curva ROC sugiere la capacidad de un modelo de clasificación binaria para separar las clases positivas de las negativas. Supongamos, por ejemplo, que un modelo de clasificación binaria separa perfectamente todas las clases negativas de todas las clases positivas:
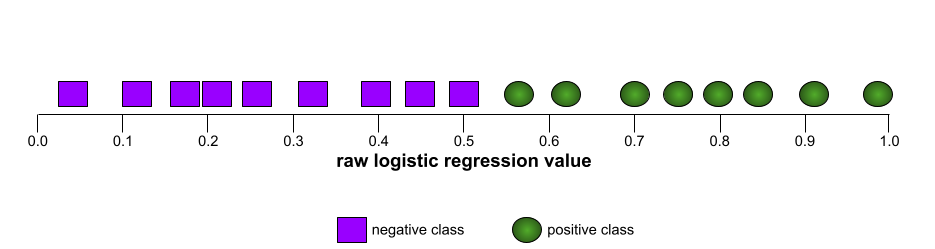
La curva ROC del modelo anterior se ve de la siguiente manera:
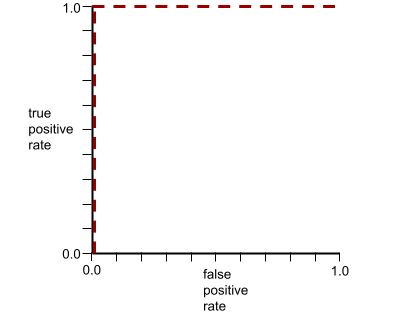
En cambio, en la siguiente ilustración, se grafican los valores de regresión logística sin procesar para un modelo deficiente que no puede separar las clases negativas de las positivas:
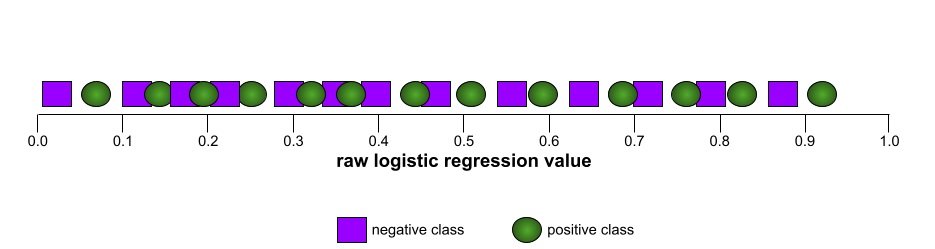
La curva ROC para este modelo se ve de la siguiente manera:
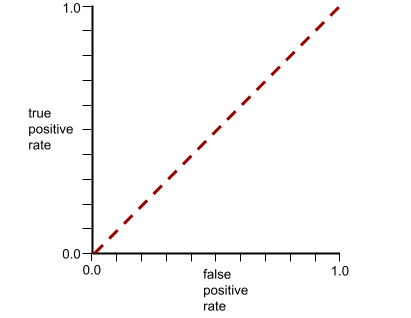
Mientras tanto, en el mundo real, la mayoría de los modelos de clasificación binaria separan las clases positivas y negativas en cierto grado, pero no de forma perfecta. Por lo tanto, una curva ROC típica se encuentra en algún punto entre los dos extremos:
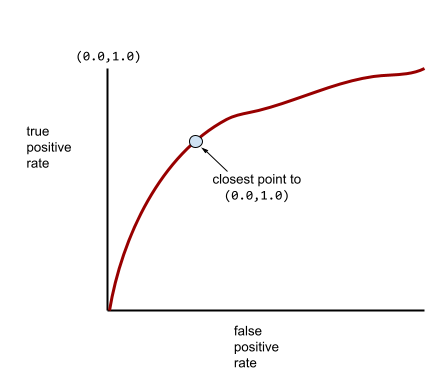
En teoría, el punto de una curva ROC más cercano a (0.0, 1.0) identifica el umbral de clasificación ideal. Sin embargo, varios otros problemas del mundo real influyen en la selección del umbral de clasificación ideal. Por ejemplo, tal vez los falsos negativos causen mucho más dolor que los falsos positivos.
Una métrica numérica llamada AUC resume la curva ROC en un solo valor de punto flotante.
Instrucciones con roles
Una instrucción, que suele comenzar con el pronombre tú, que le indica a un modelo de IA generativa que finja ser una persona o un rol determinado cuando genere la respuesta. Las instrucciones de rol pueden ayudar a un modelo de IA generativa a adoptar la "mentalidad" adecuada para generar una respuesta más útil. Por ejemplo, cualquiera de las siguientes instrucciones de rol podría ser adecuada según el tipo de respuesta que busques:
Tienes un doctorado en informática.
Eres ingeniero de software y te gusta dar explicaciones pacientes sobre Python a los estudiantes de programación nuevos.
Eres un héroe de acción con un conjunto muy particular de habilidades de programación. Asegúrame que encontrarás un elemento específico en una lista de Python.
raíz
Es el nodo inicial (la primera condición) en un árbol de decisión. Por convención, los diagramas colocan la raíz en la parte superior del árbol de decisión. Por ejemplo:
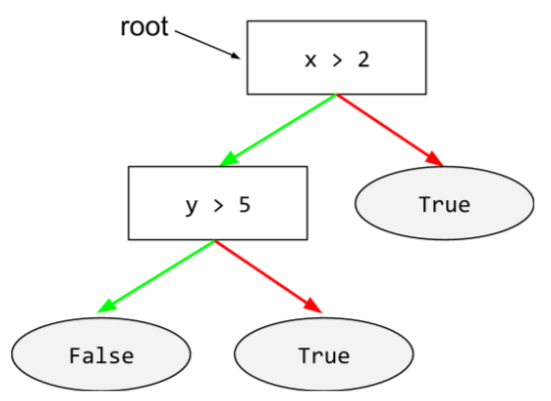
directorio raíz
Es el directorio que especificas para alojar subdirectorios del punto de control de TensorFlow y archivos de eventos de varios modelos.
Raíz cuadrada del error cuadrático medio (RMSE)
Raíz cuadrada del error cuadrático medio.
invariancia rotacional
En un problema de clasificación de imágenes, es la capacidad de un algoritmo para clasificar imágenes de forma correcta incluso cuando cambia la orientación de la imagen. Por ejemplo, el algoritmo aún puede identificar una raqueta de tenis, ya sea que apunte hacia arriba, hacia los lados o hacia abajo. Ten en cuenta que la invariancia rotacional no siempre es deseable; por ejemplo, un 9 al revés no debe clasificarse como un 9.
Consulta también invariancia de traslación y invariancia de tamaño.
ROUGE (Recall-Oriented Understudy for Gisting Evaluation)
Es una familia de métricas que evalúan los modelos de traducción automática y resumen automático. Las métricas de ROUGE determinan el grado en que un texto de referencia se superpone con el texto generado de un modelo de AA. Cada miembro de la familia ROUGE mide la superposición de una manera diferente. Las puntuaciones ROUGE más altas indican una mayor similitud entre el texto de referencia y el texto generado que las puntuaciones ROUGE más bajas.
Por lo general, cada miembro de la familia ROUGE genera las siguientes métricas:
- Precisión
- Recuperación
- F1
Para obtener detalles y ejemplos, consulta lo siguiente:
ROUGE-L
Es un miembro de la familia ROUGE que se enfoca en la longitud de la subsecuencia común más larga en el texto de referencia y el texto generado. Las siguientes fórmulas calculan la recuperación y la precisión de ROUGE-L:
Luego, puedes usar F1 para combinar la recuperación de ROUGE-L y la precisión de ROUGE-L en una sola métrica:
ROUGE-L ignora los saltos de línea en el texto de referencia y el texto generado, por lo que la subsecuencia común más larga podría abarcar varias oraciones. Cuando el texto de referencia y el texto generado involucran varias oraciones, ROUGE-Lsum, una variación de ROUGE-L, suele ser una mejor métrica. ROUGE-Lsum determina la subsecuencia común más larga para cada oración de un pasaje y, luego, calcula la media de esas subsecuencias comunes más largas.
ROUGE-N
Es un conjunto de métricas dentro de la familia ROUGE que compara los N-gramas compartidos de un tamaño determinado en el texto de referencia y el texto generado. Por ejemplo:
- ROUGE-1 mide la cantidad de tokens compartidos en el texto de referencia y el texto generado.
- ROUGE-2 mide la cantidad de bigramas (2-gramas) compartidos en el texto de referencia y el texto generado.
- ROUGE-3 mide la cantidad de trigramas (3-gramas) compartidos en el texto de referencia y el texto generado.
Puedes usar las siguientes fórmulas para calcular la recuperación de ROUGE-N y la precisión de ROUGE-N para cualquier miembro de la familia de ROUGE-N:
Luego, puedes usar F1 para resumir la recuperación de ROUGE-N y la precisión de ROUGE-N en una sola métrica:
ROUGE-S
Es una forma flexible de ROUGE-N que permite la correlación de skip-gramas. Es decir, ROUGE-N solo cuenta los n-gramas que coinciden exactamente, pero ROUGE-S también cuenta los n-gramas separados por una o más palabras. Por ejemplo, considera lo siguiente:
- Texto de referencia: Nubes blancas
- Texto generado: Nubes blancas y ondulantes
Cuando se calcula ROUGE-N, el 2-grama Nubes blancas no coincide con Nubes blancas y ondulantes. Sin embargo, cuando se calcula ROUGE-S, Nubes blancas sí coincide con Nubes blancas y ondulantes.
R al cuadrado
Es una métrica de regresión que indica qué parte de la variación en una etiqueta se debe a un atributo individual o a un conjunto de atributos. El coeficiente de determinación R² es un valor entre 0 y 1 que puedes interpretar de la siguiente manera:
- Un R al cuadrado de 0 significa que ninguna variación de la etiqueta se debe al conjunto de atributos.
- Un R al cuadrado de 1 significa que toda la variación de la etiqueta se debe al conjunto de atributos.
- Un R al cuadrado entre 0 y 1 indica en qué medida la variación de la etiqueta se puede predecir a partir de un atributo en particular o del conjunto de atributos. Por ejemplo, un R al cuadrado de 0.10 significa que el 10% de la varianza en la etiqueta se debe al conjunto de atributos, un R al cuadrado de 0.20 significa que el 20% se debe al conjunto de atributos, y así sucesivamente.
R al cuadrado es el cuadrado del coeficiente de correlación de Pearson entre los valores que predijo un modelo y la verdad fundamental.
RTE
Abreviatura de Recognizing Textual Entailment.
S
sesgo muestral
Consulta sesgo de selección.
Muestreo con reemplazo
Es un método para elegir elementos de un conjunto de elementos candidatos en el que se puede elegir el mismo elemento varias veces. La frase "con reemplazo" significa que, después de cada selección, el elemento seleccionado se devuelve al conjunto de elementos candidatos. El método inverso, muestreo sin reemplazo, significa que un elemento candidato solo se puede elegir una vez.
Por ejemplo, considera el siguiente conjunto de frutas:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}Supongamos que el sistema elige de forma aleatoria fig como el primer elemento.
Si se usa el muestreo con reemplazo, el sistema elige el segundo elemento del siguiente conjunto:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}Sí, es el mismo conjunto que antes, por lo que el sistema podría volver a elegir fig.
Si se usa el muestreo sin reemplazo, una vez que se selecciona una muestra, no se puede volver a seleccionar. Por ejemplo, si el sistema elige al azar fig como la primera muestra, no se puede volver a elegir fig. Por lo tanto, el sistema elige la segunda muestra del siguiente conjunto (reducido):
fruit = {kiwi, apple, pear, cherry, lime, mango}modelo guardado
Es el formato recomendado para guardar y recuperar modelos de TensorFlow. SavedModel es un formato de serialización recuperable y neutral con respecto al lenguaje que permite que las herramientas y los sistemas de nivel superior produzcan, consuman y transformen modelos de TensorFlow.
Para obtener más información, consulta la sección sobre cómo guardar y restablecer en la Guía para programadores de TensorFlow.
Económico
Un objeto de TensorFlow responsable de guardar controles del modelo.
escalar
Un solo número o una sola cadena que se puede representar como un tensor de rango 0. Por ejemplo, las siguientes líneas de código crean cada una un escalar en TensorFlow:
breed = tf.Variable("poodle", tf.string)
temperature = tf.Variable(27, tf.int16)
precision = tf.Variable(0.982375101275, tf.float64)escalamiento
Cualquier transformación o técnica matemática que desplace el rango de una etiqueta, un valor de atributo o ambos. Algunas formas de escalamiento son muy útiles para transformaciones como la normalización.
Entre las formas comunes de escalamiento útiles en el aprendizaje automático, se incluyen las siguientes:
- El ajuste lineal, que suele usar una combinación de resta y división para reemplazar el valor original por un número entre -1 y +1 o entre 0 y 1
- Escala logarítmica, que reemplaza el valor original por su logaritmo.
- Normalización de la puntuación Z, que reemplaza el valor original por un valor de punto flotante que representa la cantidad de desviaciones estándares desde la media de ese atributo
scikit-learn
Una plataforma de aprendizaje automático de código abierto muy popular. Consulta scikit-learn.org.
puntuación
Es la parte de un sistema de recomendación que proporciona un valor o una clasificación para cada elemento producido por la fase de generación de candidatos.
sesgo de selección
Errores en las conclusiones que se extraen de los datos muestreados debido a un proceso de selección que genera diferencias sistemáticas entre las muestras observadas en los datos y las no observadas. Existen las siguientes formas de sesgo de selección:
- Sesgo de cobertura: La población representada en el conjunto de datos no coincide con la población sobre la cual el modelo de aprendizaje automático realiza predicciones.
- Sesgo muestral: Los datos no se recopilan de forma aleatoria del grupo objetivo.
- Sesgo de no respuesta (también llamado sesgo de participación): Los usuarios de ciertos grupos rechazan realizar encuestas con frecuencias diferentes que los usuarios de otros grupos.
Por ejemplo, supongamos que creas un modelo de aprendizaje automático que predice cuánto disfrutan las personas una película. Para recopilar datos de entrenamiento, dejas una encuesta a todos en frente del lugar donde se proyecta la película. A primera vista, esto parece una forma razonable para recopilar un conjunto de datos; sin embargo, esta forma de recopilación de datos puede introducir las siguientes formas de sesgo de selección:
- sesgo de cobertura: Tomar una muestra de una población que eligió ver la película posibilita que las predicciones de tu modelo no generalicen a las personas que aún no expresaron ese nivel de interés en la película.
- sesgo muestral: En lugar de muestrear aleatoriamente desde la población prevista (todas las personas en la película), solo se muestrearon las personas en la primera fila. Es posible que las personas sentadas en la primera fila estén más interesadas en la película que aquellas en otras filas.
- sesgo de no respuesta: En general, las personas con opiniones fuertes tienden a responder a las encuestas opcionales con mayor frecuencia que las personas con opiniones moderadas. Como la encuesta de la película es opcional, es más probable que las respuestas formen una distribución bimodal en lugar de una distribución normal (con forma de campana).
Autoatención (también llamada capa de autoatención)
Capa de red neuronal que transforma una secuencia de embeddings (por ejemplo, embeddings de tokens) en otra secuencia de embeddings. Cada incorporación en la secuencia de salida se construye integrando información de los elementos de la secuencia de entrada a través de un mecanismo de atención.
La parte auto de autoatención hace referencia a la secuencia que se atiende a sí misma en lugar de a algún otro contexto. La autoatención es uno de los principales componentes básicos de los Transformers y usa terminología de búsqueda de diccionario, como "consulta", "clave" y "valor".
Una capa de autoatención comienza con una secuencia de representaciones de entrada, una para cada palabra. La representación de entrada para una palabra puede ser una incorporación simple. Para cada palabra de una secuencia de entrada, la red califica la relevancia de la palabra para cada elemento de toda la secuencia de palabras. Las puntuaciones de relevancia determinan en qué medida la representación final de la palabra incorpora las representaciones de otras palabras.
Por ejemplo, considera la siguiente oración:
El animal no cruzó la calle porque estaba demasiado cansado.
La siguiente ilustración (de Transformer: A Novel Neural Network Architecture for Language Understanding) muestra el patrón de atención de una capa de autoatención para el pronombre it, en la que la oscuridad de cada línea indica cuánto contribuye cada palabra a la representación:
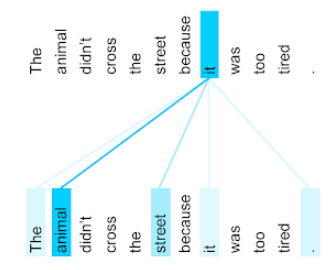
La capa de autoatención destaca las palabras que son relevantes para "it". En este caso, la capa de atención aprendió a destacar las palabras a las que podría referirse, y asignó el peso más alto a animal.
Para una secuencia de n tokens, la autoatención transforma una secuencia de embeddings n veces separadas, una vez en cada posición de la secuencia.
Consulta también atención y atención propia de varios encabezados.
aprendizaje autoguiado
Es una familia de técnicas para convertir un problema de aprendizaje automático no supervisado en un problema de aprendizaje automático supervisado creando etiquetas sustitutas a partir de ejemplos sin etiquetar.
Algunos modelos basados en Transformer, como BERT, utilizan el aprendizaje supervisado por sí mismo.
El entrenamiento autovigilado es un enfoque de aprendizaje semisupervisado.
autocapacitación
Es una variante del aprendizaje autovigilado que resulta especialmente útil cuando se cumplen todas las siguientes condiciones:
- La proporción de ejemplos sin etiquetar en relación con los ejemplos etiquetados en el conjunto de datos es alta.
- Este es un problema de clasificación.
El autoentrenamiento funciona iterando los siguientes dos pasos hasta que el modelo deja de mejorar:
- Usa el aprendizaje automático supervisado para entrenar un modelo con los ejemplos etiquetados.
- Usa el modelo creado en el paso 1 para generar predicciones (etiquetas) en los ejemplos sin etiquetar y mueve aquellos en los que haya un alto nivel de confianza a los ejemplos etiquetados con la etiqueta predicha.
Observa que cada iteración del paso 2 agrega más ejemplos etiquetados para que se entrene el paso 1.
aprendizaje semisupervisado
Entrenar un modelo con datos en los que algunos ejemplos de entrenamiento tienen etiquetas, pero otros no. Una técnica para el aprendizaje semisupervisado es inferir etiquetas para los ejemplos no etiquetados y, luego, entrenar con las etiquetas inferidas para crear un modelo nuevo. El aprendizaje semisupervisado puede ser útil si es costoso obtener las etiquetas, aun cuando los ejemplos no etiquetados son abundantes.
El autoentrenamiento es una técnica de aprendizaje semisupervisado.
atributo sensible
Un atributo humano que puede ser objeto de consideración especial por motivos legales, éticos, sociales o personales.Análisis de opiniones
Usar algoritmos estadísticos o de aprendizaje automático para determinar la actitud general de un grupo (positiva o negativa) hacia un servicio, producto, organización o tema. Por ejemplo, utilizando la comprensión del lenguaje natural, un algoritmo podría realizar un análisis de opiniones en la retroalimentación textual de un curso universitario para determinar en qué grado les gustó o disgustó el curso a los estudiantes en general.
Consulta la guía de Clasificación de texto para obtener más información.
modelo de secuencia
Es un modelo cuyas entradas tienen una dependencia secuencial. Por ejemplo, la predicción del siguiente video mirado desde una secuencia de videos mirados anteriormente.
Tarea de secuencia a secuencia
Es una tarea que convierte una secuencia de entrada de tokens en una secuencia de salida de tokens. Por ejemplo, dos tipos populares de tareas de secuencia a secuencia son los siguientes:
- Traductores:
- Secuencia de entrada de ejemplo: "Te amo".
- Secuencia de salida de ejemplo: "Je t'aime".
- Búsqueda de respuestas:
- Secuencia de entrada de ejemplo: "¿Necesito mi automóvil en la ciudad de Nueva York?"
- Secuencia de salida de ejemplo: "No. Deja el auto en casa".
modelos
Proceso de hacer que un modelo entrenado esté disponible para proporcionar predicciones a través de la inferencia en línea o la inferencia sin conexión.
forma (tensor)
Es la cantidad de elementos en cada dimensión de un tensor. La forma se representa como una lista de números enteros. Por ejemplo, el siguiente tensor bidimensional tiene una forma de [3,4]:
[[5, 7, 6, 4], [2, 9, 4, 8], [3, 6, 5, 1]]
TensorFlow usa el formato principal por filas (estilo C) para representar el orden de las dimensiones, por lo que la forma en TensorFlow es [3,4] en lugar de [4,3]. En otras palabras, en un tensor bidimensional de TensorFlow, la forma es [cantidad de filas, cantidad de columnas].
Una forma estática es una forma de tensor que se conoce en el momento de la compilación.
Una forma dinámica es desconocida en el momento de la compilación y, por lo tanto, depende de los datos del tiempo de ejecución. Este tensor se puede representar con una dimensión de marcador de posición en TensorFlow, como en [3, ?].
fragmento
Es una división lógica del conjunto de entrenamiento o del modelo. Por lo general, algún proceso crea fragmentos dividiendo los ejemplos o los parámetros en fragmentos de tamaño igual (por lo general). Luego, cada fragmento se asigna a una máquina diferente.
La fragmentación de un modelo se denomina paralelismo de modelos, y la fragmentación de datos se denomina paralelismo de datos.
Contracción
Es un hiperparámetro en el aumento de gradiente que controla el sobreajuste. La reducción en el aumento del gradiente es análoga a la tasa de aprendizaje en el descenso de gradientes. La reducción es un valor decimal entre 0.0 y 1.0. Un valor de reducción más bajo reduce el sobreajuste más que un valor de reducción más alto.
evaluación en paralelo
Comparar la calidad de dos modelos juzgando sus respuestas a la misma instrucción Por ejemplo, supongamos que se les da la siguiente instrucción a dos modelos diferentes:
Crea una imagen de un perro tierno haciendo malabares con tres pelotas.
En una evaluación comparativa, un evaluador elegiría qué imagen era "mejor" (¿más precisa? ¿Más hermosa? ¿Más linda?).
función sigmoidea
Función matemática que "comprime" un valor de entrada en un rango restringido, generalmente de 0 a 1 o de -1 a +1. Es decir, puedes pasar cualquier número (dos, un millón, mil millones negativos, lo que sea) a una sigmoide y el resultado seguirá estando en el rango restringido. El gráfico de la función de activación sigmoidea se ve de la siguiente manera:

La función sigmoidea tiene varios usos en el aprendizaje automático, incluidos los siguientes:
- Convierte el resultado sin procesar de un modelo de regresión logística o de regresión multinomial en una probabilidad.
- Actúa como una función de activación en algunas redes neuronales.
medida de similitud
En los algoritmos de agrupamiento en clústeres, es la métrica que se usa para determinar qué tan parecidos (cuán similares) son dos ejemplos cualesquiera.
Programa único / datos múltiples (SPMD)
Es una técnica de paralelismo en la que el mismo cálculo se ejecuta en diferentes datos de entrada en paralelo en diferentes dispositivos. El objetivo de SPMD es obtener resultados más rápido. Es el estilo más común de programación paralela.
invariancia de tamaño
En un problema de clasificación de imágenes, es la capacidad de un algoritmo para clasificar imágenes de forma correcta incluso cuando cambia el tamaño de la imagen. Por ejemplo, el algoritmo aún puede identificar a un gato si consume 2 millones de píxeles o 200,000 píxeles. Ten en cuenta que incluso los mejores algoritmos de clasificación de imágenes tienen límites prácticos en la invariancia de tamaño. Por ejemplo, es poco probable que un algoritmo (o persona) clasifique correctamente una imagen de gato que consuma solo 20 píxeles.
Consulta también invariancia traslacional y invariancia rotacional.
Consulta el curso sobre clustering para obtener más información.
boceto
En el aprendizaje automático no supervisado, una categoría de algoritmos que ejecutan un análisis preliminar de similitud de los ejemplos. Los algoritmos de esbozo usan una función de hash sensible a la localidad para identificar puntos que probablemente sean similares y luego juntarlos en agrupamientos.
El esbozo reduce el cómputo requerido para los cálculos de similitud en conjuntos de datos extensos. En lugar de calcular la similitud para cada par de ejemplos del conjunto de datos, se calcula la similitud solo para cada par de puntos dentro de cada discretización.
Skip-gram
Un n-grama que puede omitir (o "saltar") palabras del contexto original, lo que significa que las N palabras podrían no haber sido adyacentes originalmente. Más precisamente, un "n-grama de k-omisiones" es un n-grama para el que se pueden haber omitido hasta k palabras.
Por ejemplo, "the quick brown fox" tiene los siguientes bigramas posibles:
- "the quick"
- "quick brown"
- "zorro marrón"
Un "1-skip-2-gram" es un par de palabras que tienen como máximo 1 palabra entre ellas. Por lo tanto, "el zorro pardo rápido" tiene los siguientes 2-gramas con 1 salto:
- "el marrón"
- "quick fox"
Además, todos los 2-gramas también son 1-skip-2-gramas, ya que se puede omitir menos de una palabra.
Los skip-grams son útiles para comprender mejor el contexto que rodea a una palabra. En el ejemplo, "fox" se asoció directamente con "quick" en el conjunto de 1-skip-2-gramas, pero no en el conjunto de 2-gramas.
Los skip-grams ayudan a entrenar modelos de incorporación de palabras.
softmax
Función que determina las probabilidades para cada clase posible en un modelo de clasificación de clases múltiples. Las probabilidades suman exactamente 1.0. Por ejemplo, en la siguiente tabla, se muestra cómo la función softmax distribuye varias probabilidades:
| La imagen es… | Probabilidad |
|---|---|
| perro | .85 |
| cat | .13 |
| caballo | 0.02 |
Softmax también se denomina softmax completo.
Compara esto con el muestreo de candidatos.
Consulta Redes neuronales: clasificación de clases múltiples en el Curso intensivo de aprendizaje automático para obtener más información.
Ajuste de instrucciones secundarias
Es una técnica para ajustar un modelo de lenguaje grande para una tarea en particular, sin necesidad de un ajuste que requiera muchos recursos. En lugar de volver a entrenar todos los pesos del modelo, el ajuste de instrucciones flexible ajusta automáticamente una instrucción para lograr el mismo objetivo.
Dado un texto de instrucción, el ajuste de instrucciones con texto adicional suele agregar incorporaciones de tokens adicionales a la instrucción y usa la retropropagación para optimizar la entrada.
Una instrucción "fuerte" contiene tokens reales en lugar de incorporaciones de tokens.
atributo disperso
Es un atributo cuyos valores son predominantemente cero o están vacíos. Por ejemplo, una característica que contiene un solo valor 1 y un millón de valores 0 es dispersa. En cambio, un atributo denso tiene valores que no son predominantemente cero ni están vacíos.
En el aprendizaje automático, una cantidad sorprendente de atributos son atributos dispersos. Los atributos categóricos suelen ser atributos dispersos. Por ejemplo, de las 300 especies de árboles posibles en un bosque, un solo ejemplo podría identificar solo un arce. O bien, de los millones de videos posibles en una biblioteca de videos, un solo ejemplo podría identificar solo "Casablanca".
En un modelo, por lo general, representas los atributos dispersos con la codificación one-hot. Si la codificación one-hot es grande, puedes colocar una capa de embedding sobre la codificación one-hot para obtener una mayor eficiencia.
representación dispersa
Almacena solo las posiciones de los elementos distintos de cero en una característica dispersa.
Por ejemplo, supongamos que un atributo categórico llamado species identifica las 36 especies de árboles en un bosque en particular. Además, supongamos que cada ejemplo identifica solo una especie.
Podrías usar un vector one-hot para representar las especies de árboles en cada ejemplo.
Un vector one-hot contendría un solo 1 (para representar la especie de árbol en particular en ese ejemplo) y 35 0 (para representar las 35 especies de árboles que no se incluyen en ese ejemplo). Por lo tanto, la representación one-hot de maple podría verse de la siguiente manera:

Como alternativa, la representación dispersa simplemente identificaría la posición de la especie en particular. Si maple está en la posición 24, su representación dispersa sería la siguiente:maple
24
Observa que la representación dispersa es mucho más compacta que la representación one-hot.
Consulta Cómo trabajar con datos categóricos en el Curso intensivo de aprendizaje automático para obtener más información.
vector disperso
Vector cuyos valores son predominantemente cero. Consulta también atributo disperso y dispersión.
dispersión
Es la cantidad de elementos establecidos en cero (o nulos) en un vector o una matriz dividida por la cantidad total de entradas en ese vector o matriz. Por ejemplo, considera una matriz de 100 elementos en la que 98 celdas contienen cero. El cálculo de la dispersión es el siguiente:
La esparcidad de atributos se refiere a la esparcidad de un vector de atributos, mientras que la esparcidad del modelo se refiere a la esparcidad de los pesos del modelo.
Reducción espacial
Consulta reducción.
codificación especificacional
Proceso de escribir y mantener un archivo en un lenguaje humano (por ejemplo, inglés) que describe software. Luego, puedes pedirle a un modelo de IA generativa o a otro ingeniero de software que cree el software que cumpla con esa descripción.
El código generado automáticamente suele requerir iteraciones. En la codificación de especificaciones, iteras en el archivo de descripción. En cambio, en la programación conversacional, iteras dentro del cuadro de instrucciones. En la práctica, la generación automática de código a veces implica una combinación de ambos tipos de codificación: la específica y la conversacional.
split
En un árbol de decisión, otro nombre para una condición.
divisor
Durante el entrenamiento de un árbol de decisión, la rutina (y el algoritmo) se encargan de encontrar la mejor condición en cada nodo.
SPMD
Abreviatura de un programa y varios datos.
SQuAD
Es el acrónimo de Stanford Question Answering Dataset, que se presentó en el artículo SQuAD: 100,000+ Questions for Machine Comprehension of Text. Las preguntas de este conjunto de datos provienen de personas que hacen preguntas sobre artículos de Wikipedia. Algunas de las preguntas en SQuAD tienen respuestas, pero otras intencionalmente no las tienen. Por lo tanto, puedes usar SQuAD para evaluar la capacidad de un LLM para hacer lo siguiente:
- Responde las preguntas que se puedan responder.
- Identifica las preguntas que no se pueden responder.
Concordancia exacta en combinación con F1 son las métricas más comunes para evaluar los LLM en comparación con SQuAD.
pérdida de bisagra al cuadrado
Cuadrado de la pérdida de bisagra. La pérdida de bisagra al cuadrado penaliza los valores atípicos con mayor severidad que la pérdida de bisagra normal.
pérdida al cuadrado
Sinónimo de pérdida L2.
entrenamiento por etapas
Es una táctica para entrenar un modelo en una secuencia de etapas discretas. El objetivo puede ser acelerar el proceso de entrenamiento o lograr una mejor calidad del modelo.
A continuación, se muestra una ilustración del enfoque de apilamiento progresivo:
- La etapa 1 contiene 3 capas ocultas, la etapa 2 contiene 6 capas ocultas y la etapa 3 contiene 12 capas ocultas.
- La etapa 2 comienza el entrenamiento con los pesos aprendidos en las 3 capas ocultas de la etapa 1. La etapa 3 comienza el entrenamiento con los pesos aprendidos en las 6 capas ocultas de la etapa 2.
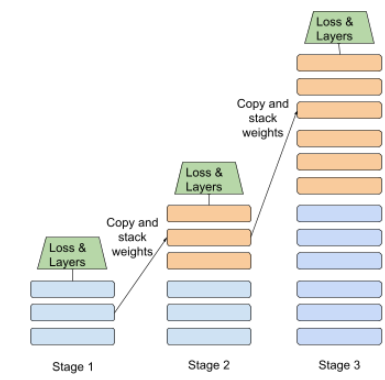
Consulta también canalización.
state
En el aprendizaje por refuerzo, son los valores de los parámetros que describen la configuración actual del entorno, que el agente usa para elegir una acción.
función de valor de estado-acción
Sinónimo de función Q.
static
Es algo que se hace una vez en lugar de continuamente. Los términos estático y sin conexión son sinónimos. A continuación, se indican los usos comunes de estático y sin conexión en el aprendizaje automático:
- Un modelo estático (o modelo sin conexión) es un modelo que se entrena una sola vez y, luego, se usa durante un tiempo.
- El entrenamiento estático (o entrenamiento sin conexión) es el proceso de entrenar un modelo estático.
- La inferencia estática (o inferencia sin conexión) es un proceso en el que un modelo genera un lote de predicciones a la vez.
Compara esto con dinámico.
Inferencia estática
Sinónimo de inferencia sin conexión.
Estacionariedad
Es una característica cuyos valores no cambian en una o más dimensiones, por lo general, el tiempo. Por ejemplo, un atributo cuyos valores se ven casi iguales en 2021 y 2023 presenta estacionariedad.
En el mundo real, muy pocas variables presentan estacionariedad. Incluso las características sinónimas de estabilidad (como el nivel del mar) cambian con el tiempo.
Compara esto con la no estacionariedad.
paso
Un pase hacia adelante y un pase hacia atrás de un lote.
Consulta Propagación hacia atrás para obtener más información sobre el pase hacia adelante y el pase hacia atrás.
tamaño del paso
Sinónimo de tasa de aprendizaje.
descenso de gradientes estocástico (SGD)
Algoritmo de descenso de gradientes en el que el tamaño del lote es uno. En otras palabras, el SGD se entrena con un solo ejemplo elegido al azar de manera uniforme de un conjunto de entrenamiento.
Consulta Regresión lineal: Hiperparámetros en el Curso intensivo de aprendizaje automático para obtener más información.
stride
En una operación convolucional o de reducción, el delta en cada dimensión de la siguiente serie de segmentos de entrada. Por ejemplo, la siguiente animación muestra un stride (1,1) durante una operación convolucional. Por lo tanto, la siguiente división de entrada comienza una posición a la derecha de la división de entrada anterior. Cuando la operación alcanza el borde derecho, la siguiente división se encuentra completamente a la izquierda, pero una posición más abajo.
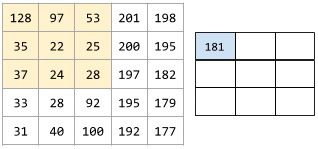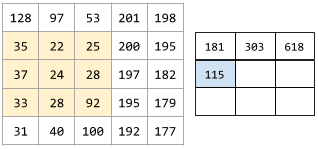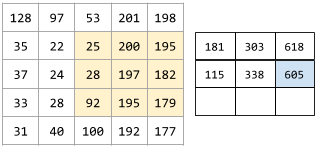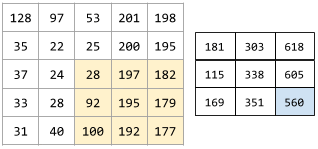
En el ejemplo anterior, se muestra un avance bidimensional. Si la matriz de entrada es tridimensional, el segmento también tendrá ese formato.
minimización del riesgo estructural (SRM)
Un algoritmo que equilibra dos objetivos:
- La necesidad de crear el modelo más predictivo (por ejemplo, la pérdida más baja)
- La necesidad de mantener el modelo lo más simple posible (por ejemplo, una regularización estricta)
Por ejemplo, una función que minimiza la pérdida + regularización en el conjunto de entrenamiento es un algoritmo de minimización del riesgo estructural.
Compara esto con la minimización del riesgo empírico.
submuestreo
Consulta reducción.
token de subpalabra
En los modelos de lenguaje, un token es una subcadena de una palabra, que puede ser la palabra completa.
Por ejemplo, una palabra como "desglosar" se puede dividir en las partes "desglos" (una raíz) y "ar" (un sufijo), cada una de las cuales se representa con su propio token. Dividir las palabras poco comunes en partes más pequeñas, llamadas subpalabras, permite que los modelos de lenguaje operen con las partes constituyentes más comunes de la palabra, como los prefijos y los sufijos.
Por el contrario, las palabras comunes, como "ir", podrían no dividirse y representarse con un solo token.
resumen
En TensorFlow, valor o conjunto de valores que se calcula en cada paso, generalmente se usa para realizar un seguimiento de las métricas del modelo durante el entrenamiento.
SuperGLUE
Es un conjunto de datos para calificar la capacidad general de un LLM para comprender y generar texto. El conjunto incluye los siguientes conjuntos de datos:
- Boolean Questions (BoolQ)
- CommitmentBank (CB)
- Elección de alternativas plausibles (COPA)
- Comprensión de lectura de varios enunciados (MultiRC)
- Conjunto de datos de comprensión de lectura con razonamiento de sentido común (ReCoRD)
- Reconocimiento de la implicación textual (RTE)
- Palabras en contexto (WiC)
- Winograd Schema Challenge (WSC)
Para obtener más detalles, consulta SuperGLUE: A Stickier Benchmark for General-Purpose Language Understanding Systems.
aprendizaje automático supervisado
Entrenar un modelo a partir de atributos y sus etiquetas correspondientes El aprendizaje automático supervisado es análogo a aprender una materia estudiando un conjunto de preguntas y sus respuestas correspondientes. Después de dominar la correlación entre preguntas y respuestas, el estudiante puede proporcionar respuestas a preguntas nuevas (nunca antes vistas) sobre el mismo tema.
Compara esto con el aprendizaje automático no supervisado.
Consulta Aprendizaje supervisado en el curso Introducción al AA para obtener más información.
atributo sintético
Un atributo que no está presente entre los atributos de entrada, pero que se ensambla a partir de uno o más de ellos. Entre los métodos para crear atributos sintéticos, se incluyen los siguientes:
- Agrupamiento de un atributo continuo en discretizaciones de rango
- Creación de una combinación de atributos
- Multiplicación (o división) de un valor de atributo por otros valores de atributos o por sí mismo Por ejemplo, si
aybson atributos de entrada, los siguientes son ejemplos de atributos sintéticos:- ab
- a2
- Aplicar una función trascendental a un valor de atributo Por ejemplo, si
ces un atributo de entrada, los siguientes son ejemplos de atributos sintéticos:- sin(c)
- ln(c)
Los atributos creados solo por normalización o escalamiento no se consideran atributos sintéticos.
T
T5
Un modelo de aprendizaje por transferencia de texto a texto introducido por Google AI en 2020. T5 es un modelo de codificador-decodificador basado en la arquitectura de Transformer y entrenado en un conjunto de datos extremadamente grande. Es eficaz en una variedad de tareas de procesamiento de lenguaje natural, como generar texto, traducir idiomas y responder preguntas de manera conversacional.
T5 recibe su nombre de las cinco letras T de "Text-to-Text Transfer Transformer".
T5X
Un framework de aprendizaje automático de código abierto diseñado para compilar y entrenar modelos de procesamiento de lenguaje natural (PLN) a gran escala. T5 se implementa en la base de código de T5X (que se basa en JAX y Flax).
Q-learning tabular
En el aprendizaje por refuerzo, se implementa el aprendizaje Q con una tabla para almacenar las funciones Q para cada combinación de estado y acción.
objetivo
Sinónimo de etiqueta.
red objetivo
En el aprendizaje profundo basado en Q, se usa una red neuronal que es una aproximación estable de la red neuronal principal, en la que esta última implementa una función Q o una política. Luego, puedes entrenar la red principal con los valores Q que predice la red objetivo. Por lo tanto, evitas el bucle de retroalimentación que se produce cuando la red principal se entrena en función de los valores Q que predice por sí misma. Si se evita esta retroalimentación, aumenta la estabilidad del entrenamiento.
tarea
Un problema que se puede resolver con técnicas de aprendizaje automático, como los siguientes:
temperatura
Es un hiperparámetro que controla el grado de aleatoriedad del resultado de un modelo. Las temperaturas más altas generan resultados más aleatorios, mientras que las temperaturas más bajas generan resultados menos aleatorios.
Elegir la mejor temperatura depende de la aplicación específica o de los valores de cadena.
datos temporales
Son los datos registrados en diferentes momentos. Por ejemplo, las ventas de abrigos de invierno registradas para cada día del año serían datos temporales.
Tensor
Es la principal estructura de datos en los programas de TensorFlow. Los tensores son estructuras de datos N-dimensionales (donde N podría ser muy grande), y los más comunes son los escalares, los vectores o las matrices. Los elementos de un tensor pueden tener valores enteros, de punto flotante o de una cadena de caracteres.
TensorBoard
Panel que muestra los resúmenes guardados durante la ejecución de uno o más programas de TensorFlow.
TensorFlow
Plataforma de aprendizaje automático distribuida a gran escala. El término también hace referencia a la capa de API base en la pila de TensorFlow, que admite la computación general en gráficos de flujo de datos.
Aunque TensorFlow se usa principalmente para el aprendizaje automático, también puedes usarlo para tareas que no son de AA y que requieren cálculos numéricos con grafos de flujo de datos.
TensorFlow Playground
Programa que visualiza cómo los diferentes hiperparámetros influyen en el entrenamiento del modelo (principalmente en las redes neuronales). Para probar TensorFlow Playground, visita http://playground.tensorflow.org.
TensorFlow Serving
Plataforma para implementar modelos entrenados en producción.
Unidad de procesamiento tensorial (TPU)
Circuito integrado específico de la aplicación (ASIC) que optimiza el rendimiento de las cargas de trabajo de aprendizaje automático. Estos ASIC se implementan como varios chips de TPU en un dispositivo de TPU.
Rango del tensor
Consulta rango (tensor).
Forma del tensor
Cantidad de elementos que contiene un Tensor en distintas dimensiones.
Por ejemplo, un tensor [5, 10] tiene una forma de 5 en una dimensión y de 10 en la otra.
Tamaño del tensor
Cantidad total de números escalares que contiene un Tensor. Por ejemplo, un tensor [5, 10] tiene un tamaño de 50.
TensorStore
Una biblioteca para leer y escribir de manera eficiente grandes arrays multidimensionales.
condición de finalización
En el aprendizaje por refuerzo, son las condiciones que determinan cuándo finaliza un episodio, por ejemplo, cuando el agente alcanza un estado determinado o supera un umbral de transiciones de estado. Por ejemplo, en tres en raya, un episodio finaliza cuando un jugador marca tres espacios consecutivos o cuando se marcan todos los espacios.
prueba
En un árbol de decisión, otro nombre para una condición.
Pérdida de prueba
Es una métrica que representa la pérdida de un modelo en relación con el conjunto de prueba. Cuando compilas un modelo, por lo general, intentas minimizar la pérdida de la prueba. Esto se debe a que una pérdida de prueba baja es un indicador de calidad más sólido que una pérdida de entrenamiento baja o una pérdida de validación baja.
A veces, una gran brecha entre la pérdida de prueba y la pérdida de entrenamiento o la pérdida de validación sugiere que debes aumentar la tasa de regularización.
conjunto de prueba
Es un subconjunto del conjunto de datos reservado para probar un modelo entrenado.
Tradicionalmente, los ejemplos del conjunto de datos se dividen en los siguientes tres subconjuntos distintos:
- un conjunto de entrenamiento
- un conjunto de validación
- un conjunto de prueba
Cada ejemplo de un conjunto de datos debe pertenecer a solo uno de los subconjuntos anteriores. Por ejemplo, un solo ejemplo no debe pertenecer al conjunto de entrenamiento y al conjunto de prueba.
El conjunto de entrenamiento y el conjunto de validación están estrechamente vinculados al entrenamiento de un modelo. Dado que el conjunto de prueba solo se asocia de forma indirecta con el entrenamiento, la pérdida de prueba es una métrica de mayor calidad y menos sesgada que la pérdida de entrenamiento o la pérdida de validación.
Consulta Conjuntos de datos: Cómo dividir el conjunto de datos original en el Curso intensivo de aprendizaje automático para obtener más información.
extensión de texto
Es el intervalo de índice del array asociado con una subsección específica de una cadena de texto.
Por ejemplo, la palabra good en la cadena de Python s="Be good now" ocupa el tramo de texto del 3 al 6.
tf.Example
Búfer de protocolo estándar que se usa para describir datos de entrada para el entrenamiento o la inferencia de modelos de aprendizaje automático.
tf.keras
Es una implementación de Keras integrada en TensorFlow.
Umbral (para árboles de decisión)
En una condición alineada con el eje, es el valor con el que se compara una característica. Por ejemplo, 75 es el valor del umbral en la siguiente condición:
grade >= 75
Consulta Divisor exacto para la clasificación binaria con atributos numéricos en el curso de Bosques de decisión para obtener más información.
análisis de series temporales
Subcampo del aprendizaje automático y la estadística que analiza datos temporales. Muchos tipos de problemas de aprendizaje automático requieren análisis de series temporales, incluidos la clasificación, el agrupamiento en clústeres, la previsión y la detección de anomalías. Por ejemplo, puedes usar el análisis de series temporales para predecir las ventas futuras de abrigos de invierno por mes en función de los datos de ventas históricos.
paso de tiempo
Una celda "desenrollada" dentro de una red neuronal recurrente. Por ejemplo, en la siguiente figura, se muestran tres pasos de tiempo (etiquetados con los subíndices t-1, t y t+1):

token
En un modelo de lenguaje, es la unidad atómica con la que el modelo entrena y realiza predicciones. Por lo general, un token es uno de los siguientes:
- Una palabra (por ejemplo, la frase "a los perros les gustan los gatos" consta de tres tokens de palabras: "perros", "les gustan" y "gatos").
- Un carácter: Por ejemplo, la frase "pez bicicleta" consta de nueve tokens de caracteres. (Ten en cuenta que el espacio en blanco cuenta como uno de los tokens).
- Subpalabras: En las que una sola palabra puede ser un token único o varios tokens. Una subpalabra consta de una raíz, un prefijo o un sufijo. Por ejemplo, un modelo de lenguaje que usa subpalabras como tokens podría ver la palabra "perros" como dos tokens (la raíz "perro" y el sufijo plural "s"). Ese mismo modelo de lenguaje podría considerar la palabra "más alto" como dos subpalabras (la raíz "alto" y el sufijo "más").
En dominios fuera de los modelos de lenguaje, los tokens pueden representar otros tipos de unidades atómicas. Por ejemplo, en la visión artificial, un token puede ser un subconjunto de una imagen.
Consulta Modelos de lenguaje grandes en el Curso intensivo de aprendizaje automático para obtener más información.
tokenizer
Es un sistema o algoritmo que traduce una secuencia de datos de entrada en tokens.
La mayoría de los modelos de base modernos son multimodales. Un tokenizador para un sistema multimodal debe traducir cada tipo de entrada al formato adecuado. Por ejemplo, con datos de entrada que incluyen texto y gráficos, el tokenizador podría traducir el texto de entrada en subpalabras y las imágenes de entrada en parches pequeños. Luego, el tokenizador debe convertir todos los tokens en un único espacio de incorporación unificado, lo que permite que el modelo "comprenda" un flujo de entrada multimodal.
Precisión del top-k
Es el porcentaje de veces que aparece una "etiqueta objetivo" en las primeras k posiciones de las listas generadas. Las listas pueden ser recomendaciones personalizadas o una lista de elementos ordenados por softmax.
La precisión del Top-k también se conoce como precisión en k.
torre
Es un componente de una red neuronal profunda que, en sí mismo, es una red neuronal profunda. En algunos casos, cada torre lee de una fuente de datos independiente, y esas torres siguen siendo independientes hasta que su resultado se combina en una capa final. En otros casos (por ejemplo, en la torre del codificador y el decodificador de muchos Transformers), las torres tienen conexiones cruzadas entre sí.
tóxico
Es el grado en que el contenido es abusivo, ofensivo o amenazante. Muchos modelos de aprendizaje automático pueden identificar, medir y clasificar la toxicidad. La mayoría de estos modelos identifican la toxicidad en función de varios parámetros, como el nivel de lenguaje abusivo y el nivel de lenguaje amenazante.
TPU
Abreviatura de unidad de procesamiento tensorial.
Chip TPU
Acelerador de álgebra lineal programable con memoria de alto ancho de banda en el chip que está optimizado para las cargas de trabajo de aprendizaje automático. Se implementan varios chips de TPU en un dispositivo de TPU.
Dispositivo de TPU
Una placa de circuito impreso (PCB) con varios chips de TPU, interfaces de red de alto ancho de banda y hardware de enfriamiento del sistema.
Nodo TPU
Es un recurso de TPU en Google Cloud con un tipo de TPU específico. El nodo TPU se conecta a tu red de VPC desde una red de VPC de intercambio de tráfico. Los nodos TPU son un recurso definido en la API de Cloud TPU.
Pod de TPU
Es una configuración específica de dispositivos de TPU en un centro de datos de Google. Todos los dispositivos de un pod de TPU están conectados entre sí a través de una red dedicada de alta velocidad. Un pod de TPU es la configuración más grande de dispositivos de TPU disponible para una versión específica de TPU.
Recurso de TPU
Es una entidad de TPU en Google Cloud que creas, administras o consumes. Por ejemplo, los nodos TPU y los tipos de TPU son recursos de TPU.
Porción de TPU
Una porción de TPU es una parte fraccionaria de los dispositivos TPU en un pod de TPU. Todos los dispositivos de una porción de TPU están conectados entre sí a través de una red dedicada de alta velocidad.
Tipo de TPU
Es una configuración de uno o más dispositivos de TPU con una versión de hardware de TPU específica. Cuando creas un nodo TPU en Google Cloud, debes seleccionar un tipo de TPU. Por ejemplo, un tipo de TPU v2-8 es un solo dispositivo TPU v2 con 8 núcleos. Un tipo de TPU v3-2048 tiene 256 dispositivos TPU v3 en red y un total de 2,048 núcleos. Los tipos de TPU son un recurso definido en la API de Cloud TPU.
Trabajador de TPU
Proceso que se ejecuta en una máquina host y ejecuta programas de aprendizaje automático en dispositivos TPU.
entrenamiento
Proceso de determinar los parámetros ideales (pesos y sesgos) que conforman un modelo. Durante el entrenamiento, un sistema lee ejemplos y ajusta los parámetros de forma gradual. El entrenamiento usa cada ejemplo desde algunas veces hasta miles de millones de veces.
Consulta Aprendizaje supervisado en el curso Introducción al AA para obtener más información.
Pérdida de entrenamiento
Es una métrica que representa la pérdida de un modelo durante una iteración de entrenamiento en particular. Por ejemplo, supongamos que la función de pérdida es el error cuadrático medio. Quizás la pérdida de entrenamiento (el error cuadrático medio) para la décima iteración sea de 2.2, y la pérdida de entrenamiento para la iteración número 100 sea de 1.9.
Una curva de pérdida representa la pérdida de entrenamiento en función de la cantidad de iteraciones. Una curva de pérdida proporciona las siguientes sugerencias sobre el entrenamiento:
- Una pendiente descendente implica que el modelo está mejorando.
- Una pendiente ascendente implica que el modelo está empeorando.
- Una pendiente plana implica que el modelo alcanzó la convergencia.
Por ejemplo, la siguiente curva de pérdida algo idealizada muestra lo siguiente:
- Una pendiente descendente pronunciada durante las iteraciones iniciales, lo que implica una mejora rápida del modelo
- Una pendiente que se aplana gradualmente (pero que sigue siendo descendente) hasta cerca del final del entrenamiento, lo que implica una mejora continua del modelo a un ritmo algo más lento que durante las iteraciones iniciales.
- Una pendiente plana hacia el final del entrenamiento, lo que sugiere convergencia.
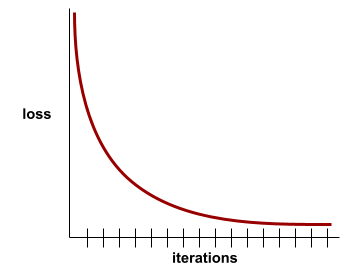
Si bien la pérdida de entrenamiento es importante, también debes consultar la generalización.
Sesgo entre el entrenamiento y la entrega
La diferencia entre el rendimiento de un modelo durante el entrenamiento y el rendimiento del mismo modelo durante la deriva.
conjunto de entrenamiento
Es el subconjunto del conjunto de datos que se usa para entrenar un modelo.
Tradicionalmente, los ejemplos del conjunto de datos se dividen en los siguientes tres subconjuntos distintos:
- un conjunto de entrenamiento
- un conjunto de validación
- un conjunto de prueba
Lo ideal es que cada ejemplo del conjunto de datos pertenezca a solo uno de los subconjuntos anteriores. Por ejemplo, un solo ejemplo no debe pertenecer al conjunto de entrenamiento y al conjunto de validación.
Consulta Conjuntos de datos: Cómo dividir el conjunto de datos original en el Curso intensivo de aprendizaje automático para obtener más información.
trayectoria
En el aprendizaje por refuerzo, una secuencia de tuplas que representan una secuencia de transiciones de estado del agente, en la que cada tupla corresponde al estado, la acción, la recompensa y el siguiente estado para una transición de estado determinada.
aprendizaje por transferencia
Transferir información de una tarea de aprendizaje automático a otra Por ejemplo, en el aprendizaje de tareas múltiples, un solo modelo resuelve varias tareas, como en el caso de un modelo profundo que tiene diferentes nodos de resultados para las distintas tareas. El aprendizaje por transferencia puede implicar la transferencia de conocimiento de la solución de una tarea más simple a una más compleja, o bien la transferencia de conocimiento de una tarea en la que hay más datos a una en la que hay menos datos.
La mayoría de los sistemas de aprendizaje automático resuelven una sola tarea. El aprendizaje por transferencia es un primer paso hacia la inteligencia artificial en el que un solo programa puede resolver varias tareas.
Transformador
Es una arquitectura de red neuronal desarrollada en Google que se basa en mecanismos de autoatención para transformar una secuencia de incorporaciones de entrada en una secuencia de incorporaciones de salida sin depender de convoluciones ni redes neuronales recurrentes. Un Transformer se puede ver como una pila de capas de autoatención.
Un Transformer puede incluir cualquiera de los siguientes elementos:
- un codificador
- un decodificador
- un codificador y un decodificador
Un codificador transforma una secuencia de embeddings en una nueva secuencia de la misma longitud. Un codificador incluye N capas idénticas, cada una de las cuales contiene dos subcapas. Estas dos subcapas se aplican en cada posición de la secuencia de incorporación de entrada, lo que transforma cada elemento de la secuencia en una nueva incorporación. La primera subcapa del codificador agrega información de toda la secuencia de entrada. La segunda subcapa del codificador transforma la información agregada en un embedding de salida.
Un decodificador transforma una secuencia de incorporaciones de entrada en una secuencia de incorporaciones de salida, posiblemente con una longitud diferente. Un decodificador también incluye N capas idénticas con tres subcapas, dos de las cuales son similares a las subcapas del codificador. La tercera subcapa del decodificador toma el resultado del codificador y aplica el mecanismo de autoatención para recopilar información de él.
La entrada de blog Transformer: A Novel Neural Network Architecture for Language Understanding proporciona una buena introducción a los Transformers.
Para obtener más información, consulta LLMs: ¿Qué es un modelo de lenguaje grande? en el Curso intensivo de aprendizaje automático.
invariancia traslacional
En un problema de clasificación de imágenes, es la capacidad de un algoritmo para clasificar imágenes de forma correcta incluso cuando cambia la posición de los objetos dentro de la imagen. Por ejemplo, el algoritmo aún puede identificar un perro, ya sea en el centro del marco o en el extremo izquierdo de este.
Consulta también invariancia de tamaño y invariancia rotacional.
trigrama
Un n-grama en el que N=3.
Búsqueda de respuestas a preguntas de trivia
Son conjuntos de datos para evaluar la capacidad de un LLM de responder preguntas de trivia. Cada conjunto de datos contiene pares de preguntas y respuestas creados por entusiastas de las trivias. Diferentes fuentes fundamentan los distintos conjuntos de datos, incluidas las siguientes:
- Búsqueda web (TriviaQA)
- Wikipedia (TriviaQA_wiki)
Para obtener más información, consulta TriviaQA: A Large Scale Distantly Supervised Challenge Dataset for Reading Comprehension.
verdadero negativo (VN)
Ejemplo en el que el modelo predice correctamente la clase negativa. Por ejemplo, el modelo infiere que un mensaje de correo electrónico en particular no es spam y, en efecto, ese mensaje no es spam.
verdadero positivo (VP)
Ejemplo en el que el modelo predice correctamente la clase positiva. Por ejemplo, el modelo infiere que un mensaje de correo electrónico en particular es spam y realmente lo es.
tasa de verdaderos positivos (TVP)
Sinónimo de recuperación. Es decir:
La tasa de verdaderos positivos es el eje Y en una curva ROC.
TTL
Abreviatura de tiempo de actividad.
Typologically Diverse Question Answering (TyDi QA)
Es un conjunto de datos grande para evaluar la competencia de un LLM a la hora de responder preguntas. El conjunto de datos contiene pares de preguntas y respuestas en muchos idiomas.
Para obtener más detalles, consulta TyDi QA: A Benchmark for Information-Seeking Question Answering in Typologically Diverse Languages.
U
Ultra
El modelo de Gemini con la mayor cantidad de parámetros. Consulta Gemini Ultra para obtener más detalles.
Desconocimiento (de un atributo sensible)
Situación en la que hay atributos sensibles, pero no se incluyen en los datos de entrenamiento. Dado que los atributos sensibles suelen correlacionarse con otros atributos de los datos de una persona, un modelo entrenado sin tener en cuenta un atributo sensible podría seguir teniendo un impacto dispar con respecto a ese atributo o incumplir otras restricciones de equidad.
Subajuste
Producir un modelo con poca capacidad predictiva porque el modelo no ha capturado por completo la complejidad de los datos de entrenamiento. El subajuste puede estar causado por varios problemas, como los siguientes:
- Entrenamiento con el conjunto incorrecto de atributos
- Entrenamiento con pocos ciclos o con una tasa de aprendizaje demasiado baja
- Entrenamiento con una tasa de regularización demasiado alta
- Establecer muy pocas capas ocultas en una red neuronal profunda
Consulta Sobreajuste en el Curso intensivo de aprendizaje automático para obtener más información.
submuestreo
Quitar ejemplos de la clase mayoritaria en un conjunto de datos con desequilibrio de clases para crear un conjunto de entrenamiento más equilibrado
Por ejemplo, considera un conjunto de datos en el que la proporción de la clase mayoritaria con respecto a la clase minoritaria es de 20:1. Para superar este desequilibrio de clases, puedes crear un conjunto de entrenamiento que incluya todos los ejemplos de la clase minoritaria, pero solo una décima parte de los ejemplos de la clase mayoritaria, lo que crearía una proporción de clases del conjunto de entrenamiento de 2:1. Gracias al submuestreo, este conjunto de entrenamiento más equilibrado podría producir un mejor modelo. Como alternativa, este conjunto de entrenamiento más equilibrado podría contener ejemplos insuficientes para entrenar un modelo eficaz.
Compara esto con el sobremuestreo.
unidireccional
Un sistema que solo evalúa el texto que precede a una sección de texto objetivo. Por el contrario, un sistema bidireccional evalúa tanto el texto que precede como el que sigue a una sección de texto objetivo. Consulta bidirectional para obtener más detalles.
modelo de lenguaje unidireccional
Un modelo de lenguaje que basa sus probabilidades solo en los tokens que aparecen antes, no después, de los tokens objetivo. Compara esto con el modelo de lenguaje bidireccional.
ejemplo sin etiqueta
Es un ejemplo que contiene atributos, pero no una etiqueta. Por ejemplo, la siguiente tabla muestra tres ejemplos sin etiquetar de un modelo de valuación de viviendas, cada uno con tres atributos, pero sin valor de la vivienda:
| Cantidad de dormitorios | Cantidad de baños | Antigüedad de la casa |
|---|---|---|
| 3 | 2 | 15 |
| 2 | 1 | 72 |
| 4 | 2 | 34 |
En el aprendizaje automático supervisado, los modelos se entrenan con ejemplos etiquetados y realizan predicciones sobre ejemplos sin etiqueta.
En el aprendizaje semisupervisado y no supervisado, los ejemplos sin etiqueta se usan durante el entrenamiento.
Compara el ejemplo sin etiqueta con el ejemplo etiquetado.
aprendizaje automático no supervisado
Entrenamiento de un modelo para encontrar patrones en un conjunto de datos, generalmente sin etiqueta.
El uso más común del aprendizaje automático no supervisado es la agrupación en clústeres de datos en grupos de ejemplos similares. Por ejemplo, un algoritmo de aprendizaje automático no supervisado puede agrupar canciones según varias propiedades de la música. Los clústeres resultantes pueden convertirse en una entrada para otros algoritmos de aprendizaje automático (por ejemplo, para un servicio de recomendación de música). El agrupamiento en clústeres puede ser útil cuando las etiquetas útiles son escasas o no están disponibles. Por ejemplo, en dominios como la protección contra el abuso y el fraude, los clústeres pueden ayudar a los humanos a comprender mejor los datos.
Compara esto con el aprendizaje automático supervisado.
Consulta ¿Qué es el aprendizaje automático? en el curso Introducción al AA para obtener más información.
modelado de aumento
Técnica de modelado que se usa comúnmente en el marketing y que modela el "efecto causal" (también conocido como "impacto incremental") de un "tratamiento" en un "individuo". A continuación, presentamos dos ejemplos:
- Los médicos pueden usar el modelado de efectividad para predecir la disminución de la mortalidad (efecto causal) de un procedimiento médico (tratamiento) según la edad y el historial médico de un paciente (individuo).
- Los especialistas en marketing pueden usar el modelado de efectividad para predecir el aumento en la probabilidad de una compra (efecto causal) debido a un anuncio (tratamiento) que se muestra a una persona (individual).
El modelado de efectividad difiere de la clasificación o la regresión en que algunas etiquetas (por ejemplo, la mitad de las etiquetas en los tratamientos binarios) siempre faltan en el modelado de efectividad. Por ejemplo, un paciente puede recibir o no un tratamiento. Por lo tanto, solo podemos observar si el paciente se curará o no en una de estas dos situaciones (pero nunca en ambas). La principal ventaja de un modelo de efectividad es que puede generar predicciones para la situación no observada (la contrafáctica) y usarlas para calcular el efecto causal.
Incremento de la ponderación
Aplicación de un peso a la clase con reducción de muestreo igual al factor por el que se realizó la reducción de muestreo.
matriz de usuarios
En los sistemas de recomendación, un vector de incorporación generado por la factorización de matrices que contiene indicadores latentes sobre las preferencias del usuario. Cada fila de la matriz de usuarios contiene información sobre la fuerza relativa de varias señales latentes para un solo usuario. Por ejemplo, considera un sistema de recomendación de películas. En este sistema, las señales latentes de la matriz de usuarios pueden representar el interés de cada usuario en géneros particulares o pueden ser señales más complicadas de interpretar que impliquen interacciones complejas entre múltiples factores.
La matriz de usuarios tiene una columna para cada atributo latente y una fila para cada usuario. Es decir, la matriz de usuarios tiene la misma cantidad de filas que la matriz objetivo que se factoriza. Por ejemplo, en un modelo de recomendación de películas para 1,000,000 de usuarios, la matriz de usuarios tendrá 1,000,000 de filas.
V
validación
Es la evaluación inicial de la calidad de un modelo. La validación verifica la calidad de las predicciones de un modelo en comparación con el conjunto de validación.
Dado que el conjunto de validación difiere del conjunto de entrenamiento, la validación ayuda a evitar el sobreajuste.
Podrías pensar que evaluar el modelo con el conjunto de validación es la primera ronda de pruebas y que evaluar el modelo con el conjunto de prueba es la segunda ronda de pruebas.
Pérdida de validación
Es una métrica que representa la pérdida de un modelo en el conjunto de validación durante una iteración particular del entrenamiento.
Consulta también curva de generalización.
conjunto de validación
Es el subconjunto del conjunto de datos que realiza la evaluación inicial con un modelo entrenado. Por lo general, evalúas el modelo entrenado con el conjunto de validación varias veces antes de evaluarlo con el conjunto de prueba.
Tradicionalmente, los ejemplos del conjunto de datos se dividen en los siguientes tres subconjuntos distintos:
- un conjunto de entrenamiento
- un conjunto de validación
- un conjunto de prueba
Lo ideal es que cada ejemplo del conjunto de datos pertenezca a solo uno de los subconjuntos anteriores. Por ejemplo, un solo ejemplo no debe pertenecer al conjunto de entrenamiento y al conjunto de validación.
Consulta Conjuntos de datos: Cómo dividir el conjunto de datos original en el Curso intensivo de aprendizaje automático para obtener más información.
Imputación de valores
Proceso de reemplazar un valor faltante por un sustituto aceptable. Cuando falta un valor, puedes descartar el ejemplo completo o usar la imputación de valores para rescatarlo.
Por ejemplo, considera un conjunto de datos que contiene un atributo temperature que se debe registrar cada hora. Sin embargo, la lectura de temperatura no estuvo disponible durante una hora en particular. Aquí se muestra una sección del conjunto de datos:
| Marca de tiempo | Temperatura |
|---|---|
| 1680561000 | 10 |
| 1680564600 | 12 |
| 1680568200 | faltante |
| 1680571800 | 20 |
| 1680575400 | 21 |
| 1680579000 | 21 |
Un sistema podría borrar el ejemplo faltante o imputar la temperatura faltante como 12, 16, 18 o 20, según el algoritmo de imputación.
Problema de desvanecimiento de gradiente
Es la tendencia de los gradientes de las primeras capas ocultas de algunas redes neuronales profundas a volverse sorprendentemente planos (bajos). Los gradientes cada vez más bajos generan cambios cada vez más pequeños en los pesos de los nodos de una red neuronal profunda, lo que lleva a un aprendizaje escaso o nulo. Los modelos que sufren el problema del desvanecimiento del gradiente se vuelven difíciles o imposibles de entrenar. Las celdas de memoria a corto plazo de larga duración abordan este problema.
Compara esto con el problema de gradiente explosivo.
Importancia de las variables
Es un conjunto de puntuaciones que indica la importancia relativa de cada atributo para el modelo.
Por ejemplo, considera un árbol de decisión que estima los precios de las casas. Supongamos que este árbol de decisión usa tres atributos: tamaño, edad y estilo. Si se calcula que un conjunto de importancias de variables para las tres características es {tamaño=5.8, edad=2.5, estilo=4.7}, entonces el tamaño es más importante para el árbol de decisión que la edad o el estilo.
Existen diferentes métricas de importancia de las variables que pueden informar a los expertos en AA sobre diferentes aspectos de los modelos.
Codificador automático variacional (VAE)
Es un tipo de autoencoder que aprovecha la discrepancia entre las entradas y las salidas para generar versiones modificadas de las entradas. Los autocodificadores variacionales son útiles para la IA generativa.
Los VAE se basan en la inferencia variacional, una técnica para estimar los parámetros de un modelo de probabilidad.
vector
Término muy sobrecargado cuyo significado varía según los diferentes campos matemáticos y científicos. En el aprendizaje automático, un vector tiene dos propiedades:
- Tipo de datos: Los vectores en el aprendizaje automático suelen contener números de punto flotante.
- Cantidad de elementos: Es la longitud del vector o su dimensión.
Por ejemplo, considera un vector de atributos que contiene ocho números de punto flotante. Este vector de atributos tiene una longitud o dimensión de ocho. Ten en cuenta que los vectores de aprendizaje automático suelen tener una gran cantidad de dimensiones.
Puedes representar muchos tipos diferentes de información como un vector. Por ejemplo:
- Cualquier posición en la superficie de la Tierra se puede representar como un vector bidimensional, en el que una dimensión es la latitud y la otra es la longitud.
- Los precios actuales de cada una de las 500 acciones se pueden representar como un vector de 500 dimensiones.
- Una distribución de probabilidad sobre una cantidad finita de clases se puede representar como un vector. Por ejemplo, un sistema de clasificación multiclase que predice uno de tres colores de salida (rojo, verde o amarillo) podría generar el vector
(0.3, 0.2, 0.5)para significarP[red]=0.3, P[green]=0.2, P[yellow]=0.5.
Los vectores se pueden concatenar. Por lo tanto, se puede representar una variedad de medios diferentes como un solo vector. Algunos modelos operan directamente en la concatenación de muchas codificaciones one-hot.
Los procesadores especializados, como las TPU, están optimizados para realizar operaciones matemáticas en vectores.
Un vector es un tensor de rango 1.
Vertex
Plataforma de Google Cloud para la IA y el aprendizaje automático. Vertex proporciona herramientas e infraestructura para compilar, implementar y administrar aplicaciones basadas en IA, incluido el acceso a los modelos de Gemini.vibe coding
Dar instrucciones a un modelo de IA generativa para crear software Es decir, tus instrucciones describen el propósito y las funciones del software, que un modelo de IA generativa traduce en código fuente. El código generado no siempre coincide con tus intenciones, por lo que la programación por intuición suele requerir iteraciones.
Andrej Karpathy acuñó el término "vibe coding" en esta publicación de X. En la publicación de X, Karpathy lo describe como "un nuevo tipo de programación… en el que te dejas llevar por el ambiente…". Por lo tanto, el término originalmente implicaba un enfoque intencionalmente flexible para crear software en el que tal vez ni siquiera se examinaba el código generado. Sin embargo, el término evolucionó rápidamente en muchos círculos para significar ahora cualquier forma de codificación generada por IA.
Para obtener una descripción más detallada de la codificación de ambiente, consulta ¿Qué es el vibe coding?.
Además, compara y contrasta el vibe coding con lo siguiente:
W
Pérdida de Wasserstein
Es una de las funciones de pérdida que se usan comúnmente en las redes adversarias generativas, basada en la distancia de movimiento de tierra entre la distribución de los datos generados y los datos reales.
peso
Es un valor por el que un modelo multiplica otro valor. El entrenamiento es el proceso de determinar los pesos ideales de un modelo; la inferencia es el proceso de usar esos pesos aprendidos para hacer predicciones.
Consulta Regresión lineal en el Curso intensivo de aprendizaje automático para obtener más información.
Mínimos cuadrados ponderados alternos (WALS)
Es un algoritmo para minimizar la función objetivo durante la factorización de matrices en los sistemas de recomendación, lo que permite una reducción de los pesos de los ejemplos faltantes. WALS minimiza el error cuadrático ponderado entre la matriz original y la reconstrucción alternando entre fijar la factorización de filas y la de columnas. Cada una de estas optimizaciones puede resolverse con optimización convexa de mínimos cuadrados. Para obtener más información, consulta el curso de Sistemas de recomendación.
suma ponderada
Es la suma de todos los valores de entrada relevantes multiplicados por sus pesos correspondientes. Por ejemplo, supongamos que las entradas pertinentes son las siguientes:
| valor de entrada | Peso de entrada |
| 2 | -1.3 |
| -1 | 0.6 |
| 3 | 0.4 |
Por lo tanto, la suma ponderada es la siguiente:
weighted sum = (2)(-1.3) + (-1)(0.6) + (3)(0.4) = -2.0
Una suma ponderada es el argumento de entrada para una función de activación.
WiC
Abreviatura de Words in Context.
modelo amplio
Es un modelo lineal que generalmente tiene muchos atributos de entrada dispersos. Se hace referencia a este modelo como "amplio" porque se trata de un tipo especial de red neuronal con un alto número de entradas que se conectan directamente con el nodo de resultado. Con frecuencia, los modelos amplios son más fáciles de inspeccionar y depurar que los modelos profundos. Si bien los modelos amplios no pueden expresar no linealidades a través de capas ocultas, pueden usar transformaciones como cruce de atributos y agrupamiento para modelar no linealidades de diferentes maneras.
Compara esto con el modelo profundo.
ancho
Es la cantidad de neuronas en una capa específica de una red neuronal.
WikiLingua (wiki_lingua)
Es un conjunto de datos para evaluar la capacidad de un LLM de resumir artículos cortos. WikiHow, una enciclopedia de artículos que explican cómo realizar diversas tareas, es la fuente escrita por humanos tanto para los artículos como para los resúmenes. Cada entrada del conjunto de datos consta de lo siguiente:
- Un artículo que se crea agregando cada paso de la versión en prosa (párrafo) de la lista numerada, sin incluir la oración inicial de cada paso.
- Un resumen de ese artículo, que consta de la oración inicial de cada paso de la lista numerada.
Para obtener más información, consulta WikiLingua: A New Benchmark Dataset for Cross-Lingual Abstractive Summarization.
Desafío de esquemas de Winograd (WSC)
Es un formato (o un conjunto de datos que se ajusta a ese formato) para evaluar la capacidad de un LLM de determinar la frase nominal a la que se refiere un pronombre.
Cada entrada en un Winograd Schema Challenge consta de lo siguiente:
- Un pasaje corto que contiene un pronombre objetivo
- Un pronombre objetivo
- Son las frases nominales candidatas, seguidas de la respuesta correcta (un valor booleano). Si el pronombre objetivo se refiere a este candidato, la respuesta es verdadero. Si el pronombre objetivo no se refiere a este candidato, la respuesta es False.
Por ejemplo:
- Pasaje: Mark le contó muchas mentiras a Pete sobre sí mismo, que Pete incluyó en su libro. Debería haber sido más sincero.
- Pronombre objetivo: Él
- Frases nominales candidatas:
- Mark: Verdadero, porque el pronombre objetivo se refiere a Mark
- Pete: Falso, porque el pronombre objetivo no se refiere a Peter.
El Winograd Schema Challenge es un componente del conjunto SuperGLUE.
Sabiduría de la multitud
La idea de que promediar las opiniones o estimaciones de un grupo grande de personas ("la multitud") suele producir resultados sorprendentemente buenos. Por ejemplo, considera un juego en el que las personas adivinan la cantidad de caramelos de goma que hay en un frasco grande. Si bien la mayoría de las conjeturas individuales serán imprecisas, se ha demostrado empíricamente que el promedio de todas las conjeturas es sorprendentemente cercano a la cantidad real de gomitas en el frasco.
Los ensambles son un análogo de software de la sabiduría de la multitud. Incluso si los modelos individuales hacen predicciones muy imprecisas, promediar las predicciones de muchos modelos suele generar predicciones sorprendentemente buenas. Por ejemplo, aunque un árbol de decisión individual puede generar predicciones deficientes, un bosque de decisión suele generar predicciones muy buenas.
WMT
Curiosamente, es la abreviatura de Conference on Machine Translation. (La abreviatura es WMT porque el nombre original era Workshop on Machine Translation). La conferencia se centra en los avances en los sistemas de traducción automática.
embedding de palabras
Representar cada palabra de un conjunto de palabras dentro de un vector de incorporación, es decir, representar cada palabra como un vector de valores de punto flotante entre 0.0 y 1.0 Las palabras con significados similares tienen representaciones más parecidas que las palabras con significados diferentes. Por ejemplo, zanahorias, apio y pepinos tendrían representaciones relativamente similares, que serían muy diferentes de las representaciones de avión, gafas de sol y pasta de dientes.
Words in Context (WiC)
Es un conjunto de datos para evaluar qué tan bien un LLM usa el contexto para comprender palabras que tienen múltiples significados. Cada entrada del conjunto de datos contiene lo siguiente:
- Dos oraciones, cada una con la palabra objetivo
- La palabra objetivo
- La respuesta correcta (un valor booleano), donde:
- Verdadero significa que la palabra objetivo tiene el mismo significado en las dos oraciones.
- Falso significa que la palabra objetivo tiene un significado diferente en las dos oraciones.
Por ejemplo:
- Dos oraciones:
- Hay mucha basura en el lecho del río.
- Cuando duermo, dejo un vaso de agua junto a mi cama.
- La palabra objetivo: cama
- Respuesta correcta: Falso, porque la palabra objetivo tiene un significado diferente en las dos oraciones.
Para obtener más detalles, consulta WiC: the Word-in-Context Dataset for Evaluating Context-Sensitive Meaning Representations.
Words in Context es un componente del conjunto SuperGLUE.
WSC
Abreviatura de Winograd Schema Challenge.
X
XLA (Accelerated Linear Algebra)
Compilador de aprendizaje automático de código abierto para GPUs, CPUs y aceleradores de AA.
El compilador de XLA toma modelos de frameworks de AA populares, como PyTorch, TensorFlow y JAX, y los optimiza para una ejecución de alto rendimiento en diferentes plataformas de hardware, incluidos los aceleradores de GPU, CPU y AA.
XL-Sum (xlsum)
Es un conjunto de datos para evaluar la competencia de un LLM en la tarea de resumir texto. XL-Sum proporciona entradas en muchos idiomas. Cada entrada del conjunto de datos contiene lo siguiente:
- Un artículo de la British Broadcasting Company (BBC).
- Es un resumen del artículo escrito por su autor. Ten en cuenta que el resumen puede contener palabras o frases que no están presentes en el artículo.
Para obtener más detalles, consulta XL-Sum: Large-Scale Multilingual Abstractive Summarization for 44 Languages.
xsum
Abreviatura de Extreme Summarization.
Z
aprendizaje sin ejemplos
Es un tipo de entrenamiento de aprendizaje automático en el que el modelo infiere una predicción para una tarea para la que no se entrenó específicamente. En otras palabras, el modelo no recibe ningún ejemplo de entrenamiento específico para la tarea, pero se le pide que realice la inferencia para esa tarea.
instrucción sin ejemplos
Una instrucción que no proporciona un ejemplo de cómo quieres que responda el modelo de lenguaje grande Por ejemplo:
| Partes de una instrucción | Notas |
|---|---|
| ¿Cuál es la moneda oficial del país especificado? | La pregunta que quieres que responda el LLM. |
| India: | Es la búsqueda real. |
El modelo de lenguaje grande podría responder con cualquiera de las siguientes opciones:
- Rupia
- INR
- ₹
- Rupia hindú
- La rupia
- La rupia india
Todas las respuestas son correctas, aunque es posible que prefieras un formato en particular.
Compara y contrasta el zero-shot prompting con los siguientes términos:
Normalización de la puntuación Z
Técnica de ajuste que reemplaza un valor de atributo sin procesar por un valor de punto flotante que representa la cantidad de desviaciones estándares desde la media de ese atributo. Por ejemplo, considera un atributo cuya media es 800 y cuya desviación estándar es 100. En la siguiente tabla, se muestra cómo la normalización de la puntuación Z mapearía el valor sin procesar a su puntuación Z:
| Valor sin procesar | Puntuación Z |
|---|---|
| 800 | 0 |
| 950 | +1.5 |
| 575 | -2.25 |
Luego, el modelo de aprendizaje automático se entrena con las puntuaciones Z de ese atributo en lugar de con los valores sin procesar.
Consulta Datos numéricos: Normalización en el Curso intensivo de aprendizaje automático para obtener más información.