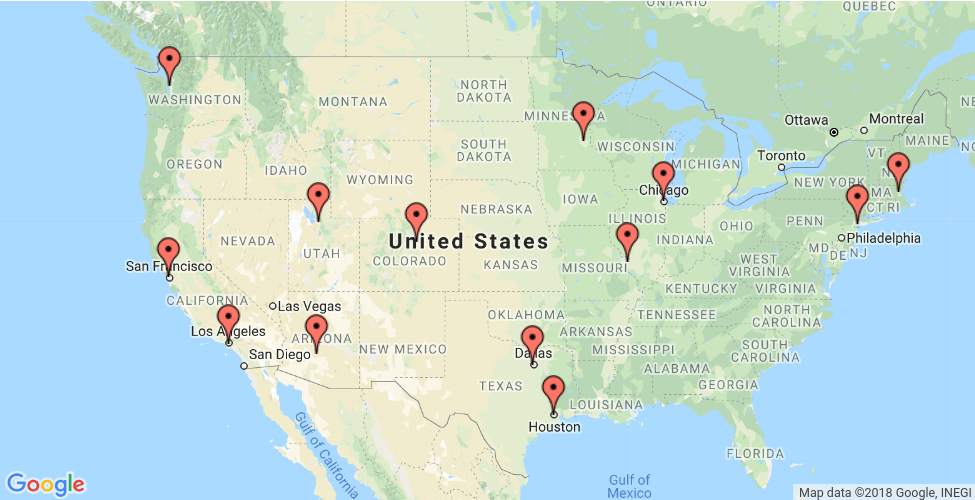
This section presents an example that shows how to solve the Traveling Salesperson Problem (TSP) for the locations shown on the map below.
The following sections present programs in Python, C++, Java, and C# that solve the TSP using OR-Tools
Create the data
The code below creates the data for the problem.
Python
def create_data_model(): """Stores the data for the problem.""" data = {} data["distance_matrix"] = [ [0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972], [2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579], [713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260], [1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987], [1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371], [1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999], [2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701], [213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099], [2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600], [875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162], [1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200], [2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504], [1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0], ] data["num_vehicles"] = 1 data["depot"] = 0 return data
C++
struct DataModel { const std::vector<std::vector<int64_t>> distance_matrix{ {0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972}, {2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579}, {713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260}, {1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987}, {1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371}, {1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999}, {2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701}, {213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099}, {2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600}, {875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162}, {1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200}, {2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504}, {1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0}, }; const int num_vehicles = 1; const RoutingIndexManager::NodeIndex depot{0}; };
Java
static class DataModel { public final long[][] distanceMatrix = { {0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972}, {2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579}, {713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260}, {1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987}, {1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371}, {1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999}, {2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701}, {213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099}, {2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600}, {875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162}, {1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200}, {2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504}, {1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0}, }; public final int vehicleNumber = 1; public final int depot = 0; }
C#
class DataModel { public long[,] DistanceMatrix = { { 0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972 }, { 2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579 }, { 713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260 }, { 1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987 }, { 1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371 }, { 1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999 }, { 2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701 }, { 213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099 }, { 2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600 }, { 875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162 }, { 1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200 }, { 2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504 }, { 1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0 }, }; public int VehicleNumber = 1; public int Depot = 0; };
The distance matrix is an array whose i, j entry is the distance from
location i to location j in miles, where the array indices correspond to the
locations in the following order:
0. New York - 1. Los Angeles - 2. Chicago - 3. Minneapolis - 4. Denver - 5. Dallas
- 6. Seattle - 7. Boston - 8. San Francisco - 9. St. Louis - 10. Houston - 11. Phoenix - 12. Salt Lake City
The data also includes:
- The number of vehicles in the problem, which is 1 because this is a TSP. (For a vehicle routing problem (VRP), the number of vehicles can be greater than 1.)
- The depot: the start and end location for the route. In this case, the depot is 0, which corresponds to New York.
Other ways to create the distance matrix
In this example, the distance matrix is explicitly defined in the program. It's also possible to use a function to calculate distances between locations: for example, the Euclidean formula for the distance between points in the plane. However, it's still more efficient to pre-compute all the distances between locations and store them in a matrix, rather than compute them at run time. See Example: drilling a circuit board for an example that creates the distance matrix this way.
Another alternative is to use the Google Maps Distance Matrix API to dynamically create a distance (or travel time) matrix for a routing problem.
Create the routing model
The following code in the main section of the programs creates the
index manager (manager) and the routing model (routing). The method
manager.IndexToNode converts the solver's internal indices (which you can
safely ignore) to the numbers for locations. Location numbers correspond to the indices for the distance matrix.
Python
data = create_data_model() manager = pywrapcp.RoutingIndexManager( len(data["distance_matrix"]), data["num_vehicles"], data["depot"] ) routing = pywrapcp.RoutingModel(manager)
C++
DataModel data; RoutingIndexManager manager(data.distance_matrix.size(), data.num_vehicles, data.depot); RoutingModel routing(manager);
Java
final DataModel data = new DataModel(); RoutingIndexManager manager = new RoutingIndexManager(data.distanceMatrix.length, data.vehicleNumber, data.depot); RoutingModel routing = new RoutingModel(manager);
C#
DataModel data = new DataModel(); RoutingIndexManager manager = new RoutingIndexManager(data.DistanceMatrix.GetLength(0), data.VehicleNumber, data.Depot); RoutingModel routing = new RoutingModel(manager);
The inputs to RoutingIndexManager are:
- The number of rows of the distance matrix, which is the number of locations (including the depot).
- The number of vehicles in the problem.
- The node corresponding to the depot.
Create the distance callback
To use the routing solver, you need to create a distance (or transit) callback: a function that takes any pair of locations and returns the distance between them. The easiest way to do this is using the distance matrix.
The following function creates the callback and registers it with the solver as
transit_callback_index.
Python
def distance_callback(from_index, to_index): """Returns the distance between the two nodes.""" # Convert from routing variable Index to distance matrix NodeIndex. from_node = manager.IndexToNode(from_index) to_node = manager.IndexToNode(to_index) return data["distance_matrix"][from_node][to_node] transit_callback_index = routing.RegisterTransitCallback(distance_callback)
C++
const int transit_callback_index = routing.RegisterTransitCallback( [&data, &manager](const int64_t from_index, const int64_t to_index) -> int64_t { // Convert from routing variable Index to distance matrix NodeIndex. const int from_node = manager.IndexToNode(from_index).value(); const int to_node = manager.IndexToNode(to_index).value(); return data.distance_matrix[from_node][to_node]; });
Java
final int transitCallbackIndex = routing.registerTransitCallback((long fromIndex, long toIndex) -> { // Convert from routing variable Index to user NodeIndex. int fromNode = manager.indexToNode(fromIndex); int toNode = manager.indexToNode(toIndex); return data.distanceMatrix[fromNode][toNode]; });
C#
int transitCallbackIndex = routing.RegisterTransitCallback((long fromIndex, long toIndex) => { // Convert from routing variable Index to // distance matrix NodeIndex. var fromNode = manager.IndexToNode(fromIndex); var toNode = manager.IndexToNode(toIndex); return data.DistanceMatrix[fromNode, toNode]; });
The callback accepts two indices, from_index and to_index, and returns the
corresponding entry of the distance matrix.
Set the cost of travel
The arc cost evaluator tells the solver how to calculate the cost of travel between any two locations — in other words, the cost of the edge (or arc) joining them in the graph for the problem. The following code sets the arc cost evaluator.
Python
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)
C++
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index);
Java
routing.setArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
C#
routing.SetArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
In this example, the arc cost evaluator is the transit_callback_index, which
is the solver's internal reference to the distance callback. This means that the
cost of travel between any two locations is just the distance between them.
However, in general the costs can involve other factors as well.
You can also define multiple arc cost evaluators that depend on which vehicle is
traveling between locations, using the method routing.SetArcCostEvaluatorOfVehicle().
For example, if the vehicles have different speeds, you could define the cost of
travel between locations to be the distance divided by the vehicle's speed
— in other words, the travel time.
Set search parameters
The following code sets the default search parameters and a heuristic method for finding the first solution:
Python
search_parameters = pywrapcp.DefaultRoutingSearchParameters() search_parameters.first_solution_strategy = ( routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC )
C++
RoutingSearchParameters searchParameters = DefaultRoutingSearchParameters(); searchParameters.set_first_solution_strategy( FirstSolutionStrategy::PATH_CHEAPEST_ARC);
Java
RoutingSearchParameters searchParameters = main.defaultRoutingSearchParameters() .toBuilder() .setFirstSolutionStrategy(FirstSolutionStrategy.Value.PATH_CHEAPEST_ARC) .build();
C#
RoutingSearchParameters searchParameters = operations_research_constraint_solver.DefaultRoutingSearchParameters(); searchParameters.FirstSolutionStrategy = FirstSolutionStrategy.Types.Value.PathCheapestArc;
The code sets the first solution strategy to PATH_CHEAPEST_ARC, which creates
an initial route for the solver by repeatedly adding edges with the least weight
that don't lead to a previously visited node (other than the depot). For other
options, see
First solution strategy.
Add the solution printer
The function that displays the solution returned by the solver is shown below. The function extracts the route from the solution and prints it to the console.
Python
def print_solution(manager, routing, solution): """Prints solution on console.""" print(f"Objective: {solution.ObjectiveValue()} miles") index = routing.Start(0) plan_output = "Route for vehicle 0:\n" route_distance = 0 while not routing.IsEnd(index): plan_output += f" {manager.IndexToNode(index)} ->" previous_index = index index = solution.Value(routing.NextVar(index)) route_distance += routing.GetArcCostForVehicle(previous_index, index, 0) plan_output += f" {manager.IndexToNode(index)}\n" plan_output += f"Route distance: {route_distance}miles\n" print(plan_output)
C++
//! @brief Print the solution. //! @param[in] manager Index manager used. //! @param[in] routing Routing solver used. //! @param[in] solution Solution found by the solver. void PrintSolution(const RoutingIndexManager& manager, const RoutingModel& routing, const Assignment& solution) { // Inspect solution. LOG(INFO) << "Objective: " << solution.ObjectiveValue() << " miles"; int64_t index = routing.Start(0); LOG(INFO) << "Route:"; int64_t distance{0}; std::stringstream route; while (!routing.IsEnd(index)) { route << manager.IndexToNode(index).value() << " -> "; const int64_t previous_index = index; index = solution.Value(routing.NextVar(index)); distance += routing.GetArcCostForVehicle(previous_index, index, int64_t{0}); } LOG(INFO) << route.str() << manager.IndexToNode(index).value(); LOG(INFO) << "Route distance: " << distance << "miles"; LOG(INFO) << ""; LOG(INFO) << "Advanced usage:"; LOG(INFO) << "Problem solved in " << routing.solver()->wall_time() << "ms"; }
Java
/// @brief Print the solution. static void printSolution( RoutingModel routing, RoutingIndexManager manager, Assignment solution) { // Solution cost. logger.info("Objective: " + solution.objectiveValue() + "miles"); // Inspect solution. logger.info("Route:"); long routeDistance = 0; String route = ""; long index = routing.start(0); while (!routing.isEnd(index)) { route += manager.indexToNode(index) + " -> "; long previousIndex = index; index = solution.value(routing.nextVar(index)); routeDistance += routing.getArcCostForVehicle(previousIndex, index, 0); } route += manager.indexToNode(routing.end(0)); logger.info(route); logger.info("Route distance: " + routeDistance + "miles"); }
C#
/// <summary> /// Print the solution. /// </summary> static void PrintSolution(in RoutingModel routing, in RoutingIndexManager manager, in Assignment solution) { Console.WriteLine("Objective: {0} miles", solution.ObjectiveValue()); // Inspect solution. Console.WriteLine("Route:"); long routeDistance = 0; var index = routing.Start(0); while (routing.IsEnd(index) == false) { Console.Write("{0} -> ", manager.IndexToNode((int)index)); var previousIndex = index; index = solution.Value(routing.NextVar(index)); routeDistance += routing.GetArcCostForVehicle(previousIndex, index, 0); } Console.WriteLine("{0}", manager.IndexToNode((int)index)); Console.WriteLine("Route distance: {0}miles", routeDistance); }
The function displays the optimal route and its distance, which is given by
ObjectiveValue().
Solve and print the solution
Finally, you can call the solver and print the solution:
Python
solution = routing.SolveWithParameters(search_parameters) if solution: print_solution(manager, routing, solution)
C++
const Assignment* solution = routing.SolveWithParameters(searchParameters); PrintSolution(manager, routing, *solution);
Java
Assignment solution = routing.solveWithParameters(searchParameters); printSolution(routing, manager, solution);
C#
Assignment solution = routing.SolveWithParameters(searchParameters); PrintSolution(routing, manager, solution);
This returns the solution and displays the optimal route.
Run the programs
When you run the programs, they display the following output.
Objective: 7293 miles Route for vehicle 0: 0 -> 7 -> 2 -> 3 -> 4 -> 12 -> 6 -> 8 -> 1 -> 11 -> 10 -> 5 -> 9 -> 0
In this example, there's only one route because it's a TSP. But in more general vehicle routing problems, the solution contains multiple routes.
Save routes to a list or array
As an alternative to printing the solution directly, you can save the route (or routes, for a VRP) to a list or array. This has the advantage of making the routes available in case you want to do something with them later. For example, you could run the program several times with different parameters and save the routes in the returned solutions to a file for comparison.
The following functions save the routes in the solution to any VRP (possibly with multiple vehicles) as a list (Python) or an array (C++).
Python
def get_routes(solution, routing, manager): """Get vehicle routes from a solution and store them in an array.""" # Get vehicle routes and store them in a two dimensional array whose # i,j entry is the jth location visited by vehicle i along its route. routes = [] for route_nbr in range(routing.vehicles()): index = routing.Start(route_nbr) route = [manager.IndexToNode(index)] while not routing.IsEnd(index): index = solution.Value(routing.NextVar(index)) route.append(manager.IndexToNode(index)) routes.append(route) return routes
C++
std::vector<std::vector<int>> GetRoutes(const Assignment& solution, const RoutingModel& routing, const RoutingIndexManager& manager) { // Get vehicle routes and store them in a two dimensional array, whose // i, j entry is the node for the jth visit of vehicle i. std::vector<std::vector<int>> routes(manager.num_vehicles()); // Get routes. for (int vehicle_id = 0; vehicle_id < manager.num_vehicles(); ++vehicle_id) { int64_t index = routing.Start(vehicle_id); routes[vehicle_id].push_back(manager.IndexToNode(index).value()); while (!routing.IsEnd(index)) { index = solution.Value(routing.NextVar(index)); routes[vehicle_id].push_back(manager.IndexToNode(index).value()); } } return routes; }
You can use these functions to get the routes in any of the VRP examples in the Routing section.
The following code displays the routes.
Python
routes = get_routes(solution, routing, manager) # Display the routes. for i, route in enumerate(routes): print('Route', i, route)
C++
const std::vector⟨std::vector⟨int⟩⟩ routes = GetRoutes(*solution, routing, manager); // Display the routes. for (int vehicle_id = 0; vehicle_id < routes.size(); ++vehicle_id) { LOG(INFO) << "Route " << vehicle_id; for (int j = 1; j < routes[vehicle_id].size(); ++j) { LOG(INFO) << routes[vehicle_id][j]; } }
For the current example, this code returns the following route:
Route 0 [0, 7, 2, 3, 4, 12, 6, 8, 1, 11, 10, 5, 9, 0]
As an exercise, modify the code above to format the output the same way as the solution printer for the program.
Complete programs
The complete TSP programs are shown below.
Python
"""Simple Travelling Salesperson Problem (TSP) between cities.""" from ortools.constraint_solver import routing_enums_pb2 from ortools.constraint_solver import pywrapcp def create_data_model(): """Stores the data for the problem.""" data = {} data["distance_matrix"] = [ [0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972], [2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579], [713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260], [1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987], [1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371], [1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999], [2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701], [213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099], [2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600], [875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162], [1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200], [2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504], [1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0], ] data["num_vehicles"] = 1 data["depot"] = 0 return data def print_solution(manager, routing, solution): """Prints solution on console.""" print(f"Objective: {solution.ObjectiveValue()} miles") index = routing.Start(0) plan_output = "Route for vehicle 0:\n" route_distance = 0 while not routing.IsEnd(index): plan_output += f" {manager.IndexToNode(index)} ->" previous_index = index index = solution.Value(routing.NextVar(index)) route_distance += routing.GetArcCostForVehicle(previous_index, index, 0) plan_output += f" {manager.IndexToNode(index)}\n" plan_output += f"Route distance: {route_distance}miles\n" print(plan_output) def main(): """Entry point of the program.""" # Instantiate the data problem. data = create_data_model() # Create the routing index manager. manager = pywrapcp.RoutingIndexManager( len(data["distance_matrix"]), data["num_vehicles"], data["depot"] ) # Create Routing Model. routing = pywrapcp.RoutingModel(manager) def distance_callback(from_index, to_index): """Returns the distance between the two nodes.""" # Convert from routing variable Index to distance matrix NodeIndex. from_node = manager.IndexToNode(from_index) to_node = manager.IndexToNode(to_index) return data["distance_matrix"][from_node][to_node] transit_callback_index = routing.RegisterTransitCallback(distance_callback) # Define cost of each arc. routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index) # Setting first solution heuristic. search_parameters = pywrapcp.DefaultRoutingSearchParameters() search_parameters.first_solution_strategy = ( routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC ) # Solve the problem. solution = routing.SolveWithParameters(search_parameters) # Print solution on console. if solution: print_solution(manager, routing, solution) if __name__ == "__main__": main()
C++
#include <cstdint> #include <cstdlib> #include <sstream> #include <vector> #include "ortools/base/logging.h" #include "ortools/constraint_solver/constraint_solver.h" #include "ortools/constraint_solver/routing.h" #include "ortools/constraint_solver/routing_enums.pb.h" #include "ortools/constraint_solver/routing_index_manager.h" #include "ortools/constraint_solver/routing_parameters.h" namespace operations_research { struct DataModel { const std::vector<std::vector<int64_t>> distance_matrix{ {0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972}, {2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579}, {713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260}, {1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987}, {1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371}, {1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999}, {2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701}, {213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099}, {2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600}, {875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162}, {1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200}, {2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504}, {1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0}, }; const int num_vehicles = 1; const RoutingIndexManager::NodeIndex depot{0}; }; //! @brief Print the solution. //! @param[in] manager Index manager used. //! @param[in] routing Routing solver used. //! @param[in] solution Solution found by the solver. void PrintSolution(const RoutingIndexManager& manager, const RoutingModel& routing, const Assignment& solution) { // Inspect solution. LOG(INFO) << "Objective: " << solution.ObjectiveValue() << " miles"; int64_t index = routing.Start(0); LOG(INFO) << "Route:"; int64_t distance{0}; std::stringstream route; while (!routing.IsEnd(index)) { route << manager.IndexToNode(index).value() << " -> "; const int64_t previous_index = index; index = solution.Value(routing.NextVar(index)); distance += routing.GetArcCostForVehicle(previous_index, index, int64_t{0}); } LOG(INFO) << route.str() << manager.IndexToNode(index).value(); LOG(INFO) << "Route distance: " << distance << "miles"; LOG(INFO) << ""; LOG(INFO) << "Advanced usage:"; LOG(INFO) << "Problem solved in " << routing.solver()->wall_time() << "ms"; } void Tsp() { // Instantiate the data problem. DataModel data; // Create Routing Index Manager RoutingIndexManager manager(data.distance_matrix.size(), data.num_vehicles, data.depot); // Create Routing Model. RoutingModel routing(manager); const int transit_callback_index = routing.RegisterTransitCallback( [&data, &manager](const int64_t from_index, const int64_t to_index) -> int64_t { // Convert from routing variable Index to distance matrix NodeIndex. const int from_node = manager.IndexToNode(from_index).value(); const int to_node = manager.IndexToNode(to_index).value(); return data.distance_matrix[from_node][to_node]; }); // Define cost of each arc. routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index); // Setting first solution heuristic. RoutingSearchParameters searchParameters = DefaultRoutingSearchParameters(); searchParameters.set_first_solution_strategy( FirstSolutionStrategy::PATH_CHEAPEST_ARC); // Solve the problem. const Assignment* solution = routing.SolveWithParameters(searchParameters); // Print solution on console. PrintSolution(manager, routing, *solution); } } // namespace operations_research int main(int /*argc*/, char* /*argv*/[]) { operations_research::Tsp(); return EXIT_SUCCESS; }
Java
package com.google.ortools.constraintsolver.samples; import com.google.ortools.Loader; import com.google.ortools.constraintsolver.Assignment; import com.google.ortools.constraintsolver.FirstSolutionStrategy; import com.google.ortools.constraintsolver.RoutingIndexManager; import com.google.ortools.constraintsolver.RoutingModel; import com.google.ortools.constraintsolver.RoutingSearchParameters; import com.google.ortools.constraintsolver.main; import java.util.logging.Logger; /** Minimal TSP using distance matrix. */ public class TspCities { private static final Logger logger = Logger.getLogger(TspCities.class.getName()); static class DataModel { public final long[][] distanceMatrix = { {0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972}, {2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579}, {713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260}, {1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987}, {1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371}, {1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999}, {2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701}, {213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099}, {2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600}, {875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162}, {1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200}, {2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504}, {1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0}, }; public final int vehicleNumber = 1; public final int depot = 0; } /// @brief Print the solution. static void printSolution( RoutingModel routing, RoutingIndexManager manager, Assignment solution) { // Solution cost. logger.info("Objective: " + solution.objectiveValue() + "miles"); // Inspect solution. logger.info("Route:"); long routeDistance = 0; String route = ""; long index = routing.start(0); while (!routing.isEnd(index)) { route += manager.indexToNode(index) + " -> "; long previousIndex = index; index = solution.value(routing.nextVar(index)); routeDistance += routing.getArcCostForVehicle(previousIndex, index, 0); } route += manager.indexToNode(routing.end(0)); logger.info(route); logger.info("Route distance: " + routeDistance + "miles"); } public static void main(String[] args) throws Exception { Loader.loadNativeLibraries(); // Instantiate the data problem. final DataModel data = new DataModel(); // Create Routing Index Manager RoutingIndexManager manager = new RoutingIndexManager(data.distanceMatrix.length, data.vehicleNumber, data.depot); // Create Routing Model. RoutingModel routing = new RoutingModel(manager); // Create and register a transit callback. final int transitCallbackIndex = routing.registerTransitCallback((long fromIndex, long toIndex) -> { // Convert from routing variable Index to user NodeIndex. int fromNode = manager.indexToNode(fromIndex); int toNode = manager.indexToNode(toIndex); return data.distanceMatrix[fromNode][toNode]; }); // Define cost of each arc. routing.setArcCostEvaluatorOfAllVehicles(transitCallbackIndex); // Setting first solution heuristic. RoutingSearchParameters searchParameters = main.defaultRoutingSearchParameters() .toBuilder() .setFirstSolutionStrategy(FirstSolutionStrategy.Value.PATH_CHEAPEST_ARC) .build(); // Solve the problem. Assignment solution = routing.solveWithParameters(searchParameters); // Print solution on console. printSolution(routing, manager, solution); } }
C#
using System; using System.Collections.Generic; using Google.OrTools.ConstraintSolver; /// <summary> /// Minimal TSP using distance matrix. /// </summary> public class TspCities { class DataModel { public long[,] DistanceMatrix = { { 0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972 }, { 2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579 }, { 713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260 }, { 1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987 }, { 1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371 }, { 1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999 }, { 2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701 }, { 213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099 }, { 2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600 }, { 875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162 }, { 1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200 }, { 2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504 }, { 1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0 }, }; public int VehicleNumber = 1; public int Depot = 0; }; /// <summary> /// Print the solution. /// </summary> static void PrintSolution(in RoutingModel routing, in RoutingIndexManager manager, in Assignment solution) { Console.WriteLine("Objective: {0} miles", solution.ObjectiveValue()); // Inspect solution. Console.WriteLine("Route:"); long routeDistance = 0; var index = routing.Start(0); while (routing.IsEnd(index) == false) { Console.Write("{0} -> ", manager.IndexToNode((int)index)); var previousIndex = index; index = solution.Value(routing.NextVar(index)); routeDistance += routing.GetArcCostForVehicle(previousIndex, index, 0); } Console.WriteLine("{0}", manager.IndexToNode((int)index)); Console.WriteLine("Route distance: {0}miles", routeDistance); } public static void Main(String[] args) { // Instantiate the data problem. DataModel data = new DataModel(); // Create Routing Index Manager RoutingIndexManager manager = new RoutingIndexManager(data.DistanceMatrix.GetLength(0), data.VehicleNumber, data.Depot); // Create Routing Model. RoutingModel routing = new RoutingModel(manager); int transitCallbackIndex = routing.RegisterTransitCallback((long fromIndex, long toIndex) => { // Convert from routing variable Index to // distance matrix NodeIndex. var fromNode = manager.IndexToNode(fromIndex); var toNode = manager.IndexToNode(toIndex); return data.DistanceMatrix[fromNode, toNode]; }); // Define cost of each arc. routing.SetArcCostEvaluatorOfAllVehicles(transitCallbackIndex); // Setting first solution heuristic. RoutingSearchParameters searchParameters = operations_research_constraint_solver.DefaultRoutingSearchParameters(); searchParameters.FirstSolutionStrategy = FirstSolutionStrategy.Types.Value.PathCheapestArc; // Solve the problem. Assignment solution = routing.SolveWithParameters(searchParameters); // Print solution on console. PrintSolution(routing, manager, solution); } }
Example: drilling a circuit board
The next example involves drilling holes in a circuit board with an automated drill. The problem is to find the shortest route for the drill to take on the board in order to drill all of the required holes. The example is taken from TSPLIB, a library of TSP problems.
Here's scatter chart of the locations for the holes:
The following sections present programs that find a good solution to the circuit board problem, using the solver's default search parameters. After that, we'll show how to find a better solution by changing the search strategy.
Create the data
The data for the problem consist of 280 points in the plane, shown in the scatter chart above. The program creates the data in an array of ordered pairs corresponding to the points in the plane, as shown below.
Python
def create_data_model(): """Stores the data for the problem.""" data = {} # Locations in block units data["locations"] = [ # fmt: off (288, 149), (288, 129), (270, 133), (256, 141), (256, 157), (246, 157), (236, 169), (228, 169), (228, 161), (220, 169), (212, 169), (204, 169), (196, 169), (188, 169), (196, 161), (188, 145), (172, 145), (164, 145), (156, 145), (148, 145), (140, 145), (148, 169), (164, 169), (172, 169), (156, 169), (140, 169), (132, 169), (124, 169), (116, 161), (104, 153), (104, 161), (104, 169), (90, 165), (80, 157), (64, 157), (64, 165), (56, 169), (56, 161), (56, 153), (56, 145), (56, 137), (56, 129), (56, 121), (40, 121), (40, 129), (40, 137), (40, 145), (40, 153), (40, 161), (40, 169), (32, 169), (32, 161), (32, 153), (32, 145), (32, 137), (32, 129), (32, 121), (32, 113), (40, 113), (56, 113), (56, 105), (48, 99), (40, 99), (32, 97), (32, 89), (24, 89), (16, 97), (16, 109), (8, 109), (8, 97), (8, 89), (8, 81), (8, 73), (8, 65), (8, 57), (16, 57), (8, 49), (8, 41), (24, 45), (32, 41), (32, 49), (32, 57), (32, 65), (32, 73), (32, 81), (40, 83), (40, 73), (40, 63), (40, 51), (44, 43), (44, 35), (44, 27), (32, 25), (24, 25), (16, 25), (16, 17), (24, 17), (32, 17), (44, 11), (56, 9), (56, 17), (56, 25), (56, 33), (56, 41), (64, 41), (72, 41), (72, 49), (56, 49), (48, 51), (56, 57), (56, 65), (48, 63), (48, 73), (56, 73), (56, 81), (48, 83), (56, 89), (56, 97), (104, 97), (104, 105), (104, 113), (104, 121), (104, 129), (104, 137), (104, 145), (116, 145), (124, 145), (132, 145), (132, 137), (140, 137), (148, 137), (156, 137), (164, 137), (172, 125), (172, 117), (172, 109), (172, 101), (172, 93), (172, 85), (180, 85), (180, 77), (180, 69), (180, 61), (180, 53), (172, 53), (172, 61), (172, 69), (172, 77), (164, 81), (148, 85), (124, 85), (124, 93), (124, 109), (124, 125), (124, 117), (124, 101), (104, 89), (104, 81), (104, 73), (104, 65), (104, 49), (104, 41), (104, 33), (104, 25), (104, 17), (92, 9), (80, 9), (72, 9), (64, 21), (72, 25), (80, 25), (80, 25), (80, 41), (88, 49), (104, 57), (124, 69), (124, 77), (132, 81), (140, 65), (132, 61), (124, 61), (124, 53), (124, 45), (124, 37), (124, 29), (132, 21), (124, 21), (120, 9), (128, 9), (136, 9), (148, 9), (162, 9), (156, 25), (172, 21), (180, 21), (180, 29), (172, 29), (172, 37), (172, 45), (180, 45), (180, 37), (188, 41), (196, 49), (204, 57), (212, 65), (220, 73), (228, 69), (228, 77), (236, 77), (236, 69), (236, 61), (228, 61), (228, 53), (236, 53), (236, 45), (228, 45), (228, 37), (236, 37), (236, 29), (228, 29), (228, 21), (236, 21), (252, 21), (260, 29), (260, 37), (260, 45), (260, 53), (260, 61), (260, 69), (260, 77), (276, 77), (276, 69), (276, 61), (276, 53), (284, 53), (284, 61), (284, 69), (284, 77), (284, 85), (284, 93), (284, 101), (288, 109), (280, 109), (276, 101), (276, 93), (276, 85), (268, 97), (260, 109), (252, 101), (260, 93), (260, 85), (236, 85), (228, 85), (228, 93), (236, 93), (236, 101), (228, 101), (228, 109), (228, 117), (228, 125), (220, 125), (212, 117), (204, 109), (196, 101), (188, 93), (180, 93), (180, 101), (180, 109), (180, 117), (180, 125), (196, 145), (204, 145), (212, 145), (220, 145), (228, 145), (236, 145), (246, 141), (252, 125), (260, 129), (280, 133) # fmt: on ] data["num_vehicles"] = 1 data["depot"] = 0 return data
C++
struct DataModel { const std::vector<std::vector<int>> locations{ {288, 149}, {288, 129}, {270, 133}, {256, 141}, {256, 157}, {246, 157}, {236, 169}, {228, 169}, {228, 161}, {220, 169}, {212, 169}, {204, 169}, {196, 169}, {188, 169}, {196, 161}, {188, 145}, {172, 145}, {164, 145}, {156, 145}, {148, 145}, {140, 145}, {148, 169}, {164, 169}, {172, 169}, {156, 169}, {140, 169}, {132, 169}, {124, 169}, {116, 161}, {104, 153}, {104, 161}, {104, 169}, {90, 165}, {80, 157}, {64, 157}, {64, 165}, {56, 169}, {56, 161}, {56, 153}, {56, 145}, {56, 137}, {56, 129}, {56, 121}, {40, 121}, {40, 129}, {40, 137}, {40, 145}, {40, 153}, {40, 161}, {40, 169}, {32, 169}, {32, 161}, {32, 153}, {32, 145}, {32, 137}, {32, 129}, {32, 121}, {32, 113}, {40, 113}, {56, 113}, {56, 105}, {48, 99}, {40, 99}, {32, 97}, {32, 89}, {24, 89}, {16, 97}, {16, 109}, {8, 109}, {8, 97}, {8, 89}, {8, 81}, {8, 73}, {8, 65}, {8, 57}, {16, 57}, {8, 49}, {8, 41}, {24, 45}, {32, 41}, {32, 49}, {32, 57}, {32, 65}, {32, 73}, {32, 81}, {40, 83}, {40, 73}, {40, 63}, {40, 51}, {44, 43}, {44, 35}, {44, 27}, {32, 25}, {24, 25}, {16, 25}, {16, 17}, {24, 17}, {32, 17}, {44, 11}, {56, 9}, {56, 17}, {56, 25}, {56, 33}, {56, 41}, {64, 41}, {72, 41}, {72, 49}, {56, 49}, {48, 51}, {56, 57}, {56, 65}, {48, 63}, {48, 73}, {56, 73}, {56, 81}, {48, 83}, {56, 89}, {56, 97}, {104, 97}, {104, 105}, {104, 113}, {104, 121}, {104, 129}, {104, 137}, {104, 145}, {116, 145}, {124, 145}, {132, 145}, {132, 137}, {140, 137}, {148, 137}, {156, 137}, {164, 137}, {172, 125}, {172, 117}, {172, 109}, {172, 101}, {172, 93}, {172, 85}, {180, 85}, {180, 77}, {180, 69}, {180, 61}, {180, 53}, {172, 53}, {172, 61}, {172, 69}, {172, 77}, {164, 81}, {148, 85}, {124, 85}, {124, 93}, {124, 109}, {124, 125}, {124, 117}, {124, 101}, {104, 89}, {104, 81}, {104, 73}, {104, 65}, {104, 49}, {104, 41}, {104, 33}, {104, 25}, {104, 17}, {92, 9}, {80, 9}, {72, 9}, {64, 21}, {72, 25}, {80, 25}, {80, 25}, {80, 41}, {88, 49}, {104, 57}, {124, 69}, {124, 77}, {132, 81}, {140, 65}, {132, 61}, {124, 61}, {124, 53}, {124, 45}, {124, 37}, {124, 29}, {132, 21}, {124, 21}, {120, 9}, {128, 9}, {136, 9}, {148, 9}, {162, 9}, {156, 25}, {172, 21}, {180, 21}, {180, 29}, {172, 29}, {172, 37}, {172, 45}, {180, 45}, {180, 37}, {188, 41}, {196, 49}, {204, 57}, {212, 65}, {220, 73}, {228, 69}, {228, 77}, {236, 77}, {236, 69}, {236, 61}, {228, 61}, {228, 53}, {236, 53}, {236, 45}, {228, 45}, {228, 37}, {236, 37}, {236, 29}, {228, 29}, {228, 21}, {236, 21}, {252, 21}, {260, 29}, {260, 37}, {260, 45}, {260, 53}, {260, 61}, {260, 69}, {260, 77}, {276, 77}, {276, 69}, {276, 61}, {276, 53}, {284, 53}, {284, 61}, {284, 69}, {284, 77}, {284, 85}, {284, 93}, {284, 101}, {288, 109}, {280, 109}, {276, 101}, {276, 93}, {276, 85}, {268, 97}, {260, 109}, {252, 101}, {260, 93}, {260, 85}, {236, 85}, {228, 85}, {228, 93}, {236, 93}, {236, 101}, {228, 101}, {228, 109}, {228, 117}, {228, 125}, {220, 125}, {212, 117}, {204, 109}, {196, 101}, {188, 93}, {180, 93}, {180, 101}, {180, 109}, {180, 117}, {180, 125}, {196, 145}, {204, 145}, {212, 145}, {220, 145}, {228, 145}, {236, 145}, {246, 141}, {252, 125}, {260, 129}, {280, 133}, }; const int num_vehicles = 1; const RoutingIndexManager::NodeIndex depot{0}; };
Java
static class DataModel { public final int[][] locations = {{288, 149}, {288, 129}, {270, 133}, {256, 141}, {256, 157}, {246, 157}, {236, 169}, {228, 169}, {228, 161}, {220, 169}, {212, 169}, {204, 169}, {196, 169}, {188, 169}, {196, 161}, {188, 145}, {172, 145}, {164, 145}, {156, 145}, {148, 145}, {140, 145}, {148, 169}, {164, 169}, {172, 169}, {156, 169}, {140, 169}, {132, 169}, {124, 169}, {116, 161}, {104, 153}, {104, 161}, {104, 169}, {90, 165}, {80, 157}, {64, 157}, {64, 165}, {56, 169}, {56, 161}, {56, 153}, {56, 145}, {56, 137}, {56, 129}, {56, 121}, {40, 121}, {40, 129}, {40, 137}, {40, 145}, {40, 153}, {40, 161}, {40, 169}, {32, 169}, {32, 161}, {32, 153}, {32, 145}, {32, 137}, {32, 129}, {32, 121}, {32, 113}, {40, 113}, {56, 113}, {56, 105}, {48, 99}, {40, 99}, {32, 97}, {32, 89}, {24, 89}, {16, 97}, {16, 109}, {8, 109}, {8, 97}, {8, 89}, {8, 81}, {8, 73}, {8, 65}, {8, 57}, {16, 57}, {8, 49}, {8, 41}, {24, 45}, {32, 41}, {32, 49}, {32, 57}, {32, 65}, {32, 73}, {32, 81}, {40, 83}, {40, 73}, {40, 63}, {40, 51}, {44, 43}, {44, 35}, {44, 27}, {32, 25}, {24, 25}, {16, 25}, {16, 17}, {24, 17}, {32, 17}, {44, 11}, {56, 9}, {56, 17}, {56, 25}, {56, 33}, {56, 41}, {64, 41}, {72, 41}, {72, 49}, {56, 49}, {48, 51}, {56, 57}, {56, 65}, {48, 63}, {48, 73}, {56, 73}, {56, 81}, {48, 83}, {56, 89}, {56, 97}, {104, 97}, {104, 105}, {104, 113}, {104, 121}, {104, 129}, {104, 137}, {104, 145}, {116, 145}, {124, 145}, {132, 145}, {132, 137}, {140, 137}, {148, 137}, {156, 137}, {164, 137}, {172, 125}, {172, 117}, {172, 109}, {172, 101}, {172, 93}, {172, 85}, {180, 85}, {180, 77}, {180, 69}, {180, 61}, {180, 53}, {172, 53}, {172, 61}, {172, 69}, {172, 77}, {164, 81}, {148, 85}, {124, 85}, {124, 93}, {124, 109}, {124, 125}, {124, 117}, {124, 101}, {104, 89}, {104, 81}, {104, 73}, {104, 65}, {104, 49}, {104, 41}, {104, 33}, {104, 25}, {104, 17}, {92, 9}, {80, 9}, {72, 9}, {64, 21}, {72, 25}, {80, 25}, {80, 25}, {80, 41}, {88, 49}, {104, 57}, {124, 69}, {124, 77}, {132, 81}, {140, 65}, {132, 61}, {124, 61}, {124, 53}, {124, 45}, {124, 37}, {124, 29}, {132, 21}, {124, 21}, {120, 9}, {128, 9}, {136, 9}, {148, 9}, {162, 9}, {156, 25}, {172, 21}, {180, 21}, {180, 29}, {172, 29}, {172, 37}, {172, 45}, {180, 45}, {180, 37}, {188, 41}, {196, 49}, {204, 57}, {212, 65}, {220, 73}, {228, 69}, {228, 77}, {236, 77}, {236, 69}, {236, 61}, {228, 61}, {228, 53}, {236, 53}, {236, 45}, {228, 45}, {228, 37}, {236, 37}, {236, 29}, {228, 29}, {228, 21}, {236, 21}, {252, 21}, {260, 29}, {260, 37}, {260, 45}, {260, 53}, {260, 61}, {260, 69}, {260, 77}, {276, 77}, {276, 69}, {276, 61}, {276, 53}, {284, 53}, {284, 61}, {284, 69}, {284, 77}, {284, 85}, {284, 93}, {284, 101}, {288, 109}, {280, 109}, {276, 101}, {276, 93}, {276, 85}, {268, 97}, {260, 109}, {252, 101}, {260, 93}, {260, 85}, {236, 85}, {228, 85}, {228, 93}, {236, 93}, {236, 101}, {228, 101}, {228, 109}, {228, 117}, {228, 125}, {220, 125}, {212, 117}, {204, 109}, {196, 101}, {188, 93}, {180, 93}, {180, 101}, {180, 109}, {180, 117}, {180, 125}, {196, 145}, {204, 145}, {212, 145}, {220, 145}, {228, 145}, {236, 145}, {246, 141}, {252, 125}, {260, 129}, {280, 133}}; public final int vehicleNumber = 1; public final int depot = 0; }
C#
class DataModel { public int[,] Locations = { { 288, 149 }, { 288, 129 }, { 270, 133 }, { 256, 141 }, { 256, 157 }, { 246, 157 }, { 236, 169 }, { 228, 169 }, { 228, 161 }, { 220, 169 }, { 212, 169 }, { 204, 169 }, { 196, 169 }, { 188, 169 }, { 196, 161 }, { 188, 145 }, { 172, 145 }, { 164, 145 }, { 156, 145 }, { 148, 145 }, { 140, 145 }, { 148, 169 }, { 164, 169 }, { 172, 169 }, { 156, 169 }, { 140, 169 }, { 132, 169 }, { 124, 169 }, { 116, 161 }, { 104, 153 }, { 104, 161 }, { 104, 169 }, { 90, 165 }, { 80, 157 }, { 64, 157 }, { 64, 165 }, { 56, 169 }, { 56, 161 }, { 56, 153 }, { 56, 145 }, { 56, 137 }, { 56, 129 }, { 56, 121 }, { 40, 121 }, { 40, 129 }, { 40, 137 }, { 40, 145 }, { 40, 153 }, { 40, 161 }, { 40, 169 }, { 32, 169 }, { 32, 161 }, { 32, 153 }, { 32, 145 }, { 32, 137 }, { 32, 129 }, { 32, 121 }, { 32, 113 }, { 40, 113 }, { 56, 113 }, { 56, 105 }, { 48, 99 }, { 40, 99 }, { 32, 97 }, { 32, 89 }, { 24, 89 }, { 16, 97 }, { 16, 109 }, { 8, 109 }, { 8, 97 }, { 8, 89 }, { 8, 81 }, { 8, 73 }, { 8, 65 }, { 8, 57 }, { 16, 57 }, { 8, 49 }, { 8, 41 }, { 24, 45 }, { 32, 41 }, { 32, 49 }, { 32, 57 }, { 32, 65 }, { 32, 73 }, { 32, 81 }, { 40, 83 }, { 40, 73 }, { 40, 63 }, { 40, 51 }, { 44, 43 }, { 44, 35 }, { 44, 27 }, { 32, 25 }, { 24, 25 }, { 16, 25 }, { 16, 17 }, { 24, 17 }, { 32, 17 }, { 44, 11 }, { 56, 9 }, { 56, 17 }, { 56, 25 }, { 56, 33 }, { 56, 41 }, { 64, 41 }, { 72, 41 }, { 72, 49 }, { 56, 49 }, { 48, 51 }, { 56, 57 }, { 56, 65 }, { 48, 63 }, { 48, 73 }, { 56, 73 }, { 56, 81 }, { 48, 83 }, { 56, 89 }, { 56, 97 }, { 104, 97 }, { 104, 105 }, { 104, 113 }, { 104, 121 }, { 104, 129 }, { 104, 137 }, { 104, 145 }, { 116, 145 }, { 124, 145 }, { 132, 145 }, { 132, 137 }, { 140, 137 }, { 148, 137 }, { 156, 137 }, { 164, 137 }, { 172, 125 }, { 172, 117 }, { 172, 109 }, { 172, 101 }, { 172, 93 }, { 172, 85 }, { 180, 85 }, { 180, 77 }, { 180, 69 }, { 180, 61 }, { 180, 53 }, { 172, 53 }, { 172, 61 }, { 172, 69 }, { 172, 77 }, { 164, 81 }, { 148, 85 }, { 124, 85 }, { 124, 93 }, { 124, 109 }, { 124, 125 }, { 124, 117 }, { 124, 101 }, { 104, 89 }, { 104, 81 }, { 104, 73 }, { 104, 65 }, { 104, 49 }, { 104, 41 }, { 104, 33 }, { 104, 25 }, { 104, 17 }, { 92, 9 }, { 80, 9 }, { 72, 9 }, { 64, 21 }, { 72, 25 }, { 80, 25 }, { 80, 25 }, { 80, 41 }, { 88, 49 }, { 104, 57 }, { 124, 69 }, { 124, 77 }, { 132, 81 }, { 140, 65 }, { 132, 61 }, { 124, 61 }, { 124, 53 }, { 124, 45 }, { 124, 37 }, { 124, 29 }, { 132, 21 }, { 124, 21 }, { 120, 9 }, { 128, 9 }, { 136, 9 }, { 148, 9 }, { 162, 9 }, { 156, 25 }, { 172, 21 }, { 180, 21 }, { 180, 29 }, { 172, 29 }, { 172, 37 }, { 172, 45 }, { 180, 45 }, { 180, 37 }, { 188, 41 }, { 196, 49 }, { 204, 57 }, { 212, 65 }, { 220, 73 }, { 228, 69 }, { 228, 77 }, { 236, 77 }, { 236, 69 }, { 236, 61 }, { 228, 61 }, { 228, 53 }, { 236, 53 }, { 236, 45 }, { 228, 45 }, { 228, 37 }, { 236, 37 }, { 236, 29 }, { 228, 29 }, { 228, 21 }, { 236, 21 }, { 252, 21 }, { 260, 29 }, { 260, 37 }, { 260, 45 }, { 260, 53 }, { 260, 61 }, { 260, 69 }, { 260, 77 }, { 276, 77 }, { 276, 69 }, { 276, 61 }, { 276, 53 }, { 284, 53 }, { 284, 61 }, { 284, 69 }, { 284, 77 }, { 284, 85 }, { 284, 93 }, { 284, 101 }, { 288, 109 }, { 280, 109 }, { 276, 101 }, { 276, 93 }, { 276, 85 }, { 268, 97 }, { 260, 109 }, { 252, 101 }, { 260, 93 }, { 260, 85 }, { 236, 85 }, { 228, 85 }, { 228, 93 }, { 236, 93 }, { 236, 101 }, { 228, 101 }, { 228, 109 }, { 228, 117 }, { 228, 125 }, { 220, 125 }, { 212, 117 }, { 204, 109 }, { 196, 101 }, { 188, 93 }, { 180, 93 }, { 180, 101 }, { 180, 109 }, { 180, 117 }, { 180, 125 }, { 196, 145 }, { 204, 145 }, { 212, 145 }, { 220, 145 }, { 228, 145 }, { 236, 145 }, { 246, 141 }, { 252, 125 }, { 260, 129 }, { 280, 133 }, }; public int VehicleNumber = 1; public int Depot = 0; };
Compute the distance matrix
The function below computes the Euclidean distance between any two points in the data and stores it in an array. Because the routing solver works over the integers, the function rounds the computed distances to integers. Rounding doesn't affect the solution in this example, but might in other cases. See Scaling the distance matrix for a way to avoid possible rounding issues.
Python
def compute_euclidean_distance_matrix(locations): """Creates callback to return distance between points.""" distances = {} for from_counter, from_node in enumerate(locations): distances[from_counter] = {} for to_counter, to_node in enumerate(locations): if from_counter == to_counter: distances[from_counter][to_counter] = 0 else: # Euclidean distance distances[from_counter][to_counter] = int( math.hypot((from_node[0] - to_node[0]), (from_node[1] - to_node[1])) ) return distances
C++
// @brief Generate distance matrix. std::vector<std::vector<int64_t>> ComputeEuclideanDistanceMatrix( const std::vector<std::vector<int>>& locations) { std::vector<std::vector<int64_t>> distances = std::vector<std::vector<int64_t>>( locations.size(), std::vector<int64_t>(locations.size(), int64_t{0})); for (int from_node = 0; from_node < locations.size(); from_node++) { for (int to_node = 0; to_node < locations.size(); to_node++) { if (from_node != to_node) distances[from_node][to_node] = static_cast<int64_t>( std::hypot((locations[to_node][0] - locations[from_node][0]), (locations[to_node][1] - locations[from_node][1]))); } } return distances; }
Java
/// @brief Compute Euclidean distance matrix from locations array. /// @details It uses an array of locations and computes /// the Euclidean distance between any two locations. private static long[][] computeEuclideanDistanceMatrix(int[][] locations) { // Calculate distance matrix using Euclidean distance. long[][] distanceMatrix = new long[locations.length][locations.length]; for (int fromNode = 0; fromNode < locations.length; ++fromNode) { for (int toNode = 0; toNode < locations.length; ++toNode) { if (fromNode == toNode) { distanceMatrix[fromNode][toNode] = 0; } else { distanceMatrix[fromNode][toNode] = (long) Math.hypot(locations[toNode][0] - locations[fromNode][0], locations[toNode][1] - locations[fromNode][1]); } } } return distanceMatrix; }
C#
/// <summary> /// Euclidean distance implemented as a callback. It uses an array of /// positions and computes the Euclidean distance between the two /// positions of two different indices. /// </summary> static long[,] ComputeEuclideanDistanceMatrix(in int[,] locations) { // Calculate the distance matrix using Euclidean distance. int locationNumber = locations.GetLength(0); long[,] distanceMatrix = new long[locationNumber, locationNumber]; for (int fromNode = 0; fromNode < locationNumber; fromNode++) { for (int toNode = 0; toNode < locationNumber; toNode++) { if (fromNode == toNode) distanceMatrix[fromNode, toNode] = 0; else distanceMatrix[fromNode, toNode] = (long)Math.Sqrt(Math.Pow(locations[toNode, 0] - locations[fromNode, 0], 2) + Math.Pow(locations[toNode, 1] - locations[fromNode, 1], 2)); } } return distanceMatrix; }
Add the distance callback
The code that creates the distance callback is almost the same as in the previous example. However, in this case the program calls the function that computes the distance matrix before adding the callback.
Python
distance_matrix = compute_euclidean_distance_matrix(data["locations"]) def distance_callback(from_index, to_index): """Returns the distance between the two nodes.""" # Convert from routing variable Index to distance matrix NodeIndex. from_node = manager.IndexToNode(from_index) to_node = manager.IndexToNode(to_index) return distance_matrix[from_node][to_node] transit_callback_index = routing.RegisterTransitCallback(distance_callback) routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)
C++
const auto distance_matrix = ComputeEuclideanDistanceMatrix(data.locations); const int transit_callback_index = routing.RegisterTransitCallback( [&distance_matrix, &manager](const int64_t from_index, const int64_t to_index) -> int64_t { // Convert from routing variable Index to distance matrix NodeIndex. const int from_node = manager.IndexToNode(from_index).value(); const int to_node = manager.IndexToNode(to_index).value(); return distance_matrix[from_node][to_node]; }); routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index);
Java
final long[][] distanceMatrix = computeEuclideanDistanceMatrix(data.locations); final int transitCallbackIndex = routing.registerTransitCallback((long fromIndex, long toIndex) -> { // Convert from routing variable Index to user NodeIndex. int fromNode = manager.indexToNode(fromIndex); int toNode = manager.indexToNode(toIndex); return distanceMatrix[fromNode][toNode]; }); routing.setArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
C#
long[,] distanceMatrix = ComputeEuclideanDistanceMatrix(data.Locations); int transitCallbackIndex = routing.RegisterTransitCallback((long fromIndex, long toIndex) => { // Convert from routing variable Index to // distance matrix NodeIndex. var fromNode = manager.IndexToNode(fromIndex); var toNode = manager.IndexToNode(toIndex); return distanceMatrix[fromNode, toNode]; }); routing.SetArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
Solution printer
The following function prints the solution to the console. To keep the output more compact, the function displays just the indices of the locations in the route.
Python
def print_solution(manager, routing, solution): """Prints solution on console.""" print(f"Objective: {solution.ObjectiveValue()}") index = routing.Start(0) plan_output = "Route:\n" route_distance = 0 while not routing.IsEnd(index): plan_output += f" {manager.IndexToNode(index)} ->" previous_index = index index = solution.Value(routing.NextVar(index)) route_distance += routing.GetArcCostForVehicle(previous_index, index, 0) plan_output += f" {manager.IndexToNode(index)}\n" print(plan_output) plan_output += f"Objective: {route_distance}m\n"
C++
//! @brief Print the solution //! @param[in] manager Index manager used. //! @param[in] routing Routing solver used. //! @param[in] solution Solution found by the solver. void PrintSolution(const RoutingIndexManager& manager, const RoutingModel& routing, const Assignment& solution) { LOG(INFO) << "Objective: " << solution.ObjectiveValue(); // Inspect solution. int64_t index = routing.Start(0); LOG(INFO) << "Route:"; int64_t distance{0}; std::stringstream route; while (!routing.IsEnd(index)) { route << manager.IndexToNode(index).value() << " -> "; const int64_t previous_index = index; index = solution.Value(routing.NextVar(index)); distance += routing.GetArcCostForVehicle(previous_index, index, int64_t{0}); } LOG(INFO) << route.str() << manager.IndexToNode(index).value(); LOG(INFO) << "Route distance: " << distance << "mm"; LOG(INFO) << ""; LOG(INFO) << "Advanced usage:"; LOG(INFO) << "Problem solved in " << routing.solver()->wall_time() << "ms"; }
Java
/// @brief Print the solution. static void printSolution( RoutingModel routing, RoutingIndexManager manager, Assignment solution) { // Solution cost. logger.info("Objective: " + solution.objectiveValue()); // Inspect solution. logger.info("Route:"); long routeDistance = 0; String route = ""; long index = routing.start(0); while (!routing.isEnd(index)) { route += manager.indexToNode(index) + " -> "; long previousIndex = index; index = solution.value(routing.nextVar(index)); routeDistance += routing.getArcCostForVehicle(previousIndex, index, 0); } route += manager.indexToNode(routing.end(0)); logger.info(route); logger.info("Route distance: " + routeDistance); }
C#
/// <summary> /// Print the solution. /// </summary> static void PrintSolution(in RoutingModel routing, in RoutingIndexManager manager, in Assignment solution) { Console.WriteLine("Objective: {0}", solution.ObjectiveValue()); // Inspect solution. Console.WriteLine("Route:"); long routeDistance = 0; var index = routing.Start(0); while (routing.IsEnd(index) == false) { Console.Write("{0} -> ", manager.IndexToNode((int)index)); var previousIndex = index; index = solution.Value(routing.NextVar(index)); routeDistance += routing.GetArcCostForVehicle(previousIndex, index, 0); } Console.WriteLine("{0}", manager.IndexToNode((int)index)); Console.WriteLine("Route distance: {0}m", routeDistance); }
Main function
The main function is essentially the same as the one in the previous example, but also includes a call to the function that creates the distance matrix.
Running the program
The complete programs are shown in the next section. When you run the program, it displays the following route:
Total distance: 2790 Route of vehicle 0: 0 -> 1 -> 279 -> 2 -> 278 -> 277 -> 247 -> 248 -> 249 -> 246 -> 244 -> 243 -> 242 -> 241 -> 240 -> 239 -> 238 -> 237 -> 236 -> 235 -> 234 -> 233 -> 232 -> 231 -> 230 -> 245 -> 250 -> 229 -> 228 -> 227 -> 226 -> 225 -> 224 -> 223 -> 222 -> 221 -> 220 -> 219 -> 218 -> 217 -> 216 -> 215 -> 214 -> 213 -> 212 -> 211 -> 210 -> 209 -> 208 -> 251 -> 254 -> 255 -> 257 -> 256 -> 253 -> 252 -> 207 -> 206 -> 205 -> 204 -> 203 -> 202 -> 142 -> 141 -> 146 -> 147 -> 140 -> 139 -> 265 -> 136 -> 137 -> 138 -> 148 -> 149 -> 177 -> 176 -> 175 -> 178 -> 179 -> 180 -> 181 -> 182 -> 183 -> 184 -> 186 -> 185 -> 192 -> 196 -> 197 -> 198 -> 144 -> 145 -> 143 -> 199 -> 201 -> 200 -> 195 -> 194 -> 193 -> 191 -> 190 -> 189 -> 188 -> 187 -> 163 -> 164 -> 165 -> 166 -> 167 -> 168 -> 169 -> 171 -> 170 -> 172 -> 105 -> 106 -> 104 -> 103 -> 107 -> 109 -> 110 -> 113 -> 114 -> 116 -> 117 -> 61 -> 62 -> 63 -> 65 -> 64 -> 84 -> 85 -> 115 -> 112 -> 86 -> 83 -> 82 -> 87 -> 111 -> 108 -> 89 -> 90 -> 91 -> 102 -> 101 -> 100 -> 99 -> 98 -> 97 -> 96 -> 95 -> 94 -> 93 -> 92 -> 79 -> 88 -> 81 -> 80 -> 78 -> 77 -> 76 -> 74 -> 75 -> 73 -> 72 -> 71 -> 70 -> 69 -> 66 -> 68 -> 67 -> 57 -> 56 -> 55 -> 54 -> 53 -> 52 -> 51 -> 50 -> 49 -> 48 -> 47 -> 46 -> 45 -> 44 -> 43 -> 58 -> 60 -> 59 -> 42 -> 41 -> 40 -> 39 -> 38 -> 37 -> 36 -> 35 -> 34 -> 33 -> 32 -> 31 -> 30 -> 29 -> 124 -> 123 -> 122 -> 121 -> 120 -> 119 -> 118 -> 156 -> 157 -> 158 -> 173 -> 162 -> 161 -> 160 -> 174 -> 159 -> 150 -> 151 -> 155 -> 152 -> 154 -> 153 -> 128 -> 129 -> 130 -> 131 -> 18 -> 19 -> 20 -> 127 -> 126 -> 125 -> 28 -> 27 -> 26 -> 25 -> 21 -> 24 -> 22 -> 23 -> 13 -> 12 -> 14 -> 11 -> 10 -> 9 -> 7 -> 8 -> 6 -> 5 -> 275 -> 274 -> 273 -> 272 -> 271 -> 270 -> 15 -> 16 -> 17 -> 132 -> 133 -> 269 -> 268 -> 134 -> 135 -> 267 -> 266 -> 264 -> 263 -> 262 -> 261 -> 260 -> 258 -> 259 -> 276 -> 3 -> 4 -> 0
Here's a graph of the corresponding route:
The OR-Tools library finds the above tour very quickly: in less than a second on a typical computer. The total length of the above tour is 2790.
Complete programs
Here are the complete programs for the circuit board example.
Python
"""Simple Travelling Salesperson Problem (TSP) on a circuit board.""" import math from ortools.constraint_solver import routing_enums_pb2 from ortools.constraint_solver import pywrapcp def create_data_model(): """Stores the data for the problem.""" data = {} # Locations in block units data["locations"] = [ # fmt: off (288, 149), (288, 129), (270, 133), (256, 141), (256, 157), (246, 157), (236, 169), (228, 169), (228, 161), (220, 169), (212, 169), (204, 169), (196, 169), (188, 169), (196, 161), (188, 145), (172, 145), (164, 145), (156, 145), (148, 145), (140, 145), (148, 169), (164, 169), (172, 169), (156, 169), (140, 169), (132, 169), (124, 169), (116, 161), (104, 153), (104, 161), (104, 169), (90, 165), (80, 157), (64, 157), (64, 165), (56, 169), (56, 161), (56, 153), (56, 145), (56, 137), (56, 129), (56, 121), (40, 121), (40, 129), (40, 137), (40, 145), (40, 153), (40, 161), (40, 169), (32, 169), (32, 161), (32, 153), (32, 145), (32, 137), (32, 129), (32, 121), (32, 113), (40, 113), (56, 113), (56, 105), (48, 99), (40, 99), (32, 97), (32, 89), (24, 89), (16, 97), (16, 109), (8, 109), (8, 97), (8, 89), (8, 81), (8, 73), (8, 65), (8, 57), (16, 57), (8, 49), (8, 41), (24, 45), (32, 41), (32, 49), (32, 57), (32, 65), (32, 73), (32, 81), (40, 83), (40, 73), (40, 63), (40, 51), (44, 43), (44, 35), (44, 27), (32, 25), (24, 25), (16, 25), (16, 17), (24, 17), (32, 17), (44, 11), (56, 9), (56, 17), (56, 25), (56, 33), (56, 41), (64, 41), (72, 41), (72, 49), (56, 49), (48, 51), (56, 57), (56, 65), (48, 63), (48, 73), (56, 73), (56, 81), (48, 83), (56, 89), (56, 97), (104, 97), (104, 105), (104, 113), (104, 121), (104, 129), (104, 137), (104, 145), (116, 145), (124, 145), (132, 145), (132, 137), (140, 137), (148, 137), (156, 137), (164, 137), (172, 125), (172, 117), (172, 109), (172, 101), (172, 93), (172, 85), (180, 85), (180, 77), (180, 69), (180, 61), (180, 53), (172, 53), (172, 61), (172, 69), (172, 77), (164, 81), (148, 85), (124, 85), (124, 93), (124, 109), (124, 125), (124, 117), (124, 101), (104, 89), (104, 81), (104, 73), (104, 65), (104, 49), (104, 41), (104, 33), (104, 25), (104, 17), (92, 9), (80, 9), (72, 9), (64, 21), (72, 25), (80, 25), (80, 25), (80, 41), (88, 49), (104, 57), (124, 69), (124, 77), (132, 81), (140, 65), (132, 61), (124, 61), (124, 53), (124, 45), (124, 37), (124, 29), (132, 21), (124, 21), (120, 9), (128, 9), (136, 9), (148, 9), (162, 9), (156, 25), (172, 21), (180, 21), (180, 29), (172, 29), (172, 37), (172, 45), (180, 45), (180, 37), (188, 41), (196, 49), (204, 57), (212, 65), (220, 73), (228, 69), (228, 77), (236, 77), (236, 69), (236, 61), (228, 61), (228, 53), (236, 53), (236, 45), (228, 45), (228, 37), (236, 37), (236, 29), (228, 29), (228, 21), (236, 21), (252, 21), (260, 29), (260, 37), (260, 45), (260, 53), (260, 61), (260, 69), (260, 77), (276, 77), (276, 69), (276, 61), (276, 53), (284, 53), (284, 61), (284, 69), (284, 77), (284, 85), (284, 93), (284, 101), (288, 109), (280, 109), (276, 101), (276, 93), (276, 85), (268, 97), (260, 109), (252, 101), (260, 93), (260, 85), (236, 85), (228, 85), (228, 93), (236, 93), (236, 101), (228, 101), (228, 109), (228, 117), (228, 125), (220, 125), (212, 117), (204, 109), (196, 101), (188, 93), (180, 93), (180, 101), (180, 109), (180, 117), (180, 125), (196, 145), (204, 145), (212, 145), (220, 145), (228, 145), (236, 145), (246, 141), (252, 125), (260, 129), (280, 133) # fmt: on ] data["num_vehicles"] = 1 data["depot"] = 0 return data def compute_euclidean_distance_matrix(locations): """Creates callback to return distance between points.""" distances = {} for from_counter, from_node in enumerate(locations): distances[from_counter] = {} for to_counter, to_node in enumerate(locations): if from_counter == to_counter: distances[from_counter][to_counter] = 0 else: # Euclidean distance distances[from_counter][to_counter] = int( math.hypot((from_node[0] - to_node[0]), (from_node[1] - to_node[1])) ) return distances def print_solution(manager, routing, solution): """Prints solution on console.""" print(f"Objective: {solution.ObjectiveValue()}") index = routing.Start(0) plan_output = "Route:\n" route_distance = 0 while not routing.IsEnd(index): plan_output += f" {manager.IndexToNode(index)} ->" previous_index = index index = solution.Value(routing.NextVar(index)) route_distance += routing.GetArcCostForVehicle(previous_index, index, 0) plan_output += f" {manager.IndexToNode(index)}\n" print(plan_output) plan_output += f"Objective: {route_distance}m\n" def main(): """Entry point of the program.""" # Instantiate the data problem. data = create_data_model() # Create the routing index manager. manager = pywrapcp.RoutingIndexManager( len(data["locations"]), data["num_vehicles"], data["depot"] ) # Create Routing Model. routing = pywrapcp.RoutingModel(manager) distance_matrix = compute_euclidean_distance_matrix(data["locations"]) def distance_callback(from_index, to_index): """Returns the distance between the two nodes.""" # Convert from routing variable Index to distance matrix NodeIndex. from_node = manager.IndexToNode(from_index) to_node = manager.IndexToNode(to_index) return distance_matrix[from_node][to_node] transit_callback_index = routing.RegisterTransitCallback(distance_callback) # Define cost of each arc. routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index) # Setting first solution heuristic. search_parameters = pywrapcp.DefaultRoutingSearchParameters() search_parameters.first_solution_strategy = ( routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC ) # Solve the problem. solution = routing.SolveWithParameters(search_parameters) # Print solution on console. if solution: print_solution(manager, routing, solution) if __name__ == "__main__": main()
C++
#include <cmath> #include <cstdint> #include <cstdlib> #include <sstream> #include <vector> #include "ortools/base/logging.h" #include "ortools/constraint_solver/constraint_solver.h" #include "ortools/constraint_solver/routing.h" #include "ortools/constraint_solver/routing_enums.pb.h" #include "ortools/constraint_solver/routing_index_manager.h" #include "ortools/constraint_solver/routing_parameters.h" namespace operations_research { struct DataModel { const std::vector<std::vector<int>> locations{ {288, 149}, {288, 129}, {270, 133}, {256, 141}, {256, 157}, {246, 157}, {236, 169}, {228, 169}, {228, 161}, {220, 169}, {212, 169}, {204, 169}, {196, 169}, {188, 169}, {196, 161}, {188, 145}, {172, 145}, {164, 145}, {156, 145}, {148, 145}, {140, 145}, {148, 169}, {164, 169}, {172, 169}, {156, 169}, {140, 169}, {132, 169}, {124, 169}, {116, 161}, {104, 153}, {104, 161}, {104, 169}, {90, 165}, {80, 157}, {64, 157}, {64, 165}, {56, 169}, {56, 161}, {56, 153}, {56, 145}, {56, 137}, {56, 129}, {56, 121}, {40, 121}, {40, 129}, {40, 137}, {40, 145}, {40, 153}, {40, 161}, {40, 169}, {32, 169}, {32, 161}, {32, 153}, {32, 145}, {32, 137}, {32, 129}, {32, 121}, {32, 113}, {40, 113}, {56, 113}, {56, 105}, {48, 99}, {40, 99}, {32, 97}, {32, 89}, {24, 89}, {16, 97}, {16, 109}, {8, 109}, {8, 97}, {8, 89}, {8, 81}, {8, 73}, {8, 65}, {8, 57}, {16, 57}, {8, 49}, {8, 41}, {24, 45}, {32, 41}, {32, 49}, {32, 57}, {32, 65}, {32, 73}, {32, 81}, {40, 83}, {40, 73}, {40, 63}, {40, 51}, {44, 43}, {44, 35}, {44, 27}, {32, 25}, {24, 25}, {16, 25}, {16, 17}, {24, 17}, {32, 17}, {44, 11}, {56, 9}, {56, 17}, {56, 25}, {56, 33}, {56, 41}, {64, 41}, {72, 41}, {72, 49}, {56, 49}, {48, 51}, {56, 57}, {56, 65}, {48, 63}, {48, 73}, {56, 73}, {56, 81}, {48, 83}, {56, 89}, {56, 97}, {104, 97}, {104, 105}, {104, 113}, {104, 121}, {104, 129}, {104, 137}, {104, 145}, {116, 145}, {124, 145}, {132, 145}, {132, 137}, {140, 137}, {148, 137}, {156, 137}, {164, 137}, {172, 125}, {172, 117}, {172, 109}, {172, 101}, {172, 93}, {172, 85}, {180, 85}, {180, 77}, {180, 69}, {180, 61}, {180, 53}, {172, 53}, {172, 61}, {172, 69}, {172, 77}, {164, 81}, {148, 85}, {124, 85}, {124, 93}, {124, 109}, {124, 125}, {124, 117}, {124, 101}, {104, 89}, {104, 81}, {104, 73}, {104, 65}, {104, 49}, {104, 41}, {104, 33}, {104, 25}, {104, 17}, {92, 9}, {80, 9}, {72, 9}, {64, 21}, {72, 25}, {80, 25}, {80, 25}, {80, 41}, {88, 49}, {104, 57}, {124, 69}, {124, 77}, {132, 81}, {140, 65}, {132, 61}, {124, 61}, {124, 53}, {124, 45}, {124, 37}, {124, 29}, {132, 21}, {124, 21}, {120, 9}, {128, 9}, {136, 9}, {148, 9}, {162, 9}, {156, 25}, {172, 21}, {180, 21}, {180, 29}, {172, 29}, {172, 37}, {172, 45}, {180, 45}, {180, 37}, {188, 41}, {196, 49}, {204, 57}, {212, 65}, {220, 73}, {228, 69}, {228, 77}, {236, 77}, {236, 69}, {236, 61}, {228, 61}, {228, 53}, {236, 53}, {236, 45}, {228, 45}, {228, 37}, {236, 37}, {236, 29}, {228, 29}, {228, 21}, {236, 21}, {252, 21}, {260, 29}, {260, 37}, {260, 45}, {260, 53}, {260, 61}, {260, 69}, {260, 77}, {276, 77}, {276, 69}, {276, 61}, {276, 53}, {284, 53}, {284, 61}, {284, 69}, {284, 77}, {284, 85}, {284, 93}, {284, 101}, {288, 109}, {280, 109}, {276, 101}, {276, 93}, {276, 85}, {268, 97}, {260, 109}, {252, 101}, {260, 93}, {260, 85}, {236, 85}, {228, 85}, {228, 93}, {236, 93}, {236, 101}, {228, 101}, {228, 109}, {228, 117}, {228, 125}, {220, 125}, {212, 117}, {204, 109}, {196, 101}, {188, 93}, {180, 93}, {180, 101}, {180, 109}, {180, 117}, {180, 125}, {196, 145}, {204, 145}, {212, 145}, {220, 145}, {228, 145}, {236, 145}, {246, 141}, {252, 125}, {260, 129}, {280, 133}, }; const int num_vehicles = 1; const RoutingIndexManager::NodeIndex depot{0}; }; // @brief Generate distance matrix. std::vector<std::vector<int64_t>> ComputeEuclideanDistanceMatrix( const std::vector<std::vector<int>>& locations) { std::vector<std::vector<int64_t>> distances = std::vector<std::vector<int64_t>>( locations.size(), std::vector<int64_t>(locations.size(), int64_t{0})); for (int from_node = 0; from_node < locations.size(); from_node++) { for (int to_node = 0; to_node < locations.size(); to_node++) { if (from_node != to_node) distances[from_node][to_node] = static_cast<int64_t>( std::hypot((locations[to_node][0] - locations[from_node][0]), (locations[to_node][1] - locations[from_node][1]))); } } return distances; } //! @brief Print the solution //! @param[in] manager Index manager used. //! @param[in] routing Routing solver used. //! @param[in] solution Solution found by the solver. void PrintSolution(const RoutingIndexManager& manager, const RoutingModel& routing, const Assignment& solution) { LOG(INFO) << "Objective: " << solution.ObjectiveValue(); // Inspect solution. int64_t index = routing.Start(0); LOG(INFO) << "Route:"; int64_t distance{0}; std::stringstream route; while (!routing.IsEnd(index)) { route << manager.IndexToNode(index).value() << " -> "; const int64_t previous_index = index; index = solution.Value(routing.NextVar(index)); distance += routing.GetArcCostForVehicle(previous_index, index, int64_t{0}); } LOG(INFO) << route.str() << manager.IndexToNode(index).value(); LOG(INFO) << "Route distance: " << distance << "mm"; LOG(INFO) << ""; LOG(INFO) << "Advanced usage:"; LOG(INFO) << "Problem solved in " << routing.solver()->wall_time() << "ms"; } void Tsp() { // Instantiate the data problem. DataModel data; // Create Routing Index Manager RoutingIndexManager manager(data.locations.size(), data.num_vehicles, data.depot); // Create Routing Model. RoutingModel routing(manager); const auto distance_matrix = ComputeEuclideanDistanceMatrix(data.locations); const int transit_callback_index = routing.RegisterTransitCallback( [&distance_matrix, &manager](const int64_t from_index, const int64_t to_index) -> int64_t { // Convert from routing variable Index to distance matrix NodeIndex. const int from_node = manager.IndexToNode(from_index).value(); const int to_node = manager.IndexToNode(to_index).value(); return distance_matrix[from_node][to_node]; }); // Define cost of each arc. routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index); // Setting first solution heuristic. RoutingSearchParameters searchParameters = DefaultRoutingSearchParameters(); searchParameters.set_first_solution_strategy( FirstSolutionStrategy::PATH_CHEAPEST_ARC); // Solve the problem. const Assignment* solution = routing.SolveWithParameters(searchParameters); // Print solution on console. PrintSolution(manager, routing, *solution); } } // namespace operations_research int main(int /*argc*/, char* /*argv*/[]) { operations_research::Tsp(); return EXIT_SUCCESS; }
Java
package com.google.ortools.constraintsolver.samples; import com.google.ortools.Loader; import com.google.ortools.constraintsolver.Assignment; import com.google.ortools.constraintsolver.FirstSolutionStrategy; import com.google.ortools.constraintsolver.RoutingIndexManager; import com.google.ortools.constraintsolver.RoutingModel; import com.google.ortools.constraintsolver.RoutingSearchParameters; import com.google.ortools.constraintsolver.main; import java.util.logging.Logger; /** Minimal TSP. */ public class TspCircuitBoard { private static final Logger logger = Logger.getLogger(TspCircuitBoard.class.getName()); static class DataModel { public final int[][] locations = {{288, 149}, {288, 129}, {270, 133}, {256, 141}, {256, 157}, {246, 157}, {236, 169}, {228, 169}, {228, 161}, {220, 169}, {212, 169}, {204, 169}, {196, 169}, {188, 169}, {196, 161}, {188, 145}, {172, 145}, {164, 145}, {156, 145}, {148, 145}, {140, 145}, {148, 169}, {164, 169}, {172, 169}, {156, 169}, {140, 169}, {132, 169}, {124, 169}, {116, 161}, {104, 153}, {104, 161}, {104, 169}, {90, 165}, {80, 157}, {64, 157}, {64, 165}, {56, 169}, {56, 161}, {56, 153}, {56, 145}, {56, 137}, {56, 129}, {56, 121}, {40, 121}, {40, 129}, {40, 137}, {40, 145}, {40, 153}, {40, 161}, {40, 169}, {32, 169}, {32, 161}, {32, 153}, {32, 145}, {32, 137}, {32, 129}, {32, 121}, {32, 113}, {40, 113}, {56, 113}, {56, 105}, {48, 99}, {40, 99}, {32, 97}, {32, 89}, {24, 89}, {16, 97}, {16, 109}, {8, 109}, {8, 97}, {8, 89}, {8, 81}, {8, 73}, {8, 65}, {8, 57}, {16, 57}, {8, 49}, {8, 41}, {24, 45}, {32, 41}, {32, 49}, {32, 57}, {32, 65}, {32, 73}, {32, 81}, {40, 83}, {40, 73}, {40, 63}, {40, 51}, {44, 43}, {44, 35}, {44, 27}, {32, 25}, {24, 25}, {16, 25}, {16, 17}, {24, 17}, {32, 17}, {44, 11}, {56, 9}, {56, 17}, {56, 25}, {56, 33}, {56, 41}, {64, 41}, {72, 41}, {72, 49}, {56, 49}, {48, 51}, {56, 57}, {56, 65}, {48, 63}, {48, 73}, {56, 73}, {56, 81}, {48, 83}, {56, 89}, {56, 97}, {104, 97}, {104, 105}, {104, 113}, {104, 121}, {104, 129}, {104, 137}, {104, 145}, {116, 145}, {124, 145}, {132, 145}, {132, 137}, {140, 137}, {148, 137}, {156, 137}, {164, 137}, {172, 125}, {172, 117}, {172, 109}, {172, 101}, {172, 93}, {172, 85}, {180, 85}, {180, 77}, {180, 69}, {180, 61}, {180, 53}, {172, 53}, {172, 61}, {172, 69}, {172, 77}, {164, 81}, {148, 85}, {124, 85}, {124, 93}, {124, 109}, {124, 125}, {124, 117}, {124, 101}, {104, 89}, {104, 81}, {104, 73}, {104, 65}, {104, 49}, {104, 41}, {104, 33}, {104, 25}, {104, 17}, {92, 9}, {80, 9}, {72, 9}, {64, 21}, {72, 25}, {80, 25}, {80, 25}, {80, 41}, {88, 49}, {104, 57}, {124, 69}, {124, 77}, {132, 81}, {140, 65}, {132, 61}, {124, 61}, {124, 53}, {124, 45}, {124, 37}, {124, 29}, {132, 21}, {124, 21}, {120, 9}, {128, 9}, {136, 9}, {148, 9}, {162, 9}, {156, 25}, {172, 21}, {180, 21}, {180, 29}, {172, 29}, {172, 37}, {172, 45}, {180, 45}, {180, 37}, {188, 41}, {196, 49}, {204, 57}, {212, 65}, {220, 73}, {228, 69}, {228, 77}, {236, 77}, {236, 69}, {236, 61}, {228, 61}, {228, 53}, {236, 53}, {236, 45}, {228, 45}, {228, 37}, {236, 37}, {236, 29}, {228, 29}, {228, 21}, {236, 21}, {252, 21}, {260, 29}, {260, 37}, {260, 45}, {260, 53}, {260, 61}, {260, 69}, {260, 77}, {276, 77}, {276, 69}, {276, 61}, {276, 53}, {284, 53}, {284, 61}, {284, 69}, {284, 77}, {284, 85}, {284, 93}, {284, 101}, {288, 109}, {280, 109}, {276, 101}, {276, 93}, {276, 85}, {268, 97}, {260, 109}, {252, 101}, {260, 93}, {260, 85}, {236, 85}, {228, 85}, {228, 93}, {236, 93}, {236, 101}, {228, 101}, {228, 109}, {228, 117}, {228, 125}, {220, 125}, {212, 117}, {204, 109}, {196, 101}, {188, 93}, {180, 93}, {180, 101}, {180, 109}, {180, 117}, {180, 125}, {196, 145}, {204, 145}, {212, 145}, {220, 145}, {228, 145}, {236, 145}, {246, 141}, {252, 125}, {260, 129}, {280, 133}}; public final int vehicleNumber = 1; public final int depot = 0; } /// @brief Compute Euclidean distance matrix from locations array. /// @details It uses an array of locations and computes /// the Euclidean distance between any two locations. private static long[][] computeEuclideanDistanceMatrix(int[][] locations) { // Calculate distance matrix using Euclidean distance. long[][] distanceMatrix = new long[locations.length][locations.length]; for (int fromNode = 0; fromNode < locations.length; ++fromNode) { for (int toNode = 0; toNode < locations.length; ++toNode) { if (fromNode == toNode) { distanceMatrix[fromNode][toNode] = 0; } else { distanceMatrix[fromNode][toNode] = (long) Math.hypot(locations[toNode][0] - locations[fromNode][0], locations[toNode][1] - locations[fromNode][1]); } } } return distanceMatrix; } /// @brief Print the solution. static void printSolution( RoutingModel routing, RoutingIndexManager manager, Assignment solution) { // Solution cost. logger.info("Objective: " + solution.objectiveValue()); // Inspect solution. logger.info("Route:"); long routeDistance = 0; String route = ""; long index = routing.start(0); while (!routing.isEnd(index)) { route += manager.indexToNode(index) + " -> "; long previousIndex = index; index = solution.value(routing.nextVar(index)); routeDistance += routing.getArcCostForVehicle(previousIndex, index, 0); } route += manager.indexToNode(routing.end(0)); logger.info(route); logger.info("Route distance: " + routeDistance); } public static void main(String[] args) throws Exception { Loader.loadNativeLibraries(); // Instantiate the data problem. final DataModel data = new DataModel(); // Create Routing Index Manager RoutingIndexManager manager = new RoutingIndexManager(data.locations.length, data.vehicleNumber, data.depot); // Create Routing Model. RoutingModel routing = new RoutingModel(manager); // Create and register a transit callback. final long[][] distanceMatrix = computeEuclideanDistanceMatrix(data.locations); final int transitCallbackIndex = routing.registerTransitCallback((long fromIndex, long toIndex) -> { // Convert from routing variable Index to user NodeIndex. int fromNode = manager.indexToNode(fromIndex); int toNode = manager.indexToNode(toIndex); return distanceMatrix[fromNode][toNode]; }); // Define cost of each arc. routing.setArcCostEvaluatorOfAllVehicles(transitCallbackIndex); // Setting first solution heuristic. RoutingSearchParameters searchParameters = main.defaultRoutingSearchParameters() .toBuilder() .setFirstSolutionStrategy(FirstSolutionStrategy.Value.PATH_CHEAPEST_ARC) .build(); // Solve the problem. Assignment solution = routing.solveWithParameters(searchParameters); // Print solution on console. printSolution(routing, manager, solution); } }
C#
using System; using System.Collections.Generic; using Google.OrTools.ConstraintSolver; /// <summary> /// Minimal TSP. /// A description of the problem can be found here: /// http://en.wikipedia.org/wiki/Travelling_salesperson_problem. /// </summary> public class TspCircuitBoard { class DataModel { public int[,] Locations = { { 288, 149 }, { 288, 129 }, { 270, 133 }, { 256, 141 }, { 256, 157 }, { 246, 157 }, { 236, 169 }, { 228, 169 }, { 228, 161 }, { 220, 169 }, { 212, 169 }, { 204, 169 }, { 196, 169 }, { 188, 169 }, { 196, 161 }, { 188, 145 }, { 172, 145 }, { 164, 145 }, { 156, 145 }, { 148, 145 }, { 140, 145 }, { 148, 169 }, { 164, 169 }, { 172, 169 }, { 156, 169 }, { 140, 169 }, { 132, 169 }, { 124, 169 }, { 116, 161 }, { 104, 153 }, { 104, 161 }, { 104, 169 }, { 90, 165 }, { 80, 157 }, { 64, 157 }, { 64, 165 }, { 56, 169 }, { 56, 161 }, { 56, 153 }, { 56, 145 }, { 56, 137 }, { 56, 129 }, { 56, 121 }, { 40, 121 }, { 40, 129 }, { 40, 137 }, { 40, 145 }, { 40, 153 }, { 40, 161 }, { 40, 169 }, { 32, 169 }, { 32, 161 }, { 32, 153 }, { 32, 145 }, { 32, 137 }, { 32, 129 }, { 32, 121 }, { 32, 113 }, { 40, 113 }, { 56, 113 }, { 56, 105 }, { 48, 99 }, { 40, 99 }, { 32, 97 }, { 32, 89 }, { 24, 89 }, { 16, 97 }, { 16, 109 }, { 8, 109 }, { 8, 97 }, { 8, 89 }, { 8, 81 }, { 8, 73 }, { 8, 65 }, { 8, 57 }, { 16, 57 }, { 8, 49 }, { 8, 41 }, { 24, 45 }, { 32, 41 }, { 32, 49 }, { 32, 57 }, { 32, 65 }, { 32, 73 }, { 32, 81 }, { 40, 83 }, { 40, 73 }, { 40, 63 }, { 40, 51 }, { 44, 43 }, { 44, 35 }, { 44, 27 }, { 32, 25 }, { 24, 25 }, { 16, 25 }, { 16, 17 }, { 24, 17 }, { 32, 17 }, { 44, 11 }, { 56, 9 }, { 56, 17 }, { 56, 25 }, { 56, 33 }, { 56, 41 }, { 64, 41 }, { 72, 41 }, { 72, 49 }, { 56, 49 }, { 48, 51 }, { 56, 57 }, { 56, 65 }, { 48, 63 }, { 48, 73 }, { 56, 73 }, { 56, 81 }, { 48, 83 }, { 56, 89 }, { 56, 97 }, { 104, 97 }, { 104, 105 }, { 104, 113 }, { 104, 121 }, { 104, 129 }, { 104, 137 }, { 104, 145 }, { 116, 145 }, { 124, 145 }, { 132, 145 }, { 132, 137 }, { 140, 137 }, { 148, 137 }, { 156, 137 }, { 164, 137 }, { 172, 125 }, { 172, 117 }, { 172, 109 }, { 172, 101 }, { 172, 93 }, { 172, 85 }, { 180, 85 }, { 180, 77 }, { 180, 69 }, { 180, 61 }, { 180, 53 }, { 172, 53 }, { 172, 61 }, { 172, 69 }, { 172, 77 }, { 164, 81 }, { 148, 85 }, { 124, 85 }, { 124, 93 }, { 124, 109 }, { 124, 125 }, { 124, 117 }, { 124, 101 }, { 104, 89 }, { 104, 81 }, { 104, 73 }, { 104, 65 }, { 104, 49 }, { 104, 41 }, { 104, 33 }, { 104, 25 }, { 104, 17 }, { 92, 9 }, { 80, 9 }, { 72, 9 }, { 64, 21 }, { 72, 25 }, { 80, 25 }, { 80, 25 }, { 80, 41 }, { 88, 49 }, { 104, 57 }, { 124, 69 }, { 124, 77 }, { 132, 81 }, { 140, 65 }, { 132, 61 }, { 124, 61 }, { 124, 53 }, { 124, 45 }, { 124, 37 }, { 124, 29 }, { 132, 21 }, { 124, 21 }, { 120, 9 }, { 128, 9 }, { 136, 9 }, { 148, 9 }, { 162, 9 }, { 156, 25 }, { 172, 21 }, { 180, 21 }, { 180, 29 }, { 172, 29 }, { 172, 37 }, { 172, 45 }, { 180, 45 }, { 180, 37 }, { 188, 41 }, { 196, 49 }, { 204, 57 }, { 212, 65 }, { 220, 73 }, { 228, 69 }, { 228, 77 }, { 236, 77 }, { 236, 69 }, { 236, 61 }, { 228, 61 }, { 228, 53 }, { 236, 53 }, { 236, 45 }, { 228, 45 }, { 228, 37 }, { 236, 37 }, { 236, 29 }, { 228, 29 }, { 228, 21 }, { 236, 21 }, { 252, 21 }, { 260, 29 }, { 260, 37 }, { 260, 45 }, { 260, 53 }, { 260, 61 }, { 260, 69 }, { 260, 77 }, { 276, 77 }, { 276, 69 }, { 276, 61 }, { 276, 53 }, { 284, 53 }, { 284, 61 }, { 284, 69 }, { 284, 77 }, { 284, 85 }, { 284, 93 }, { 284, 101 }, { 288, 109 }, { 280, 109 }, { 276, 101 }, { 276, 93 }, { 276, 85 }, { 268, 97 }, { 260, 109 }, { 252, 101 }, { 260, 93 }, { 260, 85 }, { 236, 85 }, { 228, 85 }, { 228, 93 }, { 236, 93 }, { 236, 101 }, { 228, 101 }, { 228, 109 }, { 228, 117 }, { 228, 125 }, { 220, 125 }, { 212, 117 }, { 204, 109 }, { 196, 101 }, { 188, 93 }, { 180, 93 }, { 180, 101 }, { 180, 109 }, { 180, 117 }, { 180, 125 }, { 196, 145 }, { 204, 145 }, { 212, 145 }, { 220, 145 }, { 228, 145 }, { 236, 145 }, { 246, 141 }, { 252, 125 }, { 260, 129 }, { 280, 133 }, }; public int VehicleNumber = 1; public int Depot = 0; }; /// <summary> /// Euclidean distance implemented as a callback. It uses an array of /// positions and computes the Euclidean distance between the two /// positions of two different indices. /// </summary> static long[,] ComputeEuclideanDistanceMatrix(in int[,] locations) { // Calculate the distance matrix using Euclidean distance. int locationNumber = locations.GetLength(0); long[,] distanceMatrix = new long[locationNumber, locationNumber]; for (int fromNode = 0; fromNode < locationNumber; fromNode++) { for (int toNode = 0; toNode < locationNumber; toNode++) { if (fromNode == toNode) distanceMatrix[fromNode, toNode] = 0; else distanceMatrix[fromNode, toNode] = (long)Math.Sqrt(Math.Pow(locations[toNode, 0] - locations[fromNode, 0], 2) + Math.Pow(locations[toNode, 1] - locations[fromNode, 1], 2)); } } return distanceMatrix; } /// <summary> /// Print the solution. /// </summary> static void PrintSolution(in RoutingModel routing, in RoutingIndexManager manager, in Assignment solution) { Console.WriteLine("Objective: {0}", solution.ObjectiveValue()); // Inspect solution. Console.WriteLine("Route:"); long routeDistance = 0; var index = routing.Start(0); while (routing.IsEnd(index) == false) { Console.Write("{0} -> ", manager.IndexToNode((int)index)); var previousIndex = index; index = solution.Value(routing.NextVar(index)); routeDistance += routing.GetArcCostForVehicle(previousIndex, index, 0); } Console.WriteLine("{0}", manager.IndexToNode((int)index)); Console.WriteLine("Route distance: {0}m", routeDistance); } public static void Main(String[] args) { // Instantiate the data problem. DataModel data = new DataModel(); // Create Routing Index Manager RoutingIndexManager manager = new RoutingIndexManager(data.Locations.GetLength(0), data.VehicleNumber, data.Depot); // Create Routing Model. RoutingModel routing = new RoutingModel(manager); // Define cost of each arc. long[,] distanceMatrix = ComputeEuclideanDistanceMatrix(data.Locations); int transitCallbackIndex = routing.RegisterTransitCallback((long fromIndex, long toIndex) => { // Convert from routing variable Index to // distance matrix NodeIndex. var fromNode = manager.IndexToNode(fromIndex); var toNode = manager.IndexToNode(toIndex); return distanceMatrix[fromNode, toNode]; }); routing.SetArcCostEvaluatorOfAllVehicles(transitCallbackIndex); // Setting first solution heuristic. RoutingSearchParameters searchParameters = operations_research_constraint_solver.DefaultRoutingSearchParameters(); searchParameters.FirstSolutionStrategy = FirstSolutionStrategy.Types.Value.PathCheapestArc; // Solve the problem. Assignment solution = routing.SolveWithParameters(searchParameters); // Print solution on console. PrintSolution(routing, manager, solution); } }
Changing the search strategy
The routing solver does not always return the optimal solution to a TSP, because routing problems are computationally intractable. For instance, the solution returned in the previous example is not the optimal route.
To find a better solution, you can use a more advanced search strategy, called guided local search, which enables the solver to escape a local minimum — a solution that is shorter than all nearby routes, but which is not the global minimum. After moving away from the local minimum, the solver continues the search.
The examples below show how to set a guided local search for the circuit board example.
Python
search_parameters = pywrapcp.DefaultRoutingSearchParameters() search_parameters.local_search_metaheuristic = ( routing_enums_pb2.LocalSearchMetaheuristic.GUIDED_LOCAL_SEARCH) search_parameters.time_limit.seconds = 30 search_parameters.log_search = True
C++
RoutingSearchParameters searchParameters = DefaultRoutingSearchParameters(); searchParameters.set_local_search_metaheuristic( LocalSearchMetaheuristic::GUIDED_LOCAL_SEARCH); searchParameters.mutable_time_limit()->set_seconds(30); search_parameters.set_log_search(true);
Java
Add the following `import` statement at the beginning of the program:import com.google.protobuf.Duration;
RoutingSearchParameters searchParameters = main.defaultRoutingSearchParameters() .toBuilder() .setFirstSolutionStrategy(FirstSolutionStrategy.Value.PATH_CHEAPEST_ARC) .setLocalSearchMetaheuristic(LocalSearchMetaheuristic.Value.GUIDED_LOCAL_SEARCH) .setTimeLimit(Duration.newBuilder().setSeconds(30).build()) .setLogSearch(true) .build();
C#
Add the following line at the beginning of the program:using Google.Protobuf.WellKnownTypes; // Duration
RoutingSearchParameters searchParameters =
operations_research_constraint_solver.DefaultRoutingSearchParameters();
searchParameters.FirstSolutionStrategy = FirstSolutionStrategy.Types.Value.PathCheapestArc;
searchParameters.LocalSearchMetaheuristic = LocalSearchMetaheuristic.Types.Value.GuidedLocalSearch;
searchParameters.TimeLimit = new Duration { Seconds = 30 };
searchParameters.LogSearch = true;For other local search strategies, see Local search options.
The examples above also enable logging for the search. While logging isn't required, it can be useful for debugging.
When you run the program after making the changes shown above, you get the following solution, which is shorter than the solution shown in the previous section.
Objective: 2672 Route: 0 -> 3 -> 276 -> 4 -> 5 -> 6 -> 8 -> 7 -> 9 -> 10 -> 11 -> 14 -> 12 -> 13 -> 23 -> 22 -> 24 -> 21 -> 25 -> 26 -> 27 -> 28 -> 125 -> 126 -> 127 -> 20 -> 19 -> 130 -> 129 -> 128 -> 153 -> 154 -> 152 -> 155 -> 151 -> 150 -> 177 -> 176 -> 175 -> 180 -> 161 -> 160 -> 174 -> 159 -> 158 -> 157 -> 156 -> 118 -> 119 -> 120 -> 121 -> 122 -> 123 -> 124 -> 29 -> 30 -> 31 -> 32 -> 33 -> 34 -> 35 -> 36 -> 37 -> 38 -> 39 -> 40 -> 41 -> 42 -> 59 -> 60 -> 58 -> 43 -> 44 -> 45 -> 46 -> 47 -> 48 -> 49 -> 50 -> 51 -> 52 -> 53 -> 54 -> 55 -> 56 -> 57 -> 67 -> 68 -> 66 -> 69 -> 70 -> 71 -> 72 -> 73 -> 75 -> 74 -> 76 -> 77 -> 78 -> 80 -> 81 -> 88 -> 79 -> 92 -> 93 -> 94 -> 95 -> 96 -> 97 -> 98 -> 99 -> 100 -> 101 -> 102 -> 91 -> 90 -> 89 -> 108 -> 111 -> 87 -> 82 -> 83 -> 86 -> 112 -> 115 -> 85 -> 84 -> 64 -> 65 -> 63 -> 62 -> 61 -> 117 -> 116 -> 114 -> 113 -> 110 -> 109 -> 107 -> 103 -> 104 -> 105 -> 106 -> 173 -> 172 -> 171 -> 170 -> 169 -> 168 -> 167 -> 166 -> 165 -> 164 -> 163 -> 162 -> 187 -> 188 -> 189 -> 190 -> 191 -> 192 -> 185 -> 186 -> 184 -> 183 -> 182 -> 181 -> 179 -> 178 -> 149 -> 148 -> 138 -> 137 -> 136 -> 266 -> 267 -> 135 -> 134 -> 268 -> 269 -> 133 -> 132 -> 131 -> 18 -> 17 -> 16 -> 15 -> 270 -> 271 -> 272 -> 273 -> 274 -> 275 -> 259 -> 258 -> 260 -> 261 -> 262 -> 263 -> 264 -> 265 -> 139 -> 140 -> 147 -> 146 -> 141 -> 142 -> 145 -> 144 -> 198 -> 197 -> 196 -> 193 -> 194 -> 195 -> 200 -> 201 -> 199 -> 143 -> 202 -> 203 -> 204 -> 205 -> 206 -> 207 -> 252 -> 253 -> 256 -> 257 -> 255 -> 254 -> 251 -> 208 -> 209 -> 210 -> 211 -> 212 -> 213 -> 214 -> 215 -> 216 -> 217 -> 218 -> 219 -> 220 -> 221 -> 222 -> 223 -> 224 -> 225 -> 226 -> 227 -> 232 -> 233 -> 234 -> 235 -> 236 -> 237 -> 230 -> 231 -> 228 -> 229 -> 250 -> 245 -> 238 -> 239 -> 240 -> 241 -> 242 -> 243 -> 244 -> 246 -> 249 -> 248 -> 247 -> 277 -> 278 -> 2 -> 279 -> 1 -> 0
For more search options, see Routing Options.
The best algorithms can now routinely solve TSP instances with tens of thousands of nodes. (The record at the time of writing is the pla85900 instance in TSPLIB, a VLSI application with 85,900 nodes. For certain instances with millions of nodes, solutions have been found guaranteed to be within 1% of an optimal tour.)
Scaling the distance matrix
Since the routing solver works over the integers, if your distance matrix has non-integer entries, you have to round the distances to integers. If some distances are small, rounding can affect the solution.
To avoid any issue with rounding, you can scale the distance matrix: multiply
all entries of the matrix by a large number — say 100. This multiplies the
length of any route by a factor of 100, but it doesn't change the solution. The
advantage is that now when you round the matrix entries, the rounding amount
(which is at most 0.5), is very small compared to the distances, so it won't
affect the solution significantly.
If you scale the distance matrix, you also need to change the solution printer to divide the scaled route lengths by the scaling factor, so that it displays the unscaled distances of the routes.
