Page Summary
-
The problem focuses on maximizing the expression
x + 10ysubject to specific constraints, requiring integer solutions forxandy. -
This is classified as a Mixed Integer Programming (MIP) problem, specifically an Integer Linear Programming (ILP) problem.
-
The solution involves using a solver like SCIP or CP-SAT through the OR-Tools library to find the optimal values of
xandy. -
The optimal solution is achieved when
x = 3andy = 2, resulting in a maximum objective value of23. -
The provided code examples demonstrate how to implement this solution using OR-Tools in Python, C++, Java, and C#.
The following sections present an example of a MIP problem and show how to solve it. Here's the problem:
Maximize x + 10y subject to the following constraints:
x + 7y≤ 17.5- 0 ≤
x≤ 3.5 - 0 ≤
y x,yintegers
Since the constraints are linear, this is just a linear optimization problem in which the solutions are required to be integers. The following graph shows the integer points in the feasible region for the problem.
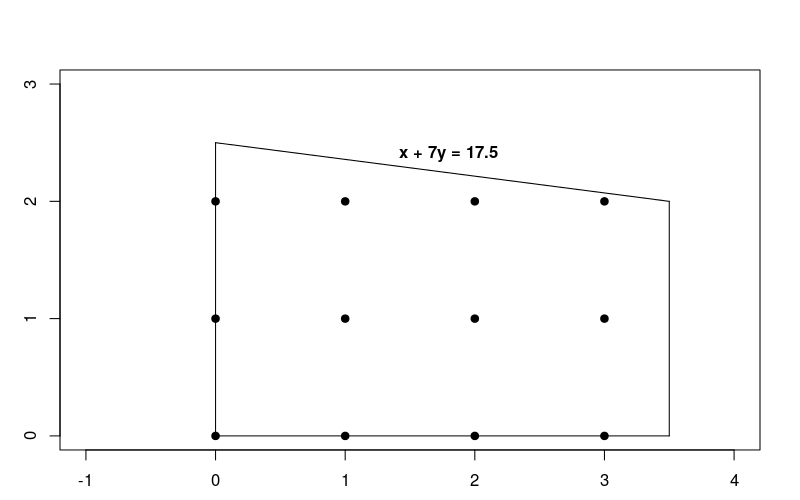
Notice that this problem is very similar to the linear optimization problem described in Solving an LP Problem, but in this case it requires the solutions to be integers.
Basic steps for solving a MIP problem
To solve a MIP problem, your program should include the following steps:
- Import the linear solver wrapper,
- declare the MIP solver,
- define the variables,
- define the constraints,
- define the objective,
- call the MIP solver and
- display the solution
Solution using the MPSolver
The following section present a program that solves the problem using the MPSolver wrapper and a MIP solver.
For integer linear problems (ILP), that is problems without continuous variables, we recommend using the CP-SAT solver.
For mixed integer problems (MIP), that is problem with both integer and continuous variables, we recommend using the SCIP solver.
Import the linear solver wrapper
Import (or include) the OR-Tools linear solver wrapper, an interface for MIP solvers and linear solvers, as shown in the following code.
Python
from ortools.linear_solver import pywraplp
C++
#include <memory> #include "absl/base/log_severity.h" #include "absl/log/globals.h" #include "ortools/base/init_google.h" #include "ortools/linear_solver/linear_solver.h"
Java
import com.google.ortools.Loader; import com.google.ortools.linearsolver.MPConstraint; import com.google.ortools.linearsolver.MPObjective; import com.google.ortools.linearsolver.MPSolver; import com.google.ortools.linearsolver.MPVariable;
C#
using System; using Google.OrTools.LinearSolver;
Declare the MIP solver
The following code declares the MIP solver for the problem. This example uses the third-party solver SCIP.
Python
# Create the mip solver with the CP-SAT backend. solver = pywraplp.Solver.CreateSolver("SAT") if not solver: return
C++
// Create the mip solver with the SCIP backend. std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP")); if (!solver) { LOG(WARNING) << "SCIP solver unavailable."; return; }
Java
// Create the linear solver with the SCIP backend. MPSolver solver = MPSolver.createSolver("SCIP"); if (solver == null) { System.out.println("Could not create solver SCIP"); return; }
C#
// Create the linear solver with the SCIP backend. Solver solver = Solver.CreateSolver("SCIP"); if (solver is null) { return; }
Define the variables
The following code defines the variables in the problem.
Python
infinity = solver.infinity() # x and y are integer non-negative variables. x = solver.IntVar(0.0, infinity, "x") y = solver.IntVar(0.0, infinity, "y") print("Number of variables =", solver.NumVariables())
C++
const double infinity = solver->infinity(); // x and y are integer non-negative variables. MPVariable* const x = solver->MakeIntVar(0.0, infinity, "x"); MPVariable* const y = solver->MakeIntVar(0.0, infinity, "y"); LOG(INFO) << "Number of variables = " << solver->NumVariables();
Java
double infinity = java.lang.Double.POSITIVE_INFINITY; // x and y are integer non-negative variables. MPVariable x = solver.makeIntVar(0.0, infinity, "x"); MPVariable y = solver.makeIntVar(0.0, infinity, "y"); System.out.println("Number of variables = " + solver.numVariables());
C#
// x and y are integer non-negative variables. Variable x = solver.MakeIntVar(0.0, double.PositiveInfinity, "x"); Variable y = solver.MakeIntVar(0.0, double.PositiveInfinity, "y"); Console.WriteLine("Number of variables = " + solver.NumVariables());
The program uses the MakeIntVar method (or a variant, depending on the coding
language) to create variables x and y that take on non-negative integer
values.
Define the constraints
The following code defines the constraints for the problem.
Python
# x + 7 * y <= 17.5. solver.Add(x + 7 * y <= 17.5) # x <= 3.5. solver.Add(x <= 3.5) print("Number of constraints =", solver.NumConstraints())
C++
// x + 7 * y <= 17.5. MPConstraint* const c0 = solver->MakeRowConstraint(-infinity, 17.5, "c0"); c0->SetCoefficient(x, 1); c0->SetCoefficient(y, 7); // x <= 3.5. MPConstraint* const c1 = solver->MakeRowConstraint(-infinity, 3.5, "c1"); c1->SetCoefficient(x, 1); c1->SetCoefficient(y, 0); LOG(INFO) << "Number of constraints = " << solver->NumConstraints();
Java
// x + 7 * y <= 17.5. MPConstraint c0 = solver.makeConstraint(-infinity, 17.5, "c0"); c0.setCoefficient(x, 1); c0.setCoefficient(y, 7); // x <= 3.5. MPConstraint c1 = solver.makeConstraint(-infinity, 3.5, "c1"); c1.setCoefficient(x, 1); c1.setCoefficient(y, 0); System.out.println("Number of constraints = " + solver.numConstraints());
C#
// x + 7 * y <= 17.5. solver.Add(x + 7 * y <= 17.5); // x <= 3.5. solver.Add(x <= 3.5); Console.WriteLine("Number of constraints = " + solver.NumConstraints());
Define the objective
The following code defines the objective function for the problem.
Python
# Maximize x + 10 * y. solver.Maximize(x + 10 * y)
C++
// Maximize x + 10 * y. MPObjective* const objective = solver->MutableObjective(); objective->SetCoefficient(x, 1); objective->SetCoefficient(y, 10); objective->SetMaximization();
Java
// Maximize x + 10 * y. MPObjective objective = solver.objective(); objective.setCoefficient(x, 1); objective.setCoefficient(y, 10); objective.setMaximization();
C#
// Maximize x + 10 * y. solver.Maximize(x + 10 * y);
Call the solver
The following code calls the solver.
Python
print(f"Solving with {solver.SolverVersion()}") status = solver.Solve()
C++
const MPSolver::ResultStatus result_status = solver->Solve(); // Check that the problem has an optimal solution. if (result_status != MPSolver::OPTIMAL) { LOG(FATAL) << "The problem does not have an optimal solution!"; }
Java
final MPSolver.ResultStatus resultStatus = solver.solve();
C#
Solver.ResultStatus resultStatus = solver.Solve();
Display the solution
The following code displays the solution.
Python
if status == pywraplp.Solver.OPTIMAL: print("Solution:") print("Objective value =", solver.Objective().Value()) print("x =", x.solution_value()) print("y =", y.solution_value()) else: print("The problem does not have an optimal solution.")
C++
LOG(INFO) << "Solution:"; LOG(INFO) << "Objective value = " << objective->Value(); LOG(INFO) << "x = " << x->solution_value(); LOG(INFO) << "y = " << y->solution_value();
Java
if (resultStatus == MPSolver.ResultStatus.OPTIMAL) { System.out.println("Solution:"); System.out.println("Objective value = " + objective.value()); System.out.println("x = " + x.solutionValue()); System.out.println("y = " + y.solutionValue()); } else { System.err.println("The problem does not have an optimal solution!"); }
C#
// Check that the problem has an optimal solution. if (resultStatus != Solver.ResultStatus.OPTIMAL) { Console.WriteLine("The problem does not have an optimal solution!"); return; } Console.WriteLine("Solution:"); Console.WriteLine("Objective value = " + solver.Objective().Value()); Console.WriteLine("x = " + x.SolutionValue()); Console.WriteLine("y = " + y.SolutionValue());
Here is the solution to the problem.
Number of variables = 2 Number of constraints = 2 Solution: Objective value = 23 x = 3 y = 2
The optimal value of the objective function is 23, which occurs at the point
x = 3, y = 2.
Complete programs
Here are the complete programs.
Python
from ortools.linear_solver import pywraplp def main(): # Create the mip solver with the CP-SAT backend. solver = pywraplp.Solver.CreateSolver("SAT") if not solver: return infinity = solver.infinity() # x and y are integer non-negative variables. x = solver.IntVar(0.0, infinity, "x") y = solver.IntVar(0.0, infinity, "y") print("Number of variables =", solver.NumVariables()) # x + 7 * y <= 17.5. solver.Add(x + 7 * y <= 17.5) # x <= 3.5. solver.Add(x <= 3.5) print("Number of constraints =", solver.NumConstraints()) # Maximize x + 10 * y. solver.Maximize(x + 10 * y) print(f"Solving with {solver.SolverVersion()}") status = solver.Solve() if status == pywraplp.Solver.OPTIMAL: print("Solution:") print("Objective value =", solver.Objective().Value()) print("x =", x.solution_value()) print("y =", y.solution_value()) else: print("The problem does not have an optimal solution.") print("\nAdvanced usage:") print(f"Problem solved in {solver.wall_time():d} milliseconds") print(f"Problem solved in {solver.iterations():d} iterations") print(f"Problem solved in {solver.nodes():d} branch-and-bound nodes") if __name__ == "__main__": main()
C++
#include <memory> #include "absl/base/log_severity.h" #include "absl/log/globals.h" #include "ortools/base/init_google.h" #include "ortools/linear_solver/linear_solver.h" namespace operations_research { void SimpleMipProgram() { // Create the mip solver with the SCIP backend. std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP")); if (!solver) { LOG(WARNING) << "SCIP solver unavailable."; return; } const double infinity = solver->infinity(); // x and y are integer non-negative variables. MPVariable* const x = solver->MakeIntVar(0.0, infinity, "x"); MPVariable* const y = solver->MakeIntVar(0.0, infinity, "y"); LOG(INFO) << "Number of variables = " << solver->NumVariables(); // x + 7 * y <= 17.5. MPConstraint* const c0 = solver->MakeRowConstraint(-infinity, 17.5, "c0"); c0->SetCoefficient(x, 1); c0->SetCoefficient(y, 7); // x <= 3.5. MPConstraint* const c1 = solver->MakeRowConstraint(-infinity, 3.5, "c1"); c1->SetCoefficient(x, 1); c1->SetCoefficient(y, 0); LOG(INFO) << "Number of constraints = " << solver->NumConstraints(); // Maximize x + 10 * y. MPObjective* const objective = solver->MutableObjective(); objective->SetCoefficient(x, 1); objective->SetCoefficient(y, 10); objective->SetMaximization(); const MPSolver::ResultStatus result_status = solver->Solve(); // Check that the problem has an optimal solution. if (result_status != MPSolver::OPTIMAL) { LOG(FATAL) << "The problem does not have an optimal solution!"; } LOG(INFO) << "Solution:"; LOG(INFO) << "Objective value = " << objective->Value(); LOG(INFO) << "x = " << x->solution_value(); LOG(INFO) << "y = " << y->solution_value(); LOG(INFO) << "\nAdvanced usage:"; LOG(INFO) << "Problem solved in " << solver->wall_time() << " milliseconds"; LOG(INFO) << "Problem solved in " << solver->iterations() << " iterations"; LOG(INFO) << "Problem solved in " << solver->nodes() << " branch-and-bound nodes"; } } // namespace operations_research int main(int argc, char* argv[]) { InitGoogle(argv[0], &argc, &argv, true); absl::SetStderrThreshold(absl::LogSeverityAtLeast::kInfo); operations_research::SimpleMipProgram(); return EXIT_SUCCESS; }
Java
package com.google.ortools.linearsolver.samples; import com.google.ortools.Loader; import com.google.ortools.linearsolver.MPConstraint; import com.google.ortools.linearsolver.MPObjective; import com.google.ortools.linearsolver.MPSolver; import com.google.ortools.linearsolver.MPVariable; /** Minimal Mixed Integer Programming example to showcase calling the solver. */ public final class SimpleMipProgram { public static void main(String[] args) { Loader.loadNativeLibraries(); // Create the linear solver with the SCIP backend. MPSolver solver = MPSolver.createSolver("SCIP"); if (solver == null) { System.out.println("Could not create solver SCIP"); return; } double infinity = java.lang.Double.POSITIVE_INFINITY; // x and y are integer non-negative variables. MPVariable x = solver.makeIntVar(0.0, infinity, "x"); MPVariable y = solver.makeIntVar(0.0, infinity, "y"); System.out.println("Number of variables = " + solver.numVariables()); // x + 7 * y <= 17.5. MPConstraint c0 = solver.makeConstraint(-infinity, 17.5, "c0"); c0.setCoefficient(x, 1); c0.setCoefficient(y, 7); // x <= 3.5. MPConstraint c1 = solver.makeConstraint(-infinity, 3.5, "c1"); c1.setCoefficient(x, 1); c1.setCoefficient(y, 0); System.out.println("Number of constraints = " + solver.numConstraints()); // Maximize x + 10 * y. MPObjective objective = solver.objective(); objective.setCoefficient(x, 1); objective.setCoefficient(y, 10); objective.setMaximization(); final MPSolver.ResultStatus resultStatus = solver.solve(); if (resultStatus == MPSolver.ResultStatus.OPTIMAL) { System.out.println("Solution:"); System.out.println("Objective value = " + objective.value()); System.out.println("x = " + x.solutionValue()); System.out.println("y = " + y.solutionValue()); } else { System.err.println("The problem does not have an optimal solution!"); } System.out.println("\nAdvanced usage:"); System.out.println("Problem solved in " + solver.wallTime() + " milliseconds"); System.out.println("Problem solved in " + solver.iterations() + " iterations"); System.out.println("Problem solved in " + solver.nodes() + " branch-and-bound nodes"); } private SimpleMipProgram() {} }
C#
using System; using Google.OrTools.LinearSolver; public class SimpleMipProgram { static void Main() { // Create the linear solver with the SCIP backend. Solver solver = Solver.CreateSolver("SCIP"); if (solver is null) { return; } // x and y are integer non-negative variables. Variable x = solver.MakeIntVar(0.0, double.PositiveInfinity, "x"); Variable y = solver.MakeIntVar(0.0, double.PositiveInfinity, "y"); Console.WriteLine("Number of variables = " + solver.NumVariables()); // x + 7 * y <= 17.5. solver.Add(x + 7 * y <= 17.5); // x <= 3.5. solver.Add(x <= 3.5); Console.WriteLine("Number of constraints = " + solver.NumConstraints()); // Maximize x + 10 * y. solver.Maximize(x + 10 * y); Solver.ResultStatus resultStatus = solver.Solve(); // Check that the problem has an optimal solution. if (resultStatus != Solver.ResultStatus.OPTIMAL) { Console.WriteLine("The problem does not have an optimal solution!"); return; } Console.WriteLine("Solution:"); Console.WriteLine("Objective value = " + solver.Objective().Value()); Console.WriteLine("x = " + x.SolutionValue()); Console.WriteLine("y = " + y.SolutionValue()); Console.WriteLine("\nAdvanced usage:"); Console.WriteLine("Problem solved in " + solver.WallTime() + " milliseconds"); Console.WriteLine("Problem solved in " + solver.Iterations() + " iterations"); Console.WriteLine("Problem solved in " + solver.Nodes() + " branch-and-bound nodes"); } }
Comparison of Linear and Integer Optimization
To compare the solution to the integer optimization problem, shown before,
with the solution to the corresponding linear optimization problem, in which
integer constraints are removed. You might guess that the solution to the
integer problem would be the integer point in the feasible region closest to the
linear solution — namely, the point x = 0, y = 2. But as you will see
next, this is not the case.
You can modify the program in the preceding section to solve the linear problem by making the following changes:
- Replace the MIP solver
with the LP solver
Python
# Create the mip solver with the CP-SAT backend. solver = pywraplp.Solver.CreateSolver("SAT") if not solver: return
C++
// Create the mip solver with the SCIP backend. std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP")); if (!solver) { LOG(WARNING) << "SCIP solver unavailable."; return; }
Java
// Create the linear solver with the SCIP backend. MPSolver solver = MPSolver.createSolver("SCIP"); if (solver == null) { System.out.println("Could not create solver SCIP"); return; }
C#
// Create the linear solver with the SCIP backend. Solver solver = Solver.CreateSolver("SCIP"); if (solver is null) { return; }
Python
# Create the linear solver with the GLOP backend. solver = pywraplp.Solver.CreateSolver("GLOP") if not solver: return
C++
// Create the linear solver with the GLOP backend. std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("GLOP"));
Java
// Create the linear solver with the GLOP backend. MPSolver solver = MPSolver.createSolver("GLOP"); if (solver == null) { System.out.println("Could not create solver SCIP"); return; }
C#
// Create the linear solver with the GLOP backend. Solver solver = Solver.CreateSolver("GLOP"); if (solver is null) { return; }
- Replace the integer variables
with continuous variables
Python
infinity = solver.infinity() # x and y are integer non-negative variables. x = solver.IntVar(0.0, infinity, "x") y = solver.IntVar(0.0, infinity, "y") print("Number of variables =", solver.NumVariables())
C++
const double infinity = solver->infinity(); // x and y are integer non-negative variables. MPVariable* const x = solver->MakeIntVar(0.0, infinity, "x"); MPVariable* const y = solver->MakeIntVar(0.0, infinity, "y"); LOG(INFO) << "Number of variables = " << solver->NumVariables();
Java
double infinity = java.lang.Double.POSITIVE_INFINITY; // x and y are integer non-negative variables. MPVariable x = solver.makeIntVar(0.0, infinity, "x"); MPVariable y = solver.makeIntVar(0.0, infinity, "y"); System.out.println("Number of variables = " + solver.numVariables());
C#
// x and y are integer non-negative variables. Variable x = solver.MakeIntVar(0.0, double.PositiveInfinity, "x"); Variable y = solver.MakeIntVar(0.0, double.PositiveInfinity, "y"); Console.WriteLine("Number of variables = " + solver.NumVariables());
Python
infinity = solver.infinity() # Create the variables x and y. x = solver.NumVar(0.0, infinity, "x") y = solver.NumVar(0.0, infinity, "y") print("Number of variables =", solver.NumVariables())
C++
const double infinity = solver->infinity(); // Create the variables x and y. MPVariable* const x = solver->MakeNumVar(0.0, infinity, "x"); MPVariable* const y = solver->MakeNumVar(0.0, infinity, "y"); LOG(INFO) << "Number of variables = " << solver->NumVariables();
Java
double infinity = java.lang.Double.POSITIVE_INFINITY; // Create the variables x and y. MPVariable x = solver.makeNumVar(0.0, infinity, "x"); MPVariable y = solver.makeNumVar(0.0, infinity, "y"); System.out.println("Number of variables = " + solver.numVariables());
C#
// Create the variables x and y. Variable x = solver.MakeNumVar(0.0, double.PositiveInfinity, "x"); Variable y = solver.MakeNumVar(0.0, double.PositiveInfinity, "y"); Console.WriteLine("Number of variables = " + solver.NumVariables());
After making these changes and running the program again, you get the following output:
Number of variables = 2 Number of constraints = 2 Objective value = 25.000000 x = 0.000000 y = 2.500000
The solution to the linear problem occurs at the point x = 0, y = 2.5, where
the objective function equals 25. Here's a graph showing the solutions to both
the linear and integer problems.
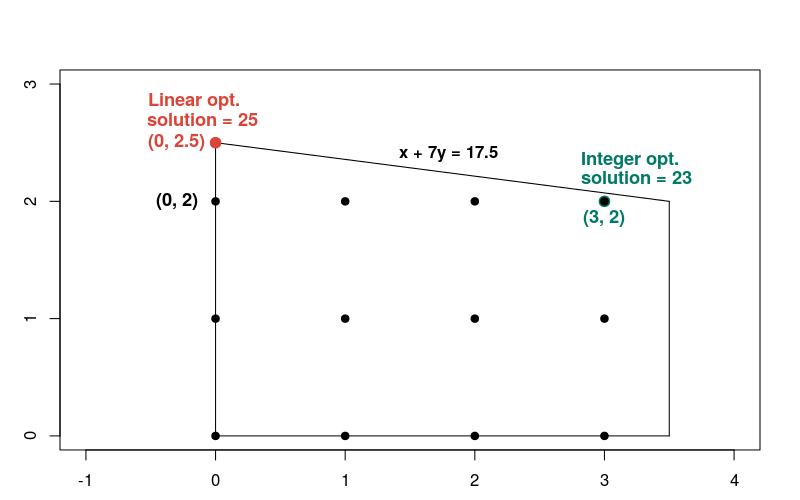
Notice that the integer solution is not close to the linear solution, compared with most other integer points in the feasible region. In general, the solutions to a linear optimization problem and the corresponding integer optimization problems can be far apart. Because of this, the two types of problems require different methods for their solution.
