Page Summary
-
Network flow problems, like transporting goods across a railway system, can be represented by graphs with nodes and links, where links have capacity limits.
-
The maximum flow problem aims to find the maximum transportable amount across a network, respecting capacity constraints.
-
OR-Tools offers various solvers in its graph libraries to address network flow problems like maximum flows and minimum cost flows.
-
Example applications of network flows include assignments with individual workers or teams, solvable using OR-Tools.
Many problems in computer science can be represented by a graph consisting of nodes and links between them. Examples are network flow problems, which involve transporting goods or material across a network, such as a railway system.
You can represent a network flow by a graph whose nodes are cities and whose arcs are rail lines between them. (They're called flows because their properties are similar to those of water flowing through a network of pipes.)
A key constraint in network flows is that each arc has a capacity — the maximum amount that can be transported across the arc in a fixed period of time.
The maximum flow problem is to determine the maximum total amount that can be transported across all arcs in the network, subject to the capacity constraints.
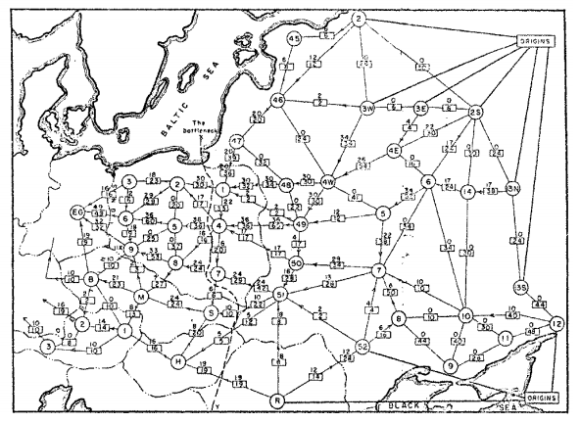
The first person to study this problem was the Russian mathematician A.N. Tolstoi, in the 1930s. The following map shows the actual railway network for which he wanted to find a maximum flow. The map itself comes from "Theodore E. Harris and Frank S. Ross. Fundamentals of a method for evaluating rail net capacities. Research Memorandum RM-1573, The RAND Corporation, Santa Monica, California, October 24, 1955. Declassified May 13, 1999".
OR-Tools provides several solvers for network flow problems in its graph libraries.
The following sections present examples of network flow problems and show how to solve them:
