Le problème des N-queens

Dans les sections suivantes, nous allons illustrer la programmation de contraintes (CP) par un problème combiné basé sur un jeu d'échecs. Aux échecs, une reine peut attaquer horizontalement, verticalement et en diagonale. Le problème de N-reens pose:

Comment les reines peuvent-elles être placées sur un échiquier NxN pour éviter qu'elles ne s'affrontent ?

Vous trouverez ci-dessous une solution possible au problème de N-reensions pour N = 4.

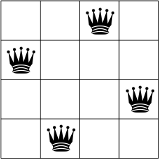
Il n'y a pas deux reines sur la même ligne, colonne ou diagonale.

Notez qu'il ne s'agit pas d'un problème d'optimisation: nous souhaitons trouver toutes les solutions possibles plutôt qu'une solution optimale, ce qui en fait une solution naturelle de programmation de contraintes. Les sections suivantes décrivent l'approche CP au problème des N-queens et présentent les programmes qui le résolvent à l'aide du résolveur CP-SAT et du résolveur CP d'origine.

Approche CP pour résoudre le problème des N-queens

Un solutionneur CP essaie systématiquement de trouver toutes les attributions de valeurs possibles aux variables d'un problème, afin de trouver les solutions réalisables. Dans le problème des quatre reines, le résolveur démarre à la colonne la plus à gauche et place successivement une reine dans chaque colonne, à un emplacement qui n'a pas été attaqué par aucune reine précédemment placée.

Propagation et retour arrière

Une recherche en programmation avec contrainte comporte deux éléments clés:

• Propagation : chaque fois que le résolveur attribue une valeur à une variable, des contraintes ajoutent des restrictions aux valeurs possibles des variables non attribuées. Ces restrictions se propagent aux futures attributions de variables. Par exemple, dans le problème des 4 reines, chaque fois que le solutionneur place une reine, il ne peut pas placer d'autres reines sur la ligne et en diagonale sur la reine actuelle. La propagation peut accélérer considérablement la recherche en réduisant l'ensemble de valeurs variables que le solutionneur doit explorer.
• Un retour arrière se produit lorsque le résolveur ne peut pas attribuer de valeur à la variable suivante en raison des contraintes ou lorsqu'il trouve une solution. Dans les deux cas, l'outil de retour arrière renvoie à une étape précédente et remplace la valeur de la variable à cette étape par une valeur qui n'a pas encore été testée. Dans l'exemple des quatre reines, cela signifie déplacer une reine vers un nouveau carré sur la colonne actuelle.

Vous verrez ensuite comment la programmation par contrainte utilise la propagation et le suivi arrière pour résoudre le problème à 4 reines.

Supposons que le solutionneur commence par placer arbitrairement une reine dans le coin supérieur gauche. C'est une sorte d'hypothèse. Il se peut peut-être qu'aucune solution n'existe avec une reine dans l'angle supérieur gauche.

Selon cette hypothèse, quelles contraintes pouvons-nous propager ? Une contrainte est qu'il ne peut y avoir qu'une seule reine dans une colonne (les X gris ci-dessous), et qu'une autre contrainte interdit deux reines sur la même diagonale (les X rouges ci-dessous).

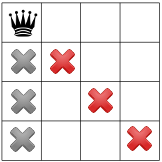
Notre troisième contrainte interdit les reines sur la même ligne:

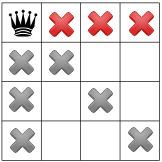
Nos contraintes se sont propagées, nous pouvons tester une autre hypothèse et placer une deuxième reine sur l'un des carrés disponibles disponibles. Notre solutionneur peut décider d'y placer le premier carré disponible dans la deuxième colonne:

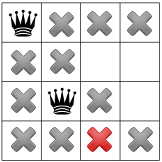
Après avoir propagé la contrainte diagonale, nous constatons qu'elle ne laisse aucun carré disponible dans la troisième colonne ou la dernière ligne:

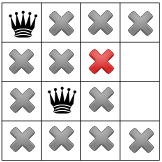
Étant donné qu'aucune solution n'est possible pour le moment, nous devons faire marche arrière. Une option permet au résolveur de choisir l'autre carré disponible dans la deuxième colonne. Toutefois, la propagation des contraintes force alors une reine dans la deuxième ligne de la troisième colonne, ne laissant aucun espace valide pour la quatrième reine:

Le résolveur doit donc revenir en arrière, cette fois jusqu'à l'emplacement de la première reine. Nous avons vu qu'aucune solution au problème des reines n'occuperait un carré d'angle.

Comme il n'y a pas de reine à l'angle, la solutionneur déplace la première reine d'un côté et se propage, ce qui ne laisse qu'un seul emplacement pour la seconde reine:

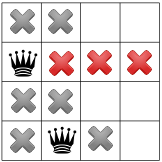
En propagé de nouveau, il ne reste plus qu'un emplacement restant pour la troisième reine:

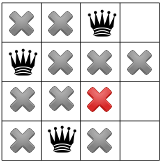
Et pour la quatrième et dernière reine:

Nous avons notre première solution ! Si nous avons demandé à notre solution de s'arrêter après avoir trouvé la première solution, elle s'arrêterait ici. Sinon, il effectuerait un retour arrière et placerait la première reine sur la troisième ligne de la première colonne.

Solution utilisant CP-SAT

Le problème de N-queens est idéal pour la programmation de contraintes. Dans cette section, nous allons parcourir un bref programme Python qui utilise le résolveur CP-SAT pour trouver toutes les solutions au problème.

Importer les bibliothèques

Le code suivant importe la bibliothèque requise.

Python

import sys
import time
from ortools.sat.python import cp_model

C++

#include <stdlib.h>

#include <sstream>
#include <string>
#include <vector>

#include "absl/strings/numbers.h"
#include "ortools/base/logging.h"
#include "ortools/sat/cp_model.h"
#include "ortools/sat/cp_model.pb.h"
#include "ortools/sat/cp_model_solver.h"
#include "ortools/sat/model.h"
#include "ortools/sat/sat_parameters.pb.h"
#include "ortools/util/sorted_interval_list.h"

Java

import com.google.ortools.Loader;
import com.google.ortools.sat.CpModel;
import com.google.ortools.sat.CpSolver;
import com.google.ortools.sat.CpSolverSolutionCallback;
import com.google.ortools.sat.IntVar;
import com.google.ortools.sat.LinearExpr;

C#

using System;
using Google.OrTools.Sat;

Déclarer le modèle

Le code suivant déclare le modèle CP-SAT.

Python

model = cp_model.CpModel()

C++

CpModelBuilder cp_model;

Java

CpModel model = new CpModel();

C#

        CpModel model = new CpModel();

        int BoardSize = 8;
        // There are `BoardSize` number of variables, one for a queen in each
        // column of the board. The value of each variable is the row that the
        // queen is in.
        IntVar[] queens = new IntVar[BoardSize];
        for (int i = 0; i < BoardSize; ++i)
        {
            queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}");
        }

        // Define constraints.
        // All rows must be different.
        model.AddAllDifferent(queens);

        // No two queens can be on the same diagonal.
        LinearExpr[] diag1 = new LinearExpr[BoardSize];
        LinearExpr[] diag2 = new LinearExpr[BoardSize];
        for (int i = 0; i < BoardSize; ++i)
        {
            diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i);
            diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i);
        }

        model.AddAllDifferent(diag1);
        model.AddAllDifferent(diag2);

        // Creates a solver and solves the model.
        CpSolver solver = new CpSolver();
        SolutionPrinter cb = new SolutionPrinter(queens);
        // Search for all solutions.
        solver.StringParameters = "enumerate_all_solutions:true";
        // And solve.
        solver.Solve(model, cb);

        Console.WriteLine("Statistics");
        Console.WriteLine($"  conflicts : {solver.NumConflicts()}");
        Console.WriteLine($"  branches  : {solver.NumBranches()}");
        Console.WriteLine($"  wall time : {solver.WallTime()} s");
        Console.WriteLine($"  number of solutions found: {cb.SolutionCount()}");
    }
}

Créer les variables

Le résolveur crée les variables du problème sous la forme d'un tableau nommé queens.

Python

# There are `board_size` number of variables, one for a queen in each column
# of the board. The value of each variable is the row that the queen is in.
queens = [model.NewIntVar(0, board_size - 1, f"x_{i}") for i in range(board_size)]

C++

// There are `board_size` number of variables, one for a queen in each column
// of the board. The value of each variable is the row that the queen is in.
std::vector<IntVar> queens;
queens.reserve(board_size);
Domain range(0, board_size - 1);
for (int i = 0; i < board_size; ++i) {
  queens.push_back(
      cp_model.NewIntVar(range).WithName("x" + std::to_string(i)));
}

Java

int boardSize = 8;
// There are `BoardSize` number of variables, one for a queen in each column of the board. The
// value of each variable is the row that the queen is in.
IntVar[] queens = new IntVar[boardSize];
for (int i = 0; i < boardSize; ++i) {
  queens[i] = model.newIntVar(0, boardSize - 1, "x" + i);
}

C#

int BoardSize = 8;
// There are `BoardSize` number of variables, one for a queen in each
// column of the board. The value of each variable is the row that the
// queen is in.
IntVar[] queens = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
    queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}");
}

Ici, nous supposons que queens[j] est le numéro de ligne de la reine dans la colonne j. En d'autres termes, queens[j] = i signifie qu'il y a une reine à la ligne i et à la colonne j.

Remarque :Lorsque vous dessinez le schéma d'une solution, vous obtenez une image différente selon que les lignes sont ordonnées de bas en haut ou de haut en bas (et selon que les colonnes sont triées de gauche à droite ou inversement). Cependant, l'ordre ne modifie pas l'ensemble de toutes les solutions possibles, mais uniquement la façon dont elles sont représentées dans un schéma.

Créer les contraintes

Voici le code qui crée les contraintes liées au problème.

Python

# All rows must be different.
model.AddAllDifferent(queens)

# No two queens can be on the same diagonal.
model.AddAllDifferent(queens[i] + i for i in range(board_size))
model.AddAllDifferent(queens[i] - i for i in range(board_size))

C++

// The following sets the constraint that all queens are in different rows.
cp_model.AddAllDifferent(queens);

// No two queens can be on the same diagonal.
std::vector<LinearExpr> diag_1;
diag_1.reserve(board_size);
std::vector<LinearExpr> diag_2;
diag_2.reserve(board_size);
for (int i = 0; i < board_size; ++i) {
  diag_1.push_back(queens[i] + i);
  diag_2.push_back(queens[i] - i);
}
cp_model.AddAllDifferent(diag_1);
cp_model.AddAllDifferent(diag_2);

Java

// All rows must be different.
model.addAllDifferent(queens);

// No two queens can be on the same diagonal.
LinearExpr[] diag1 = new LinearExpr[boardSize];
LinearExpr[] diag2 = new LinearExpr[boardSize];
for (int i = 0; i < boardSize; ++i) {
  diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build();
  diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build();
}
model.addAllDifferent(diag1);
model.addAllDifferent(diag2);

C#

// All rows must be different.
model.AddAllDifferent(queens);

// No two queens can be on the same diagonal.
LinearExpr[] diag1 = new LinearExpr[BoardSize];
LinearExpr[] diag2 = new LinearExpr[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
    diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i);
    diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i);
}

model.AddAllDifferent(diag1);
model.AddAllDifferent(diag2);

Le code utilise la méthode AddAllDifferent, qui nécessite que tous les éléments d'un tableau de variables soient différents.

Voyons comment ces contraintes garantissent les trois conditions du problème de type N-queens (reines sur différentes lignes, colonnes et diagonales).

Pas deux reines sur la même ligne

L'application de la méthode AllDifferent du résolveur à queens force les valeurs de queens[j] à être différentes pour chaque j, ce qui signifie que toutes les reines doivent figurer dans des lignes différentes.

Deux reines dans la même colonne

Cette contrainte est implicite dans la définition de queens. Étant donné que deux éléments de queens ne peuvent pas avoir le même index, aucune deux reines ne peut figurer dans la même colonne.

Deux reines sur la même diagonale

La contrainte diagonale est un peu plus délicate que la contrainte de ligne et de colonne. Tout d'abord, si deux reines se trouvent sur la même diagonale, l'une des conditions suivantes doit être remplie:

• Le numéro de ligne et le numéro de colonne de chacune des deux reines sont identiques. En d'autres termes, queens(j) + j a la même valeur pour deux index j différents.
• Le numéro de ligne moins le numéro de colonne de chacune des deux reines est égal. Dans ce cas, queens(j) - j a la même valeur pour deux index j différents.

L'une de ces conditions signifie que les reines se trouvent sur la même diagonale croissante (de gauche à droite), tandis que l'autre signifie qu'elles sont sur la même diagonale décroissante. La condition correspondant à l'ordre croissant et à l'ordre décroissant dépend de l'ordre des lignes et des colonnes. Comme indiqué dans la section précédente, le classement n'a aucun effet sur l'ensemble de solutions, mais uniquement sur leur visualisation.

Par conséquent, la contrainte diagonale est que les valeurs de queens(j) + j doivent toutes être différentes, et les valeurs de queens(j) - j doivent toutes être différentes, pour différentes valeurs j.

Pour appliquer la méthode AddAllDifferent à queens(j) + j, nous avons placé les N instances de la variable, pour j de 0 à N-1, dans un tableau, diag1, comme suit:

q1 = model.NewIntVar(0, 2 * board_size, 'diag1_%i' % i)
diag1.append(q1)
model.Add(q1 == queens[j] + j)

Ensuite, nous appliquons AddAllDifferent à diag1.

model.AddAllDifferent(diag1)

La contrainte pour queens(j) - j est créée de la même manière.

Créer une imprimante de solution

Pour imprimer toutes les solutions au problème de type N-queens, vous devez transmettre un rappel, appelé imprimante de solution, au résolveur CP-SAT. Le rappel imprime chaque nouvelle solution au fur et à mesure que le résolveur la trouve. Le code suivant crée une imprimante de solution.

Python

class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback):
    """Print intermediate solutions."""

    def __init__(self, queens):
        cp_model.CpSolverSolutionCallback.__init__(self)
        self.__queens = queens
        self.__solution_count = 0
        self.__start_time = time.time()

    def solution_count(self):
        return self.__solution_count

    def on_solution_callback(self):
        current_time = time.time()
        print(
            f"Solution {self.__solution_count}, "
            f"time = {current_time - self.__start_time} s"
        )
        self.__solution_count += 1

        all_queens = range(len(self.__queens))
        for i in all_queens:
            for j in all_queens:
                if self.Value(self.__queens[j]) == i:
                    # There is a queen in column j, row i.
                    print("Q", end=" ")
                else:
                    print("_", end=" ")
            print()
        print()

C++

int num_solutions = 0;
Model model;
model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) {
  LOG(INFO) << "Solution " << num_solutions;
  for (int i = 0; i < board_size; ++i) {
    std::stringstream ss;
    for (int j = 0; j < board_size; ++j) {
      if (SolutionIntegerValue(response, queens[j]) == i) {
        // There is a queen in column j, row i.
        ss << "Q";
      } else {
        ss << "_";
      }
      if (j != board_size - 1) ss << " ";
    }
    LOG(INFO) << ss.str();
  }
  num_solutions++;
}));

Java

static class SolutionPrinter extends CpSolverSolutionCallback {
  public SolutionPrinter(IntVar[] queensIn) {
    solutionCount = 0;
    queens = queensIn;
  }

  @Override
  public void onSolutionCallback() {
    System.out.println("Solution " + solutionCount);
    for (int i = 0; i < queens.length; ++i) {
      for (int j = 0; j < queens.length; ++j) {
        if (value(queens[j]) == i) {
          System.out.print("Q");
        } else {
          System.out.print("_");
        }
        if (j != queens.length - 1) {
          System.out.print(" ");
        }
      }
      System.out.println();
    }
    solutionCount++;
  }

  public int getSolutionCount() {
    return solutionCount;
  }

  private int solutionCount;
  private final IntVar[] queens;
}

C#

public class SolutionPrinter : CpSolverSolutionCallback
{
    public SolutionPrinter(IntVar[] queens)
    {
        queens_ = queens;
    }

    public override void OnSolutionCallback()
    {
        Console.WriteLine($"Solution {SolutionCount_}");
        for (int i = 0; i < queens_.Length; ++i)
        {
            for (int j = 0; j < queens_.Length; ++j)
            {
                if (Value(queens_[j]) == i)
                {
                    Console.Write("Q");
                }
                else
                {
                    Console.Write("_");
                }
                if (j != queens_.Length - 1)
                    Console.Write(" ");
            }
            Console.WriteLine("");
        }
        SolutionCount_++;
    }

    public int SolutionCount()
    {
        return SolutionCount_;
    }

    private int SolutionCount_;
    private IntVar[] queens_;
}

Notez que l'imprimante de la solution doit être écrite en tant que classe Python, en raison de l'interface Python avec le résolveur C++ sous-jacent.

Les solutions sont imprimées sur les lignes suivantes sur l'imprimante.

for v in self.__variables:
print('%s = %i' % (v, self.Value(v)), end = ' ')

Dans cet exemple, self.__variables est la variable queens, et chaque v correspond à l'une des huit entrées de queens. Le résultat est le suivant: x0 = queens(0) x1 = queens(1) ... x7 = queens(7), où xi est le numéro de colonne de la reine à la ligne i.

La section suivante présente un exemple de solution.

Appeler le résolveur et afficher les résultats

Le code suivant exécute le solutionneur et affiche les solutions.

Python

solver = cp_model.CpSolver()
solution_printer = NQueenSolutionPrinter(queens)
solver.parameters.enumerate_all_solutions = True
solver.Solve(model, solution_printer)

C++

// Tell the solver to enumerate all solutions.
SatParameters parameters;
parameters.set_enumerate_all_solutions(true);
model.Add(NewSatParameters(parameters));

const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model);
LOG(INFO) << "Number of solutions found: " << num_solutions;

Java

CpSolver solver = new CpSolver();
SolutionPrinter cb = new SolutionPrinter(queens);
// Tell the solver to enumerate all solutions.
solver.getParameters().setEnumerateAllSolutions(true);
// And solve.
solver.solve(model, cb);

C#

// Creates a solver and solves the model.
CpSolver solver = new CpSolver();
SolutionPrinter cb = new SolutionPrinter(queens);
// Search for all solutions.
solver.StringParameters = "enumerate_all_solutions:true";
// And solve.
solver.Solve(model, cb);

Le programme trouve 92 solutions différentes pour une carte 8x8. Voici la première.

        Q _ _ _ _ _ _ _
        _ _ _ _ _ _ Q _
        _ _ _ _ Q _ _ _
        _ _ _ _ _ _ _ Q
        _ Q _ _ _ _ _ _
        _ _ _ Q _ _ _ _
        _ _ _ _ _ Q _ _
        _ _ Q _ _ _ _ _
        ...91 other solutions displayed...
        Solutions found: 92

Vous pouvez résoudre le problème pour un board d'une taille différente en transmettant N comme argument de ligne de commande. Par exemple, si le programme s'appelle queens, python nqueens_sat.py 6 résout le problème pour une carte 6x6.

L'ensemble du programme

Voici l'intégralité du programme N-queens.

Python

"""OR-Tools solution to the N-queens problem."""
import sys
import time
from ortools.sat.python import cp_model


class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback):
    """Print intermediate solutions."""

    def __init__(self, queens):
        cp_model.CpSolverSolutionCallback.__init__(self)
        self.__queens = queens
        self.__solution_count = 0
        self.__start_time = time.time()

    def solution_count(self):
        return self.__solution_count

    def on_solution_callback(self):
        current_time = time.time()
        print(
            f"Solution {self.__solution_count}, "
            f"time = {current_time - self.__start_time} s"
        )
        self.__solution_count += 1

        all_queens = range(len(self.__queens))
        for i in all_queens:
            for j in all_queens:
                if self.Value(self.__queens[j]) == i:
                    # There is a queen in column j, row i.
                    print("Q", end=" ")
                else:
                    print("_", end=" ")
            print()
        print()



def main(board_size):
    # Creates the solver.
    model = cp_model.CpModel()

    # Creates the variables.
    # There are `board_size` number of variables, one for a queen in each column
    # of the board. The value of each variable is the row that the queen is in.
    queens = [model.NewIntVar(0, board_size - 1, f"x_{i}") for i in range(board_size)]

    # Creates the constraints.
    # All rows must be different.
    model.AddAllDifferent(queens)

    # No two queens can be on the same diagonal.
    model.AddAllDifferent(queens[i] + i for i in range(board_size))
    model.AddAllDifferent(queens[i] - i for i in range(board_size))

    # Solve the model.
    solver = cp_model.CpSolver()
    solution_printer = NQueenSolutionPrinter(queens)
    solver.parameters.enumerate_all_solutions = True
    solver.Solve(model, solution_printer)

    # Statistics.
    print("\nStatistics")
    print(f"  conflicts      : {solver.NumConflicts()}")
    print(f"  branches       : {solver.NumBranches()}")
    print(f"  wall time      : {solver.WallTime()} s")
    print(f"  solutions found: {solution_printer.solution_count()}")


if __name__ == "__main__":
    # By default, solve the 8x8 problem.
    size = 8
    if len(sys.argv) > 1:
        size = int(sys.argv[1])
    main(size)

C++

// OR-Tools solution to the N-queens problem.
#include <stdlib.h>

#include <sstream>
#include <string>
#include <vector>

#include "absl/strings/numbers.h"
#include "ortools/base/logging.h"
#include "ortools/sat/cp_model.h"
#include "ortools/sat/cp_model.pb.h"
#include "ortools/sat/cp_model_solver.h"
#include "ortools/sat/model.h"
#include "ortools/sat/sat_parameters.pb.h"
#include "ortools/util/sorted_interval_list.h"

namespace operations_research {
namespace sat {

void NQueensSat(const int board_size) {
  // Instantiate the solver.
  CpModelBuilder cp_model;

  // There are `board_size` number of variables, one for a queen in each column
  // of the board. The value of each variable is the row that the queen is in.
  std::vector<IntVar> queens;
  queens.reserve(board_size);
  Domain range(0, board_size - 1);
  for (int i = 0; i < board_size; ++i) {
    queens.push_back(
        cp_model.NewIntVar(range).WithName("x" + std::to_string(i)));
  }

  // Define constraints.
  // The following sets the constraint that all queens are in different rows.
  cp_model.AddAllDifferent(queens);

  // No two queens can be on the same diagonal.
  std::vector<LinearExpr> diag_1;
  diag_1.reserve(board_size);
  std::vector<LinearExpr> diag_2;
  diag_2.reserve(board_size);
  for (int i = 0; i < board_size; ++i) {
    diag_1.push_back(queens[i] + i);
    diag_2.push_back(queens[i] - i);
  }
  cp_model.AddAllDifferent(diag_1);
  cp_model.AddAllDifferent(diag_2);

  int num_solutions = 0;
  Model model;
  model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) {
    LOG(INFO) << "Solution " << num_solutions;
    for (int i = 0; i < board_size; ++i) {
      std::stringstream ss;
      for (int j = 0; j < board_size; ++j) {
        if (SolutionIntegerValue(response, queens[j]) == i) {
          // There is a queen in column j, row i.
          ss << "Q";
        } else {
          ss << "_";
        }
        if (j != board_size - 1) ss << " ";
      }
      LOG(INFO) << ss.str();
    }
    num_solutions++;
  }));

  // Tell the solver to enumerate all solutions.
  SatParameters parameters;
  parameters.set_enumerate_all_solutions(true);
  model.Add(NewSatParameters(parameters));

  const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model);
  LOG(INFO) << "Number of solutions found: " << num_solutions;

  // Statistics.
  LOG(INFO) << "Statistics";
  LOG(INFO) << CpSolverResponseStats(response);
}

}  // namespace sat
}  // namespace operations_research

int main(int argc, char** argv) {
  int board_size = 8;
  if (argc > 1) {
    if (!absl::SimpleAtoi(argv[1], &board_size)) {
      LOG(INFO) << "Cannot parse '" << argv[1]
                << "', using the default value of 8.";
      board_size = 8;
    }
  }
  operations_research::sat::NQueensSat(board_size);
  return EXIT_SUCCESS;
}

Java

package com.google.ortools.sat.samples;
import com.google.ortools.Loader;
import com.google.ortools.sat.CpModel;
import com.google.ortools.sat.CpSolver;
import com.google.ortools.sat.CpSolverSolutionCallback;
import com.google.ortools.sat.IntVar;
import com.google.ortools.sat.LinearExpr;

/** OR-Tools solution to the N-queens problem. */
public final class NQueensSat {
  static class SolutionPrinter extends CpSolverSolutionCallback {
    public SolutionPrinter(IntVar[] queensIn) {
      solutionCount = 0;
      queens = queensIn;
    }

    @Override
    public void onSolutionCallback() {
      System.out.println("Solution " + solutionCount);
      for (int i = 0; i < queens.length; ++i) {
        for (int j = 0; j < queens.length; ++j) {
          if (value(queens[j]) == i) {
            System.out.print("Q");
          } else {
            System.out.print("_");
          }
          if (j != queens.length - 1) {
            System.out.print(" ");
          }
        }
        System.out.println();
      }
      solutionCount++;
    }

    public int getSolutionCount() {
      return solutionCount;
    }

    private int solutionCount;
    private final IntVar[] queens;
  }

  public static void main(String[] args) {
    Loader.loadNativeLibraries();
    // Create the model.
    CpModel model = new CpModel();

    int boardSize = 8;
    // There are `BoardSize` number of variables, one for a queen in each column of the board. The
    // value of each variable is the row that the queen is in.
    IntVar[] queens = new IntVar[boardSize];
    for (int i = 0; i < boardSize; ++i) {
      queens[i] = model.newIntVar(0, boardSize - 1, "x" + i);
    }

    // Define constraints.
    // All rows must be different.
    model.addAllDifferent(queens);

    // No two queens can be on the same diagonal.
    LinearExpr[] diag1 = new LinearExpr[boardSize];
    LinearExpr[] diag2 = new LinearExpr[boardSize];
    for (int i = 0; i < boardSize; ++i) {
      diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build();
      diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build();
    }
    model.addAllDifferent(diag1);
    model.addAllDifferent(diag2);

    // Create a solver and solve the model.
    CpSolver solver = new CpSolver();
    SolutionPrinter cb = new SolutionPrinter(queens);
    // Tell the solver to enumerate all solutions.
    solver.getParameters().setEnumerateAllSolutions(true);
    // And solve.
    solver.solve(model, cb);

    // Statistics.
    System.out.println("Statistics");
    System.out.println("  conflicts : " + solver.numConflicts());
    System.out.println("  branches  : " + solver.numBranches());
    System.out.println("  wall time : " + solver.wallTime() + " s");
    System.out.println("  solutions : " + cb.getSolutionCount());
  }

  private NQueensSat() {}
}

C#

// OR-Tools solution to the N-queens problem.
using System;
using Google.OrTools.Sat;

public class NQueensSat
{
    public class SolutionPrinter : CpSolverSolutionCallback
    {
        public SolutionPrinter(IntVar[] queens)
        {
            queens_ = queens;
        }

        public override void OnSolutionCallback()
        {
            Console.WriteLine($"Solution {SolutionCount_}");
            for (int i = 0; i < queens_.Length; ++i)
            {
                for (int j = 0; j < queens_.Length; ++j)
                {
                    if (Value(queens_[j]) == i)
                    {
                        Console.Write("Q");
                    }
                    else
                    {
                        Console.Write("_");
                    }
                    if (j != queens_.Length - 1)
                        Console.Write(" ");
                }
                Console.WriteLine("");
            }
            SolutionCount_++;
        }

        public int SolutionCount()
        {
            return SolutionCount_;
        }

        private int SolutionCount_;
        private IntVar[] queens_;
    }

    static void Main()
    {
        // Constraint programming engine
        CpModel model = new CpModel();

        int BoardSize = 8;
        // There are `BoardSize` number of variables, one for a queen in each
        // column of the board. The value of each variable is the row that the
        // queen is in.
        IntVar[] queens = new IntVar[BoardSize];
        for (int i = 0; i < BoardSize; ++i)
        {
            queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}");
        }

        // Define constraints.
        // All rows must be different.
        model.AddAllDifferent(queens);

        // No two queens can be on the same diagonal.
        LinearExpr[] diag1 = new LinearExpr[BoardSize];
        LinearExpr[] diag2 = new LinearExpr[BoardSize];
        for (int i = 0; i < BoardSize; ++i)
        {
            diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i);
            diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i);
        }

        model.AddAllDifferent(diag1);
        model.AddAllDifferent(diag2);

        // Creates a solver and solves the model.
        CpSolver solver = new CpSolver();
        SolutionPrinter cb = new SolutionPrinter(queens);
        // Search for all solutions.
        solver.StringParameters = "enumerate_all_solutions:true";
        // And solve.
        solver.Solve(model, cb);

        Console.WriteLine("Statistics");
        Console.WriteLine($"  conflicts : {solver.NumConflicts()}");
        Console.WriteLine($"  branches  : {solver.NumBranches()}");
        Console.WriteLine($"  wall time : {solver.WallTime()} s");
        Console.WriteLine($"  number of solutions found: {cb.SolutionCount()}");
    }
}

Solution utilisant le résolveur CP d'origine

Les sections suivantes présentent un programme Python qui résout les N-queens à l'aide du résolveur CP d'origine. (Nous vous recommandons toutefois d'utiliser le nouveau solution CP-SAT).

Importer les bibliothèques

Le code suivant importe la bibliothèque requise.

Python

import sys
from ortools.constraint_solver import pywrapcp

C++

#include <cstdint>
#include <cstdlib>
#include <sstream>
#include <vector>

#include "ortools/base/logging.h"
#include "ortools/constraint_solver/constraint_solver.h"

Java

import com.google.ortools.Loader;
import com.google.ortools.constraintsolver.DecisionBuilder;
import com.google.ortools.constraintsolver.IntVar;
import com.google.ortools.constraintsolver.Solver;

C#

using System;
using Google.OrTools.ConstraintSolver;

Déclarer la solution

Le code suivant déclare le résolveur CP d'origine.

Python

solver = pywrapcp.Solver("n-queens")

C++

Solver solver("N-Queens");

Java

Solver solver = new Solver("N-Queens");

C#

Solver solver = new Solver("N-Queens");

Créer les variables

La méthode IntVar du résolveur crée les variables du problème sous la forme d'un tableau nommé queens.

Python

# The array index is the column, and the value is the row.
queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)]

C++

std::vector<IntVar*> queens;
queens.reserve(board_size);
for (int i = 0; i < board_size; ++i) {
  queens.push_back(
      solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i)));
}

Java

int boardSize = 8;
IntVar[] queens = new IntVar[boardSize];
for (int i = 0; i < boardSize; ++i) {
  queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i);
}

C#

const int BoardSize = 8;
IntVar[] queens = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
    queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}");
}

Pour toute solution, queens[j] = i signifie qu'il existe une reine dans la colonne j et la ligne i.

Créer les contraintes

Voici le code qui crée les contraintes liées au problème.

Python

# All rows must be different.
solver.Add(solver.AllDifferent(queens))

# No two queens can be on the same diagonal.
solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)]))
solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)]))

C++

// The following sets the constraint that all queens are in different rows.
solver.AddConstraint(solver.MakeAllDifferent(queens));

// All columns must be different because the indices of queens are all
// different. No two queens can be on the same diagonal.
std::vector<IntVar*> diag_1;
diag_1.reserve(board_size);
std::vector<IntVar*> diag_2;
diag_2.reserve(board_size);
for (int i = 0; i < board_size; ++i) {
  diag_1.push_back(solver.MakeSum(queens[i], i)->Var());
  diag_2.push_back(solver.MakeSum(queens[i], -i)->Var());
}
solver.AddConstraint(solver.MakeAllDifferent(diag_1));
solver.AddConstraint(solver.MakeAllDifferent(diag_2));

Java

// All rows must be different.
solver.addConstraint(solver.makeAllDifferent(queens));

// All columns must be different because the indices of queens are all different.
// No two queens can be on the same diagonal.
IntVar[] diag1 = new IntVar[boardSize];
IntVar[] diag2 = new IntVar[boardSize];
for (int i = 0; i < boardSize; ++i) {
  diag1[i] = solver.makeSum(queens[i], i).var();
  diag2[i] = solver.makeSum(queens[i], -i).var();
}
solver.addConstraint(solver.makeAllDifferent(diag1));
solver.addConstraint(solver.makeAllDifferent(diag2));

C#

// All rows must be different.
solver.Add(queens.AllDifferent());

// All columns must be different because the indices of queens are all different.
// No two queens can be on the same diagonal.
IntVar[] diag1 = new IntVar[BoardSize];
IntVar[] diag2 = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
    diag1[i] = solver.MakeSum(queens[i], i).Var();
    diag2[i] = solver.MakeSum(queens[i], -i).Var();
}

solver.Add(diag1.AllDifferent());
solver.Add(diag2.AllDifferent());

Ces contraintes garantissent les trois conditions du problème de nombre de N-res (nombre de lignes, de colonnes et de diagonales différents).

Pas deux reines sur la même ligne

L'application de la méthode AllDifferent du résolveur à queens force les valeurs de queens[j] à être différentes pour chaque j, ce qui signifie que toutes les reines doivent figurer dans des lignes différentes.

Deux reines dans la même colonne

Cette contrainte est implicite dans la définition de queens. Étant donné que deux éléments de queens ne peuvent pas avoir le même index, aucune deux reines ne peut figurer dans la même colonne.

Deux reines sur la même diagonale

La contrainte diagonale est un peu plus délicate que la contrainte de ligne et de colonne. Tout d'abord, si deux reines se trouvent sur la même diagonale, l'une des conditions suivantes doit être remplie:

• Si la diagonale est décroissante (de gauche à droite), le numéro de ligne et le numéro de colonne de chacune des deux reines sont identiques. Ainsi, queens(i) + i a la même valeur pour deux index i différents.
• Si la diagonale est croissante, le numéro de ligne moins le numéro de colonne de chacune des deux reines est égal. Dans ce cas, queens(i) - i a la même valeur pour deux index différents i.

Par conséquent, la contrainte diagonale est que les valeurs de queens(i) + i doivent toutes être différentes, de même que les valeurs de queens(i) - i, pour des i différentes.

Le code ci-dessus ajoute cette contrainte en appliquant la méthode AllDifferent à queens[j] + j et queens[j] - j, pour chaque i.

Ajouter le décideur

L'étape suivante consiste à créer un outil de prise de décision, qui définit la stratégie de recherche pour le problème. La stratégie de recherche peut avoir un impact majeur sur le temps de recherche, en raison de la propagation des contraintes, qui réduit le nombre de valeurs variables que le solutionneur doit explorer. Vous en avez déjà vu un exemple dans l'exemple à 4 reines.

Le code suivant crée un outil de prise de décision à l'aide de la méthode Phase du résolveur.

Python

db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE)

C++

DecisionBuilder* const db = solver.MakePhase(
    queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE);

Java

// Create the decision builder to search for solutions.
final DecisionBuilder db =
    solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);

C#

// Create the decision builder to search for solutions.
DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);

Pour en savoir plus sur les arguments d'entrée de la méthode Phase, consultez la page Générateur de décisions.

Fonctionnement du générateur de décisions dans l'exemple à 4 reines

Examinons la façon dont le décisionnaire dirige la recherche dans l'exemple à 4 reines. Le résolveur commence par queens[0], la première variable du tableau, comme indiqué par CHOOSE_FIRST_UNBOUND. Le résolveur attribue ensuite à queens[0] la plus petite valeur qui n'a pas encore été testée, soit 0 à ce stade, comme indiqué par ASSIGN_MIN_VALUE. La première reine est ainsi placée dans l'angle supérieur gauche du tableau.

Ensuite, le résolveur sélectionne queens[1], qui est maintenant la première variable non liée de queens. Après avoir propagé les contraintes, il existe deux lignes possibles pour une reine dans la colonne 1: la ligne 2 ou la ligne 3. L'option ASSIGN_MIN_VALUE demande à l'outil de résolution d'attribuer queens[1] = 2. (Si vous définissez plutôt IntValueStrategy sur ASSIGN_MAX_VALUE, le résolveur attribue queens[1] = 3.)

Vous pouvez vérifier que le reste de la recherche suit les mêmes règles.

Appeler le résolveur et afficher les résultats

Le code suivant exécute le Solveur et affiche la solution.

Python

# Iterates through the solutions, displaying each.
num_solutions = 0
solver.NewSearch(db)
while solver.NextSolution():
    # Displays the solution just computed.
    for i in range(board_size):
        for j in range(board_size):
            if queens[j].Value() == i:
                # There is a queen in column j, row i.
                print("Q", end=" ")
            else:
                print("_", end=" ")
        print()
    print()
    num_solutions += 1
solver.EndSearch()

C++

// Iterates through the solutions, displaying each.
int num_solutions = 0;

solver.NewSearch(db);
while (solver.NextSolution()) {
  // Displays the solution just computed.
  LOG(INFO) << "Solution " << num_solutions;
  for (int i = 0; i < board_size; ++i) {
    std::stringstream ss;
    for (int j = 0; j < board_size; ++j) {
      if (queens[j]->Value() == i) {
        // There is a queen in column j, row i.
        ss << "Q";
      } else {
        ss << "_";
      }
      if (j != board_size - 1) ss << " ";
    }
    LOG(INFO) << ss.str();
  }
  num_solutions++;
}
solver.EndSearch();

Java

int solutionCount = 0;
solver.newSearch(db);
while (solver.nextSolution()) {
  System.out.println("Solution " + solutionCount);
  for (int i = 0; i < boardSize; ++i) {
    for (int j = 0; j < boardSize; ++j) {
      if (queens[j].value() == i) {
        System.out.print("Q");
      } else {
        System.out.print("_");
      }
      if (j != boardSize - 1) {
        System.out.print(" ");
      }
    }
    System.out.println();
  }
  solutionCount++;
}
solver.endSearch();

C#

// Iterates through the solutions, displaying each.
int SolutionCount = 0;
solver.NewSearch(db);
while (solver.NextSolution())
{
    Console.WriteLine("Solution " + SolutionCount);
    for (int i = 0; i < BoardSize; ++i)
    {
        for (int j = 0; j < BoardSize; ++j)
        {
            if (queens[j].Value() == i)
            {
                Console.Write("Q");
            }
            else
            {
                Console.Write("_");
            }
            if (j != BoardSize - 1)
                Console.Write(" ");
        }
        Console.WriteLine("");
    }
    SolutionCount++;
}
solver.EndSearch();

Voici la première solution proposée par le programme pour une carte 8x8.

        Q _ _ _ _ _ _ _
        _ _ _ _ _ _ Q _
        _ _ _ _ Q _ _ _
        _ _ _ _ _ _ _ Q
        _ Q _ _ _ _ _ _
        _ _ _ Q _ _ _ _
        _ _ _ _ _ Q _ _
        _ _ Q _ _ _ _ _
        ...91 other solutions displayed...
        Statistics
        failures: 304
        branches: 790
        wall time: 5 ms
        Solutions found: 92

Vous pouvez résoudre le problème pour un board d'une taille différente en transmettant N comme argument de ligne de commande. Par exemple, python nqueens_cp.py 6 résout le problème d'une carte 6x6.

L'ensemble du programme

Le programme complet est présenté ci-dessous.

Python

"""OR-Tools solution to the N-queens problem."""
import sys
from ortools.constraint_solver import pywrapcp


def main(board_size):
    # Creates the solver.
    solver = pywrapcp.Solver("n-queens")

    # Creates the variables.
    # The array index is the column, and the value is the row.
    queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)]

    # Creates the constraints.
    # All rows must be different.
    solver.Add(solver.AllDifferent(queens))

    # No two queens can be on the same diagonal.
    solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)]))
    solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)]))

    db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE)

    # Iterates through the solutions, displaying each.
    num_solutions = 0
    solver.NewSearch(db)
    while solver.NextSolution():
        # Displays the solution just computed.
        for i in range(board_size):
            for j in range(board_size):
                if queens[j].Value() == i:
                    # There is a queen in column j, row i.
                    print("Q", end=" ")
                else:
                    print("_", end=" ")
            print()
        print()
        num_solutions += 1
    solver.EndSearch()

    # Statistics.
    print("\nStatistics")
    print(f"  failures: {solver.Failures()}")
    print(f"  branches: {solver.Branches()}")
    print(f"  wall time: {solver.WallTime()} ms")
    print(f"  Solutions found: {num_solutions}")


if __name__ == "__main__":
    # By default, solve the 8x8 problem.
    size = 8
    if len(sys.argv) > 1:
        size = int(sys.argv[1])
    main(size)

C++

// OR-Tools solution to the N-queens problem.
#include <cstdint>
#include <cstdlib>
#include <sstream>
#include <vector>

#include "ortools/base/logging.h"
#include "ortools/constraint_solver/constraint_solver.h"

namespace operations_research {

void NQueensCp(const int board_size) {
  // Instantiate the solver.
  Solver solver("N-Queens");

  std::vector<IntVar*> queens;
  queens.reserve(board_size);
  for (int i = 0; i < board_size; ++i) {
    queens.push_back(
        solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i)));
  }

  // Define constraints.
  // The following sets the constraint that all queens are in different rows.
  solver.AddConstraint(solver.MakeAllDifferent(queens));

  // All columns must be different because the indices of queens are all
  // different. No two queens can be on the same diagonal.
  std::vector<IntVar*> diag_1;
  diag_1.reserve(board_size);
  std::vector<IntVar*> diag_2;
  diag_2.reserve(board_size);
  for (int i = 0; i < board_size; ++i) {
    diag_1.push_back(solver.MakeSum(queens[i], i)->Var());
    diag_2.push_back(solver.MakeSum(queens[i], -i)->Var());
  }
  solver.AddConstraint(solver.MakeAllDifferent(diag_1));
  solver.AddConstraint(solver.MakeAllDifferent(diag_2));

  DecisionBuilder* const db = solver.MakePhase(
      queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE);

  // Iterates through the solutions, displaying each.
  int num_solutions = 0;

  solver.NewSearch(db);
  while (solver.NextSolution()) {
    // Displays the solution just computed.
    LOG(INFO) << "Solution " << num_solutions;
    for (int i = 0; i < board_size; ++i) {
      std::stringstream ss;
      for (int j = 0; j < board_size; ++j) {
        if (queens[j]->Value() == i) {
          // There is a queen in column j, row i.
          ss << "Q";
        } else {
          ss << "_";
        }
        if (j != board_size - 1) ss << " ";
      }
      LOG(INFO) << ss.str();
    }
    num_solutions++;
  }
  solver.EndSearch();

  // Statistics.
  LOG(INFO) << "Statistics";
  LOG(INFO) << "  failures: " << solver.failures();
  LOG(INFO) << "  branches: " << solver.branches();
  LOG(INFO) << "  wall time: " << solver.wall_time() << " ms";
  LOG(INFO) << "  Solutions found: " << num_solutions;
}

}  // namespace operations_research

int main(int argc, char** argv) {
  int board_size = 8;
  if (argc > 1) {
    board_size = std::atoi(argv[1]);
  }
  operations_research::NQueensCp(board_size);
  return EXIT_SUCCESS;
}

Java

// OR-Tools solution to the N-queens problem.
package com.google.ortools.constraintsolver.samples;
import com.google.ortools.Loader;
import com.google.ortools.constraintsolver.DecisionBuilder;
import com.google.ortools.constraintsolver.IntVar;
import com.google.ortools.constraintsolver.Solver;

/** N-Queens Problem. */
public final class NQueensCp {
  public static void main(String[] args) {
    Loader.loadNativeLibraries();
    // Instantiate the solver.
    Solver solver = new Solver("N-Queens");

    int boardSize = 8;
    IntVar[] queens = new IntVar[boardSize];
    for (int i = 0; i < boardSize; ++i) {
      queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i);
    }

    // Define constraints.
    // All rows must be different.
    solver.addConstraint(solver.makeAllDifferent(queens));

    // All columns must be different because the indices of queens are all different.
    // No two queens can be on the same diagonal.
    IntVar[] diag1 = new IntVar[boardSize];
    IntVar[] diag2 = new IntVar[boardSize];
    for (int i = 0; i < boardSize; ++i) {
      diag1[i] = solver.makeSum(queens[i], i).var();
      diag2[i] = solver.makeSum(queens[i], -i).var();
    }
    solver.addConstraint(solver.makeAllDifferent(diag1));
    solver.addConstraint(solver.makeAllDifferent(diag2));

    // Create the decision builder to search for solutions.
    final DecisionBuilder db =
        solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);

    int solutionCount = 0;
    solver.newSearch(db);
    while (solver.nextSolution()) {
      System.out.println("Solution " + solutionCount);
      for (int i = 0; i < boardSize; ++i) {
        for (int j = 0; j < boardSize; ++j) {
          if (queens[j].value() == i) {
            System.out.print("Q");
          } else {
            System.out.print("_");
          }
          if (j != boardSize - 1) {
            System.out.print(" ");
          }
        }
        System.out.println();
      }
      solutionCount++;
    }
    solver.endSearch();

    // Statistics.
    System.out.println("Statistics");
    System.out.println("  failures: " + solver.failures());
    System.out.println("  branches: " + solver.branches());
    System.out.println("  wall time: " + solver.wallTime() + "ms");
    System.out.println("  Solutions found: " + solutionCount);
  }

  private NQueensCp() {}
}

C#

// OR-Tools solution to the N-queens problem.
using System;
using Google.OrTools.ConstraintSolver;

public class NQueensCp
{
    public static void Main(String[] args)
    {
        // Instantiate the solver.
        Solver solver = new Solver("N-Queens");

        const int BoardSize = 8;
        IntVar[] queens = new IntVar[BoardSize];
        for (int i = 0; i < BoardSize; ++i)
        {
            queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}");
        }

        // Define constraints.
        // All rows must be different.
        solver.Add(queens.AllDifferent());

        // All columns must be different because the indices of queens are all different.
        // No two queens can be on the same diagonal.
        IntVar[] diag1 = new IntVar[BoardSize];
        IntVar[] diag2 = new IntVar[BoardSize];
        for (int i = 0; i < BoardSize; ++i)
        {
            diag1[i] = solver.MakeSum(queens[i], i).Var();
            diag2[i] = solver.MakeSum(queens[i], -i).Var();
        }

        solver.Add(diag1.AllDifferent());
        solver.Add(diag2.AllDifferent());

        // Create the decision builder to search for solutions.
        DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);

        // Iterates through the solutions, displaying each.
        int SolutionCount = 0;
        solver.NewSearch(db);
        while (solver.NextSolution())
        {
            Console.WriteLine("Solution " + SolutionCount);
            for (int i = 0; i < BoardSize; ++i)
            {
                for (int j = 0; j < BoardSize; ++j)
                {
                    if (queens[j].Value() == i)
                    {
                        Console.Write("Q");
                    }
                    else
                    {
                        Console.Write("_");
                    }
                    if (j != BoardSize - 1)
                        Console.Write(" ");
                }
                Console.WriteLine("");
            }
            SolutionCount++;
        }
        solver.EndSearch();

        // Statistics.
        Console.WriteLine("Statistics");
        Console.WriteLine($"  failures: {solver.Failures()}");
        Console.WriteLine($"  branches: {solver.Branches()}");
        Console.WriteLine($"  wall time: {solver.WallTime()} ms");
        Console.WriteLine($"  Solutions found: {SolutionCount}");
    }
}

Nombre de solutions

Le nombre de solutions augmente à peu près de manière exponentielle avec la taille de la carte:

Taille de la grille	Solutions	Il est temps de trouver toutes les solutions (ms)
1	1	0
2	0	0
3	0	0
4	2	0
5	10	0
6	4	0
7	40	3
8	92	9
9	352	35
10	724	95
11	2680	378
12	14200	2198
13	73712	11628
14	365596	62427
15	2279184	410701

De nombreuses solutions ne sont que des rotations d'autres, et une technique appelée "bris de symétrie" peut être utilisée pour réduire la quantité de calcul nécessaire. Nous ne l'utilisons pas ici, car notre solution ci-dessus n'est pas destinée à être rapide, mais simplement simple. Bien entendu, nous pourrions accélérer les choses en ne recherchant qu'une solution au lieu de toutes: pas plus de quelques millisecondes pour des tailles de carte allant jusqu'à 50.