En las siguientes secciones, ilustraremos la programación de restricciones (CP) con un problema combinatorio basado en el juego de ajedrez. En el ajedrez, una reina puede atacar horizontal, vertical y diagonal. El problema de N-queens pregunta:
¿Cómo se pueden colocar las reinas N en un tablero de ajedrez NxN para que ninguna de ellas ataque entre sí?
A continuación, puedes ver una posible solución al problema de N-reinas para N = 4.
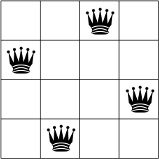
No hay dos reinas en la misma fila, columna o diagonal.
Tenga en cuenta que esto no es un problema de optimización. Queremos encontrar todas las posibles en lugar de una solución óptima, por lo que es una candidata natural para la programación de restricciones. En las siguientes secciones se describe el enfoque de CP para el problema de N-queens. presentar programas que lo resuelvan con el solucionador de problemas de CP-SAT y el uso de la API de de resolución de problemas.
Enfoque de PC para el problema de las N-queens
Un solucionador de problemas de PC funciona sistemáticamente probando todos posibles asignaciones de valores a las variables en un problema, para encontrar la soluciones factibles. En el problema de las 4 queens, el solucionador comienza en el extremo izquierdo y coloca sucesivamente una reina en cada columna, en una ubicación que se que no sea atacada por ninguna reina previamente colocada.
Propagación y seguimiento
Hay dos elementos clave en una búsqueda de programación de restricciones:
- Propagación: Cada vez que el solucionador asigna un valor a una variable, agregan restricciones a los valores posibles de la restricción variables. Estas restricciones se propagan a asignaciones de variables futuras. Por ejemplo, en el problema de las 4 reinas, cada vez que el solucionador coloca una reina, No puedes colocar otras reinas en la fila y diagonales en las que se encuentra la reina actual. La propagación puede acelerar la búsqueda significativamente al reducir el conjunto de valores de variable que el solucionador debe explorar.
- El retroceso ocurre cuando la resolución de problemas no puede asignar un valor a la siguiente variable debido a las limitaciones, o para encontrar una solución. En cualquier caso, el la resolución retroactiva a una etapa anterior y cambia el valor de la variable en en esa etapa a un valor que aún no se probó. En el ejemplo de 4-queens, esto significa mover una reina a un nuevo cuadrado en la columna actual.
A continuación, verás cómo la programación de restricciones usa la propagación y el retroceso para resolver el problema de las 4 reinas.
Supongamos que el solucionador de problemas comienza colocando de forma arbitraria una reina en la esquina superior izquierda en la esquina superior derecha. Esa es una especie de hipótesis; quizás resulte que ninguna solución existe con una reina en la esquina superior izquierda.
Considerando esta hipótesis, ¿qué restricciones podemos propagar? Una limitación es que solo puede haber una reina por columna (las X grises que aparecen debajo) y otra restricción prohíbe dos reinas en la misma diagonal (las X rojas a continuación).

Nuestra tercera restricción prohíbe que las reinas estén en la misma fila:
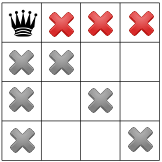
Nuestras restricciones se propagaron, podemos probar otra hipótesis y colocar un a la segunda reina de uno de los restantes cuadrados disponibles. El solucionador podría decidir para colocar en él el primer cuadrado disponible de la segunda columna:
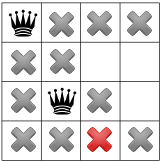
Después de propagar la restricción diagonal, vemos que no deja cuadrados disponibles en la tercera columna o en la última fila:
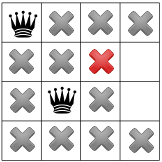
Como no hay soluciones posibles en esta etapa, debemos retroceder. Una opción es para que el solucionador elija el otro cuadrado disponible en la segunda columna. Sin embargo, la propagación de restricciones obliga a una reina a ingresar a la segunda fila de la tercera columna, sin dejar lugares válidos para la cuarta reina:

El solucionador debe retroceder de nuevo, esta vez, de la primera reina. Hemos demostrado que no hay solución para las reinas el problema ocupará un cuadrado de esquina.
Como no puede haber ninguna reina en la esquina, el solucionador hará que la primera reina baja en uno, y se propaga, dejando solo un lugar para la segunda reina:
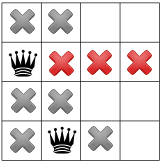
La propagación de nuevo revela solo un lugar para la tercera reina:
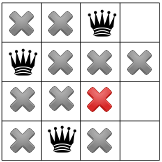
Y para la cuarta y última reina:

Tenemos nuestra primera solución. Si le indicamos a la herramienta de resolución que se detenga después de encontrar la primera solución, terminaría aquí. De lo contrario, volvería hacia atrás y coloca la primera reina en la tercera fila de la primera columna.
Solución que usa CP-SAT
El problema de N-queens es ideal para limitar la programación. En este analizaremos un breve programa de Python que usa el solucionador de problemas CP-SAT para encontrar todas las soluciones al problema.
Importa las bibliotecas
Con el siguiente código, se importa la biblioteca requerida.
Python
import sys import time from ortools.sat.python import cp_model
C++
#include <stdlib.h> #include <sstream> #include <string> #include <vector> #include "absl/strings/numbers.h" #include "ortools/base/logging.h" #include "ortools/sat/cp_model.h" #include "ortools/sat/cp_model.pb.h" #include "ortools/sat/cp_model_solver.h" #include "ortools/sat/model.h" #include "ortools/sat/sat_parameters.pb.h" #include "ortools/util/sorted_interval_list.h"
Java
import com.google.ortools.Loader; import com.google.ortools.sat.CpModel; import com.google.ortools.sat.CpSolver; import com.google.ortools.sat.CpSolverSolutionCallback; import com.google.ortools.sat.IntVar; import com.google.ortools.sat.LinearExpr;
C#
using System; using Google.OrTools.Sat;
Declara el modelo
En el siguiente código, se declara el modelo CP-SAT.
Python
model = cp_model.CpModel()
C++
CpModelBuilder cp_model;
Java
CpModel model = new CpModel();
C#
CpModel model = new CpModel(); int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2); // Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb); Console.WriteLine("Statistics"); Console.WriteLine($" conflicts : {solver.NumConflicts()}"); Console.WriteLine($" branches : {solver.NumBranches()}"); Console.WriteLine($" wall time : {solver.WallTime()} s"); Console.WriteLine($" number of solutions found: {cb.SolutionCount()}"); } }
Crea las variables
La herramienta de resolución crea las variables para el problema como un array llamado queens.
Python
# There are `board_size` number of variables, one for a queen in each column # of the board. The value of each variable is the row that the queen is in. queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)]
C++
// There are `board_size` number of variables, one for a queen in each column // of the board. The value of each variable is the row that the queen is in. std::vector<IntVar> queens; queens.reserve(board_size); Domain range(0, board_size - 1); for (int i = 0; i < board_size; ++i) { queens.push_back( cp_model.NewIntVar(range).WithName("x" + std::to_string(i))); }
Java
int boardSize = 8; // There are `BoardSize` number of variables, one for a queen in each column of the board. The // value of each variable is the row that the queen is in. IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = model.newIntVar(0, boardSize - 1, "x" + i); }
C#
int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); }
Aquí, suponemos que queens[j] es el número de fila de la reina en la columna j.
En otras palabras, queens[j] = i significa que hay una reina en la fila i y la columna j.
Crea las restricciones
Este es el código que crea las restricciones para el problema.
Python
# All rows must be different. model.add_all_different(queens) # No two queens can be on the same diagonal. model.add_all_different(queens[i] + i for i in range(board_size)) model.add_all_different(queens[i] - i for i in range(board_size))
C++
// The following sets the constraint that all queens are in different rows. cp_model.AddAllDifferent(queens); // No two queens can be on the same diagonal. std::vector<LinearExpr> diag_1; diag_1.reserve(board_size); std::vector<LinearExpr> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(queens[i] + i); diag_2.push_back(queens[i] - i); } cp_model.AddAllDifferent(diag_1); cp_model.AddAllDifferent(diag_2);
Java
// All rows must be different. model.addAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[boardSize]; LinearExpr[] diag2 = new LinearExpr[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build(); diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build(); } model.addAllDifferent(diag1); model.addAllDifferent(diag2);
C#
// All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2);
El código usa el método AddAllDifferent, que requiere todos los elementos de una
variable variable para que sea diferente.
Veamos cómo estas restricciones garantizan las tres condiciones para la reina N (reina en diferentes filas, columnas y diagonales).
No hay dos reinas en la misma fila
Si aplicas el método AllDifferent del solucionador a queens se fuerzan los valores de
queens[j] sea diferente para cada j, lo que significa que todas las reinas deben estar en
filas diferentes.
No puede haber dos reinas en la misma columna
Esta restricción está implícita en la definición de queens.
Como no puede haber dos elementos de queens con el mismo índice, no puede haber dos reinas
en la misma columna.
No hay dos reinas en la misma diagonal.
La restricción diagonal es un poco más complicada que las restricciones de filas y columnas. Primero, si dos reinas yace en la misma diagonal, una de las siguientes condiciones debe ser verdadero:
- El número de fila más el número de columna de cada una de las dos reinas son iguales.
En otras palabras,
queens(j) + jtiene el mismo valor para dos índices distintos.j - El número de fila menos el número de columna de cada una de las dos reinas son iguales.
En este caso,
queens(j) - jtiene el mismo valor para dos índices diferentes,j.
Una de estas condiciones significa que las reinas se encuentran en la misma diagonal ascendente ( de izquierda a derecha), mientras que el otro significa que se encuentran en el mismo orden descendente. diagonal. ¿Qué condición corresponde al orden ascendente y cuál a la descendente? depende de cómo ordenes las filas y columnas. Como se menciona en el artículo sección anterior, el orden no tiene efecto en el conjunto de en la forma en que las visualizas.
Por lo tanto, la restricción diagonal es que todos los valores de queens(j) + j deben ser
diferente, y los valores de queens(j) - j deben ser todos diferentes para
diferentes j.
Para aplicar el método AddAllDifferent a queens(j) + j, colocamos las N instancias
de la variable, para j de 0 a N-1, en un array, diag1, de la siguiente manera:
q1 = model.NewIntVar(0, 2 * board_size, 'diag1_%i' % i) diag1.append(q1) model.Add(q1 == queens[j] + j)
Luego, aplicamos AddAllDifferent a diag1.
model.AddAllDifferent(diag1)
La restricción para queens(j) - j se crea de manera similar.
Crear una solución de impresora
Para imprimir todas las soluciones para el problema de N-queens, debes pasar una devolución de llamada. llamada impresora de soluciones, al solucionador de problemas de CP-SAT. La devolución de llamada imprime cada una nueva solución a medida que la encuentra el solucionador. El siguiente código crea una solución impresora.
Python
class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback): """Print intermediate solutions.""" def __init__(self, queens: list[cp_model.IntVar]): cp_model.CpSolverSolutionCallback.__init__(self) self.__queens = queens self.__solution_count = 0 self.__start_time = time.time() @property def solution_count(self) -> int: return self.__solution_count def on_solution_callback(self): current_time = time.time() print( f"Solution {self.__solution_count}, " f"time = {current_time - self.__start_time} s" ) self.__solution_count += 1 all_queens = range(len(self.__queens)) for i in all_queens: for j in all_queens: if self.value(self.__queens[j]) == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print()
C++
int num_solutions = 0; Model model; model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) { LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (SolutionIntegerValue(response, queens[j]) == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; }));
Java
static class SolutionPrinter extends CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queensIn) { solutionCount = 0; queens = queensIn; } @Override public void onSolutionCallback() { System.out.println("Solution " + solutionCount); for (int i = 0; i < queens.length; ++i) { for (int j = 0; j < queens.length; ++j) { if (value(queens[j]) == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != queens.length - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } public int getSolutionCount() { return solutionCount; } private int solutionCount; private final IntVar[] queens; }
C#
public class SolutionPrinter : CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queens) { queens_ = queens; } public override void OnSolutionCallback() { Console.WriteLine($"Solution {SolutionCount_}"); for (int i = 0; i < queens_.Length; ++i) { for (int j = 0; j < queens_.Length; ++j) { if (Value(queens_[j]) == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != queens_.Length - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount_++; } public int SolutionCount() { return SolutionCount_; } private int SolutionCount_; private IntVar[] queens_; }
Ten en cuenta que la impresora de la solución se debe escribir como una clase Python, debido a la Interfaz de Python para el solucionador de C++ subyacente.
Las soluciones se imprimen con las siguientes líneas en la impresora de soluciones.
for v in self.__variables: print('%s = %i' % (v, self.Value(v)), end = ' ')
En este ejemplo, self.__variables es la variable queens, y cada v
corresponde a una de las ocho entradas de queens. Esto imprime una solución en
el siguiente formato: x0 = queens(0) x1 = queens(1) ... x7 = queens(7), donde
xi es el número de columna de la reina en la fila i.
En la siguiente sección, se muestra un ejemplo de una solución.
Cómo llamar a la herramienta de resolución y mostrar los resultados
Con el siguiente código, se ejecuta el solucionador y se muestran las soluciones.
Python
solver = cp_model.CpSolver() solution_printer = NQueenSolutionPrinter(queens) solver.parameters.enumerate_all_solutions = True solver.solve(model, solution_printer)
C++
// Tell the solver to enumerate all solutions. SatParameters parameters; parameters.set_enumerate_all_solutions(true); model.Add(NewSatParameters(parameters)); const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model); LOG(INFO) << "Number of solutions found: " << num_solutions;
Java
CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Tell the solver to enumerate all solutions. solver.getParameters().setEnumerateAllSolutions(true); // And solve. solver.solve(model, cb);
C#
// Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb);
El programa encuentra 92 soluciones diferentes para una placa de 8 × 8. Aquí va la primera.
Q _ _ _ _ _ _ _
_ _ _ _ _ _ Q _
_ _ _ _ Q _ _ _
_ _ _ _ _ _ _ Q
_ Q _ _ _ _ _ _
_ _ _ Q _ _ _ _
_ _ _ _ _ Q _ _
_ _ Q _ _ _ _ _
...91 other solutions displayed...
Solutions found: 92Puedes resolver el problema de un tablero de otro tamaño pasando N como
línea de comandos. Por ejemplo, si el programa se llama queens,
python nqueens_sat.py 6 resuelve el problema de una placa de 6 × 6.
Todo el programa
Aquí está todo el programa del programa N-queens.
Python
"""OR-Tools solution to the N-queens problem.""" import sys import time from ortools.sat.python import cp_model class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback): """Print intermediate solutions.""" def __init__(self, queens: list[cp_model.IntVar]): cp_model.CpSolverSolutionCallback.__init__(self) self.__queens = queens self.__solution_count = 0 self.__start_time = time.time() @property def solution_count(self) -> int: return self.__solution_count def on_solution_callback(self): current_time = time.time() print( f"Solution {self.__solution_count}, " f"time = {current_time - self.__start_time} s" ) self.__solution_count += 1 all_queens = range(len(self.__queens)) for i in all_queens: for j in all_queens: if self.value(self.__queens[j]) == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() def main(board_size: int) -> None: # Creates the solver. model = cp_model.CpModel() # Creates the variables. # There are `board_size` number of variables, one for a queen in each column # of the board. The value of each variable is the row that the queen is in. queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)] # Creates the constraints. # All rows must be different. model.add_all_different(queens) # No two queens can be on the same diagonal. model.add_all_different(queens[i] + i for i in range(board_size)) model.add_all_different(queens[i] - i for i in range(board_size)) # Solve the model. solver = cp_model.CpSolver() solution_printer = NQueenSolutionPrinter(queens) solver.parameters.enumerate_all_solutions = True solver.solve(model, solution_printer) # Statistics. print("\nStatistics") print(f" conflicts : {solver.num_conflicts}") print(f" branches : {solver.num_branches}") print(f" wall time : {solver.wall_time} s") print(f" solutions found: {solution_printer.solution_count}") if __name__ == "__main__": # By default, solve the 8x8 problem. size = 8 if len(sys.argv) > 1: size = int(sys.argv[1]) main(size)
C++
// OR-Tools solution to the N-queens problem. #include <stdlib.h> #include <sstream> #include <string> #include <vector> #include "absl/strings/numbers.h" #include "ortools/base/logging.h" #include "ortools/sat/cp_model.h" #include "ortools/sat/cp_model.pb.h" #include "ortools/sat/cp_model_solver.h" #include "ortools/sat/model.h" #include "ortools/sat/sat_parameters.pb.h" #include "ortools/util/sorted_interval_list.h" namespace operations_research { namespace sat { void NQueensSat(const int board_size) { // Instantiate the solver. CpModelBuilder cp_model; // There are `board_size` number of variables, one for a queen in each column // of the board. The value of each variable is the row that the queen is in. std::vector<IntVar> queens; queens.reserve(board_size); Domain range(0, board_size - 1); for (int i = 0; i < board_size; ++i) { queens.push_back( cp_model.NewIntVar(range).WithName("x" + std::to_string(i))); } // Define constraints. // The following sets the constraint that all queens are in different rows. cp_model.AddAllDifferent(queens); // No two queens can be on the same diagonal. std::vector<LinearExpr> diag_1; diag_1.reserve(board_size); std::vector<LinearExpr> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(queens[i] + i); diag_2.push_back(queens[i] - i); } cp_model.AddAllDifferent(diag_1); cp_model.AddAllDifferent(diag_2); int num_solutions = 0; Model model; model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) { LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (SolutionIntegerValue(response, queens[j]) == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; })); // Tell the solver to enumerate all solutions. SatParameters parameters; parameters.set_enumerate_all_solutions(true); model.Add(NewSatParameters(parameters)); const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model); LOG(INFO) << "Number of solutions found: " << num_solutions; // Statistics. LOG(INFO) << "Statistics"; LOG(INFO) << CpSolverResponseStats(response); } } // namespace sat } // namespace operations_research int main(int argc, char** argv) { int board_size = 8; if (argc > 1) { if (!absl::SimpleAtoi(argv[1], &board_size)) { LOG(INFO) << "Cannot parse '" << argv[1] << "', using the default value of 8."; board_size = 8; } } operations_research::sat::NQueensSat(board_size); return EXIT_SUCCESS; }
Java
package com.google.ortools.sat.samples; import com.google.ortools.Loader; import com.google.ortools.sat.CpModel; import com.google.ortools.sat.CpSolver; import com.google.ortools.sat.CpSolverSolutionCallback; import com.google.ortools.sat.IntVar; import com.google.ortools.sat.LinearExpr; /** OR-Tools solution to the N-queens problem. */ public final class NQueensSat { static class SolutionPrinter extends CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queensIn) { solutionCount = 0; queens = queensIn; } @Override public void onSolutionCallback() { System.out.println("Solution " + solutionCount); for (int i = 0; i < queens.length; ++i) { for (int j = 0; j < queens.length; ++j) { if (value(queens[j]) == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != queens.length - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } public int getSolutionCount() { return solutionCount; } private int solutionCount; private final IntVar[] queens; } public static void main(String[] args) { Loader.loadNativeLibraries(); // Create the model. CpModel model = new CpModel(); int boardSize = 8; // There are `BoardSize` number of variables, one for a queen in each column of the board. The // value of each variable is the row that the queen is in. IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = model.newIntVar(0, boardSize - 1, "x" + i); } // Define constraints. // All rows must be different. model.addAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[boardSize]; LinearExpr[] diag2 = new LinearExpr[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build(); diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build(); } model.addAllDifferent(diag1); model.addAllDifferent(diag2); // Create a solver and solve the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Tell the solver to enumerate all solutions. solver.getParameters().setEnumerateAllSolutions(true); // And solve. solver.solve(model, cb); // Statistics. System.out.println("Statistics"); System.out.println(" conflicts : " + solver.numConflicts()); System.out.println(" branches : " + solver.numBranches()); System.out.println(" wall time : " + solver.wallTime() + " s"); System.out.println(" solutions : " + cb.getSolutionCount()); } private NQueensSat() {} }
C#
// OR-Tools solution to the N-queens problem. using System; using Google.OrTools.Sat; public class NQueensSat { public class SolutionPrinter : CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queens) { queens_ = queens; } public override void OnSolutionCallback() { Console.WriteLine($"Solution {SolutionCount_}"); for (int i = 0; i < queens_.Length; ++i) { for (int j = 0; j < queens_.Length; ++j) { if (Value(queens_[j]) == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != queens_.Length - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount_++; } public int SolutionCount() { return SolutionCount_; } private int SolutionCount_; private IntVar[] queens_; } static void Main() { // Constraint programming engine CpModel model = new CpModel(); int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2); // Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb); Console.WriteLine("Statistics"); Console.WriteLine($" conflicts : {solver.NumConflicts()}"); Console.WriteLine($" branches : {solver.NumBranches()}"); Console.WriteLine($" wall time : {solver.WallTime()} s"); Console.WriteLine($" number of solutions found: {cb.SolutionCount()}"); } }
Solución con el solucionador de problemas de PC original
En las siguientes secciones se presenta un programa de Python que resuelve N-queens a través de la resolución de problemas de PC original. (Sin embargo, recomendamos usar el solucionador de problemas de CP-SAT más reciente).
Importa las bibliotecas
Con el siguiente código, se importa la biblioteca requerida.
Python
import sys from ortools.constraint_solver import pywrapcp
C++
#include <cstdint> #include <cstdlib> #include <sstream> #include <vector> #include "ortools/base/logging.h" #include "ortools/constraint_solver/constraint_solver.h"
Java
import com.google.ortools.Loader; import com.google.ortools.constraintsolver.DecisionBuilder; import com.google.ortools.constraintsolver.IntVar; import com.google.ortools.constraintsolver.Solver;
C#
using System; using Google.OrTools.ConstraintSolver;
Cómo declarar la herramienta de resolución
En el siguiente código, se declara el solucionador de problemas de CP original.
Python
solver = pywrapcp.Solver("n-queens")
C++
Solver solver("N-Queens");
Java
Solver solver = new Solver("N-Queens");
C#
Solver solver = new Solver("N-Queens");
Crea las variables
El método IntVar del solucionador crea las variables para el problema como un array
llamado queens.
Python
# The array index is the column, and the value is the row. queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)]
C++
std::vector<IntVar*> queens; queens.reserve(board_size); for (int i = 0; i < board_size; ++i) { queens.push_back( solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i))); }
Java
int boardSize = 8; IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i); }
C#
const int BoardSize = 8; IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}"); }
Para cualquier solución, queens[j] = i significa que hay una reina en la columna j y la fila
i
Crea las restricciones
Este es el código que crea las restricciones para el problema.
Python
# All rows must be different. solver.Add(solver.AllDifferent(queens)) # No two queens can be on the same diagonal. solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)])) solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)]))
C++
// The following sets the constraint that all queens are in different rows. solver.AddConstraint(solver.MakeAllDifferent(queens)); // All columns must be different because the indices of queens are all // different. No two queens can be on the same diagonal. std::vector<IntVar*> diag_1; diag_1.reserve(board_size); std::vector<IntVar*> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(solver.MakeSum(queens[i], i)->Var()); diag_2.push_back(solver.MakeSum(queens[i], -i)->Var()); } solver.AddConstraint(solver.MakeAllDifferent(diag_1)); solver.AddConstraint(solver.MakeAllDifferent(diag_2));
Java
// All rows must be different. solver.addConstraint(solver.makeAllDifferent(queens)); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[boardSize]; IntVar[] diag2 = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = solver.makeSum(queens[i], i).var(); diag2[i] = solver.makeSum(queens[i], -i).var(); } solver.addConstraint(solver.makeAllDifferent(diag1)); solver.addConstraint(solver.makeAllDifferent(diag2));
C#
// All rows must be different. solver.Add(queens.AllDifferent()); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[BoardSize]; IntVar[] diag2 = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = solver.MakeSum(queens[i], i).Var(); diag2[i] = solver.MakeSum(queens[i], -i).Var(); } solver.Add(diag1.AllDifferent()); solver.Add(diag2.AllDifferent());
Estas restricciones garantizan las tres condiciones para el problema de la N-queens ( en diferentes filas, columnas y diagonales).
No hay dos reinas en la misma fila
Si aplicas el método AllDifferent del solucionador a queens se fuerzan los valores de
queens[j] sea diferente para cada j, lo que significa que todas las reinas deben estar en
filas diferentes.
No puede haber dos reinas en la misma columna
Esta restricción está implícita en la definición de queens.
Como no puede haber dos elementos de queens con el mismo índice, no puede haber dos reinas
en la misma columna.
No hay dos reinas en la misma diagonal.
La restricción diagonal es un poco más complicada que las restricciones de filas y columnas. Primero, si dos reinas yace en la misma diagonal, una de las siguientes opciones debe ser verdadera:
- Si la diagonal es descendente (va de izquierda a derecha), el número de fila más
para cada una de las dos reinas son iguales. Entonces,
queens(i) + itiene la mismo valor para dos índices diferentesi. - Si la diagonal es ascendente, el número de fila menos el número de columna de cada
de las dos reinas son iguales. En este caso,
queens(i) - itiene el mismo valor. para dos índices diferentes,i.
Por lo tanto, la restricción diagonal es que todos los valores de queens(i) + i deben ser
diferente y, asimismo, los valores de queens(i) - i deben ser todos diferentes para
diferentes i.
El código anterior agrega esta restricción aplicando el
AllDifferent
método a queens[j] + j y queens[j] - j, para cada i.
Agrega el generador de decisiones
El próximo paso es crear un generador de decisiones, que defina la estrategia de búsqueda para resolver el problema. La estrategia de búsqueda puede tener un impacto importante en el tiempo de búsqueda debido a la propagación de restricciones, que reduce la cantidad de valores de variables el solucionador tiene que explorar. Ya viste un ejemplo de esto Ejemplo de 4-queens.
Con el siguiente código, se crea un generador de decisiones a partir del directorio
Phase
.
Python
db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE)
C++
DecisionBuilder* const db = solver.MakePhase( queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE);
Java
// Create the decision builder to search for solutions. final DecisionBuilder db = solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
C#
// Create the decision builder to search for solutions. DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
Consulta Creador de decisiones para obtener detalles sobre la
argumentos de entrada al método Phase.
Cómo funciona el generador de decisiones en el ejemplo de las 4 queens
Veamos cómo el generador de decisiones dirige la búsqueda en el
Ejemplo de 4-queens.
La resolución comienza con queens[0], la primera variable del array, como se indica.
por CHOOSE_FIRST_UNBOUND. El solucionador le asigna a queens[0] la menor
valor que aún no se probó, que es 0 en esta etapa, según lo indica
ASSIGN_MIN_VALUE Esto coloca a la primera reina en la esquina superior izquierda de la
a bordo.
A continuación, el solucionador selecciona queens[1], que ahora es la primera variable no delimitada en
queens Después de propagar las restricciones, existen dos filas posibles para un
la reina en la columna 1: fila 2 o fila 3. La opción ASSIGN_MIN_VALUE dirige al
solucionador de problemas para asignar queens[1] = 2. (Si, en cambio, configuras IntValueStrategy como
ASSIGN_MAX_VALUE, la herramienta de resolución asignaría queens[1] = 3).
Puedes comprobar que el resto de la búsqueda siga las mismas reglas.
Cómo llamar a la herramienta de resolución y mostrar los resultados
El siguiente código ejecuta el solucionador y muestra la solución.
Python
# Iterates through the solutions, displaying each. num_solutions = 0 solver.NewSearch(db) while solver.NextSolution(): # Displays the solution just computed. for i in range(board_size): for j in range(board_size): if queens[j].Value() == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() num_solutions += 1 solver.EndSearch()
C++
// Iterates through the solutions, displaying each. int num_solutions = 0; solver.NewSearch(db); while (solver.NextSolution()) { // Displays the solution just computed. LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (queens[j]->Value() == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; } solver.EndSearch();
Java
int solutionCount = 0; solver.newSearch(db); while (solver.nextSolution()) { System.out.println("Solution " + solutionCount); for (int i = 0; i < boardSize; ++i) { for (int j = 0; j < boardSize; ++j) { if (queens[j].value() == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != boardSize - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } solver.endSearch();
C#
// Iterates through the solutions, displaying each. int SolutionCount = 0; solver.NewSearch(db); while (solver.NextSolution()) { Console.WriteLine("Solution " + SolutionCount); for (int i = 0; i < BoardSize; ++i) { for (int j = 0; j < BoardSize; ++j) { if (queens[j].Value() == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != BoardSize - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount++; } solver.EndSearch();
Esta es la primera solución que encontró el programa para una placa de 8 × 8.
Q _ _ _ _ _ _ _
_ _ _ _ _ _ Q _
_ _ _ _ Q _ _ _
_ _ _ _ _ _ _ Q
_ Q _ _ _ _ _ _
_ _ _ Q _ _ _ _
_ _ _ _ _ Q _ _
_ _ Q _ _ _ _ _
...91 other solutions displayed...
Statistics
failures: 304
branches: 790
wall time: 5 ms
Solutions found: 92Puedes resolver el problema de un tablero de otro tamaño pasando N como
línea de comandos. Por ejemplo, python nqueens_cp.py 6 soluciona el problema.
para una placa de 6 x 6.
Todo el programa
El programa completo se muestra a continuación.
Python
"""OR-Tools solution to the N-queens problem.""" import sys from ortools.constraint_solver import pywrapcp def main(board_size): # Creates the solver. solver = pywrapcp.Solver("n-queens") # Creates the variables. # The array index is the column, and the value is the row. queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)] # Creates the constraints. # All rows must be different. solver.Add(solver.AllDifferent(queens)) # No two queens can be on the same diagonal. solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)])) solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)])) db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE) # Iterates through the solutions, displaying each. num_solutions = 0 solver.NewSearch(db) while solver.NextSolution(): # Displays the solution just computed. for i in range(board_size): for j in range(board_size): if queens[j].Value() == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() num_solutions += 1 solver.EndSearch() # Statistics. print("\nStatistics") print(f" failures: {solver.Failures()}") print(f" branches: {solver.Branches()}") print(f" wall time: {solver.WallTime()} ms") print(f" Solutions found: {num_solutions}") if __name__ == "__main__": # By default, solve the 8x8 problem. size = 8 if len(sys.argv) > 1: size = int(sys.argv[1]) main(size)
C++
// OR-Tools solution to the N-queens problem. #include <cstdint> #include <cstdlib> #include <sstream> #include <vector> #include "ortools/base/logging.h" #include "ortools/constraint_solver/constraint_solver.h" namespace operations_research { void NQueensCp(const int board_size) { // Instantiate the solver. Solver solver("N-Queens"); std::vector<IntVar*> queens; queens.reserve(board_size); for (int i = 0; i < board_size; ++i) { queens.push_back( solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i))); } // Define constraints. // The following sets the constraint that all queens are in different rows. solver.AddConstraint(solver.MakeAllDifferent(queens)); // All columns must be different because the indices of queens are all // different. No two queens can be on the same diagonal. std::vector<IntVar*> diag_1; diag_1.reserve(board_size); std::vector<IntVar*> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(solver.MakeSum(queens[i], i)->Var()); diag_2.push_back(solver.MakeSum(queens[i], -i)->Var()); } solver.AddConstraint(solver.MakeAllDifferent(diag_1)); solver.AddConstraint(solver.MakeAllDifferent(diag_2)); DecisionBuilder* const db = solver.MakePhase( queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE); // Iterates through the solutions, displaying each. int num_solutions = 0; solver.NewSearch(db); while (solver.NextSolution()) { // Displays the solution just computed. LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (queens[j]->Value() == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; } solver.EndSearch(); // Statistics. LOG(INFO) << "Statistics"; LOG(INFO) << " failures: " << solver.failures(); LOG(INFO) << " branches: " << solver.branches(); LOG(INFO) << " wall time: " << solver.wall_time() << " ms"; LOG(INFO) << " Solutions found: " << num_solutions; } } // namespace operations_research int main(int argc, char** argv) { int board_size = 8; if (argc > 1) { board_size = std::atoi(argv[1]); } operations_research::NQueensCp(board_size); return EXIT_SUCCESS; }
Java
// OR-Tools solution to the N-queens problem. package com.google.ortools.constraintsolver.samples; import com.google.ortools.Loader; import com.google.ortools.constraintsolver.DecisionBuilder; import com.google.ortools.constraintsolver.IntVar; import com.google.ortools.constraintsolver.Solver; /** N-Queens Problem. */ public final class NQueensCp { public static void main(String[] args) { Loader.loadNativeLibraries(); // Instantiate the solver. Solver solver = new Solver("N-Queens"); int boardSize = 8; IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i); } // Define constraints. // All rows must be different. solver.addConstraint(solver.makeAllDifferent(queens)); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[boardSize]; IntVar[] diag2 = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = solver.makeSum(queens[i], i).var(); diag2[i] = solver.makeSum(queens[i], -i).var(); } solver.addConstraint(solver.makeAllDifferent(diag1)); solver.addConstraint(solver.makeAllDifferent(diag2)); // Create the decision builder to search for solutions. final DecisionBuilder db = solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE); int solutionCount = 0; solver.newSearch(db); while (solver.nextSolution()) { System.out.println("Solution " + solutionCount); for (int i = 0; i < boardSize; ++i) { for (int j = 0; j < boardSize; ++j) { if (queens[j].value() == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != boardSize - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } solver.endSearch(); // Statistics. System.out.println("Statistics"); System.out.println(" failures: " + solver.failures()); System.out.println(" branches: " + solver.branches()); System.out.println(" wall time: " + solver.wallTime() + "ms"); System.out.println(" Solutions found: " + solutionCount); } private NQueensCp() {} }
C#
// OR-Tools solution to the N-queens problem. using System; using Google.OrTools.ConstraintSolver; public class NQueensCp { public static void Main(String[] args) { // Instantiate the solver. Solver solver = new Solver("N-Queens"); const int BoardSize = 8; IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. solver.Add(queens.AllDifferent()); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[BoardSize]; IntVar[] diag2 = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = solver.MakeSum(queens[i], i).Var(); diag2[i] = solver.MakeSum(queens[i], -i).Var(); } solver.Add(diag1.AllDifferent()); solver.Add(diag2.AllDifferent()); // Create the decision builder to search for solutions. DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE); // Iterates through the solutions, displaying each. int SolutionCount = 0; solver.NewSearch(db); while (solver.NextSolution()) { Console.WriteLine("Solution " + SolutionCount); for (int i = 0; i < BoardSize; ++i) { for (int j = 0; j < BoardSize; ++j) { if (queens[j].Value() == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != BoardSize - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount++; } solver.EndSearch(); // Statistics. Console.WriteLine("Statistics"); Console.WriteLine($" failures: {solver.Failures()}"); Console.WriteLine($" branches: {solver.Branches()}"); Console.WriteLine($" wall time: {solver.WallTime()} ms"); Console.WriteLine($" Solutions found: {SolutionCount}"); } }
Cantidad de soluciones
La cantidad de soluciones aumenta de manera exponencial en función del tamaño del tablero:
| Tamaño del tablero | Soluciones | Tiempo para encontrar todas las soluciones (ms) |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 0 | 0 |
| 3 | 0 | 0 |
| 4 | 2 | 0 |
| 5 | 10 | 0 |
| 6 | 4 | 0 |
| 7 | 40 | 3 |
| 8 | 92 | 9 |
| 9 | 352 | 35 |
| 10 | 724 | 95 |
| 11 | 2680 | 378 |
| 12 | 14200 | 2198 |
| 13 | 73712 | 11628 |
| 14 | 365596 | 62427 |
| 15 | 2279184 | 410701 |
Muchas soluciones son solo rotaciones de otras, y una técnica llamada simetría se puede usar para reducir la cantidad de cómputo necesario. No usamos eso, la solución anterior no pretende ser rápida, sino sencilla. Por supuesto, podríamos hacerlo mucho más rápido si solo quisiéramos encontrar una solución, en lugar de todos: unos pocos milisegundos para placas de hasta 50 tamaños.

