تقسیم کننده دقیق برای طبقه بندی باینری با ویژگی های عددی

در این واحد، ساده‌ترین و رایج‌ترین الگوریتم تقسیم‌کننده را بررسی می‌کنید، که شرایطی به شکل $\mathrm{feature}_i \geq t$ را در تنظیمات زیر ایجاد می‌کند:

• وظیفه طبقه بندی باینری
• بدون مقادیر از دست رفته در مثال ها
• بدون شاخص از پیش محاسبه شده در نمونه ها

مجموعه‌ای از $n$ مثال با یک ویژگی عددی و یک برچسب باینری "نارنجی" و "آبی" را فرض کنید. به طور رسمی، بیایید مجموعه داده $D$ را به صورت زیر توصیف کنیم:

$$D = \{(x_i,y_i)\}_{i\in[1,n]}$$

جایی که:

• $x_i$ مقدار یک ویژگی عددی در $\mathbb{R}$ (مجموعه اعداد واقعی) است.
• $y_i$ یک مقدار برچسب طبقه‌بندی باینری به رنگ {نارنجی، آبی} است.

هدف ما یافتن یک مقدار آستانه $t$ (آستانه) است به گونه‌ای که تقسیم مثال‌های $D$ به گروه‌های $T(rue)$ و $F(alse)$ با توجه به شرایط $x_i \geq t$ باعث بهبود جداسازی برچسب ها؛ به عنوان مثال، نمونه های "نارنجی" بیشتر در $T$ و نمونه های "آبی" بیشتر در $F$.

آنتروپی شانون معیاری برای بی نظمی است. برای یک برچسب باینری:

• زمانی که برچسب‌ها در مثال‌ها متعادل باشند (۵۰٪ آبی و ۵۰٪ نارنجی) آنتروپی شانون حداکثر است.
• آنتروپی شانون زمانی که برچسب‌های موجود در نمونه‌ها خالص هستند (100٪ آبی یا 100٪ نارنجی) در حداقل (مقدار صفر) است.

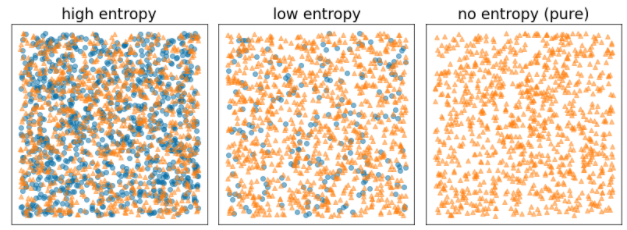
شکل 8. سه سطح آنتروپی مختلف.

به طور رسمی، می‌خواهیم شرطی را پیدا کنیم که مجموع وزنی آنتروپی توزیع برچسب‌ها را در $T$ و $F$ کاهش دهد. امتیاز مربوطه به دست آوردن اطلاعات است که تفاوت بین آنتروپی $D$ و آنتروپی {$T$,$F$} است. به این تفاوت، کسب اطلاعات می گویند .

شکل زیر یک تقسیم بد را نشان می‌دهد که در آن آنتروپی بالا و افزایش اطلاعات کم می‌ماند:

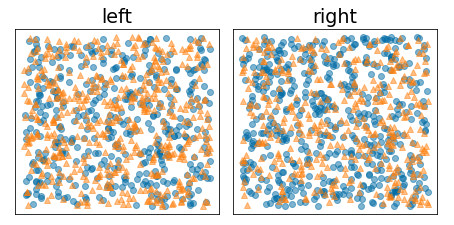
شکل 9. تقسیم بد آنتروپی برچسب را کاهش نمی دهد.

در مقابل، شکل زیر یک تقسیم بهتر را نشان می‌دهد که در آن آنتروپی کم می‌شود (و افزایش اطلاعات زیاد می‌شود):

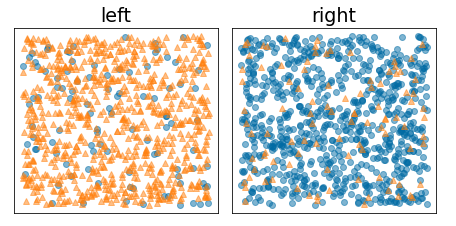
شکل 10. یک تقسیم خوب آنتروپی برچسب را کاهش می دهد.

به طور رسمی:

\[\begin{eqnarray} T & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \ge t \} \\[12pt] F & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \lt t \} \\[12pt] R(X) & = & \frac{\lvert \{ x | x \in X \ \textrm{and} \ x = \mathrm{pos} \} \rvert}{\lvert X \rvert} \\[12pt] H(X) & = & - p \log p - (1 - p) \log (1-p) \ \textrm{with} \ p = R(X)\\[12pt] IG(D,T,F) & = & H(D) - \frac {\lvert T\rvert} {\lvert D \rvert } H(T) - \frac {\lvert F \rvert} {\lvert D \rvert } H(F) \end{eqnarray}\]

جایی که:

• $IG(D,T,F)$ کسب اطلاعات حاصل از تقسیم $D$ به $T$ و $F$ است.
• $H(X)$ آنتروپی مجموعه مثال ها $X$ است.
• $|X|$ تعداد عناصر مجموعه $X$ است.
• $t$ مقدار آستانه است.
• $pos$ مقدار برچسب مثبت است، به عنوان مثال، "آبی" در مثال بالا. انتخاب یک برچسب متفاوت به عنوان "برچسب مثبت" مقدار آنتروپی یا افزایش اطلاعات را تغییر نمی دهد.
• $R(X)$ نسبت مقادیر برچسب مثبت در مثال‌های $X$ است.
• $D$ مجموعه داده است (همانطور که قبلاً در این واحد تعریف شد).

در مثال زیر، یک مجموعه داده طبقه بندی باینری را با یک ویژگی عددی واحد $x$ در نظر می گیریم. شکل زیر برای مقادیر مختلف آستانه $t$ (محور x) نشان می دهد:

1. هیستوگرام ویژگی $x$.
2. نسبت نمونه های "آبی" در $D$، $T$، و $F$ با توجه به مقدار آستانه تنظیم می شود.
3. آنتروپی در $D$، $T$ و $F$.
4. به دست آوردن اطلاعات؛ یعنی دلتای آنتروپی بین $D$ و {$T$,$F$} با تعداد نمونه وزن شده است.

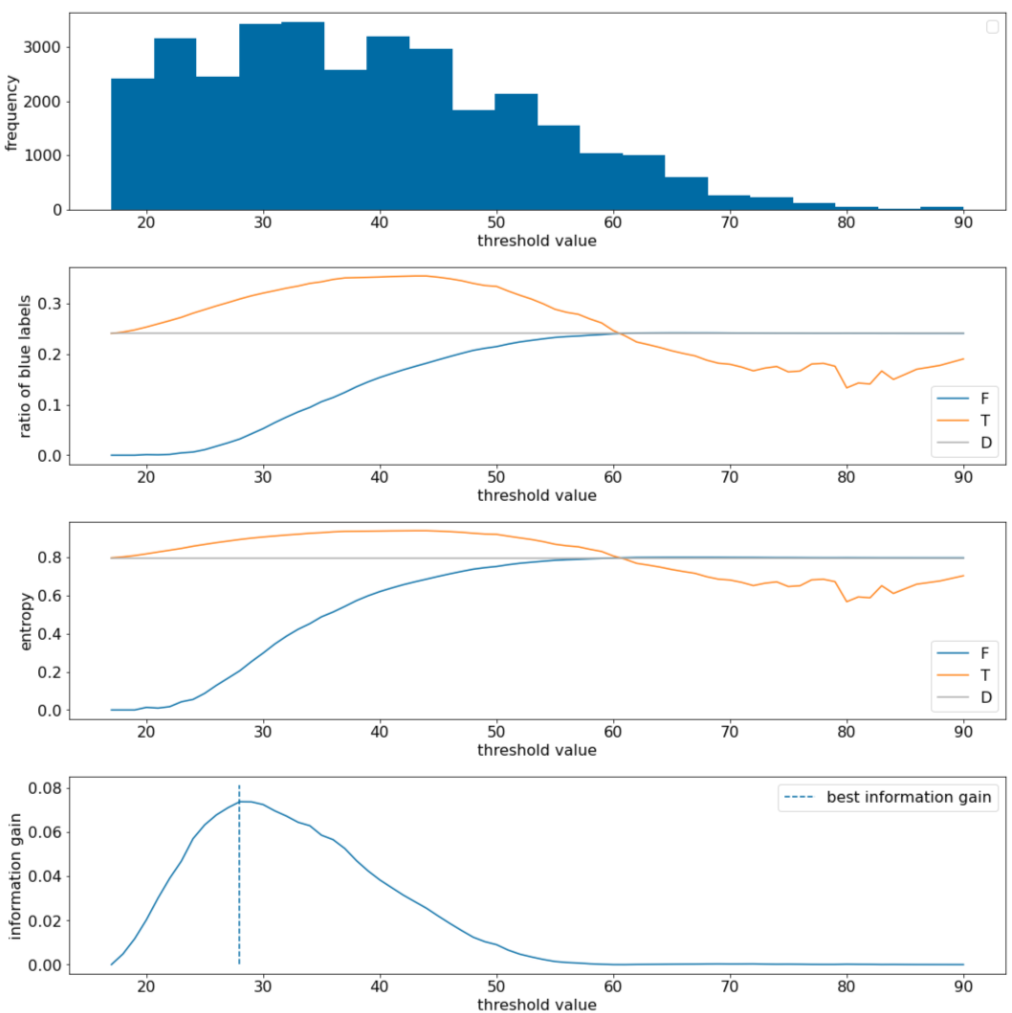
شکل 11. چهار نمودار آستانه.

این نمودارها موارد زیر را نشان می دهند:

• نمودار "فرکانس" نشان می دهد که مشاهدات با غلظت های بین 18 و 60 نسبتاً خوب پخش می شوند. گسترش مقدار گسترده به این معنی است که شکاف های بالقوه زیادی وجود دارد که برای آموزش مدل خوب است.

• نسبت برچسب های "آبی" در مجموعه داده ~25٪ است. نمودار "نسبت برچسب آبی" نشان می دهد که برای مقادیر آستانه بین 20 و 50:

  • مجموعه $T$ حاوی بیش از حد نمونه های برچسب "آبی" است (تا 35٪ برای آستانه 35).
  • مجموعه $F$ حاوی یک کسری مکمل از نمونه های برچسب "آبی" است (فقط 8٪ برای آستانه 35).

  هر دو نمودار "نسبت برچسب های آبی" و "آنتروپی" نشان می دهد که برچسب ها را می توان به خوبی در این محدوده آستانه جدا کرد.

• این مشاهده در طرح "به دست آوردن اطلاعات" تایید شده است. می بینیم که حداکثر بهره اطلاعات با t~=28 برای مقدار به دست آوردن اطلاعات ~0.074 به دست می آید. بنابراین، شرط بازگشتی توسط اسپلیتر $x \geq 28$ خواهد بود.

• کسب اطلاعات همیشه مثبت یا پوچ است. زمانی که مقدار آستانه به سمت مقدار حداکثر/حداقل آن همگرا می شود، به صفر همگرا می شود. در این موارد، $F$ یا $T$ خالی می شود در حالی که دیگری شامل کل مجموعه داده است و آنتروپی برابر با D$$ نشان می دهد. هنگامی که $H(T)$ = $H(F)$ = $H(D)$، سود اطلاعات نیز می تواند صفر باشد. در آستانه 60، نسبت برچسب های "آبی" برای هر دو $T$ و $F$ با $D$ یکسان است و سود اطلاعات صفر است.

مقادیر کاندید برای $t$ در مجموعه اعداد واقعی ($\mathbb{R}$) بی نهایت هستند. با این حال، با توجه به تعداد محدودی از مثال‌ها، تنها تعداد محدودی از تقسیم‌بندی‌های $D$ به $T$ و $F$ وجود دارد. بنابراین، فقط تعداد محدودی از مقادیر $t$ برای آزمایش معنادار است.

یک رویکرد کلاسیک این است که مقادیر x _i را به ترتیب افزایش x _s(i) مرتب کنیم به طوری که:

$$ x_{s(i)} \leq x_{s(i+1)} $$

سپس، $t$ را برای هر مقدار در نیمه راه بین مقادیر مرتب شده متوالی $x_i$ آزمایش کنید. برای مثال، فرض کنید 1000 مقدار ممیز شناور از یک ویژگی خاص دارید. پس از مرتب سازی، فرض کنید دو مقدار اول 8.5 و 8.7 باشد. در این حالت، اولین مقدار آستانه برای آزمایش 8.6 خواهد بود.

به طور رسمی، مقادیر کاندید زیر را برای t در نظر می گیریم:

$$ X = \left\{ \frac {x_{s(i)} + x_{s(i + 1)}} {2} \lvert x_{s(i)} \ne x_{s(i+1)} \right\} $$

پیچیدگی زمانی این الگوریتم $\mathcal{O} (n \log n) $ با $n$ تعداد نمونه‌های موجود در گره است (به دلیل مرتب‌سازی مقادیر ویژگی). هنگامی که بر روی درخت تصمیم اعمال می شود، الگوریتم تقسیم بر هر گره و هر ویژگی اعمال می شود. توجه داشته باشید که هر گره 1/2 از نمونه های والد خود را دریافت می کند. بنابراین، با توجه به قضیه اصلی ، پیچیدگی زمانی آموزش درخت تصمیم با این تقسیم کننده به صورت زیر است:

$$ \mathcal{O} ( m n \log^2 n ) $$

جایی که:

• $m$ تعداد ویژگی ها است.
• $n$ تعداد نمونه های آموزشی است.

در این الگوریتم، ارزش ویژگی ها مهم نیست. فقط سفارش مهم است به همین دلیل، این الگوریتم مستقل از مقیاس یا توزیع مقادیر ویژگی کار می کند. به همین دلیل است که هنگام آموزش درخت تصمیم نیازی به نرمال سازی یا مقیاس بندی ویژگی های عددی نداریم.