TensorFlow, Keras et deep learning, sans doctorat

Dans cet atelier de programmation, vous allez apprendre à créer et à entraîner un réseau de neurones capable de reconnaître des chiffres manuscrits. Au fur et à mesure que vous améliorerez votre réseau de neurones pour atteindre une précision de 99 %, vous découvrirez également les outils utilisés par les professionnels du deep learning pour entraîner efficacement leurs modèles.

Cet atelier de programmation utilise l'ensemble de données MNIST, une collection de 60 000 chiffres étiquetés qui a occupé des générations de doctorants pendant près de deux décennies. Vous résoudrez le problème avec moins de 100 lignes de code Python / TensorFlow.

Points abordés

• Qu'est-ce qu'un réseau de neurones et comment l'entraîner ?
• Créer un réseau de neurones de base à une couche à l'aide de tf.keras
• Ajouter des calques
• Configurer un calendrier du taux d'apprentissage
• Créer des réseaux de neurones convolutifs
• Utiliser des techniques de régularisation : abandon, normalisation par lot
• Qu'est-ce que le surapprentissage ?

Prérequis

Un simple navigateur. Cet atelier peut être entièrement exécuté avec Google Colaboratory.

Commentaires

N'hésitez pas à nous contacter si vous remarquez quelque chose d'inhabituel dans cet atelier ou si vous pensez qu'il devrait être amélioré. Nous traitons les commentaires via les problèmes GitHub [lien vers les commentaires].

Cet atelier utilise Google Colaboratory et ne nécessite aucune configuration de votre part. Vous pouvez l'exécuter depuis un Chromebook. Veuillez ouvrir le fichier ci-dessous et exécuter les cellules pour vous familiariser avec les notebooks Colab.

Welcome to Colab.ipynb

Vous trouverez des instructions supplémentaires ci-dessous :

Sélectionner un backend de GPU

Dans le menu Colab, sélectionnez Exécution > Modifier le type d'exécution, puis sélectionnez "GPU". La connexion au runtime se fait automatiquement lors de la première exécution. Vous pouvez également utiliser le bouton "Connect" (Se connecter) en haut à droite.

Exécution de notebooks

Exécutez les cellules une par une en cliquant sur une cellule et en utilisant Maj+ENTRÉE. Vous pouvez également exécuter l'intégralité du notebook avec Exécuter > Exécuter tout.

Sommaire

Tous les notebooks comportent une table des matières. Vous pouvez l'ouvrir à l'aide de la flèche noire sur la gauche.

Cellules masquées

Certaines cellules n'affichent que leur titre. Il s'agit d'une fonctionnalité de notebook spécifique à Colab. Vous pouvez double-cliquer dessus pour afficher le code qu'ils contiennent, mais il n'est généralement pas très intéressant. Fonctions de support ou de visualisation, généralement. Vous devez toujours exécuter ces cellules pour que les fonctions à l'intérieur soient définies.

Nous allons d'abord regarder un réseau de neurones s'entraîner. Veuillez ouvrir le notebook ci-dessous et exécuter toutes les cellules. Ne vous préoccupez pas encore du code. Nous commencerons à l'expliquer plus tard.

keras_01_mnist.ipynb

Lorsque vous exécutez le notebook, concentrez-vous sur les visualisations. Pour en savoir plus, consultez les explications ci-dessous.

Données d'entraînement

Nous disposons d'un ensemble de données de chiffres manuscrits qui ont été étiquetés afin que nous sachions ce que représente chaque image, c'est-à-dire un nombre compris entre 0 et 9. Dans le notebook, vous verrez un extrait :

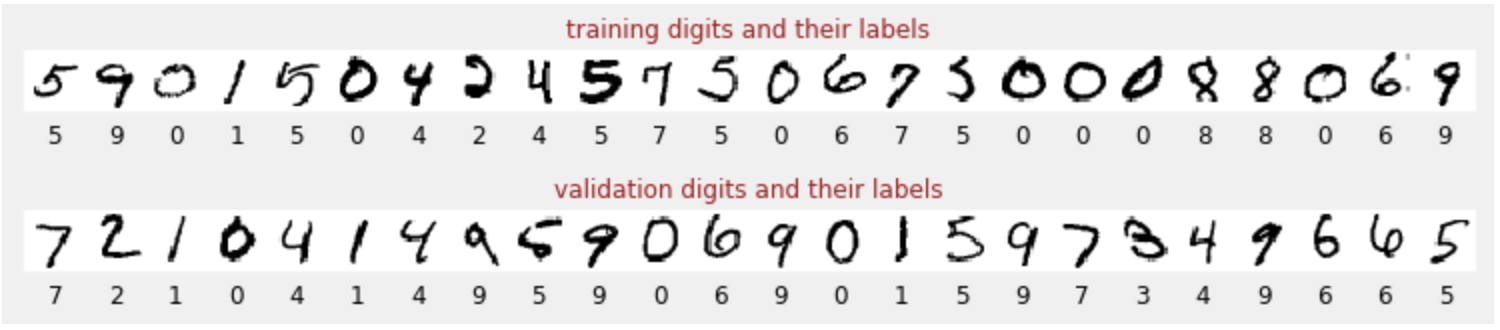
Le réseau de neurones que nous allons créer classifie les chiffres manuscrits dans leurs 10 classes (0, …, 9). Pour ce faire, il s'appuie sur des paramètres internes qui doivent avoir une valeur correcte pour que la classification fonctionne bien. Cette "valeur correcte" est apprise grâce à un processus d'entraînement qui nécessite un "ensemble de données étiquetées" avec des images et les réponses correctes associées.

Comment savoir si le réseau de neurones entraîné est performant ou non ? Utiliser l'ensemble de données d'entraînement pour tester le réseau serait de la triche. Il a déjà vu cet ensemble de données plusieurs fois pendant l'entraînement et est très certainement très performant sur celui-ci. Nous avons besoin d'un autre ensemble de données étiquetées, jamais vu pendant l'entraînement, pour évaluer les performances "réelles" du réseau. On parle alors d'ensemble de données de validation.

Cet ensemble de données contient 50 000 chiffres d'entraînement. Nous alimentons une "batch" de taille 128 dans la boucle d'entraînement à chaque itération. Le système aura ainsi vu tous les chiffres d'entraînement une fois après 391 itérations. C'est ce que nous appelons une époque.

Il existe également 10 000 chiffres de validation distincts pour tester les performances du modèle.

Formation

Au fur et à mesure de l'entraînement, un lot de données d'entraînement à la fois, les paramètres internes du modèle sont mis à jour et le modèle devient de plus en plus performant pour reconnaître les chiffres manuscrits. Vous pouvez le voir sur le graphique d'entraînement :

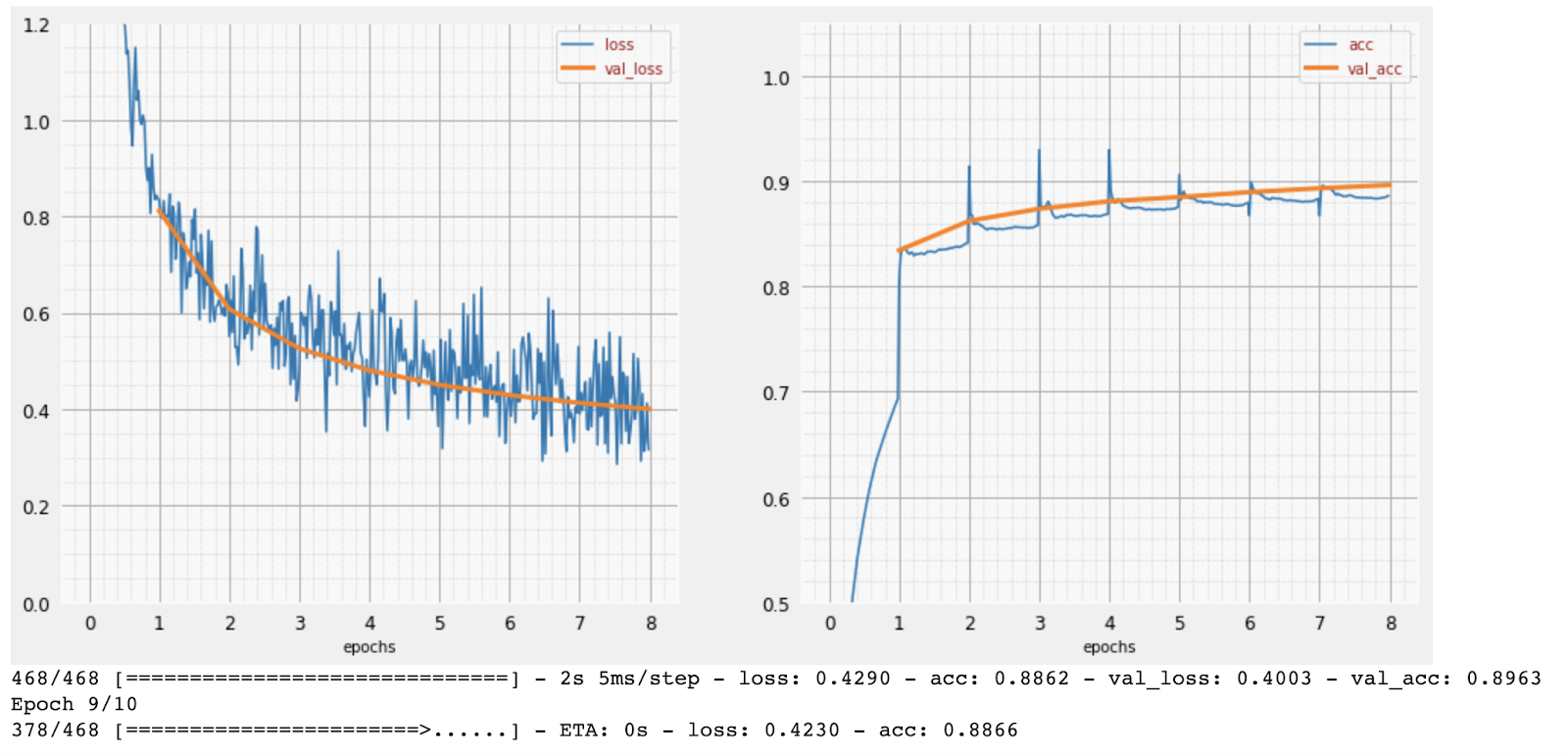
À droite, la "précision" correspond simplement au pourcentage de chiffres correctement reconnus. Elle augmente à mesure que l'entraînement progresse, ce qui est une bonne chose.

À gauche, nous pouvons voir la perte. Pour entraîner le modèle, nous allons définir une fonction de "perte", qui représente la façon dont le système reconnaît les chiffres, et essayer de la minimiser. Vous pouvez voir ici que la perte diminue à la fois pour les données d'entraînement et de validation à mesure que l'entraînement progresse. C'est une bonne chose. Cela signifie que le réseau de neurones est en train d'apprendre.

L'axe X représente le nombre d'"époques" ou d'itérations sur l'ensemble de données.

Prédictions

Une fois le modèle entraîné, nous pouvons l'utiliser pour reconnaître des chiffres manuscrits. La visualisation suivante montre ses performances sur quelques chiffres rendus à partir de polices locales (première ligne), puis sur les 10 000 chiffres de l'ensemble de données de validation. La classe prédite apparaît sous chaque chiffre. Si elle est incorrecte, elle est en rouge.

Comme vous pouvez le voir, ce modèle initial n'est pas très bon, mais il reconnaît tout de même certains chiffres correctement. La précision de la validation finale est d'environ 90 %, ce qui n'est pas si mal pour le modèle simpliste avec lequel nous commençons. Toutefois,cela signifie qu'il manque encore 1 000 chiffres de validation sur les 10 000. C'est beaucoup plus que ce qui peut être affiché. C'est pourquoi il semble que toutes les réponses soient fausses (en rouge).

Tensors

Les données sont stockées dans des matrices. Une image en niveaux de gris de 28 x 28 pixels tient dans une matrice bidimensionnelle de 28 x 28. Mais pour une image en couleur, nous avons besoin de plus de dimensions. Il existe trois valeurs de couleur par pixel (rouge, vert et bleu). Vous aurez donc besoin d'un tableau tridimensionnel avec les dimensions [28, 28, 3]. Pour stocker un lot de 128 images en couleur, il faut un tableau à quatre dimensions avec les dimensions [128, 28, 28, 3].

Ces tableaux multidimensionnels sont appelés tenseurs et la liste de leurs dimensions est leur forme.

En bref

Si vous connaissez déjà tous les termes en gras du paragraphe suivant, vous pouvez passer à l'exercice suivant. Si vous débutez dans le deep learning, bienvenue. Veuillez lire la suite.

Un classificateur de réseau de neurones est composé de plusieurs couches de neurones. Pour la classification d'images, il peut s'agir de couches denses ou, plus fréquemment, convolutionnelles. Elles sont généralement activées avec la fonction d'activation relu. La dernière couche utilise autant de neurones que de classes et est activée avec softmax. Pour la classification, l'entropie croisée est la fonction de perte la plus couramment utilisée. Elle compare les libellés encodés one-hot (c'est-à-dire les réponses correctes) avec les probabilités prédites par le réseau de neurones. Pour minimiser la perte, il est préférable de choisir un optimiseur avec un élan, par exemple Adam, et d'effectuer l'entraînement sur des lots d'images et de libellés d'entraînement.

Pour les modèles créés sous forme de séquence de couches, Keras propose l'API Sequential. Par exemple, un classificateur d'images utilisant trois couches denses peut être écrit dans Keras comme suit :

model = tf.keras.Sequential([
    tf.keras.layers.Flatten(input_shape=[28, 28, 1]),
    tf.keras.layers.Dense(200, activation="relu"),
    tf.keras.layers.Dense(60, activation="relu"),
    tf.keras.layers.Dense(10, activation='softmax') # classifying into 10 classes
])

# this configures the training of the model. Keras calls it "compiling" the model.
model.compile(
  optimizer='adam',
  loss= 'categorical_crossentropy',
  metrics=['accuracy']) # % of correct answers

# train the model
model.fit(dataset, ... )

Une seule couche dense

Les chiffres manuscrits de l'ensemble de données MNIST sont des images en niveaux de gris de 28 x 28 pixels. L'approche la plus simple pour les classer consiste à utiliser les 28 x 28=784 pixels comme entrées pour un réseau de neurones à une couche.

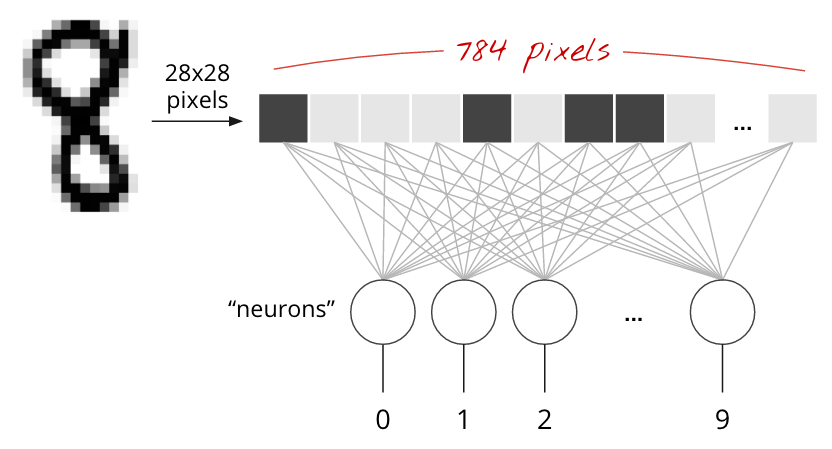
Chaque neurone d'un réseau de neurones effectue une somme pondérée de toutes ses entrées, ajoute une constante appelée "biais", puis transmet le résultat à une fonction d'activation non linéaire. Les pondérations et les biais sont des paramètres qui seront déterminés par l'entraînement. Elles sont initialement initialisées avec des valeurs aléatoires.

L'image ci-dessus représente un réseau de neurones à une couche avec 10 neurones de sortie, car nous voulons classer les chiffres en 10 classes (de 0 à 9).

Avec une multiplication matricielle

Voici comment une couche de réseau de neurones traitant une collection d'images peut être représentée par une multiplication de matrices :

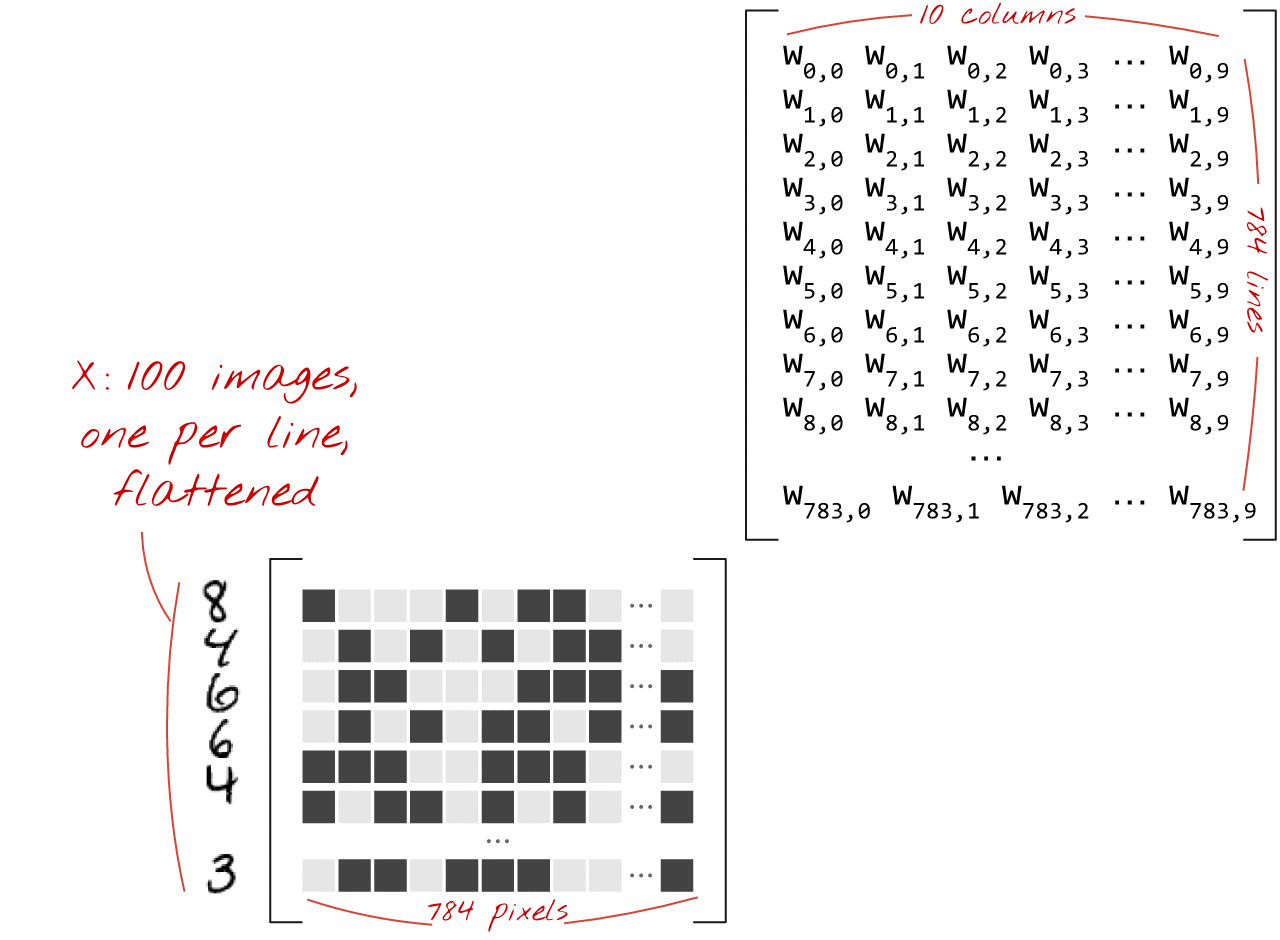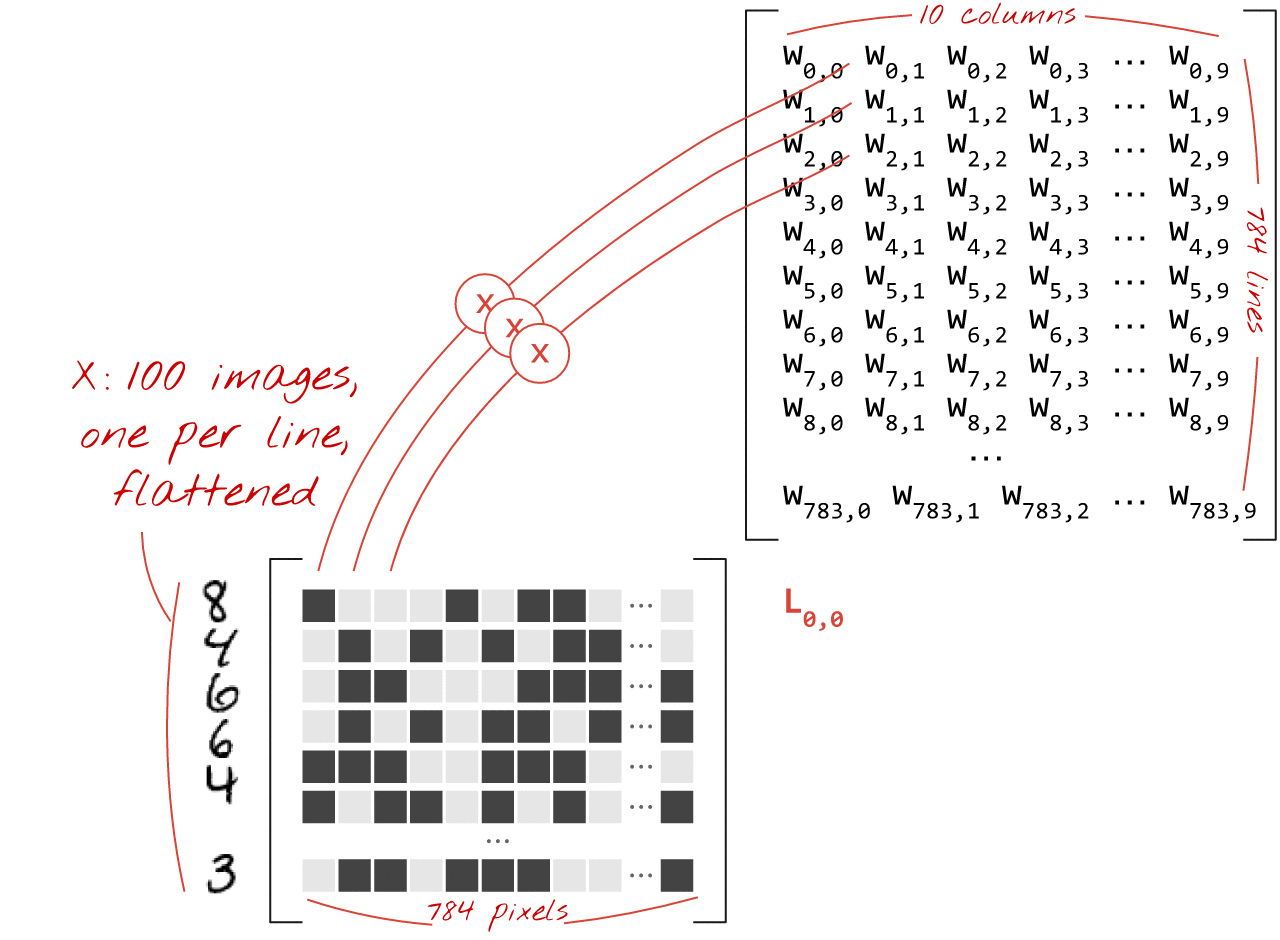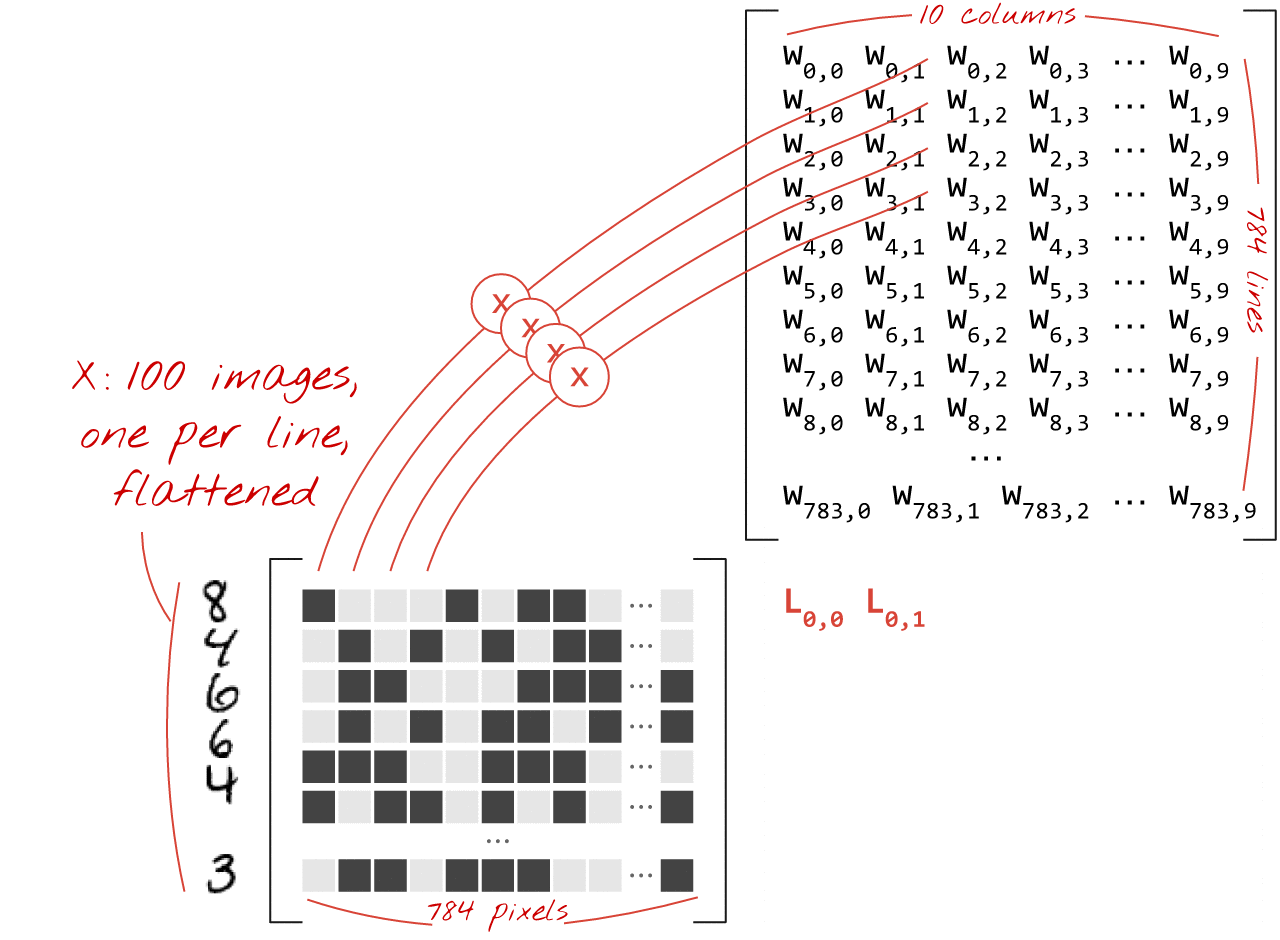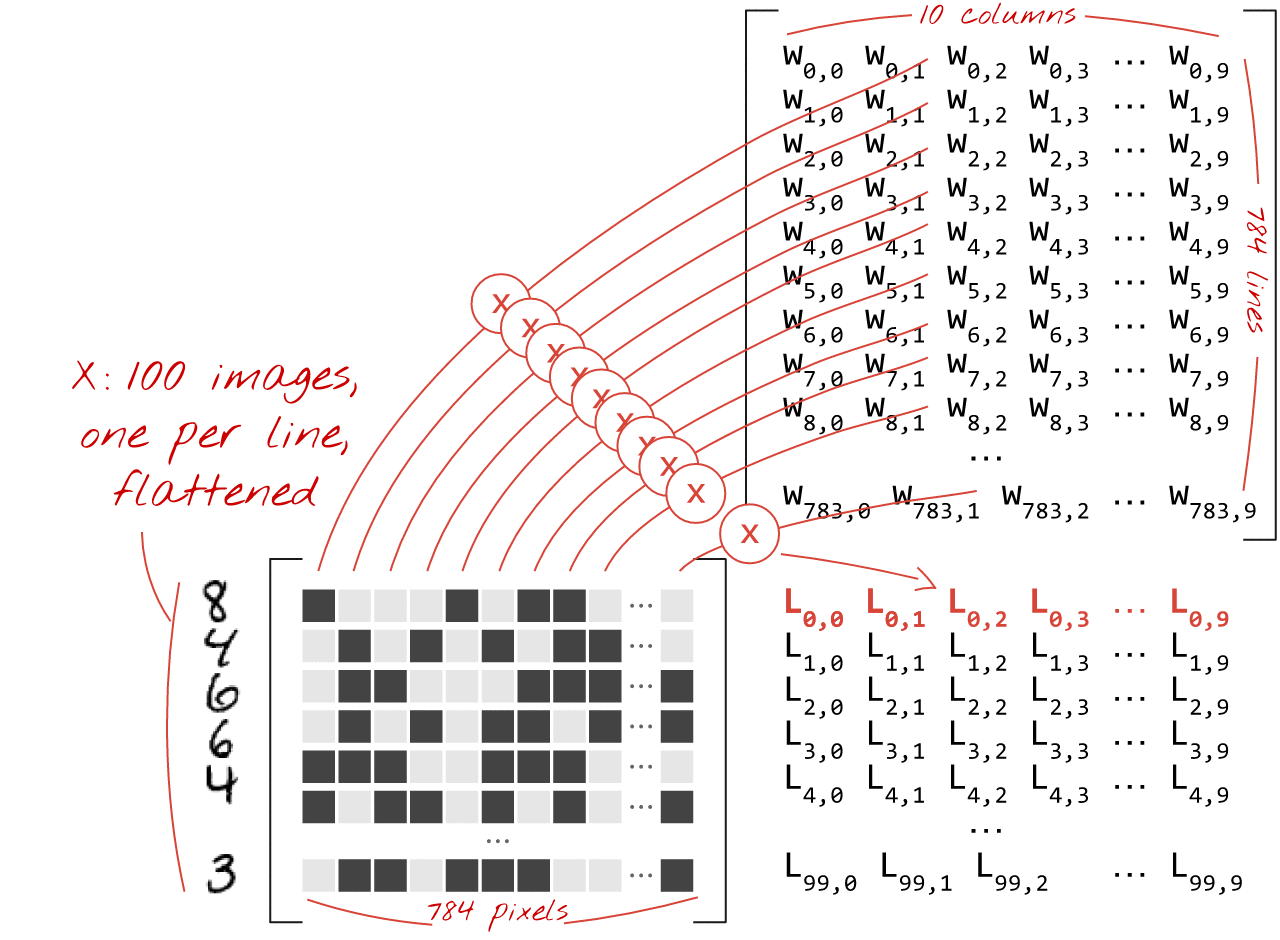
À l'aide de la première colonne de pondérations de la matrice de pondérations W, nous calculons la somme pondérée de tous les pixels de la première image. Cette somme correspond au premier neurone. En utilisant la deuxième colonne de pondérations, nous faisons de même pour le deuxième neurone, et ainsi de suite jusqu'au 10e neurone. Nous pouvons ensuite répéter l'opération pour les 99 images restantes. Si nous appelons X la matrice contenant nos 100 images, toutes les sommes pondérées pour nos 10 neurones, calculées sur 100 images, sont simplement X.W, une multiplication matricielle.

Chaque neurone doit maintenant ajouter son biais (une constante). Comme nous avons 10 neurones, nous avons 10 constantes de biais. Nous appellerons ce vecteur de 10 valeurs "b". Il doit être ajouté à chaque ligne de la matrice calculée précédemment. En utilisant une technique appelée "broadcasting", nous allons écrire cela avec un simple signe plus.

La diffusion est une astuce standard utilisée dans Python et numpy, sa bibliothèque de calcul scientifique. Elle étend le fonctionnement normal des opérations sur les matrices dont les dimensions sont incompatibles. "Diffusion d'une addition" signifie "si vous ajoutez deux matrices, mais que vous ne pouvez pas le faire, car leurs dimensions ne sont pas compatibles, essayez de répliquer la plus petite autant que nécessaire pour que cela fonctionne".

Enfin, nous appliquons une fonction d'activation, par exemple "softmax" (expliquée ci-dessous), et obtenons la formule décrivant un réseau de neurones à une couche, appliquée à 100 images :

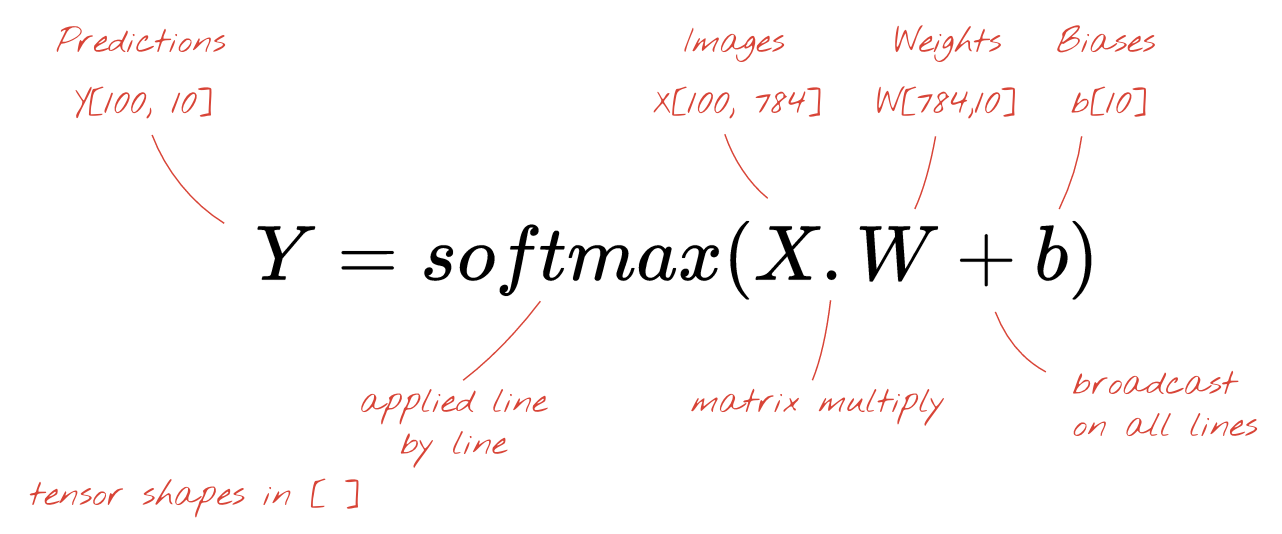
Dans Keras

Avec les bibliothèques de réseaux de neurones de haut niveau comme Keras, nous n'aurons pas besoin d'implémenter cette formule. Toutefois, il est important de comprendre qu'une couche de réseau de neurones n'est qu'un ensemble de multiplications et d'additions. Dans Keras, une couche dense s'écrirait comme suit :

tf.keras.layers.Dense(10, activation='softmax')

Aller plus loin

Il est trivial d'enchaîner les couches de réseaux de neurones. La première couche calcule les sommes pondérées des pixels. Les couches suivantes calculent les sommes pondérées des sorties des couches précédentes.

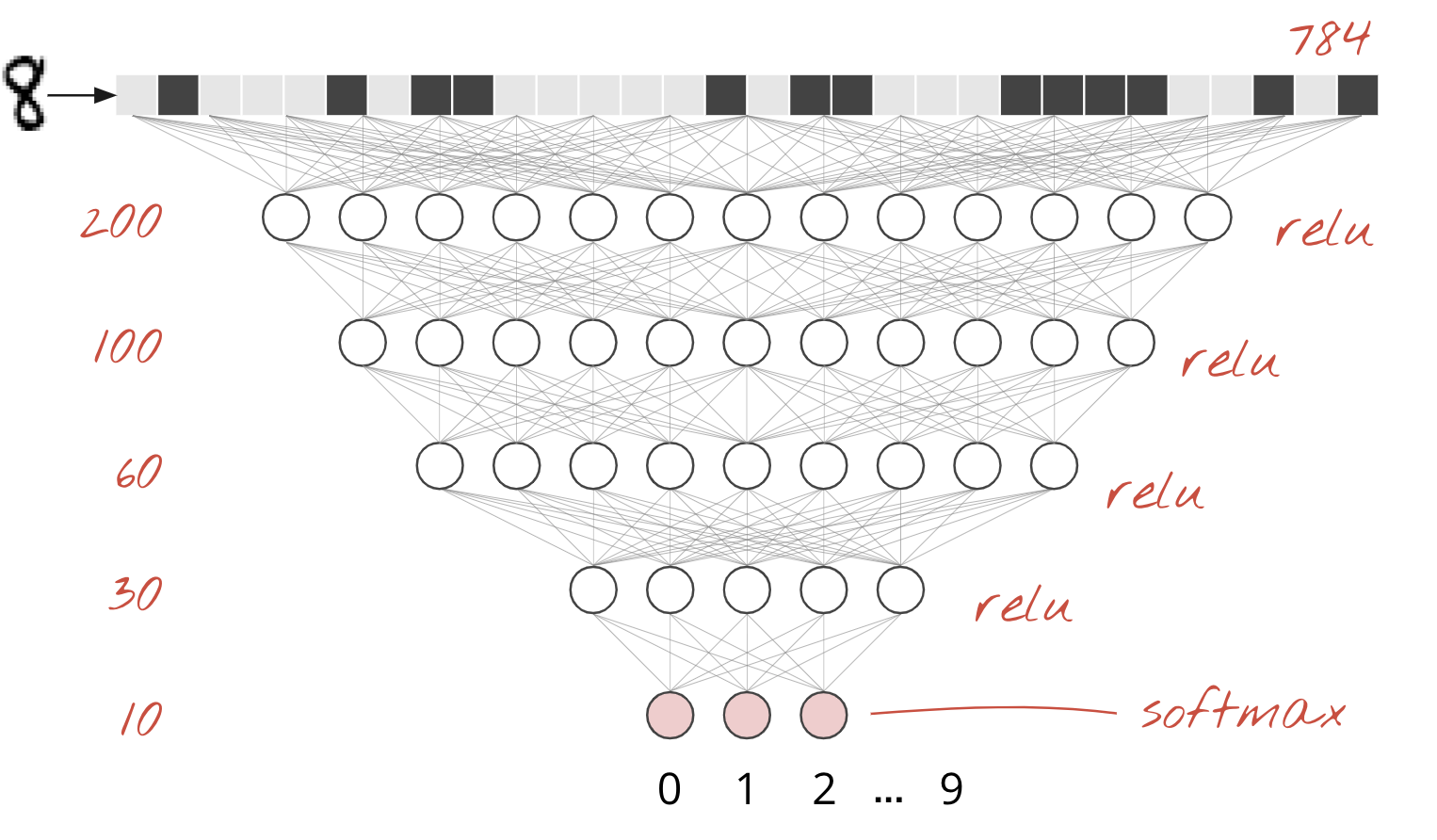
La seule différence, en dehors du nombre de neurones, sera le choix de la fonction d'activation.

Fonctions d'activation : ReLU, softmax et sigmoïde

Vous devez généralement utiliser la fonction d'activation "relu" pour toutes les couches, sauf la dernière. La dernière couche d'un classificateur utiliserait l'activation "softmax".

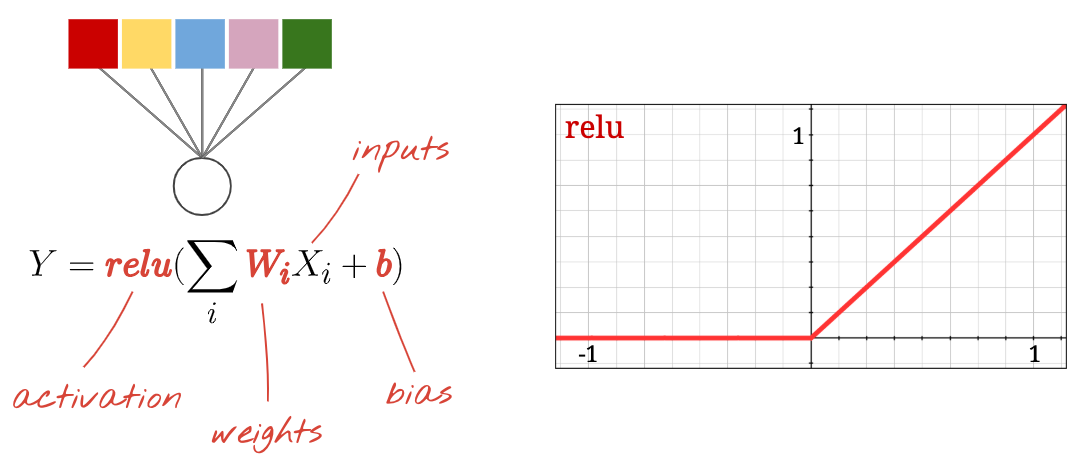
Là encore, un "neurone" calcule une somme pondérée de toutes ses entrées, ajoute une valeur appelée "biais" et transmet le résultat à la fonction d'activation.

La fonction d'activation la plus populaire est appelée RELU (Rectified Linear Unit). Comme vous pouvez le voir sur le graphique ci-dessus, il s'agit d'une fonction très simple.

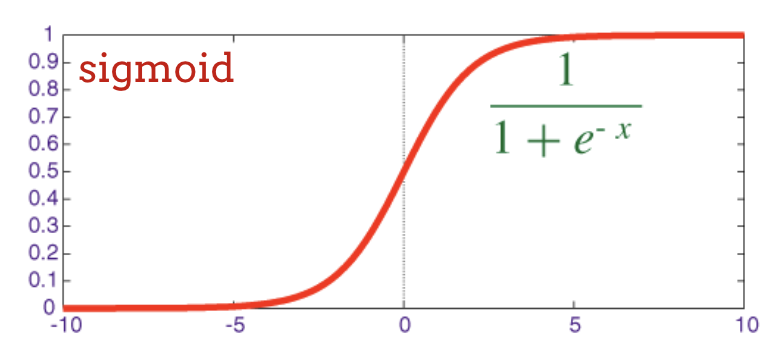
La fonction d'activation traditionnelle dans les réseaux neuronaux était la sigmoïde, mais la fonction"relu " s'est avérée avoir de meilleures propriétés de convergence presque partout et est désormais privilégiée.

Activation Softmax pour la classification

La dernière couche de notre réseau neuronal comporte 10 neurones, car nous voulons classer les chiffres manuscrits dans 10 classes (0 à 9). Il doit générer 10 nombres compris entre 0 et 1, représentant la probabilité que ce chiffre soit un 0, un 1, un 2, etc. Pour ce faire, nous utiliserons une fonction d'activation appelée softmax sur la dernière couche.

Pour appliquer la fonction softmax à un vecteur, il faut prendre l'exponentielle de chaque élément, puis normaliser le vecteur, généralement en le divisant par sa norme "L1" (c'est-à-dire la somme des valeurs absolues) afin que les valeurs normalisées totalisent 1 et puissent être interprétées comme des probabilités.

La sortie de la dernière couche, avant l'activation, est parfois appelée logits. Si ce vecteur est L = [L0, L1, L2, L3, L4, L5, L6, L7, L8, L9], alors :

Pourquoi la fonction softmax est-elle appelée ainsi ? L'exponentielle est une fonction à croissance rapide. Elle augmentera les différences entre les sorties des neurones. Ensuite, lorsque vous normalisez le vecteur, l'élément le plus grand, qui domine la norme, est normalisé à une valeur proche de 1, tandis que tous les autres éléments sont divisés par une grande valeur et normalisés à une valeur proche de 0. Le vecteur obtenu indique clairement la classe gagnante (le "max"), mais conserve l'ordre relatif initial de ses valeurs (d'où le terme "soft").

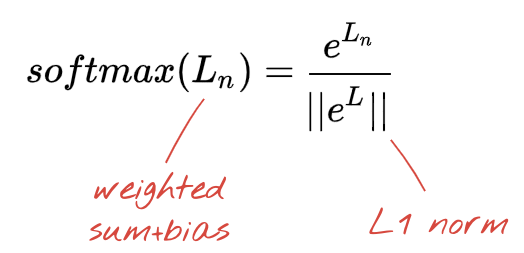
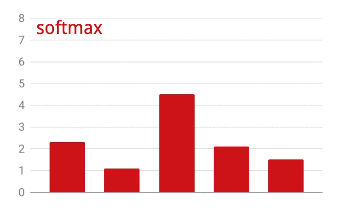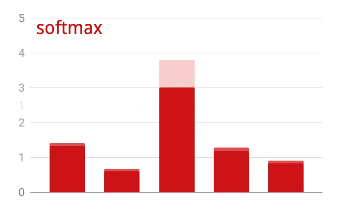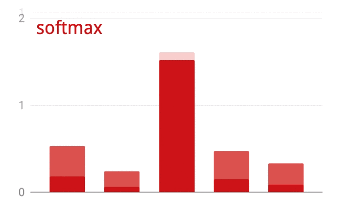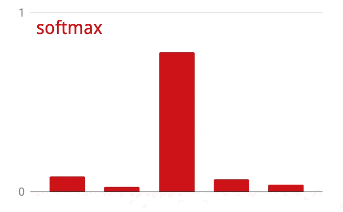
Perte d'entropie croisée

Maintenant que notre réseau de neurones produit des prédictions à partir d'images d'entrée, nous devons mesurer leur qualité, c'est-à-dire la distance entre ce que le réseau nous dit et les réponses correctes, souvent appelées "libellés". N'oubliez pas que nous disposons de libellés corrects pour toutes les images de l'ensemble de données.

N'importe quelle distance fonctionnerait, mais pour les problèmes de classification, la "distance d'entropie croisée" est la plus efficace. Nous appellerons cela notre fonction d'erreur ou de "perte" :

L'encodage one-hot signifie que vous représentez le libellé "il s'agit du chiffre 3" à l'aide d'un vecteur de 10 valeurs, toutes nulles sauf la troisième qui est égale à 1. Ce vecteur représente une probabilité de 100 % d'être le "chiffre 3". Notre réseau de neurones génère également ses prédictions sous la forme d'un vecteur de 10 valeurs de probabilité. Elles sont faciles à comparer.

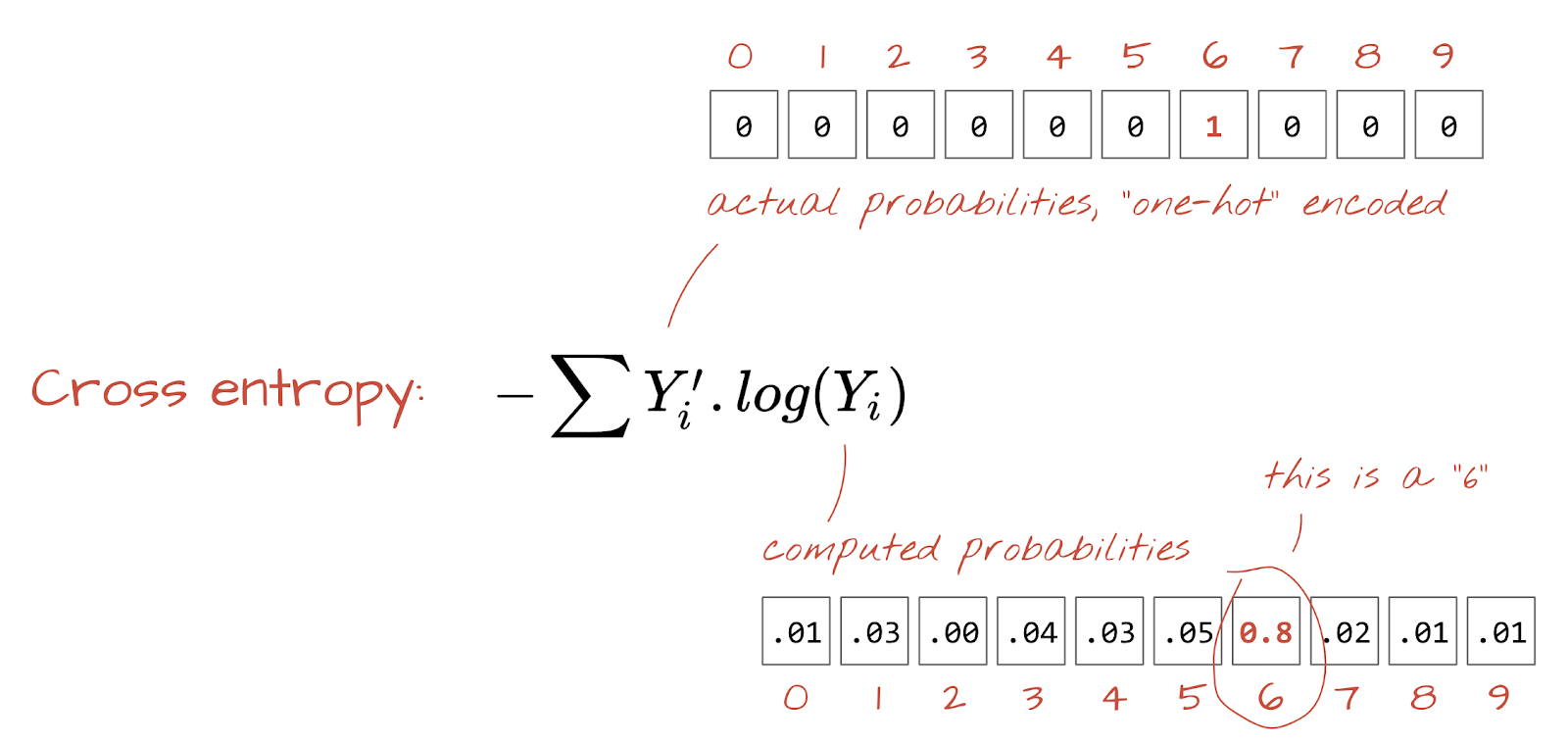
Descente de gradient

"Entraîner" le réseau de neurones signifie en fait utiliser des images et des libellés d'entraînement pour ajuster les pondérations et les biais afin de minimiser la fonction de perte d'entropie croisée. Voici comment cela fonctionne.

L'entropie croisée est une fonction des pondérations, des biais, des pixels de l'image d'entraînement et de sa classe connue.

Si nous calculons les dérivées partielles de l'entropie croisée par rapport à tous les poids et à tous les biais, nous obtenons un "gradient", calculé pour une image, un libellé et une valeur actuelle de poids et de biais donnés. N'oubliez pas que nous pouvons avoir des millions de pondérations et de biais. Le calcul du gradient semble donc être une tâche considérable. Heureusement, TensorFlow le fait pour nous. La propriété mathématique d'un gradient est qu'il pointe vers le haut. Comme nous voulons aller là où l'entropie croisée est faible, nous allons dans la direction opposée. Nous mettons à jour les pondérations et les biais par une fraction du gradient. Nous répétons ensuite la même chose encore et encore en utilisant les lots suivants d'images et d'étiquettes d'entraînement, dans une boucle d'entraînement. Nous espérons que cela converge vers un endroit où l'entropie croisée est minimale, bien que rien ne garantisse que ce minimum soit unique.

Taux d'apprentissage : vous ne pouvez pas mettre à jour vos pondérations et vos biais sur toute la longueur du gradient à chaque itération. C'est comme essayer d'atteindre le fond d'une vallée en portant des bottes de sept lieues. Vous passeriez d'un côté de la vallée à l'autre. Pour atteindre le bas, vous devez faire des pas plus petits, c'est-à-dire n'utiliser qu'une fraction du gradient, généralement de l'ordre de 1/1 000. Cette fraction est appelée "taux d'apprentissage".

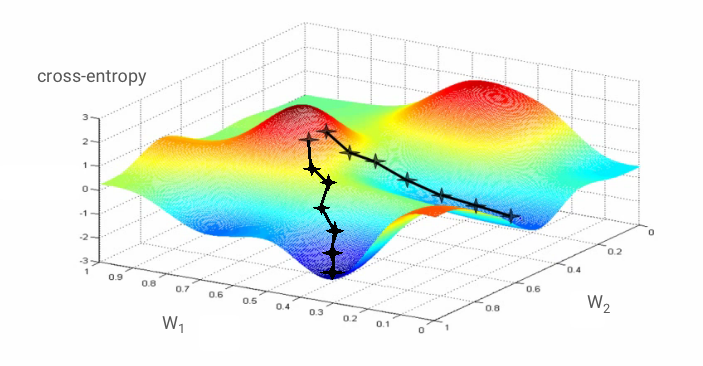
Mini-batching et momentum

Vous pouvez calculer votre gradient sur une seule image d'exemple et mettre à jour immédiatement les pondérations et les biais. Toutefois, si vous le faites sur un lot de, par exemple, 128 images, vous obtiendrez un gradient qui représente mieux les contraintes imposées par différentes images d'exemple et qui est donc susceptible de converger plus rapidement vers la solution. La taille du mini-lot est un paramètre ajustable.

Cette technique, parfois appelée "descente de gradient stochastique", présente un autre avantage plus pragmatique : travailler avec des lots signifie également travailler avec des matrices plus grandes, qui sont généralement plus faciles à optimiser sur les GPU et les TPU.

La convergence peut toutefois rester un peu chaotique et peut même s'arrêter si le vecteur de gradient est entièrement nul. Cela signifie-t-il que nous avons trouvé un minimum ? Non. Un composant de dégradé peut être nul à un minimum ou à un maximum. Avec un vecteur de gradient comportant des millions d'éléments, si tous sont nuls, la probabilité que chaque zéro corresponde à un minimum et qu'aucun ne corresponde à un point maximal est assez faible. Dans un espace à plusieurs dimensions, les points de selle sont assez courants et nous ne voulons pas nous y arrêter.

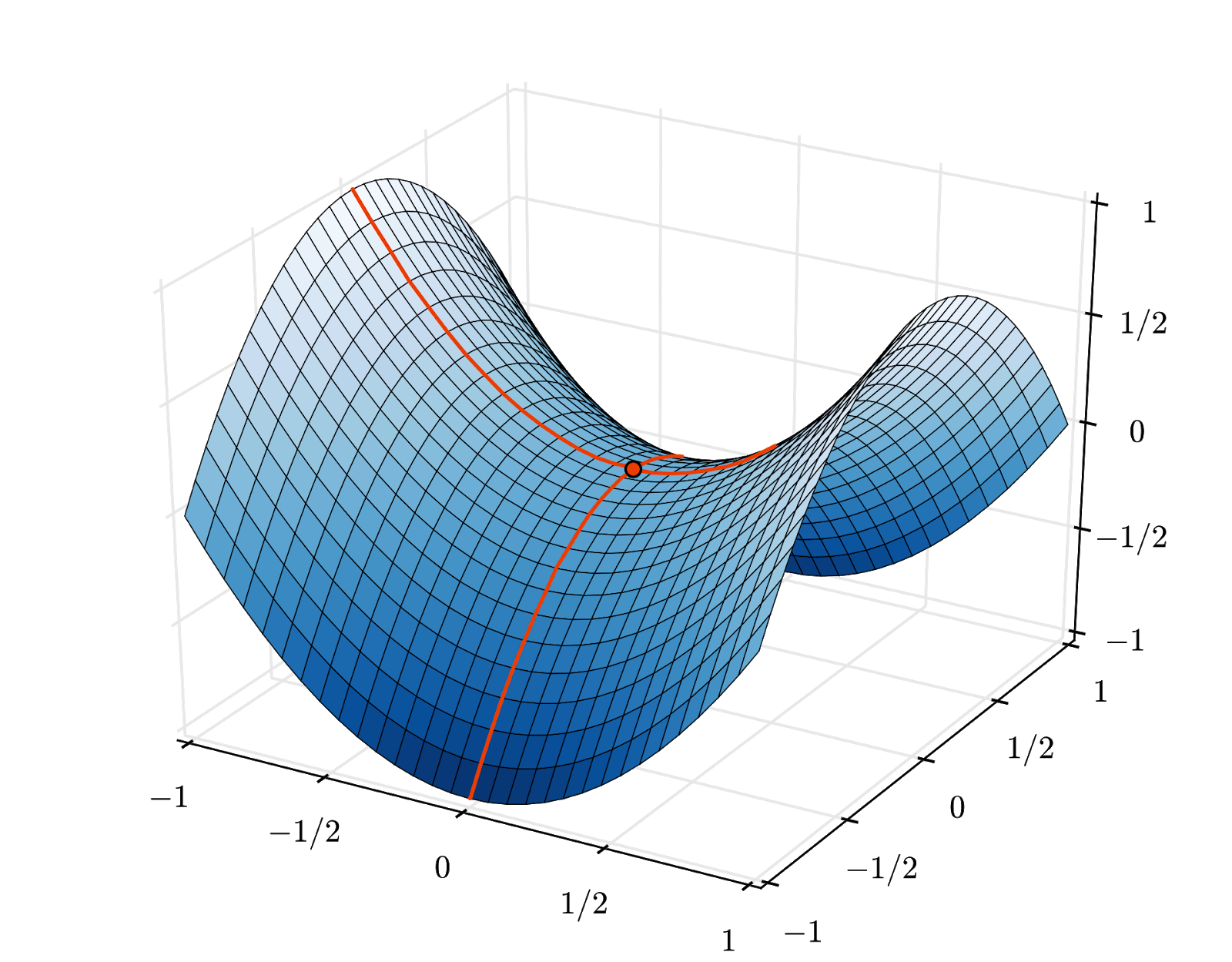
Illustration : un point-selle. Le gradient est de 0, mais il ne s'agit pas d'un minimum dans toutes les directions. (Attribution de l'image : Wikimedia : par Nicoguaro – Own work, CC BY 3.0)

La solution consiste à ajouter de l'élan à l'algorithme d'optimisation afin qu'il puisse dépasser les points-selles sans s'arrêter.

La bibliothèque TensorFlow propose toute une gamme d'optimiseurs, à commencer par tf.train.GradientDescentOptimizer. tf.train.RMSPropOptimizer et tf.train.AdamOptimizer sont des optimiseurs populaires plus avancés qui intègrent un élan.

Glossaire

Lot ou mini-lot : l'entraînement est toujours effectué sur des lots de données et d'étiquettes d'entraînement. Cela permet à l'algorithme de converger. La dimension "batch" est généralement la première dimension des Tensors de données. Par exemple, un Tensor de forme [100, 192, 192, 3] contient 100 images de 192 x 192 pixels avec trois valeurs par pixel (RVB).

Perte d'entropie croisée : fonction de perte spéciale souvent utilisée dans les classificateurs.

Couche dense : couche de neurones où chaque neurone est connecté à tous les neurones de la couche précédente.

Caractéristiques : les entrées d'un réseau de neurones sont parfois appelées "caractéristiques". L'art de déterminer quelles parties d'un ensemble de données (ou combinaisons de parties) transmettre à un réseau de neurones pour obtenir de bonnes prédictions s'appelle l'ingénierie des caractéristiques.

Libellés : autre nom pour les "classes" ou les réponses correctes dans un problème de classification supervisée

Taux d'apprentissage : fraction du gradient par laquelle les pondérations et les biais sont mis à jour à chaque itération de la boucle d'entraînement.

logits : les sorties d'une couche de neurones avant l'application de la fonction d'activation sont appelées "logits". Le terme provient de la "fonction logistique", également appelée "fonction sigmoïde", qui était la fonction d'activation la plus populaire. "Sorties de neurones avant la fonction logistique" a été raccourci en "logits".

loss : fonction d'erreur comparant les sorties du réseau de neurones aux bonnes réponses

Neurone : calcule la somme pondérée de ses entrées, ajoute un biais et transmet le résultat via une fonction d'activation.

Encodage one-hot : la classe 3 sur 5 est encodée sous forme de vecteur de cinq éléments, tous nuls sauf le troisième qui est égal à 1.

relu : unité de rectification linéaire. Fonction d'activation populaire pour les neurones.

sigmoid : autre fonction d'activation qui était populaire et qui est toujours utile dans des cas particuliers.

softmax : fonction d'activation spéciale qui agit sur un vecteur, augmente la différence entre le plus grand composant et tous les autres, et normalise également le vecteur pour que la somme soit égale à 1, afin qu'il puisse être interprété comme un vecteur de probabilités. Utilisé comme dernière étape dans les classificateurs.

Tenseur : un tenseur est semblable à une matrice, mais avec un nombre arbitraire de dimensions. Un Tensor unidimensionnel est un vecteur. Un Tensor à deux dimensions est une matrice. Vous pouvez ensuite avoir des Tensors avec 3, 4, 5 ou plus de dimensions.

Revenons au notebook d'étude et lisons le code cette fois-ci.

keras_01_mnist.ipynb

ATELIER PRATIQUE :

Dans cette section, votre tâche consiste à lire le code et à le comprendre afin de pouvoir l'améliorer ultérieurement.

Passons en revue toutes les cellules de ce notebook.

Cellule "Paramètres"

La taille du lot, le nombre d'époques d'entraînement et l'emplacement des fichiers de données sont définis ici. Les fichiers de données sont hébergés dans un bucket Google Cloud Storage (GCS), c'est pourquoi leur adresse commence par gs://.

Cellule "Importations"

Toutes les bibliothèques Python nécessaires sont importées ici, y compris TensorFlow et matplotlib pour les visualisations.

Cellule "utilitaires de visualisation [EXÉCUTER MOI]"

Cette cellule contient du code de visualisation sans intérêt. Il est réduit par défaut, mais vous pouvez l'ouvrir et examiner le code quand vous avez le temps en double-cliquant dessus.

Vous devez exécuter cette cellule (MAJ+ENTRÉE). Sinon, les fonctions définies à l'intérieur ne seront pas analysées et vous obtiendrez des erreurs par la suite.

Cellule tf.data.Dataset : analyser les fichiers et préparer les ensembles de données d'entraînement et de validation

Cette cellule a utilisé l'API tf.data.Dataset pour charger l'ensemble de données MNIST à partir des fichiers de données. Il n'est pas nécessaire de passer trop de temps sur cette cellule. Si l'API tf.data.Dataset vous intéresse, voici un tutoriel qui l'explique : Pipelines de données à la vitesse des TPU. Pour l'instant, voici les bases :

Les images et les libellés (réponses correctes) de l'ensemble de données MNIST sont stockés dans des enregistrements de longueur fixe dans quatre fichiers. Les fichiers peuvent être chargés avec la fonction d'enregistrement fixe dédiée :

imagedataset = tf.data.FixedLengthRecordDataset(image_filename, 28*28, header_bytes=16)

Nous disposons désormais d'un ensemble de données d'octets d'image. Elles doivent être décodées en images. Nous définissons une fonction pour ce faire. L'image n'étant pas compressée, la fonction n'a pas besoin de décoder quoi que ce soit (decode_raw ne fait pratiquement rien). L'image est ensuite convertie en valeurs à virgule flottante comprises entre 0 et 1. Nous pourrions le remodeler ici en tant qu'image 2D, mais nous le conservons en fait sous la forme d'un tableau plat de pixels de taille 28*28, car c'est ce que notre couche dense initiale attend.

def read_image(tf_bytestring):
    image = tf.decode_raw(tf_bytestring, tf.uint8)
    image = tf.cast(image, tf.float32)/256.0
    image = tf.reshape(image, [28*28])
    return image

Nous appliquons cette fonction à l'ensemble de données à l'aide de .map et obtenons un ensemble de données d'images :

imagedataset = imagedataset.map(read_image, num_parallel_calls=16)

Nous effectuons le même type de lecture et de décodage pour les libellés, et nous .zip les images et les libellés ensemble :

dataset = tf.data.Dataset.zip((imagedataset, labelsdataset))

Nous disposons désormais d'un ensemble de données de paires (image, libellé). C'est ce qu'attend notre modèle. Nous ne sommes pas encore prêts à l'utiliser dans la fonction d'entraînement :

dataset = dataset.cache()
dataset = dataset.shuffle(5000, reshuffle_each_iteration=True)
dataset = dataset.repeat()
dataset = dataset.batch(batch_size)
dataset = dataset.prefetch(tf.data.experimental.AUTOTUNE)

L'API tf.data.Dataset dispose de toutes les fonctions utilitaires nécessaires à la préparation des ensembles de données :

.cache met en cache l'ensemble de données dans la RAM. Comme il s'agit d'un petit ensemble de données, cela fonctionnera. .shuffle le mélange avec un tampon de 5 000 éléments. Il est important que les données d'entraînement soient bien brassées. .repeat met l'ensemble de données en boucle. Nous l'entraînerons plusieurs fois (plusieurs époques). .batch regroupe plusieurs images et libellés dans un mini-batch. Enfin, .prefetch peut utiliser le CPU pour préparer le lot suivant pendant que le lot actuel est entraîné sur le GPU.

L'ensemble de données de validation est préparé de la même manière. Nous sommes maintenant prêts à définir un modèle et à l'entraîner à l'aide de cet ensemble de données.

Cellule "Modèle Keras"

Tous nos modèles seront des séquences de couches droites. Nous pouvons donc utiliser le style tf.keras.Sequential pour les créer. Au départ, il s'agit d'une seule couche dense. Il comporte 10 neurones, car nous classons les chiffres écrits à la main dans 10 classes. Il utilise l'activation "softmax" car il s'agit de la dernière couche d'un classificateur.

Un modèle Keras doit également connaître la forme de ses entrées. tf.keras.layers.Input peut être utilisé pour le définir. Ici, les vecteurs d'entrée sont des vecteurs plats de valeurs de pixels de longueur 28*28.

model = tf.keras.Sequential(
  [
    tf.keras.layers.Input(shape=(28*28,)),
    tf.keras.layers.Dense(10, activation='softmax')
  ])

model.compile(optimizer='sgd',
              loss='categorical_crossentropy',
              metrics=['accuracy'])

# print model layers
model.summary()

# utility callback that displays training curves
plot_training = PlotTraining(sample_rate=10, zoom=1)

La configuration du modèle s'effectue dans Keras à l'aide de la fonction model.compile. Ici, nous utilisons l'optimiseur de base 'sgd' (descente de gradient stochastique). Un modèle de classification nécessite une fonction de perte d'entropie croisée, appelée 'categorical_crossentropy' dans Keras. Enfin, nous demandons au modèle de calculer la métrique 'accuracy', qui correspond au pourcentage d'images correctement classées.

Keras propose l'utilitaire model.summary(), qui est très pratique pour afficher les détails du modèle que vous avez créé. Votre sympathique instructeur a ajouté l'utilitaire PlotTraining (défini dans la cellule "visualization utilities") qui affichera différentes courbes d'entraînement pendant l'entraînement.

Cellule "Entraîner et valider le modèle"

C'est là que l'entraînement a lieu, en appelant model.fit et en transmettant les ensembles de données d'entraînement et de validation. Par défaut, Keras exécute une série de validations à la fin de chaque époque.

model.fit(training_dataset, steps_per_epoch=steps_per_epoch, epochs=EPOCHS,
          validation_data=validation_dataset, validation_steps=1,
          callbacks=[plot_training])

Dans Keras, il est possible d'ajouter des comportements personnalisés pendant l'entraînement en utilisant des rappels. C'est ainsi que le graphique d'entraînement à mise à jour dynamique a été implémenté pour cet atelier.

Cellule "Visualiser les prédictions"

Une fois le modèle entraîné, nous pouvons obtenir des prédictions en appelant model.predict() :

probabilities = model.predict(font_digits, steps=1)
predicted_labels = np.argmax(probabilities, axis=1)

Ici, nous avons préparé un ensemble de chiffres imprimés à partir de polices locales, à titre de test. N'oubliez pas que le réseau de neurones renvoie un vecteur de 10 probabilités à partir de son "softmax" final. Pour obtenir le libellé, nous devons déterminer quelle probabilité est la plus élevée. np.argmax de la bibliothèque NumPy le fait.

Pour comprendre pourquoi le paramètre axis=1 est nécessaire, n'oubliez pas que nous avons traité un lot de 128 images. Le modèle renvoie donc 128 vecteurs de probabilités. La forme du Tensor de sortie est [128, 10]. Nous calculons l'argmax sur les 10 probabilités renvoyées pour chaque image, donc axis=1 (le premier axe étant 0).

Ce modèle simple reconnaît déjà 90 % des chiffres. Ce n'est pas mal, mais vous allez maintenant l'améliorer considérablement.

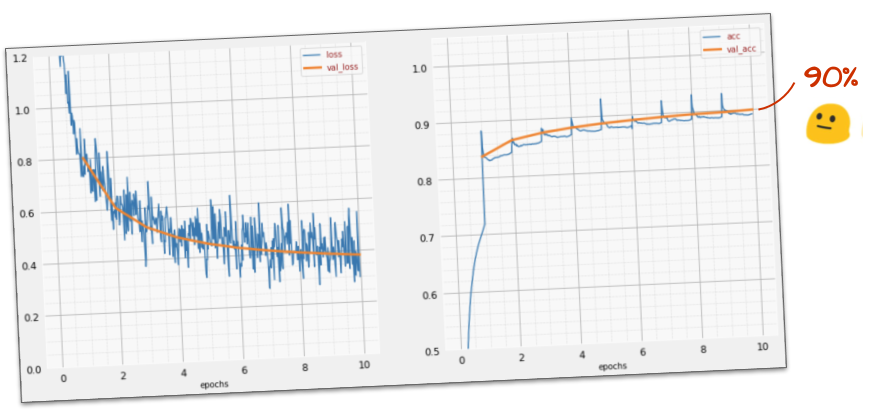
Pour améliorer la précision de la reconnaissance, nous allons ajouter des couches au réseau de neurones.

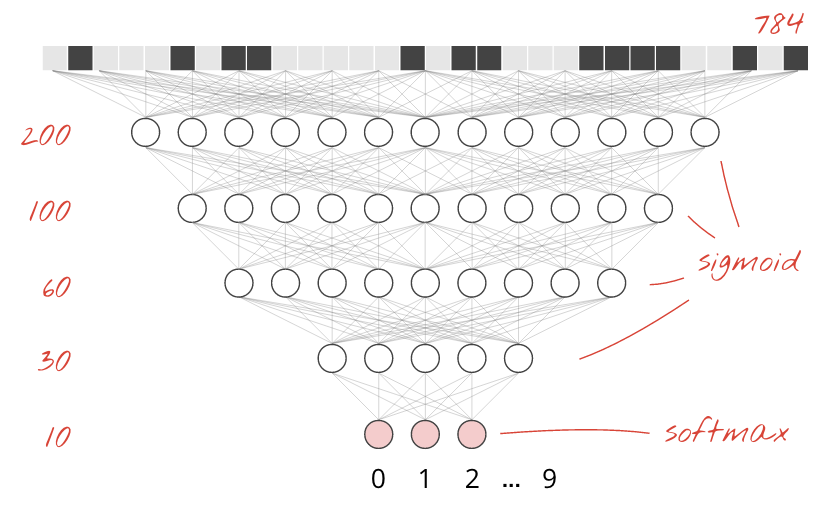
Nous conservons softmax comme fonction d'activation sur la dernière couche, car c'est ce qui fonctionne le mieux pour la classification. Cependant, nous utiliserons la fonction d'activation la plus classique sur les couches intermédiaires : la sigmoïde.

ATELIER PRATIQUE :

Veuillez ajouter quelques couches denses intermédiaires activées avec "sigmoid" avant votre couche "softmax". Le nombre de neurones peut être compris entre 784 (nombre de pixels d'entrée) et 10 (nombre de neurones de sortie). Réentraînez ensuite le modèle.

Avertissement : Pour réentraîner le modèle, vous devez réexécuter la cellule "Modèle Keras" pour définir un nouveau modèle, puis la cellule d'entraînement. Il vous suffit de réexécuter la cellule d'entraînement pour poursuivre l'entraînement de votre modèle précédent.

Par exemple, votre modèle peut ressembler à ceci (n'oubliez pas les virgules, car tf.keras.Sequential accepte une liste de calques séparés par des virgules) :

model = tf.keras.Sequential(
  [
      tf.keras.layers.Input(shape=(28*28,)),
      tf.keras.layers.Dense(200, activation='sigmoid'),
      tf.keras.layers.Dense(60, activation='sigmoid'),
      tf.keras.layers.Dense(10, activation='softmax')
  ])

Consultez le "récapitulatif" de votre modèle. Il comporte désormais au moins 10 fois plus de paramètres. Elle devrait être 10 fois meilleure ! Mais pour une raison inconnue, ce n'est pas le cas…

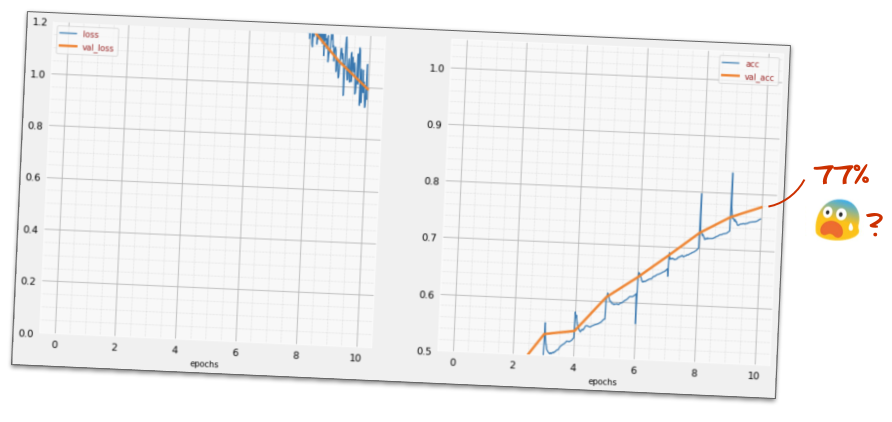
Les pertes semblent également avoir explosé. Un problème est survenu.

Vous venez de découvrir les réseaux de neurones tels qu'ils étaient conçus dans les années 1980 et 1990. Il n'est donc pas étonnant qu'ils aient abandonné l'idée, ce qui a marqué le début de ce que l'on appelle l'"hiver de l'IA". En effet, à mesure que vous ajoutez des couches, les réseaux neuronaux ont de plus en plus de mal à converger.

Il s'avère que les réseaux de neurones profonds comportant de nombreuses couches (20, 50, voire 100 aujourd'hui) peuvent très bien fonctionner, à condition d'utiliser quelques astuces mathématiques pour les faire converger. La découverte de ces astuces simples est l'une des raisons de la renaissance du deep learning dans les années 2010.

Activation RELU

La fonction d'activation sigmoïde est en fait assez problématique dans les réseaux profonds. Elle compresse toutes les valeurs entre 0 et 1. Si vous le faites de manière répétée, les sorties de neurones et leurs gradients peuvent disparaître complètement. Elle a été mentionnée pour des raisons historiques, mais les réseaux modernes utilisent la fonction RELU (Rectified Linear Unit), qui ressemble à ceci :

ATELIER PRATIQUE :

Remplacez tous les activation='sigmoid' par activation='relu' dans vos calques et entraînez de nouveau le modèle.

Pourquoi la sigmoïde est-elle problématique ? Regardez comment il se comporte sur les côtés : il s'aplatit.

Cela signifie que sa dérivée est proche de zéro. Rappelez-vous que l'entraînement progresse en suivant le gradient, qui est un vecteur de dérivées. Avec l'activation sigmoïde, en particulier s'il y a de nombreuses couches, le gradient peut devenir très petit et l'entraînement de plus en plus lent.

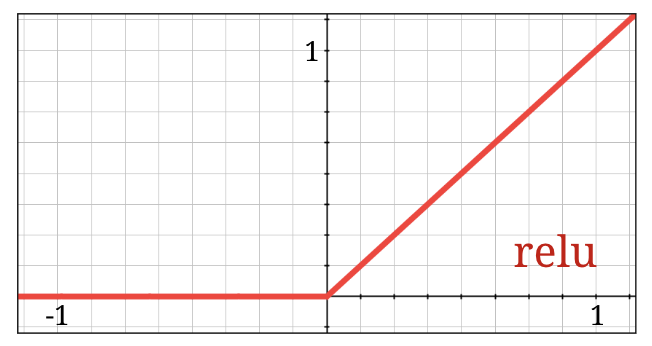
La relu, en revanche, a une dérivée de 1, au moins sur sa partie droite. Avec l'activation RELU, même si les gradients provenant de certains neurones peuvent être nuls, il y en aura toujours d'autres qui donneront un gradient non nul clair, ce qui permettra à l'entraînement de se poursuivre à un bon rythme.

Un meilleur outil d'optimisation

Dans les espaces de très grande dimension comme ici (nous avons de l'ordre de 10 000 poids et biais), les "points de selle" sont fréquents. Il s'agit de points qui ne sont pas des minima locaux, mais où le gradient est néanmoins nul et où l'optimiseur de descente de gradient reste bloqué. TensorFlow propose un éventail complet d'optimiseurs, dont certains fonctionnent avec une certaine inertie et dépassent les points de selle en toute sécurité.

ATELIER PRATIQUE :

Remplacez l'optimiseur 'sgd' par un meilleur, par exemple 'adam', puis entraînez de nouveau le modèle.

Initialisations aléatoires

L'art d'initialiser les biais de pondération avant l'entraînement est un domaine de recherche à part entière, avec de nombreux articles publiés sur le sujet. Vous pouvez consulter tous les initialiseurs disponibles dans Keras sur cette page. Heureusement, Keras fait ce qu'il faut par défaut et utilise l'initialiseur 'glorot_uniform', qui est le meilleur dans presque tous les cas.

Vous n'avez rien à faire, car Keras fait déjà ce qu'il faut.

NaN ???

La formule de l'entropie croisée implique un logarithme, et log(0) n'est pas un nombre (NaN, ou un plantage numérique si vous préférez). L'entrée de l'entropie croisée peut-elle être égale à 0 ? L'entrée provient de softmax, qui est essentiellement une exponentielle, et une exponentielle n'est jamais nulle. Nous sommes donc en sécurité !

Ah bon ? Dans le magnifique monde des mathématiques, nous serions en sécurité, mais dans le monde de l'informatique, exp(-150), représenté au format float32, est aussi proche de ZÉRO que possible et l'entropie croisée plante.

Heureusement, vous n'avez rien à faire ici non plus, car Keras s'en charge et calcule la softmax suivie de l'entropie croisée de manière particulièrement minutieuse pour assurer la stabilité numérique et éviter les redoutables NaN.

Opération réussie ?

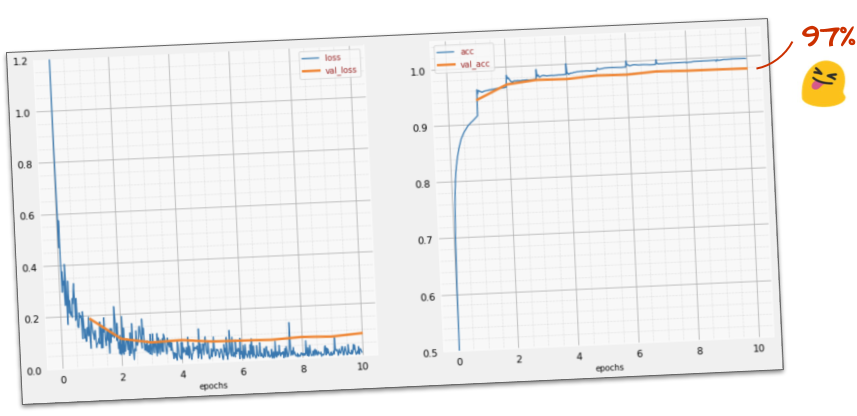
Vous devriez maintenant atteindre une précision de 97 %. L'objectif de cet atelier est de dépasser largement les 99 %, alors continuons.

Si vous êtes bloqué, voici la solution à ce stade :

keras_02_mnist_dense.ipynb

Peut-être pouvons-nous essayer d'entraîner le modèle plus rapidement ? Le taux d'apprentissage par défaut de l'optimiseur Adam est de 0,001. Essayons de l'augmenter.

ATELIER PRATIQUE :

Augmentez le taux d'apprentissage de sa valeur par défaut (0,001) à 0,01. Pour ce faire, vous devrez remplacer l'optimiseur prédéfini 'adam' par une instance réelle d'un optimiseur Adam afin d'avoir accès à ses paramètres de configuration :

optimizer=tf.keras.optimizers.Adam(lr=0.01)

Veuillez également augmenter le facteur de zoom à 5 dans PlotTraining. Cela zoome autour de 0 sur les pertes et autour de 1 sur les précisions pour vous aider à comprendre ce qui se passe : PlotTraining(sample_rate=10, zoom=5)

Accélérer ne semble pas aider beaucoup, et qu'est-ce que tout ce bruit ?

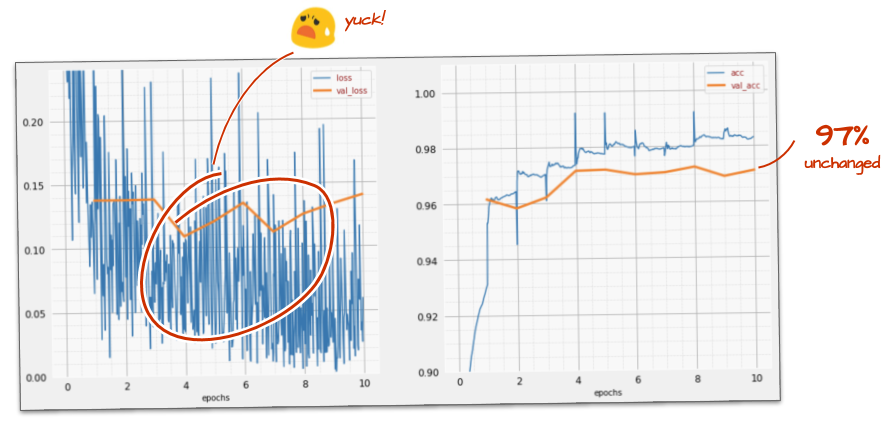
Les courbes d'entraînement sont très bruitées et les deux courbes de validation sont instables. Cela signifie que nous allons trop vite. Nous pourrions revenir à notre vitesse précédente, mais il existe une meilleure solution.

La bonne solution consiste à commencer rapidement et à réduire le taux d'apprentissage de manière exponentielle. Dans Keras, vous pouvez le faire avec le rappel tf.keras.callbacks.LearningRateScheduler.

ATELIER PRATIQUE :

Implémentez un programme de taux d'apprentissage qui diminue le taux d'apprentissage de manière exponentielle. Vous trouverez ci-dessous des extraits de code utiles.

Code utile à copier-coller :

# lr decay function
def lr_decay(epoch):
  return 0.01 * math.pow(0.6, epoch)

# lr schedule callback
lr_decay_callback = tf.keras.callbacks.LearningRateScheduler(lr_decay, verbose=True)

# important to see what you are doing
plot_learning_rate(lr_decay, EPOCHS)

N'oubliez pas d'utiliser le lr_decay_callback que vous avez créé. Ajoutez-le à la liste des rappels dans model.fit :

model.fit(...,  callbacks=[plot_training, lr_decay_callback])

L'impact de ce petit changement est spectaculaire. Vous constatez que la plupart du bruit a disparu et que la précision du test est désormais supérieure à 98 % de manière continue.

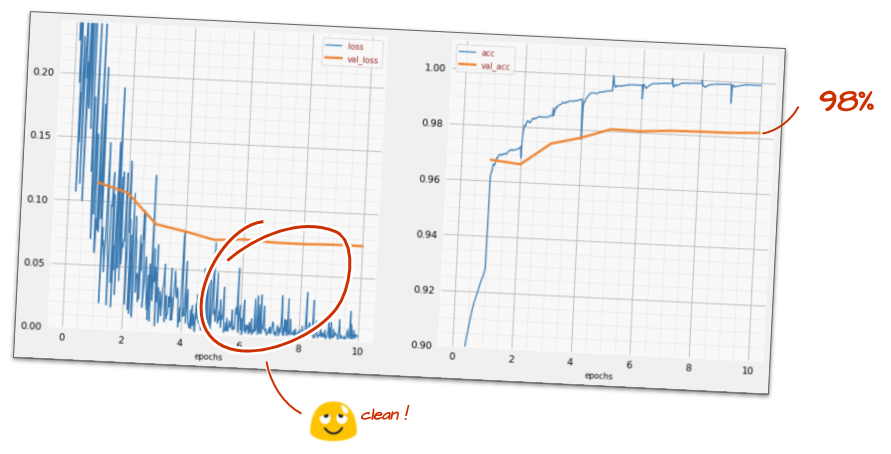
Le modèle semble maintenant converger correctement. Essayons d'aller encore plus loin.

ATELIER PRATIQUE :

Si vous ne l'avez pas encore fait, veuillez augmenter la profondeur du modèle à au moins quatre couches denses et l'entraîner à nouveau. Vous pouvez utiliser le nombre de neurones suivant dans les couches : 200, 100, 60, 10.

Veuillez également augmenter le facteur de zoom à 10 dans PlotTraining. Cela zoome autour de 0 sur les pertes et autour de 1 sur les précisions pour vous aider à comprendre ce qui se passe : PlotTraining(sample_rate=10, zoom=10)

Cela vous a-t-il aidé ?

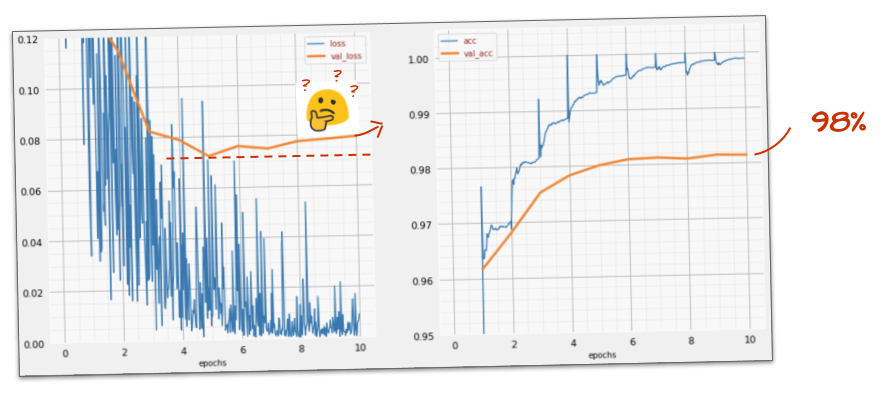
Pas vraiment, la précision est toujours bloquée à 98 % et la perte de validation est toujours élevée. Ça monte ! L'algorithme d'apprentissage ne fonctionne que sur les données d'entraînement et optimise la perte d'entraînement en conséquence. Il ne voit jamais de données de validation. Il n'est donc pas surprenant qu'au bout d'un certain temps, son travail n'ait plus d'effet sur la perte de validation, qui cesse de diminuer et remonte parfois.

Cela n'a pas d'incidence immédiate sur les capacités de reconnaissance du monde réel de votre modèle, mais cela vous empêchera d'exécuter de nombreuses itérations et indique généralement que l'entraînement n'a plus d'effet positif.

Cette déconnexion est généralement appelée "surapprentissage". Lorsque vous la constatez, vous pouvez essayer d'appliquer une technique de régularisation appelée "dropout". La technique de dropout consiste à désactiver des neurones aléatoires à chaque itération d'entraînement.

L'abandon est l'une des plus anciennes techniques de régularisation dans le deep learning. À chaque itération d'entraînement, il supprime des neurones aléatoires du réseau avec une probabilité p (généralement de 25 % à 50 %). En pratique, les sorties des neurones sont définies sur 0. Le résultat net est que ces neurones ne participeront pas au calcul de la perte cette fois-ci et que leurs pondérations ne seront pas mises à jour. Différents neurones seront supprimés à chaque itération d'entraînement.

Lorsque vous testez les performances de votre réseau, vous remettez bien sûr tous les neurones en place (taux d'abandon=0). Keras le fait automatiquement. Il vous suffit donc d'ajouter un calque tf.keras.layers.Dropout. Il aura automatiquement le bon comportement lors de l'entraînement et de l'évaluation.

Pourquoi ça marche ? La théorie est que les réseaux de neurones ont tellement de liberté entre leurs nombreuses couches qu'il est tout à fait possible qu'une couche développe un mauvais comportement et que la couche suivante le compense. Ce n'est pas une utilisation idéale des neurones. Avec l'abandon, il y a une forte probabilité que le neurone "corrigeant" le problème ne soit pas présent lors d'un cycle d'entraînement donné. Le comportement insatisfaisant de la couche incriminée devient évident et les pondérations évoluent vers un meilleur comportement.

ATELIER PRATIQUE :

Vous pouvez ajouter un dropout après chaque couche dense intermédiaire du réseau. N'ajoutez pas de dropout après votre couche softmax. Vous supprimeriez vos probabilités prédites. Vous pouvez ajouter un taux d'abandon de 25 % avec : tf.keras.layers.Dropout(0.25)

Cela a-t-il fonctionné ?

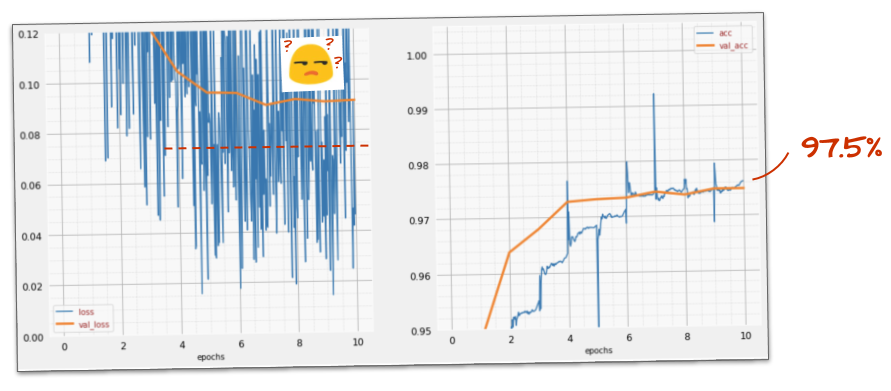
Le bruit réapparaît (ce qui n'est pas surprenant compte tenu du fonctionnement du dropout). La perte de validation ne semble plus augmenter, mais elle est globalement plus élevée qu'en l'absence de dropout. La précision de la validation a légèrement diminué. C'est un résultat assez décevant.

Il semble que le dropout n'était pas la bonne solution, ou peut-être que le "surapprentissage" est un concept plus complexe et que certaines de ses causes ne peuvent pas être résolues par un dropout.

Qu'est-ce que le "surapprentissage" ? Le surapprentissage se produit lorsqu'un réseau de neurones apprend "mal", c'est-à-dire d'une manière qui fonctionne pour les exemples d'entraînement, mais pas très bien pour les données réelles. Il existe des techniques de régularisation comme l'abandon qui peuvent l'obliger à apprendre de manière plus efficace, mais le surapprentissage a également des racines plus profondes.

Le surapprentissage de base se produit lorsqu'un réseau de neurones dispose d'un trop grand nombre de degrés de liberté pour le problème en question. Imaginez que nous ayons tellement de neurones que le réseau puisse stocker toutes nos images d'entraînement et les reconnaître par reconnaissance de formes. Il échouerait complètement sur des données réelles. Un réseau de neurones doit être quelque peu contraint afin d'être forcé à généraliser ce qu'il apprend pendant l'entraînement.

Si vous disposez de très peu de données d'entraînement, même un petit réseau peut les apprendre par cœur, et vous constaterez un "surapprentissage". En règle générale, vous avez toujours besoin de nombreuses données pour entraîner les réseaux de neurones.

Enfin, si vous avez tout fait dans les règles de l'art, expérimenté différentes tailles de réseau pour vous assurer que ses degrés de liberté sont limités, appliqué le dropout et entraîné sur de nombreuses données, vous pouvez toujours être bloqué à un niveau de performances que rien ne semble pouvoir améliorer. Cela signifie que votre réseau de neurones, dans sa forme actuelle, n'est pas en mesure d'extraire plus d'informations de vos données, comme dans notre cas ici.

Vous souvenez-vous de la façon dont nous utilisons nos images, aplaties en un seul vecteur ? C'était une très mauvaise idée. Les chiffres manuscrits sont composés de formes, et nous avons supprimé les informations sur les formes lorsque nous avons aplati les pixels. Toutefois, il existe un type de réseau de neurones qui peut tirer parti des informations sur la forme : les réseaux convolutifs. Essayons-les.

Si vous êtes bloqué, voici la solution à ce stade :

keras_03_mnist_dense_lrdecay_dropout.ipynb

En bref

Si vous connaissez déjà tous les termes en gras du paragraphe suivant, vous pouvez passer à l'exercice suivant. Si vous débutez avec les réseaux de neurones convolutifs, veuillez poursuivre votre lecture.

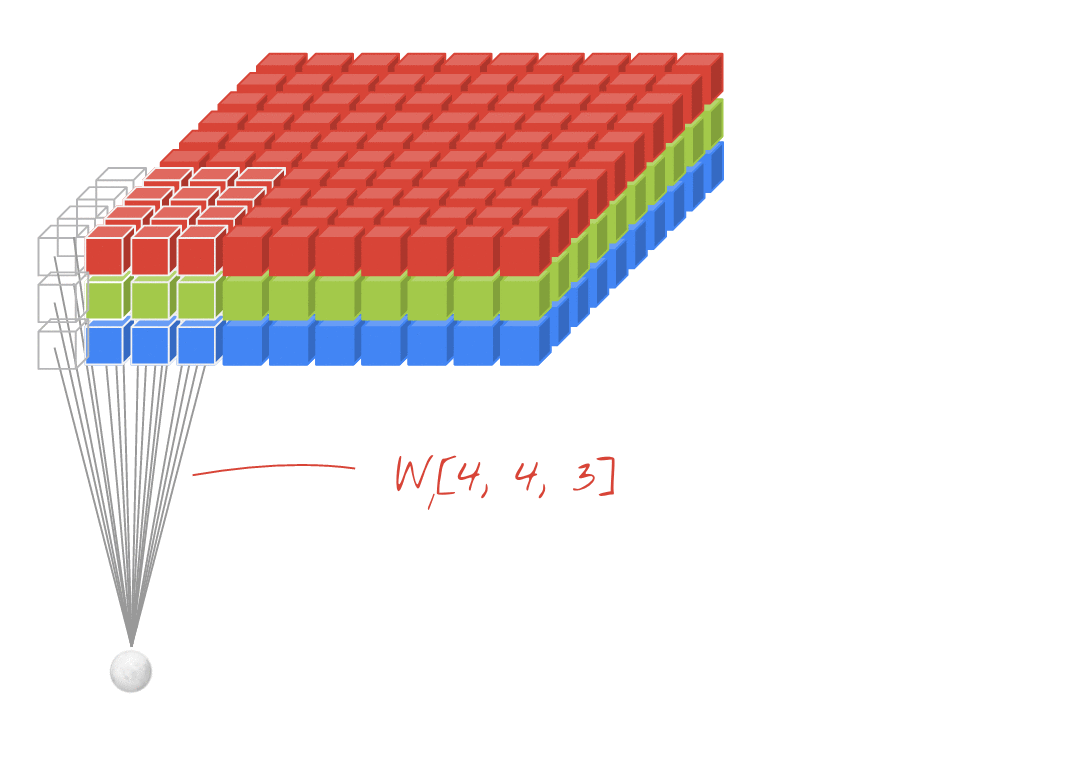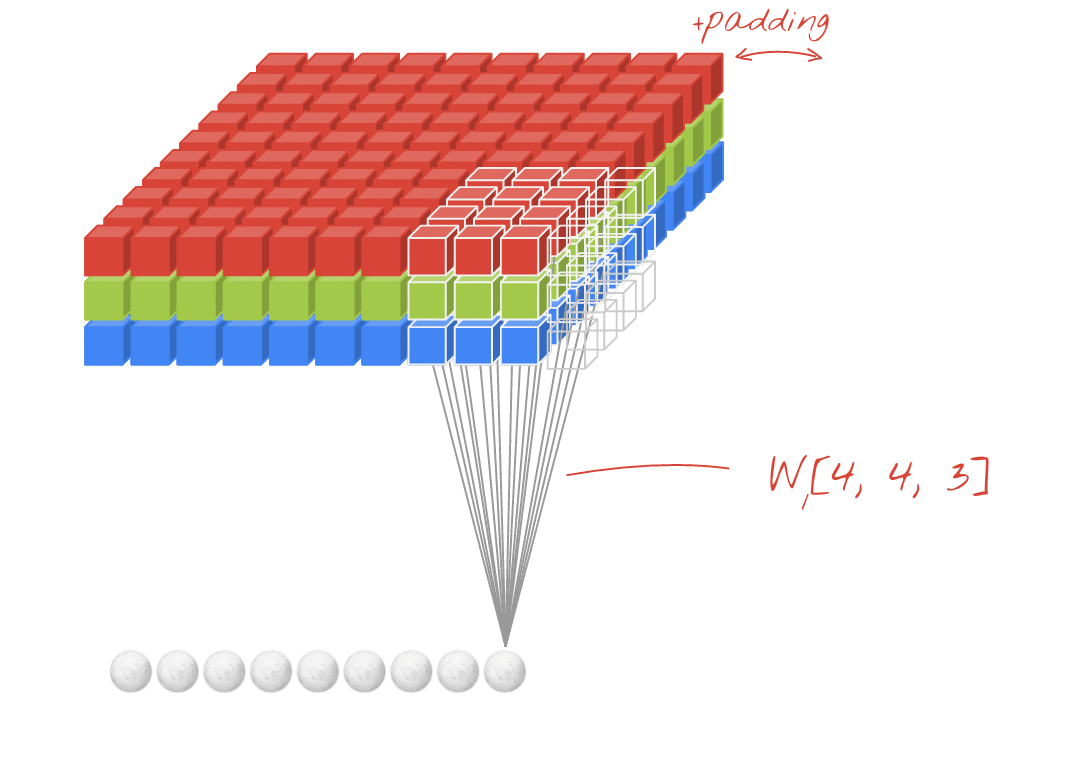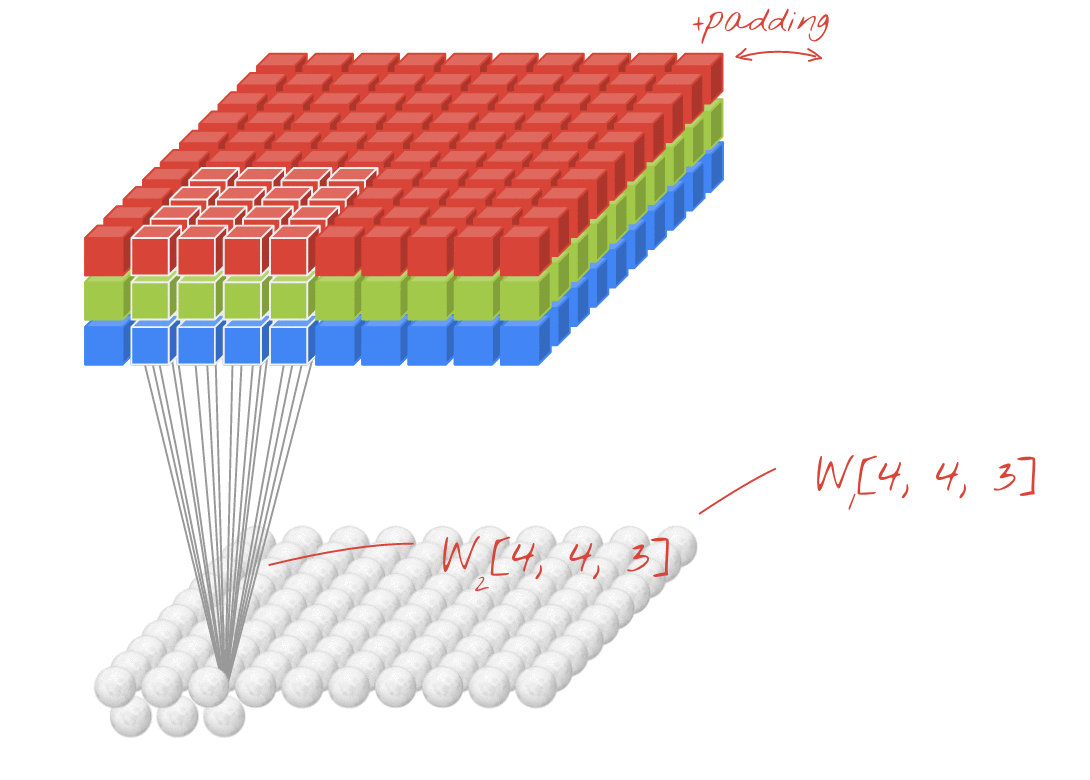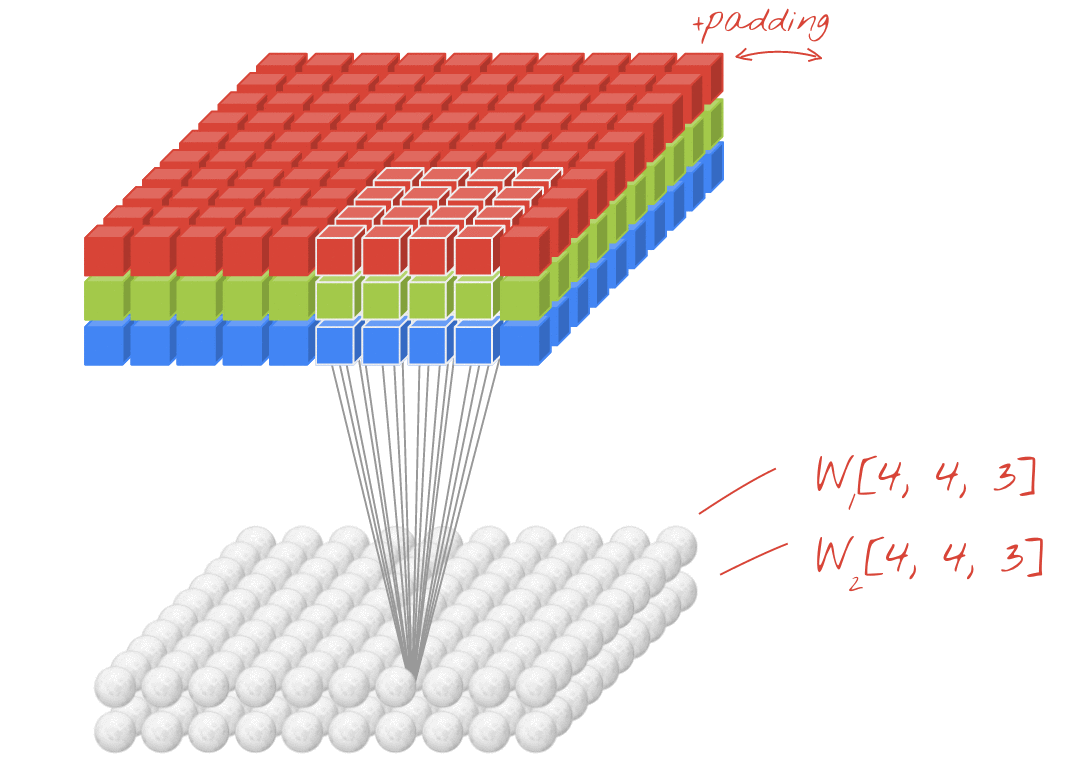
Illustration : filtrage d'une image avec deux filtres successifs composés chacun de 4 x 4 x 3=48 poids pouvant être appris.

Les réseaux de neurones convolutifs appliquent une série de filtres pouvant être appris à l'image d'entrée. Une couche de convolution est définie par la taille du filtre (ou du kernel), le nombre de filtres appliqués et le pas. L'entrée et la sortie d'une couche de convolution ont chacune trois dimensions (largeur, hauteur, nombre de canaux), en commençant par l'image d'entrée (largeur, hauteur, canaux RVB). Lorsque vous empilez des couches de convolution, vous pouvez ajuster la largeur et la hauteur de la sortie en utilisant un pas supérieur à 1 ou une opération de pooling maximal. La profondeur de la sortie (nombre de canaux) est ajustée en utilisant plus ou moins de filtres.

Voici à quoi ressemble un réseau de neurones convolutif simple dans Keras :

model = tf.keras.Sequential([
    tf.keras.layers.Reshape(input_shape=(28*28,), target_shape=(28, 28, 1)),
    tf.keras.layers.Conv2D(kernel_size=3, filters=12, activation='relu'),
    tf.keras.layers.Conv2D(kernel_size=6, filters=24, strides=2, activation='relu'),
    tf.keras.layers.Conv2D(kernel_size=6, filters=32, strides=2, activation='relu'),
    tf.keras.layers.Flatten(),
    tf.keras.layers.Dense(10, activation='softmax')
])

Dans une couche d'un réseau de convolution, un "neurone" effectue une somme pondérée des pixels situés juste au-dessus, sur une petite région de l'image uniquement. Il ajoute un biais et transmet la somme via une fonction d'activation, comme le ferait un neurone dans une couche dense classique. Cette opération est ensuite répétée sur l'ensemble de l'image en utilisant les mêmes pondérations. N'oubliez pas que dans les couches denses, chaque neurone avait ses propres pondérations. Ici, un seul "patch" de pondérations glisse sur l'image dans les deux sens (une "convolution"). La sortie comporte autant de valeurs que de pixels dans l'image (un remplissage est toutefois nécessaire sur les bords). Il s'agit d'une opération de filtrage. Dans l'illustration ci-dessus, il utilise un filtre de 4 x 4 x 3=48 poids.

Toutefois, 48 pondérations ne suffiront pas. Pour ajouter des degrés de liberté, nous répétons la même opération avec un nouvel ensemble de pondérations. Un nouvel ensemble de résultats de filtrage est alors généré. Appelons-le "canal" de sorties par analogie avec les canaux R, G et B de l'image d'entrée.

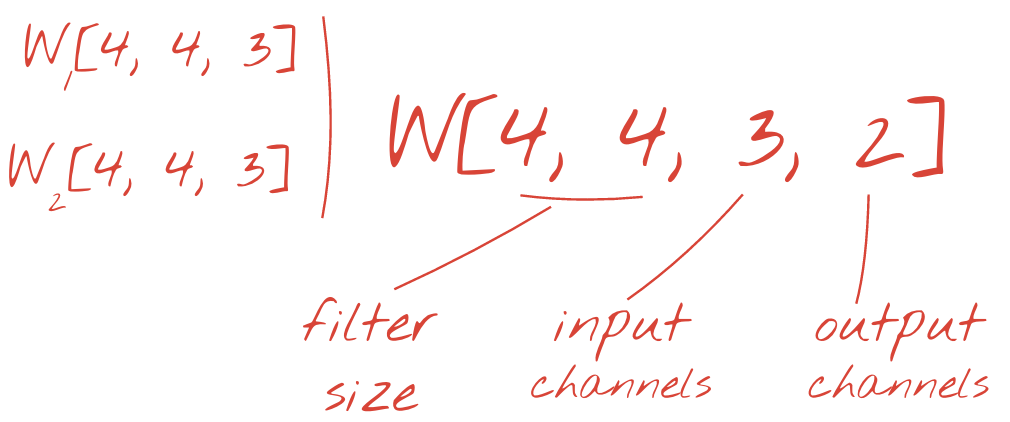
Les deux ensembles de pondérations (ou plus) peuvent être résumés en un seul Tensor en ajoutant une dimension. Cela nous donne la forme générique du Tensor de poids pour une couche de convolution. Étant donné que le nombre de canaux d'entrée et de sortie sont des paramètres, nous pouvons commencer à empiler et à enchaîner des couches de convolution.

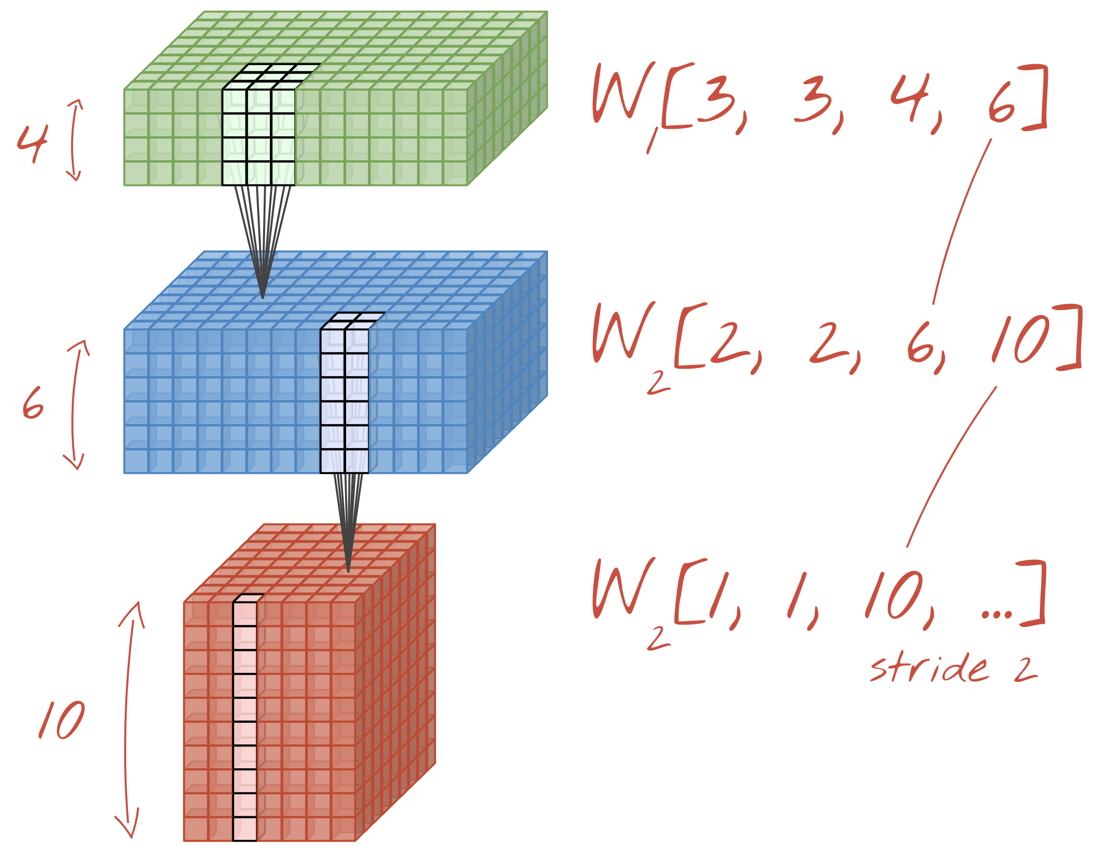
Illustration : un réseau de neurones convolutif transforme des "cubes" de données en d'autres "cubes" de données.

Convolutions avec stride, pooling maximal

En effectuant les convolutions avec un pas de 2 ou 3, nous pouvons également réduire le cube de données résultant dans ses dimensions horizontales. Pour ce faire, deux méthodes courantes s'offrent à vous :

• Convolution à pas : filtre coulissant comme ci-dessus, mais avec un pas > 1
• Pooling maximal : fenêtre glissante appliquant l'opération MAX (généralement sur des blocs 2x2, répétés tous les deux pixels)

Illustration : si vous faites glisser la fenêtre de calcul de trois pixels, vous obtiendrez moins de valeurs de sortie. Les convolutions à pas ou le pooling maximal (max sur une fenêtre 2x2 glissant par un pas de 2) permettent de réduire le cube de données dans les dimensions horizontales.

Le pooling maximal peut nous aider à comprendre intuitivement le fonctionnement des réseaux convolutionnels : si vous supposez que, pendant l'entraînement, les groupes de pondérations évoluent en filtres qui reconnaissent les formes de base (lignes horizontales et verticales, courbes, etc.), une façon de réduire les informations utiles consiste à conserver, tout au long des couches, les sorties où une forme a été reconnue avec l'intensité maximale. En pratique, dans une couche de mise en commun maximale, les sorties des neurones sont traitées par groupes de 2x2 et seule la valeur maximale est conservée.

Dernière couche

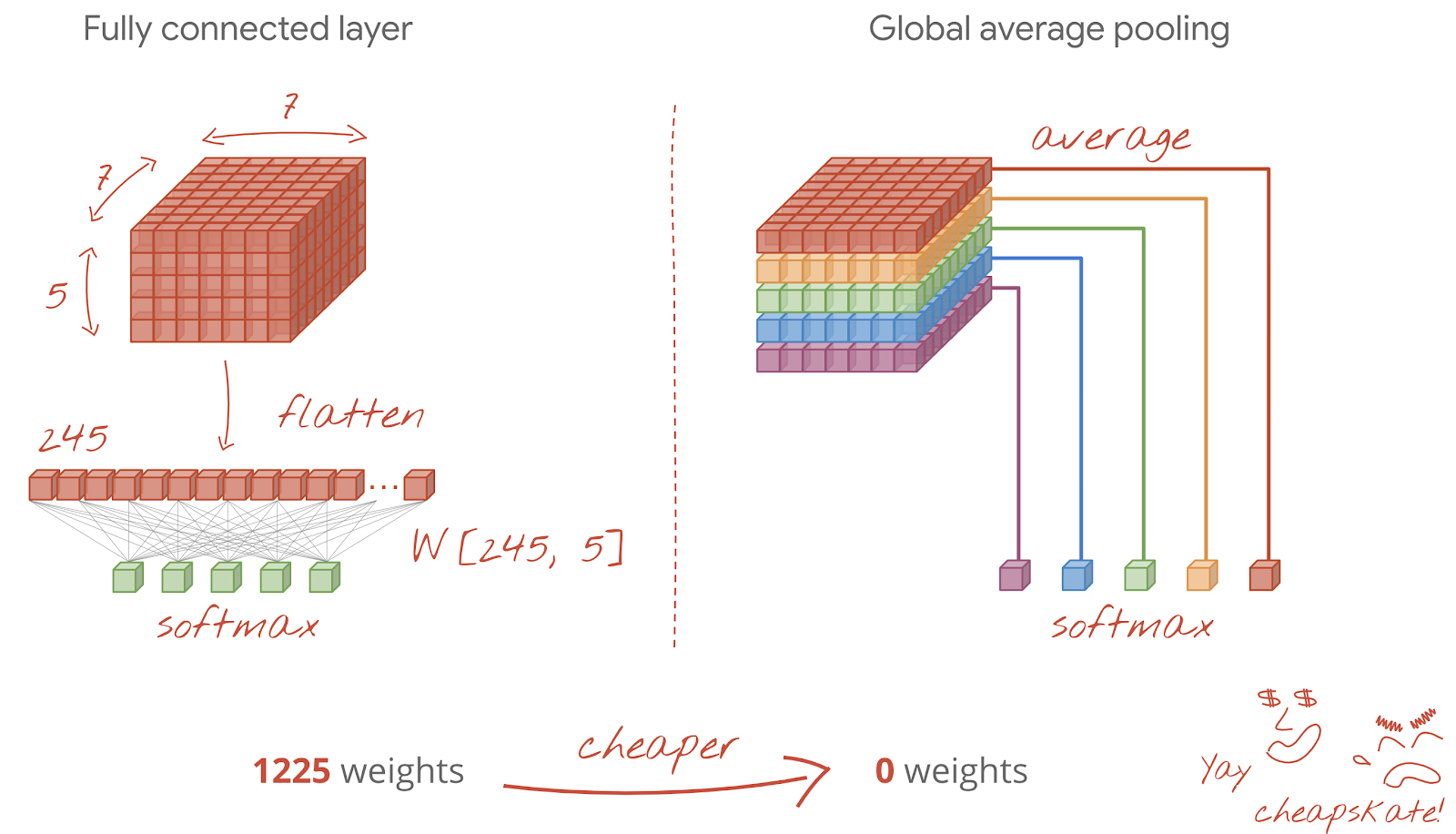
Après la dernière couche de convolution, les données se présentent sous la forme d'un "cube". Il existe deux façons de l'intégrer à la dernière couche dense.

La première consiste à aplatir le cube de données en un vecteur, puis à l'envoyer à la couche softmax. Parfois, vous pouvez même ajouter une couche dense avant la couche softmax. Cela a tendance à être coûteux en termes de nombre de pondérations. Une couche dense à la fin d'un réseau convolutif peut contenir plus de la moitié des pondérations de l'ensemble du réseau de neurones.

Au lieu d'utiliser une couche dense coûteuse, nous pouvons également diviser le "cube" de données entrantes en autant de parties que nous avons de classes, faire la moyenne de leurs valeurs et les transmettre via une fonction d'activation softmax. Cette façon de créer l'en-tête de classification ne coûte aucun poids. Dans Keras, il existe une couche pour cela : tf.keras.layers.GlobalAveragePooling2D().

Les réseaux de neurones convolutifs détectent l'emplacement des objets. Lorsqu'un filtre répond fortement à une fonctionnalité, il le fait à un emplacement (x, y) spécifique. Selon ce que vous souhaitez faire, un réseau de neurones peut être entraîné à utiliser ou à ignorer ces données de localisation. Le pooling moyen global supprime explicitement toutes les données de localisation. Cela peut convenir à un classificateur de fleurs, mais pas à d'autres tâches, comme le dénombrement des fleurs dans une image. À utiliser avec précaution.

Passez à la section suivante pour créer un réseau de convolution adapté au problème.

Construisons un réseau convolutif pour la reconnaissance des chiffres manuscrits. Nous utiliserons trois couches convolutives en haut, notre couche de lecture softmax traditionnelle en bas et les connecterons avec une couche entièrement connectée :

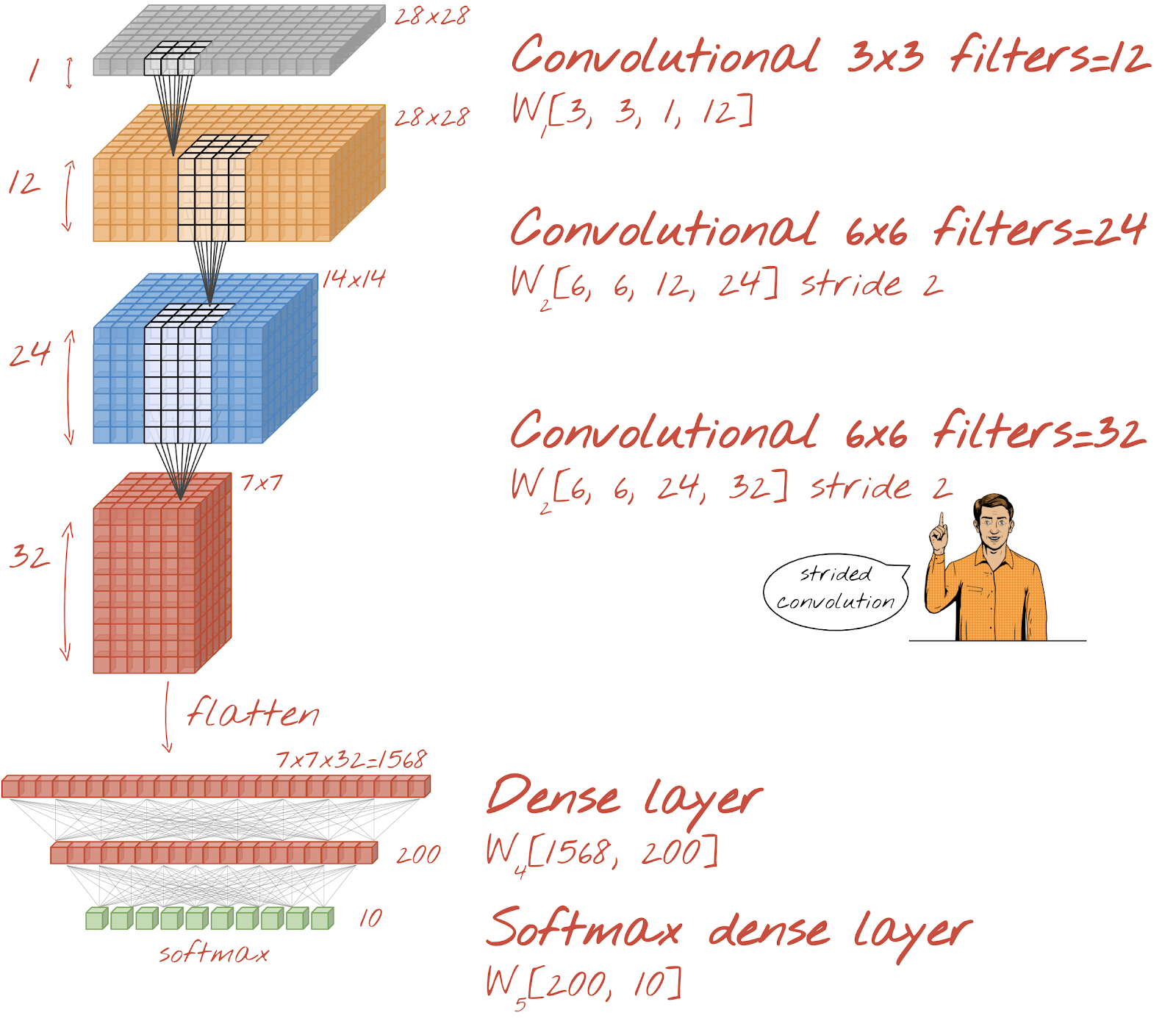
Notez que les deuxième et troisième couches de convolution ont un pas de deux, ce qui explique pourquoi elles réduisent le nombre de valeurs de sortie de 28 x 28 à 14 x 14, puis à 7 x 7.

Écrivons le code Keras.

Une attention particulière est requise avant la première couche de convolution. En effet, il s'attend à un "cube" de données en 3D, mais notre ensemble de données a jusqu'à présent été configuré pour des couches denses, et tous les pixels des images sont aplatis en un vecteur. Nous devons les remodeler en images de 28 x 28 x 1 (1 canal pour les images en niveaux de gris) :

tf.keras.layers.Reshape(input_shape=(28*28,), target_shape=(28, 28, 1))

Vous pouvez utiliser cette ligne au lieu du calque tf.keras.layers.Input que vous aviez jusqu'à présent.

Dans Keras, la syntaxe d'une couche de convolution activée par "relu" est la suivante :

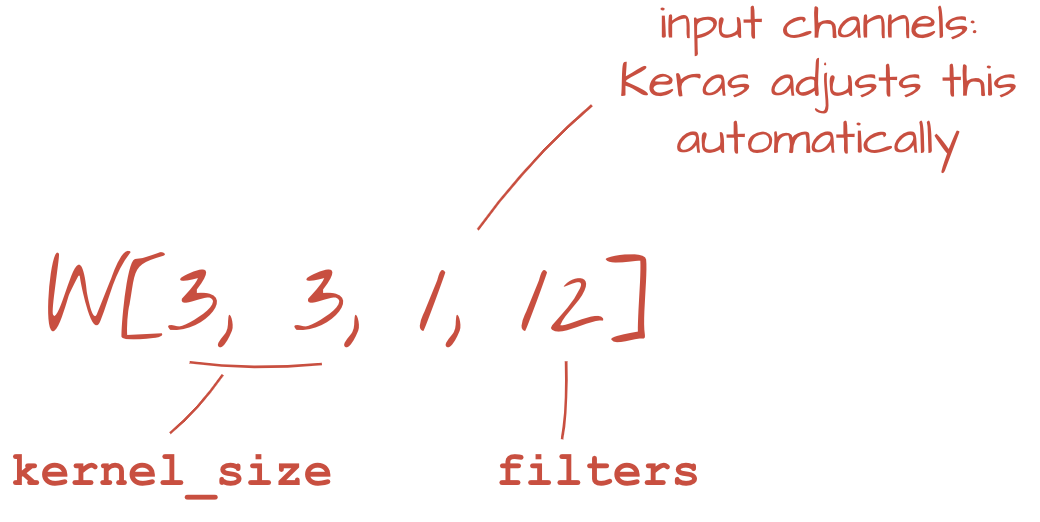
tf.keras.layers.Conv2D(kernel_size=3, filters=12, padding='same', activation='relu')

Le paramètre de marge intérieure dans les couches de convolution peut avoir deux valeurs :

• "same" : ajoute des zéros pour produire des sorties de même largeur/hauteur que l'entrée.
• "valid" : aucune marge intérieure, seuls les pixels réels sont utilisés

Nous utilisons ici un remplissage. Veuillez donc le définir sur "same" (identique).

Pour une convolution avec un pas, vous devez écrire :

tf.keras.layers.Conv2D(kernel_size=6, filters=24, padding='same', activation='relu', strides=2)

Pour aplatir un cube de données en un vecteur afin qu'il puisse être utilisé par une couche dense :

tf.keras.layers.Flatten()

Pour le calque dense, la syntaxe n'a pas changé :

tf.keras.layers.Dense(200, activation='relu')

ATELIER PRATIQUE :

Modifiez votre modèle pour le transformer en modèle convolutif. Vous pouvez utiliser les valeurs du dessin ci-dessus pour le dimensionner. Vous pouvez conserver la diminution du taux d'apprentissage tel quel, mais veuillez supprimer le dropout à ce stade.

Veuillez également augmenter le facteur de zoom à 16 dans PlotTraining. Cela zoome autour de 0 sur les pertes et autour de 1 sur les précisions pour vous aider à comprendre ce qui se passe : PlotTraining(sample_rate=10, zoom=16)

Votre modèle a-t-il dépassé la barre des 99 % de précision ? Presque… mais examinez la courbe de perte de validation. Ces problématiques vous semblent-elles familières ?

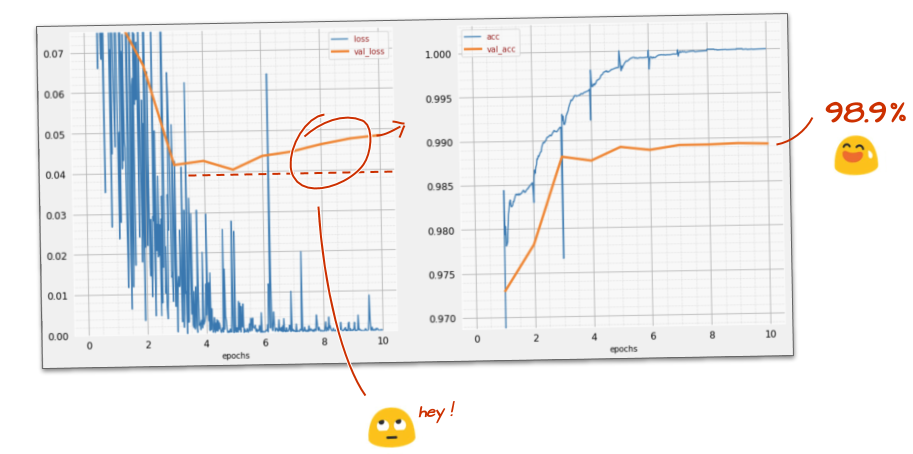
Examinez également les prédictions. Pour la première fois, vous devriez constater que la plupart des 10 000 chiffres de test sont désormais correctement reconnus. Il ne reste qu'environ 4 lignes et demie de détections incorrectes (environ 110 chiffres sur 10 000).

Si vous êtes bloqué, voici la solution à ce stade :

keras_04_mnist_convolutional.ipynb

L'entraînement précédent présente des signes évidents de surapprentissage (et n'atteint toujours pas 99 % de précision). Dois-je réessayer de déposer les enfants ?

ATELIER PRATIQUE :

Ajoutez une couche d'abandon entre les deux couches denses de votre réseau. Utilisez un taux de dropout de 40 % (=0,4) :

tf.keras.layers.Dropout(0.4)

Il est possible d'appliquer le dropout aux couches de convolution, mais cela fonctionne légèrement différemment et n'est généralement pas aussi efficace, car il y a beaucoup moins de pondérations dans les couches de convolution et donc moins de chances de mauvaise co-adaptation. Nous n'aborderons pas ce point.

Comment s'est-il passé cette fois-ci ?

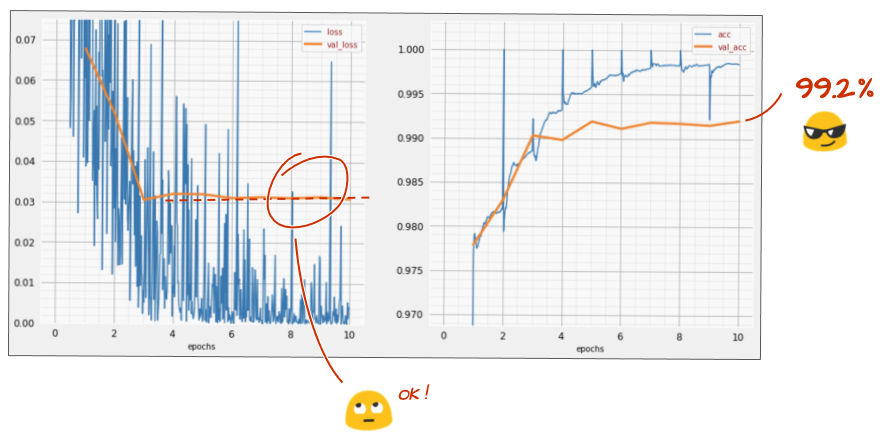
Il semble que l'abandon ait fonctionné cette fois-ci. La perte de validation n'augmente plus et la précision finale devrait être bien supérieure à 99 %. Félicitations !

La première fois que nous avons essayé d'appliquer le dropout, nous avons pensé avoir un problème de surapprentissage, alors qu'en fait, le problème se trouvait dans l'architecture du réseau de neurones. Nous ne pouvions pas aller plus loin sans couches de convolution, et le dropout n'y pouvait rien.

Cette fois, il semble que le surapprentissage soit à l'origine du problème et que le dropout ait réellement aidé. N'oubliez pas que de nombreux facteurs peuvent entraîner une déconnexion entre les courbes de perte d'entraînement et de validation, avec une augmentation progressive de la perte de validation. Le surapprentissage (trop de degrés de liberté, mal utilisés par le réseau) n'en est qu'un. Si votre ensemble de données est trop petit ou si l'architecture de votre réseau de neurones n'est pas adaptée, vous pouvez observer un comportement similaire sur les courbes de perte, mais le dropout ne vous sera d'aucune aide.

Enfin, essayons d'ajouter une normalisation par lot.

Qu'est-ce que la normalisation par lot ?

En résumé, la normalisation par lot tente de résoudre le problème de la distribution des sorties de neurones par rapport à la fonction d'activation du neurone. Dans un mini-batch de données d'entraînement, la sortie d'un neurone, avant l'activation, peut avoir les distributions suivantes :

Trop à gauche, après l'activation sigmoïde, ce neurone génère presque toujours une sortie de 0.

Trop étroit, ce neurone ne produit jamais de 0 ou de 1 clairs.

Ce n'est pas si mal. Le neurone aura un éventail de comportements équitable dans ce minibatch.

Pour résoudre ce problème, la normalisation par lot normalise les sorties de neurones sur un lot de données d'entraînement, c'est-à-dire qu'elle soustrait la moyenne et divise par l'écart type. Cependant, cela serait trop brutal. Avec une distribution parfaitement centrée et normalement large partout, tous les neurones auraient le même comportement. L'astuce consiste à introduire deux paramètres supplémentaires pouvant être appris par neurone, 𝛼 et 𝛽, et à calculer :

𝛼 . normalized_out + 𝛽

Appliquez ensuite la fonction d'activation (sigmoïde, ReLU, etc.). De cette façon, le réseau décide, grâce au machine learning, de la quantité de centrage et de remise à l'échelle à appliquer à chaque neurone. Il appartient au lecteur de vérifier qu'il existe des valeurs de 𝛼 et 𝛽 qui peuvent supprimer complètement la normalisation, si cela est approprié.

En pratique, 𝛼 et 𝛽 ne sont pas toujours nécessaires. Dans Keras, ils sont appelés "scale" et "center". Vous pouvez utiliser l'un ou l'autre de manière sélective, par exemple :

tf.keras.layers.BatchNormalization(scale=False, center=True)

Le problème avec la normalisation par lot est qu'au moment de la prédiction, vous ne disposez pas de lots d'entraînement sur lesquels vous pourriez calculer les statistiques des sorties de vos neurones. Mais vous avez toujours besoin de ces valeurs. Cette partie est un peu bidouillée. Lors de l'entraînement, une moyenne et un écart-type de sortie de neurone "typique" sont calculés sur un nombre "suffisant" de lots, en pratique à l'aide d'une moyenne exponentielle courante. Ces statistiques sont ensuite utilisées au moment de l'inférence.

La bonne nouvelle est que dans Keras, vous pouvez utiliser un calque tf.keras.layers.BatchNormalization et que toute cette comptabilité se fera automatiquement.

C'est la théorie. En pratique, il suffit de retenir quelques règles :

Batch norm "by the book" (norme par lot "dans les règles de l'art") :

1. La normalisation par lot se situe entre la sortie d'une couche et sa fonction d'activation.
2. Si vous utilisez center=True dans la normalisation par lot, vous n'avez pas besoin de biais dans votre couche. Le décalage de la normalisation par lot joue le rôle d'un biais.
3. Si vous utilisez une fonction d'activation invariante à l'échelle (c'est-à-dire dont la forme ne change pas si vous zoomez dessus), vous pouvez définir scale=False. La fonction ReLU est invariante à l'échelle. Sigmoïde ne l'est pas.

C'est la théorie, mais le seul moyen de savoir si le non-respect de ces règles est mauvais est d'essayer.

Pour l'instant, suivons les règles et ajoutons une couche de normalisation par lot à chaque couche du réseau de neurones, sauf la dernière. Ne l'ajoutez pas à la dernière couche "softmax". Il ne serait pas utile dans ce cas.

# Modify each layer: remove the activation from the layer itself.
# Set use_bias=False since batch norm will play the role of biases.
tf.keras.layers.Conv2D(..., use_bias=False),
# Batch norm goes between the layer and its activation.
# The scale factor can be turned off for Relu activation.
tf.keras.layers.BatchNormalization(scale=False, center=True),
# Finish with the activation.
tf.keras.layers.Activation('relu'),

Quelle est la précision maintenant ?

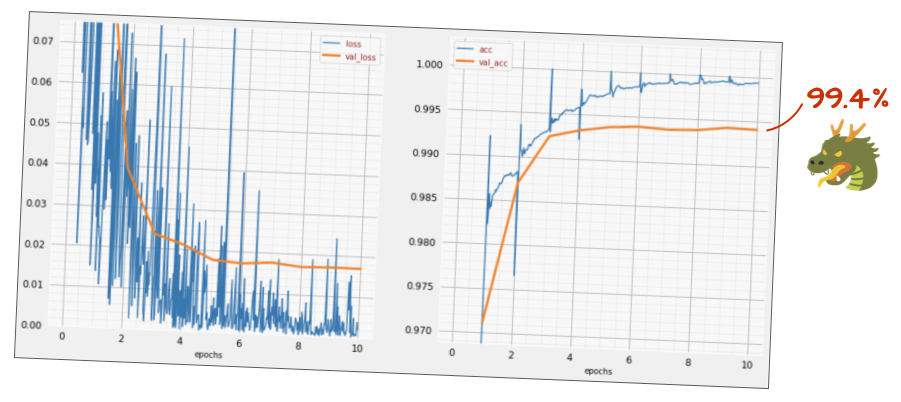
Avec quelques ajustements (BATCH_SIZE=64, paramètre de diminution du taux d'apprentissage 0,666, taux de dropout sur la couche dense 0,3) et un peu de chance, vous pouvez atteindre 99,5 %. Les ajustements du taux d'apprentissage et de l'abandon ont été effectués en suivant les "bonnes pratiques" pour l'utilisation de la normalisation par lot :

• La normalisation par lot aide les réseaux de neurones à converger et vous permet généralement de vous entraîner plus rapidement.
• La normalisation par lot est un régularisateur. Vous pouvez généralement réduire le taux d'abandon que vous utilisez, voire ne pas en utiliser du tout.

Le notebook de solution présente une exécution d'entraînement de 99,5 % :

keras_05_mnist_batch_norm.ipynb

Vous trouverez une version du code prête pour le cloud dans le dossier mlengine sur GitHub, ainsi que des instructions pour l'exécuter sur Google Cloud AI Platform. Avant de pouvoir exécuter cette partie, vous devrez créer un compte Google Cloud et activer la facturation. Les ressources nécessaires pour terminer l'atelier devraient coûter moins de deux dollars (en supposant une heure de temps d'entraînement sur un GPU). Pour préparer votre compte :

1. Créez un projet Google Cloud Platform (http://cloud.google.com/console).
2. Activez la facturation.
3. Installez les outils de ligne de commande GCP (SDK GCP ici).
4. Créez un bucket Google Cloud Storage (dans la région us-central1). Il servira à préparer le code d'entraînement et à stocker votre modèle entraîné.
5. Activez les API nécessaires et demandez les quotas requis (exécutez la commande d'entraînement une fois. Vous devriez recevoir des messages d'erreur vous indiquant ce que vous devez activer).

Vous avez créé votre premier réseau de neurones et l'avez entraîné jusqu'à atteindre une précision de 99 %. Les techniques apprises en cours de route ne sont pas spécifiques à l'ensemble de données MNIST. En fait, elles sont largement utilisées lorsque vous travaillez avec des réseaux de neurones. Pour vous remercier, voici la carte "résumé" de l'atelier, en version dessinée. Vous pouvez l'utiliser pour vous souvenir de ce que vous avez appris :

Étapes suivantes

• Après les réseaux entièrement connectés et convolutifs, vous devriez vous intéresser aux réseaux de neurones récurrents.
• Pour exécuter votre entraînement ou votre inférence dans le cloud sur une infrastructure distribuée, Google Cloud fournit AI Platform.
  
• Enfin, vos commentaires nous intéressent. N'hésitez pas à nous contacter si vous remarquez quelque chose d'inhabituel dans cet atelier ou si vous pensez qu'il devrait être amélioré. Nous traitons les commentaires via les problèmes GitHub [lien vers les commentaires].

Auteur : Martin Görner Twitter : @martin_gorner

Tous les dessins animés de cet atelier sont soumis aux droits d'auteur : alexpokusay / 123RF stock photos