En las siguientes secciones, se presenta un ejemplo de un problema de LP y se muestra cómo resolverlo. Este es el problema:
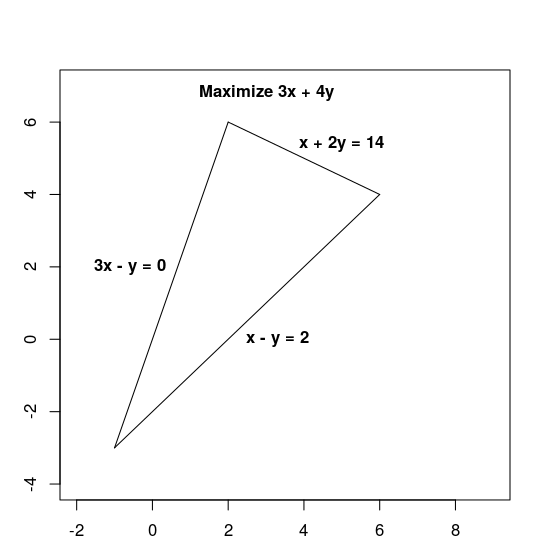
Maximizar 3x + 4y sujeto a las siguientes restricciones:
x + 2y≤ 143x - y≥ 0x - y≤ 2
Tanto la función objetivo, 3x + 4y, como las restricciones se proporcionan mediante expresiones lineales, lo que hace que este sea un problema lineal.
Las restricciones definen la región posible, que es el triángulo que se muestra a continuación, incluido su interior.
Pasos básicos para resolver un problema de LP
Para resolver un problema de LP, el programa debe incluir los siguientes pasos:
- Importa el wrapper de resolución lineal.
- declaramos el solucionador de problemas de LP,
- definir las variables,
- definir las restricciones,
- definir el objetivo
- llamar al solucionador de problemas de LP; y
- mostrar la solución
Solución con MPSolver
En la siguiente sección, se presenta un programa que resuelve el problema con el wrapper MPSolver y un solucionador de problemas LP.
Nota: Para ejecutar el programa que aparece a continuación, debes instalar las herramientas del operador OR.
La principal herramienta de resolución de optimización lineal de las herramientas del operador O es Glop, la herramienta de resolución de programación lineal interna de Google. Es rápido, eficiente en cuanto a memoria y estable en términos numéricos.
Importa el wrapper de resolución lineal
Importa (o incluye) el wrapper de resolución lineal de las herramientas OR, una interfaz para solucionadores de MIP y solucionadores lineales, como se muestra a continuación.
Python
from ortools.linear_solver import pywraplp
C++
#include <iostream> #include <memory> #include "ortools/linear_solver/linear_solver.h"
Java
import com.google.ortools.Loader; import com.google.ortools.linearsolver.MPConstraint; import com.google.ortools.linearsolver.MPObjective; import com.google.ortools.linearsolver.MPSolver; import com.google.ortools.linearsolver.MPVariable;
C#
using System; using Google.OrTools.LinearSolver;
Cómo declarar el solucionador de problemas de LP
MPsolver es un wrapper para varias soluciones diferentes, incluido Glop. El siguiente código declara el solucionador de problemas de GLOP.
Python
solver = pywraplp.Solver.CreateSolver("GLOP")
if not solver:
return
C++
std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP"));
if (!solver) {
LOG(WARNING) << "SCIP solver unavailable.";
return;
}
Java
MPSolver solver = MPSolver.createSolver("GLOP");
C#
Solver solver = Solver.CreateSolver("GLOP");
if (solver is null)
{
return;
}
Nota: Sustituye PDLP por GLOP para usar un solucionador de problemas de LP alternativo. Para obtener más detalles sobre cómo elegir solucionadores, consulta Resolución avanzada de LP y, para la instalación de solucionadores de terceros, consulta la guía de instalación.
Crea las variables
Primero, crea las variables x e y cuyos valores estén en el rango de 0 a infinito.
Python
x = solver.NumVar(0, solver.infinity(), "x")
y = solver.NumVar(0, solver.infinity(), "y")
print("Number of variables =", solver.NumVariables())
C++
const double infinity = solver->infinity(); // x and y are non-negative variables. MPVariable* const x = solver->MakeNumVar(0.0, infinity, "x"); MPVariable* const y = solver->MakeNumVar(0.0, infinity, "y"); LOG(INFO) << "Number of variables = " << solver->NumVariables();
Java
double infinity = java.lang.Double.POSITIVE_INFINITY;
// x and y are continuous non-negative variables.
MPVariable x = solver.makeNumVar(0.0, infinity, "x");
MPVariable y = solver.makeNumVar(0.0, infinity, "y");
System.out.println("Number of variables = " + solver.numVariables());
C#
Variable x = solver.MakeNumVar(0.0, double.PositiveInfinity, "x");
Variable y = solver.MakeNumVar(0.0, double.PositiveInfinity, "y");
Console.WriteLine("Number of variables = " + solver.NumVariables());
Define las restricciones
A continuación, define las restricciones de las variables. Otorga un nombre único a cada restricción (como constraint0) y, luego, define los coeficientes para la restricción.
Python
# Constraint 0: x + 2y <= 14.
solver.Add(x + 2 * y <= 14.0)
# Constraint 1: 3x - y >= 0.
solver.Add(3 * x - y >= 0.0)
# Constraint 2: x - y <= 2.
solver.Add(x - y <= 2.0)
print("Number of constraints =", solver.NumConstraints())
C++
// x + 2*y <= 14. MPConstraint* const c0 = solver->MakeRowConstraint(-infinity, 14.0); c0->SetCoefficient(x, 1); c0->SetCoefficient(y, 2); // 3*x - y >= 0. MPConstraint* const c1 = solver->MakeRowConstraint(0.0, infinity); c1->SetCoefficient(x, 3); c1->SetCoefficient(y, -1); // x - y <= 2. MPConstraint* const c2 = solver->MakeRowConstraint(-infinity, 2.0); c2->SetCoefficient(x, 1); c2->SetCoefficient(y, -1); LOG(INFO) << "Number of constraints = " << solver->NumConstraints();
Java
// x + 2*y <= 14.
MPConstraint c0 = solver.makeConstraint(-infinity, 14.0, "c0");
c0.setCoefficient(x, 1);
c0.setCoefficient(y, 2);
// 3*x - y >= 0.
MPConstraint c1 = solver.makeConstraint(0.0, infinity, "c1");
c1.setCoefficient(x, 3);
c1.setCoefficient(y, -1);
// x - y <= 2.
MPConstraint c2 = solver.makeConstraint(-infinity, 2.0, "c2");
c2.setCoefficient(x, 1);
c2.setCoefficient(y, -1);
System.out.println("Number of constraints = " + solver.numConstraints());
C#
// x + 2y <= 14.
solver.Add(x + 2 * y <= 14.0);
// 3x - y >= 0.
solver.Add(3 * x - y >= 0.0);
// x - y <= 2.
solver.Add(x - y <= 2.0);
Console.WriteLine("Number of constraints = " + solver.NumConstraints());
Define la función objetivo
El siguiente código define la función objetivo, 3x + 4y, y especifica que se trata de un problema de maximización.
Python
# Objective function: 3x + 4y. solver.Maximize(3 * x + 4 * y)
C++
// Objective function: 3x + 4y. MPObjective* const objective = solver->MutableObjective(); objective->SetCoefficient(x, 3); objective->SetCoefficient(y, 4); objective->SetMaximization();
Java
// Maximize 3 * x + 4 * y. MPObjective objective = solver.objective(); objective.setCoefficient(x, 3); objective.setCoefficient(y, 4); objective.setMaximization();
C#
// Objective function: 3x + 4y. solver.Maximize(3 * x + 4 * y);
Cómo invocar el solucionador
El siguiente código invoca el solucionador.
Python
print(f"Solving with {solver.SolverVersion()}")
status = solver.Solve()
C++
const MPSolver::ResultStatus result_status = solver->Solve();
// Check that the problem has an optimal solution.
if (result_status != MPSolver::OPTIMAL) {
LOG(FATAL) << "The problem does not have an optimal solution!";
}
Java
final MPSolver.ResultStatus resultStatus = solver.solve();
C#
Solver.ResultStatus resultStatus = solver.Solve();
Muestra la solución
El siguiente código muestra la solución.
Python
if status == pywraplp.Solver.OPTIMAL:
print("Solution:")
print(f"Objective value = {solver.Objective().Value():0.1f}")
print(f"x = {x.solution_value():0.1f}")
print(f"y = {y.solution_value():0.1f}")
else:
print("The problem does not have an optimal solution.")
C++
LOG(INFO) << "Solution:"; LOG(INFO) << "Optimal objective value = " << objective->Value(); LOG(INFO) << x->name() << " = " << x->solution_value(); LOG(INFO) << y->name() << " = " << y->solution_value();
Java
if (resultStatus == MPSolver.ResultStatus.OPTIMAL) {
System.out.println("Solution:");
System.out.println("Objective value = " + objective.value());
System.out.println("x = " + x.solutionValue());
System.out.println("y = " + y.solutionValue());
} else {
System.err.println("The problem does not have an optimal solution!");
}
C#
// Check that the problem has an optimal solution.
if (resultStatus != Solver.ResultStatus.OPTIMAL)
{
Console.WriteLine("The problem does not have an optimal solution!");
return;
}
Console.WriteLine("Solution:");
Console.WriteLine("Objective value = " + solver.Objective().Value());
Console.WriteLine("x = " + x.SolutionValue());
Console.WriteLine("y = " + y.SolutionValue());
Los programas completos
A continuación, se muestran los programas completos.
Python
from ortools.linear_solver import pywraplp
def LinearProgrammingExample():
"""Linear programming sample."""
# Instantiate a Glop solver, naming it LinearExample.
solver = pywraplp.Solver.CreateSolver("GLOP")
if not solver:
return
# Create the two variables and let them take on any non-negative value.
x = solver.NumVar(0, solver.infinity(), "x")
y = solver.NumVar(0, solver.infinity(), "y")
print("Number of variables =", solver.NumVariables())
# Constraint 0: x + 2y <= 14.
solver.Add(x + 2 * y <= 14.0)
# Constraint 1: 3x - y >= 0.
solver.Add(3 * x - y >= 0.0)
# Constraint 2: x - y <= 2.
solver.Add(x - y <= 2.0)
print("Number of constraints =", solver.NumConstraints())
# Objective function: 3x + 4y.
solver.Maximize(3 * x + 4 * y)
# Solve the system.
print(f"Solving with {solver.SolverVersion()}")
status = solver.Solve()
if status == pywraplp.Solver.OPTIMAL:
print("Solution:")
print(f"Objective value = {solver.Objective().Value():0.1f}")
print(f"x = {x.solution_value():0.1f}")
print(f"y = {y.solution_value():0.1f}")
else:
print("The problem does not have an optimal solution.")
print("\nAdvanced usage:")
print(f"Problem solved in {solver.wall_time():d} milliseconds")
print(f"Problem solved in {solver.iterations():d} iterations")
LinearProgrammingExample()
C++
#include <iostream>
#include <memory>
#include "ortools/linear_solver/linear_solver.h"
namespace operations_research {
void LinearProgrammingExample() {
std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP"));
if (!solver) {
LOG(WARNING) << "SCIP solver unavailable.";
return;
}
const double infinity = solver->infinity();
// x and y are non-negative variables.
MPVariable* const x = solver->MakeNumVar(0.0, infinity, "x");
MPVariable* const y = solver->MakeNumVar(0.0, infinity, "y");
LOG(INFO) << "Number of variables = " << solver->NumVariables();
// x + 2*y <= 14.
MPConstraint* const c0 = solver->MakeRowConstraint(-infinity, 14.0);
c0->SetCoefficient(x, 1);
c0->SetCoefficient(y, 2);
// 3*x - y >= 0.
MPConstraint* const c1 = solver->MakeRowConstraint(0.0, infinity);
c1->SetCoefficient(x, 3);
c1->SetCoefficient(y, -1);
// x - y <= 2.
MPConstraint* const c2 = solver->MakeRowConstraint(-infinity, 2.0);
c2->SetCoefficient(x, 1);
c2->SetCoefficient(y, -1);
LOG(INFO) << "Number of constraints = " << solver->NumConstraints();
// Objective function: 3x + 4y.
MPObjective* const objective = solver->MutableObjective();
objective->SetCoefficient(x, 3);
objective->SetCoefficient(y, 4);
objective->SetMaximization();
const MPSolver::ResultStatus result_status = solver->Solve();
// Check that the problem has an optimal solution.
if (result_status != MPSolver::OPTIMAL) {
LOG(FATAL) << "The problem does not have an optimal solution!";
}
LOG(INFO) << "Solution:";
LOG(INFO) << "Optimal objective value = " << objective->Value();
LOG(INFO) << x->name() << " = " << x->solution_value();
LOG(INFO) << y->name() << " = " << y->solution_value();
}
} // namespace operations_research
int main(int argc, char** argv) {
operations_research::LinearProgrammingExample();
return EXIT_SUCCESS;
}
Java
package com.google.ortools.linearsolver.samples;
import com.google.ortools.Loader;
import com.google.ortools.linearsolver.MPConstraint;
import com.google.ortools.linearsolver.MPObjective;
import com.google.ortools.linearsolver.MPSolver;
import com.google.ortools.linearsolver.MPVariable;
/** Simple linear programming example. */
public final class LinearProgrammingExample {
public static void main(String[] args) {
Loader.loadNativeLibraries();
MPSolver solver = MPSolver.createSolver("GLOP");
double infinity = java.lang.Double.POSITIVE_INFINITY;
// x and y are continuous non-negative variables.
MPVariable x = solver.makeNumVar(0.0, infinity, "x");
MPVariable y = solver.makeNumVar(0.0, infinity, "y");
System.out.println("Number of variables = " + solver.numVariables());
// x + 2*y <= 14.
MPConstraint c0 = solver.makeConstraint(-infinity, 14.0, "c0");
c0.setCoefficient(x, 1);
c0.setCoefficient(y, 2);
// 3*x - y >= 0.
MPConstraint c1 = solver.makeConstraint(0.0, infinity, "c1");
c1.setCoefficient(x, 3);
c1.setCoefficient(y, -1);
// x - y <= 2.
MPConstraint c2 = solver.makeConstraint(-infinity, 2.0, "c2");
c2.setCoefficient(x, 1);
c2.setCoefficient(y, -1);
System.out.println("Number of constraints = " + solver.numConstraints());
// Maximize 3 * x + 4 * y.
MPObjective objective = solver.objective();
objective.setCoefficient(x, 3);
objective.setCoefficient(y, 4);
objective.setMaximization();
final MPSolver.ResultStatus resultStatus = solver.solve();
if (resultStatus == MPSolver.ResultStatus.OPTIMAL) {
System.out.println("Solution:");
System.out.println("Objective value = " + objective.value());
System.out.println("x = " + x.solutionValue());
System.out.println("y = " + y.solutionValue());
} else {
System.err.println("The problem does not have an optimal solution!");
}
System.out.println("\nAdvanced usage:");
System.out.println("Problem solved in " + solver.wallTime() + " milliseconds");
System.out.println("Problem solved in " + solver.iterations() + " iterations");
}
private LinearProgrammingExample() {}
}
C#
using System;
using Google.OrTools.LinearSolver;
public class LinearProgrammingExample
{
static void Main()
{
Solver solver = Solver.CreateSolver("GLOP");
if (solver is null)
{
return;
}
// x and y are continuous non-negative variables.
Variable x = solver.MakeNumVar(0.0, double.PositiveInfinity, "x");
Variable y = solver.MakeNumVar(0.0, double.PositiveInfinity, "y");
Console.WriteLine("Number of variables = " + solver.NumVariables());
// x + 2y <= 14.
solver.Add(x + 2 * y <= 14.0);
// 3x - y >= 0.
solver.Add(3 * x - y >= 0.0);
// x - y <= 2.
solver.Add(x - y <= 2.0);
Console.WriteLine("Number of constraints = " + solver.NumConstraints());
// Objective function: 3x + 4y.
solver.Maximize(3 * x + 4 * y);
Solver.ResultStatus resultStatus = solver.Solve();
// Check that the problem has an optimal solution.
if (resultStatus != Solver.ResultStatus.OPTIMAL)
{
Console.WriteLine("The problem does not have an optimal solution!");
return;
}
Console.WriteLine("Solution:");
Console.WriteLine("Objective value = " + solver.Objective().Value());
Console.WriteLine("x = " + x.SolutionValue());
Console.WriteLine("y = " + y.SolutionValue());
Console.WriteLine("\nAdvanced usage:");
Console.WriteLine("Problem solved in " + solver.WallTime() + " milliseconds");
Console.WriteLine("Problem solved in " + solver.Iterations() + " iterations");
}
}
Solución óptima
El programa devuelve la solución óptima para el problema, como se indica a continuación.
Number of variables = 2
Number of constraints = 3
Solution:
x = 6.0
y = 4.0
Optimal objective value = 34.0
A continuación, se muestra un gráfico en el que se muestra la solución:
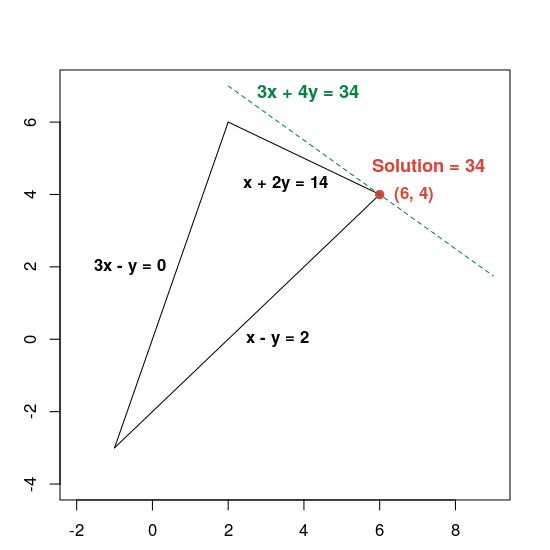
Para definir la línea verde punteada, se configura la función objetivo igual a su valor óptimo de 34. Cualquier línea cuya ecuación tenga la forma 3x + 4y = c es paralela a la línea punteada, y 34 es el valor mayor de c para el cual la línea cruza la región posible.
Si quieres obtener más información para resolver problemas de optimización lineal, consulta Solución avanzada de LP.
