في الأقسام التالية، سنوضح برمجة التقييد (CP) من خلال مشكلة انفتاحية مبنية على لعبة الشطرنج. في لعبة الشطرنج، تستطيع الملكة الهجوم أفقيًا وعموديًا وقُطريًا. تسأل مشكلة N-queens:
كيف يمكن وضع ملكات NxN على لوح شطرنج NxN حتى لا يهاجمها أي اثنان منها لبعضنا البعض؟
أدناه، يمكنك رؤية أحد الحلول الممكنة لمشكلة N-queens لـ N = 4.
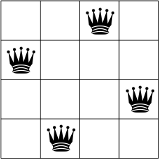
لا توجد ملكتان في الصف أو العمود أو القطر نفسه.
يُرجى العلم أنّ هذه المشكلة ليست في ما يتعلق بالتحسين، فنحن نريد إيجاد جميع بدلاً من حل واحد مثالي، مما يجعلها مرشحة بشكل طبيعي لبرمجة التقييد. تصف الأقسام التالية نهج CP لمشكلة N-queens. تقديم البرامج التي تحلها باستخدام كل من أداة حل CP-SAT وCP الأصلي للحل.
نهج CP لمشكلة N-Quens
تعمل أداة حلّ CP من خلال تجربة كل والتعيينات الممكنة للقيم للمتغيرات في مشكلة ما، لإيجاد الحلول الممكنة. في مسألة تتعلق بأربع ملكات، تبدأ أداة الحلّ من أقصى اليسار وتضع على التوالي ملكة واحدة في كل عمود، في موقع لم تتعرض للهجوم من قبل أي ملكات سبق أن تم شغلها.
الانتشار والتتبع العكسي
هناك عنصران رئيسيان لقيد البحث عن البرمجة:
- النشر: في كل مرة تخصص فيها أداة الحلّ قيمة لمتغير، قيود تضيف قيودًا على القيم المحتملة للأشخاص غير المعيَّنين المتغيرات. ويتم نشر هذه القيود إلى عمليات تعيين المتغيّرات المستقبلية. فعلى سبيل المثال، في مسألة تتعلق بالأربع ملكات، ففي كل مرة تضع فيها أداة الحلّ ملكة، فإنه لا يمكن وضع أي ملكات أخرى في الصف والأقطار التي توجد عليها الملكة الحالية. يمكن أن يؤدي الانتشار إلى تسريع عملية البحث بشكل كبير عن طريق تقليل مجموعة قيم المتغير التي يجب على أداة الحلّ استكشافها.
- يحدث التتبُّع العكسي عندما لا تتمكّن أداة الحلّ من تعيين قيمة لما يلي. متغير، أو بسبب القيود، أو إيجاد حل. في كلتا الحالتين، ترجع أداة الحلّ إلى مرحلة سابقة وتغير قيمة المتغير هذه المرحلة إلى قيمة لم تتم تجربتها بالفعل. في مثال الـ 4 ملكات، وهذا يعني نقل ملكة إلى مربع جديد في العمود الحالي.
بعد ذلك، سترى كيف تستخدم البرمجة المقيّدة النشر والتتبُّع العكسي لحل مشكلة الأربع ملكات.
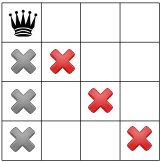
لنفرض أن أداة الحلّ تبدأ بوضع ملكة بشكل عشوائي في أعلى يسار الصفحة. العليا. هذه فرضية نوعًا ما؛ فربما يتضح أنه لا يوجد حل موجود مع ملكة في الزاوية اليسرى العليا.
بالنظر إلى هذه الفرضية، ما القيود التي يمكننا نشرها؟ يتمثل أحد القيود في يمكن أن يكون هناك ملكة واحدة فقط في عمود (حروف X الرمادية أدناه)، ملكةتين على نفس القطر (أحرف X الحمراء أدناه).
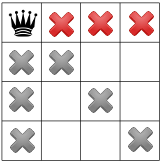
القيد الثالث يحظر ظهور الأميرات في الصف نفسه:
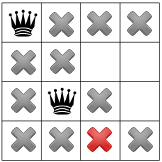
تم نشر قيودنا، يمكننا اختبار فرضية أخرى، ووضع للملكة الثانية في أحد المربعات المتبقية المتاحة. قد تقرر أداة الحلّ لدينا لوضع أول مربع متاح في العمود الثاني فيه:
وبعد نشر القيد القطري، يمكننا ملاحظة أنه لا المربعات المتاحة في العمود الثالث أو الصف الأخير:
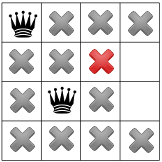
مع عدم وجود حلول ممكنة في هذه المرحلة، نحتاج إلى التراجع. هناك خيار واحد هو لتختار أداة الحلّ المربّع الآخر المتاح في العمود الثاني. ومع ذلك، فإن انتشار القيود يفرض بعد ذلك ملكة على الصف الثاني من العمود الثالث، بدون ترك أماكن صالحة للملكة الرابعة:

ولذا يجب على أداة الحلّ أن تتراجع مرة أخرى، ولكن هذه المرة كل العودة إلى للملكة الأولى. لقد أظهرنا الآن أنه لا يوجد حل للملكات أن المشكلة ستشغل مربع زاوية.
نظرًا لعدم وجود ملكة في الزاوية، تنقلك أداة الحلّ أول ملكة لأسفل واحد، وينتشر، تاركًا مكانًا واحدًا فقط للملكة الثانية:
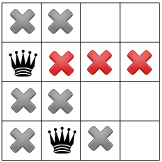
يكشف النشر مرة أخرى عن بقعة واحدة فقط للملكة الثالثة:
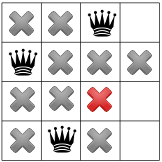
وللملكة الرابعة والأخيرة:

لدينا الحلّ الأول. إذا طلبنا من أداة الحل أن تتوقف بعد العثور الحل الأول، ستنتهي هنا. وإلا، فسيتراجع مرة أخرى ضع الملكة الأولى في الصف الثالث من العمود الأول.
حلّ باستخدام CP-SAT
تعد مشكلة N-queens مناسبة بشكل مثالي لتقييد البرمجة. في هذه الدورة، سوف نتعرف على برنامج قصير بلغة بايثون يستخدم أداة حل CP-SAT إيجاد جميع الحلول للمشكلة.
استيراد المكتبات
يستورد الرمز التالي المكتبة المطلوبة.
Python
import sys import time from ortools.sat.python import cp_model
C++
#include <stdlib.h> #include <sstream> #include <string> #include <vector> #include "absl/strings/numbers.h" #include "ortools/base/logging.h" #include "ortools/sat/cp_model.h" #include "ortools/sat/cp_model.pb.h" #include "ortools/sat/cp_model_solver.h" #include "ortools/sat/model.h" #include "ortools/sat/sat_parameters.pb.h" #include "ortools/util/sorted_interval_list.h"
Java
import com.google.ortools.Loader; import com.google.ortools.sat.CpModel; import com.google.ortools.sat.CpSolver; import com.google.ortools.sat.CpSolverSolutionCallback; import com.google.ortools.sat.IntVar; import com.google.ortools.sat.LinearExpr;
#C
using System; using Google.OrTools.Sat;
تعريف النموذج
يوضح الرمز التالي نموذج CP-SAT.
Python
model = cp_model.CpModel()
C++
CpModelBuilder cp_model;
Java
CpModel model = new CpModel();
#C
CpModel model = new CpModel(); int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2); // Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb); Console.WriteLine("Statistics"); Console.WriteLine($" conflicts : {solver.NumConflicts()}"); Console.WriteLine($" branches : {solver.NumBranches()}"); Console.WriteLine($" wall time : {solver.WallTime()} s"); Console.WriteLine($" number of solutions found: {cb.SolutionCount()}"); } }
إنشاء المتغيّرات
تنشئ أداة الحلّ المتغيّرات للمشكلة كمصفوفة اسمها queens.
Python
# There are `board_size` number of variables, one for a queen in each column # of the board. The value of each variable is the row that the queen is in. queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)]
C++
// There are `board_size` number of variables, one for a queen in each column // of the board. The value of each variable is the row that the queen is in. std::vector<IntVar> queens; queens.reserve(board_size); Domain range(0, board_size - 1); for (int i = 0; i < board_size; ++i) { queens.push_back( cp_model.NewIntVar(range).WithName("x" + std::to_string(i))); }
Java
int boardSize = 8; // There are `BoardSize` number of variables, one for a queen in each column of the board. The // value of each variable is the row that the queen is in. IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = model.newIntVar(0, boardSize - 1, "x" + i); }
#C
int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); }
نفترض هنا أن queens[j] هو رقم صف الملكة في العمود j.
بعبارة أخرى، تعني queens[j] = i أن هناك ملكة في الصف i والعمود j.
وضع القيود
إليك الرمز الذي يضع قيودًا على المشكلة.
Python
# All rows must be different. model.add_all_different(queens) # No two queens can be on the same diagonal. model.add_all_different(queens[i] + i for i in range(board_size)) model.add_all_different(queens[i] - i for i in range(board_size))
C++
// The following sets the constraint that all queens are in different rows. cp_model.AddAllDifferent(queens); // No two queens can be on the same diagonal. std::vector<LinearExpr> diag_1; diag_1.reserve(board_size); std::vector<LinearExpr> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(queens[i] + i); diag_2.push_back(queens[i] - i); } cp_model.AddAllDifferent(diag_1); cp_model.AddAllDifferent(diag_2);
Java
// All rows must be different. model.addAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[boardSize]; LinearExpr[] diag2 = new LinearExpr[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build(); diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build(); } model.addAllDifferent(diag1); model.addAllDifferent(diag2);
#C
// All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2);
يستخدم الرمز الطريقة AddAllDifferent، التي تتطلب جميع عناصر
أن تكون الصفيفة مختلفة.
لنرى كيف تضمن هذه القيود الشروط الثلاثة لـ N-queens المشكلة (الملكات في صفوف وأعمدة وأقطار مختلفة).
ما مِن ملكات في الصف نفسه
يؤدي تطبيق طريقة AllDifferent لأداة الحلّ على queens إلى فرض قيم
queens[j] على أن تكون مختلفة لكل j، مما يعني أن جميع الملكات يجب أن تكون في
صفوف مختلفة.
لا توجد ملكتان في العمود نفسه
هذا القيد ضمني في تعريف queens.
وبما أنه لا يمكن أن يضم أي عنصرين من عناصر queens الفهرس ذاته، فلا يمكن استخدام حقلين
في نفس العمود.
لا توجد ملكتان على نفس القطر
القيد القطري أصعب قليلاً من قيود الصف والعمود. أولاً، إذا كانت هناك ملكتان في نفس القطر، فإن أحد الشروط التالية يجب أن تكون true:
- رقم الصف بالإضافة إلى رقم العمود لكل من الملكتين متساويتان.
بعبارة أخرى، تحمل
queens(j) + jالقيمة نفسها لفهرسين مختلفينj - رقم الصف ناقص رقم العمود لكل من الملكتين متساويتين.
في هذه الحالة، تكون للدالة
queens(j) - jالقيمة نفسها لفهرسَين مختلفَينj.
يعني أحد هذه الشروط أن الملكات ترقدان على نفس القطر التصاعدي ( من اليسار إلى اليمين)، بينما يعني الآخر أنهما يقعان على نفس الترتيب التنازلي قُطريًا. ما الشرط الذي يتوافق مع التصاعدي وأيه تنازلي على كيفية ترتيب الصفوف والأعمدة. كما ذُكر في قسم القسم السابق، فإن الترتيب لا يؤثر في مجموعة الحلول، فقط في كيفية تصورها.
إذًا، القيد القطري هو أن جميع قيم queens(j) + j يجب أن تكون
مختلفة، ويجب أن تكون قيم queens(j) - j مختلفة جميعًا،
مختلفة j.
لتطبيق طريقة AddAllDifferent على queens(j) + j، نضع أمثلة N
من المتغير، من أجل j من 0 إلى N-1، في المصفوفة diag1 على النحو التالي:
q1 = model.NewIntVar(0, 2 * board_size, 'diag1_%i' % i) diag1.append(q1) model.Add(q1 == queens[j] + j)
بعد ذلك، نطبِّق AddAllDifferent على diag1.
model.AddAllDifferent(diag1)
يتم إنشاء القيد لـ queens(j) - j بالطريقة نفسها.
إنشاء طابعة حلول
لطباعة جميع الحلول لمشكلة N-queens، تحتاج إلى تمرير استدعاء، تُسمى طابعة الحلول، إلى أداة حل CP-SAT. تطبع كل وظيفة معاودة الاتصال الحل الجديد الذي تعثر عليه أداة الحلّ. تنشئ التعليمة البرمجية التالية حلاً الطابعة.
Python
class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback): """Print intermediate solutions.""" def __init__(self, queens: list[cp_model.IntVar]): cp_model.CpSolverSolutionCallback.__init__(self) self.__queens = queens self.__solution_count = 0 self.__start_time = time.time() @property def solution_count(self) -> int: return self.__solution_count def on_solution_callback(self): current_time = time.time() print( f"Solution {self.__solution_count}, " f"time = {current_time - self.__start_time} s" ) self.__solution_count += 1 all_queens = range(len(self.__queens)) for i in all_queens: for j in all_queens: if self.value(self.__queens[j]) == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print()
C++
int num_solutions = 0; Model model; model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) { LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (SolutionIntegerValue(response, queens[j]) == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; }));
Java
static class SolutionPrinter extends CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queensIn) { solutionCount = 0; queens = queensIn; } @Override public void onSolutionCallback() { System.out.println("Solution " + solutionCount); for (int i = 0; i < queens.length; ++i) { for (int j = 0; j < queens.length; ++j) { if (value(queens[j]) == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != queens.length - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } public int getSolutionCount() { return solutionCount; } private int solutionCount; private final IntVar[] queens; }
#C
public class SolutionPrinter : CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queens) { queens_ = queens; } public override void OnSolutionCallback() { Console.WriteLine($"Solution {SolutionCount_}"); for (int i = 0; i < queens_.Length; ++i) { for (int j = 0; j < queens_.Length; ++j) { if (Value(queens_[j]) == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != queens_.Length - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount_++; } public int SolutionCount() { return SolutionCount_; } private int SolutionCount_; private IntVar[] queens_; }
لاحظ أنه يجب كتابة طابعة الحل باعتبارها فئة بايثون، بسبب Python. إلى أداة الحلّ الأساسية C++.
تتم طباعة الحلول بواسطة السطور التالية في طابعة الحل.
for v in self.__variables: print('%s = %i' % (v, self.Value(v)), end = ' ')
في هذا المثال، تمثّل self.__variables المتغيّر queens، وكل v
مع أحد الإدخالات الثمانية لـ queens. يؤدي هذا إلى طباعة حل في
النموذج التالي: x0 = queens(0) x1 = queens(1) ... x7 = queens(7) حيث
xi هو رقم عمود الملكة في الصف i.
يعرض القسم التالي مثالاً على الحل.
عليك استدعاء أداة الحلّ وعرض النتائج.
يقوم التعليمة البرمجية التالية بتشغيل أداة الحل وعرض الحلول.
Python
solver = cp_model.CpSolver() solution_printer = NQueenSolutionPrinter(queens) solver.parameters.enumerate_all_solutions = True solver.solve(model, solution_printer)
C++
// Tell the solver to enumerate all solutions. SatParameters parameters; parameters.set_enumerate_all_solutions(true); model.Add(NewSatParameters(parameters)); const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model); LOG(INFO) << "Number of solutions found: " << num_solutions;
Java
CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Tell the solver to enumerate all solutions. solver.getParameters().setEnumerateAllSolutions(true); // And solve. solver.solve(model, cb);
#C
// Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb);
عثر البرنامج على 92 حلاً مختلفًا للوحة 8×8. آدِي أَوِّلْ إِدْخَالْ.
Q _ _ _ _ _ _ _
_ _ _ _ _ _ Q _
_ _ _ _ Q _ _ _
_ _ _ _ _ _ _ Q
_ Q _ _ _ _ _ _
_ _ _ Q _ _ _ _
_ _ _ _ _ Q _ _
_ _ Q _ _ _ _ _
...91 other solutions displayed...
Solutions found: 92يمكنك حل مشكلة لوحة ذات حجم مختلف عن طريق المرور في N كـ
وسيطة سطر الأوامر. فعلى سبيل المثال، إذا كان اسم البرنامج queens،
تحل python nqueens_sat.py 6 المشكلة المتعلقة بلوحة مقاس 6×6.
البرنامج بأكمله
إليك البرنامج الكامل لبرنامج N-queens.
Python
"""OR-Tools solution to the N-queens problem.""" import sys import time from ortools.sat.python import cp_model class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback): """Print intermediate solutions.""" def __init__(self, queens: list[cp_model.IntVar]): cp_model.CpSolverSolutionCallback.__init__(self) self.__queens = queens self.__solution_count = 0 self.__start_time = time.time() @property def solution_count(self) -> int: return self.__solution_count def on_solution_callback(self): current_time = time.time() print( f"Solution {self.__solution_count}, " f"time = {current_time - self.__start_time} s" ) self.__solution_count += 1 all_queens = range(len(self.__queens)) for i in all_queens: for j in all_queens: if self.value(self.__queens[j]) == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() def main(board_size: int) -> None: # Creates the solver. model = cp_model.CpModel() # Creates the variables. # There are `board_size` number of variables, one for a queen in each column # of the board. The value of each variable is the row that the queen is in. queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)] # Creates the constraints. # All rows must be different. model.add_all_different(queens) # No two queens can be on the same diagonal. model.add_all_different(queens[i] + i for i in range(board_size)) model.add_all_different(queens[i] - i for i in range(board_size)) # Solve the model. solver = cp_model.CpSolver() solution_printer = NQueenSolutionPrinter(queens) solver.parameters.enumerate_all_solutions = True solver.solve(model, solution_printer) # Statistics. print("\nStatistics") print(f" conflicts : {solver.num_conflicts}") print(f" branches : {solver.num_branches}") print(f" wall time : {solver.wall_time} s") print(f" solutions found: {solution_printer.solution_count}") if __name__ == "__main__": # By default, solve the 8x8 problem. size = 8 if len(sys.argv) > 1: size = int(sys.argv[1]) main(size)
C++
// OR-Tools solution to the N-queens problem. #include <stdlib.h> #include <sstream> #include <string> #include <vector> #include "absl/strings/numbers.h" #include "ortools/base/logging.h" #include "ortools/sat/cp_model.h" #include "ortools/sat/cp_model.pb.h" #include "ortools/sat/cp_model_solver.h" #include "ortools/sat/model.h" #include "ortools/sat/sat_parameters.pb.h" #include "ortools/util/sorted_interval_list.h" namespace operations_research { namespace sat { void NQueensSat(const int board_size) { // Instantiate the solver. CpModelBuilder cp_model; // There are `board_size` number of variables, one for a queen in each column // of the board. The value of each variable is the row that the queen is in. std::vector<IntVar> queens; queens.reserve(board_size); Domain range(0, board_size - 1); for (int i = 0; i < board_size; ++i) { queens.push_back( cp_model.NewIntVar(range).WithName("x" + std::to_string(i))); } // Define constraints. // The following sets the constraint that all queens are in different rows. cp_model.AddAllDifferent(queens); // No two queens can be on the same diagonal. std::vector<LinearExpr> diag_1; diag_1.reserve(board_size); std::vector<LinearExpr> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(queens[i] + i); diag_2.push_back(queens[i] - i); } cp_model.AddAllDifferent(diag_1); cp_model.AddAllDifferent(diag_2); int num_solutions = 0; Model model; model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) { LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (SolutionIntegerValue(response, queens[j]) == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; })); // Tell the solver to enumerate all solutions. SatParameters parameters; parameters.set_enumerate_all_solutions(true); model.Add(NewSatParameters(parameters)); const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model); LOG(INFO) << "Number of solutions found: " << num_solutions; // Statistics. LOG(INFO) << "Statistics"; LOG(INFO) << CpSolverResponseStats(response); } } // namespace sat } // namespace operations_research int main(int argc, char** argv) { int board_size = 8; if (argc > 1) { if (!absl::SimpleAtoi(argv[1], &board_size)) { LOG(INFO) << "Cannot parse '" << argv[1] << "', using the default value of 8."; board_size = 8; } } operations_research::sat::NQueensSat(board_size); return EXIT_SUCCESS; }
Java
package com.google.ortools.sat.samples; import com.google.ortools.Loader; import com.google.ortools.sat.CpModel; import com.google.ortools.sat.CpSolver; import com.google.ortools.sat.CpSolverSolutionCallback; import com.google.ortools.sat.IntVar; import com.google.ortools.sat.LinearExpr; /** OR-Tools solution to the N-queens problem. */ public final class NQueensSat { static class SolutionPrinter extends CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queensIn) { solutionCount = 0; queens = queensIn; } @Override public void onSolutionCallback() { System.out.println("Solution " + solutionCount); for (int i = 0; i < queens.length; ++i) { for (int j = 0; j < queens.length; ++j) { if (value(queens[j]) == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != queens.length - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } public int getSolutionCount() { return solutionCount; } private int solutionCount; private final IntVar[] queens; } public static void main(String[] args) { Loader.loadNativeLibraries(); // Create the model. CpModel model = new CpModel(); int boardSize = 8; // There are `BoardSize` number of variables, one for a queen in each column of the board. The // value of each variable is the row that the queen is in. IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = model.newIntVar(0, boardSize - 1, "x" + i); } // Define constraints. // All rows must be different. model.addAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[boardSize]; LinearExpr[] diag2 = new LinearExpr[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build(); diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build(); } model.addAllDifferent(diag1); model.addAllDifferent(diag2); // Create a solver and solve the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Tell the solver to enumerate all solutions. solver.getParameters().setEnumerateAllSolutions(true); // And solve. solver.solve(model, cb); // Statistics. System.out.println("Statistics"); System.out.println(" conflicts : " + solver.numConflicts()); System.out.println(" branches : " + solver.numBranches()); System.out.println(" wall time : " + solver.wallTime() + " s"); System.out.println(" solutions : " + cb.getSolutionCount()); } private NQueensSat() {} }
#C
// OR-Tools solution to the N-queens problem. using System; using Google.OrTools.Sat; public class NQueensSat { public class SolutionPrinter : CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queens) { queens_ = queens; } public override void OnSolutionCallback() { Console.WriteLine($"Solution {SolutionCount_}"); for (int i = 0; i < queens_.Length; ++i) { for (int j = 0; j < queens_.Length; ++j) { if (Value(queens_[j]) == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != queens_.Length - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount_++; } public int SolutionCount() { return SolutionCount_; } private int SolutionCount_; private IntVar[] queens_; } static void Main() { // Constraint programming engine CpModel model = new CpModel(); int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2); // Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb); Console.WriteLine("Statistics"); Console.WriteLine($" conflicts : {solver.NumConflicts()}"); Console.WriteLine($" branches : {solver.NumBranches()}"); Console.WriteLine($" wall time : {solver.WallTime()} s"); Console.WriteLine($" number of solutions found: {cb.SolutionCount()}"); } }
الحلّ باستخدام أداة حلّ CP الأصلية
تقدم الأقسام التالية برنامج بايثون يحل لغة N-queens باستخدام أداة حلّ CP الأصلية. (ومع ذلك، ننصح باستخدام أحدث أداة حلّ CP-SAT).
استيراد المكتبات
يستورد الرمز التالي المكتبة المطلوبة.
Python
import sys from ortools.constraint_solver import pywrapcp
C++
#include <cstdint> #include <cstdlib> #include <sstream> #include <vector> #include "ortools/base/logging.h" #include "ortools/constraint_solver/constraint_solver.h"
Java
import com.google.ortools.Loader; import com.google.ortools.constraintsolver.DecisionBuilder; import com.google.ortools.constraintsolver.IntVar; import com.google.ortools.constraintsolver.Solver;
#C
using System; using Google.OrTools.ConstraintSolver;
تضمين أداة الحلّ
يشير الرمز التالي إلى أداة حلّ CP الأصلية.
Python
solver = pywrapcp.Solver("n-queens")
C++
Solver solver("N-Queens");
Java
Solver solver = new Solver("N-Queens");
#C
Solver solver = new Solver("N-Queens");
إنشاء المتغيّرات
تنشئ طريقة IntVar في أداة الحلّ المتغيّرات للمشكلة في شكل مصفوفة.
باسم queens.
Python
# The array index is the column, and the value is the row. queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)]
C++
std::vector<IntVar*> queens; queens.reserve(board_size); for (int i = 0; i < board_size; ++i) { queens.push_back( solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i))); }
Java
int boardSize = 8; IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i); }
#C
const int BoardSize = 8; IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}"); }
بالنسبة إلى أي حلّ، تعني السمة queens[j] = i أنّ هناك ملكة في العمود j والصف.
i
وضع القيود
إليك الرمز الذي يضع قيودًا على المشكلة.
Python
# All rows must be different. solver.Add(solver.AllDifferent(queens)) # No two queens can be on the same diagonal. solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)])) solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)]))
C++
// The following sets the constraint that all queens are in different rows. solver.AddConstraint(solver.MakeAllDifferent(queens)); // All columns must be different because the indices of queens are all // different. No two queens can be on the same diagonal. std::vector<IntVar*> diag_1; diag_1.reserve(board_size); std::vector<IntVar*> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(solver.MakeSum(queens[i], i)->Var()); diag_2.push_back(solver.MakeSum(queens[i], -i)->Var()); } solver.AddConstraint(solver.MakeAllDifferent(diag_1)); solver.AddConstraint(solver.MakeAllDifferent(diag_2));
Java
// All rows must be different. solver.addConstraint(solver.makeAllDifferent(queens)); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[boardSize]; IntVar[] diag2 = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = solver.makeSum(queens[i], i).var(); diag2[i] = solver.makeSum(queens[i], -i).var(); } solver.addConstraint(solver.makeAllDifferent(diag1)); solver.addConstraint(solver.makeAllDifferent(diag2));
#C
// All rows must be different. solver.Add(queens.AllDifferent()); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[BoardSize]; IntVar[] diag2 = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = solver.MakeSum(queens[i], i).Var(); diag2[i] = solver.MakeSum(queens[i], -i).Var(); } solver.Add(diag1.AllDifferent()); solver.Add(diag2.AllDifferent());
تضمن هذه القيود الشروط الثلاثة لمشكلة N-queens ( الملكات في صفوف وأعمدة وأقطار مختلفة).
لا توجد ملكتان في الصف نفسه
يؤدي تطبيق طريقة AllDifferent لأداة الحلّ على queens إلى فرض قيم
queens[j] على أن تكون مختلفة لكل j، مما يعني أن جميع الملكات يجب أن تكون في
صفوف مختلفة.
لا توجد ملكتان في العمود نفسه
هذا القيد ضمني في تعريف queens.
وبما أنه لا يمكن أن يضم أي عنصرين من عناصر queens الفهرس ذاته، فلا يمكن استخدام حقلين
في نفس العمود.
لا توجد ملكتان على نفس القطر
القيد القطري أصعب قليلاً من قيود الصف والعمود. أولاً، إذا كانت ملكتان في نفس القطر، يجب أن يكون أحد ما يلي صحيحًا:
- إذا كان القطر تنازليًا (من اليسار إلى اليمين)، فإن رقم الصف بالإضافة إلى
رقم العمود لكل من الملكتين متساويتين. إذًا، لدى
queens(i) + iنفس القيمة لفهرسين مختلفينi. - إذا كان القطر تصاعديًا، يتم طرح رقم الصف ناقص رقم العمود لكل
الملكتان متساويتان. في هذه الحالة، تكون لـ
queens(i) - iنفس القيمة لمؤشرين مختلفينi.
إذًا، القيد القطري هو أن جميع قيم queens(i) + i يجب أن تكون
كذلك، وكذلك يجب أن تكون قيم queens(i) - i مختلفة،
مختلفة i.
يضيف التعليمة البرمجية أعلاه هذا القيد من خلال تطبيق
AllDifferent
إلى queens[j] + j وqueens[j] - j لكل i.
إضافة أداة إنشاء القرار
تتمثل الخطوة التالية في إنشاء أداة إنشاء قرارات تحدد استراتيجية البحث للمشكلة. قد يكون لاستراتيجية البحث أثر كبير في وقت البحث وذلك بسبب انتشار القيود، مما يقلل من عدد قيم المتغير التي يتعين على أداة الحلّ استكشافها. لقد رأيتَ مثالاً على ذلك من قبل في مثال لـ 4 ملكات:
تُنشئ التعليمة البرمجية التالية أداة إنشاء قرارات باستخدام
Phase
.
Python
db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE)
C++
DecisionBuilder* const db = solver.MakePhase( queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE);
Java
// Create the decision builder to search for solutions. final DecisionBuilder db = solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
#C
// Create the decision builder to search for solutions. DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
راجع أداة إنشاء القرارات للحصول على تفاصيل حول
إدخال وسيطات إلى الطريقة Phase.
كيف تعمل أداة إنشاء القرار في مثال 4 ملكات
لنلقِ نظرة على الطريقة التي توجه بها أداة إنشاء القرارات البحث في
مثال لـ 4 ملكات:
تبدأ أداة الحلّ بـ queens[0]، وهو المتغيّر الأول في الصفيف حسب التوجيهات
بواسطة CHOOSE_FIRST_UNBOUND تضع أداة الحلّ بعد ذلك queens[0] أصغر
قيمة لم تتم تجربتها من قبل، وهي 0 في هذه المرحلة، حسب توجيهات
ASSIGN_MIN_VALUE هذا يضع الملكة الأولى في الزاوية اليسرى العليا من
لوح.
بعد ذلك، تختار أداة الحلّ queens[1]، وهو الآن أول متغيّر غير مرتبط في
queens بعد نشر القيود، هناك صفان محتملان
الملكة في العمود 1: الصف 2 أو الصف 3. يوجّه الخيار ASSIGN_MIN_VALUE
أداة الحلّ لإسناد تعيين queens[1] = 2. (إذا بدلاً من ذلك، يمكنك ضبط IntValueStrategy على
ASSIGN_MAX_VALUE، ستخصّص أداة الحلّ queens[1] = 3).
يمكنك التحقّق من أنّ بقية عمليات البحث تتبع القواعد نفسها.
عليك استدعاء أداة الحلّ وعرض النتائج.
يقوم التعليمة البرمجية التالية بتشغيل أداة الحل وعرض الحل.
Python
# Iterates through the solutions, displaying each. num_solutions = 0 solver.NewSearch(db) while solver.NextSolution(): # Displays the solution just computed. for i in range(board_size): for j in range(board_size): if queens[j].Value() == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() num_solutions += 1 solver.EndSearch()
C++
// Iterates through the solutions, displaying each. int num_solutions = 0; solver.NewSearch(db); while (solver.NextSolution()) { // Displays the solution just computed. LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (queens[j]->Value() == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; } solver.EndSearch();
Java
int solutionCount = 0; solver.newSearch(db); while (solver.nextSolution()) { System.out.println("Solution " + solutionCount); for (int i = 0; i < boardSize; ++i) { for (int j = 0; j < boardSize; ++j) { if (queens[j].value() == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != boardSize - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } solver.endSearch();
#C
// Iterates through the solutions, displaying each. int SolutionCount = 0; solver.NewSearch(db); while (solver.NextSolution()) { Console.WriteLine("Solution " + SolutionCount); for (int i = 0; i < BoardSize; ++i) { for (int j = 0; j < BoardSize; ++j) { if (queens[j].Value() == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != BoardSize - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount++; } solver.EndSearch();
إليك الحل الأول الذي توصل إليه البرنامج للوحة مقاس 8×8.
Q _ _ _ _ _ _ _
_ _ _ _ _ _ Q _
_ _ _ _ Q _ _ _
_ _ _ _ _ _ _ Q
_ Q _ _ _ _ _ _
_ _ _ Q _ _ _ _
_ _ _ _ _ Q _ _
_ _ Q _ _ _ _ _
...91 other solutions displayed...
Statistics
failures: 304
branches: 790
wall time: 5 ms
Solutions found: 92يمكنك حل مشكلة لوحة ذات حجم مختلف عن طريق المرور في N كـ
وسيطة سطر الأوامر. على سبيل المثال، بإمكان python nqueens_cp.py 6 حلّ المسألة.
للوحة 6×6.
البرنامج بأكمله
يمكنك الاطّلاع أدناه على البرنامج الكامل.
Python
"""OR-Tools solution to the N-queens problem.""" import sys from ortools.constraint_solver import pywrapcp def main(board_size): # Creates the solver. solver = pywrapcp.Solver("n-queens") # Creates the variables. # The array index is the column, and the value is the row. queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)] # Creates the constraints. # All rows must be different. solver.Add(solver.AllDifferent(queens)) # No two queens can be on the same diagonal. solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)])) solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)])) db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE) # Iterates through the solutions, displaying each. num_solutions = 0 solver.NewSearch(db) while solver.NextSolution(): # Displays the solution just computed. for i in range(board_size): for j in range(board_size): if queens[j].Value() == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() num_solutions += 1 solver.EndSearch() # Statistics. print("\nStatistics") print(f" failures: {solver.Failures()}") print(f" branches: {solver.Branches()}") print(f" wall time: {solver.WallTime()} ms") print(f" Solutions found: {num_solutions}") if __name__ == "__main__": # By default, solve the 8x8 problem. size = 8 if len(sys.argv) > 1: size = int(sys.argv[1]) main(size)
C++
// OR-Tools solution to the N-queens problem. #include <cstdint> #include <cstdlib> #include <sstream> #include <vector> #include "ortools/base/logging.h" #include "ortools/constraint_solver/constraint_solver.h" namespace operations_research { void NQueensCp(const int board_size) { // Instantiate the solver. Solver solver("N-Queens"); std::vector<IntVar*> queens; queens.reserve(board_size); for (int i = 0; i < board_size; ++i) { queens.push_back( solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i))); } // Define constraints. // The following sets the constraint that all queens are in different rows. solver.AddConstraint(solver.MakeAllDifferent(queens)); // All columns must be different because the indices of queens are all // different. No two queens can be on the same diagonal. std::vector<IntVar*> diag_1; diag_1.reserve(board_size); std::vector<IntVar*> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(solver.MakeSum(queens[i], i)->Var()); diag_2.push_back(solver.MakeSum(queens[i], -i)->Var()); } solver.AddConstraint(solver.MakeAllDifferent(diag_1)); solver.AddConstraint(solver.MakeAllDifferent(diag_2)); DecisionBuilder* const db = solver.MakePhase( queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE); // Iterates through the solutions, displaying each. int num_solutions = 0; solver.NewSearch(db); while (solver.NextSolution()) { // Displays the solution just computed. LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (queens[j]->Value() == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; } solver.EndSearch(); // Statistics. LOG(INFO) << "Statistics"; LOG(INFO) << " failures: " << solver.failures(); LOG(INFO) << " branches: " << solver.branches(); LOG(INFO) << " wall time: " << solver.wall_time() << " ms"; LOG(INFO) << " Solutions found: " << num_solutions; } } // namespace operations_research int main(int argc, char** argv) { int board_size = 8; if (argc > 1) { board_size = std::atoi(argv[1]); } operations_research::NQueensCp(board_size); return EXIT_SUCCESS; }
Java
// OR-Tools solution to the N-queens problem. package com.google.ortools.constraintsolver.samples; import com.google.ortools.Loader; import com.google.ortools.constraintsolver.DecisionBuilder; import com.google.ortools.constraintsolver.IntVar; import com.google.ortools.constraintsolver.Solver; /** N-Queens Problem. */ public final class NQueensCp { public static void main(String[] args) { Loader.loadNativeLibraries(); // Instantiate the solver. Solver solver = new Solver("N-Queens"); int boardSize = 8; IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i); } // Define constraints. // All rows must be different. solver.addConstraint(solver.makeAllDifferent(queens)); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[boardSize]; IntVar[] diag2 = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = solver.makeSum(queens[i], i).var(); diag2[i] = solver.makeSum(queens[i], -i).var(); } solver.addConstraint(solver.makeAllDifferent(diag1)); solver.addConstraint(solver.makeAllDifferent(diag2)); // Create the decision builder to search for solutions. final DecisionBuilder db = solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE); int solutionCount = 0; solver.newSearch(db); while (solver.nextSolution()) { System.out.println("Solution " + solutionCount); for (int i = 0; i < boardSize; ++i) { for (int j = 0; j < boardSize; ++j) { if (queens[j].value() == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != boardSize - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } solver.endSearch(); // Statistics. System.out.println("Statistics"); System.out.println(" failures: " + solver.failures()); System.out.println(" branches: " + solver.branches()); System.out.println(" wall time: " + solver.wallTime() + "ms"); System.out.println(" Solutions found: " + solutionCount); } private NQueensCp() {} }
#C
// OR-Tools solution to the N-queens problem. using System; using Google.OrTools.ConstraintSolver; public class NQueensCp { public static void Main(String[] args) { // Instantiate the solver. Solver solver = new Solver("N-Queens"); const int BoardSize = 8; IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. solver.Add(queens.AllDifferent()); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[BoardSize]; IntVar[] diag2 = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = solver.MakeSum(queens[i], i).Var(); diag2[i] = solver.MakeSum(queens[i], -i).Var(); } solver.Add(diag1.AllDifferent()); solver.Add(diag2.AllDifferent()); // Create the decision builder to search for solutions. DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE); // Iterates through the solutions, displaying each. int SolutionCount = 0; solver.NewSearch(db); while (solver.NextSolution()) { Console.WriteLine("Solution " + SolutionCount); for (int i = 0; i < BoardSize; ++i) { for (int j = 0; j < BoardSize; ++j) { if (queens[j].Value() == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != BoardSize - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount++; } solver.EndSearch(); // Statistics. Console.WriteLine("Statistics"); Console.WriteLine($" failures: {solver.Failures()}"); Console.WriteLine($" branches: {solver.Branches()}"); Console.WriteLine($" wall time: {solver.WallTime()} ms"); Console.WriteLine($" Solutions found: {SolutionCount}"); } }
عدد الحلول
يزيد عدد المحاليل بشكل كبير تقريبًا مع زيادة حجم اللوحة:
| حجم اللوحة | الحلول | وقت العثور على كل الحلول (بالملّي ثانية) |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 0 | 0 |
| 3 | 0 | 0 |
| 4 | 2 | 0 |
| 5 | 10 | 0 |
| 6 | 4 | 0 |
| 7 | 40 | 3 |
| 8 | 92 | 9 |
| 9 | 352 | 35 |
| 10 | 724 | 95 |
| 11 | 2680 | 378 |
| 12 | 14200 | 2198 |
| 13 | 73712 | 11628 |
| 14 | 365596 | 62427 |
| 15 | 2279184 | 410701 |
العديد من الحلول هي مجرد تدويرات أخرى، وهو أسلوب يسمى التماثل يمكن استخدام الانقسام لتقليل كمية العمليات الحسابية المطلوبة. لا نستخدم ذلك هنا؛ لا يُقصد من الحل الذي نقدمه أن تكون سريعة، بل بسيطة فقط. بالطبع، يمكننا أن نجعل الأمر أسرع إذا أردنا إيجاد حل واحد فقط بدلاً من جميعها: لا تزيد عن بضع مللي ثانية لأحجام اللوحات التي تصل إلى 50.
