如何偵錯及減輕最佳化失敗的影響?
摘要:如果模型難以最佳化,請務必先修正問題,再嘗試其他做法。診斷及修正訓練失敗問題是目前的研究重點。

請注意圖 4 的下列事項:
- 變更步幅不會導致低學習率的成效下降。
- 由於不穩定,高學習率不再能有效訓練。
- 套用 1000 個步驟的學習率預熱,即可解決這個不穩定問題,並以 0.1 的學習率上限穩定訓練。
找出不穩定的工作負載
如果學習率過高,任何工作負載都會變得不穩定。不穩定性只會在迫使您使用過小的學習率時造成問題。至少有兩種訓練不穩定性值得區分:
- 初始化或訓練初期不穩定。
- 訓練期間突然不穩。
您可以採取系統性方法,透過下列方式找出工作負載的穩定性問題:
- 進行學習率掃描,找出最佳學習率 lr*。
- 繪製學習率略高於 lr* 的訓練損失曲線。
- 如果學習率 > lr* 顯示損失不穩定 (訓練期間損失上升而非下降),修正不穩定通常可改善訓練。
在訓練期間記錄完整損失梯度 L2 範數,因為離群值可能會在訓練中途造成虛假的不穩定性。這項資訊可做為依據,判斷要多積極地剪輯漸層或更新權重。
注意:部分模型在初期會出現不穩定狀態,隨後恢復穩定,但訓練速度會變慢。如果評估頻率不夠高,常見的評估時間表可能會錯過這些問題!
如要檢查這個問題,您可以訓練約 500 個步驟的縮短執行時間,但要評估每個步驟。lr = 2 * current best

常見不穩定模式的可能修正方式
針對常見的不穩定模式,請考慮下列可能的修正方式:
- 套用學習率預熱。這項功能最適合用於訓練初期不穩定的情況。
- 套用梯度限幅。這項功能有助於解決訓練初期和中期的不穩定問題,並修正熱身無法解決的初始化問題。
- 請嘗試使用新的最佳化工具。有時 Adam 可以處理 Momentum 無法處理的不穩定情況。我們正積極研究這方面。
- 請確保您為模型架構採用最佳做法和最佳初始化設定 (範例如下)。如果模型尚未包含殘差連線和正規化,請新增這些項目。
- 在殘餘值之前,將正規化做為最後一項作業。例如:
x + Norm(f(x))。 請注意,Norm(x + f(x))可能會導致問題。 - 請嘗試將剩餘分支初始化為 0。(請參閱「ReZero is All You Need: Fast Convergence at Large Depth.」)
- 降低學習率。這是最後的手段。
學習率預熱

何時套用學習率升溫

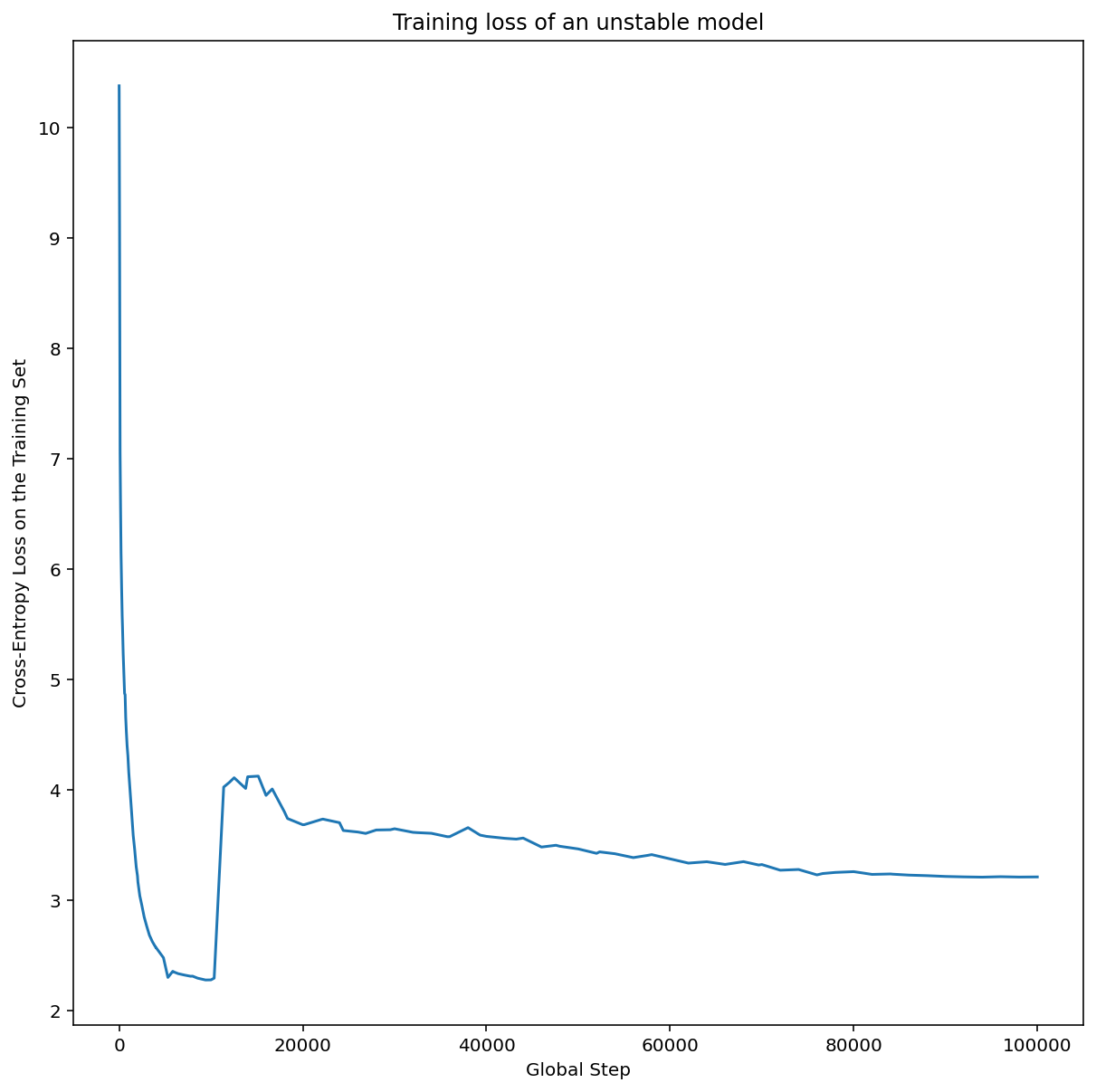
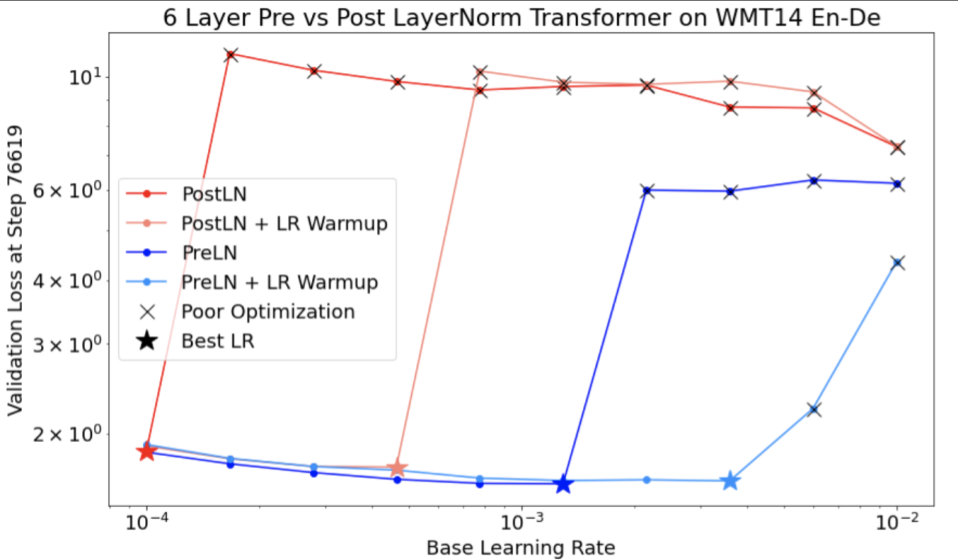
圖 7a 顯示超參數軸圖,指出模型發生最佳化不穩定情形,因為最佳學習率正好位於不穩定邊緣。
圖 7b 顯示如何檢查,方法是查看以比這個峰值大 5 倍或 10 倍的學習率訓練模型時的訓練損失。如果該圖在穩定下降後突然出現損失上升的情況 (例如上圖中步驟 ~10k 的位置),則模型可能受到最佳化不穩定性的影響。
如何套用學習率預熱
使用上述程序,找出模型變得不穩定的學習率 unstable_base_learning_rate。
預熱程序會預先加入學習率時間表,將學習率從 0 提升至某個穩定值 base_learning_rate,且該值至少比 unstable_base_learning_rate 大一個數量級。預設值為嘗試 10 倍 base_learning_rate unstable_base_learning_rate。但請注意,您可以針對 100 倍的unstable_base_learning_rate再次執行整個程序。具體時間表如下:
- 在 warmup_steps 期間,從 0 逐步調升至 base_learning_rate。
- 以固定速率訓練 post_warmup_steps。
您的目標是找出最短的 warmup_steps,讓您存取遠高於 unstable_base_learning_rate 的最高學習率。
因此,您需要針對每個 base_learning_rate 調整 warmup_steps 和 post_warmup_steps。通常將 post_warmup_steps 設為 2*warmup_steps 即可。
您可以獨立調整升溫期,不必受現有衰減時間表影響。warmup_steps
應掃過幾個不同的量級。舉例來說,假設您想研究 [10, 1000, 10,000, 100,000],最大可行點不得超過 max_train_steps 的 10%。
建立不會在 base_learning_rate 造成訓練爆炸的 warmup_steps 後,應將其套用至基準模型。基本上,只要將這個時間表加到現有時間表的前面,然後使用上述最佳檢查點選取方式,比較這項實驗與基準即可。舉例來說,如果我們原本有 10,000 個 max_train_steps,並執行了 1,000 個步驟的 warmup_steps,則新的訓練程序總共應執行 11,000 個步驟。
如果穩定訓練需要較長的 warmup_steps (>5% 的 max_train_steps),您可能需要增加 max_train_steps 來因應這項需求。
在整個工作負載範圍內,其實沒有「典型」值。有些模型只需要 100 個步驟,有些模型 (尤其是 Transformer) 則可能需要 4 萬個以上的步驟。
梯度限幅
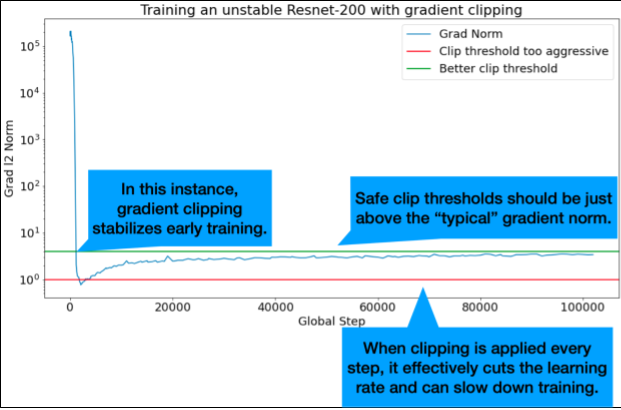
發生大型或離群漸層問題時,漸層剪輯功能最實用。漸層剪裁可修正下列任一問題:
- 早期訓練不穩定 (早期梯度範數較大)
- 訓練期間不穩定 (訓練期間梯度突然飆升)。
有時,較長的預熱期可以修正裁剪無法解決的不穩定問題;詳情請參閱「學習率預熱」。
🤖 暖機期間發生削波情形該怎麼辦?
理想的剪輯片段門檻略高於「一般」漸層常態。
以下舉例說明如何剪裁漸層:
- 如果梯度 $\left | g \right |$ 的範數大於梯度裁剪門檻 $\lambda$,則執行 ${g}'= \lambda \times \frac{g}{\left | g \right |}$,其中 ${g}'$ 是新梯度。
在訓練期間記錄未剪輯的梯度範數。根據預設,系統會產生:
- 梯度範數與步數的關係圖
- 在所有步驟中匯總的梯度範數直方圖
根據漸層常態分布的第 90 個百分位數,選擇漸層剪除門檻。門檻取決於工作負載,但 90% 是不錯的起點。如果 90% 無效,可以調整這個門檻。
🤖 採用某種自動調整策略如何?
如果嘗試梯度剪輯後,不穩定問題依然存在,可以嘗試更嚴格的剪輯,也就是縮小閾值。
極度積極的梯度剪除 (也就是超過 50% 的更新遭到剪除),本質上是一種奇怪的學習率降低方式。如果您發現自己使用極度激進的剪除方式,可能應該改為直接調降學習率。
為什麼您將學習率和其他最佳化參數稱為超參數?這些並非任何先前分配的參數。
「超參數」一詞在貝氏機器學習中具有精確的意義,因此將學習率和其他可調整的深度學習參數稱為「超參數」,可以說是濫用術語。我們偏好使用「元參數」一詞來表示學習率、架構參數,以及所有其他可調整的深度學習項目。這是因為元參數可避免誤用「超參數」一詞而造成混淆。討論貝氏最佳化時,這種混淆情況尤其可能發生,因為機率性回應曲面模型有自己的真實超參數。
很遺憾,雖然「超參數」一詞可能會造成混淆,但已在深度學習社群中廣為使用。因此,這份文件是為廣大讀者而撰寫,其中許多人可能不瞭解這項技術細節,我們選擇為這個領域的其中一個混淆來源做出貢獻,希望避免出現其他混淆。不過,我們在發布研究論文時可能會做出不同選擇,並建議在大多數情況下使用「metaparameter」一詞。
為什麼不應調整批次大小,直接提升驗證集效能?
變更批次大小,但不變更訓練管道的任何其他詳細資料,通常會影響驗證集效能。不過,如果針對每個批次大小獨立最佳化訓練管道,通常就不會出現驗證集效能差異。
與批次大小互動最密切的超參數,因此最重要的是針對每個批次大小分別調整,是最佳化工具超參數 (例如學習率、動量) 和正規化超參數。由於樣本變異數,較小的批次大小會將更多雜訊導入訓練演算法。這種雜訊可以產生正規化效果。因此,批次大小越大,越容易過度訓練,可能需要更強大的正規化和/或其他正規化技術。此外,變更批次大小時,您可能需要調整訓練步驟數。
考量所有這些影響後,沒有令人信服的證據顯示批次大小會影響可達成的最高驗證效能。詳情請參閱 Shallue 等人於 2018 年發表的論文。
所有熱門最佳化演算法的更新規則為何?
本節提供幾種熱門最佳化演算法的更新規則。
隨機梯度下降 (SGD)
\[\theta_{t+1} = \theta_{t} - \eta_t \nabla \mathcal{l}(\theta_t)\]
其中 $\eta_t$ 是步驟 $t$ 的學習率。
累積熱度
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t v_{t+1}\]
其中 $\eta_t$ 是步驟 $t$ 的學習率,$\gamma$ 則是動量係數。
Nesterov
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t ( \gamma v_{t+1} + \nabla \mathcal{l}(\theta_{t}) )\]
其中 $\eta_t$ 是步驟 $t$ 的學習率,$\gamma$ 則是動量係數。
RMSProp
\[v_0 = 1 \text{, } m_0 = 0\]
\[v_{t+1} = \rho v_{t} + (1 - \rho) \nabla \mathcal{l}(\theta_t)^2\]
\[m_{t+1} = \gamma m_{t} + \frac{\eta_t}{\sqrt{v_{t+1} + \epsilon}}\nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - m_{t+1}\]
ADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l}(\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{m_{t+1}}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
NADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l} (\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{\beta_1 m_{t+1} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]