En esta unidad, explorarás el algoritmo de divisor más simple y común, que crea condiciones de la forma $\mathrm{feature}_i \geq t$ en la siguiente configuración:
- Tarea de clasificación binaria
- Sin valores faltantes en los ejemplos
- Sin índice precalculado en los ejemplos
Supongamos un conjunto de $n$ ejemplos con un atributo numérico y una etiqueta binaria “naranja” y “azul”. Formalmente, describamos el conjunto de datos $D$ de la siguiente manera:
Donde:
- $x_i$ es el valor de un atributo numérico en $\mathbb{R}$ (el conjunto de números reales).
- $y_i$ es un valor de etiqueta de clasificación binaria en {naranja, azul}.
Nuestro objetivo es encontrar un valor umbral $t$ (umbral) de modo que dividir los ejemplos $D$ en los grupos $T(rue)$ y $F(alse)$ según la condición $x_i \geq t$ mejore la separación de las etiquetas; por ejemplo, más ejemplos “naranja” en $T$ y más ejemplos “azules” en $F$.
La entropía de Shannon es una medida del desorden. Para una etiqueta binaria, haz lo siguiente:
- La entropía de Shannon es máxima cuando las etiquetas de los ejemplos están equilibradas (50% azul y 50% naranja).
- La entropía de Shannon es mínima (valor cero) cuando las etiquetas de los ejemplos son puras (100% azul o 100% naranja).
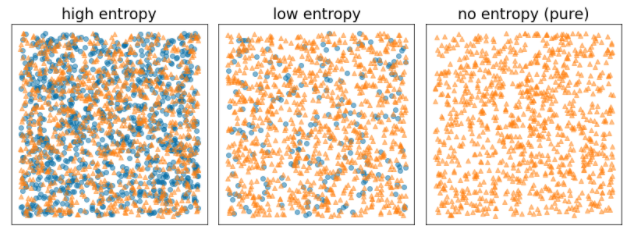
Figura 8. Tres niveles de entropía diferentes.
De forma formal, queremos encontrar una condición que disminuya la suma ponderada de la entropía de las distribuciones de etiquetas en $T$ y $F$. La puntuación correspondiente es la ganancia de información, que es la diferencia entre la entropía de $D$ y la entropía de {$T$,$F$}. A esta diferencia se la llama ganancia de información.
En la siguiente figura, se muestra una división incorrecta, en la que la entropía sigue siendo alta y la ganancia de información es baja:
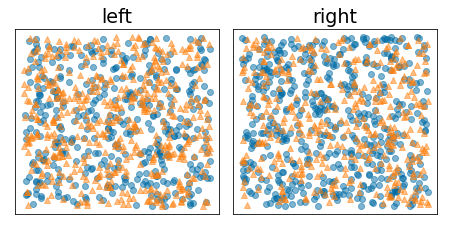
Figura 9. Una división incorrecta no reduce la entropía de la etiqueta.
Por el contrario, en la siguiente figura, se muestra una mejor división en la que la entropía se vuelve baja (y la ganancia de información alta):
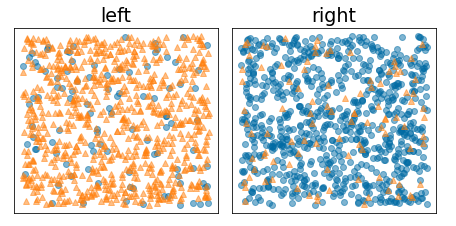
Figura 10. Una buena división reduce la entropía de la etiqueta.
De forma formal:
\[\begin{eqnarray} T & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \ge t \} \\[12pt] F & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \lt t \} \\[12pt] R(X) & = & \frac{\lvert \{ x | x \in X \ \textrm{and} \ x = \mathrm{pos} \} \rvert}{\lvert X \rvert} \\[12pt] H(X) & = & - p \log p - (1 - p) \log (1-p) \ \textrm{with} \ p = R(X)\\[12pt] IG(D,T,F) & = & H(D) - \frac {\lvert T\rvert} {\lvert D \rvert } H(T) - \frac {\lvert F \rvert} {\lvert D \rvert } H(F) \end{eqnarray}\]
Donde:
- $IG(D,T,F)$ es la ganancia de información de dividir $D$ en $T$ y $F$.
- $H(X)$ es la entropía del conjunto de ejemplos $X$.
- $|X|$ es la cantidad de elementos del conjunto $X$.
- $t$ es el valor del umbral.
- $pos$ es el valor de la etiqueta positiva, por ejemplo, "azul" en el ejemplo anterior. Elegir una etiqueta diferente para que sea la "etiqueta positiva" no cambia el valor de la entropía ni la ganancia de información.
- $R(X)$ es la proporción de valores de etiquetas positivas en los ejemplos $X$.
- $D$ es el conjunto de datos (como se definió anteriormente en esta unidad).
En el siguiente ejemplo, consideramos un conjunto de datos de clasificación binaria con un solo atributo numérico $x$. En la siguiente figura, se muestran los diferentes valores de umbral $t$ (eje x):
- El histograma de la función $x$.
- La proporción de ejemplos “azules” en los conjuntos $D$, $T$ y $F$ según el valor del umbral
- La entropía en $D$, $T$ y $F$.
- La ganancia de información, es decir, la delta de entropía entre $D$ y {$T$,$F$} ponderada por la cantidad de ejemplos
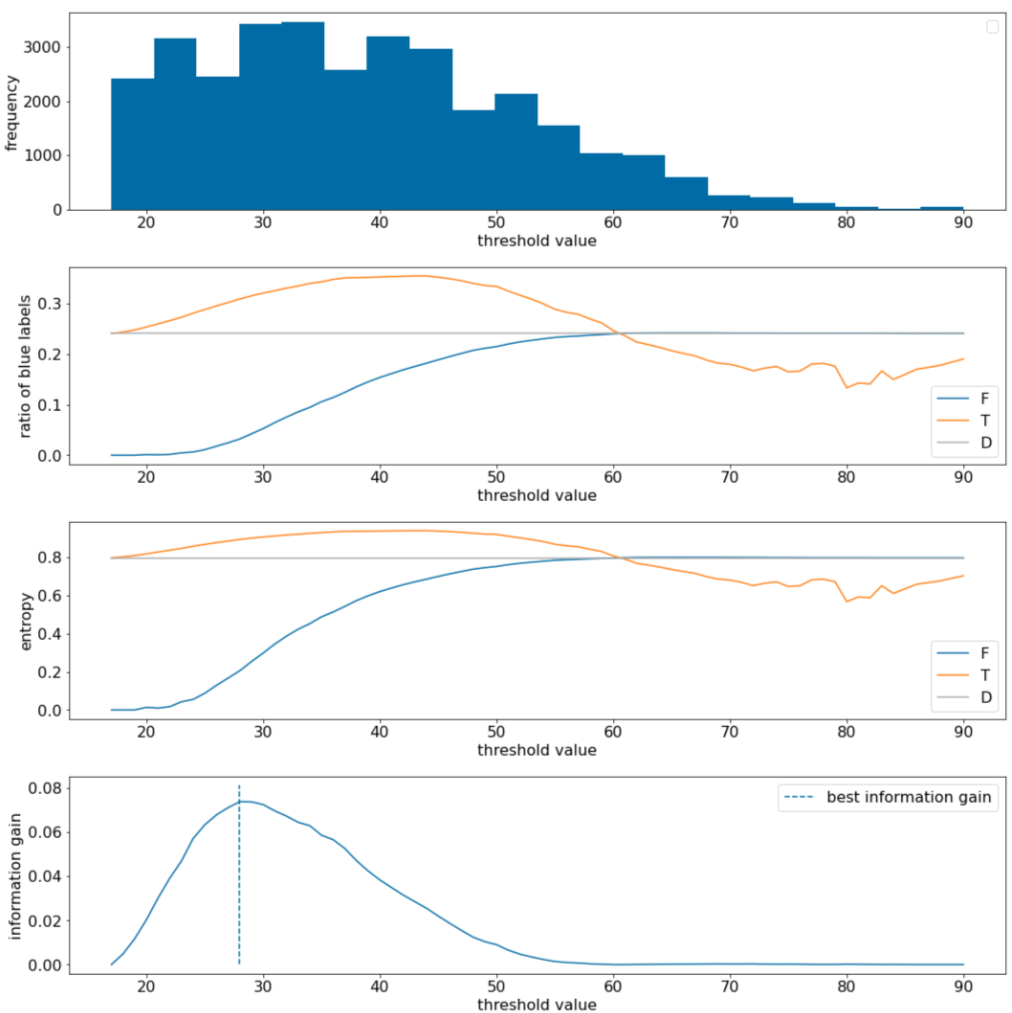
Figura 11: Cuatro gráficos de umbrales.
En estos gráficos, se muestra lo siguiente:
- El gráfico "frecuencia" muestra que las observaciones están relativamente bien distribuidas con concentraciones entre 18 y 60. Una amplia dispersión de valores significa que hay muchas posibles divisiones, lo que es bueno para entrenar el modelo.
La proporción de etiquetas "azules" en el conjunto de datos es de alrededor del 25%. El gráfico “proporción de etiqueta azul” muestra que, para valores de umbral entre 20 y 50, se produce lo siguiente:
- El conjunto $T$ contiene un exceso de ejemplos de etiquetas "azules" (hasta un 35% para el umbral 35).
- El conjunto $F$ contiene un déficit complementario de ejemplos de etiquetas "azules" (solo el 8% para el umbral 35).
Tanto el gráfico de “proporción de etiquetas azules” como el de “entropía” indican que las etiquetas pueden estar relativamente bien separadas en este rango de umbral.
Esta observación se confirma en el gráfico de “ganancia de información”. Vemos que la ganancia de información máxima se obtiene con t~=28 para un valor de ganancia de información de ~0.074. Por lo tanto, la condición que muestra el divisor será $x \geq 28$.
La ganancia de información siempre es positiva o nula. Converja a cero a medida que el valor del umbral converja hacia su valor máximo o mínimo. En esos casos, $F$ o $T$ se vacían, mientras que el otro contiene todo el conjunto de datos y muestra una entropía igual a la de $D$. La ganancia de información también puede ser cero cuando $H(T)$ = $H(F)$ = $H(D)$. En el umbral 60, las proporciones de etiquetas "azules" para $T$ y $F$ son las mismas que las de $D$, y la ganancia de información es cero.
Los valores candidatos para $t$ en el conjunto de números reales ($\mathbb{R}$) son infinitos. Sin embargo, dado un número finito de ejemplos, solo existe una cantidad finita de divisiones de $D$ en $T$ y $F$. Por lo tanto, solo una cantidad finita de valores de $t$ es significativa para probar.
Un enfoque clásico es ordenar los valores xi en orden creciente xs(i) de modo que se cumpla lo siguiente:
Luego, prueba $t$ para cada valor a mitad de camino entre valores consecutivos ordenados de $x_i$. Por ejemplo, supongamos que tienes 1,000 valores de punto flotante de una característica en particular. Después de ordenar, supongamos que los dos primeros valores son 8.5 y 8.7. En este caso, el primer valor de umbral que se probará sería 8.6.
De forma formal, consideramos los siguientes valores candidatos para t:
La complejidad temporal de este algoritmo es $\mathcal{O} ( n \log n) $, con $n$ la cantidad de ejemplos en el nodo (debido al orden de los valores de los atributos). Cuando se aplica a un árbol de decisión, el algoritmo de divisor se aplica a cada nodo y a cada atributo. Ten en cuenta que cada nodo recibe aproximadamente la mitad de sus ejemplos superiores. Por lo tanto, según el teorema maestro, la complejidad temporal de entrenar un árbol de decisión con este divisor es la siguiente:
Donde:
- $m$ es la cantidad de atributos.
- $n$ es la cantidad de ejemplos de entrenamiento.
En este algoritmo, el valor de los atributos no importa, solo el orden. Por este motivo, este algoritmo funciona independientemente de la escala o la distribución de los valores de los atributos. Por este motivo, no necesitamos normalizar ni escalar los atributos numéricos cuando entrenamos un árbol de decisión.