TensorFlow, Keras y aprendizaje profundo, sin un doctorado

En este codelab, aprenderás a compilar y entrenar una red neuronal que reconoce dígitos escritos a mano. En el camino, a medida que mejores tu red neuronal para alcanzar una precisión del 99%, también descubrirás las herramientas que usan los profesionales del aprendizaje profundo para entrenar sus modelos de manera eficiente.

En este codelab, se usa el conjunto de datos MNIST, una colección de 60,000 dígitos etiquetados que ha mantenido ocupadas a generaciones de estudiantes de doctorado durante casi dos décadas. Resolverás el problema con menos de 100 líneas de código de Python o TensorFlow.

Qué aprenderás

• Qué es una red neuronal y cómo entrenarla
• Cómo compilar una red neuronal básica de 1 capa con tf.keras
• Cómo agregar más capas
• Cómo configurar un programa de tasa de aprendizaje
• Cómo compilar redes neuronales convolucionales
• Cómo usar técnicas de regularización: abandono y normalización por lotes
• Qué es el sobreajuste

Requisitos

Solo un navegador. Este taller se puede realizar por completo con Google Colaboratory.

Comentarios

Avísanos si ves algo incorrecto en este lab o si crees que se debería mejorar. Manejamos los comentarios a través de los problemas de GitHub [vínculo de comentarios].

En este lab, se usa Google Colaboratory y no se requiere ninguna configuración de tu parte. Puedes ejecutarlo desde una Chromebook. Abre el siguiente archivo y ejecuta las celdas para familiarizarte con los notebooks de Colab.

Welcome to Colab.ipynb

A continuación, se incluyen instrucciones adicionales:

Selecciona un backend de GPU

En el menú de Colab, selecciona Entorno de ejecución > Cambiar tipo de entorno de ejecución y, luego, selecciona GPU. La conexión con el tiempo de ejecución se realizará automáticamente en la primera ejecución, o bien puedes usar el botón "Conectar" en la esquina superior derecha.

Ejecución de notebooks

Ejecuta las celdas una por una haciendo clic en una celda y usando Mayúsculas + INTRO. También puedes ejecutar todo el notebook con Runtime > Run all.

Índice

Todos los notebooks tienen un índice. Puedes abrirlo con la flecha negra que se encuentra a la izquierda.

Celdas ocultas

Algunas celdas solo mostrarán su título. Esta es una función del notebook específica de Colab. Puedes hacer doble clic en ellos para ver el código que contienen, pero, por lo general, no es muy interesante. Por lo general, son funciones de asistencia o visualización. Aún debes ejecutar estas celdas para que se definan las funciones que contienen.

Primero, veremos cómo se entrena una red neuronal. Abre el notebook que se muestra a continuación y ejecuta todas las celdas. Por el momento, no prestes atención al código. Lo explicaremos más adelante.

keras_01_mnist.ipynb

A medida que ejecutes el notebook, enfócate en las visualizaciones. Consulta las explicaciones a continuación.

Datos de entrenamiento

Tenemos un conjunto de datos de dígitos escritos a mano que se etiquetaron para que sepamos qué representa cada imagen, es decir, un número entre 0 y 9. En el notebook, verás un fragmento:

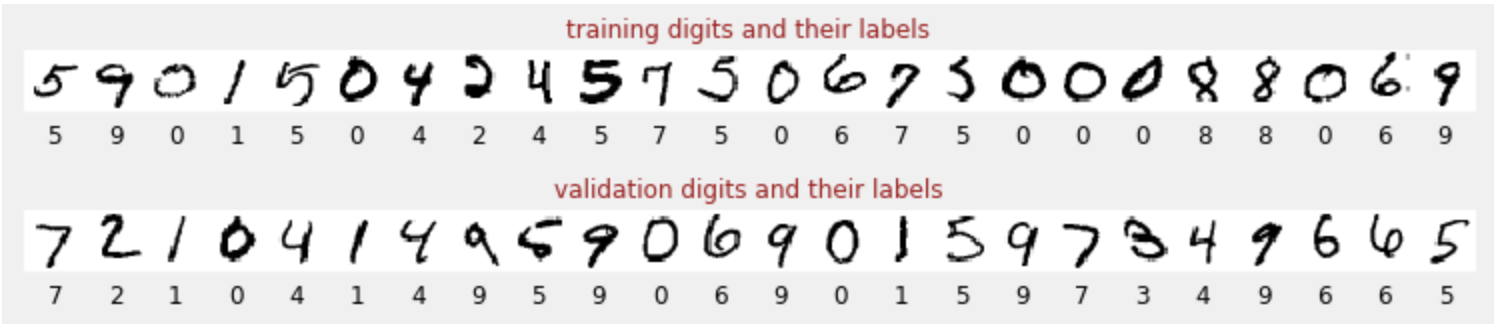
La red neuronal que crearemos clasificará los dígitos escritos a mano en sus 10 clases (0, …, 9). Lo hace en función de parámetros internos que deben tener un valor correcto para que la clasificación funcione bien. Este "valor correcto" se aprende a través de un proceso de entrenamiento que requiere un "conjunto de datos etiquetados" con imágenes y las respuestas correctas asociadas.

¿Cómo sabemos si la red neuronal entrenada funciona bien o no? Usar el conjunto de datos de entrenamiento para probar la red sería hacer trampa. Ya vio ese conjunto de datos varias veces durante el entrenamiento y, sin duda, tiene un rendimiento muy alto en él. Necesitamos otro conjunto de datos etiquetados, que no se haya visto durante el entrenamiento, para evaluar el rendimiento de la red en el "mundo real". Se denomina "conjunto de datos de validación".

Este conjunto de datos contiene 50,000 dígitos de entrenamiento. En cada iteración, alimentamos el bucle de entrenamiento con un "lote" de 128 ejemplos para que el sistema haya visto todos los dígitos de entrenamiento una vez después de 391 iteraciones. A esto lo llamamos "época".

También hay 10,000 dígitos de "validación" separados para probar el rendimiento del modelo.

Capacitación

A medida que avanza el entrenamiento, se actualizan los parámetros internos del modelo y este mejora cada vez más en el reconocimiento de los dígitos escritos a mano. Puedes verlo en el gráfico de entrenamiento:

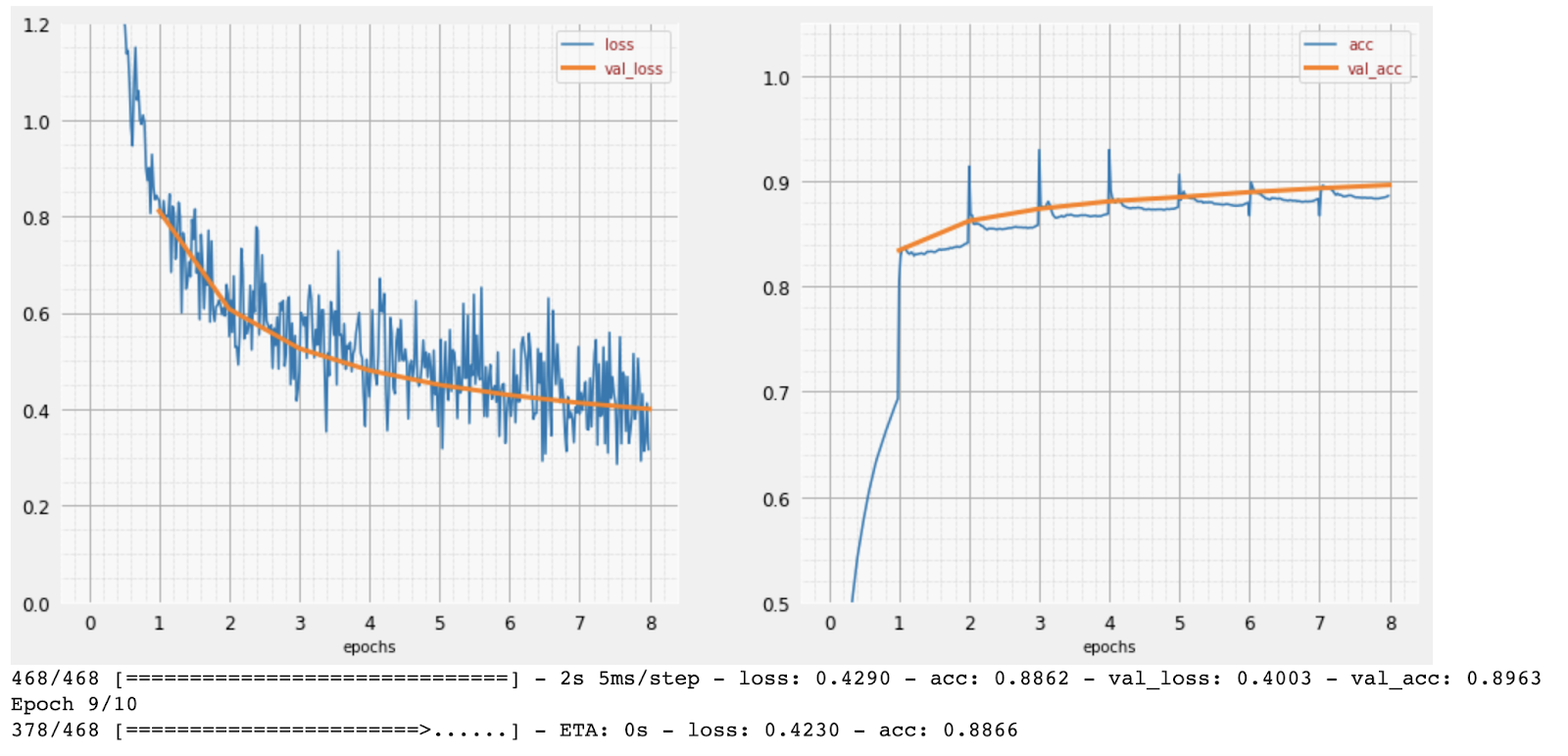
A la derecha, la "precisión" es simplemente el porcentaje de dígitos reconocidos correctamente. Aumenta a medida que avanza el entrenamiento, lo cual es bueno.

A la izquierda, podemos ver la "pérdida". Para impulsar el entrenamiento, definiremos una función de "pérdida", que representa qué tan mal reconoce el sistema los dígitos, y trataremos de minimizarla. Aquí, puedes ver que la pérdida disminuye tanto en los datos de entrenamiento como en los de validación a medida que avanza el entrenamiento, lo cual es bueno. Esto significa que la red neuronal está aprendiendo.

El eje X representa la cantidad de "épocas" o iteraciones en todo el conjunto de datos.

Predicciones

Cuando se entrena el modelo, podemos usarlo para reconocer dígitos escritos a mano. La siguiente visualización muestra qué tan bien se desempeña con algunos dígitos renderizados a partir de fuentes locales (primera línea) y, luego, con los 10,000 dígitos del conjunto de datos de validación. La clase predicha aparece debajo de cada dígito, en rojo si fue incorrecta.

Como puedes ver, este modelo inicial no es muy bueno, pero reconoce algunos dígitos correctamente. Su precisión de validación final es de alrededor del 90%, lo que no es tan malo para el modelo simplista con el que comenzamos, pero aún significa que omite 1,000 dígitos de validación de los 10,000. Esto es mucho más de lo que se puede mostrar, por lo que parece que todas las respuestas son incorrectas (rojas).

Tensores

Los datos se almacenan en matrices. Una imagen en escala de grises de 28 x 28 píxeles cabe en una matriz bidimensional de 28 x 28. Sin embargo, para una imagen a color, necesitamos más dimensiones. Hay 3 valores de color por píxel (rojo, verde y azul), por lo que se necesitará una tabla tridimensional con dimensiones [28, 28, 3]. Y para almacenar un lote de 128 imágenes en color, se necesita una tabla de cuatro dimensiones con dimensiones [128, 28, 28, 3].

Estas tablas multidimensionales se denominan "tensores", y la lista de sus dimensiones es su "forma".

En resumen

Si ya conoces todos los términos en negrita del siguiente párrafo, puedes pasar al siguiente ejercicio. Si recién comienzas a aprender sobre el aprendizaje profundo, bienvenido y sigue leyendo.

Un clasificador de red neuronal se compone de varias capas de neuronas. Para la clasificación de imágenes, estas pueden ser capas densas o, con mayor frecuencia, capas convolucionales. Por lo general, se activan con la función de activación relu. La última capa usa tantas neuronas como clases hay y se activa con softmax. Para la clasificación, la entropía cruzada es la función de pérdida más utilizada, ya que compara las etiquetas codificadas con one-hot (es decir, las respuestas correctas) con las probabilidades que predice la red neuronal. Para minimizar la pérdida, lo mejor es elegir un optimizador con impulso, por ejemplo, Adam, y entrenar con lotes de imágenes y etiquetas de entrenamiento.

Para los modelos creados como una secuencia de capas, Keras ofrece la API secuencial. Por ejemplo, un clasificador de imágenes que usa tres capas densas se puede escribir en Keras de la siguiente manera:

model = tf.keras.Sequential([
    tf.keras.layers.Flatten(input_shape=[28, 28, 1]),
    tf.keras.layers.Dense(200, activation="relu"),
    tf.keras.layers.Dense(60, activation="relu"),
    tf.keras.layers.Dense(10, activation='softmax') # classifying into 10 classes
])

# this configures the training of the model. Keras calls it "compiling" the model.
model.compile(
  optimizer='adam',
  loss= 'categorical_crossentropy',
  metrics=['accuracy']) # % of correct answers

# train the model
model.fit(dataset, ... )

Una sola capa densa

Los dígitos escritos a mano en el conjunto de datos de MNIST son imágenes en escala de grises de 28 × 28 píxeles. El enfoque más simple para clasificarlos es usar los 28 x 28=784 píxeles como entradas para una red neuronal de 1 capa.

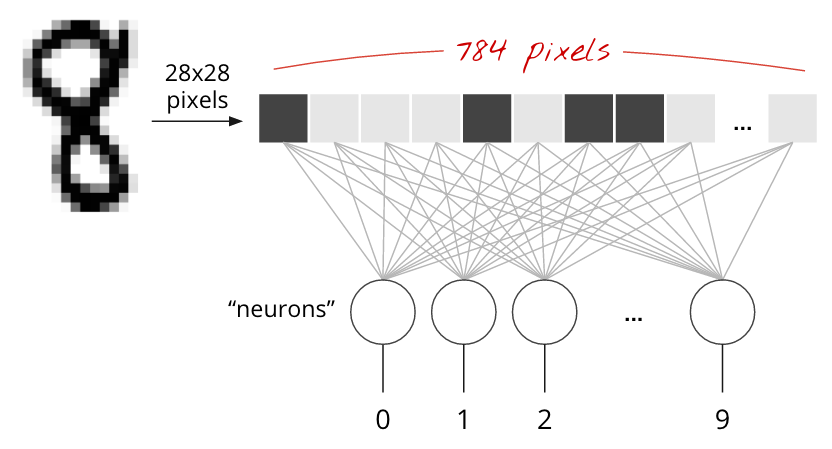
Cada "neurona" en una red neuronal realiza una suma ponderada de todas sus entradas, agrega una constante llamada "sesgo" y, luego, alimenta el resultado a través de alguna "función de activación" no lineal. Los "pesos" y los "sesgos" son parámetros que se determinarán a través del entrenamiento. Al principio, se inicializan con valores aleatorios.

La imagen anterior representa una red neuronal de 1 capa con 10 neuronas de salida, ya que queremos clasificar los dígitos en 10 clases (del 0 al 9).

Con una multiplicación de matrices

A continuación, se muestra cómo se puede representar una capa de red neuronal que procesa una colección de imágenes con una multiplicación de matrices:

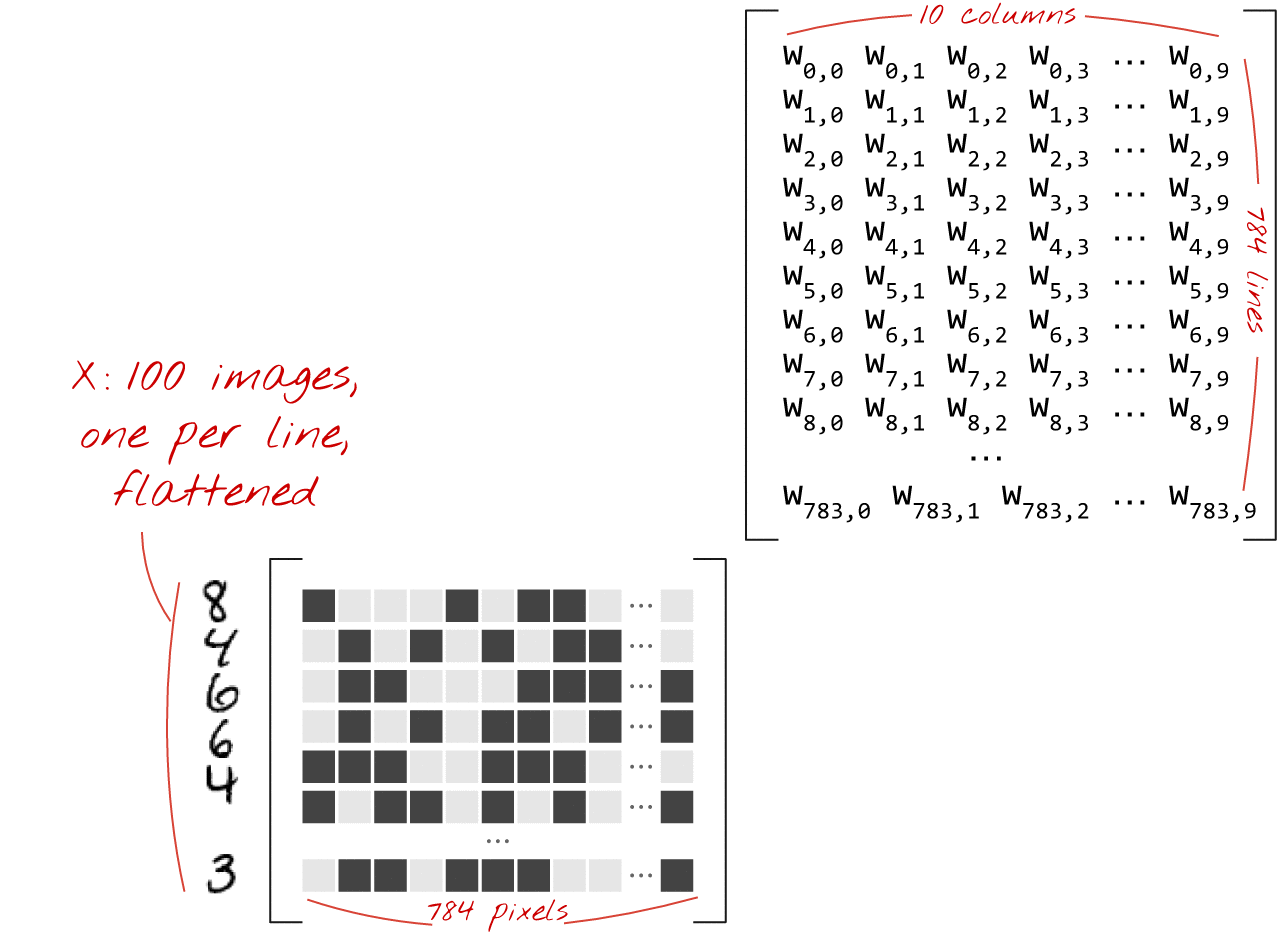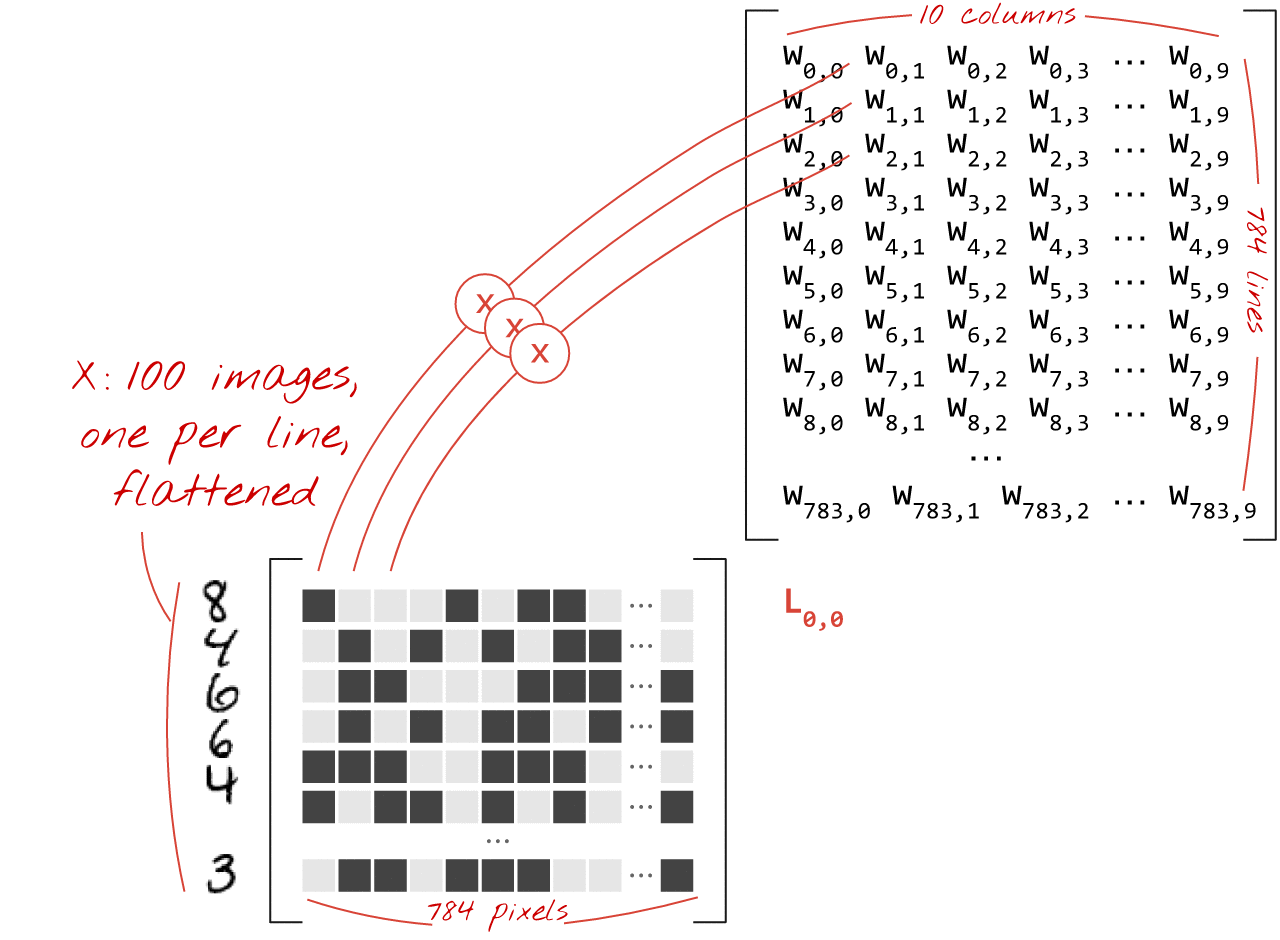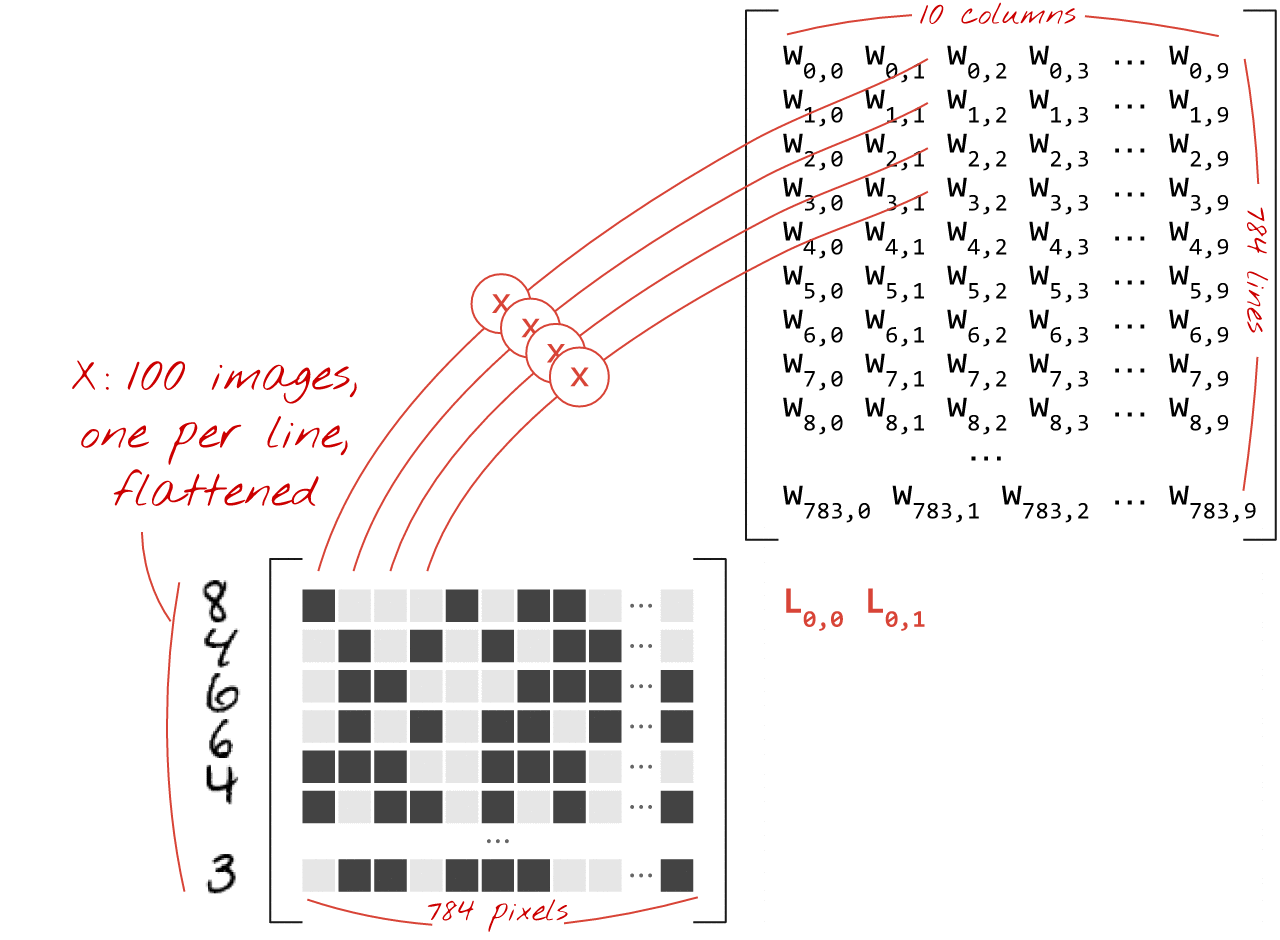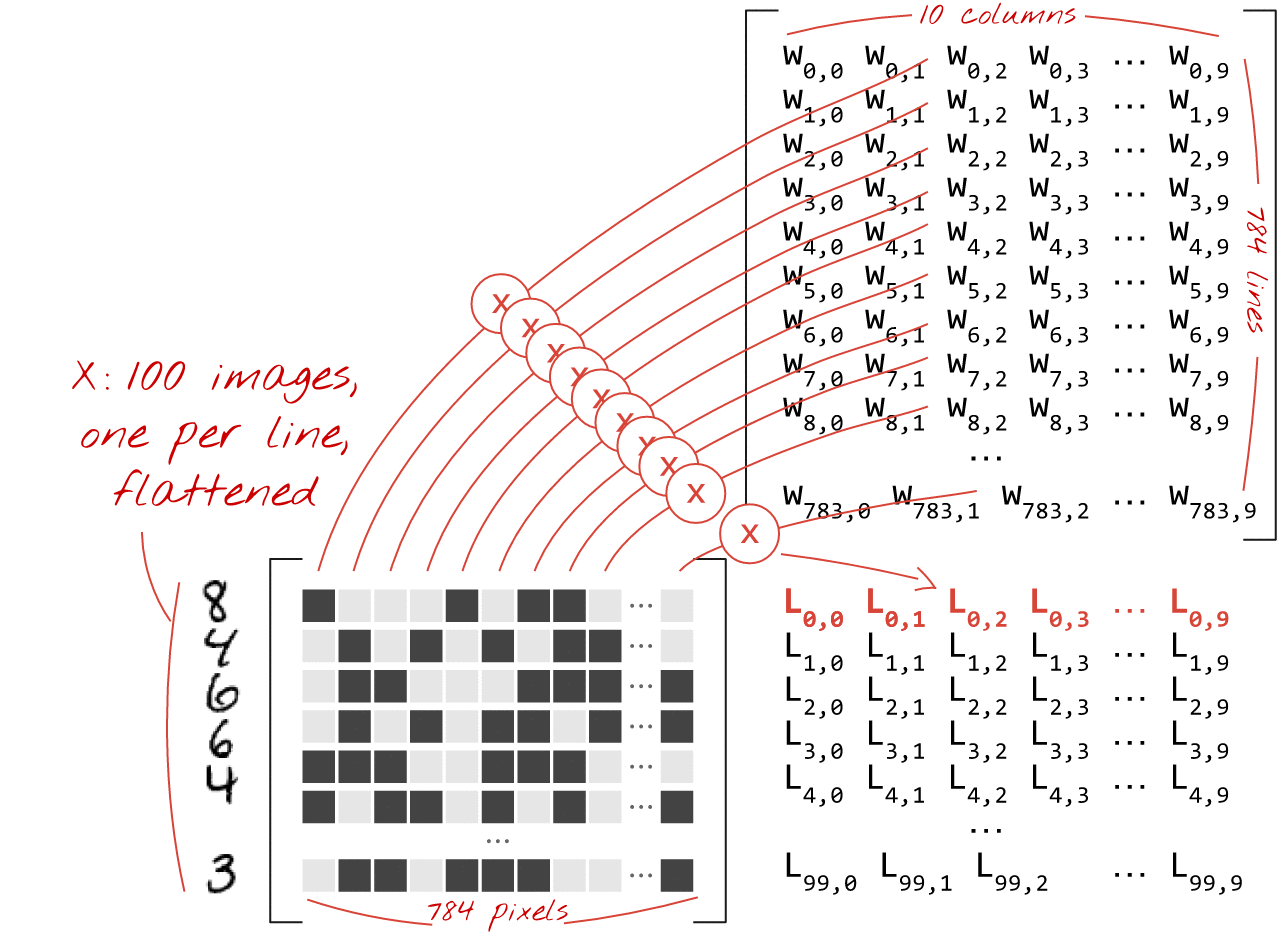
Con la primera columna de pesos de la matriz de pesos W, calculamos la suma ponderada de todos los píxeles de la primera imagen. Esta suma corresponde a la primera neurona. Con la segunda columna de pesos, hacemos lo mismo para la segunda neurona y así sucesivamente hasta la décima neurona. Luego, podemos repetir la operación para las 99 imágenes restantes. Si llamamos X a la matriz que contiene nuestras 100 imágenes, todas las sumas ponderadas de nuestras 10 neuronas, calculadas en 100 imágenes, son simplemente X.W, una multiplicación de matrices.

Ahora cada neurona debe agregar su sesgo (una constante). Como tenemos 10 neuronas, tenemos 10 constantes de sesgo. Llamaremos a este vector de 10 valores b. Se debe agregar a cada línea de la matriz calculada anteriormente. Con un poco de magia llamada "transmisión", escribiremos esto con un simple signo más.

La "transmisión" es un truco estándar que se usa en Python y en NumPy, su biblioteca de computación científica. Extiende el funcionamiento de las operaciones normales en matrices con dimensiones incompatibles. "Transmisión de suma" significa "si estás sumando dos matrices, pero no puedes hacerlo porque sus dimensiones no son compatibles, intenta replicar la más pequeña tanto como sea necesario para que funcione".

Por último, aplicamos una función de activación, por ejemplo, "softmax" (que se explica a continuación), y obtenemos la fórmula que describe una red neuronal de 1 capa, aplicada a 100 imágenes:

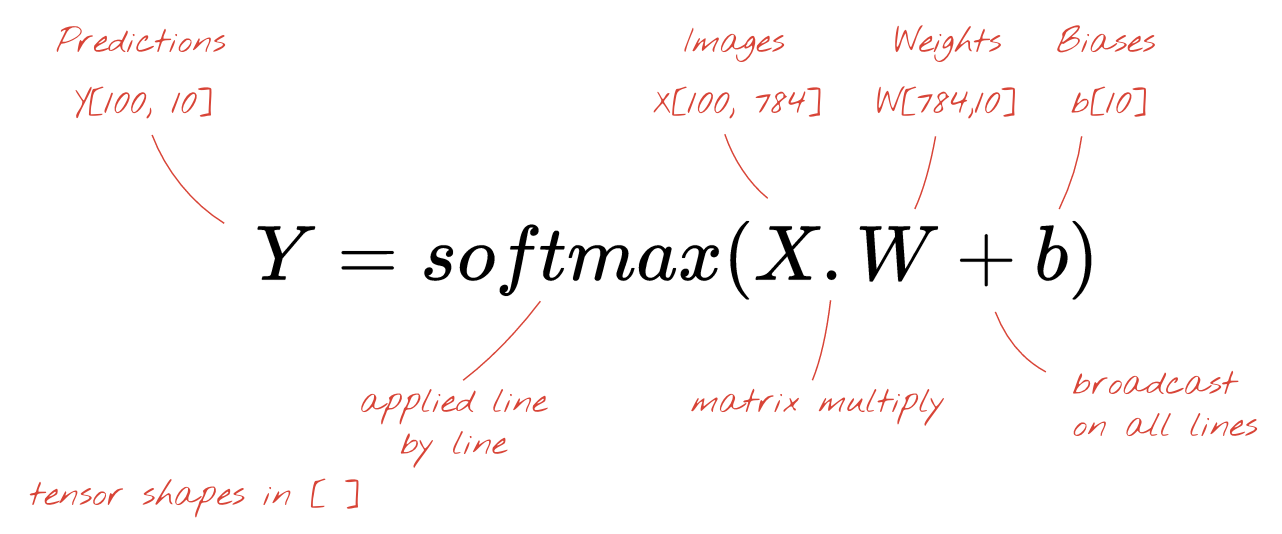
En Keras

Con bibliotecas de redes neuronales de alto nivel, como Keras, no necesitaremos implementar esta fórmula. Sin embargo, es importante comprender que una capa de red neuronal es solo un conjunto de multiplicaciones y sumas. En Keras, una capa densa se escribiría de la siguiente manera:

tf.keras.layers.Dense(10, activation='softmax')

Profundiza

Es trivial encadenar capas de redes neuronales. La primera capa calcula sumas ponderadas de píxeles. Las capas posteriores calculan sumas ponderadas de los resultados de las capas anteriores.

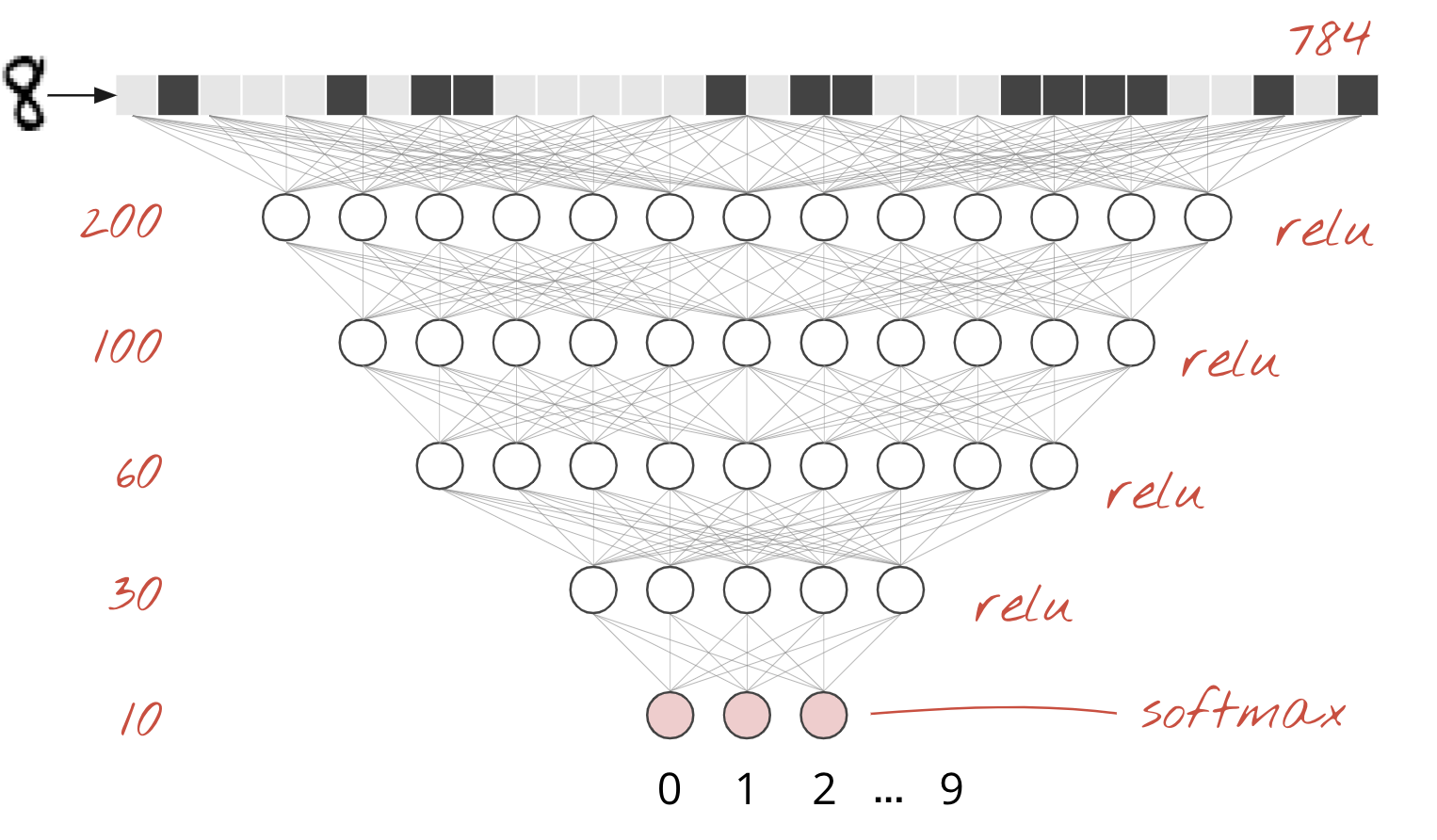
La única diferencia, además de la cantidad de neuronas, será la elección de la función de activación.

Funciones de activación: relu, softmax y sigmoide

Por lo general, usarías la función de activación "relu" para todas las capas, excepto la última. La última capa, en un clasificador, usaría la activación "softmax".

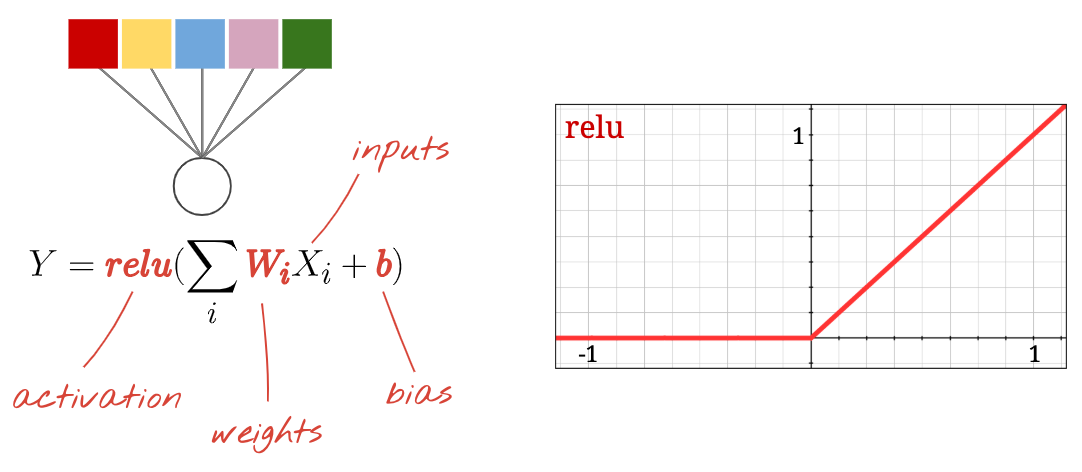
Nuevamente, una "neurona" calcula una suma ponderada de todas sus entradas, agrega un valor llamado "sesgo" y alimenta el resultado a través de la función de activación.

La función de activación más popular se llama "RELU", que significa unidad lineal rectificada. Es una función muy simple, como puedes ver en el gráfico anterior.

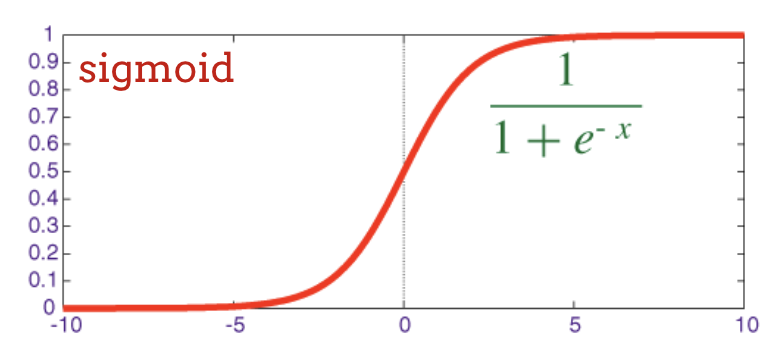
La función de activación tradicional en las redes neuronales era la "sigmoide", pero se demostró que la "relu" tiene mejores propiedades de convergencia en casi todas partes y ahora se prefiere.

Activación softmax para la clasificación

La última capa de nuestra red neuronal tiene 10 neuronas porque queremos clasificar los dígitos escritos a mano en 10 clases (0…9). Debe generar 10 números entre 0 y 1 que representen la probabilidad de que este dígito sea un 0, un 1, un 2, etcétera. Para ello, en la última capa, usaremos una función de activación llamada "softmax".

Para aplicar la función softmax a un vector, se toma la exponencial de cada elemento y, luego, se normaliza el vector, por lo general, dividiéndolo por su norma "L1" (es decir, la suma de los valores absolutos) para que los valores normalizados sumen 1 y se puedan interpretar como probabilidades.

A veces, la salida de la última capa, antes de la activación, se denomina “logits”. Si este vector es L = [L0, L1, L2, L3, L4, L5, L6, L7, L8, L9], entonces:

¿Por qué se llama "softmax"? La función exponencial es una función que aumenta de forma pronunciada. Aumentará las diferencias entre los resultados de las neuronas. Luego, a medida que normalizas el vector, el elemento más grande, que domina la norma, se normalizará a un valor cercano a 1, mientras que todos los demás elementos terminarán divididos por un valor grande y normalizados a un valor cercano a 0. El vector resultante muestra claramente cuál es la clase ganadora, la "máxima", pero conserva el orden relativo original de sus valores, por lo que es "suave".

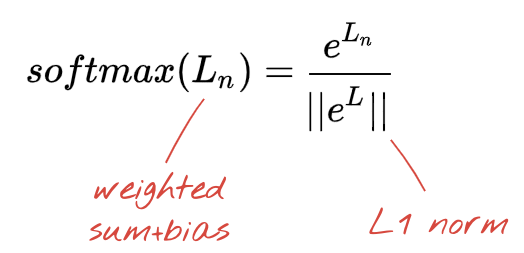
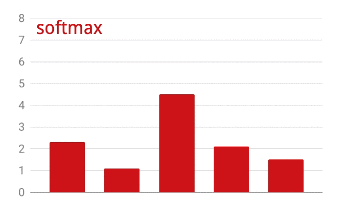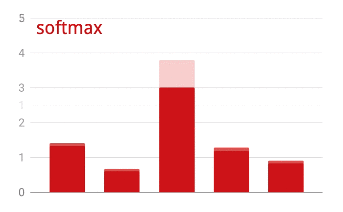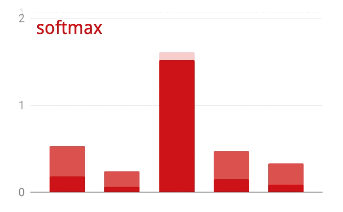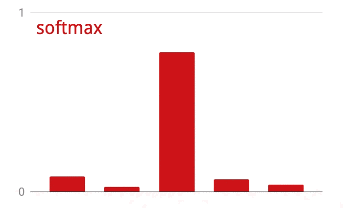
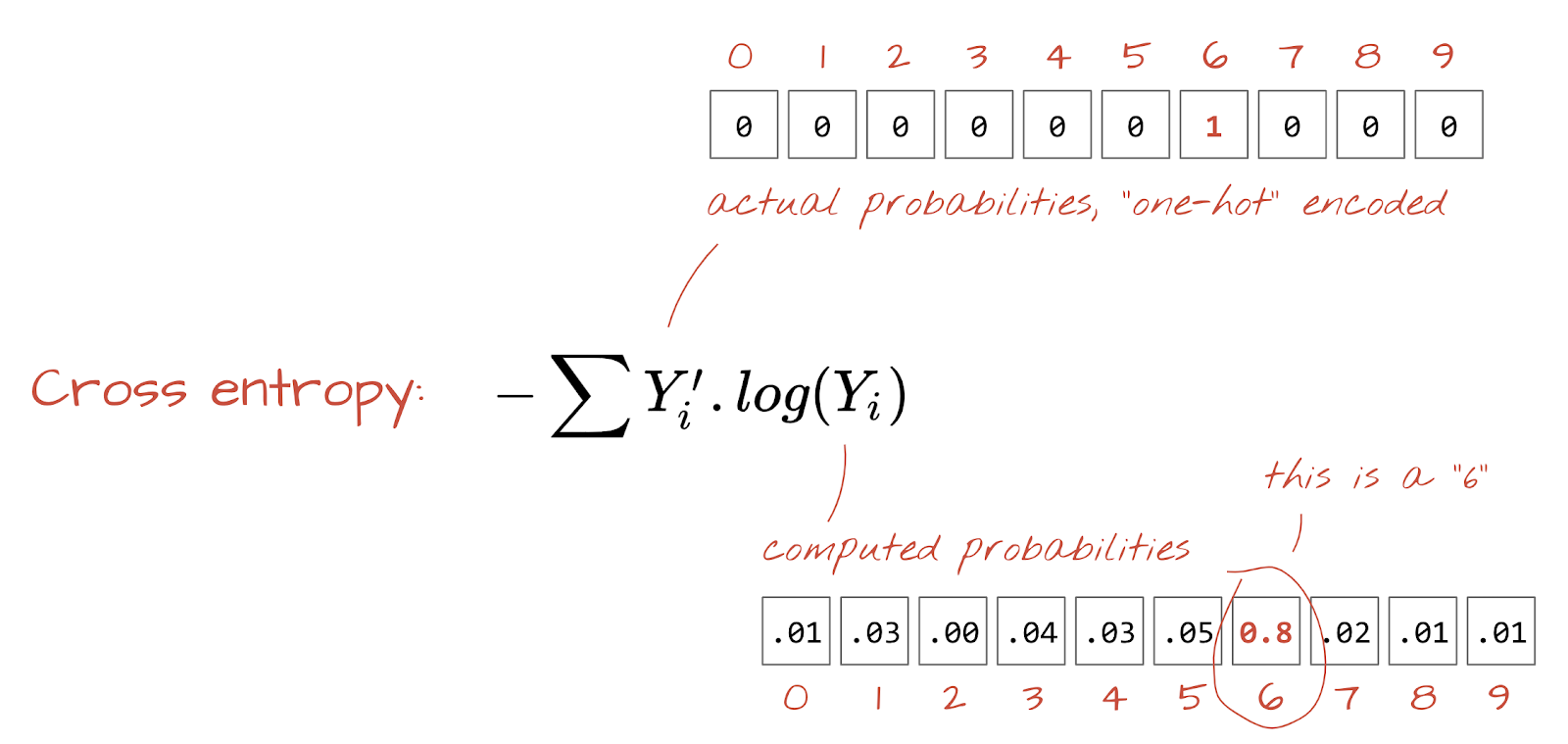
Pérdida de entropía cruzada

Ahora que nuestra red neuronal produce predicciones a partir de imágenes de entrada, debemos medir qué tan buenas son, es decir, la distancia entre lo que nos dice la red y las respuestas correctas, que a menudo se denominan "etiquetas". Recuerda que tenemos etiquetas correctas para todas las imágenes del conjunto de datos.

Cualquier distancia funcionaría, pero para los problemas de clasificación, la llamada "distancia de entropía cruzada" es la más eficaz. Llamaremos a esta nuestra función de error o "pérdida":

La codificación "one-hot" significa que representas la etiqueta "este es el dígito 3" con un vector de 10 valores, todos ceros, excepto el 3ᵉʳ valor, que es 1. Este vector representa una probabilidad del 100% de ser el "dígito 3". Nuestra red neuronal también genera sus predicciones como un vector de 10 valores de probabilidad. Son fáciles de comparar.

Descenso de gradientes

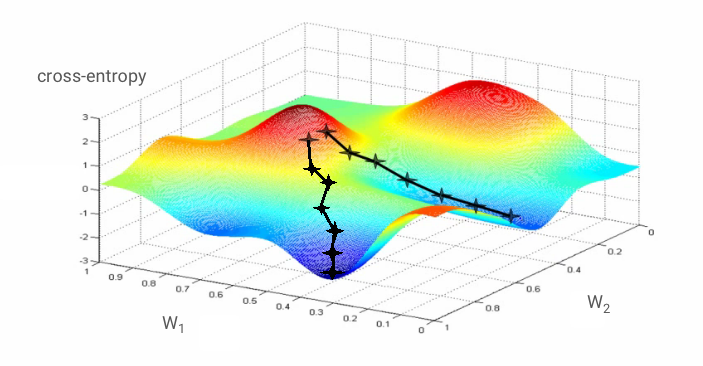
"Entrenar" la red neuronal en realidad significa usar imágenes y etiquetas de entrenamiento para ajustar los pesos y los sesgos de modo que se minimice la función de pérdida de entropía cruzada. Así es como funciona.

La entropía cruzada es una función de los pesos, las tendencias, los píxeles de la imagen de entrenamiento y su clase conocida.

Si calculamos las derivadas parciales de la entropía cruzada en relación con todos los pesos y todos los sesgos, obtenemos un "gradiente" que se calcula para una imagen, una etiqueta y un valor actual de pesos y sesgos determinados. Recuerda que podemos tener millones de pesos y sesgos, por lo que calcular el gradiente parece una tarea muy laboriosa. Afortunadamente, TensorFlow lo hace por nosotros. La propiedad matemática de un gradiente es que apunta "hacia arriba". Como queremos ir hacia donde la entropía cruzada es baja, vamos en la dirección opuesta. Actualizamos los pesos y las bias con una fracción del gradiente. Luego, repetimos el mismo proceso una y otra vez con los siguientes lotes de imágenes y etiquetas de entrenamiento, en un bucle de entrenamiento. Esperamos que esto converja en un lugar donde la entropía cruzada sea mínima, aunque nada garantiza que este mínimo sea único.

"Tasa de aprendizaje": No puedes actualizar tus pesos y sesgos con la longitud completa del gradiente en cada iteración. Sería como intentar llegar al fondo de un valle con botas de siete leguas. Saltarías de un lado del valle al otro. Para llegar al fondo, debes dar pasos más pequeños, es decir, usar solo una fracción del gradiente, por lo general, en el rango de 1/1,000. Esta fracción se denomina “tasa de aprendizaje”.

Minilotes y momento

Puedes calcular tu gradiente en una sola imagen de ejemplo y actualizar los pesos y las tendencias de inmediato, pero hacerlo en un lote de, por ejemplo, 128 imágenes proporciona un gradiente que representa mejor las restricciones impuestas por diferentes imágenes de ejemplo y, por lo tanto, es probable que converja hacia la solución más rápido. El tamaño del minilote es un parámetro ajustable.

Esta técnica, a veces denominada "descenso de gradiente estocástico", tiene otro beneficio más pragmático: trabajar con lotes también significa trabajar con matrices más grandes, que suelen ser más fáciles de optimizar en las GPU y las TPU.

Sin embargo, la convergencia puede ser un poco caótica y hasta detenerse si el vector de gradiente es todo ceros. ¿Eso significa que encontramos un mínimo? No en todos los casos. Un componente de gradiente puede ser cero en un mínimo o un máximo. Con un vector de gradiente con millones de elementos, si todos son ceros, la probabilidad de que cada cero corresponda a un mínimo y ninguno a un punto máximo es bastante baja. En un espacio de muchas dimensiones, los puntos de silla son bastante comunes y no queremos detenernos en ellos.

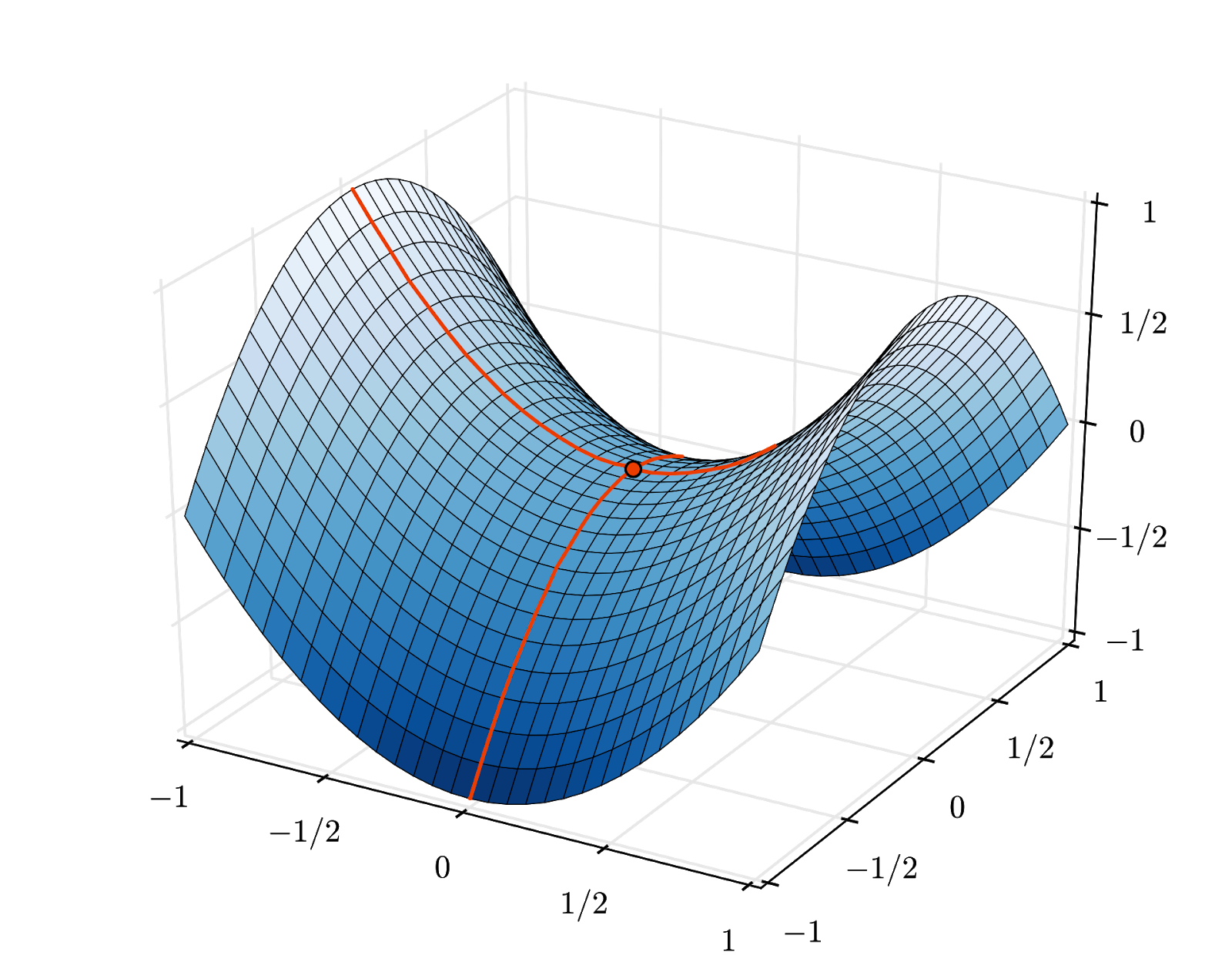
Ilustración: Un punto de silla. El gradiente es 0, pero no es un mínimo en todas las direcciones. (Atribución de la imagen Wikimedia: De Nicoguaro - Trabajo propio, CC BY 3.0)

La solución es agregar algo de impulso al algoritmo de optimización para que pueda superar los puntos de silla sin detenerse.

La biblioteca de TensorFlow proporciona una amplia variedad de optimizadores, comenzando con tf.train.GradientDescentOptimizer. Los optimizadores populares más avanzados que tienen un momentum integrado son tf.train.RMSPropOptimizer o tf.train.AdamOptimizer.

Glosario

Lote o minilote: El entrenamiento siempre se realiza en lotes de datos y etiquetas de entrenamiento. Esto ayuda a que el algoritmo converja. Por lo general, la dimensión "lote" es la primera dimensión de los tensores de datos. Por ejemplo, un tensor con la forma [100, 192, 192, 3] contiene 100 imágenes de 192 x 192 píxeles con tres valores por píxel (RGB).

Pérdida de entropía cruzada: Es una función de pérdida especial que se usa a menudo en los clasificadores.

Capa densa: Es una capa de neuronas en la que cada neurona está conectada a todas las neuronas de la capa anterior.

Atributos: Las entradas de una red neuronal a veces se denominan "atributos". El arte de determinar qué partes de un conjunto de datos (o combinaciones de partes) se deben ingresar en una red neuronal para obtener buenas predicciones se denomina "ingeniería de funciones".

etiquetas: Otro nombre para "clases" o respuestas correctas en un problema de clasificación supervisada

Tasa de aprendizaje: Es la fracción del gradiente según la cual se actualizan los pesos y las tendencias en cada iteración del ciclo de entrenamiento.

logits: Las salidas de una capa de neuronas antes de que se aplique la función de activación se denominan "logits". El término proviene de la "función logística", también conocida como "función sigmoidea", que solía ser la función de activación más popular. "Salidas de neuronas antes de la función logística" se abrevió a "logits".

pérdida: Es la función de error que compara los resultados de la red neuronal con las respuestas correctas.

Neurona: Calcula la suma ponderada de sus entradas, agrega un sesgo y pasa el resultado a través de una función de activación.

Codificación one-hot: La clase 3 de 5 se codifica como un vector de 5 elementos, todos ceros, excepto el 3º, que es 1.

relu: Unidad lineal rectificada. Es una función de activación popular para las neuronas.

sigmoid: Otra función de activación que solía ser popular y que sigue siendo útil en casos especiales.

softmax: Es una función de activación especial que actúa sobre un vector, aumenta la diferencia entre el componente más grande y todos los demás, y también normaliza el vector para que tenga una suma de 1 y se pueda interpretar como un vector de probabilidades. Se usa como el último paso en los clasificadores.

tensor: Un "tensor" es como una matriz, pero con una cantidad arbitraria de dimensiones. Un tensor unidimensional es un vector. Un tensor de 2 dimensiones es una matriz. Luego, puedes tener tensores con 3, 4, 5 o más dimensiones.

Volvamos al notebook de estudio y, esta vez, leamos el código.

keras_01_mnist.ipynb

PRÁCTICA:

Tu tarea en esta sección es leer el código y comprenderlo para que puedas mejorarlo más adelante.

Veamos todas las celdas de este notebook.

Celda "Parameters"

Aquí se definen el tamaño del lote, la cantidad de ciclos de entrenamiento y la ubicación de los archivos de datos. Los archivos de datos se alojan en un bucket de Google Cloud Storage (GCS), por lo que su dirección comienza con gs://.

Celda "Importaciones"

Aquí se importan todas las bibliotecas de Python necesarias, incluidas TensorFlow y matplotlib para las visualizaciones.

Celda "utilidades de visualización [EJECUTAR]"

Esta celda contiene código de visualización poco interesante. Está contraído de forma predeterminada, pero puedes abrirlo y ver el código cuando tengas tiempo haciendo doble clic en él.

Debes ejecutar esta celda (MAYÚSCULAS + INTRO). De lo contrario, las funciones definidas en su interior no se analizarán y recibirás errores más adelante.

Celda "tf.data.Dataset: analiza archivos y prepara conjuntos de datos de entrenamiento y validación"

En esta celda, se usó la API de tf.data.Dataset para cargar el conjunto de datos de MNIST desde los archivos de datos. No es necesario dedicar demasiado tiempo a esta celda. Si te interesa la API de tf.data.Dataset, aquí tienes un instructivo que la explica: Canalizaciones de datos con velocidades de TPU. Por ahora, los conceptos básicos son los siguientes:

Las imágenes y las etiquetas (respuestas correctas) del conjunto de datos de MNIST se almacenan en registros de longitud fija en 4 archivos. Los archivos se pueden cargar con la función de registro fijo dedicada:

imagedataset = tf.data.FixedLengthRecordDataset(image_filename, 28*28, header_bytes=16)

Ahora tenemos un conjunto de datos de bytes de imágenes. Deben decodificarse en imágenes. Definimos una función para hacerlo. La imagen no se comprime, por lo que la función no necesita decodificar nada (decode_raw básicamente no hace nada). Luego, la imagen se convierte en valores de punto flotante entre 0 y 1. Podríamos cambiarle la forma aquí como una imagen 2D, pero, en realidad, la conservamos como un array plano de píxeles de tamaño 28*28 porque eso es lo que espera nuestra capa densa inicial.

def read_image(tf_bytestring):
    image = tf.decode_raw(tf_bytestring, tf.uint8)
    image = tf.cast(image, tf.float32)/256.0
    image = tf.reshape(image, [28*28])
    return image

Aplicamos esta función al conjunto de datos con .map y obtenemos un conjunto de datos de imágenes:

imagedataset = imagedataset.map(read_image, num_parallel_calls=16)

Hacemos el mismo tipo de lectura y decodificación para las etiquetas, y .zip las imágenes y las etiquetas juntas:

dataset = tf.data.Dataset.zip((imagedataset, labelsdataset))

Ahora tenemos un conjunto de datos de pares (imagen, etiqueta). Esto es lo que espera nuestro modelo. Aún no está todo listo para usarla en la función de entrenamiento:

dataset = dataset.cache()
dataset = dataset.shuffle(5000, reshuffle_each_iteration=True)
dataset = dataset.repeat()
dataset = dataset.batch(batch_size)
dataset = dataset.prefetch(tf.data.experimental.AUTOTUNE)

La API de tf.data.Dataset tiene todas las funciones de utilidad necesarias para preparar conjuntos de datos:

.cache almacena en caché el conjunto de datos en la RAM. Este es un conjunto de datos muy pequeño, por lo que funcionará. .shuffle lo mezcla con un búfer de 5,000 elementos. Es importante que los datos de entrenamiento estén bien redistribuidos. .repeat repite el conjunto de datos. Lo entrenaremos varias veces (varios ciclos de entrenamiento). .batch reúne varias imágenes y etiquetas en un mini-natch. Por último, .prefetch puede usar la CPU para preparar el siguiente lote mientras se entrena el lote actual en la GPU.

El conjunto de datos de validación se prepara de manera similar. Ahora podemos definir un modelo y usar este conjunto de datos para entrenarlo.

Celda "Modelo de Keras"

Todos nuestros modelos serán secuencias directas de capas, por lo que podemos usar el estilo tf.keras.Sequential para crearlos. Inicialmente, aquí es una sola capa densa. Tiene 10 neuronas porque clasificamos dígitos escritos a mano en 10 clases. Utiliza la activación "softmax" porque es la última capa de un clasificador.

Un modelo de Keras también necesita conocer la forma de sus entradas. Se puede usar tf.keras.layers.Input para definirlo. Aquí, los vectores de entrada son vectores planos de valores de píxeles de longitud 28*28.

model = tf.keras.Sequential(
  [
    tf.keras.layers.Input(shape=(28*28,)),
    tf.keras.layers.Dense(10, activation='softmax')
  ])

model.compile(optimizer='sgd',
              loss='categorical_crossentropy',
              metrics=['accuracy'])

# print model layers
model.summary()

# utility callback that displays training curves
plot_training = PlotTraining(sample_rate=10, zoom=1)

La configuración del modelo se realiza en Keras con la función model.compile. Aquí usamos el optimizador básico 'sgd' (descenso de gradientes estocástico). Un modelo de clasificación requiere una función de pérdida de entropía cruzada, llamada 'categorical_crossentropy' en Keras. Por último, le pedimos al modelo que calcule la métrica 'accuracy', que es el porcentaje de imágenes clasificadas correctamente.

Keras ofrece la excelente utilidad model.summary() que imprime los detalles del modelo que creaste. Tu amable instructor agregó la utilidad PlotTraining (definida en la celda "utilidades de visualización") que mostrará varias curvas de entrenamiento durante el entrenamiento.

Celda "Train and validate the model"

Aquí es donde se realiza el entrenamiento, llamando a model.fit y pasando los conjuntos de datos de entrenamiento y validación. De forma predeterminada, Keras ejecuta una ronda de validación al final de cada ciclo de entrenamiento.

model.fit(training_dataset, steps_per_epoch=steps_per_epoch, epochs=EPOCHS,
          validation_data=validation_dataset, validation_steps=1,
          callbacks=[plot_training])

En Keras, es posible agregar comportamientos personalizados durante el entrenamiento con devoluciones de llamada. Así se implementó el gráfico de entrenamiento que se actualiza de forma dinámica para este taller.

Celda "Visualizar predicciones"

Una vez que se entrena el modelo, podemos obtener predicciones llamando a model.predict():

probabilities = model.predict(font_digits, steps=1)
predicted_labels = np.argmax(probabilities, axis=1)

Aquí preparamos un conjunto de dígitos impresos renderizados a partir de fuentes locales, como prueba. Recuerda que la red neuronal devuelve un vector de 10 probabilidades desde su "softmax" final. Para obtener la etiqueta, debemos averiguar qué probabilidad es la más alta. np.argmax de la biblioteca numpy hace eso.

Para comprender por qué se necesita el parámetro axis=1, recuerda que procesamos un lote de 128 imágenes y, por lo tanto, el modelo devuelve 128 vectores de probabilidades. La forma del tensor de salida es [128, 10]. Calculamos el argmax en las 10 probabilidades que se devuelven para cada imagen, por lo que axis=1 (el primer eje es 0).

Este modelo simple ya reconoce el 90% de los dígitos. No está mal, pero ahora lo mejorarás significativamente.

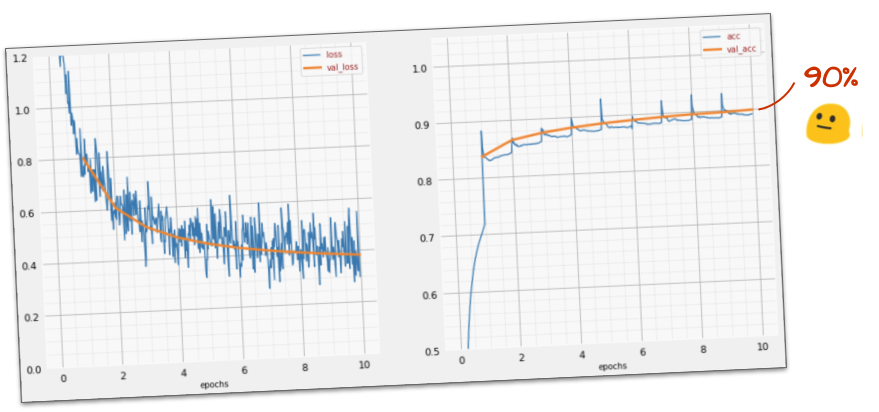
Para mejorar la precisión del reconocimiento, agregaremos más capas a la red neuronal.

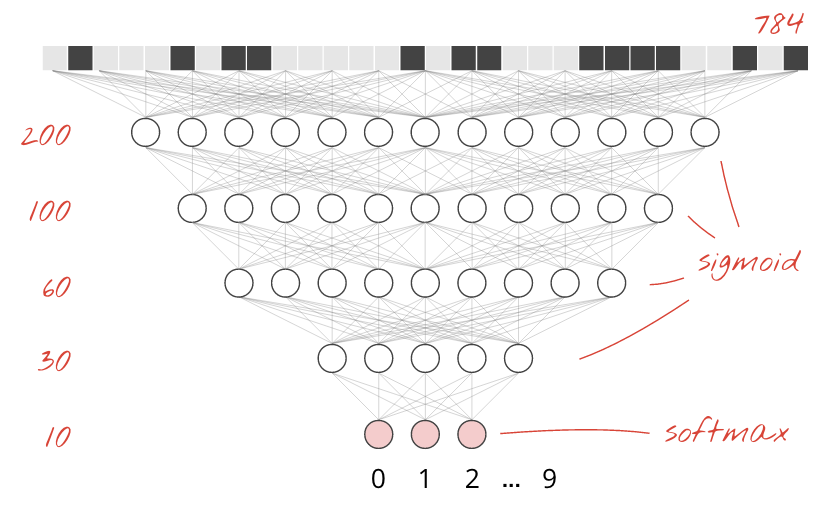
Mantenemos softmax como la función de activación en la última capa porque es lo que mejor funciona para la clasificación. Sin embargo, en las capas intermedias, usaremos la función de activación más clásica: la sigmoide:

PRÁCTICA:

Agrega un par de capas ocultas intermedias activadas con "sigmoid" antes de la capa "softmax". La cantidad de neuronas en ellas puede ser cualquier número entre 784 (la cantidad de píxeles de entrada) y 10 (la cantidad de neuronas de salida). Luego, vuelve a entrenar el modelo.

Advertencia: Para volver a entrenar el modelo, debes volver a ejecutar la celda "Modelo de Keras" para definir un modelo nuevo y, luego, la celda de entrenamiento. Si vuelves a ejecutar la celda de entrenamiento, se continuará el entrenamiento de tu modelo anterior.

Por ejemplo, tu modelo podría verse así (no olvides las comas, tf.keras.Sequential toma una lista de capas separadas por comas):

model = tf.keras.Sequential(
  [
      tf.keras.layers.Input(shape=(28*28,)),
      tf.keras.layers.Dense(200, activation='sigmoid'),
      tf.keras.layers.Dense(60, activation='sigmoid'),
      tf.keras.layers.Dense(10, activation='softmax')
  ])

Consulta el "resumen" de tu modelo. Ahora tiene al menos 10 veces más parámetros. Debería ser 10 veces mejor. Pero, por alguna razón, no lo es…

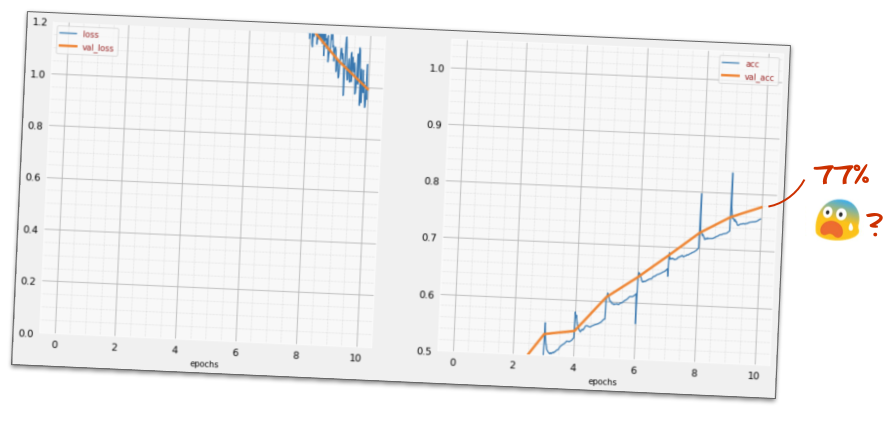
Además, parece que las pérdidas se dispararon. Algo no funciona bien.

Acabas de experimentar las redes neuronales, tal como las diseñaban las personas en los años 80 y 90. No es de extrañar que abandonaran la idea, lo que dio paso al llamado "invierno de la IA". De hecho, a medida que agregas capas, las redes neuronales tienen cada vez más dificultades para converger.

Resulta que las redes neuronales profundas con muchas capas (20, 50 o incluso 100 en la actualidad) pueden funcionar muy bien, siempre que se apliquen algunos trucos matemáticos para que converjan. El descubrimiento de estos trucos simples es uno de los motivos del renacimiento del aprendizaje profundo en la década de 2010.

Activación de ReLU

La función de activación sigmoidea es bastante problemática en las redes profundas. Comprime todos los valores entre 0 y 1, y, cuando lo haces repetidamente, las salidas de las neuronas y sus gradientes pueden desaparecer por completo. Se mencionó por motivos históricos, pero las redes modernas usan la ReLU (unidad lineal rectificada), que se ve de la siguiente manera:

PRÁCTICA:

Reemplaza todos los activation='sigmoid' por activation='relu' en tus capas y vuelve a entrenar el modelo.

¿Por qué la sigmoide es problemática? Mira cómo se comporta en los laterales: se aplana.

Y eso significa que su derivada allí es cercana a cero. Recuerda cómo progresa el entrenamiento siguiendo el gradiente, que es un vector de derivadas. Con la activación sigmoidea, especialmente si hay muchas capas, el gradiente puede volverse muy pequeño y el entrenamiento se vuelve cada vez más lento.

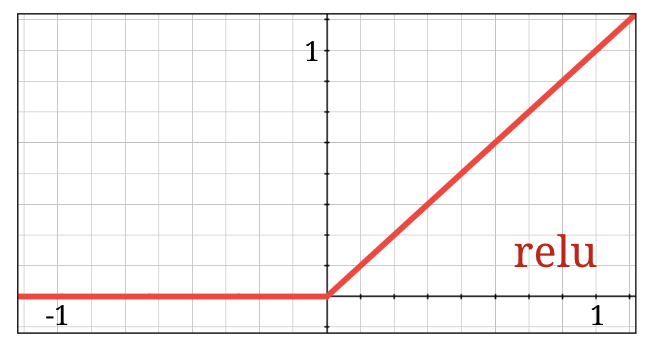
Por otro lado, la ReLU tiene una derivada de 1, al menos en su lado derecho. Con la activación de ReLU, incluso si los gradientes que provienen de algunas neuronas pueden ser cero, siempre habrá otras que proporcionen un gradiente claro distinto de cero, y el entrenamiento puede continuar a un buen ritmo.

Un mejor optimizador

En espacios de dimensiones muy altas, como aquí (tenemos alrededor de 10,000 pesos y sesgos), los "puntos silla" son frecuentes. Estos son puntos que no son mínimos locales, pero en los que el gradiente es cero y el optimizador de descenso de gradientes se queda atascado allí. TensorFlow tiene una gran variedad de optimizadores disponibles, incluidos algunos que funcionan con una cantidad de inercia y que superan de forma segura los puntos de silla.

PRÁCTICA:

Reemplaza el optimizador 'sgd' por uno mejor, por ejemplo, 'adam', y vuelve a entrenar el modelo.

Inicializaciones aleatorias

El arte de inicializar los sesgos de los pesos antes del entrenamiento es un área de investigación en sí misma, con numerosos artículos publicados sobre el tema. Puedes consultar todos los inicializadores disponibles en Keras aquí. Afortunadamente, Keras hace lo correcto de forma predeterminada y usa el inicializador 'glorot_uniform', que es el mejor en casi todos los casos.

No tienes que hacer nada, ya que Keras ya hace lo correcto.

¿NaN?

La fórmula de entropía cruzada incluye un logaritmo, y log(0) no es un número (NaN, una falla numérica si lo prefieres). ¿Puede ser 0 la entrada de la entropía cruzada? La entrada proviene de softmax, que es esencialmente una exponencial, y una exponencial nunca es cero. Así que estamos a salvo.

¿En serio? En el hermoso mundo de las matemáticas, estaríamos a salvo, pero en el mundo de las computadoras, exp(-150), representado en formato float32, es tan CERO como puede ser y la entropía cruzada falla.

Afortunadamente, tampoco tienes que hacer nada aquí, ya que Keras se encarga de esto y calcula la función softmax seguida de la entropía cruzada de una manera especialmente cuidadosa para garantizar la estabilidad numérica y evitar los temidos NaN.

¿Se completó correctamente?

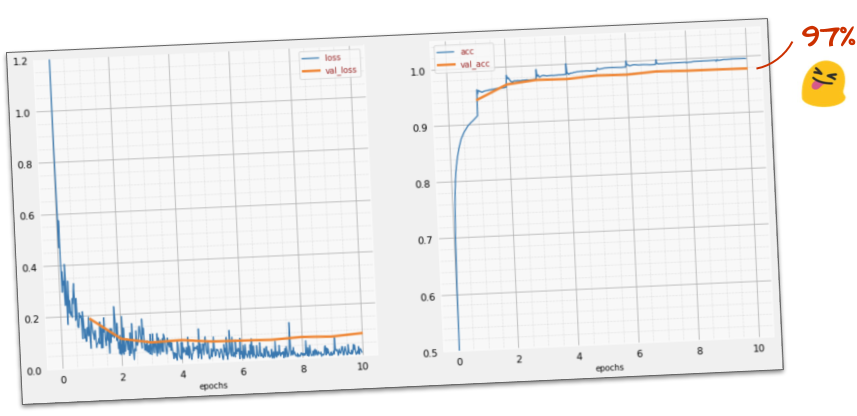
Ahora deberías alcanzar una precisión del 97%. El objetivo de este taller es superar significativamente el 99%, así que sigamos adelante.

Si no sabes cómo hacerlo, aquí tienes la solución en este punto:

keras_02_mnist_dense.ipynb

¿Quizás podamos intentar entrenar el modelo más rápido? La tasa de aprendizaje predeterminada en el optimizador de Adam es 0.001. Intentemos aumentarlo.

PRÁCTICA:

Aumenta la tasa de aprendizaje de su valor predeterminado de 0.001 a 0.01. Para ello, deberás reemplazar el optimizador predefinido 'adam' por una instancia real de un optimizador de Adam para que tengas acceso a sus parámetros de configuración:

optimizer=tf.keras.optimizers.Adam(lr=0.01)

También aumenta el factor de zoom a 5 en PlotTraining. Esto hace un acercamiento alrededor de 0 en las pérdidas y alrededor de 1 en las precisiones para ayudarte a ver qué sucede: PlotTraining(sample_rate=10, zoom=5)

Ir más rápido no parece ayudar mucho, ¿y qué es todo este ruido?

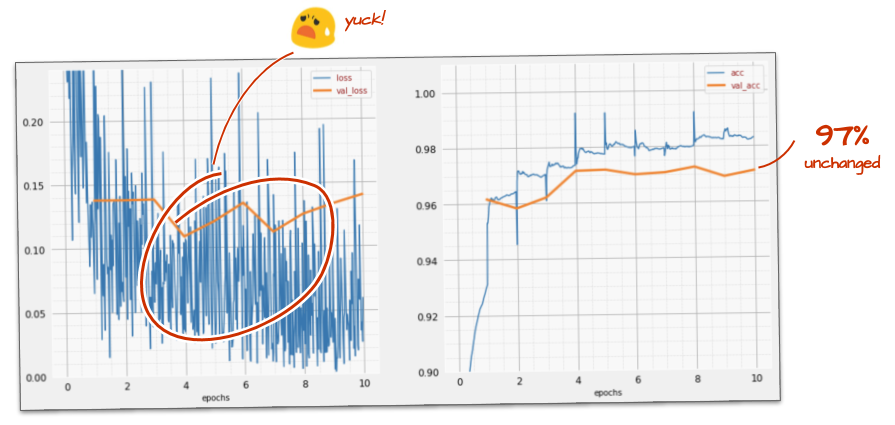
Las curvas de entrenamiento son muy ruidosas y las dos curvas de validación suben y bajan. Esto significa que vamos demasiado rápido. Podríamos volver a la velocidad anterior, pero hay una mejor manera.

La solución adecuada es comenzar rápido y reducir la tasa de aprendizaje de forma exponencial. En Keras, puedes hacerlo con la devolución de llamada tf.keras.callbacks.LearningRateScheduler.

PRÁCTICA:

Implementa un programa de la tasa de aprendizaje que la disminuya de forma exponencial. A continuación, encontrarás fragmentos de código útiles.

Código útil para copiar y pegar:

# lr decay function
def lr_decay(epoch):
  return 0.01 * math.pow(0.6, epoch)

# lr schedule callback
lr_decay_callback = tf.keras.callbacks.LearningRateScheduler(lr_decay, verbose=True)

# important to see what you are doing
plot_learning_rate(lr_decay, EPOCHS)

No olvides usar el lr_decay_callback que creaste. Agrégalo a la lista de devoluciones de llamada en model.fit:

model.fit(...,  callbacks=[plot_training, lr_decay_callback])

El impacto de este pequeño cambio es espectacular. Verás que la mayor parte del ruido desapareció y que la precisión de la prueba ahora supera el 98% de forma sostenida.

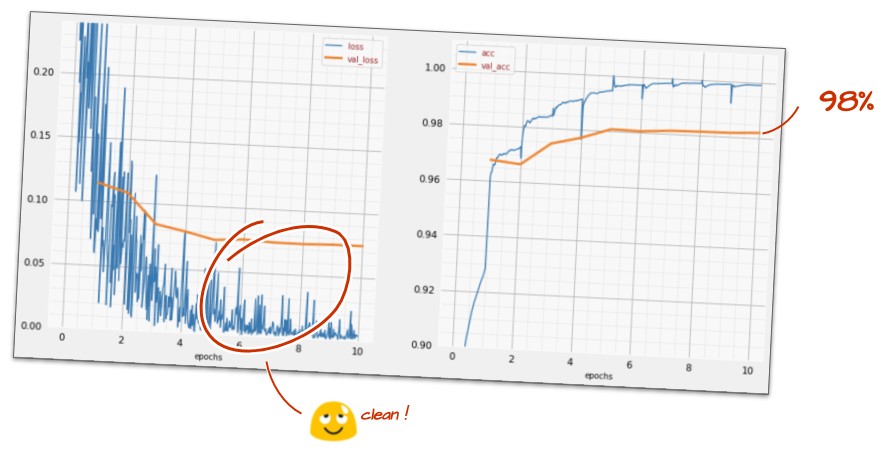
Parece que el modelo converge bien ahora. Intentemos profundizar aún más.

PRÁCTICA:

Si aún no lo hiciste, aumenta la profundidad del modelo a, al menos, 4 capas densas y vuelve a entrenarlo. Puedes usar la siguiente cantidad de neuronas en las capas: 200, 100, 60 y 10.

También aumenta el factor de zoom a 10 en PlotTraining. Esto hace un acercamiento alrededor de 0 en las pérdidas y alrededor de 1 en las precisiones para ayudarte a ver qué sucede: PlotTraining(sample_rate=10, zoom=10)

¿Te sirve?

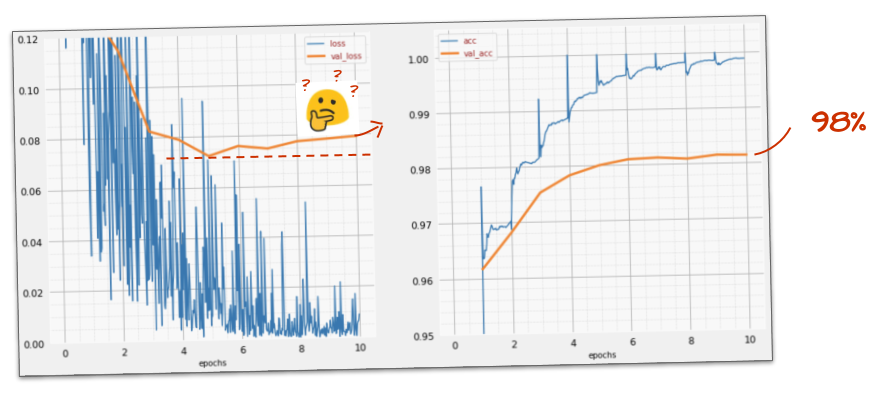
En realidad, no. La precisión sigue en el 98% y mira la pérdida de validación. ¡Está subiendo! El algoritmo de aprendizaje solo funciona con datos de entrenamiento y optimiza la pérdida de entrenamiento en consecuencia. Nunca ve datos de validación, por lo que no es sorprendente que, después de un tiempo, su trabajo ya no tenga efecto en la pérdida de validación, que deja de disminuir y, a veces, incluso vuelve a aumentar.

Esto no afecta de inmediato las capacidades de reconocimiento en el mundo real de tu modelo, pero te impedirá ejecutar muchas iteraciones y, en general, es un signo de que el entrenamiento ya no tiene un efecto positivo.

Esta desconexión suele llamarse "sobreajuste", y, cuando la veas, puedes intentar aplicar una técnica de regularización llamada "abandono". La técnica de dropout dispara neuronas aleatorias en cada iteración de entrenamiento.

El retiro es una de las técnicas de regularización más antiguas en el aprendizaje profundo. En cada iteración de entrenamiento, se descartan neuronas aleatorias de la red con una probabilidad p (por lo general, del 25% al 50%). En la práctica, las salidas de las neuronas se establecen en 0. El resultado neto es que estas neuronas no participarán en el cálculo de la pérdida esta vez y no recibirán actualizaciones de peso. En cada iteración de entrenamiento, se descartarán diferentes neuronas.

Cuando pruebas el rendimiento de tu red, por supuesto, vuelves a colocar todas las neuronas (tasa de retirados=0). Keras lo hace automáticamente, por lo que solo tienes que agregar una capa tf.keras.layers.Dropout. Tendrá el comportamiento correcto en el momento del entrenamiento y la evaluación automáticamente.

¿Por qué funciona? La teoría es que las redes neuronales tienen tanta libertad entre sus numerosas capas que es completamente posible que una capa desarrolle un comportamiento incorrecto y que la siguiente capa lo compense. Este no es un uso ideal de las neuronas. Con la deserción, existe una alta probabilidad de que la neurona que "soluciona" el problema no esté presente en una ronda de entrenamiento determinada. El comportamiento inadecuado de la capa infractora se vuelve evidente y los pesos evolucionan hacia un mejor comportamiento.

PRÁCTICA:

Puedes agregar la deserción después de cada capa oculta intermedia en la red. No agregues la función de abandono después de la capa softmax. Descartarías las probabilidades predichas. Puedes agregar una tasa de deserción del 25% con el siguiente comando: tf.keras.layers.Dropout(0.25)

¿Funcionó?

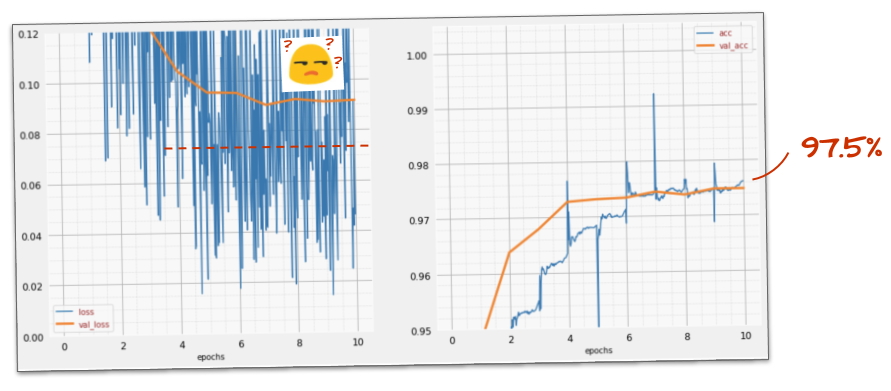
El ruido vuelve a aparecer (lo que no sorprende, dado cómo funciona la deserción). La pérdida de validación ya no parece aumentar, pero es más alta en general que sin la deserción. Y la precisión de la validación disminuyó un poco. Este es un resultado bastante decepcionante.

Parece que la deserción no fue la solución correcta o, tal vez, el "sobreajuste" es un concepto más complejo y algunas de sus causas no se pueden solucionar con la deserción.

¿Qué es el "sobreajuste"? El sobreajuste ocurre cuando una red neuronal aprende "mal", de una manera que funciona para los ejemplos de entrenamiento, pero no tan bien con los datos del mundo real. Existen técnicas de regularización, como el abandono, que pueden obligarlo a aprender de una mejor manera, pero el sobreajuste también tiene raíces más profundas.

El sobreajuste básico ocurre cuando una red neuronal tiene demasiados grados de libertad para el problema en cuestión. Imagina que tenemos tantas neuronas que la red puede almacenar todas nuestras imágenes de entrenamiento y, luego, reconocerlas por coincidencia de patrones. Fallaría por completo con datos del mundo real. Una red neuronal debe estar algo restringida para que se vea obligada a generalizar lo que aprende durante el entrenamiento.

Si tienes muy pocos datos de entrenamiento, incluso una red pequeña puede aprenderlos de memoria y verás un "sobreajuste". En general, siempre necesitas muchos datos para entrenar redes neuronales.

Por último, si hiciste todo según las instrucciones, experimentaste con diferentes tamaños de red para asegurarte de que sus grados de libertad estén restringidos, aplicaste la deserción y entrenaste con muchos datos, es posible que sigas atascado en un nivel de rendimiento que nada parece poder mejorar. Esto significa que tu red neuronal, en su forma actual, no es capaz de extraer más información de tus datos, como en nuestro caso aquí.

¿Recuerdas cómo usamos nuestras imágenes, aplanadas en un solo vector? Fue una muy mala idea. Los dígitos escritos a mano están formados por formas, y descartamos la información de las formas cuando aplanamos los píxeles. Sin embargo, existe un tipo de red neuronal que puede aprovechar la información de la forma: las redes convolucionales. Probemos.

Si no sabes cómo hacerlo, aquí tienes la solución en este punto:

keras_03_mnist_dense_lrdecay_dropout.ipynb

En resumen

Si ya conoces todos los términos en negrita del siguiente párrafo, puedes pasar al siguiente ejercicio. Si recién comienzas a usar redes neuronales convolucionales, sigue leyendo.

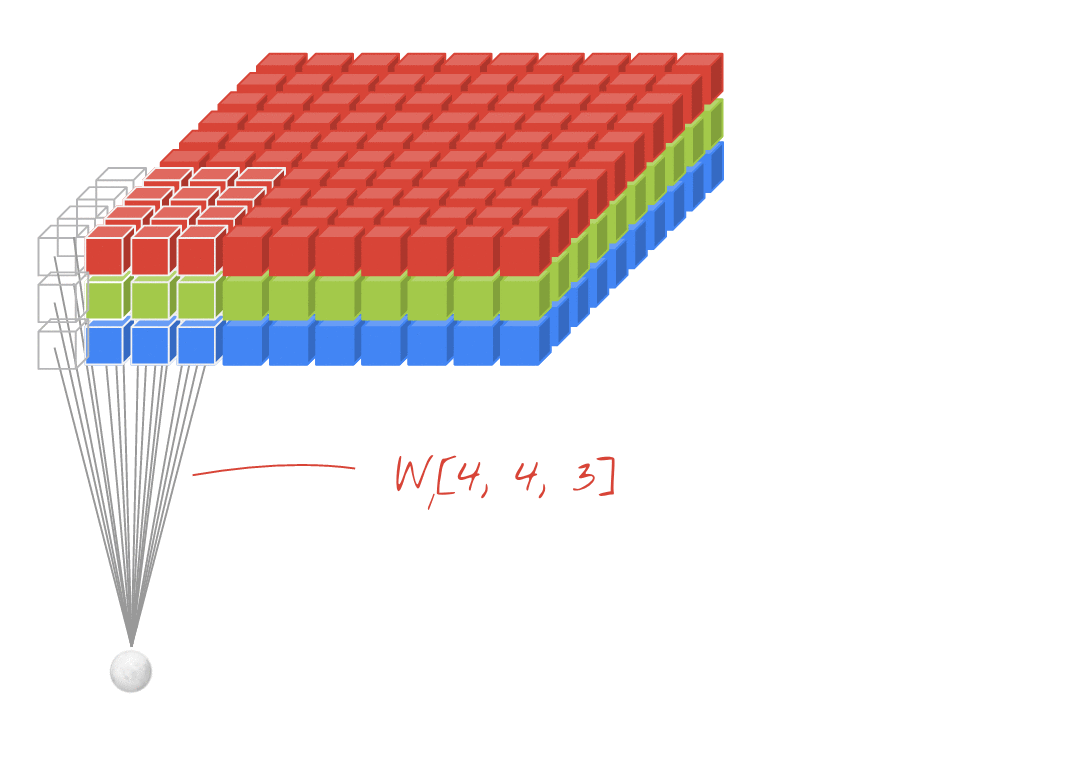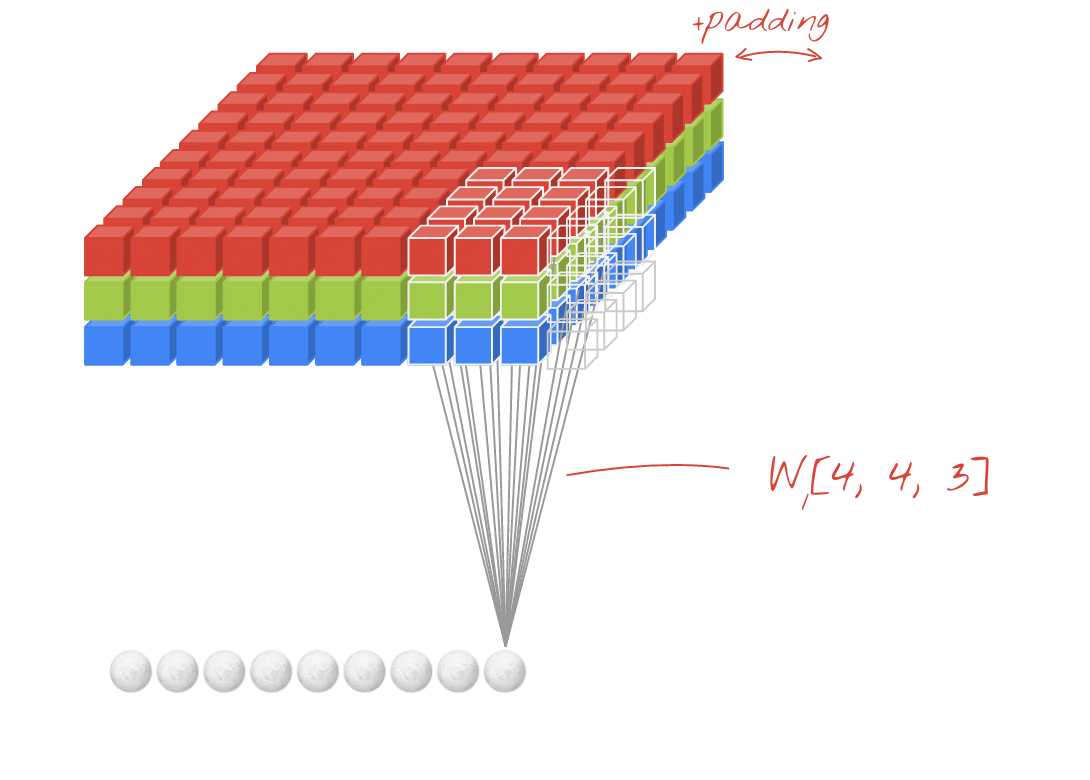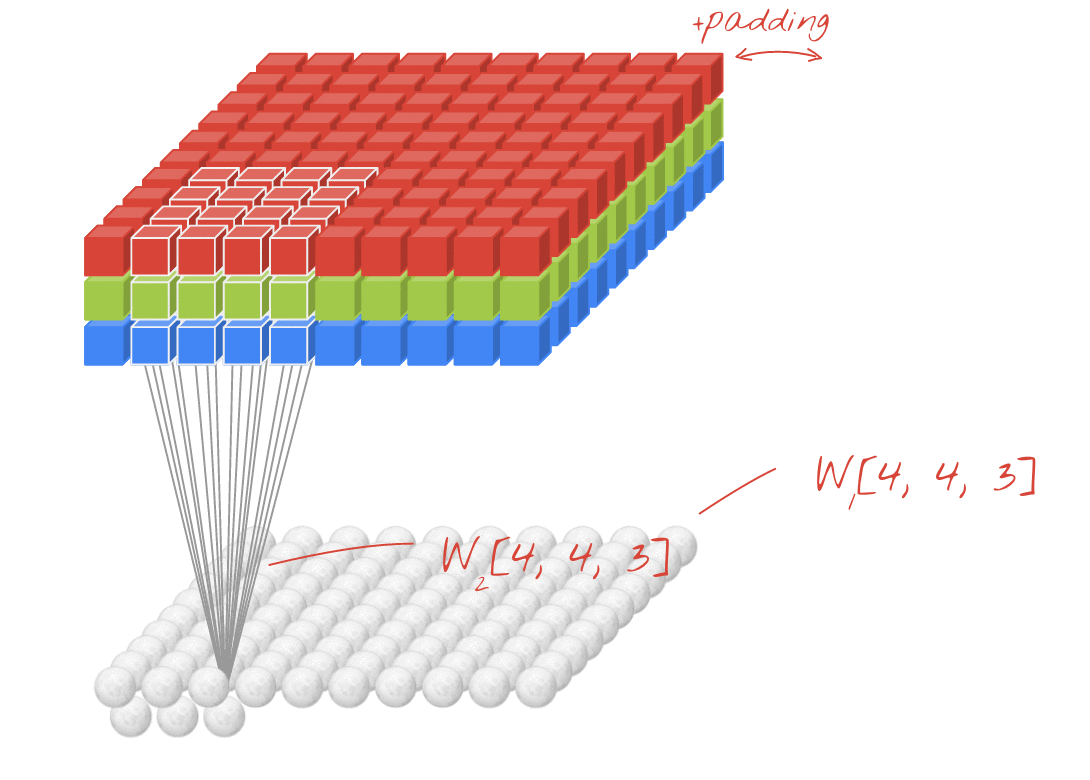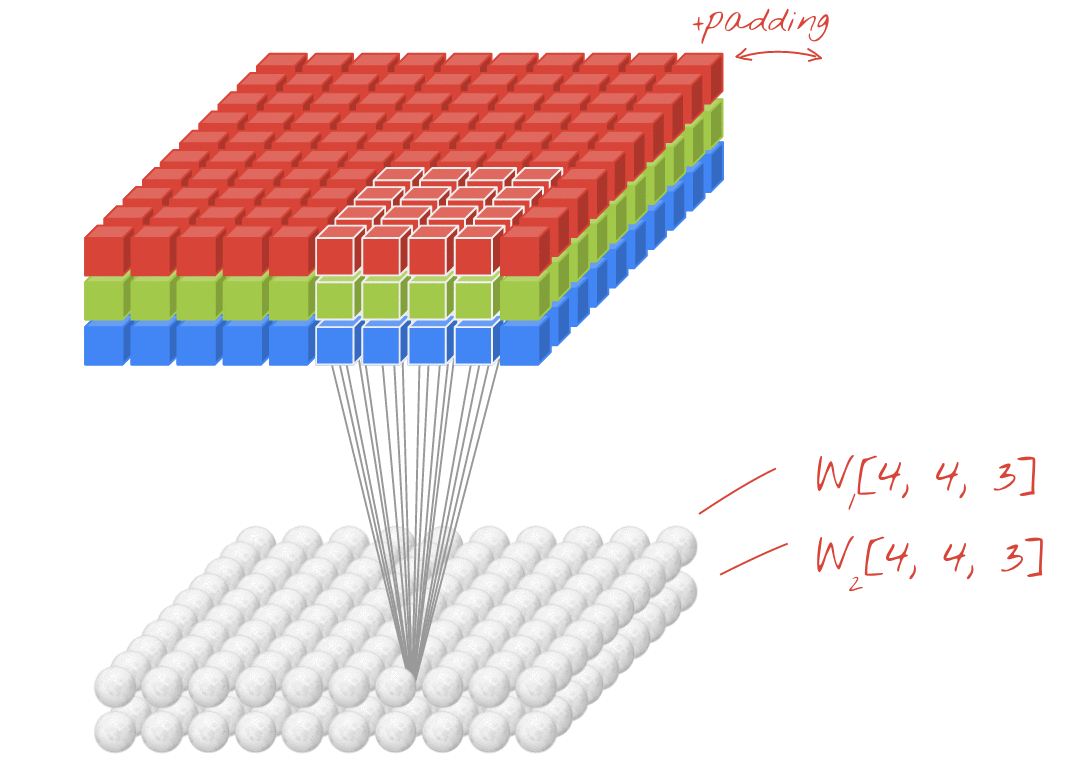
Ilustración: Filtrado de una imagen con dos filtros sucesivos compuestos por 48 pesos entrenables cada uno (4 × 4 × 3=48).

Las redes neuronales convolucionales aplican una serie de filtros entrenables a la imagen de entrada. Una capa convolucional se define por el tamaño del filtro (o kernel), la cantidad de filtros aplicados y el paso. La entrada y la salida de una capa convolucional tienen tres dimensiones cada una (ancho, alto y cantidad de canales), comenzando con la imagen de entrada (ancho, alto y canales RGB). Cuando se apilan capas convolucionales, el ancho y la altura de la salida se pueden ajustar con un stride > 1 o con una operación de max-pooling. La profundidad de la salida (cantidad de canales) se ajusta con más o menos filtros.

Así se ve una red neuronal convolucional simple en Keras:

model = tf.keras.Sequential([
    tf.keras.layers.Reshape(input_shape=(28*28,), target_shape=(28, 28, 1)),
    tf.keras.layers.Conv2D(kernel_size=3, filters=12, activation='relu'),
    tf.keras.layers.Conv2D(kernel_size=6, filters=24, strides=2, activation='relu'),
    tf.keras.layers.Conv2D(kernel_size=6, filters=32, strides=2, activation='relu'),
    tf.keras.layers.Flatten(),
    tf.keras.layers.Dense(10, activation='softmax')
])

En una capa de una red convolucional, una "neurona" realiza una suma ponderada de los píxeles que se encuentran justo arriba de ella, solo en una pequeña región de la imagen. Agrega un sesgo y alimenta la suma a través de una función de activación, tal como lo haría una neurona en una capa densa normal. Luego, esta operación se repite en toda la imagen con los mismos pesos. Recuerda que, en las capas densas, cada neurona tenía sus propios pesos. Aquí, un solo "parche" de pesos se desliza por la imagen en ambas direcciones (una "convolución"). El resultado tiene tantos valores como píxeles hay en la imagen (aunque es necesario agregar relleno en los bordes). Es una operación de filtrado. En la ilustración anterior, se usa un filtro de 4 x 4 x 3=48 pesos.

Sin embargo, 48 pesos no serán suficientes. Para agregar más grados de libertad, repetimos la misma operación con un nuevo conjunto de pesos. Esto genera un nuevo conjunto de resultados del filtro. Por analogía con los canales R,G y B de la imagen de entrada,llamémoslo "canal" de salidas.

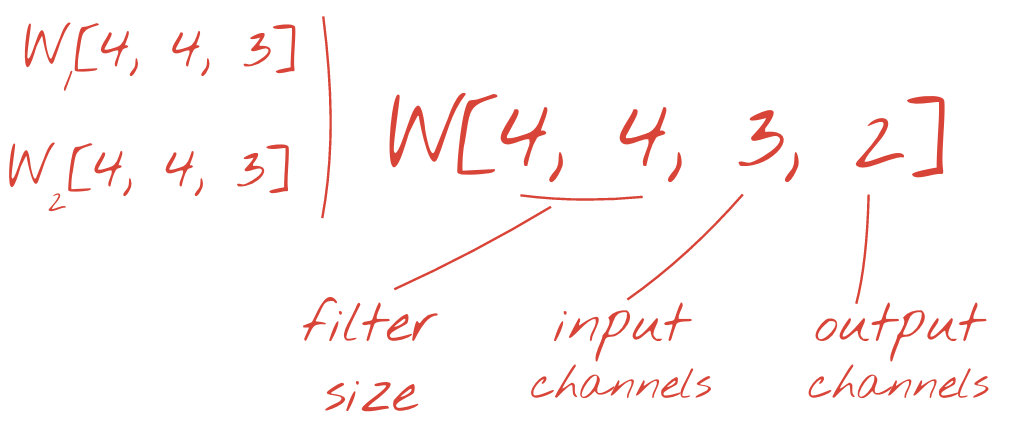
Los dos (o más) conjuntos de pesos se pueden sumar como un tensor agregando una nueva dimensión. Esto nos da la forma genérica del tensor de pesos para una capa convolucional. Dado que la cantidad de canales de entrada y salida son parámetros, podemos comenzar a apilar y encadenar capas convolucionales.

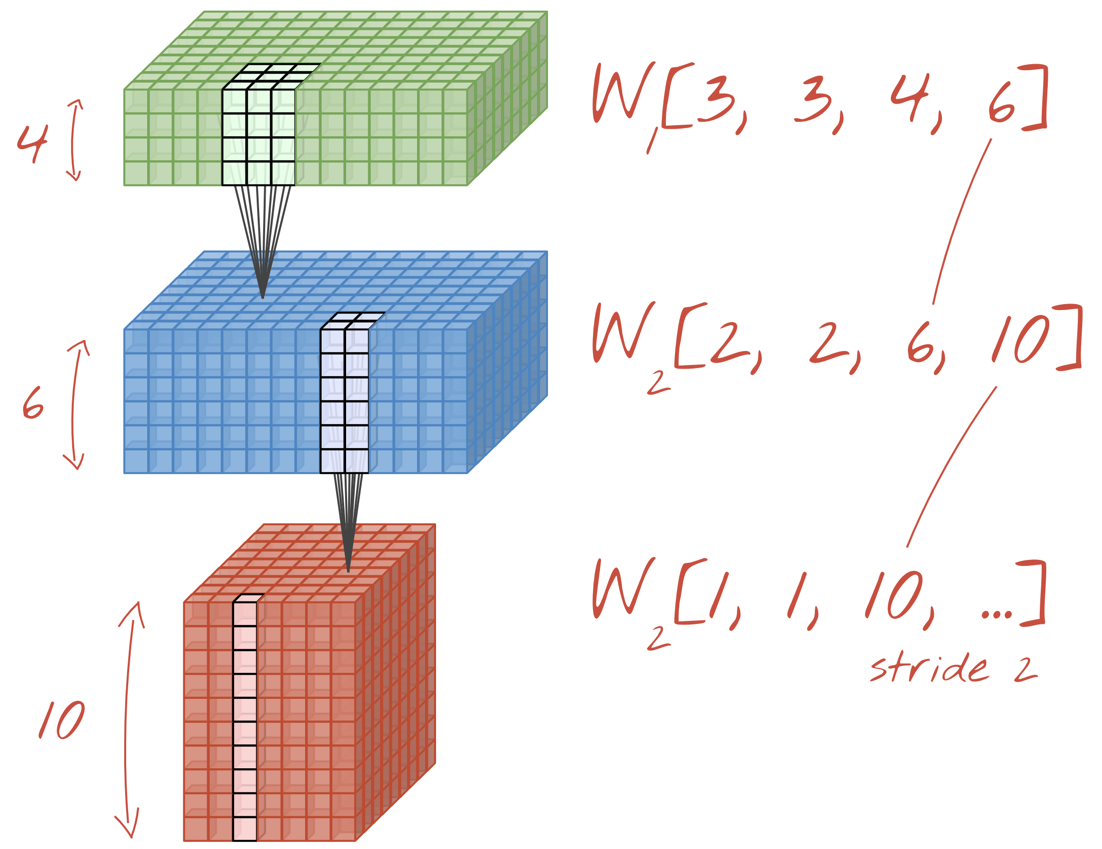
Ilustración: Una red neuronal convolucional transforma "cubos" de datos en otros "cubos" de datos.

Convoluciones con stride, reducción máxima

Si realizamos las convoluciones con un paso de 2 o 3, también podemos reducir el cubo de datos resultante en sus dimensiones horizontales. Existen dos formas comunes de hacerlo:

• Convolución con stride: Un filtro deslizante como el anterior, pero con un stride > 1
• Reducción máxima: Una ventana deslizante que aplica la operación MAX (generalmente en parches de 2×2, repetidos cada 2 píxeles)

Ilustración: Deslizar la ventana de cálculo en 3 píxeles genera menos valores de salida. Las convoluciones con segmentos o la reducción máxima (máximo en una ventana de 2x2 que se desliza con un segmento de 2) son una forma de reducir el cubo de datos en las dimensiones horizontales.

El "agrupamiento máximo" puede ayudarnos a comprender de forma intuitiva cómo operan las redes convolucionales: si suponemos que, durante el entrenamiento, los parches de pesos evolucionan a filtros que reconocen formas básicas (líneas horizontales y verticales, curvas, etcétera), una forma de reducir la información útil es mantener a través de las capas los resultados en los que se reconoció una forma con la máxima intensidad. En la práctica, en una neurona de capa de max-pooling, las salidas se procesan en grupos de 2x2 y solo se retiene el valor máximo.

La capa final

Después de la última capa convolucional, los datos tienen la forma de un "cubo". Hay dos formas de alimentarlo a través de la capa densa final.

La primera es aplanar el cubo de datos en un vector y, luego, ingresarlo en la capa softmax. A veces, incluso puedes agregar una capa densa antes de la capa softmax. Esto suele ser costoso en términos de la cantidad de pesos. Una capa densa al final de una red convolucional puede contener más de la mitad de los pesos de toda la red neuronal.

En lugar de usar una capa densa costosa, también podemos dividir el "cubo" de datos entrantes en tantas partes como clases tengamos, calcular el promedio de sus valores y pasarlos a través de una función de activación softmax. Esta forma de crear el encabezado de clasificación no requiere ningún peso. En Keras, existe una capa para esto: tf.keras.layers.GlobalAveragePooling2D().

Las redes neuronales convolucionales detectan la ubicación de los objetos. Cuando un filtro responde con intensidad a alguna característica, lo hace en una ubicación (x, y) específica. Según lo que quieras hacer, se puede entrenar una red neuronal para que use o descarte estos datos de ubicación. El uso del agrupamiento promedio global descarta explícitamente todos los datos de ubicación. Esto podría ser adecuado para un clasificador de flores, pero podría no funcionar bien para otras tareas, como contar flores en una imagen. Úsala con precaución.

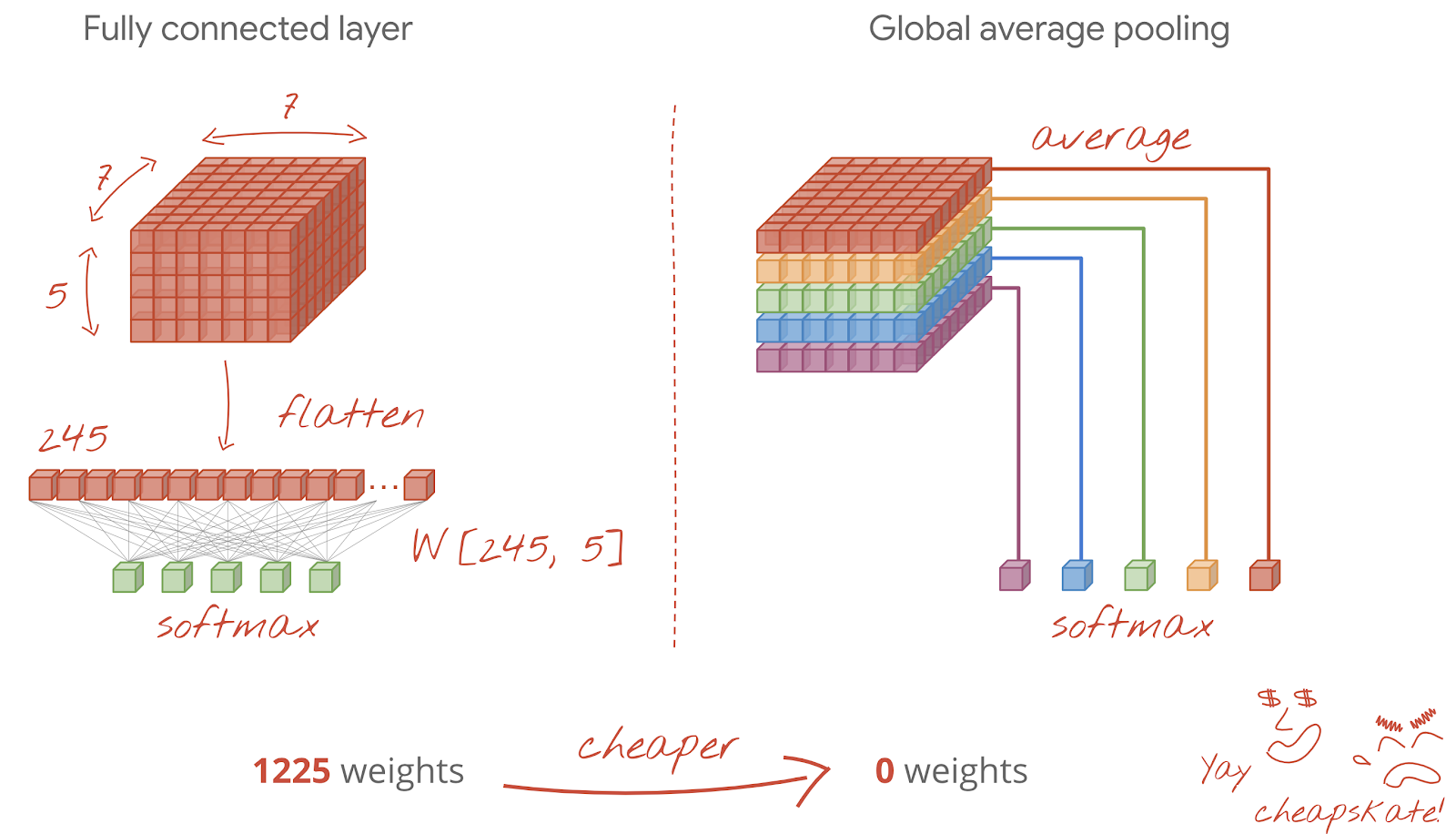
Pasa a la siguiente sección para crear una red convolucional para el problema en cuestión.

Creemos una red convolucional para el reconocimiento de dígitos escritos a mano. Usaremos tres capas convolucionales en la parte superior, nuestra tradicional capa de lectura de softmax en la parte inferior y las conectaremos con una capa completamente conectada:

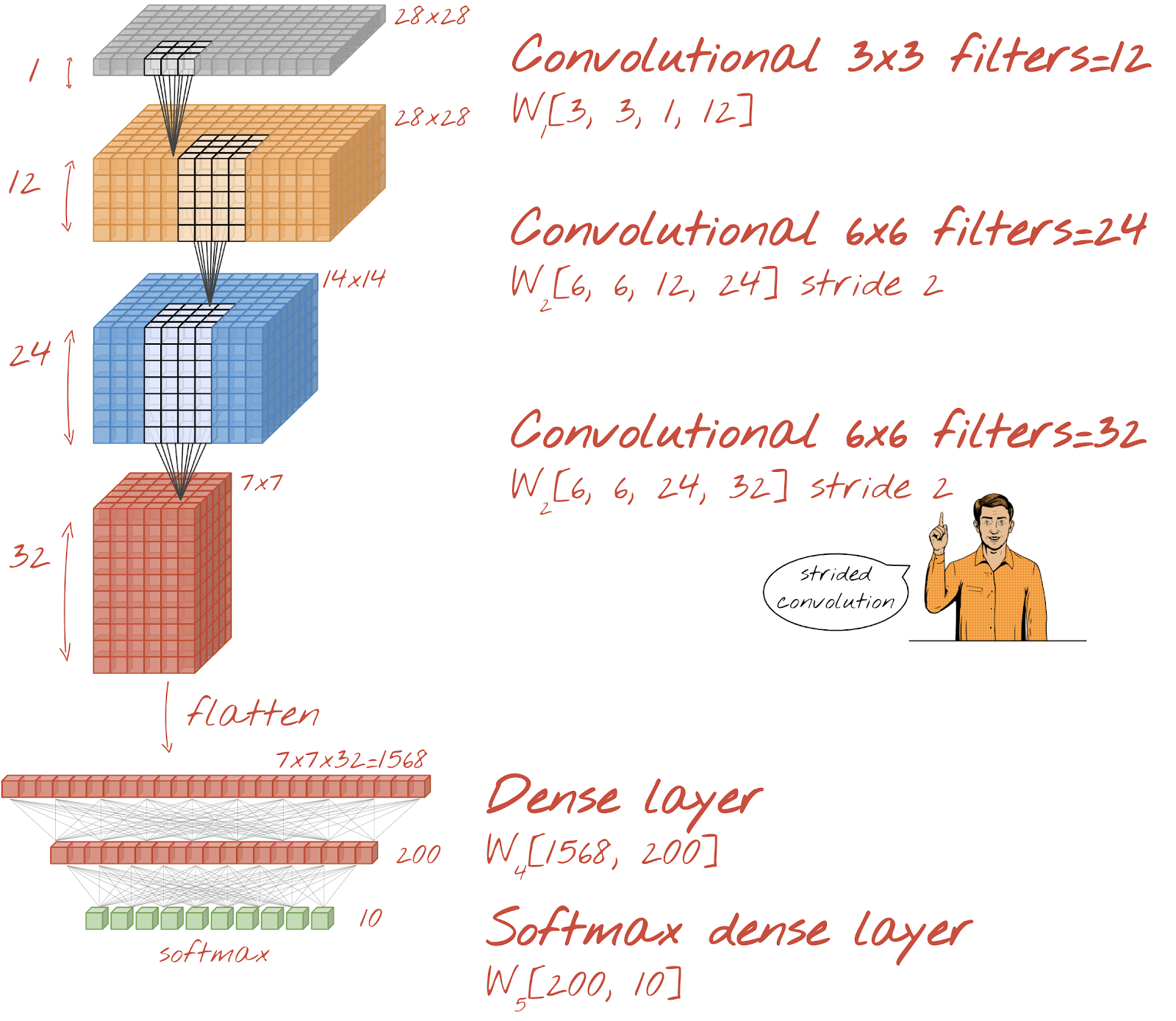
Ten en cuenta que la segunda y la tercera capa convolucional tienen un stride de dos, lo que explica por qué reducen la cantidad de valores de salida de 28 x 28 a 14 x 14 y, luego, a 7 x 7.

Escribamos el código de Keras.

Se necesita una atención especial antes de la primera capa convolucional. De hecho, espera un "cubo" de datos en 3D, pero nuestro conjunto de datos se configuró hasta ahora para capas densas, y todos los píxeles de las imágenes se aplanan en un vector. Debemos volver a darles la forma de imágenes de 28 x 28 x 1 (1 canal para imágenes en escala de grises):

tf.keras.layers.Reshape(input_shape=(28*28,), target_shape=(28, 28, 1))

Puedes usar esta línea en lugar de la capa tf.keras.layers.Input que tenías hasta ahora.

En Keras, la sintaxis para una capa convolucional activada por "relu" es la siguiente:

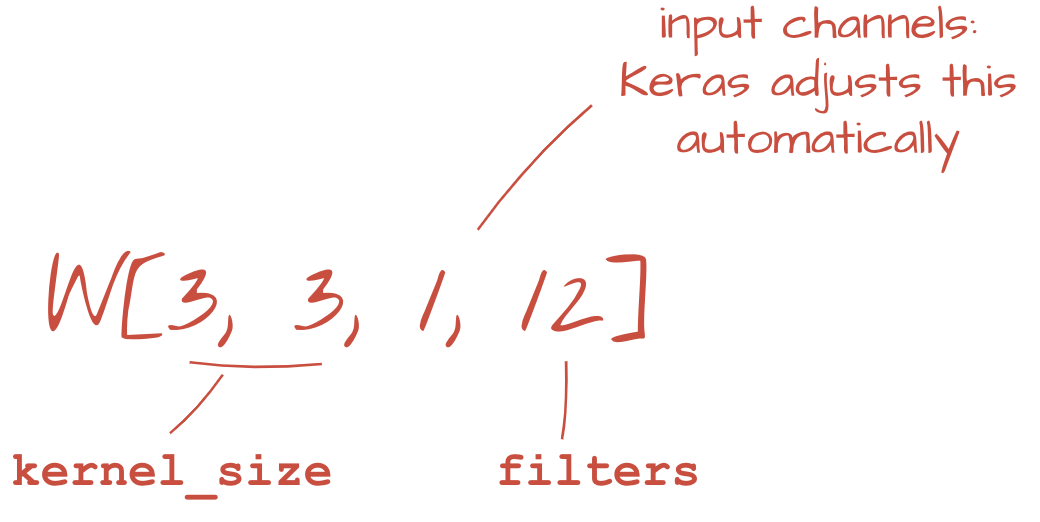
tf.keras.layers.Conv2D(kernel_size=3, filters=12, padding='same', activation='relu')

El parámetro de padding en las capas convolucionales puede tener dos valores:

• "same": Se agregan ceros para producir resultados con el mismo ancho y alto que la entrada.
• "valid": Sin relleno, solo se usan píxeles reales.

Aquí usamos el padding, así que configúralo como "same".

Para una convolución con stride, escribirías lo siguiente:

tf.keras.layers.Conv2D(kernel_size=6, filters=24, padding='same', activation='relu', strides=2)

Para aplanar un cubo de datos en un vector de modo que una capa densa pueda consumirlo, haz lo siguiente:

tf.keras.layers.Flatten()

Y para la capa densa, la sintaxis no cambió:

tf.keras.layers.Dense(200, activation='relu')

PRÁCTICA:

Modifica tu modelo para convertirlo en un modelo convolucional. Puedes usar los valores del dibujo anterior para determinar su tamaño. Puedes mantener la disminución de la tasa de aprendizaje como estaba, pero quita el abandono en este punto.

También aumenta el factor de zoom a 16 en PlotTraining. Esto hace un acercamiento alrededor de 0 en las pérdidas y alrededor de 1 en las precisiones para ayudarte a ver qué sucede: PlotTraining(sample_rate=10, zoom=16)

¿Tu modelo superó la barrera de exactitud del 99%? Casi… pero observa la curva de pérdida de validación. ¿Te suena esto?

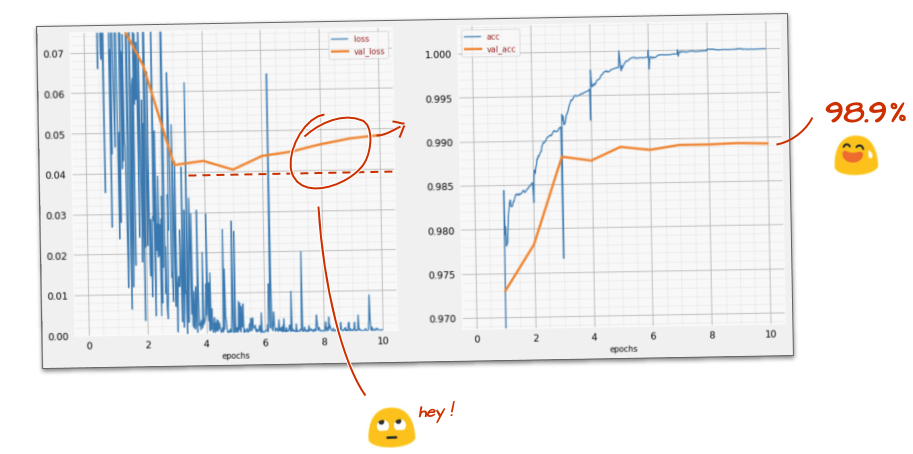
También mira las predicciones. Por primera vez, deberías ver que la mayoría de los 10,000 dígitos de prueba ahora se reconocen correctamente. Solo quedan alrededor de 4 filas y media de detecciones incorrectas (alrededor de 110 dígitos de 10,000).

Si no sabes cómo hacerlo, aquí tienes la solución en este punto:

keras_04_mnist_convolutional.ipynb

El entrenamiento anterior muestra signos claros de sobreajuste (y aún no alcanza el 99% de exactitud). ¿Deberíamos volver a probar con la exclusión?

PRÁCTICA:

Agrega una capa de retiro entre las dos capas densas de tu red. Usa una tasa de deserción del 40% (=0.4):

tf.keras.layers.Dropout(0.4)

Es posible aplicar la deserción a las capas convolucionales, pero funciona de manera ligeramente diferente y, por lo general, no es tan eficaz porque hay muchos menos pesos en las capas convolucionales y, por lo tanto, menos posibilidades de una mala coadaptación. No exploraremos este tema.

¿Cómo te fue esta vez?

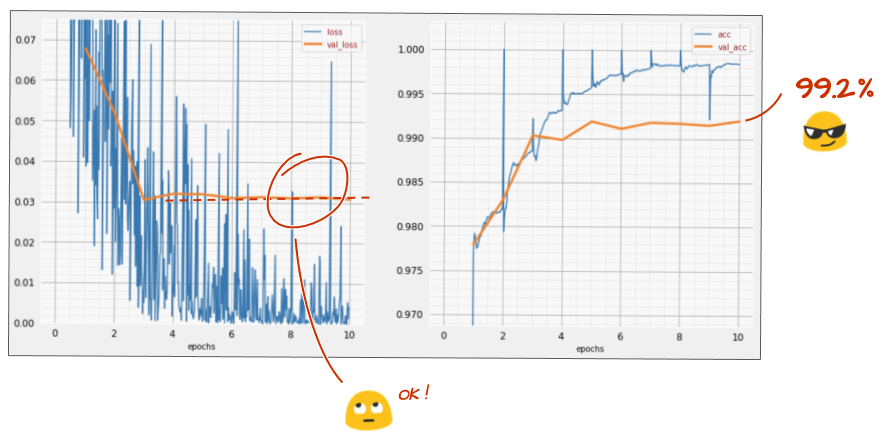
Parece que esta vez la deserción funcionó. La pérdida de validación ya no aumenta y la precisión final debería ser muy superior al 99%. ¡Felicitaciones!

La primera vez que intentamos aplicar la deserción, pensamos que teníamos un problema de sobreajuste, cuando, en realidad, el problema estaba en la arquitectura de la red neuronal. No pudimos avanzar más sin capas convolucionales, y no había nada que la deserción pudiera hacer al respecto.

Esta vez, parece que el sobreajuste fue la causa del problema y la deserción realmente ayudó. Recuerda que hay muchos factores que pueden causar una desconexión entre las curvas de pérdida de entrenamiento y validación, lo que provoca que la pérdida de validación aumente. El sobreajuste (demasiados grados de libertad, mal uso por parte de la red) es solo uno de ellos. Si tu conjunto de datos es demasiado pequeño o la arquitectura de tu red neuronal no es adecuada, es posible que veas un comportamiento similar en las curvas de pérdida, pero la deserción no ayudará.

Por último, intentemos agregar la normalización por lotes.

¿Qué es la normalización por lotes?

En pocas palabras, la normalización por lotes intenta abordar el problema de cómo se distribuyen las salidas de las neuronas en relación con la función de activación de la neurona. En un lote pequeño de datos de entrenamiento, la salida de una neurona, antes de la activación, podría tener las siguientes distribuciones:

Demasiado a la izquierda, después de la activación sigmoidea, esta neurona casi siempre genera un 0.

Demasiado estrecha: Esta neurona nunca genera un 0 o un 1 claros.

No está tan mal. La neurona tendrá un rango de comportamientos razonable en este lote pequeño.

Para solucionar este problema, la normalización por lotes normaliza las salidas de las neuronas en un lote de datos de entrenamiento, es decir, resta el promedio y divide por la desviación estándar. Sin embargo, hacer solo eso sería demasiado brutal. Con una distribución perfectamente centrada y normalmente amplia en todas partes, todas las neuronas tendrían el mismo comportamiento. El truco consiste en introducir dos parámetros adicionales que se pueden aprender por neurona, 𝛼 y 𝛽, y calcular lo siguiente:

𝛼 . normalized_out + 𝛽

Luego, aplica la función de activación (sigmoide, ReLU, etc.). De esta manera, la red decide, a través del aprendizaje automático, cuánto centrado y reescalado aplicar en cada neurona. Se deja como ejercicio para el lector verificar que existen valores de 𝛼 y 𝛽 que pueden quitar la normalización por completo, si eso es lo correcto.

En la práctica, no siempre se necesitan 𝛼 y 𝛽. En Keras, se denominan "escala" y "centrado", y puedes usar uno u otro de forma selectiva, por ejemplo:

tf.keras.layers.BatchNormalization(scale=False, center=True)

El problema con la normalización por lotes es que, en el momento de la predicción, no tienes lotes de entrenamiento con los que puedas calcular las estadísticas de las salidas de tus neuronas. Pero aún necesitas esos valores. Esta parte es un poco hacky. Durante el entrenamiento, se calcula un promedio y una desviación estándar de la salida de la neurona "típica" en una cantidad "suficiente" de lotes, que, en la práctica, se realiza con un promedio exponencial acumulado. Luego, estas estadísticas se usan durante la inferencia.

La buena noticia es que, en Keras, puedes usar una capa tf.keras.layers.BatchNormalization y toda esta contabilización se realizará automáticamente.

Esa es la teoría. En la práctica, solo recuerda un par de reglas:

Normalización por lotes "según el libro":

1. La normalización por lotes se aplica entre la salida de una capa y su función de activación.
2. Si usas center=True en la normalización por lotes, no necesitas sesgos en tu capa. El desplazamiento de la normalización por lotes desempeña el rol de una desviación.
3. Si usas una función de activación que es invariante a la escala (es decir, no cambia de forma si la acercas), puedes establecer scale=False. La función ReLU es invariante a la escala. La sigmoide no lo es.

Esta es la teoría, pero la única forma de saber si incumplir estas reglas es malo es intentarlo.

Por ahora, sigamos las reglas y agreguemos una capa de normalización por lotes en cada capa de la red neuronal, excepto la última. No lo agregues a la última capa "softmax". No sería útil allí.

# Modify each layer: remove the activation from the layer itself.
# Set use_bias=False since batch norm will play the role of biases.
tf.keras.layers.Conv2D(..., use_bias=False),
# Batch norm goes between the layer and its activation.
# The scale factor can be turned off for Relu activation.
tf.keras.layers.BatchNormalization(scale=False, center=True),
# Finish with the activation.
tf.keras.layers.Activation('relu'),

¿Cómo es la precisión ahora?

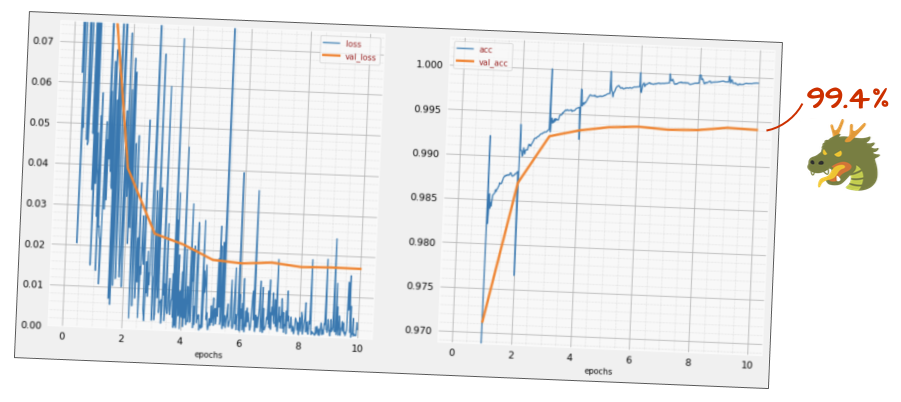
Con algunos ajustes (BATCH_SIZE=64, parámetro de decaimiento de la tasa de aprendizaje 0.666, tasa de deserción en la capa densa 0.3) y un poco de suerte, puedes alcanzar el 99.5%. Los ajustes de la tasa de aprendizaje y la tasa de abandono se realizaron siguiendo las "prácticas recomendadas" para usar la normalización por lotes:

• La normalización por lotes ayuda a que las redes neuronales converjan y, por lo general, te permite entrenar más rápido.
• La normalización por lotes es un regularizador. Por lo general, puedes disminuir la cantidad de dropout que usas o, incluso, no usarlo en absoluto.

El notebook de solución tiene una ejecución de entrenamiento del 99.5%:

keras_05_mnist_batch_norm.ipynb

Encontrarás una versión del código lista para la nube en la carpeta mlengine de GitHub, junto con instrucciones para ejecutarla en Google Cloud AI Platform. Antes de ejecutar esta parte, deberás crear una cuenta de Google Cloud y habilitar la facturación. Los recursos necesarios para completar el lab deberían costar menos de un par de dólares (suponiendo 1 h de tiempo de entrenamiento en una GPU). Para preparar tu cuenta, sigue estos pasos:

1. Crea un proyecto de Google Cloud Platform (http://cloud.google.com/console).
2. Habilita la facturación.
3. Instala las herramientas de línea de comandos de GCP (SDK de GCP aquí).
4. Crea un bucket de Google Cloud Storage (colócalo en la región us-central1). Se usará para organizar el código de entrenamiento y almacenar tu modelo entrenado.
5. Habilita las APIs necesarias y solicita las cuotas necesarias (ejecuta el comando de entrenamiento una vez y deberías recibir mensajes de error que te indiquen qué debes habilitar).

Compilaste tu primera red neuronal y la entrenaste hasta alcanzar una precisión del 99%. Las técnicas que se aprenden en el camino no son específicas del conjunto de datos MNIST, sino que se usan ampliamente cuando se trabaja con redes neuronales. Como regalo de despedida, aquí tienes la tarjeta de "notas de la clase" del lab, en versión de dibujos animados. Puedes usarlo para recordar lo que aprendiste:

Próximos pasos

• Después de las redes convolucionales y completamente conectadas, deberías echar un vistazo a las redes neuronales recurrentes.
• Para ejecutar tu entrenamiento o inferencia en la nube en una infraestructura distribuida, Google Cloud proporciona AI Platform.
  
• Por último, nos encanta recibir comentarios. Avísanos si ves algo incorrecto en este lab o si crees que se debería mejorar. Manejamos los comentarios a través de los problemas de GitHub [vínculo de comentarios].

El autor: Martin Görner Twitter: @martin_gorner

Derechos de autor de todas las imágenes de dibujos animados en este lab: alexpokusay / 123RF stock photos