Halaman ini berisi istilah glosarium Decision Forests. Untuk semua istilah glosarium, klik di sini.
A
pengambilan sampel atribut
Taktik untuk melatih hutan keputusan yang setiap pohon keputusannya hanya mempertimbangkan subset acak dari fitur yang mungkin saat mempelajari kondisi. Umumnya, subset fitur yang berbeda diambil sampelnya untuk setiap node. Sebaliknya, saat melatih pohon keputusan tanpa pengambilan sampel atribut, semua fitur yang mungkin dipertimbangkan untuk setiap node.
kondisi yang sejajar dengan sumbu
Dalam pohon keputusan, kondisi
yang hanya melibatkan satu fitur. Misalnya, jika area
adalah fitur, maka berikut adalah kondisi yang sejajar dengan sumbu:
area > 200
Berbeda dengan kondisi miring.
B
mengantongi
Metode untuk melatih ansambel dengan setiap model konstituen dilatih pada subset acak dari contoh pelatihan yang diambil sampelnya dengan penggantian. Misalnya, hutan acak adalah kumpulan pohon keputusan yang dilatih dengan bagging.
Istilah bagging adalah singkatan dari bootstrap aggregating.
Lihat Random forest dalam kursus Decision Forest untuk mengetahui informasi selengkapnya.
kondisi biner
Dalam pohon keputusan, kondisi yang hanya memiliki dua kemungkinan hasil, biasanya ya atau tidak. Misalnya, berikut adalah kondisi biner:
temperature >= 100
Berbeda dengan kondisi non-biner.
Lihat Jenis kondisi dalam kursus Decision Forests untuk mengetahui informasi selengkapnya.
C
kondisi
Dalam pohon keputusan, setiap node yang melakukan pengujian. Misalnya, pohon keputusan berikut berisi dua kondisi:
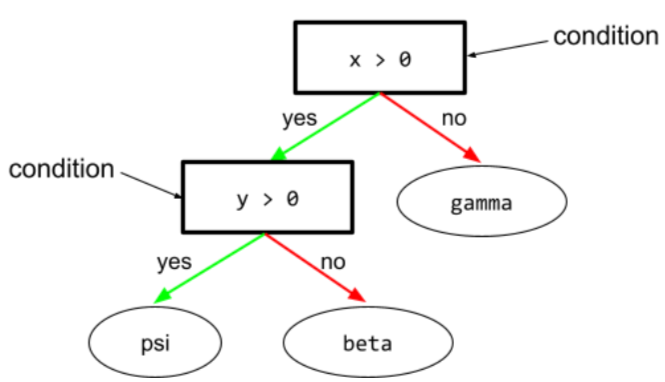
Kondisi juga disebut pemisahan atau pengujian.
Kondisi kontras dengan leaf.
Lihat juga:
Lihat Jenis kondisi dalam kursus Decision Forests untuk mengetahui informasi selengkapnya.
D
hutan keputusan
Model yang dibuat dari beberapa pohon keputusan. Hutan keputusan membuat prediksi dengan menggabungkan prediksi pohon keputusannya. Jenis hutan keputusan yang populer mencakup hutan acak dan pohon penguatan gradien.
Lihat bagian Decision Forests di kursus Decision Forests untuk mengetahui informasi selengkapnya.
pohon keputusan
Model pembelajaran terawasi yang terdiri dari serangkaian kondisi dan daun yang disusun secara hierarkis. Misalnya, berikut adalah pohon keputusan:

E
entropi
Dalam teori informasi, deskripsi tentang seberapa tidak terduganya distribusi probabilitas. Atau, entropi juga ditentukan sebagai seberapa banyak informasi yang terkandung dalam setiap contoh. Distribusi memiliki entropi tertinggi yang mungkin terjadi jika semua nilai variabel acak memiliki kemungkinan yang sama.
Entropi himpunan dengan dua kemungkinan nilai "0" dan "1" (misalnya, label dalam masalah klasifikasi biner) memiliki formula berikut:
H = -p log p - q log q = -p log p - (1-p) * log (1-p)
dalam hal ini:
- H adalah entropi.
- p adalah fraksi contoh "1".
- q adalah fraksi contoh "0". Perhatikan bahwa q = (1 - p)
- log umumnya adalah log2. Dalam hal ini, unit entropi adalah bit.
Misalnya, anggap saja hal berikut:
- 100 contoh berisi nilai "1"
- 300 contoh berisi nilai "0"
Oleh karena itu, nilai entropi adalah:
- p = 0,25
- q = 0,75
- H = (-0,25)log2(0,25) - (0,75)log2(0,75) = 0,81 bit per contoh
Kumpulan data yang seimbang sempurna (misalnya, 200 "0" dan 200 "1") akan memiliki entropi 1,0 bit per contoh. Seiring bertambahnya ketidakseimbangan dalam kumpulan data, entropinya bergerak menuju 0,0.
Dalam pohon keputusan, entropi membantu merumuskan perolehan informasi untuk membantu pemisah memilih kondisi selama pertumbuhan pohon keputusan klasifikasi.
Bandingkan entropi dengan:
- gini impurity
- Fungsi kerugian cross-entropy
Entropi sering disebut entropi Shannon.
Lihat Splitter persis untuk klasifikasi biner dengan fitur numerik dalam kursus Decision Forests untuk mengetahui informasi selengkapnya.
F
tingkat kepentingan fitur
Sinonim untuk kepentingan variabel.
G
gini impurity
Metrik yang mirip dengan entropi. Splitter menggunakan nilai yang berasal dari ketidakmurnian Gini atau entropi untuk menyusun kondisi untuk klasifikasi pohon keputusan. Perolehan informasi berasal dari entropi. Tidak ada istilah yang setara dan diterima secara universal untuk metrik yang berasal dari ketidakmurnian Gini; namun, metrik yang tidak disebutkan namanya ini sama pentingnya dengan perolehan informasi.
Ketidakmurnian Gini juga disebut indeks gini, atau cukup gini.
pohon (keputusan) penguatan gradien (GBT)
Jenis hutan keputusan yang:
- Pelatihan mengandalkan gradient boosting.
- Model lemah adalah pohon keputusan.
Lihat Gradient Boosted Decision Trees di kursus Decision Forests untuk mengetahui informasi selengkapnya.
gradient boosting
Algoritma pelatihan yang melatih model lemah secara berulang untuk meningkatkan kualitas (mengurangi kerugian) model yang kuat. Misalnya, model yang lemah dapat berupa model linear atau pohon keputusan kecil. Model kuat menjadi jumlah dari semua model lemah yang dilatih sebelumnya.
Dalam bentuk gradient boosting yang paling sederhana, pada setiap iterasi, model lemah dilatih untuk memprediksi gradien kerugian model kuat. Kemudian, output model yang kuat diperbarui dengan mengurangi gradien yang diprediksi, mirip dengan penurunan gradien.
dalam hal ini:
- $F_{0}$ adalah model awal yang kuat.
- $F_{i+1}$ adalah model kuat berikutnya.
- $F_{i}$ adalah model kuat saat ini.
- $\xi$ adalah nilai antara 0,0 dan 1,0 yang disebut penyusutan, yang analog dengan kecepatan pembelajaran dalam penurunan gradien.
- $f_{i}$ adalah model lemah yang dilatih untuk memprediksi gradien kerugian $F_{i}$.
Variasi modern dari gradient boosting juga menyertakan turunan kedua (Hessian) dari loss dalam komputasinya.
Pohon keputusan biasanya digunakan sebagai model lemah dalam gradient boosting. Lihat pohon (keputusan) penguatan gradien.
I
jalur inferensi
Dalam pohon keputusan, selama inferensi, rute yang diambil oleh contoh tertentu dari root ke kondisi lainnya, yang berakhir dengan leaf. Misalnya, dalam pohon keputusan berikut, panah yang lebih tebal menunjukkan jalur inferensi untuk contoh dengan nilai fitur berikut:
- x = 7
- y = 12
- z = -3
Jalur inferensi dalam ilustrasi berikut melewati tiga
kondisi sebelum mencapai leaf (Zeta).
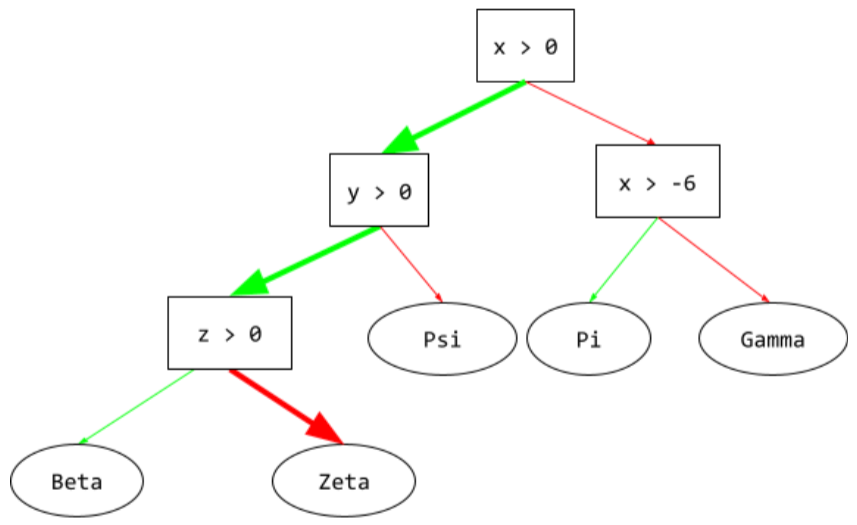
Tiga panah tebal menunjukkan jalur inferensi.
Lihat Pohon keputusan dalam kursus Decision Forests untuk mengetahui informasi selengkapnya.
perolehan informasi
Dalam hutan keputusan, perbedaan antara entropi node dan jumlah entropi node turunannya yang diberi bobot (berdasarkan jumlah contoh). Entropi node adalah entropi contoh di node tersebut.
Misalnya, pertimbangkan nilai entropi berikut:
- entropi node induk = 0,6
- entropi satu node turunan dengan 16 contoh relevan = 0,2
- entropi node turunan lain dengan 24 contoh relevan = 0,1
Jadi, 40% contoh berada di satu node turunan dan 60% berada di node turunan lainnya. Jadi:
- jumlah entropi berbobot dari node turunan = (0,4 * 0,2) + (0,6 * 0,1) = 0,14
Jadi, perolehan informasi adalah:
- perolehan informasi = entropi node induk - jumlah entropi tertimbang node turunan
- perolehan informasi = 0,6 - 0,14 = 0,46
Sebagian besar pemisah berupaya membuat kondisi yang memaksimalkan perolehan informasi.
kondisi dalam set
Dalam pohon keputusan, kondisi yang menguji keberadaan satu item dalam sekumpulan item. Misalnya, berikut adalah kondisi dalam set:
house-style in [tudor, colonial, cape]
Selama inferensi, jika nilai fitur gaya rumah adalah tudor atau colonial atau cape, kondisi ini akan bernilai Ya. Jika
nilai fitur gaya visual adalah sesuatu yang lain (misalnya, ranch),
maka kondisi ini akan bernilai Tidak.
Kondisi dalam set biasanya menghasilkan pohon keputusan yang lebih efisien daripada kondisi yang menguji fitur berenkode one-hot.
L
daun
Endpoint apa pun dalam pohon keputusan. Tidak seperti kondisi, leaf tidak melakukan pengujian. Sebaliknya, daun adalah kemungkinan prediksi. Leaf juga merupakan node terminal dari jalur inferensi.
Misalnya, pohon keputusan berikut berisi tiga daun:
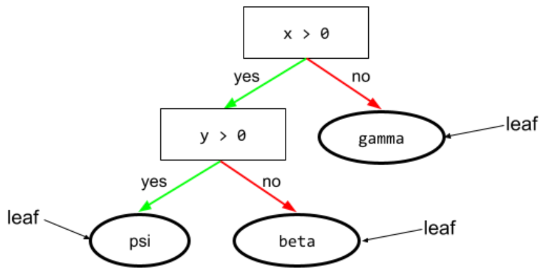
Lihat Pohon keputusan dalam kursus Decision Forests untuk mengetahui informasi selengkapnya.
T
node (pohon keputusan)
Dalam pohon keputusan, setiap kondisi atau daun.
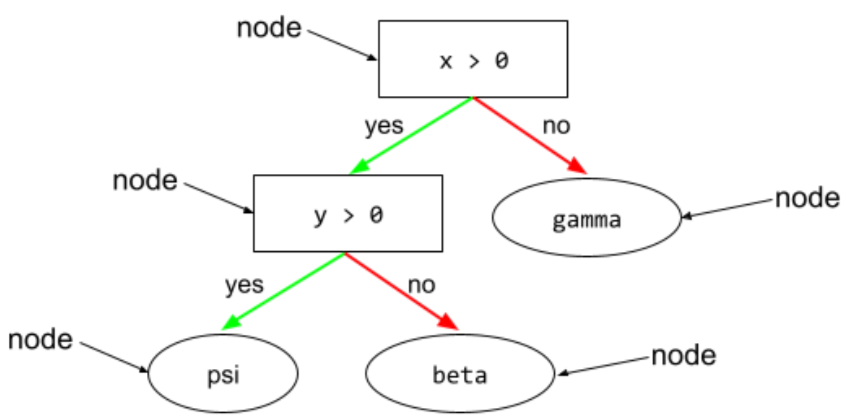
Lihat Pohon Keputusan dalam kursus Decision Forests untuk mengetahui informasi selengkapnya.
kondisi non-biner
Kondisi yang berisi lebih dari dua kemungkinan hasil. Misalnya, kondisi non-biner berikut berisi tiga kemungkinan hasil:
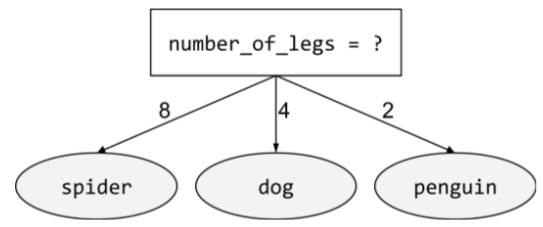
Lihat Jenis kondisi dalam kursus Decision Forests untuk mengetahui informasi selengkapnya.
O
kondisi miring
Dalam pohon keputusan, kondisi yang melibatkan lebih dari satu fitur. Misalnya, jika tinggi dan lebar adalah fitur, maka berikut adalah kondisi miring:
height > width
Berbeda dengan kondisi sejajar sumbu.
Lihat Jenis kondisi dalam kursus Decision Forests untuk mengetahui informasi selengkapnya.
evaluasi di luar paket (evaluasi OOB)
Mekanisme untuk mengevaluasi kualitas decision forest dengan menguji setiap decision tree terhadap contoh yang tidak digunakan selama pelatihan decision tree tersebut. Misalnya, dalam diagram berikut, perhatikan bahwa sistem melatih setiap pohon keputusan pada sekitar dua pertiga contoh, lalu mengevaluasinya terhadap sepertiga contoh yang tersisa.
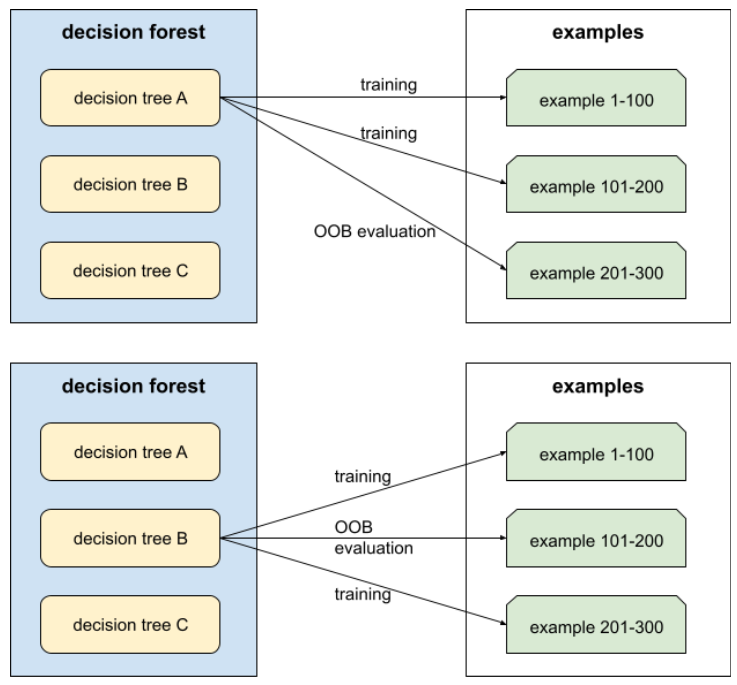
Evaluasi out-of-bag adalah perkiraan mekanisme validasi silang yang efisien secara komputasi dan konservatif. Dalam validasi silang, satu model dilatih untuk setiap putaran validasi silang (misalnya, 10 model dilatih dalam validasi silang 10 kali lipat). Dengan evaluasi OOB, satu model dilatih. Karena bagging menahan beberapa data dari setiap pohon selama pelatihan, evaluasi OOB dapat menggunakan data tersebut untuk memperkirakan validasi silang.
Lihat Evaluasi di luar sampel di kursus Decision Forests untuk mengetahui informasi selengkapnya.
P
permutation variable importances
Jenis kepentingan variabel yang mengevaluasi peningkatan error prediksi model setelah melakukan permutasi pada nilai fitur. Kepentingan variabel permutasi adalah metrik independen model.
R
hutan acak
Ensemble pohon keputusan di mana setiap pohon keputusan dilatih dengan derau acak tertentu, seperti bagging.
Hutan acak adalah jenis hutan keputusan.
Lihat Random Forest dalam kursus Decision Forests untuk mengetahui informasi selengkapnya.
root
Node awal (kondisi pertama) dalam pohon keputusan. Menurut konvensi, diagram menempatkan root di bagian atas pohon keputusan. Contoh:
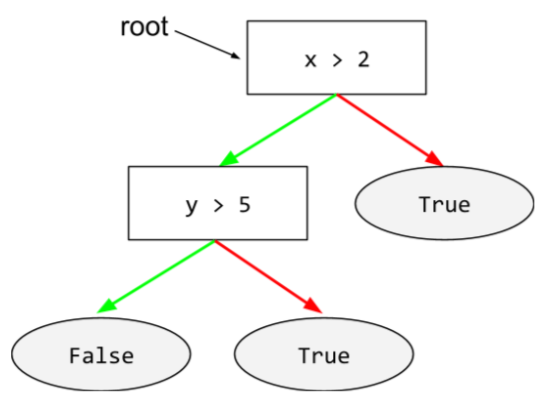
S
pengambilan sampel dengan pengembalian
Metode memilih item dari sekumpulan item kandidat yang sama dapat dipilih beberapa kali. Frasa "dengan pengembalian" berarti bahwa setelah setiap pilihan, item yang dipilih dikembalikan ke kumpulan item kandidat. Metode inversi, pengambilan sampel tanpa penggantian, berarti item kandidat hanya dapat dipilih satu kali.
Misalnya, perhatikan kumpulan buah berikut:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}Misalkan sistem memilih fig secara acak sebagai item pertama.
Jika menggunakan pengambilan sampel dengan penggantian, sistem akan memilih item kedua dari set berikut:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}Ya, itu set yang sama seperti sebelumnya, jadi sistem berpotensi memilih fig lagi.
Jika menggunakan sampling tanpa penggantian, setelah dipilih, sampel tidak dapat
dipilih lagi. Misalnya, jika sistem secara acak memilih fig sebagai
sampel pertama, maka fig tidak dapat dipilih lagi. Oleh karena itu, sistem
memilih contoh kedua dari kumpulan (yang dikurangi) berikut:
fruit = {kiwi, apple, pear, cherry, lime, mango}penyusutan
Hyperparameter dalam gradient boosting yang mengontrol overfitting. Penciutan dalam gradient boosting mirip dengan kecepatan pembelajaran dalam penurunan gradien. Penyusutan adalah nilai desimal antara 0,0 dan 1,0. Nilai penyusutan yang lebih rendah mengurangi kecocokan berlebih lebih banyak daripada nilai penyusutan yang lebih besar.
bagian
Dalam pohon keputusan, nama lain untuk kondisi.
pemisah
Saat melatih pohon keputusan, rutin (dan algoritma) yang bertanggung jawab untuk menemukan kondisi terbaik di setiap node.
T
uji
Dalam pohon keputusan, nama lain untuk kondisi.
nilai minimum (untuk pohon keputusan)
Dalam kondisi yang sejajar dengan sumbu, nilai yang dibandingkan dengan fitur. Misalnya, 75 adalah nilai batas dalam kondisi berikut:
grade >= 75
Lihat Splitter persis untuk klasifikasi biner dengan fitur numerik dalam kursus Decision Forests untuk mengetahui informasi selengkapnya.
V
kepentingan variabel
Kumpulan skor yang menunjukkan nilai penting relatif dari setiap fitur terhadap model.
Misalnya, pertimbangkan pohon keputusan yang memperkirakan harga rumah. Misalkan pohon keputusan ini menggunakan tiga fitur: ukuran, usia, dan gaya. Jika sekumpulan kepentingan variabel untuk ketiga fitur dihitung menjadi {size=5,8, age=2,5, style=4,7}, maka ukuran lebih penting bagi pohon keputusan daripada usia atau gaya.
Ada berbagai metrik kepentingan variabel yang dapat memberi tahu pakar ML tentang berbagai aspek model.
W
kebijaksanaan keramaian
Gagasan bahwa merata-ratakan pendapat atau perkiraan sekelompok besar orang ("kumpulan orang") sering kali menghasilkan hasil yang sangat baik. Misalnya, pertimbangkan game di mana orang menebak jumlah kacang jeli yang dikemas dalam toples besar. Meskipun sebagian besar tebakan individu tidak akurat, rata-rata semua tebakan secara empiris terbukti sangat mendekati jumlah sebenarnya kacang jeli dalam toples.
Ensemble adalah analog software dari kebijaksanaan kolektif. Meskipun model individual membuat prediksi yang sangat tidak akurat, merata-ratakan prediksi banyak model sering kali menghasilkan prediksi yang sangat baik. Misalnya, meskipun pohon keputusan individu mungkin membuat prediksi yang buruk, hutan keputusan sering kali membuat prediksi yang sangat baik.
