In questo tutorial verrà introdotta la metodologia di modellazione della distribuzione delle specie utilizzando Google Earth Engine. Verrà fornita una breve panoramica della modellazione della distribuzione delle specie, seguita dalla procedura di previsione e analisi dell'habitat di una specie di uccello in pericolo nota come pitta ninfa (nome scientifico: Pitta nympha).
Run me first
Esegui la cella seguente per inizializzare l'API. L'output conterrà le istruzioni su come concedere a questo blocco note l'accesso a Earth Engine utilizzando il tuo account.
import ee
# Trigger the authentication flow.
ee.Authenticate()
# Initialize the library.
ee.Initialize(project='my-project')
Breve panoramica della modellazione della distribuzione delle specie
Esploriamo cosa sono i modelli di distribuzione delle specie, i vantaggi dell'utilizzo di Google Earth Engine per il loro trattamento, i dati richiesti per i modelli e la struttura del flusso di lavoro.
Che cos'è la modellazione della distribuzione delle specie?
La modellazione della distribuzione delle specie (di seguito SDM) è la metodologia più comune utilizzata per stimare la distribuzione geografica effettiva o potenziale di una specie. Consiste nel caratterizzare le condizioni ambientali adatte a una determinata specie e quindi identificare dove queste condizioni adatte sono distribuite geograficamente.
Negli ultimi anni, la SDM è diventata un componente fondamentale della pianificazione della conservazione e sono state sviluppate varie tecniche di modellazione a questo scopo. L'implementazione di SDM in Google Earth Engine (GEE di seguito) fornisce un facile accesso a dati ambientali su larga scala, oltre a potenti funzionalità di calcolo e supporto per algoritmi di machine learning, consentendo una modellazione rapida.
Dati richiesti per SDM
In genere, l'SDM utilizza la relazione tra i record di presenza di specie note e le variabili ambientali per identificare le condizioni in cui una popolazione può sostenersi. In altre parole, sono necessari due tipi di dati di input del modello:
- Record di presenza di specie note
- Varie variabili ambientali
Questi dati vengono inseriti negli algoritmi per identificare le condizioni ambientali associate alla presenza di specie.
Flusso di lavoro di SDM che utilizza GEE
Il flusso di lavoro per SDM che utilizza GEE è il seguente:
- Raccolta e pre-elaborazione dei dati di presenza delle specie
- Definizione dell'area di interesse
- Aggiunta di variabili ambientali GEE
- Generazione di dati di pseudo-assenza
- Adattamento e previsione del modello
- Valutazione dell'importanza e dell'accuratezza delle variabili
Habitat Prediction and Analysis Using GEE
La pitta ninfa (Pitta nympha) verrà utilizzata come case study per dimostrare l'applicazione del modello di distribuzione delle specie basato su GEE. Sebbene questa specie specifica sia stata selezionata per un esempio, i ricercatori possono applicare la metodologia a qualsiasi specie target di interesse con leggere modifiche al codice sorgente fornito.
La pitta fatata è un raro uccello migratore estivo e di passaggio in Corea del Sud, la cui area di distribuzione si sta espandendo a causa del recente riscaldamento climatico nella penisola coreana. È classificato come specie rara, fauna selvatica in pericolo di estinzione di classe II, monumento naturale n. 204, valutato come estinto a livello regionale (RE) nella Lista rossa nazionale e vulnerabile (VU) secondo le categorie IUCN.
L'esecuzione di SDM per la pianificazione della conservazione della Pitta fatata sembra essere piuttosto preziosa. Ora procediamo con la previsione e l'analisi dell'habitat tramite GEE.
Innanzitutto, vengono importate le librerie Python.L'istruzione import importa l'intero contenuto di un modulo, mentre l'istruzione from import consente l'importazione di oggetti specifici da un modulo.
# Import libraries
import geemap
import geemap.colormaps as cm
import pandas as pd, geopandas as gpd
import numpy as np, matplotlib.pyplot as plt
import os, requests, math, random
from ipyleaflet import TileLayer
from statsmodels.stats.outliers_influence import variance_inflation_factor
Raccolta e preelaborazione dei dati di presenza delle specie
Ora raccogliamo i dati sulle occorrenze della Pitta fatata. Anche se al momento non hai accesso ai dati di presenza per le specie di interesse, puoi ottenere dati osservativi su specie specifiche tramite l'API GBIF. L'API GBIF è un'interfaccia che consente l'accesso ai dati di distribuzione delle specie forniti da GBIF, consentendo agli utenti di cercare, filtrare e scaricare i dati, nonché di acquisire varie informazioni relative alle specie.
Nel codice riportato di seguito, alla variabile species_name viene assegnato il nome scientifico della specie (ad es. Pitta nympha per la pitta ninfa) e alla variabile country_code viene assegnato il codice paese (ad es. KR per la Corea del Sud). La variabile base_url memorizza l'indirizzo dell'API GBIF. params è un dizionario contenente i parametri da utilizzare nella richiesta API:
scientificName: imposta il nome scientifico della specie da cercare.country: limita la ricerca a un paese specifico.hasCoordinate: garantisce che vengano cercati solo i dati con coordinate (true).basisOfRecord: Sceglie solo i record di osservazione umana (HUMAN_OBSERVATION).limit: imposta il numero massimo di risultati restituiti a 10.000.
def get_gbif_species_data(species_name, country_code):
"""
Retrieves observational data for a specific species using the GBIF API and returns it as a pandas DataFrame.
Parameters:
species_name (str): The scientific name of the species to query.
country_code (str): The country code of the where the observation data will be queried.
Returns:
pd.DataFrame: A pandas DataFrame containing the observational data.
"""
base_url = "https://api.gbif.org/v1/occurrence/search"
params = {
"scientificName": species_name,
"country": country_code,
"hasCoordinate": "true",
"basisOfRecord": "HUMAN_OBSERVATION",
"limit": 10000,
}
try:
response = requests.get(base_url, params=params)
response.raise_for_status() # Raises an exception for a response error.
data = response.json()
occurrences = data.get("results", [])
if occurrences: # If data is present
df = pd.json_normalize(occurrences)
return df
else:
print("No data found for the given species and country code.")
return pd.DataFrame() # Returns an empty DataFrame
except requests.RequestException as e:
print(f"Request failed: {e}")
return pd.DataFrame() # Returns an empty DataFrame in case of an exception
Utilizzando i parametri impostati in precedenza, eseguiamo una query sull'API GBIF per i record osservativi della pitta ninfa (Pitta nympha) e carichiamo i risultati in un DataFrame per controllare la prima riga. Un DataFrame è una struttura di dati per la gestione di dati formattati in tabelle, costituiti da righe e colonne. Se necessario, il DataFrame può essere salvato come file CSV e letto nuovamente.
# Retrieve Fairy Pitta data
df = get_gbif_species_data("Pitta nympha", "KR")
"""
# Save DataFrame to CSV and read back in.
df.to_csv("pitta_nympha_data.csv", index=False)
df = pd.read_csv("pitta_nympha_data.csv")
"""
df.head(1) # Display the first row of the DataFrame
Successivamente, convertiamo il DataFrame in un GeoDataFrame che include una colonna per le informazioni geografiche (geometry) e controlliamo la prima riga. Un GeoDataFrame può essere salvato come file GeoPackage (*.gpkg) e letto di nuovo.
# Convert DataFrame to GeoDataFrame
gdf = gpd.GeoDataFrame(
df,
geometry=gpd.points_from_xy(df.decimalLongitude,
df.decimalLatitude),
crs="EPSG:4326"
)[["species", "year", "month", "geometry"]]
"""
# Convert GeoDataFrame to GeoPackage (requires pycrs module)
%pip install -U -q pycrs
gdf.to_file("pitta_nympha_data.gpkg", driver="GPKG")
gdf = gpd.read_file("pitta_nympha_data.gpkg")
"""
gdf.head(1) # Display the first row of the GeoDataFrame
Questa volta, abbiamo creato una funzione per visualizzare la distribuzione dei dati per anno e mese dal GeoDataFrame e visualizzarli come grafico, che può essere salvato come file immagine. L'utilizzo di una mappa termica ci consente di comprendere rapidamente la frequenza di comparsa delle specie per anno e mese, fornendo una visualizzazione intuitiva dei cambiamenti e dei pattern temporali all'interno dei dati. Ciò consente di identificare i pattern temporali e le variazioni stagionali nei dati di presenza delle specie, nonché di rilevare rapidamente outlier o problemi di qualità all'interno dei dati.
# Yearly and monthly data distribution heatmap
def plot_heatmap(gdf, h_size=8):
statistics = gdf.groupby(["month", "year"]).size().unstack(fill_value=0)
# Heatmap
plt.figure(figsize=(h_size, h_size - 6))
heatmap = plt.imshow(
statistics.values, cmap="YlOrBr", origin="upper", aspect="auto"
)
# Display values above each pixel
for i in range(len(statistics.index)):
for j in range(len(statistics.columns)):
plt.text(
j, i, statistics.values[i, j], ha="center", va="center", color="black"
)
plt.colorbar(heatmap, label="Count")
plt.title("Monthly Species Count by Year")
plt.xlabel("Year")
plt.ylabel("Month")
plt.xticks(range(len(statistics.columns)), statistics.columns)
plt.yticks(range(len(statistics.index)), statistics.index)
plt.tight_layout()
plt.savefig("heatmap_plot.png")
plt.show()
plot_heatmap(gdf)
I dati del 1995 sono molto scarsi, con lacune significative rispetto ad altri anni, e anche i mesi di agosto e settembre hanno campioni limitati e mostrano caratteristiche stagionali diverse rispetto ad altri periodi. L'esclusione di questi dati potrebbe contribuire a migliorare la stabilità e la capacità predittiva del modello.
Tuttavia, è importante notare che l'esclusione dei dati può migliorare la capacità di generalizzazione del modello, ma potrebbe anche portare alla perdita di informazioni preziose pertinenti agli obiettivi della ricerca. Pertanto, queste decisioni devono essere prese con la dovuta attenzione.
# Filtering data by year and month
filtered_gdf = gdf[
(~gdf['year'].eq(1995)) &
(~gdf['month'].between(8, 9))
]
Ora il GeoDataFrame filtrato viene convertito in un oggetto Google Earth Engine.
# Convert GeoDataFrame to Earth Engine object
data_raw = geemap.geopandas_to_ee(filtered_gdf)
Successivamente, definiremo le dimensioni dei pixel raster dei risultati SDM con una risoluzione di 1 km.
# Spatial resolution setting (meters)
grain_size = 1000
Quando sono presenti più punti di occorrenza all'interno dello stesso pixel raster con risoluzione di 1 km, è molto probabile che condividano le stesse condizioni ambientali nella stessa posizione geografica. L'utilizzo diretto di questi dati nell'analisi può introdurre distorsioni nei risultati.
In altre parole, dobbiamo limitare il potenziale impatto del bias di campionamento geografico. Per raggiungere questo obiettivo, manterremo una sola posizione all'interno di ogni pixel di 1 km e rimuoveremo tutte le altre, consentendo al modello di riflettere in modo più oggettivo le condizioni ambientali.
def remove_duplicates(data, grain_size):
# Select one occurrence record per pixel at the chosen spatial resolution
random_raster = ee.Image.random().reproject("EPSG:4326", None, grain_size)
rand_point_vals = random_raster.sampleRegions(
collection=ee.FeatureCollection(data), geometries=True
)
return rand_point_vals.distinct("random")
data = remove_duplicates(data_raw, grain_size)
# Before selection and after selection
print("Original data size:", data_raw.size().getInfo())
print("Final data size:", data.size().getInfo())
Di seguito è riportata la visualizzazione che confronta la distorsione del campionamento geografico prima del pre-elaborazione (in blu) e dopo il pre-elaborazione (in rosso). Per facilitare il confronto, la mappa è stata centrata sull'area con un'alta concentrazione di coordinate di presenza di Pitta fatata nel Parco nazionale del monte Halla.
# Visualization of geographic sampling bias before (blue) and after (red) preprocessing
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
# Add the random raster layer
random_raster = ee.Image.random().reproject("EPSG:4326", None, grain_size)
Map.addLayer(
random_raster,
{"min": 0, "max": 1, "palette": ["black", "white"], "opacity": 0.5},
"Random Raster",
)
# Add the original data layer in blue
Map.addLayer(data_raw, {"color": "blue"}, "Original data")
# Add the final data layer in red
Map.addLayer(data, {"color": "red"}, "Final data")
# Set the center of the map to the coordinates
Map.setCenter(126.712, 33.516, 14)
Map
Definizione dell'area di interesse
La definizione dell'area di interesse (AOI di seguito) si riferisce al termine utilizzato dai ricercatori per indicare l'area geografica che vogliono analizzare. Ha un significato simile al termine Area di studio.
In questo contesto, abbiamo ottenuto il riquadro di selezione della geometria del livello dei punti di occorrenza e abbiamo creato un buffer di 50 chilometri intorno (con una tolleranza massima di 1000 metri) per definire l'AOI.
# Define the AOI
aoi = data.geometry().bounds().buffer(distance=50000, maxError=1000)
# Add the AOI to the map
outline = ee.Image().byte().paint(
featureCollection=aoi, color=1, width=3)
Map.remove_layer("Random Raster")
Map.addLayer(outline, {'palette': 'FF0000'}, "AOI")
Map.centerObject(aoi, 6)
Map
Aggiunta di variabili ambientali GEE
Ora aggiungiamo le variabili ambientali all'analisi. GEE fornisce un'ampia gamma di set di dati per variabili ambientali come temperatura, precipitazioni, elevazione, copertura del suolo e terreno. Questi set di dati ci consentono di analizzare in modo completo vari fattori che possono influenzare le preferenze di habitat della Pitta fatata.
La selezione delle variabili ambientali di GEE in SDM deve riflettere le caratteristiche di preferenza dell'habitat della specie. A questo scopo, è necessario condurre ricerche e revisioni della letteratura precedenti sulle preferenze di habitat della pitta fatata. Questo tutorial si concentra principalmente sul flusso di lavoro di SDM che utilizza GEE, pertanto alcuni dettagli approfonditi vengono omessi.
WorldClim V1 Bioclim: questo set di dati fornisce 19 variabili bioclimatiche derivate dai dati mensili di temperatura e precipitazioni. Copre il periodo dal 1960 al 1991 e ha una risoluzione di 927,67 metri.
# WorldClim V1 Bioclim
bio = ee.Image("WORLDCLIM/V1/BIO")
NASA SRTM Digital Elevation 30m: questo set di dati contiene dati di elevazione digitale della Shuttle Radar Topography Mission (SRTM). I dati sono stati raccolti principalmente intorno all'anno 2000 e sono forniti con una risoluzione di circa 30 metri (1 secondo d'arco). Il seguente codice calcola i livelli di elevazione, pendenza, esposizione e ombreggiatura a partire dai dati SRTM.
# NASA SRTM Digital Elevation 30m
terrain = ee.Algorithms.Terrain(ee.Image("USGS/SRTMGL1_003"))
Global Forest Cover Change (GFCC) Tree Cover Multi-Year Global 30m: il set di dati Vegetation Continuous Fields (VCF) di Landsat stima la proporzione di copertura vegetale proiettata verticalmente quando l'altezza della vegetazione è superiore a 5 metri. Questo set di dati è fornito per quattro periodi di tempo centrati sugli anni 2000, 2005, 2010 e 2015, con una risoluzione di 30 metri. Qui vengono utilizzati i valori mediani di questi quattro periodi di tempo.
# Global Forest Cover Change (GFCC) Tree Cover Multi-Year Global 30m
tcc = ee.ImageCollection("NASA/MEASURES/GFCC/TC/v3")
median_tcc = (
tcc.filterDate("2000-01-01", "2015-12-31")
.select(["tree_canopy_cover"], ["TCC"])
.median()
)
bio (variabili bioclimatiche), terrain (topografia) e median_tcc (copertura della chioma degli alberi) vengono combinate in un'unica immagine multibanda. La banda elevation viene selezionata da terrain e viene creato un watermask per le località in cui elevation è maggiore di 0. In questo modo vengono mascherate le regioni sotto il livello del mare (ad es. l'oceano) e il ricercatore è pronto ad analizzare in modo completo vari fattori ambientali per l'AOI.
# Combine bands into a multi-band image
predictors = bio.addBands(terrain).addBands(median_tcc)
# Create a water mask
watermask = terrain.select('elevation').gt(0)
# Mask out ocean pixels and clip to the area of interest
predictors = predictors.updateMask(watermask).clip(aoi)
Quando in un modello vengono incluse variabili predittive altamente correlate, possono sorgere problemi di multicollinearità. La multicollinearità è un fenomeno che si verifica quando esistono forti relazioni lineari tra le variabili indipendenti di un modello, il che comporta instabilità nella stima dei coefficienti (pesi) del modello. Questa instabilità può ridurre l'affidabilità del modello e rendere difficile fare previsioni o interpretazioni per i nuovi dati. Pertanto, prenderemo in considerazione la multicollinearità e procederemo con il processo di selezione delle variabili predittive.
Innanzitutto, genereremo 5000 punti casuali,quindi estrarremo i valori della variabile predittore della singola immagine multibanda in questi punti.
# Generate 5,000 random points
data_cor = predictors.sample(scale=grain_size, numPixels=5000, geometries=True)
# Extract predictor variable values
pvals = predictors.sampleRegions(collection=data_cor, scale=grain_size)
Convertiremo i valori dei predittori estratti per ogni punto in un DataFrame e poi controlleremo la prima riga.
# Converting predictor values from Earth Engine to a DataFrame
pvals_df = geemap.ee_to_df(pvals)
pvals_df.head(1)
# Displaying the columns
columns = pvals_df.columns
print(columns)
Calcolo dei coefficienti di correlazione di Spearman tra le variabili predittive specificate e visualizzazione in una mappa termica.
def plot_correlation_heatmap(dataframe, h_size=10, show_labels=False):
# Calculate Spearman correlation coefficients
correlation_matrix = dataframe.corr(method="spearman")
# Create a heatmap
plt.figure(figsize=(h_size, h_size-2))
plt.imshow(correlation_matrix, cmap='coolwarm', interpolation='nearest')
# Optionally display values on the heatmap
if show_labels:
for i in range(correlation_matrix.shape[0]):
for j in range(correlation_matrix.shape[1]):
plt.text(j, i, f"{correlation_matrix.iloc[i, j]:.2f}",
ha='center', va='center', color='white', fontsize=8)
columns = dataframe.columns.tolist()
plt.xticks(range(len(columns)), columns, rotation=90)
plt.yticks(range(len(columns)), columns)
plt.title("Variables Correlation Matrix")
plt.colorbar(label="Spearman Correlation")
plt.savefig('correlation_heatmap_plot.png')
plt.show()
# Plot the correlation heatmap of variables
plot_correlation_heatmap(pvals_df)
Il coefficiente di correlazione di Spearman è utile per comprendere le associazioni generali tra le variabili predittive, ma non valuta direttamente l'interazione tra più variabili, in particolare non rileva la multicollinearità.
Il fattore di inflazione della varianza (VIF di seguito) è una metrica statistica utilizzata per valutare la multicollinearità e guidare la selezione delle variabili. Indica il grado di relazione lineare di ogni variabile indipendente con le altre variabili indipendenti e valori VIF elevati possono essere la prova di multicollinearità.
In genere, quando i valori VIF superano 5 o 10, ciò suggerisce che la variabile ha una forte correlazione con altre variabili, il che potrebbe compromettere la stabilità e l'interpretabilità del modello. In questo tutorial, per la selezione delle variabili è stato utilizzato un criterio di valori VIF inferiori a 10. Le seguenti 6 variabili sono state selezionate in base al VIF.
# Filter variables based on Variance Inflation Factor (VIF)
def filter_variables_by_vif(dataframe, threshold=10):
original_columns = dataframe.columns.tolist()
remaining_columns = original_columns[:]
while True:
vif_data = dataframe[remaining_columns]
vif_values = [
variance_inflation_factor(vif_data.values, i)
for i in range(vif_data.shape[1])
]
max_vif_index = vif_values.index(max(vif_values))
max_vif = max(vif_values)
if max_vif < threshold:
break
print(f"Removing '{remaining_columns[max_vif_index]}' with VIF {max_vif:.2f}")
del remaining_columns[max_vif_index]
filtered_data = dataframe[remaining_columns]
bands = filtered_data.columns.tolist()
print("Bands:", bands)
return filtered_data, bands
filtered_pvals_df, bands = filter_variables_by_vif(pvals_df)
# Variable Selection Based on VIF
predictors = predictors.select(bands)
# Plot the correlation heatmap of variables
plot_correlation_heatmap(filtered_pvals_df, h_size=6, show_labels=True)
Successivamente, visualizziamo le sei variabili predittive selezionate sulla mappa.
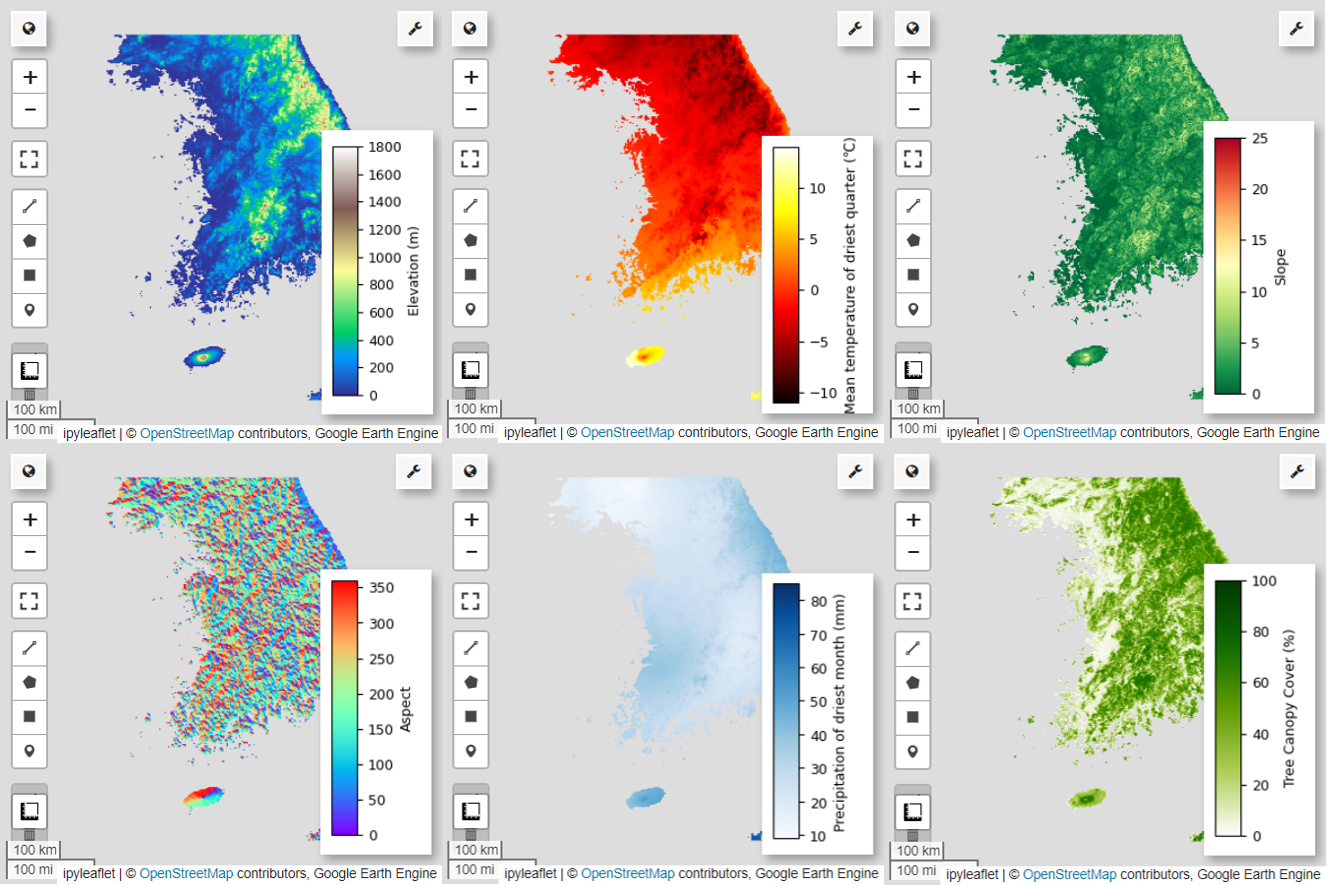
Puoi esplorare le tavolozze disponibili per la visualizzazione della mappa utilizzando il seguente codice. Ad esempio, la tavolozza terrain ha questo aspetto.
cm.plot_colormaps(width=8.0, height=0.2)
cm.plot_colormap('terrain', width=8.0, height=0.2, orientation='horizontal')
# Elevation layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['elevation'], 'min': 0, 'max': 1800, 'palette': cm.palettes.terrain}
Map.addLayer(predictors, vis_params, 'elevation')
Map.add_colorbar(vis_params, label="Elevation (m)", orientation="vertical", layer_name="elevation")
Map.centerObject(aoi, 6)
Map
# Calculate the minimum and maximum values for bio09
min_max_val = (
predictors.select("bio09")
.multiply(0.1)
.reduceRegion(reducer=ee.Reducer.minMax(), scale=1000)
.getInfo()
)
# bio09 (Mean temperature of driest quarter) layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"min": math.floor(min_max_val["bio09_min"]),
"max": math.ceil(min_max_val["bio09_max"]),
"palette": cm.palettes.hot,
}
Map.addLayer(predictors.select("bio09").multiply(0.1), vis_params, "bio09")
Map.add_colorbar(
vis_params,
label="Mean temperature of driest quarter (℃)",
orientation="vertical",
layer_name="bio09",
)
Map.centerObject(aoi, 6)
Map
# Slope layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['slope'], 'min': 0, 'max': 25, 'palette': cm.palettes.RdYlGn_r}
Map.addLayer(predictors, vis_params, 'slope')
Map.add_colorbar(vis_params, label="Slope", orientation="vertical", layer_name="slope")
Map.centerObject(aoi, 6)
Map
# Aspect layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['aspect'], 'min': 0, 'max': 360, 'palette': cm.palettes.rainbow}
Map.addLayer(predictors, vis_params, 'aspect')
Map.add_colorbar(vis_params, label="Aspect", orientation="vertical", layer_name="aspect")
Map.centerObject(aoi, 6)
Map
# Calculate the minimum and maximum values for bio14
min_max_val = (
predictors.select("bio14")
.reduceRegion(reducer=ee.Reducer.minMax(), scale=1000)
.getInfo()
)
# bio14 (Precipitation of driest month) layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"bands": ["bio14"],
"min": math.floor(min_max_val["bio14_min"]),
"max": math.ceil(min_max_val["bio14_max"]),
"palette": cm.palettes.Blues,
}
Map.addLayer(predictors, vis_params, "bio14")
Map.add_colorbar(
vis_params,
label="Precipitation of driest month (mm)",
orientation="vertical",
layer_name="bio14",
)
Map.centerObject(aoi, 6)
Map
# TCC layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"bands": ["TCC"],
"min": 0,
"max": 100,
"palette": ["ffffff", "afce56", "5f9c00", "0e6a00", "003800"],
}
Map.addLayer(predictors, vis_params, "TCC")
Map.add_colorbar(
vis_params, label="Tree Canopy Cover (%)", orientation="vertical", layer_name="TCC"
)
Map.centerObject(aoi, 6)
Map
Generazione di dati di pseudo-assenza
Nel processo di SDM, la selezione dei dati di input per una specie viene principalmente affrontata utilizzando due metodi:
Metodo presenza-sfondo: questo metodo confronta le posizioni in cui è stata osservata una determinata specie (presenza) con altre posizioni in cui la specie non è stata osservata (sfondo). In questo caso, i dati di sfondo non si riferiscono necessariamente alle aree in cui la specie non esiste, ma sono configurati per riflettere le condizioni ambientali generali dell'area di studio. Viene utilizzato per distinguere gli ambienti adatti in cui la specie potrebbe esistere da quelli meno adatti.
Metodo presenza-assenza: questo metodo confronta le località in cui è stata osservata la specie (presenza) con le località in cui non è stata osservata in modo definitivo (assenza). In questo caso, i dati di assenza rappresentano luoghi specifici in cui è noto che la specie non esiste. Non riflette le condizioni ambientali complessive dell'area di studio, ma indica piuttosto le località in cui si stima che la specie non esista.
In pratica, è spesso difficile raccogliere dati di assenza reali, quindi vengono spesso utilizzati dati di pseudo-assenza generati artificialmente. Tuttavia, è importante riconoscere i limiti e i potenziali errori di questo metodo, poiché i punti di pseudo-assenza generati artificialmente potrebbero non riflettere con precisione le vere aree di assenza.
La scelta tra questi due metodi dipende dalla disponibilità dei dati, dagli obiettivi della ricerca, dall'accuratezza e dall'affidabilità del modello, nonché dal tempo e dalle risorse. In questo caso, utilizzeremo i dati di presenza raccolti da GBIF e i dati di pseudo-assenza generati artificialmente per la modellazione utilizzando il metodo "Presenza-Assenza".
La generazione di dati di pseudo-assenza verrà eseguita tramite l'"approccio di profilazione ambientale" e i passaggi specifici sono i seguenti:
Classificazione ambientale mediante clustering K-means: l'algoritmo di clustering K-means, basato sulla distanza euclidea, verrà utilizzato per dividere i pixel all'interno dell'area di studio in due cluster. Un cluster rappresenterà le aree con caratteristiche ambientali simili a 100 località di presenza selezionate in modo casuale, mentre l'altro cluster rappresenterà le aree con caratteristiche diverse.
Generazione di dati di pseudo-assenza all'interno di cluster dissimili: all'interno del secondo cluster identificato nel primo passaggio (che ha caratteristiche ambientali diverse dai dati di presenza), verranno creati punti di pseudo-assenza generati in modo casuale. Questi punti di pseudo-assenza rappresenteranno le località in cui non è prevista la presenza della specie.
# Randomly select 100 locations for occurrence
pvals = predictors.sampleRegions(
collection=data.randomColumn().sort('random').limit(100),
properties=[],
scale=grain_size
)
# Perform k-means clustering
clusterer = ee.Clusterer.wekaKMeans(
nClusters=2,
distanceFunction="Euclidean"
).train(pvals)
cl_result = predictors.cluster(clusterer)
# Get cluster ID for locations similar to occurrence
cl_id = cl_result.sampleRegions(
collection=data.randomColumn().sort('random').limit(200),
properties=[],
scale=grain_size
)
# Define non-occurrence areas in dissimilar clusters
cl_id = ee.FeatureCollection(cl_id).reduceColumns(ee.Reducer.mode(),['cluster'])
cl_id = ee.Number(cl_id.get('mode')).subtract(1).abs()
cl_mask = cl_result.select(['cluster']).eq(cl_id)
# Presence location mask
presence_mask = data.reduceToImage(properties=['random'],
reducer=ee.Reducer.first()
).reproject('EPSG:4326', None,
grain_size).mask().neq(1).selfMask()
# Masking presence locations in non-occurrence areas and clipping to AOI
area_for_pa = presence_mask.updateMask(cl_mask).clip(aoi)
# Area for Pseudo-absence
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
Map.addLayer(area_for_pa, {'palette': 'black'}, 'AreaForPA')
Map.centerObject(aoi, 6)
Map
Adattamento e previsione del modello
Ora suddivideremo i dati in dati di addestramento e dati di test. I dati di addestramento verranno utilizzati per trovare i parametri ottimali addestrando il modello, mentre i dati di test verranno utilizzati per valutare il modello addestrato in precedenza. Un concetto importante da considerare in questo contesto è l'autocorrelazione spaziale.
L'autocorrelazione spaziale è un elemento essenziale in SDM, associato alla legge di Tobler. Rappresenta il concetto secondo cui "tutto è correlato a tutto, ma le cose vicine sono più correlate di quelle distanti". L'autocorrelazione spaziale rappresenta la relazione significativa tra la posizione delle specie e le variabili ambientali. Tuttavia, se esiste un'autocorrelazione spaziale tra i dati di addestramento e di test, l'indipendenza tra i due set di dati può essere compromessa. Ciò influisce in modo significativo sulla valutazione della capacità di generalizzazione del modello.
Un metodo per risolvere questo problema è la tecnica di convalida incrociata a blocchi spaziali, che prevede la suddivisione dei dati in set di dati di addestramento e test. Questa tecnica prevede la suddivisione dei dati in più blocchi, utilizzando ogni blocco in modo indipendente come set di dati di addestramento e test per ridurre l'impatto dell'autocorrelazione spaziale. In questo modo, viene migliorata l'indipendenza tra i set di dati, consentendo una valutazione più accurata della capacità di generalizzazione del modello.
La procedura specifica è la seguente:
- Creazione di blocchi spaziali: dividi l'intero set di dati in blocchi spaziali di dimensioni uguali (ad es. 50x50 km).
- Assegnazione dei set di addestramento e test: ogni blocco spaziale viene assegnato in modo casuale al set di addestramento (70%) o al set di test (30%). In questo modo, il modello non esegue l'overfitting dei dati di aree specifiche e mira a ottenere risultati più generalizzati.
- Convalida incrociata iterativa: l'intero processo viene ripetuto n volte (ad es. 10 volte). In ogni iterazione, i blocchi vengono suddivisi nuovamente in modo casuale in set di addestramento e test, al fine di migliorare la stabilità e l'affidabilità del modello.
- Generazione di dati di pseudo-assenza: in ogni iterazione, i dati di pseudo-assenza vengono generati in modo casuale per valutare le prestazioni del modello.
Scale = 50000
grid = watermask.reduceRegions(
collection=aoi.coveringGrid(scale=Scale, proj='EPSG:4326'),
reducer=ee.Reducer.mean()).filter(ee.Filter.neq('mean', None))
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
Map.addLayer(grid, {}, "Grid for spatial block cross validation")
Map.addLayer(outline, {'palette': 'FF0000'}, "Study Area")
Map.centerObject(aoi, 6)
Map
Ora possiamo adattare il modello. L'adattamento di un modello comporta la comprensione dei pattern nei dati e la regolazione dei parametri del modello (pesi e bias) di conseguenza. Questo processo consente al modello di fare previsioni più accurate quando vengono presentati nuovi dati. A questo scopo, abbiamo definito una funzione chiamata SDM() per adattare il modello.
Utilizzeremo l'algoritmo Random Forest.
def sdm(x):
seed = ee.Number(x)
# Random block division for training and validation
rand_blk = ee.FeatureCollection(grid).randomColumn(seed=seed).sort("random")
training_grid = rand_blk.filter(ee.Filter.lt("random", split)) # Grid for training
testing_grid = rand_blk.filter(ee.Filter.gte("random", split)) # Grid for testing
# Presence points
presence_points = ee.FeatureCollection(data)
presence_points = presence_points.map(lambda feature: feature.set("PresAbs", 1))
tr_presence_points = presence_points.filter(
ee.Filter.bounds(training_grid)
) # Presence points for training
te_presence_points = presence_points.filter(
ee.Filter.bounds(testing_grid)
) # Presence points for testing
# Pseudo-absence points for training
tr_pseudo_abs_points = area_for_pa.sample(
region=training_grid,
scale=grain_size,
numPixels=tr_presence_points.size().add(300),
seed=seed,
geometries=True,
)
# Same number of pseudo-absence points as presence points for training
tr_pseudo_abs_points = (
tr_pseudo_abs_points.randomColumn()
.sort("random")
.limit(ee.Number(tr_presence_points.size()))
)
tr_pseudo_abs_points = tr_pseudo_abs_points.map(lambda feature: feature.set("PresAbs", 0))
te_pseudo_abs_points = area_for_pa.sample(
region=testing_grid,
scale=grain_size,
numPixels=te_presence_points.size().add(100),
seed=seed,
geometries=True,
)
# Same number of pseudo-absence points as presence points for testing
te_pseudo_abs_points = (
te_pseudo_abs_points.randomColumn()
.sort("random")
.limit(ee.Number(te_presence_points.size()))
)
te_pseudo_abs_points = te_pseudo_abs_points.map(lambda feature: feature.set("PresAbs", 0))
# Merge training and pseudo-absence points
training_partition = tr_presence_points.merge(tr_pseudo_abs_points)
testing_partition = te_presence_points.merge(te_pseudo_abs_points)
# Extract predictor variable values at training points
train_pvals = predictors.sampleRegions(
collection=training_partition,
properties=["PresAbs"],
scale=grain_size,
geometries=True,
)
# Random Forest classifier
classifier = ee.Classifier.smileRandomForest(
numberOfTrees=500,
variablesPerSplit=None,
minLeafPopulation=10,
bagFraction=0.5,
maxNodes=None,
seed=seed,
)
# Presence probability: Habitat suitability map
classifier_pr = classifier.setOutputMode("PROBABILITY").train(
train_pvals, "PresAbs", bands
)
classified_img_pr = predictors.select(bands).classify(classifier_pr)
# Binary presence/absence map: Potential distribution map
classifier_bin = classifier.setOutputMode("CLASSIFICATION").train(
train_pvals, "PresAbs", bands
)
classified_img_bin = predictors.select(bands).classify(classifier_bin)
return [
classified_img_pr,
classified_img_bin,
training_partition,
testing_partition,
], classifier_pr
I blocchi spaziali sono suddivisi rispettivamente in 70% per l'addestramento del modello e 30% per il test del modello. I dati di pseudo-assenza vengono generati in modo casuale all'interno di ogni set di addestramento e test in ogni iterazione. Di conseguenza, ogni esecuzione produce diversi set di dati di presenza e pseudo-assenza per l'addestramento e il test del modello.
split = 0.7
numiter = 10
# Random Seed
runif = lambda length: [random.randint(1, 1000) for _ in range(length)]
items = runif(numiter)
# Fixed seed
# items = [287, 288, 553, 226, 151, 255, 902, 267, 419, 538]
results_list = [] # Initialize SDM results list
importances_list = [] # Initialize variable importance list
for item in items:
result, trained = sdm(item)
# Accumulate SDM results into the list
results_list.extend(result)
# Accumulate variable importance into the list
importance = ee.Dictionary(trained.explain()).get('importance')
importances_list.extend(importance.getInfo().items())
# Flatten the SDM results list
results = ee.List(results_list).flatten()
Ora possiamo visualizzare la mappa dell'idoneità dell'habitat e la mappa della potenziale distribuzione per la pitta fatata. In questo caso, la mappa dell'idoneità dell'habitat viene creata utilizzando la funzione mean() per calcolare la media per ogni posizione dei pixel in tutte le immagini, mentre la mappa della potenziale distribuzione viene generata utilizzando la funzione mode() per determinare il valore più frequente in ogni posizione dei pixel in tutte le immagini.
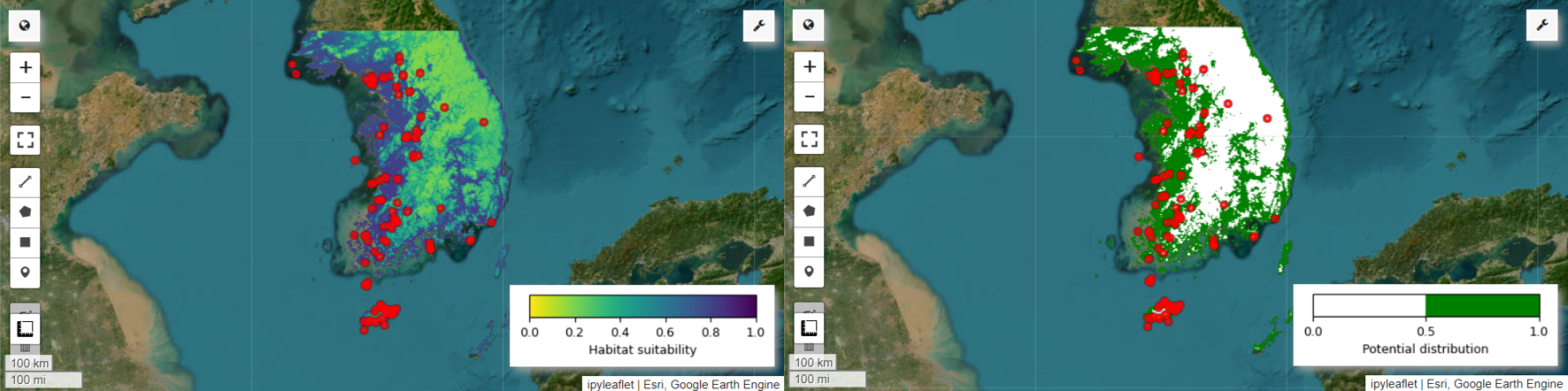
# Habitat suitability map
images = ee.List.sequence(
0, ee.Number(numiter).multiply(4).subtract(1), 4).map(
lambda x: results.get(x))
model_average = ee.ImageCollection.fromImages(images).mean()
Map = geemap.Map(layout={'height':'400px', 'width':'800px'}, basemap='Esri.WorldImagery')
vis_params = {
'min': 0,
'max': 1,
'palette': cm.palettes.viridis_r}
Map.addLayer(model_average, vis_params, 'Habitat suitability')
Map.add_colorbar(vis_params, label="Habitat suitability",
orientation="horizontal",
layer_name="Habitat suitability")
Map.addLayer(data, {'color':'red'}, 'Presence')
Map.centerObject(aoi, 6)
Map
# Potential distribution map
images2 = ee.List.sequence(1, ee.Number(numiter).multiply(4).subtract(1), 4).map(
lambda x: results.get(x)
)
distribution_map = ee.ImageCollection.fromImages(images2).mode()
Map = geemap.Map(
layout={"height": "400px", "width": "800px"}, basemap="Esri.WorldImagery"
)
vis_params = {"min": 0, "max": 1, "palette": ["white", "green"]}
Map.addLayer(distribution_map, vis_params, "Potential distribution")
Map.addLayer(data, {"color": "red"}, "Presence")
Map.add_colorbar(
vis_params,
label="Potential distribution",
discrete=True,
orientation="horizontal",
layer_name="Potential distribution",
)
Map.centerObject(data.geometry(), 6)
Map
Valutazione dell'importanza e dell'accuratezza delle variabili
Random Forest (ee.Classifier.smileRandomForest) è uno dei metodi di apprendimento ensemble, che funziona costruendo più alberi decisionali per fare previsioni. Ogni albero decisionale apprende in modo indipendente da diversi sottoinsiemi di dati e i risultati vengono aggregati per consentire previsioni più accurate e stabili.
L'importanza delle variabili è una misura che valuta l'impatto di ciascuna variabile sulle previsioni all'interno del modello Random Forest. Utilizzeremo il importances_list definito in precedenza per calcolare e stampare l'importanza media delle variabili.
def plot_variable_importance(importances_list):
# Extract each variable importance value into a list
variables = [item[0] for item in importances_list]
importances = [item[1] for item in importances_list]
# Calculate the average importance for each variable
average_importances = {}
for variable in set(variables):
indices = [i for i, var in enumerate(variables) if var == variable]
average_importance = np.mean([importances[i] for i in indices])
average_importances[variable] = average_importance
# Sort the importances in descending order of importance
sorted_importances = sorted(average_importances.items(),
key=lambda x: x[1], reverse=False)
variables = [item[0] for item in sorted_importances]
avg_importances = [item[1] for item in sorted_importances]
# Adjust the graph size
plt.figure(figsize=(8, 4))
# Plot the average importance as a horizontal bar chart
plt.barh(variables, avg_importances)
plt.xlabel('Importance')
plt.ylabel('Variables')
plt.title('Average Variable Importance')
# Display values above the bars
for i, v in enumerate(avg_importances):
plt.text(v + 0.02, i, f"{v:.2f}", va='center')
# Adjust the x-axis range
plt.xlim(0, max(avg_importances) + 5) # Adjust to the desired range
plt.tight_layout()
plt.savefig('variable_importance.png')
plt.show()
plot_variable_importance(importances_list)
Utilizzando i set di dati di test, calcoliamo AUC-ROC e AUC-PR per ogni esecuzione. Calcoliamo quindi l'AUC-ROC e l'AUC-PR medie su n iterazioni.
AUC-ROC rappresenta l'area sotto la curva del grafico "Sensibilità (richiamo) vs. 1-specificità", che illustra la relazione tra sensibilità e specificità al variare della soglia. La specificità si basa su tutte le non occorrenze osservate. Pertanto, l'AUC-ROC comprende tutti i quadranti della matrice di confusione.
AUC-PR rappresenta l'area sotto la curva del grafico "Precisione vs. Richiamo (sensibilità)", che mostra la relazione tra precisione e richiamo al variare della soglia. La precisione si basa su tutte le occorrenze previste. Pertanto, AUC-PR non include i veri negativi (TN).
def print_pres_abs_sizes(TestingDatasets, numiter):
# Check and print the sizes of presence and pseudo-absence coordinates
def get_pres_abs_size(x):
fc = ee.FeatureCollection(TestingDatasets.get(x))
presence_size = fc.filter(ee.Filter.eq("PresAbs", 1)).size()
pseudo_absence_size = fc.filter(ee.Filter.eq("PresAbs", 0)).size()
return ee.List([presence_size, pseudo_absence_size])
sizes_info = (
ee.List.sequence(0, ee.Number(numiter).subtract(1), 1)
.map(get_pres_abs_size)
.getInfo()
)
for i, sizes in enumerate(sizes_info):
presence_size = sizes[0]
pseudo_absence_size = sizes[1]
print(
f"Iteration {i + 1}: Presence Size = {presence_size}, Pseudo-absence Size = {pseudo_absence_size}"
)
# Extracting the Testing Datasets
testing_datasets = ee.List.sequence(
3, ee.Number(numiter).multiply(4).subtract(1), 4
).map(lambda x: results.get(x))
print_pres_abs_sizes(testing_datasets, numiter)
def get_acc(hsm, t_data, grain_size):
pr_prob_vals = hsm.sampleRegions(
collection=t_data, properties=["PresAbs"], scale=grain_size
)
seq = ee.List.sequence(start=0, end=1, count=25) # Divide 0 to 1 into 25 intervals
def calculate_metrics(cutoff):
# Each element of the seq list is passed as cutoff(threshold value)
# Observed present = TP + FN
pres = pr_prob_vals.filterMetadata("PresAbs", "equals", 1)
# TP (True Positive)
tp = ee.Number(
pres.filterMetadata("classification", "greater_than", cutoff).size()
)
# TPR (True Positive Rate) = Recall = Sensitivity = TP / (TP + FN) = TP / Observed present
tpr = tp.divide(pres.size())
# Observed absent = FP + TN
abs = pr_prob_vals.filterMetadata("PresAbs", "equals", 0)
# FN (False Negative)
fn = ee.Number(
pres.filterMetadata("classification", "less_than", cutoff).size()
)
# TNR (True Negative Rate) = Specificity = TN / (FP + TN) = TN / Observed absent
tn = ee.Number(abs.filterMetadata("classification", "less_than", cutoff).size())
tnr = tn.divide(abs.size())
# FP (False Positive)
fp = ee.Number(
abs.filterMetadata("classification", "greater_than", cutoff).size()
)
# FPR (False Positive Rate) = FP / (FP + TN) = FP / Observed absent
fpr = fp.divide(abs.size())
# Precision = TP / (TP + FP) = TP / Predicted present
precision = tp.divide(tp.add(fp))
# SUMSS = SUM of Sensitivity and Specificity
sumss = tpr.add(tnr)
return ee.Feature(
None,
{
"cutoff": cutoff,
"TP": tp,
"TN": tn,
"FP": fp,
"FN": fn,
"TPR": tpr,
"TNR": tnr,
"FPR": fpr,
"Precision": precision,
"SUMSS": sumss,
},
)
return ee.FeatureCollection(seq.map(calculate_metrics))
def calculate_and_print_auc_metrics(images, testing_datasets, grain_size, numiter):
# Calculate AUC-ROC and AUC-PR
def calculate_auc_metrics(x):
hsm = ee.Image(images.get(x))
t_data = ee.FeatureCollection(testing_datasets.get(x))
acc = get_acc(hsm, t_data, grain_size)
# Calculate AUC-ROC
x = ee.Array(acc.aggregate_array("FPR"))
y = ee.Array(acc.aggregate_array("TPR"))
x1 = x.slice(0, 1).subtract(x.slice(0, 0, -1))
y1 = y.slice(0, 1).add(y.slice(0, 0, -1))
auc_roc = x1.multiply(y1).multiply(0.5).reduce("sum", [0]).abs().toList().get(0)
# Calculate AUC-PR
x = ee.Array(acc.aggregate_array("TPR"))
y = ee.Array(acc.aggregate_array("Precision"))
x1 = x.slice(0, 1).subtract(x.slice(0, 0, -1))
y1 = y.slice(0, 1).add(y.slice(0, 0, -1))
auc_pr = x1.multiply(y1).multiply(0.5).reduce("sum", [0]).abs().toList().get(0)
return (auc_roc, auc_pr)
auc_metrics = (
ee.List.sequence(0, ee.Number(numiter).subtract(1), 1)
.map(calculate_auc_metrics)
.getInfo()
)
# Print AUC-ROC and AUC-PR for each iteration
df = pd.DataFrame(auc_metrics, columns=["AUC-ROC", "AUC-PR"])
df.index = [f"Iteration {i + 1}" for i in range(len(df))]
df.to_csv("auc_metrics.csv", index_label="Iteration")
print(df)
# Calculate mean and standard deviation of AUC-ROC and AUC-PR
mean_auc_roc, std_auc_roc = df["AUC-ROC"].mean(), df["AUC-ROC"].std()
mean_auc_pr, std_auc_pr = df["AUC-PR"].mean(), df["AUC-PR"].std()
print(f"Mean AUC-ROC = {mean_auc_roc:.4f} ± {std_auc_roc:.4f}")
print(f"Mean AUC-PR = {mean_auc_pr:.4f} ± {std_auc_pr:.4f}")
%%time
# Calculate AUC-ROC and AUC-PR
calculate_and_print_auc_metrics(images, testing_datasets, grain_size, numiter)
Questo tutorial ha fornito un esempio pratico di utilizzo di Google Earth Engine (GEE) per la modellazione della distribuzione delle specie (SDM). Un aspetto importante è la versatilità e la flessibilità di GEE nel campo della SDM. Sfruttare le potenti funzionalità di elaborazione dei dati geospaziali di Earth Engine apre infinite possibilità per ricercatori e ambientalisti di comprendere e preservare la biodiversità del nostro pianeta. Applicando le conoscenze e le competenze acquisite da questo tutorial, le persone possono esplorare e contribuire a questo affascinante campo della ricerca ecologica.
 Esegui in Google Colab
Esegui in Google Colab
 Visualizza il codice sorgente su GitHub
Visualizza il codice sorgente su GitHub