TensorFlow、Keras 和深度学习（无需拥有博士学位）

在此 Codelab 中，您将学习如何构建和训练可识别手写数字的神经网络。在不断改进神经网络以达到 99% 准确率的过程中，您还将发现深度学习专业人士用来高效训练模型的工具。

此 Codelab 使用 MNIST 数据集，这是一个包含 60,000 个带标签数字的集合，近 20 年来一直让一代又一代的博士生忙碌不已。您将使用不到 100 行 Python / TensorFlow 代码解决该问题。

学习内容

• 什么是神经网络以及如何训练神经网络
• 如何使用 tf.keras 构建基本的单层神经网络
• 如何添加更多图层
• 如何设置学习率安排
• 如何构建卷积神经网络
• 如何使用正规化技术：dropout、批量归一化
• 什么是过拟合

所需条件

只需一个浏览器。本研讨会完全可以使用 Google Colaboratory 运行。

反馈

如果您发现此实验有任何问题，或者认为它应该有所改进，请告诉我们。我们通过 GitHub 问题 [反馈链接] 处理反馈。

此实验使用 Google Colaboratory，无需您进行任何设置。您可以在 Chromebook 上运行该应用。请打开下面的文件，然后执行单元格，以便熟悉 Colab 笔记本。

Welcome to Colab.ipynb

其他说明如下：

选择 GPU 后端

在 Colab 菜单中，依次选择运行时 > 更改运行时类型，然后选择 GPU。首次执行时，系统会自动连接到运行时，您也可以使用右上角的“连接”按钮。

笔记本执行

点击某个单元格，然后使用 Shift-Enter 逐个执行单元格。您还可以通过依次选择运行时 > 全部运行来运行整个笔记本

目录

所有笔记本都有目录。您可以使用左侧的黑色箭头打开该菜单。

隐藏单元格

部分单元格将仅显示其标题。这是 Colab 特有的笔记本功能。您可以双击它们来查看其中的代码，但通常不会很有趣。通常是支持或可视化函数。您仍需运行这些单元格，才能定义其中的函数。

我们将首先观看神经网络的训练过程。请打开下面的笔记本，并运行所有单元格。暂时不要关注代码，我们稍后会开始讲解。

keras_01_mnist.ipynb

执行笔记本时，请重点关注可视化图表。有关说明，请参阅下文。

训练数据

我们有一个手写数字数据集，其中包含已添加标签的手写数字，因此我们知道每张图片代表什么，即 0 到 9 之间的数字。在笔记本中，您会看到一段摘录：

我们将构建的神经网络会将手写数字分类到 10 个类别（0 到 9）中。它会根据内部参数进行分类，这些参数需要具有正确的值，才能使分类功能正常运行。这种“正确值”是通过训练过程学习到的，该过程需要包含图片和相关正确答案的“已标记数据集”。

如何判断训练后的神经网络性能是否良好？使用训练数据集来测试网络属于作弊行为。在训练期间，它已经多次看到该数据集，因此在该数据集上的表现肯定非常出色。我们需要另一个在训练期间从未见过的带标签数据集，以评估网络的“实际”性能。称为“验证数据集”

此数据集中包含 5 万个训练数字。我们在每次迭代时将大小为 128 的“批次” 馈送到训练循环中，这样在 391 次迭代后，系统将看到所有训练数字一次。我们将其称为“周期”。

此外，还有 10,000 个单独的“验证”数字用于测试模型的性能。

训练

随着训练的进行，模型会一次处理一批训练数据，内部模型参数会得到更新，模型识别手写数字的能力也会越来越好。您可以在训练图表中看到它：

在右侧，“准确率”只是正确识别的数字所占的百分比。随着训练的进行，该值会上升，这是好事。

在左侧，我们可以看到 损失。为了推动训练，我们将定义一个“损失”函数，该函数表示系统识别数字的错误程度，并尝试将其最小化。您会看到，随着训练的进行，训练数据和验证数据的损失都在下降：这是好事。这意味着神经网络正在学习。

X 轴表示“周期数”，即遍历整个数据集的次数。

预测

模型训练完毕后，我们就可以使用它来识别手写数字了。下一个可视化图表显示了模型在本地字体渲染的几个数字（第一行）以及验证数据集的 10,000 个数字上的表现。预测的类别会显示在每个数字下方，如果预测错误，则以红色显示。

如您所见，此初始模型效果不太好，但仍能正确识别一些数字。其最终验证准确率约为 90%，对于我们开始使用的简单模型来说还不错，但仍意味着在 10, 000 个验证数字中，有 1,000 个数字被错误分类。这远远超出了可显示的范围，因此看起来好像所有答案都是错误的（红色）。

张量

数据存储在矩阵中。28x28 像素的灰度图片适合放入 28x28 的二维矩阵中。但对于彩色图片，我们需要更多维度。每个像素有 3 个颜色值（红色、绿色、蓝色），因此需要一个维度为 [28, 28, 3] 的三维表。若要存储一批 128 张彩色图片，则需要一个维度为 [128, 28, 28, 3] 的四维表。

这些多维表格称为“张量”，其维度列表称为“形状”。

简而言之

如果您已了解下一段中所有粗体字词，则可以继续进行下一个练习。如果您刚刚开始学习深度学习，欢迎您，请继续阅读。

神经网络分类器由多个神经元层组成。对于图像分类，这些层可以是密集层，但更常见的是卷积层。它们通常通过 relu 激活函数激活。最后一层使用的神经元数量与类别的数量相同，并使用 softmax 进行激活。对于分类，交叉熵是最常用的损失函数，用于将独热编码的标签（即正确答案）与神经网络预测的概率进行比较。为了最大限度地减少损失，最好选择具有动量的优化器（例如 Adam），并针对训练图片和标签的批次进行训练。

对于构建为层序列的模型，Keras 提供了 Sequential API。例如，使用三个密集层的图片分类器可以在 Keras 中编写为：

model = tf.keras.Sequential([
    tf.keras.layers.Flatten(input_shape=[28, 28, 1]),
    tf.keras.layers.Dense(200, activation="relu"),
    tf.keras.layers.Dense(60, activation="relu"),
    tf.keras.layers.Dense(10, activation='softmax') # classifying into 10 classes
])

# this configures the training of the model. Keras calls it "compiling" the model.
model.compile(
  optimizer='adam',
  loss= 'categorical_crossentropy',
  metrics=['accuracy']) # % of correct answers

# train the model
model.fit(dataset, ... )

单个密集层

MNIST 数据集中的手写数字是 28x28 像素的灰度图片。对这些图片进行分类的最简单方法是将 28x28=784 像素用作单层神经网络的输入。

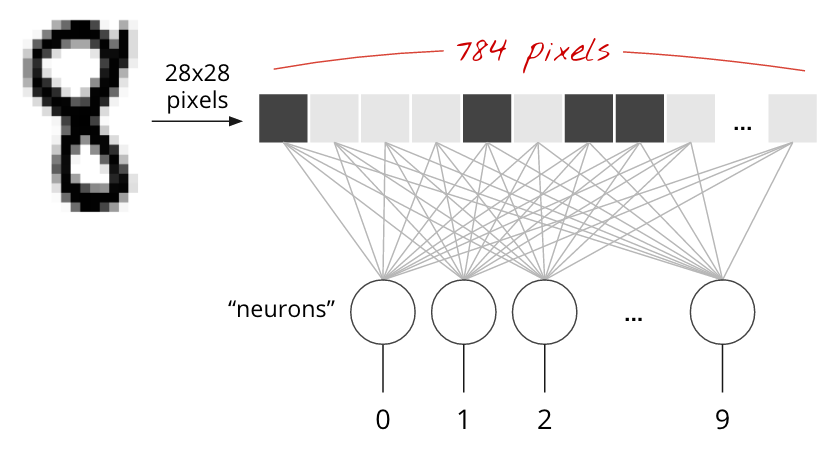
神经网络中的每个“神经元”都会对其所有输入进行加权求和，然后加上一个称为“偏差”的常量，最后通过某个非线性“激活函数”馈送结果。“权重”和“偏差”是通过训练确定的参数。它们最初使用随机值进行初始化。

上图表示一个单层神经网络，其中包含 10 个输出神经元，因为我们要将数字分为 10 个类别（0 到 9）。

使用矩阵乘法

下面展示了如何通过矩阵乘法表示处理一组图像的神经网络层：

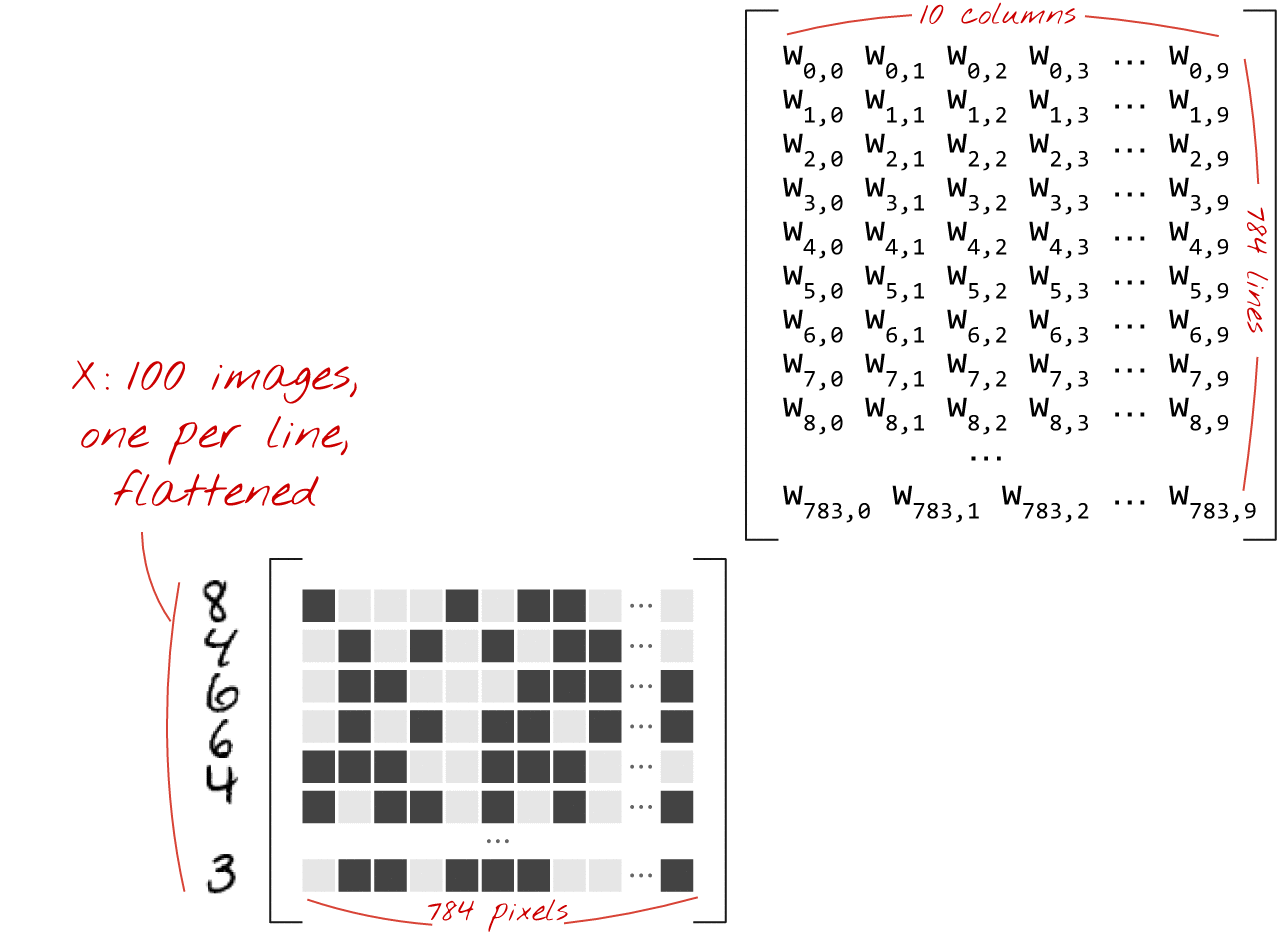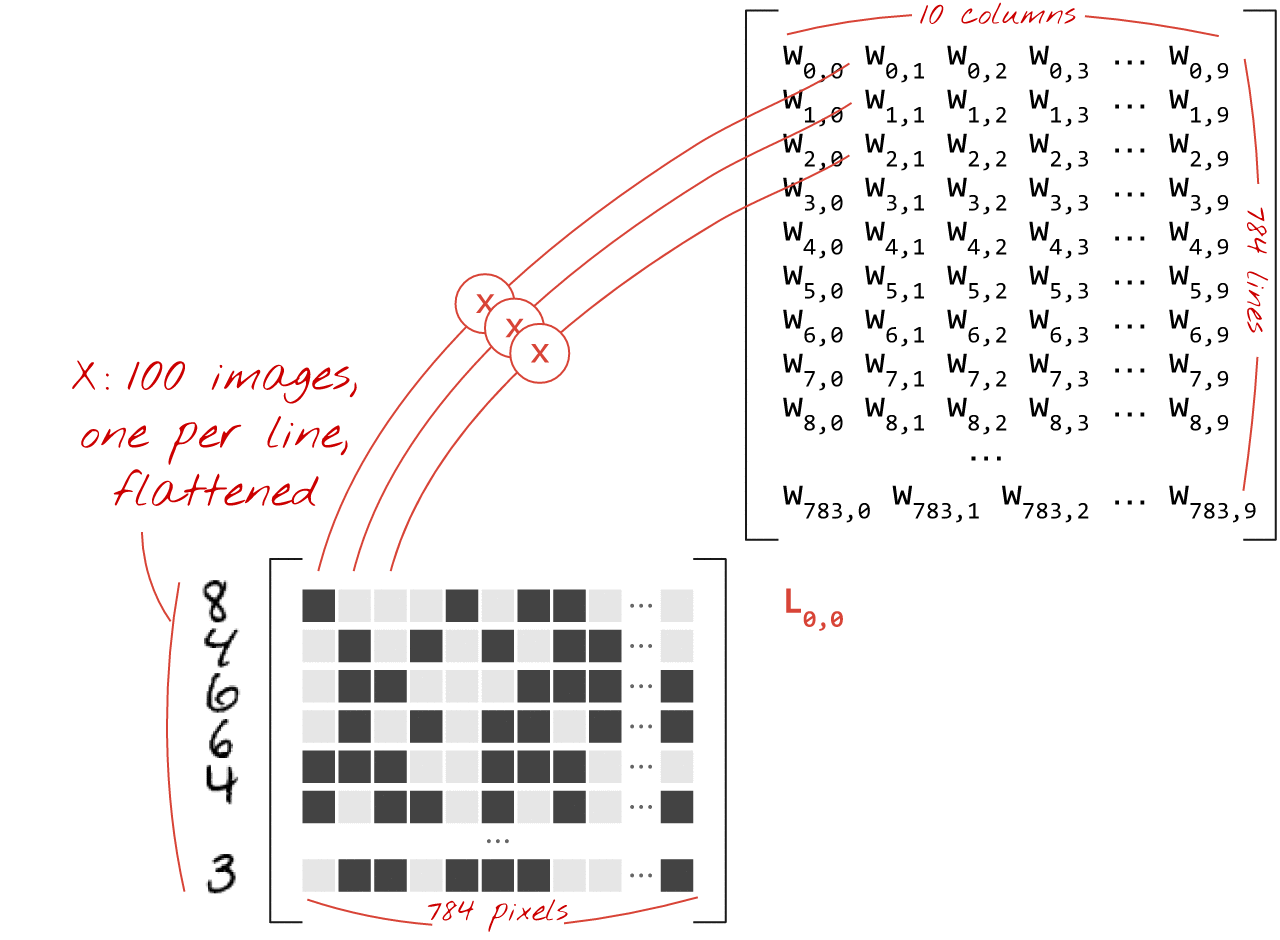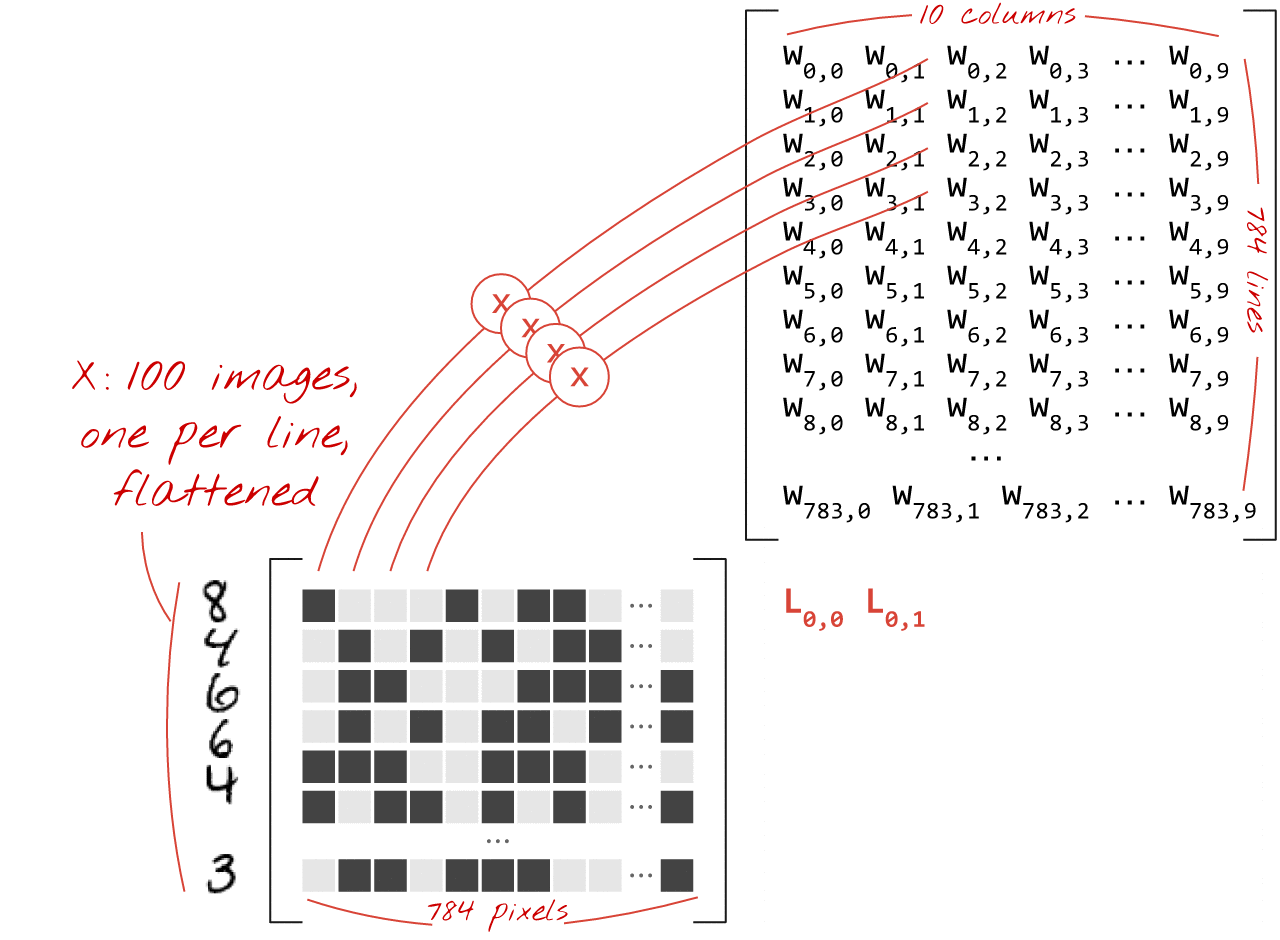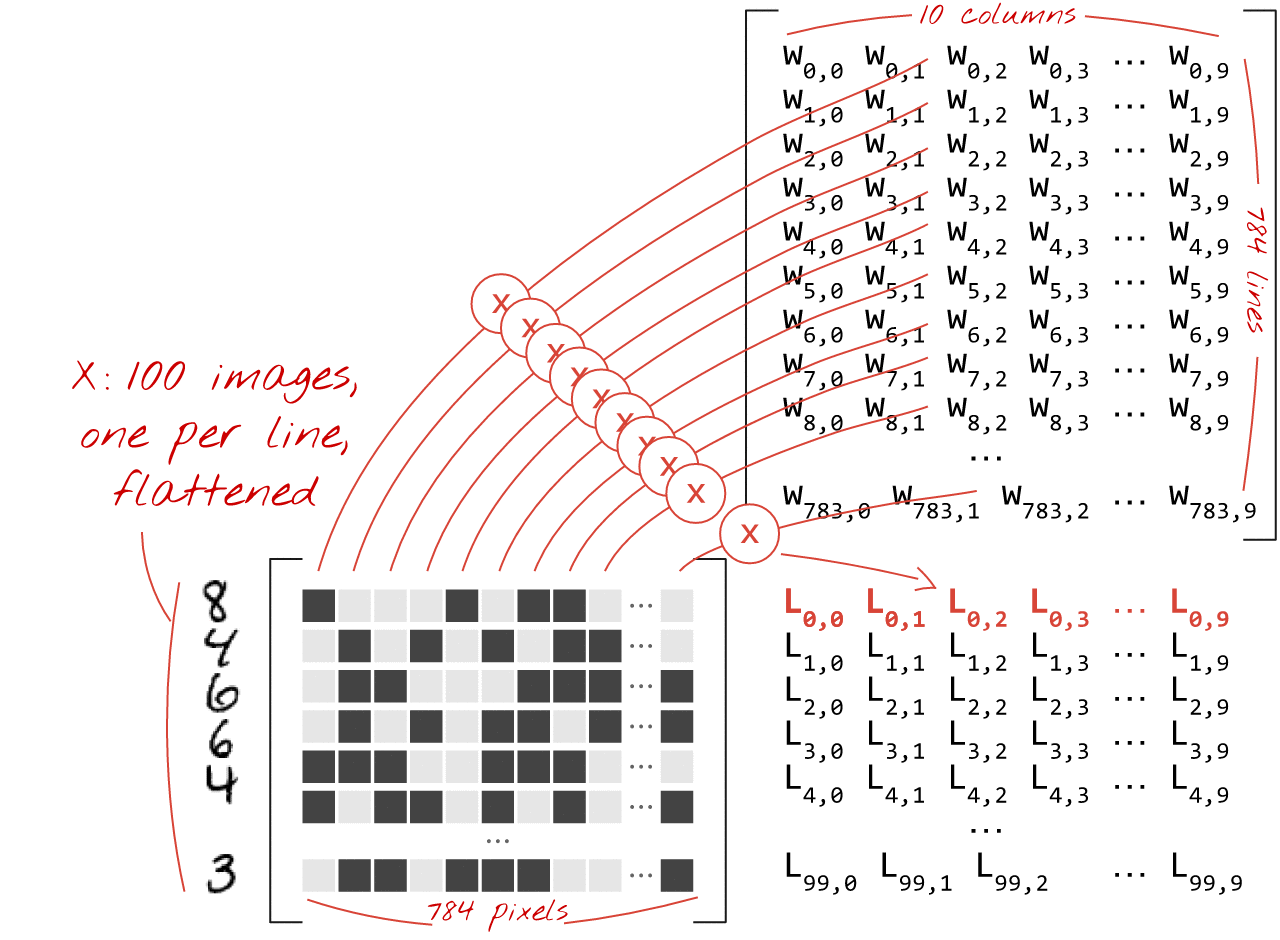
使用权重矩阵 W 中的第一列权重，计算第一个图像的所有像素的加权和。此总和对应于第一个神经元。使用第二列权重，我们对第二个神经元执行相同的操作，依此类推，直到第 10 个神经元。然后，我们可以对剩余的 99 张图片重复执行此操作。如果我们用 X 表示包含 100 张图片的矩阵，那么对 100 张图片计算出的 10 个神经元的全部加权和就是 X.W，即矩阵乘法。

每个神经元现在都必须添加其偏差（一个常数）。由于我们有 10 个神经元，因此有 10 个偏置常数。我们将这个包含 10 个值的向量称为 b。必须将其添加到之前计算的矩阵的每一行中。借助一种称为“广播”的技巧，我们可以使用简单的加号来编写此代码。

“广播”是 Python 及其科学计算库 numpy 中使用的标准技巧。它扩展了不兼容维度的矩阵的常规运算方式。“广播相加”是指“如果您要相加两个矩阵，但由于它们的维度不兼容而无法相加，请尝试根据需要尽可能多地复制较小的矩阵，以使其能够相加。”

最后，我们应用激活函数（例如“softmax”，如下所述），并获得描述应用于 100 张图片的单层神经网络的公式：

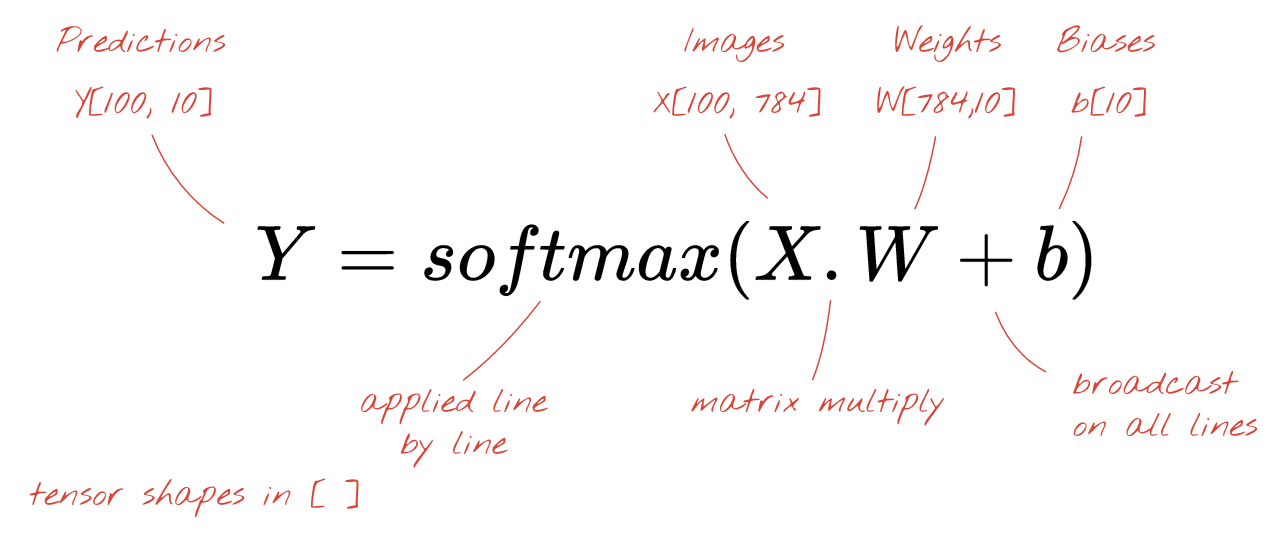
在 Keras 中

借助 Keras 等高级神经网络库，我们无需实现此公式。不过，请务必了解神经网络层只是一堆乘法和加法运算。在 Keras 中，密集层可以写为：

tf.keras.layers.Dense(10, activation='softmax')

深入了解

链接神经网络层非常简单。第一层计算像素的加权和。后续层计算前几层输出的加权和。

除了神经元数量之外，唯一的区别在于激活函数的选择。

激活函数：relu、softmax 和 sigmoid

通常，您会为除最后一层之外的所有层使用“relu”激活函数。分类器中的最后一层会使用“softmax”激活函数。

同样，“神经元”会计算所有输入的加权和，添加一个称为“偏差”的值，并通过激活函数馈送结果。

最常用的激活函数是“RELU”（修正线性单元）。如上图所示，这是一个非常简单的函数。

神经网络中的传统激活函数是 “sigmoid”，但“relu”几乎在所有地方都表现出更好的收敛特性，因此现在更受青睐。

用于分类的 Softmax 激活函数

我们神经网络的最后一层有 10 个神经元，因为我们希望将手写数字分为 10 个类别（0 到 9）。它应该输出 10 个介于 0 到 1 之间的数字，分别表示相应数字为 0、1、2 等的概率。为此，我们将在最后一层使用一个名为 “softmax”的激活函数。

对向量应用 softmax 函数的方法是，先计算每个元素的指数，然后对向量进行归一化处理，通常是将其除以“L1”范数（即绝对值之和），这样归一化后的值加起来等于 1，可以解释为概率。

激活前的最后一层的输出有时称为 “logits”。如果此向量为 L = [L0, L1, L2, L3, L4, L5, L6, L7, L8, L9]，则：

为什么“softmax”被称为 softmax？指数函数是一种陡峭递增的函数。它会增加神经元输出之间的差异。然后，当您对向量进行归一化时，占主导地位的最大元素将被归一化为接近 1 的值，而所有其他元素最终将被除以一个较大的值，并归一化为接近 0 的值。生成的向量清楚地显示了获胜的类别（即“最大”类别），但保留了其值的原始相对顺序，因此称为“软”。

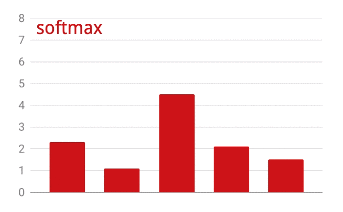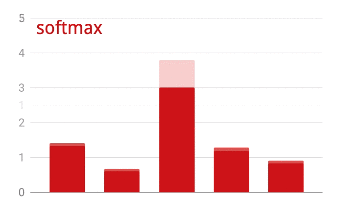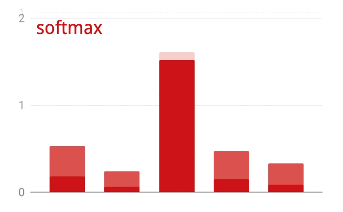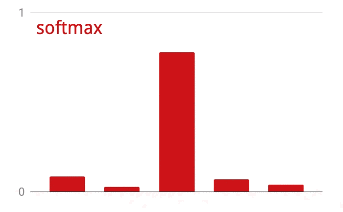
交叉熵损失

现在，我们的神经网络可以根据输入图片生成预测结果，我们需要衡量这些结果的准确性，即网络给出的结果与正确答案（通常称为“标签”）之间的距离。请注意，我们已为数据集中的所有图片添加了正确的标签。

任何距离都可以，但对于分类问题，所谓的“交叉熵距离”是最有效的。我们将此函数称为误差或“损失”函数：

“独热”编码是指使用一个包含 10 个值的向量来表示“这是数字 3”这一标签，该向量中除第 3 个值为 1 之外，其余值均为零。此向量表示是“数字 3”的概率为 100%。我们的神经网络还会以包含 10 个概率值的向量形式输出预测结果。易于比较。

梯度下降法

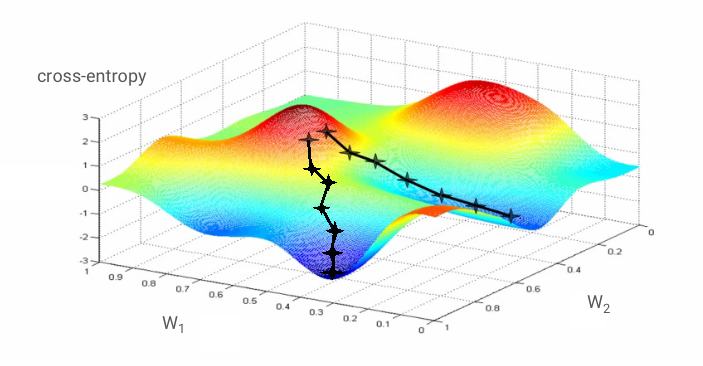
“训练”神经网络实际上是指使用训练图片和标签来调整权重和偏差，以最大限度地减少交叉熵损失函数。具体运作方式如下。

交叉熵是权重、偏差、训练图像的像素及其已知类别的函数。

如果我们计算交叉熵相对于所有权重和所有偏差的偏导数，就会得到一个“梯度”，该梯度是针对给定的图片、标签以及当前权重和偏差值计算得出的。请注意，我们可能有数百万个权重和偏差，因此计算梯度似乎是一项非常繁重的工作。幸运的是，TensorFlow 可以帮我们完成这项工作。梯度的数学属性是它指向“上方”。由于我们希望前往交叉熵较低的位置，因此我们朝相反的方向前进。我们通过梯度的一小部分来更新权重和偏差。然后，我们在训练循环中使用下一批训练图片和标签，一遍又一遍地重复上述操作。希望这会收敛到交叉熵最小的位置，尽管无法保证此最小值是唯一的。

“学习速率”：您无法在每次迭代时按梯度的整个长度更新权重和偏差。这就像穿着七里靴试图到达山谷底部一样。您会从山谷的一侧跳到另一侧。若要到达底部，您需要采取更小的步长，即仅使用梯度的一小部分，通常在 1/1000 范围内。这一分数称为“学习率”。

小批量和动量

您可以仅根据一张示例图片计算梯度并立即更新权重和偏差，但如果根据一批（例如 128 张）图片计算梯度，则梯度会更好地表示不同示例图片施加的限制，因此更有可能更快地收敛到解决方案。小批次的大小是一个可调整的参数。

这种有时称为“随机梯度下降”的技术还有另一个更实用的好处：处理批次也意味着处理更大的矩阵，而这些矩阵通常更易于在 GPU 和 TPU 上进行优化。

不过，收敛可能仍然有点混乱，如果梯度向量全为零，甚至可能会停止。这是否意味着我们找到了最小值？不一定。梯度分量在最小值或最大值处可以为零。如果梯度向量有数百万个元素，并且这些元素全部为零，那么每个零都对应一个最小值，而没有一个零对应最大值的概率非常小。在多维空间中，鞍点非常常见，我们不希望停留在鞍点。

图示：鞍点。梯度为 0，但它在所有方向上都不是最小值。（图片提供方信息 维基媒体：Nicoguaro - 自制作品，CC BY 3.0）

解决方案是为优化算法增加一些动量，使其能够顺利通过鞍点而不停止。

TensorFlow 库提供了一系列优化器，从 tf.train.GradientDescentOptimizer 开始。内置动量的更高级的主流优化器包括 tf.train.RMSPropOptimizer 或 tf.train.AdamOptimizer。

术语库

批次或小批次：始终基于批次的训练数据和标签进行训练。这样做有助于算法收敛。“批次”维度通常是数据张量的第一个维度。例如，形状为 [100, 192, 192, 3] 的张量包含 100 张 192x192 像素的图片，每张图片包含三个值（RGB）。

交叉熵损失：一种常用于分类器的特殊损失函数。

密集层：一种神经元层，其中每个神经元都与上一层中的所有神经元相连。

特征：神经网络的输入有时称为“特征”。确定将数据集的哪些部分（或部分组合）馈送到神经网络以获得良好预测结果的技巧称为“特征工程”。

标签：监督式分类问题中“类别”或正确答案的另一种名称

学习速率：在训练循环的每次迭代中，权重和偏差更新所依据的梯度分数。

logits：神经元层在应用激活函数之前的输出称为“logits”。该术语源自“logistic 函数”（也称为“sigmoid 函数”），后者曾经是最常用的激活函数。“Neuron outputs before logistic function”（逻辑函数之前的神经元输出）缩短为“logits”。

损失：比较神经网络输出与正确答案的误差函数

神经元：计算输入的加权和，添加偏差，并通过激活函数馈送结果。

独热编码：5 个类别中的第 3 个类别编码为包含 5 个元素的向量，除第 3 个元素为 1 外，其余元素均为零。

relu：修正线性单元。一种常用的神经元激活函数。

sigmoid：另一种曾经很受欢迎的激活函数，在特殊情况下仍然有用。

softmax：一种特殊的激活函数，可对向量进行运算，增大最大分量与所有其他分量之间的差值，并对向量进行归一化处理，使其总和为 1，以便将其解读为概率向量。用作分类器的最后一步。

张量：“张量”类似于矩阵，但具有任意数量的维度。一维张量是向量。二维张量是矩阵。然后，您可以拥有 3 维、4 维、5 维或更多维度的张量。

返回到学习笔记本，这次我们来阅读代码。

keras_01_mnist.ipynb

实操：

本部分中的任务是阅读并理解代码，以便稍后对其进行改进。

我们来浏览一下此笔记本中的所有单元格。

“参数”单元格

在此处定义批次大小、训练周期数和数据文件的位置。数据文件托管在 Google Cloud Storage (GCS) 存储分区中，因此其地址以 gs:// 开头

“导入”单元格

此处导入了所有必需的 Python 库，包括 TensorFlow 和用于可视化的 matplotlib。

单元格“可视化实用程序 [运行我]”

此单元格包含不重要的可视化代码。该窗口默认处于收起状态，但您可以双击它，在有时间时将其打开并查看代码。

您必须运行此单元格 (SHIFT-ENTER)，否则系统将不会解析其中定义的函数，并且您稍后会收到错误。

单元格“tf.data.Dataset：解析文件并准备训练和验证数据集”

此单元格使用 tf.data.Dataset API 从数据文件加载 MNIST 数据集。无需在此单元格上花费过多时间。如果您对 tf.data.Dataset API 感兴趣，可以参阅以下教程：TPU 速度数据流水线。目前，基础知识包括：

MNIST 数据集中的图片和标签（正确答案）存储在 4 个文件中的固定长度记录中。可以使用专用固定记录函数加载文件：

imagedataset = tf.data.FixedLengthRecordDataset(image_filename, 28*28, header_bytes=16)

现在，我们有了一个图片字节数据集。需要将它们解码为图片。为此，我们定义了一个函数。由于图片未压缩，因此该函数无需解码任何内容（decode_raw 基本上不执行任何操作）。然后，将图片转换为介于 0 到 1 之间的浮点值。我们可以在此处将其重塑为 2D 图片，但实际上，我们将其保留为大小为 28*28 的扁平像素数组，因为这是我们的初始密集层所期望的。

def read_image(tf_bytestring):
    image = tf.decode_raw(tf_bytestring, tf.uint8)
    image = tf.cast(image, tf.float32)/256.0
    image = tf.reshape(image, [28*28])
    return image

我们使用 .map 将此函数应用于数据集，并获得一个图片数据集：

imagedataset = imagedataset.map(read_image, num_parallel_calls=16)

我们对标签进行相同的读取和解码，并一起 .zip 图片和标签：

dataset = tf.data.Dataset.zip((imagedataset, labelsdataset))

现在，我们有了一个包含（图片、标签）对的数据集。这是我们模型所期望的。我们尚未准备好在训练函数中使用它：

dataset = dataset.cache()
dataset = dataset.shuffle(5000, reshuffle_each_iteration=True)
dataset = dataset.repeat()
dataset = dataset.batch(batch_size)
dataset = dataset.prefetch(tf.data.experimental.AUTOTUNE)

tf.data.Dataset API 具有用于准备数据集的所有必需的实用函数：

.cache 会将数据集缓存在 RAM 中。这是一个很小的数据集，因此可以正常运行。.shuffle 使用 5000 个元素的缓冲区对其进行随机排序。请务必对训练数据进行充分的随机化处理。.repeat 循环播放数据集。我们将多次（多个周期）对其进行训练。.batch 将多个图片和标签一起拉入一个 mini-batch 中。最后，.prefetch 可以在 GPU 上训练当前批次的同时，使用 CPU 准备下一批次。

验证数据集的准备方式类似。现在，我们可以定义模型并使用此数据集对其进行训练了。

“Keras 模型”单元格

我们的所有模型都将是层级的直线序列，因此我们可以使用 tf.keras.Sequential 样式来创建它们。最初，这里是一个密集层。它有 10 个神经元，因为我们要将手写数字分为 10 类。它使用“softmax”激活函数，因为它是分类器中的最后一层。

Keras 模型还需要知道其输入的形状。您可以使用 tf.keras.layers.Input 来定义它。在此示例中，输入向量是长度为 28*28 的像素值扁平向量。

model = tf.keras.Sequential(
  [
    tf.keras.layers.Input(shape=(28*28,)),
    tf.keras.layers.Dense(10, activation='softmax')
  ])

model.compile(optimizer='sgd',
              loss='categorical_crossentropy',
              metrics=['accuracy'])

# print model layers
model.summary()

# utility callback that displays training curves
plot_training = PlotTraining(sample_rate=10, zoom=1)

在 Keras 中，使用 model.compile 函数配置模型。这里我们使用基本优化器 'sgd'（随机梯度下降法）。分类模型需要交叉熵损失函数，在 Keras 中称为 'categorical_crossentropy'。最后，我们要求模型计算 'accuracy' 指标，即正确分类的图片所占的百分比。

Keras 提供了一个非常实用的 model.summary() 实用程序，用于输出您创建的模型的详细信息。您好心的指导员添加了 PlotTraining 实用程序（在“可视化实用程序”单元格中定义），该程序将在训练期间显示各种训练曲线。

“训练和验证模型”单元格

通过调用 model.fit 并传入训练数据集和验证数据集，即可在此处进行训练。默认情况下，Keras 会在每个周期结束时运行一轮验证。

model.fit(training_dataset, steps_per_epoch=steps_per_epoch, epochs=EPOCHS,
          validation_data=validation_dataset, validation_steps=1,
          callbacks=[plot_training])

在 Keras 中，可以使用回调在训练期间添加自定义行为。这就是本次研讨会中动态更新的训练图的实现方式。

“直观呈现预测结果”单元格

模型训练完毕后，我们可以通过调用 model.predict() 从中获取预测结果：

probabilities = model.predict(font_digits, steps=1)
predicted_labels = np.argmax(probabilities, axis=1)

我们在此准备了一组使用本地字体渲染的打印数字，以供测试。请注意，神经网络会通过最终的“softmax”返回一个包含 10 个概率的向量。为了获得标签，我们必须找出哪个概率最高。numpy 库中的 np.argmax 可以实现此目的。

如需了解为何需要 axis=1 参数，请记住我们已处理一批 128 张图片，因此模型会返回 128 个概率向量。输出张量的形状为 [128, 10]。我们正在计算每张图片返回的 10 个概率的 argmax，因此为 axis=1（第一个轴为 0）。

这个简单模型已经可以识别 90% 的数字。这个分数不算差，但您现在可以大幅提高此分数。

为了提高识别准确率，我们将向神经网络添加更多层。

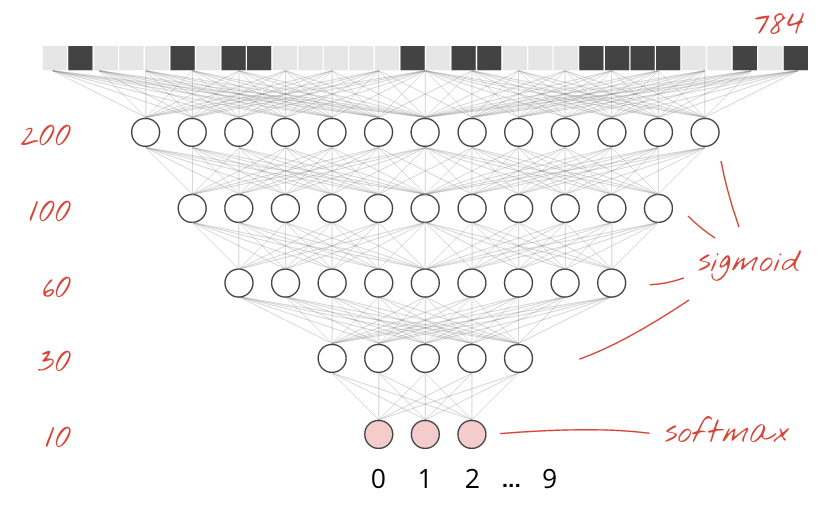
我们将 softmax 保留为最后一层的激活函数，因为这是最适合分类的函数。不过，在中间层，我们将使用最经典的激活函数：sigmoid：

实操：

请在“softmax”层之前添加几个以“sigmoid”激活的中间密集层。其中的神经元数量可以是介于 784（输入像素数）和 10（输出神经元数）之间的任意值。然后重新训练模型。

警告：如需重新训练，您必须重新运行“Keras 模型”单元格以定义新模型，然后运行训练单元格。只需重新运行训练单元格，即可继续训练之前的模型。

例如，您的模型可能如下所示（请勿忘记逗号，tf.keras.Sequential 接受以逗号分隔的层列表）：

model = tf.keras.Sequential(
  [
      tf.keras.layers.Input(shape=(28*28,)),
      tf.keras.layers.Dense(200, activation='sigmoid'),
      tf.keras.layers.Dense(60, activation='sigmoid'),
      tf.keras.layers.Dense(10, activation='softmax')
  ])

查看模型的“摘要”。现在，它的参数数量至少增加了 10 倍。效果应该好 10 倍！但由于某些原因，它不是 ...

亏损似乎也大幅增加。出了点问题。

您刚刚体验了 20 世纪 80 年代和 90 年代人们设计神经网络的方式。难怪他们放弃了这个想法，迎来了所谓的“AI 寒冬”。事实上，随着层数的增加，神经网络越来越难以收敛。

事实证明，只要采用一些数学技巧来使深度神经网络收敛，那么具有许多层（如今为 20 层、50 层甚至 100 层）的深度神经网络就可以发挥出非常出色的效果。这些简单技巧的发现是 2010 年代深度学习复兴的原因之一。

RELU 激活

在深度网络中，sigmoid 激活函数实际上存在相当大的问题。它会将所有值压缩到 0 到 1 之间，如果重复执行此操作，神经元输出及其梯度可能会完全消失。之所以提到它，是因为历史原因，但现代网络使用 RELU（修正线性单元），其外观如下所示：

实操：

将层中的所有 activation='sigmoid' 替换为 activation='relu'，然后重新训练。

为什么 sigmoid 函数存在问题？看看它在侧面的表现：变得扁平。

这意味着该点的导数接近于零。请记住，训练是通过梯度（导数向量）来推进的。使用 sigmoid 激活函数时，尤其是在层数较多的情况下，梯度可能会变得非常小，导致训练速度越来越慢。

另一方面，relu 的导数为 1（至少在其右侧）。使用 RELU 激活函数时，即使某些神经元传来的梯度可能为零，也总会有其他神经元提供清晰的非零梯度，训练可以以良好的速度继续进行。

更好的优化器

在像这里这样非常高维的空间中（我们有大约 1 万个权重和偏差），“鞍点”很常见。这些点不是局部最小值，但梯度为零，梯度下降优化器会停滞在这些点。TensorFlow 提供了各种优化器，包括一些可处理一定惯性的优化器，这些优化器可安全地通过鞍点。

实操：

将 'sgd' 优化器替换为更好的优化器（例如 'adam'），然后重新训练。

随机初始化

在训练之前初始化权重偏差是一门艺术，也是一个研究领域，有大量论文发表于此主题。您可以点击此处查看 Keras 中所有可用的初始值设定器。幸运的是，Keras 默认情况下会执行正确的操作，并使用 'glorot_uniform' 初始化程序，这在几乎所有情况下都是最佳选择。

您无需执行任何操作，因为 Keras 已经做出了正确的处理。

NaN ???

交叉熵公式涉及对数，而 log(0) 是非数字 (NaN，如果您愿意，也可以称之为数值崩溃)。交叉熵的输入可以是 0 吗？输入来自 softmax，而 softmax 本质上是指数函数，指数函数永远不会为零。所以我们是安全的！

真的吗？在美好的数学世界中，我们是安全的，但在计算机世界中，以 float32 格式表示的 exp(-150) 几乎为零，因此交叉熵会崩溃。

幸运的是，您也无需在此处执行任何操作，因为 Keras 会处理此问题，并以特别谨慎的方式计算 softmax，然后计算交叉熵，以确保数值稳定性并避免出现可怕的 NaN。

成功？

现在，您应该能达到 97% 的准确率。此工作坊的目标是将准确率大幅提高到 99% 以上，因此我们继续操作。

如果您卡住了，请尝试以下解决方案：

keras_02_mnist_dense.ipynb

也许我们可以尝试更快地训练？Adam 优化器中的默认学习速率为 0.001。我们来尝试增加它。

实操：

将学习速率从默认值 0.001 提高到 0.01。为此，您必须将 'adam' 预定义优化器替换为 Adam 优化器的实际实例，以便访问其配置参数：

optimizer=tf.keras.optimizers.Adam(lr=0.01)

另请在 PlotTraining 中将缩放系数提升到 5。这会放大损失接近 0 和准确率接近 1 的区域，以帮助您了解情况：PlotTraining(sample_rate=10, zoom=5)

加快速度似乎没有太大帮助，而且这些噪音是什么？

训练曲线非常嘈杂，并且两个验证曲线都在上下跳动。这意味着我们走得太快了。我们可以恢复到之前的速度，但还有更好的方法。

一个不错的解决方案是快速开始，然后以指数方式衰减学习速率。在 Keras 中，您可以使用 tf.keras.callbacks.LearningRateScheduler 回调来实现此目的。

实操：

实现一种以指数方式衰减学习速率的学习速率调度。您可以在下方找到有用的代码段。

可供复制粘贴的实用代码：

# lr decay function
def lr_decay(epoch):
  return 0.01 * math.pow(0.6, epoch)

# lr schedule callback
lr_decay_callback = tf.keras.callbacks.LearningRateScheduler(lr_decay, verbose=True)

# important to see what you are doing
plot_learning_rate(lr_decay, EPOCHS)

请勿忘记使用您创建的 lr_decay_callback。将其添加到 model.fit 中的回调列表中：

model.fit(...,  callbacks=[plot_training, lr_decay_callback])

这一小小的变化带来了惊人的效果。您会看到，大部分噪声都已消除，测试准确率现在持续高于 98%。

模型现在似乎正在顺利收敛。让我们尝试更深入地了解一下。

实操：

如果您尚未这样做，请将模型的深度增加到至少 4 个密集层，然后重新训练。您可以在各层中使用以下数量的神经元：200、100、60、10。

另请在 PlotTraining 中将缩放系数提升到 10。这会放大损失接近 0 和准确率接近 1 的区域，以帮助您了解情况：PlotTraining(sample_rate=10, zoom=10)

这是否有帮助？

实际上并没有，准确率仍停留在 98%，请看验证损失率。正在上涨！学习算法仅处理训练数据，并相应地优化训练损失。它永远不会看到验证数据，因此过一段时间后，它的工作不再对验证损失产生影响，验证损失停止下降，有时甚至会反弹回升，这并不令人意外。

这不会立即影响模型的实际识别能力，但会阻止您运行多次迭代，并且通常表明训练不再产生积极效果。

这种不一致通常称为“过拟合”，如果您发现这种情况，可以尝试应用一种称为“Dropout”的正则化技术。在每次训练迭代中，dropout 技术都会随机射击神经元。

Dropout 是深度学习中最古老的正则化技术之一。在每次训练迭代中，它会以概率 p（通常为 25% 到 50%）从网络中舍弃随机神经元。在实践中，神经元输出设置为 0。最终结果是，这些神经元将不会参与本次的损失计算，也不会获得权重更新。在每次训练迭代中，系统会随机舍弃不同的神经元。

在测试网络性能时，当然要将所有神经元都放回去（丢弃率为 0）。Keras 会自动执行此操作，因此您只需添加一个 tf.keras.layers.Dropout 层。它会在训练和评估时自动表现出正确的行为。

这种做法为何有效？该理论认为，神经网络在众多层之间有很大的自由度，因此某一层完全有可能演变出不良行为，而下一层则会对其进行补偿。这并非神经元的理想使用方式。使用 dropout 时，在给定的训练轮次中，解决问题的神经元很可能不存在。违规层的错误行为变得明显，权重朝着更好的行为演变。

实操：

您可以在网络中的每个中间密集层之后添加 dropout。请勿在 softmax 层之后添加 dropout。您会降低预测概率。您可以使用以下代码添加 25% 的失能率：tf.keras.layers.Dropout(0.25)

效果如何？

噪声会重新出现（考虑到 dropout 的工作方式，这并不令人意外）。验证损失似乎不再上升，但总体上高于不使用 dropout 的情况。验证准确率略有下降。这个结果相当令人失望。

看来 dropout 并不是正确的解决方案，或者“过拟合”是一个更复杂的概念，其某些原因无法通过“dropout”修复？

什么是“过拟合”？当神经网络“学习”得不好时，就会发生过拟合，即学习方式适用于训练示例，但在真实世界的数据中效果不佳。有一些正则化技术（例如 dropout）可以强制模型以更好的方式学习，但过拟合也有更深层次的原因。

当神经网络对于手头的问题具有过多的自由度时，就会发生基本的过拟合。假设我们有如此多的神经元，以至于网络可以将所有训练图片存储在其中，然后通过模式匹配来识别它们。它在真实世界的数据上会完全失败。神经网络必须受到一定的限制，这样才能被迫泛化在训练期间学到的知识。

如果您只有极少的训练数据，即使是小型网络也能记住这些数据，从而导致“过拟合”。一般来说，您始终需要大量数据来训练神经网络。

最后，如果您已按部就班地完成所有操作，尝试了不同大小的网络以确保其自由度受到限制，应用了 dropout，并使用大量数据进行了训练，但仍停留在似乎无法提高的性能水平，这意味着，您的神经网络目前无法从数据中提取更多信息，就像我们这里的情况一样。

还记得我们如何将图片展平为单个向量吗？这真是个糟糕的主意。手写数字由形状组成，我们在展平像素时舍弃了形状信息。不过，有一种神经网络可以利用形状信息，那就是卷积网络。让我们来试试吧。

如果您卡住了，请尝试以下解决方案：

keras_03_mnist_dense_lrdecay_dropout.ipynb

简而言之

如果您已了解下一段中所有粗体字词，则可以继续进行下一个练习。如果您刚刚开始使用卷积神经网络，请继续阅读。

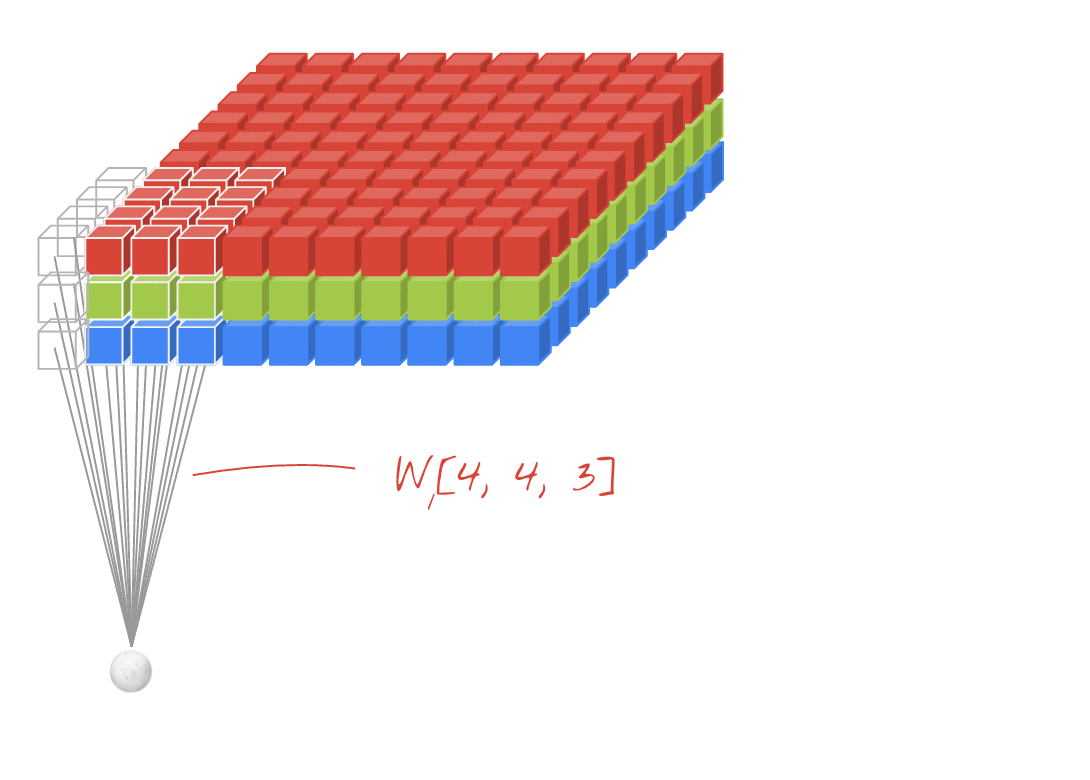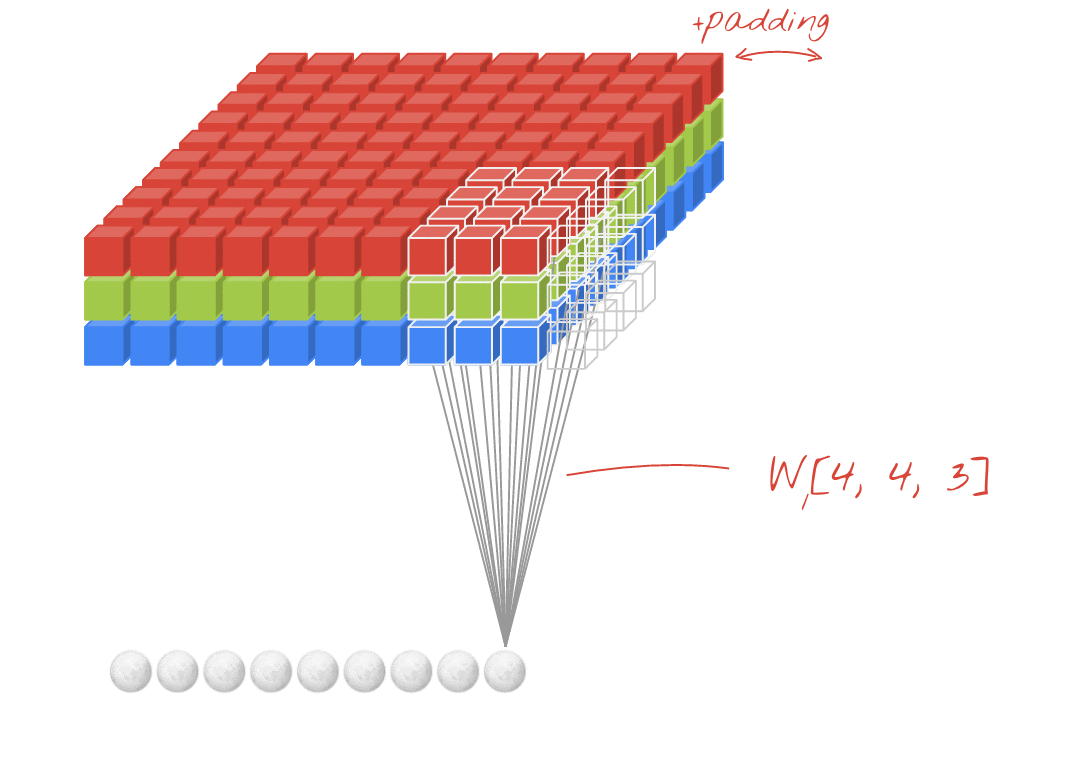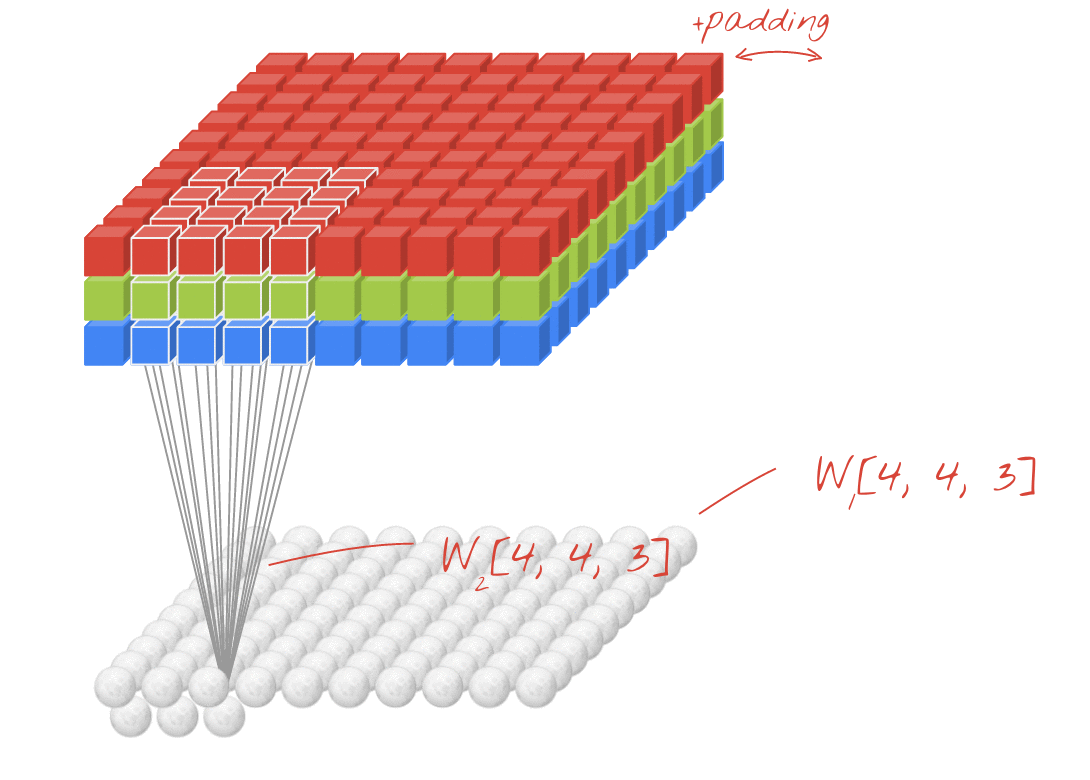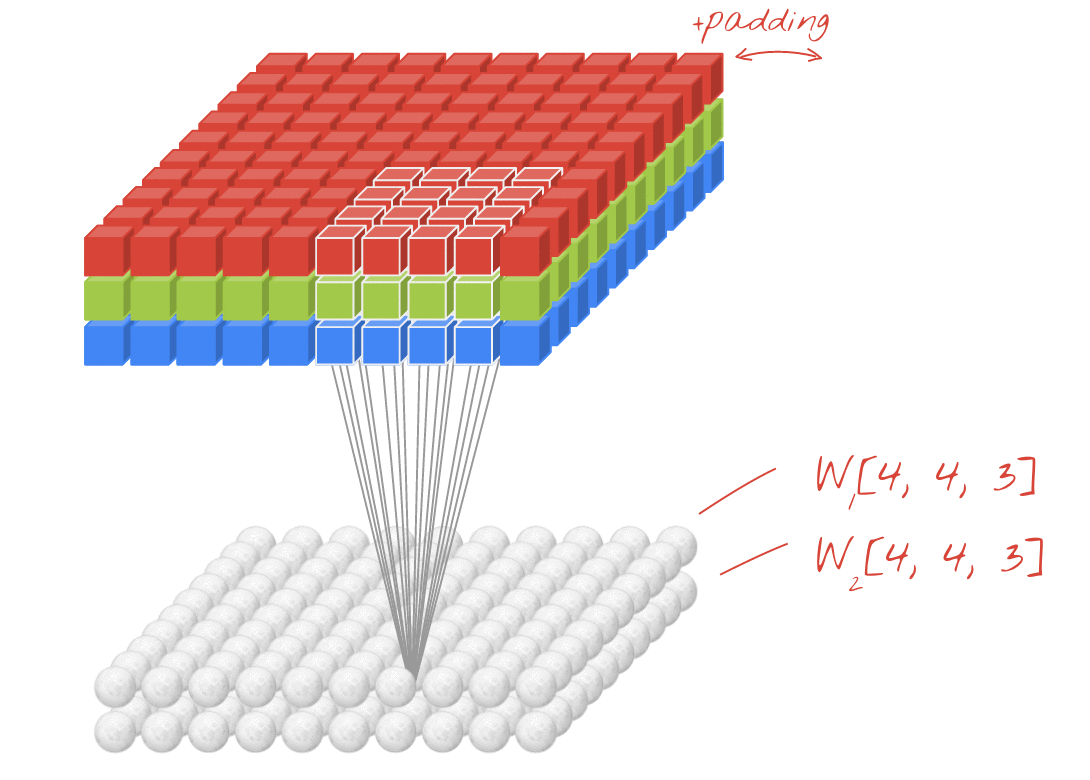
图示：使用两个连续的滤波器（每个滤波器由 4x4x3=48 个可学习的权重组成）过滤图像。

卷积神经网络会对输入图像应用一系列可学习的过滤器。卷积层由过滤条件（或内核）大小、应用的过滤条件数量和步幅定义。卷积层的输入和输出各有三个维度（宽度、高度、通道数），从输入图像（宽度、高度、RGB 通道）开始。堆叠卷积层时，可以使用步幅 >1 或通过最大池化操作来调整输出的宽度和高度。通过使用更多或更少的过滤器来调整输出的深度（渠道数量）。

以下是 Keras 中一个简单的卷积神经网络：

model = tf.keras.Sequential([
    tf.keras.layers.Reshape(input_shape=(28*28,), target_shape=(28, 28, 1)),
    tf.keras.layers.Conv2D(kernel_size=3, filters=12, activation='relu'),
    tf.keras.layers.Conv2D(kernel_size=6, filters=24, strides=2, activation='relu'),
    tf.keras.layers.Conv2D(kernel_size=6, filters=32, strides=2, activation='relu'),
    tf.keras.layers.Flatten(),
    tf.keras.layers.Dense(10, activation='softmax')
])

在卷积网络的某一层中，一个“神经元”仅对上方一小块图像区域中的像素进行加权求和。它会添加偏差，并通过激活函数馈送总和，就像常规密集层中的神经元一样。然后，使用相同的权重对整个图片重复此操作。请注意，在密集层中，每个神经元都有自己的权重。在这里，单个权重“补丁”在图像上沿两个方向滑动（即“卷积”）。输出的值数量与图片中的像素数量相同（不过边缘需要一些填充）。这是一项过滤操作。在上图中，它使用了 4x4x3=48 个权重的过滤条件。

不过，48 个权重是不够的。为了增加自由度，我们使用一组新的权重重复相同的操作。这会生成一组新的过滤输出。我们不妨将其称为输出“通道”，这与输入图像中的 R、G、B 通道类似。

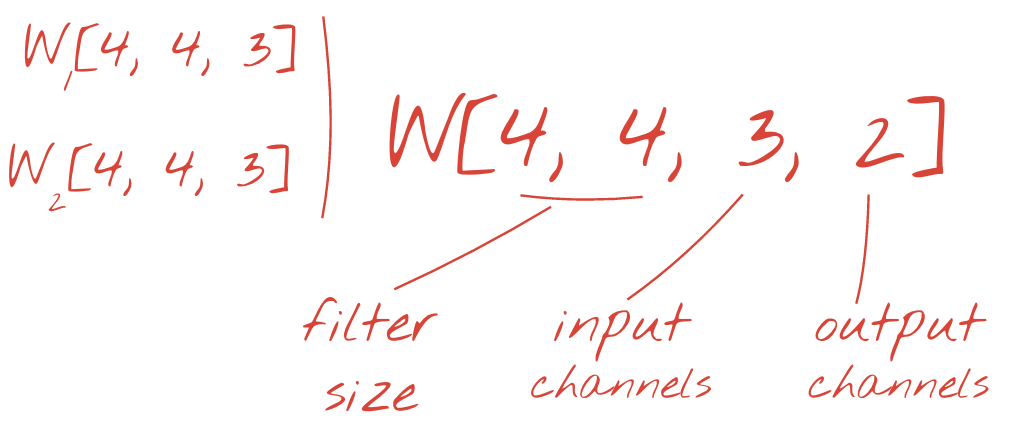
通过添加新维度，可以将两组（或更多组）权重汇总为一个张量。这样，我们就得到了卷积层权重张量的通用形状。由于输入和输出通道的数量是形参，我们可以开始堆叠和链接卷积层。

图示：卷积神经网络将数据“立方体”转换为其他数据“立方体”。

步幅卷积、最大池化

通过以 2 或 3 的步幅执行卷积，我们还可以缩小所得数据立方体的水平维度。以下是两种常见的方法：

• 步幅卷积：与上述滑动过滤器的不同之处在于，步幅大于 1
• 最大池化：应用 MAX 操作的滑动窗口（通常在 2x2 块上，每 2 个像素重复一次）

示例：将计算窗口滑动 3 个像素会减少输出值。步幅卷积或最大池化（以 2 为步幅滑动 2x2 窗口的最大值）是一种在水平维度上缩小数据立方体的方法。

“最大池化”有助于我们直观地了解卷积网络的运作方式：假设在训练期间，权重块会演变为可识别基本形状（水平线、垂直线、曲线等）的过滤器，那么一种提取有用信息的方法是，通过各层保留以最大强度识别出形状的输出。实际上，在最大池化层中，神经元输出以 2x2 为一组进行处理，并且仅保留最大值。

最后一层

在最后一个卷积层之后，数据以“立方体”的形式存在。有两种方式可将其馈送到最终的密集层。

第一种方法是将数据立方体展平为向量，然后将其馈送到 softmax 层。有时，您甚至可以在 softmax 层之前添加一个密集层。就权重数量而言，这种方法往往成本较高。卷积网络末端的密集层可能包含整个神经网络一半以上的权重。

除了使用开销较大的密集层之外，我们还可以将传入的数据“立方体”拆分为与类别数量相同的多个部分，计算这些部分的平均值，然后通过 softmax 激活函数馈送这些平均值。这种构建分类头的方式不需要任何权重。在 Keras 中，有一个专门用于此目的的层：tf.keras.layers.GlobalAveragePooling2D()。

卷积神经网络可检测事物的位置。当某个滤波器对某个特征做出强响应时，它会在特定 (x, y) 位置做出响应。根据您要执行的操作，可以训练神经网络来使用或舍弃这些位置数据。使用全局平均池化会明确舍弃所有位置数据。这对于花卉分类器来说可能没问题，但对于其他任务（例如统计图片中的花卉数量）来说可能效果不佳。请小心使用。

跳到下一部分，为当前问题构建卷积网络。

让我们构建一个用于识别手写数字的卷积网络。我们将使用顶部的三个卷积层、底部的传统 softmax 读取层，并通过一个全连接层将它们连接起来：

请注意，第二个和第三个卷积层的步幅为 2，这说明了为什么它们会将输出值的数量从 28x28 减少到 14x14，然后再减少到 7x7。

我们来编写 Keras 代码。

在第一个卷积层之前需要特别注意。实际上，它需要一个 3D 数据“立方体”，但我们的数据集目前已设置为密集层，并且图像的所有像素都已展平为向量。我们需要将它们重新调整为 28x28x1 的图片（灰度图片为 1 个通道）：

tf.keras.layers.Reshape(input_shape=(28*28,), target_shape=(28, 28, 1))

您可以使用此行代码来代替您之前使用的 tf.keras.layers.Input 层。

在 Keras 中，采用“relu”激活函数的卷积层的语法如下：

tf.keras.layers.Conv2D(kernel_size=3, filters=12, padding='same', activation='relu')

卷积层中的 padding 参数可以有两个值：

• “same”：用零填充，以生成与输入宽度/高度相同的输出
• “valid”：无内边距，仅使用实际像素

我们在此处使用了填充，因此请将填充设置为“相同”。

对于步幅卷积，您需要编写以下代码：

tf.keras.layers.Conv2D(kernel_size=6, filters=24, padding='same', activation='relu', strides=2)

将数据立方体展平为向量，以便密集层可以使用该向量：

tf.keras.layers.Flatten()

对于密集层，语法没有变化：

tf.keras.layers.Dense(200, activation='relu')

实操：

修改模型，将其转换为卷积模型。您可以使用上图中的值来调整其大小。您可以保持学习速率衰减不变，但请移除 dropout。

另请在 PlotTraining 中将缩放系数提升到 16。这会放大损失接近 0 和准确率接近 1 的区域，以帮助您了解情况：PlotTraining(sample_rate=10, zoom=16)

您的模型是否突破了 99% 的准确率？差不多了…但请查看验证损失曲线。这是否让您想起了什么？

还要查看预测结果。首次测试时，您应该会看到 10,000 个测试数字中的大多数现在都能正确识别。误检的行数仅剩约 4½ 行（在 10,000 个数字中约有 110 个）

如果您卡住了，请尝试以下解决方案：

keras_04_mnist_convolutional.ipynb

之前的训练显示出明显的过拟合迹象（并且准确率仍低于 99%）。我们是否应再次尝试丢弃？

实操：

在网络中的两个密集层之间添加一个 dropout 层。使用 40%（即 0.4）的 dropout 率：

tf.keras.layers.Dropout(0.4)

虽然可以将 dropout 应用于卷积层，但其运作方式略有不同，通常效果不如应用于全连接层，因为卷积层中的权重数量要少得多，因此出现不良共同适应的机会也更少。我们不会探讨这一点。

这次怎么样？

这次的 dropout 似乎奏效了。验证损失不再缓慢增加，最终准确率应远高于 99%。恭喜！

我们第一次尝试应用 dropout 时，以为遇到了过拟合问题，但实际上问题出在神经网络的架构上。如果没有卷积层，我们就无法继续，而 Dropout 对此也无能为力。

这次，过拟合似乎是问题的原因，而 dropout 确实有帮助。请注意，有很多因素可能会导致训练损失曲线和验证损失曲线之间出现差异，并导致验证损失逐渐增加。过拟合（自由度过高，被网络错误地使用）只是其中一种。如果您的数据集过小或神经网络的架构不够完善，您可能会在损失曲线上看到类似的行为，但 Dropout 无法提供帮助。

最后，我们尝试添加批次归一化。

什么是批量归一化？

简而言之，批归一化试图解决神经元输出相对于神经元激活函数的分布问题。在训练数据的小批次中，神经元在激活前的输出可能具有以下分布：

如果权重过小（即太靠左），经过 sigmoid 激活后，相应神经元几乎总是输出 0。

过窄，此神经元永远不会输出明确的 0 或 1。

这还不错。神经元将在此微批次中表现出相当广泛的行为。

为解决此问题，批次归一化会跨训练数据批次对神经元输出进行归一化，即减去平均值并除以标准差。不过，如果只做这些，就太残酷了。如果分布完全居中且在各处都呈正态宽分布，那么所有神经元的行为都会相同。诀窍是为每个神经元引入两个额外的可学习参数 𝛼 和 𝛽，并计算：

𝛼。normalized_out + 𝛽

然后应用激活函数（sigmoid、relu 等）。这样，网络就可以通过机器学习来决定在每个神经元处应用多少居中和重新缩放。读者可以自行验证是否存在可完全移除归一化的 𝛼 和 𝛽 值（如果这是正确做法）。

在实践中，并不总是需要同时使用 𝛼 和 𝛽。在 Keras 中，它们分别称为“scale”和“center”，您可以选择性地使用其中一个或另一个，例如：

tf.keras.layers.BatchNormalization(scale=False, center=True)

批归一化存在的问题是，在预测时，您没有可用于计算神经元输出统计信息的训练批次。但您仍然需要这些值。这部分有点 hacky。在训练期间，系统会计算“足够”数量的批次的“典型”神经元输出平均值和标准差，实际上是使用指数移动平均值。这些统计数据随后会在推理时使用。

好消息是，在 Keras 中，您可以使用 tf.keras.layers.BatchNormalization 层，系统会自动进行所有这些计算。

这是理论上的情况，但在实践中，只需记住以下几条规则：

“按部就班”的批次归一化：

1. 批次归一化位于层的输出和其激活函数之间。
2. 如果您在批次归一化中使用 center=True，则无需在层中使用偏差。批次归一化偏移量充当偏差的角色。
3. 如果您使用的激活函数具有尺度不变性（即，放大后形状不会改变），则可以设置 scale=False。ReLU 是尺度不变的。Sigmoid 则不是。

这只是理论，不过，若要了解违反这些规则是否会带来不良影响，唯一的方法就是尝试。

我们现在先按部就班地操作，在每个神经网络层（最后一层除外）上添加一个批归一化层。请勿将其添加到最后一个“softmax”层。在这种情况下，它不会有用。

# Modify each layer: remove the activation from the layer itself.
# Set use_bias=False since batch norm will play the role of biases.
tf.keras.layers.Conv2D(..., use_bias=False),
# Batch norm goes between the layer and its activation.
# The scale factor can be turned off for Relu activation.
tf.keras.layers.BatchNormalization(scale=False, center=True),
# Finish with the activation.
tf.keras.layers.Activation('relu'),

现在的准确度如何？

稍作调整（BATCH_SIZE=64，学习速率衰减参数 0.666，密集层的 dropout 率 0.3），再加上一点运气，您就可以达到 99.5% 的准确率。学习率和 dropout 调整是按照使用批次归一化的“最佳实践”进行的：

• 批次归一化有助于神经网络收敛，通常可让您更快地进行训练。
• 批次归一化是一种正则化方法。您通常可以减少所用的 dropout 量，甚至完全不使用 dropout。

解决方案笔记本的训练运行成功率为 99.5%：

keras_05_mnist_batch_norm.ipynb

您可以在 GitHub 上的 mlengine 文件夹中找到可用于云端的代码版本，以及在 Google Cloud AI Platform 上运行该代码的说明。在运行此部分之前，您必须先创建 Google Cloud 账号并启用结算功能。完成实验所需的资源应不超过几美元（假设在一个 GPU 上训练 1 小时）。准备账号：

1. 创建 Google Cloud Platform 项目 (http://cloud.google.com/console)。
2. 启用结算功能。
3. 安装 GCP 命令行工具（此处为 GCP SDK）。
4. 创建一个 Google Cloud Storage 存储分区（放在 us-central1 区域中）。它将用于暂存训练代码并存储经过训练的模型。
5. 启用必要的 API 并申请必要的配额（运行一次训练命令，您应该会收到错误消息，告知您需要启用哪些 API）。

您已构建了首个神经网络，并将其训练到 99% 的准确率。在此过程中学到的技巧并非仅适用于 MNIST 数据集，实际上它们在处理神经网络时得到了广泛应用。作为临别礼物，我们为您准备了本实验的卡通版“速记卡片”。您可以使用它来记住所学内容：

后续步骤

• 在学习了全连接网络和卷积网络之后，您应该了解一下循环神经网络。
• 如需在云端分布式基础架构上运行训练或推理，Google Cloud 提供了 AI Platform。
  
• 最后，我们非常欢迎您提供反馈。如果您发现此实验有任何问题，或者认为它应该有所改进，请告诉我们。我们通过 GitHub 问题 [反馈链接] 处理反馈。

作者：Martin Görner Twitter：@martin_gorner

本实验中的所有卡通图片版权归以下方所有：alexpokusay / 123RF stock photos