
В этой лабораторной работе вы научитесь создавать и обучать нейронную сеть, распознающую рукописные цифры. По мере того, как вы будете совершенствовать свою нейронную сеть до 99% точности, вы также познакомитесь с инструментами, которые специалисты по глубокому обучению используют для эффективного обучения своих моделей.
В этой лабораторной работе используется набор данных MNIST — коллекция из 60 000 помеченных цифр, которая вот уже почти два десятилетия даёт работу нескольким поколениям докторов наук. Вы решите задачу, используя менее 100 строк кода на Python/TensorFlow.
Чему вы научитесь
- Что такое нейронная сеть и как ее обучить
- Как построить простую однослойную нейронную сеть с использованием tf.keras
- Как добавить больше слоев
- Как настроить график скорости обучения
- Как построить сверточные нейронные сети
- Как использовать методы регуляризации: исключение, пакетная нормализация
- Что такое переобучение?
Что вам понадобится
Всего лишь браузер. Этот семинар можно провести полностью с помощью Google Colaboratory.
Обратная связь
Пожалуйста, сообщите нам, если вы заметили что-то неладное в этой лаборатории или считаете, что её следует улучшить. Мы обрабатываем отзывы через GitHub Issues [ ссылка на обратную связь ].
Эта лабораторная работа использует Google Colaboratory и не требует настройки. Вы можете запустить её на Chromebook. Откройте файл ниже и выполните команды в ячейках, чтобы ознакомиться с блокнотами Colab.
Дополнительные инструкции ниже:
Выберите бэкэнд GPU
В меню Colab выберите «Среда выполнения» > «Изменить тип среды выполнения» , а затем выберите «Графический процессор». Подключение к среде выполнения произойдет автоматически при первом запуске. Вы также можете воспользоваться кнопкой «Подключиться» в правом верхнем углу.
Ноутбук исполнение
Выполняйте ячейки по одной, щелкая по ним и нажимая Shift+ENTER. Вы также можете запустить весь блокнот, выбрав «Среда выполнения» > «Выполнить все».
Оглавление
Во всех блокнотах есть оглавление. Открыть его можно, нажав на чёрную стрелку слева.
Скрытые ячейки
В некоторых ячейках отображается только их заголовок. Это специфичная для блокнотов функция Colab. Вы можете дважды щелкнуть по ним, чтобы увидеть код внутри, но обычно он не очень интересен. Обычно это функции поддержки или визуализации. Вам всё равно нужно запустить эти ячейки, чтобы определить функции внутри.
Сначала посмотрим, как тренируется нейронная сеть. Откройте блокнот ниже и пройдитесь по всем ячейкам. Пока не обращайте внимания на код, мы начнём объяснять его позже.
Заполняя блокнот, сосредоточьтесь на визуализациях. Объяснения см. ниже.
Данные обучения
У нас есть набор данных рукописных цифр, которые были помечены так, чтобы мы знали, что представляет каждая картинка, то есть число от 0 до 9. В блокноте вы увидите отрывок:

Нейронная сеть, которую мы построим, классифицирует рукописные цифры по 10 классам (0, .., 9). Она делает это на основе внутренних параметров, которые должны иметь корректные значения для корректной классификации. Это «корректное значение» формируется в процессе обучения, для которого требуется «размеченный набор данных» с изображениями и соответствующими правильными ответами.
Как узнать, хорошо ли работает обученная нейронная сеть? Использование обучающего набора данных для тестирования сети было бы мошенничеством. Сеть уже многократно использовала этот набор данных во время обучения и, безусловно, показала на нём очень высокую эффективность. Нам нужен ещё один размеченный набор данных, который никогда не использовался во время обучения, чтобы оценить «реальную» производительность сети. Он называется « валидационным набором данных ».
Обучение
По мере обучения, по одному набору обучающих данных за раз, внутренние параметры модели обновляются, и модель всё лучше и лучше распознаёт рукописные цифры. Это можно увидеть на графике обучения:

Справа «точность» — это просто процент правильно распознанных цифр. Она растёт по мере обучения, что хорошо.
Слева мы видим «потери» . Для управления обучением мы определим функцию «потерь», которая отражает, насколько плохо система распознаёт цифры, и постараемся минимизировать её. Здесь видно, что потери уменьшаются как на обучающих, так и на проверочных данных по мере обучения: это хорошо. Это означает, что нейронная сеть обучается.
Ось X представляет собой количество «эпох» или итераций во всем наборе данных.
Прогнозы
После обучения модели мы можем использовать её для распознавания рукописных цифр. Следующая визуализация показывает, насколько хорошо она работает на нескольких цифрах, отрисованных локальными шрифтами (первая строка), а затем на 10 000 цифр из проверочного набора данных. Предсказанный класс отображается под каждой цифрой, красным цветом, если он неверен.

Как видите, эта исходная модель не очень хороша, но всё же правильно распознаёт некоторые цифры. Её итоговая точность проверки составляет около 90%, что не так уж плохо для нашей упрощённой модели, но всё равно означает, что она пропускает 1000 проверочных цифр из 10 000. Это гораздо больше, чем можно отобразить, поэтому кажется, что все ответы неверны (красный).
Тензоры
Данные хранятся в матрицах. Изображение в оттенках серого размером 28x28 пикселей помещается в двумерную матрицу размером 28x28. Но для цветного изображения требуется больше измерений. На каждый пиксель приходится 3 значения цвета (красный, зелёный, синий), поэтому потребуется трёхмерная таблица с размерами [28, 28, 3]. А для хранения пакета из 128 цветных изображений потребуется четырёхмерная таблица с размерами [128, 28, 28, 3].
Эти многомерные таблицы называются «тензорами» , а список их измерений — их «формой» .
В двух словах
Если все термины, выделенные жирным шрифтом в следующем абзаце, вам уже знакомы, можете перейти к следующему упражнению. Если же вы только начинаете изучать глубокое обучение, добро пожаловать, и, пожалуйста, продолжайте читать.

Для моделей, построенных как последовательность слоёв, Keras предлагает API Sequential. Например, классификатор изображений с тремя плотными слоями можно записать в Keras следующим образом:
model = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=[28, 28, 1]),
tf.keras.layers.Dense(200, activation="relu"),
tf.keras.layers.Dense(60, activation="relu"),
tf.keras.layers.Dense(10, activation='softmax') # classifying into 10 classes
])
# this configures the training of the model. Keras calls it "compiling" the model.
model.compile(
optimizer='adam',
loss= 'categorical_crossentropy',
metrics=['accuracy']) # % of correct answers
# train the model
model.fit(dataset, ... )
Один плотный слой
Рукописные цифры в наборе данных MNIST представляют собой изображения в оттенках серого размером 28x28 пикселей. Простейший подход к их классификации — использовать эти 28x28=784 пикселя в качестве входных данных для однослойной нейронной сети.
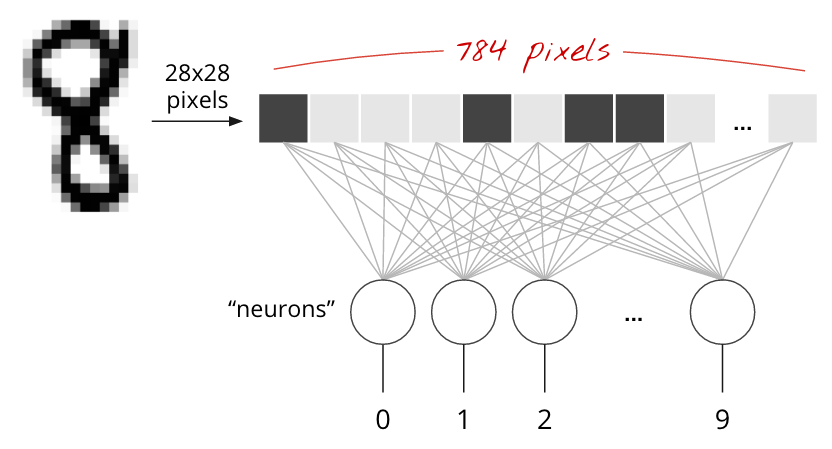
Каждый «нейрон» в нейронной сети взвешивает все свои входные данные, добавляет константу, называемую «смещением», и затем пропускает результат через нелинейную «функцию активации» . «Веса» и «смещения» — это параметры, которые определяются в процессе обучения. Сначала они инициализируются случайными значениями.
На рисунке выше представлена однослойная нейронная сеть с 10 выходными нейронами, поскольку мы хотим классифицировать цифры по 10 классам (от 0 до 9).
С помощью умножения матриц
Вот как слой нейронной сети, обрабатывающий коллекцию изображений, можно представить с помощью умножения матриц:
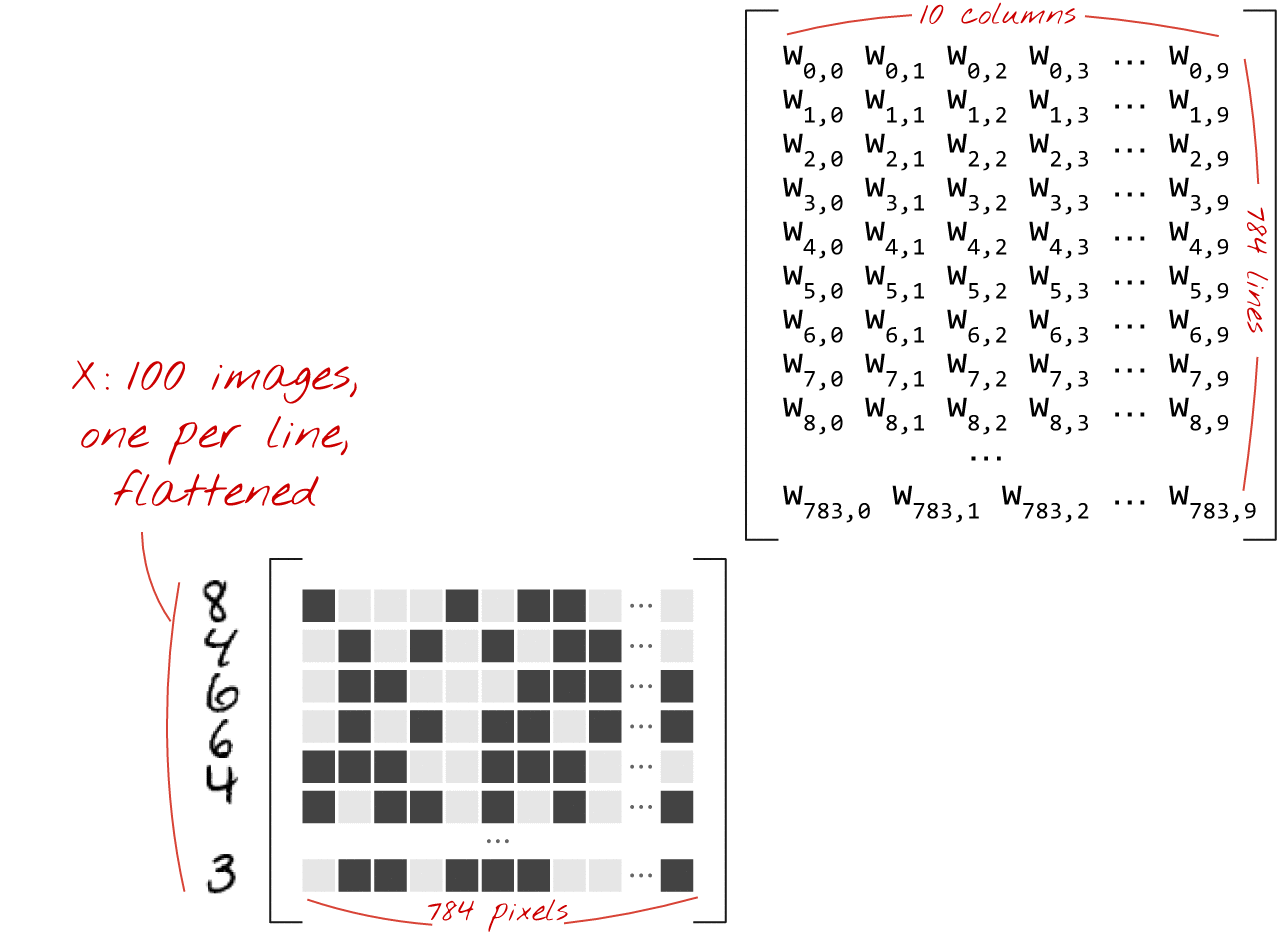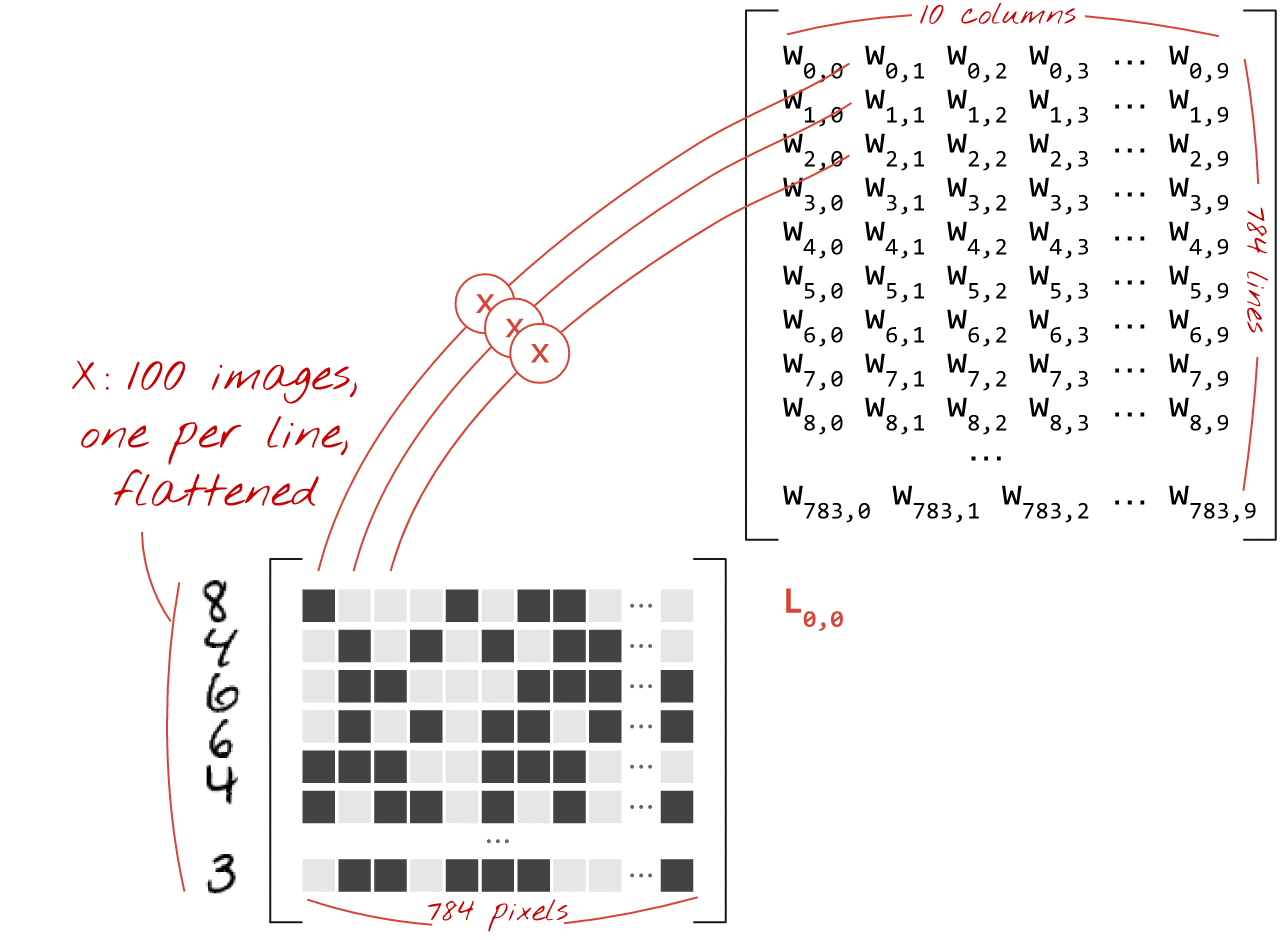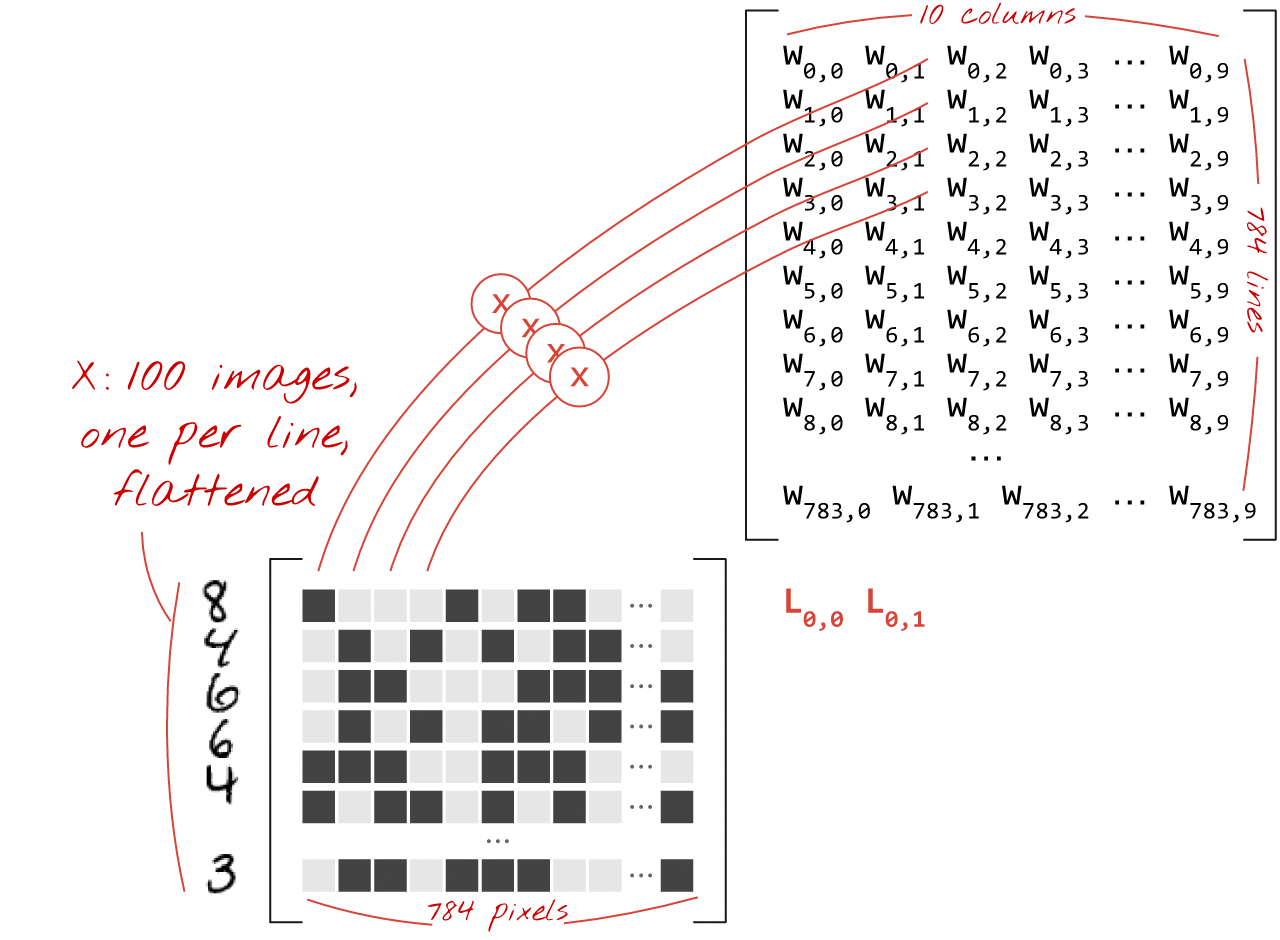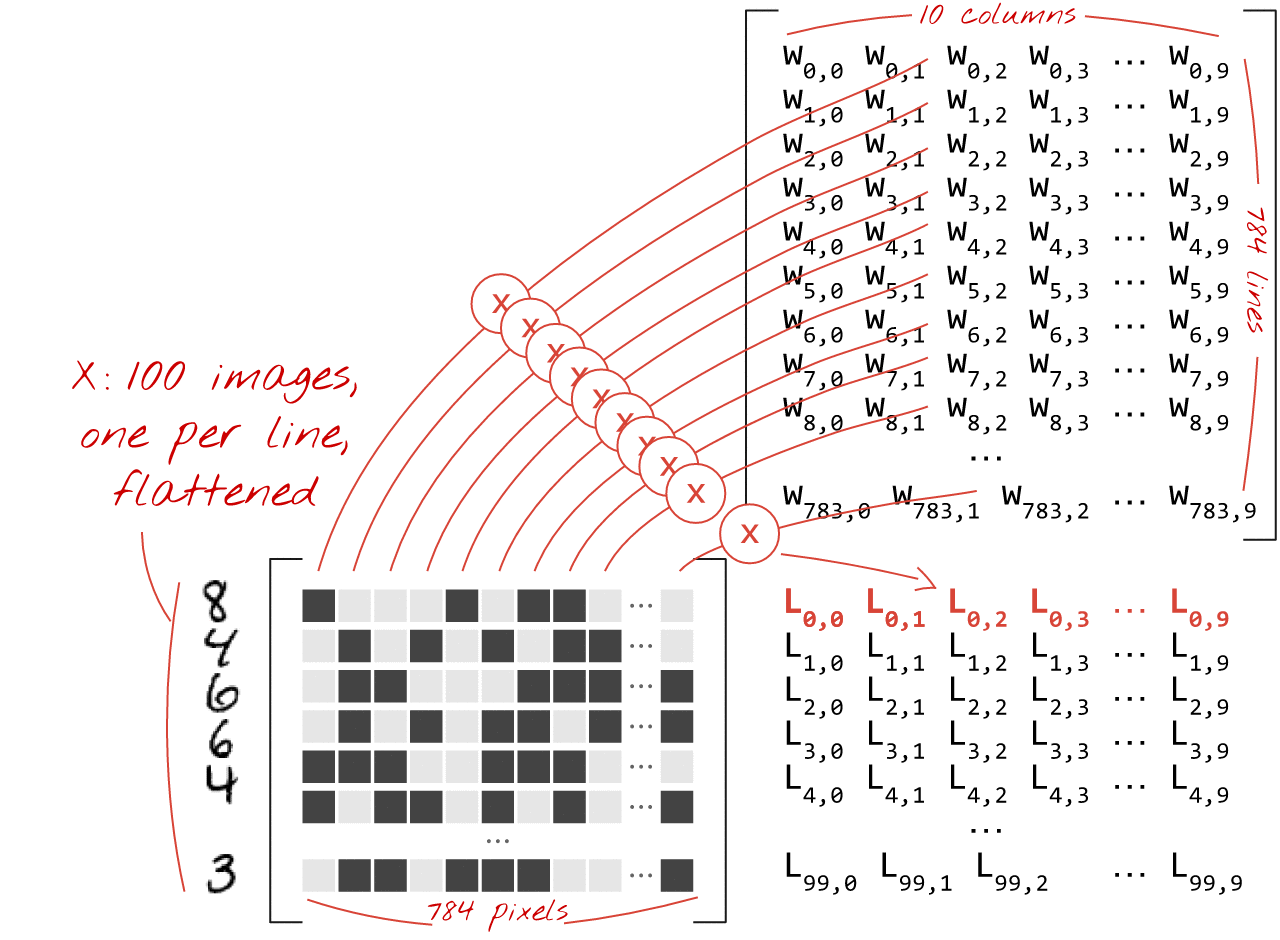
Используя первый столбец весов матрицы весов W, мы вычисляем взвешенную сумму всех пикселей первого изображения. Эта сумма соответствует первому нейрону. Используя второй столбец весов, мы делаем то же самое для второго нейрона и так далее до десятого нейрона. Затем мы можем повторить операцию для оставшихся 99 изображений. Если обозначить матрицу, содержащую наши 100 изображений, как X, то все взвешенные суммы для наших 10 нейронов, вычисленные для 100 изображений, будут просто XW, то есть умножением матриц.
Каждый нейрон теперь должен добавить своё смещение (константу). Поскольку у нас 10 нейронов, у нас есть 10 констант смещения. Назовём этот вектор из 10 значений b. Его нужно добавить к каждой строке ранее вычисленной матрицы. Используя немного магии под названием «трансляция», мы запишем это простым знаком плюс.
Наконец, применяем функцию активации, например, «softmax» (поясняется ниже), и получаем формулу, описывающую однослойную нейронную сеть, примененную к 100 изображениям:
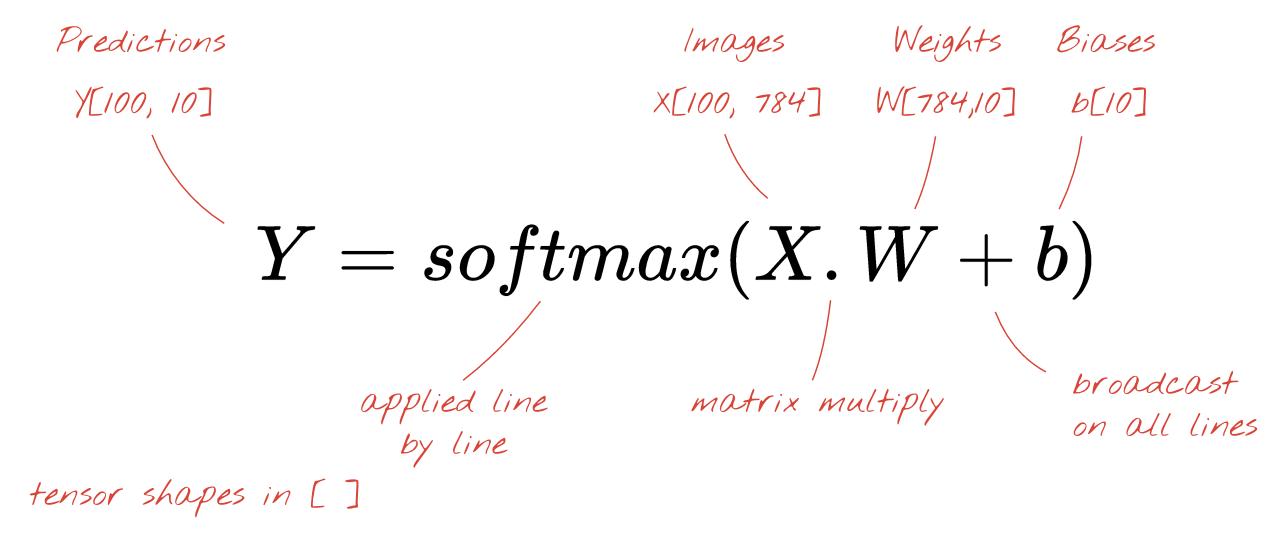
В Керасе
С помощью высокоуровневых библиотек нейронных сетей, таких как Keras, нам не потребуется реализовывать эту формулу. Однако важно понимать, что слой нейронной сети — это всего лишь набор операций умножения и сложения. В Keras плотный слой записывается так:
tf.keras.layers.Dense(10, activation='softmax')Идти глубоко
Объединение слоёв нейронной сети в цепочку — простая задача. Первый слой вычисляет взвешенные суммы пикселей. Последующие слои вычисляют взвешенные суммы выходных данных предыдущих слоёв.

Единственным отличием, помимо количества нейронов, будет выбор функции активации.
Функции активации: relu, softmax и sigmoid
Обычно для всех слоёв, кроме последнего, используется функция активации «relu». Для последнего слоя классификатора используется функция активации «softmax».

Опять же, «нейрон» вычисляет взвешенную сумму всех своих входов, добавляет значение, называемое «смещением», и передает результат через функцию активации.
Самая популярная функция активации называется «RELU» (Rectified Linear Unit). Это очень простая функция, как видно на графике выше.
Традиционной функцией активации в нейронных сетях была «сигмоида» , но было показано, что «relu» обладает лучшими свойствами сходимости практически везде и теперь является предпочтительным.

Активация Softmax для классификации
Последний слой нашей нейронной сети состоит из 10 нейронов, поскольку мы хотим классифицировать рукописные цифры по 10 классам (0,...9). Сеть должна выводить 10 чисел от 0 до 1, представляющих вероятность того, что данная цифра окажется 0, 1, 2 и так далее. Для этого на последнем слое мы используем функцию активации, называемую «softmax» .
Применение softmax к вектору осуществляется путем взятия экспоненты каждого элемента и последующей нормализации вектора, обычно путем его деления на норму «L1» (т. е. сумму абсолютных значений), так что нормализованные значения в сумме дают 1 и могут быть интерпретированы как вероятности.
Выход последнего слоя, перед активацией, иногда называют «логитами» . Если этот вектор равен L = [L0, L1, L2, L3, L4, L5, L6, L7, L8, L9], то:


Потеря перекрестной энтропии
Теперь, когда наша нейронная сеть генерирует прогнозы на основе входных изображений, нам нужно оценить их точность, то есть расстояние между тем, что нам сообщает сеть, и правильными ответами, которые часто называют «метками». Помните, что у нас есть правильные метки для всех изображений в наборе данных.
Подойдет любое расстояние, но для задач классификации наиболее эффективно так называемое «расстояние кросс-энтропии». Мы будем называть его функцией ошибок или «потерь»:

Градиентный спуск
«Обучение» нейронной сети фактически означает использование обучающих изображений и меток для корректировки весов и смещений таким образом, чтобы минимизировать функцию потерь кросс-энтропии. Вот как это работает.
Перекрестная энтропия является функцией весов, смещений, пикселей обучающего изображения и его известного класса.
Если мы вычислим частные производные перекрёстной энтропии относительно всех весов и всех смещений, мы получим «градиент», вычисленный для заданного изображения, метки и текущего значения весов и смещений. Помните, что у нас могут быть миллионы весов и смещений, поэтому вычисление градиента может показаться очень трудоёмким. К счастью, TensorFlow делает это за нас. Математическое свойство градиента заключается в том, что он направлен «вверх». Поскольку мы хотим попасть туда, где перекрёстная энтропия низкая, мы идём в противоположном направлении. Мы обновляем веса и смещения на долю градиента. Затем мы повторяем то же самое снова и снова, используя следующие партии обучающих изображений и меток в обучающем цикле. Будем надеяться, что это сходится к точке, где перекрёстная энтропия минимальна, хотя ничто не гарантирует уникальность этого минимума.
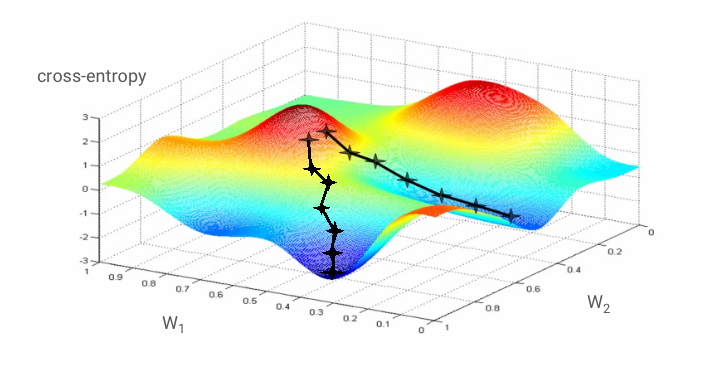
Мини-партии и импульс
Вы можете вычислить градиент только на основе одного образца изображения и сразу же обновить веса и смещения, но, используя пакет, например, из 128 изображений, вы получите градиент, который лучше отражает ограничения, накладываемые различными образцами изображений, и, следовательно, с большей вероятностью быстрее сойдется к решению. Размер мини-пакета — настраиваемый параметр.
Этот метод, иногда называемый «стохастическим градиентным спуском», имеет еще одно, более прагматичное преимущество: работа с пакетами также означает работу с большими матрицами, а их обычно проще оптимизировать на графических процессорах и тензорных процессорах.
Однако сходимость всё ещё может быть несколько хаотичной и даже остановиться, если вектор градиента состоит из одних нулей. Означает ли это, что мы нашли минимум? Не всегда. Компонента градиента может быть равна нулю как на минимуме, так и на максимуме. Если вектор градиента состоит из миллионов элементов, и все они равны нулю, вероятность того, что каждый ноль соответствует минимуму, а ни один — максимуму, довольно мала. В многомерном пространстве седловые точки встречаются довольно часто, и мы не хотим на них останавливаться.

Иллюстрация: седловая точка. Градиент равен 0, но не минимален во всех направлениях. (Источник изображения : Wikimedia: Nicoguaro — собственная работа, CC BY 3.0 )
Решение состоит в том, чтобы добавить некоторый импульс алгоритму оптимизации, чтобы он мог проходить седловые точки без остановки.
Глоссарий
Пакетное или мини-пакетное обучение: обучение всегда выполняется на пакетах обучающих данных и меток. Это способствует сходимости алгоритма. Измерение «пакет» обычно является первым измерением тензоров данных. Например, тензор формы [100, 192, 192, 3] содержит 100 изображений размером 192x192 пикселя с тремя значениями на пиксель (RGB).
кросс-энтропийные потери : особая функция потерь, часто используемая в классификаторах.
плотный слой : слой нейронов, в котором каждый нейрон связан со всеми нейронами предыдущего слоя.
Признаки : входные данные нейронной сети иногда называют «признаками». Искусство определения, какие части набора данных (или комбинации частей) следует передать нейронной сети для получения точных прогнозов, называется «инженерией признаков».
метки : другое название для «классов» или правильных ответов в задаче контролируемой классификации
Скорость обучения : доля градиента, с которой обновляются веса и смещения на каждой итерации цикла обучения.
Логиты : выходные данные слоя нейронов до применения функции активации называются «логитами». Термин происходит от «логистической функции», также известной как «сигмоидальная функция», которая ранее была самой популярной функцией активации. Термин «выходы нейронов до применения логистической функции» был сокращён до «логитами».
потеря : функция ошибки, сравнивающая выходные данные нейронной сети с правильными ответами
нейрон : вычисляет взвешенную сумму своих входных данных, добавляет смещение и передает результат через функцию активации.
прямое кодирование : класс 3 из 5 кодируется как вектор из 5 элементов, все элементы — нули, за исключением третьего, который равен 1.
relu : выпрямленная линейная единица. Популярная функция активации для нейронов.
сигмоида : еще одна функция активации, которая была популярна и все еще полезна в особых случаях.
softmax : специальная функция активации, которая воздействует на вектор, увеличивает разницу между наибольшим компонентом и всеми остальными, а также нормализует вектор, чтобы сумма его компонентов была равна 1, что позволяет интерпретировать его как вектор вероятностей. Используется на последнем этапе классификаторов.
Тензор : «Тензор» подобен матрице, но с произвольным числом измерений. Одномерный тензор — это вектор. Двумерный тензор — это матрица. Кроме того, существуют тензоры с 3, 4, 5 и более измерениями.
Вернемся к учебной тетради и на этот раз прочитаем код.
Давайте пройдемся по всем ячейкам в этой тетради.
Ячейка «Параметры»
Здесь определяются размер пакета, количество эпох обучения и расположение файлов данных. Файлы данных размещаются в контейнере Google Cloud Storage (GCS), поэтому их адрес начинается с gs://
Ячейка «Импорт»
Здесь импортированы все необходимые библиотеки Python, включая TensorFlow, а также matplotlib для визуализации.
Ячейка " утилиты визуализации [RUN ME] "
Эта ячейка содержит неинтересный код визуализации. По умолчанию она свёрнута, но вы можете открыть её и посмотреть код, когда появится время, дважды щёлкнув по ней.
Ячейка « tf.data.Dataset: анализ файлов и подготовка обучающих и проверочных наборов данных »
Эта ячейка использовала API tf.data.Dataset для загрузки набора данных MNIST из файлов данных. Нет необходимости подробно останавливаться на этой ячейке. Если вас интересует API tf.data.Dataset, вот руководство с его объяснением: Конвейеры данных на скорости TPU . На данный момент основные сведения таковы:
Изображения и метки (правильные ответы) из набора данных MNIST хранятся в записях фиксированной длины в четырёх файлах. Файлы можно загрузить с помощью специальной функции фиксированной записи:
imagedataset = tf.data.FixedLengthRecordDataset(image_filename, 28*28, header_bytes=16) Теперь у нас есть набор данных из байтов изображения. Их нужно декодировать в изображения. Мы определяем функцию для этого. Изображение не сжато, поэтому функция не должна ничего декодировать ( decode_raw по сути, ничего не делает). Затем изображение преобразуется в значения с плавающей точкой от 0 до 1. Мы могли бы преобразовать его в двумерное изображение, но на самом деле мы сохраняем его как плоский массив пикселей размером 28*28, поскольку именно этого ожидает наш исходный плотный слой.
def read_image(tf_bytestring):
image = tf.decode_raw(tf_bytestring, tf.uint8)
image = tf.cast(image, tf.float32)/256.0
image = tf.reshape(image, [28*28])
return image Мы применяем эту функцию к набору данных с помощью .map и получаем набор данных изображений:
imagedataset = imagedataset.map(read_image, num_parallel_calls=16) Мы выполняем такое же чтение и декодирование для этикеток и архивируем изображения и этикетки вместе в .zip :
dataset = tf.data.Dataset.zip((imagedataset, labelsdataset))Теперь у нас есть набор данных, состоящий из пар (изображение, метка). Именно этого ожидает наша модель. Мы пока не готовы использовать его в обучающей функции:
dataset = dataset.cache()
dataset = dataset.shuffle(5000, reshuffle_each_iteration=True)
dataset = dataset.repeat()
dataset = dataset.batch(batch_size)
dataset = dataset.prefetch(tf.data.experimental.AUTOTUNE)API tf.data.Dataset имеет все необходимые служебные функции для подготовки наборов данных:
.cache кэширует набор данных в оперативной памяти. Это небольшой набор данных, поэтому он будет работать. .shuffle перемешивает его с буфером из 5000 элементов. Важно, чтобы обучающие данные были хорошо перемешаны. .repeat зацикливает набор данных. Мы будем обучать его несколько раз (несколько эпох). .batch объединяет несколько изображений и меток в мини-пакет. Наконец, .prefetch может использовать центральный процессор для подготовки следующего пакета, пока текущий пакет обучается на графическом процессоре.
Набор данных для проверки подготавливается аналогичным образом. Теперь мы готовы определить модель и использовать этот набор данных для её обучения.
Ячейка «Модель Keras»
Все наши модели будут представлять собой прямые последовательности слоёв, поэтому для их создания мы можем использовать стиль tf.keras.Sequential . Изначально это один плотный слой. Он содержит 10 нейронов, поскольку мы классифицируем рукописные цифры по 10 классам. Он использует активацию «softmax», поскольку это последний слой классификатора.
Модель Keras также должна знать форму входных данных. Для её определения можно использовать tf.keras.layers.Input . Здесь входные векторы представляют собой плоские векторы значений пикселей длиной 28*28.
model = tf.keras.Sequential(
[
tf.keras.layers.Input(shape=(28*28,)),
tf.keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='sgd',
loss='categorical_crossentropy',
metrics=['accuracy'])
# print model layers
model.summary()
# utility callback that displays training curves
plot_training = PlotTraining(sample_rate=10, zoom=1) Настройка модели выполняется в Keras с помощью функции model.compile . Здесь мы используем базовый оптимизатор 'sgd' (стохастический градиентный спуск). Для модели классификации требуется функция потерь кросс-энтропии, которая в Keras называется 'categorical_crossentropy' . Наконец, мы просим модель вычислить метрику 'accuracy' , которая представляет собой процент правильно классифицированных изображений.
Keras предлагает замечательную утилиту model.summary() , которая выводит подробную информацию о созданной вами модели. Ваш любезный преподаватель добавил утилиту PlotTraining (определённую в ячейке «Утилиты визуализации»), которая будет отображать различные кривые обучения в процессе обучения.
Ячейка «Обучение и проверка модели»
Обучение происходит путём вызова model.fit и передачи обучающего и проверочного наборов данных. По умолчанию Keras запускает раунд проверки в конце каждой эпохи.
model.fit(training_dataset, steps_per_epoch=steps_per_epoch, epochs=EPOCHS,
validation_data=validation_dataset, validation_steps=1,
callbacks=[plot_training])В Keras можно добавлять пользовательские поведения во время обучения с помощью обратных вызовов. Именно так был реализован динамически обновляемый график обучения для этого семинара.
Ячейка «Визуализация прогнозов»
После обучения модели мы можем получать от нее прогнозы, вызывая model.predict() :
probabilities = model.predict(font_digits, steps=1)
predicted_labels = np.argmax(probabilities, axis=1)Здесь мы подготовили набор напечатанных цифр, отрисованных локальными шрифтами, для теста. Помните, что нейронная сеть возвращает вектор из 10 вероятностей из своего финального «мягкого максимума». Чтобы получить метку, нам нужно определить, какая вероятность наибольшая. Это делает np.argmax из библиотеки numpy.
Чтобы понять, зачем нужен параметр axis=1 , помните, что мы обработали партию из 128 изображений, и, следовательно, модель возвращает 128 векторов вероятностей. Форма выходного тензора — [128, 10]. Мы вычисляем argmax по 10 вероятностям, полученным для каждого изображения, поэтому axis=1 (первая ось равна 0).
Эта простая модель уже распознаёт 90% цифр. Неплохо, но теперь вы сможете значительно улучшить этот показатель.


Для повышения точности распознавания мы добавим больше слоев в нейронную сеть.
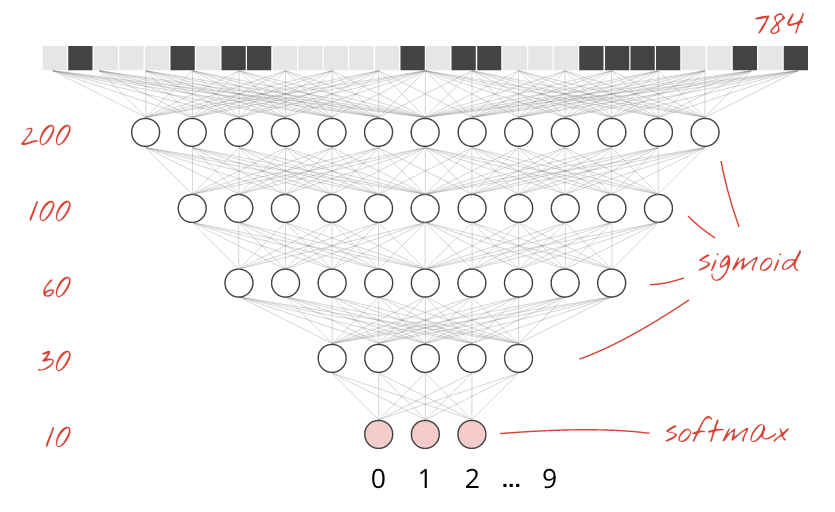
В качестве функции активации на последнем слое мы используем softmax, поскольку именно он лучше всего подходит для классификации. Однако на промежуточных слоях мы будем использовать наиболее классическую функцию активации: сигмоиду:

Например, ваша модель может выглядеть так (не забудьте запятые, tf.keras.Sequential принимает список слоев, разделенных запятыми):
model = tf.keras.Sequential(
[
tf.keras.layers.Input(shape=(28*28,)),
tf.keras.layers.Dense(200, activation='sigmoid'),
tf.keras.layers.Dense(60, activation='sigmoid'),
tf.keras.layers.Dense(10, activation='softmax')
])Посмотрите на «сводку» вашей модели. Теперь в ней как минимум в 10 раз больше параметров. Она должна быть в 10 раз лучше! Но по какой-то причине этого не происходит...

Похоже, потери тоже взлетели до небес. Что-то тут не так.
Вы только что познакомились с нейронными сетями, какими их создавали в 80-х и 90-х годах. Неудивительно, что они отказались от этой идеи, положив начало так называемой «зиме искусственного интеллекта». Действительно, по мере добавления слоёв нейронным сетям становится всё сложнее сходиться.
Оказывается, глубокие нейронные сети с большим количеством слоёв (сегодня 20, 50, а то и 100) могут работать очень хорошо, если применить пару математических трюков, чтобы добиться их сходимости. Открытие этих простых трюков стало одной из причин возрождения глубокого обучения в 2010-х годах.
активация RELU

Сигмоидальная функция активации на самом деле довольно проблематична в глубоких сетях. Она сжимает все значения от 0 до 1, и при многократном повторении этого процесса выходные сигналы нейронов и их градиенты могут полностью исчезнуть. Она упоминалась в исторических целях, но современные сети используют RELU (Rectified Linear Unit), который выглядит следующим образом:

С другой стороны, у RELU есть производная, равная 1, по крайней мере, в правой части. При активации RELU, даже если градиенты, исходящие от некоторых нейронов, могут быть нулевыми, всегда найдутся другие, дающие чёткий ненулевой градиент, и обучение может продолжаться в хорошем темпе.
Лучший оптимизатор
В пространствах очень высокой размерности, подобных этому (у нас порядка 10 тысяч весов и смещений), часто встречаются «седловые точки». Это точки, которые не являются локальными минимумами, но где градиент, тем не менее, равен нулю, и оптимизатор градиентного спуска застревает в них. TensorFlow располагает полным набором доступных оптимизаторов, включая те, которые работают с некоторой инерцией и безопасно проходят седловые точки.
Случайные инициализации
Искусство инициализации смещений весов перед обучением само по себе является областью исследований, и по этой теме опубликовано множество статей. Вы можете ознакомиться со всеми инициализаторами, доступными в Keras, здесь . К счастью, Keras по умолчанию делает всё правильно и использует инициализатор 'glorot_uniform' который является лучшим практически во всех случаях.
Вам ничего не нужно делать, так как Керас уже делает все правильно.
NaN ???
Формула перекрёстной энтропии содержит логарифм, а log(0) — это не число (NaN, или, если хотите, числовой сбой). Может ли входное значение перекрёстной энтропии быть 0? Входное значение поступает от softmax, который, по сути, является экспонентой, а экспонента никогда не равна нулю. Так что мы в безопасности!
Серьёзно? В прекрасном мире математики мы были бы в безопасности, но в компьютерном мире exp(-150), представленное в формате float32, равно НУЛЮ, и перекрёстная энтропия рушится.
К счастью, здесь вам тоже ничего не нужно делать, поскольку Keras об этом позаботится и вычислит softmax, а затем перекрестную энтропию особенно тщательно, чтобы обеспечить численную устойчивость и избежать ужасных NaN.
Успех?

Теперь ваша точность должна достигать 97%. Цель этого семинара — значительно превысить 99%, так что давайте продолжим.
Если вы застряли, вот решение на этом этапе:
Может быть, стоит попробовать тренироваться быстрее? Скорость обучения по умолчанию в оптимизаторе Adam — 0,001. Попробуем её увеличить.
Ускоренная езда, похоже, не особо помогает, да и что это за шум?

Обучающие кривые очень шумные, и посмотрите на обе контрольные: они скачут вверх и вниз. Это означает, что мы движемся слишком быстро. Мы могли бы вернуться к прежней скорости, но есть способ лучше.

Хорошее решение — начать быстро и постепенно уменьшать скорость обучения. В Keras это можно сделать с помощью функции обратного вызова tf.keras.callbacks.LearningRateScheduler .
Полезный код для копирования и вставки:
# lr decay function
def lr_decay(epoch):
return 0.01 * math.pow(0.6, epoch)
# lr schedule callback
lr_decay_callback = tf.keras.callbacks.LearningRateScheduler(lr_decay, verbose=True)
# important to see what you are doing
plot_learning_rate(lr_decay, EPOCHS)Не забудьте использовать созданный вами коллбэк lr_decay_callback . Добавьте его в список коллбэков в model.fit :
model.fit(..., callbacks=[plot_training, lr_decay_callback])Эффект от этого небольшого изменения впечатляет. Видно, что большая часть шума исчезла, а точность теста теперь стабильно превышает 98%.

Похоже, модель сейчас хорошо сходится. Давайте попробуем копнуть ещё глубже.
Помогает ли это?

Не совсем, точность всё ещё держится на 98%, а посмотрите на потери при валидации. Они растут! Алгоритм обучения работает только с тренировочными данными и соответствующим образом оптимизирует потери при обучении. Он никогда не видит данные валидации, поэтому неудивительно, что через некоторое время его работа перестаёт влиять на потери при валидации, которые перестают падать, а иногда даже возвращаются к норме.
Это не оказывает немедленного влияния на возможности распознавания реальных данных вашей модели, но не позволяет вам выполнять много итераций и, как правило, является признаком того, что обучение больше не оказывает положительного эффекта.

Такое расхождение обычно называют «переобучением», и если вы его заметили, попробуйте применить метод регуляризации, называемый «выпадением». Метод «выпадения» генерирует случайные нейроны на каждой итерации обучения.
Сработало?

Шум появляется вновь (неудивительно, учитывая, как работает выпадение). Потеря проверки, кажется, больше не ползуется, но в целом она выше, чем без отсева. И точность проверки немного снизилась. Это довольно разочаровывающий результат.
Похоже, что отсечение не было правильным решением, или, может быть, «переосмысление» - более сложная концепция, и некоторые из его причин не поддаются исправлению «выпадающих»?
Что такое «переживание»? Персиджение происходит, когда нейронная сеть учится «плохо», так как это работает для примеров обучения, но не так хорошо для реальных данных. Существуют методы регуляризации, такие как выпадение, которые могут заставить его учиться лучше, но переосмысление также имеет более глубокие корни.

Основное переживание происходит, когда нейронная сеть имеет слишком много степеней свободы для проблемы. Представьте себе, что у нас так много нейронов, что сеть может хранить все наши учебные изображения в них, а затем распознавать их по сопоставлению рисунков. Это потерпит неудачу в реальных данных полностью. Нейронная сеть должна быть несколько ограничена, чтобы она была вынуждена обобщать то, что она учится во время обучения.
Если у вас очень мало учебных данных, даже небольшая сеть может изучить их наизусть, и вы увидите «переосмысление». Вообще говоря, вам всегда нужно много данных для обучения нейронных сетей.
Наконец, если вы все сделали по книге, экспериментировали с различными размерами сети, чтобы убедиться, что ее степени свободы ограничены, применялись и обучались большим количеством данных, которые вы все равно можете застрять на уровне производительности, что, кажется, не может улучшить. Это означает, что ваша нейронная сеть в своей нынешней форме не способна извлечь больше информации из ваших данных, как в нашем случае здесь.
Помните, как мы используем наши изображения, сплющенные в один вектор? Это была действительно плохая идея. Рукописные цифры изготовлены из форм, и мы отбросили информацию о форме, когда мы сгладили пиксели. Тем не менее, существует тип нейронной сети, которая может воспользоваться информацией о форме: сверточные сети. Давайте попробуем их.
Если вы застряли, вот решение на данный момент:
В двух словах
Если все термины в следующем абзаце уже известны вам, вы можете перейти к следующему упражнению. Если вы только начинаете с сверточных нейронных сетей, пожалуйста, читайте дальше.
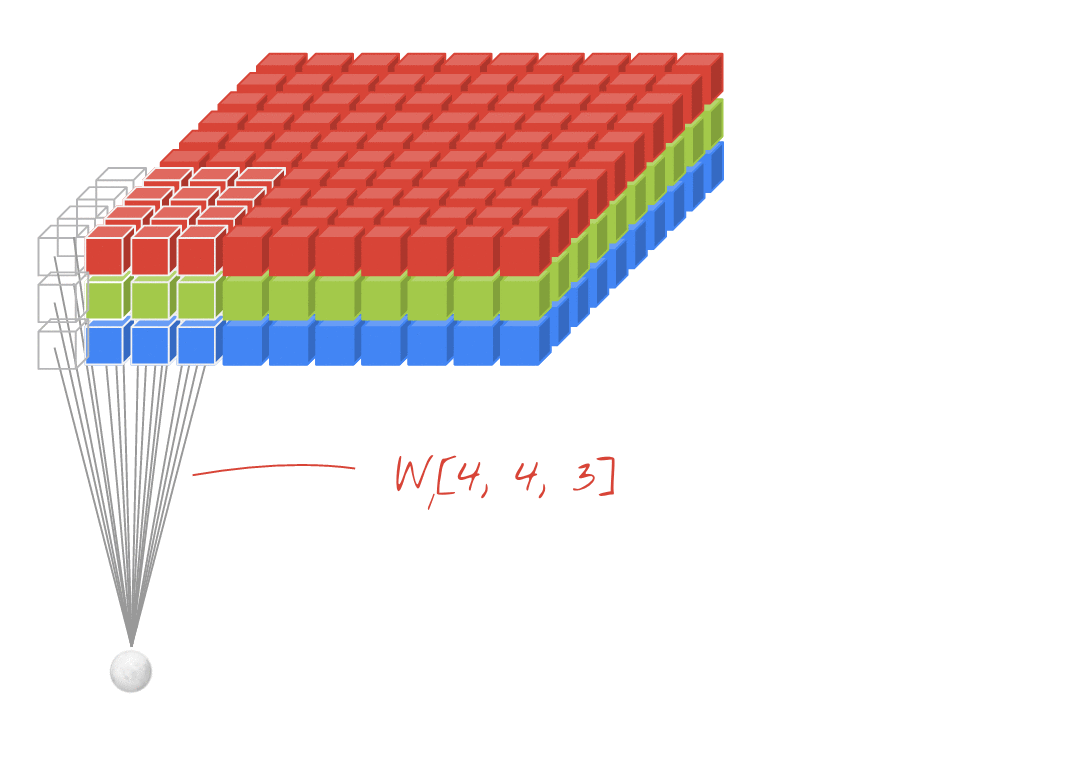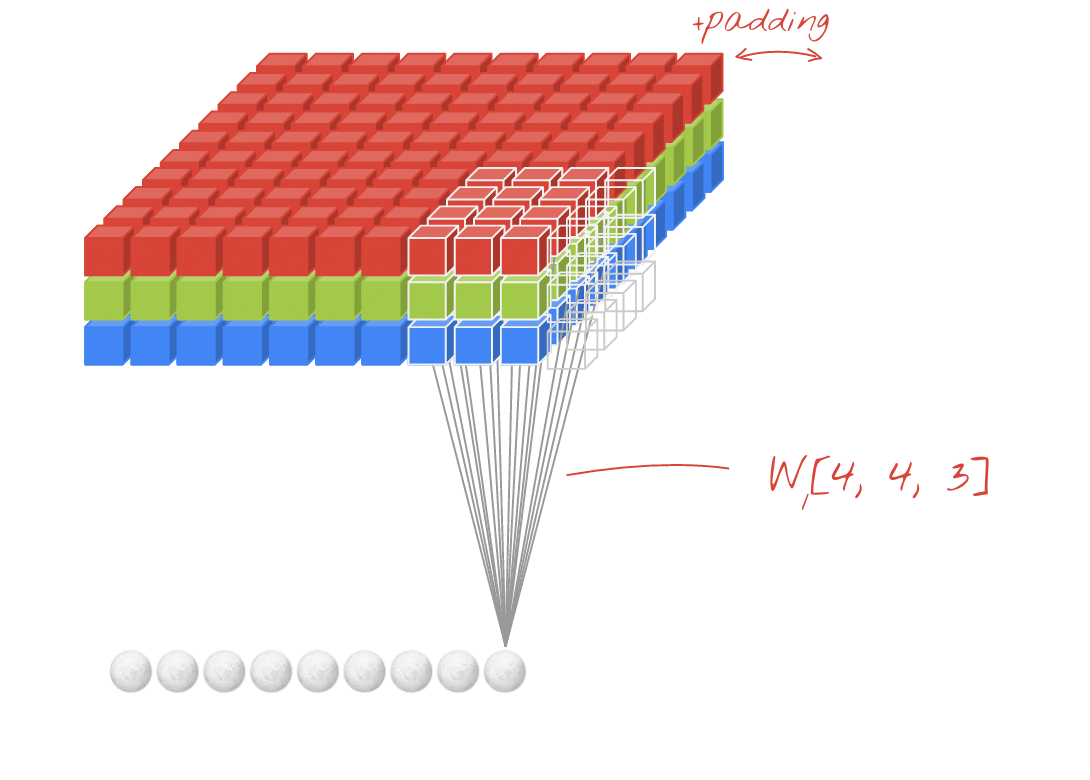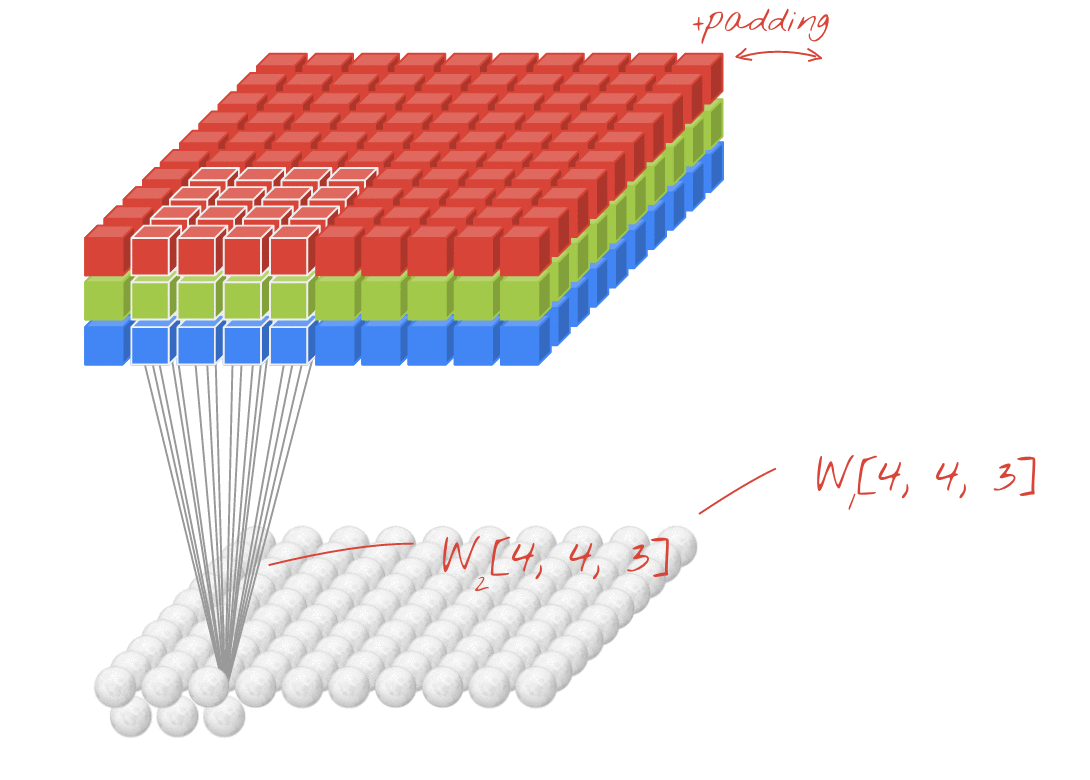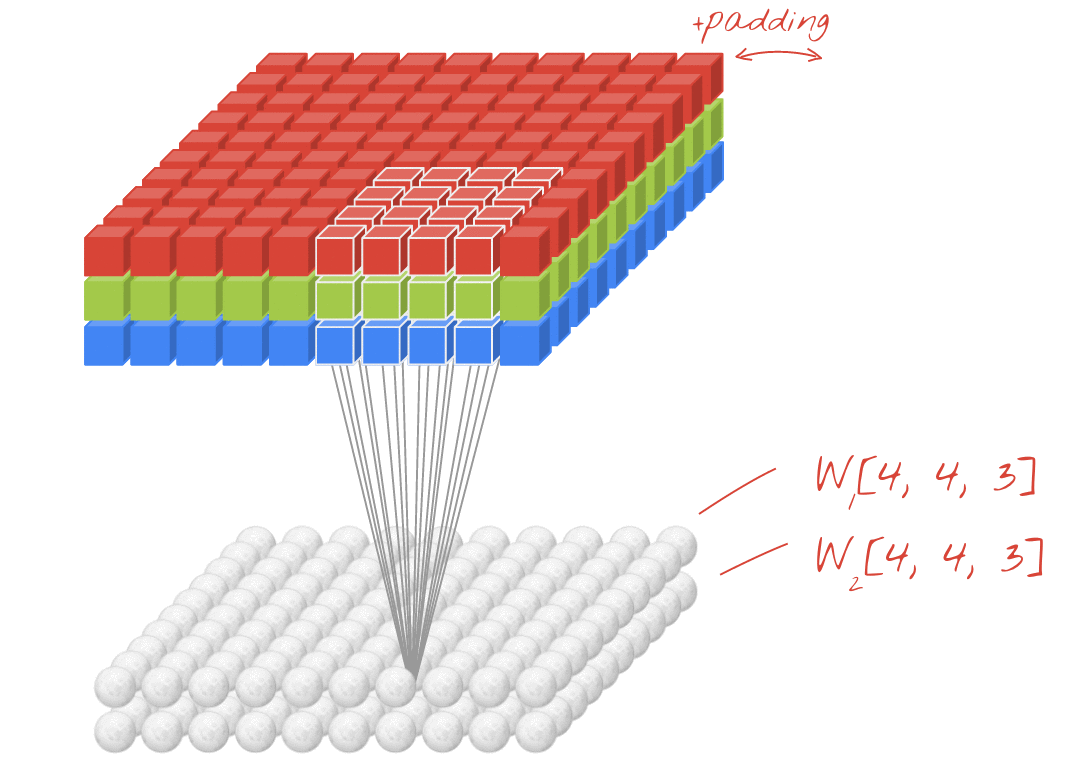
Иллюстрация: фильтрация изображения с двумя последовательными фильтрами, изготовленными из 4x4x3 = 48 обучаемых весов в каждом.
Так выглядит простая сверточная нейронная сеть в керасе:
model = tf.keras.Sequential([
tf.keras.layers.Reshape(input_shape=(28*28,), target_shape=(28, 28, 1)),
tf.keras.layers.Conv2D(kernel_size=3, filters=12, activation='relu'),
tf.keras.layers.Conv2D(kernel_size=6, filters=24, strides=2, activation='relu'),
tf.keras.layers.Conv2D(kernel_size=6, filters=32, strides=2, activation='relu'),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(10, activation='softmax')
])
В слое сверточной сети один «нейрон» выполняет взвешенную сумму пикселей прямо над ней, только через небольшую область изображения. Он добавляет смещение и питает сумму через функцию активации, так же как нейрон в обычном плотном слое. Эта операция затем повторяется по всему изображению, используя те же веса. Помните, что в плотных слоях у каждого нейрона были свои веса. Здесь один «патч» веса скользит по изображению в обоих направлениях («свертка»). Вывод имеет столько значений, сколько и пикселей в изображении (хотя на краях необходимо некоторая заполнение). Это операция фильтрации. На приведенной выше иллюстрации он использует фильтр 4x4x3 = 48 веса.
Тем не менее, 48 весов будут недостаточно. Чтобы добавить больше степеней свободы, мы повторяем ту же операцию с новым набором весов. Это создает новый набор выходов фильтра. Давайте назовем это «каналом» выходов по аналогии с каналами R, G, B на входном изображении.
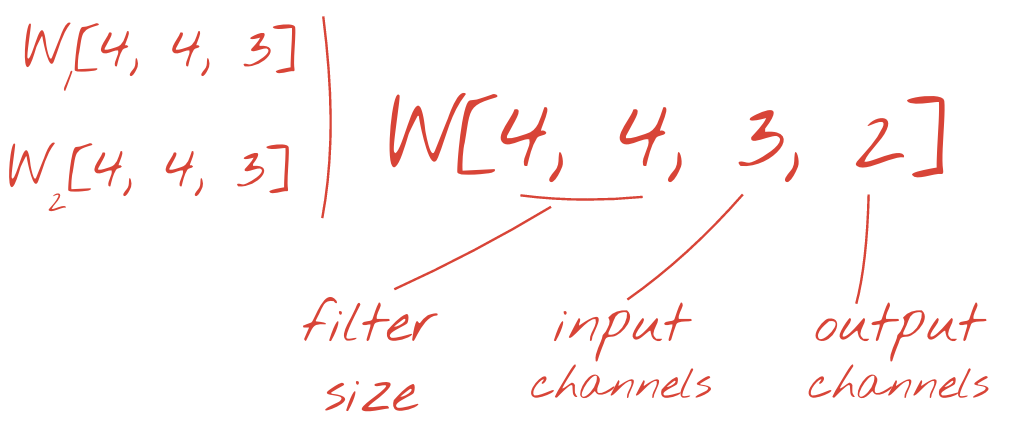
Два (или более) набора весов могут быть обобщены как один тензор, добавив новое измерение. Это дает нам общую форму тензора веса для сверточного слоя. Поскольку количество входных и выходных каналов является параметрами, мы можем начать складывание и цепочку сверточных слоев.

Иллюстрация: сверточная нейронная сеть превращает «кубики» данных в другие «кубики» данных.
Подчеркнутые свертки, максимальное объединение
Выполняя свертывание с шагом 2 или 3, мы также можем уменьшить полученный кубик данных в его горизонтальных измерениях. Есть два распространенных способа сделать это:
- Униженная свертка: скользящий фильтр, как указано выше, но с шагом> 1
- MAX Pooling: раздвижное окно, применяющее максимальную работу (обычно на пятнах 2x2, повторяется каждые 2 пикселя)

Иллюстрация: скольжение вычислительного окна на 3 пикселя приводит к меньшему количеству выходных значений. Униженные сознания или максимальное объединение (максимум в окне 2x2, скользящего по шагу 2), являются способом сокращения куба данных в горизонтальных измерениях.
Последний слой
После последнего сверточного слоя данные находятся в форме «куба». Есть два способа кормить его через последний плотный слой.
Первым является выравнивание куба данных в вектор, а затем подавать его к слою Softmax. Иногда вы можете даже добавить плотный слой перед слоем Softmax. Это, как правило, дорого с точки зрения количества весов. Плотный слой в конце сверточной сети может содержать более половины весов всей нейронной сети.
Вместо использования дорогостоящего плотного слоя мы также можем разделить входящие данные «куб» на столько же частей, сколько у нас есть классы, средние их значения и подавать их с помощью функции активации Softmax. Этот способ построения классификационной головки стоит 0 весов. В Keras есть слой для этого: tf.keras.layers.GlobalAveragePooling2D() .

Перейдите к следующему разделу, чтобы построить сверточную сеть для задачи.
Давайте создадим сверточную сеть для рукописного распознавания цифр. Мы будем использовать три сверточных слоя сверху, наш традиционный слой считывания Softmax внизу и подключим их с одним полностью подключенным слоем:

Обратите внимание, что второй и третий сверточный слои имеют шаг из двух, что объясняет, почему они снижают количество выходных значений с 28x28 до 14x14, а затем 7x7.
Давайте напишем код кераса.
Особое внимание необходимо перед первым сверточным слоем. Действительно, он ожидает трехмерного куба данных, но наш набор данных до сих пор был настроен для плотных слоев, и все пиксели изображений сгладиваются в вектор. Нам нужно изменить их обратно на изображения 28x28x1 (1 канал для изображений серого):
tf.keras.layers.Reshape(input_shape=(28*28,), target_shape=(28, 28, 1))Вы можете использовать эту линию вместо слоя tf.keras.layers.Input который у вас был до сих пор.
В керах синтаксис для активированного на резолюционном слое:

tf.keras.layers.Conv2D(kernel_size=3, filters=12, padding='same', activation='relu')Для укрепленной сверты, вы бы написали:
tf.keras.layers.Conv2D(kernel_size=6, filters=24, padding='same', activation='relu', strides=2)Чтобы сгладить куб данных в вектор, чтобы его можно было поглощать плотным слоем:
tf.keras.layers.Flatten()И для плотного слоя синтаксис не изменился:
tf.keras.layers.Dense(200, activation='relu')Ваша модель преодолела барьер точности 99%? Довольно близко ... но посмотрите на кривую потери проверки. Это звонит колоколом?

Также посмотрите на прогнозы. Впервые вы должны увидеть, что большинство из 10000 тестовых цифр теперь правильно распознаются. Осталось только около 4½ рядов ошибок (около 110 цифр из 10 000)

Если вы застряли, вот решение на данный момент:
Предыдущая тренировка демонстрирует четкие признаки переосмысления (и до сих пор не соответствует точке 99%). Стоит ли снова попробовать выбросить?
Как все прошло на этот раз?

Похоже, что отступление сработало на этот раз. Потеря проверки больше не ползуется, и окончательная точность должна быть намного выше 99%. Поздравляю!
В первый раз, когда мы попытались применить отступление, мы думали, что у нас есть проблема с переосмыслением, когда на самом деле проблема была в архитектуре нейронной сети. Мы не могли бы пойти дальше без сверточных слоев, и с этим ничего не может сделать.
На этот раз это похоже на то, что переживание было причиной проблемы, и выброс фактически помог. Помните, что есть много вещей, которые могут вызвать разрыв между кривыми обучения и потери проверки, причем потери валидации ползутся. Переполнение (слишком много степеней свободы, которые плохо используются сетью) - это только один из них. Если ваш набор данных слишком мал или архитектура вашей нейронной сети не является адекватной, вы можете увидеть аналогичное поведение на кривых потери, но отсевание не поможет.
Наконец, давайте попробуем добавить нормализацию партии.
Это теория, на практике, просто помните пару правил:
Давайте пока играем у книги и добавим партированный слой нормы на каждом уровне нейронной сети, но в последний. Не добавляйте его к последнему слою «Softmax». Там не было бы полезно.
# Modify each layer: remove the activation from the layer itself.
# Set use_bias=False since batch norm will play the role of biases.
tf.keras.layers.Conv2D(..., use_bias=False),
# Batch norm goes between the layer and its activation.
# The scale factor can be turned off for Relu activation.
tf.keras.layers.BatchNormalization(scale=False, center=True),
# Finish with the activation.
tf.keras.layers.Activation('relu'),Как сейчас точность?

При небольшой настройке (batch_size = 64, параметр распада скорости обучения 0,666, скорость отсева на плотном уровне 0,3) и немного удачи, вы можете добраться до 99,5%. Корректировки уровня обучения и отсева были выполнены после «лучших практик» для использования пакетной нормы:
- Пакетная норма помогает нейронным сетям сходиться и обычно позволяет тренироваться быстрее.
- Пакетная норма - регулятор. Обычно вы можете уменьшить количество выбывшего, которое вы используете, или даже не использовать отсевание вообще.
The Solution Notebook имеет 99,5% тренировочный запуск:

Вы найдете готовую к облаку версии кода в папке Mlengine на GitHub , а также инструкции по его запуску на платформе Google Cloud AI . Прежде чем вы сможете запустить эту часть, вам придется создать учетную запись Google Cloud и включить выставление счетов. Ресурсы, необходимые для завершения лаборатории, должны составлять менее пары долларов (при условии 1 часа обучения на одном графическом процессоре). Чтобы подготовить свою учетную запись:
- Создайте проект Google Cloud Platform ( http://cloud.google.com/console ).
- Включить биллинг.
- Установите инструменты командной строки GCP ( GCP SDK здесь ).
- Создайте ведро Google Cloud Storage (PLOT в регионе
us-central1). Он будет использоваться для постановки учебного кода и хранения вашей обученной модели. - Включите необходимые API и запросите необходимые квоты (запустите команду обучения один раз, и вы должны получить сообщения об ошибках, сообщающие вам, что для включения).
Вы построили свою первую нейронную сеть и обучили ее до конца 99% точности. Методы, изученные на этом пути, не являются специфическими для набора данных MNIST, на самом деле они широко используются при работе с нейронными сетями. В качестве прощального подарка, вот карта «Примечания Клиффа» для лаборатории, в мультипликационной версии. Вы можете использовать его, чтобы вспомнить, что вы узнали:

Следующие шаги
- После полностью связанных и сверточных сетей вы должны взглянуть на повторяющиеся нейронные сети .
- Чтобы запустить обучение или вывод в облаке на распределенной инфраструктуре, Google Cloud предоставляет платформу AI .
- Наконец, мы любим обратную связь. Пожалуйста, скажите нам, если вы видите что -то не так, как в этой лаборатории или вы думаете, что это должно быть улучшено. Мы обрабатываем обратную связь через проблемы GitHub [ ссылка на обратную связь ].

Автор: Мартин Горнер Twitter: @martin_gorner |
|
Все мультипликационные изображения в этой лаборатории Copyright: Alexpokusay / 123RF Стоковые фотографии




