
In questo codelab imparerai a creare e addestrare una rete neurale che riconosce le cifre scritte a mano. Lungo il percorso, mentre migliori la tua rete neurale per raggiungere un'accuratezza del 99%, scoprirai anche gli strumenti del mestiere che i professionisti del deep learning utilizzano per addestrare i loro modelli in modo efficiente.
Questo codelab utilizza il set di dati MNIST, una raccolta di 60.000 cifre etichettate che ha tenuto occupate generazioni di dottorandi per quasi due decenni. Risolvi il problema con meno di 100 righe di codice Python / TensorFlow.
Obiettivi didattici
- Che cos'è una rete neurale e come addestrarla
- Come creare una rete neurale di base a un livello utilizzando tf.keras
- Come aggiungere altri livelli
- Come impostare una pianificazione del tasso di apprendimento
- Come creare reti neurali convoluzionali
- Come utilizzare le tecniche di regolarizzazione: abbandono, normalizzazione batch
- Che cos'è l'overfitting
Che cosa ti serve
Solo un browser. Questo workshop può essere eseguito interamente con Google Colaboratory.
Feedback
Segnalaci eventuali problemi riscontrati in questo lab o se ritieni che debba essere migliorato. Gestiamo i feedback tramite i problemi di GitHub [link al feedback].
Questo lab utilizza Google Colaboratory e non richiede alcuna configurazione da parte tua. Puoi eseguirlo da un Chromebook. Apri il file qui sotto ed esegui le celle per acquisire familiarità con i notebook Colab.
Ulteriori istruzioni di seguito:
Seleziona un backend GPU
Nel menu Colab, seleziona Runtime > Cambia tipo di runtime e poi seleziona GPU. La connessione al runtime avverrà automaticamente alla prima esecuzione oppure puoi utilizzare il pulsante "Connetti" nell'angolo in alto a destra.
Esecuzione del notebook
Esegui le celle una alla volta facendo clic su una cella e utilizzando Maiusc+INVIO. Puoi anche eseguire l'intero notebook con Runtime > Esegui tutto.
Sommario
Tutti i notebook hanno un indice. Puoi aprirlo utilizzando la freccia nera a sinistra.
Celle nascoste
Alcune celle mostreranno solo il titolo. Questa è una funzionalità specifica dei notebook di Colab. Puoi fare doppio clic per visualizzare il codice all'interno, ma di solito non è molto interessante. In genere funzioni di supporto o visualizzazione. Devi comunque eseguire queste celle per definire le funzioni al loro interno.
Per prima cosa, osserveremo l'addestramento di una rete neurale. Apri il notebook di seguito ed esegui tutte le celle. Non prestare ancora attenzione al codice, inizieremo a spiegarlo più avanti.
Mentre esegui il blocco note, concentrati sulle visualizzazioni. Vedi di seguito le spiegazioni.
Dati di addestramento
Abbiamo un set di dati di cifre scritte a mano che sono state etichettate in modo da sapere cosa rappresenta ogni immagine, ovvero un numero compreso tra 0 e 9. Nel notebook vedrai un estratto:
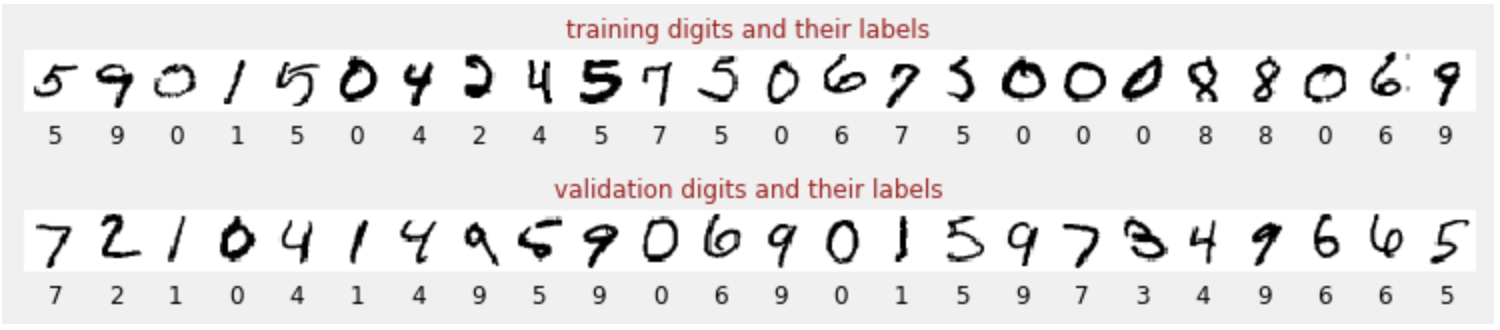
La rete neurale che creeremo classifica le cifre scritte a mano nelle 10 classi (0, …, 9). Lo fa in base a parametri interni che devono avere un valore corretto affinché la classificazione funzioni correttamente. Questo "valore corretto" viene appreso attraverso un processo di addestramento che richiede un "set di dati etichettato" con immagini e le risposte corrette associate.
Come facciamo a sapere se la rete neurale addestrata funziona bene o meno? Utilizzare il set di dati di addestramento per testare la rete sarebbe un imbroglio. Ha già visto questo set di dati più volte durante l'addestramento ed è sicuramente molto performante. Abbiamo bisogno di un altro set di dati etichettato, mai visto durante l'addestramento, per valutare le prestazioni "reali" della rete. Si chiama "set di dati di convalida".
Addestramento
Man mano che l'addestramento procede, un batch di dati di addestramento alla volta, i parametri interni del modello vengono aggiornati e il modello diventa sempre più bravo a riconoscere le cifre scritte a mano. Puoi visualizzarlo nel grafico di addestramento:
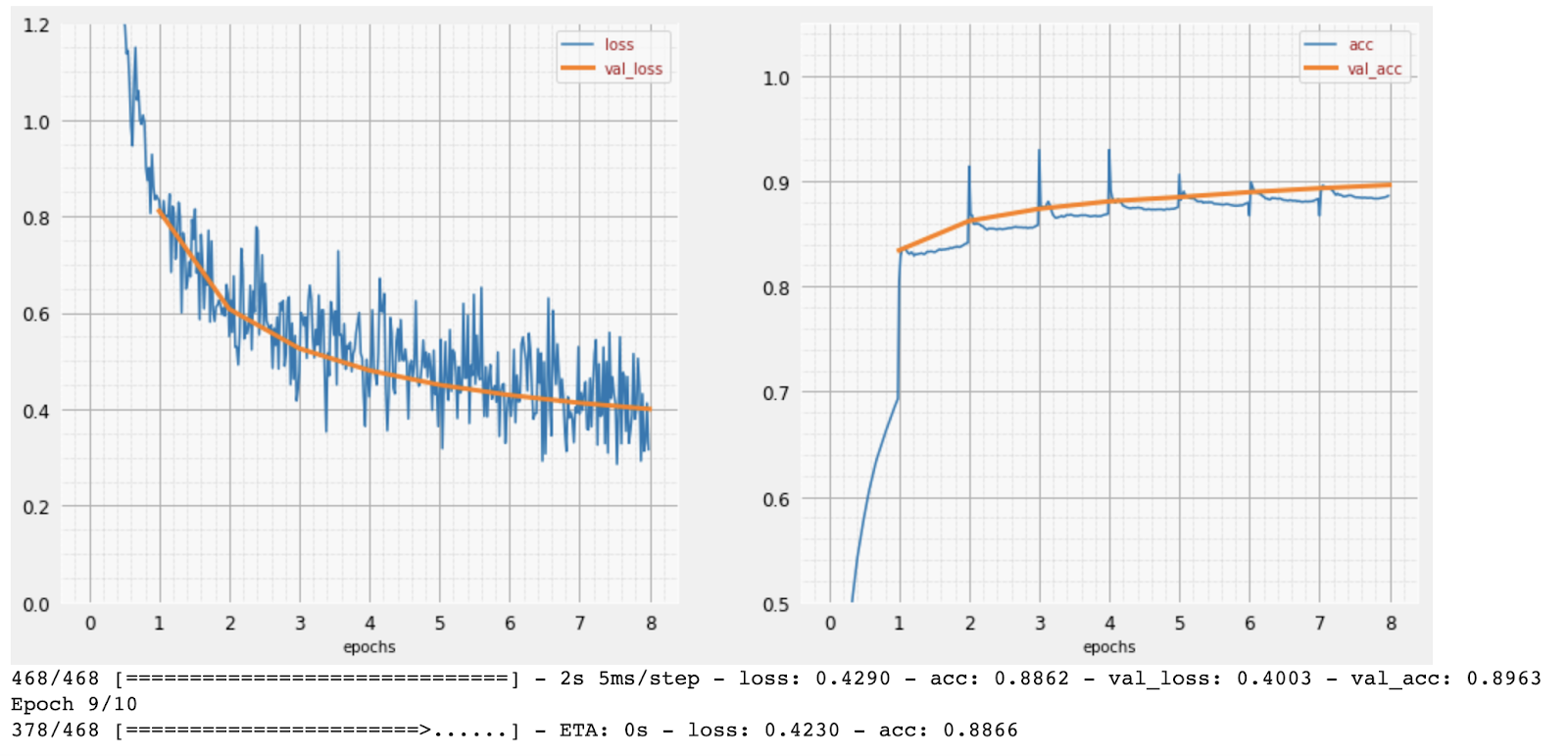
A destra, l'accuratezza è semplicemente la percentuale di cifre riconosciute correttamente. Aumenta man mano che l'addestramento procede, il che è positivo.
A sinistra, possiamo vedere la "perdita". Per guidare l'addestramento, definiremo una funzione "loss", che rappresenta il grado di difficoltà con cui il sistema riconosce le cifre, e cercheremo di ridurla al minimo. Come puoi vedere, la perdita diminuisce sia sui dati di addestramento che su quelli di convalida man mano che l'addestramento procede: questo è un buon segno. Significa che la rete neurale sta imparando.
L'asse X rappresenta il numero di "epoche" o iterazioni nell'intero set di dati.
Previsioni
Una volta addestrato, il modello può essere utilizzato per riconoscere i numeri scritti a mano. La visualizzazione successiva mostra il rendimento su alcune cifre eseguite con caratteri locali (prima riga) e poi sulle 10.000 cifre del set di dati di convalida. La classe prevista viene visualizzata sotto ogni cifra, in rosso se è errata.

Come puoi vedere, questo modello iniziale non è molto efficace, ma riconosce comunque correttamente alcune cifre. La sua precisione di convalida finale è di circa il 90%, il che non è male per il modello semplificato con cui stiamo iniziando,ma significa comunque che mancano 1000 cifre di convalida su 10.000. Sono molte di più di quelle che possono essere visualizzate, motivo per cui sembra che tutte le risposte siano errate (rosse).
Tensori
I dati vengono archiviati in matrici. Un'immagine in scala di grigi di 28 x 28 pixel si adatta a una matrice bidimensionale di 28 x 28. Per un'immagine a colori, però, abbiamo bisogno di più dimensioni. Esistono tre valori di colore per pixel (rosso, verde, blu), quindi sarà necessaria una tabella tridimensionale con dimensioni [28, 28, 3]. Per memorizzare un batch di 128 immagini a colori, è necessaria una tabella quadridimensionale con dimensioni [128, 28, 28, 3].
Queste tabelle multidimensionali sono chiamate "tensori" e l'elenco delle loro dimensioni è la loro "forma".
In sintesi
Se conosci già tutti i termini in grassetto nel paragrafo successivo, puoi passare all'esercizio successivo. Se hai appena iniziato a utilizzare il deep learning, benvenuto e continua a leggere.

Per i modelli creati come sequenza di livelli, Keras offre l'API Sequential. Ad esempio, un classificatore di immagini che utilizza tre strati densi può essere scritto in Keras come:
model = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=[28, 28, 1]),
tf.keras.layers.Dense(200, activation="relu"),
tf.keras.layers.Dense(60, activation="relu"),
tf.keras.layers.Dense(10, activation='softmax') # classifying into 10 classes
])
# this configures the training of the model. Keras calls it "compiling" the model.
model.compile(
optimizer='adam',
loss= 'categorical_crossentropy',
metrics=['accuracy']) # % of correct answers
# train the model
model.fit(dataset, ... )
Un singolo livello denso
Le cifre scritte a mano nel set di dati MNIST sono immagini in scala di grigi di 28 x 28 pixel. L'approccio più semplice per classificarli è utilizzare i 28 x 28=784 pixel come input per una rete neurale a un livello.
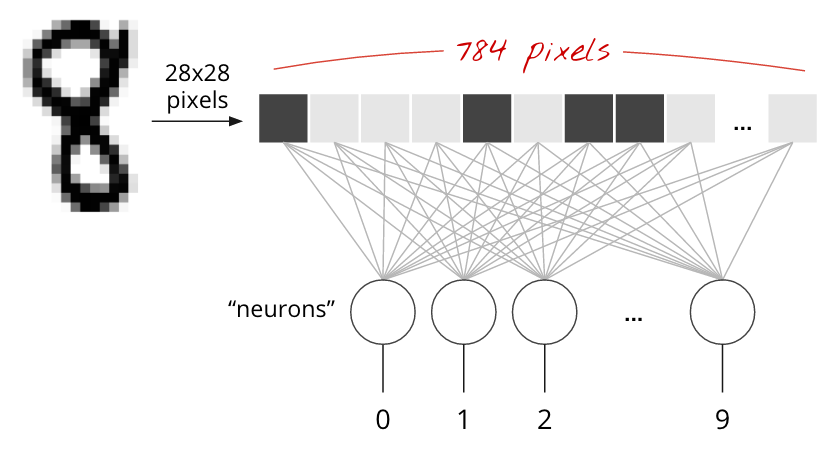
Ogni "neurone" in una rete neurale esegue una somma ponderata di tutti i suoi input, aggiunge una costante chiamata "bias" e poi inserisce il risultato in una "funzione di attivazione" non lineare. Le "ponderazioni" e i "bias" sono parametri che verranno determinati tramite l'addestramento. All'inizio vengono inizializzati con valori casuali.
L'immagine sopra rappresenta una rete neurale a un livello con 10 neuroni di output, poiché vogliamo classificare le cifre in 10 classi (da 0 a 9).
Con una moltiplicazione di matrici
Ecco come uno strato di rete neurale, che elabora una raccolta di immagini, può essere rappresentato da una moltiplicazione di matrici:
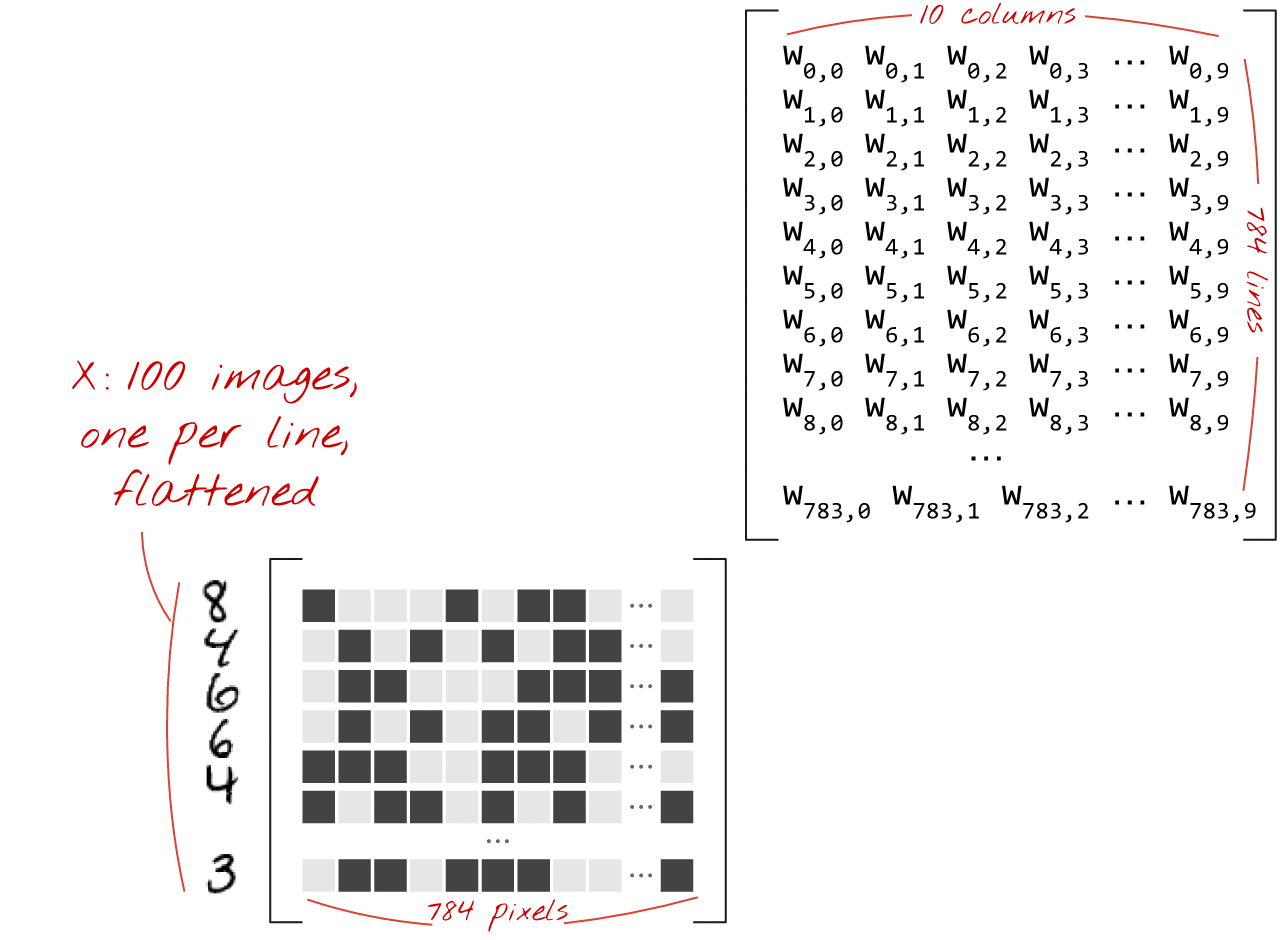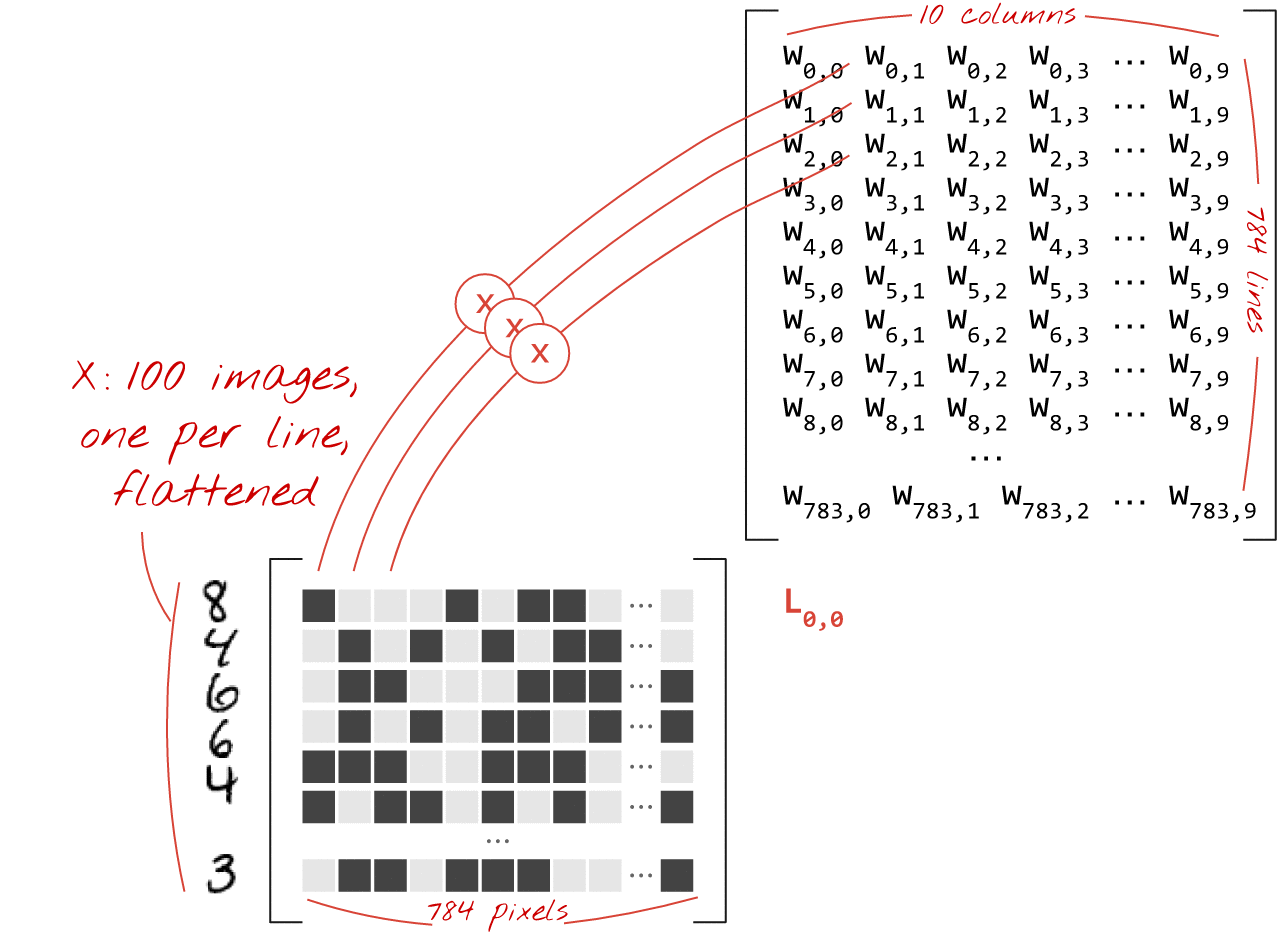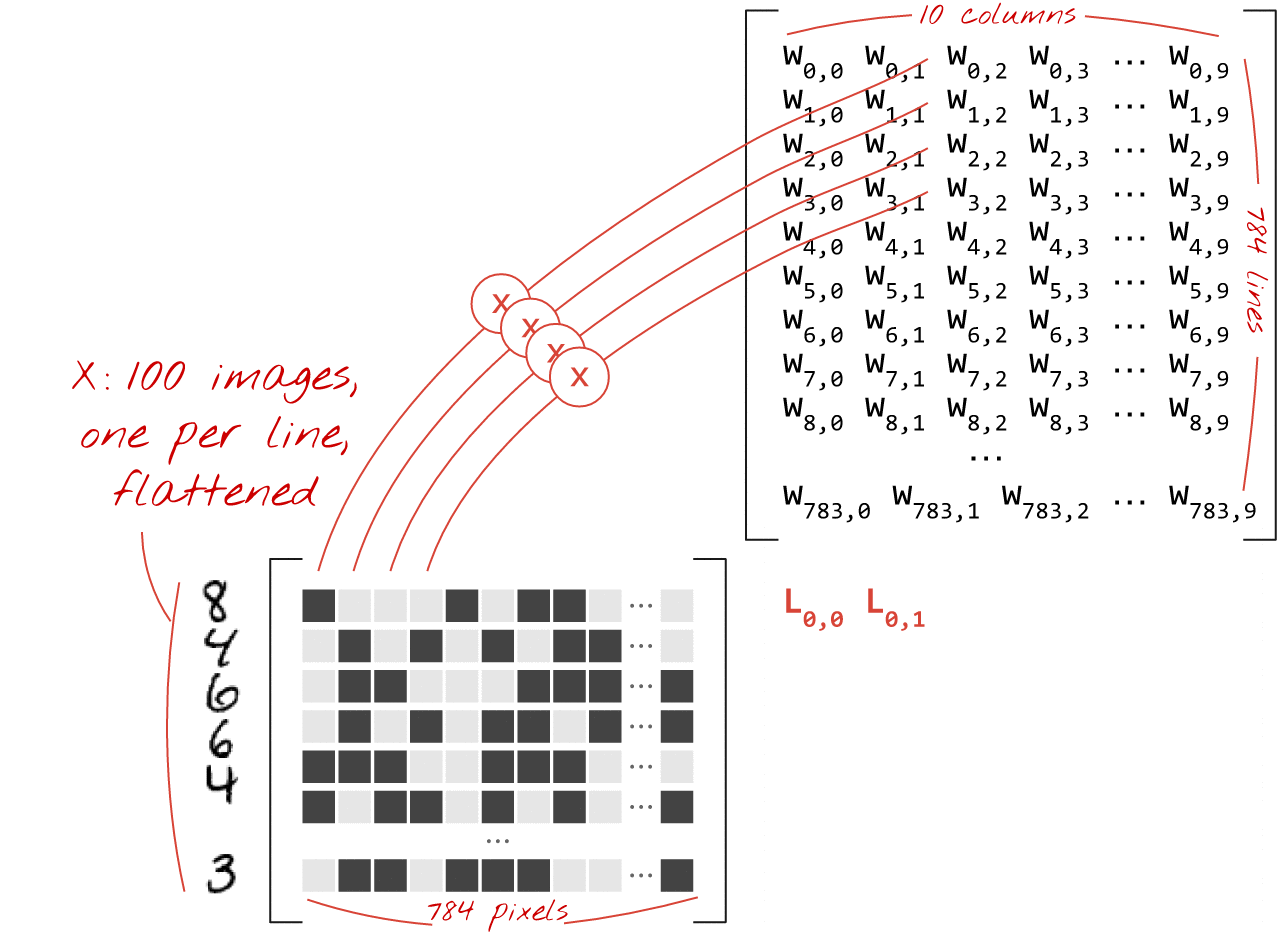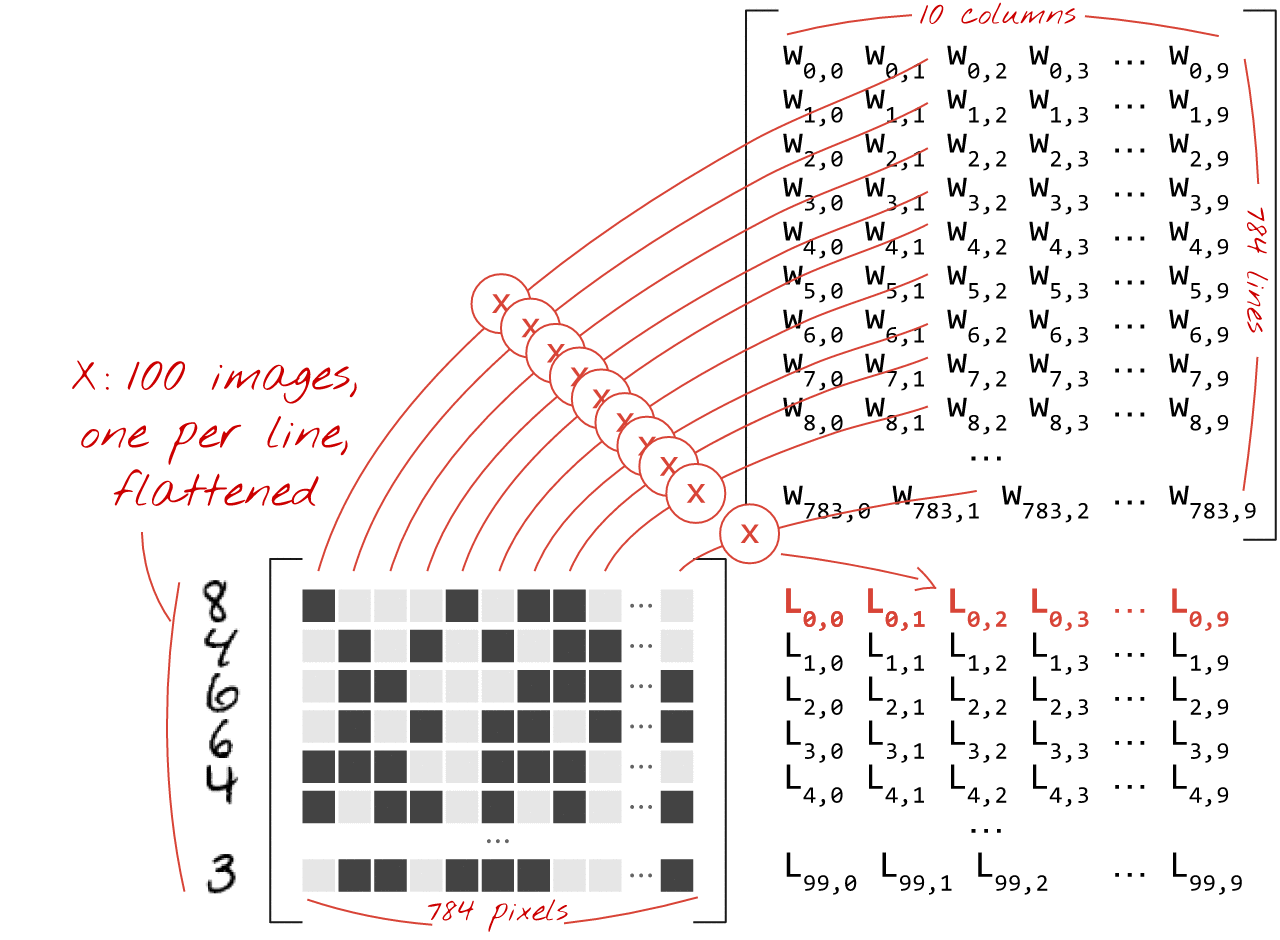
Utilizzando la prima colonna dei pesi nella matrice dei pesi W, calcoliamo la somma ponderata di tutti i pixel della prima immagine. Questa somma corrisponde al primo neurone. Utilizzando la seconda colonna di pesi, eseguiamo la stessa operazione per il secondo neurone e così via fino al decimo neurone. Possiamo quindi ripetere l'operazione per le restanti 99 immagini. Se chiamiamo X la matrice contenente le nostre 100 immagini, tutte le somme ponderate per i nostri 10 neuroni, calcolate su 100 immagini, sono semplicemente X.W, una moltiplicazione di matrici.
Ogni neurone deve ora aggiungere il proprio bias (una costante). Poiché abbiamo 10 neuroni, abbiamo 10 costanti di bias. Chiameremo questo vettore di 10 valori b. Deve essere aggiunto a ogni riga della matrice calcolata in precedenza. Utilizzando un po' di magia chiamata "trasmissione", scriveremo questa formula con un semplice segno più.
Infine, applichiamo una funzione di attivazione, ad esempio "softmax" (spiegata di seguito) e otteniamo la formula che descrive una rete neurale a un livello, applicata a 100 immagini:
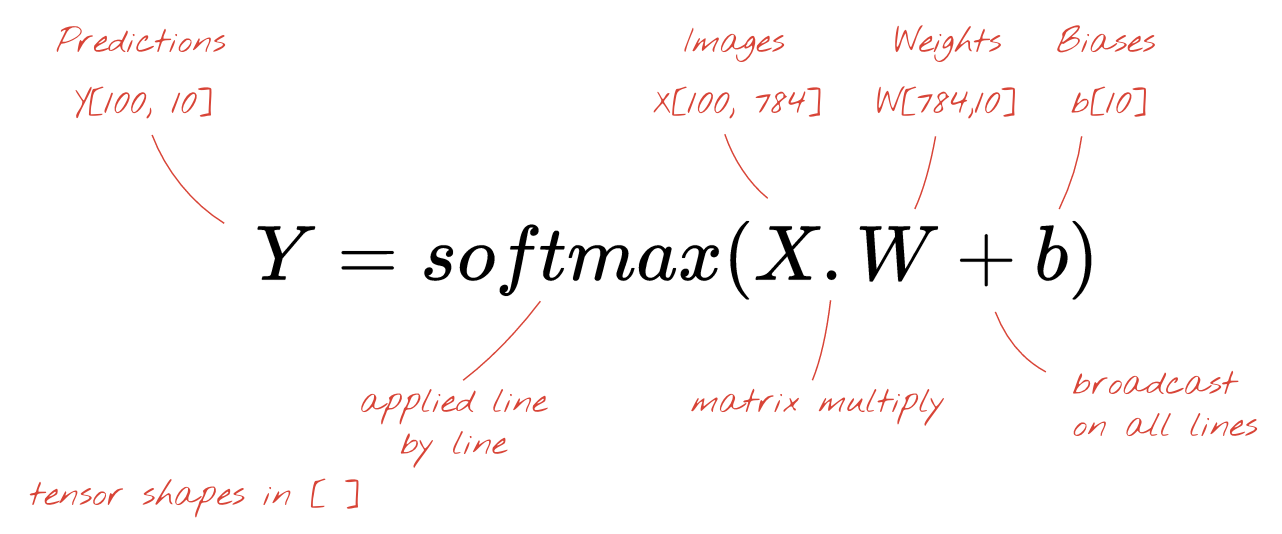
In Keras
Con librerie di reti neurali di alto livello come Keras, non sarà necessario implementare questa formula. Tuttavia, è importante capire che un livello di rete neurale è solo un insieme di moltiplicazioni e addizioni. In Keras, un livello denso verrebbe scritto come segue:
tf.keras.layers.Dense(10, activation='softmax')Approfondimento
È banale concatenare i livelli della rete neurale. Il primo livello calcola le somme ponderate dei pixel. Gli strati successivi calcolano le somme ponderate degli output degli strati precedenti.
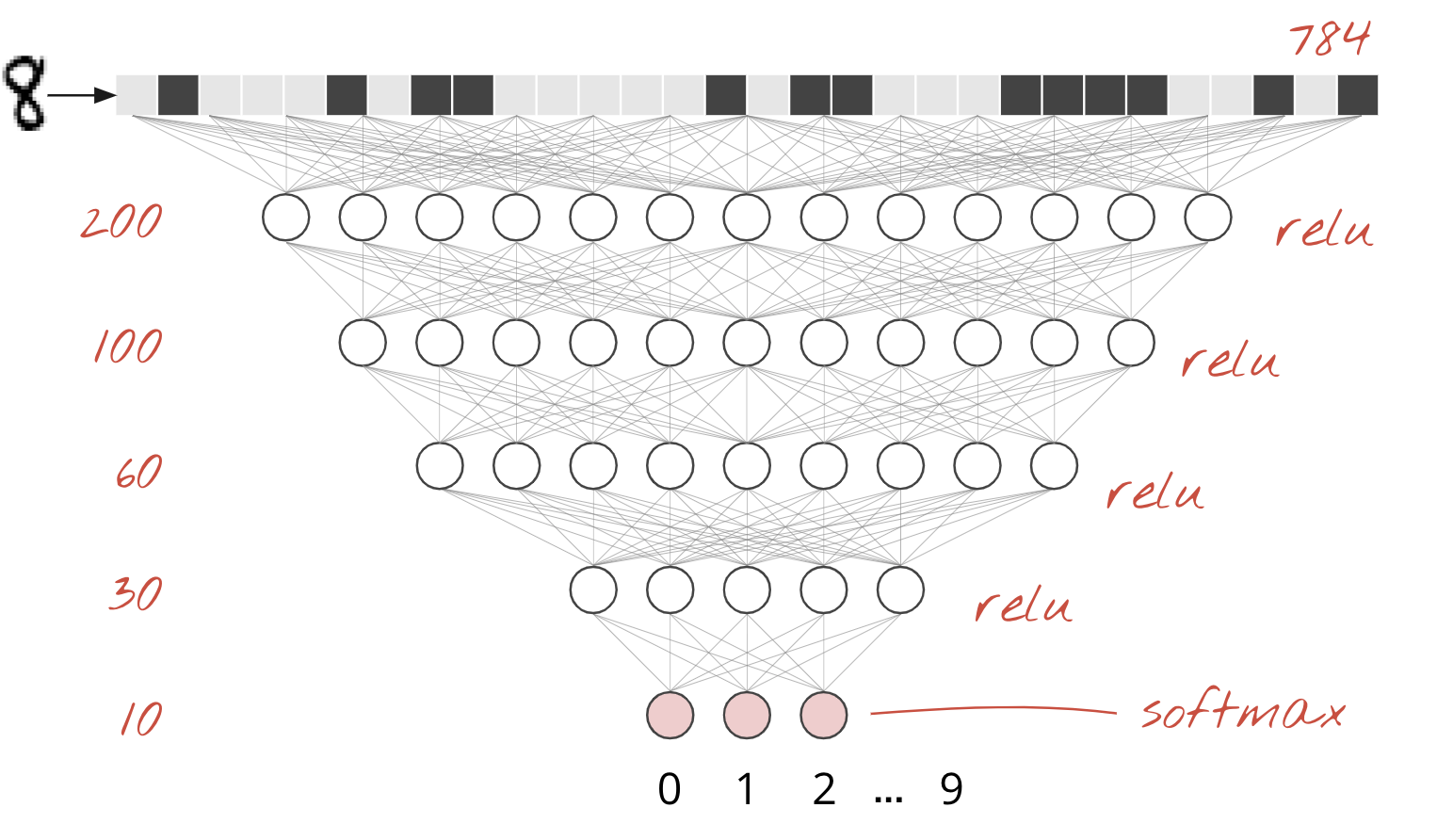
L'unica differenza, a parte il numero di neuroni, sarà la scelta della funzione di attivazione.
Funzioni di attivazione: relu, softmax e sigmoide
In genere, utilizzeresti la funzione di attivazione "relu" per tutti i livelli tranne l'ultimo. L'ultimo livello di un classificatore utilizzerebbe l'attivazione "softmax".
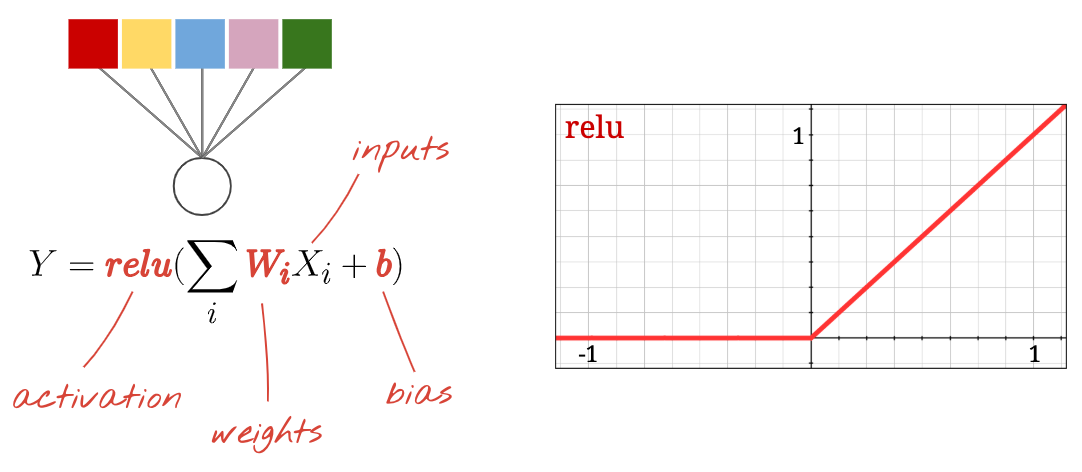
Anche in questo caso, un "neurone" calcola una somma ponderata di tutti i suoi input, aggiunge un valore chiamato "bias" e inserisce il risultato nella funzione di attivazione.
La funzione di attivazione più popolare è chiamata "RELU", acronimo di Rectified Linear Unit. È una funzione molto semplice, come puoi vedere nel grafico sopra.
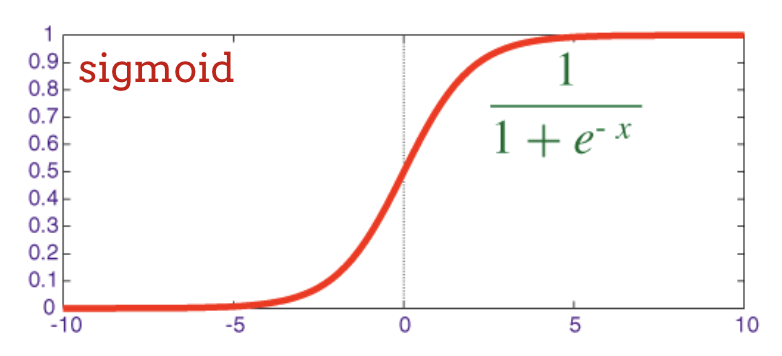
La funzione di attivazione tradizionale nelle reti neurali era la "sigmoide", ma è stato dimostrato che la "relu" ha proprietà di convergenza migliori quasi ovunque ed è ora preferita.
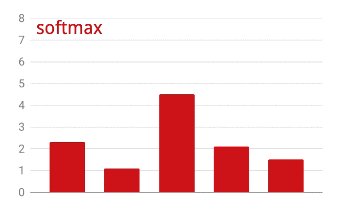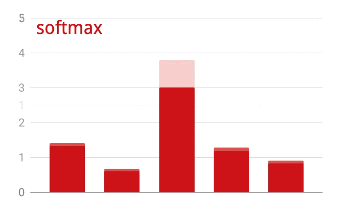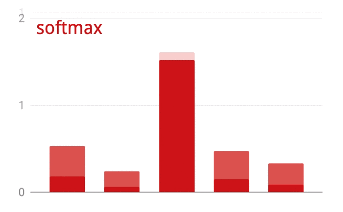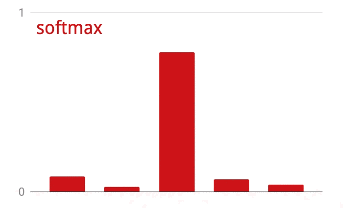
Attivazione Softmax per la classificazione
L'ultimo livello della nostra rete neurale ha 10 neuroni perché vogliamo classificare le cifre scritte a mano in 10 classi (0-9). Deve restituire 10 numeri compresi tra 0 e 1 che rappresentano la probabilità che questa cifra sia 0, 1, 2 e così via. A questo scopo, nell'ultimo livello utilizzeremo una funzione di attivazione chiamata "softmax".
L'applicazione di softmax a un vettore viene eseguita prendendo l'esponenziale di ogni elemento e poi normalizzando il vettore, in genere dividendolo per la sua norma "L1" (ovvero la somma dei valori assoluti) in modo che i valori normalizzati sommati diano 1 e possano essere interpretati come probabilità.
L'output dell'ultimo livello, prima dell'attivazione, viene talvolta chiamato "logits". Se questo vettore è L = [L0, L1, L2, L3, L4, L5, L6, L7, L8, L9], allora:

Perdita di entropia incrociata
Ora che la nostra rete neurale produce previsioni dalle immagini di input, dobbiamo misurare la loro qualità, ovvero la distanza tra ciò che ci dice la rete e le risposte corrette, spesso chiamate "etichette". Ricorda che abbiamo le etichette corrette per tutte le immagini del set di dati.
Qualsiasi distanza andrebbe bene, ma per i problemi di classificazione la cosiddetta "distanza di entropia incrociata" è la più efficace. La chiameremo funzione di errore o "perdita":
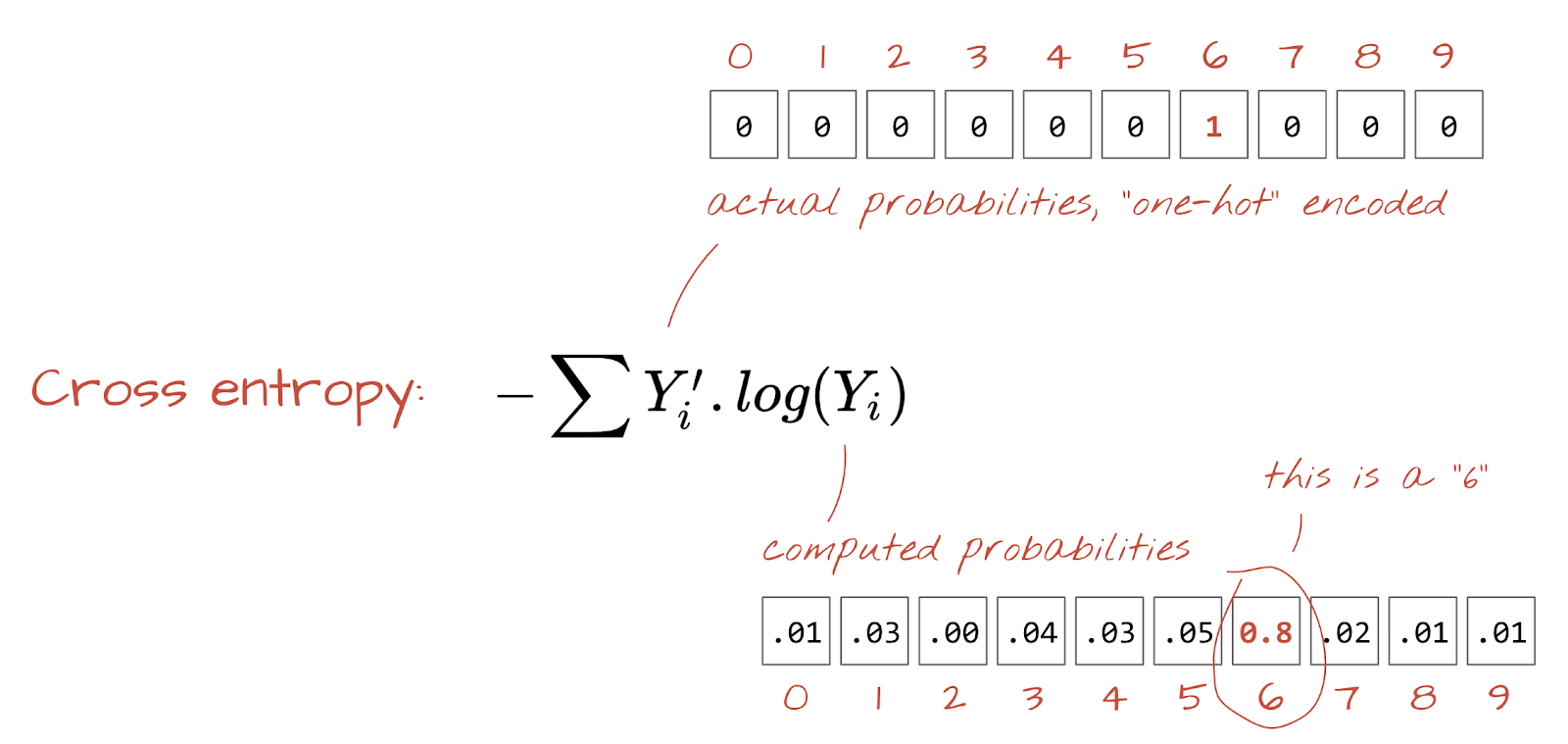
Discesa del gradiente
"Addestrare" la rete neurale significa utilizzare immagini e etichette di addestramento per regolare pesi e bias in modo da ridurre al minimo la funzione di perdita di entropia incrociata. Ecco come funziona.
L'entropia incrociata è una funzione di pesi, bias, pixel dell'immagine di addestramento e della sua classe nota.
Se calcoliamo le derivate parziali dell'entropia incrociata rispetto a tutti i pesi e a tutti i bias, otteniamo un "gradiente", calcolato per una determinata immagine, etichetta e valore attuale di pesi e bias. Ricorda che possiamo avere milioni di pesi e bias, quindi il calcolo del gradiente sembra un'attività molto impegnativa. Fortunatamente, TensorFlow lo fa per noi. La proprietà matematica di un gradiente è che punta "verso l'alto". Poiché vogliamo andare dove l'entropia incrociata è bassa, andiamo nella direzione opposta. Aggiorniamo pesi e bias di una frazione del gradiente. Quindi, ripetiamo la stessa operazione più e più volte utilizzando i batch successivi di immagini e etichette di addestramento, in un ciclo di addestramento. Si spera che questo converga in un punto in cui l'entropia incrociata sia minima, anche se nulla garantisce che questo minimo sia unico.
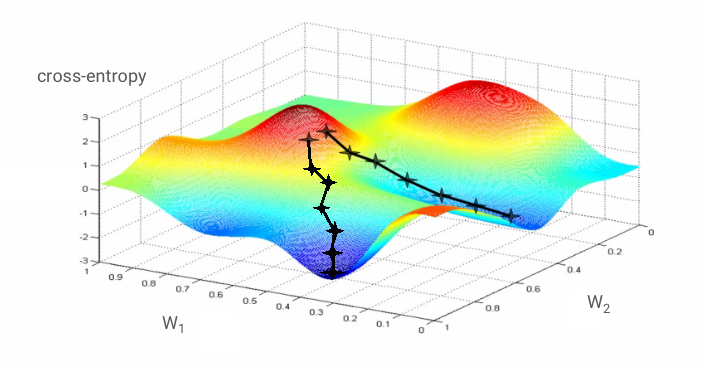
Mini-batching e momentum
Puoi calcolare il gradiente su una sola immagine di esempio e aggiornare immediatamente i pesi e i bias, ma farlo su un batch di, ad esempio, 128 immagini fornisce un gradiente che rappresenta meglio i vincoli imposti da diverse immagini di esempio e quindi è più probabile che converga più rapidamente verso la soluzione. La dimensione del mini-batch è un parametro regolabile.
Questa tecnica, a volte chiamata "discesa del gradiente stocastico", ha un altro vantaggio più pragmatico: lavorare con i batch significa anche lavorare con matrici più grandi, che di solito sono più facili da ottimizzare su GPU e TPU.
La convergenza può comunque essere un po' caotica e può persino interrompersi se il vettore gradiente è tutto zero. Significa che abbiamo trovato un minimo? Non sempre. Un componente gradiente può essere zero su un minimo o un massimo. Con un vettore gradiente con milioni di elementi, se sono tutti zero, la probabilità che ogni zero corrisponda a un punto minimo e nessuno a un punto massimo è piuttosto bassa. In uno spazio con molte dimensioni, i punti di sella sono piuttosto comuni e non vogliamo fermarci.
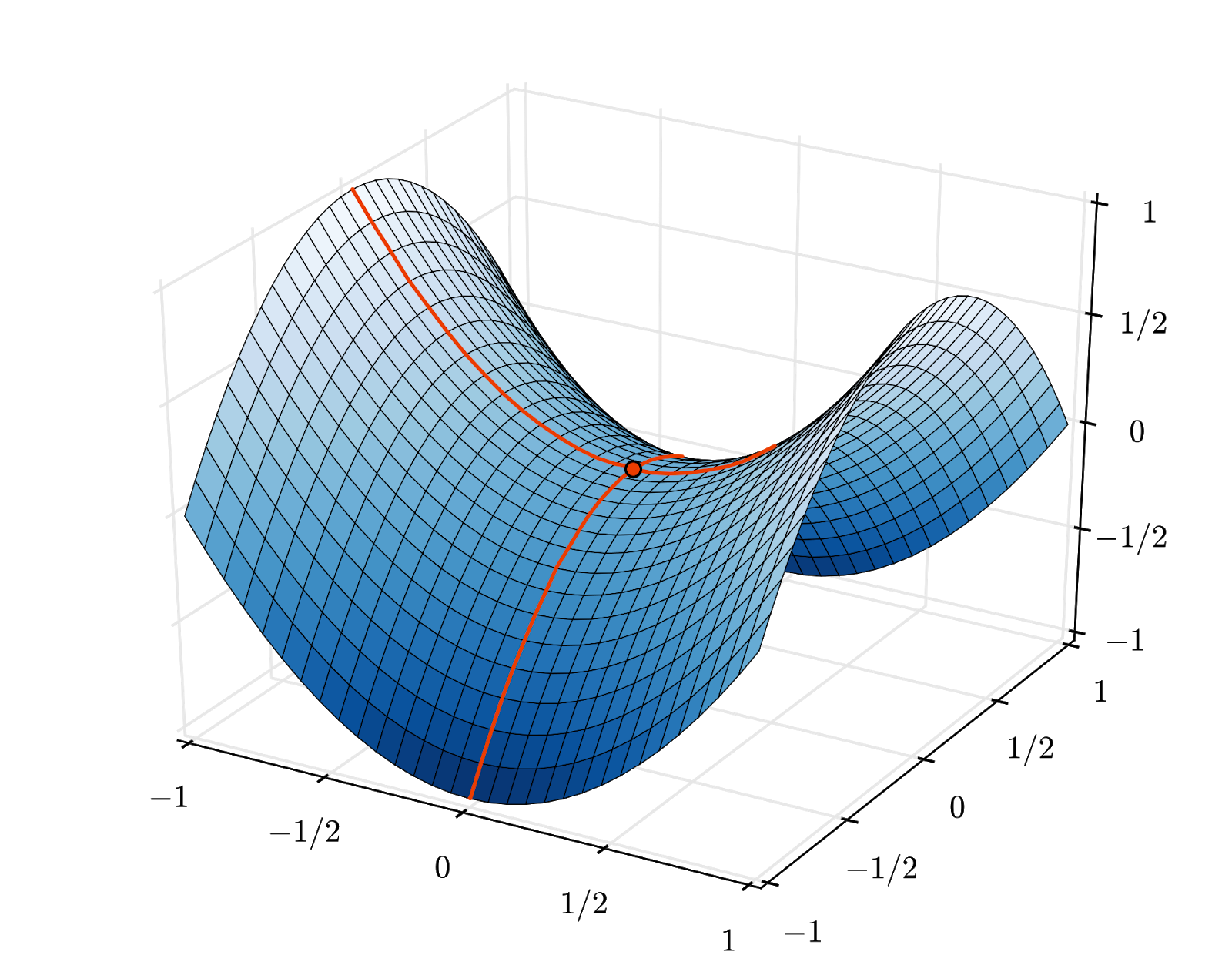
Illustrazione: un punto di sella. Il gradiente è 0, ma non è un minimo in tutte le direzioni. (Attribuzione immagine Wikimedia: di Nicoguaro - Opera propria, CC BY 3.0)
La soluzione consiste nell'aggiungere un po' di slancio all'algoritmo di ottimizzazione in modo che possa superare i punti di sella senza fermarsi.
Glossario
Batch o mini-batch: l'addestramento viene sempre eseguito su batch di dati di addestramento ed etichette. In questo modo, l'algoritmo può convergere. La dimensione "batch" è in genere la prima dimensione dei tensori di dati. Ad esempio, un tensore di forma [100, 192, 192, 3] contiene 100 immagini di 192 x 192 pixel con tre valori per pixel (RGB).
Perdita di entropia incrociata: una funzione di perdita speciale spesso utilizzata nei classificatori.
Strato denso: uno strato di neuroni in cui ogni neurone è collegato a tutti i neuroni dello strato precedente.
Caratteristiche: gli input di una rete neurale a volte vengono chiamati "caratteristiche". L'arte di capire quali parti di un set di dati (o combinazioni di parti) inserire in una rete neurale per ottenere buone previsioni è chiamata "ingegneria delle funzionalità".
Etichette: un altro nome per "classi" o risposte corrette in un problema di classificazione supervisionata
Tasso di apprendimento: frazione del gradiente in base alla quale pesi e bias vengono aggiornati a ogni iterazione del ciclo di addestramento.
Logit: gli output di un livello di neuroni prima dell'applicazione della funzione di attivazione sono chiamati "logit". Il termine deriva dalla "funzione logistica", nota anche come "funzione sigmoide", che in passato era la funzione di attivazione più popolare. "Neuron outputs before logistic function" (Output dei neuroni prima della funzione logistica) è stato abbreviato in "logits".
Perdita: la funzione di errore che confronta gli output della rete neurale con le risposte corrette
Neurone: calcola la somma ponderata dei suoi input, aggiunge un bias e trasmette il risultato tramite una funzione di attivazione.
Codifica one-hot: la classe 3 su 5 viene codificata come un vettore di 5 elementi, tutti pari a zero tranne il terzo, che è pari a 1.
relu: unità lineare rettificata. Una funzione di attivazione popolare per i neuroni.
sigmoid: un'altra funzione di attivazione che era popolare e che è ancora utile in casi speciali.
Softmax: una funzione di attivazione speciale che agisce su un vettore, aumenta la differenza tra il componente più grande e tutti gli altri e normalizza il vettore in modo che la somma sia pari a 1, in modo che possa essere interpretato come un vettore di probabilità. Utilizzato come ultimo passaggio nei classificatori.
Tensore: un "tensore" è come una matrice, ma con un numero arbitrario di dimensioni. Un tensore unidimensionale è un vettore. Un tensore bidimensionale è una matrice. Poi puoi avere tensori con 3, 4, 5 o più dimensioni.
Torniamo al notebook dello studio e questa volta leggiamo il codice.
Esaminiamo tutte le celle di questo notebook.
Cella "Parametri"
Qui vengono definiti le dimensioni del batch, il numero di epoche di addestramento e la posizione dei file di dati. I file di dati sono ospitati in un bucket Google Cloud Storage (GCS), motivo per cui il loro indirizzo inizia con gs://
Cella "Importazioni"
Qui vengono importate tutte le librerie Python necessarie, tra cui TensorFlow e matplotlib per le visualizzazioni.
Cella "utilità di visualizzazione [ESEGUI]"
Questa cella contiene codice di visualizzazione non interessante. È compresso per impostazione predefinita, ma puoi aprirlo e dare un'occhiata al codice quando hai tempo facendo doppio clic.
Cella "tf.data.Dataset: parse files and prepare training and validation datasets"
Questa cella ha utilizzato l'API tf.data.Dataset per caricare il set di dati MNIST dai file di dati. Non è necessario dedicare troppo tempo a questa cella. Se ti interessa l'API tf.data.Dataset, ecco un tutorial che la spiega: Pipeline di dati a velocità TPU. Per ora, le nozioni di base sono:
Le immagini e le etichette (risposte corrette) del set di dati MNIST sono archiviate in record a lunghezza fissa in 4 file. I file possono essere caricati con la funzione di record fisso dedicata:
imagedataset = tf.data.FixedLengthRecordDataset(image_filename, 28*28, header_bytes=16)Ora abbiamo un set di dati di byte di immagini. Devono essere decodificati in immagini. Definiamo una funzione per farlo. L'immagine non viene compressa, quindi la funzione non deve decodificare nulla (decode_raw non fa praticamente nulla). L'immagine viene quindi convertita in valori a rappresentazione in virgola mobile compresi tra 0 e 1. Potremmo rimodellarla qui come immagine 2D, ma in realtà la manteniamo come array piatto di pixel di dimensioni 28 x 28 perché è ciò che si aspetta il nostro livello denso iniziale.
def read_image(tf_bytestring):
image = tf.decode_raw(tf_bytestring, tf.uint8)
image = tf.cast(image, tf.float32)/256.0
image = tf.reshape(image, [28*28])
return imageApplichiamo questa funzione al set di dati utilizzando .map e otteniamo un set di dati di immagini:
imagedataset = imagedataset.map(read_image, num_parallel_calls=16)Eseguiamo lo stesso tipo di lettura e decodifica per le etichette e .zip immagini ed etichette insieme:
dataset = tf.data.Dataset.zip((imagedataset, labelsdataset))Ora abbiamo un set di dati di coppie (immagine, etichetta). Questo è ciò che si aspetta il nostro modello. Non siamo ancora pronti per utilizzarlo nella funzione di addestramento:
dataset = dataset.cache()
dataset = dataset.shuffle(5000, reshuffle_each_iteration=True)
dataset = dataset.repeat()
dataset = dataset.batch(batch_size)
dataset = dataset.prefetch(tf.data.experimental.AUTOTUNE)L'API tf.data.Dataset dispone di tutte le funzioni di utilità necessarie per preparare i set di dati:
.cache memorizza nella cache il set di dati nella RAM. Si tratta di un set di dati molto piccolo, quindi funzionerà. .shuffle lo riproduce in ordine casuale con un buffer di 5000 elementi. È importante che i dati di addestramento siano ben mischiati. .repeat esegue il loop del set di dati. L'addestramento verrà eseguito più volte (più epoche). .batch raccoglie più immagini ed etichette in una mini-natch. Infine, .prefetch può utilizzare la CPU per preparare il batch successivo mentre quello attuale viene addestrato sulla GPU.
Il set di dati di convalida viene preparato in modo simile. Ora possiamo definire un modello e utilizzare questo set di dati per addestrarlo.
Cella "Modello Keras"
Tutti i nostri modelli saranno sequenze lineari di livelli, quindi possiamo utilizzare lo stile tf.keras.Sequential per crearli. Inizialmente qui è un singolo strato denso. Ha 10 neuroni perché stiamo classificando le cifre scritte a mano in 10 classi. Utilizza l'attivazione "softmax" perché è l'ultimo livello di un classificatore.
Un modello Keras deve anche conoscere la forma dei suoi input. tf.keras.layers.Input può essere utilizzato per definirlo. Qui, i vettori di input sono vettori piatti di valori dei pixel di lunghezza 28*28.
model = tf.keras.Sequential(
[
tf.keras.layers.Input(shape=(28*28,)),
tf.keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='sgd',
loss='categorical_crossentropy',
metrics=['accuracy'])
# print model layers
model.summary()
# utility callback that displays training curves
plot_training = PlotTraining(sample_rate=10, zoom=1)La configurazione del modello viene eseguita in Keras utilizzando la funzione model.compile. Qui utilizziamo l'ottimizzatore di base 'sgd' (Stochastic Gradient Descent). Un modello di classificazione richiede una funzione di perdita di entropia incrociata, chiamata 'categorical_crossentropy' in Keras. Infine, chiediamo al modello di calcolare la metrica 'accuracy', ovvero la percentuale di immagini classificate correttamente.
Keras offre l'utilità model.summary() molto utile che stampa i dettagli del modello che hai creato. Il tuo gentile istruttore ha aggiunto l'utilità PlotTraining (definita nella cella "Utilità di visualizzazione") che mostrerà varie curve di allenamento durante l'allenamento.
Cella "Addestra e convalida il modello"
È qui che avviene l'addestramento, chiamando model.fit e passando sia i set di dati di addestramento che di convalida. Per impostazione predefinita, Keras esegue un ciclo di convalida al termine di ogni epoca.
model.fit(training_dataset, steps_per_epoch=steps_per_epoch, epochs=EPOCHS,
validation_data=validation_dataset, validation_steps=1,
callbacks=[plot_training])In Keras è possibile aggiungere comportamenti personalizzati durante l'addestramento utilizzando i callback. È così che è stato implementato il grafico di addestramento con aggiornamento dinamico per questo workshop.
Cella "Visualizza previsioni"
Una volta addestrato il modello, possiamo ottenere previsioni chiamando model.predict():
probabilities = model.predict(font_digits, steps=1)
predicted_labels = np.argmax(probabilities, axis=1)Qui abbiamo preparato un insieme di cifre stampate eseguite con caratteri locali, a scopo di test. Ricorda che la rete neurale restituisce un vettore di 10 probabilità dal suo "softmax" finale. Per ottenere l'etichetta, dobbiamo scoprire qual è la probabilità più alta. np.argmax della libreria numpy.
Per capire perché è necessario il parametro axis=1, ricorda che abbiamo elaborato un batch di 128 immagini e pertanto il modello restituisce 128 vettori di probabilità. La forma del tensore di output è [128, 10]. Calcoliamo l'argmax tra le 10 probabilità restituite per ogni immagine, quindi axis=1 (il primo asse è 0).
Questo semplice modello riconosce già il 90% delle cifre. Non male, ma ora migliorerai notevolmente.

Per migliorare l'accuratezza del riconoscimento, aggiungeremo altri strati alla rete neurale.
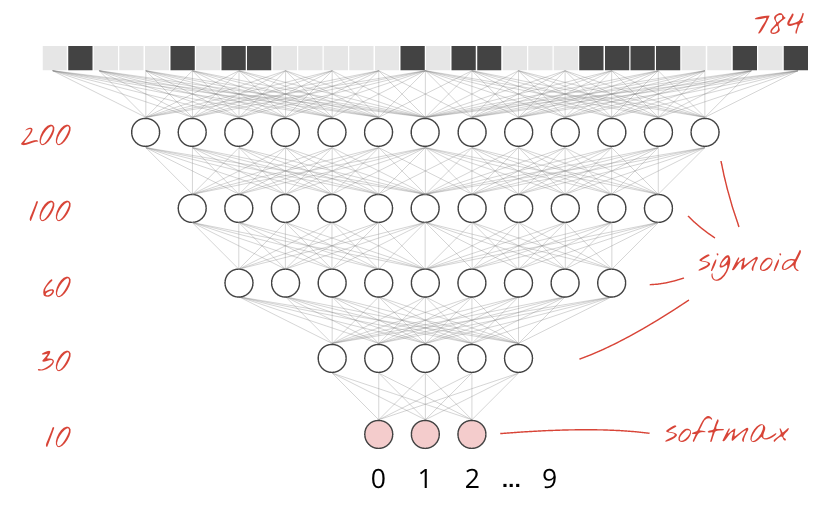
Manteniamo softmax come funzione di attivazione nell'ultimo livello perché è quella che funziona meglio per la classificazione. Nei livelli intermedi, tuttavia, utilizzeremo la funzione di attivazione più classica: la sigmoide:

Ad esempio, il modello potrebbe avere il seguente aspetto (non dimenticare le virgole, tf.keras.Sequential accetta un elenco di livelli separati da virgole):
model = tf.keras.Sequential(
[
tf.keras.layers.Input(shape=(28*28,)),
tf.keras.layers.Dense(200, activation='sigmoid'),
tf.keras.layers.Dense(60, activation='sigmoid'),
tf.keras.layers.Dense(10, activation='softmax')
])Guarda il "riepilogo" del modello. Ora ha almeno 10 volte più parametri. Dovrebbe essere 10 volte migliore. Ma per qualche motivo non è così…
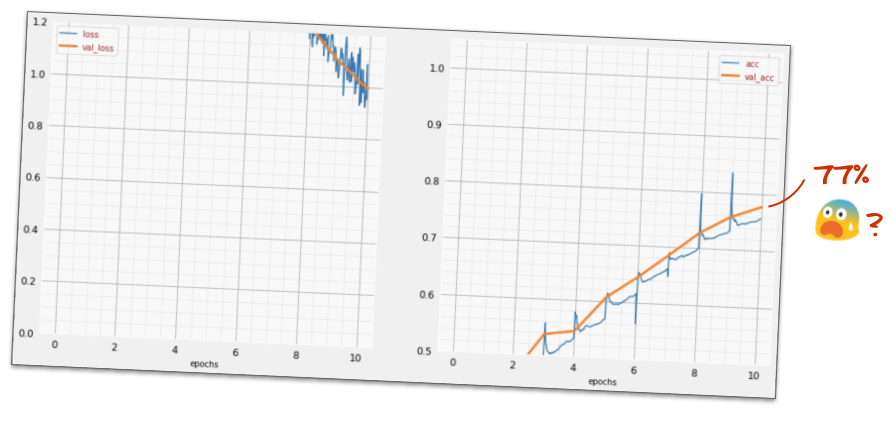
Anche le perdite sembrano essere aumentate vertiginosamente. Si è verificato un problema.
Hai appena sperimentato le reti neurali, come venivano progettate negli anni'80 e'90. Non sorprende che abbiano abbandonato l'idea, dando il via al cosiddetto "inverno dell'AI". Infatti, man mano che aggiungi livelli, le reti neurali hanno sempre più difficoltà a convergere.
Si è scoperto che le reti neurali profonde con molti strati (20, 50, persino 100 oggi) possono funzionare molto bene, a condizione che vengano utilizzati un paio di trucchi matematici per farle convergere. La scoperta di questi semplici trucchi è uno dei motivi della rinascita del deep learning negli anni 2010.
Attivazione RELU

La funzione di attivazione sigmoidea è in realtà piuttosto problematica nelle reti profonde. Comprime tutti i valori tra 0 e 1 e, se lo fai ripetutamente, gli output dei neuroni e i relativi gradienti possono scomparire completamente. È stato menzionato per motivi storici, ma le reti moderne utilizzano la ReLU (Rectified Linear Unit), che ha questo aspetto:
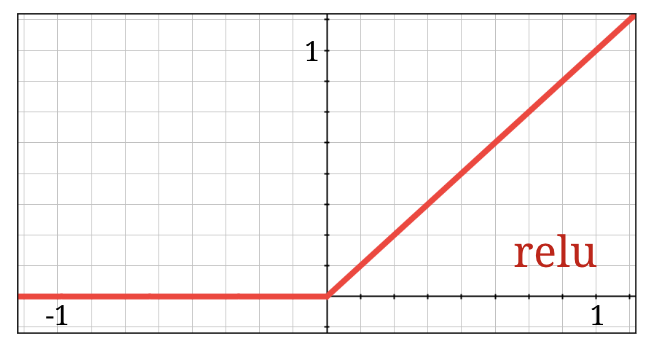
La ReLU, invece, ha una derivata di 1, almeno sul lato destro. Con l'attivazione ReLU, anche se i gradienti provenienti da alcuni neuroni possono essere pari a zero, ce ne saranno sempre altri che forniscono un gradiente diverso da zero e l'addestramento può continuare a un buon ritmo.
Un ottimizzatore migliore
In spazi con un numero molto elevato di dimensioni come in questo caso, in cui abbiamo circa 10.000 pesi e bias, i "punti di sella" sono frequenti. Questi sono punti che non sono minimi locali, ma in cui il gradiente è comunque zero e l'ottimizzatore di discesa del gradiente rimane bloccato. TensorFlow dispone di una gamma completa di ottimizzatori disponibili, inclusi alcuni che funzionano con una certa inerzia e superano in sicurezza i punti di sella.
Inizializzazioni casuali
L'arte di inizializzare i bias dei pesi prima dell'addestramento è un campo di ricerca a sé stante, con numerosi articoli pubblicati sull'argomento. Puoi dare un'occhiata a tutti gli inizializzatori disponibili in Keras qui. Fortunatamente, Keras esegue l'operazione giusta per impostazione predefinita e utilizza l'inizializzatore 'glorot_uniform', che è il migliore in quasi tutti i casi.
Non devi fare nulla, perché Keras fa già la cosa giusta.
NaN ???
La formula dell'entropia incrociata include un logaritmo e log(0) non è un numero (NaN, un errore numerico, se preferisci). L'input dell'entropia incrociata può essere 0? L'input proviene dalla funzione softmax, che è essenzialmente un esponenziale e un esponenziale non è mai zero. Quindi siamo al sicuro.
Davvero? Nel bellissimo mondo della matematica, saremmo al sicuro, ma nel mondo informatico, exp(-150), rappresentato in formato float32, è ZERO e l'entropia incrociata si arresta in modo anomalo.
Fortunatamente, non devi fare nulla neanche qui, poiché Keras si occupa di questo e calcola la funzione softmax seguita dall'entropia incrociata in modo particolarmente attento per garantire la stabilità numerica ed evitare i temuti NaN.
Operazione riuscita?
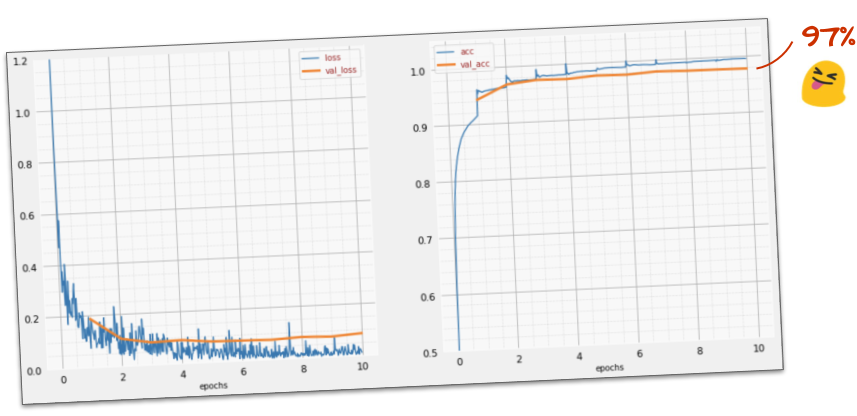
Ora dovresti raggiungere un'accuratezza del 97%. L'obiettivo di questo workshop è superare di gran lunga il 99%, quindi continuiamo.
Se non riesci ad andare avanti, ecco la soluzione a questo punto:
Forse possiamo provare ad allenarci più velocemente? Il tasso di apprendimento predefinito nell'ottimizzatore Adam è 0,001. Proviamo ad aumentarlo.
Andare più veloce non sembra aiutare molto e cos'è tutto questo rumore?
Le curve di addestramento sono molto irregolari e guarda entrambe le curve di convalida: oscillano su e giù. Ciò significa che stiamo andando troppo veloci. Potremmo tornare alla velocità precedente, ma c'è un modo migliore.

La soluzione migliore è iniziare rapidamente e ridurre il tasso di apprendimento in modo esponenziale. In Keras, puoi farlo con il callback tf.keras.callbacks.LearningRateScheduler.
Codice utile per il copia e incolla:
# lr decay function
def lr_decay(epoch):
return 0.01 * math.pow(0.6, epoch)
# lr schedule callback
lr_decay_callback = tf.keras.callbacks.LearningRateScheduler(lr_decay, verbose=True)
# important to see what you are doing
plot_learning_rate(lr_decay, EPOCHS)Non dimenticare di utilizzare il lr_decay_callback che hai creato. Aggiungilo all'elenco dei callback in model.fit:
model.fit(..., callbacks=[plot_training, lr_decay_callback])L'impatto di questa piccola modifica è spettacolare. Noti che la maggior parte del rumore è scomparsa e che l'accuratezza del test è ora superiore al 98% in modo costante.
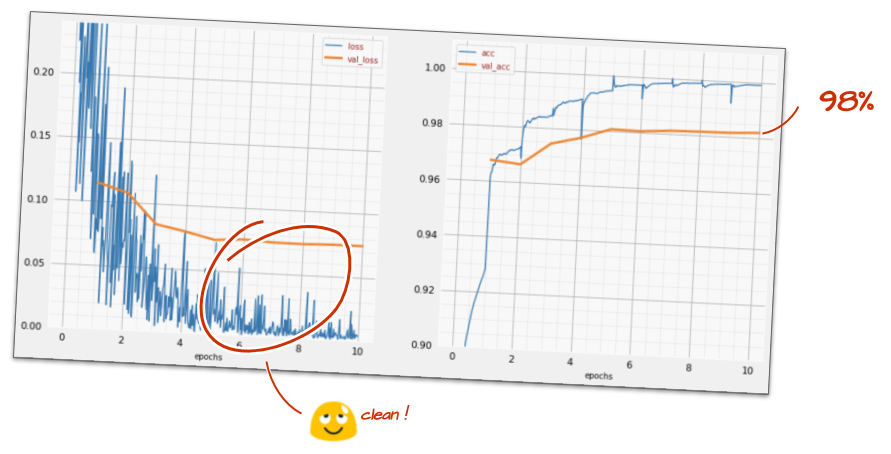
Il modello sembra convergere bene ora. Cerchiamo di andare ancora più a fondo.
Ti è stato utile?
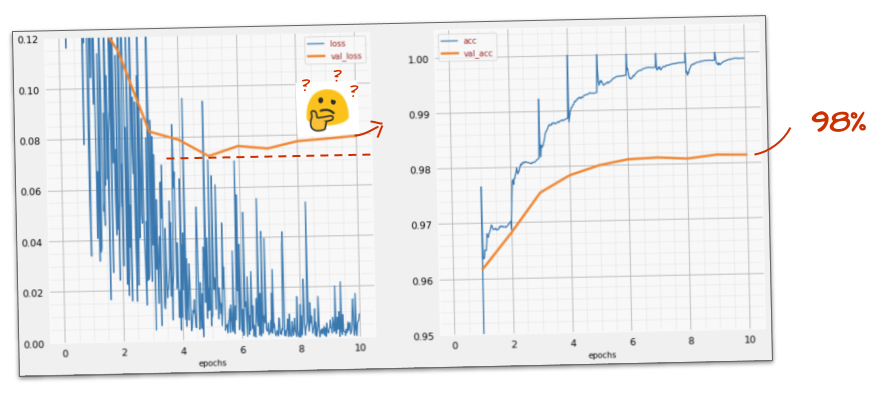
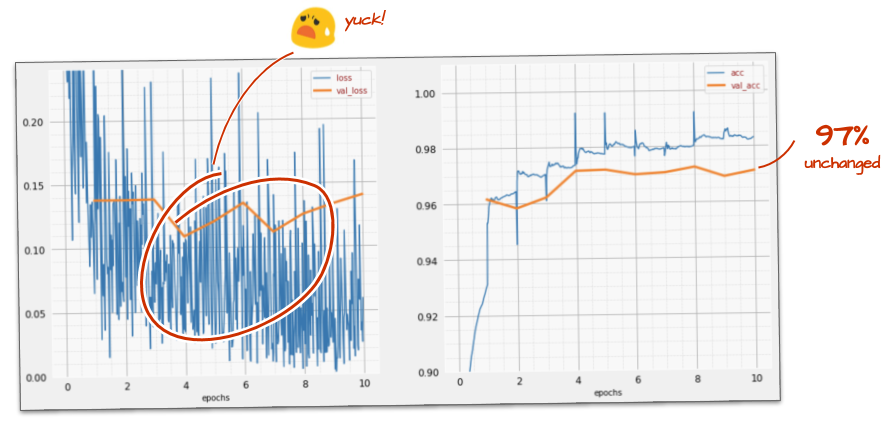
Non proprio, l'accuratezza è ancora bloccata al 98% e guarda la perdita di convalida. Sta salendo. L'algoritmo di apprendimento funziona solo sui dati di addestramento e ottimizza la perdita di addestramento di conseguenza. Non vede mai i dati di convalida, quindi non sorprende che dopo un po' il suo lavoro non abbia più effetto sulla perdita di convalida, che smette di diminuire e a volte addirittura rimbalza verso l'alto.
Ciò non influisce immediatamente sulle capacità di riconoscimento nel mondo reale del tuo modello, ma ti impedirà di eseguire molte iterazioni ed è generalmente un segno che l'addestramento non sta più avendo un effetto positivo.

Questa disconnessione viene solitamente chiamata "overfitting" e, quando la noti, puoi provare ad applicare una tecnica di regolarizzazione chiamata "dropout". La tecnica di dropout disattiva neuroni casuali a ogni iterazione di addestramento.
Ha funzionato?
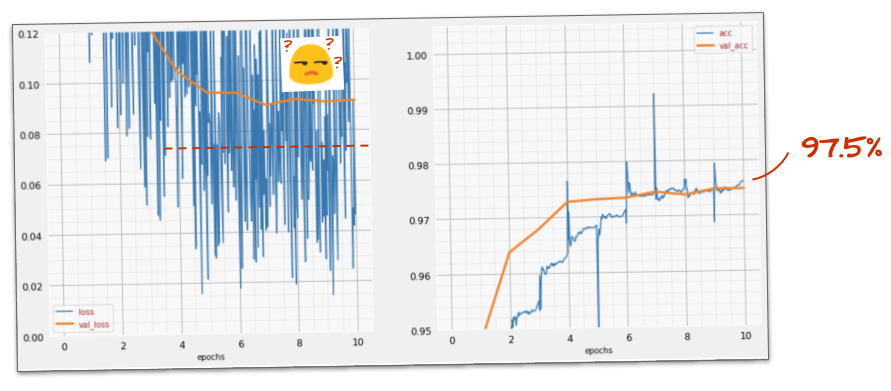
Il rumore ricompare (come prevedibile, dato il funzionamento dell'interruzione). La perdita di convalida non sembra più aumentare, ma è complessivamente superiore rispetto a quando non viene utilizzato il dropout. e l'accuratezza della convalida è diminuita leggermente. Si tratta di un risultato piuttosto deludente.
Sembra che il dropout non sia la soluzione corretta o forse l'overfitting è un concetto più complesso e alcune delle sue cause non sono risolvibili con un "dropout".
Che cos'è l'"overfitting"? L'overfitting si verifica quando una rete neurale apprende "male", in un modo che funziona per gli esempi di addestramento, ma non altrettanto bene sui dati reali. Esistono tecniche di regolarizzazione come il dropout che possono forzare l'apprendimento in modo migliore, ma l'overfitting ha anche radici più profonde.

L'overfitting di base si verifica quando una rete neurale ha troppi gradi di libertà per il problema in questione. Immagina di avere così tanti neuroni che la rete può memorizzare tutte le immagini di addestramento e riconoscerle tramite il riconoscimento di pattern. Non funzionerebbe affatto con dati reali. Una rete neurale deve essere in qualche modo vincolata in modo da essere costretta a generalizzare ciò che apprende durante l'addestramento.
Se hai pochissimi dati di addestramento, anche una rete di piccole dimensioni può impararli a memoria e si verifica un "overfitting". In generale, hai sempre bisogno di molti dati per addestrare le reti neurali.
Infine, se hai fatto tutto a regola d'arte, hai sperimentato diverse dimensioni della rete per assicurarti che i suoi gradi di libertà siano vincolati, hai applicato il dropout e hai eseguito l'addestramento su molti dati, potresti comunque essere bloccato a un livello di prestazioni che sembra impossibile migliorare. Ciò significa che la tua rete neurale, nella sua forma attuale, non è in grado di estrarre ulteriori informazioni dai tuoi dati, come nel nostro caso.
Ricordi come utilizziamo le nostre immagini, compresse in un unico vettore? È stata una pessima idea. Le cifre scritte a mano sono composte da forme e abbiamo scartato le informazioni sulle forme quando abbiamo appiattito i pixel. Tuttavia, esiste un tipo di rete neurale che può sfruttare le informazioni sulla forma: le reti convoluzionali. Proviamoli.
Se non riesci ad andare avanti, ecco la soluzione a questo punto:
In sintesi
Se conosci già tutti i termini in grassetto nel paragrafo successivo, puoi passare all'esercizio successivo. Se hai appena iniziato a utilizzare le reti neurali convoluzionali, continua a leggere.
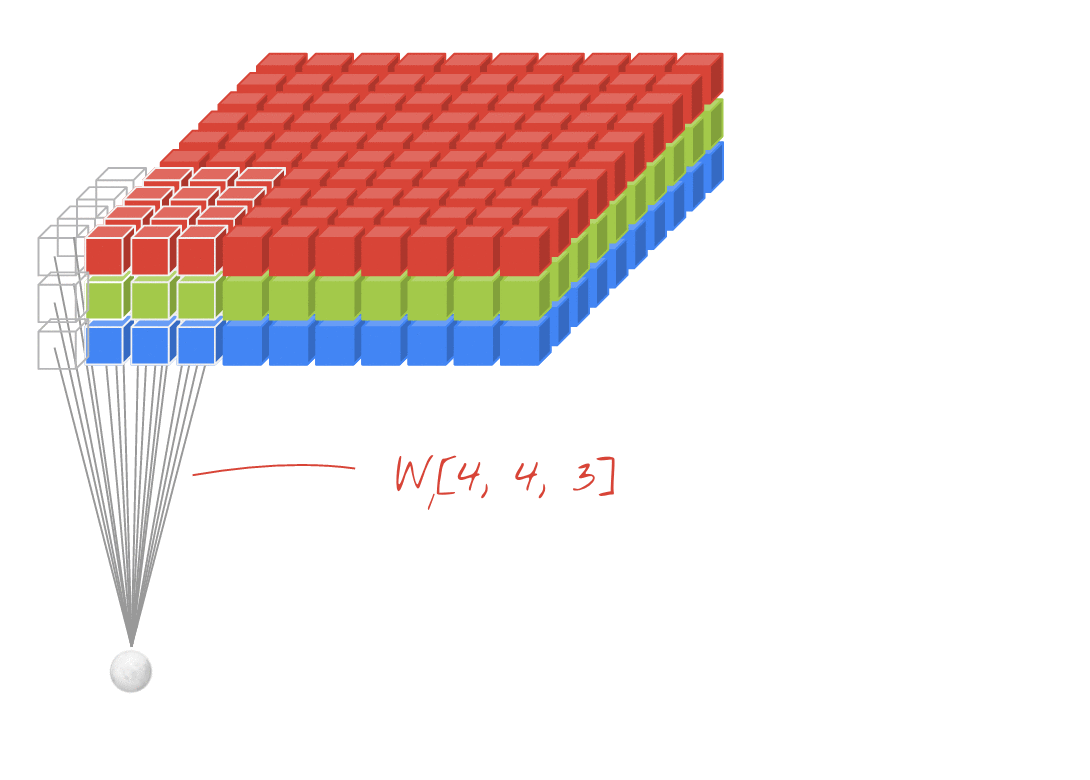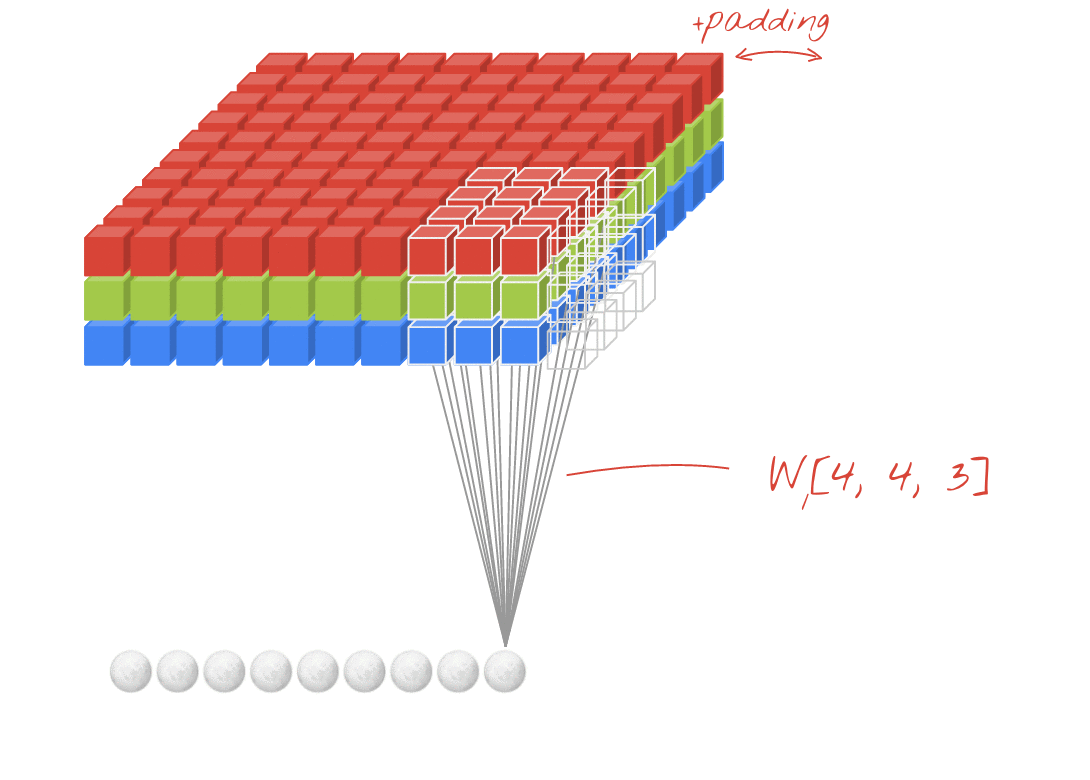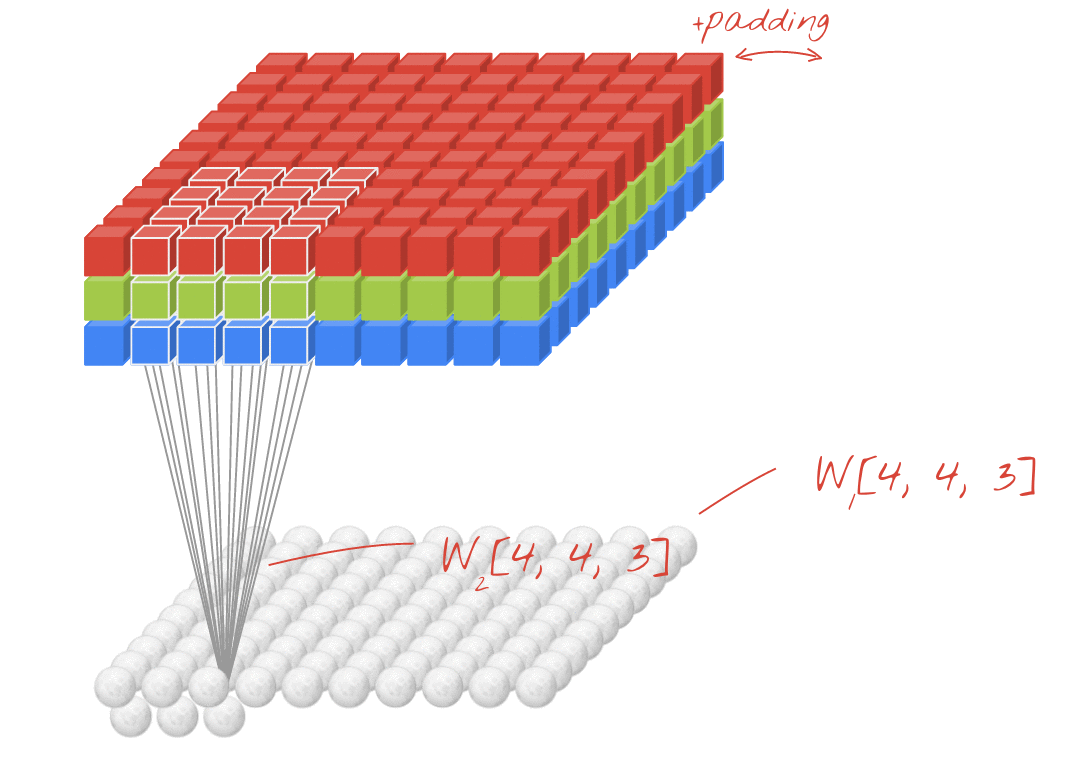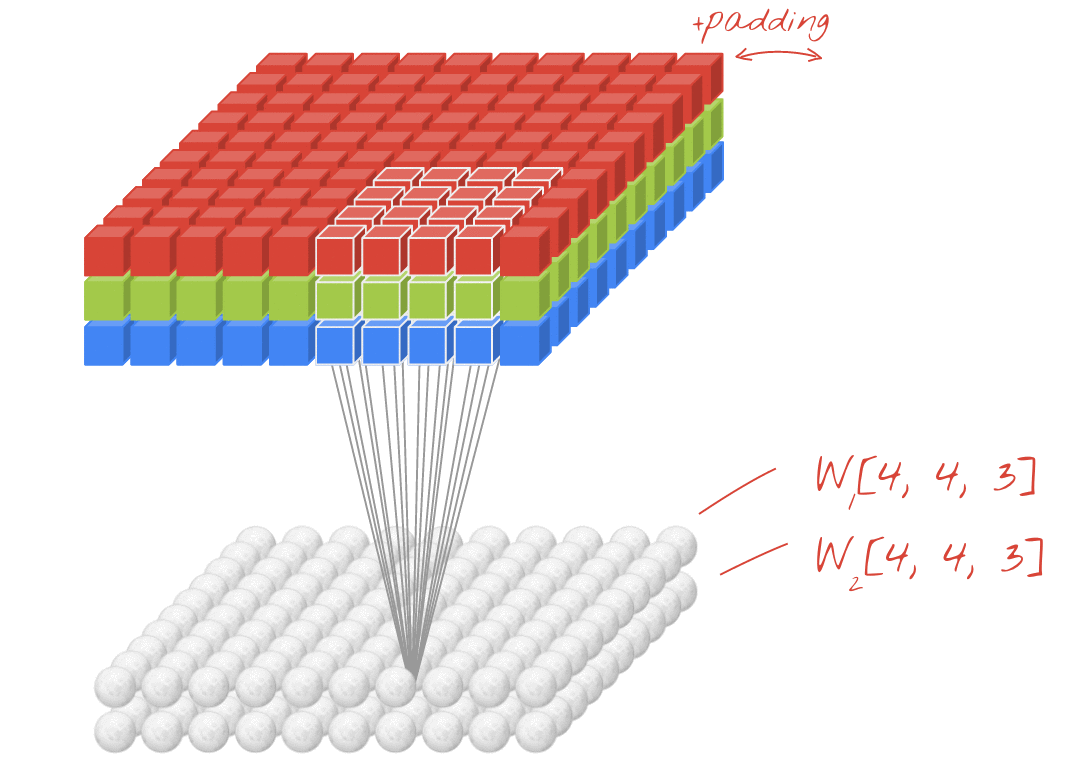
Illustrazione: filtro di un'immagine con due filtri successivi composti da 48 pesi apprendibili ciascuno (4x4x3).
Ecco come appare una semplice rete neurale convoluzionale in Keras:
model = tf.keras.Sequential([
tf.keras.layers.Reshape(input_shape=(28*28,), target_shape=(28, 28, 1)),
tf.keras.layers.Conv2D(kernel_size=3, filters=12, activation='relu'),
tf.keras.layers.Conv2D(kernel_size=6, filters=24, strides=2, activation='relu'),
tf.keras.layers.Conv2D(kernel_size=6, filters=32, strides=2, activation='relu'),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(10, activation='softmax')
])
In un livello di una rete convoluzionale, un "neurone" esegue una somma ponderata dei pixel appena sopra, solo in una piccola regione dell'immagine. Aggiunge un bias e alimenta la somma tramite una funzione di attivazione, proprio come farebbe un neurone in un normale livello denso. Questa operazione viene poi ripetuta sull'intera immagine utilizzando gli stessi pesi. Ricorda che negli strati densi ogni neurone aveva i propri pesi. Qui, una singola "patch" di pesi scorre sull'immagine in entrambe le direzioni (una "convoluzione"). L'output ha tanti valori quanti sono i pixel nell'immagine (anche se è necessario un po' di padding ai bordi). Si tratta di un'operazione di filtraggio. Nell'illustrazione precedente, utilizza un filtro di 4x4x3=48 pesi.
Tuttavia, 48 pesi non saranno sufficienti. Per aggiungere altri gradi di libertà, ripetiamo la stessa operazione con un nuovo insieme di pesi. Viene generata una nuova serie di output del filtro. Chiamiamolo "canale " di output per analogia con i canali R, G e B dell'immagine di input.
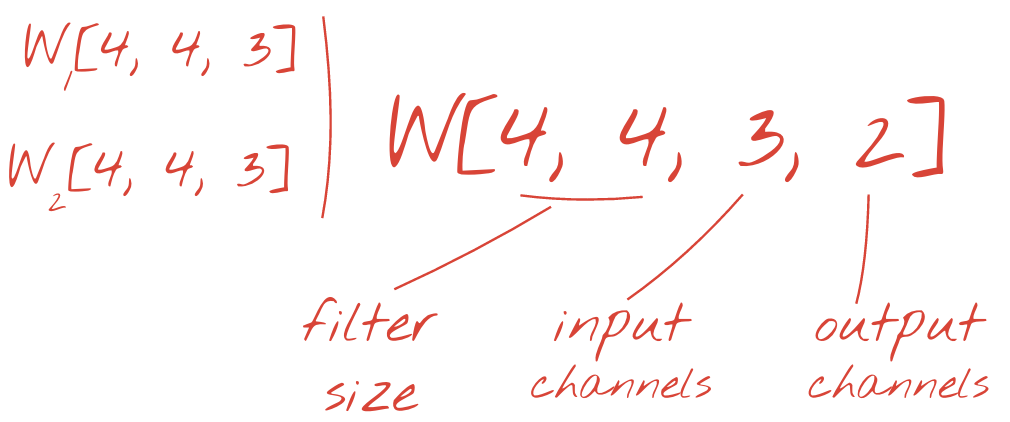
I due (o più) insiemi di pesi possono essere riassunti in un unico tensore aggiungendo una nuova dimensione. In questo modo otteniamo la forma generica del tensore dei pesi per un livello convoluzionale. Poiché il numero di canali di input e output sono parametri, possiamo iniziare ad accumulare e concatenare i livelli convoluzionali.
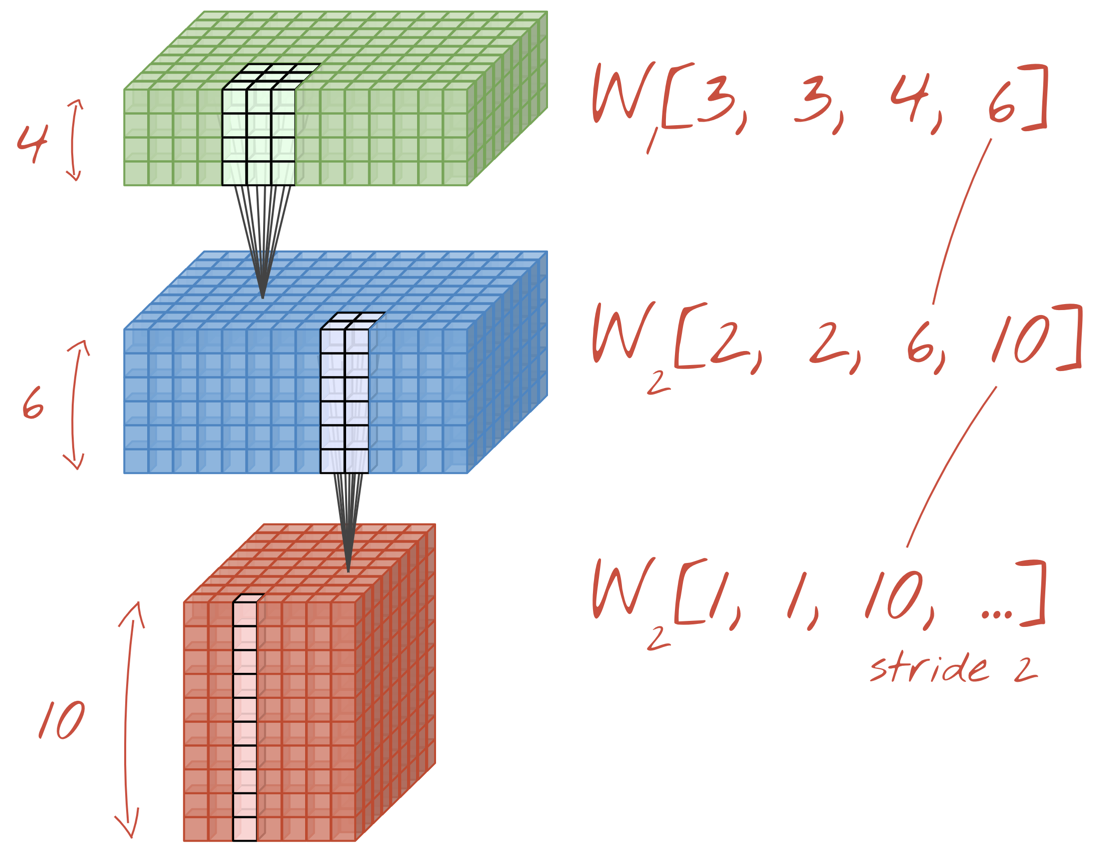
Illustrazione: una rete neurale convoluzionale trasforma "cubi" di dati in altri "cubi" di dati.
Convoluzioni con passo, max pooling
Eseguendo le convoluzioni con uno stride di 2 o 3, possiamo anche ridurre il cubo di dati risultante nelle sue dimensioni orizzontali. Esistono due modi comuni per farlo:
- Convoluzione con passo: un filtro scorrevole come sopra, ma con un passo > 1
- Max pooling: una finestra scorrevole che applica l'operazione MAX (in genere su patch 2x2, ripetute ogni 2 pixel)

Illustrazione: se la finestra di calcolo viene spostata di 3 pixel, si ottengono meno valori di output. Le convoluzioni con passo o il max pooling (massimo in una finestra 2x2 che scorre con un passo di 2) sono un modo per ridurre il cubo di dati nelle dimensioni orizzontali.
Il livello finale
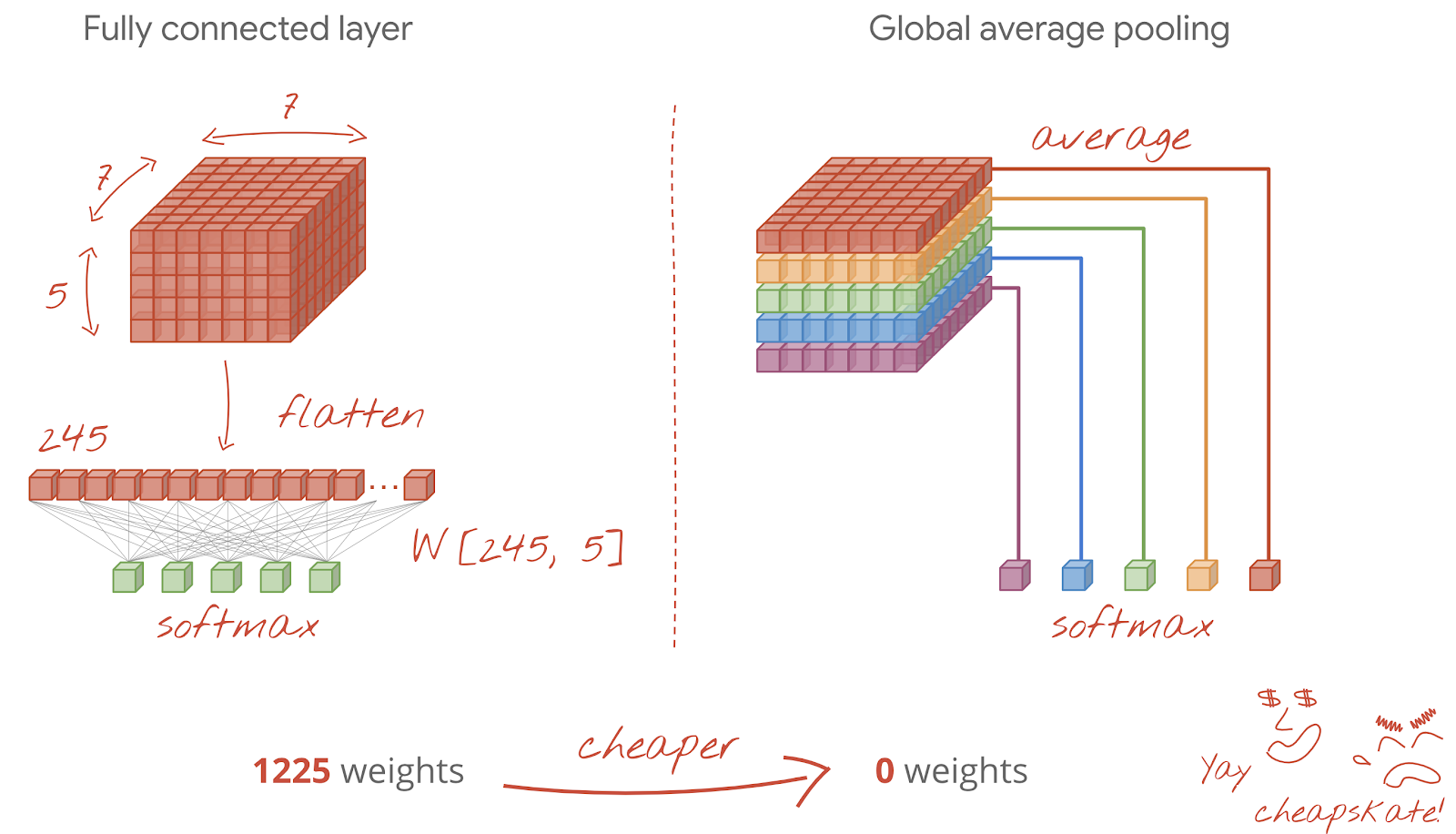
Dopo l'ultimo livello convoluzionale, i dati si trovano sotto forma di "cubo". Esistono due modi per alimentarlo attraverso l'ultimo strato denso.
Il primo consiste nell'appiattire il cubo di dati in un vettore e poi inserirlo nel livello softmax. A volte, puoi persino aggiungere un livello denso prima del livello softmax. Questa operazione tende a essere costosa in termini di numero di pesi. Un livello denso alla fine di una rete convoluzionale può contenere più della metà dei pesi dell'intera rete neurale.
Anziché utilizzare un costoso livello denso, possiamo anche dividere il "cubo" di dati in entrata in tante parti quante sono le classi, calcolare la media dei loro valori e inserirli in una funzione di attivazione softmax. Questo modo di creare l'intestazione di classificazione costa 0 pesi. In Keras esiste un livello per questo: tf.keras.layers.GlobalAveragePooling2D().
Passa alla sezione successiva per creare una rete convoluzionale per il problema in questione.
Creiamo una rete convoluzionale per il riconoscimento di cifre scritte a mano. Utilizzeremo tre livelli convoluzionali nella parte superiore, il nostro tradizionale livello di lettura softmax nella parte inferiore e li collegheremo con un livello completamente connesso:
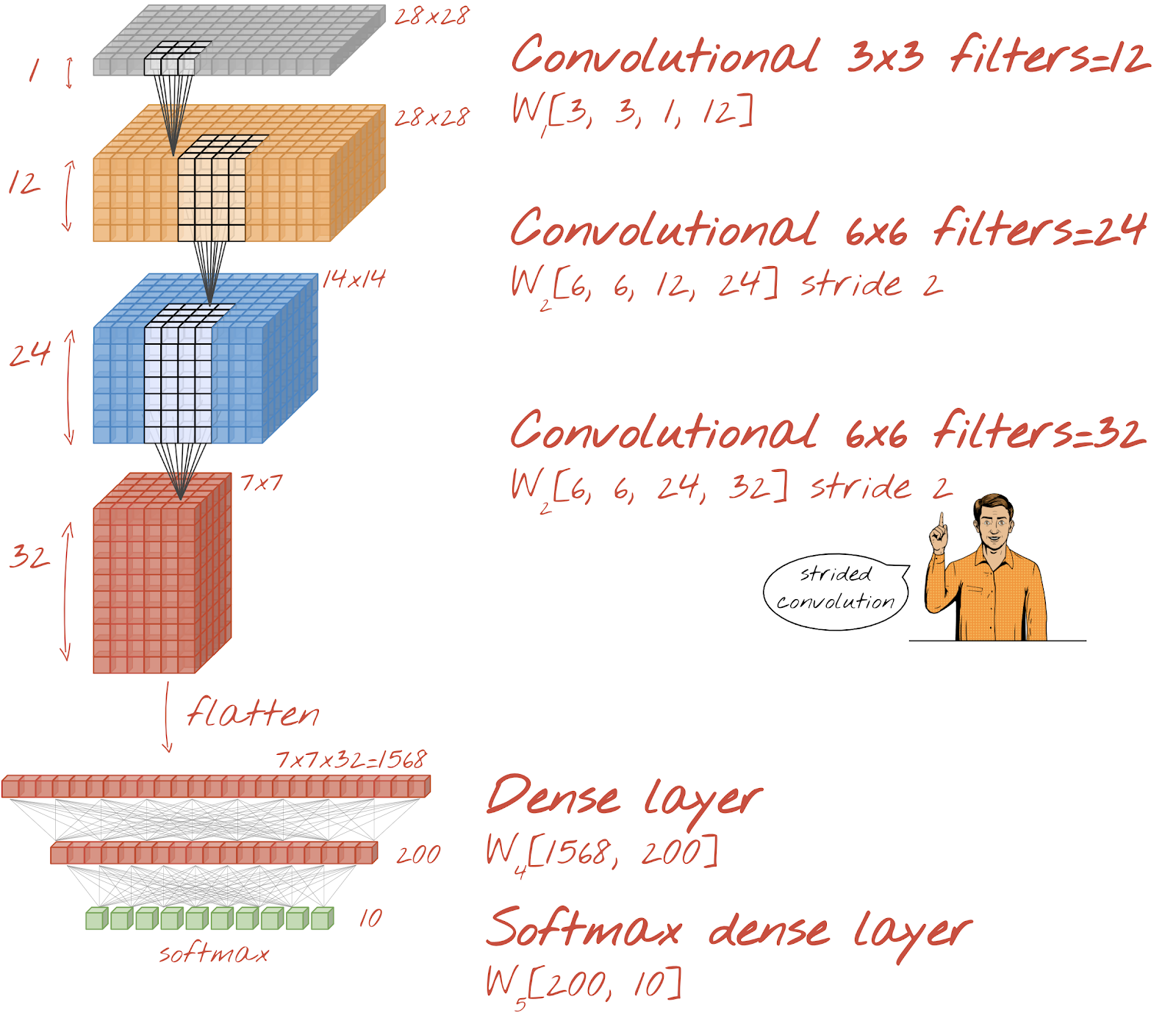
Nota che il secondo e il terzo livello convoluzionale hanno uno stride di due, il che spiega perché riducono il numero di valori di output da 28x28 a 14x14 e poi a 7x7.
Scriviamo il codice Keras.
È necessaria un'attenzione particolare prima del primo livello convoluzionale. Infatti, si aspetta un "cubo" di dati 3D, ma il nostro set di dati è stato finora configurato per i livelli densi e tutti i pixel delle immagini sono appiattiti in un vettore. Dobbiamo rimodellarle in immagini 28x28x1 (1 canale per le immagini in scala di grigi):
tf.keras.layers.Reshape(input_shape=(28*28,), target_shape=(28, 28, 1))Puoi utilizzare questa linea anziché il livello tf.keras.layers.Input che avevi finora.
In Keras, la sintassi per un livello convoluzionale attivato da "relu" è:
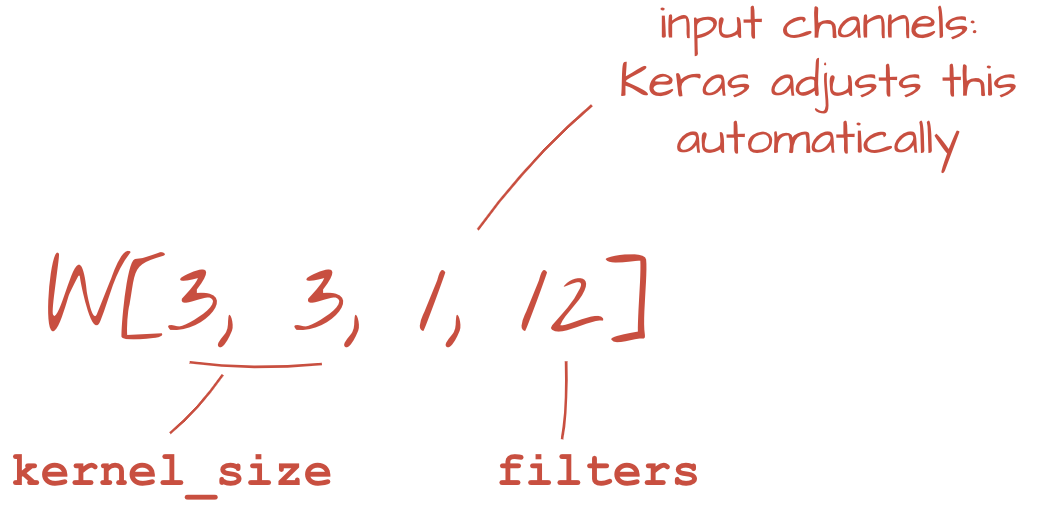
tf.keras.layers.Conv2D(kernel_size=3, filters=12, padding='same', activation='relu')Per una convoluzione con passo, scriveresti:
tf.keras.layers.Conv2D(kernel_size=6, filters=24, padding='same', activation='relu', strides=2)Per appiattire un cubo di dati in un vettore in modo che possa essere utilizzato da un livello denso:
tf.keras.layers.Flatten()Per il livello denso, la sintassi è rimasta invariata:
tf.keras.layers.Dense(200, activation='relu')Il tuo modello ha superato la barriera di accuratezza del 99%? Ci siamo quasi… ma guarda la curva di perdita di convalida. Tutto questo ti è familiare?
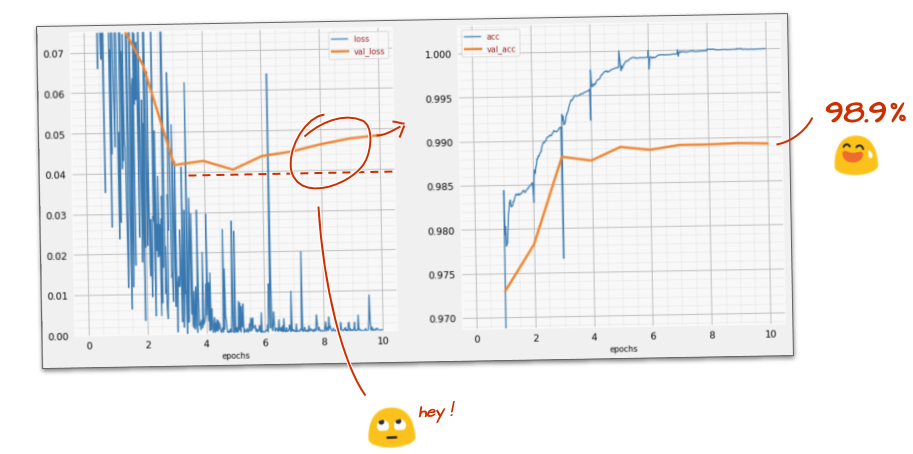
Controlla anche le previsioni. Per la prima volta, dovresti notare che la maggior parte delle 10.000 cifre di test viene ora riconosciuta correttamente. Rimangono solo circa 4 righe e mezzo di rilevamenti errati (circa 110 cifre su 10.000)

Se non riesci ad andare avanti, ecco la soluzione a questo punto:
L'addestramento precedente mostra chiari segni di overfitting (e non raggiunge comunque il 99% di accuratezza). Vuoi provare di nuovo a interrompere la riproduzione?
Com'è andata questa volta?
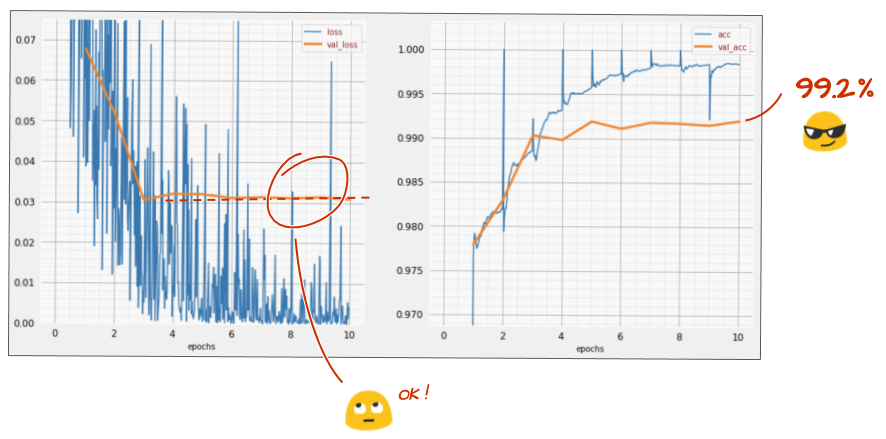
Sembra che questa volta l'abbandono sia andato a buon fine. La perdita di convalida non aumenta più e l'accuratezza finale dovrebbe essere superiore al 99%. Complimenti!
La prima volta che abbiamo provato ad applicare il dropout, abbiamo pensato di avere un problema di overfitting, quando in realtà il problema era nell'architettura della rete neurale. Non potevamo andare oltre senza i livelli convoluzionali e il dropout non poteva fare nulla al riguardo.
Questa volta, sembra che l'overfitting sia stata la causa del problema e il dropout abbia effettivamente aiutato. Ricorda che ci sono molti fattori che possono causare una discrepanza tra le curve di perdita di addestramento e convalida, con la perdita di convalida che aumenta. L'overfitting (troppi gradi di libertà, utilizzati male dalla rete) è solo uno di questi. Se il set di dati è troppo piccolo o l'architettura della rete neurale non è adeguata, potresti notare un comportamento simile nelle curve di perdita, ma il dropout non sarà utile.
Infine, proviamo ad aggiungere la normalizzazione batch.
Questa è la teoria, in pratica, ricorda solo un paio di regole:
Per ora seguiamo le regole e aggiungiamo un livello di normalizzazione batch a ogni livello della rete neurale, tranne l'ultimo. Non aggiungerlo all'ultimo livello "softmax". Non sarebbe utile.
# Modify each layer: remove the activation from the layer itself.
# Set use_bias=False since batch norm will play the role of biases.
tf.keras.layers.Conv2D(..., use_bias=False),
# Batch norm goes between the layer and its activation.
# The scale factor can be turned off for Relu activation.
tf.keras.layers.BatchNormalization(scale=False, center=True),
# Finish with the activation.
tf.keras.layers.Activation('relu'),Qual è l'accuratezza attuale?
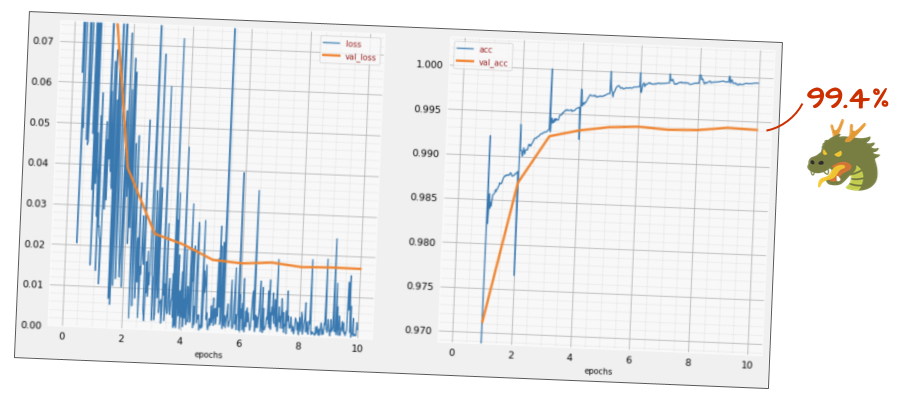
Con qualche modifica (BATCH_SIZE=64, parametro di decadimento del tasso di apprendimento 0,666, tasso di dropout sul livello denso 0,3) e un po' di fortuna, puoi raggiungere il 99,5%. Gli aggiustamenti del tasso di apprendimento e del dropout sono stati eseguiti seguendo le "best practice" per l'utilizzo della normalizzazione batch:
- La normalizzazione batch aiuta le reti neurali a convergere e di solito consente di eseguire l'addestramento più rapidamente.
- La normalizzazione batch è un regolarizzatore. In genere puoi ridurre la quantità di dropout che utilizzi o non utilizzarlo affatto.
Il notebook della soluzione ha una sessione di addestramento del 99,5%:

Troverai una versione del codice pronta per il cloud nella cartella mlengine su GitHub, insieme alle istruzioni per eseguirlo su Google Cloud AI Platform. Prima di poter eseguire questa parte, devi creare un account Google Cloud e attivare la fatturazione. Le risorse necessarie per completare il lab dovrebbero costare meno di un paio di dollari (supponendo 1 ora di tempo di addestramento su una GPU). Per preparare l'account:
- Crea un progetto Google Cloud (http://cloud.google.com/console).
- Abilita la fatturazione.
- Installa gli strumenti a riga di comando di Google Cloud (GCP SDK qui).
- Crea un bucket Google Cloud Storage (inserisci la regione
us-central1). Verrà utilizzato per preparare il codice di addestramento e archiviare il modello addestrato. - Abilita le API necessarie e richiedi le quote necessarie (esegui il comando di addestramento una volta e dovresti ricevere messaggi di errore che ti indicano cosa abilitare).
Hai creato la tua prima rete neurale e l'hai addestrata fino a raggiungere una precisione del 99%. Le tecniche apprese durante il percorso non sono specifiche del set di dati MNIST, ma sono ampiamente utilizzate quando si lavora con le reti neurali. Come regalo di addio, ecco la scheda "riassunto" del lab, in versione cartoon. Puoi utilizzarlo per ricordare ciò che hai imparato:

Passaggi successivi
- Dopo le reti completamente connesse e convoluzionali, dovresti dare un'occhiata alle reti neurali ricorrenti.
- Per eseguire l'addestramento o l'inferenza nel cloud su un'infrastruttura distribuita, Google Cloud fornisce AI Platform.
- Infine, ci piacerebbe ricevere un tuo feedback. Segnalaci eventuali problemi riscontrati in questo lab o se ritieni che debba essere migliorato. Gestiamo i feedback tramite i problemi di GitHub [link al feedback].

Autore: Martin Görner Twitter: @martin_gorner |
|
Copyright di tutte le immagini di cartoni animati in questo lab: alexpokusay / 123RF stock photos




