W tym module przedstawiamy pojęcia związane z regresją liniową.
Regresja liniowa to technika statystyczna służąca do znajdowania zależności między zmiennymi. W kontekście uczenia maszynowego regresja liniowa znajduje zależność między cechami a etykietą.
Załóżmy na przykład, że chcemy przewidzieć zużycie paliwa w milach na galon na podstawie masy samochodu. Mamy do dyspozycji taki zbiór danych:
| Funty w tysiącach (funkcja) | Mile na galon (etykieta) |
|---|---|
| 3,5 | 18 |
| 3,69 | 15 |
| 3,44 | 18 |
| 3,43 | 16 |
| 4,34 | 15 |
| 4,42 | 14 |
| 2,37 | 24 |
Jeśli naniesiemy te punkty, otrzymamy taki wykres:
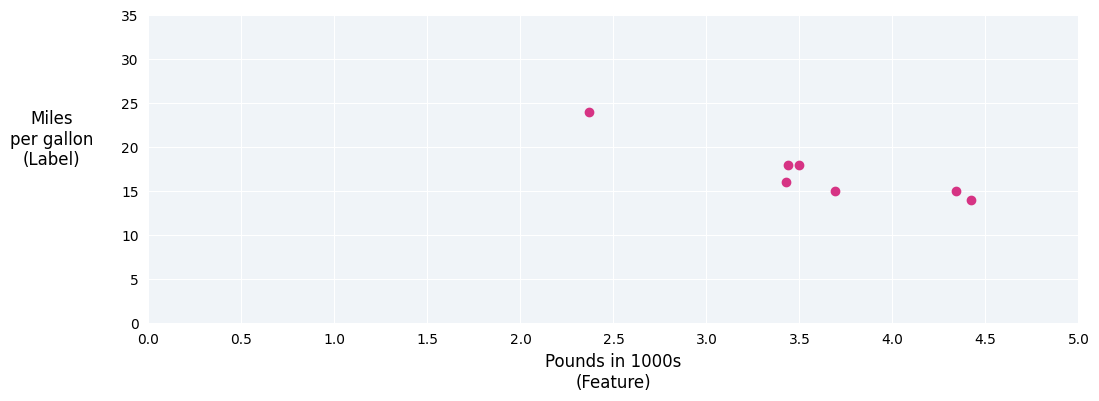
Rysunek 1. Masa samochodu (w funtach) w porównaniu z oceną mil na galon. Wraz ze wzrostem masy samochodu jego zużycie paliwa na milę zwykle maleje.
Możemy utworzyć własny model, rysując przez punkty linię najlepszego dopasowania:

Rysunek 2. Linia najlepszego dopasowania narysowana na podstawie danych z poprzedniego rysunku.
Równanie regresji liniowej
W języku algebry model ten można zdefiniować jako $ y = mx + b $, gdzie
- $ y $ to liczba mil na galon – wartość, którą chcemy przewidzieć.
- $ m $ to nachylenie linii.
- $ x $ to wartość wejściowa w funtach.
- $ b $ to punkt przecięcia z osią Y.
W uczeniu maszynowym równanie modelu regresji liniowej ma postać:
gdzie:
- $ y'$ to prognozowana etykieta – dane wyjściowe.
- $ b $ to błąd modelu. Zależność ta jest taka sama jak w przypadku przecięcia z osią y w równaniu algebraicznym linii. W ML błąd systematyczny jest czasami nazywany $ w_0 $. Jest to parametr modelu, który jest obliczany podczas treningu.
- $ w_1 $ to waga tej cechy. Waga to ta sama koncepcja co nachylenie $ m $ w równaniu algebraicznym linii. Waga jest parametrem modelu i jest obliczana podczas trenowania.
- $ x_1 $ to cecha – dane wejściowe.
Podczas trenowania model oblicza wagę i uświadczenia, które dają najlepszy model.

Rysunek 3. Matematyczne przedstawienie modelu liniowego.
W naszym przykładzie obliczymy wagę i uparty z wykresowanej linii. Współczynnik jest równy 34 (gdzie linia przecina oś Y), a waga –4,6 (nachylenie linii). Model zostałby zdefiniowany jako $ y' = 34 + (-4.6)(x_1)$ i można go byłoby używać do tworzenia prognoz. Na przykład według tego modelu przewidywana wydajność spalania paliwa w przypadku samochodu o masie 4000 funtów wynosi 15,6 mil na galon.

Rysunek 4. Na podstawie tego modelu przewidywany współczynnik zużycia paliwa dla samochodu o masie 4000 funtów wynosi 15,6 mil na galon.
Modele z wieloma funkcjami
Przykład w tej sekcji wykorzystuje tylko jedną cechę – ciężar samochodu – ale bardziej zaawansowany model może opierać się na wielu cechach, z których każda ma osobną wagę ($ w_1 $, $ w_2 $ itd.). Na przykład model, który korzysta z 5 cech, będzie wyglądał tak:
$ y' = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 $
Na przykład model przewidujący zużycie paliwa może dodatkowo używać takich cech:
- Pojemność skokowa silnika
- Przyspieszenie
- Liczba cylindrów
- Koń parowy
Ten model będzie wyglądał tak:

Rysunek 5. Model z 5 cechami do prognozowania mil na galon dla samochodu.
Na wykresach przedstawiających niektóre z tych dodatkowych funkcji widać, że mają one również charakter liniowy w stosunku do etykiety „mile na galon”:

Rysunek 6. pojemność skokowa silnika w cm3 i ocena w MPG, Wraz ze wzrostem pojemności silnika samochodu jego zużycie paliwa na milę zwykle maleje.

Rysunek 7. przyspieszenie samochodu i wartość mil na galon. Im dłużej trwa przyspieszanie samochodu, tym wyższa jest średnia liczba mil na galon.

Rysunek 8. Moc silnika i liczba mil na galon. Wraz ze wzrostem mocy silnika samochodu liczba mil na galon zwykle maleje.
