Làm cách nào để gỡ lỗi và giảm thiểu các lỗi tối ưu hoá?
Tóm tắt: Nếu mô hình gặp khó khăn trong việc tối ưu hoá, bạn cần khắc phục những khó khăn đó trước khi thử các cách khác. Chẩn đoán và khắc phục các lỗi huấn luyện là một lĩnh vực nghiên cứu đang phát triển mạnh mẽ.

Hãy lưu ý những điều sau đây về Hình 4:
- Việc thay đổi bước sải không làm giảm hiệu suất ở tốc độ học tập thấp.
- Tốc độ học tập cao không còn được huấn luyện tốt do tính không ổn định.
- Việc áp dụng 1000 bước khởi động tốc độ học sẽ giải quyết trường hợp không ổn định cụ thể này, cho phép huấn luyện ổn định ở tốc độ học tối đa là 0,1.
Xác định khối lượng công việc không ổn định
Mọi khối lượng công việc đều trở nên không ổn định nếu tốc độ học quá lớn. Tính không ổn định chỉ là vấn đề khi nó buộc bạn phải sử dụng tốc độ học quá nhỏ. Có ít nhất 2 loại bất ổn trong quá trình huấn luyện mà bạn nên phân biệt:
- Tính không ổn định khi khởi tạo hoặc trong giai đoạn đầu của quá trình huấn luyện.
- Đột ngột mất ổn định trong quá trình huấn luyện.
Bạn có thể áp dụng một phương pháp có hệ thống để xác định các vấn đề về độ ổn định trong khối lượng công việc của mình bằng cách thực hiện những việc sau:
- Thực hiện quét tốc độ học và tìm tốc độ học tốt nhất lr*.
- Vẽ các đường cong tổn thất huấn luyện cho tốc độ học tập ngay trên lr*.
- Nếu tốc độ học tập > lr* cho thấy sự bất ổn về tổn thất (tổn thất tăng lên chứ không giảm xuống trong các giai đoạn huấn luyện), thì việc khắc phục sự bất ổn thường sẽ cải thiện quá trình huấn luyện.
Ghi lại chuẩn L2 của toàn bộ độ dốc tổn thất trong quá trình huấn luyện, vì các giá trị ngoại lai có thể gây ra sự bất ổn giả tạo ở giữa quá trình huấn luyện. Điều này có thể cho biết mức độ cắt các độ dốc hoặc mức độ cập nhật trọng số.
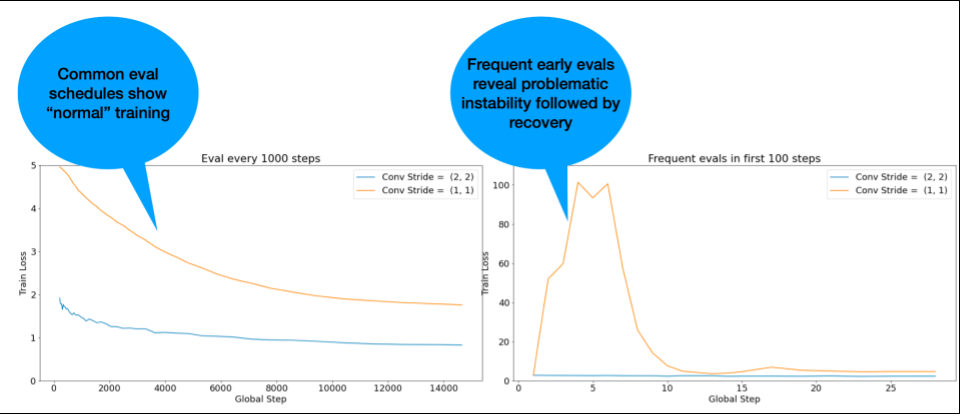
LƯU Ý: Một số mô hình cho thấy tình trạng không ổn định từ rất sớm, sau đó là quá trình khôi phục dẫn đến quá trình huấn luyện chậm nhưng ổn định. Các lịch đánh giá thông thường có thể bỏ sót những vấn đề này do không đánh giá đủ thường xuyên!
Để kiểm tra điều này, bạn có thể huấn luyện cho một lần chạy rút gọn chỉ khoảng 500 bước bằng cách sử dụng lr = 2 * current best, nhưng đánh giá từng bước.
Các cách khắc phục có thể áp dụng cho các mẫu bất ổn thường gặp
Hãy cân nhắc những cách khắc phục có thể sau đây đối với các mẫu bất ổn thường gặp:
- Áp dụng giai đoạn khởi động tốc độ học. Điều này phù hợp nhất với tình trạng không ổn định trong quá trình huấn luyện ban đầu.
- Áp dụng tính năng giới hạn độ dốc. Điều này tốt cho cả tình trạng không ổn định khi bắt đầu và giữa quá trình huấn luyện, đồng thời có thể khắc phục một số lỗi khởi tạo ban đầu mà quá trình khởi động không thể khắc phục.
- Hãy thử một trình tối ưu hoá mới. Đôi khi, Adam có thể xử lý những điểm không ổn định mà Momentum không thể. Đây là một lĩnh vực nghiên cứu đang phát triển mạnh mẽ.
- Đảm bảo rằng bạn đang sử dụng các phương pháp hay nhất và chế độ khởi tạo tốt nhất cho cấu trúc mô hình của mình (các ví dụ sẽ được trình bày sau). Thêm các kết nối còn lại và chuẩn hoá nếu mô hình chưa có các kết nối này.
- Chuẩn hoá là thao tác cuối cùng trước phần dư. Ví dụ:
x + Norm(f(x)). Xin lưu ý rằngNorm(x + f(x))có thể gây ra vấn đề. - Hãy thử khởi tạo các nhánh còn lại thành 0. (Xem ReZero is All You Need: Fast Convergence at Large Depth (ReZero là tất cả những gì bạn cần: Hội tụ nhanh ở độ sâu lớn).)
- Giảm tốc độ học. Đây là biện pháp cuối cùng.
Giai đoạn khởi động tốc độ học

Thời điểm áp dụng giai đoạn khởi động tốc độ học


Hình 7a cho thấy một biểu đồ trục siêu tham số cho biết một mô hình đang gặp phải tình trạng không ổn định khi tối ưu hoá, vì tốc độ học tập tốt nhất nằm ngay ở rìa của sự không ổn định.
Hình 7b cho thấy cách kiểm tra lại điều này bằng cách xem xét tổn thất khi huấn luyện của một mô hình được huấn luyện với tốc độ học tập lớn hơn 5 lần hoặc 10 lần so với mức đỉnh này. Nếu biểu đồ đó cho thấy tổn thất tăng đột ngột sau khi giảm đều (ví dụ: ở bước ~10k trong hình trên), thì có thể mô hình gặp phải tình trạng không ổn định khi tối ưu hoá.
Cách áp dụng giai đoạn khởi động tốc độ học

Đặt unstable_base_learning_rate là tốc độ học mà mô hình trở nên không ổn định, bằng cách sử dụng quy trình trước đó.
Giai đoạn khởi động bao gồm việc thêm trước một lịch trình tốc độ học tập giúp tăng tốc độ học tập từ 0 lên một giá trị base_learning_rate ổn định nào đó, ít nhất là lớn hơn unstable_base_learning_rate một bậc.
Theo mặc định, hệ thống sẽ thử base_learning_rate có kích thước gấp 10 lần unstable_base_learning_rate. Mặc dù lưu ý rằng bạn có thể chạy lại toàn bộ quy trình này cho khoảng 100 lần unstable_base_learning_rate. Lịch trình cụ thể như sau:
- Tăng tốc từ 0 đến base_learning_rate trong warmup_steps.
- Huấn luyện ở tốc độ không đổi cho post_warmup_steps.
Mục tiêu của bạn là tìm ra số lượng warmup_steps ngắn nhất cho phép bạn truy cập vào tốc độ học tập cao hơn nhiều so với unstable_base_learning_rate.
Vì vậy, đối với mỗi base_learning_rate, bạn cần điều chỉnh warmup_steps và post_warmup_steps. Bạn thường có thể đặt post_warmup_steps thành 2*warmup_steps.
Bạn có thể điều chỉnh giai đoạn khởi động một cách độc lập với lịch biểu giảm dần hiện có. warmup_steps cần được quét ở một số bậc độ lớn khác nhau. Ví dụ: một nghiên cứu mẫu có thể thử [10, 1000, 10,000, 100,000]. Điểm lớn nhất có thể không được vượt quá 10% của max_train_steps.
Sau khi thiết lập được một warmup_steps không làm tăng tốc độ huấn luyện ở base_learning_rate, bạn nên áp dụng warmup_steps đó cho mô hình cơ sở.
Về cơ bản, hãy thêm lịch biểu này vào lịch biểu hiện có và sử dụng lựa chọn điểm kiểm tra tối ưu đã thảo luận ở trên để so sánh thử nghiệm này với đường cơ sở. Ví dụ: nếu ban đầu chúng ta có 10.000 max_train_steps và thực hiện warmup_steps trong 1.000 bước, thì quy trình huấn luyện mới sẽ chạy tổng cộng 11.000 bước.
Nếu cần warmup_steps dài để huấn luyện ổn định (>5% max_train_steps), bạn có thể cần tăng max_train_steps để tính đến điều này.
Không có giá trị "điển hình" nào trên toàn bộ phạm vi khối lượng công việc. Một số mô hình chỉ cần 100 bước, trong khi những mô hình khác (đặc biệt là các mô hình biến đổi) có thể cần đến 40.000 bước trở lên.
Giới hạn độ dốc

Tính năng giới hạn độ dốc hữu ích nhất khi xảy ra các vấn đề về độ dốc lớn hoặc độ dốc bất thường. Tính năng Cắt chuyển sắc có thể khắc phục một trong hai vấn đề sau:
- Tính không ổn định trong quá trình huấn luyện ban đầu (chuẩn độ dốc lớn từ sớm)
- Sự không ổn định trong quá trình huấn luyện (đột ngột tăng độ dốc trong quá trình huấn luyện).
Đôi khi, thời gian khởi động dài hơn có thể khắc phục những điểm không ổn định mà việc cắt không khắc phục được; để biết thông tin chi tiết, hãy xem phần Khởi động tốc độ học tập.
🤖 Vậy còn việc cắt đoạn trong quá trình khởi động thì sao?
Ngưỡng lý tưởng cho đoạn trích nằm ngay trên mức chuẩn "điển hình".
Sau đây là ví dụ về cách thực hiện việc cắt chuyển màu:
- Nếu chuẩn của độ dốc $\left | g \right |$ lớn hơn ngưỡng cắt độ dốc $\lambda$, thì hãy thực hiện ${g}'= \lambda \times \frac{g}{\left | g \right |}$ trong đó ${g}'$ là độ dốc mới.
Ghi lại chuẩn độ dốc chưa được cắt trong quá trình huấn luyện. Theo mặc định, hãy tạo:
- Biểu đồ chuẩn độ dốc so với bước
- Biểu đồ tần suất của các chuẩn độ dốc được tổng hợp trên tất cả các bước
Chọn một ngưỡng cắt theo độ dốc dựa trên phân vị thứ 90 của các chuẩn độ dốc. Ngưỡng này phụ thuộc vào khối lượng công việc, nhưng 90% là một điểm khởi đầu tốt. Nếu 90% không hiệu quả, bạn có thể điều chỉnh ngưỡng này.
🤖 Thế còn một chiến lược thích ứng thì sao?
Nếu bạn thử cắt chuyển màu và vấn đề về độ ổn định vẫn còn, bạn có thể thử cắt chuyển màu mạnh hơn; tức là bạn có thể giảm ngưỡng.
Việc cắt gradient cực kỳ mạnh (tức là >50% các bản cập nhật bị cắt) về cơ bản là một cách lạ để giảm tốc độ học. Nếu thấy mình đang sử dụng tính năng giới hạn cực kỳ mạnh mẽ, có lẽ bạn chỉ nên giảm tốc độ học.
Tại sao bạn gọi tốc độ học và các tham số tối ưu hoá khác là siêu tham số? Chúng không phải là các tham số của bất kỳ bản phân phối nào trước đó.
Thuật ngữ "siêu tham số" có ý nghĩa chính xác trong công nghệ học máy Bayesian, vì vậy, việc coi tốc độ học và hầu hết các tham số học sâu có thể điều chỉnh khác là "siêu tham số" có thể coi là sử dụng sai thuật ngữ. Chúng tôi muốn sử dụng thuật ngữ "siêu tham số" cho tốc độ học, tham số kiến trúc và tất cả những thứ có thể điều chỉnh khác trong học sâu. Đó là vì siêu tham số tránh được khả năng gây nhầm lẫn do sử dụng sai từ "siêu tham số". Sự nhầm lẫn này đặc biệt dễ xảy ra khi thảo luận về việc tối ưu hoá theo phương pháp Bayesian, trong đó các mô hình bề mặt phản hồi xác suất có siêu tham số thực riêng.
Rất tiếc, mặc dù có thể gây nhầm lẫn, nhưng thuật ngữ "siêu tham số" đã trở nên cực kỳ phổ biến trong cộng đồng học sâu. Do đó, đối với tài liệu này (dành cho nhiều đối tượng, bao gồm cả những người không biết đến thuật ngữ kỹ thuật này), chúng tôi đã chọn đóng góp vào một nguồn gây nhầm lẫn trong lĩnh vực này với hy vọng tránh được một nguồn khác. Tuy nhiên, chúng tôi có thể đưa ra lựa chọn khác khi xuất bản một bài nghiên cứu và chúng tôi khuyến khích người khác sử dụng "siêu tham số" thay vì "tham số" trong hầu hết các bối cảnh.
Tại sao không nên điều chỉnh kích thước lô để cải thiện trực tiếp hiệu suất của tập hợp xác thực?
Việc thay đổi kích thước lô mà không thay đổi bất kỳ chi tiết nào khác của quy trình huấn luyện thường ảnh hưởng đến hiệu suất của tập hợp xác thực. Tuy nhiên, sự khác biệt về hiệu suất của tập hợp xác thực giữa hai kích thước lô thường biến mất nếu quy trình huấn luyện được tối ưu hoá độc lập cho từng kích thước lô.
Các siêu tham số tương tác mạnh nhất với kích thước lô và do đó, quan trọng nhất để điều chỉnh riêng cho từng kích thước lô là các siêu tham số của trình tối ưu hoá (ví dụ: tốc độ học, động lượng) và các siêu tham số điều chuẩn. Kích thước lô nhỏ hơn sẽ tạo ra nhiều nhiễu hơn cho thuật toán huấn luyện do phương sai mẫu. Nhiễu này có thể có tác dụng điều chỉnh. Do đó, kích thước lô lớn hơn có thể dễ bị điều chỉnh quá mức hơn và có thể yêu cầu điều chỉnh mạnh hơn và/hoặc các kỹ thuật điều chỉnh bổ sung. Ngoài ra, bạn có thể cần điều chỉnh số lượng bước huấn luyện khi thay đổi kích thước lô.
Sau khi xem xét tất cả những hiệu ứng này, không có bằng chứng thuyết phục nào cho thấy kích thước lô ảnh hưởng đến hiệu suất xác thực tối đa có thể đạt được. Để biết thông tin chi tiết, hãy xem Shallue và cộng sự, 2018.
Những quy tắc cập nhật cho tất cả các thuật toán tối ưu hoá phổ biến là gì?
Phần này cung cấp các quy tắc cập nhật cho một số thuật toán tối ưu hoá phổ biến.
Phương pháp giảm độ dốc ngẫu nhiên (SGD)
\[\theta_{t+1} = \theta_{t} - \eta_t \nabla \mathcal{l}(\theta_t)\]
Trong đó, $\eta_t$ là tốc độ học tại bước $t$.
Đà phát triển
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t v_{t+1}\]
Trong đó $\eta_t$ là tốc độ học tại bước $t$ và $\gamma$ là hệ số động lượng.
Nesterov
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t ( \gamma v_{t+1} + \nabla \mathcal{l}(\theta_{t}) )\]
Trong đó $\eta_t$ là tốc độ học tại bước $t$ và $\gamma$ là hệ số động lượng.
RMSProp
\[v_0 = 1 \text{, } m_0 = 0\]
\[v_{t+1} = \rho v_{t} + (1 - \rho) \nabla \mathcal{l}(\theta_t)^2\]
\[m_{t+1} = \gamma m_{t} + \frac{\eta_t}{\sqrt{v_{t+1} + \epsilon}}\nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - m_{t+1}\]
ADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l}(\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{m_{t+1}}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
NADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l} (\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{\beta_1 m_{t+1} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]