จะแก้ไขข้อบกพร่องและลดปัญหาการเพิ่มประสิทธิภาพที่ไม่สำเร็จได้อย่างไร
สรุป: หากโมเดลพบปัญหาในการเพิ่มประสิทธิภาพ คุณควรแก้ไขปัญหาก่อนที่จะลองทำอย่างอื่น การวินิจฉัยและการแก้ไข การฝึกที่ไม่สำเร็จเป็นประเด็นที่ยังมีการศึกษาวิจัยกันอย่างต่อเนื่อง

โปรดสังเกตสิ่งต่อไปนี้เกี่ยวกับรูปที่ 4
- การเปลี่ยนระยะก้าวย่างไม่ทำให้ประสิทธิภาพลดลงที่อัตราการเรียนรู้ต่ำ
- อัตราการเรียนรู้ที่สูงจะฝึกโมเดลได้ไม่ดีอีกต่อไปเนื่องจากความไม่เสถียร
- การใช้การวอร์มอัตรการเรียนรู้ 1, 000 ขั้นตอนจะช่วยแก้ปัญหาความไม่เสถียรในกรณีนี้ได้ ทำให้การฝึกเสถียรที่อัตรการเรียนรู้สูงสุด 0.1
การระบุภาระงานที่ไม่เสถียร
เวิร์กโหลดจะไม่มีเสถียรภาพหากอัตราการเรียนรู้มีขนาดใหญ่เกินไป ความไม่เสถียรจะเป็นปัญหาเมื่อทำให้คุณต้องใช้อัตราการเรียนรู้ ที่เล็กเกินไป ความไม่เสถียรของการฝึกมีอย่างน้อย 2 ประเภทที่ควรแยกแยะ ได้แก่
- ความไม่เสถียรเมื่อเริ่มต้นหรือในช่วงต้นของการฝึก
- ความไม่เสถียรอย่างกะทันหันในช่วงกลางของการฝึก
คุณสามารถใช้แนวทางที่เป็นระบบเพื่อระบุปัญหาด้านความเสถียรใน เวิร์กโหลดได้โดยทำดังนี้
- ทำการสวอปอัตราการเรียนรู้และค้นหาอัตราการเรียนรู้ที่ดีที่สุด lr*
- พล็อตเส้นโค้งการสูญเสียการฝึกสำหรับอัตราการเรียนรู้ที่สูงกว่า lr* เล็กน้อย
- หากอัตราการเรียนรู้ > lr* แสดงความไม่เสถียรของ Loss (Loss เพิ่มขึ้น ไม่ ลดลงในช่วงการฝึก) การแก้ไขความไม่เสถียร มักจะปรับปรุงการฝึก
บันทึกบรรทัดฐาน L2 ของการไล่ระดับการสูญเสียทั้งหมดระหว่างการฝึก เนื่องจากค่าที่ผิดปกติ อาจทำให้เกิดความไม่เสถียรที่ไม่ถูกต้องในช่วงกลางของการฝึก ซึ่งจะช่วย บอกระดับความรุนแรงในการตัดเกรดหรืออัปเดตน้ำหนัก
หมายเหตุ: โมเดลบางรุ่นแสดงความไม่เสถียรในช่วงแรกๆ ตามด้วยการกู้คืนที่ ส่งผลให้การฝึกช้าแต่เสถียร กำหนดการประเมินทั่วไปอาจพลาดปัญหาเหล่านี้ เนื่องจากไม่ได้ประเมินบ่อยพอ
หากต้องการตรวจสอบ ให้ฝึกโมเดลโดยใช้การเรียกใช้แบบย่อเพียงประมาณ 500 ขั้นตอน
โดยใช้ lr = 2 * current best แต่ให้ประเมินทุกขั้นตอน

การแก้ไขที่เป็นไปได้สำหรับรูปแบบความไม่เสถียรที่พบบ่อย
ลองใช้วิธีแก้ไขต่อไปนี้สำหรับรูปแบบความไม่เสถียรที่พบได้ทั่วไป
- ใช้การวอร์มอัพอัตราการเรียนรู้ วิธีนี้เหมาะที่สุดสำหรับความไม่เสถียรของการฝึกในช่วงแรก
- ใช้การตัดการไล่ระดับสี ซึ่งเหมาะสำหรับความไม่เสถียรทั้งในช่วงต้นและช่วงกลางของการฝึก และอาจแก้ไขการเริ่มต้นที่ไม่ดีบางอย่างที่การวอร์มอัพทำไม่ได้
- ลองใช้เครื่องมือเพิ่มประสิทธิภาพใหม่ บางครั้ง Adam ก็จัดการความไม่เสถียรที่ Momentum ทำไม่ได้ ซึ่งเป็นประเด็นที่ยังมีการศึกษาวิจัยกันอย่างต่อเนื่อง
- ตรวจสอบว่าคุณใช้แนวทางปฏิบัติแนะนำและการเริ่มต้นที่ดีที่สุด สำหรับสถาปัตยกรรมโมเดล (ตัวอย่างที่จะตามมา) เพิ่มการเชื่อมต่อที่เหลือ และการทำให้เป็นมาตรฐานหากโมเดลยังไม่มี
- ปรับให้เป็นมาตรฐานเป็นการดำเนินการสุดท้ายก่อนที่ค่าที่เหลือ ตัวอย่างเช่น
x + Norm(f(x))โปรดทราบว่าNorm(x + f(x))อาจทำให้เกิดปัญหา - ลองเริ่มต้นกิ่งก้านที่เหลือเป็น 0 (ดู ReZero is All You Need: Fast Convergence at Large Depth)
- ลดอัตราการเรียนรู้ นี่เป็นทางเลือกสุดท้าย
การวอร์มอัพอัตราการเรียนรู้

กรณีที่ควรใช้การวอร์มอัพอัตราการเรียนรู้

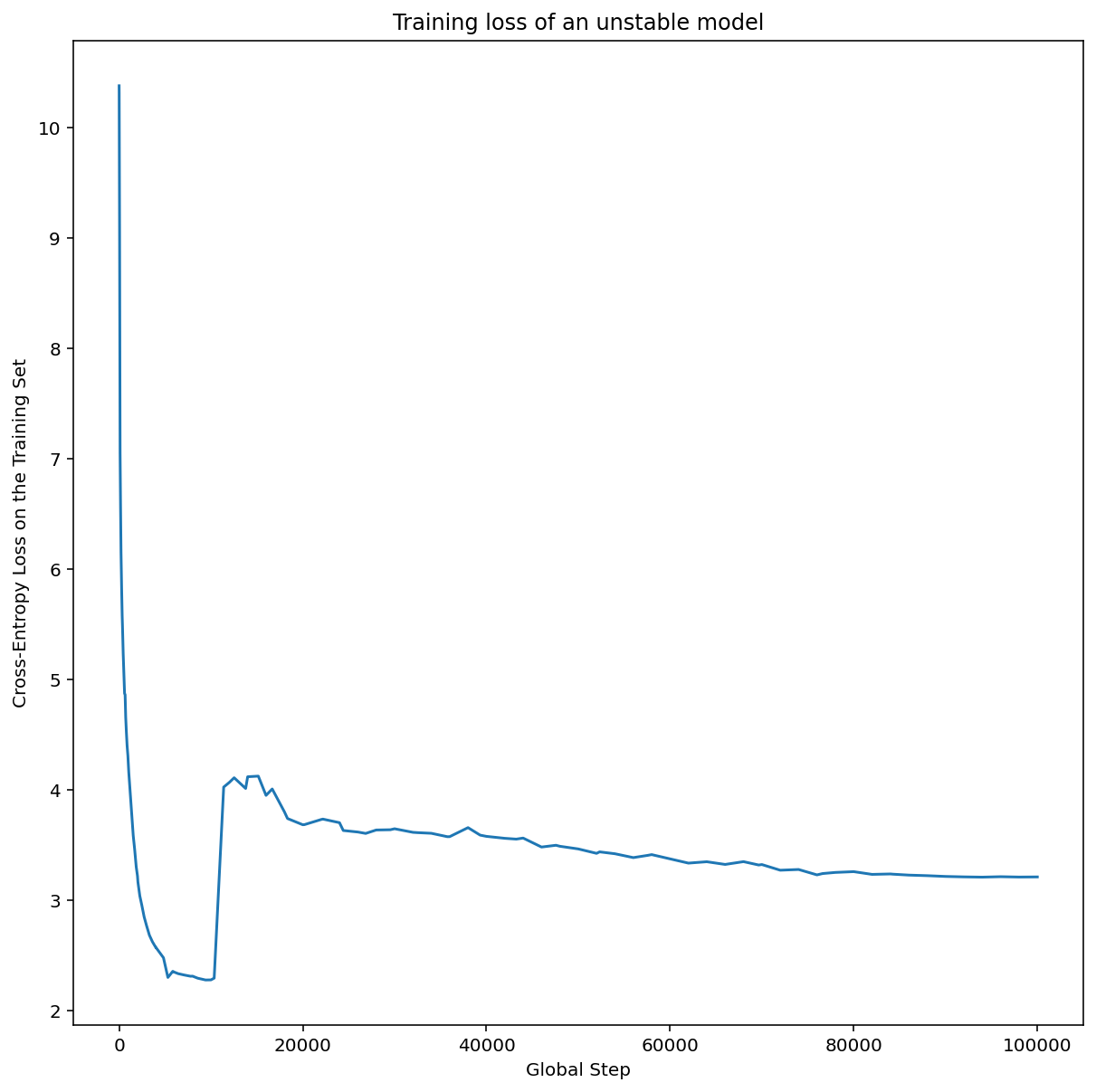
รูปที่ 7ก แสดงพล็อตแกนไฮเปอร์พารามิเตอร์ที่ระบุโมเดล ที่ประสบปัญหาความไม่เสถียรในการเพิ่มประสิทธิภาพ เนื่องจากอัตราการเรียนรู้ที่ดีที่สุด อยู่ตรงขอบของความไม่เสถียร
รูปที่ 7b แสดงวิธีตรวจสอบอีกครั้งโดยการตรวจสอบการสูญเสียจากการฝึกของโมเดลที่ฝึกด้วยอัตราการเรียนรู้ที่ใหญ่กว่าจุดสูงสุดนี้ 5 เท่าหรือ 10 เท่า หากพล็อตดังกล่าวแสดงการเพิ่มขึ้นอย่างฉับพลันของการสูญเสียหลังจากที่ลดลงอย่างต่อเนื่อง (เช่น ที่ขั้นตอน ~10,000 ในรูปด้านบน) แสดงว่าโมเดลอาจประสบปัญหาความไม่เสถียรในการเพิ่มประสิทธิภาพ
วิธีใช้การวอร์มอัพอัตราการเรียนรู้

ให้ unstable_base_learning_rate เป็นอัตราการเรียนรู้ที่โมเดล
เริ่มไม่เสถียรโดยใช้กระบวนการก่อนหน้า
การวอร์มอัพเกี่ยวข้องกับการเพิ่มกำหนดการอัตราการเรียนรู้ที่เพิ่มอัตราการเรียนรู้จาก 0 เป็นค่า base_learning_rate ที่เสถียร ซึ่งมีขนาดใหญ่กว่า unstable_base_learning_rate อย่างน้อย 10 เท่า
ค่าเริ่มต้นคือการลองใช้ base_learning_rate ที่มีขนาด 10 เท่า
unstable_base_learning_rate แม้ว่าคุณจะทำตามขั้นตอนทั้งหมดนี้อีกครั้งสำหรับค่าประมาณ 100 เท่า
unstable_base_learning_rateได้ กำหนดการที่เฉพาะเจาะจงมีดังนี้
- เพิ่มจาก 0 เป็น base_learning_rate ในช่วง warmup_steps
- ฝึกที่อัตราคงที่สำหรับ post_warmup_steps
เป้าหมายของคุณคือการค้นหาจำนวน warmup_steps ที่น้อยที่สุดซึ่งช่วยให้คุณ
เข้าถึงอัตราการเรียนรู้สูงสุดที่สูงกว่า
unstable_base_learning_rate มาก
ดังนั้นสำหรับ base_learning_rate แต่ละรายการ คุณต้องปรับ warmup_steps และ
post_warmup_steps โดยปกติแล้วคุณสามารถตั้งค่า post_warmup_steps เป็น
2*warmup_steps ได้
คุณปรับการวอร์มอัพแยกจากกำหนดการลดอัตราการเรียนรู้ที่มีอยู่ได้ warmup_steps
ควรมีการกวาดที่ลำดับขนาดที่แตกต่างกัน 2-3 รายการ เช่น การศึกษาตัวอย่างอาจลองใช้ [10, 1000, 10,000, 100,000] จุดที่ใหญ่ที่สุดที่เป็นไปได้
ไม่ควรเกิน 10% ของ max_train_steps
เมื่อสร้าง warmup_steps ที่ไม่ทำให้การฝึกโมเดลที่ base_learning_rate
ล้มเหลวแล้ว ก็ควรนำไปใช้กับโมเดลพื้นฐาน
โดยพื้นฐานแล้ว ให้เพิ่มกำหนดการนี้ไว้ที่ด้านหน้าของกำหนดการที่มีอยู่ และใช้
การเลือกจุดตรวจสอบที่เหมาะสมซึ่งกล่าวถึงข้างต้นเพื่อเปรียบเทียบการทดสอบนี้
กับเกณฑ์พื้นฐาน ตัวอย่างเช่น หากเดิมเรามี 10,000 max_train_steps
และทำ warmup_steps เป็นเวลา 1,000 ขั้นตอน กระบวนการฝึกใหม่ควร
ทำงานเป็นเวลา 11,000 ขั้นตอนโดยรวม
หากต้องใช้ warmup_steps นานเพื่อให้การฝึกเสถียร (>5% ของ
max_train_steps) คุณอาจต้องเพิ่ม max_train_steps เพื่อให้สอดคล้องกับ
ข้อกำหนดนี้
จริงๆ แล้วไม่มีค่า "ทั่วไป" ในช่วงภาระงานทั้งหมด โมเดลบางอย่างต้องการเพียง 100 ขั้นตอน ในขณะที่โมเดลอื่นๆ (โดยเฉพาะ Transformer) อาจต้องการ 40, 000 ขั้นตอนขึ้นไป
การตัดการไล่ระดับสี

การตัดเกรดเดียนต์จะมีประโยชน์มากที่สุดเมื่อเกิดปัญหาเกี่ยวกับเกรดเดียนต์ขนาดใหญ่หรือค่าผิดปกติ การตัดเกรดสามารถแก้ไขปัญหาต่อไปนี้ได้
- ความไม่เสถียรของการฝึกในช่วงแรก (ค่าบรรทัดฐานของเกรเดียนต์ขนาดใหญ่ในช่วงแรก)
- ความไม่เสถียรระหว่างการฝึก (การเพิ่มขึ้นของค่าการไล่ระดับอย่างฉับพลันระหว่างการฝึก)
บางครั้งระยะเวลาการวอร์มอัพที่นานขึ้นอาจแก้ไขความไม่เสถียรที่การคลิปทำไม่ได้ ดูรายละเอียดได้ที่การวอร์มอัพอัตราการเรียนรู้
🤖 แล้วการตัดต่อระหว่างการวอร์มอัพล่ะ
เกณฑ์คลิปที่เหมาะสมจะอยู่เหนือค่าปกติของค่าการไล่ระดับสี "ทั่วไป"
ต่อไปนี้เป็นตัวอย่างวิธีใช้การตัดเกรด
- หากบรรทัดฐานของเกรเดียนต์ $\left | g \right |$ มากกว่า เกณฑ์การตัดเกรเดียนต์ $\lambda$ ให้ทำ ${g}'= \lambda \times \frac{g}{\left | g \right |}$ โดยที่ ${g}'$ คือเกรเดียนต์ใหม่
บันทึกบรรทัดฐานการไล่ระดับที่ไม่ได้ตัดระหว่างการฝึก โดยค่าเริ่มต้น ระบบจะสร้าง
- พล็อตของบรรทัดฐานการไล่ระดับสีเทียบกับขั้น
- ฮิสโทแกรมของบรรทัดฐานการไล่ระดับที่รวบรวมไว้ในทุกขั้นตอน
เลือกเกณฑ์การตัดการไล่ระดับสีตามเปอร์เซ็นไทล์ที่ 90 ของ ค่ามาตรฐานการไล่ระดับสี เกณฑ์จะขึ้นอยู่กับปริมาณงาน แต่ 90% เป็นจุดเริ่มต้นที่ดี หาก 90% ไม่ได้ผล คุณสามารถปรับเกณฑ์นี้ได้
🤖 แล้วกลยุทธ์แบบปรับเปลี่ยนได้ล่ะ
หากลองใช้การตัดค่าความชันแล้ว แต่ปัญหาความไม่เสถียรยังคงอยู่ คุณสามารถลองใช้การตัดค่าความชันที่เข้มงวดมากขึ้นได้ นั่นคือลดเกณฑ์ให้ต่ำลง
การจำกัดค่าความชันที่รุนแรงมาก (กล่าวคือ มีการจำกัดการอัปเดตมากกว่า 50%) เป็นวิธีที่แปลกในการลดอัตราการเรียนรู้ หากคุณพบว่าตัวเองใช้การจำกัดค่าที่รุนแรงมาก คุณอาจ ควรลดอัตราการเรียนรู้แทน
เหตุใดคุณจึงเรียกอัตราการเรียนรู้และพารามิเตอร์การเพิ่มประสิทธิภาพอื่นๆ ว่าไฮเปอร์พารามิเตอร์ โดยไม่ใช่พารามิเตอร์ของการแจกแจงก่อนหน้า
คำว่า "ไฮเปอร์พารามิเตอร์" มีความหมายที่แน่นอนในแมชชีนเลิร์นนิงแบบเบย์ ดังนั้นการอ้างอิงอัตราการเรียนรู้และพารามิเตอร์ดีปเลิร์นนิงอื่นๆ ที่ปรับได้ส่วนใหญ่เป็น "ไฮเปอร์พารามิเตอร์" จึงอาจเป็นการใช้คำศัพท์ในทางที่ผิด เราขอแนะนำให้ใช้คำว่า "Metaparameter" สำหรับอัตราการเรียนรู้ พารามิเตอร์สถาปัตยกรรม และสิ่งอื่นๆ ทั้งหมดที่ปรับได้ในการเรียนรู้เชิงลึก เนื่องจากเมตาพารามิเตอร์ช่วยหลีกเลี่ยงความสับสนที่อาจเกิดขึ้นจากการใช้คำว่า "ไฮเปอร์พารามิเตอร์" ในทางที่ผิด ความสับสนนี้มีแนวโน้มที่จะเกิดขึ้นโดยเฉพาะ เมื่อพูดถึงการเพิ่มประสิทธิภาพแบบเบย์ ซึ่งโมเดลพื้นผิวการตอบสนองเชิงความน่าจะเป็น มีไฮเปอร์พารามิเตอร์ที่แท้จริงของตัวเอง
ขออภัย แม้ว่าคำว่า "ไฮเปอร์พารามิเตอร์" อาจทำให้เกิดความสับสน แต่ก็เป็นคำที่ใช้กันอย่างแพร่หลายในชุมชนดีปเลิร์นนิง ดังนั้น สำหรับเอกสารนี้ซึ่งมีไว้สำหรับกลุ่มเป้าหมายในวงกว้าง ซึ่งรวมถึง ผู้คนจำนวนมากที่ไม่น่าจะทราบถึงรายละเอียดทางเทคนิคนี้ เราจึงเลือกที่จะ เป็นส่วนหนึ่งของแหล่งที่มาของความสับสนในฟิลด์นี้ โดยหวังว่าจะหลีกเลี่ยง ความสับสนอีกแหล่งหนึ่งได้ อย่างไรก็ตาม เราอาจเลือกใช้คำอื่นเมื่อ เผยแพร่เอกสารงานวิจัย และขอแนะนำให้ผู้อื่นใช้คำว่า "พารามิเตอร์เมตา" แทนในบริบทส่วนใหญ่
เหตุใดจึงไม่ควรปรับขนาดกลุ่มโดยตรงเพื่อปรับปรุงประสิทธิภาพชุดข้อมูลการตรวจสอบ
การเปลี่ยนขนาดกลุ่มโดยไม่เปลี่ยนรายละเอียดอื่นๆ ของไปป์ไลน์การฝึกมักจะส่งผลต่อประสิทธิภาพชุดข้อมูลการตรวจสอบ อย่างไรก็ตาม ความแตกต่างของประสิทธิภาพชุดการตรวจสอบระหว่างขนาดกลุ่ม 2 ขนาดมักจะหายไปหากไปป์ไลน์การฝึกได้รับการเพิ่มประสิทธิภาพแยกกันสำหรับแต่ละขนาดกลุ่ม
ไฮเปอร์พารามิเตอร์ที่มีปฏิสัมพันธ์กับขนาดกลุ่มมากที่สุด และมีความสําคัญที่สุดในการปรับแยกกันสําหรับขนาดกลุ่มแต่ละขนาด คือไฮเปอร์พารามิเตอร์ของเครื่องมือเพิ่มประสิทธิภาพ (เช่น อัตราการเรียนรู้ โมเมนตัม) และไฮเปอร์พารามิเตอร์การกําหนดค่า ขนาดกลุ่มเล็กจะทำให้เกิด สัญญาณรบกวนมากขึ้นในอัลกอริทึมการฝึกเนื่องจากความแปรปรวนของตัวอย่าง ซึ่งอาจ มีผลในการปรับค่า ดังนั้น ขนาดกลุ่มที่ใหญ่ขึ้นจึงมีแนวโน้มที่จะเกิดการปรับมากเกินไปได้มากกว่า และอาจต้องใช้การทำให้เป็นปกติที่เข้มงวดขึ้นและ/หรือเทคนิคการทำให้เป็นปกติเพิ่มเติม นอกจากนี้ คุณอาจต้องปรับจำนวน ขั้นตอนการฝึกเมื่อเปลี่ยน ขนาดกลุ่ม
เมื่อพิจารณาถึงผลกระทบทั้งหมดเหล่านี้แล้ว ก็ไม่มีหลักฐานที่น่าเชื่อถือว่าขนาดกลุ่มมีผลต่อประสิทธิภาพการตรวจสอบสูงสุดที่ทำได้ ดูรายละเอียดได้ที่ Shallue et al. 2018
กฎการอัปเดตสำหรับอัลกอริทึมการเพิ่มประสิทธิภาพยอดนิยมทั้งหมดมีอะไรบ้าง
ส่วนนี้จะอัปเดตกฎสำหรับอัลกอริทึมการเพิ่มประสิทธิภาพยอดนิยมหลายรายการ
การไล่ระดับสีแบบสุ่ม (SGD)
\[\theta_{t+1} = \theta_{t} - \eta_t \nabla \mathcal{l}(\theta_t)\]
โดย $\eta_t$ คืออัตราการเรียนรู้ที่ขั้นตอน $t$
สร้างกระแส
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t v_{t+1}\]
โดย $\eta_t$ คืออัตราการเรียนรู้ที่ขั้นตอน $t$ และ $\gamma$ คือสัมประสิทธิ์โมเมนตัม
Nesterov
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t ( \gamma v_{t+1} + \nabla \mathcal{l}(\theta_{t}) )\]
โดย $\eta_t$ คืออัตราการเรียนรู้ที่ขั้นตอน $t$ และ $\gamma$ คือสัมประสิทธิ์โมเมนตัม
RMSProp
\[v_0 = 1 \text{, } m_0 = 0\]
\[v_{t+1} = \rho v_{t} + (1 - \rho) \nabla \mathcal{l}(\theta_t)^2\]
\[m_{t+1} = \gamma m_{t} + \frac{\eta_t}{\sqrt{v_{t+1} + \epsilon}}\nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - m_{t+1}\]
ADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l}(\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{m_{t+1}}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
NADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l} (\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{\beta_1 m_{t+1} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]