最適化の失敗をデバッグして軽減するにはどうすればよいですか?
概要: モデルの最適化で問題が発生している場合は、他のことを試す前に問題を解決することが重要です。トレーニングの失敗を診断して修正することは、活発な研究分野です。

図 4 については、次の点に注意してください。
- ストライドを変更しても、学習率が低い場合にパフォーマンスが低下することはありません。
- 不安定なため、高い学習率ではうまくトレーニングできなくなります。
- 学習率のウォームアップを 1, 000 ステップ適用すると、この特定の不安定なインスタンスが解決され、最大学習率 0.1 で安定したトレーニングが可能になります。
不安定なワークロードの特定
学習率が大きすぎると、ワークロードが不安定になります。不安定さは、学習率を小さくせざるを得ない場合にのみ問題になります。トレーニングの不安定さには、少なくとも次の 2 つのタイプがあります。
- 初期化時またはトレーニングの初期段階での不安定性。
- トレーニング中に突然不安定になる。
次の操作を行うことで、ワークロードの安定性の問題を体系的に特定できます。
- 学習率スイープを実行して、最適な学習率 lr* を見つけます。
- lr* のわずかに上の学習率のトレーニング損失曲線をプロットします。
- 学習率が lr* より大きい場合に損失の不安定性(トレーニング期間中に損失が減少せずに増加する)が見られる場合は、不安定性を修正すると通常はトレーニングが改善されます。
トレーニング中に完全な損失勾配の L2 ノルムを記録します。外れ値によってトレーニングの途中で偽の不安定性が生じる可能性があるためです。これにより、グラデーションや重みの更新をどの程度積極的にクリップするかを判断できます。
注: 一部のモデルでは、非常に早い段階で不安定な状態になり、その後回復して、トレーニングが遅いながらも安定した状態になります。一般的な評価スケジュールでは、評価の頻度が十分でないため、これらの問題を見逃す可能性があります。
これを確認するには、lr = 2 * current best を使用して約 500 ステップの短縮実行でトレーニングしますが、各ステップを評価します。

一般的な不安定性のパターンに対する修正候補
一般的な不安定性のパターンに対する次の解決策を検討してください。
- 学習率のウォームアップを適用します。これは、トレーニングの初期の不安定性に最適です。
- 勾配のクリッピングを適用します。これはトレーニングの初期と中期の両方の不安定さに有効で、ウォームアップでは修正できない初期化の誤りを修正できる可能性があります。
- 新しいオプティマイザーを試してください。Adam は、Momentum では処理できない不安定さを処理できる場合があります。これは現在活発に研究が進められている分野です。
- モデル アーキテクチャにベスト プラクティスと最適な初期化を使用していることを確認します(例は後述)。モデルにまだ残差接続と正規化が含まれていない場合は、追加します。
- 残差の前の最後のオペレーションとして正規化します。(例:
x + Norm(f(x)))。Norm(x + f(x))は問題を引き起こす可能性があることに注意してください。 - 残差ブランチを 0 に初期化してみてください。(ReZero is All You Need: Fast Convergence at Large Depth. を参照)。
- 学習率を下げる。これは最後の手段です。
学習率のウォームアップ

学習率のウォームアップを適用するタイミング


図 7a は、最適な学習率が不安定性の境界にあるため、最適化の不安定性を経験しているモデルを示すハイパーパラメータ軸プロットです。
図 7b は、このピークの 5 倍または 10 倍の学習率でトレーニングされたモデルのトレーニング損失を調べることで、このことを再確認する方法を示しています。そのプロットで、損失が着実に減少した後で急激に増加している場合(上の図のステップ 10k など)、モデルは最適化の不安定性に苦しんでいる可能性があります。
学習率のウォームアップを適用する方法

上記の手順を使用して、モデルが不安定になる学習率を unstable_base_learning_rate とします。
ウォームアップでは、学習率を 0 から unstable_base_learning_rate より 1 桁以上大きい安定した base_learning_rate まで徐々に増やす学習率スケジュールを先頭に追加します。デフォルトでは、unstable_base_learning_rate の 10 倍の base_learning_rate が試行されます。ただし、この手順全体を 100 倍の unstable_base_learning_rate で再度実行することは可能です。具体的なスケジュールは次のとおりです。
- warmup_steps にわたって 0 から base_learning_rate までランプアップします。
- post_warmup_steps の間、一定のレートでトレーニングします。
目標は、unstable_base_learning_rate よりもはるかに高いピーク学習率にアクセスできる warmup_steps の最小数を見つけることです。そのため、各 base_learning_rate に対して warmup_steps と post_warmup_steps を調整する必要があります。通常は、post_warmup_steps を 2*warmup_steps に設定しても問題ありません。
ウォームアップは、既存の減衰スケジュールとは別に調整できます。warmup_steps は、いくつかの異なる桁でスイープする必要があります。たとえば、サンプルスタディで [10, 1000, 10,000, 100,000] を試すことができます。実行可能な最大ポイントは max_train_steps の 10% を超えないようにしてください。
base_learning_rate でトレーニングが爆発しない warmup_steps が確立されたら、ベースライン モデルに適用する必要があります。基本的には、このスケジュールを既存のスケジュールの先頭に追加し、上記の最適なチェックポイント選択を使用して、このテストをベースラインと比較します。たとえば、元々 10,000 個の max_train_steps があり、1,000 ステップで warmup_steps を実行した場合、新しいトレーニング手順は合計 11,000 ステップで実行されます。
安定したトレーニングに長い warmup_steps が必要な場合(max_train_steps の 5% 超)、これを考慮して max_train_steps を増やす必要がある場合があります。
ワークロードの全範囲にわたって「典型的な」値は存在しません。モデルによっては 100 ステップで済むものもあれば、4 万ステップ以上必要なものもあります(特にトランスフォーマー)。
勾配クリッピング
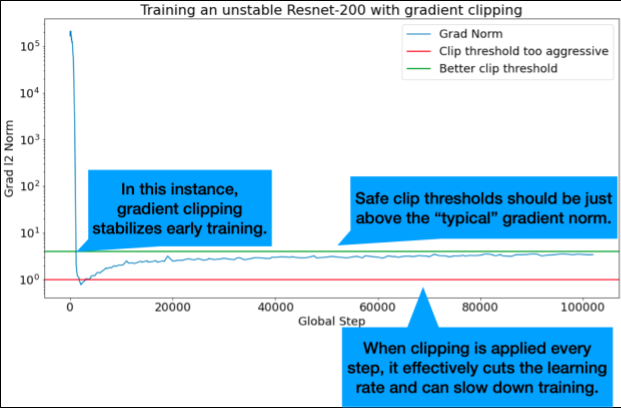
グラデーションのクリッピングは、グラデーションの大きな問題や外れ値の問題が発生した場合に最も役立ちます。グラデーション クリッピングは、次のいずれかの問題を解決できます。
- トレーニングの初期の不安定性(初期の大きなグラデーション ノルム)
- トレーニング中の不安定性(トレーニング中に突然勾配が急上昇する)。
クリッピングでは修正できない不安定さを、ウォームアップ期間を長くすることで修正できる場合があります。詳しくは、学習率のウォームアップをご覧ください。
🤖 ウォームアップ中のクリッピングはどうなりますか?
理想的なクリップしきい値は、「標準」のグラデーション ノルムをわずかに上回る値です。
以下に、グラデーション クリッピングの例を示します。
- グラデーションのノルム $\left | g \right |$ がグラデーション クリッピングしきい値 $\lambda$ より大きい場合は、${g}'= \lambda \times \frac{g}{\left | g \right |}$ を実行します。ここで、${g}'$ は新しいグラデーションです。
トレーニング中にクリップされていないグラデーション ノルムをログに記録します。デフォルトで生成:
- 勾配ノルムとステップのプロット
- すべてのステップで集計された勾配ノルムのヒストグラム
グラデーションのノルムの 90 パーセンタイルに基づいて、グラデーションのクリッピングしきい値を選択します。しきい値はワークロードによって異なりますが、90% から始めることをおすすめします。90% でうまくいかない場合は、このしきい値を調整できます。
🤖 適応型戦略のようなものはないのでしょうか?
グラデーション クリッピングを試しても不安定性の問題が解決しない場合は、しきい値を小さくして、より厳しくグラデーション クリッピングを試すことができます。
非常にアグレッシブな勾配クリッピング(つまり、更新の 50% 以上がクリップされる)は、本質的に学習率を下げる奇妙な方法です。クリッピングを過度に大きくしている場合は、学習率をカットする方がよいでしょう。
学習率やその他の最適化パラメータがハイパーパラメータと呼ばれるのはなぜですか?これらは事前分布のパラメータではありません。
「ハイパーパラメータ」という用語は、ベイズ ML では正確な意味を持ちます。そのため、学習率や他のほとんどの調整可能なディープ ラーニング パラメータを「ハイパーパラメータ」と呼ぶのは、用語の誤用と言えるでしょう。学習率、アーキテクチャ パラメータ、その他すべての調整可能なディープ ラーニングについては、「メタパラメータ」という用語を使用することをおすすめします。これは、メタパラメータが「ハイパーパラメータ」という単語の誤用による混乱を避けるためです。この混乱は、確率的応答曲面モデルに独自の真のハイパーパラメータがあるベイズ最適化について説明する場合に特に起こりやすくなります。
残念ながら、混乱を招く可能性はありますが、「ハイパーパラメータ」という用語は、ディープ ラーニング コミュニティで非常に一般的になっています。そのため、この技術的な詳細を認識していない可能性のある多くのユーザーを含む幅広いユーザーを対象としたこのドキュメントでは、別の混乱を避けるために、この分野の混乱の原因の 1 つに貢献することを選択しました。ただし、研究論文を公開する際には別の選択をする可能性があり、ほとんどのコンテキストでは「メタパラメータ」を使用することをおすすめします。
バッチサイズを調整して検証セットのパフォーマンスを直接改善すべきでないのはなぜですか?
バッチサイズを変更すると、トレーニング パイプラインの他の詳細を変更しなくても、検証セットのパフォーマンスに影響することがよくあります。ただし、トレーニング パイプラインがバッチサイズごとに個別に最適化されている場合、通常は 2 つのバッチサイズ間の検証セットのパフォーマンスの差はなくなります。
バッチサイズと最も強く相互作用し、したがってバッチサイズごとに個別に調整することが最も重要なハイパーパラメータは、オプティマイザーのハイパーパラメータ(学習率、モーメンタムなど)と正則化のハイパーパラメータです。バッチサイズが小さいほど、サンプル分散によりトレーニング アルゴリズムにノイズが多くなります。このノイズには正則化効果があります。したがって、バッチサイズが大きいほど過適合が発生しやすくなり、より強力な正則化や追加の正則化手法が必要になる可能性があります。また、バッチサイズを変更するときにトレーニング ステップ数を調整する必要がある場合もあります。
これらの影響をすべて考慮すると、バッチサイズが達成可能な最大検証パフォーマンスに影響するという説得力のある証拠はありません。詳しくは、Shallue et al. 2018 をご覧ください。
一般的な最適化アルゴリズムの更新ルールを教えてください。
このセクションでは、一般的な最適化アルゴリズムの更新ルールについて説明します。
確率的勾配降下法(SGD)
\[\theta_{t+1} = \theta_{t} - \eta_t \nabla \mathcal{l}(\theta_t)\]
ここで、$\eta_t$ はステップ $t$ の学習率です。
モメンタム
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t v_{t+1}\]
ここで、$\eta_t$ はステップ $t$ の学習率、$\gamma$ はモメンタム係数です。
Nesterov
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t ( \gamma v_{t+1} + \nabla \mathcal{l}(\theta_{t}) )\]
ここで、$\eta_t$ はステップ $t$ の学習率、$\gamma$ はモメンタム係数です。
RMSProp
\[v_0 = 1 \text{, } m_0 = 0\]
\[v_{t+1} = \rho v_{t} + (1 - \rho) \nabla \mathcal{l}(\theta_t)^2\]
\[m_{t+1} = \gamma m_{t} + \frac{\eta_t}{\sqrt{v_{t+1} + \epsilon}}\nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - m_{t+1}\]
ADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l}(\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{m_{t+1}}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
NADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l} (\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{\beta_1 m_{t+1} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]