พจนานุกรมศัพท์นี้จะให้คำจำกัดความของคำศัพท์เกี่ยวกับปัญญาประดิษฐ์
A
การจี้
เทคนิคในการประเมินความสำคัญของฟีเจอร์ หรือคอมโพเนนต์โดยนำออกชั่วคราวจากโมเดล จากนั้นให้ ฝึกโมเดลใหม่โดยไม่มีฟีเจอร์หรือคอมโพเนนต์นั้น และหากโมเดลที่ฝึกใหม่ มีประสิทธิภาพแย่ลงอย่างเห็นได้ชัด แสดงว่าฟีเจอร์หรือคอมโพเนนต์ที่นำออก อาจมีความสำคัญ
เช่น สมมติว่าคุณฝึกโมเดลการจัดประเภท ในฟีเจอร์ 10 รายการและได้ความแม่นยำ 88% ใน ชุดทดสอบ หากต้องการตรวจสอบความสำคัญ ของฟีเจอร์แรก คุณสามารถฝึกโมเดลอีกครั้งโดยใช้เฉพาะฟีเจอร์อื่นๆ อีก 9 รายการ หากโมเดลที่ฝึกใหม่มีประสิทธิภาพแย่ลงอย่างมาก (เช่น ความแม่นยำต่ำกว่า 55%) แสดงว่าฟีเจอร์ที่นำออกอาจมีความสำคัญ ในทางกลับกัน หากโมเดลที่ฝึกใหม่ทำงานได้ดีเท่ากัน แสดงว่าฟีเจอร์นั้นอาจ ไม่สำคัญมากนัก
นอกจากนี้ การตัดทอนยังช่วยระบุความสำคัญของสิ่งต่อไปนี้ได้ด้วย
- คอมโพเนนต์ขนาดใหญ่ เช่น ทั้งระบบย่อยของระบบ ML ขนาดใหญ่
- กระบวนการหรือเทคนิค เช่น ขั้นตอนการประมวลผลข้อมูลเบื้องต้น
ในทั้ง 2 กรณี คุณจะสังเกตเห็นว่าประสิทธิภาพของระบบเปลี่ยนแปลง (หรือไม่เปลี่ยนแปลง) หลังจากนำคอมโพเนนต์ออก
การทดสอบ A/B
วิธีทางสถิติในการเปรียบเทียบเทคนิค 2 อย่าง (หรือมากกว่า) ซึ่งก็คือ A และ B โดยปกติแล้ว A คือเทคนิคที่มีอยู่ และ B คือเทคนิคใหม่ การทดสอบ A/B ไม่เพียงแต่ระบุว่าเทคนิคใดทำงานได้ดีกว่า แต่ยังระบุว่าความแตกต่างนั้นมีนัยสำคัญทางสถิติหรือไม่ด้วย
โดยปกติแล้วการทดสอบ A/B จะเปรียบเทียบเมตริกเดียวใน 2 เทคนิค เช่น ความแม่นยำของโมเดลเป็นอย่างไรเมื่อเปรียบเทียบกับ 2 เทคนิค อย่างไรก็ตาม การทดสอบ A/B ยังเปรียบเทียบเมตริกจำนวนจำกัดได้ด้วย
ชิปตัวเร่ง
หมวดหมู่ของคอมโพเนนต์ฮาร์ดแวร์เฉพาะทางที่ออกแบบมาเพื่อทำการคำนวณที่สำคัญ ซึ่งจำเป็นสำหรับอัลกอริทึมการเรียนรู้เชิงลึก
ชิปตัวเร่ง (หรือเรียกสั้นๆ ว่าตัวเร่ง) สามารถเพิ่มความเร็วและประสิทธิภาพของงานการฝึกและอนุมานได้อย่างมาก เมื่อเทียบกับ CPU แบบอเนกประสงค์ ซึ่งเหมาะอย่างยิ่งสำหรับการฝึก โครงข่ายประสาทเทียมและงานที่ต้องใช้การคำนวณอย่างหนักที่คล้ายกัน
ตัวอย่างชิปเร่งความเร็ว ได้แก่
- Tensor Processing Unit (TPU) ของ Google ที่มีฮาร์ดแวร์เฉพาะ สำหรับการเรียนรู้เชิงลึก
- GPU ของ NVIDIA ซึ่งแม้จะออกแบบมาเพื่อการประมวลผลกราฟิกในตอนแรก แต่ก็ออกแบบมาเพื่อเปิดใช้การประมวลผลแบบคู่ขนาน ซึ่งจะช่วยเพิ่มความเร็วในการประมวลผลได้อย่างมาก
ความแม่นยำ
จำนวนการคาดการณ์การจัดประเภทที่ถูกต้องหารด้วยจำนวนการคาดการณ์ทั้งหมด โดยการ
เช่น โมเดลที่คาดการณ์ถูกต้อง 40 รายการและคาดการณ์ไม่ถูกต้อง 10 รายการ จะมีความแม่นยำดังนี้
การแยกประเภทแบบไบนารีจะระบุชื่อที่เฉพาะเจาะจง สำหรับหมวดหมู่ต่างๆ ของการคาดการณ์ที่ถูกต้องและ การคาดการณ์ที่ไม่ถูกต้อง ดังนั้น สูตรความแม่นยำสำหรับการจัดประเภทแบบไบนารี จึงเป็นดังนี้
ที่ไหน
- TP คือจำนวนผลบวกจริง (การคาดการณ์ที่ถูกต้อง)
- TN คือจำนวนผลลบจริง (การคาดการณ์ที่ถูกต้อง)
- FP คือจำนวนผลบวกลวง (การคาดการณ์ที่ไม่ถูกต้อง)
- FN คือจำนวนผลลบลวง (การคาดการณ์ที่ไม่ถูกต้อง)
เปรียบเทียบความแม่นยำกับความเที่ยงตรงและความอ่อนไหว
ดูข้อมูลเพิ่มเติมได้ที่การจัดประเภท: ความแม่นยำ การเรียกคืน ความเที่ยงตรง และเมตริกที่เกี่ยวข้อง ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
การดำเนินการ
ในการเรียนรู้แบบเสริมกำลัง กลไกที่เอเจนต์ เปลี่ยนระหว่างสถานะของ สภาพแวดล้อม โดย Agent จะเลือกการดำเนินการโดยใช้นโยบาย
ฟังก์ชันการเปิดใช้งาน
ฟังก์ชันที่ช่วยให้โครงข่ายประสาทเทียมเรียนรู้ความสัมพันธ์ที่ไม่ใช่เชิงเส้น (ซับซ้อน) ระหว่างฟีเจอร์ กับป้ายกำกับ
ฟังก์ชันการเปิดใช้งานที่ได้รับความนิยมมีดังนี้
พล็อตของฟังก์ชันการเปิดใช้งานจะไม่ใช่เส้นตรงเส้นเดียว ตัวอย่างเช่น พล็อตของฟังก์ชันกระตุ้น ReLU ประกอบด้วยเส้นตรง 2 เส้น ดังนี้

กราฟของฟังก์ชันการกระตุ้นแบบซิคมอยด์มีลักษณะดังนี้

ดูข้อมูลเพิ่มเติมได้ที่โครงข่ายประสาทเทียม: ฟังก์ชันการเปิดใช้งาน ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
การเรียนรู้แบบลงมือปฏิบัติ
แนวทางการฝึกที่อัลกอริทึมเลือกข้อมูลบางส่วนที่เรียนรู้ การเรียนรู้แบบแอ็กทีฟ มีประโยชน์อย่างยิ่งเมื่อตัวอย่างที่มีป้ายกำกับ หายากหรือมีราคาสูง อัลกอริทึมการเรียนรู้แบบลงมือปฏิบัติจะเลือกหาตัวอย่างในช่วงที่ต้องการสำหรับการเรียนรู้ แทนที่จะหาตัวอย่างที่หลากหลายซึ่งติดป้ายกำกับไว้โดยไม่พิจารณา
AdaGrad
อัลกอริทึมการไล่ระดับขั้นสูงที่ปรับขนาดการไล่ระดับของพารามิเตอร์แต่ละรายการ ซึ่งจะทำให้พารามิเตอร์แต่ละรายการมีอัตราการเรียนรู้ที่เป็นอิสระ ดูคำอธิบายฉบับเต็มได้ที่ Adaptive Subgradient Methods for Online Learning and Stochastic Optimization
การดัดแปลง
คำพ้องความหมายของการปรับแต่งหรือการปรับแต่งอย่างละเอียด
ตัวแทน
ซอฟต์แวร์ที่สามารถให้เหตุผลเกี่ยวกับอินพุตของผู้ใช้แบบมัลติโมดัลเพื่อวางแผนและ ดำเนินการในนามของผู้ใช้
ในการเรียนรู้แบบเสริมกำลัง เอเจนต์คือเอนทิตีที่ใช้นโยบายเพื่อเพิ่มผลตอบแทนที่คาดไว้ให้ได้มากที่สุดจากการ เปลี่ยนสถานะของสภาพแวดล้อม
เป็น Agent
รูปแบบคำคุณศัพท์ของagent Agentic หมายถึงคุณสมบัติ ที่เอเจนต์มี (เช่น ความเป็นอิสระ)
เวิร์กโฟลว์ของเอเจนต์
กระบวนการแบบไดนามิกที่เอเจนต์วางแผนและ ดำเนินการโดยอัตโนมัติเพื่อให้บรรลุเป้าหมาย กระบวนการนี้อาจเกี่ยวข้องกับการให้เหตุผล การเรียกใช้เครื่องมือภายนอก และการแก้ไขแผนด้วยตนเอง
การจัดกลุ่มแบบรวมกลุ่ม
AI slop
เอาต์พุตจากระบบ Generative AI ที่เน้นปริมาณมากกว่าคุณภาพ เช่น หน้าเว็บที่มีเนื้อหาที่ AI สร้างขึ้นอย่างลวกๆ จะเต็มไปด้วยเนื้อหาคุณภาพต่ำที่ AI สร้างขึ้นอย่างง่ายๆ
การตรวจจับความผิดปกติ
กระบวนการระบุค่าผิดปกติ ตัวอย่างเช่น หากค่าเฉลี่ย ของฟีเจอร์หนึ่งๆ คือ 100 โดยมีค่าเบี่ยงเบนมาตรฐานเป็น 10 การตรวจหาความผิดปกติควรแจ้งค่า 200 ว่าน่าสงสัย
AR
ตัวย่อของ Augmented Reality
พื้นที่ใต้กราฟ PR
พื้นที่ใต้กราฟ ROC
ปัญญาประดิษฐ์ทั่วไป
กลไกที่ไม่ใช่มนุษย์ซึ่งแสดงให้เห็นถึงความหลากหลายในการแก้ปัญหา ความคิดสร้างสรรค์ และความสามารถในการปรับตัว เช่น โปรแกรมที่แสดงให้เห็นถึงปัญญาประดิษฐ์ อเนกประสงค์สามารถแปลข้อความ แต่งซิมโฟนี และเล่นเกมที่ยังไม่มีใครเคยประดิษฐ์ได้เก่ง
ปัญญาประดิษฐ์ (AI)
โปรแกรมหรือโมเดลที่ไม่ใช่มนุษย์ซึ่งสามารถแก้โจทย์ที่ซับซ้อนได้ ตัวอย่างเช่น โปรแกรมหรือโมเดลที่แปลข้อความ หรือโปรแกรมหรือโมเดลที่ ระบุโรคจากภาพรังสีวิทยาล้วนแสดงให้เห็นถึงปัญญาประดิษฐ์
ในทางเทคนิคแล้ว แมชชีนเลิร์นนิงเป็นสาขาย่อยของปัญญาประดิษฐ์ (AI) อย่างไรก็ตาม ในช่วงไม่กี่ปีที่ผ่านมา องค์กรบางแห่งเริ่มใช้คำว่าปัญญาประดิษฐ์และแมชชีนเลิร์นนิงสลับกัน
โปรดทราบ
กลไกที่ใช้ในโครงข่ายประสาทเทียมซึ่งบ่งบอกถึงความสำคัญของคำหรือส่วนของคำหนึ่งๆ Attention จะบีบอัด ปริมาณข้อมูลที่โมเดลต้องใช้ในการคาดการณ์โทเค็น/คำถัดไป กลไกการให้ความสนใจทั่วไปอาจประกอบด้วยผลรวมแบบถ่วงน้ำหนักของชุดอินพุต โดยน้ำหนักสำหรับอินพุตแต่ละรายการจะคำนวณโดยส่วนอื่นของโครงข่ายประสาทเทียม
ดูการทำ Self-Attention และ การทำ Self-Attention แบบหลายหัว ซึ่งเป็น องค์ประกอบพื้นฐานของTransformer ด้วย
ดูข้อมูลเพิ่มเติมเกี่ยวกับ Self-Attention ได้ที่ LLM: โมเดลภาษาขนาดใหญ่คืออะไร ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
แอตทริบิวต์
คำพ้องความหมายของฟีเจอร์
ในความเท่าเทียมของแมชชีนเลิร์นนิง แอตทริบิวต์มักหมายถึง ลักษณะที่เกี่ยวข้องกับบุคคล
การสุ่มตัวอย่างแอตทริบิวต์
กลยุทธ์สำหรับการฝึกDecision Forest ซึ่งแต่ละDecision Tree จะพิจารณาเฉพาะชุดย่อยแบบสุ่มของฟีเจอร์ที่เป็นไปได้เมื่อเรียนรู้เงื่อนไข โดยทั่วไป ระบบจะสุ่มตัวอย่างฟีเจอร์ชุดย่อยที่แตกต่างกันสำหรับแต่ละโหนด ในทางตรงกันข้าม เมื่อฝึกต้นไม้ตัดสินใจโดยไม่ใช้การสุ่มตัวอย่างแอตทริบิวต์ ระบบจะพิจารณาลักษณะที่เป็นไปได้ทั้งหมดสำหรับแต่ละโหนด
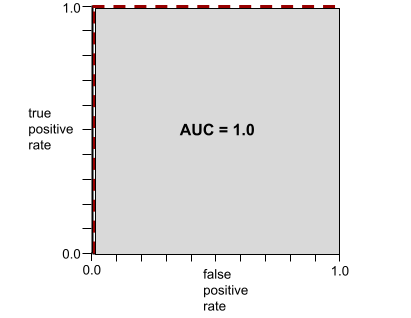
AUC (พื้นที่ใต้กราฟ ROC)
ตัวเลขระหว่าง 0.0 ถึง 1.0 ซึ่งแสดงถึงความสามารถของโมเดลการจัดประเภทแบบไบนารี ในการแยกคลาสที่เป็นบวกออกจากคลาสที่เป็นลบ ยิ่ง AUC ใกล้ 1.0 มากเท่าใด ความสามารถของโมเดลในการแยก คลาสออกจากกันก็จะยิ่งดีขึ้นเท่านั้น
ตัวอย่างเช่น ภาพต่อไปนี้แสดงโมเดลการจัดประเภทที่แยกคลาสเชิงบวก (วงรีสีเขียว) ออกจากคลาสเชิงลบ (สี่เหลี่ยมผืนผ้าสีม่วง) ได้อย่างสมบูรณ์ โมเดลที่สมบูรณ์แบบอย่างไม่สมจริงนี้มี AUC เท่ากับ 1.0

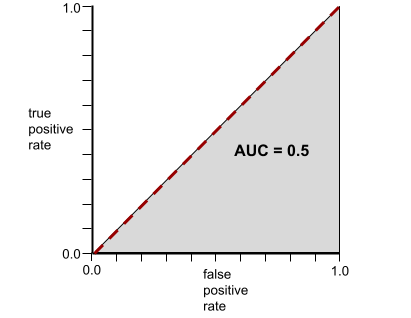
ในทางกลับกัน ภาพประกอบต่อไปนี้แสดงผลลัพธ์ของโมเดลการจัดประเภทที่สร้างผลลัพธ์แบบสุ่ม โมเดลนี้มี AUC เท่ากับ 0.5

ใช่ โมเดลก่อนหน้ามี AUC เท่ากับ 0.5 ไม่ใช่ 0.0
โมเดลส่วนใหญ่จะอยู่ระหว่าง 2 สุดขั้วนี้ ตัวอย่างเช่น โมเดลต่อไปนี้จะแยกผลลัพธ์เชิงบวกออกจากเชิงลบได้ในระดับหนึ่ง ดังนั้น จึงมี AUC อยู่ระหว่าง 0.5 ถึง 1.0

AUC จะไม่สนใจค่าที่คุณตั้งไว้สำหรับ เกณฑ์การจัดประเภท แต่ AUC จะพิจารณาเกณฑ์การแยกประเภทที่เป็นไปได้ทั้งหมด
ดูข้อมูลเพิ่มเติมได้ที่การแยกประเภท: ROC และ AUC ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
เสมือนจริงจำลอง
เทคโนโลยีที่ซ้อนภาพที่คอมพิวเตอร์สร้างขึ้นบนมุมมองโลกแห่งความเป็นจริงของผู้ใช้ จึงทำให้เกิดมุมมองแบบผสม
ออโต้เอนโค้ดเดอร์
ระบบที่เรียนรู้ที่จะดึงข้อมูลที่สำคัญที่สุดจากอินพุต Autoencoder คือการรวมกันของEncoder และ Decoder Autoencoder ใช้กระบวนการ 2 ขั้นตอนต่อไปนี้
- ตัวเข้ารหัสจะแมปอินพุตกับรูปแบบที่มีการสูญเสียข้อมูลในมิติที่ต่ำกว่า (โดยทั่วไป) (รูปแบบกลาง)
- ตัวถอดรหัสจะสร้างเวอร์ชันที่มีการสูญเสียของอินพุตต้นฉบับโดยการแมปรูปแบบที่มีมิติต่ำกว่ากับรูปแบบอินพุตต้นฉบับที่มีมิติสูงกว่า
Autoencoder ได้รับการฝึกแบบครบวงจรโดยให้ตัวถอดรหัสพยายาม สร้างอินพุตต้นฉบับจากรูปแบบกลางของตัวเข้ารหัส ให้ใกล้เคียงที่สุด เนื่องจากรูปแบบกลางมีขนาดเล็กกว่า (มีมิติที่ต่ำกว่า) รูปแบบเดิม ออโต้เอนโคดเดอร์จึงต้อง เรียนรู้ว่าข้อมูลใดในอินพุตที่จำเป็น และเอาต์พุตจะไม่ เหมือนกับอินพุตทุกประการ
เช่น
- หากข้อมูลอินพุตเป็นกราฟิก สำเนาที่ไม่ตรงกันจะคล้ายกับกราฟิกต้นฉบับ แต่มีการแก้ไขเล็กน้อย อาจเป็นเพราะ สำเนาที่ไม่ตรงกันจะนำสัญญาณรบกวนออกจากกราฟิกต้นฉบับหรือเติม พิกเซลที่ขาดหายไป
- หากข้อมูลอินพุตเป็นข้อความ ออโต้เอนโค้ดเดอร์จะสร้างข้อความใหม่ที่ เลียนแบบ (แต่ไม่เหมือนกับ) ข้อความต้นฉบับ
ดูVariational Autoencoders ด้วย
การประเมินอัตโนมัติ
การใช้ซอฟต์แวร์เพื่อตัดสินคุณภาพของเอาต์พุตของโมเดล
เมื่อเอาต์พุตของโมเดลค่อนข้างตรงไปตรงมา สคริปต์หรือโปรแกรมจะ เปรียบเทียบเอาต์พุตของโมเดลกับคำตอบที่ถูกต้องได้ บางครั้งเราเรียกการประเมินอัตโนมัติประเภทนี้ว่าการประเมินแบบเป็นโปรแกรม เมตริก เช่น ROUGE หรือ BLEU มักมีประโยชน์สำหรับการประเมินแบบเป็นโปรแกรม
เมื่อเอาต์พุตของโมเดลมีความซับซ้อนหรือไม่มีคำตอบที่ถูกต้องเพียงคำตอบเดียว บางครั้งโปรแกรม ML แยกต่างหากที่เรียกว่าเครื่องมือให้คะแนนอัตโนมัติจะทำการประเมินอัตโนมัติ
เปรียบเทียบกับการประเมินโดยเจ้าหน้าที่
อคติจากการทำงานอัตโนมัติ
เมื่อผู้มีอำนาจตัดสินใจที่เป็นมนุษย์ชอบคำแนะนำที่ระบบการตัดสินใจอัตโนมัติสร้างขึ้นมากกว่าข้อมูลที่สร้างขึ้นโดยไม่มีการทำงานอัตโนมัติ แม้ว่าระบบการตัดสินใจอัตโนมัติจะทำผิดพลาดก็ตาม
ดูข้อมูลเพิ่มเติมได้ที่ความเป็นธรรม: ประเภทของ อคติ ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
AutoML
กระบวนการอัตโนมัติใดๆ สำหรับการสร้างแมชชีนเลิร์นนิง โมเดล AutoML สามารถทำงานต่างๆ โดยอัตโนมัติได้ เช่น
- ค้นหาโมเดลที่เหมาะสมที่สุด
- ปรับแต่งไฮเปอร์พารามิเตอร์
- เตรียมข้อมูล (รวมถึงการสร้างฟีเจอร์)
- ทำให้โมเดลที่ได้ใช้งานได้
AutoML มีประโยชน์สำหรับนักวิทยาศาสตร์ข้อมูลเนื่องจากช่วยประหยัดเวลาและ ความพยายามในการพัฒนาไปป์ไลน์แมชชีนเลิร์นนิง และปรับปรุงความแม่นยำในการคาดการณ์ นอกจากนี้ยังเป็นประโยชน์ต่อผู้ที่ไม่เชี่ยวชาญด้วยการทำให้งานแมชชีนเลิร์นนิงที่ซับซ้อนเข้าถึงได้ง่ายขึ้น
ดูข้อมูลเพิ่มเติมได้ที่แมชชีนเลิร์นนิงอัตโนมัติ (AutoML) ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การประเมิน Autorater
กลไกแบบผสมสำหรับการตัดสินคุณภาพของเอาต์พุตของโมเดลGenerative AI ซึ่งรวมการประเมินโดยเจ้าหน้าที่เข้ากับการประเมินอัตโนมัติ โปรแกรมให้คะแนนอัตโนมัติคือโมเดล ML ที่ฝึกโดยใช้ข้อมูลที่สร้างขึ้นจากการประเมินโดยเจ้าหน้าที่ ในอุดมคติแล้ว โปรแกรมให้คะแนนอัตโนมัติ จะเรียนรู้ที่จะเลียนแบบผู้ประเมินที่เป็นมนุษย์มีเครื่องมือให้คะแนนอัตโนมัติที่สร้างไว้ล่วงหน้า แต่เครื่องมือให้คะแนนอัตโนมัติที่ดีที่สุดคือเครื่องมือที่ ได้รับการปรับแต่งมาโดยเฉพาะสำหรับงานที่คุณกำลังประเมิน
โมเดลอัตตาถดถอย
โมเดลที่อนุมานการคาดการณ์ตามการคาดการณ์ก่อนหน้าของตัวเอง เช่น โมเดลภาษาแบบถดถอยอัตโนมัติจะคาดการณ์โทเค็นถัดไปโดยอิงตามโทเค็นที่คาดการณ์ไว้ก่อนหน้านี้ โมเดลภาษาขนาดใหญ่ที่อิงตาม Transformer ทั้งหมดเป็นแบบ Auto-Regressive
ในทางตรงกันข้าม โมเดลรูปภาพที่อิงตาม GAN มักจะไม่ใช่แบบถดถอยอัตโนมัติ เนื่องจากสร้างรูปภาพในการส่งต่อครั้งเดียว ไม่ใช่แบบวนซ้ำใน ขั้นตอนต่างๆ อย่างไรก็ตาม โมเดลการสร้างรูปภาพบางโมเดลเป็นแบบถดถอยอัตโนมัติเนื่องจาก สร้างรูปภาพเป็นขั้นตอน
การสูญเสียเสริม
Loss Function ซึ่งใช้ร่วมกับโครงข่ายประสาทเทียม โมเดลหลัก Loss Function ที่ช่วยเร่งการฝึกระหว่าง การทำซ้ำในช่วงแรกๆ เมื่อมีการเริ่มต้นน้ำหนักแบบสุ่ม
ฟังก์ชันการสูญเสียเสริมจะส่งการไล่ระดับสีที่มีประสิทธิภาพ ไปยังเลเยอร์ก่อนหน้า ซึ่งช่วยให้การบรรจบกันในระหว่างการฝึก ง่ายขึ้นด้วยการแก้ปัญหาการไล่ระดับสีที่หายไป
ความแม่นยำเฉลี่ยที่ k
เมตริกสำหรับสรุปประสิทธิภาพของโมเดลในพรอมต์เดียวที่สร้างผลลัพธ์ที่จัดอันดับ เช่น รายการคำแนะนำหนังสือที่มีหมายเลข ความแม่นยำเฉลี่ยที่ k คือค่าเฉลี่ยของค่า ความแม่นยำที่ k สำหรับผลลัพธ์ที่เกี่ยวข้องแต่ละรายการ ดังนั้น สูตรสำหรับความแม่นยำเฉลี่ยที่ k คือ
\[{\text{average precision at k}} = \frac{1}{n} \sum_{i=1}^n {\text{precision at k for each relevant item} } \]
ที่ไหน
- \(n\) คือจำนวนสินค้าที่เกี่ยวข้องในรายการ
เปรียบเทียบกับ Recall ที่ k
เงื่อนไขที่สอดคล้องกับแกน
ในแผนผังการตัดสินใจ เงื่อนไข
ที่มีฟีเจอร์เดียวเท่านั้น ตัวอย่างเช่น หาก area
เป็นฟีเจอร์ เงื่อนไขที่สอดคล้องกับแกนจะเป็นดังนี้
area > 200
เทียบกับเงื่อนไขที่คลุมเครือ
B
การแพร่ย้อนกลับ
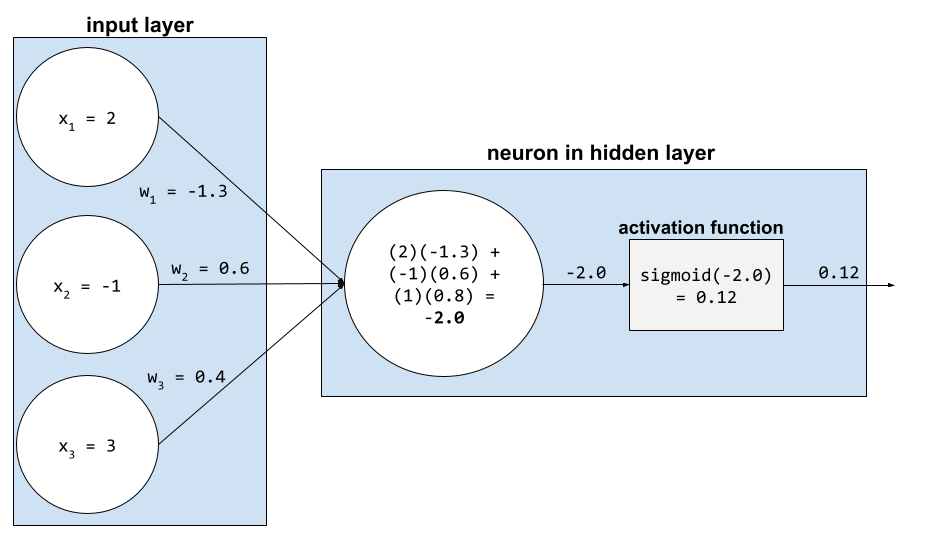
อัลกอริทึมที่ใช้การไล่ระดับการลดในโครงข่ายประสาทเทียม
การฝึกโครงข่ายประสาทเทียมต้องใช้การทำซ้ำหลายครั้ง ในวงจร 2 รอบต่อไปนี้
- ในระหว่างการส่งต่อ ระบบจะประมวลผลกลุ่มของ ตัวอย่างเพื่อให้ได้การคาดการณ์ ระบบจะเปรียบเทียบค่าการคาดการณ์แต่ละค่ากับค่าป้ายกำกับแต่ละค่า ความแตกต่างระหว่างค่าการคาดการณ์และค่าป้ายกำกับคือการสูญเสียสำหรับตัวอย่างนั้น ระบบจะรวมการสูญเสียสำหรับตัวอย่างทั้งหมดเพื่อคำนวณการสูญเสียทั้งหมดสำหรับกลุ่มปัจจุบัน
- ในการส่งผ่านย้อนกลับ (การแพร่ย้อนกลับ) ระบบจะลดการสูญเสียโดยการ ปรับน้ำหนักของนิวรอนทั้งหมดในเลเยอร์ที่ซ่อนอยู่ทั้งหมด
โดยมักจะมีนิวรอนจำนวนมากในเลเยอร์ที่ซ่อนอยู่หลายเลเยอร์ นิวรอนแต่ละตัวมีส่วนทำให้เกิดการสูญเสียโดยรวมในรูปแบบต่างๆ การแพร่ย้อนกลับจะพิจารณาว่าจะเพิ่มหรือลดน้ำหนัก ที่ใช้กับนิวรอนเฉพาะหรือไม่
อัตราการเรียนรู้คือตัวคูณที่ควบคุม ระดับที่แต่ละการส่งผ่านย้อนกลับจะเพิ่มหรือลดน้ำหนักแต่ละรายการ อัตราการเรียนรู้ที่สูงจะเพิ่มหรือลดน้ำหนักแต่ละรายการมากกว่าอัตราการเรียนรู้ที่ต่ำ
ในแง่ของแคลคูลัส การแพร่ย้อนกลับจะใช้กฎลูกโซ่ จากแคลคูลัส กล่าวคือ การแพร่ย้อนกลับจะคำนวณอนุพันธ์ย่อยของข้อผิดพลาดที่ เกี่ยวข้องกับแต่ละพารามิเตอร์
เมื่อหลายปีก่อน ผู้ปฏิบัติงานด้าน ML ต้องเขียนโค้ดเพื่อใช้การแพร่ย้อนกลับ API ของ ML รุ่นใหม่ เช่น Keras จะใช้การแพร่ย้อนกลับให้คุณ ในที่สุด
ดูข้อมูลเพิ่มเติมได้ที่โครงข่ายประสาทเทียม ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การใส่ถุง
วิธีการฝึกกลุ่ม โดยที่โมเดลแต่ละรายการจะฝึกในชุดย่อยแบบสุ่มของตัวอย่างการฝึกที่สุ่มโดยมีการแทนที่ ตัวอย่างเช่น Random Forest คือชุดของDecision Tree ที่ฝึกด้วยการ Bagging
คำว่า Bagging ย่อมาจาก Bootstrap Aggregating
ดูข้อมูลเพิ่มเติมได้ที่Random Forests ในหลักสูตร Decision Forests
Bag of Words
การแสดงคำในวลีหรือข้อความ โดยไม่คำนึงถึงลำดับ ตัวอย่างเช่น ถุงคำจะแสดงวลี 3 วลีต่อไปนี้เหมือนกัน
- สุนัขกระโดด
- กระโดดข้ามสุนัข
- สุนัขกระโดด
ระบบจะแมปแต่ละคำกับดัชนีในเวกเตอร์แบบกระจัดกระจาย โดยที่เวกเตอร์มีดัชนีสำหรับทุกคำในคำศัพท์ เช่น วลี the dog jumps จะได้รับการแมปเป็นเวกเตอร์ฟีเจอร์ที่มีค่าที่ไม่ใช่ 0 ที่ดัชนี 3 รายการซึ่งสอดคล้องกับคำว่า the, dog และ jumps ค่าที่ไม่ใช่ 0 อาจเป็นค่าใดค่าหนึ่งต่อไปนี้
- 1 เพื่อระบุว่ามีคำนั้นอยู่
- จำนวนครั้งที่คำปรากฏในกระเป๋า เช่น หากวลีคือ หมาสีน้ำตาลแดงเป็นหมาที่มีขนสีน้ำตาลแดง ทั้งคำว่าน้ำตาลแดงและหมาจะแสดงเป็น 2 ส่วนคำอื่นๆ จะแสดงเป็น 1
- ค่าอื่นๆ เช่น ลอการิทึมของจำนวนครั้งที่คำปรากฏในถุง
พื้นฐาน
โมเดลที่ใช้เป็นจุดอ้างอิงในการเปรียบเทียบประสิทธิภาพของโมเดลอื่น (โดยปกติจะเป็นโมเดลที่ซับซ้อนกว่า) เช่น โมเดลการถดถอยโลจิสติกอาจเป็นพื้นฐานที่ดีสำหรับโมเดล Deep Learning
สำหรับปัญหาหนึ่งๆ เกณฑ์พื้นฐานจะช่วยให้นักพัฒนาโมเดลระบุปริมาณ ประสิทธิภาพขั้นต่ำที่คาดหวังซึ่งโมเดลใหม่ต้องทำให้ได้เพื่อให้โมเดลใหม่ มีประโยชน์
โมเดลพื้นฐาน
โมเดลที่ผ่านการฝึกมาก่อนซึ่งใช้เป็นจุดเริ่มต้นสำหรับการปรับแต่งเพื่อจัดการกับงานหรือแอปพลิเคชันที่เฉพาะเจาะจงได้
ดูโมเดลก่อนการฝึก และโมเดลพื้นฐานด้วย
กลุ่ม
ชุดตัวอย่างที่ใช้ในการฝึก 1 รอบ ขนาดกลุ่มจะกำหนดจำนวนตัวอย่างในกลุ่ม
ดูคำอธิบายว่ากลุ่มข้อมูลเกี่ยวข้องกับ Epoch อย่างไรได้ที่Epoch
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยเชิงเส้น: ไฮเปอร์พารามิเตอร์ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การอนุมานแบบกลุ่ม
กระบวนการอนุมานการคาดการณ์ในหลาย ตัวอย่างที่ไม่มีป้ายกำกับซึ่งแบ่งออกเป็น ชุดข้อมูลย่อย ("แบทช์") ที่เล็กลง
การอนุมานแบบกลุ่มสามารถใช้ประโยชน์จากฟีเจอร์การประมวลผลแบบคู่ขนานของชิปตัวเร่ง กล่าวคือ ตัวเร่งหลายตัว สามารถอนุมานการคาดการณ์ในกลุ่มตัวอย่างที่ไม่มีป้ายกำกับ ที่แตกต่างกันได้พร้อมกัน ซึ่งจะเพิ่มจำนวนการอนุมานต่อวินาทีอย่างมาก
ดูข้อมูลเพิ่มเติมได้ที่ระบบ ML ในการใช้งานจริง: การอนุมานแบบคงที่เทียบกับการอนุมานแบบไดนามิก ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
การแปลงข้อมูลเป็นรูปแบบมาตรฐานแบบกลุ่ม
การปรับให้เป็นมาตรฐานอินพุตหรือเอาต์พุตของฟังก์ชันกระตุ้นในเลเยอร์ที่ซ่อนอยู่ การทําให้เป็นมาตรฐานแบบกลุ่มมีประโยชน์ดังนี้
- ทำให้โครงข่ายประสาทเทียมมีความเสถียรมากขึ้นด้วยการป้องกัน ค่าผิดปกติ
- เปิดใช้อัตราการเรียนรู้ที่สูงขึ้น ซึ่งจะช่วย เร่งการฝึก
- ลดการปรับมากเกินไป
ขนาดกลุ่ม
จำนวนตัวอย่างในกลุ่ม เช่น หากขนาดกลุ่มคือ 100 โมเดลจะประมวลผลตัวอย่าง 100 รายการต่อการทำซ้ำ
กลยุทธ์ขนาดกลุ่มยอดนิยมมีดังนี้
- การไล่ระดับสีแบบสุ่ม (SGD) ซึ่งมีขนาดกลุ่มเท่ากับ 1
- การประมวลผลแบบกลุ่มเต็ม ซึ่งขนาดกลุ่มคือจํานวนตัวอย่างในชุดการฝึกทั้งหมด เช่น หากชุดการฝึกมีตัวอย่าง 1 ล้านรายการ ขนาดกลุ่มจะเท่ากับตัวอย่าง 1 ล้านรายการ โดยปกติแล้ว การประมวลผลแบบกลุ่มทั้งหมดมักเป็นกลยุทธ์ที่ไม่มีประสิทธิภาพ
- มินิแบตช์ ซึ่งโดยปกติแล้วขนาดแบตช์จะอยู่ระหว่าง 10 ถึง 1,000 โดยปกติแล้ว มินิแบตช์เป็นกลยุทธ์ที่มีประสิทธิภาพมากที่สุด
โปรดดูข้อมูลเพิ่มเติมที่ด้านล่าง
- ระบบ ML ที่ใช้งานจริง: การอนุมานแบบคงที่เทียบกับแบบไดนามิก ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
- Playbook การปรับแต่ง Deep Learning
โครงข่ายประสาทเทียมแบบ Bayesian
โครงข่ายประสาทเทียมเชิงความน่าจะเป็นที่พิจารณา ความไม่แน่นอนในน้ำหนักและเอาต์พุต โดยปกติแล้วโมเดลการถดถอยของโครงข่ายประสาทเทียมมาตรฐานจะคาดการณ์ค่าสเกลาร์ เช่น โมเดลมาตรฐานคาดการณ์ราคาบ้าน ที่ 853,000 ในทางตรงกันข้าม เครือข่ายประสาทแบบเบย์จะคาดการณ์การกระจายค่า ตัวอย่างเช่น โมเดลเบย์คาดการณ์ราคาบ้านที่ 853,000 โดยมี ส่วนเบี่ยงเบนมาตรฐานที่ 67,200
โครงข่ายประสาทแบบเบย์ใช้ ทฤษฎีบทของเบย์ เพื่อคำนวณความไม่แน่นอนในน้ำหนักและการคาดการณ์ โครงข่ายประสาทเทียมแบบเบย์มีประโยชน์ในกรณีที่ต้องวัดปริมาณความไม่แน่นอน เช่น ในโมเดลที่เกี่ยวข้องกับยา นอกจากนี้ เครือข่ายประสาทแบบเบย์ยังช่วย ป้องกันการปรับมากเกินไปได้ด้วย
การเพิ่มประสิทธิภาพ Bayesian
เทคนิคโมเดลการถดถอยเชิงความน่าจะเป็น ในการเพิ่มประสิทธิภาพฟังก์ชันออบเจ็กทีฟที่ใช้การคำนวณสูง โดยการเพิ่มประสิทธิภาพตัวแทนแทน ซึ่งจะวัดปริมาณความไม่แน่นอนโดยใช้เทคนิคการเรียนรู้แบบเบส์ เนื่องจากการเพิ่มประสิทธิภาพแบบเบย์เองก็มีค่าใช้จ่ายสูงมาก จึงมักใช้เพื่อเพิ่มประสิทธิภาพงานที่มีค่าใช้จ่ายสูงในการประเมินซึ่งมีพารามิเตอร์จำนวนน้อย เช่น การเลือกไฮเปอร์พารามิเตอร์
สมการเบลแมน
ในการเรียนรู้แบบเสริมกำลัง ฟังก์ชัน Q ที่ดีที่สุดจะตรงกับเอกลักษณ์ต่อไปนี้
\[Q(s, a) = r(s, a) + \gamma \mathbb{E}_{s'|s,a} \max_{a'} Q(s', a')\]
อัลกอริทึมการเรียนรู้แบบเสริมกำลังใช้ข้อมูลประจำตัวนี้ เพื่อสร้างการเรียนรู้แบบ Q โดยใช้กฎการอัปเดตต่อไปนี้
\[Q(s,a) \gets Q(s,a) + \alpha \left[r(s,a) + \gamma \displaystyle\max_{\substack{a_1}} Q(s',a') - Q(s,a) \right] \]
นอกจากเรื่องการเรียนรู้แบบเสริมกำลังแล้ว สมการเบลแมนยังนำไปใช้กับ การเขียนโปรแกรมแบบไดนามิกได้ด้วย ดู รายการใน Wikipedia สำหรับสมการเบลแมน
BERT (Bidirectional Encoder Representations from Transformers)
สถาปัตยกรรมโมเดลสำหรับการแสดงข้อความ โมเดล BERT ที่ฝึกแล้วสามารถทำหน้าที่เป็นส่วนหนึ่งของโมเดลขนาดใหญ่สำหรับการจัดประเภทข้อความหรืองาน ML อื่นๆ ได้
BERT มีลักษณะดังนี้
- ใช้สถาปัตยกรรม Transformer จึงต้องอาศัยการใส่ใจตนเอง
- ใช้ส่วนEncoder ของ Transformer หน้าที่ของตัวเข้ารหัส คือการสร้างการแสดงข้อความที่ดี ไม่ใช่การทำงานเฉพาะ อย่าง เช่น การจัดประเภท
- แบบ 2 ทิศทาง
- ใช้การมาสก์สำหรับ การฝึกที่ไม่มีการควบคุมดูแล
รูปแบบต่างๆ ของ BERT มีดังนี้
ดูภาพรวมของ BERT ได้ที่การเปิดซอร์ส BERT: การฝึกแบบล่วงหน้าที่ล้ำสมัยที่สุดสำหรับการประมวลผลภาษาธรรมชาติ
อคติ (จริยธรรม/ความยุติธรรม)
1. การเหมารวม อคติ หรือการเข้าข้างสิ่งต่างๆ บุคคล หรือกลุ่มบางกลุ่มมากกว่ากลุ่มอื่นๆ อคติเหล่านี้อาจส่งผลต่อการเก็บรวบรวมและการตีความข้อมูล การออกแบบระบบ และวิธีที่ผู้ใช้โต้ตอบกับระบบ รูปแบบของอคติประเภทนี้ ได้แก่
- อคติในการทำงานอัตโนมัติ
- อคติยืนยันความคิดตัวเอง
- อคติของผู้ทดลอง
- อคติในการระบุแหล่งที่มาของกลุ่ม
- อคติโดยไม่รู้ตัว
- อคติในกลุ่ม
- อคติการมองว่ากลุ่มภายนอกมีความเหมือนกัน
2. ข้อผิดพลาดของระบบที่เกิดจากขั้นตอนการสุ่มตัวอย่างหรือการรายงาน รูปแบบของอคติประเภทนี้ ได้แก่
- อคติในการครอบคลุม
- ความลำเอียงจากการไม่ตอบ
- อคติในการเข้าร่วม
- อคติในการรายงาน
- อคติในการสุ่มตัวอย่าง
- อคติในการเลือก
อย่าสับสนกับคำว่าอคติในโมเดลแมชชีนเลิร์นนิง หรืออคติในการคาดการณ์
ดูข้อมูลเพิ่มเติมได้ที่ความเป็นธรรม: ประเภทของอคติใน หลักสูตรเร่งรัดแมชชีนเลิร์นนิง
อคติ (คณิตศาสตร์) หรือเทอมอคติ
การดักจับหรือการชดเชยจากต้นทาง อคติเป็นพารามิเตอร์ในโมเดลแมชชีนเลิร์นนิง ซึ่งแสดงด้วยสัญลักษณ์ต่อไปนี้
- ข
- w0
ตัวอย่างเช่น อคติคือ b ในสูตรต่อไปนี้
ในเส้น 2 มิติแบบง่าย อคติหมายถึง "จุดตัดแกน y" ตัวอย่างเช่น อคติของเส้นในภาพต่อไปนี้คือ 2
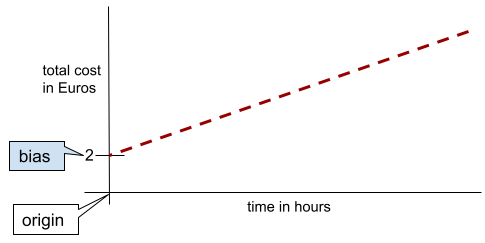
ความเอนเอียงเกิดขึ้นเนื่องจากโมเดลบางรายการไม่ได้เริ่มต้นจากจุดกำเนิด (0,0) ตัวอย่างเช่น สมมติว่าค่าเข้าสวนสนุกคือ 20 บาท และมีค่าใช้จ่ายเพิ่มเติม 5 บาทต่อชั่วโมงที่ลูกค้าอยู่ในสวนสนุก ดังนั้น โมเดลที่แมปต้นทุนทั้งหมดจึงมีอคติเป็น 2 เนื่องจากต้นทุนต่ำสุดคือ 2 ยูโร
อย่าสับสนระหว่างอคติกับอคติในด้านจริยธรรมและความเป็นธรรม หรืออคติในการคาดการณ์
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยเชิงเส้น ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
แบบ 2 ทิศทาง
คำที่ใช้เพื่ออธิบายระบบที่ประเมินข้อความที่อยู่ก่อนหน้า และต่อท้ายส่วนข้อความเป้าหมาย ในทางตรงกันข้าม ระบบแบบทิศทางเดียวจะประเมินเฉพาะข้อความที่อยู่ก่อนข้อความเป้าหมาย
ตัวอย่างเช่น ลองพิจารณาโมเดลภาษาที่ปิดบังซึ่ง ต้องกำหนดความน่าจะเป็นของคำหรือคำที่แสดงถึงขีดเส้นใต้ใน คำถามต่อไปนี้
คุณเป็นอะไร
โมเดลภาษาแบบทิศทางเดียวจะต้องอิงความน่าจะเป็นจากบริบทที่คำว่า "What", "is" และ "the" เท่านั้น ในทางตรงกันข้าม โมเดลภาษาแบบสองทิศทางยังสามารถรับบริบทจากคำว่า "กับ" และ "คุณ" ซึ่งอาจช่วยให้โมเดลสร้างการคาดการณ์ได้ดียิ่งขึ้น
โมเดลภาษาแบบ 2 ทิศทาง
โมเดลภาษาที่กำหนดความน่าจะเป็นที่โทเค็นที่กำหนดจะอยู่ในตำแหน่งที่กำหนดในข้อความที่ตัดตอนโดยอิงตามข้อความก่อนหน้าและถัดไป
ไบแกรม
N-gram ที่ N=2
การจัดประเภทแบบไบนารี
ประเภทของงานการจัดประเภทที่ คาดการณ์คลาสใดคลาสหนึ่งใน 2 คลาสที่แยกกันโดยสิ้นเชิง
ตัวอย่างเช่น โมเดลแมชชีนเลิร์นนิง 2 รายการต่อไปนี้แต่ละรายการทําการ การจัดประเภทไบนารี
- โมเดลที่พิจารณาว่าข้อความอีเมลเป็นจดหมายขยะ (คลาสเชิงบวก) หรือไม่ใช่จดหมายขยะ (คลาสเชิงลบ)
- โมเดลที่ประเมินอาการทางการแพทย์เพื่อพิจารณาว่าบุคคล เป็นโรคใดโรคหนึ่ง (คลาสบวก) หรือไม่เป็นโรคดังกล่าว (คลาสลบ)
แตกต่างจากการจัดประเภทแบบหลายคลาส
ดูเพิ่มเติมที่การถดถอยโลจิสติกและ เกณฑ์การจัดประเภท
ดูข้อมูลเพิ่มเติมได้ที่การจัดประเภท ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
เงื่อนไขไบนารี
ในแผนผังการตัดสินใจ เงื่อนไข ที่มีผลลัพธ์ที่เป็นไปได้เพียง 2 อย่าง โดยปกติคือใช่หรือไม่ใช่ ตัวอย่างเช่น เงื่อนไขต่อไปนี้เป็นเงื่อนไขแบบไบนารี
temperature >= 100
เปรียบเทียบกับเงื่อนไขที่ไม่ใช่แบบไบนารี
ดูข้อมูลเพิ่มเติมได้ที่ประเภทของเงื่อนไข ในหลักสูตร Decision Forests
การจัดกลุ่ม
คำพ้องความหมายของการจัดกลุ่ม
โมเดลกล่องดำ
โมเดลที่มี "การให้เหตุผล" ที่มนุษย์ไม่สามารถเข้าใจได้หรือเข้าใจได้ยาก กล่าวคือ แม้ว่ามนุษย์จะเห็นว่าพรอมต์ ส่งผลต่อคำตอบอย่างไร แต่ก็ไม่สามารถระบุได้อย่างแน่ชัดว่าโมเดลกล่องดำ กำหนดคำตอบอย่างไร กล่าวคือ โมเดลกล่องดำไม่มีความสามารถในการตีความ
โมเดลเชิงลึกและ โมเดลภาษาขนาดใหญ่ส่วนใหญ่เป็นกล่องดำ
BLEU (Bilingual Evaluation Understudy)
เมตริกระหว่าง 0.0 ถึง 1.0 สำหรับการประเมินการแปลด้วยเครื่อง เช่น จากภาษาสเปนเป็นภาษาญี่ปุ่น
โดยปกติแล้ว BLEU จะเปรียบเทียบการแปลของโมเดล ML (ข้อความที่สร้างขึ้น) กับการแปลของมนุษย์ผู้เชี่ยวชาญ (ข้อความอ้างอิง) เพื่อคำนวณคะแนน ระดับที่ N-gram ในข้อความที่สร้างขึ้นและ ข้อความอ้างอิงตรงกันจะเป็นตัวกำหนดคะแนน BLEU
เอกสารต้นฉบับเกี่ยวกับเมตริกนี้คือ BLEU: a Method for Automatic Evaluation of Machine Translation
ดู BLEURT เพิ่มเติม
BLEURT (Bilingual Evaluation Understudy from Transformers)
เมตริกสําหรับการประเมินการแปลด้วยเครื่อง จากภาษาหนึ่งเป็นอีกภาษาหนึ่ง โดยเฉพาะอย่างยิ่งจากและเป็นภาษาอังกฤษ
สำหรับการแปลเป็นและจากภาษาอังกฤษ BLEURT จะสอดคล้องกับการให้คะแนนของมนุษย์มากกว่า BLEU BLEURT เน้นความคล้ายคลึงกันทางความหมาย (ความหมาย) และรองรับการถอดความ ซึ่งแตกต่างจาก BLEU
BLEURT ใช้โมเดลภาษาขนาดใหญ่ที่ฝึกล่วงหน้า (BERT อย่างแม่นยำ) ซึ่งจะปรับแต่ง ในข้อความจากนักแปลที่เป็นมนุษย์
เอกสารต้นฉบับเกี่ยวกับเมตริกนี้คือ BLEURT: Learning Robust Metrics for Text Generation
การเพิ่ม
เทคนิคแมชชีนเลิร์นนิงที่รวมชุดโมเดลการแยกประเภทอย่างง่ายที่ไม่แม่นยำนัก (เรียกว่า "ตัวแยกประเภทแบบอ่อน") เข้ากับโมเดลการแยกประเภทที่มีความแม่นยำสูง ("ตัวแยกประเภทแบบเข้ม") โดยเพิ่มน้ำหนักให้กับตัวอย่างที่โมเดลแยกประเภทผิดในปัจจุบัน
ดูข้อมูลเพิ่มเติมได้ที่Gradient Boosted Decision Trees? ในหลักสูตร Decision Forests
กรอบล้อมรอบ
ในรูปภาพ พิกัด (x, y) ของสี่เหลี่ยมผืนผ้ารอบพื้นที่ที่น่าสนใจ เช่น สุนัขในรูปภาพด้านล่าง

การออกอากาศ
การขยายรูปร่างของตัวถูกดำเนินการในการดำเนินการทางคณิตศาสตร์ของเมทริกซ์ให้เป็นมิติที่เข้ากันได้กับการดำเนินการนั้น ตัวอย่างเช่น พีชคณิตเชิงเส้นกำหนดให้ตัวถูกดำเนินการทั้ง 2 ตัวในการดำเนินการบวกเมทริกซ์ ต้องมีมิติข้อมูลเดียวกัน ดังนั้น คุณจึงเพิ่มเมทริกซ์ที่มีรูปร่าง (m, n) ลงในเวกเตอร์ที่มีความยาว n ไม่ได้ การออกอากาศช่วยให้ดำเนินการนี้ได้โดย ขยายเวกเตอร์ที่มีความยาว n เป็นเมทริกซ์ที่มีรูปร่าง (m, n) โดย ทำซ้ำค่าเดียวกันในแต่ละคอลัมน์
ดูรายละเอียดเพิ่มเติมได้ที่คำอธิบายต่อไปนี้ของ การออกอากาศใน NumPy
การจัดกลุ่ม
การแปลงฟีเจอร์เดียวเป็นฟีเจอร์ไบนารีหลายรายการ ที่เรียกว่ากลุ่มหรือถัง โดยปกติจะอิงตามช่วงค่า โดยปกติแล้ว ฟีเจอร์ที่ถูกตัดจะเป็นฟีเจอร์ต่อเนื่อง
ตัวอย่างเช่น แทนที่จะแสดงอุณหภูมิเป็นฟีเจอร์ทศนิยมต่อเนื่องเดียว คุณสามารถแบ่งช่วงอุณหภูมิ ออกเป็นกลุ่มที่ไม่ต่อเนื่องได้ เช่น
- <= 10 องศาเซลเซียสจะเป็นกลุ่ม "เย็น"
- 11-24 องศาเซลเซียสจะอยู่ในกลุ่ม "อบอุ่น"
- >= 25 องศาเซลเซียสจะอยู่ในกลุ่ม "อุ่น"
โมเดลจะถือว่าค่าทุกค่าในกลุ่มเดียวกันเหมือนกัน ตัวอย่างเช่น ค่า 13 และ 22 อยู่ในกลุ่มอุณหภูมิปานกลางทั้งคู่ ดังนั้นโมเดลจึงถือว่าค่าทั้ง 2 เหมือนกัน
ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลเชิงตัวเลข: การจัดกลุ่ม ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
C
เลเยอร์การปรับเทียบ
การปรับหลังการคาดการณ์ ซึ่งโดยปกติจะใช้เพื่ออธิบายอคติในการคาดการณ์ การคาดการณ์และความน่าจะเป็นที่ปรับแล้วควรตรงกับการกระจายของชุดป้ายกำกับที่สังเกตได้
การสร้างตัวเลือก
ชุดคำแนะนำเริ่มต้นที่ระบบการแนะนำเลือก ตัวอย่างเช่น ลองพิจารณาร้านหนังสือที่มีหนังสือ 100,000 ชื่อ ระยะการสร้างรายการตัวเลือกจะสร้างรายการหนังสือที่เหมาะสมสำหรับผู้ใช้รายหนึ่งๆ ซึ่งมีขนาดเล็กลงมาก เช่น 500 รายการ แต่หนังสือ 500 เล่มก็ยังมากเกินไปที่จะแนะนำให้ผู้ใช้ ระยะต่อๆ ไปของระบบการแนะนำซึ่งมีค่าใช้จ่ายสูงกว่า (เช่น การให้คะแนนและ การจัดอันดับใหม่) จะลดจำนวนวิดีโอ 500 รายการนั้นให้เหลือชุดคำแนะนำที่เล็กลงมาก และมีประโยชน์มากขึ้น
ดูข้อมูลเพิ่มเติมได้ที่ภาพรวมการสร้างแคนดิเดต ในหลักสูตรระบบการแนะนำ
การสุ่มตัวอย่างผู้สมัคร
การเพิ่มประสิทธิภาพในเวลาฝึกที่คำนวณความน่าจะเป็นสำหรับป้ายกำกับเชิงบวกทั้งหมด โดยใช้เช่น softmax แต่ใช้เฉพาะกับตัวอย่างป้ายกำกับเชิงลบแบบสุ่ม เช่น หากมีตัวอย่างที่ติดป้ายกำกับว่า บีเกิลและสุนัข การสุ่มตัวอย่างผู้สมัครจะคำนวณความน่าจะเป็นที่คาดการณ์ และข้อกำหนดการสูญเสียที่เกี่ยวข้องสำหรับ
- บีเกิล
- สุนัข
- กลุ่มย่อยแบบสุ่มของคลาสเชิงลบที่เหลือ (เช่น cat lollipop fence)
แนวคิดคือคลาสเชิงลบสามารถเรียนรู้จากการเสริมแรงเชิงลบที่เกิดขึ้นไม่บ่อยนักได้ ตราบใดที่คลาสเชิงบวกได้รับการเสริมแรงเชิงบวกที่เหมาะสมอยู่เสมอ และเราก็สังเกตเห็นสิ่งนี้ได้จากการศึกษาเชิงประจักษ์
การสุ่มตัวอย่างผู้สมัครมีประสิทธิภาพด้านการคำนวณมากกว่าอัลกอริทึมการฝึกที่คำนวณการคาดการณ์สำหรับคลาสเชิงลบทั้งหมด โดยเฉพาะอย่างยิ่งเมื่อจำนวนคลาสเชิงลบมีจำนวนมาก
ข้อมูลเชิงหมวดหมู่
ฟีเจอร์ที่มีชุดค่าที่เป็นไปได้ที่เฉพาะเจาะจง ตัวอย่างเช่น
พิจารณาฟีเจอร์เชิงหมวดหมู่ชื่อ traffic-light-state ซึ่งมีค่าได้เพียงค่าใดค่าหนึ่งจาก 3 ค่าต่อไปนี้
redyellowgreen
การแสดง traffic-light-state เป็นฟีเจอร์เชิงหมวดหมู่
จะช่วยให้โมเดลเรียนรู้
ผลกระทบที่แตกต่างกันของ red, green และ yellow ต่อพฤติกรรมของผู้ขับขี่ได้
บางครั้งฟีเจอร์เชิงหมวดหมู่จะเรียกว่า ฟีเจอร์ไม่ต่อเนื่อง
เปรียบเทียบกับข้อมูลเชิงตัวเลข
ดูข้อมูลเพิ่มเติมได้ที่การทำงานกับข้อมูลเชิงหมวดหมู่ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
โมเดลภาษาแบบเป็นเหตุเป็นผล
คำพ้องความหมายของโมเดลภาษาแบบทิศทางเดียว
ดูโมเดลภาษาแบบสองทิศทางเพื่อเปรียบเทียบแนวทางแบบทิศทางต่างๆ ในการสร้างโมเดลภาษา
จุดศูนย์กลาง
จุดศูนย์กลางของคลัสเตอร์ตามที่กำหนดโดยอัลกอริทึม k-means หรือ k-median เช่น หาก k คือ 3 อัลกอริทึม k-means หรือ k-median จะพบจุดศูนย์กลาง 3 จุด
ดูข้อมูลเพิ่มเติมได้ที่อัลกอริทึมการจัดกลุ่ม ในหลักสูตรการจัดกลุ่ม
การจัดกลุ่มตามเซนทรอยด์
หมวดหมู่อัลกอริทึมการจัดกลุ่มที่จัดระเบียบข้อมูล เป็นคลัสเตอร์แบบไม่เป็นลำดับชั้น K-means เป็นอัลกอริทึมการจัดกลุ่มตามจุดศูนย์กลางที่ใช้กันอย่างแพร่หลายมากที่สุด
เปรียบเทียบกับอัลกอริทึมการจัดกลุ่มแบบลำดับชั้น
ดูข้อมูลเพิ่มเติมได้ที่อัลกอริทึมการจัดกลุ่ม ในหลักสูตรการจัดกลุ่ม
การเขียนพรอมต์แบบเชนออฟทอท
เทคนิคการออกแบบพรอมต์ที่กระตุ้นให้โมเดลภาษาขนาดใหญ่ (LLM) อธิบายการให้เหตุผลทีละขั้นตอน ตัวอย่างเช่น ลองพิจารณาพรอมต์ต่อไปนี้ โดยให้ความสนใจเป็นพิเศษกับประโยคที่ 2
ผู้ขับขี่จะได้รับแรง G เท่าไรในรถยนต์ที่วิ่งจาก 0 ถึง 60 ไมล์ต่อชั่วโมงใน 7 วินาที แสดงการคำนวณที่เกี่ยวข้องทั้งหมดในคำตอบ
คำตอบของ LLM มีแนวโน้มที่จะเป็นดังนี้
- แสดงลำดับสูตรฟิสิกส์ โดยเสียบค่า 0, 60 และ 7 ในตำแหน่งที่เหมาะสม
- อธิบายเหตุผลที่เลือกใช้สูตรเหล่านั้นและความหมายของตัวแปรต่างๆ
การแจ้งแบบลูกโซ่จะบังคับให้ LLM ทำการคำนวณทั้งหมด ซึ่งอาจนำไปสู่คำตอบที่ถูกต้องมากขึ้น นอกจากนี้ การแจ้งแบบลูกโซ่ความคิด ยังช่วยให้ผู้ใช้ตรวจสอบขั้นตอนของ LLM เพื่อพิจารณาว่าคำตอบสมเหตุสมผลหรือไม่
คะแนน F ของ N-gram อักขระ (ChrF)
เมตริกสำหรับประเมินโมเดลการแปลด้วยเครื่อง คะแนน F ของ N-gram อักขระจะกำหนดระดับที่ N-gram ในข้อความอ้างอิงซ้อนทับกับ N-gram ในข้อความที่สร้างขึ้นของโมเดล ML
คะแนน F ของ N-gram อักขระคล้ายกับเมตริกในกลุ่ม ROUGE และ BLEU ยกเว้นว่า
- คะแนน F ของ N-gram อักขระจะทำงานกับ N-gram อักขระ
- ROUGE และ BLEU ทำงานกับ N-gram ของคำหรือโทเค็น
แชท
เนื้อหาของบทสนทนาไปมากับระบบ ML ซึ่งโดยทั่วไปคือโมเดลภาษาขนาดใหญ่ การโต้ตอบก่อนหน้าในแชท (สิ่งที่คุณพิมพ์และวิธีที่โมเดลภาษาขนาดใหญ่ตอบกลับ) จะกลายเป็น บริบทสำหรับส่วนต่อๆ ไปของแชท
แชทบ็อตคือแอปพลิเคชันของโมเดลภาษาขนาดใหญ่
จุดตรวจ
ข้อมูลที่บันทึกสถานะของพารามิเตอร์ของโมเดล ไม่ว่าจะ ระหว่างการฝึกหรือหลังจากการฝึกเสร็จสมบูรณ์ ตัวอย่างเช่น ในระหว่างการฝึก คุณจะทำสิ่งต่อไปนี้ได้
- หยุดการฝึก อาจโดยตั้งใจหรืออาจเป็นผลมาจาก ข้อผิดพลาดบางอย่าง
- บันทึกจุดตรวจสอบ
- จากนั้นให้โหลดจุดตรวจสอบซ้ำ ซึ่งอาจทำในฮาร์ดแวร์อื่น
- เริ่มการฝึกอีกครั้ง
คลาส
หมวดหมู่ที่ป้ายกำกับสามารถเป็นของได้ เช่น
- ในโมเดลการจัดประเภทแบบไบนารีที่ตรวจหาสแปม คลาสทั้ง 2 อาจเป็นสแปมและไม่ใช่สแปม
- ในโมเดลการจัดประเภทแบบหลายคลาส ที่ระบุสายพันธุ์สุนัข คลาสอาจเป็นพุดเดิล บีเกิล ปั๊ก และอื่นๆ
โมเดลการจัดประเภทจะคาดการณ์คลาส ในทางตรงกันข้าม โมเดลการถดถอยจะคาดการณ์ตัวเลข แทนที่จะเป็นคลาส
ดูข้อมูลเพิ่มเติมได้ที่การจัดประเภท ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ชุดข้อมูลที่สมดุลของคลาส
ชุดข้อมูลที่มีป้ายกำกับ เชิงหมวดหมู่ ซึ่งจำนวนอินสแตนซ์ของแต่ละหมวดหมู่มีค่าเท่ากันโดยประมาณ ตัวอย่างเช่น พิจารณาชุดข้อมูลพฤกษศาสตร์ที่มีป้ายกำกับไบนารี ซึ่งอาจเป็นพืชพื้นเมืองหรือพืชที่ไม่ใช่พื้นเมือง
- ชุดข้อมูลที่มีพืชพื้นเมือง 515 ชนิดและพืชที่ไม่ใช่พืชพื้นเมือง 485 ชนิดคือชุดข้อมูลที่สมดุลของคลาส
- ชุดข้อมูลที่มีพืชพื้นเมือง 875 ชนิดและพืชที่ไม่ใช่พืชพื้นเมือง 125 ชนิดคือชุดข้อมูลที่มีความไม่สมดุลของคลาส
ไม่มีเส้นแบ่งอย่างเป็นทางการระหว่างชุดข้อมูลที่สมดุลของคลาสกับชุดข้อมูลที่ไม่สมดุลของคลาส ความแตกต่างนี้จะมีความสําคัญก็ต่อเมื่อโมเดลที่ฝึกในชุดข้อมูลที่มีความไม่สมดุลของคลาสสูงไม่สามารถบรรจบกันได้ ดูรายละเอียดได้ที่ ชุดข้อมูล: ชุดข้อมูลที่ไม่สมดุล ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
โมเดลการจัดประเภท
โมเดลที่มีการคาดการณ์เป็นคลาส ตัวอย่างเช่น โมเดลการแยกประเภทต่อไปนี้เป็นโมเดลการแยกประเภททั้งหมด
- โมเดลที่คาดการณ์ภาษาของประโยคอินพุต (ฝรั่งเศสใช่ไหม สเปน อิตาลี)
- โมเดลที่คาดการณ์สายพันธุ์ของต้นไม้ (เมเปิล Oak บาวบับ)
- โมเดลที่คาดการณ์คลาสที่เป็นบวกหรือลบสำหรับ ภาวะทางการแพทย์ที่เฉพาะเจาะจง
ในทางกลับกัน โมเดลการเกิดปัญหาซ้ำจะคาดการณ์ตัวเลข แทนที่จะเป็นคลาส
โมเดลการจัดประเภทที่ใช้กันทั่วไปมี 2 ประเภท ได้แก่
เกณฑ์การจัดประเภท
ในการจัดประเภทแบบไบนารี ค่า ระหว่าง 0 ถึง 1 ที่แปลงเอาต์พุตดิบของโมเดลการถดถอยลอจิสติก เป็นการคาดการณ์คลาสที่เป็นบวก หรือคลาสที่เป็นลบ โปรดทราบว่าเกณฑ์การแยกประเภทคือค่าที่มนุษย์เลือก ไม่ใช่ค่าที่ได้จากการฝึกโมเดล
โมเดลการถดถอยโลจิสติกจะแสดงผลค่าดิบระหว่าง 0 ถึง 1 จากนั้นให้ทำดังนี้
- หากค่าดิบนี้มากกว่าเกณฑ์การจัดประเภท ระบบจะคาดการณ์ คลาสที่เป็นบวก
- หากค่าดิบนี้น้อยกว่าเกณฑ์การจัดประเภท ระบบจะคาดการณ์คลาสเชิงลบ
ตัวอย่างเช่น สมมติว่าเกณฑ์การแยกประเภทคือ 0.8 หากค่าดิบ เป็น 0.9 โมเดลจะคาดการณ์คลาสเชิงบวก หากค่าดิบเป็น 0.7 โมเดลจะคาดการณ์คลาสเชิงลบ
การเลือกเกณฑ์การแยกประเภทมีผลอย่างมากต่อจำนวนผลบวกลวงและผลลบลวง
ดูข้อมูลเพิ่มเติมได้ที่เกณฑ์และเมทริกซ์ความสับสน ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ตัวแยกประเภท
คำที่ใช้กันทั่วไปสำหรับโมเดลการแยกประเภท
ชุดข้อมูลที่มีความไม่สมดุลของคลาส
ชุดข้อมูลสำหรับการแยกประเภท ซึ่งจำนวนป้ายกำกับทั้งหมดของคลาสแต่ละคลาส แตกต่างกันอย่างมาก ตัวอย่างเช่น พิจารณาชุดข้อมูลการจัดประเภทแบบไบนารีที่มีป้ายกำกับ 2 รายการ ซึ่งแบ่งออกเป็นดังนี้
- ป้ายกำกับเชิงลบ 1,000,000 รายการ
- ป้ายกำกับค่าบวก 10 รายการ
อัตราส่วนของป้ายกำกับเชิงลบต่อป้ายกำกับเชิงบวกคือ 100,000 ต่อ 1 ดังนั้นนี่จึงเป็นชุดข้อมูลที่มีความไม่สมดุลของคลาส
ในทางตรงกันข้าม ชุดข้อมูลต่อไปนี้เป็นคลาสที่สมดุลเนื่องจากอัตราส่วนของป้ายกำกับเชิงลบต่อป้ายกำกับเชิงบวกค่อนข้างใกล้เคียงกับ 1
- ป้ายกำกับเชิงลบ 517 รายการ
- ป้ายกำกับค่าบวก 483 รายการ
ชุดข้อมูลแบบหลายคลาสอาจไม่สมดุลในระดับคลาสได้เช่นกัน ตัวอย่างเช่น ชุดข้อมูลการจัดประเภทแบบหลายคลาสต่อไปนี้ยังเป็นชุดข้อมูลที่มีความไม่สมดุลของคลาสด้วย เนื่องจากป้ายกำกับหนึ่งมีตัวอย่างมากกว่าอีก 2 ป้ายกำกับมาก
- ป้ายกำกับ 1,000,000 รายการที่มีคลาส "สีเขียว"
- ป้ายกำกับ 200 รายการที่มีคลาส "สีม่วง"
- ป้ายกำกับ 350 รายการที่มีคลาส "ส้ม"
การฝึกโมเดลด้วยชุดข้อมูลที่มีความไม่สมดุลของคลาสอาจเป็นเรื่องที่ท้าทายเป็นพิเศษ ดูรายละเอียดได้ที่ ชุดข้อมูลที่ไม่สมดุล ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ดูเอนโทรปี คลาสส่วนใหญ่ และคลาสส่วนน้อยด้วย
การตัด
เทคนิคในการจัดการค่าผิดปกติโดยทำอย่างใดอย่างหนึ่งหรือทั้ง 2 อย่างต่อไปนี้
- การลดค่าฟีเจอร์ที่มากกว่าเกณฑ์สูงสุด ลงมาที่เกณฑ์สูงสุดนั้น
- การเพิ่มค่าฟีเจอร์ที่ต่ำกว่าเกณฑ์ขั้นต่ำให้สูงถึงเกณฑ์ขั้นต่ำนั้น
ตัวอย่างเช่น สมมติว่าค่าสำหรับฟีเจอร์หนึ่งๆ น้อยกว่า 0.5% อยู่ นอกช่วง 40–60 ในกรณีนี้ คุณสามารถดำเนินการต่อไปนี้ได้
- ตัดค่าทั้งหมดที่มากกว่า 60 (เกณฑ์สูงสุด) ให้เป็น 60
- คลิปค่าทั้งหมดที่ต่ำกว่า 40 (เกณฑ์ขั้นต่ำ) ให้เป็น 40
ค่าผิดปกติอาจทำให้โมเดลเสียหาย และบางครั้งอาจทำให้น้ำหนัก ล้นระหว่างการฝึก ค่าผิดปกติบางค่าอาจทำให้เมตริกต่างๆ เช่น ความแม่นยำ เสียหายอย่างมาก การตัดเสียงเป็นเทคนิคที่ใช้กันทั่วไปเพื่อจำกัด ความเสียหาย
การจำกัดค่าความชันจะบังคับให้ค่าความชันอยู่ในช่วงที่กำหนดระหว่างการฝึก
ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลตัวเลข: การปรับค่าให้เป็นมาตรฐาน ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
Cloud TPU
ตัวเร่งฮาร์ดแวร์เฉพาะทางที่ออกแบบมาเพื่อเพิ่มความเร็วของภาระงานแมชชีน เลิร์นนิงใน Google Cloud
การจัดกลุ่ม
การจัดกลุ่มตัวอย่างที่เกี่ยวข้อง โดยเฉพาะในช่วงการเรียนรู้แบบไม่มีผู้ดูแล เมื่อจัดกลุ่มตัวอย่างทั้งหมดแล้ว เจ้าหน้าที่สามารถเลือกให้ความหมายแก่แต่ละคลัสเตอร์ได้
มีอัลกอริทึมการจัดกลุ่มมากมาย ตัวอย่างเช่น อัลกอริทึม k-means จัดกลุ่มตัวอย่างตามระยะใกล้กับจุดศูนย์กลาง ดังในแผนภาพต่อไปนี้

จากนั้นนักวิจัยจะตรวจสอบคลัสเตอร์และติดป้ายกำกับคลัสเตอร์ 1 เป็น "ต้นไม้แคระ" และคลัสเตอร์ 2 เป็น "ต้นไม้ขนาดเต็ม" ได้ เป็นต้น
อีกตัวอย่างหนึ่งคือพิจารณาอัลกอริทึมการจัดกลุ่มตามระยะห่างของตัวอย่างจากจุดศูนย์กลาง ดังภาพต่อไปนี้

ดูข้อมูลเพิ่มเติมได้ที่หลักสูตรการจัดกลุ่ม
การปรับตัวร่วมกัน
ลักษณะการทำงานที่ไม่พึงประสงค์ซึ่งนิวรอนคาดการณ์รูปแบบใน ข้อมูลการฝึกโดยอาศัยเอาต์พุตของนิวรอนอื่นๆ ที่เฉพาะเจาะจงเกือบทั้งหมด แทนที่จะอาศัยลักษณะการทำงานของเครือข่ายโดยรวม เมื่อรูปแบบที่ทำให้เกิดการปรับร่วมไม่มีอยู่ในข้อมูลการตรวจสอบ การปรับร่วมจะทำให้เกิดการปรับมากเกินไป การทำให้เป็นค่าปกติแบบ Dropout ช่วยลดการปรับตัวร่วมกัน เนื่องจาก Dropout ทำให้มั่นใจได้ว่านิวรอนจะไม่พึ่งพานิวรอนอื่นๆ ที่เฉพาะเจาะจงเพียงอย่างเดียว
การกรองร่วมกัน
การคาดการณ์ความสนใจของผู้ใช้รายหนึ่ง โดยอิงตามความสนใจของผู้ใช้คนอื่นๆ จำนวนมาก การกรองร่วม มักใช้ในระบบแนะนำ
ดูข้อมูลเพิ่มเติมได้ที่การกรอง ร่วมกัน ในหลักสูตรระบบการแนะนำ
โมเดลแบบกะทัดรัด
โมเดลขนาดเล็กที่ออกแบบมาเพื่อทำงานในอุปกรณ์ขนาดเล็กที่มีทรัพยากรการคำนวณจำกัด เช่น โมเดลขนาดเล็กสามารถทำงานบนโทรศัพท์มือถือ แท็บเล็ต หรือ ระบบฝังตัวได้
คำนวณ
(คำนาม) ทรัพยากรการคำนวณที่โมเดลหรือระบบใช้ เช่น กำลังประมวลผล หน่วยความจำ และพื้นที่เก็บข้อมูล
การดริฟต์ของแนวคิด
การเปลี่ยนแปลงความสัมพันธ์ระหว่างฟีเจอร์กับค่ายเพลง เมื่อเวลาผ่านไป แนวคิดดริฟต์จะลดคุณภาพของโมเดล
ในระหว่างการฝึก โมเดลจะเรียนรู้ความสัมพันธ์ระหว่างฟีเจอร์กับ ป้ายกำกับในชุดการฝึก หากป้ายกำกับในชุดการฝึกเป็น ตัวแทนที่ดีสำหรับโลกแห่งความเป็นจริง โมเดลควรทำการคาดการณ์ในโลกแห่งความเป็นจริงได้ดี อย่างไรก็ตาม เนื่องจากแนวคิดที่เปลี่ยนแปลงไป การคาดการณ์ของโมเดลจึงมีแนวโน้มที่จะเสื่อมถอยลงเมื่อเวลาผ่านไป
ตัวอย่างเช่น ลองพิจารณาโมเดลการจัดประเภทแบบไบนารี ที่คาดการณ์ว่ารถยนต์รุ่นหนึ่งๆ "ประหยัดน้ำมัน" หรือไม่ กล่าวคือ ฟีเจอร์อาจเป็น
- น้ำหนักรถ
- การบีบอัดเครื่องยนต์
- ประเภทเกียร์
ขณะที่ป้ายกำกับมีสถานะอย่างใดอย่างหนึ่งต่อไปนี้
- ประหยัดเชื้อเพลิง
- ไม่ประหยัดเชื้อเพลิง
อย่างไรก็ตาม แนวคิดเรื่อง "รถยนต์ประหยัดน้ำมัน" มีการเปลี่ยนแปลงอยู่เสมอ รถยนต์รุ่นที่ติดป้ายกำกับว่าประหยัดน้ำมันในปี 1994 จะต้อง ติดป้ายกำกับว่าไม่ประหยัดน้ำมันในปี 2024 อย่างแน่นอน โมเดลที่ได้รับผลกระทบจากการเปลี่ยนแปลงแนวคิด มักจะทำการคาดการณ์ที่มีประโยชน์น้อยลงเรื่อยๆ เมื่อเวลาผ่านไป
เปรียบเทียบกับความไม่คงที่
เงื่อนไข
ในแผนผังการตัดสินใจ โหนดใดก็ตามที่ ทำการทดสอบ ตัวอย่างเช่น แผนผังการตัดสินใจต่อไปนี้มี เงื่อนไข 2 ข้อ
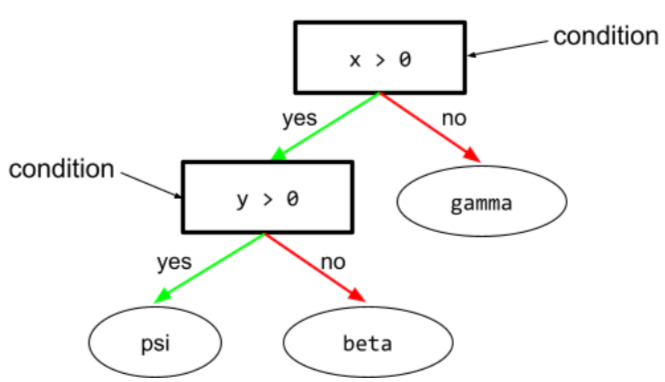
เงื่อนไขนี้เรียกอีกอย่างว่าการแยกหรือการทดสอบ
สภาพคอนทราสต์ที่มีใบไม้
และดู:
ดูข้อมูลเพิ่มเติมได้ที่ประเภทของเงื่อนไข ในหลักสูตร Decision Forests
การแต่งเรื่อง
คำพ้องความหมายของอาการหลอน
การแต่งเรื่องอาจเป็นคำที่ถูกต้องในเชิงเทคนิคมากกว่าคำว่าหลอน อย่างไรก็ตาม การหลอนได้รับความนิยมก่อน
การกำหนดค่า
กระบวนการกำหนดค่าพร็อพเพอร์ตี้เริ่มต้นที่ใช้ฝึกโมเดล ซึ่งรวมถึง
- เลเยอร์การแต่งเพลงของโมเดล
- ตำแหน่งของข้อมูล
- ไฮเปอร์พารามิเตอร์ เช่น
ในโปรเจ็กต์แมชชีนเลิร์นนิง คุณสามารถกำหนดค่าผ่านไฟล์การกำหนดค่าพิเศษหรือใช้ไลบรารีการกำหนดค่า เช่น ไลบรารีต่อไปนี้
อคติยืนยันความคิดตัวเอง
แนวโน้มที่จะค้นหา ตีความ ชื่นชอบ และจดจำข้อมูลในลักษณะที่ยืนยันความเชื่อหรือสมมติฐานที่มีอยู่ก่อนแล้ว นักพัฒนาแมชชีนเลิร์นนิงอาจเก็บรวบรวมหรือติดป้ายกำกับ ข้อมูลโดยไม่ตั้งใจในลักษณะที่ส่งผลต่อผลลัพธ์ที่สนับสนุนความเชื่อที่มีอยู่ อคติแฝงรูปแบบหนึ่งคืออคติยืนยันความคิดตัวเอง
อคติของผู้ทดลองเป็นรูปแบบหนึ่งของอคติในการยืนยัน ซึ่งผู้ทดลองจะฝึกโมเดลต่อไปจนกว่าจะมีการยืนยันสมมติฐานที่มีอยู่ก่อนแล้ว
เมตริกความสับสน
ตาราง NxN ที่สรุปจำนวนการคาดการณ์ที่ถูกต้องและไม่ถูกต้อง ที่โมเดลการจัดประเภทสร้างขึ้น ตัวอย่างเช่น ลองดูเมทริกซ์ความสับสนต่อไปนี้สําหรับโมเดลการจัดประเภทแบบไบนารี
| เนื้องอก (คาดการณ์) | ไม่ใช่เนื้องอก (คาดการณ์) | |
|---|---|---|
| เนื้องอก (ข้อมูลจากการสังเกตการณ์โดยตรง) | 18 (TP) | 1 (FN) |
| ไม่ใช่เนื้องอก (ข้อมูลจากการสังเกตการณ์โดยตรง) | 6 (FP) | 452 (TN) |
เมตริกความสับสนก่อนหน้าแสดงข้อมูลต่อไปนี้
- จากการคาดการณ์ 19 รายการที่ข้อมูลที่ระบุว่าถูกต้องโดยเจ้าหน้าที่เป็นเนื้องอก โมเดลจัดประเภทได้อย่างถูกต้อง 18 รายการและจัดประเภทไม่ถูกต้อง 1 รายการ
- จากการคาดการณ์ 458 รายการซึ่งข้อมูลที่ระบุว่าถูกต้องโดยเจ้าหน้าที่คือ "ไม่ใช่เนื้องอก" โมเดล จัดประเภทได้อย่างถูกต้อง 452 รายการและจัดประเภทไม่ถูกต้อง 6 รายการ
เมทริกซ์ความสับสนสำหรับปัญหาการจัดประเภทแบบหลายคลาส ช่วยให้คุณระบุรูปแบบของข้อผิดพลาดได้ ตัวอย่างเช่น ลองพิจารณาเมทริกซ์ความสับสนต่อไปนี้สําหรับโมเดลการจัดประเภทแบบหลายคลาส 3 คลาส ที่จัดประเภทไอริส 3 ประเภทที่แตกต่างกัน (เวอร์จินิกา เวอร์ซิคอลอร์ และเซโตซา) เมื่อข้อมูลที่ระบุว่าถูกต้องโดยเจ้าหน้าที่คือ Virginica เมทริกซ์ความสับสนจะแสดงให้เห็นว่าโมเดลมีแนวโน้มที่จะคาดการณ์ Versicolor มากกว่า Setosa โดยไม่ถูกต้อง
| Setosa (คาดการณ์) | Versicolor (คาดการณ์) | เวอร์จิเนีย (คาดการณ์) | |
|---|---|---|---|
| Setosa (ข้อมูลจากการสังเกตการณ์โดยตรง) | 88 | 12 | 0 |
| Versicolor (ข้อมูลจากการสังเกตการณ์โดยตรง) | 6 | 141 | 7 |
| เวอร์จินิกา (ข้อมูลจากการสังเกตการณ์โดยตรง) | 2 | 27 | 109 |
อีกตัวอย่างหนึ่งคือเมทริกซ์ความสับสนอาจเผยให้เห็นว่าโมเดลที่ฝึกมา เพื่อจดจำตัวเลขที่เขียนด้วยลายมือมักจะทำนายผิดเป็น 9 แทนที่จะเป็น 4 หรือทำนายผิดเป็น 1 แทนที่จะเป็น 7
เมทริกซ์ความสับสนมีข้อมูลเพียงพอที่จะคํานวณเมตริกประสิทธิภาพที่หลากหลาย รวมถึงความแม่นยํา และการเรียกคืน
การแยกวิเคราะห์ส่วนประกอบ
การแบ่งประโยคออกเป็นโครงสร้างทางไวยากรณ์ที่เล็กลง ("ส่วนประกอบ") ส่วนที่เหลือของระบบ ML เช่น โมเดลความเข้าใจภาษาธรรมชาติ จะแยกวิเคราะห์องค์ประกอบได้ง่ายกว่าประโยคเดิม ตัวอย่างเช่น ลองพิจารณาประโยคต่อไปนี้
เพื่อนของฉันรับเลี้ยงแมว 2 ตัว
ตัวแยกวิเคราะห์แบบ Constituency จะแบ่งประโยคนี้ออกเป็นส่วนประกอบ 2 ส่วนต่อไปนี้
- เพื่อนของฉันเป็นวลีนาม
- รับเลี้ยงแมว 2 ตัวเป็นวลีที่มีคำกริยา
โดยองค์ประกอบเหล่านี้สามารถแบ่งย่อยออกเป็นองค์ประกอบที่เล็กลงได้อีก เช่น วลีที่มีคำกริยา
รับเลี้ยงแมว 2 ตัว
สามารถแบ่งย่อยออกเป็น
- adopted เป็นคำกริยา
- แมว 2 ตัวเป็นวลีนามอีกวลีหนึ่ง
การฝังภาษาตามบริบท
การฝังที่เข้าใกล้ "ความเข้าใจ" คำ และวลีในแบบที่ผู้พูดที่เป็นมนุษย์สามารถทำได้ การฝังภาษาตามบริบท สามารถเข้าใจไวยากรณ์ ความหมาย และบริบทที่ซับซ้อน
ตัวอย่างเช่น ลองพิจารณาการฝังคำว่า cow ในภาษาอังกฤษ การฝังรุ่นเก่า เช่น word2vec สามารถแสดงคำภาษาอังกฤษ ในลักษณะที่ระยะทางในพื้นที่การฝัง จาก cow ถึง bull จะคล้ายกับระยะทางจาก ewe (แกะตัวเมีย) ถึง ram (แกะตัวผู้) หรือจาก female ถึง male การฝังภาษาตามบริบทสามารถก้าวไปอีกขั้นด้วยการรับรู้ว่าบางครั้งผู้พูดภาษาอังกฤษ ใช้คำว่าcow ในความหมายของวัวตัวเมียหรือวัวตัวผู้
หน้าต่างบริบท
จำนวนโทเค็นที่โมเดลประมวลผลได้ในพรอมต์ที่กำหนด ยิ่งหน้าต่างบริบทมีขนาดใหญ่เท่าใด โมเดลก็จะใช้ข้อมูลได้มากขึ้นเท่านั้น เพื่อสร้างคำตอบที่สอดคล้องและสมเหตุสมผล กับพรอมต์
ฟีเจอร์ต่อเนื่อง
ฟีเจอร์ทศนิยมที่มีค่าที่เป็นไปได้ไม่สิ้นสุด เช่น อุณหภูมิหรือน้ำหนัก
เปรียบเทียบกับฟีเจอร์ที่ไม่ต่อเนื่อง
การสุ่มตัวอย่างแบบตามสะดวก
การใช้ชุดข้อมูลที่ไม่ได้รวบรวมอย่างเป็นวิทยาศาสตร์เพื่อทำการทดสอบอย่างรวดเร็ว ในภายหลัง คุณจะต้องเปลี่ยนไปใช้ชุดข้อมูลที่รวบรวมมาอย่างเป็นระบบ
การบรรจบกัน
สถานะที่เกิดขึ้นเมื่อค่าloss เปลี่ยนแปลงน้อยมากหรือ ไม่เปลี่ยนแปลงเลยในแต่ละการทำซ้ำ ตัวอย่างเช่น เส้นโค้งการสูญเสียต่อไปนี้แสดงให้เห็นว่าการบรรจบกันเกิดขึ้นที่ประมาณ 700 การวนซ้ำ
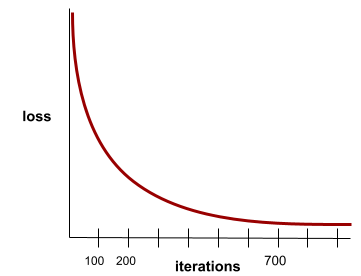
โมเดลจะบรรจบกันเมื่อการฝึกเพิ่มเติมไม่ ปรับปรุงโมเดล
ในดีปเลิร์นนิง บางครั้งค่าการสูญเสียจะคงที่หรือ เกือบคงที่สำหรับการวนซ้ำหลายครั้งก่อนที่จะลดลงในที่สุด ในช่วงระยะเวลานาน ที่ค่าการสูญเสียคงที่ คุณอาจรู้สึกว่าค่าต่างๆ บรรจบกันอย่างไม่ถูกต้องชั่วคราว
ดูการหยุดก่อนกำหนดด้วย
ดูข้อมูลเพิ่มเติมได้ที่เส้นโค้งการบรรจบกันของโมเดลและการสูญเสีย ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การเขียนโค้ดแบบสนทนา
กล่องโต้ตอบแบบวนซ้ำระหว่างคุณกับโมเดล Generative AI เพื่อวัตถุประสงค์ ในการสร้างซอฟต์แวร์ คุณป้อนพรอมต์ที่อธิบายซอฟต์แวร์บางอย่าง จากนั้น โมเดลจะใช้คำอธิบายดังกล่าวเพื่อสร้างโค้ด จากนั้นคุณจะออกพรอมต์ใหม่ เพื่อแก้ไขข้อบกพร่องในพรอมต์ก่อนหน้าหรือในโค้ดที่สร้างขึ้น และโมเดลจะสร้างโค้ดที่อัปเดตแล้ว คุณทั้ง 2 คนจะสลับกันไปมาจนกว่าซอฟต์แวร์ที่สร้างขึ้นจะดีพอ
การเขียนโค้ดการสนทนาเป็นความหมายดั้งเดิมของการเขียนโค้ดไวบ์
เปรียบเทียบกับการเขียนโค้ดตามข้อกำหนด
ฟังก์ชันนูน
ฟังก์ชันที่ภูมิภาคเหนือกราฟของฟังก์ชันเป็นเซตแบบนูน ฟังก์ชันนูนต้นแบบมีลักษณะคล้ายตัวอักษร U ตัวอย่างเช่น ฟังก์ชันต่อไปนี้ เป็นฟังก์ชันนูนทั้งหมด
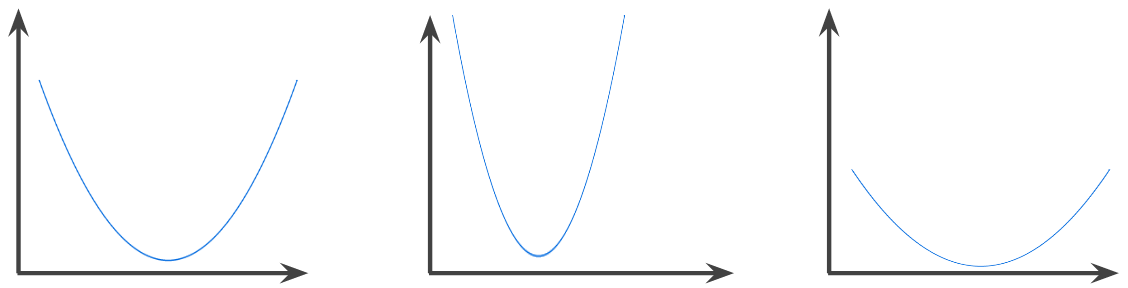
ในทางตรงกันข้าม ฟังก์ชันต่อไปนี้ไม่ใช่ฟังก์ชันเว้า โปรดสังเกตว่า พื้นที่เหนือกราฟไม่ใช่เซตแบบนูน

ฟังก์ชันนูนอย่างแท้จริงมีจุดต่ำสุดเฉพาะที่เพียงจุดเดียว ซึ่งเป็นจุดต่ำสุดส่วนกลางด้วย ฟังก์ชันรูปตัว U แบบคลาสสิกคือฟังก์ชันนูนอย่างแท้จริง อย่างไรก็ตาม ฟังก์ชันนูนบางอย่าง (เช่น เส้นตรง) ไม่ได้มีรูปร่างเป็นตัว U
ดูข้อมูลเพิ่มเติมได้ที่ฟังก์ชันการบรรจบกันและฟังก์ชันนูน ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
การเพิ่มประสิทธิภาพแบบนูน
กระบวนการใช้เทคนิคทางคณิตศาสตร์ เช่น การไล่ระดับการไล่ระดับ เพื่อค้นหาค่าต่ำสุดของฟังก์ชันนูน การวิจัยด้านแมชชีนเลิร์นนิงจำนวนมากมุ่งเน้นไปที่การกำหนดปัญหาต่างๆ เป็นปัญหาการเพิ่มประสิทธิภาพแบบนูน และการแก้ปัญหาเหล่านั้นอย่างมีประสิทธิภาพมากขึ้น
ดูรายละเอียดทั้งหมดได้ที่ Boyd และ Vandenberghe, Convex Optimization
เซตนูน
เซตย่อยของปริภูมิแบบยุคลิดซึ่งเส้นที่ลากระหว่างจุด 2 จุดในเซตย่อย จะยังคงอยู่ภายในเซตย่อยนั้นอย่างสมบูรณ์ ตัวอย่างเช่น รูปร่าง 2 รูปต่อไปนี้ เป็นเซตคอนเวกซ์

ในทางตรงกันข้าม รูปร่าง 2 แบบต่อไปนี้ไม่ใช่เซตคอนเวกซ์

การสังวัตนาการ
ในทางคณิตศาสตร์ การผสมฟังก์ชัน 2 ฟังก์ชัน ในแมชชีนเลิร์นนิง คอนโวลูชันจะผสมฟิลเตอร์คอนโวลูชันและเมทริกซ์อินพุต เพื่อฝึกน้ำหนัก
คำว่า "การสังวัตนาการ" ในแมชชีนเลิร์นนิงมักเป็นวิธีเรียกแบบย่อ เพื่ออ้างอิงถึงการดำเนินการสังวัตนาการ หรือเลเยอร์สังวัตนาการ
หากไม่มี Convolution อัลกอริทึมแมชชีนเลิร์นนิงจะต้องเรียนรู้ น้ำหนักแยกกันสำหรับทุกเซลล์ในเทนเซอร์ขนาดใหญ่ ตัวอย่างเช่น อัลกอริทึมแมชชีนเลิร์นนิงที่ฝึกกับรูปภาพขนาด 2K x 2K จะต้อง ค้นหาน้ำหนักแยกกัน 4 ล้านรายการ เนื่องจาก Convolution อัลกอริทึมแมชชีนเลิร์นนิง จึงต้องค้นหาน้ำหนักสำหรับแต่ละเซลล์ใน ฟิลเตอร์ Convolutional ซึ่งช่วยลด หน่วยความจำที่จำเป็นในการฝึกโมเดลได้อย่างมาก เมื่อใช้ฟิลเตอร์แบบ Convolutional จะมีการทำซ้ำในเซลล์เพื่อให้แต่ละเซลล์คูณด้วยฟิลเตอร์
ดูข้อมูลเพิ่มเติมได้ที่การแนะนำเครือข่ายประสาทแบบคอนโวลูชัน ในหลักสูตรการแยกประเภทรูปภาพ
ฟิลเตอร์ Convolutional
หนึ่งใน 2 ตัวดำเนินการในการดำเนินการแบบ Convolution (ส่วนนักแสดงอีกคน คือส่วนหนึ่งของเมทริกซ์อินพุต) ฟิลเตอร์ Convolutional คือเมทริกซ์ที่มีอันดับเดียวกันกับเมทริกซ์อินพุต แต่มีรูปร่างเล็กกว่า เช่น เมื่อกำหนดเมทริกซ์อินพุตขนาด 28x28 ตัวกรองอาจเป็นเมทริกซ์ 2 มิติใดก็ได้ ที่มีขนาดเล็กกว่า 28x28
ในการดัดแปลงภาพถ่าย โดยทั่วไปแล้วเซลล์ทั้งหมดในฟิลเตอร์ Convolutional จะ ตั้งค่าเป็นรูปแบบคงที่ของ 1 และ 0 ในแมชชีนเลิร์นนิง โดยปกติแล้วฟิลเตอร์ Convolution จะเริ่มต้นด้วยตัวเลขสุ่ม จากนั้น เครือข่ายจะฝึกค่าที่เหมาะสม
ดูข้อมูลเพิ่มเติมได้ที่การสังวัตนาการ ในหลักสูตรการแยกประเภทรูปภาพ
เลเยอร์ Convolutional
เลเยอร์ของโครงข่ายประสาทแบบลึกซึ่งฟิลเตอร์ Convolutional จะส่งต่อเมทริกซ์อินพุต ตัวอย่างเช่น ลองพิจารณาฟิลเตอร์ Convolutional ขนาด 3x3 ต่อไปนี้
![เมทริกซ์ 3x3 ที่มีค่าต่อไปนี้ [[0,1,0], [1,0,1], [0,1,0]]](https://developers.google.com/static/machine-learning/glossary/images/ConvolutionalFilter33.svg?hl=th)
ภาพเคลื่อนไหวต่อไปนี้แสดงเลเยอร์ Convolutional ซึ่งประกอบด้วยการดำเนินการ Convolutional 9 รายการที่เกี่ยวข้องกับเมทริกซ์อินพุตขนาด 5x5 โปรดสังเกตว่าการดำเนินการแบบ Convolution แต่ละครั้งจะทำงานกับสไลซ์ 3x3 ที่แตกต่างกันของเมทริกซ์อินพุต เมทริกซ์ 3x3 ที่ได้ (ทางด้านขวา) ประกอบด้วยผลลัพธ์ของการดำเนินการ Convolutional 9 รายการ ดังนี้
![ภาพเคลื่อนไหวที่แสดงเมทริกซ์ 2 รายการ เมทริกซ์แรกคือเมทริกซ์ 5x5
[[128,97,53,201,198], [35,22,25,200,195],
[37,24,28,197,182], [33,28,92,195,179], [31,40,100,192,177]]
เมทริกซ์ที่ 2 คือเมทริกซ์ 3x3 ดังนี้
[[181,303,618], [115,338,605], [169,351,560]]
เมทริกซ์ที่ 2 คํานวณโดยใช้ตัวกรองแบบ Convolution
[[0, 1, 0], [1, 0, 1], [0, 1, 0]] กับ
เซตย่อย 3x3 ที่แตกต่างกันของเมทริกซ์ 5x5](https://developers.google.com/static/machine-learning/glossary/images/AnimatedConvolution.gif?hl=th)
ดูข้อมูลเพิ่มเติมได้ที่เลเยอร์ที่เชื่อมต่ออย่างสมบูรณ์ ในหลักสูตรการแยกประเภทรูปภาพ
โครงข่ายประสาทแบบคอนโวลูชัน
โครงข่ายประสาทที่มีอย่างน้อย 1 เลเยอร์เป็นเลเยอร์ Convolutional โดยทั่วไปแล้ว โครงข่ายประสาทเทียมแบบ Convolutional จะประกอบด้วยเลเยอร์ต่อไปนี้
โครงข่ายประสาทเทียมแบบคอนโวลูชันประสบความสำเร็จอย่างมากในปัญหาบางประเภท เช่น การจดจำรูปภาพ
การดำเนินการแบบ Convolution
การดำเนินการทางคณิตศาสตร์ 2 ขั้นตอนต่อไปนี้
- การคูณแบบทีละองค์ประกอบของฟิลเตอร์ Convolutional และชิ้นส่วนของเมทริกซ์อินพุต (ชิ้นส่วนของเมทริกซ์อินพุตมีอันดับและขนาดเท่ากับฟิลเตอร์ Convolutional)
- ผลรวมของค่าทั้งหมดในเมทริกซ์ผลิตภัณฑ์ที่ได้
ตัวอย่างเช่น ลองพิจารณาเมทริกซ์อินพุต 5x5 ต่อไปนี้
![เมทริกซ์ 5x5: [[128,97,53,201,198], [35,22,25,200,195],
[37,24,28,197,182], [33,28,92,195,179], [31,40,100,192,177]]](https://developers.google.com/static/machine-learning/glossary/images/ConvolutionalLayerInputMatrix.svg?hl=th)
ตอนนี้ลองนึกถึงฟิลเตอร์การแปลงแบบ Convolution ขนาด 2x2 ต่อไปนี้
![เมทริกซ์ 2x2: [[1, 0], [0, 1]]](https://developers.google.com/static/machine-learning/glossary/images/ConvolutionalLayerFilter.svg?hl=th)
การดำเนินการแบบ Convolution แต่ละครั้งจะเกี่ยวข้องกับสไลซ์ขนาด 2x2 เดียวของเมทริกซ์อินพุต เช่น สมมติว่าเราใช้ชิ้นส่วนขนาด 2x2 ที่ ด้านซ้ายบนของเมทริกซ์อินพุต ดังนั้น การดำเนินการ Convolution ใน ชิ้นนี้จึงมีลักษณะดังนี้
![การใช้ตัวกรอง Convolutional [[1, 0], [0, 1]] กับส่วน 2x2 ด้านซ้ายบนของเมทริกซ์อินพุต ซึ่งคือ [[128,97], [35,22]]
ฟิลเตอร์ Convolutional จะคงค่า 128 และ 22 ไว้ แต่จะตั้งค่า 97 และ 35 เป็น 0
ดังนั้น การดำเนินการ Convolution จึงให้ผลลัพธ์เป็น
ค่า 150 (128+22)](https://developers.google.com/static/machine-learning/glossary/images/ConvolutionalLayerOperation.svg?hl=th)
เลเยอร์ Convolutional ประกอบด้วย ชุดการดำเนินการ Convolutional ซึ่งแต่ละรายการจะทำงานกับส่วนที่แตกต่างกัน ของเมทริกซ์อินพุต
ต้นทุน
คำพ้องความหมายของการสูญเสีย
การฝึกร่วม
แนวทางการเรียนรู้แบบกึ่งกำกับดูแล มีประโยชน์อย่างยิ่งเมื่อเงื่อนไขต่อไปนี้ทั้งหมดเป็นจริง
- อัตราส่วนของตัวอย่างที่ไม่มีป้ายกำกับต่อตัวอย่างที่มีป้ายกำกับในชุดข้อมูลสูง
- นี่คือปัญหาการจัดประเภท (ไบนารีหรือ หลายคลาส)
- ชุดข้อมูลมีฟีเจอร์เชิงคาดการณ์ 2 ชุดที่แตกต่างกัน ซึ่งเป็นอิสระต่อกันและเสริมซึ่งกันและกัน
การฝึกร่วมกันจะขยายสัญญาณอิสระให้เป็นสัญญาณที่แรงขึ้น เช่น พิจารณาโมเดลการแยกประเภทที่ จัดหมวดหมู่รถมือสองแต่ละคันเป็นดีหรือไม่ดี ฟีเจอร์การคาดการณ์ชุดหนึ่งอาจมุ่งเน้นลักษณะโดยรวม เช่น ปี ยี่ห้อ และรุ่นของรถยนต์ ส่วนฟีเจอร์การคาดการณ์อีกชุดหนึ่งอาจมุ่งเน้นบันทึกการขับขี่ของเจ้าของคนก่อนและประวัติการบำรุงรักษารถยนต์
เอกสารสำคัญเกี่ยวกับการฝึกร่วมคือ Combining Labeled and Unlabeled Data with Co-Training โดย Blum และ Mitchell
ความเป็นธรรมแบบข้อเท็จจริง
เมตริกความเป็นธรรมที่ตรวจสอบว่าโมเดลการจัดประเภทให้ผลลัพธ์เดียวกันสำหรับบุคคลหนึ่งกับอีกบุคคลหนึ่งที่เหมือนกับบุคคลแรกหรือไม่ ยกเว้นในส่วนของแอตทริบิวต์ที่มีความละเอียดอ่อนอย่างน้อย 1 รายการ การประเมินโมเดลการจัดประเภทเพื่อความยุติธรรมแบบข้อเท็จจริงสมมติเป็น วิธีหนึ่งในการระบุแหล่งที่มาของความเอนเอียงที่อาจเกิดขึ้นในโมเดล
โปรดดูข้อมูลเพิ่มเติมในแหล่งข้อมูลต่อไปนี้
- ความเป็นธรรม: ความเป็นธรรมแบบข้อเท็จจริงที่ขัดแย้ง ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
- เมื่อโลกมาบรรจบกัน: การผสานรวมสมมติฐานแบบ Counterfactual ที่แตกต่างกัน ในความเท่าเทียม
อคติในการครอบคลุม
การขยายตัวของคำ
ประโยคหรือวลีที่มีความหมายกำกวม Crash Blossom เป็นปัญหาสำคัญในการทำความเข้าใจภาษาธรรมชาติ ตัวอย่างเช่น พาดหัวข่าวRed Tape Holds Up Skyscraper เป็น การใช้คำที่ทำให้เกิดความสับสนเนื่องจากโมเดล NLU อาจตีความพาดหัวข่าวตามตัวอักษรหรือ ในเชิงเปรียบเทียบ
นักวิจารณ์
คำพ้องความหมายของ Deep Q-Network
ครอสเอนโทรปี
การสรุปการสูญเสียบันทึกเป็น ปัญหาการจัดประเภทแบบหลายคลาส Cross-entropy จะวัดความแตกต่างระหว่างการแจกแจงความน่าจะเป็น 2 แบบ ดูเพิ่มเติม perplexity
การตรวจสอบแบบไขว้
กลไกในการประมาณว่าโมเดลจะทำงานกับข้อมูลใหม่ได้ดีเพียงใดโดยการทดสอบโมเดลกับชุดข้อมูลย่อยที่ไม่ทับซ้อนกันอย่างน้อย 1 ชุด ซึ่งได้มาจากชุดการฝึก
ฟังก์ชันการกระจายสะสม (CDF)
ฟังก์ชันที่กำหนดความถี่ของตัวอย่างที่น้อยกว่าหรือเท่ากับค่าเป้าหมาย ตัวอย่างเช่น พิจารณาการกระจายปกติของค่าต่อเนื่อง CDF บอกคุณว่าตัวอย่างประมาณ 50% ควรน้อยกว่าหรือเท่ากับค่าเฉลี่ย และตัวอย่างประมาณ 84% ควรน้อยกว่าหรือเท่ากับค่าเบี่ยงเบนมาตรฐาน 1 ค่าเหนือค่าเฉลี่ย
D
การวิเคราะห์ข้อมูล
ทำความเข้าใจข้อมูลโดยพิจารณาตัวอย่าง การวัดผล และการแสดงข้อมูลเป็นภาพ การวิเคราะห์ข้อมูลมีประโยชน์อย่างยิ่งเมื่อได้รับชุดข้อมูลเป็นครั้งแรก ก่อนที่จะสร้างโมเดลแรก นอกจากนี้ ยังมีความสำคัญอย่างยิ่งในการทำความเข้าใจการทดสอบและการแก้ไขข้อบกพร่องของระบบ
การเพิ่มข้อมูล
การเพิ่มช่วงและจำนวนตัวอย่างการฝึกโดยการแปลงตัวอย่างที่มีอยู่เพื่อสร้างตัวอย่างเพิ่มเติม ตัวอย่างเช่น สมมติว่ารูปภาพเป็นหนึ่งในฟีเจอร์ของคุณ แต่ชุดข้อมูลไม่มีตัวอย่างรูปภาพเพียงพอให้โมเดลเรียนรู้ความสัมพันธ์ที่เป็นประโยชน์ คุณควรเพิ่มรูปภาพที่ติดป้ายกำกับให้เพียงพอลงในชุดข้อมูลเพื่อช่วยให้โมเดลฝึกได้อย่างถูกต้อง หากทำไม่ได้ การเพิ่มข้อมูล จะหมุน ยืด และพลิกรูปภาพแต่ละรูปเพื่อสร้างรูปภาพต้นฉบับ ในรูปแบบต่างๆ ซึ่งอาจให้ข้อมูลที่ติดป้ายกำกับเพียงพอที่จะช่วยให้การฝึก มีประสิทธิภาพยอดเยี่ยม
DataFrame
ประเภทข้อมูล pandas ยอดนิยมสำหรับแสดงชุดข้อมูลในหน่วยความจำ
DataFrame คล้ายกับตารางหรือสเปรดชีต แต่ละคอลัมน์ของ DataFrame มีชื่อ (ส่วนหัว) และแต่ละแถวจะระบุด้วยหมายเลขที่ไม่ซ้ำกัน
แต่ละคอลัมน์ใน DataFrame มีโครงสร้างเหมือนอาร์เรย์ 2 มิติ ยกเว้นว่า แต่ละคอลัมน์สามารถกำหนดประเภทข้อมูลของตัวเองได้
นอกจากนี้ โปรดดูหน้าข้อมูลอ้างอิง pandas.DataFrame อย่างเป็นทางการด้วย
การประมวลผลแบบคู่ขนาน
วิธีปรับขนาดการฝึกหรือการอนุมาน ที่จำลองโมเดลทั้งหมดไปยัง อุปกรณ์หลายเครื่อง แล้วส่งชุดข้อมูลย่อยของข้อมูลอินพุตไปยังแต่ละอุปกรณ์ การขนานข้อมูลช่วยให้ฝึกและอนุมานได้ด้วยขนาดกลุ่มที่ใหญ่มาก แต่การขนานข้อมูลกำหนดให้โมเดลต้องมีขนาดเล็กพอที่จะพอดีกับอุปกรณ์ทั้งหมด
โดยปกติแล้วการประมวลผลแบบคู่ขนานของข้อมูลจะช่วยเร่งการฝึกและการอนุมาน
ดูการทำงานแบบขนานของโมเดลด้วย
Dataset API (tf.data)
API TensorFlow ระดับสูงสําหรับการอ่านข้อมูลและ
แปลงข้อมูลให้อยู่ในรูปแบบที่อัลกอริทึมแมชชีนเลิร์นนิงต้องการ
ออบเจ็กต์ tf.data.Dataset แสดงลำดับขององค์ประกอบ ซึ่งแต่ละองค์ประกอบมี Tensor อย่างน้อย 1 รายการ ออบเจ็กต์ tf.data.Iterator
ช่วยให้เข้าถึงองค์ประกอบของ Dataset ได้
ชุดข้อมูล
ชุดข้อมูลดิบที่มักจะ (แต่ไม่เสมอไป) จัดระเบียบในรูปแบบใดรูปแบบหนึ่งต่อไปนี้
- สเปรดชีต
- ไฟล์ในรูปแบบ CSV (ค่าที่คั่นด้วยคอมมา)
ขอบเขตการตัดสินใจ
เส้นแบ่งระหว่างคลาสที่โมเดลเรียนรู้ในคลาสแบบไบนารีหรือปัญหาการจัดประเภทแบบหลายคลาส ตัวอย่างเช่น ในรูปภาพต่อไปนี้ซึ่งแสดงถึงปัญหาการแยกประเภทแบบไบนารี ขอบเขตการตัดสินใจคือเส้นแบ่งระหว่างคลาสสีส้มกับ คลาสสีน้ำเงิน

Decision Forest
โมเดลที่สร้างจากต้นไม้ตัดสินใจหลายต้น Decision Forest จะทำการคาดการณ์โดยการรวบรวมการคาดการณ์ของ Decision Tree ประเภทของป่าการตัดสินใจที่ได้รับความนิยม ได้แก่ Random Forest และ Gradient Boosted Tree
ดูข้อมูลเพิ่มเติมได้ที่ส่วนDecision Forests ในหลักสูตร Decision Forests
เกณฑ์การตัดสินใจ
คำพ้องความหมายของเกณฑ์การจัดประเภท
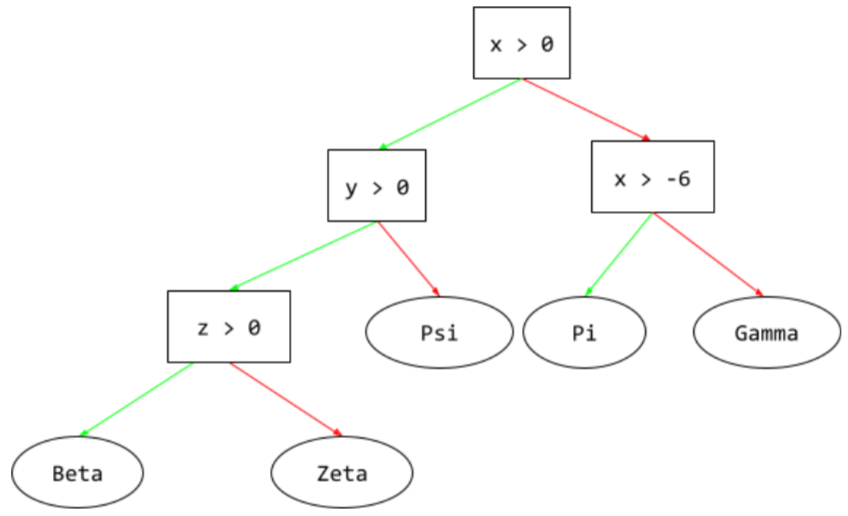
แผนผังการตัดสินใจ
โมเดลการเรียนรู้ภายใต้การควบคุมดูแลซึ่งประกอบด้วยชุดเงื่อนไขและลีฟที่จัดระเบียบตามลำดับชั้น ตัวอย่างเช่น แผนผังการตัดสินใจมีลักษณะดังนี้
เครื่องมือถอดรหัส
โดยทั่วไปแล้ว ระบบ ML ใดๆ ที่แปลงจากรูปแบบที่ประมวลผลแล้ว หนาแน่น หรือภายในเป็นรูปแบบที่ดิบกว่า กระจัดกระจาย หรือภายนอก
ดีโคดเดอร์มักเป็นส่วนประกอบของโมเดลขนาดใหญ่ ซึ่งมักจะ จับคู่กับเอนโคดเดอร์
ในงานแบบลำดับต่อลำดับ ดีโคดเดอร์ จะเริ่มต้นด้วยสถานะภายในที่เอนโคดเดอร์สร้างขึ้นเพื่อคาดการณ์ลำดับ ถัดไป
ดูคำจำกัดความของตัวถอดรหัสภายในสถาปัตยกรรม Transformer ได้ที่Transformer
ดูข้อมูลเพิ่มเติมได้ที่โมเดลภาษาขนาดใหญ่ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
โมเดลเชิงลึก
โครงข่ายประสาทเทียมที่มีเลเยอร์ที่ซ่อนอยู่มากกว่า 1 เลเยอร์
โมเดลแบบลึกเรียกอีกอย่างว่าโครงข่ายประสาทแบบลึก
เปรียบเทียบกับโมเดลแบบกว้าง
โครงข่ายประสาทแบบลึก
คำพ้องความหมายของโมเดลเชิงลึก
เครือข่าย Deep Q (DQN)
ในการเรียนรู้แบบ Q โครงข่ายประสาทแบบลึก ที่คาดการณ์ฟังก์ชัน Q
Critic เป็นคำพ้องความหมายของ Deep Q-Network
ความเท่าเทียมทางประชากร
เมตริกความเป็นธรรมที่ตรงตามเงื่อนไขต่อไปนี้ ผลลัพธ์ของการจัดประเภทของโมเดลไม่ขึ้นอยู่กับแอตทริบิวต์ที่ละเอียดอ่อนที่กำหนด
ตัวอย่างเช่น หากทั้งชาวลิลิพุตและชาวโบรบดิงแนกสมัครเข้าเรียนที่มหาวิทยาลัยกลับดับดริบ ความเท่าเทียมกันทางประชากรจะเกิดขึ้นหากเปอร์เซ็นต์ของชาวลิลิพุตที่ได้รับการตอบรับเท่ากับเปอร์เซ็นต์ของชาวโบรบดิงแนกที่ได้รับการตอบรับ ไม่ว่ากลุ่มใดกลุ่มหนึ่งจะมีคุณสมบัติมากกว่าอีกกลุ่มหนึ่งโดยเฉลี่ยหรือไม่ก็ตาม
แตกต่างจากโอกาสที่เท่าเทียมกันและ ความเท่าเทียมกันของโอกาส ซึ่งอนุญาตให้ ผลการจัดประเภทโดยรวมขึ้นอยู่กับแอตทริบิวต์ที่ละเอียดอ่อน แต่ไม่อนุญาตให้ผลการจัดประเภทสำหรับป้ายกำกับความจริงพื้นฐานที่ระบุบางอย่างขึ้นอยู่กับแอตทริบิวต์ที่ละเอียดอ่อน ดูภาพ "การต่อสู้กับการเลือกปฏิบัติด้วยแมชชีนเลิร์นนิงที่ชาญฉลาดยิ่งขึ้น" เพื่อสำรวจการแลกเปลี่ยนเมื่อเพิ่มประสิทธิภาพเพื่อความเท่าเทียมกันทางข้อมูลประชากร
ดูข้อมูลเพิ่มเติมได้ที่ความเป็นธรรม: ความเท่าเทียมกันทางประชากร ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การลดสัญญาณรบกวน
แนวทางทั่วไปสำหรับการเรียนรู้แบบกำกับดูแลตนเอง ซึ่งมีลักษณะดังนี้
- สัญญาณรบกวนจะเพิ่มลงในชุดข้อมูลโดยอัตโนมัติ
- โมเดลจะพยายามตัดเสียงรบกวน
การลดสัญญาณรบกวนช่วยให้เรียนรู้จากตัวอย่างที่ไม่มีป้ายกำกับได้ ชุดข้อมูลเดิมทำหน้าที่เป็นเป้าหมายหรือป้ายกำกับ และข้อมูลที่มีสัญญาณรบกวนทำหน้าที่เป็นอินพุต
โมเดลภาษาที่มาสก์บางรายการใช้การลดสัญญาณรบกวน ดังนี้
- ระบบจะเพิ่มสัญญาณรบกวนลงในประโยคที่ไม่มีป้ายกำกับโดยการมาสก์โทเค็นบางส่วน
- โมเดลจะพยายามคาดการณ์โทเค็นต้นฉบับ
ฟีเจอร์หนาแน่น
ฟีเจอร์ที่ค่าส่วนใหญ่หรือทั้งหมดไม่ใช่ศูนย์ โดยปกติจะเป็นเทนเซอร์ของค่าทศนิยม ตัวอย่างเช่น เทนเซอร์ 10 องค์ประกอบต่อไปนี้ เป็นแบบหนาแน่นเนื่องจากค่า 9 ค่าเป็นค่าที่ไม่ใช่ 0
| 8 | 3 | 7 | 5 | 2 | 4 | 0 | 4 | 9 | 6 |
แตกต่างจากฟีเจอร์แบบกระจัดกระจาย
เลเยอร์หนาแน่น
คำพ้องความหมายของเลเยอร์ที่เชื่อมต่ออย่างเต็มรูปแบบ
ความลึก
ผลรวมของรายการต่อไปนี้ในโครงข่ายประสาทเทียม
- จำนวนเลเยอร์ที่ซ่อน
- จำนวนเลเยอร์เอาต์พุต ซึ่งโดยปกติคือ 1
- จำนวนเลเยอร์การฝัง
เช่น โครงข่ายประสาทที่มีเลเยอร์ที่ซ่อนไว้ 5 เลเยอร์และเลเยอร์เอาต์พุต 1 เลเยอร์ มีความลึกเท่ากับ 6
โปรดทราบว่าเลเยอร์อินพุตไม่มีผลต่อความลึก
โครงข่ายประสาทแบบลึกแบบแยกส่วนตามความลึก (sepCNN)
สถาปัตยกรรมโครงข่ายประสาทเทียมแบบคอนโวลูชัน ที่อิงตาม Inception แต่จะแทนที่โมดูล Inception ด้วยคอนโวลูชันแบบแยกตามความลึก หรือที่เรียกว่า Xception
การ Convolution ที่แยกความลึกได้ (เรียกอีกอย่างว่า Convolution ที่แยกได้) จะแยก Convolution 3 มิติมาตรฐานออกเป็น 2 การดำเนินการ Convolution แยกกัน ซึ่งมีประสิทธิภาพในการคำนวณมากกว่า โดยขั้นแรกคือ Convolution ที่แยกความลึกได้ ที่มีความลึกเป็น 1 (n ✕ n ✕ 1) และขั้นที่ 2 คือ Convolution แบบ Pointwise ที่มีความยาวและความกว้างเป็น 1 (1 ✕ 1 ✕ n)
ดูข้อมูลเพิ่มเติมได้ที่ Xception: Deep Learning with Depthwise Separable Convolutions
ป้ายกำกับที่ได้มา
คำพ้องความหมายของป้ายกำกับพร็อกซี
อุปกรณ์
คำที่มีความหมายหลายอย่างซึ่งมีคำจำกัดความที่เป็นไปได้ 2 อย่างต่อไปนี้
- หมวดหมู่ฮาร์ดแวร์ที่เรียกใช้เซสชัน TensorFlow ได้ ซึ่งรวมถึง CPU, GPU และ TPU
- เมื่อฝึกโมเดล ML ในชิปตัวเร่ง (GPU หรือ TPU) ส่วนของระบบที่จัดการเทนเซอร์และการฝังจริง อุปกรณ์ทำงานบนชิปตัวเร่ง ในทางตรงกันข้าม โฮสต์ มักจะทำงานบน CPU
Differential Privacy
ในแมชชีนเลิร์นนิง แนวทางในการปกปิดข้อมูลระบุตัวบุคคลเพื่อปกป้องข้อมูลที่ละเอียดอ่อน (เช่น ข้อมูลส่วนบุคคลของบุคคล) ที่รวมอยู่ในชุดข้อมูลการฝึกของโมเดลไม่ให้มีการเปิดเผย วิธีนี้ช่วยให้มั่นใจได้ว่าโมเดลจะไม่เรียนรู้หรือจดจำข้อมูลเกี่ยวกับบุคคลใดบุคคลหนึ่งมากนัก ซึ่งทำได้โดยการสุ่มตัวอย่างและเพิ่มสัญญาณรบกวนระหว่างการฝึกโมเดลเพื่อปกปิดจุดข้อมูลแต่ละจุด ซึ่งจะช่วยลดความเสี่ยงในการเปิดเผยข้อมูลการฝึกที่ละเอียดอ่อน
นอกจากนี้ยังมีการใช้ Differential Privacy นอกเหนือจากแมชชีนเลิร์นนิงด้วย ตัวอย่างเช่น นักวิทยาศาสตร์ด้านข้อมูลบางครั้งใช้ Differential Privacy เพื่อปกป้องความเป็นส่วนตัวของแต่ละบุคคล เมื่อคำนวณสถิติการใช้งานผลิตภัณฑ์สำหรับกลุ่มประชากรต่างๆ
การลดมิติ
การลดจำนวนมิติข้อมูลที่ใช้เพื่อแสดงฟีเจอร์หนึ่งๆ ในเวกเตอร์ฟีเจอร์ โดยปกติจะทำโดย การแปลงเป็นเวกเตอร์การฝัง
ขนาด
คำที่มีการโอเวอร์โหลดซึ่งมีคำจำกัดความต่อไปนี้
จำนวนระดับของพิกัดในTensor เช่น
- สเกลาร์มี 0 มิติ เช่น
["Hello"] - เวกเตอร์มี 1 มิติ เช่น
[3, 5, 7, 11] - เมทริกซ์มี 2 มิติ เช่น
[[2, 4, 18], [5, 7, 14]]คุณระบุเซลล์หนึ่งๆ ในเวกเตอร์แบบ 1 มิติได้โดยใช้พิกัด 1 ตำแหน่ง ส่วนการระบุเซลล์หนึ่งๆ ในเมทริกซ์แบบ 2 มิติจะต้องใช้พิกัด 2 ตำแหน่ง
- สเกลาร์มี 0 มิติ เช่น
จำนวนรายการในเวกเตอร์ฟีเจอร์
จำนวนองค์ประกอบในเลเยอร์การฝัง
การเขียนพรอมต์โดยตรง
คำพ้องความหมายของการเขียนพรอมต์แบบ Zero-Shot Prompting
ฟีเจอร์ที่ไม่ต่อเนื่อง
ฟีเจอร์ที่มีชุดค่าที่เป็นไปได้แบบจำกัด เช่น ฟีเจอร์ที่มีค่าเป็น animal, vegetable หรือ mineral เท่านั้นคือฟีเจอร์ แบบไม่ต่อเนื่อง (หรือแบบหมวดหมู่)
เปรียบเทียบกับฟีเจอร์ต่อเนื่อง
โมเดลแยกแยะ
โมเดลที่คาดการณ์ป้ายกำกับจากชุดฟีเจอร์อย่างน้อย 1 รายการ ในรูปแบบที่เป็นทางการมากขึ้น โมเดลแบบแยกแยะจะกำหนด ความน่าจะเป็นแบบมีเงื่อนไขของเอาต์พุตที่กำหนดฟีเจอร์และ น้ำหนัก นั่นคือ
p(output | features, weights)
เช่น โมเดลที่คาดการณ์ว่าอีเมลเป็นสแปมหรือไม่จากฟีเจอร์ และน้ำหนักคือโมเดลจำแนก
โมเดลการเรียนรู้ภายใต้การดูแลส่วนใหญ่ รวมถึงโมเดลการจัดประเภท และโมเดลการถดถอย เป็นโมเดลเชิงเลือก
แตกต่างจากโมเดล Generative
ตัวแบ่ง
ระบบที่ระบุว่าตัวอย่างเป็นของจริงหรือปลอม
หรืออาจเป็นระบบย่อยภายในเครือข่าย ปฏิปักษ์แบบสร้างสรรค์ที่กำหนดว่าตัวอย่างที่สร้างโดยเครื่องกำเนิดเป็นของจริงหรือของปลอม
ดูข้อมูลเพิ่มเติมได้ที่ตัวแยกแยะ ในหลักสูตร GAN
ผลกระทบที่แตกต่าง
การตัดสินใจเกี่ยวกับผู้คนซึ่งส่งผลกระทบต่อกลุ่มย่อยของประชากรที่แตกต่างกันอย่างไม่สมส่วน โดยปกติแล้วจะหมายถึงสถานการณ์ ที่กระบวนการตัดสินใจของอัลกอริทึมส่งผลเสียหรือส่งผลดี ต่อกลุ่มย่อยบางกลุ่มมากกว่ากลุ่มอื่นๆ
ตัวอย่างเช่น สมมติว่าอัลกอริทึมที่พิจารณาการมีสิทธิ์ของชาวลิลิพุต ในการขอสินเชื่อบ้านขนาดเล็กมีแนวโน้มที่จะจัดประเภท ชาวลิลิพุตเป็น "ไม่มีสิทธิ์" หากที่อยู่จัดส่งมีรหัสไปรษณีย์ที่เฉพาะเจาะจง หากชาวลิลิพุตที่ใช้บิ๊กเอนเดียนมีแนวโน้มที่จะมี ที่อยู่จัดส่งที่มีรหัสไปรษณีย์นี้มากกว่าชาวลิลิพุตที่ใช้ลิทเทิลเอนเดียน อัลกอริทึมนี้อาจส่งผลให้เกิดผลกระทบที่ไม่เท่าเทียมกัน
แตกต่างจากการเลือกปฏิบัติ ซึ่งมุ่งเน้นความแตกต่างที่เกิดขึ้นเมื่อลักษณะของกลุ่มย่อย เป็นอินพุตที่ชัดเจนในกระบวนการตัดสินใจเชิงอัลกอริทึม
การเลือกปฏิบัติ
การนำแอตทริบิวต์ที่ละเอียดอ่อนของกลุ่มตัวอย่าง มาพิจารณาในกระบวนการตัดสินใจแบบอัลกอริทึมเพื่อให้ กลุ่มย่อยต่างๆ ได้รับการปฏิบัติที่แตกต่างกัน
ตัวอย่างเช่น ลองพิจารณาอัลกอริทึมที่ กำหนดสิทธิ์ของชาวลิลิพุตในการขอสินเชื่อบ้านขนาดเล็กตาม ข้อมูลที่ระบุไว้ในใบสมัครขอสินเชื่อ หากอัลกอริทึมใช้ความเกี่ยวข้องของ Lilliputian เป็น Big-Endian หรือ Little-Endian เป็นอินพุต อัลกอริทึม จะใช้การปฏิบัติที่แตกต่างกันตามมิตินั้น
แตกต่างจากผลกระทบที่ไม่เท่าเทียมกัน ซึ่งมุ่งเน้น ความแตกต่างในผลกระทบต่อสังคมของการตัดสินใจตามอัลกอริทึมที่มีต่อกลุ่มย่อย โดยไม่คำนึงว่ากลุ่มย่อยเหล่านั้นจะเป็นอินพุตของโมเดลหรือไม่
การกลั่น
กระบวนการลดขนาดโมเดลหนึ่ง (เรียกว่าโมเดลครู) ให้เป็นโมเดลที่เล็กลง (เรียกว่าโมเดลนักเรียน) ซึ่งเลียนแบบ การคาดการณ์ของโมเดลต้นฉบับให้ได้มากที่สุด การกลั่น มีประโยชน์เนื่องจากโมเดลขนาดเล็กมีข้อดี 2 ประการที่สำคัญกว่าโมเดลขนาดใหญ่ (ครู) ดังนี้
- เวลาอนุมานที่เร็วขึ้น
- ลดการใช้หน่วยความจำและพลังงาน
อย่างไรก็ตาม โดยทั่วไปแล้วการคาดการณ์ของนักเรียนมักจะไม่ดีเท่าการคาดการณ์ของครู
การกลั่นจะฝึกโมเดลนักเรียนเพื่อลดฟังก์ชันการสูญเสียตามความแตกต่างระหว่างเอาต์พุต ของการคาดการณ์ของโมเดลนักเรียนและโมเดลครู
เปรียบเทียบการกลั่นกับคำต่อไปนี้
ดูข้อมูลเพิ่มเติมได้ที่ LLM: การปรับแต่ง การกลั่น และการออกแบบพรอมต์ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การเผยแพร่
ความถี่และช่วงของค่าต่างๆ สำหรับฟีเจอร์หรือป้ายกำกับที่กำหนด การกระจายจะบันทึกความน่าจะเป็นของค่าหนึ่งๆ
รูปภาพต่อไปนี้แสดงฮิสโทแกรมของการกระจาย 2 แบบที่แตกต่างกัน
- ทางด้านซ้ายคือการกระจายความมั่งคั่งตามกฎกำลังเทียบกับจำนวนผู้ ที่มีความมั่งคั่งนั้น
- ทางด้านขวาคือการแจกแจงความสูงแบบปกติเทียบกับจำนวนคน ที่มีความสูงนั้น
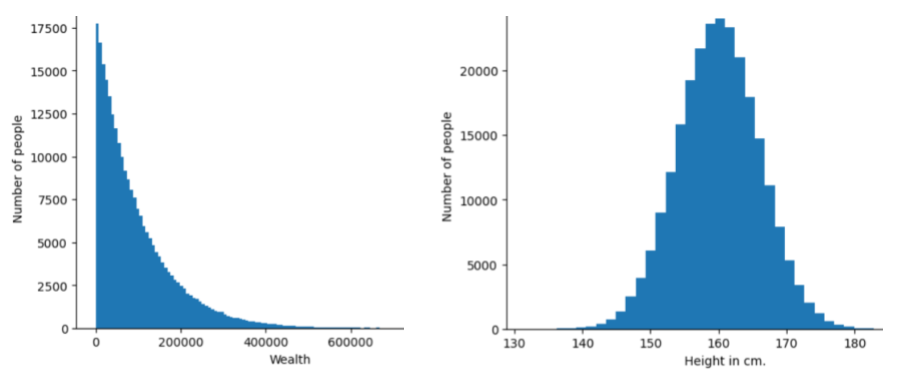
การทำความเข้าใจการกระจายของฟีเจอร์และป้ายกำกับแต่ละรายการจะช่วยให้คุณทราบวิธีปรับค่าให้เป็นมาตรฐานและตรวจหาค่าผิดปกติ
วลีไม่อยู่ในการกระจายหมายถึงค่าที่ไม่ปรากฏในชุดข้อมูล หรือพบน้อยมาก เช่น รูปภาพของดาวเสาร์จะถือว่าอยู่นอกการกระจายสำหรับชุดข้อมูลที่ประกอบด้วยรูปภาพแมว
การจัดกลุ่มแบบแบ่งแยก
การลดความละเอียด
คำที่ใช้มากเกินไปซึ่งอาจหมายถึงสิ่งต่อไปนี้
- การลดปริมาณข้อมูลในฟีเจอร์เพื่อฝึกโมเดลให้มีประสิทธิภาพมากขึ้น เช่น ก่อนฝึกโมเดลการจดจำรูปภาพ ให้ดาวน์แซมปลิงรูปภาพที่มีความละเอียดสูง เป็นรูปแบบที่มีความละเอียดต่ำกว่า
- การฝึกกับตัวอย่างคลาสที่มีการแสดงมากเกินไปในเปอร์เซ็นต์ที่ต่ำอย่างไม่สมส่วน เพื่อปรับปรุงการฝึกโมเดลในคลาสที่มีการแสดงน้อย เช่น ในชุดข้อมูล ที่ไม่สมดุลของคลาส โมเดลมักจะเรียนรู้เกี่ยวกับ คลาสส่วนใหญ่เป็นจำนวนมาก และเรียนรู้เกี่ยวกับ คลาสส่วนน้อยไม่เพียงพอ การดาวน์แซมปลิงช่วย ปรับสมดุลปริมาณการฝึกในคลาสส่วนใหญ่และคลาสส่วนน้อย
ดูข้อมูลเพิ่มเติมได้ที่ชุดข้อมูล: ชุดข้อมูลที่ไม่สมดุล ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
DQN
ตัวย่อของ Deep Q-Network
การทำให้เป็นปกติแบบ Dropout
รูปแบบของการทำให้เป็นปกติที่มีประโยชน์ในการฝึกโครงข่ายประสาทเทียม การทําให้เป็นปกติแบบ Dropout จะนําหน่วยที่เลือกแบบสุ่มจํานวนหนึ่งในเลเยอร์ เครือข่ายออกสําหรับขั้นตอนการไล่ระดับสีเดียว ยิ่งมีหน่วยหลุดออกไปมากเท่าใด การทำให้เป็นปกติก็จะยิ่งเข้มงวดมากขึ้นเท่านั้น ซึ่งคล้ายกับการฝึกโครงข่ายให้เลียนแบบกลุ่มโครงข่ายขนาดเล็กจำนวนมาก ดูรายละเอียดทั้งหมดได้ที่ Dropout: A Simple Way to Prevent Neural Networks from Overfitting
ไดนามิก
สิ่งที่ทำบ่อยๆ หรืออย่างต่อเนื่อง คำว่าไดนามิกและออนไลน์มีความหมายเหมือนกันในแมชชีนเลิร์นนิง การใช้งาน dynamic และ online ที่พบบ่อยในแมชชีนเลิร์นนิงมีดังนี้
- โมเดลแบบไดนามิก (หรือโมเดลออนไลน์) คือโมเดล ที่ได้รับการฝึกซ้ำบ่อยครั้งหรืออย่างต่อเนื่อง
- การฝึกแบบไดนามิก (หรือการฝึกออนไลน์) คือกระบวนการฝึก อย่างต่อเนื่องหรือสม่ำเสมอ
- การอนุมานแบบไดนามิก (หรือการอนุมานออนไลน์) คือกระบวนการ สร้างการคาดการณ์ตามต้องการ
โมเดลแบบไดนามิก
โมเดลที่ได้รับการฝึกซ้ำบ่อยๆ (อาจจะอย่างต่อเนื่องด้วย) โมเดลแบบไดนามิกคือ "ผู้เรียนรู้ตลอดชีวิต" ที่ ปรับตัวให้เข้ากับข้อมูลที่เปลี่ยนแปลงอยู่เสมอ โมเดลแบบไดนามิกเรียกอีกอย่างว่าโมเดลออนไลน์
แตกต่างจากโมเดลคงที่
E
Eager Execution
สภาพแวดล้อมการเขียนโปรแกรม TensorFlow ซึ่งการดำเนินการ จะทำงานทันที ในทางตรงกันข้าม การดำเนินการที่เรียกใช้ในการดำเนินการกราฟจะไม่ทำงานจนกว่าจะมีการประเมินอย่างชัดเจน การดำเนินการแบบกระตือรือร้นคืออินเทอร์เฟซแบบคำสั่ง ซึ่งคล้ายกับโค้ดในภาษาโปรแกรมส่วนใหญ่ โดยทั่วไปแล้ว โปรแกรมการดำเนินการแบบกระตือรือร้นจะแก้ไขข้อบกพร่องได้ง่ายกว่าโปรแกรมการดำเนินการแบบกราฟมาก
การหยุดก่อนกำหนด
วิธีการสำหรับการทำให้เป็นปกติที่เกี่ยวข้องกับการสิ้นสุดการฝึก ก่อนที่การสูญเสียการฝึกจะลดลง การหยุดก่อนเวลาคือการหยุดฝึกโมเดลโดยตั้งใจ เมื่อการสูญเสียในชุดข้อมูลการตรวจสอบเริ่ม เพิ่มขึ้น นั่นคือเมื่อประสิทธิภาพการสรุปทั่วไปแย่ลง
แตกต่างจากการออกก่อนเวลา
ระยะทางของ Earth Mover (EMD)
การวัดความคล้ายคลึงกันของการกระจาย 2 รายการ ยิ่งระยะทางของ Earth Mover ต่ำเท่าใด การกระจายก็จะยิ่งคล้ายกันมากขึ้นเท่านั้น
ระยะทางแก้ไข
การวัดว่าสตริงข้อความ 2 รายการมีความคล้ายกันมากน้อยเพียงใด ในแมชชีนเลิร์นนิง ระยะทางในการแก้ไขมีประโยชน์ด้วยเหตุผลต่อไปนี้
- การคำนวณระยะทางแก้ไขทำได้ง่าย
- ระยะทางในการแก้ไขสามารถเปรียบเทียบสตริง 2 รายการที่ทราบว่าคล้ายกัน
- ระยะทางในการแก้ไขจะกำหนดระดับที่สตริงต่างๆ คล้ายกับสตริงที่กำหนด
มีคำจำกัดความหลายอย่างของระยะทางเอดิท ซึ่งแต่ละคำจำกัดความใช้การดำเนินการกับสตริงที่แตกต่างกัน ดูตัวอย่างได้ที่ระยะทางเลเวนชไตน์
สัญกรณ์ Einsum
สัญกรณ์ที่มีประสิทธิภาพสำหรับอธิบายวิธีรวมเทนเซอร์ 2 รายการ ระบบจะรวมเทนเซอร์โดยการคูณองค์ประกอบของเทนเซอร์หนึ่ง กับองค์ประกอบของเทนเซอร์อีกอัน แล้วจึงนำผลคูณมาบวกกัน สัญกรณ์ Einsum ใช้สัญลักษณ์เพื่อระบุแกนของแต่ละเทนเซอร์ และจะจัดเรียงสัญลักษณ์เดียวกันเหล่านั้นใหม่เพื่อระบุรูปร่างของเทนเซอร์ใหม่ที่ได้
NumPy มีการใช้งาน Einsum ทั่วไป
เลเยอร์การฝัง
เลเยอร์ที่ซ่อนอยู่พิเศษที่ฝึกในฟีเจอร์เชิงหมวดหมู่ที่มีมิติสูงเพื่อค่อยๆ เรียนรู้เวกเตอร์การฝังที่มีมิติต่ำกว่า เลเยอร์การฝังช่วยให้โครงข่ายประสาทเทียมฝึกได้มีประสิทธิภาพมากกว่าการฝึกเฉพาะฟีเจอร์เชิงหมวดหมู่ที่มีมิติสูง
ตัวอย่างเช่น ปัจจุบัน Earth รองรับต้นไม้ประมาณ 73,000 สายพันธุ์ สมมติว่า
สายพันธุ์ต้นไม้เป็นฟีเจอร์ในโมเดล ดังนั้นเลเยอร์
อินพุตของโมเดลจึงมีเวกเตอร์แบบ One-Hot ที่มีความยาว 73,000
องค์ประกอบ
ตัวอย่างเช่น baobab อาจแสดงผลดังนี้

อาร์เรย์ที่มีองค์ประกอบ 73,000 รายการนั้นยาวมาก หากคุณไม่เพิ่มเลเยอร์การฝัง ลงในโมเดล การฝึกจะใช้เวลานานมากเนื่องจาก การคูณ 0 จำนวน 72,999 ตัว สมมติว่าคุณเลือกเลเยอร์การฝังที่มีมิติข้อมูล 12 รายการ ดังนั้น เลเยอร์การฝังจะค่อยๆ เรียนรู้ เวกเตอร์การฝังใหม่สำหรับต้นไม้แต่ละสายพันธุ์
ในบางสถานการณ์ การแฮชเป็นทางเลือกที่สมเหตุสมผล แทนเลเยอร์การฝัง
ดูข้อมูลเพิ่มเติมได้ที่การฝัง ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
พื้นที่การฝัง
ปริภูมิเวกเตอร์ d มิติที่แมปฟีเจอร์จากปริภูมิเวกเตอร์ที่มีมิติสูงกว่า ระบบจะฝึกพื้นที่การฝังเพื่อจับโครงสร้าง ที่มีความหมายสําหรับแอปพลิเคชันที่ต้องการ
ดอทโปรดักต์ ของการฝัง 2 รายการคือการวัดความคล้ายคลึงกัน
เวกเตอร์การฝัง
กล่าวโดยกว้างๆ คือ อาร์เรย์ของจำนวนจุดลอยที่นำมาจากเลเยอร์ที่ซ่อน ใดก็ได้ซึ่งอธิบายอินพุตไปยังเลเยอร์ที่ซ่อนนั้น เวกเตอร์การฝังมักจะเป็นอาร์เรย์ของจำนวนจุดลอยที่ฝึกในเลเยอร์การฝัง เช่น สมมติว่าเลเยอร์การฝังต้องเรียนรู้เวกเตอร์การฝังสําหรับต้นไม้แต่ละสายพันธุ์จากทั้งหมด 73,000 สายพันธุ์บนโลก เวกเตอร์การฝังสำหรับต้นบาวบับอาจเป็นอาร์เรย์ต่อไปนี้

เวกเตอร์การฝังไม่ใช่กลุ่มตัวเลขแบบสุ่ม เลเยอร์การฝัง จะกำหนดค่าเหล่านี้ผ่านการฝึก ซึ่งคล้ายกับวิธีที่ โครงข่ายประสาทเทียมเรียนรู้น้ำหนักอื่นๆ ระหว่างการฝึก องค์ประกอบแต่ละรายการของอาร์เรย์ คือการจัดประเภทตามลักษณะบางอย่างของสายพันธุ์ต้นไม้ องค์ประกอบใดแสดงลักษณะของต้นไม้สายพันธุ์ใด ซึ่งเป็นสิ่งที่มนุษย์ ระบุได้ยากมาก
ส่วนที่น่าทึ่งในทางคณิตศาสตร์ของเวกเตอร์การฝังคือรายการที่คล้ายกันจะมีชุดตัวเลขทศนิยมที่คล้ายกัน เช่น ต้นไม้สายพันธุ์ที่คล้ายกันจะมีชุดตัวเลขทศนิยมที่คล้ายกันมากกว่าต้นไม้สายพันธุ์ที่แตกต่างกัน ต้นเรดวูดและต้นซีคัวญ่าเป็นต้นไม้ที่อยู่ในสายพันธุ์เดียวกัน ดังนั้นชุดตัวเลขทศนิยมแบบลอยจึงมีความคล้ายคลึงกันมากกว่า ต้นเรดวูดและต้นมะพร้าว ตัวเลขในเวกเตอร์การฝังจะ เปลี่ยนทุกครั้งที่คุณฝึกโมเดลใหม่ แม้ว่าคุณจะฝึกโมเดลใหม่ ด้วยอินพุตที่เหมือนกันก็ตาม
ฟังก์ชันการกระจายสะสมเชิงประจักษ์ (eCDF หรือ EDF)
ฟังก์ชันการกระจายสะสม อิงตามการวัดเชิงประจักษ์จากชุดข้อมูลจริง ค่าของฟังก์ชันที่จุดใดก็ตามตามแกน x คือเศษส่วนของการสังเกตในชุดข้อมูลที่น้อยกว่าหรือเท่ากับค่าที่ระบุ
การลดความเสี่ยงเชิงประจักษ์ (ERM)
เลือกฟังก์ชันที่ลดการสูญเสียในชุดการฝึกให้เหลือน้อยที่สุด เปรียบเทียบกับการลดความเสี่ยงเชิงโครงสร้าง
โปรแกรมเปลี่ยนไฟล์
โดยทั่วไปแล้ว ระบบ ML ใดๆ ที่แปลงจากรูปแบบดิบ แบบกระจัดกระจาย หรือภายนอก เป็นรูปแบบที่ประมวลผลแล้ว หนาแน่นขึ้น หรือเป็นรูปแบบภายในมากขึ้น
โดยมักเป็นส่วนประกอบของโมเดลขนาดใหญ่ ซึ่งมักจะใช้ร่วมกับดีโคดเดอร์ Transformer บางตัวจะจับคู่ตัวเข้ารหัสกับตัวถอดรหัส แต่ Transformer ตัวอื่นๆ จะใช้เฉพาะตัวเข้ารหัส หรือเฉพาะตัวถอดรหัส
บางระบบใช้เอาต์พุตของตัวเข้ารหัสเป็นอินพุตไปยังเครือข่ายการจัดประเภทหรือการถดถอย
ในงานแบบลำดับต่อลำดับ ตัวเข้ารหัส จะรับลำดับอินพุตและส่งคืนสถานะภายใน (เวกเตอร์) จากนั้นดีโคดเดอร์จะใช้สถานะภายในนั้นเพื่อคาดการณ์ลำดับถัดไป
ดูคำจำกัดความของตัวเข้ารหัสในสถาปัตยกรรม Transformer ได้ที่Transformer
ดูข้อมูลเพิ่มเติมได้ที่LLM: โมเดลภาษาขนาดใหญ่คืออะไรในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
อุปกรณ์ปลายทาง
ตำแหน่งที่เข้าถึงได้ในเครือข่าย (โดยปกติคือ URL) ซึ่งใช้เข้าถึงบริการได้
วงดนตรี
ชุดโมเดลที่ฝึกแยกกันซึ่งมีการหาค่าเฉลี่ยหรือการรวบรวมการคาดการณ์ ในหลายกรณี การรวมโมเดลจะให้การคาดการณ์ที่ดีกว่าโมเดลเดียว เช่น Random Forest เป็นการรวมกันที่สร้างจากDecision Tree หลายรายการ โปรดทราบว่าDecision Forest บางรายการไม่ใช่กลุ่ม
ดูข้อมูลเพิ่มเติมได้ที่Random Forest ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
เอนโทรปี
ใน ทฤษฎีข้อมูล คำอธิบายเกี่ยวกับความไม่แน่นอนของการกระจายความน่าจะเป็น หรืออาจกล่าวได้ว่าเอนโทรปีคือปริมาณข้อมูลที่ตัวอย่างแต่ละรายการมี การกระจายจะมี เอนโทรปีสูงสุดที่เป็นไปได้เมื่อค่าทั้งหมดของตัวแปรสุ่มมี โอกาสเท่ากัน
เอนโทรปีของชุดที่มีค่าที่เป็นไปได้ 2 ค่าคือ "0" และ "1" (เช่น ป้ายกำกับในปัญหาการแยกประเภทแบบไบนารี) มีสูตรดังนี้
H = -p log p - q log q = -p log p - (1-p) * log (1-p)
ที่ไหน
- H คือเอนโทรปี
- p คือเศษส่วนของตัวอย่าง "1"
- q คือเศษส่วนของตัวอย่าง "0" โปรดทราบว่า q = (1 - p)
- log โดยทั่วไปคือ log2 ในกรณีนี้ หน่วยเอนโทรปี คือบิต
ตัวอย่างเช่น สมมติว่ามีข้อมูลต่อไปนี้
- ตัวอย่าง 100 รายการมีค่า "1"
- ตัวอย่าง 300 รายการมีค่า "0"
ดังนั้นค่าเอนโทรปีจึงเป็น
- p = 0.25
- q = 0.75
- H = (-0.25)log2(0.25) - (0.75)log2(0.75) = 0.81 บิตต่อตัวอย่าง
ชุดข้อมูลที่สมดุลอย่างสมบูรณ์ (เช่น "0" 200 รายการและ "1" 200 รายการ) จะมีเอนโทรปี 1.0 บิตต่อตัวอย่าง เมื่อชุดข้อมูลมีความไม่สมดุลมากขึ้น เอนโทรปีจะเข้าใกล้ 0.0
ในแผนผังการตัดสินใจ เอนโทรปีช่วยสร้างการได้ข้อมูลเพื่อช่วยให้ตัวแยกเลือกเงื่อนไข ในระหว่างการเติบโตของแผนผังการตัดสินใจแบบการจัดประเภท
เปรียบเทียบเอนโทรปีกับ
- ความไม่บริสุทธิ์ของ Gini
- ฟังก์ชันการสูญเสียเอนโทรปีครอส
โดยมักเรียกเอนโทรปีว่าเอนโทรปีของแชนนอน
ดูข้อมูลเพิ่มเติมได้ที่ตัวแยกที่แน่นอนสำหรับการแยกประเภทแบบไบนารีที่มีฟีเจอร์เชิงตัวเลข ในหลักสูตร Decision Forests
สภาพแวดล้อม
ในการเรียนรู้แบบเสริมกำลัง โลกที่มีเอเจนต์ และอนุญาตให้เอเจนต์สังเกตสถานะของโลกนั้น เช่น โลกที่แสดงอาจเป็นเกมอย่างหมากรุก หรือโลกจริงอย่างเขาวงกต เมื่อเอเจนต์ใช้การดำเนินการกับสภาพแวดล้อม สภาพแวดล้อมจะเปลี่ยนสถานะ
ตอน
ในการเรียนรู้แบบเสริมกำลัง ความพยายามซ้ำๆ ของเอเจนต์แต่ละครั้งเพื่อเรียนรู้สภาพแวดล้อม
Epoch
การส่งผ่านการฝึกแบบเต็มทั้งชุดการฝึก เพื่อให้ระบบประมวลผลตัวอย่างแต่ละรายการ 1 ครั้ง
Epoch แสดงถึงN/ขนาดกลุ่ม
การวนซ้ำของการฝึก โดย N คือ
จํานวนตัวอย่างทั้งหมด
เช่น สมมติว่ามีข้อมูลต่อไปนี้
- ชุดข้อมูลประกอบด้วยตัวอย่าง 1,000 รายการ
- ขนาดกลุ่มคือ 50 ตัวอย่าง
ดังนั้น 1 Epoch จึงต้องมีการวนซ้ำ 20 ครั้ง
1 epoch = (N/batch size) = (1,000 / 50) = 20 iterations
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยเชิงเส้น: ไฮเปอร์พารามิเตอร์ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
นโยบายแบบเอปซิลอนกรีด
ในการเรียนรู้แบบเสริมกำลัง นโยบายที่ทำตาม นโยบายแบบสุ่มที่มีความน่าจะเป็นเป็นเอปซิลอน หรือ นโยบายแบบตะกละในกรณีอื่นๆ ตัวอย่างเช่น หากเอปซิลอนเป็น 0.9 นโยบายจะทำตามนโยบายแบบสุ่ม 90% ของเวลาและนโยบายแบบตะกละ 10% ของเวลา
ในตอนต่อๆ ไป อัลกอริทึมจะลดค่าของเอปซิลอนเพื่อเปลี่ยนจากการปฏิบัติตามนโยบายแบบสุ่มเป็นการปฏิบัติตามนโยบายแบบตะกละ การเปลี่ยนนโยบายทำให้เอเจนต์สำรวจสภาพแวดล้อมแบบสุ่มก่อน แล้วจึงใช้ประโยชน์จากผลลัพธ์ของการสำรวจแบบสุ่มอย่างตะกละตะกลาม
ความเท่าเทียมของโอกาส
เมตริกความเป็นธรรมเพื่อประเมินว่าโมเดล คาดการณ์ผลลัพธ์ที่ต้องการได้ดีเท่าๆ กันสำหรับค่าทั้งหมดของแอตทริบิวต์ที่ละเอียดอ่อนหรือไม่ กล่าวอีกนัยหนึ่งคือ หากคลาสที่เป็นบวกคือผลลัพธ์ที่ต้องการสำหรับโมเดล เป้าหมายคือการทำให้อัตราผลบวกจริงเท่ากันสำหรับทุกกลุ่ม
ความเท่าเทียมกันของโอกาสเกี่ยวข้องกับอัตราส่วนที่เท่ากัน ซึ่งกำหนดให้ทั้งอัตราผลบวกจริงและ อัตราผลบวกลวงต้องเหมือนกันสำหรับทุกกลุ่ม
สมมติว่ามหาวิทยาลัยกลับดับดริบรับทั้งชาวลิลิปุตและชาวบรอบดิงแนก เข้าโปรแกรมคณิตศาสตร์ที่เข้มงวด โรงเรียนมัธยมศึกษาของชาวลิลิพุตมี หลักสูตรที่แข็งแกร่งสำหรับชั้นเรียนคณิตศาสตร์ และนักเรียนส่วนใหญ่ มีคุณสมบัติเหมาะสมสำหรับโปรแกรมมหาวิทยาลัย โรงเรียนมัธยมของชาวบร็อบดิงแน็กไม่ เปิดสอนวิชาคณิตศาสตร์เลย และด้วยเหตุนี้ นักเรียนที่ มีคุณสมบัติจึงมีจำนวนน้อยกว่ามาก โอกาสที่เท่าเทียมกันจะเกิดขึ้นสำหรับป้ายกำกับที่ต้องการ "รับเข้า" ในส่วนที่เกี่ยวข้องกับสัญชาติ (ชาวลิลิพุตหรือชาวบร็อบดิงแนก) หากนักเรียน/นักศึกษาที่มีคุณสมบัติเหมาะสมมีโอกาสได้รับการรับเข้าเท่ากัน ไม่ว่าจะเป็นชาวลิลิพุตหรือชาวบร็อบดิงแนก
ตัวอย่างเช่น สมมติว่ามีชาวลิลิพุต 100 คนและชาวโบรบดิงแนก 100 คนสมัครเข้าเรียนที่ มหาวิทยาลัยกลับบ์ดับดริบ และการตัดสินใจรับเข้าเรียนมีดังนี้
ตารางที่ 1 ผู้สมัครจากลิลิพุต (90% มีคุณสมบัติ)
| เข้าเกณฑ์ | คุณสมบัติไม่ครบ | |
|---|---|---|
| ยอมรับ | 45 | 3 |
| ถูกปฏิเสธ | 45 | 7 |
| รวม | 90 | 10 |
|
เปอร์เซ็นต์ของนักเรียนที่มีคุณสมบัติเหมาะสมที่ได้รับการตอบรับ: 45/90 = 50% เปอร์เซ็นต์ของนักเรียนที่ไม่มีคุณสมบัติเหมาะสมที่ถูกปฏิเสธ: 7/10 = 70% เปอร์เซ็นต์รวมของนักเรียนจากลิลิพุตที่ได้รับการตอบรับ: (45+3)/100 = 48% |
||
ตารางที่ 2 ผู้สมัครจาก Brobdingnag (10% มีคุณสมบัติ):
| เข้าเกณฑ์ | คุณสมบัติไม่ครบ | |
|---|---|---|
| ยอมรับ | 5 | 9 |
| ถูกปฏิเสธ | 5 | 81 |
| รวม | 10 | 90 |
|
เปอร์เซ็นต์ของนักเรียนที่มีคุณสมบัติเหมาะสมที่ได้รับการตอบรับ: 5/10 = 50% เปอร์เซ็นต์ของนักเรียนที่ไม่มีคุณสมบัติเหมาะสมที่ถูกปฏิเสธ: 81/90 = 90% เปอร์เซ็นต์รวมของนักเรียน Brobdingnagian ที่ได้รับการตอบรับ: (5+9)/100 = 14% |
||
ตัวอย่างก่อนหน้านี้เป็นไปตามความเท่าเทียมกันในโอกาสที่จะได้รับการยอมรับ ของนักเรียน/นักศึกษาที่มีคุณสมบัติเหมาะสม เนื่องจากทั้งชาวลิลิปุตและชาวบร็อบดิงแน็ก มีโอกาส 50% ที่จะได้รับการตอบรับ
แม้ว่าโอกาสจะเท่าเทียมกัน แต่เมตริกความเป็นธรรม 2 รายการต่อไปนี้ ยังไม่เป็นไปตามข้อกำหนด
- ความเท่าเทียมกันทางประชากร: ชาวลิลิพุตและชาวบรอบดิงแนกได้รับการรับเข้ามหาวิทยาลัยในอัตราที่แตกต่างกัน โดยมีนักเรียนชาวลิลิพุต 48% ได้รับการรับเข้า แต่มีนักเรียนชาวบรอบดิงแนกเพียง 14% เท่านั้นที่ได้รับการรับเข้า
- โอกาสที่เท่าเทียมกัน: แม้ว่านักเรียน/นักศึกษาชาวลิลิพุตและชาวบร็อบดิงแนกที่มีคุณสมบัติเหมาะสมจะมีโอกาสได้รับการตอบรับเท่ากัน แต่ข้อจำกัดเพิ่มเติมที่ว่านักเรียน/นักศึกษาชาวลิลิพุตและชาวบร็อบดิงแนกที่ไม่มีคุณสมบัติเหมาะสมจะมีโอกาสถูกปฏิเสธเท่ากันนั้นไม่เป็นจริง ชาวลิลิพุตที่ไม่ผ่านเกณฑ์มีอัตราการปฏิเสธ 70% ในขณะที่ชาวบร็อบดิงแนกที่ไม่ผ่านเกณฑ์มีอัตราการปฏิเสธ 90%
ดูข้อมูลเพิ่มเติมได้ที่ความเป็นธรรม: ความเท่าเทียมกันของ โอกาส ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
โอกาสที่เท่าเทียมกัน
เมตริกความเป็นธรรมเพื่อประเมินว่าโมเดลคาดการณ์ผลลัพธ์ได้ดีเท่ากันสำหรับค่าทั้งหมดของแอตทริบิวต์ที่ละเอียดอ่อนหรือไม่ โดยคำนึงถึงทั้งคลาสบวกและคลาสลบ ไม่ใช่แค่คลาสใดคลาสหนึ่งเท่านั้น กล่าวอีกนัยหนึ่งคือ อัตราผลบวกจริง และอัตราผลลบลวงควรเท่ากันสำหรับ ทุกกลุ่ม
โอกาสที่เท่าเทียมกันเกี่ยวข้องกับ ความเท่าเทียมกันของโอกาส ซึ่งมุ่งเน้นเฉพาะ อัตราข้อผิดพลาดสำหรับคลาสเดียว (บวกหรือลบ)
ตัวอย่างเช่น สมมติว่ามหาวิทยาลัยกลับดับดริบรับทั้งชาวลิลิพุตและชาวบร็อบดิงแนกเข้าเรียนในหลักสูตรคณิตศาสตร์ที่เข้มงวด โรงเรียนมัธยมของชาวลิลิพุต มีหลักสูตรที่แข็งแกร่งสำหรับชั้นเรียนคณิตศาสตร์ และนักเรียนส่วนใหญ่ มีคุณสมบัติเหมาะสมสำหรับโปรแกรมมหาวิทยาลัย โรงเรียนมัธยมของชาวบร็อบดิงแนกไม่มีชั้นเรียนคณิตศาสตร์เลย และด้วยเหตุนี้ นักเรียนของพวกเขาจึงมีคุณสมบัติน้อยกว่ามาก โอกาสที่เท่าเทียมกันจะเกิดขึ้นได้ก็ต่อเมื่อไม่ว่าผู้สมัครจะเป็นชาวลิลิปุตหรือชาวบร็อบดิงแน็ก หากมีคุณสมบัติครบถ้วน ก็มีโอกาสเท่ากันที่จะได้รับการยอมรับให้เข้าร่วมโปรแกรม และหากไม่มีคุณสมบัติครบถ้วน ก็มีโอกาสเท่ากันที่จะถูกปฏิเสธ
สมมติว่าชาวลิลิปุต 100 คนและชาวบร็อบดิงแนก 100 คนสมัครเข้าเรียนที่มหาวิทยาลัยกลับบ์ดับดริบ และมีการตัดสินใจรับเข้าเรียนดังนี้
ตารางที่ 3 ผู้สมัครจากลิลิพุต (90% มีคุณสมบัติ)
| เข้าเกณฑ์ | คุณสมบัติไม่ครบ | |
|---|---|---|
| ยอมรับ | 45 | 2 |
| ถูกปฏิเสธ | 45 | 8 |
| รวม | 90 | 10 |
|
เปอร์เซ็นต์ของนักเรียนที่มีคุณสมบัติผ่านที่ได้รับการตอบรับ: 45/90 = 50% เปอร์เซ็นต์ของนักเรียนที่ไม่มีคุณสมบัติผ่านที่ถูกปฏิเสธ: 8/10 = 80% เปอร์เซ็นต์รวมของนักเรียนชาวลิลิพุตที่ได้รับการตอบรับ: (45+2)/100 = 47% |
||
ตารางที่ 4 ผู้สมัครจาก Brobdingnag (10% มีคุณสมบัติ):
| เข้าเกณฑ์ | คุณสมบัติไม่ครบ | |
|---|---|---|
| ยอมรับ | 5 | 18 |
| ถูกปฏิเสธ | 5 | 72 |
| รวม | 10 | 90 |
|
เปอร์เซ็นต์ของนักเรียนที่มีคุณสมบัติเหมาะสมที่ได้รับการตอบรับ: 5/10 = 50% เปอร์เซ็นต์ของนักเรียนที่ไม่มีคุณสมบัติเหมาะสมที่ถูกปฏิเสธ: 72/90 = 80% เปอร์เซ็นต์รวมของนักเรียนจาก Brobdingnag ที่ได้รับการตอบรับ: (5+18)/100 = 23% |
||
โอกาสที่เท่าเทียมกันเป็นไปตามเงื่อนไขเนื่องจากนักเรียนที่มีคุณสมบัติทั้งชาวลิลิพุตและชาวบร็อบดิงแนก มีโอกาส 50% ที่จะได้รับการตอบรับ และนักเรียนที่ไม่มีคุณสมบัติทั้งชาวลิลิพุต และชาวบร็อบดิงแนกมีโอกาส 80% ที่จะถูกปฏิเสธ
ความน่าจะเป็นที่เท่ากันมีการกำหนดอย่างเป็นทางการใน "ความเท่าเทียมกันของ โอกาสในการเรียนรู้ภายใต้การกำกับดูแล" ดังนี้ "ตัวทำนาย Ŷ มีความน่าจะเป็นที่เท่ากันเมื่อเทียบกับ แอตทริบิวต์ที่ได้รับการคุ้มครอง A และผลลัพธ์ Y หาก Ŷ และ A เป็นอิสระ โดยมีเงื่อนไขเป็น Y"
เครื่องมือประมาณค่า
API ของ TensorFlow ที่เลิกใช้งานแล้ว ใช้ tf.keras แทน Estimators
evals
ใช้เป็นตัวย่อสำหรับการประเมิน LLM เป็นหลัก ในวงกว้าง evals เป็นคำย่อของการประเมินในรูปแบบใดก็ได้
การประเมิน
กระบวนการวัดคุณภาพของโมเดลหรือการเปรียบเทียบโมเดลต่างๆ กับโมเดลอื่นๆ
โดยปกติแล้ว คุณจะประเมินโมเดลแมชชีนเลิร์นนิงที่มีการควบคุมดูแล โดยเปรียบเทียบกับชุดการตรวจสอบ และชุดการทดสอบ การประเมิน LLM โดยทั่วไปจะเกี่ยวข้องกับการประเมินคุณภาพและความปลอดภัยในวงกว้าง
การทำงานแบบตรง
เมตริกแบบทั้งหมดหรือไม่มีเลยซึ่งเอาต์พุตของโมเดลจะตรงกับข้อมูลจากการสังเกตการณ์โดยตรงหรือข้อความอ้างอิง อย่างใดอย่างหนึ่ง เช่น หากข้อมูลจากการสังเกตการณ์โดยตรงคือ orange ผลลัพธ์ของโมเดลเดียวที่ตรงกับการทำงานแบบตรงทั้งหมดคือ orange
การจับคู่ที่แน่นอนยังประเมินโมเดลที่มีเอาต์พุตเป็นลำดับ (รายการที่จัดอันดับของรายการ) ได้ด้วย โดยทั่วไป การทำงานแบบตรงกำหนดให้รายการที่จัดอันดับที่สร้างขึ้นต้องตรงกับความจริงพื้นฐานทุกประการ นั่นคือ รายการแต่ละรายการในทั้ง 2 รายการต้องอยู่ในลำดับเดียวกัน อย่างไรก็ตาม หากข้อมูลจากการสังเกตการณ์โดยตรง ประกอบด้วยลำดับที่ถูกต้องหลายลำดับ การจับคู่ที่แน่นอนจะกำหนดให้เอาต์พุตของโมเดลตรงกับลำดับที่ถูกต้องลำดับใดลำดับหนึ่งเท่านั้น
ตัวอย่าง
ค่าของแถวหนึ่งของ features และอาจมี label ตัวอย่างในการเรียนรู้แบบมีผู้ดูแลแบ่งออกเป็น 2 หมวดหมู่ทั่วไป ดังนี้
- ตัวอย่างที่มีป้ายกำกับประกอบด้วยฟีเจอร์อย่างน้อย 1 รายการ และป้ายกำกับ ตัวอย่างที่มีป้ายกำกับจะใช้ในระหว่างการฝึก
- ตัวอย่างที่ไม่มีป้ายกำกับประกอบด้วยฟีเจอร์อย่างน้อย 1 รายการแต่ไม่มีป้ายกำกับ ระบบจะใช้ตัวอย่างที่ไม่มีป้ายกำกับในระหว่างการอนุมาน
เช่น สมมติว่าคุณกำลังฝึกโมเดลเพื่อพิจารณาอิทธิพล ของสภาพอากาศต่อคะแนนสอบของนักเรียน ตัวอย่างที่มีป้ายกำกับ 3 รายการมีดังนี้
| ฟีเจอร์ | ป้ายกำกับ | ||
|---|---|---|---|
| อุณหภูมิ | ความชื้น | ความกดอากาศ | คะแนนสอบ |
| 15 | 47 | 998 | ดี |
| 19 | 34 | 1020 | ดีมาก |
| 18 | 92 | 1012 | แย่ |
ตัวอย่างที่ไม่มีป้ายกำกับ 3 รายการมีดังนี้
| อุณหภูมิ | ความชื้น | ความกดอากาศ | |
|---|---|---|---|
| 12 | 62 | 1014 | |
| 21 | 47 | 1017 | |
| 19 | 41 | 1021 |
โดยปกติแล้ว แถวของชุดข้อมูลจะเป็นแหล่งที่มาดิบสำหรับตัวอย่าง กล่าวคือ ตัวอย่างมักประกอบด้วยชุดย่อยของคอลัมน์ในชุดข้อมูล นอกจากนี้ ฟีเจอร์ในตัวอย่างยังอาจรวมถึงฟีเจอร์สังเคราะห์ เช่น การรวมฟีเจอร์
ดูข้อมูลเพิ่มเติมได้ที่การเรียนรู้แบบมีผู้ดูแลใน หลักสูตรข้อมูลเบื้องต้นเกี่ยวกับแมชชีนเลิร์นนิง
การเล่นประสบการณ์ซ้ำ
ในรีอินฟอร์ซเมนต์เลิร์นนิง เทคนิค DQN ใช้เพื่อลดความสัมพันธ์ตามเวลาในข้อมูลการฝึก Agent จะจัดเก็บการเปลี่ยนสถานะไว้ในบัฟเฟอร์การเล่นซ้ำ จากนั้น จะสุ่มตัวอย่างการเปลี่ยนสถานะจากบัฟเฟอร์การเล่นซ้ำเพื่อสร้างข้อมูลการฝึก
อคติของผู้ทดลอง
ปัญหาการไล่ระดับสีที่ระเบิด
แนวโน้มที่การไล่ระดับสีใน โครงข่ายประสาทแบบลึก (โดยเฉพาะ โครงข่ายประสาทแบบเกิดซ้ำ) จะชัน (สูง) อย่างน่าประหลาดใจ การไล่ระดับที่ชันมักทำให้เกิดการอัปเดตขนาดใหญ่มาก ในน้ำหนักของโหนดแต่ละรายการใน โครงข่ายประสาทเทียมแบบลึก
โมเดลที่ประสบปัญหาการไล่ระดับสีที่เพิ่มขึ้นอย่างรวดเร็วจะฝึกได้ยาก หรือฝึกไม่ได้เลย การจำกัดค่าความชัน ช่วยลดปัญหานี้ได้
เปรียบเทียบกับปัญหาการไล่ระดับสีที่หายไป
F
F1
เมตริกการจัดประเภทแบบไบนารี "การสรุป" ที่ อิงตามทั้งความแม่นยำและความอ่อนไหว สูตรมีดังนี้
ข้อเท็จจริง
ในโลกของ ML พร็อพเพอร์ตี้ที่อธิบายโมเดลซึ่งเอาต์พุตอิงตามความเป็นจริง ความถูกต้องตามข้อเท็จจริงเป็นแนวคิด ไม่ใช่เมตริก เช่น สมมติว่าคุณส่งพรอมต์ต่อไปนี้ ไปยังโมเดลภาษาขนาดใหญ่
สูตรเคมีของเกลือแกงคืออะไร
โมเดลที่เพิ่มประสิทธิภาพความถูกต้องจะตอบว่า
NaCl
การคิดว่าโมเดลทั้งหมดควรอิงตามข้อเท็จจริงเป็นสิ่งที่น่าดึงดูดใจ อย่างไรก็ตาม พรอมต์บางอย่าง เช่น พรอมต์ต่อไปนี้ ควรทำให้โมเดล Generative AI เพิ่มประสิทธิภาพความคิดสร้างสรรค์มากกว่าความถูกต้องตามข้อเท็จจริง
เล่าร้อยกรองลิเมอริกเกี่ยวกับนักบินอวกาศและหนอนผีเสื้อให้ฟังหน่อย
ไม่น่าเป็นไปได้ที่กลอนตลกที่ได้จะอิงตามความเป็นจริง
เปรียบเทียบกับความสมเหตุสมผล
ข้อจำกัดด้านความเป็นธรรม
การใช้ข้อจำกัดกับอัลกอริทึมเพื่อให้มั่นใจว่ามีการปฏิบัติตามคำจำกัดความของความเป็นธรรมอย่างน้อย 1 รายการ ตัวอย่างข้อจำกัดด้านความเป็นธรรม ได้แก่- การประมวลผลภายหลังเอาต์พุตของโมเดล
- การแก้ไขฟังก์ชันการสูญเสียเพื่อรวมค่าปรับ สำหรับการละเมิดเมตริกความเป็นธรรม
- การเพิ่มข้อจํากัดทางคณิตศาสตร์ลงในปัญหาการเพิ่มประสิทธิภาพโดยตรง
เมตริกความเป็นธรรม
คำจำกัดความทางคณิตศาสตร์ของ "ความเป็นธรรม" ที่วัดได้ ตัวอย่างเมตริกความเป็นธรรมที่ใช้กันโดยทั่วไปมีดังนี้
- โอกาสที่เท่าเทียมกัน
- ความเท่าเทียมในการคาดการณ์
- ความเป็นธรรมแบบข้อเท็จจริง
- ความเท่าเทียมกันของข้อมูลประชากร
เมตริกความเป็นธรรมหลายรายการไม่สามารถใช้ร่วมกันได้ โปรดดูความไม่เข้ากันของเมตริกความเป็นธรรม
ผลลบลวง (FN)
ตัวอย่างที่โมเดลคาดการณ์คลาสเชิงลบผิดพลาด ตัวอย่างเช่น โมเดล คาดการณ์ว่าข้อความอีเมลหนึ่งไม่ใช่จดหมายขยะ (คลาสเชิงลบ) แต่ข้อความอีเมลนั้นเป็นจดหมายขยะจริง
อัตราผลลบลวง
สัดส่วนของตัวอย่างผลบวกจริงที่โมเดลคาดการณ์คลาสเชิงลบผิดพลาด สูตรต่อไปนี้ใช้ในการคำนวณอัตราผลลบลวง
ดูข้อมูลเพิ่มเติมได้ที่เกณฑ์และเมทริกซ์ความสับสน ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ผลบวกลวง (FP)
ตัวอย่างที่โมเดลคาดการณ์คลาสบวกอย่างไม่ถูกต้อง เช่น โมเดลคาดการณ์ว่าข้อความอีเมลหนึ่งๆ เป็นจดหมายขยะ (คลาสบวก) แต่ข้อความอีเมลนั้นไม่ใช่จดหมายขยะ
ดูข้อมูลเพิ่มเติมได้ที่เกณฑ์และเมทริกซ์ความสับสน ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
อัตราผลบวกลวง (FPR)
สัดส่วนของตัวอย่างเชิงลบจริงที่โมเดลคาดการณ์คลาสเชิงบวกผิดพลาด สูตรต่อไปนี้ใช้ในการคำนวณอัตราผลบวกลวง
อัตราผลบวกลวงคือแกน x ในกราฟ ROC
ดูข้อมูลเพิ่มเติมได้ที่การแยกประเภท: ROC และ AUC ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ลดลงอย่างรวดเร็ว
เทคนิคการฝึกเพื่อปรับปรุงประสิทธิภาพของ LLM Fast decay involves rapidly decreasing the learning rate during training. กลยุทธ์นี้ช่วยป้องกันไม่ให้โมเดลโอเวอร์ฟิตกับ ข้อมูลการฝึก และปรับปรุงการสรุป
ฟีเจอร์
ตัวแปรอินพุตของโมเดลแมชชีนเลิร์นนิง ตัวอย่าง ประกอบด้วยฟีเจอร์อย่างน้อย 1 รายการ เช่น สมมติว่าคุณกำลังฝึกโมเดลเพื่อพิจารณาอิทธิพลของสภาพอากาศต่อคะแนนสอบของนักเรียน ตารางต่อไปนี้แสดงตัวอย่าง 3 รายการ ซึ่งแต่ละรายการมีฟีเจอร์ 3 รายการและป้ายกำกับ 1 รายการ
| ฟีเจอร์ | ป้ายกำกับ | ||
|---|---|---|---|
| อุณหภูมิ | ความชื้น | ความกดอากาศ | คะแนนสอบ |
| 15 | 47 | 998 | 92 |
| 19 | 34 | 1020 | 84 |
| 18 | 92 | 1012 | 87 |
คอนทราสต์กับป้ายกำกับ
ดูข้อมูลเพิ่มเติมได้ที่การเรียนรู้แบบมีผู้สอน ในหลักสูตรข้อมูลเบื้องต้นเกี่ยวกับแมชชีนเลิร์นนิง
ฟีเจอร์ข้าม
ฟีเจอร์สังเคราะห์ที่เกิดจากการ "ครอส" ฟีเจอร์เชิงหมวดหมู่หรือแบบจัดกลุ่ม
ตัวอย่างเช่น ลองพิจารณารูปแบบ "การพยากรณ์อารมณ์" ที่แสดง อุณหภูมิในกลุ่มใดกลุ่มหนึ่งต่อไปนี้
freezingchillytemperatewarm
และแสดงความเร็วลมในกลุ่มใดกลุ่มหนึ่งต่อไปนี้
stilllightwindy
หากไม่มีการรวมฟีเจอร์ โมเดลเชิงเส้นจะฝึกแยกกันในแต่ละกลุ่มต่างๆ 7 กลุ่มก่อนหน้า
ดังนั้น โมเดลจะฝึกจาก เช่น
freezing โดยไม่ขึ้นอยู่กับการฝึกจาก เช่น
windy
หรือจะสร้างฟีเจอร์ครอสของอุณหภูมิและ ความเร็วลมก็ได้ ฟีเจอร์สังเคราะห์นี้จะมีค่าที่เป็นไปได้ 12 ค่าดังนี้
freezing-stillfreezing-lightfreezing-windychilly-stillchilly-lightchilly-windytemperate-stilltemperate-lighttemperate-windywarm-stillwarm-lightwarm-windy
การรวมฟีเจอร์ช่วยให้โมเดลเรียนรู้ความแตกต่างของอารมณ์
ระหว่างfreezing-windyวันที่มีฝนตกกับfreezing-stillวันที่แดดออกได้
หากคุณสร้างฟีเจอร์สังเคราะห์จากฟีเจอร์ 2 รายการซึ่งแต่ละรายการมีกลุ่มต่างๆ จำนวนมาก การครอสฟีเจอร์ที่ได้จะมีชุดค่าผสมที่เป็นไปได้จำนวนมาก เช่น หากฟีเจอร์หนึ่งมี 1,000 กลุ่ม และอีกฟีเจอร์หนึ่งมี 2,000 กลุ่ม ฟีเจอร์ครอสที่ได้จะมี 2,000,000 กลุ่ม
ในทางคณิตศาสตร์ ครอสคือผลคูณคาร์ทีเซียน
โดยส่วนใหญ่แล้วฟีเจอร์ครอสจะใช้กับโมเดลเชิงเส้นและไม่ค่อยได้ใช้กับ โครงข่ายประสาทเทียม
ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลเชิงหมวดหมู่: การรวมฟีเจอร์ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
Feature Engineering
กระบวนการที่มีขั้นตอนต่อไปนี้
- การพิจารณาว่าฟีเจอร์ใดบ้างที่อาจมีประโยชน์ ในการฝึกโมเดล
- การแปลงข้อมูลดิบจากชุดข้อมูลเป็นฟีเจอร์เวอร์ชันที่มีประสิทธิภาพ
เช่น คุณอาจพิจารณาว่า temperature อาจเป็นฟีเจอร์ที่มีประโยชน์
จากนั้นคุณอาจทดลองใช้การจัดกลุ่ม
เพื่อเพิ่มประสิทธิภาพสิ่งที่โมเดลสามารถเรียนรู้จากtemperatureช่วงต่างๆ ได้
บางครั้งเราเรียกการปรับแต่งฟีเจอร์ว่า การดึงฟีเจอร์หรือ การสร้างฟีเจอร์
ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลเชิงตัวเลข: วิธีที่โมเดลรับข้อมูลโดยใช้เวกเตอร์ฟีเจอร์ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การแยกฟีเจอร์
คำที่โอเวอร์โหลดซึ่งมีคำจำกัดความอย่างใดอย่างหนึ่งต่อไปนี้
- การดึงการแสดงฟีเจอร์ระดับกลางที่คำนวณโดยโมเดลแบบไม่มีการกำกับดูแลหรือโมเดลที่ฝึกไว้ล่วงหน้า (เช่น ค่าเลเยอร์ที่ซ่อนอยู่ในโครงข่ายประสาทเทียม) เพื่อใช้ในโมเดลอื่นเป็นอินพุต
- คำพ้องความหมายของ Feature Engineering
ความสำคัญของฟีเจอร์
คำพ้องความหมายสำหรับความสำคัญของตัวแปร
ชุดฟีเจอร์
กลุ่มฟีเจอร์ที่โมเดลแมชชีนเลิร์นนิงของคุณใช้ฝึก ตัวอย่างเช่น ชุดฟีเจอร์ที่เรียบง่ายสำหรับโมเดลที่คาดการณ์ราคาที่อยู่อาศัย อาจประกอบด้วยรหัสไปรษณีย์ ขนาดที่พัก และสภาพที่พัก
ข้อมูลจำเพาะของฟีเจอร์
อธิบายข้อมูลที่จำเป็นในการดึงข้อมูลฟีเจอร์ จากบัฟเฟอร์โปรโตคอล tf.Example เนื่องจากบัฟเฟอร์โปรโตคอล tf.Example เป็นเพียงคอนเทนเนอร์สำหรับข้อมูล คุณจึงต้องระบุข้อมูลต่อไปนี้
- ข้อมูลที่จะดึง (เช่น คีย์สำหรับฟีเจอร์)
- ประเภทข้อมูล (เช่น ลอยหรือจำนวนเต็ม)
- ความยาว (คงที่หรือเปลี่ยนแปลงได้)
เวกเตอร์ฟีเจอร์
อาร์เรย์ของค่า feature ที่ประกอบกันเป็น example เวกเตอร์ฟีเจอร์เป็นอินพุตระหว่างการฝึกและระหว่างการอนุมาน ตัวอย่างเช่น เวกเตอร์ฟีเจอร์สําหรับโมเดลที่มีฟีเจอร์ที่ไม่ต่อเนื่อง 2 รายการ อาจเป็นดังนี้
[0.92, 0.56]
ตัวอย่างแต่ละรายการจะให้ค่าที่แตกต่างกันสำหรับเวกเตอร์ฟีเจอร์ ดังนั้น เวกเตอร์ฟีเจอร์สำหรับตัวอย่างถัดไปอาจมีลักษณะดังนี้
[0.73, 0.49]
การออกแบบฟีเจอร์จะกำหนดวิธีแสดงฟีเจอร์ในเวกเตอร์ฟีเจอร์ เช่น ฟีเจอร์เชิงหมวดหมู่แบบไบนารีที่มีค่าที่เป็นไปได้ 5 ค่าอาจแสดงด้วยการเข้ารหัสแบบ One-Hot ในกรณีนี้ ส่วนของเวกเตอร์ฟีเจอร์สำหรับตัวอย่างหนึ่งๆ จะประกอบด้วยเลข 0 จำนวน 4 ตัวและ เลข 1.0 ตัวเดียวในตำแหน่งที่ 3 ดังนี้
[0.0, 0.0, 1.0, 0.0, 0.0]
อีกตัวอย่างหนึ่ง สมมติว่าโมเดลของคุณประกอบด้วยฟีเจอร์ 3 รายการ
- ฟีเจอร์เชิงหมวดหมู่แบบไบนารีที่มีค่าที่เป็นไปได้ 5 ค่าซึ่งแสดงด้วย
การเข้ารหัสแบบ One-Hot เช่น
[0.0, 1.0, 0.0, 0.0, 0.0] - ฟีเจอร์เชิงหมวดหมู่แบบไบนารีอีกรายการที่มีค่าที่เป็นไปได้3 ค่าซึ่งแสดง
ด้วยการเข้ารหัสแบบ One-hot เช่น
[0.0, 0.0, 1.0] - ฟีเจอร์แบบจุดลอยตัว เช่น
8.3
ในกรณีนี้ เวกเตอร์ฟีเจอร์สำหรับแต่ละตัวอย่างจะแสดงด้วยค่า9 ค่า จากค่าตัวอย่างในรายการก่อนหน้า เวกเตอร์ฟีเจอร์จะเป็นดังนี้
0.0 1.0 0.0 0.0 0.0 0.0 0.0 1.0 8.3
ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลเชิงตัวเลข: วิธีที่โมเดลรับข้อมูลโดยใช้เวกเตอร์ฟีเจอร์ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การสร้างฟีเจอร์
กระบวนการดึงฟีเจอร์จากแหล่งที่มาของอินพุต เช่น เอกสารหรือวิดีโอ และการแมปฟีเจอร์เหล่านั้นลงใน เวกเตอร์ฟีเจอร์
ผู้เชี่ยวชาญด้าน ML บางคนใช้การสร้างฟีเจอร์เป็นคำพ้องความหมายของ การออกแบบฟีเจอร์หรือ การดึงฟีเจอร์
การเรียนรู้แบบสมาพันธ์
แนวทางแมชชีนเลิร์นนิงแบบกระจายที่ฝึก โมเดลแมชชีนเลิร์นนิงโดยใช้ตัวอย่างแบบกระจายที่อยู่ในอุปกรณ์ต่างๆ เช่น สมาร์ทโฟน ในการเรียนรู้แบบรวมศูนย์ อุปกรณ์บางส่วนจะดาวน์โหลดโมเดลปัจจุบัน จากเซิร์ฟเวอร์ส่วนกลางที่ทำหน้าที่ประสานงาน อุปกรณ์จะใช้ตัวอย่างที่จัดเก็บไว้ ในอุปกรณ์เพื่อปรับปรุงโมเดล จากนั้นอุปกรณ์จะอัปโหลด การปรับปรุงโมเดล (แต่ไม่ใช่ตัวอย่างการฝึก) ไปยังเซิร์ฟเวอร์ ที่ประสานงาน ซึ่งจะรวบรวมการปรับปรุงเหล่านี้กับการอัปเดตอื่นๆ เพื่อให้ได้โมเดล ส่วนกลางที่ได้รับการปรับปรุง หลังจากการรวบรวมแล้ว ระบบจะไม่จำเป็นต้องใช้การอัปเดตโมเดลที่อุปกรณ์คำนวณอีกต่อไป และสามารถทิ้งได้
เนื่องจากไม่มีการอัปโหลดตัวอย่างการฝึก Federated Learning จึงเป็นไปตาม หลักการด้านความเป็นส่วนตัวของการเก็บรวบรวมข้อมูลที่มุ่งเน้นและการลดข้อมูลให้เหลือน้อยที่สุด
ดูรายละเอียดเพิ่มเติมได้ที่การ์ตูนการเรียนรู้แบบรวมศูนย์ (ใช่ การ์ตูน)
วงจรความคิดเห็น
ในแมชชีนเลิร์นนิง สถานการณ์ที่การคาดการณ์ของโมเดลมีอิทธิพลต่อ ข้อมูลการฝึกของโมเดลเดียวกันหรือโมเดลอื่น ตัวอย่างเช่น โมเดลที่ แนะนำภาพยนตร์จะส่งผลต่อภาพยนตร์ที่ผู้คนเห็น ซึ่งจะ ส่งผลต่อโมเดลการแนะนำภาพยนตร์ในภายหลัง
ดูข้อมูลเพิ่มเติมได้ที่ระบบ ML ในเวอร์ชันที่ใช้งานจริง: คำถามที่ควร ถาม ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
ฟีดฟอร์เวิร์ดนิวรอลเน็ตเวิร์ก (FFN)
โครงข่ายประสาทเทียมที่ไม่มีการเชื่อมต่อแบบวนซ้ำหรือแบบเรียกซ้ำ ตัวอย่างเช่น โครงข่ายประสาทแบบลึกแบบเดิมคือ โครงข่ายประสาทแบบฟีดฟอร์เวิร์ด ซึ่งแตกต่างจากเครือข่ายประสาท แบบเกิดซ้ำซึ่งเป็นแบบวนซ้ำ
การเรียนรู้แบบ Few-Shot
แนวทางแมชชีนเลิร์นนิงซึ่งมักใช้สำหรับการจัดประเภทออบเจ็กต์ ออกแบบมาเพื่อฝึกโมเดลการจัดประเภทที่มีประสิทธิภาพ จากตัวอย่างการฝึกเพียงไม่กี่รายการ
ดูการเรียนรู้แบบนัดเดียวจบและ การเรียนรู้แบบศูนย์ช็อตด้วย
Few-Shot Prompting
พรอมต์ที่มีตัวอย่างมากกว่า 1 รายการ ("ไม่กี่") ซึ่งแสดงให้เห็นว่าโมเดลภาษาขนาดใหญ่ ควรตอบสนองอย่างไร ตัวอย่างเช่น พรอมต์ยาวต่อไปนี้มีตัวอย่าง 2 รายการที่แสดงให้โมเดลภาษาขนาดใหญ่เห็นวิธีตอบคำค้นหา
| ส่วนต่างๆ ของพรอมต์ | หมายเหตุ |
|---|---|
| สกุลเงินทางการของประเทศที่ระบุคืออะไร | คำถามที่คุณต้องการให้ LLM ตอบ |
| ฝรั่งเศส: EUR | ตัวอย่าง |
| สหราชอาณาจักร: GBP | อีกตัวอย่าง |
| อินเดีย: | คำค้นหาจริง |
โดยทั่วไปแล้ว การแจ้งแบบ Few-Shot จะให้ผลลัพธ์ที่ต้องการมากกว่าการแจ้งแบบ Zero-Shot และการแจ้งแบบ One-Shot อย่างไรก็ตาม Few-Shot Prompting ต้องใช้พรอมต์ที่ยาวกว่า
Few-Shot Prompting เป็นรูปแบบหนึ่งของการเรียนรู้แบบ Few-Shot ที่ใช้กับการเรียนรู้แบบใช้พรอมต์
ดูข้อมูลเพิ่มเติมได้ที่พรอมต์ เอ็นจิเนียริง ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ฟิดเดิล
ไลบรารีการกำหนดค่าที่ใช้ Python เป็นหลักซึ่งกำหนดค่า ฟังก์ชันและคลาสโดยไม่ต้องใช้โค้ดหรือโครงสร้างพื้นฐานที่รบกวน ในกรณีของ Pax และโค้ดเบส ML อื่นๆ ฟังก์ชันและ คลาสเหล่านี้แสดงถึงโมเดลและการฝึก ไฮเปอร์พารามิเตอร์
Fiddle ถือว่าโดยทั่วไปแล้วโค้ดเบสของแมชชีนเลิร์นนิงจะแบ่งออกเป็นส่วนต่างๆ ดังนี้
- โค้ดไลบรารีที่กำหนดเลเยอร์และตัวเพิ่มประสิทธิภาพ
- โค้ด "กาว" ของชุดข้อมูล ซึ่งเรียกใช้ไลบรารีและเชื่อมโยงทุกอย่างเข้าด้วยกัน
Fiddle จะบันทึกโครงสร้างการเรียกของโค้ดกาวในรูปแบบที่ยังไม่ได้ประเมินและ เปลี่ยนแปลงได้
การปรับแต่ง
การฝึกครั้งที่ 2 ที่เจาะจงงานซึ่งดำเนินการกับโมเดลที่ฝึกล่วงหน้าเพื่อปรับแต่งพารามิเตอร์สำหรับกรณีการใช้งานที่เฉพาะเจาะจง ตัวอย่างเช่น ลำดับการฝึกแบบเต็มสำหรับโมเดลภาษาขนาดใหญ่บางรุ่นมีดังนี้
- การฝึกเบื้องต้น: ฝึกโมเดลภาษาขนาดใหญ่ในชุดข้อมูลทั่วไปจำนวนมาก เช่น หน้า Wikipedia ทั้งหมดในภาษาอังกฤษ
- การปรับแต่ง: ฝึกโมเดลที่ผ่านการฝึกมาก่อนให้ทำงานเฉพาะเจาะจง เช่น ตอบคำค้นหาทางการแพทย์ โดยปกติแล้ว การปรับแต่งอย่างละเอียดต้องใช้ตัวอย่างหลายร้อยหรือหลายพันรายการที่มุ่งเน้นงานที่เฉพาะเจาะจง
อีกตัวอย่างหนึ่งคือลำดับการฝึกแบบเต็มสำหรับโมเดลรูปภาพขนาดใหญ่มีดังนี้
- การฝึกเบื้องต้น: ฝึกโมเดลรูปภาพขนาดใหญ่ในชุดข้อมูลรูปภาพทั่วไปจำนวนมาก เช่น รูปภาพทั้งหมดใน Wikimedia Commons
- การปรับแต่ง: ฝึกโมเดลที่ฝึกไว้ล่วงหน้าให้ทำงานเฉพาะเจาะจง เช่น สร้างรูปภาพของวาฬเพชฌฆาต
การปรับแต่งอาจเกี่ยวข้องกับกลยุทธ์ต่อไปนี้
- การแก้ไขทั้งหมดของพารามิเตอร์ที่มีอยู่ของโมเดลที่ฝึกไว้ล่วงหน้า ซึ่งบางครั้งเรียกว่าการปรับแต่งแบบละเอียด
- การแก้ไขเฉพาะพารามิเตอร์บางส่วนที่มีอยู่ของโมเดลที่ผ่านการฝึกมาก่อน (โดยปกติคือเลเยอร์ที่อยู่ใกล้เลเยอร์เอาต์พุตมากที่สุด) ในขณะที่พารามิเตอร์อื่นๆ ที่มีอยู่จะไม่มีการเปลี่ยนแปลง (โดยปกติคือเลเยอร์ที่อยู่ใกล้เลเยอร์อินพุตมากที่สุด) ดูการปรับแต่งที่มีประสิทธิภาพด้านพารามิเตอร์
- การเพิ่มเลเยอร์อื่นๆ โดยปกติจะอยู่เหนือเลเยอร์ที่มีอยู่ซึ่งอยู่ใกล้กับ เลเยอร์เอาต์พุตมากที่สุด
การปรับแต่งโมเดลเป็นรูปแบบหนึ่งของการเรียนรู้แบบโอน ดังนั้น การปรับแต่งอาจใช้ Loss Function หรือโมเดล ประเภทอื่นที่แตกต่างจากที่ใช้ฝึกโมเดลที่ผ่านการฝึกมาก่อน เช่น คุณอาจ ปรับแต่งโมเดลรูปภาพขนาดใหญ่ที่ฝึกไว้ล่วงหน้าเพื่อสร้างโมเดลการถดถอยที่ แสดงจำนวนนกในรูปภาพอินพุต
เปรียบเทียบการปรับแต่งโมเดลกับคำศัพท์ต่อไปนี้
ดูข้อมูลเพิ่มเติมได้ที่การปรับแต่ง ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
โมเดล Flash
กลุ่มโมเดล Gemini ขนาดค่อนข้างเล็กที่เพิ่มประสิทธิภาพเพื่อความเร็ว และเวลาในการตอบสนองต่ำ โมเดล Flash ออกแบบมาสําหรับแอปพลิเคชันที่หลากหลาย ซึ่งการตอบกลับที่รวดเร็วและปริมาณงานสูงเป็นสิ่งสําคัญ
เหลืองแฟลกซ์
ไลบรารีโอเพนซอร์สที่มีประสิทธิภาพสูง สำหรับดีปเลิร์นนิงที่สร้างขึ้นบน JAX Flax มีฟังก์ชันสำหรับการฝึก โครงข่ายประสาทเทียม รวมถึงวิธีการประเมินประสิทธิภาพ
Flaxformer
Transformer library โอเพนซอร์สที่สร้างขึ้นจาก Flax ซึ่งออกแบบมาเพื่อการประมวลผลภาษาธรรมชาติ และการวิจัยแบบมัลติโมดอลเป็นหลัก
ลืมประตู
ส่วนของเซลล์หน่วยความจำระยะยาวแบบสั้น ที่ควบคุมการไหลของข้อมูลผ่านเซลล์ Forget Gate จะรักษาบริบทโดยการตัดสินใจว่าจะทิ้งข้อมูลใดจากสถานะของเซลล์
โมเดลพื้นฐาน
โมเดลที่ได้รับการฝึกเบื้องต้นขนาดใหญ่มาก ซึ่งได้รับการฝึกจากชุดการฝึกที่หลากหลายและมีขนาดใหญ่ โมเดลพื้นฐานสามารถทำทั้ง 2 อย่างต่อไปนี้ได้
- ตอบสนองต่อคำขอที่หลากหลายได้ดี
- ใช้เป็นโมเดลพื้นฐานสำหรับการปรับแต่งเพิ่มเติมหรือการปรับแต่งอื่นๆ
กล่าวคือ โมเดลพื้นฐานมีความสามารถสูงอยู่แล้วในแง่ทั่วไป แต่สามารถปรับแต่งเพิ่มเติมให้มีประโยชน์มากยิ่งขึ้นสำหรับงานที่เฉพาะเจาะจงได้
เศษส่วนของความสำเร็จ
เมตริกสําหรับประเมินข้อความที่สร้างขึ้นของโมเดล ML เศษส่วนของความสำเร็จคือจำนวนเอาต์พุตข้อความที่สร้างขึ้นซึ่ง "สำเร็จ" หารด้วยจำนวนเอาต์พุตข้อความที่สร้างขึ้นทั้งหมด ตัวอย่างเช่น หากโมเดลภาษาขนาดใหญ่สร้างโค้ด 10 บล็อก และมี 5 บล็อกที่สำเร็จ เศษส่วนของความสำเร็จ จะเป็น 50%
แม้ว่าเศษส่วนของความสำเร็จจะมีประโยชน์อย่างกว้างขวางในสถิติ แต่ใน ML เมตริกนี้มีประโยชน์หลักในการวัดงานที่ตรวจสอบได้ เช่น การสร้างโค้ดหรือปัญหาทางคณิตศาสตร์
full softmax
คำพ้องความหมายของ softmax
แตกต่างจากการสุ่มตัวอย่างผู้สมัคร
ดูข้อมูลเพิ่มเติมได้ที่โครงข่ายประสาทเทียม: การจัดประเภทหลายคลาส ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
เลเยอร์ที่เชื่อมต่ออย่างเต็มรูปแบบ
เลเยอร์ที่ซ่อนซึ่งแต่ละโหนดเชื่อมต่อกับทุกโหนดในเลเยอร์ที่ซ่อนถัดไป
เลเยอร์ที่เชื่อมต่ออย่างเต็มรูปแบบเรียกอีกอย่างว่าเลเยอร์หนาแน่น
การแปลงฟังก์ชัน
ฟังก์ชันที่รับฟังก์ชันเป็นอินพุตและแสดงผลฟังก์ชันที่แปลงแล้ว เป็นเอาต์พุต JAX ใช้การแปลงฟังก์ชัน
G
GAN
ตัวย่อของเครือข่าย ปฏิปักษ์แบบ Generative
Gemini
ระบบนิเวศที่ประกอบด้วย AI ที่ทันสมัยที่สุดของ Google องค์ประกอบของระบบนิเวศนี้ ประกอบด้วย
- โมเดล Gemini ต่างๆ
- อินเทอร์เฟซการสนทนาแบบอินเทอร์แอกทีฟกับโมเดล Gemini ผู้ใช้พิมพ์พรอมต์และ Gemini จะตอบกลับพรอมต์เหล่านั้น
- Gemini API ต่างๆ
- ผลิตภัณฑ์ทางธุรกิจต่างๆ ที่อิงตามโมเดล Gemini เช่น Gemini สำหรับ Google Cloud
โมเดลต่างๆ ของ Gemini
Transformer ที่ทันสมัยของ Google โมเดลหลายรูปแบบ โมเดล Gemini ได้รับการออกแบบมาโดยเฉพาะ เพื่อผสานรวมกับเอเจนต์
ผู้ใช้โต้ตอบกับโมเดล Gemini ได้หลายวิธี รวมถึงผ่าน อินเทอร์เฟซกล่องโต้ตอบแบบอินเทอร์แอกทีฟและผ่าน SDK
Gemma
โมเดลโอเพนซอร์สแบบน้ำหนักเบาตระกูลหนึ่งที่สร้างขึ้นจากงานวิจัยและเทคโนโลยีเดียวกันกับที่ใช้สร้างโมเดล Gemini มีโมเดล Gemma หลายรุ่นให้เลือกใช้ ซึ่งแต่ละรุ่นก็มีฟีเจอร์ที่แตกต่างกัน เช่น วิชัน, โค้ด และการปฏิบัติตามคำสั่ง ดูรายละเอียดได้ที่ Gemma
GenAI หรือ genAI
คำย่อของ Generative AI
การสรุป
ความสามารถของโมเดลในการคาดการณ์ข้อมูลใหม่ที่ไม่เคยเห็นมาก่อนได้อย่างถูกต้อง โมเดลที่สามารถสรุปได้จะตรงกันข้ามกับโมเดลที่โอเวอร์ฟิต
ดูข้อมูลเพิ่มเติมได้ที่การสรุปทั่วไป ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
เส้นโค้งการสรุป
พล็อตของทั้งการสูญเสียการฝึกและ การสูญเสียการตรวจสอบเป็นฟังก์ชันของจำนวนการทำซ้ำ
เส้นโค้งการสรุปทั่วไปช่วยให้คุณตรวจพบการปรับมากเกินไปที่อาจเกิดขึ้นได้ ตัวอย่างเช่น เส้นโค้งการสรุปทั่วไปต่อไปนี้ บ่งบอกถึงการปรับมากเกินไปเนื่องจาก Loss ของการตรวจสอบ ในท้ายที่สุดจะสูงกว่า Loss ของการฝึกอย่างมาก
ดูข้อมูลเพิ่มเติมได้ที่การสรุปทั่วไป ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
โมเดลเชิงเส้นทั่วไป
การสรุปการถดถอยกำลังสองน้อยที่สุด ซึ่งอิงตาม สัญญาณรบกวนแบบ Gaussian ไปยังโมเดลประเภทอื่นๆ ที่อิงตามสัญญาณรบกวนประเภทอื่นๆ เช่น สัญญาณรบกวนแบบปัวซอง หรือ สัญญาณรบกวนแบบหมวดหมู่ ตัวอย่างของโมเดลเชิงเส้นทั่วไป ได้แก่
- การถดถอยแบบโลจิสติก
- การถดถอยแบบหลายคลาส
- การถดถอยแบบกำลังสองน้อยที่สุด
คุณดูพารามิเตอร์ของโมเดลเชิงเส้นทั่วไปได้ผ่านการเพิ่มประสิทธิภาพแบบนูน
โมเดลเชิงเส้นทั่วไปมีคุณสมบัติดังต่อไปนี้
- ค่าคาดการณ์เฉลี่ยของโมเดลการถดถอยแบบกำลังสองน้อยที่สุดที่เหมาะสมจะเท่ากับป้ายกำกับเฉลี่ยในข้อมูลการฝึก
- ความน่าจะเป็นเฉลี่ยที่โมเดลการถดถอยโลจิสติกส์ที่เหมาะสมคาดการณ์จะเท่ากับป้ายกำกับเฉลี่ยในข้อมูลการฝึก
ความสามารถของโมเดลเชิงเส้นทั่วไปถูกจำกัดด้วยฟีเจอร์ของโมเดล โมเดลเชิงเส้นทั่วไป "เรียนรู้ฟีเจอร์ใหม่" ไม่ได้ ซึ่งต่างจากโมเดลเชิงลึก
ข้อความที่สร้างขึ้น
โดยทั่วไปคือข้อความที่โมเดล ML แสดง เมื่อประเมินโมเดลภาษาขนาดใหญ่ เมตริกบางอย่างจะเปรียบเทียบข้อความที่สร้างขึ้นกับข้อความอ้างอิง ตัวอย่างเช่น สมมติว่าคุณ พยายามพิจารณาว่าโมเดล ML แปลจากภาษาฝรั่งเศส เป็นภาษาดัตช์ได้มีประสิทธิภาพเพียงใด ในกรณีนี้
- ข้อความที่สร้างขึ้นคือคำแปลภาษาดัตช์ที่โมเดล ML แสดง
- ข้อความอ้างอิงคือคำแปลภาษาดัตช์ที่นักแปลที่เป็นมนุษย์ (หรือซอฟต์แวร์) สร้างขึ้น
โปรดทราบว่ากลยุทธ์การประเมินบางอย่างไม่มีข้อความอ้างอิง
Generative Adversarial Network (GAN)
ระบบที่ใช้สร้างข้อมูลใหม่ซึ่งเครื่องกำเนิดสร้างข้อมูล และตัวแยกแยะจะพิจารณาว่าข้อมูลที่สร้างขึ้นนั้นถูกต้องหรือไม่
ดูข้อมูลเพิ่มเติมได้ที่หลักสูตร Generative Adversarial Networks
Generative AI
สาขาที่กำลังเกิดใหม่ซึ่งมีการเปลี่ยนแปลงโดยไม่มีคำจำกัดความที่เป็นทางการ อย่างไรก็ตาม ผู้เชี่ยวชาญส่วนใหญ่เห็นพ้องต้องกันว่าโมเดล Generative AI สามารถ สร้าง ("สร้าง") เนื้อหาที่มีลักษณะดังต่อไปนี้
- ซับซ้อน
- สอดคล้องกัน
- เดิม
ตัวอย่างของ Generative AI ได้แก่
- โมเดลภาษาขนาดใหญ่ที่สามารถสร้าง ข้อความต้นฉบับที่ซับซ้อนและตอบคำถามได้
- โมเดลการสร้างรูปภาพที่สร้างรูปภาพที่ไม่ซ้ำใครได้
- โมเดลการสร้างเสียงและเพลง ซึ่งสามารถแต่งเพลงต้นฉบับหรือ สร้างคำพูดที่สมจริง
- โมเดลการสร้างวิดีโอที่สร้างวิดีโอต้นฉบับได้
เทคโนโลยีรุ่นก่อนๆ บางอย่าง รวมถึง LSTM และ RNN ก็สร้างเนื้อหาต้นฉบับและ สอดคล้องกันได้เช่นกัน ผู้เชี่ยวชาญบางคนมองว่าเทคโนโลยีรุ่นก่อนๆ เหล่านี้เป็น Generative AI ขณะที่บางคนรู้สึกว่า Generative AI ที่แท้จริงต้องมีเอาต์พุตที่ซับซ้อนกว่าที่เทคโนโลยีรุ่นก่อนๆ เหล่านั้นสร้างขึ้นได้
แตกต่างจาก ML เชิงคาดการณ์
โมเดลแบบ Generative
ในทางปฏิบัติ โมเดลที่ทำสิ่งใดสิ่งหนึ่งต่อไปนี้
- สร้าง (สร้าง) ตัวอย่างใหม่จากชุดข้อมูลการฝึก ตัวอย่างเช่น โมเดล Generative สามารถสร้างบทกวีได้หลังจากฝึก ในชุดข้อมูลบทกวี ส่วนเครื่องกำเนิดของเครือข่าย Generative Adversarial จัดอยู่ในหมวดหมู่นี้
- กำหนดความน่าจะเป็นที่ตัวอย่างใหม่จะมาจากชุดการฝึก หรือสร้างขึ้นจากกลไกเดียวกันกับที่สร้างชุดการฝึก ตัวอย่างเช่น หลังจากฝึกโมเดล Generative ด้วยชุดข้อมูลที่ประกอบด้วยประโยคภาษาอังกฤษ โมเดลจะสามารถระบุความน่าจะเป็นที่อินพุตใหม่จะเป็นประโยคภาษาอังกฤษที่ถูกต้อง
ในทางทฤษฎีแล้ว โมเดล Generative สามารถแยกแยะการกระจายตัวของตัวอย่าง หรือฟีเจอร์ที่เฉพาะเจาะจงในชุดข้อมูลได้ โดยการ
p(examples)
โมเดลการเรียนรู้ที่ไม่มีการควบคุมดูแลเป็นแบบ Generative
แตกต่างจากโมเดลจำแนก
โปรแกรมสร้างแผนผังไซต์
ระบบย่อยภายในGenerative Adversarial Network ที่สร้างตัวอย่างใหม่
เทียบกับโมเดลการเลือกปฏิบัติ
ความไม่บริสุทธิ์ของจีนี
เมตริกที่คล้ายกับเอนโทรปี ตัวแยก ใช้ค่าที่ได้จากความไม่บริสุทธิ์ของ Gini หรือเอนโทรปีเพื่อสร้าง เงื่อนไขสำหรับการจัดประเภท ต้นไม้ตัดสินใจ การได้ข้อมูลได้มาจากเอนโทรปี ไม่มีคำที่เทียบเท่าซึ่งเป็นที่ยอมรับในระดับสากลสำหรับเมตริกที่ได้จากความไม่บริสุทธิ์ของ Gini อย่างไรก็ตาม เมตริกที่ไม่มีชื่อนี้มีความสำคัญไม่แพ้การได้ข้อมูล
ความไม่บริสุทธิ์ของจีนียังเรียกว่าดัชนีจีนี หรือเรียกสั้นๆ ว่าจีนี
ชุดข้อมูลทองคำ
ชุดข้อมูลที่ดูแลจัดการด้วยตนเองซึ่งบันทึกความจริงพื้นฐาน ทีมสามารถใช้ชุดข้อมูลทองอย่างน้อย 1 ชุดเพื่อประเมินคุณภาพของโมเดล
ชุดข้อมูลทองคำบางชุดจะบันทึกโดเมนย่อยที่แตกต่างกันของความจริงพื้นฐาน เช่น ชุดข้อมูลทองคำสำหรับการแยกประเภทรูปภาพอาจบันทึกสภาพแสง และความละเอียดของรูปภาพ
คำตอบดี
คำตอบที่ทราบว่าดี ตัวอย่างเช่น เมื่อระบุพรอมต์ต่อไปนี้
2 + 2
คำตอบที่ดีที่สุดคือ
4
Google AI Studio
เครื่องมือของ Google ที่มีอินเทอร์เฟซที่ใช้งานง่าย สำหรับการทดลองและสร้างแอปพลิเคชันโดยใช้โมเดลภาษาขนาดใหญ่ของ Google ดูรายละเอียดได้ที่หน้าแรกของ Google AI Studio
GPT (Generative Pre-trained Transformer)
ตระกูลโมเดลภาษาขนาดใหญ่ที่อิงตามTransformer ซึ่งพัฒนาโดยOpenAI
รูปแบบ GPT สามารถใช้กับรูปแบบต่างๆ ได้ ซึ่งรวมถึง
- การสร้างรูปภาพ (เช่น ImageGPT)
- การสร้างรูปภาพจากข้อความ (เช่น DALL-E)
ไล่ระดับ
เวกเตอร์ของอนุพันธ์ย่อยที่เทียบกับ ตัวแปรอิสระทั้งหมด ในแมชชีนเลิร์นนิง เกรเดียนต์คือ เวกเตอร์ของอนุพันธ์ย่อยของฟังก์ชันโมเดล จุดการไล่ระดับสี ในทิศทางที่ชันที่สุด
การสะสมการไล่ระดับสี
เทคนิคการแพร่ย้อนกลับที่อัปเดตพารามิเตอร์เพียงครั้งเดียวต่อ Epoch แทนที่จะอัปเดตครั้งเดียวต่อการวนซ้ำ หลังจากประมวลผลมินิแบตช์แต่ละรายการ การสะสมการไล่ระดับสีจะอัปเดตผลรวมของการไล่ระดับสี จากนั้นหลังจาก ประมวลผลมินิแบตช์สุดท้ายในยุคแล้ว ระบบจะอัปเดต พารามิเตอร์ตามการเปลี่ยนแปลงการไล่ระดับสีทั้งหมด
การสะสมการไล่ระดับสีจะมีประโยชน์เมื่อขนาดกลุ่มมีขนาดใหญ่มากเมื่อเทียบกับปริมาณหน่วยความจำที่พร้อมใช้งานสำหรับการฝึก เมื่อหน่วยความจำมีปัญหา แนวโน้มตามธรรมชาติคือการลดขนาดกลุ่ม อย่างไรก็ตาม การลดขนาดกลุ่มในการแพร่ย้อนกลับปกติจะเพิ่ม จํานวนการอัปเดตพารามิเตอร์ การสะสมการไล่ระดับสีช่วยให้โมเดล หลีกเลี่ยงปัญหาเกี่ยวกับหน่วยความจำ แต่ยังคงฝึกได้อย่างมีประสิทธิภาพ
Gradient Boosted (Decision) Trees (GBT)
ป่าการตัดสินใจประเภทหนึ่งซึ่งมีลักษณะดังนี้
- การฝึกใช้ การเพิ่มประสิทธิภาพแบบไล่ระดับ
- โมเดลที่อ่อนแอคือแผนผังการตัดสินใจ
ดูข้อมูลเพิ่มเติมได้ที่ต้นไม้ตัดสินใจแบบ Gradient Boosting ในหลักสูตร Decision Forests
การเพิ่มประสิทธิภาพการไล่ระดับ
อัลกอริทึมการฝึกที่ฝึกโมเดลที่อ่อนแอเพื่อปรับปรุงคุณภาพ (ลดการสูญเสีย) ของโมเดลที่แข็งแกร่งอย่างต่อเนื่อง เช่น โมเดลที่อ่อนแออาจเป็นโมเดลเชิงเส้นหรือโมเดลต้นไม้ตัดสินใจขนาดเล็ก โมเดลที่แข็งแกร่งจะกลายเป็นผลรวมของโมเดลที่อ่อนแอทั้งหมดที่ได้รับการฝึกก่อนหน้านี้
ในรูปแบบที่ง่ายที่สุดของการเพิ่มประสิทธิภาพแบบไล่ระดับ ในแต่ละการทำซ้ำ โมเดลที่อ่อนแอจะได้รับการฝึกให้คาดการณ์การไล่ระดับการสูญเสียของโมเดลที่แข็งแกร่ง จากนั้น ระบบจะอัปเดตเอาต์พุตของโมเดลที่มีประสิทธิภาพโดยการลบการไล่ระดับที่คาดการณ์ไว้ ซึ่งคล้ายกับการไล่ระดับการลด
ที่ไหน
- $F_{0}$ คือโมเดลเริ่มต้นอย่างมั่นคง
- $F_{i+1}$ คือโมเดลที่แข็งแกร่งถัดไป
- $F_{i}$ คือโมเดลที่แข็งแกร่งในปัจจุบัน
- $\xi$ คือค่าระหว่าง 0.0 ถึง 1.0 ที่เรียกว่าการหดตัว ซึ่งคล้ายกับ อัตราการเรียนรู้ใน การไล่ระดับการลด
- $f_{i}$ คือโมเดลแบบอ่อนที่ได้รับการฝึกให้คาดการณ์การไล่ระดับการสูญเสียของ $F_{i}$
การปรับปรุงการเพิ่มแบบไล่ระดับสมัยใหม่ยังรวมอนุพันธ์อันดับที่ 2 (เมทริกซ์เฮสเซียน) ของการสูญเสียในการคำนวณด้วย
แผนผังการตัดสินใจมักใช้เป็นโมเดลที่อ่อนแอใน การเพิ่มประสิทธิภาพแบบไล่ระดับ ดูGradient Boosted (Decision) Trees
การตัดการไล่ระดับสี
กลไกที่ใช้กันโดยทั่วไปเพื่อลดปัญหาการไล่ระดับสีที่เพิ่มขึ้นโดยการจำกัดค่าสูงสุดของการไล่ระดับสี (การตัด) โดยเทียมเมื่อใช้การไล่ระดับสีเพื่อฝึกโมเดล
การไล่ระดับความชัน
เทคนิคทางคณิตศาสตร์เพื่อลดการสูญเสีย การไล่ระดับความชันจะปรับน้ำหนักและอคติซ้ำๆ เพื่อค้นหาการผสมผสานที่ดีที่สุดในการลดการสูญเสียทีละน้อย
การไล่ระดับความชันมีมานานกว่าแมชชีนเลิร์นนิงมาก
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยเชิงเส้น: การไล่ระดับ การไล่ระดับ ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
กราฟ
ใน TensorFlow ข้อมูลจำเพาะของการคำนวณ โหนดในกราฟ แสดงถึงการดำเนินการ ขอบมีทิศทางและแสดงการส่งผลลัพธ์ ของการดำเนินการ (Tensor) เป็น ตัวถูกดำเนินการไปยังการดำเนินการอื่น ใช้ TensorBoard เพื่อแสดงภาพกราฟ
การดำเนินการกราฟ
สภาพแวดล้อมการเขียนโปรแกรม TensorFlow ซึ่งโปรแกรมจะสร้างกราฟก่อน แล้วจึงเรียกใช้กราฟทั้งหมดหรือบางส่วน การดำเนินการกราฟ เป็นโหมดการดำเนินการเริ่มต้นใน TensorFlow 1.x
แตกต่างจากการดำเนินการอย่างกระตือรือร้น
นโยบายที่การละเมิดถือว่าร้ายแรง
ในการเรียนรู้แบบเสริมกำลัง นโยบายที่เลือกการดำเนินการที่มีผลตอบแทนที่คาดไว้สูงสุดเสมอ
ความสมเหตุสมผล
คุณสมบัติของโมเดลที่มีเอาต์พุตอิงตาม (ยึดตาม) เนื้อหาแหล่งที่มาที่เฉพาะเจาะจง ตัวอย่างเช่น สมมติว่าคุณป้อนตำราฟิสิกส์ทั้งเล่มเป็นอินพุต ("บริบท") ให้กับโมเดลภาษาขนาดใหญ่ จากนั้นคุณจะป้อนคำสั่งให้โมเดลภาษาขนาดใหญ่ด้วยคำถามเกี่ยวกับฟิสิกส์ หากคำตอบของโมเดลแสดงข้อมูลในตำราเรียนนั้น แสดงว่าโมเดลนั้นอิงตามตำราเรียนดังกล่าวโปรดทราบว่าโมเดลที่มีการอ้างอิงไม่ได้เป็นโมเดลข้อเท็จจริงเสมอไป เช่น ตำราฟิสิกส์ที่ป้อนอาจมีข้อผิดพลาด
ข้อมูลจากการสังเกตการณ์โดยตรง
เรียลลิตี้
สิ่งที่เกิดขึ้นจริง
ตัวอย่างเช่น ลองพิจารณาการจัดประเภทแบบไบนารี โมเดลที่คาดการณ์ว่านักศึกษาปี 1 ในมหาวิทยาลัย จะสำเร็จการศึกษาภายใน 6 ปีหรือไม่ ข้อมูลจากการสังเกตการณ์โดยตรงสำหรับโมเดลนี้คือการที่นักเรียน คนนั้นจบการศึกษาภายใน 6 ปีหรือไม่
อคติในการระบุแหล่งที่มาของกลุ่ม
การสันนิษฐานว่าสิ่งที่จริงสำหรับบุคคลหนึ่งก็จริงสำหรับทุกคน ในกลุ่มนั้นด้วย ผลกระทบของอคติในการระบุแหล่งที่มาของกลุ่มอาจรุนแรงขึ้น หากใช้การสุ่มตัวอย่างตามความสะดวก ในการเก็บรวบรวมข้อมูล ในกลุ่มตัวอย่างที่ไม่เป็นตัวแทน ระบบอาจทำการระบุแหล่งที่มา ซึ่งไม่ตรงกับความเป็นจริง
ดูอคติความเหมือนกันของกลุ่มนอก และอคติในกลุ่มด้วย นอกจากนี้ โปรดดูข้อมูลเพิ่มเติมในความเป็นธรรม: ประเภทของอคติ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
H
อาการหลอนของ AI
การสร้างเอาต์พุตที่ดูสมเหตุสมผลแต่ไม่ถูกต้องตามข้อเท็จจริงโดยโมเดลGenerative AI ซึ่งอ้างว่าเป็นการยืนยันเกี่ยวกับโลกแห่งความเป็นจริง ตัวอย่างเช่น โมเดล Generative AI ที่อ้างว่าบารัก โอบามา เสียชีวิตในปี 1865 หลอน
การแฮช
ในแมชชีนเลิร์นนิง กลไกสำหรับการจัดกลุ่มข้อมูลเชิงหมวดหมู่ โดยเฉพาะอย่างยิ่งเมื่อจำนวนหมวดหมู่มีมาก แต่จำนวนหมวดหมู่ที่ปรากฏจริงในชุดข้อมูลมีน้อยกว่า
ตัวอย่างเช่น โลกมีต้นไม้ประมาณ 73,000 สายพันธุ์ คุณสามารถ แสดงต้นไม้แต่ละสายพันธุ์จาก 73,000 สายพันธุ์ในที่เก็บข้อมูลแบบหมวดหมู่แยกกัน 73,000 ที่ หรือหากมีต้นไม้เพียง 200 ชนิดที่ปรากฏในชุดข้อมูล คุณอาจใช้การแฮชเพื่อแบ่งต้นไม้เป็น 500 บัคเก็ต
ถังเดียวอาจมีต้นไม้หลายสายพันธุ์ เช่น การแฮช อาจทำให้ baobab และ red maple ซึ่งเป็นสายพันธุ์ที่แตกต่างกันทางพันธุกรรม ไปอยู่ในกลุ่มเดียวกัน อย่างไรก็ตาม การแฮชยังคงเป็นวิธีที่ดีในการ แมปชุดหมวดหมู่ขนาดใหญ่ลงในจำนวนถังที่เลือก การแฮชจะเปลี่ยนฟีเจอร์เชิงหมวดหมู่ที่มีค่าที่เป็นไปได้จำนวนมากให้เป็นค่าจำนวนน้อยลงมากโดยการจัดกลุ่มค่าในลักษณะที่กำหนด
ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลเชิงหมวดหมู่: คำศัพท์และการเข้ารหัสแบบ One-Hot ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
ฮิวริสติก
โซลูชันที่เรียบง่ายและนำไปใช้ได้อย่างรวดเร็วเพื่อแก้ปัญหา เช่น "เมื่อใช้ฮิวริสติก เรามีความแม่นยำ 86% เมื่อเราเปลี่ยนไปใช้ ดีปนิวรัลเน็ตเวิร์ก ความแม่นยำก็เพิ่มขึ้นเป็น 98%"
เลเยอร์ที่ซ่อนอยู่
เลเยอร์ในโครงข่ายประสาทเทียมระหว่างเลเยอร์อินพุต (ฟีเจอร์) กับเลเยอร์เอาต์พุต (การคาดการณ์) เลเยอร์ที่ซ่อนแต่ละเลเยอร์ประกอบด้วยนิวรอนอย่างน้อย 1 ตัว ตัวอย่างเช่น เครือข่ายประสาทต่อไปนี้มีเลเยอร์ที่ซ่อนอยู่ 2 เลเยอร์ เลเยอร์แรกมีนิวรอน 3 ตัว และเลเยอร์ที่ 2 มีนิวรอน 2 ตัว
โครงข่ายประสาทแบบลึกมีเลเยอร์ที่ซ่อนอยู่มากกว่า 1 เลเยอร์ ตัวอย่างเช่น ภาพประกอบก่อนหน้านี้เป็นโครงข่ายประสาทเทียมแบบลึกเนื่องจากโมเดลมีเลเยอร์ที่ซ่อนอยู่ 2 เลเยอร์
ดูข้อมูลเพิ่มเติมได้ที่โครงข่ายประสาท: โหนดและเลเยอร์ที่ซ่อนอยู่ ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
การจัดกลุ่มแบบลำดับชั้น
หมวดหมู่อัลกอริทึมการจัดกลุ่มที่สร้างแผนผังคลัสเตอร์ การจัดกลุ่มแบบลำดับชั้นเหมาะกับข้อมูลลำดับชั้น เช่น การจัดหมวดหมู่ทางพฤกษศาสตร์ อัลกอริทึมการจัดกลุ่มแบบลำดับชั้นมี 2 ประเภท ได้แก่
- การจัดกลุ่มแบบรวมกลุ่มจะกำหนดตัวอย่างทั้งหมดให้กับคลัสเตอร์ของตัวเองก่อน และผสานคลัสเตอร์ที่ใกล้ที่สุดซ้ำๆ เพื่อสร้างแผนผังแบบลำดับชั้น
- การจัดกลุ่มแบบแบ่งจะจัดกลุ่มตัวอย่างทั้งหมดไว้ในคลัสเตอร์เดียวก่อน จากนั้นจะแบ่งคลัสเตอร์ออกเป็นแผนภูมิลำดับชั้นซ้ำๆ
เปรียบเทียบกับการจัดกลุ่มตามเซนทรอยด์
ดูข้อมูลเพิ่มเติมได้ที่อัลกอริทึม การจัดกลุ่ม ในหลักสูตรการจัดกลุ่ม
การปีนเขา
อัลกอริทึมสำหรับการปรับปรุงโมเดลแมชชีนเลิร์นนิงซ้ำๆ ("เดินขึ้นเขา") จนกว่า โมเดลจะหยุดการปรับปรุง ("ขึ้นถึงยอดเขา") รูปแบบทั่วไป ของอัลกอริทึมมีดังนี้
- สร้างโมเดลเริ่มต้น
- สร้างโมเดลผู้สมัครใหม่โดยปรับเปลี่ยนเล็กน้อยในวิธีที่คุณฝึกหรือปรับแต่ง ซึ่งอาจต้อง ทำงานกับชุดการฝึกที่แตกต่างกันเล็กน้อยหรือ ไฮเปอร์พารามิเตอร์ที่แตกต่างกัน
- ประเมินโมเดลผู้สมัครใหม่และดำเนินการอย่างใดอย่างหนึ่งต่อไปนี้
- หากโมเดลผู้ท้าชิงมีประสิทธิภาพเหนือกว่าโมเดลเริ่มต้น โมเดลผู้ท้าชิงนั้นจะกลายเป็นโมเดลเริ่มต้นใหม่ ในกรณีนี้ ให้ทำขั้นตอนที่ 1, 2 และ 3 ซ้ำ
- หากไม่มีโมเดลใดมีประสิทธิภาพเหนือกว่าโมเดลเริ่มต้น แสดงว่าคุณมาถึงจุดสูงสุดแล้วและควรหยุดการทำซ้ำ
ดูคำแนะนำเกี่ยวกับการปรับแต่งไฮเปอร์พารามิเตอร์ได้ที่Playbook การปรับแต่ง Deep Learning ดูคำแนะนำเกี่ยวกับการสร้างฟีเจอร์ได้ที่โมดูลข้อมูลของหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การสูญเสียบานพับ
ตระกูลฟังก์ชันการสูญเสียสำหรับการจัดประเภทที่ออกแบบมาเพื่อค้นหาขอบเขตการตัดสินใจให้ไกลที่สุดจากตัวอย่างการฝึกแต่ละรายการ จึงเป็นการเพิ่มระยะขอบระหว่างตัวอย่างกับขอบเขตให้ได้มากที่สุด KSVM ใช้การสูญเสียแบบบานพับ (หรือฟังก์ชันที่เกี่ยวข้อง เช่น การสูญเสียแบบบานพับยกกำลังสอง) สําหรับการจัดประเภทแบบไบนารี ฟังก์ชันการสูญเสียแบบบานพับ จะกําหนดดังนี้
โดย y คือป้ายกำกับที่แท้จริง ซึ่งอาจเป็น -1 หรือ +1 และ y' คือเอาต์พุตดิบ ของโมเดลการแยกประเภท
ดังนั้น พล็อตของฟังก์ชันการสูญเสียแบบบานพับเทียบกับ (y * y') จะมีลักษณะดังนี้

อคติทางประวัติศาสตร์
อคติประเภทหนึ่งที่มีอยู่แล้วในโลกและแทรกซึมเข้าไปในชุดข้อมูล อคติเหล่านี้มักจะสะท้อนถึง การเหมารวมทางวัฒนธรรมที่มีอยู่ ความไม่เท่าเทียมกันทางประชากร และอคติที่มีต่อกลุ่ม ทางสังคมบางกลุ่ม
ตัวอย่างเช่น ลองพิจารณาโมเดลการจัดประเภทที่ คาดการณ์ว่าผู้สมัครขอสินเชื่อจะผิดนัดชำระหนี้หรือไม่ ซึ่งได้รับการ ฝึกจากข้อมูลการผิดนัดชำระหนี้ย้อนหลังตั้งแต่ปี 1980 จากธนาคารท้องถิ่นใน 2 ชุมชนที่แตกต่างกัน หากผู้สมัครจากชุมชน ก ในอดีตมีแนวโน้มที่จะผิดนัดชำระหนี้มากกว่าผู้สมัครจากชุมชน ข ถึง 6 เท่า โมเดลอาจเรียนรู้จากอคติในอดีต ซึ่งส่งผลให้โมเดลมีแนวโน้มน้อยที่จะอนุมัติเงินกู้ในชุมชน ก แม้ว่าเงื่อนไขในอดีตที่ส่งผลให้อัตราการผิดนัดชำระหนี้ในชุมชนนั้นสูงขึ้นจะไม่มีความเกี่ยวข้องอีกต่อไปก็ตาม
ดูข้อมูลเพิ่มเติมได้ที่ความเป็นธรรม: ประเภทของ อคติ ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
ข้อมูลที่แยกไว้
ตัวอย่างที่ไม่ได้ใช้ ("กันไว้") โดยเจตนาในระหว่างการฝึก ชุดข้อมูลการตรวจสอบและชุดข้อมูลการทดสอบเป็นตัวอย่างของข้อมูลที่แยกไว้ ข้อมูลที่กันไว้ ช่วยประเมินความสามารถของโมเดลในการสรุปข้อมูลอื่นๆ นอกเหนือจาก ข้อมูลที่ใช้ฝึกโมเดล การสูญเสียในชุดข้อมูลที่แยกไว้จะช่วยให้ประมาณการสูญเสียในชุดข้อมูลที่ไม่เคยเห็นได้ดีกว่าการสูญเสียในชุดข้อมูลการฝึก
ผู้จัด
เมื่อฝึกโมเดล ML ในชิปตัวเร่ง (GPU หรือ TPU) ส่วนของระบบ ที่ควบคุมทั้ง 2 อย่างต่อไปนี้
- โฟลว์โดยรวมของโค้ด
- การแยกและการแปลงไปป์ไลน์อินพุต
โดยปกติแล้วโฮสต์จะทำงานบน CPU ไม่ใช่ชิปตัวเร่ง ส่วนอุปกรณ์จะจัดการเทนเซอร์บนชิปตัวเร่ง
การประเมินโดยมนุษย์
กระบวนการที่ผู้ใช้ประเมินคุณภาพของเอาต์พุตโมเดล ML เช่น การให้ผู้ใช้ที่พูดได้ 2 ภาษาประเมินคุณภาพของโมเดลการแปลด้วย ML การประเมินโดยเจ้าหน้าที่จะมีประโยชน์อย่างยิ่งในการประเมินโมเดลที่ไม่มีคำตอบที่ถูกต้องเพียงคำตอบเดียว
เปรียบเทียบกับการประเมินอัตโนมัติและ การประเมินโดยผู้ให้คะแนนอัตโนมัติ
ต้องมีคนคอยตรวจสอบ (HITL)
สำนวนที่ไม่ได้กำหนดไว้อย่างชัดเจนซึ่งอาจหมายถึงสิ่งใดสิ่งหนึ่งต่อไปนี้
- นโยบายการดูผลลัพธ์ของ Generative AI อย่างมีวิจารณญาณหรือ อย่างไม่ปักใจเชื่อ
- กลยุทธ์หรือระบบที่ช่วยให้มั่นใจว่าผู้คนจะช่วยกำหนด ประเมิน และปรับแต่ง ลักษณะการทำงานของโมเดล การให้มนุษย์เข้ามามีส่วนร่วมจะช่วยให้ AI ได้รับประโยชน์จาก ทั้งสติปัญญาของเครื่องจักรและสติปัญญาของมนุษย์ ตัวอย่างเช่น ระบบที่ AI สร้างโค้ดซึ่งวิศวกรซอฟต์แวร์จะตรวจสอบในภายหลังถือเป็นระบบที่มีมนุษย์เป็นผู้ควบคุม
ไฮเปอร์พารามิเตอร์
ตัวแปรที่คุณหรือบริการปรับแต่ง Hyperparameter ปรับในระหว่างการฝึกโมเดลที่รันต่อเนื่อง ตัวอย่างเช่น อัตราการเรียนรู้เป็นไฮเปอร์พารามิเตอร์ คุณสามารถ ตั้งค่าอัตราการเรียนรู้เป็น 0.01 ก่อนเซสชันการฝึก 1 ครั้ง หากพิจารณาแล้วว่า 0.01 สูงเกินไป คุณอาจตั้งค่าอัตราการเรียนรู้เป็น 0.003 สำหรับเซสชันการฝึกครั้งถัดไป
ในทางตรงกันข้าม พารามิเตอร์คือน้ำหนักและอคติต่างๆ ที่โมเดลเรียนรู้ระหว่างการฝึก
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยเชิงเส้น: ไฮเปอร์พารามิเตอร์ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ระนาบไฮเปอร์
ขอบเขตที่แบ่งพื้นที่ออกเป็น 2 พื้นที่ย่อย เช่น เส้นคือ ระนาบไฮเปอร์ใน 2 มิติ และระนาบคือระนาบไฮเปอร์ใน 3 มิติ โดยทั่วไปในแมชชีนเลิร์นนิง ไฮเปอร์เพลนคือขอบเขตที่แยกพื้นที่ที่มีมิติสูง Kernel Support Vector Machines ใช้ ระนาบไฮเปอร์เพื่อแยกคลาสที่เป็นบวกออกจากคลาสที่เป็นลบ ซึ่งมักจะอยู่ในพื้นที่ ที่มีมิติสูงมาก
I
i.i.d.
ตัวย่อของการแจกแจงแบบอิสระและเหมือนกัน
การรู้จำรูปภาพ
กระบวนการที่จัดประเภทออบเจ็กต์ รูปแบบ หรือแนวคิดในรูปภาพ การจดจำรูปภาพเรียกอีกอย่างว่าการจัดประเภทรูปภาพ
ดูข้อมูลเพิ่มเติมได้ที่ ML Practicum: Image Classification
ดูข้อมูลเพิ่มเติมได้ที่ML Practicum: Image Classification course
ชุดข้อมูลที่ไม่สมดุล
คำพ้องความหมายของชุดข้อมูลที่มีความไม่สมดุลของคลาส
อคติโดยไม่รู้ตัว
การเชื่อมโยงหรือการคาดเดาโดยอัตโนมัติตามโมเดลความคิดและความทรงจำของบุคคล อคติโดยปริยายอาจส่งผลต่อสิ่งต่อไปนี้
- วิธีเก็บรวบรวมและจัดประเภทข้อมูล
- วิธีออกแบบและพัฒนาระบบแมชชีนเลิร์นนิง
ตัวอย่างเช่น เมื่อสร้างโมเดลการจัดประเภท เพื่อระบุรูปภาพงานแต่งงาน วิศวกรอาจใช้การมีชุดสีขาว ในรูปภาพเป็นฟีเจอร์ อย่างไรก็ตาม ชุดสีขาวเป็นธรรมเนียมเฉพาะในบางยุคและบางวัฒนธรรมเท่านั้น
ดูอคติยืนยันความคิดตัวเองด้วย
การใส่ค่า
รูปแบบย่อของการประมาณค่า
ความไม่เข้ากันของเมตริกความเป็นธรรม
แนวคิดที่ว่าแนวคิดเรื่องความยุติธรรมบางอย่างไม่สามารถใช้ร่วมกันได้และ ไม่สามารถตอบสนองพร้อมกันได้ ด้วยเหตุนี้ จึงไม่มีเมตริกเดียวที่ใช้ได้ทั่วไป สําหรับการวัดความเป็นธรรม ซึ่งนําไปใช้กับปัญหา ML ทั้งหมดได้
แม้ว่าอาจดูเหมือนว่าการเปรียบเทียบเมตริกความเป็นธรรมจะทำไม่ได้ แต่การที่เมตริกความเป็นธรรมไม่สามารถเปรียบเทียบกันได้ไม่ได้หมายความว่าความพยายามที่จะสร้างความเป็นธรรมนั้นไร้ผล แต่กลับแนะนําว่า ต้องกําหนดความเป็นธรรมตามบริบทสําหรับปัญหา ML ที่กําหนด โดยมี เป้าหมายเพื่อป้องกันอันตรายที่เฉพาะเจาะจงกับ Use Case ของปัญหา
ดูรายละเอียดเพิ่มเติมเกี่ยวกับการไม่สามารถใช้เมตริกความเป็นธรรมร่วมกันได้ที่ "On the (im)possibility of fairness"
การเรียนรู้ในบริบท
คำพ้องความหมายของ Few-Shot Prompting
มีการแจกแจงแบบอิสระและเหมือนกัน (i.i.d)
ข้อมูลที่ดึงมาจากการกระจายที่ไม่เปลี่ยนแปลง และค่าแต่ละค่า ที่ดึงมาจะไม่ขึ้นอยู่กับค่าที่ดึงมาก่อนหน้านี้ i.i.d. คือก๊าซในอุดมคติ ของแมชชีน เลิร์นนิง ซึ่งเป็นโครงสร้างทางคณิตศาสตร์ที่มีประโยชน์ แต่แทบจะไม่พบในโลกแห่งความเป็นจริง ตัวอย่างเช่น การกระจายของผู้เข้าชมหน้าเว็บ อาจเป็นแบบ i.i.d. ในช่วงเวลาสั้นๆ นั่นคือ การกระจายจะไม่ เปลี่ยนแปลงในช่วงเวลาสั้นๆ นั้น และโดยทั่วไปแล้วการเข้าชมของบุคคลหนึ่งจะ ไม่ขึ้นอยู่กับการเข้าชมของอีกบุคคลหนึ่ง อย่างไรก็ตาม หากขยายกรอบเวลาดังกล่าว ความแตกต่างตามฤดูกาลของผู้เข้าชมหน้าเว็บอาจปรากฏขึ้น
ดูความไม่คงที่ด้วย
ความเป็นธรรมต่อบุคคล
เมตริกความเป็นธรรมที่ตรวจสอบว่าบุคคลที่คล้ายกันได้รับการจัดประเภท ในลักษณะเดียวกันหรือไม่ ตัวอย่างเช่น Brobdingnagian Academy อาจต้องการตอบสนอง ความเป็นธรรมของแต่ละบุคคลโดยการรับประกันว่านักเรียน 2 คนที่มีเกรด และคะแนนสอบมาตรฐานเหมือนกันมีโอกาสเท่ากันที่จะได้รับการตอบรับ
โปรดทราบว่าความเป็นธรรมในระดับบุคคลขึ้นอยู่กับวิธีที่คุณกำหนด "ความคล้ายคลึง" (ในกรณีนี้คือเกรดและคะแนนสอบ) และคุณอาจเสี่ยงต่อการ สร้างปัญหาด้านความเป็นธรรมใหม่ๆ หากเมตริกความคล้ายคลึงพลาดข้อมูลสำคัญ (เช่น ความเข้มงวดของหลักสูตรของนักเรียน)
ดูรายละเอียดเพิ่มเติมเกี่ยวกับการพิจารณาความเป็นธรรมในแต่ละบุคคลได้ที่ "Fairness Through Awareness"
การอนุมาน
ในแมชชีนเลิร์นนิงแบบเดิม กระบวนการคาดการณ์จะทำโดย ใช้โมเดลที่ฝึกแล้วกับตัวอย่างที่ไม่มีป้ายกำกับ ดูข้อมูลเพิ่มเติมได้ที่การเรียนรู้ภายใต้การควบคุมในหลักสูตร "ข้อมูลเบื้องต้นเกี่ยวกับ ML"
ในโมเดลภาษาขนาดใหญ่ การอนุมานคือ กระบวนการใช้โมเดลที่ฝึกแล้วเพื่อสร้างคำตอบ สำหรับพรอมต์ที่ป้อน
การอนุมานมีความหมายที่แตกต่างออกไปเล็กน้อยในสถิติ ดูรายละเอียดได้ที่ บทความวิกิพีเดียเกี่ยวกับการอนุมานทางสถิติ
เส้นทางการอนุมาน
ในแผนผังการตัดสินใจ ระหว่างการอนุมาน เส้นทางที่ตัวอย่างหนึ่งๆ ใช้จากรูทไปยังเงื่อนไขอื่นๆ ซึ่งสิ้นสุดด้วยลีฟ ตัวอย่างเช่น ในแผนผังการตัดสินใจต่อไปนี้ ลูกศรที่หนาขึ้นแสดงเส้นทางการอนุมานสำหรับตัวอย่างที่มีค่าฟีเจอร์ต่อไปนี้
- x = 7
- y = 12
- z = -3
เส้นทางการอนุมานในภาพประกอบต่อไปนี้จะผ่านเงื่อนไข 3 ข้อ
ก่อนที่จะไปถึงลีฟ (Zeta)
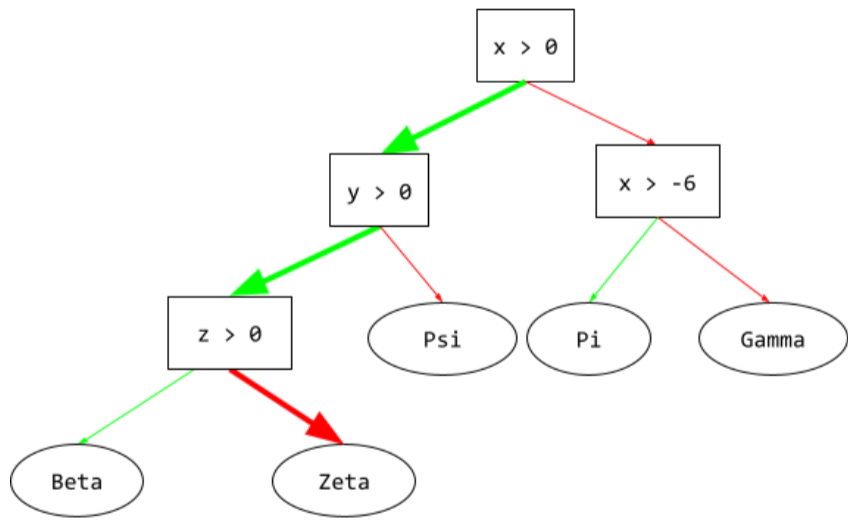
ลูกศรหนา 3 ตัวแสดงเส้นทางการอนุมาน
ดูข้อมูลเพิ่มเติมได้ที่แผนผังการตัดสินใจ ในหลักสูตร Decision Forests
การได้ข้อมูล
ในป่าการตัดสินใจ ความแตกต่างระหว่างเอนโทรปีของโหนดกับผลรวมของเอนโทรปีของโหนดลูกที่ถ่วงน้ำหนัก (ตามจำนวนตัวอย่าง) เอนโทรปีของโหนดคือเอนโทรปี ของตัวอย่างในโหนดนั้น
ตัวอย่างเช่น ลองพิจารณาค่าเอนโทรปีต่อไปนี้
- เอนโทรปีของโหนดหลัก = 0.6
- เอนโทรปีของโหนดลูก 1 โหนดที่มีตัวอย่างที่เกี่ยวข้อง 16 รายการ = 0.2
- เอนโทรปีของโหนดย่อยอีกโหนดหนึ่งที่มีตัวอย่างที่เกี่ยวข้อง 24 รายการ = 0.1
ดังนั้น 40% ของตัวอย่างจึงอยู่ในโหนดย่อยหนึ่ง และ 60% อยู่ในโหนดย่อยอีกโหนดหนึ่ง ดังนั้น
- ผลรวมของเอนโทรปีแบบถ่วงน้ำหนักของโหนดย่อย = (0.4 * 0.2) + (0.6 * 0.1) = 0.14
ดังนั้น การได้ข้อมูลจึงเป็นดังนี้
- การได้ข้อมูล = เอนโทรปีของโหนดแม่ - ผลรวมของเอนโทรปีแบบถ่วงน้ำหนักของโหนดลูก
- การได้ข้อมูล = 0.6 - 0.14 = 0.46
ตัวแยกส่วนใหญ่พยายามสร้างเงื่อนไข ที่เพิ่มการรับข้อมูลสูงสุด
อคติในกลุ่ม
การแสดงความลำเอียงต่อกลุ่มหรือลักษณะของตนเอง หากผู้ทดสอบหรือผู้ให้คะแนนเป็นเพื่อน ครอบครัว หรือเพื่อนร่วมงานของนักพัฒนาแมชชีนเลิร์นนิง อคติในกลุ่มอาจทำให้การทดสอบผลิตภัณฑ์ หรือชุดข้อมูลไม่ถูกต้อง
อคติในกลุ่มเป็นรูปแบบหนึ่งของอคติในการระบุแหล่งที่มาของกลุ่ม ดูอคติความเหมือนกันของกลุ่มนอกด้วย
ดูข้อมูลเพิ่มเติมได้ที่ความเป็นธรรม: ประเภทของอคติใน หลักสูตรเร่งรัดแมชชีนเลิร์นนิง
เครื่องมือสร้างอินพุต
กลไกที่ใช้โหลดข้อมูลลงในโครงข่ายประสาท
คุณอาจคิดว่าเครื่องมือสร้างอินพุตเป็นคอมโพเนนต์ที่รับผิดชอบในการประมวลผล ข้อมูลดิบเป็นเทนเซอร์ ซึ่งจะมีการทำซ้ำเพื่อสร้างกลุ่มสำหรับการ ฝึก การประเมิน และการอนุมาน
เลเยอร์อินพุต
เลเยอร์ของโครงข่ายระบบประสาทเทียมที่ เก็บเวกเตอร์ฟีเจอร์ กล่าวคือ เลเยอร์อินพุต มีตัวอย่างสำหรับการฝึกหรือ การอนุมาน ตัวอย่างเช่น เลเยอร์อินพุตใน โครงข่ายประสาทเทียมต่อไปนี้ประกอบด้วยฟีเจอร์ 2 รายการ
เงื่อนไขในชุด
ในแผนผังการตัดสินใจ เงื่อนไข ที่ทดสอบการมีอยู่ของรายการหนึ่งในชุดรายการ ตัวอย่างเช่น เงื่อนไขในชุดมีดังนี้
house-style in [tudor, colonial, cape]
ในระหว่างการอนุมาน หากค่าของฟีเจอร์
รูปแบบของบ้านเป็น tudor หรือ colonial หรือ cape เงื่อนไขนี้จะประเมินเป็น "ใช่" หากค่าของฟีเจอร์สไตล์บ้านเป็นอย่างอื่น (เช่น ranch)
เงื่อนไขนี้จะประเมินเป็น "ไม่"
โดยปกติแล้ว เงื่อนไขในชุดจะทำให้เกิดแผนผังการตัดสินใจที่มีประสิทธิภาพมากกว่าเงื่อนไขที่ทดสอบฟีเจอร์ที่เข้ารหัสแบบ One-Hot
อินสแตนซ์
คำพ้องความหมายของตัวอย่าง
การปรับแต่งคำสั่ง
รูปแบบหนึ่งของการปรับแต่งที่ช่วยเพิ่มความสามารถของโมเดล Generative AI ในการทำตามคำสั่ง การปรับแต่งคำสั่งเกี่ยวข้องกับการฝึกโมเดลในชุดพรอมต์คำสั่ง ซึ่งโดยทั่วไปจะครอบคลุมงานหลากหลายประเภท จากนั้นโมเดลที่ปรับแต่งตามคำสั่งมักจะ สร้างคำตอบที่มีประโยชน์สำหรับ พรอมต์แบบ Zero-Shot ในงานต่างๆ
เปรียบเทียบกับ
ความสามารถในการตีความ
ความสามารถในการอธิบายหรือนำเสนอการให้เหตุผลของโมเดล ML ใน คำที่มนุษย์เข้าใจได้
เช่น โมเดลการถดถอยเชิงเส้นส่วนใหญ่สามารถตีความได้สูง (คุณเพียงแค่ต้องดูน้ำหนักที่ฝึกแล้วสำหรับแต่ละฟีเจอร์) นอกจากนี้ Decision Forest ยังตีความได้สูงอีกด้วย อย่างไรก็ตาม โมเดลบางอย่าง ต้องใช้การแสดงภาพที่ซับซ้อนจึงจะตีความได้
คุณใช้ เครื่องมือการตีความการเรียนรู้ (LIT) เพื่อตีความโมเดล ML ได้
ความสอดคล้องระหว่างผู้ประเมิน
การวัดความถี่ที่ผู้ประเมินที่เป็นมนุษย์เห็นด้วยเมื่อทํางาน หากผู้ตรวจสอบไม่เห็นด้วย คุณอาจต้องปรับปรุงวิธีการของงาน บางครั้งเรียกว่าความสอดคล้องระหว่างผู้ใส่คำอธิบายประกอบหรือ ความน่าเชื่อถือระหว่างผู้ให้คะแนน ดูค่า Kappa ของ Cohen ซึ่งเป็นหนึ่งในการวัดข้อตกลงระหว่างผู้ให้คะแนนที่ได้รับความนิยมมากที่สุด
ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลเชิงหมวดหมู่: ปัญหาที่พบบ่อย ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
Intersection over Union (IoU)
อินเทอร์เซกชันของ 2 ชุดหารด้วยยูเนียนของชุดทั้ง 2 ในงานตรวจจับรูปภาพของแมชชีนเลิร์นนิง IoU ใช้เพื่อวัดความแม่นยำของกรอบล้อมรอบที่โมเดลคาดการณ์เทียบกับกรอบล้อมรอบข้อมูลจากการสังเกตการณ์โดยตรง ในกรณีนี้ IoU สำหรับกรอบ 2 กรอบคืออัตราส่วนระหว่างพื้นที่ที่ซ้อนทับกันกับพื้นที่ทั้งหมด และค่าของ IoU จะอยู่ในช่วงตั้งแต่ 0 (ไม่มีการซ้อนทับกันของกรอบล้อมรอบที่คาดการณ์ไว้กับกรอบล้อมรอบจากการสังเกตการณ์โดยตรง) ถึง 1 (กรอบล้อมรอบที่คาดการณ์ไว้กับกรอบล้อมรอบจากการสังเกตการณ์โดยตรงมีพิกัดเดียวกันทุกประการ)
ตัวอย่างเช่น ในรูปภาพด้านล่าง
- กรอบล้อมรอบที่คาดการณ์ (พิกัดที่กำหนดขอบเขตตำแหน่งที่โมเดล คาดการณ์ว่าโต๊ะข้างเตียงในภาพวาดอยู่) จะมีเส้นขอบสีม่วง
- กรอบล้อมรอบความจริงภาคพื้น (พิกัดที่กำหนดขอบเขตของตำแหน่งที่โต๊ะข้างเตียงในภาพวาดอยู่จริง) จะมีเส้นขอบสีเขียว
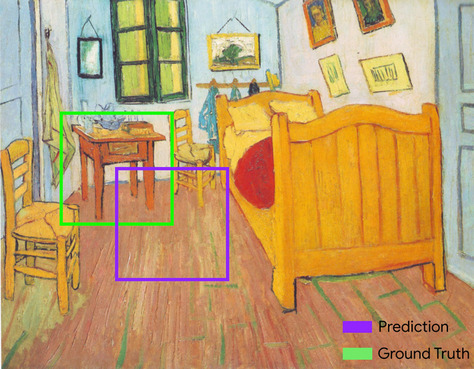
ในที่นี้ ส่วนที่ตัดกันของกรอบล้อมรอบสำหรับการคาดการณ์และข้อมูลจากการสังเกตการณ์โดยตรง (ด้านล่างซ้าย) คือ 1 และส่วนที่รวมกันของกรอบล้อมรอบสำหรับการคาดการณ์และข้อมูลจากการสังเกตการณ์โดยตรง (ด้านล่างขวา) คือ 7 ดังนั้น IoU จึงเท่ากับ \(\frac{1}{7}\)
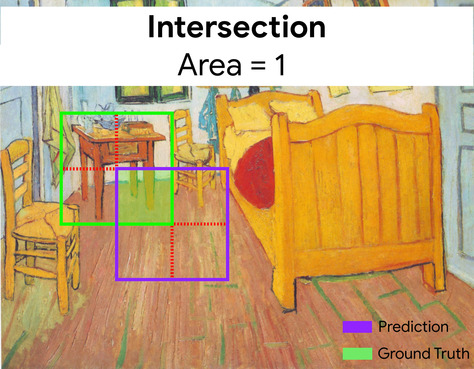
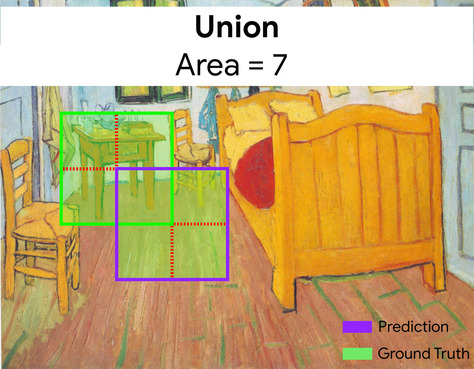
IoU
ตัวย่อของ Intersection over Union
เมทริกซ์รายการ
ในระบบการแนะนำ เมทริกซ์ของเวกเตอร์การฝังที่สร้างขึ้นโดยการแยกตัวประกอบเมทริกซ์ ซึ่งมีสัญญาณแฝงเกี่ยวกับรายการแต่ละรายการ แต่ละแถวของเมทริกซ์สินค้าจะมีค่าของฟีเจอร์แฝงเดียวสำหรับสินค้าทั้งหมด ตัวอย่างเช่น พิจารณาระบบแนะนำภาพยนตร์ แต่ละคอลัมน์ ในเมทริกซ์รายการจะแสดงภาพยนตร์ 1 เรื่อง สัญญาณแฝง อาจแสดงถึงประเภท หรืออาจเป็นสัญญาณที่ตีความได้ยากกว่า ซึ่งเกี่ยวข้องกับการโต้ตอบที่ซับซ้อนระหว่างประเภทภาพยนตร์ ดารา อายุของภาพยนตร์ หรือปัจจัยอื่นๆ
เมทริกซ์รายการมีจำนวนคอลัมน์เท่ากับเมทริกซ์เป้าหมาย ที่กำลังแยกตัวประกอบ ตัวอย่างเช่น หากมีระบบแนะนำภาพยนตร์ที่ประเมินชื่อภาพยนตร์ 10,000 เรื่อง เมทริกซ์รายการจะมี 10,000 คอลัมน์
รายการ
ในระบบการแนะนำ เอนทิตีที่ ระบบแนะนำ เช่น วิดีโอคือรายการที่ร้านวิดีโอแนะนำ ส่วนหนังสือคือรายการที่ร้านหนังสือแนะนำ
การทำซ้ำ
การอัปเดตพารามิเตอร์ของโมเดลเพียงครั้งเดียว ซึ่งก็คือน้ำหนักและอคติของโมเดลระหว่างการฝึก ขนาดกลุ่มจะกำหนด จำนวนตัวอย่างที่โมเดลประมวลผลในการทำซ้ำครั้งเดียว เช่น หากขนาดกลุ่มคือ 20 โมเดลจะประมวลผลตัวอย่าง 20 รายการก่อน ปรับพารามิเตอร์
เมื่อฝึกโครงข่ายระบบประสาทเทียม การทำซ้ำครั้งเดียว จะเกี่ยวข้องกับการส่งผ่าน 2 ครั้งต่อไปนี้
- การส่งต่อเพื่อประเมินการสูญเสียในกลุ่มเดียว
- การส่งผ่านย้อนกลับ (การแพร่ย้อนกลับ) เพื่อปรับพารามิเตอร์ของโมเดลตามการสูญเสียและอัตราการเรียนรู้
ดูข้อมูลเพิ่มเติมได้ที่การไล่ระดับ ความชัน ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
J
JAX
ไลบรารีการประมวลผลอาร์เรย์ที่รวมXLA (Accelerated Linear Algebra) และการหาอนุพันธ์อัตโนมัติ สำหรับการประมวลผลเชิงตัวเลขประสิทธิภาพสูง JAX มี API ที่เรียบง่ายและมีประสิทธิภาพ สำหรับการเขียนโค้ดเชิงตัวเลขที่เร่งความเร็วด้วยการเปลี่ยนรูปแบบที่ประกอบได้ JAX มีฟีเจอร์ต่างๆ เช่น
grad(การหาอนุพันธ์อัตโนมัติ)jit(การคอมไพล์แบบทันที)vmap(การแปลงเป็นเวกเตอร์หรือการจัดกลุ่มอัตโนมัติ)pmap(การประมวลผลแบบคู่ขนาน)
JAX เป็นภาษาสำหรับแสดงและเรียบเรียงการแปลงโค้ดตัวเลข ซึ่งคล้ายกับไลบรารี NumPy ของ Python แต่มีขอบเขตที่กว้างกว่ามาก (ในความเป็นจริงแล้ว ไลบรารี .numpy ใน JAX มีฟังก์ชันการทำงานเทียบเท่ากัน แต่เป็นเวอร์ชันที่เขียนใหม่ทั้งหมดของไลบรารี NumPy ของ Python)
JAX เหมาะอย่างยิ่งสำหรับการเร่งความเร็วงานแมชชีนเลิร์นนิงหลายอย่าง โดยการแปลงโมเดลและข้อมูลให้อยู่ในรูปแบบที่เหมาะกับการทำงานแบบคู่ขนาน ใน GPU และTPU ชิปตัวเร่ง
Flax, Optax, Pax และไลบรารีอื่นๆ อีกมากมาย สร้างขึ้นบนโครงสร้างพื้นฐานของ JAX
K
Keras
API แมชชีนเลิร์นนิงของ Python ที่ได้รับความนิยม Keras ทํางานบน เฟรมเวิร์กการเรียนรู้เชิงลึกหลายรายการ รวมถึง TensorFlow ซึ่งพร้อมใช้งานเป็น tf.keras
Kernel Support Vector Machines (KSVM)
อัลกอริทึมการจัดประเภทที่พยายามเพิ่มระยะขอบระหว่างคลาสเชิงบวกและคลาสเชิงลบให้ได้มากที่สุดโดยการแมปเวกเตอร์ข้อมูลอินพุตไปยังพื้นที่ที่มีมิติสูงขึ้น ตัวอย่างเช่น พิจารณาปัญหาการจัดประเภท ซึ่งชุดข้อมูลอินพุต มีฟีเจอร์ 100 รายการ KSVM สามารถจับคู่ฟีเจอร์เหล่านั้นภายในเป็นพื้นที่ที่มีมิติข้อมูล 1 ล้านมิติเพื่อเพิ่มระยะขอบระหว่าง คลาสที่เป็นบวกและคลาสที่เป็นลบให้สูงสุด KSVM ใช้ Loss Function ที่เรียกว่า Hinge Loss
คีย์พอยต์
พิกัดของฟีเจอร์ที่เฉพาะเจาะจงในรูปภาพ เช่น สำหรับโมเดลการจดจำรูปภาพที่แยกแยะสายพันธุ์ดอกไม้ จุดสำคัญอาจเป็นจุดกึ่งกลางของกลีบดอกแต่ละกลีบ ก้าน เกสรตัวผู้ และอื่นๆ
การตรวจสอบความถูกต้องแบบไขว้ k-fold
อัลกอริทึมสําหรับการคาดการณ์ความสามารถของโมเดลในการสรุปข้อมูลใหม่ k ใน k-fold หมายถึงจำนวนกลุ่มที่เท่ากันที่คุณแบ่งตัวอย่างของชุดข้อมูลออกเป็น นั่นคือ คุณฝึกและทดสอบโมเดล k ครั้ง สำหรับการฝึกและทดสอบแต่ละรอบ กลุ่มที่แตกต่างกันจะเป็นชุดทดสอบ และกลุ่มที่เหลือทั้งหมดจะกลายเป็นชุดฝึก หลังจากฝึกและทดสอบ k รอบแล้ว ให้คำนวณค่าเฉลี่ยและ ส่วนเบี่ยงเบนมาตรฐานของเมตริกการทดสอบที่เลือก
เช่น สมมติว่าชุดข้อมูลมีตัวอย่าง 120 รายการ สมมติว่าคุณตัดสินใจตั้งค่า k เป็น 4 ดังนั้นหลังจากสับเปลี่ยนตัวอย่างแล้ว คุณจะแบ่งชุดข้อมูลออกเป็น 4 กลุ่มเท่าๆ กัน กลุ่มละ 30 ตัวอย่าง และทำการฝึกและทดสอบ 4 รอบ ดังนี้
เช่น ความคลาดเคลื่อนเฉลี่ยกำลังสอง (MSE) อาจเป็นเมตริกที่มีความหมายมากที่สุดสำหรับโมเดลการถดถอยเชิงเส้น ดังนั้น คุณ จึงควรหาค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของ MSE ในทั้ง 4 รอบ
k-means
อัลกอริทึมการจัดกลุ่มยอดนิยมที่จัดกลุ่มตัวอย่าง ในการเรียนรู้แบบไม่มีการควบคุมดูแล โดยพื้นฐานแล้ว อัลกอริทึม K-means จะทำสิ่งต่อไปนี้
- กำหนดจุดศูนย์กลาง k ที่ดีที่สุดซ้ำๆ (เรียกว่าเซนทรอยด์)
- กำหนดตัวอย่างแต่ละรายการไปยังเซนทรอยด์ที่ใกล้ที่สุด ตัวอย่างที่อยู่ใกล้ จุดศูนย์กลางเดียวกันจะอยู่ในกลุ่มเดียวกัน
อัลกอริทึม k-means จะเลือกตำแหน่งจุดศูนย์กลางเพื่อลดกำลังสองสะสมของระยะทางจากแต่ละตัวอย่างไปยังจุดศูนย์กลางที่ใกล้ที่สุด
ตัวอย่างเช่น ลองดูแผนภาพความสูงของสุนัขเทียบกับความกว้างของสุนัขต่อไปนี้

หาก k=3 อัลกอริทึม K-means จะกำหนดจุดศูนย์กลาง 3 จุด ระบบจะกำหนดตัวอย่างแต่ละรายการ ให้กับจุดศูนย์กลางที่ใกล้ที่สุด ทำให้เกิด 3 กลุ่ม ดังนี้

สมมติว่าผู้ผลิตต้องการกำหนดขนาดที่เหมาะสมที่สุดสำหรับเสื้อสเวตเตอร์ขนาดเล็ก กลาง และใหญ่สำหรับสุนัข เซนทรอยด์ทั้ง 3 ระบุความสูงเฉลี่ยและความกว้างเฉลี่ยของสุนัขแต่ละตัวในคลัสเตอร์นั้น ดังนั้น ผู้ผลิต ควรใช้จุดศูนย์กลางทั้ง 3 จุดนี้เป็นพื้นฐานในการกำหนดขนาดเสื้อสเวตเตอร์ โปรดทราบว่า โดยทั่วไปแล้ว เซนทรอยด์ของคลัสเตอร์ไม่ใช่ตัวอย่างในคลัสเตอร์
ภาพประกอบก่อนหน้าแสดง K-Means สำหรับตัวอย่างที่มีฟีเจอร์เพียง 2 รายการ (ความสูงและความกว้าง) โปรดทราบว่า K-Means สามารถจัดกลุ่มตัวอย่าง ในฟีเจอร์ต่างๆ ได้
ดูข้อมูลเพิ่มเติมได้ที่การจัดกลุ่ม K-means คืออะไร ในหลักสูตรการจัดกลุ่ม
k-median
อัลกอริทึมการจัดกลุ่มที่เกี่ยวข้องอย่างใกล้ชิดกับ k-means ความแตกต่างในทางปฏิบัติระหว่างทั้ง 2 อย่างมีดังนี้
- ใน K-Means เซนทรอยด์จะกำหนดโดยการลดผลรวมของกำลังสองของระยะห่างระหว่างเซนทรอยด์ที่เป็นไปได้กับแต่ละตัวอย่าง
- ใน k-median จะกำหนดจุดศูนย์กลางโดยการลดผลรวมของ ระยะห่างระหว่างจุดศูนย์กลางที่เป็นไปได้กับตัวอย่างแต่ละรายการ
โปรดทราบว่าคำจำกัดความของระยะทางก็แตกต่างกันด้วย
- K-means อาศัยระยะทางแบบยุคลิดจาก จุดศูนย์กลางไปยังตัวอย่าง (ใน 2 มิติ ระยะทางแบบยุคลิดหมายถึงการใช้ทฤษฎีบทพีทาโกรัสเพื่อคำนวณด้านตรงข้ามมุมฉาก) ตัวอย่างเช่น ระยะทาง k-means ระหว่าง (2,2) กับ (5,-2) จะเป็นดังนี้
- k-median อาศัย ระยะทางแมนฮัตตัน จากจุดศูนย์กลางไปยังตัวอย่าง ระยะทางนี้คือผลรวมของ เดลต้าสัมบูรณ์ในแต่ละมิติ ตัวอย่างเช่น ระยะทาง k-มัธยฐาน ระหว่าง (2,2) กับ (5,-2) จะเป็นดังนี้
L
Regularization แบบ L0
การทำให้เป็นปกติประเภทหนึ่งที่ ลงโทษจำนวนทั้งหมดของน้ำหนักที่ไม่ใช่ศูนย์ ในโมเดล เช่น โมเดลที่มีน้ำหนักที่ไม่ใช่ 0 จำนวน 11 รายการ จะถูกลงโทษมากกว่าโมเดลที่คล้ายกันซึ่งมีน้ำหนักที่ไม่ใช่ 0 จำนวน 10 รายการ
บางครั้งเราเรียก Regularization แบบ L0 ว่า Regularization แบบ L0-norm
แพ้ 1 นัด
ฟังก์ชันการสูญเสียที่คำนวณค่าสัมบูรณ์ ของความแตกต่างระหว่างค่าป้ายกำกับจริงกับ ค่าที่โมเดลคาดการณ์ ตัวอย่างเช่น ต่อไปนี้คือการคำนวณการสูญเสีย L1 สำหรับกลุ่มตัวอย่าง 5 รายการ
| มูลค่าที่แท้จริงของตัวอย่าง | ค่าที่โมเดลคาดการณ์ | ค่าสัมบูรณ์ของเดลต้า |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 3 |
| 4 | 6 | 2 |
| 9 | 8 | 1 |
| 8 = การสูญเสีย L1 | ||
การสูญเสีย L1 มีความไวต่อค่าผิดปกติน้อยกว่าการสูญเสีย L2
ค่าเฉลี่ยความผิดพลาดสัมบูรณ์คือค่าเฉลี่ยของ L1 loss ต่อตัวอย่าง
ดูข้อมูลเพิ่มเติมได้ที่ การถดถอยเชิงเส้น: การสูญเสีย ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
Regularization แบบ L1
การทำให้เป็นปกติประเภทหนึ่งที่ลงโทษน้ำหนักตามสัดส่วนของผลรวมค่าสัมบูรณ์ของน้ำหนัก การปรับค่า L1 ช่วยให้ค่าถ่วงน้ำหนักของฟีเจอร์ที่ไม่เกี่ยวข้อง หรือแทบไม่เกี่ยวข้องกลายเป็น0 อย่างแน่นอน ฟีเจอร์ที่มีน้ำหนักเป็น 0 จะถูกนำออกจากโมเดล
เปรียบเทียบกับ L2 Regularization
การสูญเสีย L2
ฟังก์ชันการสูญเสียที่คำนวณกำลังสองของความแตกต่างระหว่างค่าป้ายกำกับจริงกับค่าที่โมเดลคาดการณ์ ตัวอย่างเช่น ต่อไปนี้คือการคำนวณการสูญเสีย L2 สำหรับกลุ่มของตัวอย่าง 5 รายการ
| มูลค่าที่แท้จริงของตัวอย่าง | ค่าที่โมเดลคาดการณ์ | กำลังสองของเดลต้า |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 9 |
| 4 | 6 | 4 |
| 9 | 8 | 1 |
| 16 = L2 loss | ||
เนื่องจากการยกกำลังสอง การสูญเสีย L2 จึงขยายอิทธิพลของค่าผิดปกติ กล่าวคือ การสูญเสีย L2 จะตอบสนองต่อการคาดการณ์ที่ไม่ดีมากกว่าการสูญเสีย L1 เช่น การสูญเสีย L1 สำหรับกลุ่มก่อนหน้าจะเป็น 8 แทนที่จะเป็น 16 โปรดสังเกตว่าบัญชีที่ผิดปกติเพียงบัญชีเดียว คิดเป็น 9 จาก 16 รายการ
โมเดลการถดถอยมักใช้ Loss L2 เป็น Loss Function
ความคลาดเคลื่อนเฉลี่ยกำลังสองคือการสูญเสีย L2 โดยเฉลี่ยต่อตัวอย่าง Squared loss เป็นอีกชื่อหนึ่งของ L2 loss
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยโลจิสติก: การสูญเสียและ การทำให้เป็นปกติ ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
Regularization แบบ L2
การทำให้เป็นปกติประเภทหนึ่งที่ลงโทษน้ำหนักตามสัดส่วนของผลยกกำลังสองของน้ำหนัก การปรับค่า L2 ช่วยให้ค่าถ่วงน้ำหนักค่าผิดปกติ (ค่าที่มีค่าบวกสูงหรือค่าลบต่ำ) เข้าใกล้ 0 มากขึ้น แต่ไม่ถึง 0 ฟีเจอร์ที่มีค่าใกล้ 0 มากจะยังคงอยู่ในโมเดล แต่จะไม่ส่งผลต่อการคาดการณ์ของโมเดลมากนัก
การปรับค่า L2 จะปรับปรุงการสรุปในโมเดลเชิงเส้นเสมอ
เปรียบเทียบกับ L1 Regularization
ดูข้อมูลเพิ่มเติมได้ที่การปรับมากเกินไป: การทำให้เป็นปกติ L2 ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ป้ายกำกับ
ในแมชชีนเลิร์นนิงที่มีการควบคุมดูแล ส่วน "คำตอบ" หรือ "ผลลัพธ์" ของตัวอย่าง
ตัวอย่างที่ติดป้ายกำกับแต่ละรายการประกอบด้วยฟีเจอร์อย่างน้อย 1 รายการและป้ายกำกับ ตัวอย่างเช่น ในชุดข้อมูลการตรวจหาสแปม ป้ายกำกับอาจเป็น "สแปม" หรือ "ไม่ใช่สแปม" ในชุดข้อมูลปริมาณน้ำฝน ป้ายกำกับอาจเป็นปริมาณ น้ำฝนที่ตกลงมาในช่วงเวลาหนึ่ง
ดูข้อมูลเพิ่มเติมได้ที่การเรียนรู้แบบมีผู้ดูแล ในข้อมูลเบื้องต้นเกี่ยวกับแมชชีนเลิร์นนิง
ตัวอย่างที่มีป้ายกำกับ
ตัวอย่างที่มีฟีเจอร์อย่างน้อย 1 รายการและป้ายกำกับ ตัวอย่างเช่น ตารางต่อไปนี้แสดงตัวอย่างที่ติดป้ายกำกับ 3 รายการจากโมเดลการประเมินบ้าน โดยแต่ละรายการมีฟีเจอร์ 3 รายการและป้ายกำกับ 1 รายการ
| จำนวนห้องนอน | จำนวนห้องน้ำ | อายุของบ้าน | ราคาบ้าน (ป้ายกำกับ) |
|---|---|---|---|
| 3 | 2 | 15 | $345,000 |
| 2 | 1 | 72 | $179,000 |
| 4 | 2 | 34 | $392,000 |
ในแมชชีนเลิร์นนิงที่มีการควบคุมดูแล โมเดลจะฝึกกับตัวอย่างที่ติดป้ายกำกับและทำการคาดการณ์กับ ตัวอย่างที่ไม่มีป้ายกำกับ
เปรียบเทียบตัวอย่างที่มีป้ายกำกับกับตัวอย่างที่ไม่มีป้ายกำกับ
ดูข้อมูลเพิ่มเติมได้ที่การเรียนรู้แบบมีผู้ดูแล ในข้อมูลเบื้องต้นเกี่ยวกับแมชชีนเลิร์นนิง
การรั่วไหลของป้ายกำกับ
ข้อบกพร่องในการออกแบบโมเดลที่ฟีเจอร์เป็นพร็อกซีสำหรับป้ายกำกับ ตัวอย่างเช่น ลองพิจารณารูปแบบการจัดประเภทแบบไบนารีที่คาดการณ์ว่า
ผู้มีโอกาสเป็นลูกค้าจะซื้อผลิตภัณฑ์หนึ่งๆ หรือไม่
สมมติว่าฟีเจอร์หนึ่งของโมเดลเป็นบูลีนชื่อ
SpokeToCustomerAgent สมมติว่าระบบจะมอบหมายตัวแทนลูกค้าหลังจากผู้มีโอกาสเป็นลูกค้าซื้อผลิตภัณฑ์จริงแล้วเท่านั้น ในระหว่างการฝึก โมเดลจะเรียนรู้ความสัมพันธ์
ระหว่าง SpokeToCustomerAgent กับป้ายกำกับอย่างรวดเร็ว
ดูข้อมูลเพิ่มเติมได้ที่การตรวจสอบ ไปป์ไลน์ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
lambda
คำพ้องความหมายของอัตราการปรับ
Lambda เป็นคำที่มีการใช้งานมากเกินไป ในที่นี้เราจะมุ่งเน้นที่คำจำกัดความของคำว่า ภายในการทำให้เป็นปกติ
LaMDA (โมเดลภาษาสำหรับแอปพลิเคชันด้านการโต้ตอบ หรือ Language Model for Dialogue Applications)
โมเดลภาษาขนาดใหญ่ที่อิงตามTransformer พัฒนาโดย Google ซึ่งได้รับการฝึกด้วย ชุดข้อมูลการสนทนาขนาดใหญ่ที่สร้างคำตอบที่สมจริงได้
LaMDA: เทคโนโลยีการสนทนา ที่ก้าวล้ำของเราจะให้ภาพรวม
จุดสังเกต
คำพ้องความหมายของประเด็นสำคัญ
โมเดลภาษา
โมเดลที่ประมาณความน่าจะเป็นของโทเค็น หรือลำดับของโทเค็นที่เกิดขึ้นในลำดับโทเค็นที่ยาวขึ้น
ดูข้อมูลเพิ่มเติมได้ที่โมเดลภาษาคืออะไร ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
โมเดลภาษาขนาดใหญ่
อย่างน้อยที่สุดคือโมเดลภาษาที่มีพารามิเตอร์จำนวนมาก หรือจะพูดอย่างไม่เป็นทางการก็ได้ว่าโมเดลภาษาที่อิงตามTransformer เช่น Gemini หรือ GPT
ดูข้อมูลเพิ่มเติมได้ที่โมเดลภาษาขนาดใหญ่ (LLM) ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
เวลาในการตอบสนอง
เวลาที่โมเดลใช้ในการประมวลผลอินพุตและสร้างคำตอบ การตอบสนองที่มีเวลาในการตอบสนองสูงจะใช้เวลาในการสร้างนานกว่าการตอบสนองที่มีเวลาในการตอบสนองต่ำ
ปัจจัยที่มีผลต่อเวลาในการตอบสนองของโมเดลภาษาขนาดใหญ่ ได้แก่
- ความยาวของโทเค็นอินพุตและเอาต์พุต [token]
- ความซับซ้อนของโมเดล
- โครงสร้างพื้นฐานที่โมเดลทำงานอยู่
การเพิ่มประสิทธิภาพเพื่อลดเวลาในการตอบสนองเป็นสิ่งสำคัญในการสร้างแอปพลิเคชันที่ตอบสนองได้ดีและเป็นมิตรต่อผู้ใช้
พื้นที่แฝง
คำพ้องความหมายของพื้นที่การฝัง
เลเยอร์
ชุดนิวรอนในโครงข่ายระบบประสาทเทียม เลเยอร์ 3 ประเภทที่ใช้กันทั่วไป มีดังนี้
- เลเยอร์อินพุต ซึ่งให้ค่าสำหรับฟีเจอร์ทั้งหมด
- เลเยอร์ที่ซ่อนอย่างน้อย 1 เลเยอร์ ซึ่งจะค้นหา ความสัมพันธ์แบบไม่เชิงเส้นระหว่างฟีเจอร์กับป้ายกำกับ
- เลเยอร์เอาต์พุตซึ่งให้การคาดการณ์
ตัวอย่างเช่น ภาพต่อไปนี้แสดงโครงข่ายประสาทเทียมที่มีเลเยอร์อินพุต 1 เลเยอร์ เลเยอร์ที่ซ่อน 2 เลเยอร์ และเลเยอร์เอาต์พุต 1 เลเยอร์
ใน TensorFlow เลเยอร์ยังเป็นฟังก์ชัน Python ที่รับ Tensor และตัวเลือกการกำหนดค่าเป็นอินพุต และ สร้าง Tensor อื่นๆ เป็นเอาต์พุต
Layers API (tf.layers)
TensorFlow API สำหรับสร้างดีปนิวรัลเน็ตเวิร์ก เป็นองค์ประกอบของเลเยอร์ Layers API ช่วยให้คุณสร้างเลเยอร์ประเภทต่างๆ เช่น
tf.layers.Denseสำหรับเลเยอร์ที่เชื่อมต่ออย่างเต็มรูปแบบtf.layers.Conv2Dสำหรับเลเยอร์ Convolutional
Layers API เป็นไปตามรูปแบบ API ของเลเยอร์ Keras กล่าวคือ นอกเหนือจากคำนำหน้าที่แตกต่างกัน ฟังก์ชันทั้งหมดใน Layers API มีชื่อและลายเซ็นเหมือนกับฟังก์ชันที่เทียบเท่าใน Keras layers API
ใบไม้
แผนผังการตัดสินใจ เงื่อนไขต่างจากลีฟตรงที่ลีฟไม่ได้ทำการทดสอบ แต่ใบไม้คือการคาดการณ์ที่เป็นไปได้ ใบไม้ยังเป็นโหนดสุดท้ายของเส้นทางการอนุมานด้วย
ตัวอย่างเช่น แผนผังการตัดสินใจต่อไปนี้มี 3 ใบ
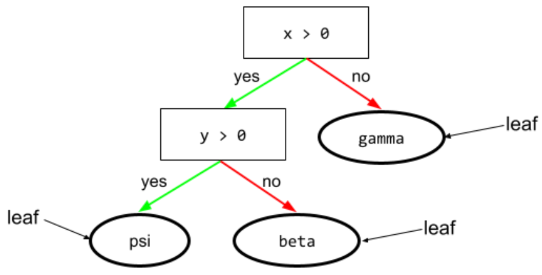
ดูข้อมูลเพิ่มเติมได้ที่แผนผังการตัดสินใจ ในหลักสูตร Decision Forests
เครื่องมือความสามารถในการตีความการเรียนรู้ (LIT)
เครื่องมือแบบภาพและแบบอินเทอร์แอกทีฟสำหรับทำความเข้าใจโมเดลและการแสดงข้อมูลด้วยภาพ
คุณสามารถใช้ LIT แบบโอเพนซอร์สเพื่อ ตีความโมเดล หรือเพื่อแสดงภาพข้อความ รูปภาพ และ ข้อมูลตารางได้
อัตราการเรียนรู้
จำนวนทศนิยมที่บอกอัลกอริทึมการไล่ระดับสี ว่าควรปรับน้ำหนักและอคติในแต่ละการทำซ้ำมากน้อยเพียงใด ตัวอย่างเช่น อัตราการเรียนรู้ที่ 0.3 จะปรับน้ำหนักและอคติได้แรงกว่าอัตราการเรียนรู้ที่ 0.1 ถึง 3 เท่า
อัตราการเรียนรู้เป็นไฮเปอร์พารามิเตอร์ที่สำคัญ หากตั้งค่า อัตราการเรียนรู้ต่ำเกินไป การฝึกจะใช้เวลานานเกินไป หาก คุณตั้งค่าอัตราการเรียนรู้สูงเกินไป การไล่ระดับการไล่ระดับมักมีปัญหาในการ เข้าถึงการบรรจบกัน
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยเชิงเส้น: ไฮเปอร์พารามิเตอร์ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การถดถอยแบบกำลังสองน้อยที่สุด
โมเดลการถดถอยเชิงเส้นที่ฝึกโดยการลด การสูญเสีย L
ระยะทางเลเวนชไตน์
เมตริกระยะทางในการแก้ไขที่คำนวณการดำเนินการลบ แทรก และแทนที่ที่น้อยที่สุดซึ่งจำเป็นต่อการเปลี่ยนคำหนึ่งเป็นอีกคำหนึ่ง ตัวอย่างเช่น ระยะทางเลเวนชไตน์ระหว่างคำว่า "heart" กับ "darts" คือ 3 เนื่องจากมีการแก้ไข 3 รายการต่อไปนี้ ซึ่งเป็นการเปลี่ยนแปลงที่น้อยที่สุดในการเปลี่ยน คำหนึ่งเป็นอีกคำหนึ่ง
- heart → deart (แทนที่ "h" ด้วย "d")
- deart → dart (ลบ "e")
- dart → darts (แทรก "s")
โปรดทราบว่าลำดับก่อนหน้าไม่ใช่เส้นทางการแก้ไข 3 รายการเพียงเส้นทางเดียว
เชิงเส้น
ความสัมพันธ์ระหว่างตัวแปรตั้งแต่ 2 ตัวขึ้นไปซึ่งแสดงได้โดยการบวกและการคูณเท่านั้น
พล็อตของความสัมพันธ์เชิงเส้นคือเส้นตรง
แตกต่างจากไม่ปรากฏร่วมกับเนื้อหา
รูปแบบเชิงเส้น
โมเดลที่กำหนดน้ำหนัก 1 รายการต่อฟีเจอร์เพื่อทำการคาดการณ์ (โมเดลเชิงเส้นยังรวมอคติด้วย) ในทางตรงกันข้าม ความสัมพันธ์ของฟีเจอร์กับการคาดการณ์ในโมเดลแบบลึก โดยทั่วไปแล้วจะไม่เป็นเชิงเส้น
โดยปกติแล้ว โมเดลเชิงเส้นจะฝึกได้ง่ายกว่าและตีความได้มากกว่าโมเดลเชิงลึก อย่างไรก็ตาม โมเดลเชิงลึกสามารถเรียนรู้ความสัมพันธ์ที่ซับซ้อนระหว่างฟีเจอร์ต่างๆ ได้
การถดถอยเชิงเส้นและ การถดถอยโลจิสติกเป็นโมเดลเชิงเส้น 2 ประเภท
การถดถอยเชิงเส้น
โมเดลแมชชีนเลิร์นนิงประเภทหนึ่งซึ่งมีลักษณะดังต่อไปนี้
- โมเดลนี้เป็นโมเดลเชิงเส้น
- การคาดการณ์เป็นค่าทศนิยม (นี่คือส่วนการถดถอยของการถดถอยเชิงเส้น)
เปรียบเทียบการถดถอยเชิงเส้นกับการถดถอยแบบโลจิสติก นอกจากนี้ ให้เปรียบเทียบการถดถอยกับการจัดประเภทด้วย
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยเชิงเส้น ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
LIT
ตัวย่อของ เครื่องมือการตีความการเรียนรู้ (LIT) ซึ่งก่อนหน้านี้เรียกว่าเครื่องมือการตีความภาษา
LLM
ตัวย่อของโมเดลภาษาขนาดใหญ่
การประเมิน LLM (Evals)
ชุดเมตริกและการเปรียบเทียบสำหรับประเมินประสิทธิภาพของโมเดลภาษาขนาดใหญ่ (LLM) การประเมิน LLM ในระดับสูงมีดังนี้
- ช่วยนักวิจัยระบุจุดที่ LLM ต้องปรับปรุง
- มีประโยชน์ในการเปรียบเทียบ LLM ต่างๆ และระบุ LLM ที่ดีที่สุดสำหรับงานหนึ่งๆ
- ช่วยให้มั่นใจว่า LLM จะปลอดภัยและมีจริยธรรมในการใช้งาน
ดูข้อมูลเพิ่มเติมได้ที่โมเดลภาษาขนาดใหญ่ (LLM) ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การถดถอยแบบโลจิสติก
โมเดลการถดถอยประเภทหนึ่งที่คาดการณ์ความน่าจะเป็น โมเดลการถดถอยลอจิสติกมีลักษณะดังนี้
- ป้ายกำกับเป็นหมวดหมู่ โดยปกติแล้วคำว่าการถดถอยโลจิสติกจะหมายถึงการถดถอยโลจิสติกแบบไบนารี ซึ่งก็คือ โมเดลที่คำนวณความน่าจะเป็นสำหรับป้ายกำกับที่มีค่าที่เป็นไปได้ 2 ค่า การถดถอยโลจิสติกแบบมัลติโนเมียล ซึ่งเป็นรูปแบบที่พบได้น้อยกว่า จะคำนวณ ความน่าจะเป็นสำหรับป้ายกำกับที่มีค่าที่เป็นไปได้มากกว่า 2 ค่า
- ฟังก์ชันการสูญเสียระหว่างการฝึกคือLog Loss (วางหน่วย Log Loss หลายหน่วยแบบขนานกันสําหรับป้ายกํากับที่มีค่าที่เป็นไปได้มากกว่า 2 ค่าได้)
- โมเดลมีสถาปัตยกรรมเชิงเส้น ไม่ใช่โครงข่ายประสาทเทียมแบบลึก อย่างไรก็ตาม คําจํากัดความที่เหลือนี้ยังใช้กับโมเดลเชิงลึกที่คาดการณ์ความน่าจะเป็น สําหรับป้ายกํากับเชิงหมวดหมู่ด้วย
ตัวอย่างเช่น พิจารณาโมเดลการถดถอยโลจิสติกที่คำนวณ ความน่าจะเป็นของอีเมลขาเข้าว่าเป็นสแปมหรือไม่ ในระหว่างการอนุมาน สมมติว่าโมเดลคาดการณ์ 0.72 ดังนั้น โมเดลจึงประมาณค่าต่อไปนี้
- มีโอกาส 72% ที่อีเมลจะเป็นจดหมายขยะ
- มีโอกาส 28% ที่อีเมลจะไม่ใช่จดหมายขยะ
โมเดลการถดถอยโลจิสติกใช้สถาปัตยกรรม 2 ขั้นตอนต่อไปนี้
- โมเดลสร้างการคาดการณ์ดิบ (y') โดยใช้ฟังก์ชันเชิงเส้น ของฟีเจอร์อินพุต
- โมเดลใช้การคาดการณ์ดิบดังกล่าวเป็นอินพุตสำหรับฟังก์ชันซิกมอยด์ ซึ่งจะแปลงการคาดการณ์ดิบเป็นค่าระหว่าง 0 ถึง 1 โดยไม่รวม 0 และ 1
โมเดลการถดถอยแบบโลจิสติกคาดการณ์ตัวเลขเช่นเดียวกับโมเดลการถดถอยอื่นๆ อย่างไรก็ตาม โดยปกติแล้วตัวเลขนี้จะกลายเป็นส่วนหนึ่งของโมเดลการจัดประเภทแบบไบนารี ดังนี้
- หากตัวเลขที่คาดการณ์มากกว่า เกณฑ์การจัดประเภท โมเดลการจัดประเภทแบบไบนารีจะคาดการณ์คลาสที่เป็นบวก
- หากตัวเลขที่คาดการณ์น้อยกว่าเกณฑ์การจัดประเภท โมเดลการจัดประเภทแบบไบนารีจะคาดการณ์คลาสเชิงลบ
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยโลจิสติก ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ลอจิท
เวกเตอร์ของการคาดการณ์ดิบ (ไม่ได้รับการทำให้เป็นมาตรฐาน) ที่โมเดลการจัดประเภท สร้างขึ้น ซึ่งโดยปกติแล้วจะส่งไปยังฟังก์ชันการทำให้เป็นมาตรฐาน หากโมเดลกำลังแก้ปัญหาการแยกประเภทหลายคลาส โดยทั่วไปแล้ว ลอจิทจะกลายเป็นอินพุตของฟังก์ชัน ซอฟต์แม็กซ์ จากนั้นฟังก์ชัน Softmax จะสร้างเวกเตอร์ของความน่าจะเป็น (ที่ทำให้เป็นมาตรฐานแล้ว) โดยมีค่า 1 ค่าสำหรับแต่ละคลาสที่เป็นไปได้
การสูญเสียของบันทึก
Loss Function ที่ใช้ในการถดถอยโลจิสติกแบบไบนารี
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยโลจิสติก: การสูญเสียและการทำให้เป็นปกติ ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
ล็อกออดส์
ลอการิทึมของอัตราต่อรองของเหตุการณ์หนึ่งๆ
หน่วยความจำระยะยาวแบบสั้น (LSTM)
ประเภทของเซลล์ในเครือข่ายประสาทแบบเกิดซ้ำที่ใช้ในการประมวลผลลำดับข้อมูลในแอปพลิเคชันต่างๆ เช่น การจดจำลายมือ การแปลด้วยเครื่อง และการสร้างคำบรรยายภาพ LSTM แก้ปัญหาการไล่ระดับสีที่หายไปซึ่ง เกิดขึ้นเมื่อฝึก RNN เนื่องจากลำดับข้อมูลที่ยาวโดยการเก็บประวัติไว้ใน สถานะหน่วยความจำภายในตามอินพุตใหม่และบริบทจากเซลล์ก่อนหน้าใน RNN
LoRA
คำย่อของ Low-Rank Adaptability
แพ้
ในระหว่างการฝึกโมเดลภายใต้การควบคุม จะมีการวัดว่าการคาดการณ์ของโมเดลอยู่ห่างจากป้ายกำกับของโมเดลมากน้อยเพียงใด
ฟังก์ชันการสูญเสียจะคำนวณการสูญเสีย
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยเชิงเส้น: การสูญเสีย ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
ผู้รวบรวมข้อมูลการสูญเสีย
อัลกอริทึมแมชชีนเลิร์นนิงประเภทหนึ่งที่ ปรับปรุงประสิทธิภาพของโมเดล โดยการรวมการคาดการณ์ของโมเดลหลายรายการและ ใช้การคาดการณ์เหล่านั้นเพื่อทำการคาดการณ์รายการเดียว ด้วยเหตุนี้ เครื่องมือรวบรวมการสูญเสียจึงช่วยลดความแปรปรวนของการคาดการณ์และ ปรับปรุงความแม่นยำของการคาดการณ์ได้
เส้นโค้งการสูญเสีย
พล็อตของการสูญเสียเป็นฟังก์ชันของจำนวนการทำซ้ำในการฝึก พล็อตต่อไปนี้แสดงเส้นโค้งการสูญเสียทั่วไป
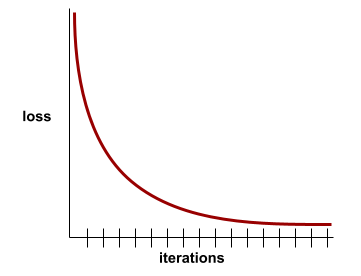
เส้นโค้งการสูญเสียช่วยให้คุณพิจารณาได้ว่าโมเดลบรรจบหรือฟิตมากเกินไปเมื่อใด
เส้นโค้งการสูญเสียสามารถพล็อตการสูญเสียประเภทต่อไปนี้ทั้งหมด
ดูเส้นโค้งการสรุปด้วย
ดูข้อมูลเพิ่มเติมได้ที่การปรับมากเกินไป: การตีความเส้นโค้งการสูญเสีย ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
ฟังก์ชันการสูญเสีย
ในระหว่างการฝึกหรือการทดสอบ ฟังก์ชันทางคณิตศาสตร์ที่คำนวณ การสูญเสียในกลุ่มตัวอย่าง ฟังก์ชันการสูญเสียจะส่งคืนการสูญเสียที่ต่ำกว่า สำหรับโมเดลที่ทำการคาดการณ์ได้ดีกว่าโมเดลที่ทำการคาดการณ์ได้ไม่ดี
โดยปกติแล้วเป้าหมายของการฝึกคือการลดการสูญเสียที่ฟังก์ชันการสูญเสีย ส่งคืน
ฟังก์ชันการสูญเสียมีอยู่หลายประเภท เลือกฟังก์ชันการสูญเสียที่เหมาะสม สำหรับโมเดลประเภทที่คุณกำลังสร้าง เช่น
- การสูญเสีย L2 (หรือข้อผิดพลาดกำลังสองเฉลี่ย) คือฟังก์ชันการสูญเสียสำหรับการถดถอยเชิงเส้น
- Log Loss คือฟังก์ชันการสูญเสียสำหรับ การถดถอยโลจิสติก
พื้นผิวการสูญเสีย
กราฟของน้ำหนักเทียบกับความสูญเสีย การไล่ระดับความชันมีเป้าหมาย เพื่อค้นหาน้ำหนักที่พื้นผิวการสูญเสียอยู่ที่ค่าต่ำสุดในพื้นที่
เอฟเฟกต์หลงทางกลาง
แนวโน้มของ LLM ในการใช้ข้อมูลจากจุดเริ่มต้นและจุดสิ้นสุดของหน้าต่างบริบทที่ยาวนานอย่างมีประสิทธิภาพมากกว่าข้อมูลจากตรงกลาง กล่าวคือ เมื่อมีบริบทที่ยาว เอฟเฟกต์ "หลงทางตรงกลาง" จะทำให้ความแม่นยำเป็นดังนี้
- ค่อนข้างสูงเมื่อข้อมูลที่เกี่ยวข้องในการสร้างคำตอบอยู่ใกล้จุดเริ่มต้นหรือจุดสิ้นสุดของบริบท
- ค่อนข้างต่ำ เมื่อข้อมูลที่เกี่ยวข้องในการสร้างคำตอบอยู่ตรงกลางของบริบท
คำนี้มาจากบทความLost in the Middle: How Language Models Use Long Contexts
การปรับตัวแบบ Low-Rank (LoRA)
เทคนิคประหยัดพารามิเตอร์สำหรับ การปรับแต่งที่ "ตรึง" น้ำหนักที่ฝึกไว้ล่วงหน้าของโมเดล (เพื่อให้แก้ไขไม่ได้อีกต่อไป) แล้วแทรกชุดน้ำหนักที่ฝึกได้ขนาดเล็ก ลงในโมเดล ชุดน้ำหนักที่ฝึกได้นี้ (หรือที่เรียกว่า "เมทริกซ์การอัปเดต") มีขนาดเล็กกว่าโมเดลพื้นฐานอย่างมาก จึงฝึกได้เร็วกว่ามาก
LoRA มีประโยชน์ดังนี้
- ปรับปรุงคุณภาพการคาดการณ์ของโมเดลสำหรับโดเมนที่มีการปรับแต่ง
- ปรับแต่งได้เร็วกว่าเทคนิคที่ต้องปรับแต่งพารามิเตอร์ทั้งหมดของโมเดล
- ลดต้นทุนการคำนวณของการอนุมานโดยการเปิดใช้ การแสดงผลพร้อมกันของโมเดลเฉพาะทางหลายรายการที่ใช้โมเดลพื้นฐานเดียวกัน
LSTM
ตัวย่อของ Long Short-Term Memory
M
แมชชีนเลิร์นนิง
โปรแกรมหรือระบบที่ฝึกโมเดลจากข้อมูลที่ป้อน โมเดลที่ฝึกแล้วสามารถ ทําการคาดการณ์ที่เป็นประโยชน์จากข้อมูลใหม่ (ไม่เคยเห็นมาก่อน) ซึ่งดึงมาจาก การกระจายเดียวกันกับที่ใช้ฝึกโมเดล
แมชชีนเลิร์นนิงยังหมายถึงสาขาวิชาที่เกี่ยวข้องกับโปรแกรมหรือระบบเหล่านี้ด้วย
ดูข้อมูลเพิ่มเติมได้ที่หลักสูตรข้อมูลเบื้องต้นเกี่ยวกับแมชชีนเลิร์นนิง
การแปลด้วยคอมพิวเตอร์
การใช้ซอฟต์แวร์ (โดยปกติคือโมเดลแมชชีนเลิร์นนิง) เพื่อแปลงข้อความจาก ภาษาหนึ่งของมนุษย์เป็นอีกภาษาหนึ่งของมนุษย์ เช่น จากอังกฤษเป็น ญี่ปุ่น
คลาสส่วนใหญ่
ป้ายกำกับที่พบบ่อยกว่าในชุดข้อมูลที่มีความไม่สมดุลของคลาส ตัวอย่างเช่น หากชุดข้อมูลมีป้ายกำกับเชิงลบ 99% และป้ายกำกับเชิงบวก 1% ป้ายกำกับเชิงลบจะเป็นคลาสส่วนใหญ่
เปรียบเทียบกับคลาสส่วนน้อย
ดูข้อมูลเพิ่มเติมได้ที่ชุดข้อมูล: ชุดข้อมูลที่ไม่สมดุล ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
กระบวนการตัดสินใจแบบมาร์คอฟ (MDP)
กราฟที่แสดงรูปแบบการตัดสินใจซึ่งมีการตัดสินใจ (หรือการดำเนินการ) เพื่อไปยังลำดับของสถานะภายใต้สมมติฐานว่าคุณสมบัติมาร์คอฟเป็นจริง ในการเรียนรู้แบบเสริมกำลัง การเปลี่ยนสถานะเหล่านี้ จะแสดงผลรางวัลที่เป็นตัวเลข
คุณสมบัติมาร์คอฟ
คุณสมบัติของสภาพแวดล้อมบางอย่าง ซึ่งการเปลี่ยนสถานะ จะกำหนดโดยข้อมูลที่อยู่ในสถานะปัจจุบันและการดำเนินการของเอเจนต์
โมเดลภาษาที่ปิดบัง
โมเดลภาษาที่คาดการณ์ความน่าจะเป็นของ โทเค็นผู้สมัครเพื่อเติมช่องว่างในลำดับ ตัวอย่างเช่น โมเดลภาษาที่มาสก์สามารถคำนวณความน่าจะเป็นของคำที่ต้องการ เพื่อแทนที่ขีดเส้นใต้ในประโยคต่อไปนี้ได้
____ ในหมวกกลับมาแล้ว
โดยปกติแล้ว เอกสารจะใช้สตริง "MASK" แทนขีดล่าง เช่น
"MASK" ในหมวกกลับมาแล้ว
โมเดลภาษาที่มาสก์สมัยใหม่ส่วนใหญ่เป็นแบบสองทิศทาง
matplotlib
ไลบรารีการพล็อต 2 มิติของ Python แบบโอเพนซอร์ส matplotlib ช่วยให้คุณแสดงภาพ แง่มุมต่างๆ ของแมชชีนเลิร์นนิงได้
การแยกตัวประกอบเมทริกซ์
ในคณิตศาสตร์ กลไกในการค้นหาเมทริกซ์ที่มีผลคูณจุดประมาณเมทริกซ์เป้าหมาย
ในระบบการแนะนำ เมทริกซ์เป้าหมาย มักจะมีการให้คะแนนของผู้ใช้เกี่ยวกับรายการ ตัวอย่างเช่น เมทริกซ์เป้าหมาย สำหรับระบบแนะนำภาพยนตร์อาจมีลักษณะดัง ต่อไปนี้ โดยจำนวนเต็มบวกคือคะแนนที่ผู้ใช้ให้ และ 0 หมายความว่าผู้ใช้ไม่ได้ให้คะแนนภาพยนตร์
| คาสซาบลางกา | The Philadelphia Story | แบล็ค แพนเธอร์ (Black Panther) | Wonder Woman | Pulp Fiction | |
|---|---|---|---|---|---|
| ผู้ใช้ 1 | 5.0 | 3.0 | 0.0 | 2.0 | 0.0 |
| ผู้ใช้ 2 | 4.0 | 0.0 | 0.0 | 1.0 | 5.0 |
| ผู้ใช้ 3 | 3.0 | 1.0 | 4.0 | 5.0 | 0.0 |
ระบบแนะนำภาพยนตร์มีเป้าหมายเพื่อคาดการณ์คะแนนของผู้ใช้สำหรับภาพยนตร์ที่ยังไม่ได้รับการจัดประเภท เช่น ผู้ใช้ 1 จะชอบ Black Panther ไหม
แนวทางหนึ่งสำหรับระบบการแนะนำคือการใช้การแยกตัวประกอบเมทริกซ์ เพื่อสร้างเมทริกซ์ 2 รายการต่อไปนี้
- เมทริกซ์ผู้ใช้ในรูปแบบจํานวนผู้ใช้ X จํานวนมิติข้อมูลการฝัง
- เมทริกซ์รายการ ซึ่งมีรูปร่างเป็นจำนวนมิติการฝัง X จำนวนรายการ
ตัวอย่างเช่น การใช้การแยกเมทริกซ์กับผู้ใช้ 3 รายและสินค้า 5 รายการ อาจให้เมทริกซ์ผู้ใช้และเมทริกซ์สินค้าต่อไปนี้
User Matrix Item Matrix 1.1 2.3 0.9 0.2 1.4 2.0 1.2 0.6 2.0 1.7 1.2 1.2 -0.1 2.1 2.5 0.5
ผลคูณของเมทริกซ์ผู้ใช้และเมทริกซ์รายการจะให้เมทริกซ์คำแนะนำ ซึ่งไม่เพียงมีคะแนนของผู้ใช้เดิม แต่ยังมีค่าคาดการณ์ สำหรับภาพยนตร์ที่ผู้ใช้แต่ละคนยังไม่เคยดูด้วย ตัวอย่างเช่น ลองพิจารณาคะแนนที่ผู้ใช้ 1 ให้กับคาซาบลังกา ซึ่งเท่ากับ 5.0 ผลิตภัณฑ์ที่สอดคล้องกับเซลล์นั้นในเมทริกซ์คำแนะนำควรมีค่าประมาณ 5.0 และเป็นเช่นนั้นจริง
(1.1 * 0.9) + (2.3 * 1.7) = 4.9และที่สำคัญที่สุดคือ ผู้ใช้ 1 จะชอบ Black Panther ไหม การหาผลคูณจุด ที่สอดคล้องกับแถวแรกและคอลัมน์ที่สามจะให้คะแนนที่คาดการณ์ไว้ เป็น 4.3
(1.1 * 1.4) + (2.3 * 1.2) = 4.3โดยปกติแล้วการแยกตัวประกอบเมทริกซ์จะให้เมทริกซ์ผู้ใช้และเมทริกซ์สินค้าที่เมื่อรวมกันแล้วจะกะทัดรัดกว่าเมทริกซ์เป้าหมายอย่างมาก
ค่าเฉลี่ยความคลาดเคลื่อนสัมบูรณ์ (MAE)
การสูญเสียเฉลี่ยต่อตัวอย่างเมื่อใช้การสูญเสีย L1 คำนวณค่าเฉลี่ยความผิดพลาดสัมบูรณ์ดังนี้
- คำนวณการสูญเสีย L1 สำหรับกลุ่ม
- หารการสูญเสีย L1 ด้วยจำนวนตัวอย่างในกลุ่ม
เช่น ลองพิจารณาการคำนวณการสูญเสีย L1 ในชุดตัวอย่าง 5 รายการต่อไปนี้
| มูลค่าที่แท้จริงของตัวอย่าง | ค่าที่โมเดลคาดการณ์ | การสูญเสีย (ความแตกต่างระหว่างค่าจริงกับค่าที่คาดการณ์) |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 3 |
| 4 | 6 | 2 |
| 9 | 8 | 1 |
| 8 = การสูญเสีย L1 | ||
ดังนั้น ค่าความสูญเสีย L1 คือ 8 และจำนวนตัวอย่างคือ 5 ดังนั้นค่าเฉลี่ยความผิดพลาดสัมบูรณ์จึงเป็นดังนี้
Mean Absolute Error = L1 loss / Number of Examples Mean Absolute Error = 8/5 = 1.6
เปรียบเทียบค่าเฉลี่ยความคลาดเคลื่อนสัมบูรณ์กับความคลาดเคลื่อนเฉลี่ยกำลังสองและ สแควรูทของความคลาดเคลื่อนกำลังสองเฉลี่ย
ความแม่นยำของค่าเฉลี่ยที่ k (mAP@k)
ค่าเฉลี่ยทางสถิติของคะแนนความแม่นยำเฉลี่ยที่ k ทั้งหมดในชุดข้อมูลการตรวจสอบ การใช้ความแม่นยำเฉลี่ยที่ตำแหน่ง k อย่างหนึ่งคือการประเมิน คุณภาพของคำแนะนำที่สร้างโดยระบบแนะนำ
แม้ว่าวลี "ค่าเฉลี่ย" จะฟังดูซ้ำซ้อน แต่ชื่อของเมตริกก็เหมาะสมแล้ว เนื่องจากเมตริกนี้จะหาค่าเฉลี่ยของค่าความแม่นยำเฉลี่ยที่ k หลายค่า
ความคลาดเคลื่อนเฉลี่ยกำลังสอง (MSE)
การสูญเสียเฉลี่ยต่อตัวอย่างเมื่อใช้L2 loss คำนวณความคลาดเคลื่อนเฉลี่ยกำลังสองดังนี้
- คำนวณการสูญเสีย L2 สำหรับกลุ่ม
- หารการสูญเสีย L2 ด้วยจำนวนตัวอย่างในกลุ่ม
ตัวอย่างเช่น ลองพิจารณาการสูญเสียในกลุ่มตัวอย่าง 5 รายการต่อไปนี้
| มูลค่าที่แท้จริง | การคาดการณ์ของโมเดล | แพ้ | การสูญเสียกำลังสอง |
|---|---|---|---|
| 7 | 6 | 1 | 1 |
| 5 | 4 | 1 | 1 |
| 8 | 11 | 3 | 9 |
| 4 | 6 | 2 | 4 |
| 9 | 8 | 1 | 1 |
| 16 = L2 loss | |||
ดังนั้น ความคลาดเคลื่อนเฉลี่ยกำลังสองจึงเป็น
Mean Squared Error = L2 loss / Number of Examples Mean Squared Error = 16/5 = 3.2
ความคลาดเคลื่อนเฉลี่ยกำลังสองเป็นเครื่องมือเพิ่มประสิทธิภาพการฝึกยอดนิยม โดยเฉพาะอย่างยิ่งสำหรับการถดถอยเชิงเส้น
เปรียบเทียบความคลาดเคลื่อนกำลังสองเฉลี่ยกับค่าเฉลี่ยความคลาดเคลื่อนสัมบูรณ์และค่าเฉลี่ยความคลาดเคลื่อนกำลังสอง
TensorFlow Playground ใช้ข้อผิดพลาดกำลังสองเฉลี่ย เพื่อคำนวณค่าการสูญเสีย
Mesh
ในการเขียนโปรแกรมแบบขนาน ML คำที่เชื่อมโยงกับการกำหนดข้อมูลและโมเดลให้กับชิป TPU และการกำหนดวิธีที่จะแยกส่วนหรือจำลองค่าเหล่านี้
Mesh เป็นคำที่มีความหมายหลากหลาย ซึ่งอาจหมายถึงสิ่งใดสิ่งหนึ่งต่อไปนี้
- เลย์เอาต์จริงของชิป TPU
- โครงสร้างเชิงตรรกะแบบนามธรรมสำหรับการแมปข้อมูลและโมเดลกับชิป TPU
ไม่ว่าในกรณีใดก็ตาม ระบบจะระบุ Mesh เป็นรูปร่าง
การเรียนรู้แบบเมตา
ส่วนย่อยของแมชชีนเลิร์นนิงที่ค้นพบหรือปรับปรุงอัลกอริทึมการเรียนรู้ ระบบเมตาเลิร์นนิงยังสามารถมุ่งฝึกโมเดลให้เรียนรู้งานใหม่ได้อย่างรวดเร็ว จากข้อมูลจำนวนเล็กน้อยหรือจากประสบการณ์ที่ได้รับในงานก่อนหน้า โดยทั่วไปแล้ว อัลกอริทึมเมตาเลิร์นนิงจะพยายามทำให้ได้ผลลัพธ์ต่อไปนี้
- ปรับปรุงหรือเรียนรู้ฟีเจอร์ที่สร้างขึ้นด้วยมือ (เช่น ตัวเริ่มต้นหรือ ตัวเพิ่มประสิทธิภาพ)
- มีประสิทธิภาพด้านข้อมูลและการประมวลผลมากขึ้น
- ปรับปรุงการสรุป
Meta-learning เกี่ยวข้องกับการเรียนรู้แบบ Few-Shot
เมตริก
สถิติที่คุณสนใจ
วัตถุประสงค์คือเมตริกที่ระบบแมชชีนเลิร์นนิง พยายามเพิ่มประสิทธิภาพ
Metrics API (tf.metrics)
API ของ TensorFlow สำหรับการประเมินโมเดล เช่น tf.metrics.accuracy
จะกำหนดความถี่ที่การคาดการณ์ของโมเดลตรงกับป้ายกำกับ
มินิแบทช์
ชุดข้อมูลย่อยที่เลือกแบบสุ่มขนาดเล็กของกลุ่มที่ประมวลผลในการทำซ้ำครั้งเดียว โดยปกติแล้ว ขนาดกลุ่มของมินิแบตช์จะอยู่ ระหว่าง 10 ถึง 1,000 ตัวอย่าง
ตัวอย่างเช่น สมมติว่าชุดการฝึกทั้งหมด (กลุ่มทั้งหมด) ประกอบด้วยตัวอย่าง 1,000 รายการ สมมติว่าคุณตั้งค่าขนาดกลุ่มของมินิแบตช์แต่ละรายการเป็น 20 ดังนั้น การทำซ้ำแต่ละครั้งจะกำหนดการสูญเสียในตัวอย่างแบบสุ่ม 20 รายการจาก 1,000 รายการ แล้วจึง ปรับน้ำหนักและอคติตามนั้น
การคำนวณการสูญเสียในมินิแบทช์มีประสิทธิภาพมากกว่าการคำนวณการสูญเสียในตัวอย่างทั้งหมดในฟูลแบทช์มาก
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยเชิงเส้น: ไฮเปอร์พารามิเตอร์ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การไล่ระดับสีแบบสุ่มของมินิแบทช์
อัลกอริทึมการไล่ระดับความชันที่ใช้ มินิแบตช์ กล่าวอีกนัยหนึ่ง การไล่ระดับความชันแบบสุ่มของมินิแบตช์จะประมาณค่าการไล่ระดับความชันโดยอิงตามชุดข้อมูลการฝึกขนาดเล็ก การไล่ระดับสีแบบสุ่มปกติจะใช้ มินิแบตช์ขนาด 1
การสูญเสียแบบมินิแม็กซ์
ฟังก์ชันการสูญเสียสำหรับGenerative Adversarial Network โดยอิงตามCross-Entropy ระหว่างการกระจาย ของข้อมูลที่สร้างขึ้นและข้อมูลจริง
การสูญเสียแบบมินิแม็กซ์ใช้ในเอกสารฉบับแรกเพื่ออธิบาย Generative Adversarial Network
ดูข้อมูลเพิ่มเติมได้ที่ฟังก์ชันการสูญเสียใน หลักสูตร Generative Adversarial Networks
ชนชั้นที่เป็นชนกลุ่มน้อย
ป้ายกำกับที่พบน้อยกว่าในชุดข้อมูลที่มีความไม่สมดุลของคลาส เช่น หากชุดข้อมูลมีป้ายกำกับเชิงลบ 99% และป้ายกำกับเชิงบวก 1% ป้ายกำกับเชิงบวกจะเป็นคลาสส่วนน้อย
เปรียบเทียบกับชั้นเรียนส่วนใหญ่
ดูข้อมูลเพิ่มเติมได้ที่ชุดข้อมูล: ชุดข้อมูลที่ไม่สมดุล ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
Mixture of Experts
รูปแบบการเพิ่มประสิทธิภาพเครือข่ายประสาทโดย ใช้เฉพาะชุดย่อยของพารามิเตอร์ (เรียกว่าผู้เชี่ยวชาญ) เพื่อประมวลผล โทเค็นหรือตัวอย่างที่กำหนด เครือข่ายการควบคุมการเข้าถึงจะกำหนดเส้นทางโทเค็นอินพุตหรือตัวอย่างแต่ละรายการไปยังผู้เชี่ยวชาญที่เหมาะสม
โปรดดูรายละเอียดในเอกสารต่อไปนี้
- โครงข่ายระบบประสาทเทียมขนาดใหญ่มาก: เลเยอร์ Sparsely-Gated Mixture-of-Experts
- Mixture-of-Experts พร้อมการกำหนดเส้นทางตามตัวเลือกของผู้เชี่ยวชาญ
ML
ตัวย่อของแมชชีนเลิร์นนิง
MMIT
คำย่อของ multimodal instruction-tuned
MNIST
ชุดข้อมูลโดเมนสาธารณะที่รวบรวมโดย LeCun, Cortes และ Burges ซึ่งมีรูปภาพ 60,000 รูป โดยแต่ละรูปแสดงวิธีที่มนุษย์เขียนตัวเลข 0-9 ด้วยตนเอง ระบบจะจัดเก็บรูปภาพแต่ละรูปเป็นอาร์เรย์จำนวนเต็มขนาด 28x28 โดย จำนวนเต็มแต่ละรายการคือค่าระดับสีเทาระหว่าง 0 ถึง 255 (รวม)
MNIST เป็นชุดข้อมูล Canonical สำหรับแมชชีนเลิร์นนิง ซึ่งมักใช้ในการทดสอบแนวทางใหม่ๆ ของแมชชีนเลิร์นนิง ดูรายละเอียดได้ที่ ฐานข้อมูล MNIST ของตัวเลขที่เขียนด้วยลายมือ
รูปแบบ
หมวดหมู่ข้อมูลระดับสูง ตัวอย่างเช่น ตัวเลข ข้อความ รูปภาพ วิดีโอ และเสียงเป็นรูปแบบที่แตกต่างกัน 5 รูปแบบ
รุ่น
โดยทั่วไปแล้ว โครงสร้างทางคณิตศาสตร์ใดๆ ที่ประมวลผลข้อมูลอินพุตและส่งคืน เอาต์พุต กล่าวอีกนัยหนึ่งคือ โมเดลคือชุดพารามิเตอร์และโครงสร้าง ที่ระบบต้องใช้ในการคาดการณ์ ในแมชชีนเลิร์นนิงที่มีการควบคุมดูแล โมเดลจะใช้ตัวอย่างเป็นข้อมูลป้อนเข้าและอนุมานการคาดการณ์เป็นข้อมูลผลลัพธ์ ภายในแมชชีนเลิร์นนิงที่มีการควบคุมดูแล โมเดลจะแตกต่างกันเล็กน้อย เช่น
- โมเดลการถดถอยเชิงเส้นประกอบด้วยชุดน้ำหนัก และอคติ
- โมเดลโครงข่ายประสาทเทียมประกอบด้วยองค์ประกอบต่อไปนี้
- ชุดเลเยอร์ที่ซ่อนอยู่ ซึ่งแต่ละเลเยอร์มีนิวรอนอย่างน้อย 1 ตัว
- น้ำหนักและความเอนเอียงที่เชื่อมโยงกับแต่ละนิวรอน
- โมเดลแผนผังการตัดสินใจประกอบด้วยองค์ประกอบต่อไปนี้
- รูปร่างของต้นไม้ ซึ่งก็คือรูปแบบที่เชื่อมต่อเงื่อนไข และใบไม้
- เงื่อนไขและใบไม้
คุณสามารถบันทึก กู้คืน หรือทำสำเนารูปแบบได้
แมชชีนเลิร์นนิงแบบไม่มีการกำกับดูแลยังสร้างโมเดลด้วย โดยปกติจะเป็นฟังก์ชันที่สามารถเชื่อมโยงตัวอย่างอินพุตกับคลัสเตอร์ที่เหมาะสมที่สุด
ความจุของโมเดล
ความซับซ้อนของปัญหาที่โมเดลสามารถเรียนรู้ได้ ยิ่งโมเดลเรียนรู้ปัญหาที่ซับซ้อนได้มากเท่าใด ความสามารถของโมเดลก็จะยิ่งสูงขึ้นเท่านั้น โดยปกติแล้ว ความจุของโมเดลจะเพิ่มขึ้นตามจำนวนพารามิเตอร์ของโมเดล ดูคำจำกัดความอย่างเป็นทางการของความจุโมเดลการจัดประเภทได้ที่มิติข้อมูล VC
การเรียงซ้อนโมเดล
ระบบที่เลือกโมเดลที่เหมาะสมที่สุดสําหรับการอนุมาน คําค้นหาที่เฉพาะเจาะจง
ลองนึกถึงกลุ่มโมเดลที่มีตั้งแต่ขนาดใหญ่มาก (มีพารามิเตอร์จำนวนมาก) ไปจนถึงขนาดเล็กกว่ามาก (มีพารามิเตอร์น้อยกว่ามาก) โมเดลขนาดใหญ่มากใช้ทรัพยากรการคำนวณมากกว่าในเวลาการอนุมานเมื่อเทียบกับโมเดลขนาดเล็ก อย่างไรก็ตาม โดยทั่วไปแล้วโมเดลขนาดใหญ่มากจะอนุมานคำขอที่ซับซ้อนกว่าโมเดลขนาดเล็กได้ การเรียงซ้อนโมเดลจะกำหนดความซับซ้อนของคำค้นหาการอนุมาน จากนั้นจะเลือกโมเดลที่เหมาะสมเพื่อทำการอนุมาน แรงจูงใจหลักในการเรียงซ้อนโมเดลคือการลดต้นทุนการอนุมานโดย โดยทั่วไปแล้วจะเลือกโมเดลขนาดเล็กกว่า และเลือกโมเดลขนาดใหญ่กว่าเฉพาะสำหรับคำค้นหาที่ซับซ้อนกว่า
ลองนึกภาพว่าโมเดลขนาดเล็กทำงานบนโทรศัพท์และโมเดลเวอร์ชันที่ใหญ่กว่า ทำงานบนเซิร์ฟเวอร์ระยะไกล การเรียงต่อโมเดลที่ดีจะช่วยลดต้นทุนและเวลาในการตอบสนองโดยการเปิดให้โมเดลขนาดเล็กจัดการคำขอที่เรียบง่าย และเรียกใช้โมเดลระยะไกลเพื่อจัดการคำขอที่ซับซ้อนเท่านั้น
ดูเราเตอร์รุ่นเพิ่มเติม
การขนานโมเดล
วิธีปรับขนาดการฝึกหรือการอนุมานที่วางส่วนต่างๆ ของโมเดลหนึ่งไว้ในอุปกรณ์ต่างๆ การขนานโมเดล ช่วยให้ใช้โมเดลที่มีขนาดใหญ่เกินกว่าจะพอดีกับอุปกรณ์เครื่องเดียวได้
โดยทั่วไปแล้ว ระบบจะดำเนินการต่อไปนี้เพื่อใช้การขนานกันของโมเดล
- แบ่ง (แยก) โมเดลออกเป็นส่วนเล็กๆ
- กระจายการฝึกส่วนเล็กๆ เหล่านั้นไปยังโปรเซสเซอร์หลายตัว โปรเซสเซอร์แต่ละตัวจะฝึกโมเดลในส่วนของตัวเอง
- รวมผลลัพธ์เพื่อสร้างโมเดลเดียว
การขนานโมเดลทำให้การฝึกช้าลง
ดูการประมวลผลแบบขนานของข้อมูลด้วย
เราเตอร์รุ่น
อัลกอริทึมที่กำหนดโมเดลที่เหมาะสมที่สุดสำหรับ การอนุมานในการเรียงซ้อนโมเดล โดยปกติแล้วเราเตอร์โมเดลจะเป็นโมเดลแมชชีนเลิร์นนิงที่ ค่อยๆ เรียนรู้วิธีเลือกโมเดลที่ดีที่สุดสำหรับอินพุตที่กำหนด อย่างไรก็ตาม บางครั้งเราเตอร์โมเดลอาจเป็นอัลกอริทึมที่ไม่ใช่แมชชีนเลิร์นนิงที่เรียบง่ายกว่า
การฝึกโมเดล
กระบวนการพิจารณาโมเดลที่ดีที่สุด
MOE
คำย่อของMixture of Experts
สร้างกระแส
อัลกอริทึมการไล่ระดับที่ซับซ้อนซึ่งขั้นตอนการเรียนรู้ไม่ได้ขึ้นอยู่กับอนุพันธ์ในขั้นตอนปัจจุบันเท่านั้น แต่ยังขึ้นอยู่กับอนุพันธ์ของขั้นตอนก่อนหน้าด้วย โมเมนตัมเกี่ยวข้องกับการคำนวณค่าเฉลี่ยเคลื่อนที่ถ่วงน้ำหนักแบบเอ็กซ์โปเนนเชียลของค่าการไล่ระดับเมื่อเวลาผ่านไป ซึ่งคล้ายกับโมเมนตัมในฟิสิกส์ โมเมนตัมบางครั้งช่วยให้การเรียนรู้ไม่ ติดอยู่ในค่าต่ำสุดเฉพาะที่
MT
ตัวย่อของการแปลด้วยคอมพิวเตอร์
การจัดประเภทแบบหลายคลาส
ใน Supervised Learning ปัญหาการจัดประเภท ซึ่งชุดข้อมูลมีป้ายกำกับมากกว่า 2 คลาส ตัวอย่างเช่น ป้ายกำกับในชุดข้อมูล Iris ต้องเป็นหนึ่งใน 3 คลาสต่อไปนี้
- Iris setosa
- Iris virginica
- ไอริส เวอร์ซิโคเลอร์
โมเดลที่ฝึกในชุดข้อมูล Iris ซึ่งคาดการณ์ประเภท Iris ในตัวอย่างใหม่ จะทำการจัดประเภทแบบหลายคลาส
ในทางตรงกันข้าม ปัญหาการจัดประเภทที่แยกความแตกต่างระหว่าง 2 คลาสอย่างชัดเจนคือโมเดลการจัดประเภทแบบไบนารี ตัวอย่างเช่น โมเดลอีเมลที่คาดการณ์ว่าจะเป็นสแปมหรือไม่ใช่สแปม คือโมเดลการจัดประเภทแบบไบนารี
ในปัญหาการจัดกลุ่ม การจัดประเภทแบบหลายคลาสหมายถึงคลัสเตอร์มากกว่า 2 คลัสเตอร์
ดูข้อมูลเพิ่มเติมได้ที่โครงข่ายประสาทเทียม: การจัดประเภทแบบหลายคลาส ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
การถดถอยแบบโลจิสติกหลายคลาส
การใช้การถดถอยโลจิสติกในปัญหาการจัดประเภทแบบหลายคลาส
Multi-Head Self-Attention
ส่วนขยายของการใส่ใจตนเองที่ใช้กลไกการใส่ใจตนเองหลายครั้งสำหรับแต่ละตำแหน่งในลำดับอินพุต
Transformer ได้เปิดตัวการทำ Self-Attention แบบหลายหัว
ได้รับการปรับแต่งสำหรับการสอนแบบหลายรูปแบบ
โมเดลที่ปรับแต่งตามคำสั่งซึ่งประมวลผลอินพุตได้ นอกเหนือจากข้อความ เช่น รูปภาพ วิดีโอ และเสียง
โมเดลแบบ Multimodal
โมเดลที่มีอินพุต เอาต์พุต หรือทั้ง 2 อย่างเป็นรูปแบบมากกว่า 1 รายการ ตัวอย่างเช่น พิจารณาโมเดลที่รับทั้ง รูปภาพและคำบรรยายข้อความ (2 รูปแบบ) เป็นฟีเจอร์ และ แสดงคะแนนที่บ่งบอกว่าคำบรรยายข้อความเหมาะสมกับรูปภาพเพียงใด ดังนั้นอินพุตของโมเดลนี้จึงเป็นแบบหลายรูปแบบและเอาต์พุตเป็นแบบรูปแบบเดียว
การจัดประเภทแบบหลายกลุ่ม
คำพ้องความหมายของการจัดประเภทแบบหลายคลาส
การถดถอยแบบมัลติโนเมียล
คำพ้องความหมายสำหรับ การถดถอยแบบโลจิสติกหลายคลาส
ทำงานหลายอย่างพร้อมกัน
เทคนิคแมชชีนเลิร์นนิงที่ใช้โมเดลเดียว เพื่อฝึกให้ทำงานหลายอย่าง
โมเดลแบบมัลติทาสก์สร้างขึ้นโดยการฝึกข้อมูลที่เหมาะสมกับแต่ละงาน ซึ่งจะช่วยให้โมเดลเรียนรู้ที่จะแชร์ ข้อมูลในงานต่างๆ ซึ่งจะช่วยให้โมเดลเรียนรู้ได้อย่างมีประสิทธิภาพมากขึ้น
โมเดลที่ฝึกสำหรับหลายงานมักจะมีความสามารถในการสร้างข้อมูลทั่วไปที่ดีขึ้น และสามารถจัดการข้อมูลประเภทต่างๆ ได้อย่างมีประสิทธิภาพมากขึ้น
N
Nano
โมเดล Gemini ขนาดค่อนข้างเล็กซึ่งออกแบบมาเพื่อใช้ในอุปกรณ์ ดูรายละเอียดได้ที่ Gemini Nano
กับดัก NaN
เมื่อตัวเลขหนึ่งในโมเดลกลายเป็น NaN ระหว่างการฝึก ซึ่งทำให้ตัวเลขอื่นๆ ในโมเดล กลายเป็น NaN ในที่สุด
NaN เป็นตัวย่อของ Not a Number
การประมวลผลภาษาธรรมชาติ
สาขาการสอนคอมพิวเตอร์ให้ประมวลผลสิ่งที่ผู้ใช้พูดหรือพิมพ์โดยใช้ กฎทางภาษา การประมวลผลภาษาธรรมชาติสมัยใหม่เกือบทั้งหมดอาศัย แมชชีนเลิร์นนิงความเข้าใจภาษาธรรมชาติ
กลุ่มย่อยของการประมวลผลภาษาธรรมชาติ ที่กำหนดเจตนาของสิ่งที่พูดหรือพิมพ์ ความเข้าใจภาษาธรรมชาติ สามารถก้าวข้ามการประมวลผลภาษาธรรมชาติเพื่อพิจารณาลักษณะที่ซับซ้อน ของภาษา เช่น บริบท การประชดประชัน และความรู้สึก
คลาสที่เป็นลบ
ในการจัดประเภทแบบไบนารี คลาสหนึ่งเรียกว่าบวกและอีกคลาสหนึ่งเรียกว่าลบ คลาสที่เป็นบวกคือ สิ่งหรือเหตุการณ์ที่โมเดลทดสอบ และคลาสที่เป็นลบคือ ความเป็นไปได้อื่นๆ เช่น
- คลาสเชิงลบในการตรวจทางการแพทย์อาจเป็น "ไม่ใช่มะเร็ง"
- คลาสเชิงลบในโมเดลการจัดประเภทอีเมลอาจเป็น "ไม่ใช่จดหมายขยะ"
เปรียบเทียบกับคลาสที่เป็นบวก
การสุ่มตัวอย่างเชิงลบ
คำพ้องความหมายของการสุ่มตัวอย่างแคมเปญ
Neural Architecture Search (NAS)
เทคนิคในการออกแบบสถาปัตยกรรมของโครงข่ายประสาทเทียมโดยอัตโนมัติ อัลกอริทึม NAS ช่วยลดเวลาและทรัพยากรที่ต้องใช้ในการฝึกโครงข่ายประสาทได้
โดยปกติแล้ว NAS จะใช้สิ่งต่อไปนี้
- พื้นที่ค้นหา ซึ่งเป็นชุดสถาปัตยกรรมที่เป็นไปได้
- ฟังก์ชันความเหมาะสม ซึ่งเป็นการวัดว่าสถาปัตยกรรมหนึ่งๆ ทำงานได้ดีเพียงใดในงานที่กำหนด
โดยปกติแล้ว อัลกอริทึม NAS จะเริ่มต้นด้วยชุดสถาปัตยกรรมที่เป็นไปได้ขนาดเล็ก และค่อยๆ ขยายพื้นที่ค้นหาเมื่ออัลกอริทึมเรียนรู้เพิ่มเติมเกี่ยวกับสถาปัตยกรรมที่มีประสิทธิภาพ โดยปกติแล้ว ฟังก์ชันความเหมาะสมจะอิงตามประสิทธิภาพของสถาปัตยกรรมในชุดการฝึก และโดยปกติแล้ว อัลกอริทึมจะได้รับการฝึกโดยใช้เทคนิคการเรียนรู้แบบเสริมกำลัง
อัลกอริทึม NAS ได้รับการพิสูจน์แล้วว่ามีประสิทธิภาพในการค้นหาสถาปัตยกรรมที่มีประสิทธิภาพสูงสำหรับงานต่างๆ ซึ่งรวมถึงการจัดหมวดหมู่รูปภาพ การจัดหมวดหมู่ข้อความ และการแปลด้วยเครื่อง
โครงข่ายระบบประสาทเทียม
โมเดลที่มีเลเยอร์ที่ซ่อนอยู่อย่างน้อย 1 รายการ โครงข่ายประสาทแบบลึกเป็นโครงข่ายประสาทประเภทหนึ่ง ที่มีเลเยอร์ที่ซ่อนอยู่มากกว่า 1 เลเยอร์ ตัวอย่างเช่น ไดอะแกรมต่อไปนี้ แสดงโครงข่ายประสาทเทียมแบบลึกที่มีเลเยอร์ซ่อน 2 เลเยอร์
นิวรอนแต่ละตัวในโครงข่ายประสาทจะเชื่อมต่อกับโหนดทั้งหมดในเลเยอร์ถัดไป ตัวอย่างเช่น ในแผนภาพก่อนหน้า คุณจะเห็นว่านิวรอนทั้ง 3 ตัว ในเลเยอร์ที่ซ่อนเลเยอร์แรกเชื่อมต่อกับนิวรอนทั้ง 2 ตัวใน เลเยอร์ที่ซ่อนเลเยอร์ที่ 2 แยกกัน
บางครั้งเราเรียกโครงข่ายประสาทเทียมที่ใช้ในคอมพิวเตอร์ว่าโครงข่ายประสาทเทียมเพื่อแยกความแตกต่างจากโครงข่ายประสาทที่พบในสมองและระบบประสาทอื่นๆ
โครงข่ายประสาทเทียมบางอย่างสามารถเลียนแบบความสัมพันธ์แบบไม่เชิงเส้นที่ซับซ้อนอย่างยิ่ง ระหว่างฟีเจอร์ต่างๆ กับป้ายกำกับ
ดูเพิ่มเติมที่โครงข่ายประสาทเทียมแบบคอนโวลูชันและ โครงข่ายประสาทเทียมแบบเกิดซ้ำ
ดูข้อมูลเพิ่มเติมได้ที่โครงข่ายประสาทเทียม ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
เซลล์ประสาท
ในแมชชีนเลิร์นนิง หน่วยที่แตกต่างกันภายในเลเยอร์ที่ซ่อนอยู่ ของโครงข่ายประสาทเทียม นิวรอนแต่ละตัวจะดำเนินการ 2 ขั้นตอนต่อไปนี้
- คำนวณผลรวมแบบถ่วงน้ำหนักของค่าอินพุตที่คูณ ด้วยน้ำหนักที่เกี่ยวข้อง
- ส่งผลรวมแบบถ่วงน้ำหนักเป็นอินพุตไปยังฟังก์ชันการเปิดใช้งาน
นิวรอนในเลเยอร์ซ่อนชั้นแรกจะรับอินพุตจากค่าฟีเจอร์ ในเลเยอร์อินพุต นิวรอนในเลเยอร์ที่ซ่อนใดๆ ที่อยู่ถัดจากเลเยอร์แรกจะรับอินพุตจากนิวรอนในเลเยอร์ที่ซ่อนก่อนหน้า ตัวอย่างเช่น นิวรอนในเลเยอร์ที่ซ่อนที่ 2 จะรับอินพุตจากนิวรอนในเลเยอร์ที่ซ่อนที่ 1
ภาพต่อไปนี้ไฮไลต์นิวรอน 2 ตัวและอินพุตของนิวรอนเหล่านั้น
นิวรอนในโครงข่ายประสาทเทียมจะเลียนแบบพฤติกรรมของนิวรอนในสมองและ ส่วนอื่นๆ ของระบบประสาท
N-gram
ลำดับของคำ N คำ เช่น truly madly เป็น 2-gram เนื่องจากลำดับมีความเกี่ยวข้อง madly truly จึงเป็น 2-gram ที่แตกต่างจาก truly madly
| N | ชื่อของ N-gram ประเภทนี้ | ตัวอย่าง |
|---|---|---|
| 2 | ไบแกรมหรือ 2-แกรม | ไป ไปที่ กินอาหารกลางวัน กินอาหารเย็น |
| 3 | ไตรแกรมหรือ 3-แกรม | กินมากไป มีความสุขตลอดกาล เสียงระฆังดัง |
| 4 | 4-gram | walk in the park, dust in the wind, the boy ate lentils |
โมเดลการทำความเข้าใจภาษาธรรมชาติจำนวนมากอาศัย N-gram เพื่อคาดเดาคำถัดไปที่ผู้ใช้จะพิมพ์ หรือพูด เช่น สมมติว่าผู้ใช้พิมพ์ happily ever โมเดล NLU ที่อิงตามไตรแกรมมีแนวโน้มที่จะคาดการณ์ว่าผู้ใช้จะพิมพ์คำว่าหลังจากเป็นคำถัดไป
เปรียบเทียบ N-gram กับ bag of words ซึ่งเป็น ชุดคำที่ไม่มีการจัดเรียง
ดูข้อมูลเพิ่มเติมได้ที่โมเดลภาษาขนาดใหญ่ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
NLP
ตัวย่อของการประมวลผลภาษาธรรมชาติ
NLU
ตัวย่อของความเข้าใจภาษาธรรมชาติ
โหนด (แผนผังการตัดสินใจ)
ในแผนผังการตัดสินใจ จะมี เงื่อนไขหรือโหนดปลายสุด
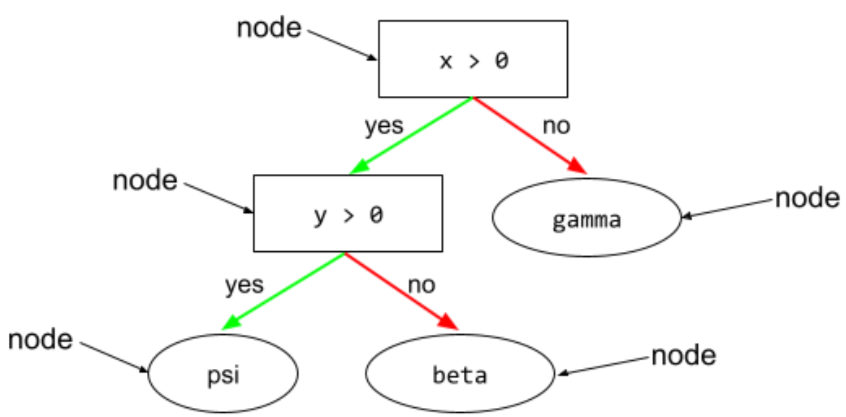
ดูข้อมูลเพิ่มเติมได้ที่แผนผังการตัดสินใจ ในหลักสูตร Decision Forests
โหนด (โครงข่ายประสาทเทียม)
ดูข้อมูลเพิ่มเติมได้ที่โครงข่ายประสาทเทียม ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
โหนด (กราฟ TensorFlow)
การดำเนินการในกราฟ TensorFlow
เสียงรบกวน
โดยทั่วไปแล้ว สิ่งใดก็ตามที่บดบังสัญญาณในชุดข้อมูล ระบบอาจใส่สัญญาณรบกวนลงในข้อมูลได้หลายวิธี เช่น
- ผู้ให้คะแนนที่เป็นมนุษย์อาจติดป้ายกำกับผิดพลาด
- มนุษย์และเครื่องมือบันทึกค่าฟีเจอร์ผิดพลาดหรือละเว้นค่า
เงื่อนไขนอนไบนารี
เงื่อนไขที่มีผลลัพธ์ที่เป็นไปได้มากกว่า 2 รายการ ตัวอย่างเช่น เงื่อนไขแบบไม่ใช่ไบนารีต่อไปนี้มีผลลัพธ์ที่เป็นไปได้ 3 อย่าง
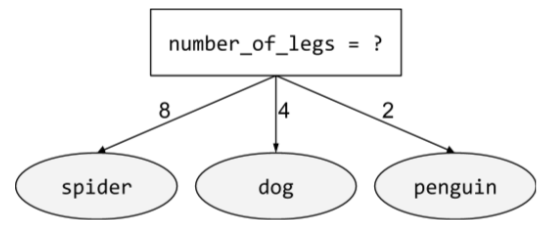
ดูข้อมูลเพิ่มเติมได้ที่ประเภทของเงื่อนไข ในหลักสูตร Decision Forests
ไม่ใช่แบบดั้งเดิม
ความสัมพันธ์ระหว่างตัวแปรตั้งแต่ 2 ตัวขึ้นไปซึ่งไม่สามารถแสดงได้โดยใช้การบวกและการคูณเพียงอย่างเดียว ความสัมพันธ์เชิงเส้นแสดงเป็นเส้นได้ แต่ความสัมพันธ์ที่ไม่ใช่เชิงเส้นแสดงเป็นเส้นไม่ได้ ตัวอย่างเช่น ลองพิจารณารูปแบบ 2 รูปแบบที่แต่ละรูปแบบเชื่อมโยง ฟีเจอร์เดียวกับป้ายกำกับเดียว โมเดลทางด้านซ้ายเป็นแบบเชิงเส้น และโมเดลทางด้านขวาเป็นแบบไม่เชิงเส้น

ดูโครงข่ายประสาทเทียม: โหนดและเลเยอร์ที่ซ่อนอยู่ ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิงเพื่อทดลองใช้ฟังก์ชันที่ไม่ใช่เชิงเส้นประเภทต่างๆ
อคติจากการไม่ตอบ
ความไม่คงที่
ฟีเจอร์ที่มีค่าเปลี่ยนแปลงในมิติข้อมูลอย่างน้อย 1 รายการ ซึ่งมักจะเป็นเวลา ตัวอย่างเช่น ลองพิจารณาตัวอย่างต่อไปนี้ของความไม่คงที่
- จำนวนชุดว่ายน้ำที่ขายในร้านค้าหนึ่งๆ จะแตกต่างกันไปตามฤดูกาล
- ปริมาณผลไม้ชนิดหนึ่งที่เก็บเกี่ยวในภูมิภาคหนึ่งๆ เป็น 0 ในช่วงเวลาส่วนใหญ่ของปี แต่มีปริมาณมากในช่วงเวลาสั้นๆ
- การเปลี่ยนแปลงสภาพภูมิอากาศทำให้อุณหภูมิเฉลี่ยรายปีเปลี่ยนแปลงไป
คอนทราสต์กับความคงที่
ไม่มีคำตอบที่ถูกต้องเพียงคำตอบเดียว (NORA)
พรอมต์ที่มีคำตอบที่ถูกต้องหลายรายการ ตัวอย่างเช่น พรอมต์ต่อไปนี้ไม่มีคำตอบที่ถูกต้องเพียงคำตอบเดียว
เล่าเรื่องตลกเกี่ยวกับช้างให้ฟังหน่อย
การประเมินคำตอบของพรอมต์ที่ไม่มีคำตอบที่ถูกต้องเพียงคำตอบเดียว มักจะมีความเป็นอัตนัยมากกว่าการประเมินพรอมต์ที่มีคำตอบที่ถูกต้องเพียงคำตอบเดียว เช่น การประเมินมุกตลกเกี่ยวกับช้างต้องมีวิธีที่เป็นระบบเพื่อพิจารณาว่ามุกตลกนั้นตลกมากน้อยเพียงใด
NORA
คำย่อของไม่มีคำตอบที่ตายตัว
การแปลงเป็นรูปแบบมาตรฐาน
โดยทั่วไป กระบวนการแปลงช่วงค่าจริงของตัวแปร เป็นช่วงค่ามาตรฐาน เช่น
- -1 ถึง +1
- 0 ถึง 1
- คะแนนมาตรฐาน (Z-Score) (ประมาณ -3 ถึง +3)
เช่น สมมติว่าช่วงค่าจริงของฟีเจอร์หนึ่งคือ 800 ถึง 2,400 ในส่วนของการออกแบบฟีเจอร์ คุณสามารถปรับค่าจริงให้เป็นช่วงมาตรฐานได้ เช่น -1 ถึง +1
การปรับให้เป็นมาตรฐานเป็นงานที่พบบ่อยในการออกแบบฟีเจอร์ โดยปกติแล้ว โมเดลจะฝึกได้เร็วขึ้น (และให้การคาดการณ์ที่ดีขึ้น) เมื่อฟีเจอร์ที่เป็นตัวเลขทุกรายการในเวกเตอร์ฟีเจอร์มีช่วงที่ใกล้เคียงกัน
ดูการปรับให้เป็นมาตรฐาน Z-score ด้วย
ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลตัวเลข: การปรับให้เป็นมาตรฐาน ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
Notebook LM
เครื่องมือที่ทำงานด้วย Gemini ซึ่งช่วยให้ผู้ใช้อัปโหลดเอกสาร แล้วใช้พรอมต์เพื่อถามคำถาม สรุป หรือจัดระเบียบเอกสารเหล่านั้นได้ ตัวอย่างเช่น นักเขียนอาจอัปโหลดเรื่องสั้นหลายเรื่อง และขอให้ NotebookLM ค้นหาธีมร่วมหรือระบุว่าเรื่องใด เหมาะที่จะนำไปสร้างเป็นภาพยนตร์มากที่สุด
การตรวจหาความแปลกใหม่
กระบวนการพิจารณาว่าตัวอย่างใหม่ (ที่ไม่เคยเห็น) มาจากการกระจายเดียวกันกับชุดการฝึกหรือไม่ กล่าวคือ หลังจากฝึกโมเดลในชุดข้อมูลการฝึกแล้ว การตรวจหาความแปลกใหม่จะพิจารณาว่าตัวอย่างใหม่ (ในระหว่างการอนุมานหรือการฝึกเพิ่มเติม) เป็นค่าผิดปกติหรือไม่
เปรียบเทียบกับการตรวจจับค่าผิดปกติ
ข้อมูลเชิงตัวเลข
ฟีเจอร์แสดงเป็นจำนวนเต็มหรือจำนวนจริง เช่น โมเดลการประเมินบ้านอาจแสดงขนาด ของบ้าน (เป็นตารางฟุตหรือตารางเมตร) เป็นข้อมูลตัวเลข การแสดงฟีเจอร์เป็นข้อมูลตัวเลขบ่งชี้ว่าค่าของฟีเจอร์มีความสัมพันธ์ทางคณิตศาสตร์กับป้ายกำกับ กล่าวคือ จำนวนตารางเมตรในบ้านอาจมีความสัมพันธ์ทางคณิตศาสตร์กับมูลค่าของบ้าน
ข้อมูลจำนวนเต็มบางรายการไม่ควรแสดงเป็นข้อมูลตัวเลข ตัวอย่างเช่น
รหัสไปรษณีย์ในบางส่วนของโลกเป็นจำนวนเต็ม แต่ไม่ควรแสดงรหัสไปรษณีย์ที่เป็นจำนวนเต็ม
เป็นข้อมูลตัวเลขในโมเดล เนื่องจากรหัสไปรษณีย์ 20000 ไม่ได้มีประสิทธิภาพเป็น 2 เท่า (หรือครึ่งหนึ่ง) ของรหัสไปรษณีย์ 10000
นอกจากนี้ แม้ว่ารหัสไปรษณีย์ที่แตกต่างกันจะสัมพันธ์กับมูลค่าอสังหาริมทรัพย์ที่แตกต่างกัน แต่เราก็ไม่สามารถสรุปได้ว่ามูลค่าอสังหาริมทรัพย์ที่รหัสไปรษณีย์ 20000 มีมูลค่าเป็น 2 เท่าของมูลค่าอสังหาริมทรัพย์ที่รหัสไปรษณีย์ 10000
ควรแสดงรหัสไปรษณีย์เป็นข้อมูลเชิงหมวดหมู่แทน
บางครั้งฟีเจอร์ที่เป็นตัวเลขจะเรียกว่า ฟีเจอร์ต่อเนื่อง
ดูข้อมูลเพิ่มเติมได้ที่การทำงานกับข้อมูลตัวเลข ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
NumPy
ไลบรารีคณิตศาสตร์แบบโอเพนซอร์ส ที่ให้การดำเนินการกับอาร์เรย์อย่างมีประสิทธิภาพใน Python pandas สร้างขึ้นบน NumPy
O
วัตถุประสงค์
เมตริกที่อัลกอริทึมพยายามเพิ่มประสิทธิภาพ
ฟังก์ชันออบเจ็กต์
สูตรทางคณิตศาสตร์หรือเมตริกที่โมเดลต้องการเพิ่มประสิทธิภาพ เช่น ฟังก์ชันออบเจกทีฟสำหรับการถดถอยเชิงเส้นมักจะเป็นการสูญเสียกำลังสองเฉลี่ย ดังนั้น เมื่อฝึกโมเดลการถดถอยเชิงเส้น การฝึกจึงมุ่งเน้นที่การลดการสูญเสียค่าเฉลี่ยกำลังสอง
ในบางกรณี เป้าหมายคือการเพิ่มฟังก์ชันออบเจ็กต์ให้ได้มากที่สุด เช่น หากฟังก์ชันออบเจ็กทีฟคือความแม่นยำ เป้าหมายคือ การเพิ่มความแม่นยำสูงสุด
ดูการสูญเสียด้วย
เงื่อนไขเฉียง
ในแผนผังการตัดสินใจ เงื่อนไขที่เกี่ยวข้องกับฟีเจอร์มากกว่า 1 รายการ ตัวอย่างเช่น หากความสูงและความกว้างเป็นทั้งฟีเจอร์ เงื่อนไขที่อ้อมค้อมจะเป็นดังนี้
height > width
เปรียบเทียบกับเงื่อนไขที่สอดคล้องกับแกน
ดูข้อมูลเพิ่มเติมได้ที่ประเภทของเงื่อนไข ในหลักสูตร Decision Forests
ออฟไลน์
คำพ้องความหมายของ static
การอนุมานแบบออฟไลน์
กระบวนการที่โมเดลสร้างการคาดการณ์ เป็นชุด แล้วแคช (บันทึก) การคาดการณ์เหล่านั้น จากนั้นแอปจะเข้าถึงการคาดคะเนที่อนุมานได้จากแคชแทนที่จะเรียกใช้โมเดลอีกครั้ง
ตัวอย่างเช่น ลองพิจารณาโมเดลที่สร้างพยากรณ์อากาศในพื้นที่ (การคาดการณ์) ทุกๆ 4 ชั่วโมง หลังจากเรียกใช้โมเดลแต่ละครั้ง ระบบจะ แคชพยากรณ์อากาศในพื้นที่ทั้งหมด แอปสภาพอากาศจะดึงข้อมูลพยากรณ์อากาศ จากแคช
การอนุมานแบบออฟไลน์เรียกอีกอย่างว่าการอนุมานแบบคงที่
แตกต่างจากการอนุมานแบบออนไลน์ ดูข้อมูลเพิ่มเติมได้ที่ระบบ ML ที่ใช้งานจริง: การอนุมานแบบคงที่เทียบกับการอนุมานแบบไดนามิก ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การเข้ารหัสแบบ One-hot
การแสดงข้อมูลเชิงหมวดหมู่เป็นเวกเตอร์ซึ่งมีลักษณะดังนี้
- ตั้งค่าองค์ประกอบหนึ่งเป็น 1
- และตั้งค่าองค์ประกอบอื่นๆ ทั้งหมดเป็น 0
โดยทั่วไปแล้ว การเข้ารหัสแบบ One-Hot จะใช้เพื่อแสดงสตริงหรือตัวระบุที่มีชุดค่าที่เป็นไปได้แบบจำกัด
ตัวอย่างเช่น สมมติว่าฟีเจอร์เชิงหมวดหมู่หนึ่งชื่อ
Scandinavia มีค่าที่เป็นไปได้ 5 ค่าดังนี้
- "เดนมาร์ก"
- "สวีเดน"
- "นอร์เวย์"
- "ฟินแลนด์"
- "ไอซ์แลนด์"
การเข้ารหัสแบบ One-Hot สามารถแสดงค่าทั้ง 5 ค่าได้ดังนี้
| ประเทศ | เวกเตอร์ | ||||
|---|---|---|---|---|---|
| "เดนมาร์ก" | 1 | 0 | 0 | 0 | 0 |
| "สวีเดน" | 0 | 1 | 0 | 0 | 0 |
| "นอร์เวย์" | 0 | 0 | 1 | 0 | 0 |
| "ฟินแลนด์" | 0 | 0 | 0 | 1 | 0 |
| "ไอซ์แลนด์" | 0 | 0 | 0 | 0 | 1 |
การเข้ารหัสแบบ One-Hot ช่วยให้โมเดลเรียนรู้การเชื่อมต่อต่างๆ ตามประเทศทั้ง 5 ประเทศได้
การแสดงฟีเจอร์เป็นข้อมูลตัวเลขเป็นทางเลือกแทนการเข้ารหัสแบบ One-hot ขออภัย การแสดงประเทศในแถบสแกนดิเนเวียเป็นตัวเลขไม่ใช่ตัวเลือกที่ดี ตัวอย่างเช่น ลองพิจารณาการแสดงตัวเลขต่อไปนี้
- "เดนมาร์ก" คือ 0
- "สวีเดน" คือ 1
- "นอร์เวย์" คือ 2
- "ฟินแลนด์" คือ 3
- "ไอซ์แลนด์" คือ 4
เมื่อใช้การเข้ารหัสตัวเลข โมเดลจะตีความตัวเลขดิบในเชิงคณิตศาสตร์และจะพยายามฝึกกับตัวเลขเหล่านั้น อย่างไรก็ตาม ในความเป็นจริงแล้ว ไอซ์แลนด์ไม่ได้มีประชากรมากกว่า (หรือน้อยกว่า) นอร์เวย์ 2 เท่า โมเดลจึงอาจสรุปผลที่แปลกประหลาดได้
ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลเชิงหมวดหมู่: คำศัพท์และการเข้ารหัสแบบ One-Hot ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
คำตอบที่ถูกต้องเพียงคำตอบเดียว (ORA)
พรอมต์ที่มีคำตอบที่ถูกต้องเพียงคำตอบเดียว ตัวอย่างเช่น ลองพิจารณาพรอมต์ต่อไปนี้
จริงหรือเท็จ: ดาวเสาร์มีขนาดใหญ่กว่าดาวอังคาร
คำตอบที่ถูกต้องเพียงอย่างเดียวคือ true
เปรียบเทียบกับไม่มีคำตอบที่ถูกต้อง
การเรียนรู้แบบครั้งเดียว
แนวทางแมชชีนเลิร์นนิงซึ่งมักใช้สำหรับการแยกประเภทออบเจ็กต์ ออกแบบมาเพื่อเรียนรู้โมเดลการแยกประเภทที่มีประสิทธิภาพ จากตัวอย่างการฝึกเพียงรายการเดียว
ดูการเรียนรู้แบบไม่กี่ช็อตและ การเรียนรู้แบบศูนย์ช็อตด้วย
การเขียนพรอมต์แบบ One-Shot Prompting
พรอมต์ที่มีตัวอย่างหนึ่งตัวอย่างที่แสดงให้เห็นว่าโมเดลภาษาขนาดใหญ่ควรตอบสนองอย่างไร ตัวอย่างเช่น พรอมต์ต่อไปนี้มีตัวอย่างหนึ่งที่แสดงให้โมเดลภาษาขนาดใหญ่เห็นว่า ควรตอบคำค้นหาอย่างไร
| ส่วนต่างๆ ของพรอมต์ | หมายเหตุ |
|---|---|
| สกุลเงินทางการของประเทศที่ระบุคืออะไร | คำถามที่คุณต้องการให้ LLM ตอบ |
| ฝรั่งเศส: EUR | ตัวอย่าง |
| อินเดีย: | คำค้นหาจริง |
เปรียบเทียบการแจ้งแบบนัดเดียวกับคำศัพท์ต่อไปนี้
หนึ่งเทียบกับทั้งหมด
เมื่อพิจารณาปัญหาการแยกประเภทที่มี N คลาส โซลูชันที่ประกอบด้วยโมเดลการจัดประเภทแบบไบนารีแยกกัน N โมเดล ซึ่งเป็นโมเดลการจัดประเภทแบบไบนารี 1 โมเดลสำหรับผลลัพธ์ที่เป็นไปได้แต่ละรายการ เช่น หากมีโมเดล ที่จัดประเภทตัวอย่างเป็นสัตว์ พืช หรือแร่ธาตุ โซลูชันแบบหนึ่งเทียบกับทั้งหมด จะให้โมเดลการจัดประเภทแบบไบนารี 3 โมเดลแยกกัน ดังนี้
- สัตว์เทียบกับไม่ใช่สัตว์
- ผักกับไม่ใช่ผัก
- แร่ธาตุเทียบกับไม่ใช่แร่ธาตุ
ออนไลน์
คำพ้องความหมายของไดนามิก
การอนุมานแบบออนไลน์
สร้างการคาดการณ์ตามต้องการ ตัวอย่างเช่น สมมติว่าแอปส่งอินพุตไปยังโมเดลและส่งคำขอสำหรับ การคาดการณ์ ระบบที่ใช้การอนุมานออนไลน์จะตอบสนองต่อคำขอโดยการเรียกใช้โมเดล (และส่งคืนการคาดการณ์ไปยังแอป)
เปรียบเทียบกับการอนุมานแบบออฟไลน์
ดูข้อมูลเพิ่มเติมได้ที่ระบบ ML ที่ใช้งานจริง: การอนุมานแบบคงที่เทียบกับการอนุมานแบบไดนามิก ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การดำเนินการ (op)
ใน TensorFlow คือกระบวนการใดๆ ที่สร้าง จัดการ หรือทำลาย Tensor ตัวอย่างเช่น การคูณเมทริกซ์เป็นการดำเนินการที่รับเทนเซอร์ 2 รายการเป็นอินพุตและสร้างเทนเซอร์ 1 รายการเป็นเอาต์พุต
Optax
ไลบรารีการประมวลผลและการเพิ่มประสิทธิภาพการไล่ระดับสีสำหรับ JAX Optax ช่วยอำนวยความสะดวกในการวิจัยโดยการจัดหาองค์ประกอบพื้นฐานที่สามารถ รวมกันใหม่ในรูปแบบที่กำหนดเองเพื่อเพิ่มประสิทธิภาพโมเดลพารามิเตอร์ เช่น ดีปนิวรัลเน็ตเวิร์ก เป้าหมายอื่นๆ ได้แก่
- การใช้งานที่อ่านง่าย มีการทดสอบอย่างดี และมีประสิทธิภาพของ คอมโพเนนต์หลัก
- การปรับปรุงประสิทธิภาพด้วยการทำให้สามารถรวมส่วนผสมระดับต่ำ เข้ากับเครื่องมือเพิ่มประสิทธิภาพที่กำหนดเอง (หรือคอมโพเนนต์การประมวลผลแบบไล่ระดับอื่นๆ)
- เร่งการนำแนวคิดใหม่ๆ มาใช้ด้วยการทำให้ทุกคนร่วมให้ข้อมูลได้ง่าย
เครื่องมือเพิ่มประสิทธิภาพ
การใช้งานอัลกอริทึมการไล่ระดับการไล่ระดับ ที่เฉพาะเจาะจง เครื่องมือเพิ่มประสิทธิภาพที่ได้รับความนิยมมีดังนี้
- AdaGrad ซึ่งย่อมาจาก ADAptive GRADient descent
- Adam ซึ่งย่อมาจาก ADAptive with Momentum
ORA
ตัวย่อสำหรับคำตอบที่ถูกต้องเพียงข้อเดียว
อคติความเหมือนกันของกลุ่มนอก
แนวโน้มที่จะมองว่าสมาชิกนอกกลุ่มมีความคล้ายคลึงกันมากกว่าสมาชิกในกลุ่ม เมื่อเปรียบเทียบทัศนคติ คุณค่า ลักษณะบุคลิกภาพ และลักษณะอื่นๆ กลุ่มในหมายถึงผู้ที่คุณโต้ตอบด้วยเป็นประจำ กลุ่มนอกหมายถึงผู้ที่คุณไม่ได้โต้ตอบด้วยเป็นประจำ หากคุณ สร้างชุดข้อมูลโดยขอให้ผู้คนระบุแอตทริบิวต์เกี่ยวกับ กลุ่มนอก แอตทริบิวต์เหล่านั้นอาจมีความแตกต่างน้อยกว่าและเป็นแบบเหมารวมมากกว่า แอตทริบิวต์ที่ผู้เข้าร่วมระบุสำหรับผู้คนในกลุ่มของตน
ตัวอย่างเช่น ชาวลิลิปุตอาจอธิบายบ้านของชาวลิลิปุตคนอื่นๆ อย่างละเอียด โดยอ้างถึงความแตกต่างเล็กๆ น้อยๆ ในรูปแบบสถาปัตยกรรม หน้าต่าง ประตู และขนาด แต่ชาวลิลิปุตคนเดียวกันนี้อาจกล่าวว่า ชาวบร็อบดิงแน็กทุกคนอาศัยอยู่ในบ้านที่เหมือนกัน
อคติความเหมือนกันของกลุ่มนอกเป็นรูปแบบหนึ่งของอคติในการระบุแหล่งที่มาของกลุ่ม
ดูอคติในกลุ่มด้วย
การตรวจจับค่าผิดปกติ
กระบวนการระบุค่าผิดปกติในชุดการฝึก
แตกต่างจากการตรวจหาความแปลกใหม่
ค่าผิดปกติ
ค่าที่แตกต่างจากค่าอื่นๆ ส่วนใหญ่ ในแมชชีนเลิร์นนิง รายการต่อไปนี้ถือเป็นค่าผิดปกติ
- ป้อนข้อมูลที่มีค่ามากกว่าค่าเบี่ยงเบนมาตรฐานประมาณ 3 ค่า จากค่าเฉลี่ย
- น้ำหนักที่มีค่าสัมบูรณ์สูง
- ค่าที่คาดการณ์ไว้ค่อนข้างห่างจากค่าจริง
ตัวอย่างเช่น สมมติว่า widget-price เป็นฟีเจอร์ของโมเดลหนึ่ง
สมมติว่าค่าเฉลี่ย widget-price คือ 7 ยูโร โดยมีค่าเบี่ยงเบนมาตรฐาน
เท่ากับ 1 ยูโร ตัวอย่างที่มี widget-price 12 ยูโรหรือ 2 ยูโร
จึงถือเป็นค่าผิดปกติ เนื่องจากราคาแต่ละรายการ
อยู่ห่างจากค่าเฉลี่ย 5 ส่วนเบี่ยงเบนมาตรฐาน
ค่าผิดปกติมักเกิดจากการพิมพ์ผิดหรือข้อผิดพลาดอื่นๆ ในการป้อนข้อมูล ในกรณีอื่นๆ ค่าผิดปกติไม่ใช่ข้อผิดพลาด เนื่องจากค่าที่อยู่ห่างจากค่าเฉลี่ย 5 ส่วนเบี่ยงเบนมาตรฐานนั้นพบได้ยากแต่ก็ไม่ใช่ว่าจะไม่มีเลย
ค่าผิดปกติมักทำให้เกิดปัญหาในการฝึกโมเดล การตัดค่าสุดโต่ง เป็นวิธีหนึ่งในการจัดการค่าผิดปกติ
ดูข้อมูลเพิ่มเติมได้ที่การทำงานกับข้อมูลตัวเลข ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
การประเมินนอกกลุ่มตัวอย่าง (การประเมิน OOB)
กลไกในการประเมินคุณภาพของDecision Forest โดยการทดสอบDecision Tree แต่ละรายการกับตัวอย่างที่ไม่ได้ใช้ในระหว่างการฝึก Decision Tree นั้น ตัวอย่างเช่น ใน แผนภาพต่อไปนี้ โปรดสังเกตว่าระบบจะฝึกต้นไม้ตัดสินใจแต่ละต้น กับตัวอย่างประมาณ 2 ใน 3 แล้วประเมินกับ ตัวอย่างที่เหลืออีก 1 ใน 3
การประเมินนอกกลุ่มตัวอย่างเป็นการประมาณกลไกการตรวจสอบแบบไขว้ที่ประหยัดการคำนวณและมีความระมัดระวัง ในการตรวจสอบความถูกต้องแบบไขว้ ระบบจะฝึกโมเดล 1 รายการสําหรับการตรวจสอบความถูกต้องแบบไขว้แต่ละรอบ (เช่น ฝึกโมเดล 10 รายการในการตรวจสอบความถูกต้องแบบไขว้ 10 เท่า) การประเมิน OOB จะฝึกโมเดลเดียว เนื่องจากการสุ่มตัวอย่างแบบแทนที่ จะละเว้นข้อมูลบางส่วนจากแต่ละทรีระหว่างการฝึก การประเมิน OOB จึงใช้ข้อมูลดังกล่าวเพื่อประมาณค่าการตรวจสอบแบบไขว้ได้
ดูข้อมูลเพิ่มเติมได้ที่การประเมินนอกกลุ่มตัวอย่าง ในหลักสูตร Decision Forests
เลเยอร์เอาต์พุต
เลเยอร์ "สุดท้าย" ของโครงข่ายประสาทเทียม เลเยอร์เอาต์พุตมีการคาดการณ์
ภาพต่อไปนี้แสดงโครงข่ายประสาทแบบลึกขนาดเล็กที่มีเลเยอร์อินพุต เลเยอร์ที่ซ่อน 2 เลเยอร์ และเลเยอร์เอาต์พุต
Overfitting
การสร้างโมเดลที่ตรงกับข้อมูลการฝึกอย่างใกล้ชิดมากจนโมเดลไม่สามารถคาดการณ์ข้อมูลใหม่ได้อย่างถูกต้อง
การทำให้เป็นปกติจะช่วยลดการปรับมากเกินไปได้ การฝึกในชุดการฝึกขนาดใหญ่และหลากหลายยังช่วยลดการเกิด Overfitting ได้ด้วย
ดูข้อมูลเพิ่มเติมได้ที่การเกิด Overfitting ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การโอเวอร์แซมปลิง
การนำตัวอย่างของคลาสส่วนน้อย ในชุดข้อมูลที่มีคลาสไม่สมดุลมาใช้ซ้ำเพื่อ สร้างชุดการฝึกที่สมดุลมากขึ้น
ตัวอย่างเช่น พิจารณาปัญหาการแยกประเภทแบบไบนารี ซึ่งอัตราส่วนของคลาสส่วนใหญ่ต่อคลาสส่วนน้อยคือ 5,000:1 หากชุดข้อมูลมีตัวอย่าง 1 ล้านรายการ ชุดข้อมูลจะมีตัวอย่างของคลาสส่วนน้อยเพียงประมาณ 200 รายการ ซึ่งอาจมีตัวอย่างน้อยเกินไปสำหรับการฝึกที่มีประสิทธิภาพ คุณอาจแก้ปัญหานี้ได้โดยการสุ่มตัวอย่างมากเกินไป (นำกลับมาใช้ใหม่) ตัวอย่าง 200 รายการนั้นหลายครั้ง ซึ่งอาจทำให้มีตัวอย่างเพียงพอสำหรับการฝึกที่เป็นประโยชน์
คุณต้องระมัดระวังเรื่องการปรับมากเกินไปเมื่อ ทำการสุ่มตัวอย่างเกิน
เปรียบเทียบกับการสุ่มตัวอย่างน้อยเกินไป
P
ข้อมูลที่แพ็ก
แนวทางในการจัดเก็บข้อมูลอย่างมีประสิทธิภาพมากขึ้น
ข้อมูลที่แพ็กจะจัดเก็บข้อมูลโดยใช้รูปแบบที่บีบอัดหรือใน วิธีอื่นๆ ที่ช่วยให้เข้าถึงข้อมูลได้อย่างมีประสิทธิภาพมากขึ้น ข้อมูลที่แพ็กจะลดปริมาณหน่วยความจำและการคำนวณที่จำเป็นต่อการเข้าถึงข้อมูล ซึ่งจะช่วยให้การฝึกเร็วขึ้นและการอนุมานโมเดลมีประสิทธิภาพมากขึ้น
มักใช้ข้อมูลที่แพ็กแล้วร่วมกับเทคนิคอื่นๆ เช่น การเพิ่มข้อมูลและการทำให้เป็นปกติ เพื่อปรับปรุงประสิทธิภาพของโมเดลให้ดียิ่งขึ้น
PaLM
ตัวย่อของ โมเดลภาษา Pathways
แพนด้า
API การวิเคราะห์ข้อมูลแบบคอลัมน์ที่สร้างขึ้นบน numpy เฟรมเวิร์กแมชชีนเลิร์นนิงหลายรายการ รวมถึง TensorFlow รองรับโครงสร้างข้อมูล pandas เป็นอินพุต ดูรายละเอียดได้ที่ เอกสารประกอบของ Pandas
พารามิเตอร์
น้ำหนักและอคติที่โมเดลเรียนรู้ระหว่างการฝึก ตัวอย่างเช่น ในโมเดลการถดถอยเชิงเส้น พารามิเตอร์ประกอบด้วย อคติ (b) และน้ำหนักทั้งหมด (w1, w2 และอื่นๆ) ในสูตรต่อไปนี้
ในทางตรงกันข้าม ไฮเปอร์พารามิเตอร์คือค่าที่คุณ (หรือบริการการปรับไฮเปอร์พารามิเตอร์) จัดหาให้แก่โมเดล เช่น อัตราการเรียนรู้เป็นไฮเปอร์พารามิเตอร์
การปรับแต่งที่มีประสิทธิภาพด้านพารามิเตอร์
ชุดเทคนิคในการปรับแต่งโมเดลภาษาขนาดใหญ่ ที่ได้รับการฝึกมาก่อน (PLM) อย่างมีประสิทธิภาพมากกว่าการปรับแต่งแบบเต็ม การปรับแต่งที่มีประสิทธิภาพด้านพารามิเตอร์มักจะปรับแต่งพารามิเตอร์น้อยกว่าการปรับแต่งแบบเต็มมาก แต่โดยทั่วไปแล้วจะสร้างโมเดลภาษาขนาดใหญ่ที่มีประสิทธิภาพดี (หรือเกือบดี) เท่ากับโมเดลภาษาขนาดใหญ่ที่สร้างจากการปรับแต่งแบบเต็ม
เปรียบเทียบการปรับแต่งที่มีประสิทธิภาพด้านพารามิเตอร์กับ
การปรับแต่งที่มีประสิทธิภาพด้านพารามิเตอร์เรียกอีกอย่างว่าการปรับแต่งแบบละเอียดที่มีประสิทธิภาพด้านพารามิเตอร์
เซิร์ฟเวอร์พารามิเตอร์ (PS)
งานที่ติดตามพารามิเตอร์ของโมเดลใน การตั้งค่าแบบกระจาย
การอัปเดตพารามิเตอร์
การดำเนินการปรับพารามิเตอร์ของโมเดลระหว่างการฝึก โดยปกติจะอยู่ในการทำซ้ำครั้งเดียวของ การไล่ระดับสี
อนุพันธ์ย่อย
อนุพันธ์ที่ถือว่าตัวแปรทั้งหมดเป็นค่าคงที่ ยกเว้นตัวแปร 1 ตัว ตัวอย่างเช่น อนุพันธ์ย่อยของ f(x, y) เทียบกับ x คืออนุพันธ์ของ f ที่ถือว่าเป็นฟังก์ชันของ x เพียงอย่างเดียว (นั่นคือคงค่า y ไว้) อนุพันธ์ย่อยของ f เทียบกับ x จะมุ่งเน้นเฉพาะ วิธีที่ x เปลี่ยนแปลง และไม่สนใจตัวแปรอื่นๆ ทั้งหมดในสมการ
อคติจากการเข้าร่วม
คำพ้องความหมายของอคติจากการไม่ตอบ ดูอคติในการเลือก
กลยุทธ์การแบ่งพาร์ติชัน
อัลกอริทึมที่ใช้ในการแบ่งตัวแปรในเซิร์ฟเวอร์พารามิเตอร์
pass at k (pass@k)
เมตริกที่ใช้กำหนดคุณภาพของโค้ด (เช่น Python) ที่โมเดลภาษาขนาดใหญ่สร้างขึ้น กล่าวอย่างเจาะจงคือ การส่งผ่านที่ k จะบอกความน่าจะเป็นที่โค้ดอย่างน้อย 1 บล็อกจากโค้ด k บล็อกที่สร้างขึ้นจะผ่านการทดสอบหน่วยทั้งหมด
โมเดลภาษาขนาดใหญ่มักประสบปัญหาในการสร้างโค้ดที่ดีสำหรับปัญหาการเขียนโปรแกรมที่ซับซ้อน วิศวกรซอฟต์แวร์ปรับตัวให้เข้ากับปัญหานี้โดย การแจ้งโมเดลภาษาขนาดใหญ่ให้สร้างโซลูชันหลายรายการ (k) สำหรับปัญหาเดียวกัน จากนั้นวิศวกรซอฟต์แวร์จะทดสอบโซลูชันแต่ละรายการ กับการทดสอบหน่วย การคำนวณการผ่านที่ k จะขึ้นอยู่กับผลลัพธ์ ของการทดสอบหน่วย
- หากโซลูชันอย่างน้อย 1 รายการผ่านการทดสอบหน่วย แสดงว่า LLM ผ่านความท้าทายในการสร้างโค้ดนั้น
- หากไม่มีโซลูชันใดผ่านการทดสอบหน่วย LLM จะไม่ผ่านความท้าทายในการสร้างโค้ดนั้น
สูตรสำหรับพาสที่ k มีดังนี้
\[\text{pass at k} = \frac{\text{total number of passes}} {\text{total number of challenges}}\]
โดยทั่วไปแล้ว ค่า k ที่สูงขึ้นจะทำให้ได้คะแนนที่ผ่านเกณฑ์ที่สูงขึ้น อย่างไรก็ตาม ค่า k ที่สูงขึ้นต้องใช้โมเดลภาษาขนาดใหญ่และการทดสอบหน่วย มากขึ้น
โมเดลภาษา Pathways (PaLM)
โมเดลรุ่นเก่าและรุ่นก่อนหน้าของโมเดล Gemini
Pax
เฟรมเวิร์กการเขียนโปรแกรมที่ออกแบบมาเพื่อฝึกโมเดล โครงข่ายระบบประสาทเทียมขนาดใหญ่ ซึ่งมีขนาดใหญ่มากจนครอบคลุมชิป TPU ตัวเร่ง ชิ้น หรือพ็อดหลายรายการ
Pax สร้างขึ้นบน Flax ซึ่งสร้างขึ้นบน JAX
เพอร์เซปตรอน
ระบบ (ทั้งฮาร์ดแวร์หรือซอฟต์แวร์) ที่รับค่าอินพุตอย่างน้อย 1 ค่า เรียกใช้ฟังก์ชันกับผลรวมแบบถ่วงน้ำหนักของอินพุต และคำนวณค่า เอาต์พุตเดียว ในแมชชีนเลิร์นนิง ฟังก์ชันมักจะเป็นแบบไม่เชิงเส้น เช่น ReLU, sigmoid หรือ tanh ตัวอย่างเช่น เพอร์เซปตรอนต่อไปนี้ใช้ฟังก์ชันซิกมอยด์เพื่อประมวลผล ค่าอินพุต 3 ค่า
ในภาพประกอบต่อไปนี้ เพอร์เซ็ปตรอนรับอินพุต 3 รายการ ซึ่งแต่ละรายการ จะได้รับการแก้ไขด้วยน้ำหนักก่อนเข้าสู่เพอร์เซ็ปตรอน

เพอร์เซ็ปตรอนคือนิวรอนในโครงข่ายประสาทเทียม
การแสดง
คำที่มีความหมายหลายอย่างต่อไปนี้
- ความหมายมาตรฐานในวิศวกรรมซอฟต์แวร์ กล่าวคือ ซอฟต์แวร์นี้ทำงานได้เร็ว (หรือมีประสิทธิภาพ) เพียงใด
- ความหมายในแมชชีนเลิร์นนิง ในที่นี้ ประสิทธิภาพจะตอบคำถามต่อไปนี้ โมเดลนี้ถูกต้องเพียงใด กล่าวคือ การคาดการณ์ของโมเดลดีเพียงใด
ความสําคัญของตัวแปรการเรียงสับเปลี่ยน
ประเภทความสําคัญของตัวแปรที่ประเมิน การเพิ่มขึ้นของข้อผิดพลาดในการคาดการณ์ของโมเดลหลังจากสลับค่าของฟีเจอร์ ความสําคัญของตัวแปรการสับเปลี่ยนเป็นเมตริกที่ไม่ขึ้นอยู่กับโมเดล
Perplexity
มาตรวัดหนึ่งที่ใช้ประเมินว่าโมเดลทํางานได้ดีเพียงใด เช่น สมมติว่างานของคุณคือการอ่านตัวอักษร 2-3 ตัวแรกของคำ ที่ผู้ใช้พิมพ์บนแป้นพิมพ์โทรศัพท์ และแสดงรายการคำที่เป็นไปได้ เพื่อเติมคำให้สมบูรณ์ ค่าความซับซ้อน P สำหรับงานนี้คือจำนวนคำที่ต้องเดาโดยประมาณเพื่อให้รายการของคุณมีคำจริงที่ผู้ใช้พยายามพิมพ์
Perplexity เกี่ยวข้องกับครอสเอนโทรปีดังนี้
ไปป์ไลน์
โครงสร้างพื้นฐานที่อยู่รอบๆ อัลกอริทึมแมชชีนเลิร์นนิง ไปป์ไลน์ ประกอบด้วยการรวบรวมข้อมูล การใส่ข้อมูลลงในไฟล์ข้อมูลการฝึก การฝึกโมเดลอย่างน้อย 1 รายการ และการส่งออกโมเดลไปยังการใช้งานจริง
ดูข้อมูลเพิ่มเติมได้ที่ไปป์ไลน์ ML ในหลักสูตรการจัดการโปรเจ็กต์ ML
การไปป์ไลน์
รูปแบบของการทำงานแบบขนานของโมเดลซึ่งการประมวลผลของโมเดล จะแบ่งออกเป็นหลายขั้นตอนต่อเนื่องกัน และแต่ละขั้นตอนจะดำเนินการ ในอุปกรณ์ที่แตกต่างกัน ในขณะที่สเตจหนึ่งประมวลผลชุดข้อมูลหนึ่ง สเตจก่อนหน้า จะประมวลผลชุดข้อมูลถัดไปได้
ดูการฝึกอบรมแบบแบ่งระยะด้วย
pjit
ฟังก์ชัน JAX ที่แยกโค้ดเพื่อเรียกใช้ในชิปตัวเร่งหลายตัว ผู้ใช้ส่งฟังก์ชันไปยัง pjit ซึ่งจะแสดงผลฟังก์ชันที่มีความหมายเทียบเท่ากัน แต่ได้รับการคอมไพล์ เป็นการคำนวณ XLA ที่ทำงานในอุปกรณ์หลายเครื่อง (เช่น GPU หรือแกน TPU)
pjit ช่วยให้ผู้ใช้แบ่งการคำนวณออกเป็นส่วนๆ ได้โดยไม่ต้องเขียนใหม่ด้วยการใช้ตัวแบ่งพาร์ติชัน SPMD
ตั้งแต่เดือนมีนาคม 2023 เป็นต้นมา เราได้รวม pjit เข้ากับ jit แล้ว ดูรายละเอียดเพิ่มเติมได้ที่
อาร์เรย์แบบกระจายและการ
ประมวลผลแบบขนานอัตโนมัติ
PLM
คำย่อของโมเดลภาษาที่ฝึกล่วงหน้า
pmap
ฟังก์ชัน JAX ที่เรียกใช้สำเนาของฟังก์ชันอินพุต ในอุปกรณ์ฮาร์ดแวร์พื้นฐานหลายเครื่อง (CPU, GPU หรือ TPU) โดยมีค่าอินพุตที่แตกต่างกัน pmap อาศัย SPMD
policy
ในการเรียนรู้แบบเสริมกำลัง การแมปเชิงความน่าจะเป็นของเอเจนต์จากสถานะไปยังการดำเนินการ
การรวม
การลดขนาดเมทริกซ์ (หรือเมทริกซ์) ที่สร้างขึ้นโดยเลเยอร์ Convolutional ก่อนหน้าให้เป็นเมทริกซ์ขนาดเล็กลง โดยปกติการรวมจะเกี่ยวข้องกับการใช้ค่าสูงสุดหรือค่าเฉลี่ย ในพื้นที่ที่รวม ตัวอย่างเช่น สมมติว่าเรามีเมทริกซ์ 3x3 ดังนี้
![เมทริกซ์ 3x3 [[5,3,1], [8,2,5], [9,4,3]]](https://developers.google.com/static/machine-learning/glossary/images/PoolingStart.svg?hl=th)
การดำเนินการพูลจะแบ่งเมทริกซ์ออกเป็นชิ้นๆ แล้วเลื่อนการดำเนินการ Convolutional ตามระยะก้าวย่าง เช่นเดียวกับการดำเนินการ Convolutional ตัวอย่างเช่น สมมติว่าการดำเนินการพูล แบ่งเมทริกซ์การแปลงเป็นชิ้นๆ ขนาด 2x2 โดยมีระยะก้าวยาว 1x1 ดังที่แผนภาพต่อไปนี้แสดงให้เห็น การดำเนินการพูลจะเกิดขึ้น 4 ครั้ง สมมติว่าการดำเนินการจัดกลุ่มแต่ละครั้งเลือกค่าสูงสุดของ ทั้ง 4 รายการในสไลซ์นั้น
![เมทริกซ์อินพุตคือ 3x3 ที่มีค่า [[5,3,1], [8,2,5], [9,4,3]]
เมทริกซ์ย่อย 2x2 ด้านซ้ายบนของเมทริกซ์อินพุตคือ [[5,3], [8,2]] ดังนั้น
การดำเนินการพูลด้านซ้ายบนจึงให้ค่า 8 (ซึ่งเป็นค่าสูงสุดของ
5, 3, 8 และ 2) เมทริกซ์ย่อย 2x2 ด้านขวาบนของเมทริกซ์อินพุตคือ [[3,1], [2,5]] ดังนั้นการดำเนินการพูลด้านขวาบนจึงให้ค่า 5 เมทริกซ์ย่อย 2x2 ด้านซ้ายล่างของเมทริกซ์อินพุตคือ
[[8,2], [9,4]] ดังนั้นการดำเนินการ Pooling ด้านซ้ายล่างจึงให้ค่า
9 เมทริกซ์ย่อย 2x2 ด้านขวาล่างของเมทริกซ์อินพุตคือ
[[2,5], [4,3]] ดังนั้นการดำเนินการ Pooling ด้านขวาล่างจึงให้ค่า
5 โดยสรุป การดำเนินการพูลจะให้เมทริกซ์ 2x2
[[8,5], [9,5]]](https://developers.google.com/static/machine-learning/glossary/images/PoolingConvolution.svg?hl=th)
พูลช่วยบังคับใช้ความไม่แปรเปลี่ยนตามการแปลในเมทริกซ์อินพุต
การรวมกลุ่มสำหรับแอปพลิเคชันวิชันซิสเต็มเรียกอย่างเป็นทางการว่าการรวมกลุ่มเชิงพื้นที่ โดยปกติแล้ว แอปพลิเคชันอนุกรมเวลาจะอ้างอิงถึงการรวมเป็นการรวมเชิงเวลา การพูลมักเรียกว่าการสุ่มตัวอย่างย่อยหรือการดาวน์แซมปลิง
ดูขอแนะนำโครงข่ายประสาทแบบคอนโวลูชัน ในหลักสูตร ML Practicum: การแยกประเภทรูปภาพ
การเข้ารหัสตำแหน่ง
เทคนิคในการเพิ่มข้อมูลเกี่ยวกับตำแหน่งของโทเค็นในลำดับไปยัง การฝังโทเค็น โมเดล Transformer ใช้การเข้ารหัสตำแหน่งเพื่อทำความเข้าใจความสัมพันธ์ระหว่างส่วนต่างๆ ของลำดับได้ดียิ่งขึ้น
การติดตั้งใช้งานการเข้ารหัสตำแหน่งโดยทั่วไปจะใช้ฟังก์ชันไซน์ (กล่าวอย่างเจาะจงคือ ความถี่และแอมพลิจูดของฟังก์ชันไซน์จะกำหนดโดยตำแหน่งของโทเค็นในลำดับ) เทคนิคนี้ ช่วยให้โมเดล Transformer เรียนรู้ที่จะให้ความสนใจกับส่วนต่างๆ ของ ลําดับตามตําแหน่งของส่วนนั้นๆ
คลาสที่เป็นบวก
ชั้นเรียนที่คุณกำลังทดสอบ
เช่น คลาสที่เป็นบวกในโมเดลมะเร็งอาจเป็น "เนื้องอก" คลาสที่เป็นบวกในโมเดลการจัดประเภทอีเมล อาจเป็น "จดหมายขยะ"
เปรียบเทียบกับคลาสที่เป็นลบ
หลังการประมวลผล
การปรับเอาต์พุตของโมเดลหลังจากเรียกใช้โมเดลแล้ว การประมวลผลภายหลังสามารถใช้เพื่อบังคับใช้ข้อจํากัดด้านความเป็นธรรมโดยไม่ต้อง แก้ไขโมเดลด้วยตนเอง
ตัวอย่างเช่น อาจใช้การประมวลผลภายหลังกับโมเดลการจัดประเภทแบบไบนารีโดยการตั้งค่าเกณฑ์การจัดประเภทเพื่อให้ความเท่าเทียมกันของโอกาสยังคงอยู่ สําหรับแอตทริบิวต์บางอย่างโดยตรวจสอบว่าอัตราผลบวกจริง เหมือนกันสําหรับค่าทั้งหมดของแอตทริบิวต์นั้น
โมเดลที่ฝึกภายหลัง
คำที่กำหนดอย่างกว้างๆ ซึ่งโดยทั่วไปหมายถึงโมเดลที่ผ่านการฝึกมาก่อนซึ่งผ่านการประมวลผลภายหลังมาแล้ว เช่น การประมวลผลอย่างน้อย 1 รายการต่อไปนี้
PR AUC (พื้นที่ใต้กราฟ PR)
พื้นที่ใต้กราฟ Precision-Recall ที่ประมาณค่าระหว่างจุดต่างๆ ซึ่งได้จากการพล็อตจุด (ความอ่อนไหว ความแม่นยำ) สำหรับค่าต่างๆ ของเกณฑ์การจัดประเภท
Praxis
ไลบรารี ML หลักที่มีประสิทธิภาพสูงของ Pax โดยมักจะเรียกว่า "ไลบรารีเลเยอร์"
Praxis ไม่ได้มีเพียงคำจำกัดความของคลาส Layer เท่านั้น แต่ยังมีคอมโพเนนต์สนับสนุนส่วนใหญ่ด้วย ซึ่งรวมถึง
- ข้อมูลอินพุต
- ไลบรารีการกำหนดค่า (HParam และ Fiddle)
- optimizers
Praxis มีคำจำกัดความสำหรับคลาส Model
ความแม่นยำ
เมตริกสําหรับโมเดลการจัดประเภทที่ตอบคําถามต่อไปนี้
เมื่อโมเดลคาดการณ์คลาสเชิงบวก การคาดการณ์กี่เปอร์เซ็นต์ที่ถูกต้อง
สูตรมีดังนี้
ที่ไหน
- ผลบวกจริงหมายความว่าโมเดลคาดการณ์คลาสที่เป็นบวกได้อย่างถูกต้อง
- ผลบวกลวงหมายความว่าโมเดลคาดการณ์คลาสที่เป็นบวกอย่างไม่ถูกต้อง
เช่น สมมติว่าโมเดลทำการคาดการณ์เชิงบวก 200 รายการ จากการคาดการณ์ที่เป็นบวก 200 รายการ
- 150 รายการเป็นผลบวกจริง
- 50 รายการเป็นการตรวจจับที่ผิดพลาด
ในกรณีนี้
เปรียบเทียบกับความแม่นยำและการเรียกคืน
ดูข้อมูลเพิ่มเติมได้ที่การจัดประเภท: ความแม่นยำ การเรียกคืน ความเที่ยงตรง และเมตริกที่เกี่ยวข้อง ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
ความแม่นยำที่ k (precision@k)
เมตริกสําหรับการประเมินรายการที่จัดอันดับ (เรียงลําดับ) ความแม่นยำที่ k ระบุเศษส่วนของรายการแรก k ในรายการนั้น ซึ่ง "เกี่ยวข้อง" โดยการ
\[\text{precision at k} = \frac{\text{relevant items in first k items of the list}} {\text{k}}\]
ค่าของ k ต้องน้อยกว่าหรือเท่ากับความยาวของรายการที่แสดง โปรดทราบว่าความยาวของรายการที่แสดงจะไม่รวมอยู่ในการคำนวณ
ความเกี่ยวข้องมักเป็นเรื่องส่วนบุคคล แม้แต่ผู้ประเมินที่เป็นมนุษย์ซึ่งเป็นผู้เชี่ยวชาญก็มักจะมีความเห็นไม่ตรงกันว่ารายการใดเกี่ยวข้อง
เปรียบเทียบกับ:
เส้นโค้ง Precision-Recall
กราฟของความแม่นยำเทียบกับความอ่อนไหวที่เกณฑ์การจัดประเภทต่างๆ
การคาดการณ์
เอาต์พุตของโมเดล เช่น
- การคาดการณ์ของโมเดลการจัดประเภทแบบไบนารีคือคลาสที่เป็นบวกหรือคลาสที่เป็นลบ
- การคาดการณ์ของโมเดลการจัดประเภทแบบหลายคลาสคือ 1 คลาส
- การคาดการณ์ของโมเดลการถดถอยเชิงเส้นคือตัวเลข
อคติในการคาดคะเน
ค่าที่ระบุว่าค่าเฉลี่ยของการคาดการณ์อยู่ห่างจากค่าเฉลี่ยของป้ายกำกับ ในชุดข้อมูลมากน้อยเพียงใด
อย่าสับสนกับคำว่าอคติในโมเดลแมชชีนเลิร์นนิง หรืออคติในด้านจริยธรรมและความยุติธรรม
ML เชิงคาดการณ์
ระบบแมชชีนเลิร์นนิงมาตรฐาน ("คลาสสิก")
คำว่า ML เชิงคาดการณ์ไม่มีคำจำกัดความที่เป็นทางการ แต่คำนี้ใช้เพื่อแยกหมวดหมู่ของระบบ ML ที่ไม่ได้อิงตามGenerative AI
ความเท่าเทียมในการคาดการณ์
เมตริกความเป็นธรรมที่ตรวจสอบว่าสำหรับโมเดลการแยกประเภทที่กำหนด อัตราความแม่นยำเทียบเท่ากับกลุ่มย่อยที่อยู่ระหว่างการพิจารณาหรือไม่
ตัวอย่างเช่น โมเดลที่คาดการณ์การตอบรับเข้าวิทยาลัยจะตรงตาม ความเท่าเทียมเชิงคาดการณ์สำหรับสัญชาติ หากอัตราความแม่นยำเท่ากัน สำหรับชาวลิลิปุตและชาวโบรบดิงแนก
บางครั้งเราเรียกความเท่าเทียมในการคาดการณ์ว่าความเท่าเทียมของอัตราการคาดการณ์
ดูรายละเอียดเพิ่มเติมเกี่ยวกับความเท่าเทียมในการคาดการณ์ได้ที่ "คำอธิบายคำจำกัดความของความเป็นธรรม" (ส่วนที่ 3.2.1)
ความเท่าเทียมของราคาเชิงคาดการณ์
อีกชื่อหนึ่งของความเท่าเทียมในการคาดการณ์
การประมวลผลล่วงหน้า
การประมวลผลข้อมูลก่อนที่จะนำไปใช้ฝึกโมเดล การประมวลผลล่วงหน้าอาจ ง่ายๆ เพียงแค่การนำคำออกจากคลังข้อความภาษาอังกฤษที่ไม่ได้ อยู่ในพจนานุกรมภาษาอังกฤษ หรืออาจซับซ้อนถึงขั้นการแสดง จุดข้อมูลใหม่ในลักษณะที่กำจัดแอตทริบิวต์ที่สัมพันธ์กับแอตทริบิวต์ที่ละเอียดอ่อนให้ได้มากที่สุด การประมวลผลล่วงหน้าช่วยให้เป็นไปตามข้อจำกัดด้านความเป็นธรรมได้โมเดลที่ฝึกไว้ล่วงหน้า
แม้ว่าคำนี้จะหมายถึงโมเดลหรือเวกเตอร์การฝังที่ผ่านการฝึกมาแล้ว แต่ปัจจุบันโมเดลที่ผ่านการฝึกเบื้องต้นมักหมายถึงโมเดลภาษาขนาดใหญ่ที่ผ่านการฝึกมาแล้ว หรือโมเดล Generative AI รูปแบบอื่นๆ ที่ผ่านการฝึกมาแล้ว
ดูโมเดลพื้นฐานและ โมเดลพื้นฐานด้วย
การฝึกล่วงหน้า
การฝึกโมเดลเบื้องต้นในชุดข้อมูลขนาดใหญ่ โมเดลที่ผ่านการฝึกมาก่อนบางโมเดล เป็นโมเดลขนาดใหญ่ที่ทำงานได้ไม่ดีนักและมักจะต้องได้รับการปรับแต่งผ่านการฝึกเพิ่มเติม ตัวอย่างเช่น ผู้เชี่ยวชาญด้าน ML อาจฝึกล่วงหน้าโมเดลภาษาขนาดใหญ่ในชุดข้อมูลข้อความขนาดใหญ่ เช่น หน้าภาษาอังกฤษทั้งหมดในวิกิพีเดีย หลังจากการฝึกเบื้องต้น โมเดลที่ได้อาจได้รับการปรับแต่งเพิ่มเติมผ่านเทคนิคต่อไปนี้
ความเชื่อเบื้องต้น
สิ่งที่คุณเชื่อเกี่ยวกับข้อมูลก่อนเริ่มฝึกโมเดล ตัวอย่างเช่น การทำให้เป็นปกติ L2 อาศัย ความเชื่อก่อนหน้าว่าน้ำหนักควรมีขนาดเล็กและมีการกระจายตัวตามปกติ รอบๆ ศูนย์
Pro
โมเดล Gemini ที่มีพารามิเตอร์น้อยกว่า Ultra แต่มีพารามิเตอร์มากกว่า Nano ดูรายละเอียดได้ที่ Gemini Pro
โมเดลการถดถอยเชิงความน่าจะเป็น
โมเดลการถดถอยที่ใช้ไม่เพียงแต่น้ำหนักสำหรับฟีเจอร์แต่ละรายการ แต่ยังรวมถึงความไม่แน่นอนของน้ำหนักเหล่านั้นด้วย โมเดลการถดถอยเชิงความน่าจะเป็นจะสร้าง การคาดการณ์และความไม่แน่นอนของการคาดการณ์นั้น เช่น โมเดลการถดถอยเชิงความน่าจะเป็นอาจให้ผลการคาดการณ์เป็น 325 โดยมี ส่วนเบี่ยงเบนมาตรฐานเป็น 12 ดูข้อมูลเพิ่มเติมเกี่ยวกับโมเดลการถดถอยเชิงความน่าจะเป็นได้ใน Colab นี้ใน tensorflow.org
ฟังก์ชันความหนาแน่นของความน่าจะเป็น
ฟังก์ชันที่ระบุความถี่ของตัวอย่างข้อมูลที่มีค่าใดค่าหนึ่งตรงกัน เมื่อค่าของชุดข้อมูลเป็นตัวเลขทศนิยมแบบต่อเนื่อง
การจับคู่ที่ตรงกันทั้งหมดจะเกิดขึ้นได้ยาก อย่างไรก็ตาม การหาปริพันธ์ของฟังก์ชันความหนาแน่นของความน่าจะเป็นจากค่า x ถึงค่า y จะให้ความถี่ที่คาดหวังของตัวอย่างข้อมูลระหว่าง x และ y
ตัวอย่างเช่น พิจารณาการแจกแจงปกติที่มีค่าเฉลี่ย 200 และค่าเบี่ยงเบนมาตรฐาน 30 หากต้องการกำหนดความถี่ที่คาดไว้ของตัวอย่างข้อมูล ที่อยู่ในช่วง 211.4 ถึง 218.7 คุณสามารถรวมฟังก์ชันความหนาแน่นของความน่าจะเป็น สำหรับการแจกแจงแบบปกติจาก 211.4 ถึง 218.7
prompt
ข้อความใดก็ตามที่ป้อนเป็นอินพุตไปยังโมเดลภาษาขนาดใหญ่ เพื่อกำหนดให้โมเดลทำงานในลักษณะใดลักษณะหนึ่ง พรอมต์อาจสั้นเพียง วลีเดียวหรือยาวเท่าใดก็ได้ (เช่น ข้อความทั้งหมดของนวนิยาย) พรอมต์ จะอยู่ในหลายหมวดหมู่ รวมถึงหมวดหมู่ที่แสดงในตารางต่อไปนี้
| หมวดหมู่พรอมต์ | ตัวอย่าง | หมายเหตุ |
|---|---|---|
| คำถาม | นกพิราบบินได้เร็วแค่ไหน | |
| โรงเรียนฝึกอบรม | แต่งกลอนขำๆ เกี่ยวกับการเก็งกำไร | พรอมต์ที่ขอให้โมเดลภาษาขนาดใหญ่ทำบางอย่าง |
| ตัวอย่าง | แปลโค้ด Markdown เป็น HTML เช่น
มาร์กดาวน์: * รายการ HTML: <ul> <li>รายการ</li> </ul> |
ประโยคแรกในพรอมต์ตัวอย่างนี้คือคำสั่ง ส่วนที่เหลือของพรอมต์คือตัวอย่าง |
| บทบาท | อธิบายเหตุผลที่ใช้การไล่ระดับความชันในการฝึกแมชชีนเลิร์นนิงให้ ผู้ที่จบปริญญาเอกสาขาฟิสิกส์ | ส่วนแรกของประโยคคือคำสั่ง ส่วนวลี "to a PhD in Physics" คือส่วนบทบาท |
| อินพุตบางส่วนเพื่อให้โมเดลทำให้เสร็จสมบูรณ์ | นายกรัฐมนตรีของสหราชอาณาจักรอาศัยอยู่ที่ | พรอมต์อินพุตบางส่วนอาจสิ้นสุดอย่างกะทันหัน (ดังตัวอย่างนี้) หรือลงท้ายด้วยขีดล่าง |
โมเดล Generative AI สามารถตอบสนองต่อพรอมต์ด้วยข้อความ โค้ด รูปภาพ การฝัง วิดีโอ และอื่นๆ อีกมากมาย
การเรียนรู้ตามพรอมต์
ความสามารถของโมเดลบางอย่างที่ช่วยให้โมเดลปรับเปลี่ยน ลักษณะการทำงานเพื่อตอบสนองต่อข้อความที่ป้อนโดยพลการ (พรอมต์) ได้ ในกระบวนทัศน์การเรียนรู้ตามพรอมต์ทั่วไป โมเดลภาษาขนาดใหญ่จะตอบกลับพรอมต์โดยการสร้างข้อความ ตัวอย่างเช่น สมมติว่าผู้ใช้ป้อนพรอมต์ต่อไปนี้
สรุปกฎการเคลื่อนที่ข้อที่ 3 ของนิวตัน
โมเดลที่ใช้การเรียนรู้ตามพรอมต์ไม่ได้ผ่านการฝึกมาเพื่อตอบพรอมต์ก่อนหน้าโดยเฉพาะ แต่โมเดล "รู้" ข้อเท็จจริงมากมายเกี่ยวกับฟิสิกส์ กฎเกณฑ์ทางภาษาทั่วไป และสิ่งที่ประกอบกันเป็นคำตอบที่มีประโยชน์โดยทั่วไป ความรู้นั้นเพียงพอที่จะให้คำตอบที่ (หวังว่า) จะเป็นประโยชน์ ความคิดเห็นเพิ่มเติมจากเจ้าหน้าที่ ("คำตอบนั้นซับซ้อนเกินไป" หรือ "รีแอ็กชันคืออะไร") จะช่วยให้ระบบการเรียนรู้บางอย่างที่อิงตามพรอมต์ค่อยๆ ปรับปรุงประโยชน์ของคำตอบ
การออกแบบพรอมต์
คำพ้องความหมายของวิศวกรรมพรอมต์
วิศวกรรมพรอมต์
ศิลปะการสร้างพรอมต์ที่กระตุ้นให้คำตอบที่ต้องการจากโมเดลภาษาขนาดใหญ่ มนุษย์จะทำพรอมต์ เอ็นจิเนียริง การเขียนพรอมต์ที่มีโครงสร้างดีเป็นส่วนสำคัญในการรับประกัน คำตอบที่เป็นประโยชน์จากโมเดลภาษาขนาดใหญ่ การออกแบบพรอมต์ขึ้นอยู่กับหลายปัจจัย ได้แก่
- ชุดข้อมูลที่ใช้ในการฝึกโมเดลภาษาขนาดใหญ่ล่วงหน้าและอาจใช้ปรับแต่ง
- อุณหภูมิและพารามิเตอร์การถอดรหัสอื่นๆ ที่โมเดลใช้ในการสร้างคำตอบ
การออกแบบพรอมต์เป็นคำพ้องความหมายของวิศวกรรมพรอมต์
ดูรายละเอียดเพิ่มเติมเกี่ยวกับการเขียนพรอมต์ที่เป็นประโยชน์ได้ที่ ข้อมูลเบื้องต้นเกี่ยวกับการออกแบบพรอมต์
ชุดพรอมต์
กลุ่มพรอมต์สำหรับการประเมิน โมเดลภาษาขนาดใหญ่ ตัวอย่างเช่น ภาพต่อไปนี้ แสดงชุดพรอมต์ที่ประกอบด้วยพรอมต์ 3 รายการ
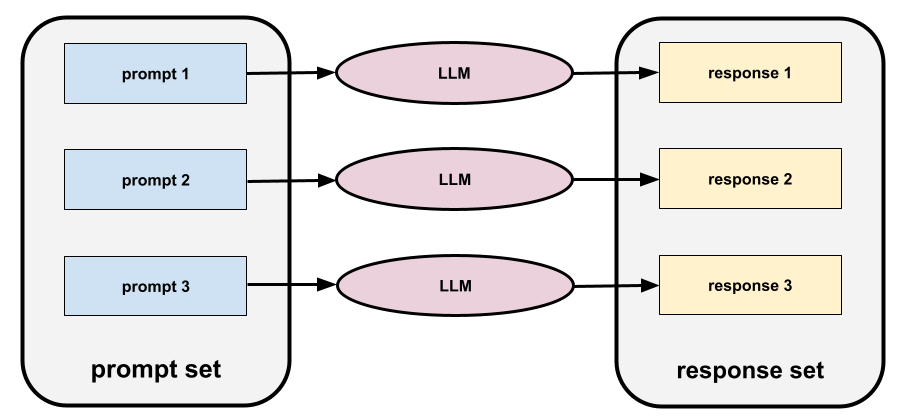
ชุดพรอมต์ที่ดีประกอบด้วยคอลเล็กชันพรอมต์ที่ "หลากหลาย" เพียงพอที่จะ ประเมินความปลอดภัยและประโยชน์ของโมเดลภาษาขนาดใหญ่อย่างละเอียด
ดูชุดคำตอบด้วย
การปรับแต่งพรอมต์
กลไกการปรับแต่งที่มีประสิทธิภาพของพารามิเตอร์ ซึ่งจะเรียนรู้ "คำนำหน้า" ที่ระบบจะเพิ่มไว้หน้าพรอมต์จริง
การปรับพรอมต์รูปแบบหนึ่งซึ่งบางครั้งเรียกว่าการปรับคำนำหน้าคือการ เพิ่มคำนำหน้าที่ทุกเลเยอร์ ในทางตรงกันข้าม การปรับพรอมต์ส่วนใหญ่จะเพิ่มคำนำหน้าให้กับเลเยอร์อินพุตเท่านั้น
พร็อกซี (แอตทริบิวต์ที่ละเอียดอ่อน)
แอตทริบิวต์ที่ใช้แทนแอตทริบิวต์ที่ละเอียดอ่อน เช่น รหัสไปรษณีย์ของบุคคลอาจใช้เป็นตัวแทนของรายได้ เชื้อชาติ หรือกลุ่มชาติพันธุ์ป้ายกำกับพร็อกซี
ข้อมูลที่ใช้ในการประมาณป้ายกำกับซึ่งไม่มีในชุดข้อมูลโดยตรง
ตัวอย่างเช่น สมมติว่าคุณต้องฝึกโมเดลเพื่อคาดการณ์ระดับความเครียดของพนักงาน ชุดข้อมูลของคุณมีฟีเจอร์การคาดการณ์จำนวนมาก แต่ไม่มีป้ายกำกับที่ชื่อระดับความเครียด คุณจึงเลือก "อุบัติเหตุในที่ทำงาน" เป็นป้ายกำกับพร็อกซีสำหรับ ระดับความเครียด เพราะพนักงานที่อยู่ภายใต้ความเครียดสูงมีแนวโน้มที่จะเกิดอุบัติเหตุมากกว่าพนักงานที่ใจเย็น หรือว่าไม่ อุบัติเหตุในที่ทำงานอาจเพิ่มขึ้นและลดลงด้วยเหตุผลหลายประการ
ตัวอย่างที่ 2 สมมติว่าคุณต้องการให้ is it raining? เป็นป้ายกำกับบูลีน สำหรับชุดข้อมูล แต่ชุดข้อมูลไม่มีข้อมูลฝน หากมีรูปถ่าย คุณอาจสร้างรูปภาพของผู้คน ที่ถือร่มเป็นป้ายกำกับพร็อกซีสำหรับ ฝนตกไหม ป้ายกำกับนี้เป็น พร็อกซีที่ดีไหม อาจเป็นไปได้ แต่ผู้คนในบางวัฒนธรรมอาจมีแนวโน้มที่จะพกร่มเพื่อป้องกันแสงแดดมากกว่าฝน
ป้ายกำกับพร็อกซีมักไม่สมบูรณ์ หากเป็นไปได้ ให้เลือกป้ายกำกับจริงแทน ป้ายกำกับพร็อกซี อย่างไรก็ตาม หากไม่มีป้ายกำกับจริง ให้เลือกป้ายกำกับพร็อกซีอย่างระมัดระวัง โดยเลือกป้ายกำกับพร็อกซีที่แย่น้อยที่สุด
ดูข้อมูลเพิ่มเติมได้ที่ชุดข้อมูล: ป้ายกำกับ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ฟังก์ชันบริสุทธิ์
ฟังก์ชันที่มีเอาต์พุตอิงตามอินพุตของฟังก์ชันนั้นๆ เท่านั้น และไม่มีผลข้างเคียง กล่าวคือ ฟังก์ชันบริสุทธิ์จะไม่ใช้หรือเปลี่ยนแปลงสถานะส่วนกลางใดๆ เช่น เนื้อหาของไฟล์หรือค่าของตัวแปรนอกฟังก์ชัน
คุณสามารถใช้ฟังก์ชันบริสุทธิ์เพื่อสร้างโค้ดที่ปลอดภัยต่อเธรด ซึ่งจะเป็นประโยชน์ เมื่อทำการ Sharding โค้ดโมเดลในชิปตัวเร่งหลายตัว
วิธีการเปลี่ยนรูปแบบฟังก์ชันของ JAX กำหนดให้ฟังก์ชันอินพุตต้องเป็นฟังก์ชันบริสุทธิ์
Q
ฟังก์ชัน Q
ในการเรียนรู้แบบเสริมกำลัง ฟังก์ชันที่คาดการณ์ผลตอบแทนที่คาดไว้จากการทำการดำเนินการในสถานะหนึ่งๆ แล้วทำตามนโยบายที่กำหนด
ฟังก์ชัน Q เรียกอีกอย่างว่าฟังก์ชันค่าสถานะ-การดำเนินการ
Q-learning
ในการเรียนรู้แบบเสริมกำลัง อัลกอริทึมที่ อนุญาตให้เอเจนต์ เรียนรู้ฟังก์ชัน Q ที่ดีที่สุดของ กระบวนการตัดสินใจแบบมาร์คอฟ โดยใช้สมการเบลแมน กระบวนการตัดสินใจแบบ Markov สร้างโมเดลสภาพแวดล้อม
ควอนไทล์
กลุ่มแต่ละกลุ่มในการจัดกลุ่มควอนไทล์
การจัดกลุ่มตามควอนไทล์
การกระจายค่าของฟีเจอร์ลงในกลุ่มเพื่อให้แต่ละกลุ่มมีจำนวนตัวอย่างเท่ากัน (หรือเกือบเท่ากัน) ตัวอย่างเช่น รูปต่อไปนี้แบ่งคะแนน 44 คะแนนออกเป็น 4 กลุ่ม โดยแต่ละกลุ่ม มีคะแนน 11 คะแนน เพื่อให้ที่เก็บข้อมูลแต่ละรายการในรูปมีจำนวนจุดเท่ากัน ที่เก็บข้อมูลบางรายการจึงครอบคลุมค่า x ที่มีความกว้างต่างกัน

ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลเชิงตัวเลข: การจัดกลุ่ม ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การหาปริมาณ
คำที่มีความหมายหลายอย่างซึ่งอาจใช้ในลักษณะใดก็ได้ต่อไปนี้
- การใช้การจัดกลุ่มตามควอนไทล์ ในฟีเจอร์ที่เฉพาะเจาะจง
- การเปลี่ยนข้อมูลเป็น 0 และ 1 เพื่อให้จัดเก็บ ฝึก และอนุมานได้เร็วขึ้น เนื่องจากข้อมูลบูลีนมีความทนทานต่อสัญญาณรบกวนและข้อผิดพลาดมากกว่า รูปแบบอื่นๆ การหาปริมาณจึงช่วยปรับปรุงความถูกต้องของโมเดลได้ เทคนิคการหาปริมาณประกอบด้วยการปัดเศษ การตัดทอน และการจัดกลุ่ม
การลดจำนวนบิตที่ใช้จัดเก็บพารามิเตอร์ของโมเดล ตัวอย่างเช่น สมมติว่าพารามิเตอร์ของโมเดล จัดเก็บเป็นจำนวนจุดลอยตัวแบบ 32 บิต การหาปริมาณจะแปลงพารามิเตอร์เหล่านั้นจาก 32 บิตเป็น 4, 8 หรือ 16 บิต การกำหนดค่าควอนไทซ์จะช่วยลด สิ่งต่อไปนี้
- การใช้งาน Compute, หน่วยความจำ, ดิสก์ และเครือข่าย
- เวลาในการอนุมานการคาดการณ์
- การใช้พลังงาน
อย่างไรก็ตาม การวัดปริมาณอาจลดความถูกต้องของการคาดการณ์ของโมเดลในบางครั้ง
คิว
การดำเนินการ TensorFlow ที่ใช้โครงสร้างข้อมูลคิว มักใช้ใน I/O
R
RAG
คำย่อของ การสร้างข้อความโดยใช้การดึงข้อมูล
ป่าสุ่ม
กลุ่มของต้นไม้ตัดสินใจใน ซึ่งต้นไม้ตัดสินใจแต่ละต้นได้รับการฝึกด้วยสัญญาณรบกวนแบบสุ่มที่เฉพาะเจาะจง เช่น Bagging
Random Forest เป็นDecision Forest ประเภทหนึ่ง
ดูข้อมูลเพิ่มเติมได้ที่Random Forest ในหลักสูตร Decision Forests
นโยบายแบบสุ่ม
ในการเรียนรู้แบบเสริมกำลัง นโยบายที่เลือกการดำเนินการแบบสุ่ม
อันดับ (ลำดับ)
ตำแหน่งลำดับของคลาสในปัญหาแมชชีนเลิร์นนิงที่จัดหมวดหมู่ คลาสจากสูงสุดไปต่ำสุด ตัวอย่างเช่น ระบบการจัดอันดับพฤติกรรม สามารถจัดอันดับรางวัลของสุนัขจากสูงสุด (สเต็ก) ไปยัง ต่ำสุด (คะน้าเหี่ยว)
อันดับ (Tensor)
จำนวนมิติข้อมูลในTensor เช่น สเกลาร์มีอันดับ 0 เวกเตอร์มีอันดับ 1 และเมทริกซ์มีอันดับ 2
อย่าสับสนกับอันดับ (ลำดับ)
การจัดอันดับ
การเรียนรู้ที่มีการควบคุมดูแลประเภทหนึ่งซึ่งมี วัตถุประสงค์เพื่อจัดลำดับรายการ
ผู้ให้คะแนน
บุคคลที่ให้ป้ายกำกับสำหรับตัวอย่าง "ผู้ใส่คำอธิบายประกอบ" เป็นอีกชื่อหนึ่งของผู้จัดประเภท
ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลเชิงหมวดหมู่: ปัญหาที่พบบ่อย ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
การเรียกคืน
เมตริกสําหรับโมเดลการจัดประเภทที่ตอบคําถามต่อไปนี้
เมื่อความจริงพื้นฐานคือคลาสที่เป็นบวก โมเดลระบุการคาดการณ์เป็นคลาสที่เป็นบวกได้อย่างถูกต้องกี่เปอร์เซ็นต์
สูตรมีดังนี้
\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]
ที่ไหน
- ผลบวกจริงหมายความว่าโมเดลคาดการณ์คลาสที่เป็นบวกได้อย่างถูกต้อง
- ผลลบลวงหมายความว่าโมเดลคาดการณ์ผิดพลาดว่า คลาสเชิงลบ
เช่น สมมติว่าโมเดลของคุณทำการคาดการณ์ 200 รายการในตัวอย่างที่ความจริงพื้นฐานเป็นคลาสเชิงบวก โดยการคาดการณ์ 200 รายการนี้มีรายละเอียดดังนี้
- 180 รายการเป็นผลบวกจริง
- 20 รายการเป็นผลลบลวง
ในกรณีนี้
\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]
ดูข้อมูลเพิ่มเติมได้ที่การจัดประเภท: ความแม่นยำ การเรียกคืน ความแม่นยำ และเมตริกที่เกี่ยวข้อง
ความอ่อนไหวที่ k (recall@k)
เมตริกสําหรับประเมินระบบที่แสดงรายการสินค้าที่จัดอันดับ (เรียงลําดับ) การเรียกคืนที่ k ระบุเศษส่วนของสินค้าที่เกี่ยวข้องในสินค้า k รายการแรก ในรายการนั้นจากจำนวนสินค้าที่เกี่ยวข้องทั้งหมดที่แสดงผล
\[\text{recall at k} = \frac{\text{relevant items in first k items of the list}} {\text{total number of relevant items in the list}}\]
คอนทราสต์ที่มีความแม่นยำที่ k
ระบบการแนะนำ
ระบบที่เลือกไอเทมที่ต้องการจำนวนค่อนข้างน้อยสำหรับผู้ใช้แต่ละรายจากคลังขนาดใหญ่ ตัวอย่างเช่น ระบบแนะนำวิดีโออาจแนะนำวิดีโอ 2 รายการ จากคลังวิดีโอ 100,000 รายการ โดยเลือกคาซาบลังกาและ The Philadelphia Story ให้แก่ผู้ใช้รายหนึ่ง และเลือกWonder Woman กับ Black Panther ให้แก่ผู้ใช้รายอื่น ระบบวิดีโอแนะนำอาจ อิงตามปัจจัยต่างๆ เช่น
- ภาพยนตร์ที่ผู้ใช้ที่คล้ายกันให้คะแนนหรือดู
- ประเภทภาพยนตร์ ผู้กำกับ นักแสดง กลุ่มเป้าหมาย...
ดูข้อมูลเพิ่มเติมได้ในหลักสูตรระบบการแนะนำ
หน่วยเชิงเส้นที่มีการแก้ไข (ReLU)
ฟังก์ชันการเปิดใช้งานที่มีลักษณะการทำงานดังนี้
- หากอินพุตเป็นค่าลบหรือ 0 เอาต์พุตจะเป็น 0
- หากอินพุตเป็นค่าบวก เอาต์พุตจะเท่ากับอินพุต
เช่น
- หากอินพุตคือ -3 เอาต์พุตจะเป็น 0
- หากอินพุตคือ +3 เอาต์พุตจะเป็น 3.0
นี่คือพล็อตของ ReLU
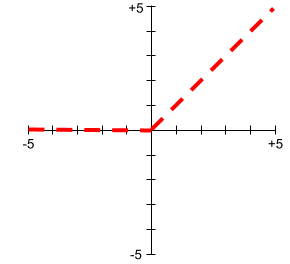
ReLU เป็นฟังก์ชันการเปิดใช้งานที่ได้รับความนิยมอย่างมาก แม้จะมีลักษณะการทำงานที่เรียบง่าย แต่ ReLU ก็ยังช่วยให้โครงข่ายประสาทเทียมเรียนรู้ความสัมพันธ์แบบไม่เชิงเส้นระหว่างฟีเจอร์กับป้ายกำกับได้
โครงข่ายประสาทแบบเกิดซ้ำ
โครงข่ายประสาทเทียมที่ตั้งใจเรียกใช้หลายครั้ง โดยที่ส่วนหนึ่งของการเรียกใช้แต่ละครั้งจะป้อนเข้าสู่การเรียกใช้ครั้งถัดไป กล่าวคือ เลเยอร์ที่ซ่อนจากการเรียกใช้ก่อนหน้าจะให้ข้อมูลส่วนหนึ่ง แก่เลเยอร์ที่ซ่อนเดียวกันในการเรียกใช้ครั้งถัดไป Recurrent Neural Network มีประโยชน์อย่างยิ่งในการประเมินลำดับ เพื่อให้เลเยอร์ที่ซ่อนอยู่ สามารถเรียนรู้จากการทำงานก่อนหน้าของ Neural Network ในส่วนก่อนหน้าของ ลำดับ
ตัวอย่างเช่น รูปต่อไปนี้แสดงโครงข่ายประสาทแบบเกิดซ้ำที่ ทำงาน 4 ครั้ง โปรดสังเกตว่าค่าที่ได้เรียนรู้ในเลเยอร์ที่ซ่อนไว้จากการรันครั้งแรกจะกลายเป็นส่วนหนึ่งของอินพุตไปยังเลเยอร์ที่ซ่อนไว้เดียวกันในการรันครั้งที่ 2 ในทำนองเดียวกัน ค่าที่ได้เรียนรู้ในเลเยอร์ที่ซ่อนในการรันครั้งที่ 2 จะกลายเป็นส่วนหนึ่งของอินพุตไปยังเลเยอร์ที่ซ่อนเดียวกันในการรันครั้งที่ 3 ด้วยวิธีนี้ เครือข่ายประสาทแบบเกิดซ้ำจะค่อยๆ ฝึกและ คาดการณ์ความหมายของลำดับทั้งหมด แทนที่จะเป็นเพียงความหมาย ของคำแต่ละคำ

ข้อความอ้างอิง
คำตอบจากผู้เชี่ยวชาญสำหรับพรอมต์ เช่น หากได้รับพรอมต์ต่อไปนี้
แปลคำถาม "คุณชื่ออะไร" จากภาษาอังกฤษเป็นภาษาฝรั่งเศส
คำตอบของผู้เชี่ยวชาญอาจเป็นดังนี้
Comment vous appelez-vous?
เมตริกต่างๆ (เช่น ROUGE) จะวัดระดับที่ข้อความอ้างอิง ตรงกับข้อความที่สร้างขึ้นของโมเดล ML
ทบทวนความคิด
กลยุทธ์ในการปรับปรุงคุณภาพของเวิร์กโฟลว์แบบเอเจนต์โดยการตรวจสอบ (พิจารณา) เอาต์พุตของขั้นตอนหนึ่งๆ ก่อนที่จะส่งเอาต์พุตนั้นไปยังขั้นตอนถัดไป
โดยปกติแล้ว ผู้ตรวจสอบจะเป็น LLM ตัวเดียวกับที่สร้างคำตอบ (แม้ว่าอาจเป็น LLM อื่นก็ได้) LLM เดียวกันที่สร้างคำตอบจะเป็นผู้ตัดสินที่ยุติธรรมสำหรับคำตอบของตัวเองได้อย่างไร "เคล็ดลับ" คือการทำให้ LLM มีความคิดเชิงวิพากษ์ (ไตร่ตรอง) กระบวนการนี้คล้ายกับนักเขียนที่ใช้ความคิดสร้างสรรค์ ในการเขียนฉบับร่างแรก แล้วเปลี่ยนไปใช้ความคิดเชิงวิพากษ์ เพื่อแก้ไข
ตัวอย่างเช่น ลองนึกถึงเวิร์กโฟลว์แบบเอเจนต์ซึ่งมีขั้นตอนแรกเป็นการสร้าง ข้อความสำหรับแก้วกาแฟ ข้อความแจ้งสำหรับขั้นตอนนี้อาจเป็น
คุณเป็นครีเอเตอร์ สร้างข้อความตลกๆ ที่ไม่ซ้ำใครซึ่งมีความยาวไม่เกิน 50 อักขระ เหมาะสำหรับแก้วกาแฟ
ตอนนี้ลองนึกถึงพรอมต์การไตร่ตรองต่อไปนี้
คุณเป็นคนดื่มกาแฟ คุณคิดว่าคำตอบก่อนหน้านี้ตลกไหม
จากนั้นเวิร์กโฟลว์อาจส่งต่อเฉพาะข้อความที่ได้รับคะแนนการสะท้อนสูง ไปยังขั้นตอนถัดไป
โมเดลการเกิดปัญหาซ้ำ
โดยทั่วไปแล้ว โมเดลที่สร้างการคาดการณ์เชิงตัวเลข (ในทางตรงกันข้าม โมเดลการแยกประเภทจะสร้างการคาดการณ์คลาส) ตัวอย่างเช่น โมเดลการถดถอยต่อไปนี้เป็นโมเดลการถดถอยทั้งหมด
- โมเดลที่คาดการณ์มูลค่าของบ้านหลังหนึ่งในสกุลเงินยูโร เช่น 423,000
- โมเดลที่คาดการณ์อายุคาดเฉลี่ยของต้นไม้หนึ่งๆ เป็นปี เช่น 23.2
- โมเดลที่คาดการณ์ปริมาณฝนเป็นนิ้วที่จะตกในเมืองหนึ่งๆ ในอีก 6 ชั่วโมงข้างหน้า เช่น 0.18
โมเดลการถดถอยที่ใช้กันทั่วไปมี 2 ประเภท ได้แก่
- การถดถอยเชิงเส้น ซึ่งค้นหาเส้นที่เหมาะสมที่สุด กับค่าป้ายกำกับสำหรับฟีเจอร์
- การถดถอยแบบโลจิสติก ซึ่งสร้าง ความน่าจะเป็นระหว่าง 0.0 ถึง 1.0 ที่ระบบมักจะแมปกับการคาดการณ์ คลาส
ไม่ใช่ทุกโมเดลที่แสดงผลการคาดการณ์เชิงตัวเลขจะเป็นโมเดลการถดถอย ในบางกรณี การคาดการณ์ที่เป็นตัวเลขก็เป็นเพียงโมเดลการจัดประเภท ที่มีชื่อคลาสเป็นตัวเลข ตัวอย่างเช่น โมเดลที่คาดการณ์รหัสไปรษณีย์ที่เป็นตัวเลขคือโมเดลการจัดประเภท ไม่ใช่โมเดลการถดถอย
Regularization
กลไกที่ช่วยลดการปรับมากเกินไป การทำให้เป็นปกติประเภทที่ได้รับความนิยมมีดังนี้
- การทำให้เป็นค่าปกติ L1
- การทำให้เป็นค่าปกติ L2
- การทำให้เป็นค่าปกติของ Dropout
- การหยุดก่อนเวลา (นี่ไม่ใช่ วิธีการปรับค่าปกติอย่างเป็นทางการ แต่สามารถจำกัดการปรับมากเกินไปได้อย่างมีประสิทธิภาพ)
นอกจากนี้ การทำให้เป็นปกติยังอาจกำหนดเป็นค่าปรับสำหรับความซับซ้อนของโมเดลได้ด้วย
ดูข้อมูลเพิ่มเติมได้ที่การปรับมากเกินไป: ความซับซ้อนของโมเดล ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
อัตราการปรับค่าปกติ
ตัวเลขที่ระบุความสําคัญสัมพัทธ์ของการกําหนดค่าปกติระหว่างการฝึก การเพิ่ม อัตราการทำให้เป็นปกติจะช่วยลดการปรับมากเกินไป แต่ก็อาจ ลดความสามารถในการคาดการณ์ของโมเดล ในทางกลับกัน การลดหรือละเว้น อัตราการทำให้เป็นปกติจะเพิ่มการปรับมากเกินไป
ดูข้อมูลเพิ่มเติมได้ที่การปรับมากเกินไป: การทำให้เป็นปกติ L2 ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การเรียนรู้แบบเสริมกำลัง (RL)
กลุ่มอัลกอริทึมที่เรียนรู้นโยบายที่เหมาะสมที่สุด โดยมีเป้าหมาย เพื่อเพิ่มผลตอบแทนสูงสุดเมื่อโต้ตอบกับสภาพแวดล้อม ตัวอย่างเช่น รางวัลสูงสุดของเกมส่วนใหญ่คือชัยชนะ ระบบการเรียนรู้แบบเสริมกำลังสามารถกลายเป็นผู้เชี่ยวชาญในการเล่นเกมที่ซับซ้อน ได้โดยการประเมินลำดับการเดินเกมก่อนหน้านี้ที่นำไปสู่ชัยชนะในท้ายที่สุด และลำดับที่นำไปสู่ความพ่ายแพ้ในท้ายที่สุด
การเรียนรู้แบบเสริมกำลังจากฟีดแบ็กของมนุษย์ (Reinforcement Learning from Human Feedback หรือ RLHF)
การใช้ความคิดเห็นจากผู้ให้คะแนนที่เป็นมนุษย์เพื่อปรับปรุงคุณภาพคำตอบของโมเดล ตัวอย่างเช่น กลไก RLHF สามารถขอให้ผู้ใช้ ให้คะแนนคุณภาพของคำตอบของโมเดลด้วยอีโมจิ 👍 หรือ 👎 จากนั้นระบบ จะปรับคำตอบในอนาคตตามความคิดเห็นนั้น
ReLU
ตัวย่อของ Rectified Linear Unit
บัฟเฟอร์การเล่นซ้ำ
ในอัลกอริทึมที่คล้ายกับ DQN หน่วยความจำที่เอเจนต์ใช้ เพื่อจัดเก็บการเปลี่ยนสถานะสำหรับใช้ใน การเล่นประสบการณ์ซ้ำ
ตัวจำลอง
สำเนา (หรือส่วนหนึ่ง) ของชุดข้อมูลการฝึกหรือโมเดล ซึ่งโดยทั่วไปจะจัดเก็บไว้ในเครื่องอื่น ตัวอย่างเช่น ระบบอาจใช้กลยุทธ์ต่อไปนี้ในการใช้การประมวลผลแบบขนานของข้อมูล
- วางสำเนาของโมเดลที่มีอยู่บนเครื่องหลายเครื่อง
- ส่งชุดย่อยที่แตกต่างกันของชุดการฝึกไปยังแต่ละสำเนา
- รวบรวมการอัปเดตพารามิเตอร์
นอกจากนี้ รีพลิกายังอ้างอิงถึงสำเนาอื่นของเซิร์ฟเวอร์การอนุมาน ได้ด้วย การเพิ่มจำนวนรีพลิกาจะเพิ่มจำนวนคำขอที่ระบบสามารถให้บริการได้พร้อมกัน แต่ก็เพิ่มค่าใช้จ่ายในการแสดงโฆษณาด้วย
อคติในการรายงาน
ความถี่ที่ผู้คนเขียนถึงการกระทำ ผลลัพธ์ หรือพร็อพเพอร์ตี้ไม่ได้สะท้อนถึงความถี่ในโลกแห่งความเป็นจริงหรือระดับที่พร็อพเพอร์ตี้เป็นลักษณะเฉพาะของกลุ่มบุคคล อคติในการรายงานอาจส่งผลต่อองค์ประกอบ ของข้อมูลที่ระบบแมชชีนเลิร์นนิงเรียนรู้
เช่น ในหนังสือ คำว่าหัวเราะพบได้บ่อยกว่าคำว่าหายใจ โมเดลแมชชีนเลิร์นนิงที่ประมาณความถี่สัมพัทธ์ของการหัวเราะและการหายใจจากคลังหนังสืออาจระบุว่าการหัวเราะพบได้บ่อยกว่าการหายใจ
ดูข้อมูลเพิ่มเติมได้ที่ความเป็นธรรม: ประเภทของอคติ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การเป็นตัวแทน
กระบวนการแมปข้อมูลกับฟีเจอร์ที่มีประโยชน์
การจัดอันดับใหม่
ขั้นตอนสุดท้ายของระบบแนะนำ ซึ่งในระหว่างนี้ ระบบอาจจัดเกรดรายการที่ได้คะแนนใหม่ตามอัลกอริทึมอื่นๆ (โดยปกติคืออัลกอริทึมที่ไม่ใช่ ML) การจัดอันดับใหม่จะประเมินรายการสินค้า ที่สร้างขึ้นในระยะการให้คะแนน โดยจะดำเนินการต่างๆ เช่น
- การนำรายการที่ผู้ใช้ซื้อไปแล้วออก
- เพิ่มคะแนนของรายการที่ใหม่กว่า
ดูข้อมูลเพิ่มเติมได้ที่การจัดอันดับใหม่ ในหลักสูตรระบบการแนะนำ
การตอบกลับ
ข้อความ รูปภาพ เสียง หรือวิดีโอที่โมเดล Generative AI อนุมาน กล่าวอีกนัยหนึ่งคือ พรอมต์คืออินพุตของโมเดล Generative AI และคำตอบคือเอาต์พุต
ชุดคำตอบ
การรวบรวมคำตอบที่โมเดลภาษาขนาดใหญ่ส่งกลับไปยังชุดพรอมต์ที่ป้อน
การสร้างเสริมด้วยการดึงข้อมูล (RAG)
เทคนิคในการปรับปรุงคุณภาพของเอาต์พุตโมเดลภาษาขนาดใหญ่ (LLM) โดยการอ้างอิงแหล่งความรู้ที่ดึงมาหลังจากฝึกโมเดลแล้ว RAG ช่วยปรับปรุงความแม่นยำของคำตอบของ LLM โดยให้ LLM ที่ผ่านการฝึกเข้าถึงข้อมูลที่ดึงมาจากฐานความรู้หรือเอกสารที่เชื่อถือได้
แรงจูงใจที่พบบ่อยในการใช้การสร้างที่เพิ่มการดึงข้อมูล ได้แก่
- เพิ่มความถูกต้องตามข้อเท็จจริงของคำตอบที่โมเดลสร้างขึ้น
- การให้สิทธิ์โมเดลเข้าถึงความรู้ที่ไม่ได้ฝึก
- การเปลี่ยนความรู้ที่โมเดลใช้
- การเปิดใช้โมเดลเพื่ออ้างอิงแหล่งที่มา
ตัวอย่างเช่น สมมติว่าแอปเคมีใช้ PaLM API เพื่อสร้างข้อมูลสรุป ที่เกี่ยวข้องกับคำค้นหาของผู้ใช้ เมื่อแบ็กเอนด์ของแอปได้รับการค้นหา แบ็กเอนด์จะดำเนินการต่อไปนี้
- ค้นหา ("ดึง") ข้อมูลที่เกี่ยวข้องกับคําค้นหาของผู้ใช้
- ผนวก ("เพิ่ม") ข้อมูลเคมีที่เกี่ยวข้องกับคำค้นหาของผู้ใช้
- สั่งให้ LLM สร้างข้อมูลสรุปตามข้อมูลที่ต่อท้าย
รีเทิร์น
ในการเรียนรู้แบบเสริมกำลัง เมื่อกำหนดนโยบายและสถานะหนึ่งๆ แล้ว ผลตอบแทนคือผลรวมของรางวัลทั้งหมดที่เอเจนต์คาดว่าจะได้รับเมื่อปฏิบัติตามนโยบายจากสถานะจนถึงตอนจบของตอน เอเจนต์ จะพิจารณาถึงลักษณะที่ล่าช้าของรางวัลที่คาดหวังโดยการลดรางวัล ตามการเปลี่ยนสถานะที่จำเป็นต่อการได้รับรางวัล
ดังนั้น หากปัจจัยส่วนลดคือ \(\gamma\)และ \(r_0, \ldots, r_{N}\) แสดงถึงรางวัลจนกว่าจะจบตอน การคำนวณผลตอบแทน จะเป็นดังนี้
รางวัล
ในการเรียนรู้แบบเสริมกำลัง ผลลัพธ์ที่เป็นตัวเลขของการดำเนินการในสถานะตามที่กำหนดโดยสภาพแวดล้อม
การปรับค่า Ridge
คำพ้องความหมายของ L2 Regularization คำว่า การทำให้เป็นปกติแบบริดจ์มักใช้ในบริบทของสถิติล้วนๆ ขณะที่การทำให้เป็นปกติแบบ L2 มักใช้ในแมชชีนเลิร์นนิง มากกว่า
RNN
ตัวย่อของโครงข่ายประสาทแบบเกิดซ้ำ
เส้นโค้ง ROC (Receiver Operating Characteristic)
กราฟอัตราผลบวกจริงเทียบกับ อัตราผลบวกลวงสำหรับเกณฑ์การจัดประเภทต่างๆ ในการจัดประเภทแบบไบนารี
รูปร่างของเส้นโค้ง ROC แสดงให้เห็นความสามารถของโมเดลการจัดประเภทแบบไบนารี ในการแยกคลาสที่เป็นบวกออกจากคลาสที่เป็นลบ สมมติว่าโมเดลการจัดประเภทแบบไบนารีแยกคลาสเชิงลบทั้งหมดออกจากคลาสเชิงบวกทั้งหมดได้อย่างสมบูรณ์ ดังนี้
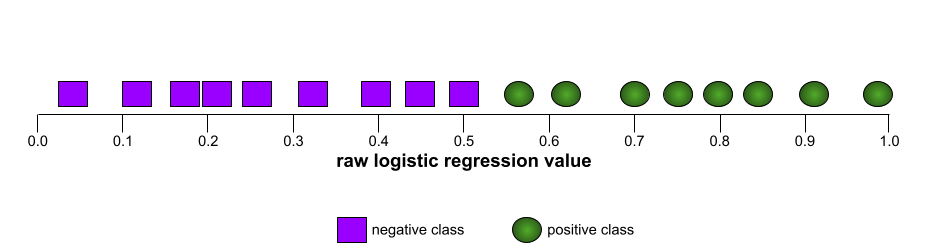
เส้นโค้ง ROC สำหรับโมเดลก่อนหน้ามีลักษณะดังนี้
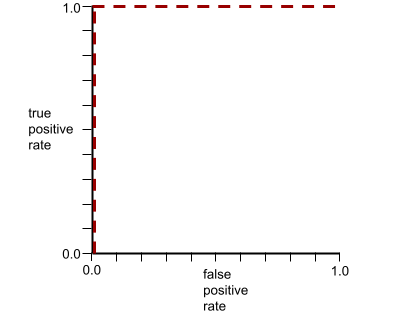
ในทางตรงกันข้าม ภาพประกอบต่อไปนี้แสดงกราฟค่าการถดถอยโลจิสติกแบบดิบ สำหรับโมเดลที่แย่ซึ่งแยกคลาสเชิงลบออกจาก คลาสเชิงบวกไม่ได้เลย
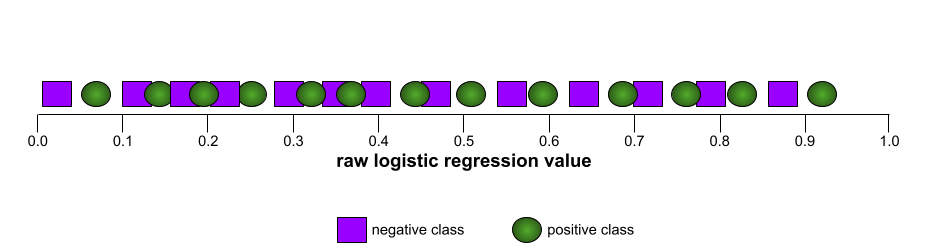
เส้นโค้ง ROC สำหรับโมเดลนี้มีลักษณะดังนี้
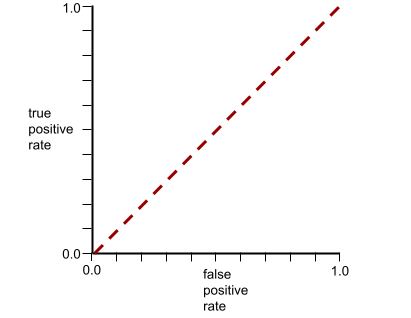
ในขณะเดียวกัน ในโลกแห่งความเป็นจริง โมเดลการจัดประเภทแบบไบนารีส่วนใหญ่จะแยก คลาสที่เป็นบวกและลบในระดับหนึ่ง แต่โดยปกติแล้วจะไม่สมบูรณ์ ดังนั้น กราฟ ROC ทั่วไปจะอยู่ระหว่าง 2 สุดขั้วนี้
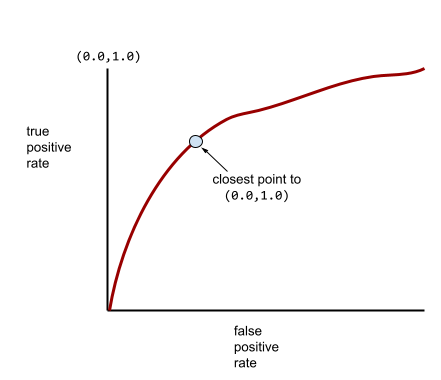
จุดบนเส้นโค้ง ROC ที่ใกล้กับ (0.0,1.0) มากที่สุดในทางทฤษฎีจะระบุ เกณฑ์การแยกประเภทที่เหมาะสม อย่างไรก็ตาม ปัญหาอื่นๆ ในโลกแห่งความเป็นจริง มีผลต่อการเลือกเกณฑ์การแยกประเภทที่เหมาะสม ตัวอย่างเช่น ผลลบเท็จอาจสร้างความเจ็บปวดมากกว่าผลบวกเท็จ
เมตริกเชิงตัวเลขที่เรียกว่า AUC จะสรุปเส้นโค้ง ROC เป็นค่าทศนิยมค่าเดียว
การเขียนพรอมต์ตามบทบาท
พรอมต์ที่มักขึ้นต้นด้วยคำสรรพนาม คุณ ซึ่ง บอกโมเดล Generative AI ให้แสร้งเป็นบุคคลหรือบทบาทหนึ่งๆ เมื่อสร้างคำตอบ การใช้พรอมต์ตามบทบาทจะช่วยให้โมเดล Generative AI มี "แนวคิด" ที่เหมาะสม เพื่อสร้างคำตอบที่เป็นประโยชน์มากขึ้น ตัวอย่างเช่น พรอมต์บทบาทต่อไปนี้อาจเหมาะสม ทั้งนี้ขึ้นอยู่กับประเภทของคำตอบที่คุณต้องการ
คุณจบการศึกษาระดับปริญญาเอกสาขาวิทยาการคอมพิวเตอร์
คุณเป็นวิศวกรซอฟต์แวร์ที่ชอบอธิบายเรื่อง Python ให้แก่นักเรียนที่เพิ่งเริ่มเรียนการเขียนโปรแกรมอย่างอดทน
คุณเป็นฮีโร่แอ็กชันที่มีทักษะการเขียนโปรแกรมที่เฉพาะเจาะจงมาก โปรดยืนยันว่าคุณจะค้นหารายการที่เฉพาะเจาะจงในรายการ Python
รูท
โหนดเริ่มต้น (เงื่อนไขแรก) ในแผนผังการตัดสินใจ ตามธรรมเนียมแล้ว แผนภาพจะวางรูทไว้ที่ด้านบนของแผนผังการตัดสินใจ เช่น
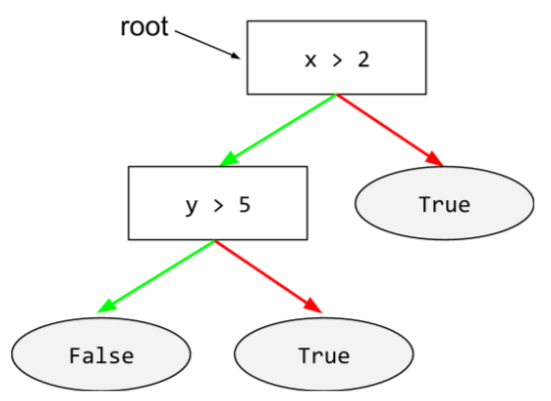
ไดเรกทอรีราก
ไดเรกทอรีที่คุณระบุสำหรับการโฮสต์ไดเรกทอรีย่อยของไฟล์จุดตรวจสอบและเหตุการณ์ TensorFlow ของโมเดลหลายรายการ
ค่าเฉลี่ยความคลาดเคลื่อนกำลังสอง (RMSE)
รากที่ 2 ของความคลาดเคลื่อนเฉลี่ยกำลังสอง
ความไม่แปรเปลี่ยนภายใต้การหมุน
ในปัญหาการแยกประเภทรูปภาพ ความสามารถของอัลกอริทึมในการแยกประเภทรูปภาพได้สำเร็จ แม้ว่าการวางแนวของรูปภาพจะเปลี่ยนไปก็ตาม ตัวอย่างเช่น อัลกอริทึมยังคงระบุไม้เทนนิสได้ไม่ว่าจะชี้ขึ้น ด้านข้าง หรือลง โปรดทราบว่าการไม่เปลี่ยนแปลงเมื่อหมุนไม่ได้เป็นสิ่งที่ต้องการเสมอไป เช่น ไม่ควรจัดประเภท 9 ที่กลับหัวเป็น 9
ดูความไม่แปรเปลี่ยนตามการเลื่อนและ ความไม่แปรเปลี่ยนตามขนาดด้วย
ROUGE (Recall-Oriented Understudy for Gisting Evaluation)
กลุ่มเมตริกที่ประเมินโมเดลการสรุปอัตโนมัติและการแปลด้วยเครื่อง เมตริก ROUGE จะกำหนดระดับที่ข้อความอ้างอิงซ้อนทับกับข้อความที่โมเดล ML สร้างขึ้น สมาชิกแต่ละคนในตระกูล ROUGE จะวัดการทับซ้อนกันในลักษณะที่แตกต่างกัน คะแนน ROUGE ที่สูงขึ้นแสดงถึง ความคล้ายกันระหว่างข้อความอ้างอิงกับข้อความที่สร้างขึ้นมากกว่าคะแนน ROUGE ที่ต่ำกว่า
โดยปกติแล้ว สมาชิกแต่ละคนในตระกูล ROUGE จะสร้างเมตริกต่อไปนี้
- ความแม่นยำ
- การจดจำ
- F1
ดูรายละเอียดและตัวอย่างได้ที่
ROUGE-L
สมาชิกในตระกูล ROUGE มุ่งเน้นที่ความยาวของลำดับย่อยร่วมที่ยาวที่สุด ในข้อความอ้างอิงและข้อความที่สร้างขึ้น สูตรต่อไปนี้จะคำนวณการเรียกคืนและความแม่นยำสำหรับ ROUGE-L
จากนั้นคุณจะใช้ F1 เพื่อสรุปการเรียกคืน ROUGE-L และความแม่นยำของ ROUGE-L เป็นเมตริกเดียวได้โดยทำดังนี้
ROUGE-L จะไม่สนใจบรรทัดใหม่ในข้อความอ้างอิงและข้อความที่สร้างขึ้น ดังนั้น ลำดับย่อยร่วมที่ยาวที่สุดอาจข้ามหลายประโยค เมื่อข้อความอ้างอิงและข้อความที่สร้างขึ้นมีหลายประโยค โดยทั่วไปแล้ว ROUGE-Lsum ซึ่งเป็นรูปแบบหนึ่งของ ROUGE-L จะเป็นเมตริกที่ดีกว่า ROUGE-Lsum จะกำหนดลำดับย่อยร่วมที่ยาวที่สุดสำหรับประโยค ในข้อความ จากนั้นจะคำนวณค่าเฉลี่ยของลำดับย่อยร่วมที่ยาวที่สุดเหล่านั้น
ROUGE-N
ชุดเมตริกภายในตระกูล ROUGE ที่เปรียบเทียบ N-gram ที่แชร์ซึ่งมีขนาดหนึ่งๆ ในข้อความอ้างอิง และข้อความที่สร้างขึ้น เช่น
- ROUGE-1 จะวัดจำนวนโทเค็นที่ใช้ร่วมกันในข้อความอ้างอิงและ ข้อความที่สร้างขึ้น
- ROUGE-2 จะวัดจำนวน bigram (2-gram) ที่ใช้ร่วมกัน ในข้อความอ้างอิงและข้อความที่สร้างขึ้น
- ROUGE-3 จะวัดจำนวน trigram (3-gram) ที่ใช้ร่วมกัน ในข้อความอ้างอิงและข้อความที่สร้างขึ้น
คุณใช้สูตรต่อไปนี้เพื่อคํานวณการเรียกคืน ROUGE-N และความแม่นยําของ ROUGE-N สําหรับสมาชิกใดก็ได้ในตระกูล ROUGE-N
จากนั้นคุณจะใช้ F1 เพื่อสรุปการเรียกคืน ROUGE-N และความแม่นยำของ ROUGE-N เป็นเมตริกเดียวได้
ROUGE-S
รูปแบบ ROUGE-N ที่ยืดหยุ่นซึ่งช่วยให้การจับคู่ skip-gram เป็นไปได้ กล่าวคือ ROUGE-N จะนับเฉพาะ N-gram ที่ตรงกันทุกประการ แต่ ROUGE-S จะนับ N-gram ที่คั่นด้วยคำอย่างน้อย 1 คำด้วย เช่น โปรดคำนึงถึงสิ่งต่อไปนี้
- ข้อความอ้างอิง: เมฆสีขาว
- ข้อความที่สร้างขึ้น: เมฆสีขาวที่ลอยเป็นปุย
เมื่อคำนวณ ROUGE-N ไดแกรม 2 คำ White clouds จะไม่ตรงกับ White billowing clouds อย่างไรก็ตาม เมื่อคำนวณ ROUGE-S เมฆสีขาว จะตรงกับเมฆสีขาวที่ลอยเป็นปุย
R-squared
เมตริกการถดถอยที่ระบุความผันแปรของป้ายกำกับที่เกิดจากฟีเจอร์แต่ละรายการหรือชุดฟีเจอร์ R-squared คือค่าระหว่าง 0 ถึง 1 ซึ่งคุณสามารถตีความได้ดังนี้
- ค่า R-squared ที่ 0 หมายความว่าความแปรปรวนของป้ายกำกับไม่ได้เกิดจากชุดฟีเจอร์
- ค่า R-squared ที่ 1 หมายความว่าความแปรปรวนทั้งหมดของป้ายกำกับเกิดจาก ชุดฟีเจอร์
- ค่า R-squared ระหว่าง 0 ถึง 1 แสดงให้เห็นถึงขอบเขตที่สามารถคาดการณ์ความแปรปรวนของป้ายกำกับได้จากฟีเจอร์หรือชุดฟีเจอร์หนึ่งๆ เช่น ค่า R ยกกำลังสองที่ 0.10 หมายความว่าความแปรปรวน 10% ในป้ายกำกับเกิดจากชุดฟีเจอร์ ค่า R ยกกำลังสองที่ 0.20 หมายความว่า 20% เกิดจากชุดฟีเจอร์ และอื่นๆ
ค่า R ยกกำลังสองคือค่ากำลังสองของสัมประสิทธิ์สหสัมพันธ์ของ Pearson ระหว่างค่าที่โมเดลคาดการณ์กับข้อมูลจากการสังเกตการณ์โดยตรง
S
อคติในการสุ่มตัวอย่าง
การสุ่มตัวอย่างแบบแทนที่
วิธีการเลือกรายการจากชุดรายการที่อาจเป็นไปได้ ซึ่งสามารถเลือกรายการเดียวกันได้หลายครั้ง วลี "แบบแทนที่" หมายความว่า หลังจากเลือกแต่ละครั้ง ระบบจะส่งคืนรายการที่เลือกไปยังกลุ่ม ของรายการที่อาจเป็นไปได้ ส่วนวิธีผกผันหรือการสุ่มตัวอย่างแบบไม่แทนที่ หมายความว่าเลือกรายการที่ต้องการได้เพียงครั้งเดียว
ตัวอย่างเช่น ลองพิจารณาชุดผลไม้ต่อไปนี้
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}สมมติว่าระบบสุ่มเลือก fig เป็นรายการแรก
หากใช้การสุ่มตัวอย่างแบบแทนที่ ระบบจะเลือกรายการที่ 2 จากชุดต่อไปนี้
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}ใช่ ชุดคำถามนี้เป็นชุดเดียวกับก่อนหน้านี้ ดังนั้นระบบอาจ
เลือกfigอีกครั้ง
หากใช้การสุ่มตัวอย่างแบบไม่แทนที่ เมื่อเลือกแล้ว จะเลือกตัวอย่างนั้นอีกไม่ได้
ตัวอย่างเช่น หากระบบสุ่มเลือก fig เป็น
ตัวอย่างแรก ระบบจะเลือก fig อีกไม่ได้ ดังนั้น ระบบ
จะเลือกตัวอย่างที่ 2 จากชุด (ที่ลดลง) ต่อไปนี้
fruit = {kiwi, apple, pear, cherry, lime, mango}SavedModel
รูปแบบที่แนะนำสำหรับการบันทึกและกู้คืนโมเดล TensorFlow SavedModel เป็นรูปแบบการซีเรียลไลซ์ที่กู้คืนได้และไม่ขึ้นกับภาษา ซึ่งช่วยให้ระบบและเครื่องมือระดับสูง สร้าง ใช้ และแปลงโมเดล TensorFlow ได้
ดูรายละเอียดทั้งหมดได้ที่ ส่วนการบันทึกและกู้คืน ในคู่มือโปรแกรมเมอร์ TensorFlow
ประหยัด
ออบเจ็กต์ TensorFlow ที่รับผิดชอบในการบันทึกจุดตรวจของโมเดล
สเกลาร์
ตัวเลขหรือสตริงเดียวที่แสดงเป็นเทนเซอร์ของอันดับ 0 ตัวอย่างเช่น บรรทัดโค้ดต่อไปนี้ แต่ละบรรทัดจะสร้างสเกลาร์ 1 รายการใน TensorFlow
breed = tf.Variable("poodle", tf.string)
temperature = tf.Variable(27, tf.int16)
precision = tf.Variable(0.982375101275, tf.float64)การปรับขนาด
การแปลงหรือเทคนิคทางคณิตศาสตร์ที่เปลี่ยนช่วงของป้ายกำกับ ค่าฟีเจอร์ หรือทั้ง 2 อย่าง การปรับขนาดบางรูปแบบมีประโยชน์อย่างมากสำหรับ การแปลง เช่น การปรับให้เป็นมาตรฐาน
รูปแบบการปรับขนาดที่ใช้กันทั่วไปในแมชชีนเลิร์นนิง ได้แก่
- การปรับขนาดเชิงเส้น ซึ่งโดยปกติจะใช้การลบและการหารร่วมกันเพื่อแทนที่ค่าเดิมด้วยตัวเลขระหว่าง -1 ถึง +1 หรือระหว่าง 0 ถึง 1
- การปรับขนาดแบบลอการิทึม ซึ่งจะแทนที่ค่าเดิมด้วย ลอการิทึมของค่าดังกล่าว
- การปรับให้เป็นมาตรฐาน Z-score ซึ่งจะแทนที่ค่าเดิมด้วยค่าทศนิยมที่แสดงถึงจำนวนส่วนเบี่ยงเบนมาตรฐานจากค่าเฉลี่ยของฟีเจอร์นั้น
scikit-learn
แพลตฟอร์มแมชชีนเลิร์นนิงแบบโอเพนซอร์สที่ได้รับความนิยม ดูที่ scikit-learn.org
การให้คะแนน
ส่วนหนึ่งของระบบการแนะนำที่ ให้ค่าหรือการจัดอันดับสำหรับแต่ละรายการที่สร้างขึ้นใน ระยะการสร้างแคนดิเดต
อคติในการเลือก
ข้อผิดพลาดในข้อสรุปที่ได้จากข้อมูลที่สุ่มตัวอย่างเนื่องจากกระบวนการเลือก ที่สร้างความแตกต่างอย่างเป็นระบบระหว่างตัวอย่างที่สังเกตได้ในข้อมูล กับตัวอย่างที่สังเกตไม่ได้ อคติในการเลือกมีรูปแบบดังนี้
- อคติจากความครอบคลุม: ประชากรที่แสดงในชุดข้อมูลไม่ตรงกับประชากรที่โมเดลแมชชีนเลิร์นนิงใช้คาดการณ์
- อคติในการสุ่มตัวอย่าง: ไม่ได้เก็บรวบรวมข้อมูลแบบสุ่มจากกลุ่มเป้าหมาย
- อคติจากการไม่ตอบ (หรือที่เรียกว่าอคติจากการเข้าร่วม): ผู้ใช้จาก บางกลุ่มเลือกไม่เข้าร่วมตอบแบบสำรวจในอัตราที่แตกต่างจากผู้ใช้จาก กลุ่มอื่นๆ
ตัวอย่างเช่น สมมติว่าคุณกำลังสร้างโมเดลแมชชีนเลิร์นนิงที่คาดการณ์ ความชอบภาพยนตร์ของผู้คน หากต้องการรวบรวมข้อมูลการฝึก คุณจะแจกแบบสำรวจให้ทุกคนที่นั่งแถวหน้าในโรงภาพยนตร์ ที่ฉายภาพยนตร์ ในแง่หนึ่ง วิธีนี้อาจดูเหมือนเป็นวิธีที่สมเหตุสมผลในการรวบรวมชุดข้อมูล แต่การเก็บรวบรวมข้อมูลในรูปแบบนี้อาจทำให้เกิดอคติในการเลือกในรูปแบบต่อไปนี้
- อคติในการครอบคลุม: การสุ่มตัวอย่างจากประชากรที่เลือกดู ภาพยนตร์ อาจทำให้การคาดการณ์ของโมเดลไม่สามารถสรุปผลไปยังผู้ที่ ยังไม่ได้แสดงความสนใจในภาพยนตร์ในระดับนั้น
- อคติในการสุ่มตัวอย่าง: แทนที่จะสุ่มตัวอย่างจากประชากรเป้าหมาย (ทุกคนที่อยู่ในโรงภาพยนตร์) คุณกลับสุ่มตัวอย่างเฉพาะคนที่นั่งแถวหน้า เป็นไปได้ว่าผู้ที่นั่งแถวหน้าจะสนใจภาพยนตร์มากกว่าผู้ที่นั่งแถวอื่นๆ
- อคติจากการไม่ตอบ: โดยทั่วไปแล้ว ผู้ที่มีความคิดเห็นอย่างชัดเจนมักจะตอบแบบสำรวจที่ไม่บังคับบ่อยกว่าผู้ที่มีความคิดเห็นแบบกลางๆ เนื่องจากแบบสำรวจภาพยนตร์เป็นแบบไม่บังคับ คำตอบจึงมีแนวโน้มที่จะสร้างการกระจายแบบสองค่ามากกว่าการกระจายแบบปกติ (รูประฆัง)
Self-Attention (หรือที่เรียกว่าเลเยอร์ Self-Attention)
เลเยอร์โครงข่ายประสาทเทียมที่แปลงลําดับของ การฝัง (เช่น การฝังโทเค็น) เป็นลําดับการฝังอีกชุดหนึ่ง การฝังแต่ละรายการในลำดับเอาต์พุตจะสร้างขึ้นโดยการผสานรวมข้อมูลจากองค์ประกอบของลำดับอินพุตผ่านกลไกความสนใจ
ส่วนตนเองของการใส่ใจตนเองหมายถึงลำดับที่ใส่ใจ ตัวมันเองแทนที่จะเป็นบริบทอื่นๆ Self-Attention เป็นหนึ่งในองค์ประกอบหลัก ของ Transformer และใช้คำศัพท์ในการค้นหาพจนานุกรม เช่น "คำค้นหา" "คีย์" และ "ค่า"
เลเยอร์การใส่ใจตนเองเริ่มต้นด้วยลำดับของการแสดงอินพุต ซึ่งมี 1 รายการสำหรับแต่ละคำ การแสดงอินพุตสำหรับคำอาจเป็นเพียงการฝัง สำหรับแต่ละคำในลำดับอินพุต เครือข่ายจะให้คะแนนความเกี่ยวข้องของคำกับทุกองค์ประกอบในลำดับคำทั้งหมด คะแนนความเกี่ยวข้องจะกำหนดว่าการแสดงคำสุดท้าย จะรวมการแสดงคำอื่นๆ ไว้มากน้อยเพียงใด
ตัวอย่างเช่น ลองพิจารณาประโยคต่อไปนี้
สัตว์ตัวนั้นไม่ข้ามถนนเพราะเหนื่อยเกินไป
ภาพต่อไปนี้ (จากTransformer: A Novel Neural Network Architecture for Language Understanding) แสดงรูปแบบการใส่ใจของเลเยอร์การใส่ใจตนเองสำหรับคำสรรพนาม it โดยความเข้มของแต่ละบรรทัดจะบ่งบอกว่าแต่ละคำมีส่วนช่วยในการแสดงมากน้อยเพียงใด
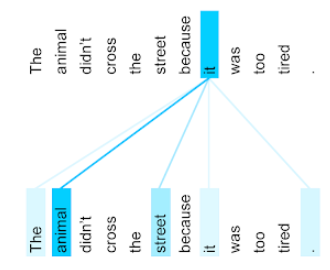
เลเยอร์การสนใจตนเองจะไฮไลต์คำที่เกี่ยวข้องกับ "มัน" ในกรณีนี้ เลเยอร์ความสนใจได้เรียนรู้ที่จะไฮไลต์คำที่เลเยอร์อาจอ้างอิงถึง โดยกำหนดน้ำหนักสูงสุดให้กับคำว่าสัตว์
สำหรับลำดับของโทเค็น การใส่ใจตนเองจะเปลี่ยนลำดับของการฝัง n ครั้งแยกกัน โดยจะเปลี่ยน 1 ครั้งในแต่ละตำแหน่งในลำดับ
ดูกลไกการทำงานของ Attention และ กลไกการทำงานของ Multi-Head Self-Attention ด้วย
การเรียนรู้แบบควบคุมดูแลด้วยตนเอง
กลุ่มเทคนิคสำหรับการเปลี่ยนปัญหาแมชชีนเลิร์นนิงแบบไม่มีการควบคุมดูแล ให้เป็นปัญหาแมชชีนเลิร์นนิงที่มีการควบคุมดูแล โดยการสร้างป้ายกำกับแทนจากตัวอย่างที่ไม่มีป้ายกำกับ
โมเดลบางรายการที่อิงตาม Transformer เช่น BERT ใช้ การเรียนรู้แบบกำกับดูแลตนเอง
การฝึกแบบกำกับดูแลตนเองเป็นแนวทางการเรียนรู้แบบกึ่งกำกับดูแล
การฝึกด้วยตนเอง
การเรียนรู้แบบกำกับดูแลตนเองรูปแบบหนึ่งซึ่งมีประโยชน์อย่างยิ่งเมื่อเงื่อนไขต่อไปนี้ทั้งหมดเป็นจริง
- อัตราส่วนของตัวอย่างที่ไม่มีป้ายกำกับต่อตัวอย่างที่มีป้ายกำกับในชุดข้อมูลสูง
- นี่คือปัญหาการจัดประเภท
การฝึกด้วยตนเองจะทำงานโดยการทำซ้ำ 2 ขั้นตอนต่อไปนี้จนกว่าโมเดลจะหยุดการพัฒนา
- ใช้แมชชีนเลิร์นนิงที่มีการควบคุมดูแลเพื่อ ฝึกโมเดลในตัวอย่างที่ติดป้ายกำกับ
- ใช้โมเดลที่สร้างขึ้นในขั้นตอนที่ 1 เพื่อสร้างการคาดการณ์ (ป้ายกำกับ) ใน ตัวอย่างที่ไม่มีป้ายกำกับ โดยย้ายตัวอย่างที่มีความเชื่อมั่นสูงไปยัง ตัวอย่างที่มีป้ายกำกับพร้อมป้ายกำกับที่คาดการณ์ไว้
โปรดสังเกตว่าการทำซ้ำแต่ละครั้งของขั้นตอนที่ 2 จะเพิ่มตัวอย่างที่มีป้ายกำกับมากขึ้นสำหรับขั้นตอนที่ 1 เพื่อใช้ในการฝึก
การเรียนรู้แบบกึ่งควบคุม
การฝึกโมเดลในข้อมูลที่ตัวอย่างการฝึกบางรายการมีป้ายกำกับ แต่ตัวอย่างอื่นๆ ไม่มี เทคนิคหนึ่งสำหรับการเรียนรู้แบบกึ่งควบคุมดูแลคือการอนุมานป้ายกำกับสำหรับ ตัวอย่างที่ไม่มีป้ายกำกับ แล้วฝึกโมเดลโดยใช้ป้ายกำกับที่อนุมานเพื่อสร้างโมเดลใหม่ การเรียนรู้ที่มีการควบคุมดูแลบางส่วนอาจมีประโยชน์หากการได้ป้ายกำกับมีค่าใช้จ่ายสูง แต่มีตัวอย่างที่ไม่มีป้ายกำกับจำนวนมาก
การฝึกด้วยตนเองเป็นเทคนิคหนึ่งสำหรับการเรียนรู้แบบกึ่งกำกับดูแล
แอตทริบิวต์ที่มีความละเอียดอ่อน
คุณลักษณะของบุคคลที่อาจได้รับการพิจารณาเป็นพิเศษด้วยเหตุผลทางกฎหมาย จริยธรรม สังคม หรือส่วนบุคคลการวิเคราะห์ความเห็น
การใช้อัลกอริทึมทางสถิติหรือแมชชีนเลิร์นนิงเพื่อพิจารณาทัศนคติโดยรวมของกลุ่ม ไม่ว่าจะเป็นเชิงบวกหรือเชิงลบต่อบริการ ผลิตภัณฑ์ องค์กร หรือหัวข้อ ตัวอย่างเช่น การใช้ความเข้าใจภาษาธรรมชาติ อัลกอริทึมสามารถวิเคราะห์ความรู้สึกในความคิดเห็นที่เป็นข้อความ จากหลักสูตรของมหาวิทยาลัยเพื่อพิจารณาว่าโดยทั่วไปแล้วนักเรียน ชอบหรือไม่ชอบหลักสูตรมากน้อยเพียงใด
ดูข้อมูลเพิ่มเติมได้ที่คู่มือการจัดประเภทข้อความ
โมเดลลำดับ
โมเดลที่มีอินพุตซึ่งมีความขึ้นต่อกันตามลำดับ เช่น การคาดการณ์ วิดีโอถัดไปที่ดูจากลำดับวิดีโอที่ดูไปก่อนหน้านี้
งานแบบลำดับต่อลำดับ
งานที่แปลงลำดับอินพุตของโทเค็นเป็นลำดับเอาต์พุตของโทเค็น ตัวอย่างเช่น งานแบบลำดับต่อลำดับที่ได้รับความนิยม 2 ประเภท ได้แก่
- ผู้แปล
- ลำดับอินพุตตัวอย่าง: "ฉันรักเธอ"
- ลำดับเอาต์พุตตัวอย่าง: "Je t'aime"
- การตอบคำถาม
- ลำดับอินพุตตัวอย่าง: "ฉันต้องใช้รถในนิวยอร์กไหม"
- ลำดับเอาต์พุตตัวอย่าง: "ไม่ เก็บรถไว้ที่บ้าน"
หน่วยบริโภค
กระบวนการทำให้โมเดลที่ฝึกแล้วพร้อมใช้งานเพื่อแสดงการคาดการณ์ผ่านการอนุมานแบบออนไลน์หรือการอนุมานแบบออฟไลน์
รูปร่าง (Tensor)
จำนวนองค์ประกอบในมิติข้อมูลแต่ละรายการของ เทนเซอร์ รูปร่างจะแสดงเป็นรายการจำนวนเต็ม ตัวอย่างเช่น เทนเซอร์ 2 มิติต่อไปนี้มีรูปร่างเป็น [3,4]
[[5, 7, 6, 4], [2, 9, 4, 8], [3, 6, 5, 1]]
TensorFlow ใช้รูปแบบแถวหลัก (สไตล์ C) เพื่อแสดงลำดับของ
มิติข้อมูล ซึ่งเป็นเหตุผลที่รูปร่างใน TensorFlow คือ [3,4] ไม่ใช่
[4,3] กล่าวอีกนัยหนึ่งคือ ในเทนเซอร์ TensorFlow แบบ 2 มิติ รูปร่าง
คือ [จำนวนแถว จำนวนคอลัมน์]
รูปร่างคงที่คือรูปร่างของเทนเซอร์ที่ทราบในเวลาคอมไพล์
รูปร่างแบบไดนามิกจะไม่รู้จักในเวลาคอมไพล์และ
จึงขึ้นอยู่กับข้อมูลรันไทม์ Tensor นี้อาจแสดงด้วยมิติข้อมูลตัวยึดตำแหน่งใน TensorFlow ดังใน [3, ?]
ชาร์ด
การแบ่งชุดการฝึกหรือโมเดลอย่างมีเหตุผล โดยปกติแล้ว กระบวนการบางอย่างจะสร้าง Shard โดยการแบ่งตัวอย่างหรือพารามิเตอร์ออกเป็นกลุ่มที่มีขนาดเท่ากัน (โดยปกติ) จากนั้นระบบจะกำหนดแต่ละ Shard ให้กับเครื่องที่แตกต่างกัน
การแบ่งพาร์ติชันโมเดลเรียกว่าการทำงานแบบขนานของโมเดล การแบ่งพาร์ติชันข้อมูลเรียกว่าการทำงานแบบขนานของข้อมูล
การหดตัว
ไฮเปอร์พารามิเตอร์ใน การเพิ่มประสิทธิภาพแบบไล่ระดับที่ควบคุม การปรับมากเกินไป การลดขนาดในการเพิ่มประสิทธิภาพแบบไล่ระดับ จะคล้ายกับอัตราการเรียนรู้ใน การไล่ระดับการลด การหดตัวคือค่าทศนิยม ระหว่าง 0.0 ถึง 1.0 ค่าการหดตัวที่ต่ำกว่าจะลดการปรับมากเกินไป ได้มากกว่าค่าการหดตัวที่สูงกว่า
การประเมินแบบเทียบเคียง
การเปรียบเทียบคุณภาพของโมเดล 2 รายการโดยการประเมินคำตอบของโมเดลต่อพรอมต์เดียวกัน เช่น สมมติว่า มีการป้อนพรอมต์ต่อไปนี้ให้กับโมเดลที่แตกต่างกัน 2 โมเดล
สร้างรูปสุนัขน่ารักที่กำลังโยนลูกบอล 3 ลูก
ในการประเมินแบบเทียบกัน ผู้ประเมินจะเลือกรูปภาพที่ "ดีกว่า" (แม่นยำกว่า สวยขึ้น น่ารักกว่าไหม)
ฟังก์ชันซิกมอยด์
ฟังก์ชันทางคณิตศาสตร์ที่ "บีบ" ค่าอินพุตให้อยู่ในช่วงที่จำกัด โดยปกติคือ 0 ถึง 1 หรือ -1 ถึง +1 กล่าวคือ คุณสามารถส่งตัวเลขใดก็ได้ (2, 1 ล้าน, -1 พันล้าน หรืออะไรก็ตาม) ไปยังฟังก์ชัน Sigmoid และเอาต์พุตจะยังคงอยู่ในช่วงที่จำกัด กราฟของฟังก์ชันการกระตุ้นแบบซิคมอยด์มีลักษณะดังนี้

ฟังก์ชันซิกมอยด์มีการใช้งานหลายอย่างในแมชชีนเลิร์นนิง ซึ่งรวมถึง
- การแปลงเอาต์พุตดิบของโมเดลการถดถอยแบบโลจิสติก หรือโมเดลการถดถอยแบบมัลติโนเมียลเป็นความน่าจะเป็น
- ทำหน้าที่เป็นฟังก์ชันการเปิดใช้งานใน โครงข่ายประสาทเทียมบางส่วน
การวัดความคล้ายคลึง
ในอัลกอริทึมการจัดกลุ่ม เมตริกที่ใช้ในการพิจารณา ความเหมือน (ความคล้ายคลึง) ของตัวอย่าง 2 รายการ
โปรแกรมเดียว / ข้อมูลหลายรายการ (SPMD)
เทคนิคการทำงานแบบขนานที่ใช้การคำนวณเดียวกันกับข้อมูลอินพุตที่แตกต่างกัน แบบขนานในอุปกรณ์ต่างๆ เป้าหมายของ SPMD คือการได้รับผลลัพธ์ เร็วขึ้น ซึ่งเป็นรูปแบบการเขียนโปรแกรมแบบขนานที่พบบ่อยที่สุด
ความไม่แปรเปลี่ยนตามขนาด
ในปัญหาการแยกประเภทรูปภาพ ความสามารถของอัลกอริทึมในการแยกประเภทรูปภาพได้สำเร็จ แม้ว่าขนาดของรูปภาพจะเปลี่ยนแปลงไปก็ตาม เช่น อัลกอริทึมยังคงระบุ แมวได้ไม่ว่าจะใช้ 2 ล้านพิกเซลหรือ 2 แสนพิกเซล โปรดทราบว่าแม้แต่ อัลกอริทึมการจัดประเภทรูปภาพที่ดีที่สุดก็ยังมีข้อจำกัดในทางปฏิบัติเกี่ยวกับความไม่แปรเปลี่ยนของขนาด ตัวอย่างเช่น อัลกอริทึม (หรือมนุษย์) อาจไม่สามารถจัดประเภทรูปภาพแมวที่มีขนาดเพียง 20 พิกเซลได้อย่างถูกต้อง
ดูความไม่แปรเปลี่ยนตามการเลื่อนและ ความไม่แปรเปลี่ยนตามการหมุนด้วย
ดูข้อมูลเพิ่มเติมได้ที่หลักสูตรการจัดกลุ่ม
การสเก็ตช์ภาพ
ในแมชชีนเลิร์นนิงที่ไม่มีการควบคุมดูแล ซึ่งเป็นหมวดหมู่อัลกอริทึมที่ทำการวิเคราะห์ความคล้ายคลึงเบื้องต้น ในตัวอย่าง อัลกอริทึมการสเก็ตช์ใช้ ฟังก์ชันแฮชที่คำนึงถึงตำแหน่ง เพื่อระบุจุดที่มีแนวโน้มที่จะคล้ายกัน แล้วจัดกลุ่ม จุดเหล่านั้นลงในที่เก็บข้อมูล
การสเก็ตช์ช่วยลดการคำนวณที่จำเป็นสำหรับการคำนวณความคล้ายคลึงกัน ในชุดข้อมูลขนาดใหญ่ แทนที่จะคำนวณความคล้ายคลึงกันสำหรับตัวอย่างแต่ละคู่ในชุดข้อมูล เราจะคำนวณความคล้ายคลึงกันสำหรับคู่ของจุดแต่ละคู่ภายในแต่ละกลุ่มเท่านั้น
Skip-gram
N-gram ซึ่งอาจละเว้น (หรือ "ข้าม") คำจากบริบทเดิม ซึ่งหมายความว่าคำ N คำอาจไม่ได้อยู่ติดกันตั้งแต่แรก กล่าวอย่างเจาะจงยิ่งขึ้น "k-skip-n-gram" คือ n-gram ที่อาจมีการข้ามคำได้สูงสุด k คำ
เช่น "the quick brown fox" มี 2-แกรมที่เป็นไปได้ดังนี้
- "the quick"
- "quick brown"
- "หมาป่าสีน้ำตาล"
"1-skip-2-gram" คือคู่คำที่มีคำคั่นระหว่างกันไม่เกิน 1 คำ ดังนั้น "the quick brown fox" จึงมี 1-skip 2-grams ดังนี้
- "the brown"
- "quick fox"
นอกจากนี้ 2-gram ทั้งหมดยังเป็น 1-skip-2-gram ด้วย เนื่องจากอาจข้ามคำน้อยกว่า 1 คำ
Skip-gram มีประโยชน์ในการทำความเข้าใจบริบทโดยรอบของคำให้มากขึ้น ในตัวอย่างนี้ "fox" เชื่อมโยงกับ "quick" โดยตรงในชุดของ 1-skip-2-gram แต่ไม่ได้อยู่ในชุดของ 2-gram
Skip-gram ช่วยฝึกโมเดลการฝังคำ
softmax
ฟังก์ชันที่กำหนดความน่าจะเป็นสำหรับแต่ละคลาสที่เป็นไปได้ในโมเดลการจัดประเภทแบบหลายคลาส ความน่าจะเป็นรวมกัน เป็น 1.0 พอดี ตัวอย่างเช่น ตารางต่อไปนี้แสดงวิธีที่ Softmax กระจาย ความน่าจะเป็นต่างๆ
| รูปภาพเป็น... | Probability |
|---|---|
| สุนัข | .85 |
| cat | .13 |
| ม้า | .02 |
Softmax เรียกอีกอย่างว่า full softmax
แตกต่างจากการสุ่มตัวอย่างผู้สมัคร
ดูข้อมูลเพิ่มเติมได้ที่โครงข่ายประสาทเทียม: การจัดประเภทแบบหลายคลาส ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
การปรับแต่งพรอมต์แบบซอฟต์
เทคนิคในการปรับโมเดลภาษาขนาดใหญ่ สำหรับงานหนึ่งๆ โดยไม่ต้องใช้การปรับแต่งที่ต้องใช้ทรัพยากรจำนวนมาก การปรับพรอมต์แบบซอฟต์จะปรับพรอมต์โดยอัตโนมัติเพื่อบรรลุเป้าหมายเดียวกัน แทนที่จะฝึกน้ำหนักทั้งหมดในโมเดลใหม่
เมื่อได้รับพรอมต์ที่เป็นข้อความ การปรับพรอมต์แบบซอฟต์ โดยทั่วไปจะผนวกการฝังโทเค็นเพิ่มเติมลงในพรอมต์และใช้ การแพร่ย้อนกลับเพื่อเพิ่มประสิทธิภาพอินพุต
พรอมต์ "ฮาร์ด" มีโทเค็นจริงแทนที่จะเป็นโทเค็นแบบฝัง
ฟีเจอร์ Sparse
ฟีเจอร์ที่มีค่าเป็น 0 หรือว่างเปล่าเป็นส่วนใหญ่ เช่น ฟีเจอร์ที่มีค่า 1 เพียงค่าเดียวและค่า 0 จำนวน 1 ล้านค่าถือเป็นฟีเจอร์แบบกระจัดกระจาย ในทางตรงกันข้าม ฟีเจอร์แบบหนาแน่นมีค่าที่ส่วนใหญ่ ไม่ใช่ 0 หรือว่างเปล่า
ในแมชชีนเลิร์นนิง ฟีเจอร์จำนวนมากอย่างน่าประหลาดใจเป็นฟีเจอร์แบบเบาบาง ฟีเจอร์เชิงหมวดหมู่มักเป็นฟีเจอร์แบบกระจัดกระจาย ตัวอย่างเช่น จากต้นไม้ 300 สายพันธุ์ที่เป็นไปได้ในป่า ตัวอย่างเดียวอาจระบุได้แค่ต้นเมเปิล หรือจากวิดีโอหลายล้านรายการ ในคลังวิดีโอ ตัวอย่างเดียวอาจระบุ เพียง "คาซาบลังกา"
ในโมเดล คุณมักจะแสดงฟีเจอร์แบบกระจัดกระจายด้วยการเข้ารหัสแบบ One-hot หากการเข้ารหัสแบบ One-hot มีขนาดใหญ่ คุณอาจวางเลเยอร์การฝังไว้ด้านบน การเข้ารหัสแบบ One-hot เพื่อเพิ่มประสิทธิภาพ
การแสดงแบบกระจัดกระจาย
จัดเก็บเฉพาะตำแหน่งขององค์ประกอบที่ไม่ใช่ศูนย์ในฟีเจอร์แบบกระจัดกระจาย
ตัวอย่างเช่น สมมติว่าฟีเจอร์เชิงหมวดหมู่ชื่อ species ระบุพันธุ์ไม้ 36
ชนิดในป่าแห่งหนึ่ง สมมติว่าตัวอย่างแต่ละรายการระบุเพียงสายพันธุ์เดียว
คุณสามารถใช้เวกเตอร์แบบ One-Hot เพื่อแสดงสายพันธุ์ของต้นไม้ในแต่ละตัวอย่าง
เวกเตอร์แบบ One-Hot จะมี 1 เพียงรายการเดียว (เพื่อแสดงถึง
สายพันธุ์ต้นไม้ที่เฉพาะเจาะจงในตัวอย่างนั้น) และมี 0 35 รายการ (เพื่อแสดงถึง
สายพันธุ์ต้นไม้ 35 สายพันธุ์ที่ไม่ได้อยู่ในตัวอย่างนั้น) ดังนั้นการแสดงแบบ One-Hot ของ maple อาจมีลักษณะดังนี้

หรือการแสดงแบบกระจัดกระจายจะระบุตำแหน่งของ
สายพันธุ์ที่เฉพาะเจาะจง หาก maple อยู่ที่ตำแหน่ง 24 การแสดงแบบกระจัดกระจาย
ของ maple จะเป็นดังนี้
24
โปรดสังเกตว่าการแสดงแบบกระจัดกระจายนั้นกะทัดรัดกว่าการแสดงแบบ One-Hot มาก
ดูข้อมูลเพิ่มเติมได้ที่การทำงานกับข้อมูลเชิงหมวดหมู่ ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
เวกเตอร์แบบกระจัดกระจาย
เวกเตอร์ที่มีค่าเป็น 0 เป็นส่วนใหญ่ ดูฟีเจอร์แบบกระจัดกระจาย และความกระจัดกระจายด้วย
การขาดแคลนข้อมูล
จำนวนองค์ประกอบที่ตั้งค่าเป็น 0 (หรือ Null) ในเวกเตอร์หรือเมทริกซ์หารด้วยจำนวนรายการทั้งหมดในเวกเตอร์หรือเมทริกซ์นั้น ตัวอย่างเช่น ลองพิจารณาเมทริกซ์ที่มี 100 องค์ประกอบซึ่งมีเซลล์ 98 เซลล์ที่มีค่าเป็น 0 การคำนวณความกระจัดกระจาย มีดังนี้
ความกระจัดกระจายของฟีเจอร์หมายถึงความกระจัดกระจายของเวกเตอร์ฟีเจอร์ ความกระจัดกระจายของโมเดลหมายถึงความกระจัดกระจายของน้ำหนักโมเดล
การรวมกลุ่มเชิงพื้นที่
การเขียนโค้ดตามข้อกำหนด
กระบวนการเขียนและดูแลรักษาไฟล์ในภาษาที่มนุษย์ใช้ (เช่น ภาษาอังกฤษ) ซึ่งอธิบายซอฟต์แวร์ จากนั้นคุณสามารถบอกโมเดล Generative AI หรือ วิศวกรซอฟต์แวร์คนอื่นๆ ให้สร้างซอฟต์แวร์ที่ตรงกับคำอธิบายนั้น
โดยทั่วไปแล้ว โค้ดที่สร้างขึ้นโดยอัตโนมัติต้องมีการทำซ้ำ ในการเขียนโค้ดตามข้อกำหนด คุณจะวนซ้ำในไฟล์คำอธิบาย ในทางตรงกันข้าม การเขียนโค้ดแบบสนทนาจะวนซ้ำภายใน ช่องพรอมต์ ในทางปฏิบัติ การสร้างโค้ดอัตโนมัติบางครั้งเกี่ยวข้องกับทั้งการเขียนโค้ดตามข้อกำหนดและการเขียนโค้ดแบบสนทนา
แยก
ในแผนผังการตัดสินใจ ซึ่งเป็นอีกชื่อหนึ่งของเงื่อนไข
ตัวแยก
ขณะฝึกต้นไม้ตัดสินใจ รูทีน (และอัลกอริทึม) ที่รับผิดชอบในการค้นหาเงื่อนไขที่ดีที่สุดในแต่ละโหนด
SPMD
ตัวย่อของโปรแกรมเดียว / ข้อมูลหลายรายการ
SQuAD
คำย่อของ Stanford Question Answering Dataset ซึ่งเปิดตัวในเอกสาร SQuAD: 100,000+ Questions for Machine Comprehension of Text คำถามในชุดข้อมูลนี้มาจากผู้ที่ถามคำถามเกี่ยวกับบทความใน วิกิพีเดีย คำถามบางข้อใน SQuAD มีคำตอบ แต่คำถามอื่นๆ ไม่มีคำตอบโดยตั้งใจ ดังนั้น คุณจึงใช้ SQuAD เพื่อประเมินความสามารถของ LLM ในการทำสิ่งต่อไปนี้ได้
- ตอบคำถามที่ตอบได้
- ระบุคำถามที่ตอบไม่ได้
การทำงานแบบตรงทั้งหมดร่วมกับ F1 เป็นเมตริกที่พบบ่อยที่สุดสําหรับ การประเมิน LLM กับ SQuAD
การสูญเสียบานพับกำลังสอง
กำลังสองของการสูญเสียแบบบานพับ การสูญเสียบานพับกำลังสองจะลงโทษค่าผิดปกติ อย่างรุนแรงกว่าการสูญเสียบานพับปกติ
การสูญเสียกำลังสอง
คำพ้องความหมายของการสูญเสียL2
การฝึกแบบเป็นขั้น
กลยุทธ์ในการฝึกโมเดลในลำดับของขั้นตอนที่แยกจากกัน เป้าหมายอาจเป็นการเร่งกระบวนการฝึก หรือเพื่อให้ได้โมเดลที่มีคุณภาพดีขึ้น
ภาพแสดงวิธีการซ้อนแบบก้าวหน้ามีดังนี้
- โดยระยะที่ 1 มีเลเยอร์ที่ซ่อนอยู่ 3 เลเยอร์ ระยะที่ 2 มีเลเยอร์ที่ซ่อนอยู่ 6 เลเยอร์ และ ระยะที่ 3 มีเลเยอร์ที่ซ่อนอยู่ 12 เลเยอร์
- ระยะที่ 2 เริ่มฝึกด้วยน้ำหนักที่ได้เรียนรู้ในเลเยอร์ที่ซ่อนอยู่ 3 เลเยอร์ ของระยะที่ 1 Stage 3 เริ่มการฝึกด้วยน้ำหนักที่ได้เรียนรู้ในเลเยอร์ที่ซ่อนอยู่ 6 เลเยอร์ของ Stage 2
ดูการส่งผ่านคำสั่งด้วย
รัฐ
ในการเรียนรู้แบบเสริมกำลัง ค่าพารามิเตอร์ที่อธิบายการกำหนดค่าปัจจุบันของสภาพแวดล้อม ซึ่งเอเจนต์ใช้เพื่อเลือกการดำเนินการ
ฟังก์ชันค่าสถานะ-การดำเนินการ
คำพ้องความหมายของฟังก์ชัน Q
คงที่
สิ่งที่ทำครั้งเดียวแทนที่จะทำอย่างต่อเนื่อง คำว่าคงที่และออฟไลน์มีความหมายเหมือนกัน การใช้งาน แบบคงที่และออฟไลน์ที่พบบ่อยในแมชชีนเลิร์นนิงมีดังนี้
- โมเดลแบบคงที่ (หรือโมเดลออฟไลน์) คือโมเดลที่ได้รับการฝึกเพียงครั้งเดียวและ นำไปใช้เป็นระยะเวลาหนึ่ง
- การฝึกแบบคงที่ (หรือการฝึกแบบออฟไลน์) คือกระบวนการฝึก โมเดลแบบคงที่
- การอนุมานแบบคงที่ (หรือการอนุมานแบบออฟไลน์) คือกระบวนการที่โมเดลสร้างการคาดการณ์แบบกลุ่มครั้งละ 1 กลุ่ม
คอนทราสต์กับไดนามิก
การอนุมานแบบคงที่
คำพ้องความหมายของการอนุมานแบบออฟไลน์
ความคงที่
ฟีเจอร์ที่มีค่าไม่เปลี่ยนแปลงในมิติข้อมูลอย่างน้อย 1 รายการ ซึ่งมักจะเป็นเวลา ตัวอย่างเช่น ฟีเจอร์ที่มีค่าที่ดูเหมือนกันในปี 2021 และ 2023 จะแสดงความคงที่
ในโลกแห่งความเป็นจริง มีฟีเจอร์เพียงไม่กี่อย่างที่แสดงความคงที่ แม้แต่ฟีเจอร์ที่ มีความหมายเหมือนกันกับความเสถียร (เช่น ระดับน้ำทะเล) ก็เปลี่ยนแปลงไปตามกาลเวลา
แตกต่างจากความไม่คงที่
ขั้นตอน
การส่งต่อและการส่งย้อนกลับของกลุ่ม
ดู backpropagation สำหรับข้อมูลเพิ่มเติมเกี่ยวกับการส่งผ่านไปข้างหน้าและการส่งผ่านไปข้างหลัง
ขนาดก้าว
คำพ้องความหมายสำหรับอัตราการเรียนรู้ -
การไล่ระดับสีแบบสุ่ม (SGD)
อัลกอริทึมการไล่ระดับสีซึ่งมีขนาดกลุ่มเป็น 1 กล่าวอีกนัยหนึ่งคือ SGD ฝึกกับ ตัวอย่างเดียวที่เลือกแบบสุ่ม อย่างสม่ำเสมอจากชุดการฝึก
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยเชิงเส้น: ไฮเปอร์พารามิเตอร์ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ก้าว
ในการดำเนินการแบบ Convolutional หรือการรวมกลุ่ม เดลต้าในแต่ละมิติของ ชุดอินพุตสไลซ์ถัดไป ตัวอย่างเช่น ภาพเคลื่อนไหวต่อไปนี้ แสดงการก้าวย่าง (1,1) ระหว่างการดำเนินการแบบ Convolution ดังนั้น อินพุตสไลซ์ถัดไปจะเริ่มต้นที่ตำแหน่งทางขวาของอินพุต สไลซ์ก่อนหน้า 1 ตำแหน่ง เมื่อการดำเนินการไปถึงขอบด้านขวา ส่วนถัดไปจะอยู่ทางด้านซ้ายสุด แต่เลื่อนลงมา 1 ตำแหน่ง
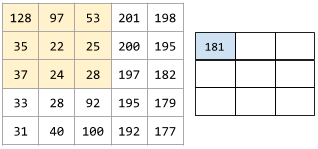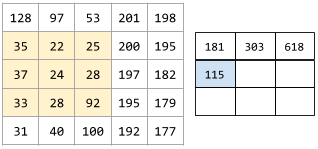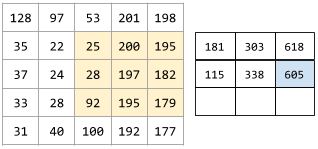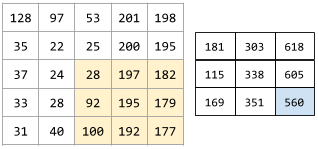
ตัวอย่างก่อนหน้าแสดงการก้าวย่างแบบ 2 มิติ หากเมทริกซ์อินพุต เป็นแบบ 3 มิติ สไตรด์ก็จะเป็นแบบ 3 มิติด้วย
การลดความเสี่ยงเชิงโครงสร้าง (SRM)
อัลกอริทึมที่สร้างสมดุลระหว่างเป้าหมาย 2 อย่าง
- ความจำเป็นในการสร้างโมเดลที่มีความสามารถในการคาดการณ์มากที่สุด (เช่น มีการสูญเสียต่ำสุด)
- ความจำเป็นในการทำให้โมเดลเรียบง่ายที่สุดเท่าที่จะเป็นไปได้ (เช่น การควบคุมที่เข้มงวด)
ตัวอย่างเช่น ฟังก์ชันที่ลดการสูญเสีย + การทำให้เป็นปกติในชุดข้อมูลการฝึกเป็นอัลกอริทึมการลดความเสี่ยงเชิงโครงสร้าง
เทียบกับการลดความเสี่ยงเชิงประจักษ์
การสุ่มย่อย
ดูการรวมกลุ่ม -
โทเค็นคำย่อย
ในโมเดลภาษา โทเค็นคือสตริงย่อยของคำ ซึ่งอาจเป็นคำทั้งคำ
เช่น คำว่า "itemize" อาจแบ่งออกเป็น "item" (คำหลัก) และ "ize" (คำต่อท้าย) ซึ่งแต่ละคำจะแสดงด้วยโทเค็นของตัวเอง การแยกคำที่ไม่ค่อยพบออกเป็นส่วนๆ ดังกล่าวเรียกว่าคำย่อย ซึ่งช่วยให้ โมเดลภาษาทำงานกับส่วนประกอบที่พบบ่อยกว่าของคำ เช่น คำนำหน้าและคำต่อท้าย
ในทางกลับกัน คำที่ใช้กันทั่วไป เช่น "going" อาจไม่ถูกแบ่งและอาจ แสดงด้วยโทเค็นเดียว
สรุป
ใน TensorFlow ค่าหรือชุดค่าที่คำนวณในขั้นตอนหนึ่งๆ มักใช้เพื่อติดตามเมตริกของโมเดลระหว่างการฝึก
แมชชีนเลิร์นนิงที่มีการควบคุมดูแล
การฝึกโมเดลจากฟีเจอร์และป้ายกำกับที่เกี่ยวข้อง แมชชีนเลิร์นนิงที่มีการควบคุมดูแลเปรียบเสมือน การเรียนรู้เรื่องหนึ่งๆ โดยการศึกษาชุดคำถามและคำตอบที่ เกี่ยวข้อง หลังจากเข้าใจความสัมพันธ์ระหว่างคำถามและคำตอบแล้ว นักเรียนจะสามารถตอบคำถามใหม่ (ที่ไม่เคยเห็นมาก่อน) ในหัวข้อเดียวกันได้
เปรียบเทียบกับแมชชีนเลิร์นนิงที่ไม่มีการควบคุมดูแล
ดูข้อมูลเพิ่มเติมได้ที่การเรียนรู้แบบมีผู้ดูแล ในหลักสูตรข้อมูลเบื้องต้นเกี่ยวกับ ML
ฟีเจอร์สังเคราะห์
ฟีเจอร์ที่ไม่มีในฟีเจอร์อินพุต แต่ ประกอบขึ้นจากฟีเจอร์อินพุตอย่างน้อย 1 รายการ วิธีการสร้างฟีเจอร์สังเคราะห์ มีดังนี้
- การจัดกลุ่มฟีเจอร์ต่อเนื่องลงในกลุ่มช่วง
- การสร้างฟีเจอร์ครอส
- การคูณ (หรือหาร) ค่าฟีเจอร์หนึ่งด้วยค่าฟีเจอร์อื่นๆ
หรือด้วยค่าของฟีเจอร์นั้นเอง ตัวอย่างเช่น หาก
aและbเป็นฟีเจอร์อินพุต ตัวอย่างฟีเจอร์สังเคราะห์มีดังนี้- ab
- a2
- การใช้ฟังก์ชันอดิศัยกับค่าฟีเจอร์ ตัวอย่างเช่น หาก
cเป็นฟีเจอร์อินพุต ตัวอย่างฟีเจอร์สังเคราะห์จะมีดังนี้- sin(c)
- ln(c)
ฟีเจอร์ที่สร้างขึ้นโดยการปรับให้เป็นมาตรฐานหรือปรับขนาด เพียงอย่างเดียวไม่ถือเป็นฟีเจอร์สังเคราะห์
T
T5
โมเดล การเรียนรู้แบบถ่ายโอนจากข้อความสู่ข้อความ เปิดตัวโดย Google AI ในปี 2020 T5 เป็นโมเดลตัวเข้ารหัส-ตัวถอดรหัสที่อิงตามสถาปัตยกรรม Transformer ซึ่งได้รับการฝึกในชุดข้อมูลขนาดใหญ่มาก โมเดลนี้มีประสิทธิภาพในการทำงานด้านการประมวลผลภาษาธรรมชาติที่หลากหลาย เช่น การสร้างข้อความ การแปลภาษา และการตอบคำถามในลักษณะการสนทนา
T5 ได้ชื่อมาจากตัวอักษร T 5 ตัวใน "Text-to-Text Transfer Transformer"
T5X
เฟรมเวิร์กแมชชีนเลิร์นนิงโอเพนซอร์สที่ออกแบบมา เพื่อสร้างและฝึกโมเดลการประมวลผลภาษาธรรมชาติ (NLP) ขนาดใหญ่ T5 ได้รับการติดตั้งใช้งานในโค้ดเบส T5X (ซึ่งสร้างขึ้นจาก JAX และ Flax)
Q-Learning แบบตาราง
ในการเรียนรู้แบบเสริมกำลัง การใช้การเรียนรู้แบบ Q โดยใช้ตารางเพื่อจัดเก็บฟังก์ชัน Q สำหรับชุดค่าผสมทั้งหมดของสถานะและการดำเนินการ
เป้าหมาย
คำพ้องความหมายของป้ายกำกับ
เครือข่ายเป้าหมาย
ใน Deep Q-learning โครงข่ายประสาทที่เสถียร โดยประมาณของโครงข่ายประสาทหลัก ซึ่งโครงข่ายประสาทหลัก จะใช้ ฟังก์ชัน Q หรือนโยบาย จากนั้นคุณจะฝึกเครือข่ายหลักเกี่ยวกับค่า Q ที่เครือข่ายเป้าหมายคาดการณ์ได้ ดังนั้น คุณจึงป้องกันลูปความคิดเห็นที่เกิดขึ้นเมื่อเครือข่ายหลัก ฝึกค่า Q ที่เครือข่ายหลักคาดการณ์เอง การหลีกเลี่ยงความคิดเห็นนี้จะช่วยเพิ่มความเสถียรในการฝึก
งาน
ปัญหาที่แก้ไขได้โดยใช้เทคนิคแมชชีนเลิร์นนิง เช่น
อุณหภูมิ
ไฮเปอร์พารามิเตอร์ที่ควบคุมระดับความสุ่ม ของเอาต์พุตของโมเดล อุณหภูมิที่สูงขึ้นจะทำให้เอาต์พุตสุ่มมากขึ้น ในขณะที่อุณหภูมิที่ต่ำลงจะทำให้เอาต์พุตสุ่มน้อยลง
การเลือกอุณหภูมิที่ดีที่สุดขึ้นอยู่กับการใช้งานเฉพาะและ/หรือค่าสตริง
ข้อมูลเชิงเวลา
ข้อมูลที่บันทึกไว้ในช่วงเวลาต่างๆ ตัวอย่างเช่น ยอดขายเสื้อโค้ทฤดูหนาว ที่บันทึกไว้ในแต่ละวันของปีจะเป็นข้อมูลตามเวลา
Tensor
โครงสร้างข้อมูลหลักในโปรแกรม TensorFlow Tensor เป็นโครงสร้างข้อมูล N มิติ (โดย N อาจมีค่ามาก) ซึ่งส่วนใหญ่เป็นสเกลาร์ เวกเตอร์ หรือเมทริกซ์ องค์ประกอบของเทนเซอร์สามารถเก็บค่าจำนวนเต็ม ค่าทศนิยม หรือค่าสตริงได้
TensorBoard
แดชบอร์ดที่แสดงข้อมูลสรุปที่บันทึกไว้ระหว่างการเรียกใช้โปรแกรม TensorFlow อย่างน้อย 1 โปรแกรม
TensorFlow
แพลตฟอร์มแมชชีนเลิร์นนิงแบบกระจายขนาดใหญ่ คำนี้ยังหมายถึง เลเยอร์ API พื้นฐานในสแต็ก TensorFlow ซึ่งรองรับการคำนวณทั่วไป ในกราฟ Dataflow
แม้ว่า TensorFlow จะใช้สำหรับแมชชีนเลิร์นนิงเป็นหลัก แต่คุณก็ใช้ TensorFlow สำหรับงานที่ไม่ใช่ ML ซึ่งต้องมีการคำนวณตัวเลขโดยใช้กราฟโฟลว์ของข้อมูลได้เช่นกัน
TensorFlow Playground
โปรแกรมที่แสดงให้เห็นว่าไฮเปอร์พารามิเตอร์ต่างๆ ส่งผลต่อการฝึกโมเดล (โดยหลักคือโครงข่ายประสาทเทียม) อย่างไร ไปที่ http://playground.tensorflow.org เพื่อทดลองใช้ TensorFlow Playground
TensorFlow Serving
แพลตฟอร์มสำหรับการติดตั้งใช้งานโมเดลที่ฝึกแล้วในเวอร์ชันที่ใช้งานจริง
Tensor Processing Unit (TPU)
วงจรรวมเฉพาะแอปพลิเคชัน (ASIC) ที่เพิ่มประสิทธิภาพ ปริมาณงานของแมชชีนเลิร์นนิง ASIC เหล่านี้ได้รับการติดตั้งใช้งานเป็นชิป TPU หลายตัวในอุปกรณ์ TPU
อันดับของ Tensor
รูปร่างของ Tensor
จํานวนองค์ประกอบที่ Tensor มีในมิติข้อมูลต่างๆ
เช่น [5, 10]เทนเซอร์มีรูปร่างเป็น 5 ในมิติหนึ่งและ 10
ในอีกมิติหนึ่ง
ขนาดของเทนเซอร์
จำนวนสเกลาร์ทั้งหมดที่ Tensor มี เช่น [5, 10]เทนเซอร์มีขนาด 50
TensorStore
ไลบรารีสำหรับการอ่านและเขียนอาร์เรย์หลายมิติขนาดใหญ่อย่างมีประสิทธิภาพ
เงื่อนไขการสิ้นสุด
ในการเรียนรู้แบบเสริมกำลัง เงื่อนไขที่ กำหนดเวลาสิ้นสุดตอน เช่น เมื่อเอเจนต์ไปถึง สถานะหนึ่งๆ หรือเกินจำนวนการเปลี่ยนสถานะตามเกณฑ์ ตัวอย่างเช่น ในเกม Tic-Tac-Toe (หรือที่รู้จักกันในชื่อเกม O-X) ตอนจะจบลงเมื่อผู้เล่นทำเครื่องหมายในช่อง 3 ช่องติดต่อกันหรือเมื่อมีการทำเครื่องหมายในทุกช่อง
ทดสอบ
ในแผนผังการตัดสินใจ ซึ่งเป็นอีกชื่อหนึ่งของเงื่อนไข
การสูญเสียการทดสอบ
เมตริกที่แสดงถึง Loss ของโมเดลเทียบกับ ชุดทดสอบ เมื่อสร้างโมเดล คุณ มักจะพยายามลดการสูญเสียในการทดสอบ เนื่องจากค่าการสูญเสียในการทดสอบที่ต่ำเป็นสัญญาณคุณภาพที่แข็งแกร่งกว่าค่าการสูญเสียในการฝึกหรือค่าการสูญเสียในการตรวจสอบที่ต่ำ
ช่องว่างขนาดใหญ่ระหว่างการสูญเสียจากการทดสอบกับการสูญเสียจากการฝึกหรือการสูญเสียจากการตรวจสอบในบางครั้ง บ่งชี้ว่าคุณต้องเพิ่มอัตราการทำให้เป็นปกติ
ชุดทดสอบ
ชุดข้อมูลย่อยของชุดข้อมูลที่สงวนไว้สำหรับการทดสอบ โมเดลที่ฝึกแล้ว
โดยปกติแล้ว คุณจะแบ่งตัวอย่างในชุดข้อมูลออกเป็น 3 กลุ่มย่อยที่แตกต่างกันดังนี้
- ชุดฝึก
- ชุดข้อมูลสำหรับตรวจสอบความถูกต้อง
- ชุดทดสอบ
ตัวอย่างแต่ละรายการในชุดข้อมูลควรอยู่ในชุดข้อมูลย่อยเพียงชุดเดียวจากชุดข้อมูลย่อยที่กล่าวถึงก่อนหน้านี้ เช่น ตัวอย่างเดียวไม่ควรอยู่ในทั้งชุดการฝึกและชุดทดสอบ
ทั้งชุดการฝึกและชุดการตรวจสอบมีความเกี่ยวข้องอย่างใกล้ชิดกับการฝึกโมเดล เนื่องจากชุดทดสอบเชื่อมโยงกับการฝึกโดยอ้อมเท่านั้น การสูญเสียจากการทดสอบจึงเป็นเมตริกที่มีคุณภาพสูงกว่าและมีอคติน้อยกว่าการสูญเสียจากการฝึกหรือการสูญเสียจากการตรวจสอบ
ดูข้อมูลเพิ่มเติมได้ที่ชุดข้อมูล: การแบ่งชุดข้อมูลเดิม ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ช่วงข้อความ
ช่วงดัชนีอาร์เรย์ที่เชื่อมโยงกับส่วนย่อยที่เฉพาะเจาะจงของสตริงข้อความ
เช่น คำว่า good ในสตริง Python s="Be good now" จะครอบครอง
ช่วงข้อความตั้งแต่ 3 ถึง 6
tf.Example
Protocol Buffer มาตรฐานสำหรับอธิบายข้อมูลอินพุตสำหรับการฝึกหรือการอนุมานโมเดลแมชชีนเลิร์นนิง
tf.keras
การติดตั้งใช้งาน Keras ที่ผสานรวมเข้ากับ TensorFlow
เกณฑ์ (สำหรับต้นไม้ตัดสินใจ)
ในเงื่อนไขที่สอดคล้องกับแกน ค่าที่ฟีเจอร์กำลังเปรียบเทียบด้วย ตัวอย่างเช่น 75 คือค่าเกณฑ์ในเงื่อนไขต่อไปนี้
grade >= 75
ดูข้อมูลเพิ่มเติมได้ที่ตัวแยกที่แน่นอนสำหรับการแยกประเภทไบนารีที่มีฟีเจอร์เชิงตัวเลข ในหลักสูตร Decision Forests
การวิเคราะห์อนุกรมเวลา
สาขาย่อยของแมชชีนเลิร์นนิงและสถิติที่วิเคราะห์ข้อมูลตามเวลา ปัญหาแมชชีนเลิร์นนิงหลายประเภทต้องใช้การวิเคราะห์อนุกรมเวลา ซึ่งรวมถึงการจัดประเภท การจัดกลุ่ม การคาดการณ์ และการตรวจหาความผิดปกติ ตัวอย่างเช่น คุณอาจใช้ การวิเคราะห์อนุกรมเวลาเพื่อคาดการณ์ยอดขายเสื้อโค้ทฤดูหนาวในอนาคตเป็นรายเดือน โดยอิงตามข้อมูลยอดขายที่ผ่านมา
ช่วงเวลา
เซลล์ "คลี่" หนึ่งเซลล์ภายในโครงข่ายประสาทแบบเกิดซ้ำ ตัวอย่างเช่น รูปต่อไปนี้แสดงไทม์สเต็ป 3 รายการ (ติดป้ายกำกับด้วย ตัวห้อย t-1, t และ t+1)

โทเค็น
ในโมเดลภาษา หน่วยย่อยที่โมเดลใช้ ฝึกและคาดการณ์ โดยทั่วไปแล้ว โทเค็นจะเป็นอย่างใดอย่างหนึ่งต่อไปนี้
- คำ เช่น วลี "dogs like cats" ประกอบด้วยโทเค็นคำ 3 คำ ได้แก่ "dogs", "like" และ "cats"
- อักขระ เช่น วลี "bike fish" ประกอบด้วยโทเค็นอักขระ 9 รายการ (โปรดทราบว่าช่องว่างจะนับเป็นโทเค็น 1 รายการ)
- คำย่อย ซึ่งคำเดียวอาจเป็นโทเค็นเดียวหรือหลายโทเค็นก็ได้ คำย่อยประกอบด้วยคำหลัก คำนำหน้า หรือคำต่อท้าย ตัวอย่างเช่น โมเดลภาษาที่ใช้คำย่อยเป็นโทเค็นอาจมองคำว่า "dogs" เป็น 2 โทเค็น (คำหลัก "dog" และคำต่อท้ายพหูพจน์ "s") โมเดลภาษาเดียวกันนี้อาจมองคำว่า "สูงกว่า" เป็นคำย่อย 2 คำ (คำหลัก "สูง" และคำต่อท้าย "กว่า")
ในโดเมนที่อยู่นอกโมเดลภาษา โทเค็นสามารถแสดงหน่วยย่อยอื่นๆ ได้ เช่น ในคอมพิวเตอร์วิทัศน์ โทเค็นอาจเป็นเซ็ตย่อย ของรูปภาพ
ดูข้อมูลเพิ่มเติมได้ที่โมเดลภาษาขนาดใหญ่ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
เครื่องมือแปลงข้อความเป็นโทเค็น
ระบบหรืออัลกอริทึมที่แปลลําดับของข้อมูลที่ป้อนเป็นโทเค็น
โมเดลพื้นฐานที่ทันสมัยส่วนใหญ่เป็นโมเดลหลายรูปแบบ ตัวแยกโทเค็นสำหรับระบบมัลติโมดัล ต้องแปลอินพุตแต่ละประเภทเป็นรูปแบบที่เหมาะสม ตัวอย่างเช่น เมื่อได้รับข้อมูลอินพุตซึ่งประกอบด้วยทั้งข้อความและกราฟิก ตัวแยกโทเค็นอาจ แปลข้อความอินพุตเป็นคำย่อยและแปลรูปภาพอินพุตเป็นแพตช์ขนาดเล็ก จากนั้นโทเค็นไนเซอร์ต้องแปลงโทเค็นทั้งหมดเป็นพื้นที่ฝังแบบรวมเดียว ซึ่งช่วยให้โมเดล "เข้าใจ" สตรีมอินพุตมัลติโมดัลได้
ความแม่นยำสูงสุด k
เปอร์เซ็นต์ของจำนวนครั้งที่ "ป้ายกำกับเป้าหมาย" ปรากฏภายในk ตำแหน่งแรกของรายการที่สร้างขึ้น รายการอาจเป็นคำแนะนำที่ปรับเปลี่ยนในแบบของคุณ หรือรายการสินค้าที่จัดเรียงตาม softmax
ความแม่นยำสูงสุด k เรียกอีกอย่างว่าความแม่นยำที่ k
หอคอย
องค์ประกอบของโครงข่ายประสาทแบบลึกซึ่งเป็นโครงข่ายประสาทแบบลึกในตัว ในบางกรณี แต่ละทาวเวอร์จะอ่านจากแหล่งข้อมูลอิสระ และทาวเวอร์เหล่านั้นจะยังคงเป็นอิสระจนกว่าจะมีการรวมเอาต์พุตไว้ในเลเยอร์สุดท้าย ในกรณีอื่นๆ (เช่น ในเอนโค้ดเดอร์และดีโค้ดเดอร์ของ Transformer หลายๆ ตัว) ทาวเวอร์มีการเชื่อมต่อข้าม ซึ่งกันและกัน
ความเชื่อผิดๆ
ระดับของเนื้อหาที่เป็นการละเมิด ข่มขู่ หรือไม่เหมาะสม โมเดลแมชชีน เลิร์นนิงหลายโมเดลสามารถระบุและวัดระดับความเป็นพิษได้ โมเดลส่วนใหญ่ระบุ ความเป็นพิษตามพารามิเตอร์ต่างๆ เช่น ระดับของภาษาที่ละเมิดและ ระดับของภาษาที่คุกคาม
TPU
ตัวย่อของ Tensor Processing Unit
ชิป TPU
ตัวเร่งพีชคณิตเชิงเส้นที่ตั้งโปรแกรมได้พร้อมหน่วยความจำแบนด์วิดท์สูงบนชิป ซึ่งได้รับการเพิ่มประสิทธิภาพสำหรับภาระงานของแมชชีนเลิร์นนิง ชิป TPU หลายตัวได้รับการติดตั้งใช้งานในอุปกรณ์ TPU
อุปกรณ์ TPU
แผงวงจรพิมพ์ (PCB) ที่มีชิป TPU หลายตัว อินเทอร์เฟซเครือข่ายที่มีแบนด์วิดท์สูง และฮาร์ดแวร์ระบายความร้อนของระบบ
โหนด TPU
ทรัพยากร TPU ใน Google Cloud ที่มีประเภท TPU ที่เฉพาะเจาะจง โหนด TPU จะเชื่อมต่อกับเครือข่าย VPC จากเครือข่าย VPC ที่มีการเชื่อมต่อแบบเพียร์ โหนด TPU เป็นทรัพยากรที่กำหนดไว้ใน Cloud TPU API
พ็อด TPU
การกำหนดค่าที่เฉพาะเจาะจงของอุปกรณ์ TPU ในศูนย์ข้อมูลของ Google อุปกรณ์ทั้งหมดใน TPU Pod จะเชื่อมต่อกัน ผ่านเครือข่ายความเร็วสูงเฉพาะ TPU Pod เป็นการกำหนดค่าที่ใหญ่ที่สุดของอุปกรณ์ TPU ที่พร้อมใช้งานสำหรับ TPU เวอร์ชันที่เฉพาะเจาะจง
ทรัพยากร TPU
เอนทิตี TPU ใน Google Cloud ที่คุณสร้าง จัดการ หรือใช้ เช่น โหนด TPU และประเภท TPU คือ ทรัพยากร TPU
Slice TPU
TPU Slice คือส่วนย่อยของอุปกรณ์ TPU ใน พ็อด TPU อุปกรณ์ทั้งหมดใน TPU Slice จะเชื่อมต่อ กันผ่านเครือข่ายความเร็วสูงเฉพาะ
ประเภท TPU
การกำหนดค่าอุปกรณ์ TPU อย่างน้อย 1 เครื่องที่มี
ฮาร์ดแวร์ TPU เวอร์ชันที่เฉพาะเจาะจง คุณเลือกประเภท TPU เมื่อสร้างโหนด TPU ใน Google Cloud เช่น v2-8
ประเภท TPU คืออุปกรณ์ TPU v2 เครื่องเดียวที่มี 8 คอร์ v3-2048 ประเภท TPU มีอุปกรณ์ TPU v3 ที่เชื่อมต่อเครือข่าย 256 เครื่องและมีคอร์ทั้งหมด 2048 คอร์ ประเภท TPU เป็นทรัพยากรที่
กำหนดไว้ใน
Cloud TPU API
TPU Worker
กระบวนการที่ทำงานบนเครื่องโฮสต์และเรียกใช้โปรแกรมแมชชีนเลิร์นนิง ในอุปกรณ์ TPU
การฝึกอบรม
กระบวนการในการกำหนดพารามิเตอร์ (น้ำหนักและความเอนเอียง) ที่เหมาะสม ซึ่งประกอบกันเป็นโมเดล ในระหว่างการฝึก ระบบจะอ่านตัวอย่างและค่อยๆ ปรับพารามิเตอร์ การฝึกจะใช้ตัวอย่างแต่ละรายการตั้งแต่ไม่กี่ครั้งไปจนถึงหลายพันล้านครั้ง
ดูข้อมูลเพิ่มเติมได้ที่การเรียนรู้แบบมีผู้ดูแล ในหลักสูตรข้อมูลเบื้องต้นเกี่ยวกับ ML
การสูญเสียการฝึก
เมตริกที่แสดงการสูญเสียของโมเดลระหว่างการฝึก ในรอบการฝึกที่เฉพาะเจาะจง เช่น สมมติว่าฟังก์ชันการสูญเสีย คือความคลาดเคลื่อนกำลังสองเฉลี่ย เช่น การสูญเสียการฝึก (ข้อผิดพลาดกำลังสองเฉลี่ย) สำหรับการทำซ้ำครั้งที่ 10 คือ 2.2 และการสูญเสียการฝึกสำหรับการทำซ้ำครั้งที่ 100 คือ 1.9
เส้นโค้งการสูญเสียจะพล็อตการสูญเสียการฝึกเทียบกับจำนวน การทำซ้ำ เส้นโค้งการสูญเสียจะให้คำแนะนำต่อไปนี้เกี่ยวกับการฝึก
- ความชันลงแสดงว่าโมเดลกำลังปรับปรุง
- ความชันที่เพิ่มขึ้นหมายความว่าโมเดลแย่ลง
- ความชันที่แบนราบแสดงว่าโมเดลถึงการบรรจบกันแล้ว
ตัวอย่างเช่น เส้นโค้งการสูญเสีย ต่อไปนี้แสดงให้เห็นว่า
- ความชันที่ลดลงอย่างรวดเร็วในระหว่างการทำซ้ำครั้งแรก ซึ่งหมายถึงการปรับปรุงโมเดลอย่างรวดเร็ว
- ความชันที่ค่อยๆ แบนราบ (แต่ยังคงลดลง) จนกระทั่งใกล้สิ้นสุด การฝึก ซึ่งหมายถึงการปรับปรุงโมเดลอย่างต่อเนื่องในอัตราที่ช้าลงเล็กน้อย กว่าในช่วงการทำซ้ำครั้งแรก
- ความชันที่ราบเรียบในช่วงท้ายของการฝึก ซึ่งบ่งบอกถึงการบรรจบกัน
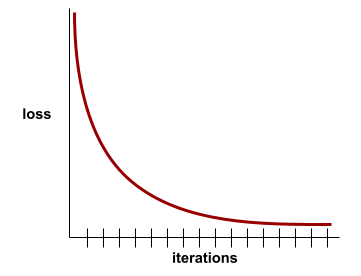
แม้ว่าการสูญเสียจากการฝึกจะมีความสําคัญ แต่โปรดดูการวางนัยทั่วไปด้วย
ความคลาดเคลื่อนระหว่างการฝึกและการให้บริการ
ความแตกต่างระหว่างประสิทธิภาพของโมเดลในระหว่างการฝึกกับประสิทธิภาพของโมเดลเดียวกันในระหว่างการแสดง
ชุดฝึก
ชุดย่อยของชุดข้อมูลที่ใช้ฝึกโมเดล
โดยปกติแล้ว ตัวอย่างในชุดข้อมูลจะแบ่งออกเป็นชุดย่อยที่แตกต่างกัน 3 ชุดต่อไปนี้
ในอุดมคติ ตัวอย่างแต่ละรายการในชุดข้อมูลควรอยู่ในชุดย่อยก่อนหน้าเพียงชุดเดียว เช่น ตัวอย่างเดียวไม่ควรอยู่ในทั้งชุดข้อมูลการฝึกและชุดข้อมูลการตรวจสอบ
ดูข้อมูลเพิ่มเติมได้ที่ชุดข้อมูล: การแบ่งชุดข้อมูลเดิม ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
วิถี
ในการเรียนรู้แบบเสริมกำลัง ลำดับของทูเพิลที่แสดงถึงลำดับของสถานะการเปลี่ยนของเอเจนต์ โดยแต่ละทูเพิลจะสอดคล้องกับสถานะ การดำเนินการ รางวัล และสถานะถัดไปสำหรับการเปลี่ยนสถานะที่กำหนด
การเรียนรู้แบบโอน
การโอนข้อมูลจากงานแมชชีนเลิร์นนิงหนึ่งไปยังอีกงานหนึ่ง ตัวอย่างเช่น ในการเรียนรู้แบบหลายงาน โมเดลเดียวจะแก้โจทย์หลายข้อ เช่น โมเดลเชิงลึกที่มีโหนดเอาต์พุตที่แตกต่างกันสำหรับ งานต่างๆ การเรียนรู้แบบถ่ายโอนอาจเกี่ยวข้องกับการถ่ายโอนความรู้ จากโซลูชันของงานที่ง่ายกว่าไปยังงานที่ซับซ้อนกว่า หรือเกี่ยวข้องกับ การถ่ายโอนความรู้จากงานที่มีข้อมูลมากกว่าไปยังงานที่มีข้อมูลน้อยกว่า
ระบบแมชชีนเลิร์นนิงส่วนใหญ่จะแก้ปัญหางานเดียว การเรียนรู้แบบถ่ายโอนเป็นหลายงาน
Transformer
สถาปัตยกรรมโครงข่ายประสาทเทียมที่พัฒนาขึ้นที่ Google ซึ่ง อาศัยกลไกการสนใจตนเองเพื่อเปลี่ยน ลำดับของ Embedding อินพุตเป็นลำดับของ Embedding เอาต์พุต โดยไม่ต้องอาศัยการสังวัตนาการหรือ โครงข่ายประสาทเทียมแบบเกิดซ้ำ Transformer สามารถมองได้ว่าเป็นเลเยอร์การใส่ใจตนเองที่ซ้อนกัน
Transformer อาจมีสิ่งต่อไปนี้
- โปรแกรมเปลี่ยนไฟล์
- ตัวถอดรหัส
- ทั้งตัวเข้ารหัสและตัวถอดรหัส
เอนโคดเดอร์จะแปลงลำดับของการฝังเป็นลำดับใหม่ที่มีความยาวเท่ากัน โดยตัวเข้ารหัสประกอบด้วยเลเยอร์ที่เหมือนกัน N เลเยอร์ ซึ่งแต่ละเลเยอร์มีเลเยอร์ย่อย 2 เลเยอร์ เลเยอร์ย่อยทั้ง 2 นี้จะใช้กับแต่ละตำแหน่งของลำดับการฝังอินพุต เพื่อเปลี่ยนแต่ละองค์ประกอบของลำดับเป็นการฝังใหม่ เลเยอร์ย่อยของตัวเข้ารหัสแรกจะรวบรวมข้อมูลจากทั่วทั้ง ลำดับอินพุต เลเยอร์ย่อยของตัวเข้ารหัสที่ 2 จะแปลงข้อมูลที่รวบรวมแล้ว เป็นเวกเตอร์การฝังเอาต์พุต
ดีโคดเดอร์จะแปลงลำดับของเวกเตอร์การฝังอินพุตเป็นลำดับของเวกเตอร์การฝังเอาต์พุต ซึ่งอาจมีความยาวแตกต่างกัน นอกจากนี้ ตัวถอดรหัสยังมี เลเยอร์ที่เหมือนกัน N เลเยอร์ซึ่งมีเลเยอร์ย่อย 3 เลเยอร์ โดย 2 เลเยอร์คล้ายกับ เลเยอร์ย่อยของตัวเข้ารหัส เลเยอร์ย่อยตัวถอดรหัสที่สามจะรับเอาต์พุตของ ตัวเข้ารหัสและใช้กลไกการทำ Self-Attention เพื่อ รวบรวมข้อมูลจากเอาต์พุตดังกล่าว
บล็อกโพสต์ Transformer: สถาปัตยกรรมโครงข่ายระบบประสาทเทียมแบบใหม่สำหรับการทำความเข้าใจภาษา เป็นข้อมูลเบื้องต้นที่ดีเกี่ยวกับ Transformer
ดูข้อมูลเพิ่มเติมได้ที่ LLM: โมเดลภาษาขนาดใหญ่คืออะไร ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ความไม่แปรเปลี่ยนตามการเลื่อน
ในปัญหาการแยกประเภทรูปภาพ ความสามารถของอัลกอริทึมในการ แยกประเภทรูปภาพได้สำเร็จแม้ว่าตำแหน่งของออบเจ็กต์ภายในรูปภาพจะเปลี่ยนไปก็ตาม ตัวอย่างเช่น อัลกอริทึมยังคงระบุสุนัขได้ ไม่ว่าจะอยู่ตรงกลางเฟรมหรือที่ขอบด้านซ้ายของเฟรม
ดูความไม่แปรเปลี่ยนตามขนาดและ ความไม่แปรเปลี่ยนตามการหมุนด้วย
ไตรแกรม
N-gram ที่ N=3
ผลลบจริง (TN)
ตัวอย่างที่โมเดลคาดการณ์อย่างถูกต้อง คลาสเชิงลบ ตัวอย่างเช่น โมเดลอนุมานว่าข้อความอีเมลหนึ่งไม่ใช่จดหมายขยะ และข้อความอีเมลนั้นไม่ใช่จดหมายขยะจริงๆ
ผลบวกจริง (TP)
ตัวอย่างที่โมเดลคาดการณ์อย่างถูกต้อง คลาสที่เป็นบวก เช่น โมเดลอนุมานว่า ข้อความอีเมลหนึ่งๆ เป็นจดหมายขยะ และข้อความอีเมลนั้นเป็นจดหมายขยะจริงๆ
อัตราผลบวกจริง (TPR)
คำพ้องความหมายของการเรียกคืน โดยการ
อัตราผลบวกจริงคือแกน y ในกราฟ ROC
TTL
ตัวย่อของ Time to Live
U
Ultra
โมเดล Gemini ที่มีพารามิเตอร์มากที่สุด ดูรายละเอียดได้ที่ Gemini Ultra
การไม่รับรู้ (ต่อแอตทริบิวต์ที่มีความละเอียดอ่อน)
สถานการณ์ที่แอตทริบิวต์ที่มีความละเอียดอ่อนมีอยู่ แต่ไม่ได้รวมอยู่ในข้อมูลการฝึก เนื่องจากแอตทริบิวต์ที่ละเอียดอ่อน มักจะมีความสัมพันธ์กับแอตทริบิวต์อื่นๆ ของข้อมูล โมเดลที่ได้รับการฝึก โดยไม่ทราบเกี่ยวกับแอตทริบิวต์ที่ละเอียดอ่อนจึงอาจยังคงมีผลกระทบที่ไม่เท่าเทียมกันเกี่ยวกับแอตทริบิวต์นั้น หรือละเมิดข้อจํากัดด้านความเป็นธรรมอื่นๆ
Underfitting
สร้างโมเดลที่มีความสามารถในการคาดการณ์ต่ำเนื่องจากโมเดล ไม่ได้รับความซับซ้อนของข้อมูลการฝึกอย่างเต็มที่ ปัญหาหลายอย่าง อาจทำให้เกิดการปรับให้พอดีน้อยเกินไป ได้แก่
- การฝึกเกี่ยวกับชุดฟีเจอร์ที่ไม่ถูกต้อง
- การฝึกที่Epoch น้อยเกินไปหรือมีอัตราการเรียนรู้ต่ำเกินไป
- การฝึกที่มีอัตราการทำให้เป็นปกติสูงเกินไป
- การระบุเลเยอร์ที่ซ่อนน้อยเกินไปใน โครงข่ายประสาทเทียมแบบลึก
ดูข้อมูลเพิ่มเติมได้ที่การเกิด Overfitting ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การสุ่มตัวอย่างน้อยเกินไป
การนำตัวอย่างออกจาก คลาสส่วนใหญ่ใน ชุดข้อมูลที่มีคลาสไม่สมดุลเพื่อ สร้างชุดการฝึกที่สมดุลมากขึ้น
ตัวอย่างเช่น พิจารณาชุดข้อมูลที่อัตราส่วนของคลาสส่วนใหญ่ต่อคลาสส่วนน้อยคือ 20:1 หากต้องการแก้ไขปัญหาความไม่สมดุลของคลาสนี้ คุณสามารถสร้างชุดการฝึกที่มีตัวอย่างคลาสส่วนน้อยทั้งหมด แต่มีตัวอย่างคลาสส่วนใหญ่เพียงหนึ่งในสิบ ซึ่งจะสร้างอัตราส่วนคลาสของชุดการฝึกเป็น 2:1 การสุ่มตัวอย่างแบบ Under Sampling อาจทำให้ชุดการฝึกที่สมดุลมากขึ้นนี้สร้างโมเดลที่ดีขึ้นได้ อีกทางหนึ่ง ชุดการฝึกที่สมดุลมากขึ้นนี้อาจมีตัวอย่างไม่เพียงพอที่จะฝึกโมเดลที่มีประสิทธิภาพ
คอนทราสต์กับการโอเวอร์แซมปลิง
แบบทิศทางเดียว
ระบบที่ประเมินเฉพาะข้อความที่อยู่ก่อนข้อความส่วนเป้าหมาย ในทางตรงกันข้าม ระบบแบบสองทิศทางจะประเมินทั้งข้อความที่อยู่ก่อนและอยู่หลังส่วนข้อความเป้าหมาย ดูรายละเอียดเพิ่มเติมได้ที่สองทิศทาง
โมเดลภาษาแบบทิศทางเดียว
โมเดลภาษาที่อิงความน่าจะเป็นจากโทเค็นที่ปรากฏก่อนโทเค็นเป้าหมายเท่านั้น ไม่ใช่หลังโทเค็นเป้าหมาย เปรียบเทียบกับโมเดลภาษาแบบสองทิศทาง
ตัวอย่างที่ไม่มีป้ายกำกับ
ตัวอย่างที่มีฟีเจอร์แต่ไม่มีป้ายกำกับ ตัวอย่างเช่น ตารางต่อไปนี้แสดงตัวอย่างที่ไม่ได้ติดป้ายกำกับ 3 รายการจากโมเดลการประเมินบ้าน โดยแต่ละรายการมีฟีเจอร์ 3 รายการแต่ไม่มีมูลค่าบ้าน
| จำนวนห้องนอน | จำนวนห้องน้ำ | อายุของบ้าน |
|---|---|---|
| 3 | 2 | 15 |
| 2 | 1 | 72 |
| 4 | 2 | 34 |
ในแมชชีนเลิร์นนิงที่มีการควบคุมดูแล โมเดลจะฝึกกับตัวอย่างที่ติดป้ายกำกับและทำการคาดการณ์กับ ตัวอย่างที่ไม่มีป้ายกำกับ
ในการเรียนรู้แบบกึ่งควบคุมดูแลและไม่มีการควบคุมดูแล จะมีการใช้ตัวอย่างที่ไม่มีป้ายกำกับในระหว่างการฝึก
เปรียบเทียบตัวอย่างที่ไม่มีป้ายกำกับกับตัวอย่างที่มีป้ายกำกับ
แมชชีนเลิร์นนิงที่ไม่มีการควบคุมดูแล
การฝึกโมเดลเพื่อค้นหารูปแบบในชุดข้อมูล ซึ่งโดยปกติจะเป็นชุดข้อมูลที่ไม่มีป้ายกำกับ
การใช้งานแมชชีนเลิร์นนิงแบบไม่มีการกำกับดูแลที่พบบ่อยที่สุดคือการจัดกลุ่มข้อมูล เป็นกลุ่มของตัวอย่างที่คล้ายกัน ตัวอย่างเช่น อัลกอริทึมแมชชีนเลิร์นนิงแบบไม่มีการกำกับดูแล สามารถจัดกลุ่มเพลงตามพร็อพเพอร์ตี้ต่างๆ ของเพลง คลัสเตอร์ที่ได้จะกลายเป็นอินพุตสำหรับอัลกอริทึมแมชชีนเลิร์นนิงอื่นๆ (เช่น สำหรับบริการแนะนำเพลง) การจัดกลุ่มช่วยได้ในกรณีที่ป้ายกำกับที่มีประโยชน์หายากหรือไม่มีเลย ตัวอย่างเช่น ในโดเมนต่างๆ เช่น การต่อต้านการละเมิดและการฉ้อโกง คลัสเตอร์จะช่วยให้ มนุษย์เข้าใจข้อมูลได้ดีขึ้น
เปรียบเทียบกับแมชชีนเลิร์นนิงที่มีการควบคุมดูแล
ดูข้อมูลเพิ่มเติมได้ที่แมชชีนเลิร์นนิงคืออะไร ในหลักสูตรข้อมูลเบื้องต้นเกี่ยวกับ ML
การประมาณการเพิ่มขึ้น
เทคนิคการประมาณที่ใช้กันทั่วไปในการตลาด ซึ่งจะประมาณ "ผลเชิงสาเหตุ" (หรือที่เรียกว่า "ผลกระทบที่เพิ่มขึ้น") ของ "การรักษา" ที่มีต่อ "บุคคล" ต่อไปนี้เป็นตัวอย่างสองตัวอย่าง:
- แพทย์อาจใช้การประมาณการเพิ่มเพื่อคาดการณ์การลดอัตราการเสียชีวิต (ผลเชิงสาเหตุ) ของกระบวนการทางการแพทย์ (การรักษา) โดยขึ้นอยู่กับ อายุและประวัติทางการแพทย์ของผู้ป่วย (แต่ละบุคคล)
- นักการตลาดอาจใช้การประมาณการเพิ่มเพื่อคาดการณ์การเพิ่มขึ้นของ ความน่าจะเป็นในการซื้อ (ผลลัพธ์เชิงสาเหตุ) อันเนื่องมาจากโฆษณา (การรักษา) ที่มีต่อบุคคล (แต่ละบุคคล)
การประมาณการเพิ่มขึ้นแตกต่างจากการจัดประเภทหรือ การถดถอยตรงที่ป้ายกำกับบางรายการ (เช่น ป้ายกำกับครึ่งหนึ่งในทรีตเมนต์ไบนารี) จะหายไปเสมอในการประมาณการเพิ่มขึ้น ตัวอย่างเช่น ผู้ป่วยอาจได้รับการรักษาหรือไม่ได้รับการรักษา ดังนั้น เราจึงสังเกตได้ว่าผู้ป่วยจะหายหรือไม่หายในสถานการณ์ใดสถานการณ์หนึ่งเท่านั้น (แต่จะไม่ใช่ทั้ง 2 สถานการณ์) ข้อได้เปรียบหลักของโมเดลการเพิ่มคือสามารถสร้างการคาดการณ์ สำหรับสถานการณ์ที่สังเกตไม่ได้ (ข้อเท็จจริงที่ขัดแย้งกับความจริงที่ตั้งขึ้น) และใช้เพื่อคำนวณ ผลกระทบเชิงสาเหตุ
การเพิ่มน้ำหนัก
การกำหนดค่าถ่วงน้ำหนักให้กับคลาสที่ดาวน์แซมเปิลเท่ากับปัจจัยที่คุณใช้ดาวน์แซมเปิล
เมทริกซ์ผู้ใช้
ในระบบการแนะนำ เวกเตอร์การฝังที่สร้างขึ้นโดยการแยกเมทริกซ์ ซึ่งมีสัญญาณแฝงเกี่ยวกับค่ากำหนดของผู้ใช้ แต่ละแถวของเมทริกซ์ผู้ใช้จะมีข้อมูลเกี่ยวกับความแรงสัมพัทธ์ของสัญญาณแฝงต่างๆ สำหรับผู้ใช้รายเดียว ตัวอย่างเช่น พิจารณาระบบแนะนำภาพยนตร์ ในระบบนี้ สัญญาณแฝงในเมทริกซ์ผู้ใช้อาจแสดงถึงความสนใจของผู้ใช้แต่ละราย ในประเภทที่เฉพาะเจาะจง หรืออาจเป็นสัญญาณที่ตีความได้ยากกว่าซึ่งเกี่ยวข้องกับ การโต้ตอบที่ซับซ้อนในหลายปัจจัย
เมทริกซ์ผู้ใช้มีคอลัมน์สำหรับฟีเจอร์ที่ซ่อนอยู่แต่ละรายการ และแถวสำหรับผู้ใช้แต่ละราย กล่าวคือ เมทริกซ์ผู้ใช้มีจำนวนแถวเท่ากับเมทริกซ์เป้าหมายที่กำลังแยกตัวประกอบ ตัวอย่างเช่น หากมีระบบแนะนำภาพยนตร์สำหรับผู้ใช้ 1,000,000 คน เมทริกซ์ผู้ใช้จะมี 1,000,000 แถว
V
การตรวจสอบความถูกต้อง
การประเมินคุณภาพของโมเดลในขั้นต้น การตรวจสอบจะตรวจสอบคุณภาพของการคาดการณ์ของโมเดลเทียบกับชุดข้อมูลการตรวจสอบ
เนื่องจากชุดข้อมูลการตรวจสอบแตกต่างจากชุดข้อมูลการฝึก การตรวจสอบจึงช่วยป้องกันการเกิด Overfitting
คุณอาจคิดว่าการประเมินโมเดลกับชุดการตรวจสอบเป็นการทดสอบรอบแรก และการประเมินโมเดลกับชุดการทดสอบเป็นการทดสอบรอบที่ 2
การสูญเสียการตรวจสอบ
เมตริกที่แสดงการสูญเสียของโมเดลในชุดข้อมูลการตรวจสอบระหว่างการทำซ้ำของการฝึก
ดูเส้นโค้งการสรุปด้วย
ชุดข้อมูลสำหรับตรวจสอบความถูกต้อง
ชุดย่อยของชุดข้อมูลที่ใช้ในการประเมินเบื้องต้นกับโมเดลที่ฝึกแล้ว โดยปกติแล้ว คุณจะประเมิน โมเดลที่ฝึกกับชุดข้อมูลการตรวจสอบหลายครั้ง ก่อนที่จะประเมินโมเดลกับชุดข้อมูลทดสอบ
โดยปกติแล้ว คุณจะแบ่งตัวอย่างในชุดข้อมูลออกเป็น 3 ชุดย่อยที่แตกต่างกันดังนี้
ในอุดมคติ ตัวอย่างแต่ละรายการในชุดข้อมูลควรอยู่ในชุดย่อยก่อนหน้าเพียงชุดเดียว เช่น ตัวอย่างเดียวไม่ควรอยู่ในทั้งชุดข้อมูลการฝึกและชุดข้อมูลการตรวจสอบ
ดูข้อมูลเพิ่มเติมได้ที่ชุดข้อมูล: การแบ่งชุดข้อมูลเดิม ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การประมาณค่า
กระบวนการแทนที่ค่าที่ขาดหายไปด้วยค่าทดแทนที่ยอมรับได้ เมื่อไม่มีค่า คุณจะทิ้งตัวอย่างทั้งหมดหรือใช้การประมาณค่าเพื่อกอบกู้ตัวอย่างก็ได้
ตัวอย่างเช่น พิจารณาชุดข้อมูลที่มีฟีเจอร์ temperature ซึ่งควรบันทึกทุกชั่วโมง อย่างไรก็ตาม ค่าอุณหภูมิที่อ่านได้
ไม่พร้อมใช้งานในชั่วโมงหนึ่งๆ ส่วนหนึ่งของชุดข้อมูลมีดังนี้
| การประทับเวลา | อุณหภูมิ |
|---|---|
| 1680561000 | 10 |
| 1680564600 | 12 |
| 1680568200 | ขาดหายไป |
| 1680571800 | 20 |
| 1680575400 | 21 |
| 1680579000 | 21 |
ระบบอาจลบตัวอย่างที่ขาดหายไปหรือใส่ค่าอุณหภูมิที่ขาดหายไปเป็น 12, 16, 18 หรือ 20 ขึ้นอยู่กับอัลกอริทึมการใส่ค่า
ปัญหาการไล่ระดับที่หายไป
แนวโน้มที่การไล่ระดับสีของเลเยอร์ที่ซ่อนอยู่ตอนต้นของเครือข่ายประสาทเทียมแบบลึกบางเครือข่ายจะกลายเป็นแบนราบอย่างน่าประหลาดใจ (ต่ำ) การไล่ระดับที่ต่ำลงเรื่อยๆ จะส่งผลให้การเปลี่ยนแปลงน้ำหนักในโหนดในโครงข่ายประสาทแบบลึกมีขนาดเล็กลงเรื่อยๆ ซึ่งจะทำให้เกิดการเรียนรู้น้อยมากหรือไม่มีเลย โมเดลที่ประสบปัญหาการไล่ระดับสีที่หายไป จะฝึกได้ยากหรือฝึกไม่ได้ เซลล์หน่วยความจำระยะสั้นที่ยาวจะช่วยแก้ปัญหานี้
เปรียบเทียบกับปัญหาการไล่ระดับสีที่ขยาย
ความสําคัญของตัวแปร
ชุดคะแนนที่บ่งบอกถึงความสำคัญที่สัมพันธ์กันของแต่ละฟีเจอร์ต่อโมเดล
ตัวอย่างเช่น ลองพิจารณาแผนผังการตัดสินใจที่ ประมาณราคาบ้าน สมมติว่าแผนผังการตัดสินใจนี้ใช้ฟีเจอร์ 3 อย่าง ได้แก่ ขนาด อายุ และสไตล์ หากระบบคำนวณชุดความสำคัญของตัวแปร สำหรับฟีเจอร์ทั้ง 3 รายการได้เป็น {size=5.8, age=2.5, style=4.7} แสดงว่าขนาดมีความสำคัญต่อ Decision Tree มากกว่าอายุหรือสไตล์
มีเมตริกความสําคัญของตัวแปรที่แตกต่างกัน ซึ่งจะช่วยให้ผู้เชี่ยวชาญด้าน ML ทราบถึงแง่มุมต่างๆ ของโมเดล
Variational Autoencoder (VAE)
ออโต้เอนโค้ดเดอร์ประเภทหนึ่งที่ใช้ประโยชน์จากความคลาดเคลื่อน ระหว่างอินพุตและเอาต์พุตเพื่อสร้างอินพุตเวอร์ชันที่แก้ไขแล้ว Variational Autoencoder มีประโยชน์สำหรับ Generative AI
VAE อิงตามการอนุมานแบบแปรผัน ซึ่งเป็นเทคนิคในการประมาณ พารามิเตอร์ของโมเดลความน่าจะเป็น
เวกเตอร์
คำที่มีการใช้มากเกินไปซึ่งมีความหมายแตกต่างกันในสาขาคณิตศาสตร์ และวิทยาศาสตร์ต่างๆ ในแมชชีนเลิร์นนิง เวกเตอร์มี 2 คุณสมบัติดังนี้
- ประเภทข้อมูล: เวกเตอร์ในแมชชีนเลิร์นนิงมักจะมีตัวเลขทศนิยม
- จำนวนองค์ประกอบ: นี่คือความยาวของเวกเตอร์หรือมิติข้อมูล
เช่น ลองพิจารณาเวกเตอร์ฟีเจอร์ที่มีตัวเลขทศนิยม 8 ตัว เวกเตอร์ฟีเจอร์นี้มีความยาวหรือมิติข้อมูล 8 โปรดทราบว่าเวกเตอร์แมชชีนเลิร์นนิงมักมีมิติข้อมูลจำนวนมาก
คุณสามารถแสดงข้อมูลหลายประเภทเป็นเวกเตอร์ได้ เช่น
- ตำแหน่งใดๆ บนพื้นผิวโลกสามารถแสดงเป็นเวกเตอร์ 2 มิติ ได้ โดยมิติหนึ่งคือละติจูดและอีกมิติหนึ่งคือลองจิจูด
- ราคาปัจจุบันของหุ้นแต่ละตัวจาก 500 ตัวสามารถแสดงเป็นเวกเตอร์ 500 มิติได้
- การกระจายความน่าจะเป็นในจำนวนชั้นเรียนที่จำกัดสามารถแสดงเป็นเวกเตอร์ได้
เช่น ระบบการแยกประเภทแบบหลายคลาสที่
คาดการณ์สีเอาต์พุต 1 ใน 3 สี (แดง เขียว หรือเหลือง) อาจแสดงเวกเตอร์
(0.3, 0.2, 0.5)เพื่อหมายถึงP[red]=0.3, P[green]=0.2, P[yellow]=0.5
เวกเตอร์สามารถต่อกันได้ ดังนั้นสื่อต่างๆ จึงสามารถแสดงเป็นเวกเตอร์เดียวได้ โมเดลบางรุ่นทำงานโดยตรงกับ การต่อกันของการเข้ารหัสแบบ One-hot หลายรายการ
โปรเซสเซอร์เฉพาะทาง เช่น TPU ได้รับการเพิ่มประสิทธิภาพให้ดำเนินการ ทางคณิตศาสตร์กับเวกเตอร์
เวกเตอร์คือเทนเซอร์ที่มีอันดับ 1
Vertex
แพลตฟอร์มของ Google Cloud สำหรับ AI และแมชชีนเลิร์นนิง Vertex มีเครื่องมือ และโครงสร้างพื้นฐานสำหรับการสร้าง การติดตั้งใช้งาน และการจัดการแอปพลิเคชัน AI รวมถึงสิทธิ์เข้าถึงโมเดล GeminiVibe Coding
การป้อนพรอมต์ให้โมเดล Generative AI สร้างซอฟต์แวร์ กล่าวคือ พรอมต์ของคุณ จะอธิบายวัตถุประสงค์และฟีเจอร์ของซอฟต์แวร์ ซึ่งโมเดล Generative AI จะแปลเป็นซอร์สโค้ด โค้ดที่สร้างขึ้นอาจไม่ตรงกับ ความตั้งใจของคุณเสมอไป ดังนั้นการเขียนโค้ดแบบไวบ์จึงมักต้องมีการทำซ้ำ
Andrej Karpathy เป็นผู้บัญญัติคำว่า vibe coding ในโพสต์บน X นี้ ในโพสต์บน X คาร์พาธีอธิบายว่า "การเขียนโค้ดรูปแบบใหม่...ที่คุณปล่อยใจไปกับฟีลลิ่งอย่างเต็มที่..." ดังนั้น คำนี้จึงหมายถึงแนวทางที่ตั้งใจให้หลวมๆ ในการสร้างซอฟต์แวร์ ซึ่งคุณอาจไม่ได้ตรวจสอบโค้ดที่สร้างขึ้นด้วยซ้ำ อย่างไรก็ตาม คำนี้ได้พัฒนาอย่างรวดเร็วในหลายวงการจนปัจจุบันหมายถึงการเขียนโค้ดที่ AI สร้างขึ้นทุกรูปแบบ
ดูคำอธิบายโดยละเอียดเกี่ยวกับการเขียนโค้ด Vibe ได้ที่ Vibe Coding คืออะไร
นอกจากนี้ ให้เปรียบเทียบการเข้ารหัสอารมณ์กับสิ่งต่อไปนี้
W
การสูญเสีย Wasserstein
ฟังก์ชันการสูญเสียอย่างหนึ่งที่ใช้กันทั่วไปในGenerative Adversarial Network โดยอิงตามระยะทางของ Earth Mover ระหว่าง การกระจายข้อมูลที่สร้างขึ้นและข้อมูลจริง
น้ำหนัก
ค่าที่โมเดลคูณด้วยค่าอื่น การฝึกคือกระบวนการกำหนดน้ำหนักที่เหมาะสมของโมเดล การอนุมานคือกระบวนการใช้น้ำหนักที่เรียนรู้เหล่านั้นเพื่อ ทำการคาดการณ์
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยเชิงเส้น ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
วิธีกำลังสองน้อยที่สุดแบบสลับถ่วงน้ำหนัก (WALS)
อัลกอริทึมสำหรับการลดฟังก์ชันออบเจ็กทีฟให้เหลือน้อยที่สุดระหว่างการแยกตัวประกอบเมทริกซ์ในระบบการแนะนำ ซึ่งช่วยให้การลดน้ำหนักของตัวอย่างที่ขาดหายไป WALS จะลดข้อผิดพลาดกำลังสองแบบถ่วงน้ำหนักระหว่างเมทริกซ์เดิมกับการสร้างใหม่โดยสลับระหว่างการแก้ไขการแยกตัวประกอบแถวและการแยกตัวประกอบคอลัมน์ การเพิ่มประสิทธิภาพแต่ละอย่างเหล่านี้สามารถแก้ไขได้โดยใช้การเพิ่มประสิทธิภาพแบบนูนด้วยวิธีกำลังสองน้อยที่สุด โปรดดูรายละเอียดที่หลักสูตรระบบการแนะนำ
ผลรวมแบบถ่วงน้ำหนัก
ผลรวมของค่าอินพุตที่เกี่ยวข้องทั้งหมดคูณด้วย ค่าถ่วงน้ำหนักที่สอดคล้องกัน ตัวอย่างเช่น สมมติว่าอินพุตที่เกี่ยวข้องประกอบด้วยข้อมูลต่อไปนี้
| ค่าอินพุต | น้ำหนักอินพุต |
| 2 | -1.3 |
| -1 | 0.6 |
| 3 | 0.4 |
ดังนั้น ผลรวมแบบถ่วงน้ำหนักจึงเป็นดังนี้
weighted sum = (2)(-1.3) + (-1)(0.6) + (3)(0.4) = -2.0
ผลรวมแบบถ่วงน้ำหนักคืออาร์กิวเมนต์อินพุตของฟังก์ชันกระตุ้น
โมเดลแบบกว้าง
โมเดลเชิงเส้นซึ่งมักจะมีฟีเจอร์อินพุตแบบกระจัดกระจายจำนวนมาก เราเรียกโมเดลนี้ว่า "กว้าง" เนื่องจากโมเดลดังกล่าวเป็นโครงข่ายประสาทเทียมประเภทพิเศษที่มี อินพุตจำนวนมากซึ่งเชื่อมต่อกับโหนดเอาต์พุตโดยตรง โมเดลแบบกว้าง มักจะแก้ไขข้อบกพร่องและตรวจสอบได้ง่ายกว่าโมเดลแบบลึก แม้ว่าโมเดลแบบกว้างจะไม่สามารถแสดงความไม่เชิงเส้นผ่านเลเยอร์ที่ซ่อนอยู่ได้ แต่โมเดลแบบกว้างสามารถใช้การแปลง เช่น การรวมฟีเจอร์และ การแบ่งกลุ่มเพื่อสร้างโมเดลความไม่เชิงเส้นในรูปแบบต่างๆ
เปรียบเทียบกับโมเดลเชิงลึก
ความกว้าง
จำนวนนิวรอนในเลเยอร์หนึ่งๆ ของโครงข่ายประสาทเทียม
ภูมิปัญญาของมวลชน
แนวคิดที่ว่าการหาค่าเฉลี่ยของความคิดเห็นหรือการประมาณค่าจากกลุ่มคนจำนวนมาก ("ฝูงชน") มักจะให้ผลลัพธ์ที่ดีอย่างน่าประหลาดใจ ตัวอย่างเช่น ลองพิจารณาเกมที่ผู้คนทายจำนวน เยลลี่บีนที่บรรจุในโหลขนาดใหญ่ แม้ว่าการคาดเดาของแต่ละคนส่วนใหญ่จะไม่ถูกต้อง แต่ค่าเฉลี่ยของการคาดเดาทั้งหมดได้รับการพิสูจน์แล้วว่าใกล้เคียงกับจำนวนจริงของลูกอมในขวดอย่างน่าประหลาดใจ
กลุ่มเป็นซอฟต์แวร์ที่เทียบเท่ากับภูมิปัญญาของมวลชน แม้ว่าโมเดลแต่ละรายการจะทําการคาดการณ์ที่คลาดเคลื่อนอย่างมาก แต่การหาค่าเฉลี่ยของการคาดการณ์ของโมเดลจํานวนมากมักจะสร้างการคาดการณ์ที่ดีอย่างน่าประหลาดใจ ตัวอย่างเช่น แม้ว่าแผนผังการตัดสินใจแต่ละรายการอาจให้การคาดการณ์ที่ไม่ดี แต่ป่าการตัดสินใจมักจะให้การคาดการณ์ที่ดีมาก
Word Embedding
การแสดงคำแต่ละคำในชุดคำภายในเวกเตอร์การฝัง นั่นคือการแสดงคำแต่ละคำเป็นเวกเตอร์ของค่าทศนิยมระหว่าง 0.0 ถึง 1.0 คำที่มีความหมายคล้ายกัน จะมีตัวแทนที่คล้ายกันมากกว่าคำที่มีความหมายต่างกัน ตัวอย่างเช่น แครอท ขึ้นฉ่าย และแตงกวาจะมีลักษณะที่คล้ายกัน ในระดับหนึ่ง ซึ่งจะแตกต่างจากลักษณะของเครื่องบิน แว่นกันแดด และยาสีฟัน
X
XLA (Accelerated Linear Algebra)
คอมไพเลอร์แมชชีนเลิร์นนิงแบบโอเพนซอร์สสำหรับ GPU, CPU และตัวเร่ง ML
คอมไพเลอร์ XLA รับโมเดลจากเฟรมเวิร์ก ML ยอดนิยม เช่น PyTorch TensorFlow และ JAX แล้วเพิ่มประสิทธิภาพ เพื่อให้ดำเนินการประสิทธิภาพสูงในแพลตฟอร์มฮาร์ดแวร์ต่างๆ ซึ่งรวมถึง GPU, CPU และตัวเร่งความเร็ว ML
Z
การเรียนรู้แบบศูนย์ช็อต
การฝึกแมชชีนเลิร์นนิงประเภทหนึ่งซึ่งโมเดลจะอนุมานการคาดการณ์สำหรับงานที่ไม่ได้ฝึกมาโดยเฉพาะ กล่าวคือ โมเดล ไม่ได้รับการฝึกตัวอย่างเฉพาะงานเลย แต่ได้รับคำสั่ง ให้ทำการอนุมานสำหรับงานนั้น
Zero-Shot Prompting
พรอมต์ที่ไม่ได้ระบุตัวอย่างวิธีที่คุณต้องการให้โมเดลภาษาขนาดใหญ่ตอบ เช่น
| ส่วนต่างๆ ของพรอมต์ | หมายเหตุ |
|---|---|
| สกุลเงินทางการของประเทศที่ระบุคืออะไร | คำถามที่คุณต้องการให้ LLM ตอบ |
| อินเดีย: | คำค้นหาจริง |
โมเดลภาษาขนาดใหญ่อาจตอบกลับด้วยข้อความต่อไปนี้
- รูปี
- INR
- ₹
- รูปีอินเดีย
- รูปี
- รูปีอินเดีย
คำตอบทั้งหมดถูกต้อง แต่คุณอาจชอบรูปแบบใดรูปแบบหนึ่งมากกว่า
เปรียบเทียบการแจ้งแบบศูนย์ช็อตกับคำต่อไปนี้
การแปลงข้อมูลเป็นรูปแบบมาตรฐาน Z-Score
เทคนิคการปรับขนาดที่แทนที่ค่าฟีเจอร์ดิบด้วยค่าทศนิยมที่แสดงถึงจำนวนค่าเบี่ยงเบนมาตรฐานจากค่าเฉลี่ยของฟีเจอร์นั้น ตัวอย่างเช่น ลองพิจารณาฟีเจอร์ที่มีค่าเฉลี่ย 800 และค่าเบี่ยงเบนมาตรฐาน 100 ตารางต่อไปนี้แสดงวิธีที่การทําให้เป็นปกติของคะแนนมาตรฐาน จะจับคู่ค่าดิบกับคะแนนมาตรฐาน
| ค่าดิบ | คะแนนมาตรฐาน (Z-Score) |
|---|---|
| 800 | 0 |
| 950 | +1.5 |
| 575 | -2.25 |
จากนั้นโมเดลแมชชีนเลิร์นนิงจะฝึกกับคะแนน Z สำหรับฟีเจอร์นั้นแทนที่จะฝึกกับค่าดิบ
ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลตัวเลข: การปรับให้เป็นมาตรฐาน ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
พจนานุกรมคำศัพท์นี้จะให้คำจำกัดความของคำศัพท์เกี่ยวกับแมชชีนเลิร์นนิง