このチュートリアルでは、Google Earth Engine を使用した種の分布モデリングの方法論を紹介します。種分布モデリングの概要を簡単に説明した後、妖精ピッタ(学名: Pitta nympha)という絶滅危惧種の鳥の生息地を予測して分析するプロセスについて説明します。
Run me first
次のセルを実行して API を初期化します。出力には、アカウントを使用してこのノートブックに Earth Engine へのアクセス権を付与する方法の手順が含まれます。
import ee
# Trigger the authentication flow.
ee.Authenticate()
# Initialize the library.
ee.Initialize(project='my-project')
種分布モデリングの概要
種分布モデルとは何か、その処理に Google Earth Engine を使用するメリット、モデルに必要なデータ、ワークフローの構造について説明します。
種分布モデリングとは
種分布モデリング(以下 SDM)は、種の実際の地理的分布または潜在的な地理的分布を推定するために使用される最も一般的な方法論です。特定の種に適した環境条件を特徴付け、これらの適した条件が地理的にどこに分布しているかを特定します。
SDM は近年、保全計画の重要な要素として登場しており、この目的のためにさまざまなモデリング手法が開発されています。Google Earth Engine(以下、GEE)に SDM を実装すると、大規模な環境データに簡単にアクセスできるだけでなく、強力なコンピューティング機能と ML アルゴリズムのサポートにより、迅速なモデリングが可能になります。
SDM に必要なデータ
SDM は通常、既知の種の出現記録と環境変数の関係を利用して、個体群が維持できる条件を特定します。つまり、次の 2 種類のモデル入力データが必要です。
- 既知の種の出現記録
- さまざまな環境変数
これらのデータは、種の存在に関連する環境条件を特定するアルゴリズムに入力されます。
GEE を使用した SDM のワークフロー
GEE を使用した SDM のワークフローは次のとおりです。
- 種の出現データの収集と前処理
- 関心のある地域の定義
- GEE 環境変数の追加
- 疑似欠席データの生成
- モデルの適合と予測
- 変数の重要度と精度の評価
GEE を使用した生息地の予測と分析
ヤイロチョウ(Pitta nympha)をケーススタディとして使用し、GEE ベースの SDM の適用方法を示します。この例では特定の種が選択されていますが、研究者は、提供されたソースコードを少し変更するだけで、対象となる任意の種にこの方法論を適用できます。
ヤイロチョウは韓国では珍しい夏鳥と通過鳥であり、朝鮮半島の近年の気候温暖化により分布域が拡大しています。希少種、絶滅危惧種 II 類、天然記念物第 204 号に分類され、国のレッドリストでは地域絶滅(RE)と評価され、IUCN のカテゴリでは絶滅危惧(VU)と評価されています。
ヤイロチョウの保全計画に SDM を実施することは、非常に有益であると思われます。それでは、GEE を使用して生息地の予測と分析に進みましょう。
まず、Python ライブラリがインポートされます。import ステートメントはモジュールの内容全体を取り込み、from import ステートメントはモジュールから特定のオブジェクトをインポートできるようにします。
# Import libraries
import geemap
import geemap.colormaps as cm
import pandas as pd, geopandas as gpd
import numpy as np, matplotlib.pyplot as plt
import os, requests, math, random
from ipyleaflet import TileLayer
from statsmodels.stats.outliers_influence import variance_inflation_factor
種の出現データの収集と前処理
では、ヤイロチョウの出現データを収集しましょう。現在、対象種の出現データにアクセスできない場合でも、GBIF API を介して特定の種に関する観測データを取得できます。GBIF API は、GBIF が提供する種の分布データへのアクセスを可能にするインターフェースです。ユーザーは、データの検索、フィルタリング、ダウンロードのほか、種に関連するさまざまな情報を取得できます。
次のコードでは、species_name 変数に種の学名(例: Pitta nympha(ヤイロチョウ))、country_code 変数には国コード(例: 韓国の場合は KR)。base_url 変数には GBIF API のアドレスが格納されます。params は、API リクエストで使用されるパラメータを含む辞書です。
scientificName: 検索する種の学名を設定します。country: 検索対象を特定の国に制限します。hasCoordinate: 座標を持つデータのみが検索されるようにします(true)。basisOfRecord: 人間の観察(HUMAN_OBSERVATION)のレコードのみを選択します。limit: 返される結果の最大数を 10,000 に設定します。
def get_gbif_species_data(species_name, country_code):
"""
Retrieves observational data for a specific species using the GBIF API and returns it as a pandas DataFrame.
Parameters:
species_name (str): The scientific name of the species to query.
country_code (str): The country code of the where the observation data will be queried.
Returns:
pd.DataFrame: A pandas DataFrame containing the observational data.
"""
base_url = "https://api.gbif.org/v1/occurrence/search"
params = {
"scientificName": species_name,
"country": country_code,
"hasCoordinate": "true",
"basisOfRecord": "HUMAN_OBSERVATION",
"limit": 10000,
}
try:
response = requests.get(base_url, params=params)
response.raise_for_status() # Raises an exception for a response error.
data = response.json()
occurrences = data.get("results", [])
if occurrences: # If data is present
df = pd.json_normalize(occurrences)
return df
else:
print("No data found for the given species and country code.")
return pd.DataFrame() # Returns an empty DataFrame
except requests.RequestException as e:
print(f"Request failed: {e}")
return pd.DataFrame() # Returns an empty DataFrame in case of an exception
前に設定したパラメータを使用して、GBIF API に Fairy pitta(Pitta nympha)の観測記録をクエリし、結果を DataFrame に読み込んで最初の行を確認します。DataFrame は、行と列で構成されるテーブル形式のデータを処理するためのデータ構造です。必要に応じて、DataFrame を CSV ファイルとして保存し、読み取り直すことができます。
# Retrieve Fairy Pitta data
df = get_gbif_species_data("Pitta nympha", "KR")
"""
# Save DataFrame to CSV and read back in.
df.to_csv("pitta_nympha_data.csv", index=False)
df = pd.read_csv("pitta_nympha_data.csv")
"""
df.head(1) # Display the first row of the DataFrame
次に、DataFrame を地理情報(geometry)の列を含む GeoDataFrame に変換し、最初の行を確認します。GeoDataFrame は GeoPackage ファイル(*.gpkg)として保存し、読み取り直すことができます。
# Convert DataFrame to GeoDataFrame
gdf = gpd.GeoDataFrame(
df,
geometry=gpd.points_from_xy(df.decimalLongitude,
df.decimalLatitude),
crs="EPSG:4326"
)[["species", "year", "month", "geometry"]]
"""
# Convert GeoDataFrame to GeoPackage (requires pycrs module)
%pip install -U -q pycrs
gdf.to_file("pitta_nympha_data.gpkg", driver="GPKG")
gdf = gpd.read_file("pitta_nympha_data.gpkg")
"""
gdf.head(1) # Display the first row of the GeoDataFrame
今回は、GeoDataFrame から年と月ごとのデータの分布を可視化し、グラフとして表示する関数を作成しました。このグラフは画像ファイルとして保存できます。ヒートマップを使用すると、種別の出現頻度を年と月ごとにすばやく把握でき、データ内の時間的変化とパターンを直感的に可視化できます。これにより、種の出現データにおける時間的パターンと季節変動を特定し、データ内の外れ値や品質の問題を迅速に検出できます。
# Yearly and monthly data distribution heatmap
def plot_heatmap(gdf, h_size=8):
statistics = gdf.groupby(["month", "year"]).size().unstack(fill_value=0)
# Heatmap
plt.figure(figsize=(h_size, h_size - 6))
heatmap = plt.imshow(
statistics.values, cmap="YlOrBr", origin="upper", aspect="auto"
)
# Display values above each pixel
for i in range(len(statistics.index)):
for j in range(len(statistics.columns)):
plt.text(
j, i, statistics.values[i, j], ha="center", va="center", color="black"
)
plt.colorbar(heatmap, label="Count")
plt.title("Monthly Species Count by Year")
plt.xlabel("Year")
plt.ylabel("Month")
plt.xticks(range(len(statistics.columns)), statistics.columns)
plt.yticks(range(len(statistics.index)), statistics.index)
plt.tight_layout()
plt.savefig("heatmap_plot.png")
plt.show()
plot_heatmap(gdf)
1995 年のデータは非常にまばらで、他の年と比較して大きなギャップがあります。また、8 月と 9 月はサンプルが少なく、他の期間と比較して季節的な特徴が異なります。このデータを除外することで、モデルの安定性と予測能力の向上に貢献できます。
ただし、データを除外するとモデルの汎化能力が向上する可能性がありますが、研究目標に関連する貴重な情報が失われる可能性もあります。そのため、このような決定は慎重に検討する必要があります。
# Filtering data by year and month
filtered_gdf = gdf[
(~gdf['year'].eq(1995)) &
(~gdf['month'].between(8, 9))
]
フィルタリングされた GeoDataFrame が Google Earth Engine オブジェクトに変換されます。
# Convert GeoDataFrame to Earth Engine object
data_raw = geemap.geopandas_to_ee(filtered_gdf)
次に、SDM 結果のラスター ピクセルサイズを 1 km の解像度として定義します。
# Spatial resolution setting (meters)
grain_size = 1000
同じ 1 km 解像度のラスター ピクセル内に複数の発生地点がある場合、それらは同じ地理的位置で同じ環境条件を共有している可能性が高くなります。このようなデータを分析に直接使用すると、結果にバイアスが生じる可能性があります。
つまり、地域別のサンプリング バイアスの影響を制限する必要があります。このため、1 km ピクセル内の 1 つの場所のみを保持し、他の場所をすべて削除することで、モデルが環境条件をより客観的に反映できるようにします。
def remove_duplicates(data, grain_size):
# Select one occurrence record per pixel at the chosen spatial resolution
random_raster = ee.Image.random().reproject("EPSG:4326", None, grain_size)
rand_point_vals = random_raster.sampleRegions(
collection=ee.FeatureCollection(data), geometries=True
)
return rand_point_vals.distinct("random")
data = remove_duplicates(data_raw, grain_size)
# Before selection and after selection
print("Original data size:", data_raw.size().getInfo())
print("Final data size:", data.size().getInfo())
次の図は、前処理前(青)と前処理後(赤)の地理的サンプリング バイアスを比較した可視化を示しています。比較しやすいように、地図は漢拏山国立公園のヤイロチョウの出現座標が集中しているエリアを中心に表示されています。
# Visualization of geographic sampling bias before (blue) and after (red) preprocessing
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
# Add the random raster layer
random_raster = ee.Image.random().reproject("EPSG:4326", None, grain_size)
Map.addLayer(
random_raster,
{"min": 0, "max": 1, "palette": ["black", "white"], "opacity": 0.5},
"Random Raster",
)
# Add the original data layer in blue
Map.addLayer(data_raw, {"color": "blue"}, "Original data")
# Add the final data layer in red
Map.addLayer(data, {"color": "red"}, "Final data")
# Set the center of the map to the coordinates
Map.setCenter(126.712, 33.516, 14)
Map
関心のある地域の定義
関心領域(以下の AOI)の定義とは、研究者が分析対象の地理的領域を示すために使用する用語を指します。Study Area という用語と似た意味です。
このコンテキストでは、発生地点レイヤのジオメトリのバウンディング ボックスを取得し、その周囲に 50 km のバッファ(最大許容誤差 1,000 メートル)を作成して AOI を定義しました。
# Define the AOI
aoi = data.geometry().bounds().buffer(distance=50000, maxError=1000)
# Add the AOI to the map
outline = ee.Image().byte().paint(
featureCollection=aoi, color=1, width=3)
Map.remove_layer("Random Raster")
Map.addLayer(outline, {'palette': 'FF0000'}, "AOI")
Map.centerObject(aoi, 6)
Map
GEE 環境変数の追加
次に、環境変数を分析に追加します。GEE は、気温、降水量、標高、土地被覆、地形などの環境変数に関する幅広いデータセットを提供します。これらのデータセットにより、ヤイロチョウの生息地の好みに影響を与える可能性のあるさまざまな要因を包括的に分析できます。
SDM での GEE 環境変数の選択は、種の生息地の好みの特徴を反映している必要があります。そのためには、ヤイロチョウの生息地の好みを事前に調査し、文献をレビューする必要があります。このチュートリアルでは、主に GEE を使用した SDM のワークフローに焦点を当てているため、詳細な説明は省略されています。
WorldClim V1 Bioclim: このデータセットは、月ごとの気温と降水量のデータから導出された 19 個の生物気候変数を提供します。1960 年から 1991 年までの期間を対象とし、解像度は 927.67 メートルです。
# WorldClim V1 Bioclim
bio = ee.Image("WORLDCLIM/V1/BIO")
NASA SRTM Digital Elevation 30m: このデータセットには、スペースシャトル レーダー地形ミッション(SRTM)の数値標高データが含まれています。データは主に 2000 年頃に収集され、約 30 メートル(1 秒角)の解像度で提供されます。次のコードは、SRTM データから標高、傾斜、方位、陰影のレイヤを計算します。
# NASA SRTM Digital Elevation 30m
terrain = ee.Algorithms.Terrain(ee.Image("USGS/SRTMGL1_003"))
Global Forest Cover Change(GFCC)Tree Cover Multi-Year Global 30m: Landsat の Vegetation Continuous Fields(VCF)データセットは、植生の高さが 5 メートルを超える場合の垂直投影植生被覆率を推定します。このデータセットは、2000 年、2005 年、2010 年、2015 年を中心とした 4 つの期間について、30 メートルの解像度で提供されます。ここでは、これら 4 つの期間の中央値が使用されます。
# Global Forest Cover Change (GFCC) Tree Cover Multi-Year Global 30m
tcc = ee.ImageCollection("NASA/MEASURES/GFCC/TC/v3")
median_tcc = (
tcc.filterDate("2000-01-01", "2015-12-31")
.select(["tree_canopy_cover"], ["TCC"])
.median()
)
bio(気候変動変数)、terrain(地形)、median_tcc(樹冠被覆)が 1 つのマルチバンド画像に統合されます。elevation バンドが terrain から選択され、elevation が 0 より大きい場所の watermask が作成されます。これにより、海面下の領域(海など)がマスクされ、研究者は AOI のさまざまな環境要因を包括的に分析できるようになります。
# Combine bands into a multi-band image
predictors = bio.addBands(terrain).addBands(median_tcc)
# Create a water mask
watermask = terrain.select('elevation').gt(0)
# Mask out ocean pixels and clip to the area of interest
predictors = predictors.updateMask(watermask).clip(aoi)
相関性の高い予測変数がモデルに同時に含まれていると、多重共線性の問題が発生する可能性があります。多重共線性は、モデル内の独立変数間に強い線形関係がある場合に発生する現象で、モデルの係数(重み)の推定が不安定になります。この不安定さにより、モデルの信頼性が低下し、新しいデータに対する予測や解釈が困難になる可能性があります。したがって、多重共線性を考慮して、予測変数の選択プロセスを進めます。
まず、5,000 個のランダムなポイントを生成し、それらのポイントで単一のマルチバンド画像の予測変数値を抽出します。
# Generate 5,000 random points
data_cor = predictors.sample(scale=grain_size, numPixels=5000, geometries=True)
# Extract predictor variable values
pvals = predictors.sampleRegions(collection=data_cor, scale=grain_size)
抽出した各ポイントの予測値は DataFrame に変換し、最初の行を確認します。
# Converting predictor values from Earth Engine to a DataFrame
pvals_df = geemap.ee_to_df(pvals)
pvals_df.head(1)
# Displaying the columns
columns = pvals_df.columns
print(columns)
指定された予測変数間のスピアマン相関係数を計算し、ヒートマップで可視化します。
def plot_correlation_heatmap(dataframe, h_size=10, show_labels=False):
# Calculate Spearman correlation coefficients
correlation_matrix = dataframe.corr(method="spearman")
# Create a heatmap
plt.figure(figsize=(h_size, h_size-2))
plt.imshow(correlation_matrix, cmap='coolwarm', interpolation='nearest')
# Optionally display values on the heatmap
if show_labels:
for i in range(correlation_matrix.shape[0]):
for j in range(correlation_matrix.shape[1]):
plt.text(j, i, f"{correlation_matrix.iloc[i, j]:.2f}",
ha='center', va='center', color='white', fontsize=8)
columns = dataframe.columns.tolist()
plt.xticks(range(len(columns)), columns, rotation=90)
plt.yticks(range(len(columns)), columns)
plt.title("Variables Correlation Matrix")
plt.colorbar(label="Spearman Correlation")
plt.savefig('correlation_heatmap_plot.png')
plt.show()
# Plot the correlation heatmap of variables
plot_correlation_heatmap(pvals_df)
スピアマンの相関係数は、予測変数間の一般的な関連性を理解するのに役立ちますが、複数の変数がどのように相互作用するかを直接評価することはできません。特に、多重共線性を検出することはできません。
分散拡大係数(以下 VIF)は、多重共線性を評価し、変数の選択をガイドするために使用される統計指標です。各独立変数と他の独立変数との線形関係の程度を示します。VIF 値が高い場合は、多重共線性の証拠となる可能性があります。
通常、VIF 値が 5 または 10 を超えると、その変数が他の変数と強い相関関係にあり、モデルの安定性と解釈可能性が損なわれる可能性があることを示します。このチュートリアルでは、変数選択の基準として VIF 値が 10 未満であることを使用しました。VIF に基づいて、次の 6 つの変数が選択されました。
# Filter variables based on Variance Inflation Factor (VIF)
def filter_variables_by_vif(dataframe, threshold=10):
original_columns = dataframe.columns.tolist()
remaining_columns = original_columns[:]
while True:
vif_data = dataframe[remaining_columns]
vif_values = [
variance_inflation_factor(vif_data.values, i)
for i in range(vif_data.shape[1])
]
max_vif_index = vif_values.index(max(vif_values))
max_vif = max(vif_values)
if max_vif < threshold:
break
print(f"Removing '{remaining_columns[max_vif_index]}' with VIF {max_vif:.2f}")
del remaining_columns[max_vif_index]
filtered_data = dataframe[remaining_columns]
bands = filtered_data.columns.tolist()
print("Bands:", bands)
return filtered_data, bands
filtered_pvals_df, bands = filter_variables_by_vif(pvals_df)
# Variable Selection Based on VIF
predictors = predictors.select(bands)
# Plot the correlation heatmap of variables
plot_correlation_heatmap(filtered_pvals_df, h_size=6, show_labels=True)
次に、選択した 6 つの予測変数について地図上に可視化します。
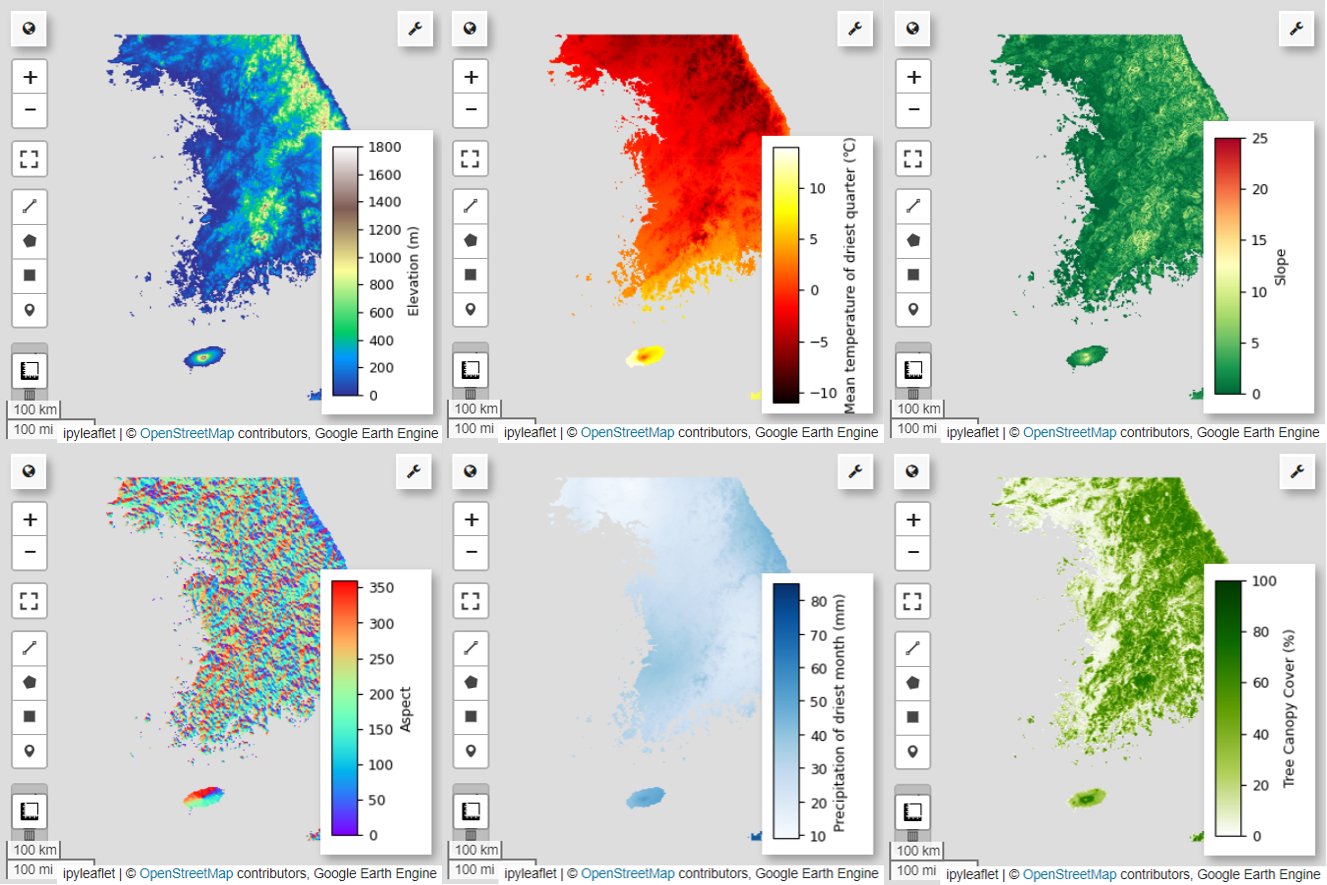
次のコードを使用して、地図の可視化に使用できるパレットを確認できます。たとえば、terrain パレットは次のようになります。
cm.plot_colormaps(width=8.0, height=0.2)
cm.plot_colormap('terrain', width=8.0, height=0.2, orientation='horizontal')
# Elevation layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['elevation'], 'min': 0, 'max': 1800, 'palette': cm.palettes.terrain}
Map.addLayer(predictors, vis_params, 'elevation')
Map.add_colorbar(vis_params, label="Elevation (m)", orientation="vertical", layer_name="elevation")
Map.centerObject(aoi, 6)
Map
# Calculate the minimum and maximum values for bio09
min_max_val = (
predictors.select("bio09")
.multiply(0.1)
.reduceRegion(reducer=ee.Reducer.minMax(), scale=1000)
.getInfo()
)
# bio09 (Mean temperature of driest quarter) layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"min": math.floor(min_max_val["bio09_min"]),
"max": math.ceil(min_max_val["bio09_max"]),
"palette": cm.palettes.hot,
}
Map.addLayer(predictors.select("bio09").multiply(0.1), vis_params, "bio09")
Map.add_colorbar(
vis_params,
label="Mean temperature of driest quarter (℃)",
orientation="vertical",
layer_name="bio09",
)
Map.centerObject(aoi, 6)
Map
# Slope layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['slope'], 'min': 0, 'max': 25, 'palette': cm.palettes.RdYlGn_r}
Map.addLayer(predictors, vis_params, 'slope')
Map.add_colorbar(vis_params, label="Slope", orientation="vertical", layer_name="slope")
Map.centerObject(aoi, 6)
Map
# Aspect layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['aspect'], 'min': 0, 'max': 360, 'palette': cm.palettes.rainbow}
Map.addLayer(predictors, vis_params, 'aspect')
Map.add_colorbar(vis_params, label="Aspect", orientation="vertical", layer_name="aspect")
Map.centerObject(aoi, 6)
Map
# Calculate the minimum and maximum values for bio14
min_max_val = (
predictors.select("bio14")
.reduceRegion(reducer=ee.Reducer.minMax(), scale=1000)
.getInfo()
)
# bio14 (Precipitation of driest month) layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"bands": ["bio14"],
"min": math.floor(min_max_val["bio14_min"]),
"max": math.ceil(min_max_val["bio14_max"]),
"palette": cm.palettes.Blues,
}
Map.addLayer(predictors, vis_params, "bio14")
Map.add_colorbar(
vis_params,
label="Precipitation of driest month (mm)",
orientation="vertical",
layer_name="bio14",
)
Map.centerObject(aoi, 6)
Map
# TCC layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"bands": ["TCC"],
"min": 0,
"max": 100,
"palette": ["ffffff", "afce56", "5f9c00", "0e6a00", "003800"],
}
Map.addLayer(predictors, vis_params, "TCC")
Map.add_colorbar(
vis_params, label="Tree Canopy Cover (%)", orientation="vertical", layer_name="TCC"
)
Map.centerObject(aoi, 6)
Map
疑似欠席データの生成
SDM のプロセスでは、種の入力データの選択は主に次の 2 つの方法で行われます。
Presence-Background メソッド: このメソッドは、特定の種が観察された場所(存在)と、その種が観察されなかった他の場所(バックグラウンド)を比較します。ここで、バックグラウンド データは、必ずしも種が存在しない領域を意味するのではなく、調査地域の全体的な環境条件を反映するように設定されています。このモデルは、種が生息できる適切な環境と、そうでない環境を区別するために使用されます。
存在 / 不在法: この方法は、種の存在が確認された場所と、種の存在が確認されなかった場所を比較します。ここで、不在データは、その種が存在しないことがわかっている特定の場所を表します。調査地域の全体的な環境条件を反映するものではなく、その種が存在しないと推定される場所を示しています。
実際には、真の欠損データを収集することは困難なことが多いため、人工的に生成された疑似欠損データが頻繁に使用されます。ただし、人工的に生成された疑似欠損点が実際の欠損領域を正確に反映していない可能性があるため、この方法の制限と潜在的なエラーを認識することが重要です。
どちらの方法を選択するかは、データの可用性、調査の目的、モデルの精度と信頼性、時間とリソースによって異なります。ここでは、GBIF から収集した出現データと人工的に生成した疑似欠損データを使用して、「Presence-Absence」メソッドでモデル化します。
疑似欠席データの生成は「環境プロファイリング アプローチ」で行われ、具体的な手順は次のとおりです。
k 平均法クラスタリングを使用した環境分類: ユークリッド距離に基づく k 平均法クラスタリング アルゴリズムを使用して、調査地域のピクセルを 2 つのクラスタに分割します。一方のクラスタは、ランダムに選択された 100 個のプレゼンス ロケーションと類似した環境特性を持つエリアを表し、もう一方のクラスタは、異なる特性を持つエリアを表します。
類似性の低いクラスタ内での疑似欠損データの生成: 最初のステップで特定された 2 番目のクラスタ(存在データとは異なる環境特性を持つ)内で、疑似欠損ポイントがランダムに生成されます。これらの疑似欠損点は、その種が存在しないと予想される場所を表します。
# Randomly select 100 locations for occurrence
pvals = predictors.sampleRegions(
collection=data.randomColumn().sort('random').limit(100),
properties=[],
scale=grain_size
)
# Perform k-means clustering
clusterer = ee.Clusterer.wekaKMeans(
nClusters=2,
distanceFunction="Euclidean"
).train(pvals)
cl_result = predictors.cluster(clusterer)
# Get cluster ID for locations similar to occurrence
cl_id = cl_result.sampleRegions(
collection=data.randomColumn().sort('random').limit(200),
properties=[],
scale=grain_size
)
# Define non-occurrence areas in dissimilar clusters
cl_id = ee.FeatureCollection(cl_id).reduceColumns(ee.Reducer.mode(),['cluster'])
cl_id = ee.Number(cl_id.get('mode')).subtract(1).abs()
cl_mask = cl_result.select(['cluster']).eq(cl_id)
# Presence location mask
presence_mask = data.reduceToImage(properties=['random'],
reducer=ee.Reducer.first()
).reproject('EPSG:4326', None,
grain_size).mask().neq(1).selfMask()
# Masking presence locations in non-occurrence areas and clipping to AOI
area_for_pa = presence_mask.updateMask(cl_mask).clip(aoi)
# Area for Pseudo-absence
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
Map.addLayer(area_for_pa, {'palette': 'black'}, 'AreaForPA')
Map.centerObject(aoi, 6)
Map
モデルの適合と予測
ここで、データをトレーニング データとテストデータに分割します。トレーニング データは、モデルをトレーニングして最適なパラメータを見つけるために使用され、テストデータは、事前にトレーニングされたモデルを評価するために使用されます。このコンテキストで考慮すべき重要なコンセプトは、空間自己相関です。
空間自己相関は、SDM の重要な要素であり、トブラーの法則に関連しています。これは、「すべてはすべてに関連しているが、近いものは遠いものよりも関連性が高い」という概念を体現しています。空間自己相関は、種の分布と環境変数との間の有意な関係を表します。ただし、トレーニング データとテストデータ間に空間自己相関が存在する場合、2 つのデータセット間の独立性が損なわれる可能性があります。これは、モデルの一般化能力の評価に大きな影響を与えます。
この問題に対処する 1 つの方法は、空間ブロック交差検証手法です。この手法では、データをトレーニング データセットとテスト データセットに分割します。この手法では、データを複数のブロックに分割し、各ブロックをトレーニング データセットとテスト データセットとして個別に使用して、空間自己相関の影響を軽減します。これにより、データセット間の独立性が高まり、モデルの汎化性能をより正確に評価できます。
具体的な手順は次のとおりです。
- 空間ブロックの作成: データセット全体を同じサイズの空間ブロックに分割します(例: 50x50 km)。
- トレーニング セットとテストセットの割り当て: 各空間ブロックは、トレーニング セット(70%)またはテストセット(30%)のいずれかにランダムに割り当てられます。これにより、モデルが特定の地域のデータに過剰適合することを防ぎ、より一般化された結果を得ることができます。
- 反復交差検証: プロセス全体が n 回繰り返されます(例: 10 回)。各反復処理で、ブロックはトレーニング セットとテストセットにランダムに分割されます。これは、モデルの安定性と信頼性を向上させることを目的としています。
- 疑似欠損データの生成: 各反復処理で、モデルのパフォーマンスを評価するために疑似欠損データがランダムに生成されます。
Scale = 50000
grid = watermask.reduceRegions(
collection=aoi.coveringGrid(scale=Scale, proj='EPSG:4326'),
reducer=ee.Reducer.mean()).filter(ee.Filter.neq('mean', None))
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
Map.addLayer(grid, {}, "Grid for spatial block cross validation")
Map.addLayer(outline, {'palette': 'FF0000'}, "Study Area")
Map.centerObject(aoi, 6)
Map
これで、モデルを適合させることができます。モデルの適合には、データのパターンを理解し、それに応じてモデルのパラメータ(重みとバイアス)を調整することが含まれます。このプロセスにより、新しいデータが提示されたときに、モデルがより正確な予測を行うことができます。このため、モデルを適合させる SDM() という関数を定義しました。
ランダム フォレスト アルゴリズムを使用します。
def sdm(x):
seed = ee.Number(x)
# Random block division for training and validation
rand_blk = ee.FeatureCollection(grid).randomColumn(seed=seed).sort("random")
training_grid = rand_blk.filter(ee.Filter.lt("random", split)) # Grid for training
testing_grid = rand_blk.filter(ee.Filter.gte("random", split)) # Grid for testing
# Presence points
presence_points = ee.FeatureCollection(data)
presence_points = presence_points.map(lambda feature: feature.set("PresAbs", 1))
tr_presence_points = presence_points.filter(
ee.Filter.bounds(training_grid)
) # Presence points for training
te_presence_points = presence_points.filter(
ee.Filter.bounds(testing_grid)
) # Presence points for testing
# Pseudo-absence points for training
tr_pseudo_abs_points = area_for_pa.sample(
region=training_grid,
scale=grain_size,
numPixels=tr_presence_points.size().add(300),
seed=seed,
geometries=True,
)
# Same number of pseudo-absence points as presence points for training
tr_pseudo_abs_points = (
tr_pseudo_abs_points.randomColumn()
.sort("random")
.limit(ee.Number(tr_presence_points.size()))
)
tr_pseudo_abs_points = tr_pseudo_abs_points.map(lambda feature: feature.set("PresAbs", 0))
te_pseudo_abs_points = area_for_pa.sample(
region=testing_grid,
scale=grain_size,
numPixels=te_presence_points.size().add(100),
seed=seed,
geometries=True,
)
# Same number of pseudo-absence points as presence points for testing
te_pseudo_abs_points = (
te_pseudo_abs_points.randomColumn()
.sort("random")
.limit(ee.Number(te_presence_points.size()))
)
te_pseudo_abs_points = te_pseudo_abs_points.map(lambda feature: feature.set("PresAbs", 0))
# Merge training and pseudo-absence points
training_partition = tr_presence_points.merge(tr_pseudo_abs_points)
testing_partition = te_presence_points.merge(te_pseudo_abs_points)
# Extract predictor variable values at training points
train_pvals = predictors.sampleRegions(
collection=training_partition,
properties=["PresAbs"],
scale=grain_size,
geometries=True,
)
# Random Forest classifier
classifier = ee.Classifier.smileRandomForest(
numberOfTrees=500,
variablesPerSplit=None,
minLeafPopulation=10,
bagFraction=0.5,
maxNodes=None,
seed=seed,
)
# Presence probability: Habitat suitability map
classifier_pr = classifier.setOutputMode("PROBABILITY").train(
train_pvals, "PresAbs", bands
)
classified_img_pr = predictors.select(bands).classify(classifier_pr)
# Binary presence/absence map: Potential distribution map
classifier_bin = classifier.setOutputMode("CLASSIFICATION").train(
train_pvals, "PresAbs", bands
)
classified_img_bin = predictors.select(bands).classify(classifier_bin)
return [
classified_img_pr,
classified_img_bin,
training_partition,
testing_partition,
], classifier_pr
空間ブロックは、モデル トレーニング用に 70%、モデル テスト用に 30% に分割されます。疑似不在データは、各イテレーションのトレーニング セットとテストセット内でランダムに生成されます。その結果、各実行で、モデルのトレーニングとテストに使用する存在データと疑似不在データの異なるセットが生成されます。
split = 0.7
numiter = 10
# Random Seed
runif = lambda length: [random.randint(1, 1000) for _ in range(length)]
items = runif(numiter)
# Fixed seed
# items = [287, 288, 553, 226, 151, 255, 902, 267, 419, 538]
results_list = [] # Initialize SDM results list
importances_list = [] # Initialize variable importance list
for item in items:
result, trained = sdm(item)
# Accumulate SDM results into the list
results_list.extend(result)
# Accumulate variable importance into the list
importance = ee.Dictionary(trained.explain()).get('importance')
importances_list.extend(importance.getInfo().items())
# Flatten the SDM results list
results = ee.List(results_list).flatten()
これで、ヤイロチョウの生息適地マップと潜在分布マップを可視化できます。この場合、生息地の適性マップは、mean() 関数を使用してすべての画像で各ピクセル位置の平均値を計算することで作成され、潜在的な分布マップは、mode() 関数を使用してすべての画像で各ピクセル位置で最も頻繁に出現する値を特定することで生成されます。
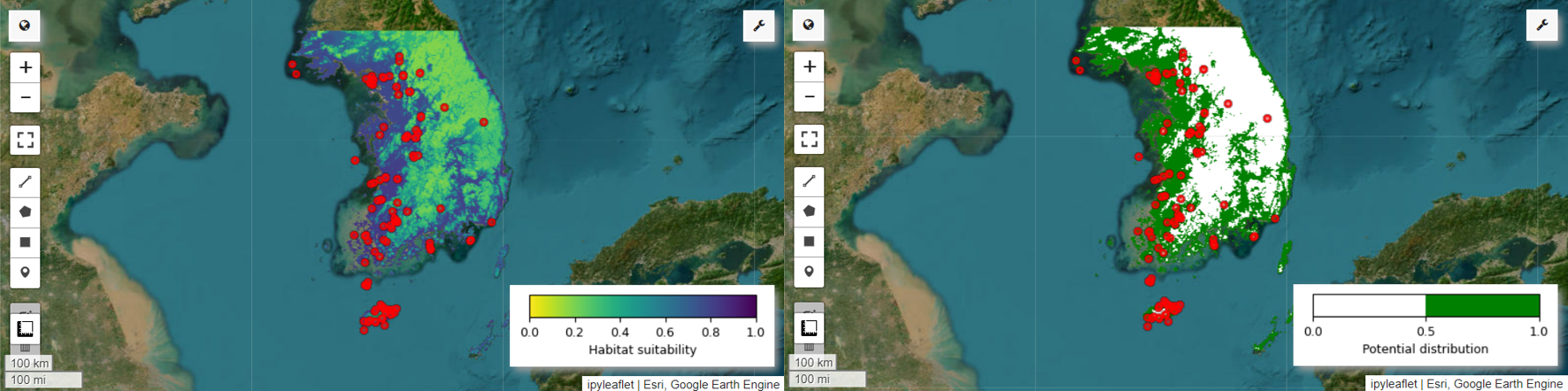
# Habitat suitability map
images = ee.List.sequence(
0, ee.Number(numiter).multiply(4).subtract(1), 4).map(
lambda x: results.get(x))
model_average = ee.ImageCollection.fromImages(images).mean()
Map = geemap.Map(layout={'height':'400px', 'width':'800px'}, basemap='Esri.WorldImagery')
vis_params = {
'min': 0,
'max': 1,
'palette': cm.palettes.viridis_r}
Map.addLayer(model_average, vis_params, 'Habitat suitability')
Map.add_colorbar(vis_params, label="Habitat suitability",
orientation="horizontal",
layer_name="Habitat suitability")
Map.addLayer(data, {'color':'red'}, 'Presence')
Map.centerObject(aoi, 6)
Map
# Potential distribution map
images2 = ee.List.sequence(1, ee.Number(numiter).multiply(4).subtract(1), 4).map(
lambda x: results.get(x)
)
distribution_map = ee.ImageCollection.fromImages(images2).mode()
Map = geemap.Map(
layout={"height": "400px", "width": "800px"}, basemap="Esri.WorldImagery"
)
vis_params = {"min": 0, "max": 1, "palette": ["white", "green"]}
Map.addLayer(distribution_map, vis_params, "Potential distribution")
Map.addLayer(data, {"color": "red"}, "Presence")
Map.add_colorbar(
vis_params,
label="Potential distribution",
discrete=True,
orientation="horizontal",
layer_name="Potential distribution",
)
Map.centerObject(data.geometry(), 6)
Map
変数の重要度と精度の評価
ランダム フォレスト(ee.Classifier.smileRandomForest)は、複数のディシジョン ツリーを構築して予測を行うアンサンブル学習手法の 1 つです。各決定木はデータの異なるサブセットから個別に学習し、その結果が集約されて、より正確で安定した予測が可能になります。
変数の重要度は、ランダム フォレスト モデル内の予測に対する各変数の影響を評価する指標です。前に定義した importances_list を使用して、平均変数重要度を計算して出力します。
def plot_variable_importance(importances_list):
# Extract each variable importance value into a list
variables = [item[0] for item in importances_list]
importances = [item[1] for item in importances_list]
# Calculate the average importance for each variable
average_importances = {}
for variable in set(variables):
indices = [i for i, var in enumerate(variables) if var == variable]
average_importance = np.mean([importances[i] for i in indices])
average_importances[variable] = average_importance
# Sort the importances in descending order of importance
sorted_importances = sorted(average_importances.items(),
key=lambda x: x[1], reverse=False)
variables = [item[0] for item in sorted_importances]
avg_importances = [item[1] for item in sorted_importances]
# Adjust the graph size
plt.figure(figsize=(8, 4))
# Plot the average importance as a horizontal bar chart
plt.barh(variables, avg_importances)
plt.xlabel('Importance')
plt.ylabel('Variables')
plt.title('Average Variable Importance')
# Display values above the bars
for i, v in enumerate(avg_importances):
plt.text(v + 0.02, i, f"{v:.2f}", va='center')
# Adjust the x-axis range
plt.xlim(0, max(avg_importances) + 5) # Adjust to the desired range
plt.tight_layout()
plt.savefig('variable_importance.png')
plt.show()
plot_variable_importance(importances_list)
テスト データセットを使用して、実行ごとに AUC-ROC と AUC-PR を計算します。次に、n 回の反復で AUC-ROC と AUC-PR の平均を計算します。
AUC-ROC は、「感度(再現率)対 1 - 特異度」グラフの曲線下面積を表します。これは、しきい値が変化するにつれて感度と特異度の関係がどのように変化するかを示しています。特異度は、観測されたすべての非発生に基づいて計算されます。したがって、AUC-ROC には混同行列のすべての象限が含まれます。
AUC-PR は、「適合率と再現率(感度)」グラフの曲線下面積を表します。これは、しきい値が変化するにつれて適合率と再現率の関係がどのように変化するかを示します。適合率は、予測されたすべての発生回数に基づいています。したがって、AUC-PR には真陰性(TN)は含まれません。
def print_pres_abs_sizes(TestingDatasets, numiter):
# Check and print the sizes of presence and pseudo-absence coordinates
def get_pres_abs_size(x):
fc = ee.FeatureCollection(TestingDatasets.get(x))
presence_size = fc.filter(ee.Filter.eq("PresAbs", 1)).size()
pseudo_absence_size = fc.filter(ee.Filter.eq("PresAbs", 0)).size()
return ee.List([presence_size, pseudo_absence_size])
sizes_info = (
ee.List.sequence(0, ee.Number(numiter).subtract(1), 1)
.map(get_pres_abs_size)
.getInfo()
)
for i, sizes in enumerate(sizes_info):
presence_size = sizes[0]
pseudo_absence_size = sizes[1]
print(
f"Iteration {i + 1}: Presence Size = {presence_size}, Pseudo-absence Size = {pseudo_absence_size}"
)
# Extracting the Testing Datasets
testing_datasets = ee.List.sequence(
3, ee.Number(numiter).multiply(4).subtract(1), 4
).map(lambda x: results.get(x))
print_pres_abs_sizes(testing_datasets, numiter)
def get_acc(hsm, t_data, grain_size):
pr_prob_vals = hsm.sampleRegions(
collection=t_data, properties=["PresAbs"], scale=grain_size
)
seq = ee.List.sequence(start=0, end=1, count=25) # Divide 0 to 1 into 25 intervals
def calculate_metrics(cutoff):
# Each element of the seq list is passed as cutoff(threshold value)
# Observed present = TP + FN
pres = pr_prob_vals.filterMetadata("PresAbs", "equals", 1)
# TP (True Positive)
tp = ee.Number(
pres.filterMetadata("classification", "greater_than", cutoff).size()
)
# TPR (True Positive Rate) = Recall = Sensitivity = TP / (TP + FN) = TP / Observed present
tpr = tp.divide(pres.size())
# Observed absent = FP + TN
abs = pr_prob_vals.filterMetadata("PresAbs", "equals", 0)
# FN (False Negative)
fn = ee.Number(
pres.filterMetadata("classification", "less_than", cutoff).size()
)
# TNR (True Negative Rate) = Specificity = TN / (FP + TN) = TN / Observed absent
tn = ee.Number(abs.filterMetadata("classification", "less_than", cutoff).size())
tnr = tn.divide(abs.size())
# FP (False Positive)
fp = ee.Number(
abs.filterMetadata("classification", "greater_than", cutoff).size()
)
# FPR (False Positive Rate) = FP / (FP + TN) = FP / Observed absent
fpr = fp.divide(abs.size())
# Precision = TP / (TP + FP) = TP / Predicted present
precision = tp.divide(tp.add(fp))
# SUMSS = SUM of Sensitivity and Specificity
sumss = tpr.add(tnr)
return ee.Feature(
None,
{
"cutoff": cutoff,
"TP": tp,
"TN": tn,
"FP": fp,
"FN": fn,
"TPR": tpr,
"TNR": tnr,
"FPR": fpr,
"Precision": precision,
"SUMSS": sumss,
},
)
return ee.FeatureCollection(seq.map(calculate_metrics))
def calculate_and_print_auc_metrics(images, testing_datasets, grain_size, numiter):
# Calculate AUC-ROC and AUC-PR
def calculate_auc_metrics(x):
hsm = ee.Image(images.get(x))
t_data = ee.FeatureCollection(testing_datasets.get(x))
acc = get_acc(hsm, t_data, grain_size)
# Calculate AUC-ROC
x = ee.Array(acc.aggregate_array("FPR"))
y = ee.Array(acc.aggregate_array("TPR"))
x1 = x.slice(0, 1).subtract(x.slice(0, 0, -1))
y1 = y.slice(0, 1).add(y.slice(0, 0, -1))
auc_roc = x1.multiply(y1).multiply(0.5).reduce("sum", [0]).abs().toList().get(0)
# Calculate AUC-PR
x = ee.Array(acc.aggregate_array("TPR"))
y = ee.Array(acc.aggregate_array("Precision"))
x1 = x.slice(0, 1).subtract(x.slice(0, 0, -1))
y1 = y.slice(0, 1).add(y.slice(0, 0, -1))
auc_pr = x1.multiply(y1).multiply(0.5).reduce("sum", [0]).abs().toList().get(0)
return (auc_roc, auc_pr)
auc_metrics = (
ee.List.sequence(0, ee.Number(numiter).subtract(1), 1)
.map(calculate_auc_metrics)
.getInfo()
)
# Print AUC-ROC and AUC-PR for each iteration
df = pd.DataFrame(auc_metrics, columns=["AUC-ROC", "AUC-PR"])
df.index = [f"Iteration {i + 1}" for i in range(len(df))]
df.to_csv("auc_metrics.csv", index_label="Iteration")
print(df)
# Calculate mean and standard deviation of AUC-ROC and AUC-PR
mean_auc_roc, std_auc_roc = df["AUC-ROC"].mean(), df["AUC-ROC"].std()
mean_auc_pr, std_auc_pr = df["AUC-PR"].mean(), df["AUC-PR"].std()
print(f"Mean AUC-ROC = {mean_auc_roc:.4f} ± {std_auc_roc:.4f}")
print(f"Mean AUC-PR = {mean_auc_pr:.4f} ± {std_auc_pr:.4f}")
%%time
# Calculate AUC-ROC and AUC-PR
calculate_and_print_auc_metrics(images, testing_datasets, grain_size, numiter)
このチュートリアルでは、Google Earth Engine(GEE)を使用して種分布モデリング(SDM)を行う実践的な例を示しました。重要なポイントは、SDM の分野における GEE の汎用性と柔軟性です。Earth Engine の強力な地理空間データ処理機能を活用することで、研究者や環境保護活動家は地球上の生物多様性を理解し、保護するための無限の可能性を切り開くことができます。このチュートリアルで得た知識とスキルを応用することで、生態学研究という魅力的な分野を探求し、貢献することができます。
 Google Colab で実行
Google Colab で実行
 GitHub 上のソースを見る
GitHub 上のソースを見る