En este instructivo, se presentará la metodología del modelado de distribución de especies con Google Earth Engine. Se proporcionará una breve descripción general del modelado de la distribución de especies, seguida del proceso de predicción y análisis del hábitat de una especie de ave en peligro de extinción conocida como Pitta ninfa (nombre científico: Pitta nympha).
Ejecútame primero
Ejecuta la siguiente celda para inicializar la API. El resultado contendrá instrucciones para otorgar acceso a este notebook a Earth Engine con tu cuenta.
import ee
# Trigger the authentication flow.
ee.Authenticate()
# Initialize the library.
ee.Initialize(project='my-project')
Breve descripción general del modelado de la distribución de especies
Exploremos qué son los modelos de distribución de especies, las ventajas de usar Google Earth Engine para su procesamiento, los datos requeridos para los modelos y cómo se estructura el flujo de trabajo.
¿Qué es el modelado de distribución de especies?
El modelado de distribución de especies (SDM, por sus siglas en inglés) es la metodología más común que se utiliza para estimar la distribución geográfica real o potencial de una especie. Consiste en caracterizar las condiciones ambientales adecuadas para una especie en particular y, luego, identificar dónde se distribuyen geográficamente estas condiciones adecuadas.
En los últimos años, el SDM se convirtió en un componente fundamental de la planificación de la conservación, y se desarrollaron varias técnicas de modelado para este propósito. La implementación del SDM en Google Earth Engine (GEE a continuación) proporciona acceso fácil a datos ambientales a gran escala, junto con potentes capacidades de procesamiento y compatibilidad con algoritmos de aprendizaje automático, lo que permite un modelado rápido.
Datos obligatorios para el SDM
Por lo general, el SDM utiliza la relación entre los registros conocidos de ocurrencia de especies y las variables ambientales para identificar las condiciones en las que una población puede mantenerse. En otras palabras, se requieren dos tipos de datos de entrada del modelo:
- Registros de ocurrencia de especies conocidas
- Diversas variables ambientales
Estos datos se ingresan en algoritmos para identificar las condiciones ambientales asociadas con la presencia de especies.
Flujo de trabajo del SDM con GEE
El flujo de trabajo para el SDM con GEE es el siguiente:
- Recopilación y procesamiento previo de datos de ocurrencia de especies
- Definición del área de interés
- Se agregaron variables ambientales de GEE
- Generación de datos de pseudoausencia
- Ajuste y predicción del modelo
- Evaluación de la importancia y la precisión de las variables
Análisis y predicción de hábitats con GEE
La pitta hada (Pitta nympha) se usará como caso de estudio para demostrar la aplicación del SDM basado en GEE. Si bien esta especie específica se seleccionó para un ejemplo, los investigadores pueden aplicar la metodología a cualquier especie objetivo de interés con pequeñas modificaciones en el código fuente proporcionado.
La pitta hada es una especie migratoria de verano y de paso poco común en Corea del Sur, cuya área de distribución se está expandiendo debido al reciente calentamiento climático en la península coreana. Se clasifica como una especie rara, vida silvestre en peligro de extinción de clase II, Monumento Natural núm. 204, evaluada como Extinta a nivel regional (RE) en la Lista Roja Nacional y Vulnerable (VU) según las categorías de la UICN.
La realización de SDM para la planificación de la conservación de la pitta hada parece ser bastante valiosa. Ahora, continuemos con la predicción y el análisis de hábitats a través de GEE.
Primero, se importan las bibliotecas de Python.La instrucción import incorpora todo el contenido de un módulo, mientras que la instrucción from import permite importar objetos específicos de un módulo.
# Import libraries
import geemap
import geemap.colormaps as cm
import pandas as pd, geopandas as gpd
import numpy as np, matplotlib.pyplot as plt
import os, requests, math, random
from ipyleaflet import TileLayer
from statsmodels.stats.outliers_influence import variance_inflation_factor
Recopilación y preprocesamiento de datos de ocurrencia de especies
Ahora, recopilemos datos de ocurrencia para la pitta hada. Incluso si actualmente no tienes acceso a los datos de ocurrencia de las especies de interés, puedes obtener datos de observación sobre especies específicas a través de la API del GBIF. La API de GBIF es una interfaz que permite acceder a los datos de distribución de especies que proporciona GBIF, lo que permite a los usuarios buscar, filtrar y descargar datos, así como adquirir diversa información relacionada con las especies.
En el siguiente código, a la variable species_name se le asigna el nombre científico de la especie (p.ej., Pitta nympha para Pitta ninfa) y a la variable country_code se le asigna el código de país (p.ej., KR para Corea del Sur). La variable base_url almacena la dirección de la API de GBIF. params es un diccionario que contiene los parámetros que se usarán en la solicitud a la API:
scientificName: Establece el nombre científico de la especie que se buscará.country: Limita la búsqueda a un país específico.hasCoordinate: Garantiza que solo se busquen datos con coordenadas (verdadero).basisOfRecord: Elige solo los registros de observación humana (HUMAN_OBSERVATION).limit: Establece la cantidad máxima de resultados devueltos en 10,000.
def get_gbif_species_data(species_name, country_code):
"""
Retrieves observational data for a specific species using the GBIF API and returns it as a pandas DataFrame.
Parameters:
species_name (str): The scientific name of the species to query.
country_code (str): The country code of the where the observation data will be queried.
Returns:
pd.DataFrame: A pandas DataFrame containing the observational data.
"""
base_url = "https://api.gbif.org/v1/occurrence/search"
params = {
"scientificName": species_name,
"country": country_code,
"hasCoordinate": "true",
"basisOfRecord": "HUMAN_OBSERVATION",
"limit": 10000,
}
try:
response = requests.get(base_url, params=params)
response.raise_for_status() # Raises an exception for a response error.
data = response.json()
occurrences = data.get("results", [])
if occurrences: # If data is present
df = pd.json_normalize(occurrences)
return df
else:
print("No data found for the given species and country code.")
return pd.DataFrame() # Returns an empty DataFrame
except requests.RequestException as e:
print(f"Request failed: {e}")
return pd.DataFrame() # Returns an empty DataFrame in case of an exception
Con los parámetros establecidos anteriormente, consultamos la API de GBIF para obtener registros de observación de la pitta ninfa (Pitta nympha) y cargamos los resultados en un DataFrame para verificar la primera fila. Un DataFrame es una estructura de datos para controlar datos con formato de tabla, que consta de filas y columnas. Si es necesario, el DataFrame se puede guardar como un archivo CSV y volver a leer.
# Retrieve Fairy Pitta data
df = get_gbif_species_data("Pitta nympha", "KR")
"""
# Save DataFrame to CSV and read back in.
df.to_csv("pitta_nympha_data.csv", index=False)
df = pd.read_csv("pitta_nympha_data.csv")
"""
df.head(1) # Display the first row of the DataFrame
A continuación, convertimos el DataFrame en un GeoDataFrame que incluye una columna para la información geográfica (geometry) y verificamos la primera fila. Un GeoDataFrame se puede guardar como un archivo GeoPackage (*.gpkg) y volver a leer.
# Convert DataFrame to GeoDataFrame
gdf = gpd.GeoDataFrame(
df,
geometry=gpd.points_from_xy(df.decimalLongitude,
df.decimalLatitude),
crs="EPSG:4326"
)[["species", "year", "month", "geometry"]]
"""
# Convert GeoDataFrame to GeoPackage (requires pycrs module)
%pip install -U -q pycrs
gdf.to_file("pitta_nympha_data.gpkg", driver="GPKG")
gdf = gpd.read_file("pitta_nympha_data.gpkg")
"""
gdf.head(1) # Display the first row of the GeoDataFrame
Esta vez, creamos una función para visualizar la distribución de los datos por año y mes del GeoDataFrame, y mostrarla como un gráfico que se puede guardar como un archivo de imagen. El uso de un mapa de calor nos permite comprender rápidamente la frecuencia de aparición de las especies por año y mes, lo que proporciona una visualización intuitiva de los cambios y patrones temporales dentro de los datos. Esto permite identificar patrones temporales y variaciones estacionales en los datos de ocurrencia de especies, así como detectar rápidamente valores atípicos o problemas de calidad en los datos.
# Yearly and monthly data distribution heatmap
def plot_heatmap(gdf, h_size=8):
statistics = gdf.groupby(["month", "year"]).size().unstack(fill_value=0)
# Heatmap
plt.figure(figsize=(h_size, h_size - 6))
heatmap = plt.imshow(
statistics.values, cmap="YlOrBr", origin="upper", aspect="auto"
)
# Display values above each pixel
for i in range(len(statistics.index)):
for j in range(len(statistics.columns)):
plt.text(
j, i, statistics.values[i, j], ha="center", va="center", color="black"
)
plt.colorbar(heatmap, label="Count")
plt.title("Monthly Species Count by Year")
plt.xlabel("Year")
plt.ylabel("Month")
plt.xticks(range(len(statistics.columns)), statistics.columns)
plt.yticks(range(len(statistics.index)), statistics.index)
plt.tight_layout()
plt.savefig("heatmap_plot.png")
plt.show()
plot_heatmap(gdf)
Los datos de 1995 son muy dispersos, con brechas significativas en comparación con otros años, y los meses de agosto y septiembre también tienen muestras limitadas y exhiben diferentes características estacionales en comparación con otros períodos. Excluir estos datos podría contribuir a mejorar la estabilidad y el poder predictivo del modelo.
Sin embargo, es importante tener en cuenta que excluir datos puede mejorar la capacidad de generalización del modelo, pero también podría provocar la pérdida de información valiosa pertinente para los objetivos de la investigación. Por lo tanto, estas decisiones deben tomarse con cuidado.
# Filtering data by year and month
filtered_gdf = gdf[
(~gdf['year'].eq(1995)) &
(~gdf['month'].between(8, 9))
]
Ahora, el GeoDataFrame filtrado se convierte en un objeto de Google Earth Engine.
# Convert GeoDataFrame to Earth Engine object
data_raw = geemap.geopandas_to_ee(filtered_gdf)
A continuación, definiremos el tamaño de píxel ráster de los resultados del SDM como una resolución de 1 km.
# Spatial resolution setting (meters)
grain_size = 1000
Cuando hay varios puntos de ocurrencia dentro del mismo píxel ráster con una resolución de 1 km, es muy probable que compartan las mismas condiciones ambientales en la misma ubicación geográfica. Usar esos datos directamente en el análisis puede introducir sesgos en los resultados.
En otras palabras, debemos limitar el posible impacto del sesgo de muestreo geográfico. Para lograrlo, conservaremos solo una ubicación dentro de cada píxel de 1 km y quitaremos todas las demás, lo que permitirá que el modelo refleje de manera más objetiva las condiciones ambientales.
def remove_duplicates(data, grain_size):
# Select one occurrence record per pixel at the chosen spatial resolution
random_raster = ee.Image.random().reproject("EPSG:4326", None, grain_size)
rand_point_vals = random_raster.sampleRegions(
collection=ee.FeatureCollection(data), geometries=True
)
return rand_point_vals.distinct("random")
data = remove_duplicates(data_raw, grain_size)
# Before selection and after selection
print("Original data size:", data_raw.size().getInfo())
print("Final data size:", data.size().getInfo())
A continuación, se muestra la visualización que compara el sesgo de muestreo geográfico antes del preprocesamiento (en azul) y después del preprocesamiento (en rojo). Para facilitar la comparación, el mapa se centró en el área con una alta concentración de coordenadas de ocurrencia de la pitta hada en el parque nacional Hallasan.
# Visualization of geographic sampling bias before (blue) and after (red) preprocessing
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
# Add the random raster layer
random_raster = ee.Image.random().reproject("EPSG:4326", None, grain_size)
Map.addLayer(
random_raster,
{"min": 0, "max": 1, "palette": ["black", "white"], "opacity": 0.5},
"Random Raster",
)
# Add the original data layer in blue
Map.addLayer(data_raw, {"color": "blue"}, "Original data")
# Add the final data layer in red
Map.addLayer(data, {"color": "red"}, "Final data")
# Set the center of the map to the coordinates
Map.setCenter(126.712, 33.516, 14)
Map
Definición del área de interés
La definición del área de interés (AOI, por sus siglas en inglés) hace referencia al término que usan los investigadores para denotar el área geográfica que desean analizar. Tiene un significado similar al término Área de estudio.
En este contexto, obtuvimos el cuadro delimitador de la geometría de la capa de puntos de ocurrencia y creamos un búfer de 50 kilómetros a su alrededor (con una tolerancia máxima de 1,000 metros) para definir el AOI.
# Define the AOI
aoi = data.geometry().bounds().buffer(distance=50000, maxError=1000)
# Add the AOI to the map
outline = ee.Image().byte().paint(
featureCollection=aoi, color=1, width=3)
Map.remove_layer("Random Raster")
Map.addLayer(outline, {'palette': 'FF0000'}, "AOI")
Map.centerObject(aoi, 6)
Map
Se agregaron variables ambientales de GEE
Ahora, agreguemos variables ambientales al análisis. GEE proporciona una amplia variedad de conjuntos de datos para variables ambientales, como temperatura, precipitación, elevación, cobertura terrestre y terreno. Estos conjuntos de datos nos permiten analizar de forma integral diversos factores que pueden influir en las preferencias de hábitat de la pitta hada.
La selección de variables ambientales de GEE en el SDM debe reflejar las características de preferencia de hábitat de la especie. Para ello, se deben realizar investigaciones previas y una revisión de la literatura sobre las preferencias de hábitat de la pitta hada. Este instructivo se enfoca principalmente en el flujo de trabajo del SDM con GEE, por lo que se omiten algunos detalles profundos.
WorldClim V1 Bioclim: Este conjunto de datos proporciona 19 variables bioclimáticas derivadas de datos mensuales de temperatura y precipitación. Abarca el período de 1960 a 1991 y tiene una resolución de 927.67 metros.
# WorldClim V1 Bioclim
bio = ee.Image("WORLDCLIM/V1/BIO")
NASA SRTM Digital Elevation 30m: Este conjunto de datos contiene datos de elevación digital de la misión Shuttle Radar Topography Mission (SRTM). Los datos se recopilaron principalmente alrededor del año 2000 y se proporcionan con una resolución de aproximadamente 30 metros (1 segundo de arco). El siguiente código calcula las capas de elevación, pendiente, orientación y sombreado del relieve a partir de los datos de SRTM.
# NASA SRTM Digital Elevation 30m
terrain = ee.Algorithms.Terrain(ee.Image("USGS/SRTMGL1_003"))
Global Forest Cover Change (GFCC) Tree Cover Multi-Year Global 30m: El conjunto de datos de campos continuos de vegetación (VCF) de Landsat estima la proporción de cobertura vegetal proyectada verticalmente cuando la altura de la vegetación es superior a 5 metros. Este conjunto de datos se proporciona para cuatro períodos centrados en los años 2000, 2005, 2010 y 2015, con una resolución de 30 metros. Aquí se usan los valores de la mediana de estos cuatro períodos.
# Global Forest Cover Change (GFCC) Tree Cover Multi-Year Global 30m
tcc = ee.ImageCollection("NASA/MEASURES/GFCC/TC/v3")
median_tcc = (
tcc.filterDate("2000-01-01", "2015-12-31")
.select(["tree_canopy_cover"], ["TCC"])
.median()
)
bio (variables bioclimáticas), terrain (topografía) y median_tcc (cobertura del dosel de los árboles) se combinan en una sola imagen multibanda. Se selecciona la banda elevation de terrain y se crea un watermask para las ubicaciones en las que elevation es mayor que 0. Esto enmascara las regiones por debajo del nivel del mar (p.ej., el océano) y prepara al investigador para analizar de forma integral diversos factores ambientales del AOI.
# Combine bands into a multi-band image
predictors = bio.addBands(terrain).addBands(median_tcc)
# Create a water mask
watermask = terrain.select('elevation').gt(0)
# Mask out ocean pixels and clip to the area of interest
predictors = predictors.updateMask(watermask).clip(aoi)
Cuando se incluyen variables predictoras altamente correlacionadas en un mismo modelo, pueden surgir problemas de multicolinealidad. La multicolinealidad es un fenómeno que ocurre cuando existen relaciones lineales sólidas entre las variables independientes de un modelo, lo que genera inestabilidad en la estimación de los coeficientes (ponderaciones) del modelo. Esta inestabilidad puede reducir la confiabilidad del modelo y dificultar las predicciones o interpretaciones para los datos nuevos. Por lo tanto, tendremos en cuenta la multicolinealidad y continuaremos con el proceso de selección de variables predictoras.
Primero, generaremos 5,000 puntos aleatorios y, luego, extraeremos los valores de las variables predictoras de la única imagen multibanda en esos puntos.
# Generate 5,000 random points
data_cor = predictors.sample(scale=grain_size, numPixels=5000, geometries=True)
# Extract predictor variable values
pvals = predictors.sampleRegions(collection=data_cor, scale=grain_size)
Convertiremos los valores del predictor extraídos para cada punto en un DataFrame y, luego, verificaremos la primera fila.
# Converting predictor values from Earth Engine to a DataFrame
pvals_df = geemap.ee_to_df(pvals)
pvals_df.head(1)
# Displaying the columns
columns = pvals_df.columns
print(columns)
Calcula los coeficientes de correlación de Spearman entre las variables predictoras proporcionadas y los visualiza en un mapa de calor.
def plot_correlation_heatmap(dataframe, h_size=10, show_labels=False):
# Calculate Spearman correlation coefficients
correlation_matrix = dataframe.corr(method="spearman")
# Create a heatmap
plt.figure(figsize=(h_size, h_size-2))
plt.imshow(correlation_matrix, cmap='coolwarm', interpolation='nearest')
# Optionally display values on the heatmap
if show_labels:
for i in range(correlation_matrix.shape[0]):
for j in range(correlation_matrix.shape[1]):
plt.text(j, i, f"{correlation_matrix.iloc[i, j]:.2f}",
ha='center', va='center', color='white', fontsize=8)
columns = dataframe.columns.tolist()
plt.xticks(range(len(columns)), columns, rotation=90)
plt.yticks(range(len(columns)), columns)
plt.title("Variables Correlation Matrix")
plt.colorbar(label="Spearman Correlation")
plt.savefig('correlation_heatmap_plot.png')
plt.show()
# Plot the correlation heatmap of variables
plot_correlation_heatmap(pvals_df)
El coeficiente de correlación de Spearman es útil para comprender las asociaciones generales entre las variables predictoras, pero no evalúa directamente cómo interactúan varias variables, en particular, no detecta la multicolinealidad.
El factor de inflación de la varianza (VIF a continuación) es una métrica estadística que se usa para evaluar la multicolinealidad y guiar la selección de variables. Indica el grado de relación lineal de cada variable independiente con las demás variables independientes, y los valores altos del VIF pueden ser evidencia de multicolinealidad.
Por lo general, cuando los valores del VIF superan el 5 o el 10, se sugiere que la variable tiene una correlación sólida con otras variables, lo que podría comprometer la estabilidad y la interpretabilidad del modelo. En este instructivo, se usó un criterio de valores del VIF inferiores a 10 para la selección de variables. Las siguientes 6 variables se seleccionaron en función del VIF.
# Filter variables based on Variance Inflation Factor (VIF)
def filter_variables_by_vif(dataframe, threshold=10):
original_columns = dataframe.columns.tolist()
remaining_columns = original_columns[:]
while True:
vif_data = dataframe[remaining_columns]
vif_values = [
variance_inflation_factor(vif_data.values, i)
for i in range(vif_data.shape[1])
]
max_vif_index = vif_values.index(max(vif_values))
max_vif = max(vif_values)
if max_vif < threshold:
break
print(f"Removing '{remaining_columns[max_vif_index]}' with VIF {max_vif:.2f}")
del remaining_columns[max_vif_index]
filtered_data = dataframe[remaining_columns]
bands = filtered_data.columns.tolist()
print("Bands:", bands)
return filtered_data, bands
filtered_pvals_df, bands = filter_variables_by_vif(pvals_df)
# Variable Selection Based on VIF
predictors = predictors.select(bands)
# Plot the correlation heatmap of variables
plot_correlation_heatmap(filtered_pvals_df, h_size=6, show_labels=True)
A continuación, visualizaremos las 6 variables predictoras seleccionadas en el mapa.
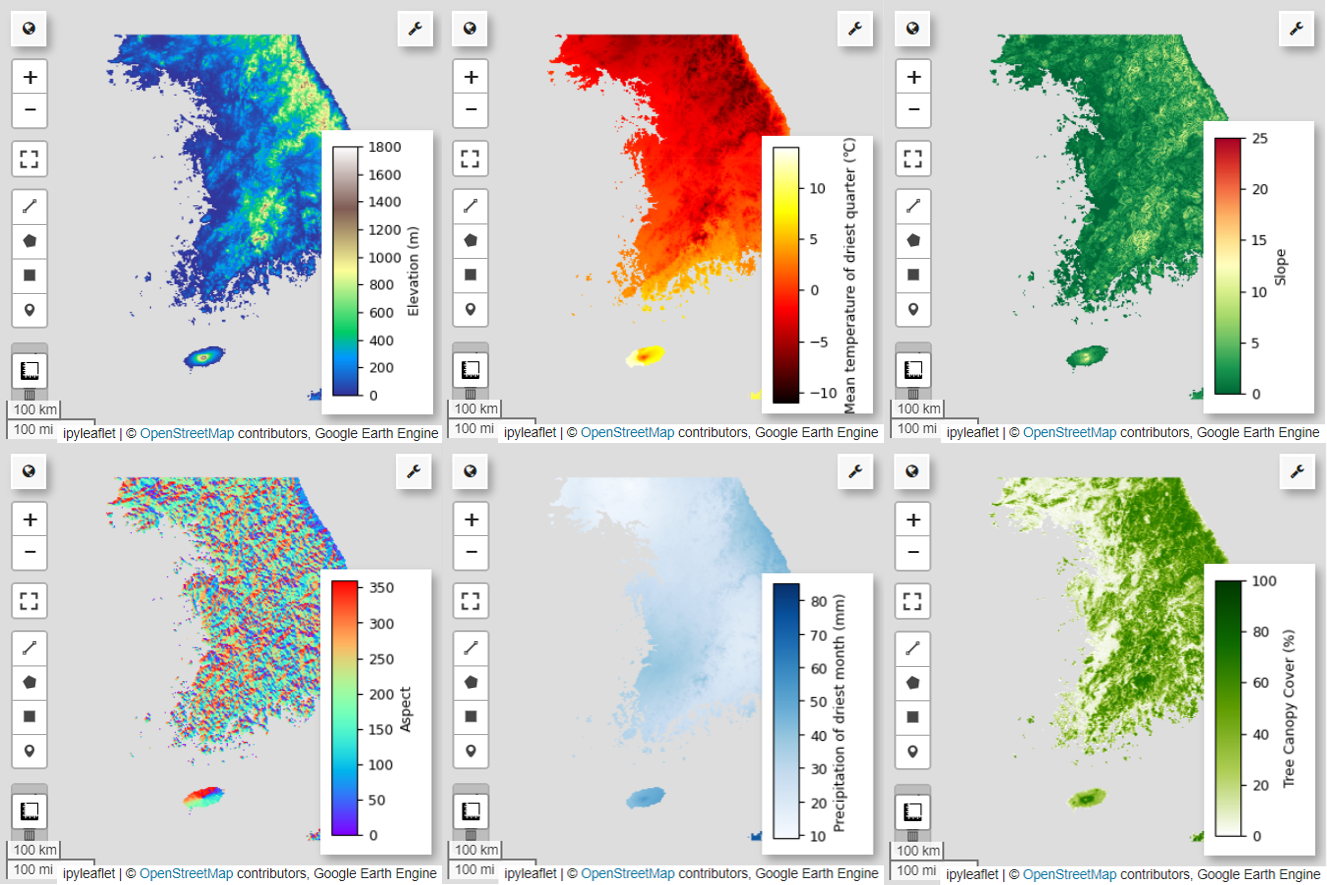
Puedes explorar las paletas disponibles para la visualización del mapa con el siguiente código. Por ejemplo, la paleta terrain se ve de la siguiente manera.
cm.plot_colormaps(width=8.0, height=0.2)
cm.plot_colormap('terrain', width=8.0, height=0.2, orientation='horizontal')
# Elevation layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['elevation'], 'min': 0, 'max': 1800, 'palette': cm.palettes.terrain}
Map.addLayer(predictors, vis_params, 'elevation')
Map.add_colorbar(vis_params, label="Elevation (m)", orientation="vertical", layer_name="elevation")
Map.centerObject(aoi, 6)
Map
# Calculate the minimum and maximum values for bio09
min_max_val = (
predictors.select("bio09")
.multiply(0.1)
.reduceRegion(reducer=ee.Reducer.minMax(), scale=1000)
.getInfo()
)
# bio09 (Mean temperature of driest quarter) layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"min": math.floor(min_max_val["bio09_min"]),
"max": math.ceil(min_max_val["bio09_max"]),
"palette": cm.palettes.hot,
}
Map.addLayer(predictors.select("bio09").multiply(0.1), vis_params, "bio09")
Map.add_colorbar(
vis_params,
label="Mean temperature of driest quarter (℃)",
orientation="vertical",
layer_name="bio09",
)
Map.centerObject(aoi, 6)
Map
# Slope layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['slope'], 'min': 0, 'max': 25, 'palette': cm.palettes.RdYlGn_r}
Map.addLayer(predictors, vis_params, 'slope')
Map.add_colorbar(vis_params, label="Slope", orientation="vertical", layer_name="slope")
Map.centerObject(aoi, 6)
Map
# Aspect layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['aspect'], 'min': 0, 'max': 360, 'palette': cm.palettes.rainbow}
Map.addLayer(predictors, vis_params, 'aspect')
Map.add_colorbar(vis_params, label="Aspect", orientation="vertical", layer_name="aspect")
Map.centerObject(aoi, 6)
Map
# Calculate the minimum and maximum values for bio14
min_max_val = (
predictors.select("bio14")
.reduceRegion(reducer=ee.Reducer.minMax(), scale=1000)
.getInfo()
)
# bio14 (Precipitation of driest month) layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"bands": ["bio14"],
"min": math.floor(min_max_val["bio14_min"]),
"max": math.ceil(min_max_val["bio14_max"]),
"palette": cm.palettes.Blues,
}
Map.addLayer(predictors, vis_params, "bio14")
Map.add_colorbar(
vis_params,
label="Precipitation of driest month (mm)",
orientation="vertical",
layer_name="bio14",
)
Map.centerObject(aoi, 6)
Map
# TCC layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"bands": ["TCC"],
"min": 0,
"max": 100,
"palette": ["ffffff", "afce56", "5f9c00", "0e6a00", "003800"],
}
Map.addLayer(predictors, vis_params, "TCC")
Map.add_colorbar(
vis_params, label="Tree Canopy Cover (%)", orientation="vertical", layer_name="TCC"
)
Map.centerObject(aoi, 6)
Map
Generación de datos de pseudoausencia
En el proceso de SDM, la selección de datos de entrada para una especie se aborda principalmente con dos métodos:
Método de presencia y ausencia: Este método compara las ubicaciones en las que se observó una especie en particular (presencia) con otras ubicaciones en las que no se observó la especie (ausencia). Aquí, los datos de fondo no necesariamente significan áreas donde no existe la especie, sino que se configuran para reflejar las condiciones ambientales generales del área de estudio. Se usa para distinguir los entornos adecuados en los que podría existir la especie de los menos adecuados.
Método de presencia-ausencia: Este método compara las ubicaciones en las que se observó la especie (presencia) con las ubicaciones en las que definitivamente no se observó (ausencia). Aquí, los datos de ausencia representan ubicaciones específicas en las que se sabe que no existe la especie. No refleja las condiciones ambientales generales del área de estudio, sino que indica las ubicaciones en las que se estima que no existe la especie.
En la práctica, suele ser difícil recopilar datos de ausencia reales, por lo que se suelen usar datos de pseudoausencia generados de forma artificial. Sin embargo, es importante reconocer las limitaciones y los posibles errores de este método, ya que los puntos de pseudoausencia generados artificialmente pueden no reflejar con precisión las verdaderas áreas de ausencia.
La elección entre estos dos métodos depende de la disponibilidad de los datos, los objetivos de la investigación, la precisión y confiabilidad del modelo, así como el tiempo y los recursos. Aquí, usaremos los datos de ocurrencia recopilados del GBIF y los datos de pseudoausencia generados artificialmente para modelar con el método "Presencia-Ausencia".
La generación de datos de pseudoausencia se realizará a través del "enfoque de generación de perfiles ambientales", y los pasos específicos son los siguientes:
Clasificación ambiental con agrupamiento en clústeres k-means: El algoritmo de agrupamiento en clústeres k-means, basado en la distancia euclidiana, se usará para dividir los píxeles dentro del área de estudio en dos clústeres. Un clúster representará las áreas con características ambientales similares a las 100 ubicaciones de presencia seleccionadas de forma aleatoria, mientras que el otro clúster representará las áreas con características diferentes.
Generación de datos de pseudoausencia en clústeres disímiles: En el segundo clúster identificado en el primer paso (que tiene características ambientales diferentes de los datos de presencia), se crearán puntos de pseudoausencia generados de forma aleatoria. Estos puntos de pseudoausencia representarán las ubicaciones en las que no se espera que exista la especie.
# Randomly select 100 locations for occurrence
pvals = predictors.sampleRegions(
collection=data.randomColumn().sort('random').limit(100),
properties=[],
scale=grain_size
)
# Perform k-means clustering
clusterer = ee.Clusterer.wekaKMeans(
nClusters=2,
distanceFunction="Euclidean"
).train(pvals)
cl_result = predictors.cluster(clusterer)
# Get cluster ID for locations similar to occurrence
cl_id = cl_result.sampleRegions(
collection=data.randomColumn().sort('random').limit(200),
properties=[],
scale=grain_size
)
# Define non-occurrence areas in dissimilar clusters
cl_id = ee.FeatureCollection(cl_id).reduceColumns(ee.Reducer.mode(),['cluster'])
cl_id = ee.Number(cl_id.get('mode')).subtract(1).abs()
cl_mask = cl_result.select(['cluster']).eq(cl_id)
# Presence location mask
presence_mask = data.reduceToImage(properties=['random'],
reducer=ee.Reducer.first()
).reproject('EPSG:4326', None,
grain_size).mask().neq(1).selfMask()
# Masking presence locations in non-occurrence areas and clipping to AOI
area_for_pa = presence_mask.updateMask(cl_mask).clip(aoi)
# Area for Pseudo-absence
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
Map.addLayer(area_for_pa, {'palette': 'black'}, 'AreaForPA')
Map.centerObject(aoi, 6)
Map
Ajuste y predicción del modelo
Ahora dividiremos los datos en datos de entrenamiento y datos de prueba. Los datos de entrenamiento se usarán para encontrar los parámetros óptimos entrenando el modelo, mientras que los datos de prueba se usarán para evaluar el modelo entrenado previamente. Un concepto importante que se debe tener en cuenta en este contexto es la autocorrelación espacial.
La autocorrelación espacial es un elemento esencial del SDM, asociado a la ley de Tobler. Incorpora el concepto de que "todo está relacionado con todo lo demás, pero las cosas cercanas están más relacionadas que las cosas distantes". La autocorrelación espacial representa la relación significativa entre la ubicación de las especies y las variables ambientales. Sin embargo, si existe autocorrelación espacial entre los datos de entrenamiento y los de prueba, se puede comprometer la independencia entre los dos conjuntos de datos. Esto afecta significativamente la evaluación de la capacidad de generalización del modelo.
Un método para abordar este problema es la técnica de validación cruzada de bloques espaciales, que implica dividir los datos en conjuntos de datos de entrenamiento y prueba. Esta técnica implica dividir los datos en varios bloques y usar cada bloque de forma independiente como conjuntos de datos de entrenamiento y prueba para reducir el impacto de la autocorrelación espacial. Esto mejora la independencia entre los conjuntos de datos, lo que permite una evaluación más precisa de la capacidad de generalización del modelo.
El procedimiento específico es el siguiente:
- Creación de bloques espaciales: Divide todo el conjunto de datos en bloques espaciales de igual tamaño (p.ej., 50 km x 50 km).
- Asignación de conjuntos de entrenamiento y prueba: Cada bloque espacial se asigna de forma aleatoria al conjunto de entrenamiento (70%) o al conjunto de prueba (30%). Esto evita que el modelo se sobreajuste a los datos de áreas específicas y tiene como objetivo lograr resultados más generalizados.
- Validación cruzada iterativa: Todo el proceso se repite n veces (p.ej., 10 veces). En cada iteración, los bloques se dividen de forma aleatoria en conjuntos de entrenamiento y prueba nuevamente, lo que tiene como objetivo mejorar la estabilidad y confiabilidad del modelo.
- Generación de datos de pseudoausencia: En cada iteración, se generan datos de pseudoausencia de forma aleatoria para evaluar el rendimiento del modelo.
Scale = 50000
grid = watermask.reduceRegions(
collection=aoi.coveringGrid(scale=Scale, proj='EPSG:4326'),
reducer=ee.Reducer.mean()).filter(ee.Filter.neq('mean', None))
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
Map.addLayer(grid, {}, "Grid for spatial block cross validation")
Map.addLayer(outline, {'palette': 'FF0000'}, "Study Area")
Map.centerObject(aoi, 6)
Map
Ahora podemos ajustar el modelo. Ajustar un modelo implica comprender los patrones en los datos y ajustar los parámetros del modelo (pesos y sesgos) según corresponda. Este proceso permite que el modelo realice predicciones más precisas cuando se le presentan datos nuevos. Para ello, definimos una función llamada SDM() para ajustar el modelo.
Usaremos el algoritmo de bosque aleatorio.
def sdm(x):
seed = ee.Number(x)
# Random block division for training and validation
rand_blk = ee.FeatureCollection(grid).randomColumn(seed=seed).sort("random")
training_grid = rand_blk.filter(ee.Filter.lt("random", split)) # Grid for training
testing_grid = rand_blk.filter(ee.Filter.gte("random", split)) # Grid for testing
# Presence points
presence_points = ee.FeatureCollection(data)
presence_points = presence_points.map(lambda feature: feature.set("PresAbs", 1))
tr_presence_points = presence_points.filter(
ee.Filter.bounds(training_grid)
) # Presence points for training
te_presence_points = presence_points.filter(
ee.Filter.bounds(testing_grid)
) # Presence points for testing
# Pseudo-absence points for training
tr_pseudo_abs_points = area_for_pa.sample(
region=training_grid,
scale=grain_size,
numPixels=tr_presence_points.size().add(300),
seed=seed,
geometries=True,
)
# Same number of pseudo-absence points as presence points for training
tr_pseudo_abs_points = (
tr_pseudo_abs_points.randomColumn()
.sort("random")
.limit(ee.Number(tr_presence_points.size()))
)
tr_pseudo_abs_points = tr_pseudo_abs_points.map(lambda feature: feature.set("PresAbs", 0))
te_pseudo_abs_points = area_for_pa.sample(
region=testing_grid,
scale=grain_size,
numPixels=te_presence_points.size().add(100),
seed=seed,
geometries=True,
)
# Same number of pseudo-absence points as presence points for testing
te_pseudo_abs_points = (
te_pseudo_abs_points.randomColumn()
.sort("random")
.limit(ee.Number(te_presence_points.size()))
)
te_pseudo_abs_points = te_pseudo_abs_points.map(lambda feature: feature.set("PresAbs", 0))
# Merge training and pseudo-absence points
training_partition = tr_presence_points.merge(tr_pseudo_abs_points)
testing_partition = te_presence_points.merge(te_pseudo_abs_points)
# Extract predictor variable values at training points
train_pvals = predictors.sampleRegions(
collection=training_partition,
properties=["PresAbs"],
scale=grain_size,
geometries=True,
)
# Random Forest classifier
classifier = ee.Classifier.smileRandomForest(
numberOfTrees=500,
variablesPerSplit=None,
minLeafPopulation=10,
bagFraction=0.5,
maxNodes=None,
seed=seed,
)
# Presence probability: Habitat suitability map
classifier_pr = classifier.setOutputMode("PROBABILITY").train(
train_pvals, "PresAbs", bands
)
classified_img_pr = predictors.select(bands).classify(classifier_pr)
# Binary presence/absence map: Potential distribution map
classifier_bin = classifier.setOutputMode("CLASSIFICATION").train(
train_pvals, "PresAbs", bands
)
classified_img_bin = predictors.select(bands).classify(classifier_bin)
return [
classified_img_pr,
classified_img_bin,
training_partition,
testing_partition,
], classifier_pr
Los bloques espaciales se dividen en un 70% para el entrenamiento del modelo y un 30% para la prueba del modelo, respectivamente. Los datos de pseudoausencia se generan de forma aleatoria dentro de cada conjunto de entrenamiento y prueba en cada iteración. Como resultado, cada ejecución genera diferentes conjuntos de datos de presencia y pseudoausencia para el entrenamiento y la prueba del modelo.
split = 0.7
numiter = 10
# Random Seed
runif = lambda length: [random.randint(1, 1000) for _ in range(length)]
items = runif(numiter)
# Fixed seed
# items = [287, 288, 553, 226, 151, 255, 902, 267, 419, 538]
results_list = [] # Initialize SDM results list
importances_list = [] # Initialize variable importance list
for item in items:
result, trained = sdm(item)
# Accumulate SDM results into the list
results_list.extend(result)
# Accumulate variable importance into the list
importance = ee.Dictionary(trained.explain()).get('importance')
importances_list.extend(importance.getInfo().items())
# Flatten the SDM results list
results = ee.List(results_list).flatten()
Ahora podemos visualizar el mapa de idoneidad del hábitat y el mapa de distribución potencial de la pitta hada. En este caso, el mapa de idoneidad del hábitat se crea con la función mean() para calcular el promedio de cada ubicación de píxel en todas las imágenes, y el mapa de distribución potencial se genera con la función mode() para determinar el valor que se repite con mayor frecuencia en cada ubicación de píxel en todas las imágenes.
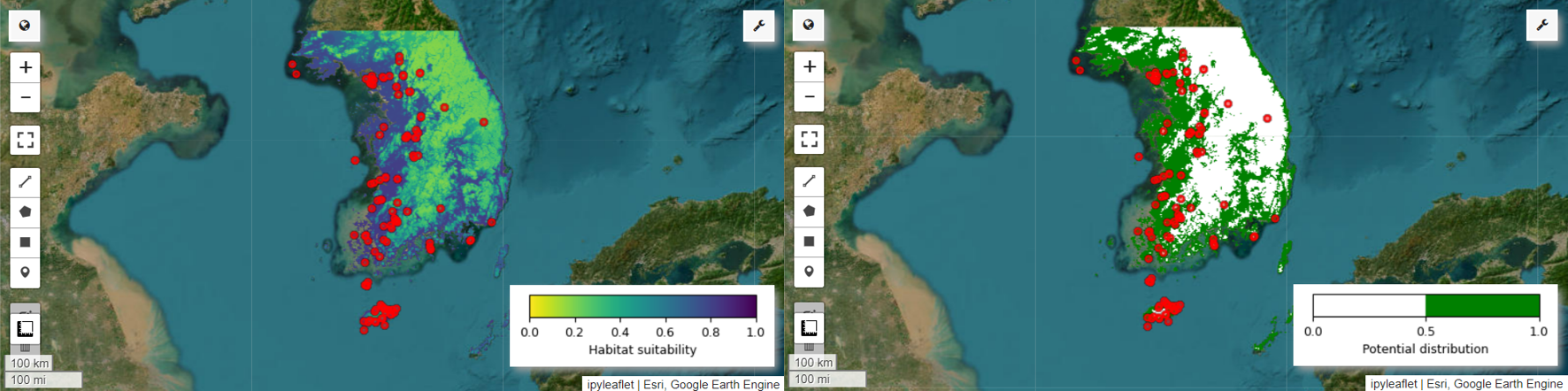
# Habitat suitability map
images = ee.List.sequence(
0, ee.Number(numiter).multiply(4).subtract(1), 4).map(
lambda x: results.get(x))
model_average = ee.ImageCollection.fromImages(images).mean()
Map = geemap.Map(layout={'height':'400px', 'width':'800px'}, basemap='Esri.WorldImagery')
vis_params = {
'min': 0,
'max': 1,
'palette': cm.palettes.viridis_r}
Map.addLayer(model_average, vis_params, 'Habitat suitability')
Map.add_colorbar(vis_params, label="Habitat suitability",
orientation="horizontal",
layer_name="Habitat suitability")
Map.addLayer(data, {'color':'red'}, 'Presence')
Map.centerObject(aoi, 6)
Map
# Potential distribution map
images2 = ee.List.sequence(1, ee.Number(numiter).multiply(4).subtract(1), 4).map(
lambda x: results.get(x)
)
distribution_map = ee.ImageCollection.fromImages(images2).mode()
Map = geemap.Map(
layout={"height": "400px", "width": "800px"}, basemap="Esri.WorldImagery"
)
vis_params = {"min": 0, "max": 1, "palette": ["white", "green"]}
Map.addLayer(distribution_map, vis_params, "Potential distribution")
Map.addLayer(data, {"color": "red"}, "Presence")
Map.add_colorbar(
vis_params,
label="Potential distribution",
discrete=True,
orientation="horizontal",
layer_name="Potential distribution",
)
Map.centerObject(data.geometry(), 6)
Map
Evaluación de la importancia y la precisión de las variables
El bosque aleatorio (ee.Classifier.smileRandomForest) es uno de los métodos de aprendizaje por ensamble, que funciona construyendo varios árboles de decisión para realizar predicciones. Cada árbol de decisión aprende de forma independiente de diferentes subconjuntos de los datos, y sus resultados se agregan para permitir predicciones más precisas y estables.
La importancia de las variables es una medida que evalúa el impacto de cada variable en las predicciones dentro del modelo de bosque aleatorio. Usaremos la variable importances_list definida anteriormente para calcular e imprimir la importancia promedio de la variable.
def plot_variable_importance(importances_list):
# Extract each variable importance value into a list
variables = [item[0] for item in importances_list]
importances = [item[1] for item in importances_list]
# Calculate the average importance for each variable
average_importances = {}
for variable in set(variables):
indices = [i for i, var in enumerate(variables) if var == variable]
average_importance = np.mean([importances[i] for i in indices])
average_importances[variable] = average_importance
# Sort the importances in descending order of importance
sorted_importances = sorted(average_importances.items(),
key=lambda x: x[1], reverse=False)
variables = [item[0] for item in sorted_importances]
avg_importances = [item[1] for item in sorted_importances]
# Adjust the graph size
plt.figure(figsize=(8, 4))
# Plot the average importance as a horizontal bar chart
plt.barh(variables, avg_importances)
plt.xlabel('Importance')
plt.ylabel('Variables')
plt.title('Average Variable Importance')
# Display values above the bars
for i, v in enumerate(avg_importances):
plt.text(v + 0.02, i, f"{v:.2f}", va='center')
# Adjust the x-axis range
plt.xlim(0, max(avg_importances) + 5) # Adjust to the desired range
plt.tight_layout()
plt.savefig('variable_importance.png')
plt.show()
plot_variable_importance(importances_list)
Con los conjuntos de datos de prueba, calculamos el AUC-ROC y el AUC-PR para cada ejecución. Luego, calculamos el promedio del AUC-ROC y el AUC-PR en n iteraciones.
El AUC-ROC representa el área bajo la curva del gráfico "Sensibilidad (recuperación) vs. 1-Especificidad", que ilustra la relación entre la sensibilidad y la especificidad a medida que cambia el umbral. La especificidad se basa en todos los no sucesos observados. Por lo tanto, el AUC-ROC abarca todos los cuadrantes de la matriz de confusión.
El AUC-PR representa el área bajo la curva del gráfico "Precisión vs. Recuperación (sensibilidad)", que muestra la relación entre la precisión y la recuperación a medida que varía el umbral. La precisión se basa en todas las ocurrencias predichas. Por lo tanto, el AUC-PR no incluye los negativos verdaderos (TN).
def print_pres_abs_sizes(TestingDatasets, numiter):
# Check and print the sizes of presence and pseudo-absence coordinates
def get_pres_abs_size(x):
fc = ee.FeatureCollection(TestingDatasets.get(x))
presence_size = fc.filter(ee.Filter.eq("PresAbs", 1)).size()
pseudo_absence_size = fc.filter(ee.Filter.eq("PresAbs", 0)).size()
return ee.List([presence_size, pseudo_absence_size])
sizes_info = (
ee.List.sequence(0, ee.Number(numiter).subtract(1), 1)
.map(get_pres_abs_size)
.getInfo()
)
for i, sizes in enumerate(sizes_info):
presence_size = sizes[0]
pseudo_absence_size = sizes[1]
print(
f"Iteration {i + 1}: Presence Size = {presence_size}, Pseudo-absence Size = {pseudo_absence_size}"
)
# Extracting the Testing Datasets
testing_datasets = ee.List.sequence(
3, ee.Number(numiter).multiply(4).subtract(1), 4
).map(lambda x: results.get(x))
print_pres_abs_sizes(testing_datasets, numiter)
def get_acc(hsm, t_data, grain_size):
pr_prob_vals = hsm.sampleRegions(
collection=t_data, properties=["PresAbs"], scale=grain_size
)
seq = ee.List.sequence(start=0, end=1, count=25) # Divide 0 to 1 into 25 intervals
def calculate_metrics(cutoff):
# Each element of the seq list is passed as cutoff(threshold value)
# Observed present = TP + FN
pres = pr_prob_vals.filterMetadata("PresAbs", "equals", 1)
# TP (True Positive)
tp = ee.Number(
pres.filterMetadata("classification", "greater_than", cutoff).size()
)
# TPR (True Positive Rate) = Recall = Sensitivity = TP / (TP + FN) = TP / Observed present
tpr = tp.divide(pres.size())
# Observed absent = FP + TN
abs = pr_prob_vals.filterMetadata("PresAbs", "equals", 0)
# FN (False Negative)
fn = ee.Number(
pres.filterMetadata("classification", "less_than", cutoff).size()
)
# TNR (True Negative Rate) = Specificity = TN / (FP + TN) = TN / Observed absent
tn = ee.Number(abs.filterMetadata("classification", "less_than", cutoff).size())
tnr = tn.divide(abs.size())
# FP (False Positive)
fp = ee.Number(
abs.filterMetadata("classification", "greater_than", cutoff).size()
)
# FPR (False Positive Rate) = FP / (FP + TN) = FP / Observed absent
fpr = fp.divide(abs.size())
# Precision = TP / (TP + FP) = TP / Predicted present
precision = tp.divide(tp.add(fp))
# SUMSS = SUM of Sensitivity and Specificity
sumss = tpr.add(tnr)
return ee.Feature(
None,
{
"cutoff": cutoff,
"TP": tp,
"TN": tn,
"FP": fp,
"FN": fn,
"TPR": tpr,
"TNR": tnr,
"FPR": fpr,
"Precision": precision,
"SUMSS": sumss,
},
)
return ee.FeatureCollection(seq.map(calculate_metrics))
def calculate_and_print_auc_metrics(images, testing_datasets, grain_size, numiter):
# Calculate AUC-ROC and AUC-PR
def calculate_auc_metrics(x):
hsm = ee.Image(images.get(x))
t_data = ee.FeatureCollection(testing_datasets.get(x))
acc = get_acc(hsm, t_data, grain_size)
# Calculate AUC-ROC
x = ee.Array(acc.aggregate_array("FPR"))
y = ee.Array(acc.aggregate_array("TPR"))
x1 = x.slice(0, 1).subtract(x.slice(0, 0, -1))
y1 = y.slice(0, 1).add(y.slice(0, 0, -1))
auc_roc = x1.multiply(y1).multiply(0.5).reduce("sum", [0]).abs().toList().get(0)
# Calculate AUC-PR
x = ee.Array(acc.aggregate_array("TPR"))
y = ee.Array(acc.aggregate_array("Precision"))
x1 = x.slice(0, 1).subtract(x.slice(0, 0, -1))
y1 = y.slice(0, 1).add(y.slice(0, 0, -1))
auc_pr = x1.multiply(y1).multiply(0.5).reduce("sum", [0]).abs().toList().get(0)
return (auc_roc, auc_pr)
auc_metrics = (
ee.List.sequence(0, ee.Number(numiter).subtract(1), 1)
.map(calculate_auc_metrics)
.getInfo()
)
# Print AUC-ROC and AUC-PR for each iteration
df = pd.DataFrame(auc_metrics, columns=["AUC-ROC", "AUC-PR"])
df.index = [f"Iteration {i + 1}" for i in range(len(df))]
df.to_csv("auc_metrics.csv", index_label="Iteration")
print(df)
# Calculate mean and standard deviation of AUC-ROC and AUC-PR
mean_auc_roc, std_auc_roc = df["AUC-ROC"].mean(), df["AUC-ROC"].std()
mean_auc_pr, std_auc_pr = df["AUC-PR"].mean(), df["AUC-PR"].std()
print(f"Mean AUC-ROC = {mean_auc_roc:.4f} ± {std_auc_roc:.4f}")
print(f"Mean AUC-PR = {mean_auc_pr:.4f} ± {std_auc_pr:.4f}")
%%time
# Calculate AUC-ROC and AUC-PR
calculate_and_print_auc_metrics(images, testing_datasets, grain_size, numiter)
En este instructivo, se proporcionó un ejemplo práctico del uso de Google Earth Engine (GEE) para el modelado de la distribución de especies (SDM). Una conclusión importante es la versatilidad y la flexibilidad de GEE en el campo del SDM. Aprovechar las potentes capacidades de procesamiento de datos geoespaciales de Earth Engine abre un sinfín de posibilidades para que los investigadores y los conservacionistas comprendan y preserven la biodiversidad de nuestro planeta. Si aplican los conocimientos y las habilidades que adquirieron en este instructivo, las personas pueden explorar este fascinante campo de la investigación ecológica y contribuir a él.
 Ejecutar en Google Colab
Ejecutar en Google Colab
 Ver código fuente en GitHub
Ver código fuente en GitHub