TensorFlow, Keras e aprendizado profundo, sem um doutorado

Neste codelab, você vai aprender a criar e treinar uma rede neural que reconhece dígitos escritos à mão. Ao longo do caminho, enquanto você aprimora sua rede neural para atingir 99% de acurácia, também vai descobrir as ferramentas que os profissionais de aprendizado profundo usam para treinar os modelos com eficiência.

Este codelab usa o conjunto de dados MNIST, uma coleção de 60.000 dígitos rotulados que mantiveram gerações de doutores ocupados por quase duas décadas. Você vai resolver o problema com menos de 100 linhas de código Python / TensorFlow.

O que você vai aprender

• O que é uma rede neural e como treiná-la
• Como criar uma rede neural básica de uma camada usando o tf.keras
• Como adicionar mais camadas
• Como configurar uma programação de taxa de aprendizado
• Como criar redes neurais convolucionais
• Como usar técnicas de regularização: eliminação, normalização de lotes
• O que é overfitting

O que é necessário

Apenas um navegador. Este workshop pode ser realizado totalmente com o Google Colaboratory.

Feedback

Informe se você notar algo errado neste laboratório ou se achar que ele precisa ser melhorado. Tratamos o feedback por problemas do GitHub [link de feedback].

Este laboratório usa o Google Colaboratory e não exige configuração da sua parte. É possível executar em um Chromebook. Abra o arquivo abaixo e execute as células para se familiarizar com os notebooks do Colab.

Welcome to Colab.ipynb

Confira outras instruções abaixo:

Selecionar um back-end de GPU

No menu do Colab, selecione Ambiente de execução > Alterar o tipo de ambiente de execução e escolha GPU. A conexão com o ambiente de execução acontece automaticamente na primeira execução, ou você pode usar o botão "Conectar" no canto superior direito.

Execução do notebook

Execute as células uma por vez clicando em uma delas e usando Shift + ENTER. Você também pode executar o notebook inteiro com Ambiente de execução > Executar tudo.

Índice

Todos os notebooks têm um sumário. É possível abrir usando a seta preta à esquerda.

Células ocultas

Algumas células vão mostrar apenas o título. Esse é um recurso específico do notebook do Colab. Clique duas vezes neles para ver o código, mas geralmente não é muito interessante. Normalmente, funções de suporte ou visualização. Ainda é necessário executar essas células para que as funções sejam definidas.

Primeiro, vamos assistir ao treinamento de uma rede neural. Abra o notebook abaixo e execute todas as células. Não preste atenção ao código ainda. Vamos começar a explicar isso mais tarde.

keras_01_mnist.ipynb

Ao executar o notebook, concentre-se nas visualizações. Confira as explicações abaixo.

Dados de treinamento

Temos um conjunto de dados de dígitos escritos à mão que foram rotulados para que saibamos o que cada imagem representa, ou seja, um número entre 0 e 9. No notebook, você vai encontrar um trecho:

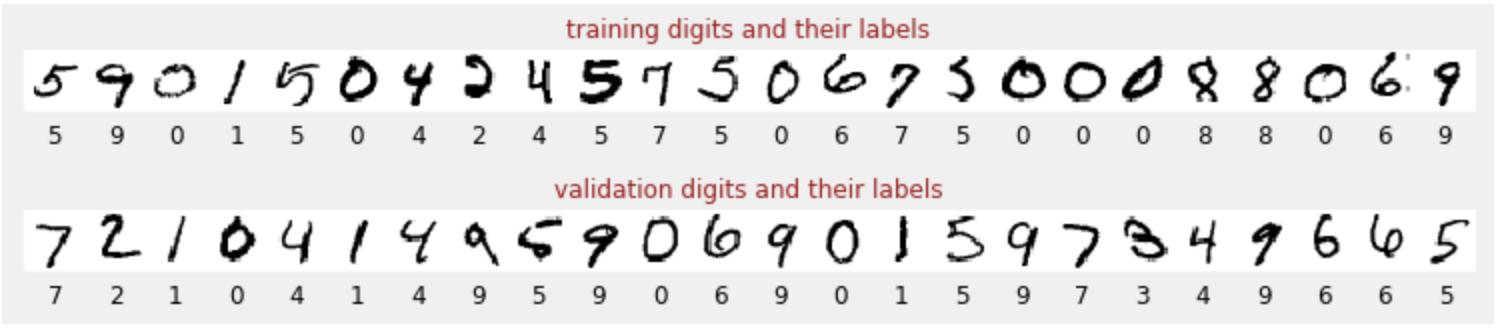
A rede neural que vamos criar classifica os dígitos manuscritos em 10 classes (0, ..., 9). Isso é feito com base em parâmetros internos que precisam ter um valor correto para que a classificação funcione bem. Esse "valor correto" é aprendido por um processo de treinamento que exige um "conjunto de dados rotulado" com imagens e as respostas corretas associadas.

Como saber se a rede neural treinada tem um bom desempenho? Usar o conjunto de dados de treinamento para testar a rede seria trapaça. Ele já viu esse conjunto de dados várias vezes durante o treinamento e certamente tem um desempenho muito bom nele. Precisamos de outro conjunto de dados rotulado, nunca visto durante o treinamento, para avaliar o desempenho "real" da rede. Ele é chamado de conjunto de dados de validação.

Há 50.000 dígitos de treinamento nesse conjunto de dados. A cada iteração, alimentamos um lote de tamanho 128 no loop de treinamento. Assim, o sistema terá visto todos os dígitos de treinamento uma vez após 391 iterações. Chamamos isso de "época".

Há também 10.000 dígitos de validação separados para testar o desempenho do modelo.

Treinamento

À medida que o treinamento avança, um lote de dados de treinamento por vez, os parâmetros internos do modelo são atualizados, e o modelo fica cada vez melhor em reconhecer os dígitos manuscritos. Confira no gráfico de treinamento:

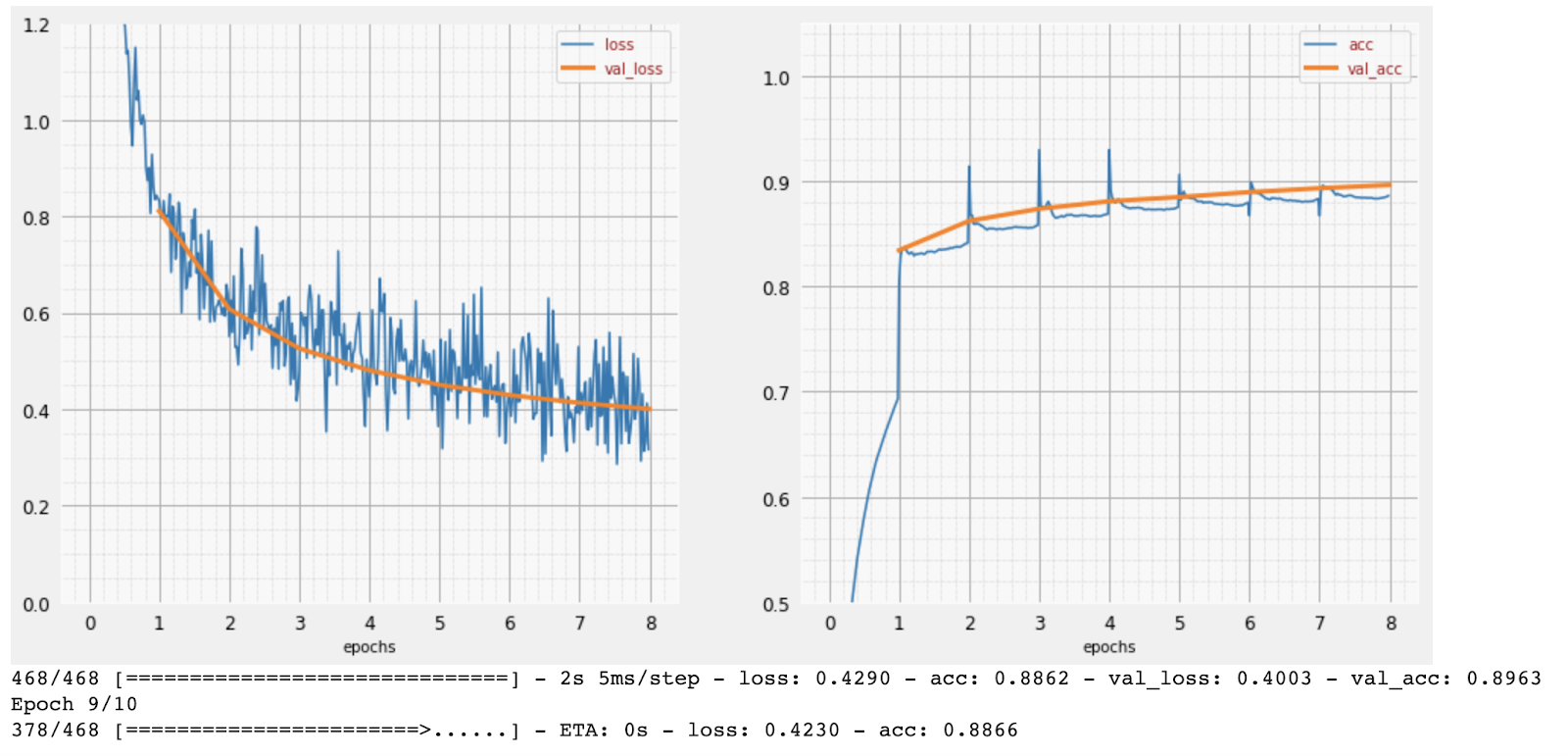
À direita, a "acurácia" é simplesmente a porcentagem de dígitos reconhecidos corretamente. Ele aumenta conforme o treinamento avança, o que é bom.

À esquerda, podemos ver a perda. Para impulsionar o treinamento, vamos definir uma função de "perda", que representa o quão mal o sistema reconhece os dígitos, e tentar minimizar essa função. O que você vê aqui é que a perda diminui nos dados de treinamento e de validação à medida que o treinamento avança. Isso é bom. Isso significa que a rede neural está aprendendo.

O eixo X representa o número de "épocas" ou iterações em todo o conjunto de dados.

Previsões

Quando o modelo é treinado, podemos usá-lo para reconhecer dígitos escritos à mão. A próxima visualização mostra o desempenho em alguns dígitos renderizados de fontes locais (primeira linha) e nos 10.000 dígitos do conjunto de dados de validação. A classe prevista aparece abaixo de cada dígito, em vermelho se estiver errada.

Como você pode ver, esse modelo inicial não é muito bom, mas ainda reconhece alguns dígitos corretamente. A acurácia final da validação é de cerca de 90%, o que não é tão ruim para o modelo simplista com que estamos começando,mas ainda significa que ele perde 1.000 dígitos de validação dos 10.000. Isso é muito mais do que pode ser mostrado, por isso parece que todas as respostas estão erradas (vermelho).

Tensores

Os dados são armazenados em matrizes. Uma imagem em escala de cinza de 28 x 28 pixels se encaixa em uma matriz bidimensional de 28 x 28. Mas, para uma imagem colorida, precisamos de mais dimensões. Há três valores de cor por pixel (vermelho, verde e azul). Portanto, uma tabela tridimensional será necessária com dimensões [28, 28, 3]. Para armazenar um lote de 128 imagens coloridas, é necessária uma tabela quadridimensional com dimensões [128, 28, 28, 3].

Essas tabelas multidimensionais são chamadas de tensores, e a lista das dimensões é a forma.

Em resumo

Se você já conhece todos os termos em negrito no próximo parágrafo, passe para o próximo exercício. Se você está começando no aprendizado profundo, seja bem-vindo e continue lendo.

Um classificador de rede neural é composto por várias camadas de neurônios. Para classificação de imagens, elas podem ser camadas densas ou, mais frequentemente, convolucionais. Elas geralmente são ativadas com a função de ativação relu. A última camada usa tantos neurônios quanto há classes e é ativada com softmax. Para classificação, a entropia cruzada é a função de perda mais usada, comparando os rótulos codificados one-hot (ou seja, respostas corretas) com as probabilidades previstas pela rede neural. Para minimizar a perda, é melhor escolher um otimizador com momentum, como o Adam, e treinar em batches de imagens e rótulos de treinamento.

Para modelos criados como uma sequência de camadas, o Keras oferece a API Sequential. Por exemplo, um classificador de imagens usando três camadas densas pode ser escrito em Keras da seguinte maneira:

model = tf.keras.Sequential([
    tf.keras.layers.Flatten(input_shape=[28, 28, 1]),
    tf.keras.layers.Dense(200, activation="relu"),
    tf.keras.layers.Dense(60, activation="relu"),
    tf.keras.layers.Dense(10, activation='softmax') # classifying into 10 classes
])

# this configures the training of the model. Keras calls it "compiling" the model.
model.compile(
  optimizer='adam',
  loss= 'categorical_crossentropy',
  metrics=['accuracy']) # % of correct answers

# train the model
model.fit(dataset, ... )

Uma única camada densa

Os dígitos manuscritos no conjunto de dados MNIST são imagens em escala de cinza de 28 x 28 pixels. A abordagem mais simples para classificá-los é usar os 28x28=784 pixels como entradas para uma rede neural de uma camada.

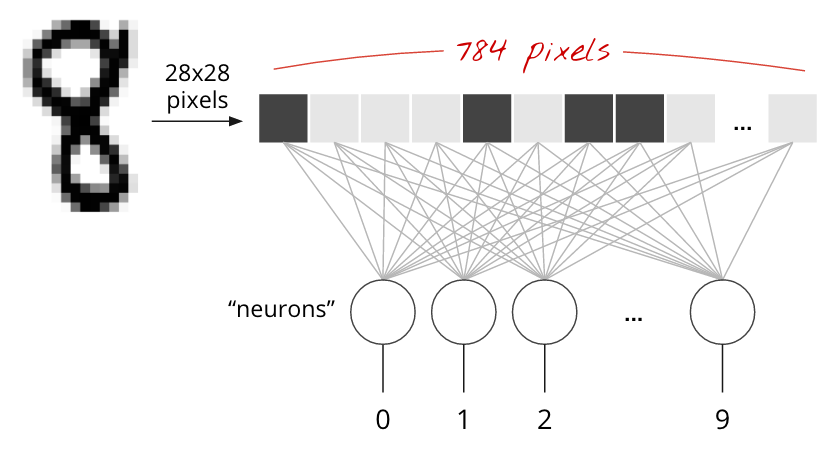
Cada "neurônio" em uma rede neural faz uma soma ponderada de todas as entradas, adiciona uma constante chamada "tendência" e transmite o resultado por uma "função de ativação" não linear. Os pesos e os vieses são parâmetros que serão determinados pelo treinamento. Elas são inicializadas com valores aleatórios no início.

A imagem acima representa uma rede neural de uma camada com 10 neurônios de saída, já que queremos classificar dígitos em 10 classes (0 a 9).

Com uma multiplicação de matrizes

Veja como uma camada de rede neural, que processa uma coleção de imagens, pode ser representada por uma multiplicação de matrizes:

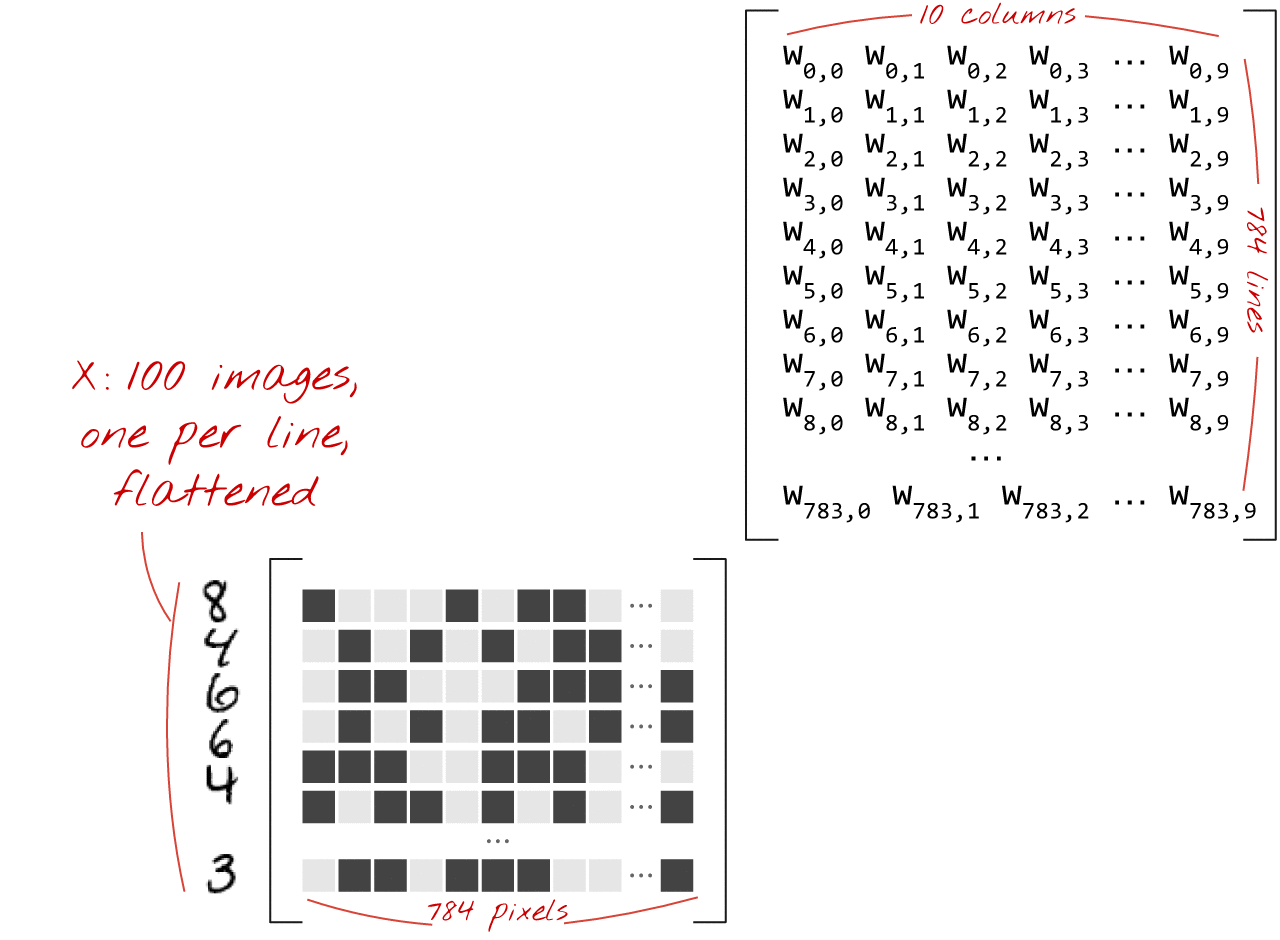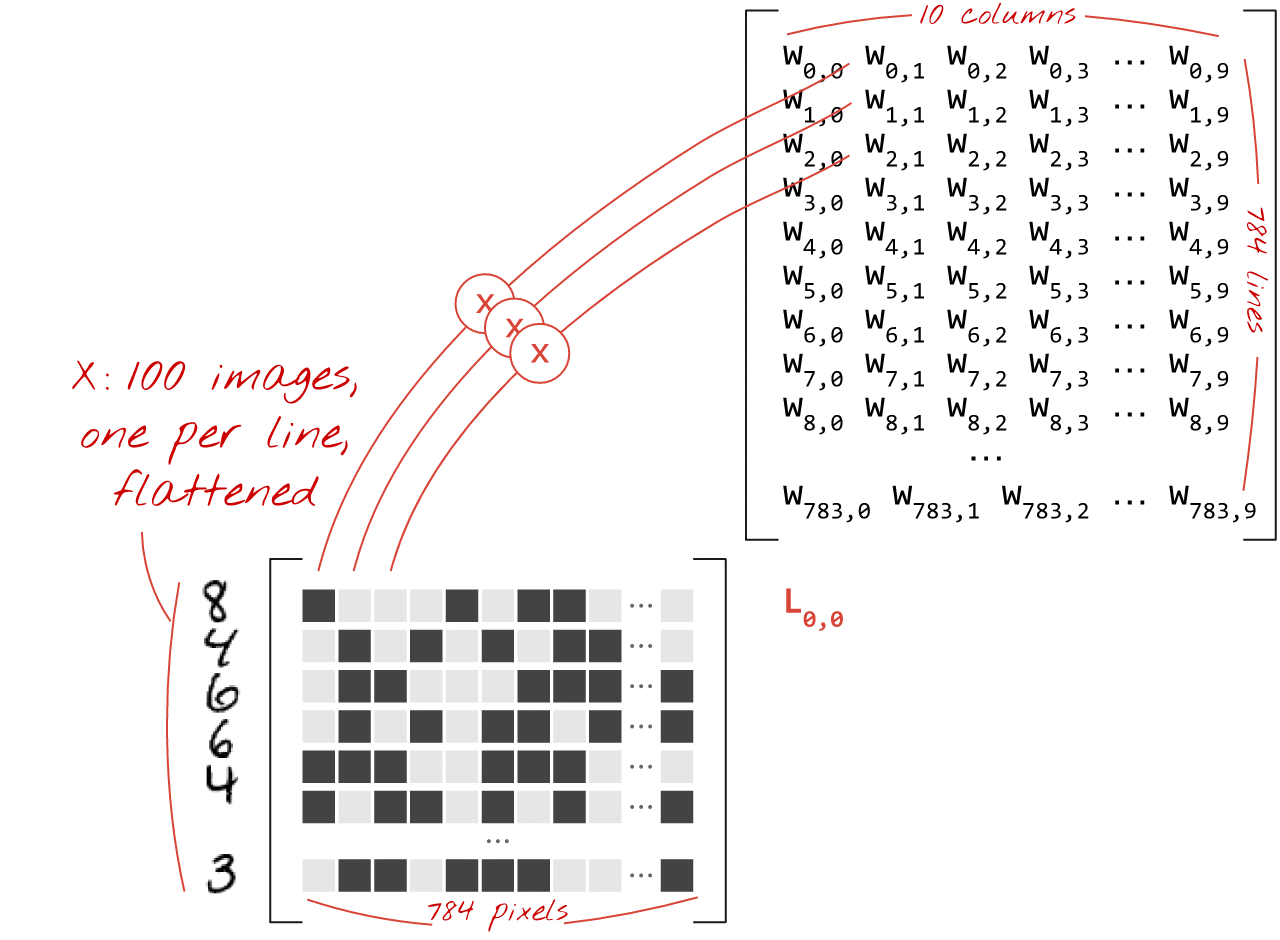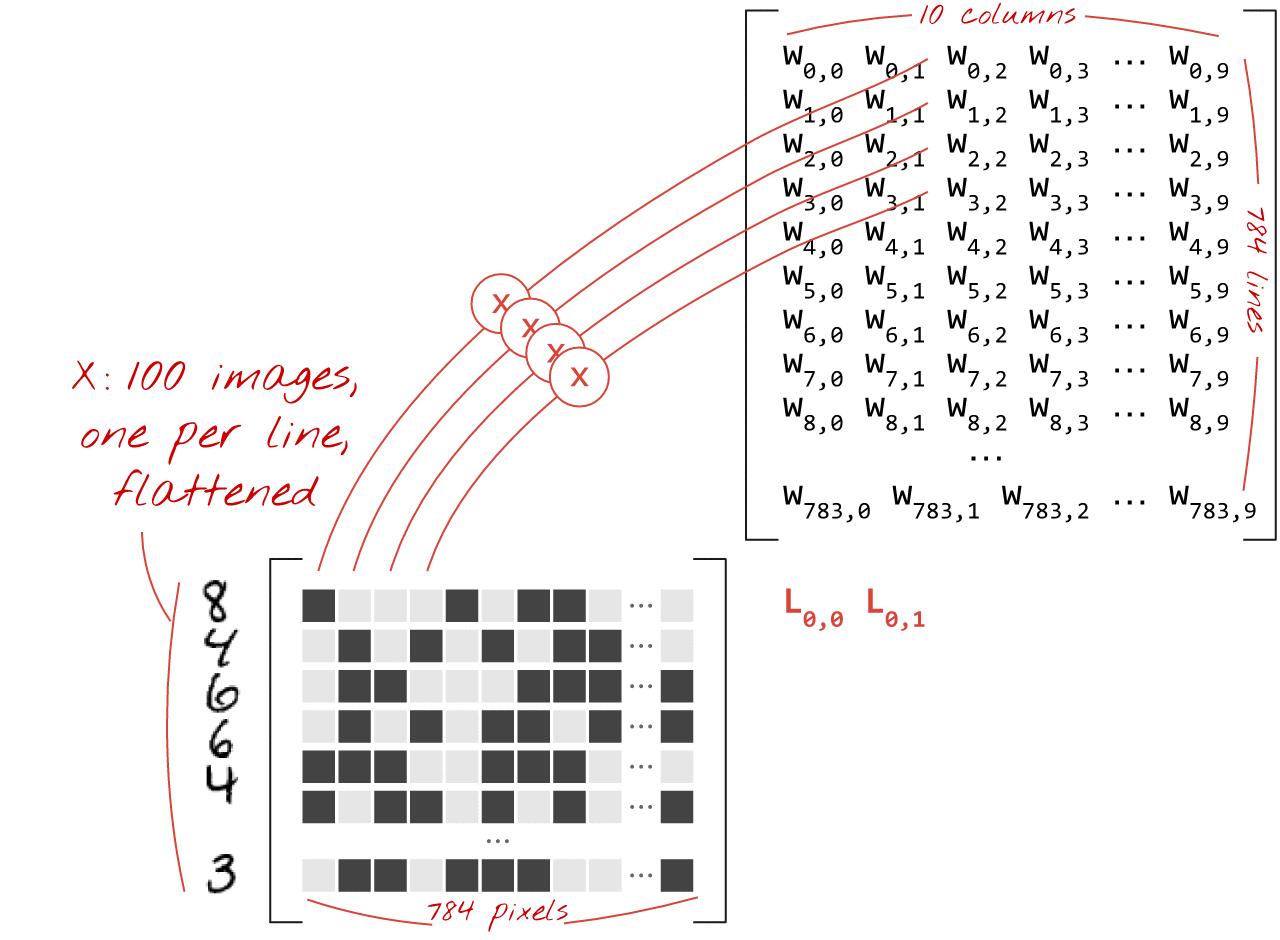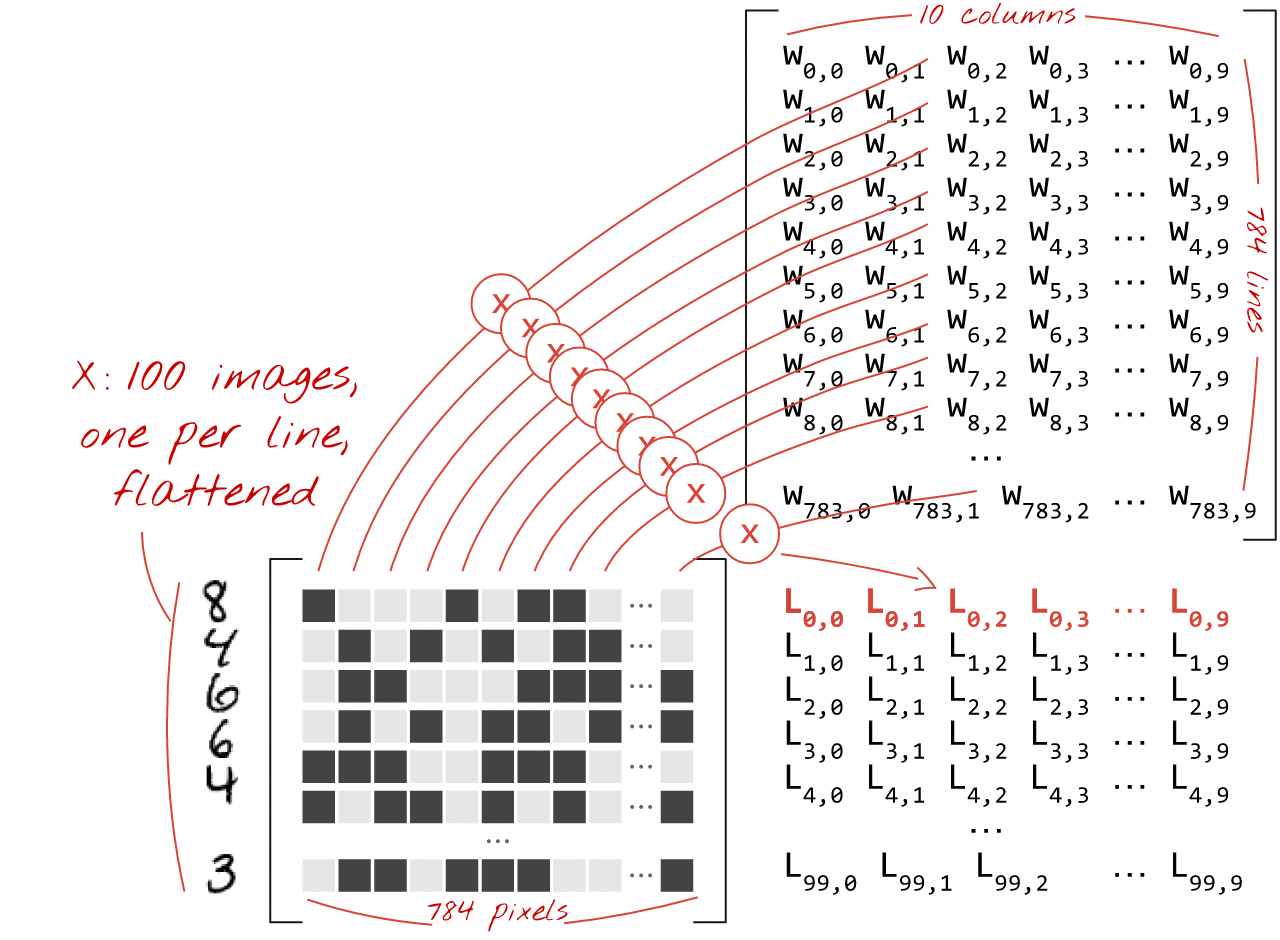
Usando a primeira coluna de pesos na matriz W, calculamos a soma ponderada de todos os pixels da primeira imagem. Essa soma corresponde ao primeiro neurônio. Usando a segunda coluna de pesos, fazemos o mesmo para o segundo neurônio e assim por diante até o 10º neurônio. Em seguida, podemos repetir a operação para as 99 imagens restantes. Se chamarmos X a matriz que contém nossas 100 imagens, todas as somas ponderadas dos nossos 10 neurônios, calculadas em 100 imagens, serão simplesmente X.W, uma multiplicação de matrizes.

Cada neurônio agora precisa adicionar o próprio viés (uma constante). Como temos 10 neurônios, temos 10 constantes de viés. Vamos chamar esse vetor de 10 valores de b. Ele precisa ser adicionado a cada linha da matriz calculada anteriormente. Usando um pouco de mágica chamada "transmissão", vamos escrever isso com um sinal de adição simples.

Transmissão é um truque padrão usado em Python e numpy, a biblioteca de computação científica. Ele estende o funcionamento das operações normais em matrizes com dimensões incompatíveis. "Transmissão de adição" significa: "se você estiver adicionando duas matrizes, mas não puder porque as dimensões delas não são compatíveis, tente replicar a pequena o quanto for necessário para que funcione".

Por fim, aplicamos uma função de ativação, por exemplo, "softmax" (explicada abaixo) e obtemos a fórmula que descreve uma rede neural de uma camada, aplicada a 100 imagens:

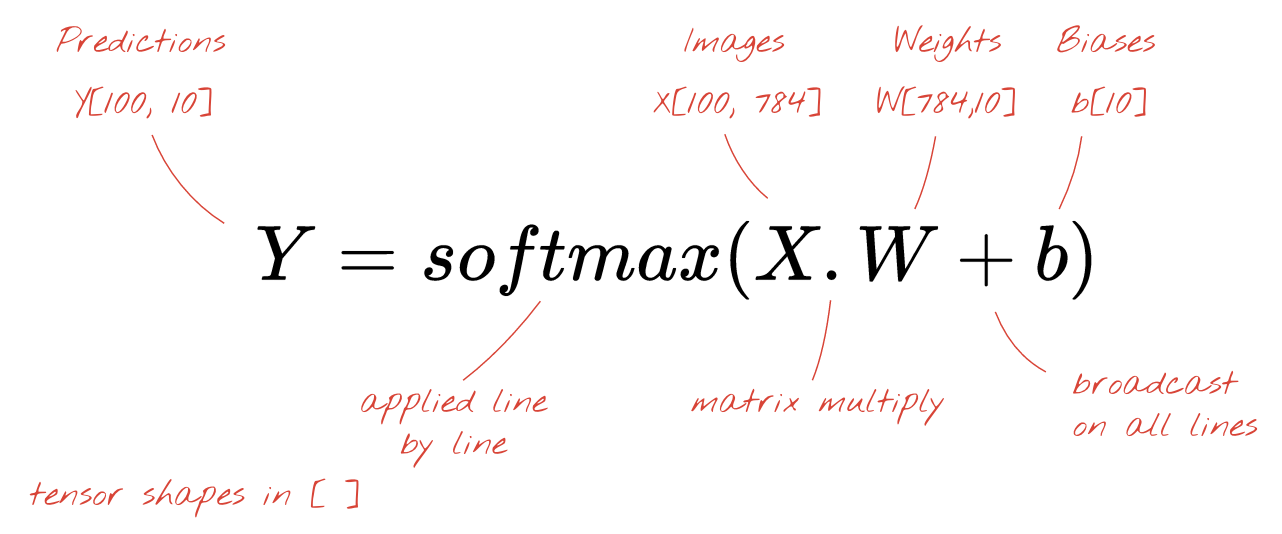
No Keras

Com bibliotecas de redes neurais de alto nível, como o Keras, não precisamos implementar essa fórmula. No entanto, é importante entender que uma camada de rede neural é apenas um monte de multiplicações e adições. No Keras, uma camada densa seria escrita assim:

tf.keras.layers.Dense(10, activation='softmax')

Vá além

É trivial encadear camadas de rede neural. A primeira camada calcula somas ponderadas de pixels. As camadas subsequentes calculam somas ponderadas das saídas das camadas anteriores.

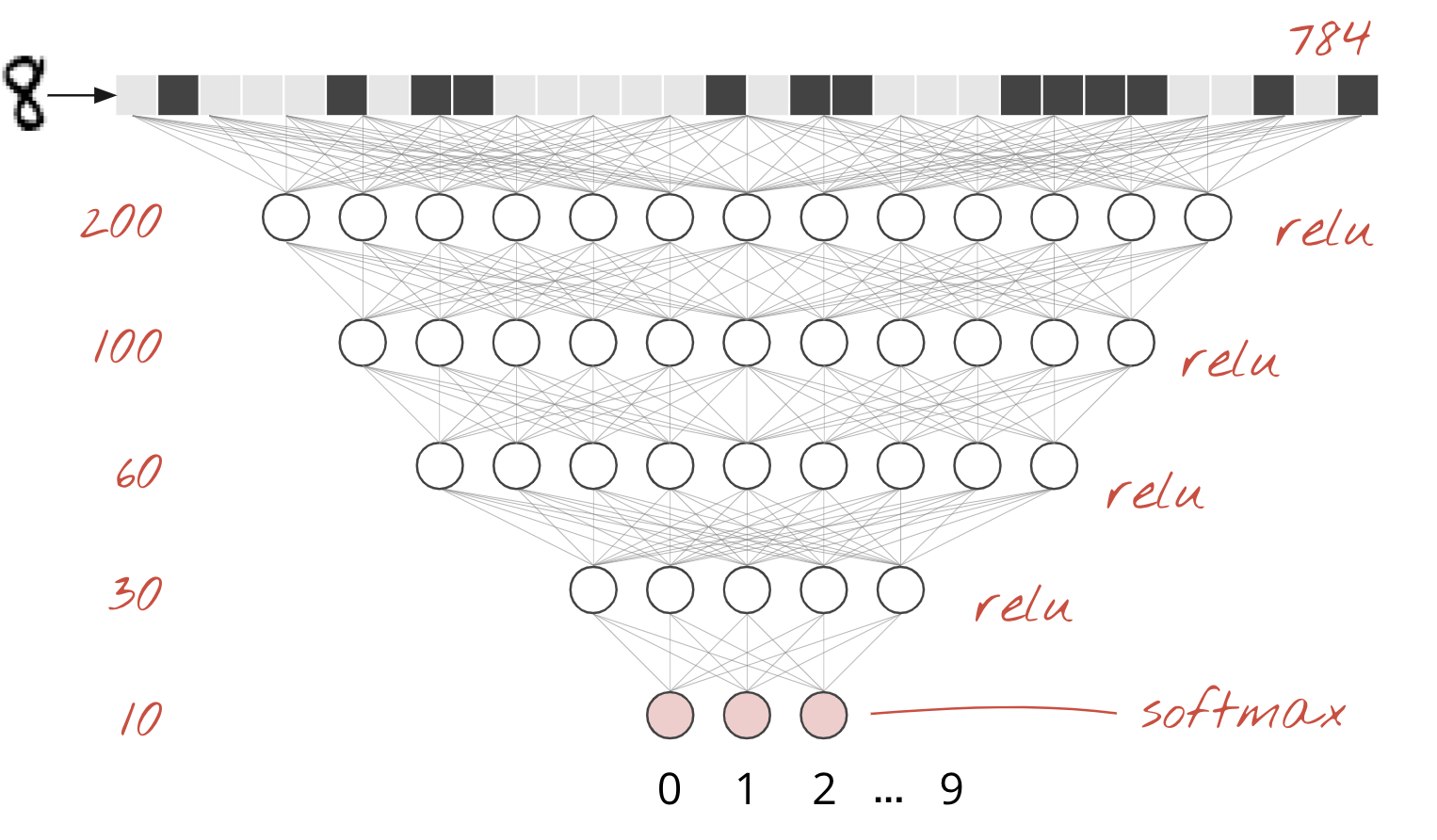
A única diferença, além do número de neurônios, será a escolha da função de ativação.

Funções de ativação: relu, softmax e sigmoid

Normalmente, você usa a função de ativação "relu" em todas as camadas, exceto a última. A última camada, em um classificador, usaria a ativação "softmax".

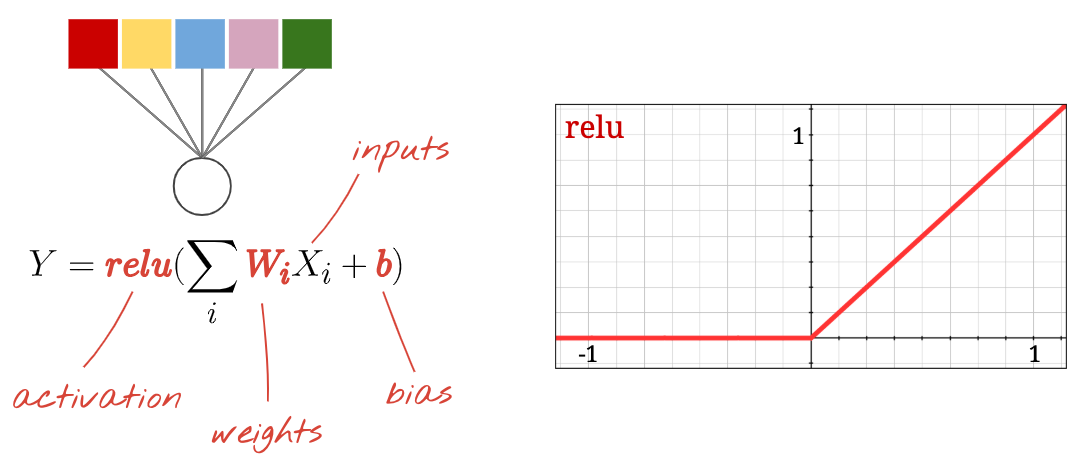
De novo, um "neurônio" calcula uma soma ponderada de todas as entradas, adiciona um valor chamado "tendência" e transmite o resultado pela função de ativação.

A função de ativação mais popular é chamada de "RELU", de Unidade Linear Retificada. É uma função muito simples, como você pode ver no gráfico acima.

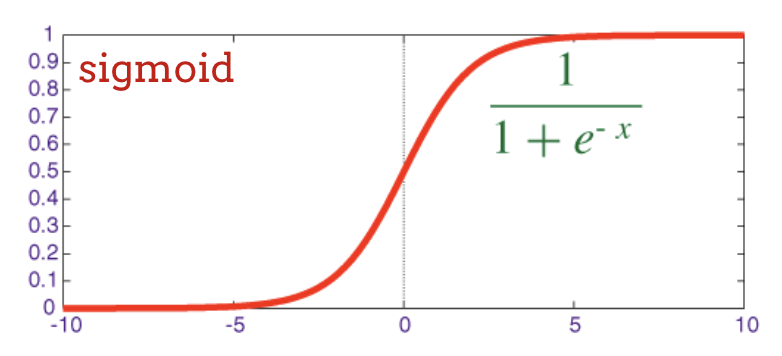
A função de ativação tradicional em redes neurais era a "sigmoide", mas a "relu" mostrou ter melhores propriedades de convergência em quase todos os lugares e agora é a preferida.

Ativação softmax para classificação

A última camada da nossa rede neural tem 10 neurônios porque queremos classificar dígitos manuscritos em 10 classes (0 a 9). Ele precisa gerar 10 números entre 0 e 1 que representam a probabilidade de o dígito ser 0, 1, 2 e assim por diante. Para isso, na última camada, vamos usar uma função de ativação chamada "softmax".

Para aplicar o softmax em um vetor, pegue o exponencial de cada elemento e normalize o vetor, geralmente dividindo-o pela norma "L1" (ou seja, a soma dos valores absolutos) para que os valores normalizados somem 1 e possam ser interpretados como probabilidades.

A saída da última camada, antes da ativação, às vezes é chamada de "logits". Se esse vetor for L = [L0, L1, L2, L3, L4, L5, L6, L7, L8, L9], então:

Por que "softmax" é chamado de softmax? A exponencial é uma função de crescimento acentuado. Isso vai aumentar as diferenças entre as saídas dos neurônios. Em seguida, ao normalizar o vetor, o maior elemento, que domina a norma, será normalizado para um valor próximo a 1, enquanto todos os outros elementos serão divididos por um valor grande e normalizados para algo próximo a 0. O vetor resultante mostra claramente qual é a classe vencedora, o "máximo", mas mantém a ordem relativa original dos valores, daí o "suave".

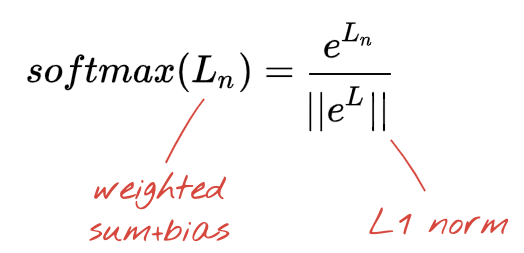
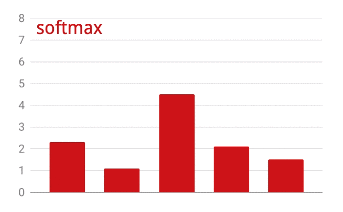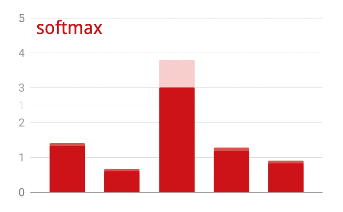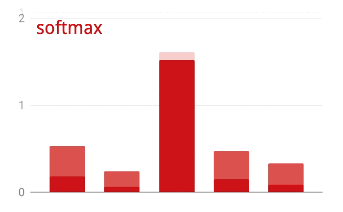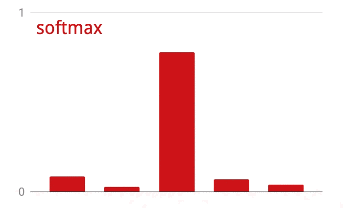
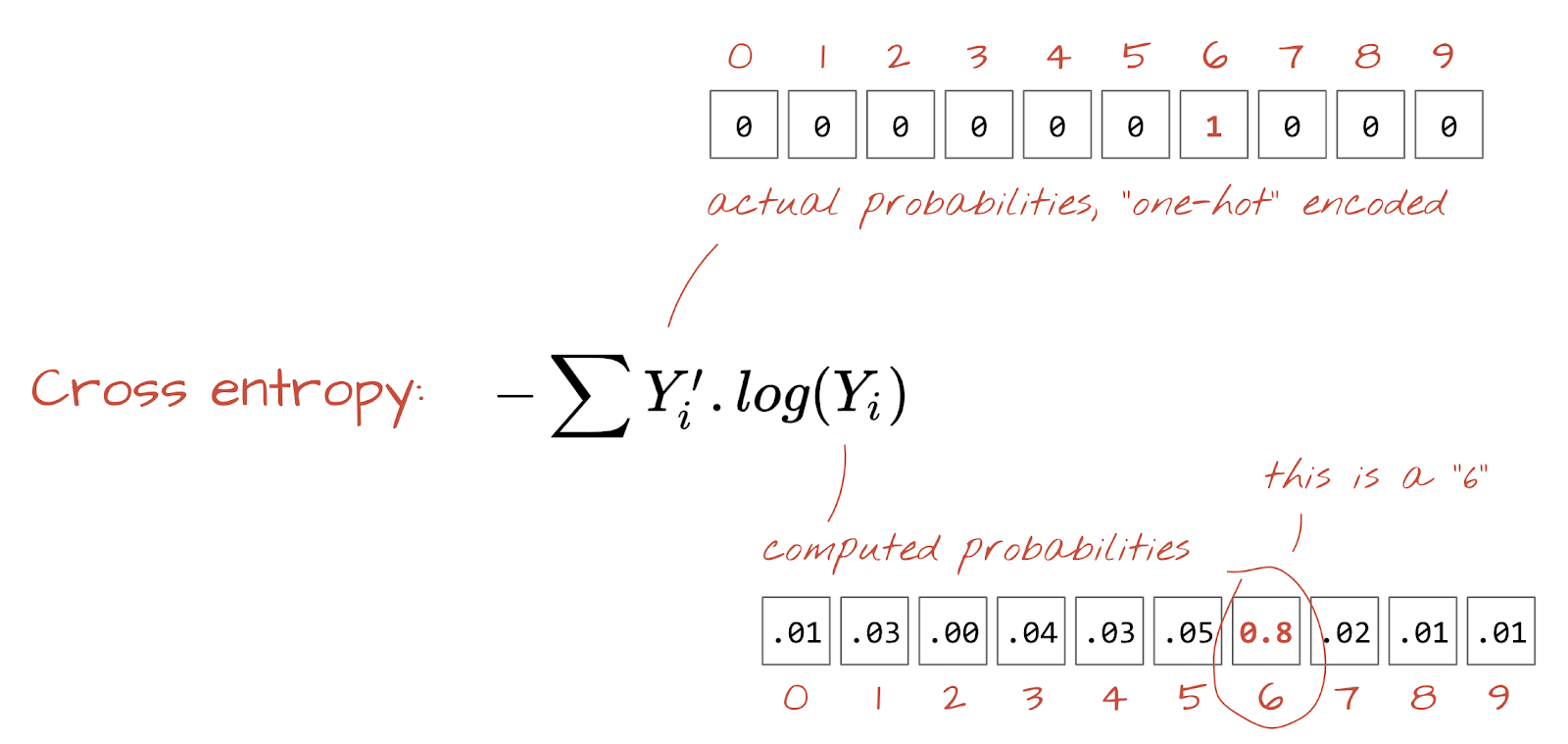
Perda de entropia cruzada

Agora que nossa rede neural gera previsões com base em imagens de entrada, precisamos medir a qualidade delas, ou seja, a distância entre o que a rede nos diz e as respostas corretas, geralmente chamadas de "rótulos". Lembre-se de que temos rótulos corretos para todas as imagens no conjunto de dados.

Qualquer distância funcionaria, mas para problemas de classificação, a chamada "distância de entropia cruzada" é a mais eficaz. Vamos chamar isso de função de erro ou "perda":

A codificação one-hot significa que você representa o rótulo "este é o dígito 3" usando um vetor de 10 valores, todos zeros, exceto o terceiro valor, que é 1. Esse vetor representa uma probabilidade de 100% de ser o "dígito 3". Nossa rede neural também gera as previsões como um vetor de 10 valores de probabilidade. Elas são fáceis de comparar.

Gradiente descendente

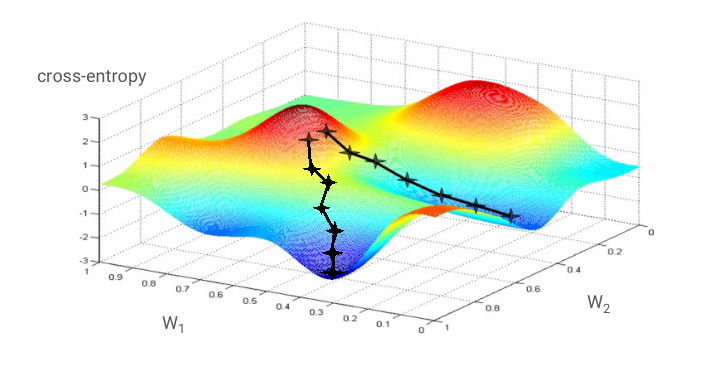
"Treinar" a rede neural significa usar imagens e rótulos de treinamento para ajustar pesos e vieses e minimizar a função de perda de entropia cruzada. Confira como funciona.

A entropia cruzada é uma função de pesos, vieses, pixels da imagem de treinamento e da classe conhecida.

Se calcularmos as derivadas parciais da entropia cruzada em relação a todos os pesos e vieses, vamos obter um "gradiente", calculado para uma determinada imagem, rótulo e valor atual de pesos e vieses. Lembre-se de que podemos ter milhões de pesos e vieses, então calcular o gradiente parece muito trabalhoso. Felizmente, o TensorFlow faz isso por nós. A propriedade matemática de um gradiente é que ele aponta para cima. Como queremos ir para onde a entropia cruzada é baixa, vamos na direção oposta. Atualizamos os pesos e os vieses por uma fração do gradiente. Em seguida, fazemos a mesma coisa repetidamente usando os próximos lotes de imagens e rótulos de treinamento, em um loop de treinamento. Esperamos que isso convirja para um lugar em que a entropia cruzada seja mínima, embora nada garanta que esse mínimo seja único.

Taxa de aprendizado: não é possível atualizar os pesos e os vieses por todo o comprimento do gradiente em cada iteração. É como tentar chegar ao fundo de um vale usando botas de sete léguas. Você estaria pulando de um lado para o outro do vale. Para chegar ao final, é preciso fazer etapas menores, ou seja, usar apenas uma fração do gradiente, normalmente na faixa de 1/1000. Essa fração é chamada de "taxa de aprendizado".

Minilotes e momentum

Você pode calcular o gradiente em apenas uma imagem de exemplo e atualizar os pesos e os vieses imediatamente, mas fazer isso em um lote de, por exemplo, 128 imagens, gera um gradiente que representa melhor as restrições impostas por diferentes imagens de exemplo e, portanto, provavelmente converge para a solução mais rapidamente. O tamanho do minilote é um parâmetro ajustável.

Essa técnica, às vezes chamada de "descida do gradiente estocástico", tem outro benefício mais pragmático: trabalhar com lotes também significa trabalhar com matrizes maiores, que geralmente são mais fáceis de otimizar em GPUs e TPUs.

No entanto, a convergência ainda pode ser um pouco caótica e até parar se o vetor de gradiente for todo zero. Isso significa que encontramos um mínimo? Nem sempre. Um componente de gradiente pode ser zero em um mínimo ou um máximo. Com um vetor de gradiente com milhões de elementos, se todos forem zeros, a probabilidade de que cada zero corresponda a um mínimo e nenhum deles a um ponto máximo é muito pequena. Em um espaço de muitas dimensões, os pontos de sela são bem comuns, e não queremos parar neles.

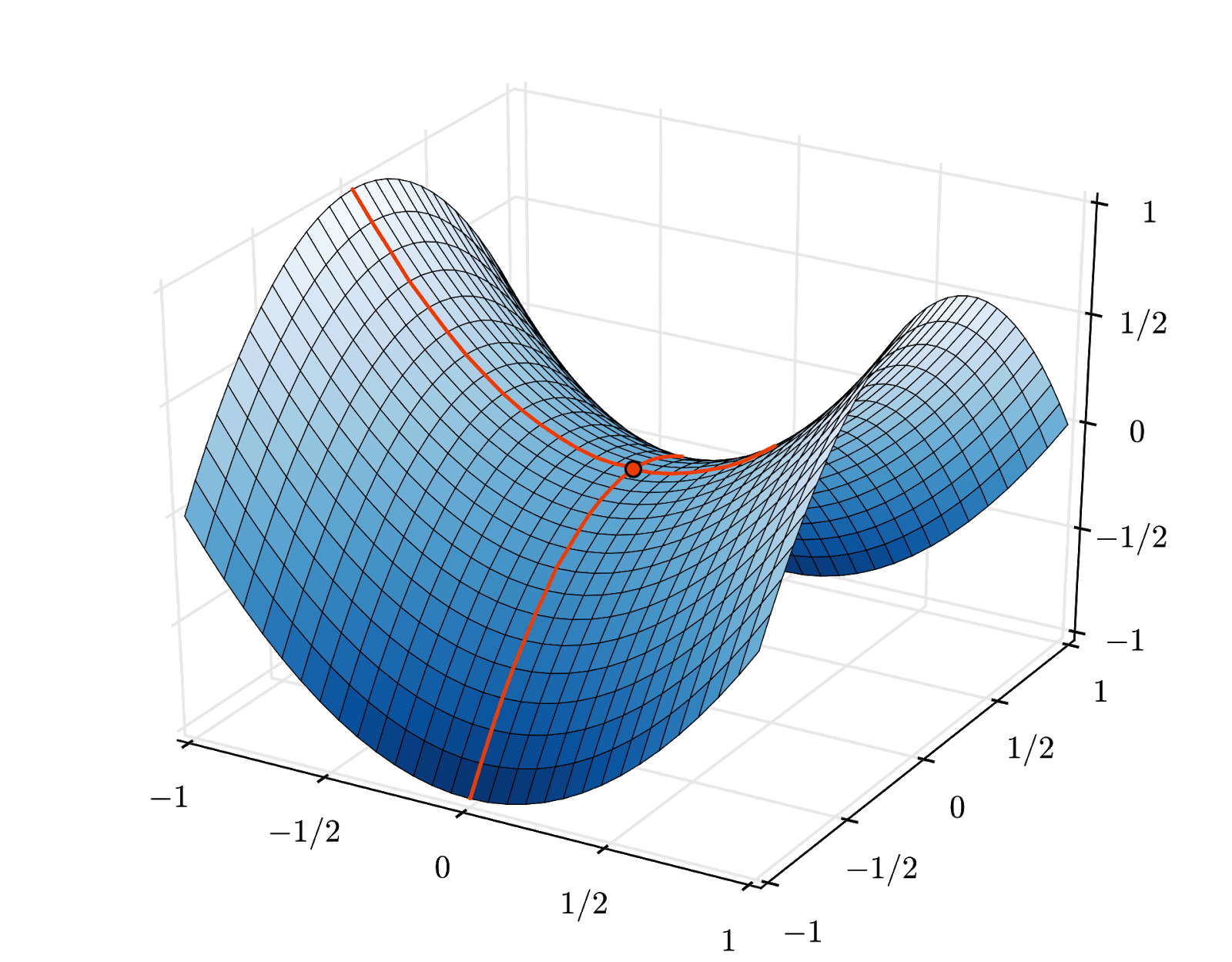
Ilustração: um ponto de sela. O gradiente é 0, mas não é um mínimo em todas as direções. (Atribuição da imagem: Wikimedia: Por Nicoguaro - Trabalho próprio, CC BY 3.0)

A solução é adicionar um pouco de impulso ao algoritmo de otimização para que ele possa passar pelos pontos de sela sem parar.

A biblioteca do TensorFlow oferece uma variedade de otimizadores, começando com tf.train.GradientDescentOptimizer. O tf.train.RMSPropOptimizer e o tf.train.AdamOptimizer são otimizadores populares mais avançados que têm um momentum integrado.

Glossário

Lote ou minilote: o treinamento é sempre realizado em lotes de dados e rótulos de treinamento. Isso ajuda o algoritmo a convergir. A dimensão "lote" geralmente é a primeira dimensão dos tensores de dados. Por exemplo, um tensor de forma [100, 192, 192, 3] contém 100 imagens de 192 x 192 pixels com três valores por pixel (RGB).

Perda de entropia cruzada: uma função de perda especial usada com frequência em classificadores.

Camada densa: uma camada de neurônios em que cada neurônio está conectado a todos os neurônios da camada anterior.

Atributos: as entradas de uma rede neural às vezes são chamadas de "atributos". A arte de descobrir quais partes de um conjunto de dados (ou combinações de partes) alimentar em uma rede neural para receber boas previsões é chamada de "engenharia de recursos".

rótulos: outro nome para "classes" ou respostas corretas em um problema de classificação supervisionada

Taxa de aprendizado: fração do gradiente pela qual os pesos e os vieses são atualizados em cada iteração do loop de treinamento.

Logits: as saídas de uma camada de neurônios antes da aplicação da função de ativação são chamadas de "logits". O termo vem da "função logística", também conhecida como "função sigmoide", que era a função de ativação mais usada. "Saídas de neurônios antes da função logística" foi abreviado para "logits".

Perda: a função de erro que compara as saídas da rede neural com as respostas corretas.

Neurônio: calcula a soma ponderada das entradas, adiciona um viés e transmite o resultado por uma função de ativação.

Codificação one-hot: a classe 3 de 5 é codificada como um vetor de 5 elementos, todos zeros, exceto o terceiro, que é 1.

relu: unidade linear retificada. Uma função de ativação comum para neurônios.

sigmoid: outra função de ativação que era popular e ainda é útil em casos especiais.

Softmax: uma função de ativação especial que atua em um vetor, aumenta a diferença entre o maior componente e todos os outros e também normaliza o vetor para ter uma soma de 1, de modo que possa ser interpretado como um vetor de probabilidades. Usado como a última etapa nos classificadores.

Tensor: um "tensor" é como uma matriz, mas com um número arbitrário de dimensões. Um tensor unidimensional é um vetor. Um tensor bidimensional é uma matriz. E você pode ter tensores com 3, 4, 5 ou mais dimensões.

Volte ao notebook de estudo e, desta vez, leia o código.

keras_01_mnist.ipynb

PRÁTICA:

Nesta seção, sua tarefa é ler e entender o código para poder melhorá-lo depois.

Vamos analisar todas as células deste notebook.

Célula "Parâmetros"

O tamanho do lote, o número de períodos de treinamento e o local dos arquivos de dados são definidos aqui. Os arquivos de dados são hospedados em um bucket do Google Cloud Storage (GCS), por isso o endereço deles começa com gs://.

Célula "Importações"

Todas as bibliotecas necessárias do Python são importadas aqui, incluindo o TensorFlow e o matplotlib para visualizações.

Célula "utilitários de visualização [EXECUTE ME]"

Essa célula contém um código de visualização sem interesse. Ele fica recolhido por padrão, mas você pode abrir e analisar o código quando tiver tempo clicando duas vezes nele.

Execute essa célula (SHIFT-ENTER). Caso contrário, as funções definidas nela não serão analisadas, e você vai receber erros mais tarde.

Célula "tf.data.Dataset: analisar arquivos e preparar conjuntos de dados de treinamento e validação"

Esta célula usou a API tf.data.Dataset para carregar o conjunto de dados MNIST dos arquivos de dados. Não é necessário passar muito tempo nessa célula. Se você tiver interesse na API tf.data.Dataset, confira este tutorial que explica como ela funciona: Pipelines de dados com velocidade de TPU. Por enquanto, os princípios básicos são:

As imagens e os rótulos (respostas corretas) do conjunto de dados MNIST são armazenados em registros de comprimento fixo em quatro arquivos. Os arquivos podem ser carregados com a função dedicada de registro fixo:

imagedataset = tf.data.FixedLengthRecordDataset(image_filename, 28*28, header_bytes=16)

Agora temos um conjunto de dados de bytes de imagem. Elas precisam ser decodificadas em imagens. Definimos uma função para isso. A imagem não é compactada, então a função não precisa decodificar nada (decode_raw basicamente não faz nada). Em seguida, a imagem é convertida em valores de ponto flutuante entre 0 e 1. Podemos remodelar como uma imagem 2D, mas vamos manter como uma matriz plana de pixels de tamanho 28*28, porque é isso que nossa camada densa inicial espera.

def read_image(tf_bytestring):
    image = tf.decode_raw(tf_bytestring, tf.uint8)
    image = tf.cast(image, tf.float32)/256.0
    image = tf.reshape(image, [28*28])
    return image

Aplicamos essa função ao conjunto de dados usando .map e obtemos um conjunto de dados de imagens:

imagedataset = imagedataset.map(read_image, num_parallel_calls=16)

Fazemos o mesmo tipo de leitura e decodificação para rótulos e .zip imagens e rótulos juntos:

dataset = tf.data.Dataset.zip((imagedataset, labelsdataset))

Agora temos um conjunto de dados de pares (imagem, rótulo). É isso que nosso modelo espera. Ainda não estamos prontos para usar na função de treinamento:

dataset = dataset.cache()
dataset = dataset.shuffle(5000, reshuffle_each_iteration=True)
dataset = dataset.repeat()
dataset = dataset.batch(batch_size)
dataset = dataset.prefetch(tf.data.experimental.AUTOTUNE)

A API tf.data.Dataset tem todas as funções utilitárias necessárias para preparar conjuntos de dados:

O .cache armazena o conjunto de dados em cache na RAM. Esse é um conjunto de dados pequeno, então vai funcionar. .shuffle embaralha com um buffer de 5.000 elementos. É importante que os dados de treinamento estejam bem embaralhados. O .repeat faz um loop no conjunto de dados. Vamos treinar várias vezes (vários períodos). O .batch reúne várias imagens e rótulos em um mini-natch. Por fim, o .prefetch pode usar a CPU para preparar o próximo lote enquanto o lote atual está sendo treinado na GPU.

O conjunto de dados de validação é preparado de maneira semelhante. Agora estamos prontos para definir um modelo e usar esse conjunto de dados para treiná-lo.

Célula "Modelo do Keras"

Todos os nossos modelos serão sequências diretas de camadas. Por isso, podemos usar o estilo tf.keras.Sequential para criá-los. Inicialmente, é uma única camada densa. Ele tem 10 neurônios porque estamos classificando dígitos manuscritos em 10 classes. Ele usa a ativação "softmax" porque é a última camada em um classificador.

Um modelo do Keras também precisa saber o formato das entradas. tf.keras.layers.Input pode ser usado para definir isso. Aqui, os vetores de entrada são vetores simples de valores de pixels de comprimento 28*28.

model = tf.keras.Sequential(
  [
    tf.keras.layers.Input(shape=(28*28,)),
    tf.keras.layers.Dense(10, activation='softmax')
  ])

model.compile(optimizer='sgd',
              loss='categorical_crossentropy',
              metrics=['accuracy'])

# print model layers
model.summary()

# utility callback that displays training curves
plot_training = PlotTraining(sample_rate=10, zoom=1)

A configuração do modelo é feita no Keras usando a função model.compile. Aqui usamos o otimizador básico 'sgd' (gradiente descendente estocástico). Um modelo de classificação requer uma função de perda de entropia cruzada, chamada 'categorical_crossentropy' no Keras. Por fim, pedimos ao modelo para calcular a métrica 'accuracy', que é a porcentagem de imagens classificadas corretamente.

O Keras oferece o utilitário model.summary(), que imprime os detalhes do modelo criado. Seu instrutor adicionou a utilidade PlotTraining (definida na célula "Utilitários de visualização"), que vai mostrar várias curvas de treinamento durante o processo.

Célula "Treinar e validar o modelo"

É aqui que o treinamento acontece, chamando model.fit e transmitindo os conjuntos de dados de treinamento e validação. Por padrão, o Keras executa uma rodada de validação ao final de cada época.

model.fit(training_dataset, steps_per_epoch=steps_per_epoch, epochs=EPOCHS,
          validation_data=validation_dataset, validation_steps=1,
          callbacks=[plot_training])

No Keras, é possível adicionar comportamentos personalizados durante o treinamento usando callbacks. É assim que o gráfico de treinamento com atualização dinâmica foi implementado neste workshop.

Célula "Visualizar previsões"

Depois que o modelo é treinado, podemos receber previsões dele chamando model.predict():

probabilities = model.predict(font_digits, steps=1)
predicted_labels = np.argmax(probabilities, axis=1)

Aqui, preparamos um conjunto de dígitos impressos renderizados de fontes locais, como um teste. Lembre-se de que a rede neural retorna um vetor de 10 probabilidades do "softmax" final. Para receber o rótulo, precisamos descobrir qual probabilidade é a mais alta. np.argmax da biblioteca numpy faz isso.

Para entender por que o parâmetro axis=1 é necessário, lembre-se de que processamos um lote de 128 imagens e, portanto, o modelo retorna 128 vetores de probabilidades. O formato do tensor de saída é [128, 10]. Estamos calculando o argmax nas 10 probabilidades retornadas para cada imagem. Portanto, axis=1 (o primeiro eixo é 0).

Esse modelo simples já reconhece 90% dos dígitos. Não está ruim, mas agora você vai melhorar muito.

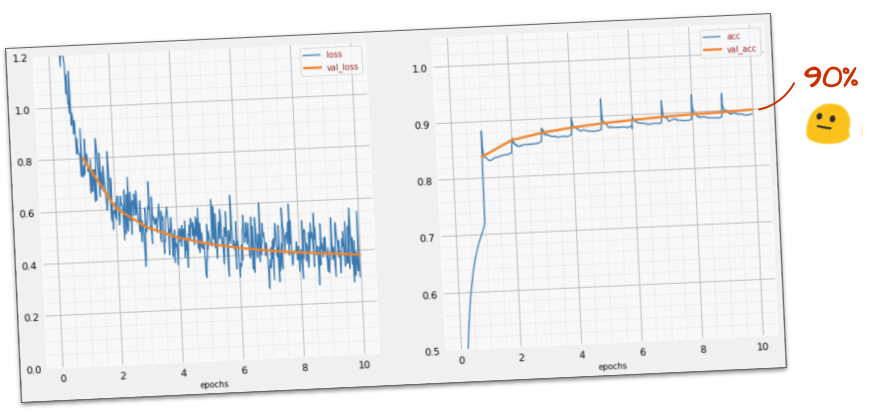
Para melhorar a precisão do reconhecimento, vamos adicionar mais camadas à rede neural.

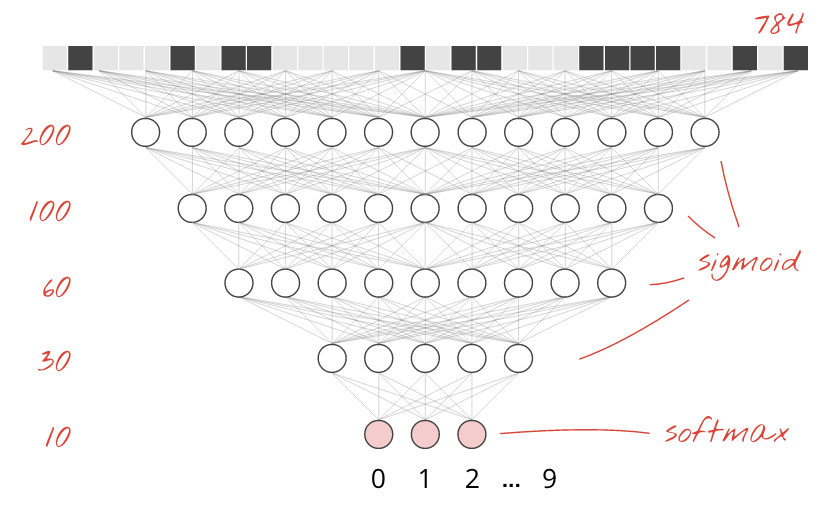
Mantemos o softmax como a função de ativação na última camada porque é o que funciona melhor para classificação. Nas camadas intermediárias, usaremos a função de ativação mais clássica: a sigmoide.

PRÁTICA:

Adicione algumas camadas densas intermediárias ativadas com "sigmoid" antes da camada "softmax". O número de neurônios pode ser qualquer valor entre 784 (o número de pixels de entrada) e 10 (o número de neurônios de saída). Em seguida, treine o modelo novamente.

Aviso: para treinar novamente, execute de novo a célula "Modelo do Keras" para definir um novo modelo e, em seguida, a célula de treinamento. Basta executar novamente a célula de treinamento para continuar o treinamento do modelo anterior.

Por exemplo, seu modelo pode ser assim (não se esqueça das vírgulas, tf.keras.Sequential usa uma lista de camadas separada por vírgulas):

model = tf.keras.Sequential(
  [
      tf.keras.layers.Input(shape=(28*28,)),
      tf.keras.layers.Dense(200, activation='sigmoid'),
      tf.keras.layers.Dense(60, activation='sigmoid'),
      tf.keras.layers.Dense(10, activation='softmax')
  ])

Confira o "resumo" do seu modelo. Agora ele tem pelo menos 10 vezes mais parâmetros. Ele precisa ser 10 vezes melhor! Mas, por algum motivo, não é ...

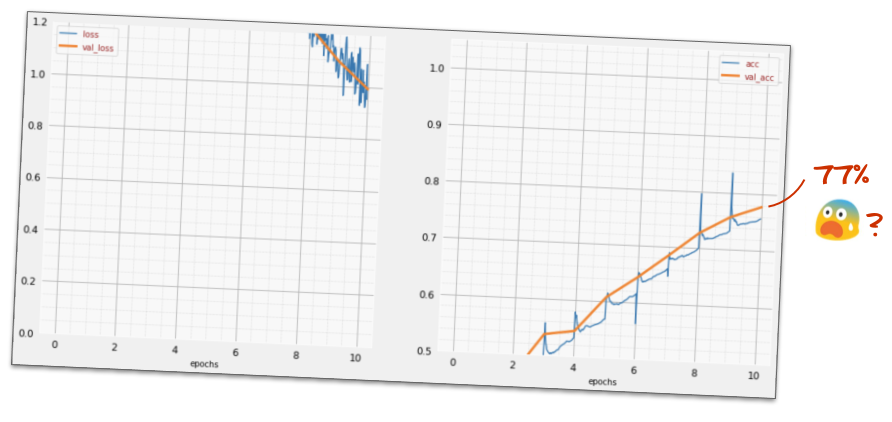
A perda também parece ter aumentado muito. Algo não está certo.

Você acabou de conhecer as redes neurais, como as pessoas costumavam projetá-las nos anos 80 e 90. Não é de se admirar que eles tenham desistido da ideia, inaugurando o chamado "inverno da IA". Na verdade, conforme você adiciona camadas, as redes neurais têm cada vez mais dificuldades para convergir.

Acontece que redes neurais profundas com muitas camadas (20, 50 ou até 100 hoje em dia) podem funcionar muito bem, desde que sejam usados alguns truques matemáticos para fazê-las convergir. A descoberta desses truques simples é um dos motivos para o renascimento do aprendizado profundo na década de 2010.

Ativação RELU

A função de ativação sigmoide é bastante problemática em redes profundas. Ele reduz todos os valores entre 0 e 1 e, quando isso é feito repetidamente, as saídas dos neurônios e seus gradientes podem desaparecer completamente. Ele foi mencionado por motivos históricos, mas as redes modernas usam a RELU (unidade linear retificada), que tem esta aparência:

PRÁTICA:

Substitua todos os activation='sigmoid' por activation='relu' nas camadas e treine novamente.

Por que a sigmoide é problemática? Veja como ele se comporta nas laterais: fica plano.

Isso significa que a derivada está perto de zero. Lembre-se de como o treinamento progride seguindo o gradiente, que é um vetor de derivadas. Com a ativação sigmoide, principalmente se houver muitas camadas, o gradiente pode ficar muito pequeno, e o treinamento fica cada vez mais lento.

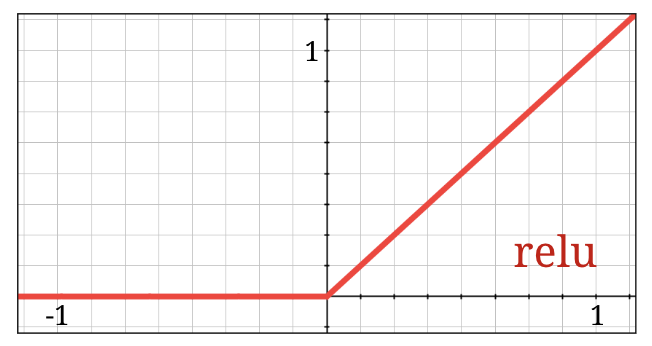
A ReLU, por outro lado, tem uma derivada de 1, pelo menos no lado direito. Com a ativação do RELU, mesmo que os gradientes provenientes de alguns neurônios possam ser zero, sempre haverá outros apresentando um gradiente claro diferente de zero e o treinamento pode continuar em um bom ritmo.

Um otimizador melhor

Em espaços de alta dimensão, como aqui, em que temos cerca de 10 mil pesos e vieses, os "pontos de sela" são frequentes. Esses são pontos que não são mínimos locais, mas onde o gradiente é zero e o otimizador de gradiente descendente fica preso. O TensorFlow tem uma variedade completa de otimizadores disponíveis, incluindo alguns que funcionam com uma quantidade de inércia e passam com segurança pelos pontos de sela.

PRÁTICA:

Substitua o otimizador 'sgd' por um melhor, por exemplo, 'adam', e treine novamente.

Inicializações aleatórias

A arte de inicializar vieses de peso antes do treinamento é uma área de pesquisa em si, com vários artigos publicados sobre o assunto. Confira todos os inicializadores disponíveis no Keras neste link. Felizmente, a Keras faz a coisa certa por padrão e usa o inicializador 'glorot_uniform', que é o melhor em quase todos os casos.

Não é preciso fazer nada, já que o Keras já faz o certo.

NaN ???

A fórmula de entropia cruzada envolve um logaritmo, e log(0) não é um número (NaN, uma falha numérica, se preferir). A entrada da entropia cruzada pode ser 0? A entrada vem da softmax, que é essencialmente uma exponencial, e uma exponencial nunca é zero. Então estamos seguros!

Mesmo? No mundo maravilhoso da matemática, estaríamos seguros, mas no mundo da computação, exp(-150), representado no formato float32, é ZERO e a entropia cruzada falha.

Felizmente, você não precisa fazer nada aqui também, já que o Keras cuida disso e calcula o softmax seguido da entropia cruzada de uma maneira especialmente cuidadosa para garantir a estabilidade numérica e evitar os temidos NaNs.

Sucesso?

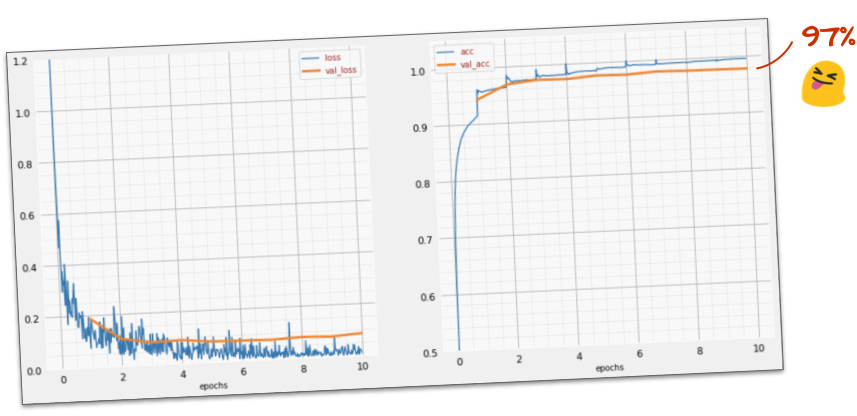
Agora você deve estar chegando a 97% de acurácia. O objetivo deste workshop é ficar significativamente acima de 99%. Então, vamos continuar.

Se você não souber o que fazer, confira a solução neste ponto:

keras_02_mnist_dense.ipynb

Talvez possamos tentar treinar mais rápido? A taxa de aprendizado padrão no otimizador Adam é 0,001. Vamos tentar aumentar.

PRÁTICA:

Aumente a taxa de aprendizado do valor padrão de 0,001 para 0,01. Para isso, substitua o otimizador predefinido 'adam' por uma instância real de um otimizador Adam para ter acesso aos parâmetros de configuração dele:

optimizer=tf.keras.optimizers.Adam(lr=0.01)

Aumente também o fator de zoom para 5 em PlotTraining. Isso aumenta o zoom em torno de 0 nas perdas e em torno de 1 nas acurácias para ajudar você a entender o que está acontecendo: PlotTraining(sample_rate=10, zoom=5)

Aumentar a velocidade não parece ajudar muito, e o que é todo esse barulho?

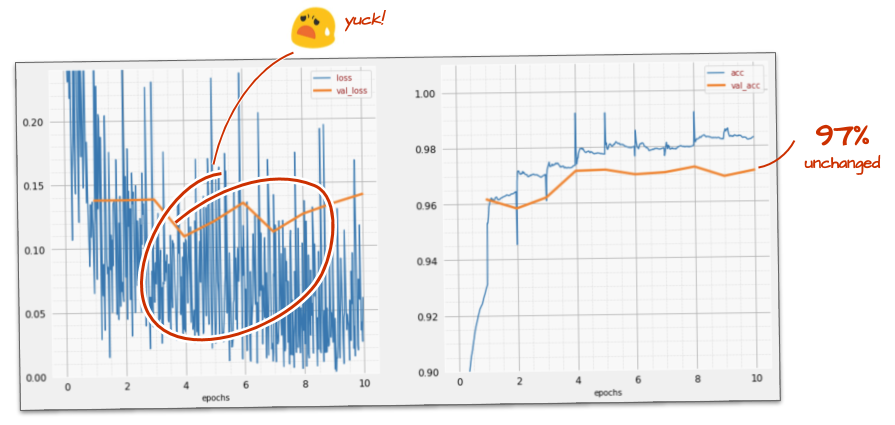
As curvas de treinamento são muito ruidosas e mostram as duas curvas de validação, que estão subindo e descendo. Isso significa que estamos indo muito rápido. Podemos voltar à velocidade anterior, mas há uma maneira melhor.

A solução ideal é começar rápido e reduzir a taxa de aprendizado exponencialmente. No Keras, é possível fazer isso com o callback tf.keras.callbacks.LearningRateScheduler.

PRÁTICA:

Implemente uma programação de taxa de aprendizado que diminua a taxa de aprendizado exponencialmente. Confira abaixo alguns snippets de código úteis.

Código útil para copiar e colar:

# lr decay function
def lr_decay(epoch):
  return 0.01 * math.pow(0.6, epoch)

# lr schedule callback
lr_decay_callback = tf.keras.callbacks.LearningRateScheduler(lr_decay, verbose=True)

# important to see what you are doing
plot_learning_rate(lr_decay, EPOCHS)

Não se esqueça de usar o lr_decay_callback que você criou. Adicione-o à lista de callbacks em model.fit:

model.fit(...,  callbacks=[plot_training, lr_decay_callback])

O impacto dessa pequena mudança é espetacular. Você vai notar que a maior parte do ruído desapareceu e a acurácia do teste agora está acima de 98% de forma consistente.

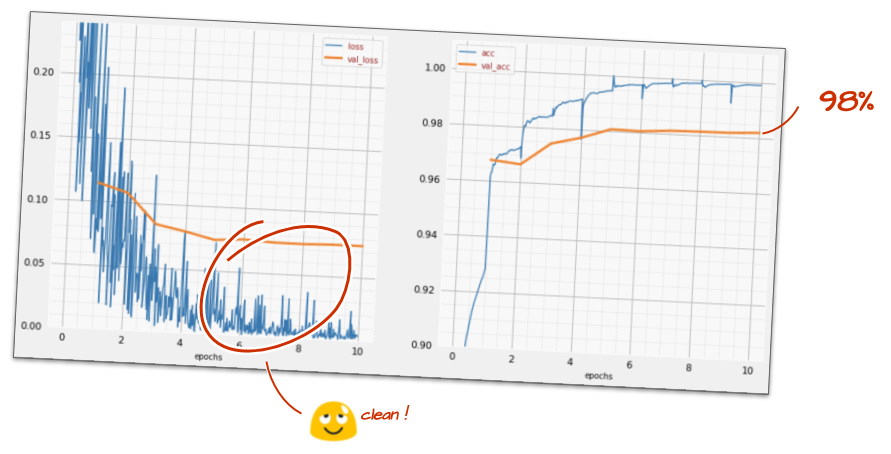
O modelo parece estar convergindo bem agora. Vamos tentar ir ainda mais fundo.

PRÁTICA:

Se você ainda não fez isso, aumente a profundidade do modelo para pelo menos quatro camadas densas e treine novamente. Você pode usar o seguinte número de neurônios nas camadas: 200, 100, 60, 10.

Aumente também o fator de zoom para 10 em PlotTraining. Isso aumenta o zoom em torno de 0 nas perdas e em torno de 1 nas acurácias para ajudar você a entender o que está acontecendo: PlotTraining(sample_rate=10, zoom=10)

Isso ajuda?

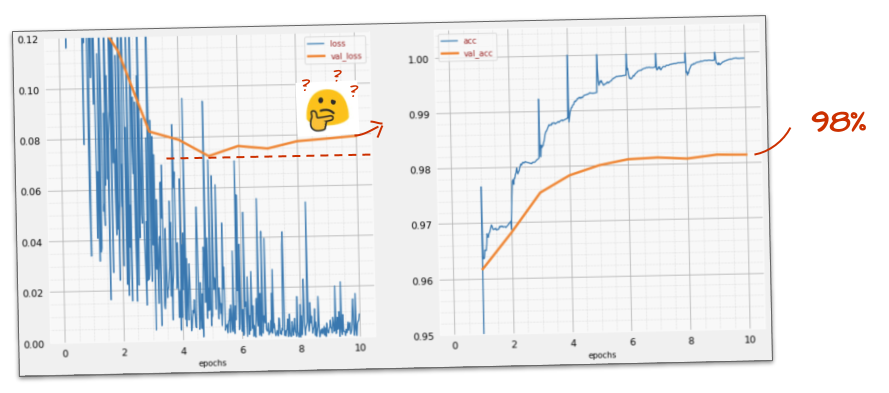
Não, a acurácia ainda está em 98%, e observe a perda de validação. Está subindo! O algoritmo de aprendizado funciona apenas com dados de treinamento e otimiza a perda de treinamento de acordo. Ele nunca vê dados de validação. Portanto, não é surpreendente que, depois de um tempo, o trabalho dele não tenha mais efeito na perda de validação, que para de diminuir e às vezes até volta a aumentar.

Isso não afeta imediatamente os recursos de reconhecimento do seu modelo no mundo real, mas impede que você execute muitas iterações e geralmente é um sinal de que o treinamento não está mais tendo um efeito positivo.

Essa desconexão geralmente é chamada de "overfitting". Quando isso acontece, tente aplicar uma técnica de regularização chamada "dropout". A técnica de dropout desativa neurônios aleatórios em cada iteração de treinamento.

O dropout é uma das técnicas de regularização mais antigas no aprendizado profundo. Em cada iteração de treinamento, ele descarta neurônios aleatórios da rede com uma probabilidade p (normalmente de 25% a 50%). Na prática, as saídas de neurônios são definidas como 0. O resultado é que esses neurônios não vão participar do cálculo da perda desta vez e não vão receber atualizações de peso. Diferentes neurônios serão descartados em cada iteração de treinamento.

Ao testar o desempenho da rede, você coloca todos os neurônios de volta (taxa de dropout=0). O Keras faz isso automaticamente. Basta adicionar uma camada tf.keras.layers.Dropout. Ele terá o comportamento correto automaticamente durante o treinamento e a avaliação.

Por que isso funciona? A teoria é que as redes neurais têm tanta liberdade entre as inúmeras camadas que é totalmente possível que uma camada desenvolva um comportamento ruim e que a próxima compense isso. Esse não é um uso ideal de neurônios. Com o dropout, há uma alta probabilidade de que o neurônio que "corrige" o problema não esteja presente em uma determinada rodada de treinamento. O mau comportamento da camada ofensiva se torna óbvio, e os pesos evoluem para um comportamento melhor.

PRÁTICA:

É possível adicionar dropout após cada camada intermediária densa na rede. Não adicione dropout após a camada softmax. Você estaria descartando as probabilidades previstas. Você pode adicionar uma taxa de desistência de 25% com: tf.keras.layers.Dropout(0.25)

Funcionou?

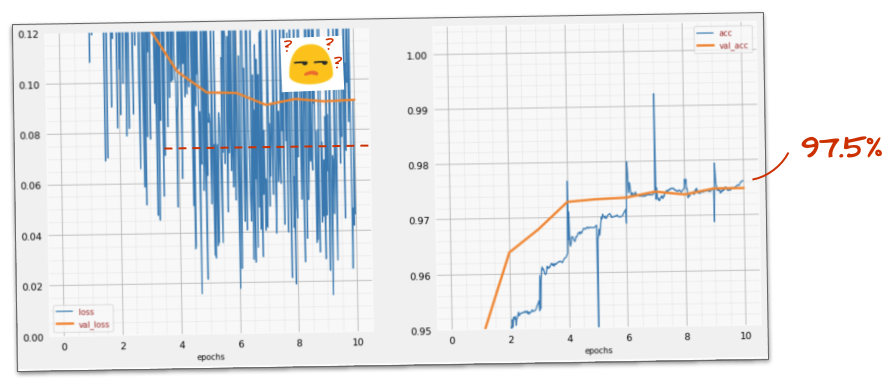
O ruído reaparece (o que não é surpreendente, considerando como o dropout funciona). A perda de validação não parece estar aumentando mais, mas é maior no geral do que sem o dropout. e a acurácia da validação diminuiu um pouco. Esse é um resultado bastante decepcionante.

Parece que o dropout não foi a solução correta, ou talvez o overfitting seja um conceito mais complexo e algumas das causas não sejam adequadas para uma correção de dropout.

O que é "overfitting"? O overfitting acontece quando uma rede neural aprende "mal", de uma forma que funciona para os exemplos de treinamento, mas não tão bem com dados do mundo real. Existem técnicas de regularização, como o dropout, que podem forçar o aprendizado de uma maneira melhor, mas o overfitting também tem raízes mais profundas.

O overfitting básico acontece quando uma rede neural tem muitos graus de liberdade para o problema em questão. Imagine que temos tantos neurônios que a rede pode armazenar todas as imagens de treinamento neles e reconhecê-las por correspondência de padrões. Ele falharia completamente em dados do mundo real. Uma rede neural precisa ser um pouco restrita para que seja forçada a generalizar o que aprende durante o treinamento.

Se você tiver poucos dados de treinamento, até mesmo uma rede pequena poderá aprender de cor, e você vai notar um "overfitting". Em geral, você sempre precisa de muitos dados para treinar redes neurais.

Por fim, se você fez tudo certo, testou diferentes tamanhos de rede para garantir que os graus de liberdade dela estejam restritos, aplicou o dropout e treinou com muitos dados, ainda pode estar preso em um nível de performance que nada parece melhorar. Isso significa que sua rede neural, na forma atual, não consegue extrair mais informações dos seus dados, como no nosso caso aqui.

Você se lembra de como estamos usando nossas imagens, transformadas em um único vetor? Essa foi uma ideia muito ruim. Os dígitos manuscritos são feitos de formas, e descartamos as informações de forma quando achatamos os pixels. No entanto, há um tipo de rede neural que pode aproveitar as informações de forma: as redes convolucionais. Vamos testar.

Se você não souber o que fazer, confira a solução neste ponto:

keras_03_mnist_dense_lrdecay_dropout.ipynb

Em resumo

Se você já conhece todos os termos em negrito no próximo parágrafo, passe para o próximo exercício. Se você está começando a usar redes neurais convolucionais, continue lendo.

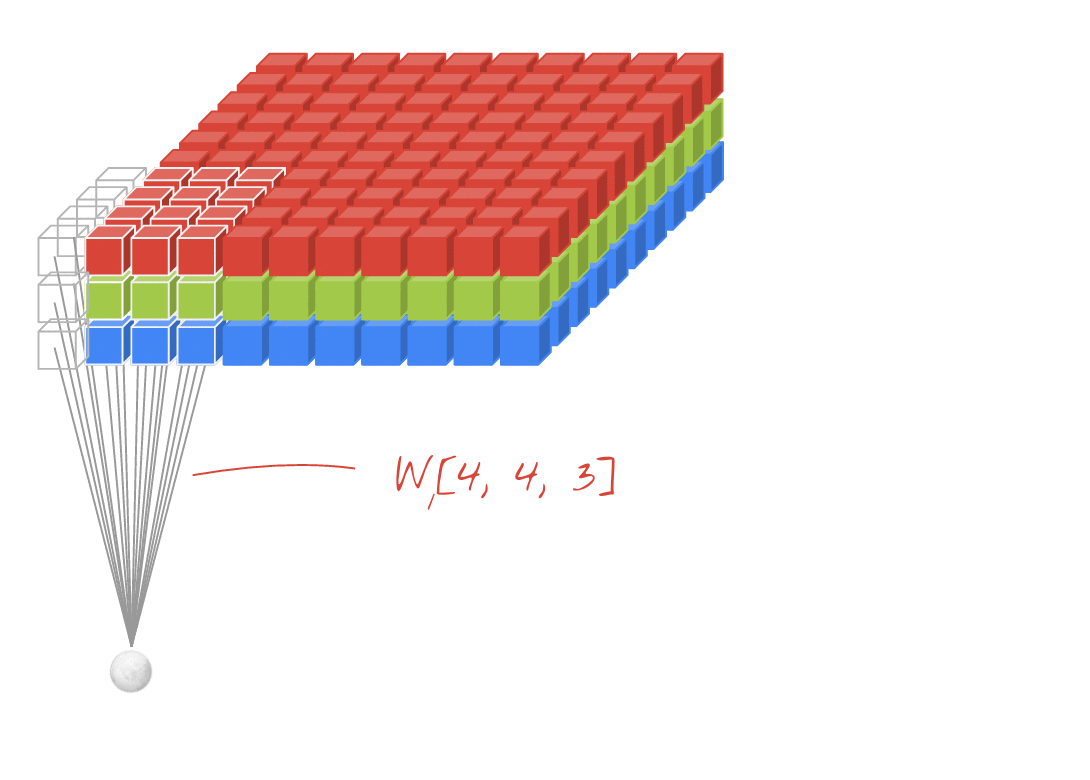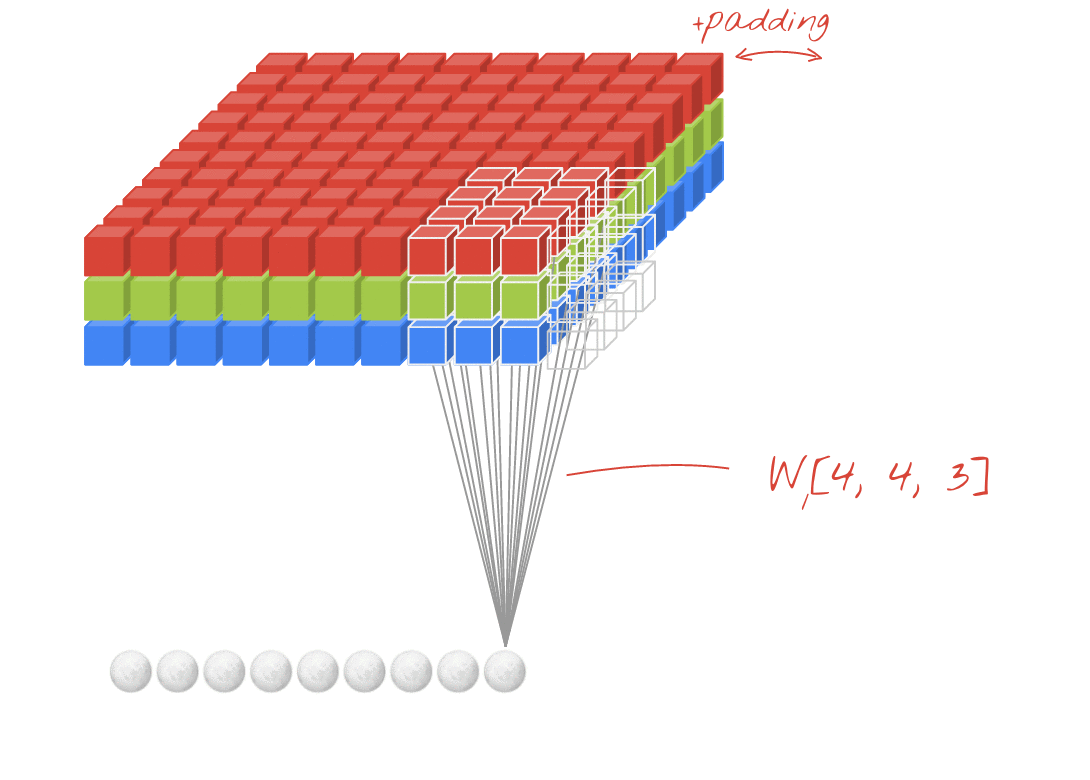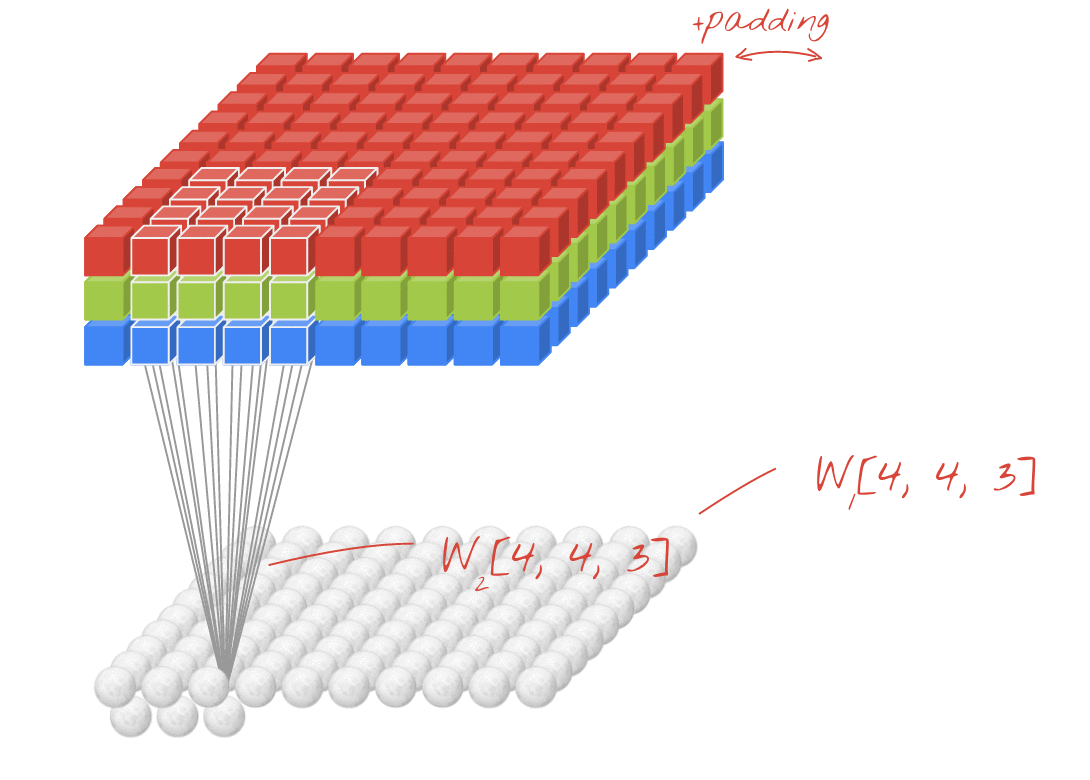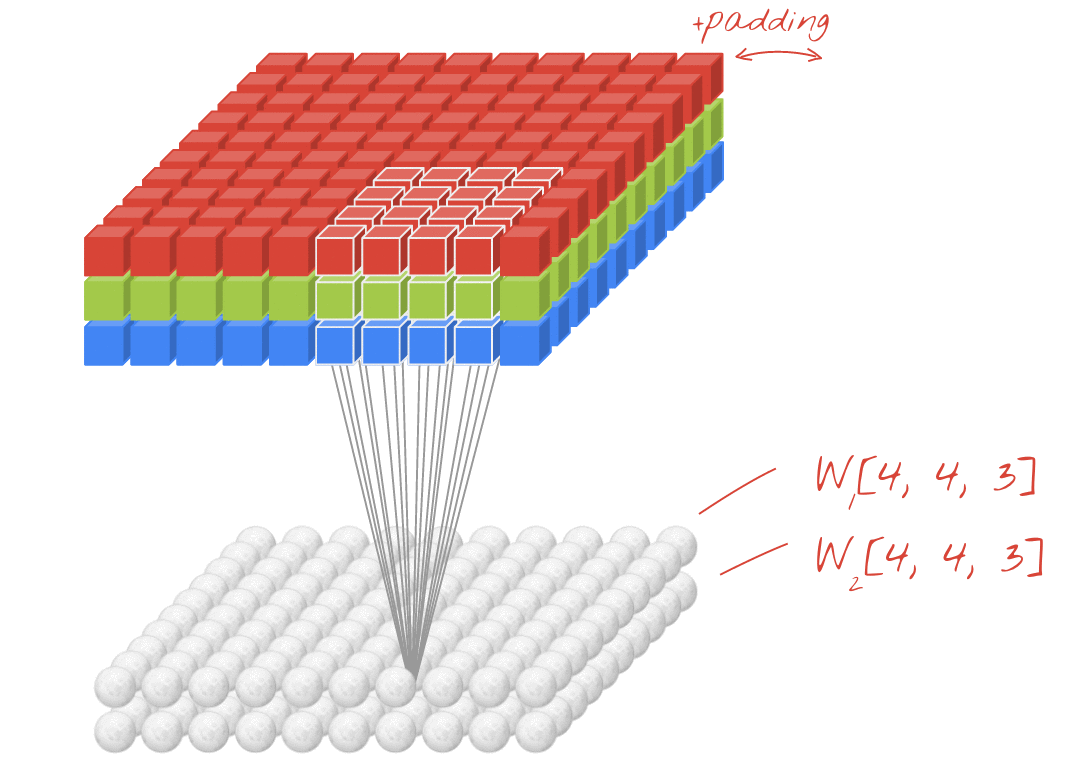
Ilustração: filtragem de uma imagem com dois filtros sucessivos feitos de 4x4x3=48 pesos aprendíveis cada.

As redes neurais convolucionais aplicam uma série de filtros aprendidos à imagem de entrada. Uma camada convolucional é definida pelo tamanho do filtro (ou kernel), pelo número de filtros aplicados e pelo stride. A entrada e a saída de uma camada convolucional têm três dimensões (largura, altura, número de canais), começando com a imagem de entrada (largura, altura, canais RGB). Ao empilhar camadas convolucionais, a largura e a altura da saída podem ser ajustadas usando uma passada >1 ou com uma operação de max-pooling. A profundidade da saída (número de canais) é ajustada usando mais ou menos filtros.

Esta é a aparência de uma rede neural convolucional simples no Keras:

model = tf.keras.Sequential([
    tf.keras.layers.Reshape(input_shape=(28*28,), target_shape=(28, 28, 1)),
    tf.keras.layers.Conv2D(kernel_size=3, filters=12, activation='relu'),
    tf.keras.layers.Conv2D(kernel_size=6, filters=24, strides=2, activation='relu'),
    tf.keras.layers.Conv2D(kernel_size=6, filters=32, strides=2, activation='relu'),
    tf.keras.layers.Flatten(),
    tf.keras.layers.Dense(10, activation='softmax')
])

Em uma camada de uma rede convolucional, um "neurônio" faz uma soma ponderada dos pixels logo acima dele, em uma pequena região da imagem. Ele adiciona um viés e alimenta a soma por uma função de ativação, assim como um neurônio em uma camada densa regular. Essa operação é repetida em toda a imagem usando os mesmos pesos. Nas camadas densas, cada neurônio tem os próprios pesos. Aqui, um único "patch" de pesos desliza pela imagem nas duas direções (uma "convolução"). A saída tem tantos valores quanto pixels na imagem (embora seja necessário um pouco de padding nas bordas). É uma operação de filtragem. Na ilustração acima, ele usa um filtro de 4x4x3=48 pesos.

No entanto, 48 ponderações não serão suficientes. Para adicionar mais graus de liberdade, repetimos a mesma operação com um novo conjunto de pesos. Isso gera um novo conjunto de saídas de filtro. Vamos chamar isso de "canal" de saídas por analogia com os canais R, G e B na imagem de entrada.

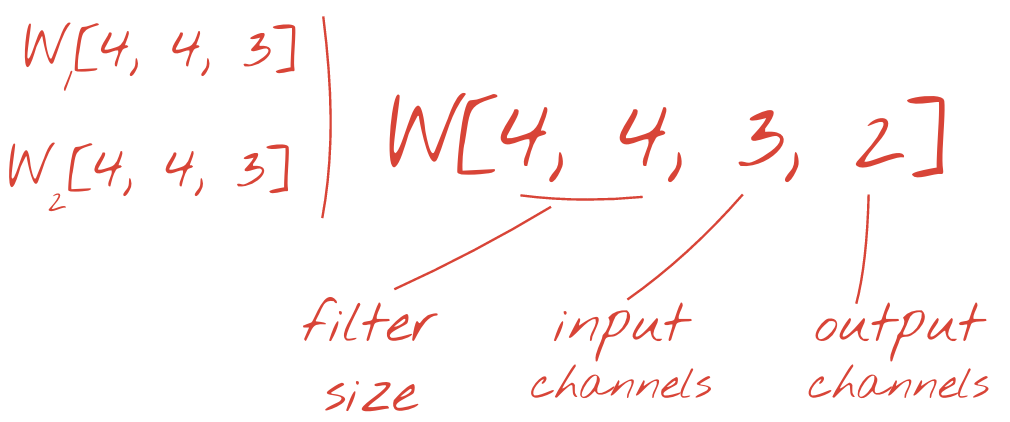
Os dois (ou mais) conjuntos de pesos podem ser somados como um tensor adicionando uma nova dimensão. Isso nos dá a forma genérica do tensor de pesos para uma camada convolucional. Como o número de canais de entrada e saída são parâmetros, podemos começar a empilhar e encadear camadas convolucionais.

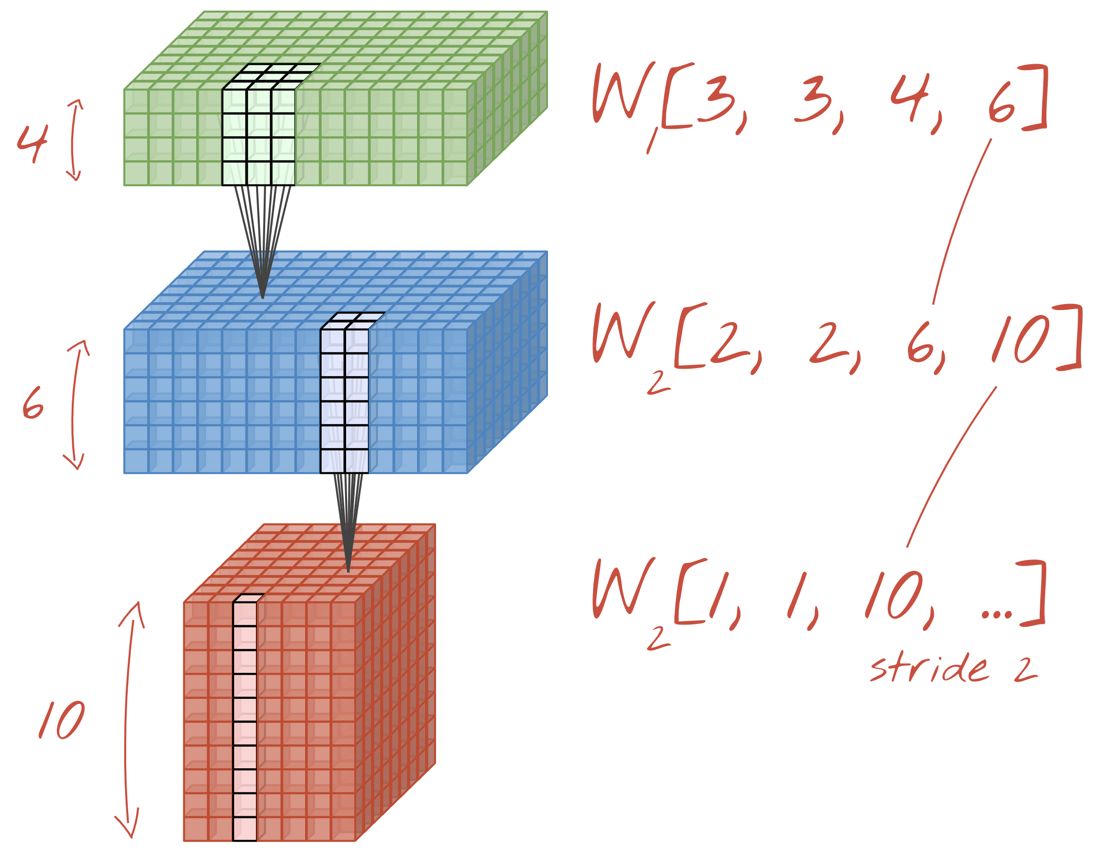
Ilustração: uma rede neural convolucional transforma "cubos" de dados em outros "cubos" de dados.

Convoluções com stride, max pooling

Ao realizar as convoluções com uma taxa de 2 ou 3, também podemos reduzir o cubo de dados resultante nas dimensões horizontais. Há duas maneiras comuns de fazer isso:

• Convolução com stride: um filtro deslizante como acima, mas com um stride > 1
• Agrupamento máximo: uma janela deslizante que aplica a operação MAX (normalmente em patches de 2x2, repetidos a cada 2 pixels)

Ilustração: deslizar a janela de computação em 3 pixels resulta em menos valores de saída. As convoluções com strides ou o agrupamento máximo (máximo em uma janela 2x2 com stride de 2) são uma maneira de reduzir o cubo de dados nas dimensões horizontais.

O max-pooling pode ajudar a entender intuitivamente como as redes convolucionais funcionam: se você presumir que, durante o treinamento, os patches de pesos evoluem para filtros que reconhecem formas básicas (linhas horizontais e verticais, curvas etc.), uma maneira de reduzir as informações úteis é manter nas camadas as saídas em que uma forma foi reconhecida com a intensidade máxima. Na prática, em uma camada de max-pooling, as saídas de neurônios são processadas em grupos de 2x2, e apenas o valor máximo é mantido.

A camada final

Depois da última camada convolucional, os dados estão na forma de um "cubo". Há duas maneiras de fazer isso pela última camada densa.

A primeira é transformar o cubo de dados em um vetor e alimentá-lo na camada softmax. Às vezes, é possível adicionar uma camada densa antes da camada softmax. Isso tende a ser caro em termos de número de pesos. Uma camada densa no final de uma rede convolucional pode conter mais da metade dos pesos de toda a rede neural.

Em vez de usar uma camada densa cara, também podemos dividir o "cubo" de dados recebidos em tantas partes quanto temos classes, calcular a média dos valores e alimentar esses dados com uma função de ativação softmax. Essa forma de criar o cabeçalho de classificação custa 0 pesos. No Keras, há uma camada para isso: tf.keras.layers.GlobalAveragePooling2D().

As redes neurais convolucionais detectam a localização das coisas. Quando um filtro responde fortemente a algum recurso, ele faz isso em um local específico (x, y). Dependendo do que você quer fazer, uma rede neural pode ser treinada para usar ou descartar esses dados de local. Usar o pooling médio global descarta explicitamente todos os dados de local. Isso pode ser bom para um classificador de flores, mas não funciona bem para outras tarefas, como contar flores em uma imagem. Use com cuidado.

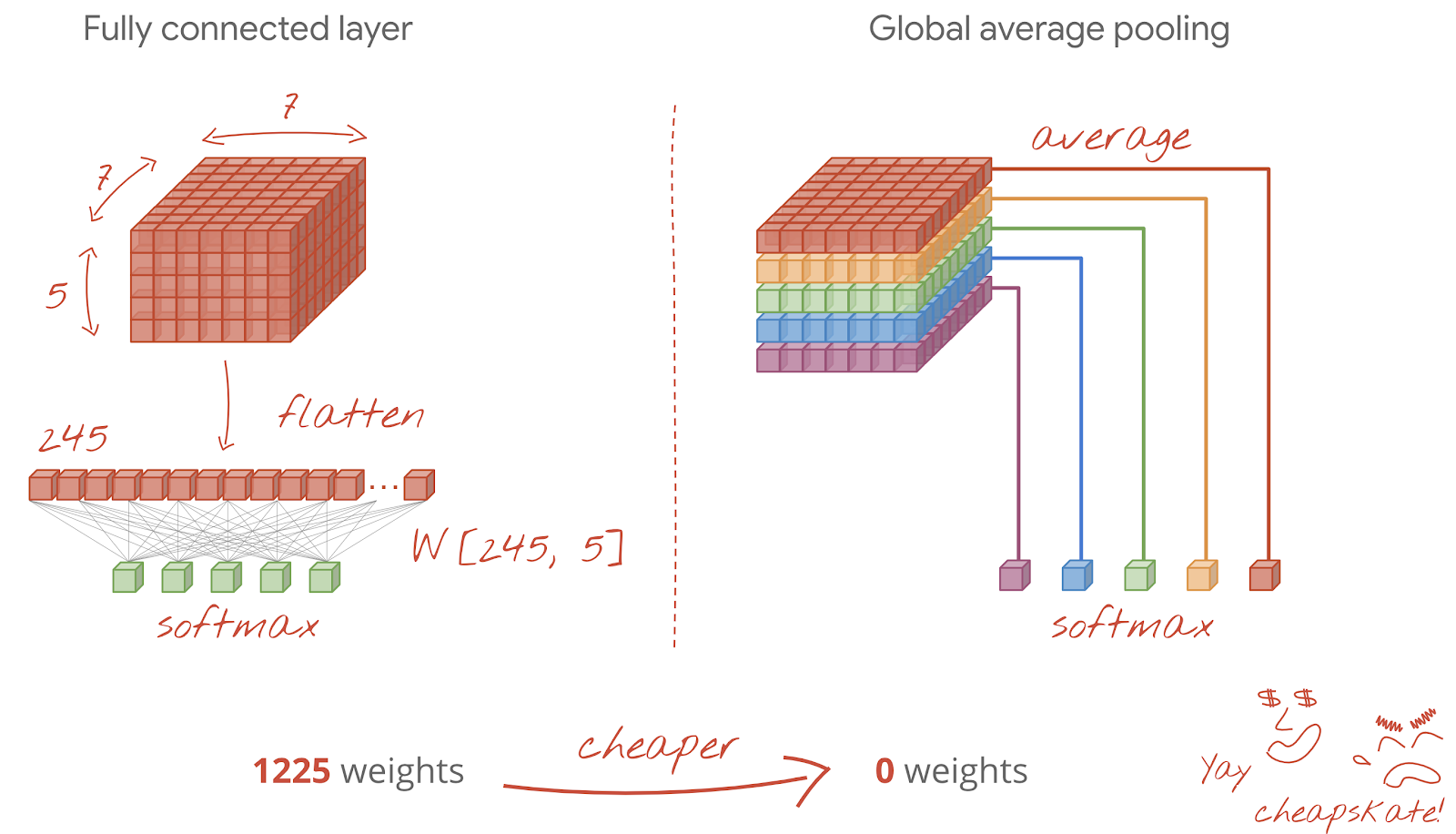
Pule para a próxima seção para criar uma rede convolucional para o problema em questão.

Vamos criar uma rede convolucional para reconhecimento de dígitos escritos à mão. Vamos usar três camadas convolucionais na parte de cima, nossa camada de leitura softmax tradicional na parte de baixo e conectá-las com uma camada totalmente conectada:

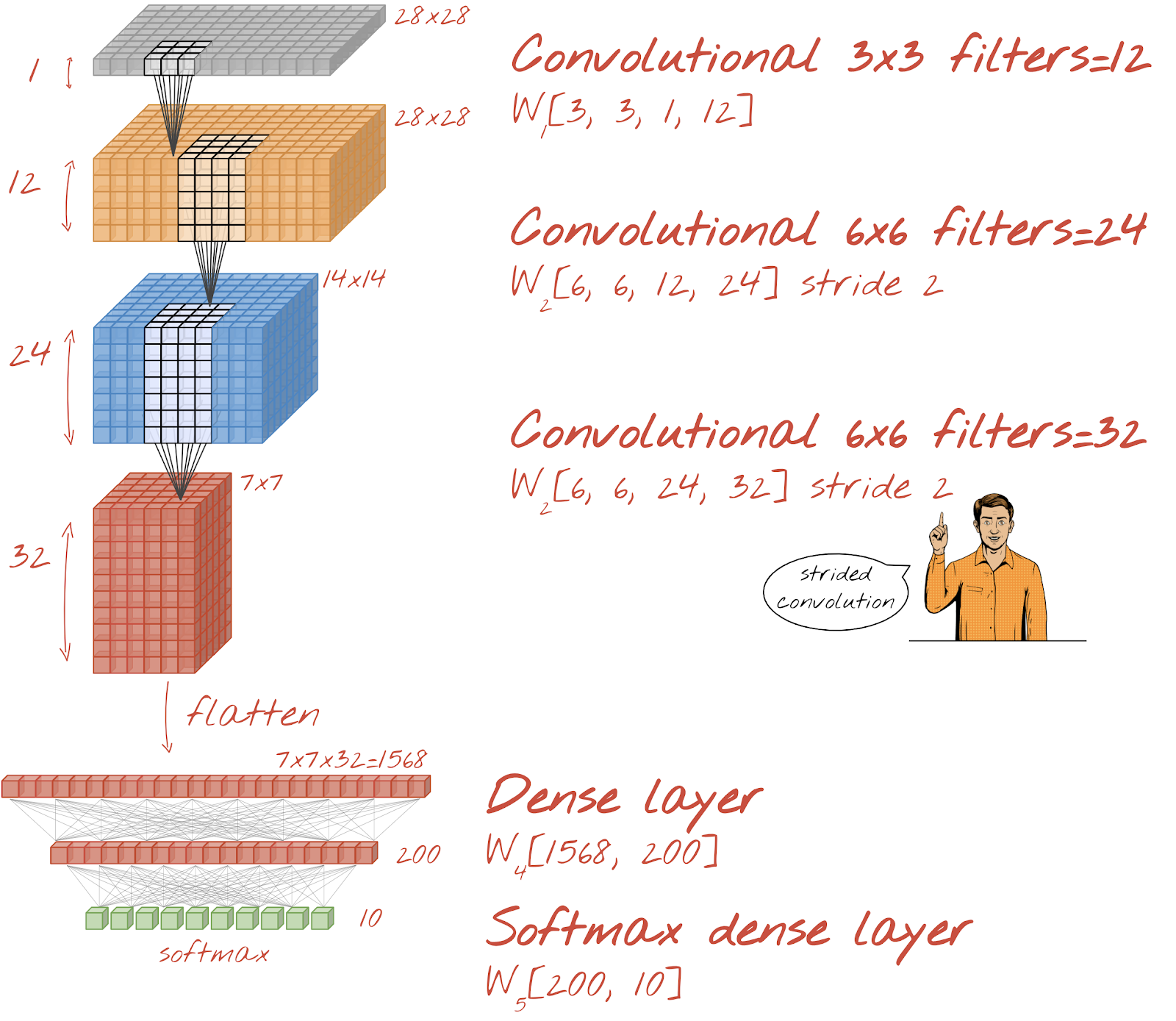
As segunda e terceira camadas convolucionais têm uma passada de dois, o que explica por que elas reduzem o número de valores de saída de 28x28 para 14x14 e depois para 7x7.

Vamos escrever o código do Keras.

É necessário ter atenção especial antes da primeira camada convolucional. Na verdade, ele espera um "cubo" 3D de dados, mas nosso conjunto de dados foi configurado para camadas densas, e todos os pixels das imagens são achatados em um vetor. Precisamos remodelar as imagens de volta para 28x28x1 (1 canal para imagens em escala de cinza):

tf.keras.layers.Reshape(input_shape=(28*28,), target_shape=(28, 28, 1))

Você pode usar essa linha em vez da camada tf.keras.layers.Input que tinha até agora.

Em Keras, a sintaxe de uma camada convolucional ativada por "relu" é:

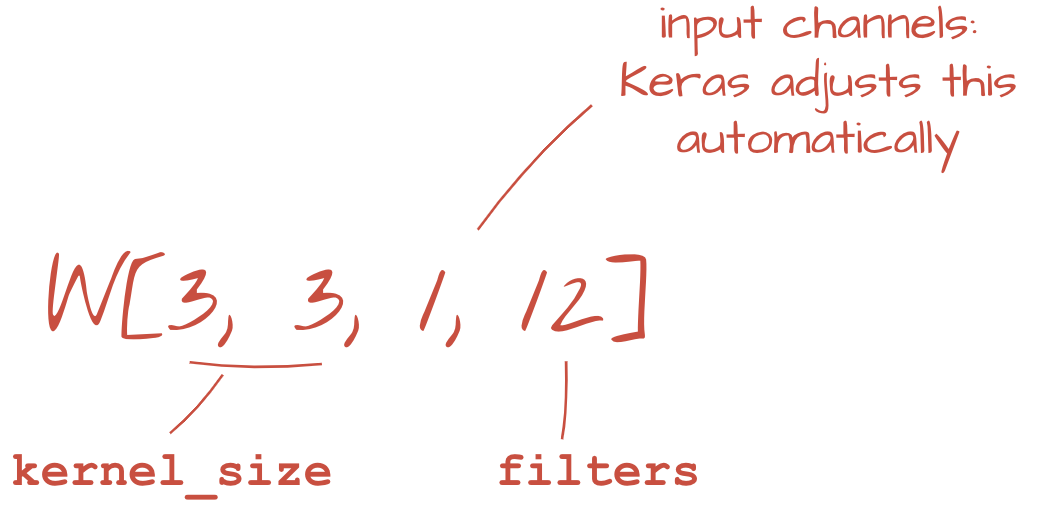
tf.keras.layers.Conv2D(kernel_size=3, filters=12, padding='same', activation='relu')

O parâmetro de padding em camadas convolucionais pode ter dois valores:

• "same": preenche com zeros para produzir saídas da mesma largura/altura da entrada
• "valid": sem padding, apenas pixels reais

Usamos padding aqui. Portanto, defina o padding como "same".

Para uma convolução com strides, você escreveria:

tf.keras.layers.Conv2D(kernel_size=6, filters=24, padding='same', activation='relu', strides=2)

Para transformar um cubo de dados em um vetor para que ele possa ser consumido por uma camada densa:

tf.keras.layers.Flatten()

E para a camada densa, a sintaxe não mudou:

tf.keras.layers.Dense(200, activation='relu')

PRÁTICA:

Modifique seu modelo para transformá-lo em um modelo convolucional. Use os valores do desenho acima para dimensionar. Você pode manter a redução da taxa de aprendizado como estava, mas remova o dropout neste momento.

Aumente também o fator de zoom para 16 em PlotTraining. Isso aumenta o zoom em torno de 0 nas perdas e em torno de 1 nas acurácias para ajudar você a entender o que está acontecendo: PlotTraining(sample_rate=10, zoom=16)

Seu modelo ultrapassou a barreira de 99% de acurácia? Quase lá… mas observe a curva de perda de validação. Isso te lembra de algo?

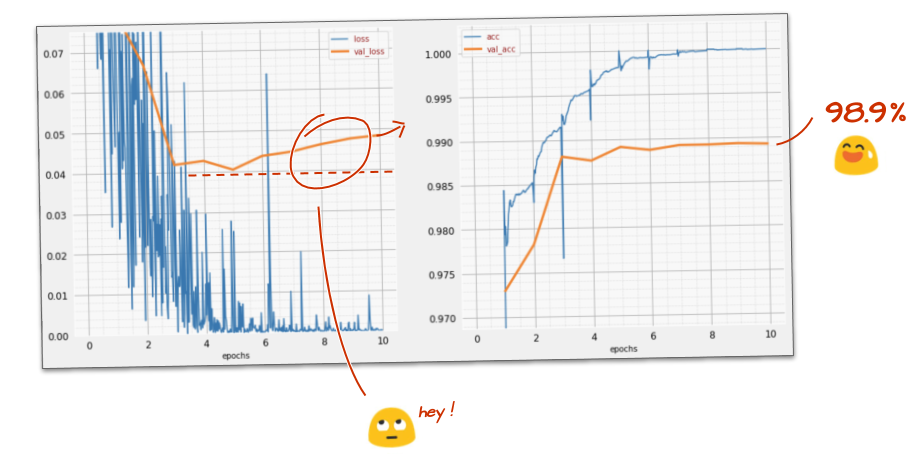
Confira também as previsões. Pela primeira vez, você vai notar que a maioria dos 10.000 dígitos de teste agora é reconhecida corretamente. Restam apenas cerca de 4½ linhas de detecções incorretas (cerca de 110 dígitos de 10.000).

Se você não souber o que fazer, confira a solução neste ponto:

keras_04_mnist_convolutional.ipynb

O treinamento anterior mostra sinais claros de overfitting e ainda não atinge 99% de acurácia. Vamos tentar o dropout de novo?

PRÁTICA:

Adicione uma camada de eliminação entre as duas camadas densas na sua rede. Use uma taxa de dropout de 40% (=0,4):

tf.keras.layers.Dropout(0.4)

É possível aplicar o dropout às camadas convolucionais, mas ele funciona de maneira um pouco diferente e geralmente não é tão eficaz porque há muito menos pesos nas camadas convolucionais e, portanto, menos chances de uma adaptação conjunta ruim. Não vamos abordar isso.

Como foi dessa vez?

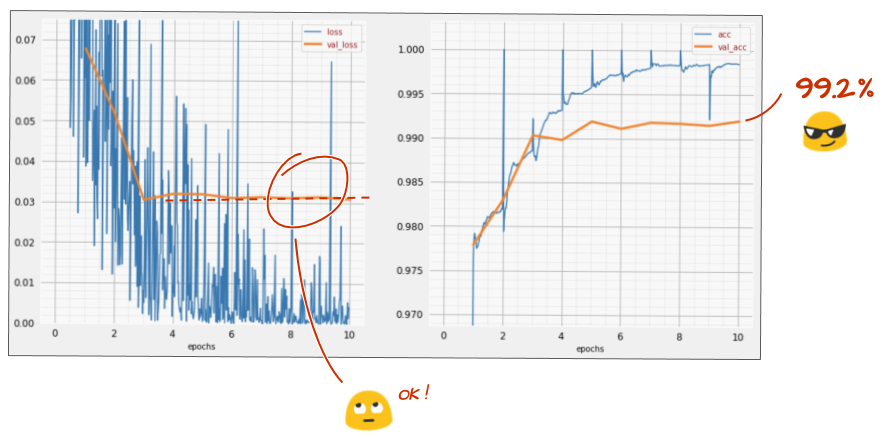
Parece que o dropout funcionou desta vez. A perda de validação não está mais aumentando, e a acurácia final deve ser muito maior que 99%. Parabéns!

Na primeira vez que tentamos aplicar o dropout, achamos que tínhamos um problema de overfitting, quando, na verdade, o problema estava na arquitetura da rede neural. Não poderíamos ir mais longe sem camadas convolucionais, e o dropout não poderia fazer nada a respeito.

Desta vez, parece que o overfitting foi a causa do problema, e o dropout ajudou. Há muitos fatores que podem causar uma desconexão entre as curvas de perda de treinamento e validação, com a perda de validação aumentando. O overfitting (muitos graus de liberdade, usados de maneira inadequada pela rede) é apenas um deles. Se o conjunto de dados for muito pequeno ou a arquitetura da rede neural não for adequada, você poderá observar um comportamento semelhante nas curvas de perda, mas o dropout não vai ajudar.

Por fim, vamos tentar adicionar a normalização em lote.

O que é normalização em lote?

Em resumo, a normalização em lote tenta resolver o problema de como as saídas dos neurônios são distribuídas em relação à função de ativação do neurônio. Em um mini-lote de dados de treinamento, uma saída de neurônio, antes da ativação, pode ter as seguintes distribuições:

Muito à esquerda, depois da ativação sigmoide, esse neurônio quase sempre gera 0.

Muito estreito, esse neurônio nunca gera um 0 ou 1 claro.

Não é tão ruim. O neurônio terá uma variedade razoável de comportamentos nessa minibatches.

Para corrigir isso, a normalização em lote normaliza as saídas de neurônios em um lote de dados de treinamento.Ou seja, ela subtrai a média e divide pelo desvio padrão. No entanto, fazer apenas isso seria muito brutal. Com uma distribuição perfeitamente centralizada e normalmente ampla em todos os lugares, todos os neurônios teriam o mesmo comportamento. O truque é introduzir dois parâmetros aprendíveis adicionais por neurônio, 𝛼 e 𝛽, e calcular:

𝛼 . normalized_out + 𝛽

Em seguida, aplique a função de ativação (sigmoide, relu etc.). Assim, a rede decide, usando o aprendizado de máquina, quanto centralizar e redimensionar em cada neurônio. Fica como exercício para o leitor verificar se há valores de 𝛼 e 𝛽 que podem remover a normalização completamente, se for a coisa certa a fazer.

Na prática, nem sempre é necessário usar 𝛼 e 𝛽. No Keras, eles são chamados de "escala" e "centralização", e você pode usar um ou outro seletivamente. Por exemplo:

tf.keras.layers.BatchNormalization(scale=False, center=True)

O problema com a normalização em lote é que, no momento da previsão, você não tem lotes de treinamento para calcular as estatísticas das saídas dos neurônios. Mas você ainda precisa desses valores. Essa parte é um pouco improvisada. Durante o treinamento, uma média e um desvio padrão de saída de neurônios "típicos" são calculados em um número "suficiente" de lotes, na prática usando uma média exponencial móvel. Essas estatísticas são usadas no momento da inferência.

A boa notícia é que, no Keras, você pode usar uma camada tf.keras.layers.BatchNormalization, e toda essa contabilidade acontece automaticamente.

Essa é a teoria. Na prática, basta lembrar algumas regras:

Normalização em lote "de acordo com o livro":

1. A normalização em lote fica entre a saída de uma camada e a função de ativação dela.
2. Se você usar center=True na normalização em lote, não precisará de vieses na camada. O deslocamento da normalização em lote desempenha a função de uma polarização.
3. Se você usar uma função de ativação invariante de escala (ou seja, que não muda de forma ao ser ampliada), defina scale=False. A ReLU é invariante de escala. A sigmoide não é.

Essa é a teoria, mas a única maneira de descobrir se violar essas regras é ruim é tentar.

Vamos seguir as regras por enquanto e adicionar uma camada de normalização em lote a cada camada da rede neural, exceto a última. Não adicione à última camada "softmax". Não seria útil.

# Modify each layer: remove the activation from the layer itself.
# Set use_bias=False since batch norm will play the role of biases.
tf.keras.layers.Conv2D(..., use_bias=False),
# Batch norm goes between the layer and its activation.
# The scale factor can be turned off for Relu activation.
tf.keras.layers.BatchNormalization(scale=False, center=True),
# Finish with the activation.
tf.keras.layers.Activation('relu'),

Como está a precisão agora?

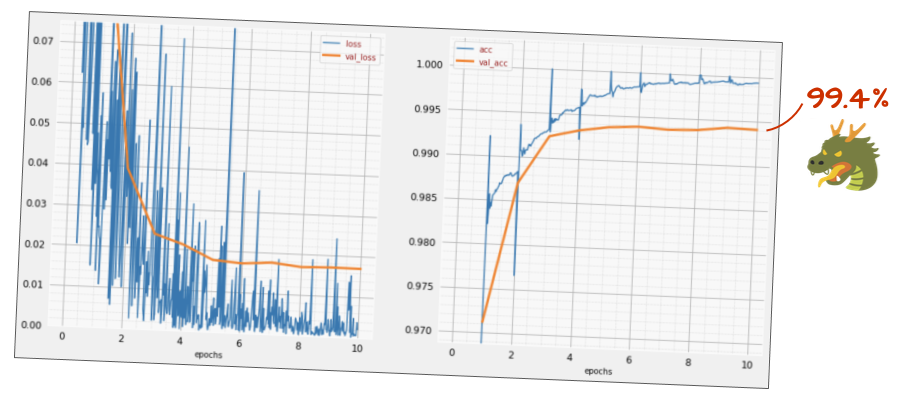
Com um pouco de ajuste (BATCH_SIZE=64, parâmetro de decaimento da taxa de aprendizado 0,666, taxa de dropout na camada densa 0,3) e um pouco de sorte, você pode chegar a 99,5%. As taxas de aprendizado e os ajustes de dropout foram feitos seguindo as práticas recomendadas para usar a normalização em lote:

• A normalização em lote ajuda as redes neurais a convergir e geralmente permite treinar mais rápido.
• A normalização em lote é um regularizador. Normalmente, é possível diminuir a quantidade de dropout usada ou até mesmo não usar esse recurso.

O notebook da solução tem uma execução de treinamento de 99,5%:

keras_05_mnist_batch_norm.ipynb

Você vai encontrar uma versão do código pronta para a nuvem na pasta mlengine no GitHub, além de instruções para executá-la no Google Cloud AI Platform. Antes de executar esta parte, crie uma conta do Google Cloud e ative o faturamento. Os recursos necessários para concluir o laboratório custam menos de alguns dólares (considerando uma hora de treinamento em uma GPU). Para preparar sua conta:

1. Crie um projeto do Google Cloud Platform (http://cloud.google.com/console).
2. Ative o faturamento.
3. Instale as ferramentas de linha de comando do GCP (SDK do GCP aqui).
4. Crie um bucket do Google Cloud Storage (na região us-central1). Ele será usado para testar o código de treinamento e armazenar o modelo treinado.
5. Ative as APIs necessárias e solicite as cotas necessárias. Execute o comando de treinamento uma vez para receber mensagens de erro informando o que precisa ser ativado.

Você criou sua primeira rede neural e a treinou até atingir uma acurácia de 99%. As técnicas aprendidas ao longo do caminho não são específicas do conjunto de dados MNIST. Na verdade, elas são amplamente usadas ao trabalhar com redes neurais. Como um presente de despedida, aqui está o cartão "Cliff's Notes" do laboratório, em versão de desenho animado. Use-o para lembrar o que você aprendeu:

Próximas etapas

• Depois das redes totalmente conectadas e convolucionais, confira as redes neurais recorrentes.
• Para executar o treinamento ou a inferência na nuvem em uma infraestrutura distribuída, o Google Cloud oferece a AI Platform.
  
• Por fim, adoramos receber feedback. Informe se você notar algo errado neste laboratório ou se achar que ele precisa ser melhorado. Tratamos o feedback por problemas do GitHub [link de feedback].

O autor: Martin Görner Twitter: @martin_gorner

Todos os direitos autorais das imagens de desenhos animados neste laboratório: alexpokusay / 123RF stock photos