TensorFlow, Keras ולמידה עמוקה (Deep Learning), ללא דוקטורט

ב-codelab הזה תלמדו איך לבנות ולאמן רשת נוירונים שמזהה ספרות בכתב יד. במהלך התהליך, כשתשפרו את הרשת העצבית כדי להגיע לדיוק של 99%, תגלו גם את הכלים המקצועיים שמשמשים מומחים ללמידה עמוקה לאימון יעיל של המודלים שלהם.

ב-codelab הזה נשתמש במערך הנתונים MNIST, אוסף של 60,000 ספרות מתויגות שהעסיק דורות של דוקטורנטים במשך כמעט שני עשורים. תפתרו את הבעיה עם פחות מ-100 שורות קוד של Python / TensorFlow.

מה תלמדו

• מהי רשת נוירונים ואיך מאמנים אותה
• איך בונים רשת עצבית בסיסית עם שכבה אחת באמצעות tf.keras
• איך מוסיפים עוד שכבות
• איך מגדירים לוח זמנים של שיעורי למידה
• איך יוצרים רשתות נוירונים מלאכותיות
• איך משתמשים בטכניקות רגולריזציה: dropout, batch normalization
• מהי התאמת יתר (overfitting)

מה נדרש

רק דפדפן. אפשר להשתמש בסדנה הזו באופן מלא באמצעות Google Colaboratory.

משוב

אם נתקלתם בבעיה ב-Google Lab הזה או שיש לכם הצעות לשיפור, נשמח לשמוע מכם. אנחנו מטפלים במשוב באמצעות בעיות ב-GitHub [קישור למשוב].

בשיעור ה-Lab הזה נעשה שימוש ב-Google Colaboratory, ולא נדרשת הגדרה מצדכם. אפשר להריץ אותו מ-Chromebook. כדאי לפתוח את הקובץ שלמטה ולהריץ את התאים כדי להכיר את קובצי ה-notebook של Colab.

Welcome to Colab.ipynb

הוראות נוספות מפורטות בהמשך:

בחירת קצה עורפי של GPU

בתפריט Colab, בוחרים באפשרות סביבת זמן הריצה > שינוי הסוג של סביבת זמן הריצה ואז בוחרים באפשרות GPU. החיבור לסביבת זמן הריצה יתבצע באופן אוטומטי בהרצה הראשונה, או שתוכלו להשתמש בלחצן 'חיבור' בפינה השמאלית העליונה.

ביצוע של Notebook

כדי להריץ תאים בזה אחר זה, לוחצים על תא ומקישים על Shift-ENTER. אפשר גם להריץ את כל ה-notebook באמצעות סביבת זמן הריצה > הפעלת הכול

תוכן העניינים

לכל מחברת יש תוכן עניינים. אפשר לפתוח אותו באמצעות החץ השחור בצד ימין.

תאים מוסתרים

בחלק מהתאים יוצג רק השם שלהם. זוהי תכונה ספציפית של מחברת Colab. אפשר ללחוץ עליהם לחיצה כפולה כדי לראות את הקוד שבתוכם, אבל בדרך כלל זה לא מעניין במיוחד. בדרך כלל תומכות בפונקציות של תמיכה או ויזואליזציה. עדיין צריך להריץ את התאים האלה כדי שהפונקציות שבתוכם יוגדרו.

קודם נצפה באימון של רשת נוירונים. עליך לפתוח את ה-notebook שבהמשך ולהריץ את כל התאים. אל תתייחסו לקוד עדיין, נסביר אותו בהמשך.

keras_01_mnist.ipynb

בזמן שמריצים את ה-notebook, מתמקדים בהדמיות. הסברים מופיעים בהמשך.

נתוני אימון

יש לנו מערך נתונים של ספרות בכתב יד שסומנו כך שאנחנו יודעים מה כל תמונה מייצגת, כלומר מספר בין 0 ל-9. במחברת יופיע קטע:

רשת הנוירונים שנבנה תסווג את הספרות הכתובות בכתב יד ב-10 הכיתות שלהן (0, .., 9). הסיווג מתבצע על סמך פרמטרים פנימיים שצריכים להיות בעלי ערך נכון כדי שהסיווג יפעל בצורה טובה. הערך הנכון הזה נלמד בתהליך אימון שדורש 'מערך נתונים עם תוויות' שכולל תמונות ואת התשובות הנכונות שמשויכות אליהן.

איך אפשר לדעת אם רשת הנוירונים שאומנה פועלת טוב או לא? שימוש במערך הנתונים לאימון כדי לבדוק את הרשת יהיה רמאות. המודל כבר ראה את מערך הנתונים הזה כמה פעמים במהלך האימון, והביצועים שלו בו טובים מאוד. אנחנו צריכים עוד מערך נתונים עם תוויות, שלא נראה במהלך האימון, כדי להעריך את הביצועים של הרשת ב'עולם האמיתי'. הוא נקרא מערך נתונים לאימות

קבוצת הנתונים הזו כוללת 50,000 ספרות לאימון. אנחנו מזינים "קבוצה" של 128 ספרות ללולאת האימון בכל איטרציה, כך שהמערכת תראה את כל הספרות לאימון פעם אחת אחרי 391 איטרציות. אנחנו קוראים לזה "תקופה".

יש גם 10,000 ספרות נפרדות של אימות לבדיקת הביצועים של המודל.

הדרכה

במהלך האימון, כל פעם קבוצה אחת של נתוני אימון, הפרמטרים הפנימיים של המודל מתעדכנים והמודל משתפר יותר ויותר בזיהוי הספרות בכתב יד. אפשר לראות את זה בתרשים האימון:

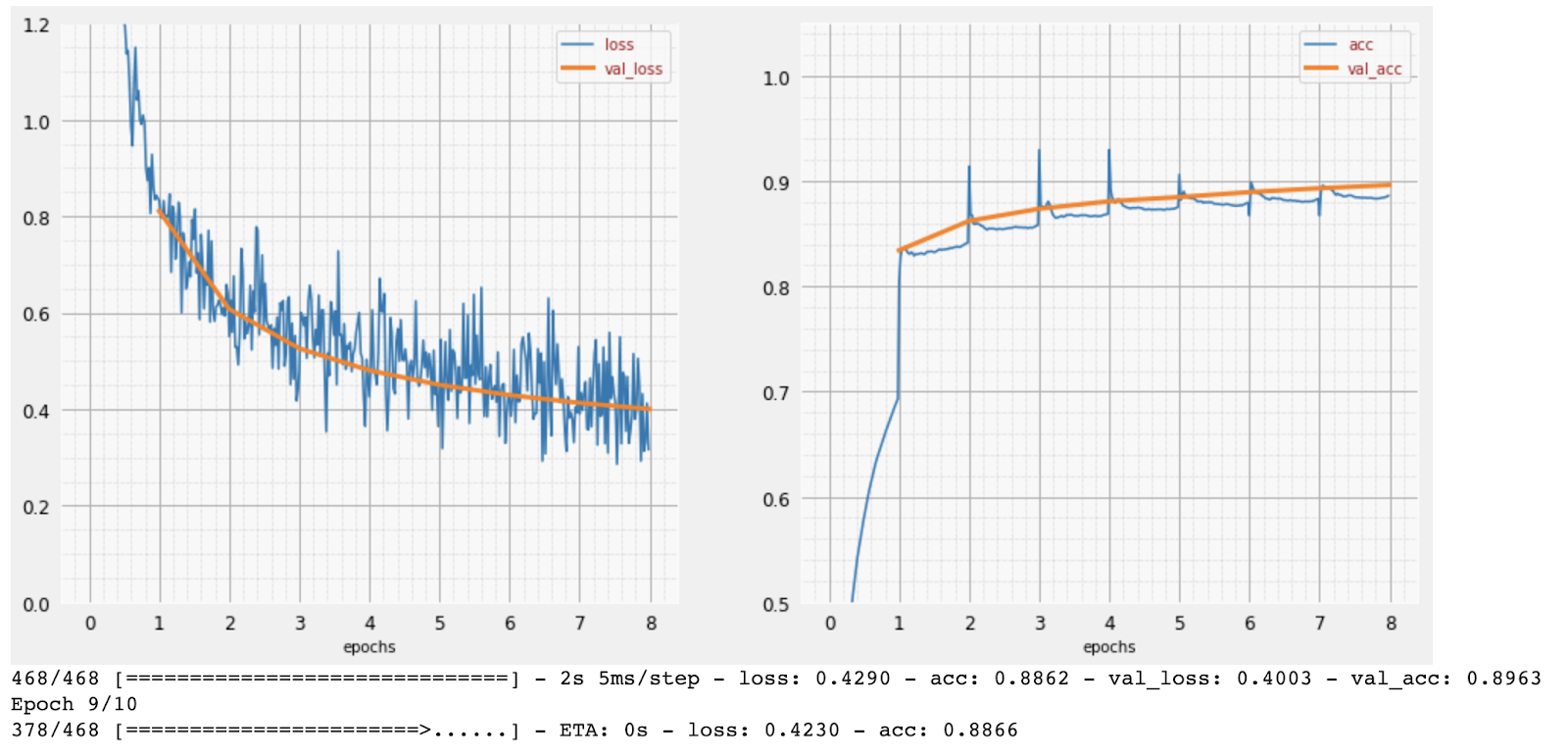
בצד שמאל, הדיוק הוא פשוט אחוז הספרות שזוהו בצורה נכונה. הערך הזה עולה ככל שהאימון מתקדם, וזה טוב.

בצד ימין אפשר לראות את הנתון 'הפסד'. כדי להפעיל את האימון, נגדיר פונקציית הפסד שמייצגת את רמת הדיוק של המערכת בזיהוי הספרות, וננסה למזער אותה. אפשר לראות שההפסד יורד גם בנתוני האימון וגם בנתוני האימות ככל שהאימון מתקדם: זה טוב. כלומר, רשת הנוירונים לומדת.

ציר ה-X מייצג את מספר התקופות של זמן מערכת (epochs) או את מספר האיטרציות על פני מערך הנתונים כולו.

תחזיות

אחרי שהמודל מאומן, אפשר להשתמש בו כדי לזהות ספרות בכתב יד. בתצוגה החזותית הבאה אפשר לראות את הביצועים של המודל על כמה ספרות שרנדרו מגופנים מקומיים (השורה הראשונה), ואז על 10,000 הספרות של מערך הנתונים לאימות. הסיווג החזוי מופיע מתחת לכל ספרה, באדום אם הוא שגוי.

כפי שאפשר לראות, המודל הראשוני הזה לא טוב במיוחד, אבל הוא עדיין מזהה חלק מהספרות בצורה נכונה. רמת הדיוק הסופית של האימות היא בערך 90%, שזה לא רע בשביל מודל פשוט שאיתו אנחנו מתחילים, אבל זה עדיין אומר שהוא מפספס 1,000 ספרות אימות מתוך 10,000. זה הרבה יותר ממה שאפשר להציג, ולכן נראה שכל התשובות שגויות (אדום).

טנסורים

הנתונים מאוחסנים במטריצות. תמונה בגווני אפור בגודל 28x28 פיקסלים מתאימה למטריצה דו-ממדית בגודל 28x28. אבל כדי להגדיר תמונה צבעונית, צריך להגדיר יותר ממד אחד. יש 3 ערכי צבע לכל פיקסל (אדום, ירוק, כחול), ולכן צריך טבלה תלת-ממדית עם המאפיינים [28, 28, 3]. כדי לאחסן קבוצה של 128 תמונות צבעוניות, צריך טבלה ארבע-ממדית עם הממדים [128, 28, 28, 3].

הטבלאות הרב-ממדיות האלה נקראות טנסורים, והרשימה של הממדים שלהן נקראת צורה.

בקצרה

אם אתם כבר מכירים את כל המונחים מודגשים בפסקה הבאה, אתם יכולים לעבור לתרגיל הבא. אם אתם רק מתחילים ללמוד על למידה עמוקה, אתם מוזמנים להמשיך לקרוא.

מסווג רשת נוירונים מורכב מכמה שכבות של נוירונים. לסיווג תמונות, אלה יכולות להיות שכבות צפופות או, בתדירות גבוהה יותר, שכבות קונבולוציוניות. בדרך כלל הן מופעלות באמצעות פונקציית ההפעלה relu. השכבה האחרונה משתמשת במספר נוירונים ששווה למספר הכיתות, והיא מופעלת באמצעות softmax. לסיווג, אנטרופיה צולבת היא פונקציית ההפסד הנפוצה ביותר, שמשווה בין תוויות (כלומר תשובות נכונות) עם קידוד one-hot לבין הסתברויות שחזתה הרשת העצבית. כדי למזער את האובדן, מומלץ לבחור אופטימיזציה עם מומנטום, למשל Adam, ולאמן על קבוצות של תמונות וסיווגים לאימון.

למודלים שנבנים כרצף של שכבות, Keras מציעה את Sequential API. לדוגמה, אפשר לכתוב ב-Keras מסווג תמונות עם שלוש שכבות צפופות כך:

model = tf.keras.Sequential([
    tf.keras.layers.Flatten(input_shape=[28, 28, 1]),
    tf.keras.layers.Dense(200, activation="relu"),
    tf.keras.layers.Dense(60, activation="relu"),
    tf.keras.layers.Dense(10, activation='softmax') # classifying into 10 classes
])

# this configures the training of the model. Keras calls it "compiling" the model.
model.compile(
  optimizer='adam',
  loss= 'categorical_crossentropy',
  metrics=['accuracy']) # % of correct answers

# train the model
model.fit(dataset, ... )

שכבת צפיפות אחת

ספרות בכתב יד במערך הנתונים MNIST הן תמונות בגווני אפור בגודל 28x28 פיקסלים. הגישה הפשוטה ביותר לסיווג שלהם היא להשתמש ב-‎28x28=784 פיקסלים כקלט לרשת עצבית עם שכבה אחת.

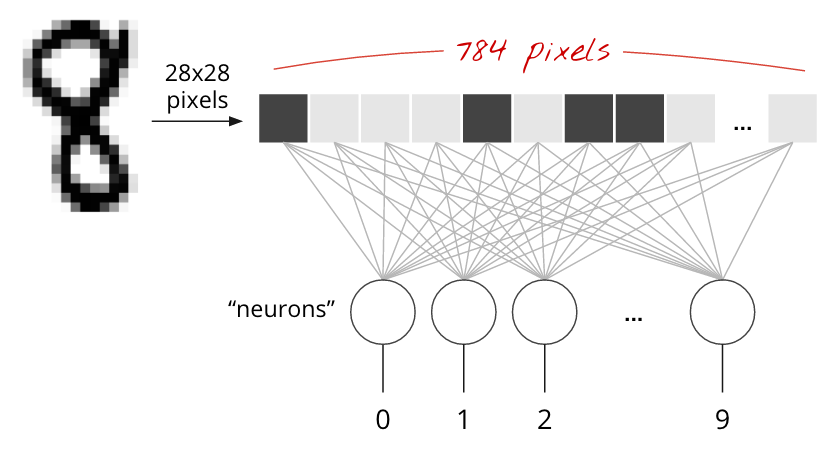
כל נוירון ברשת נוירונים מבצע סכום משוקלל של כל הקלטים שלו, מוסיף קבוע שנקרא 'הטיה' ואז מעביר את התוצאה דרך פונקציית הפעלה לא ליניארית. הפרמטרים weights ו-biases ייקבעו באמצעות אימון. בהתחלה, הם מאותחלים עם ערכים אקראיים.

התמונה שלמעלה מייצגת רשת נוירונים עם שכבה אחת ו-10 נוירונים של פלט, כי אנחנו רוצים לסווג ספרות ל-10 מחלקות (0 עד 9).

באמצעות כפל מטריצות

כך אפשר לייצג שכבת רשת נוירונים, שמבצעת עיבוד של אוסף תמונות, באמצעות כפל מטריצות:

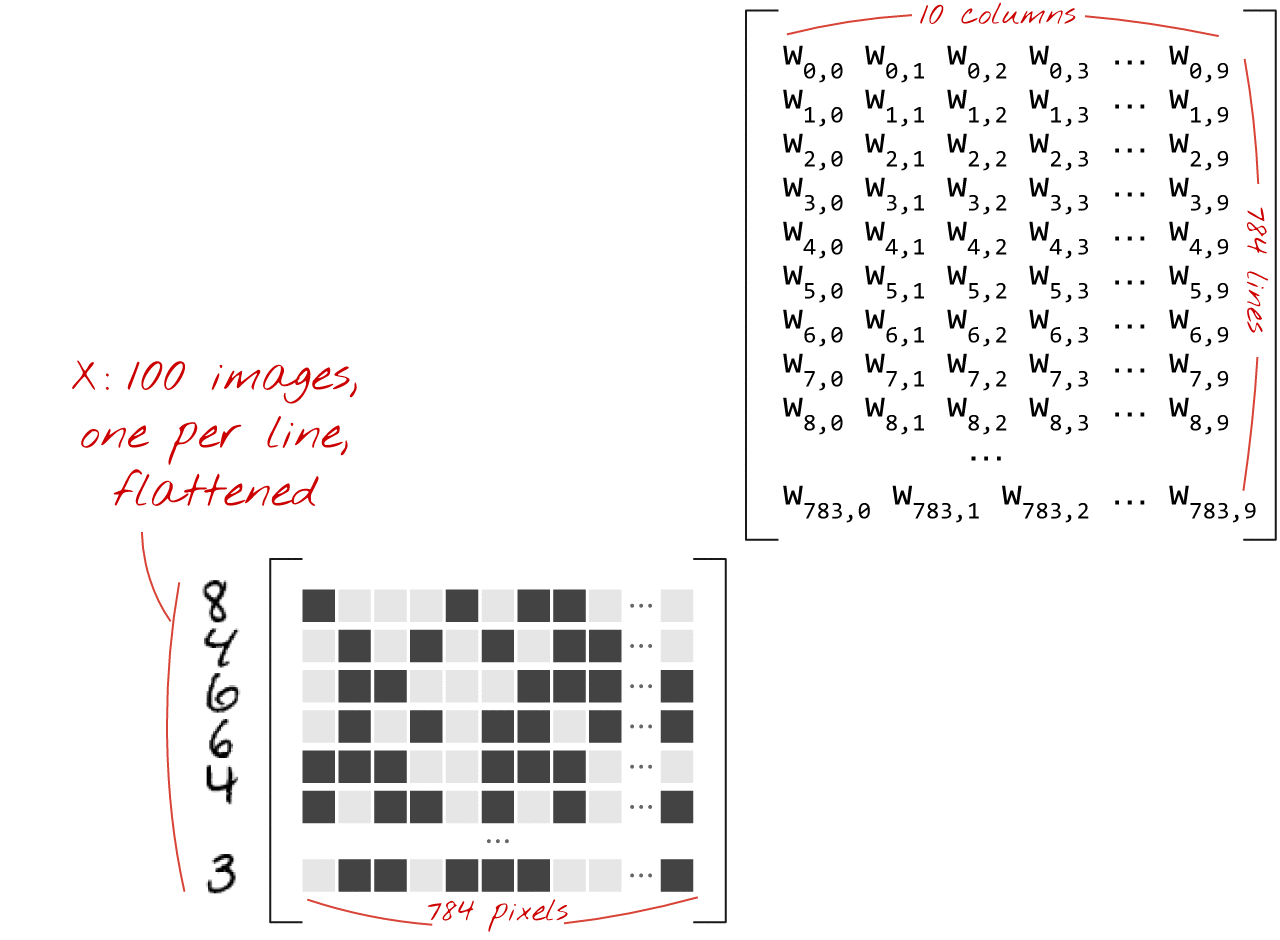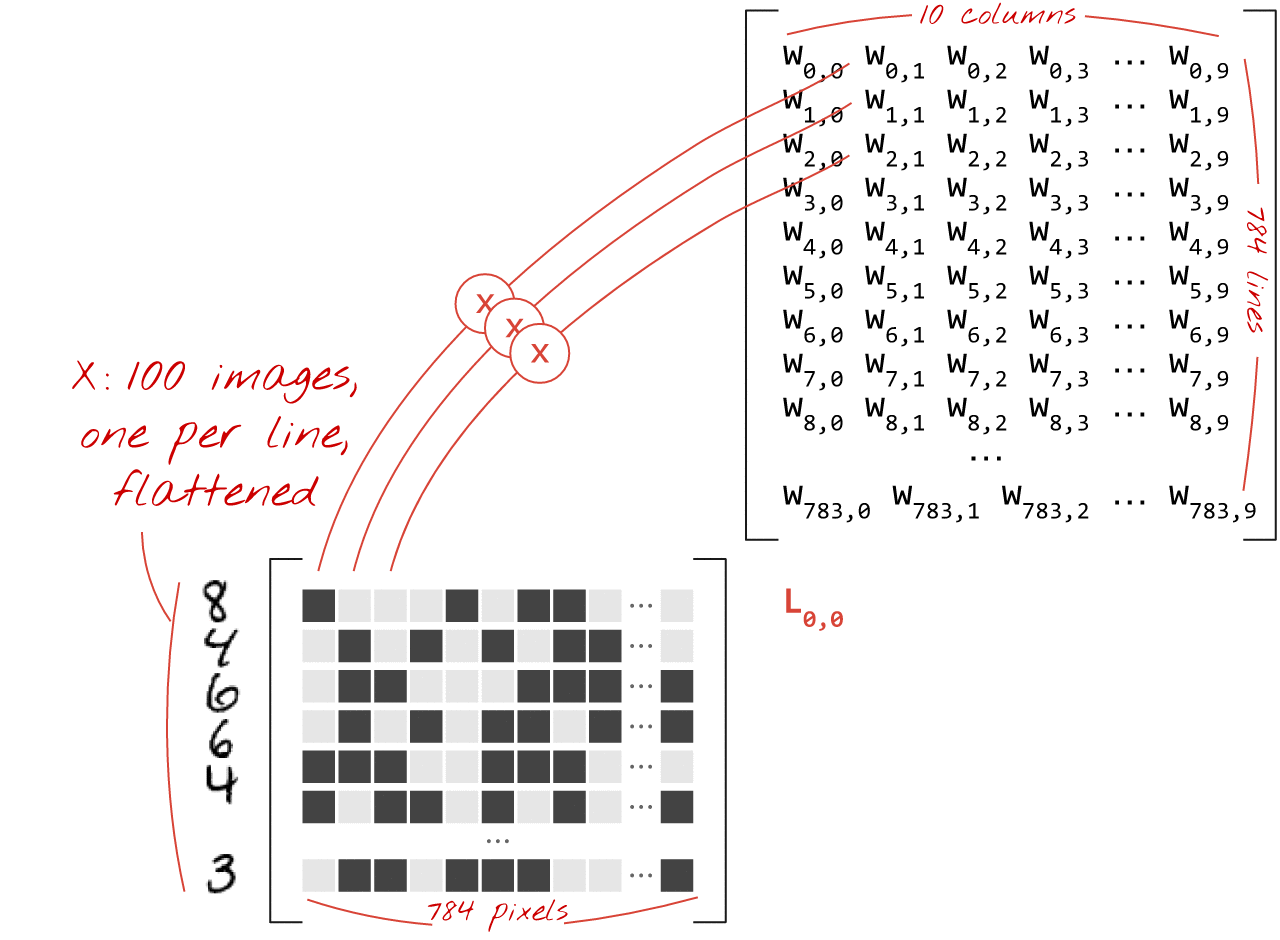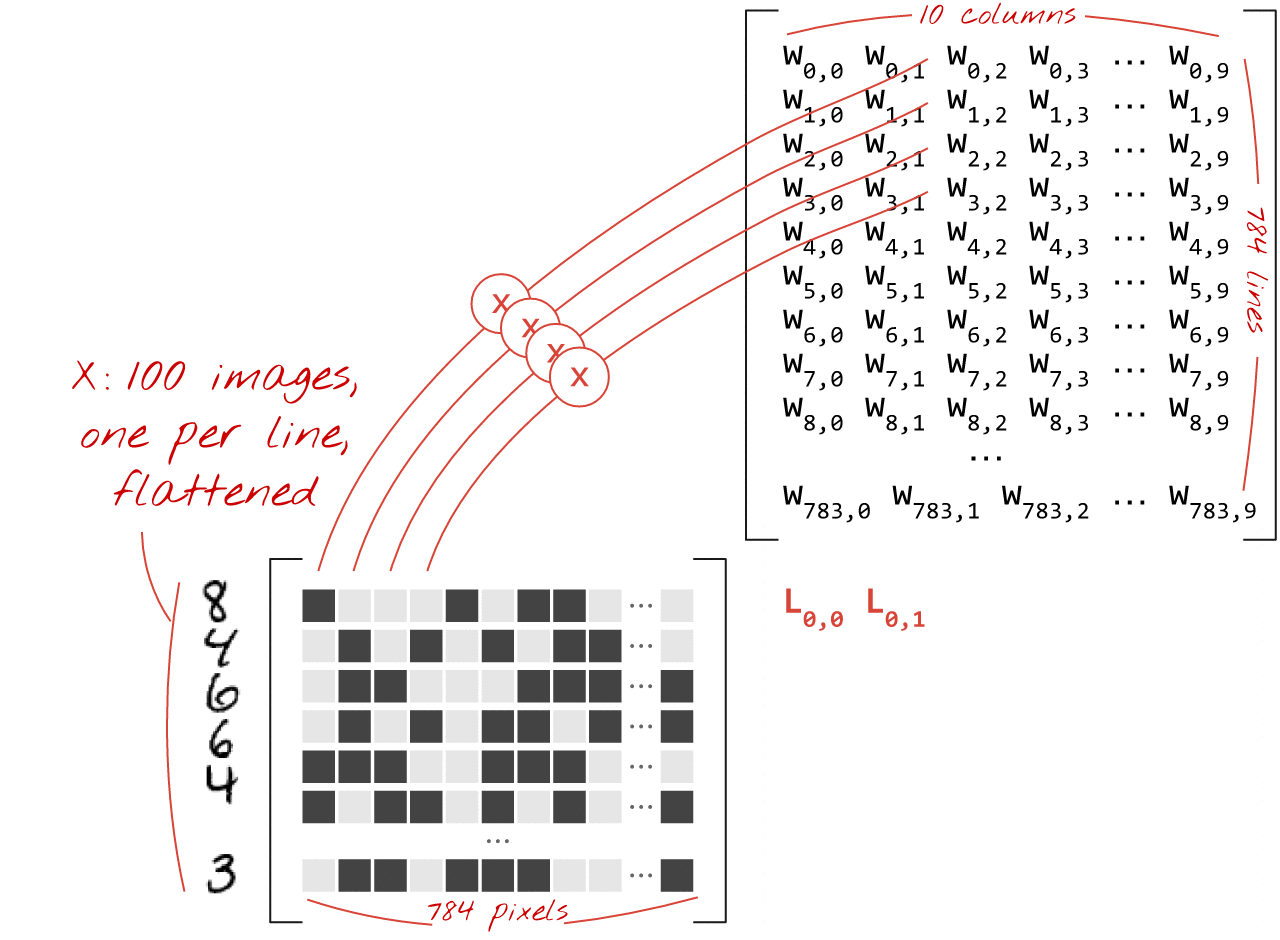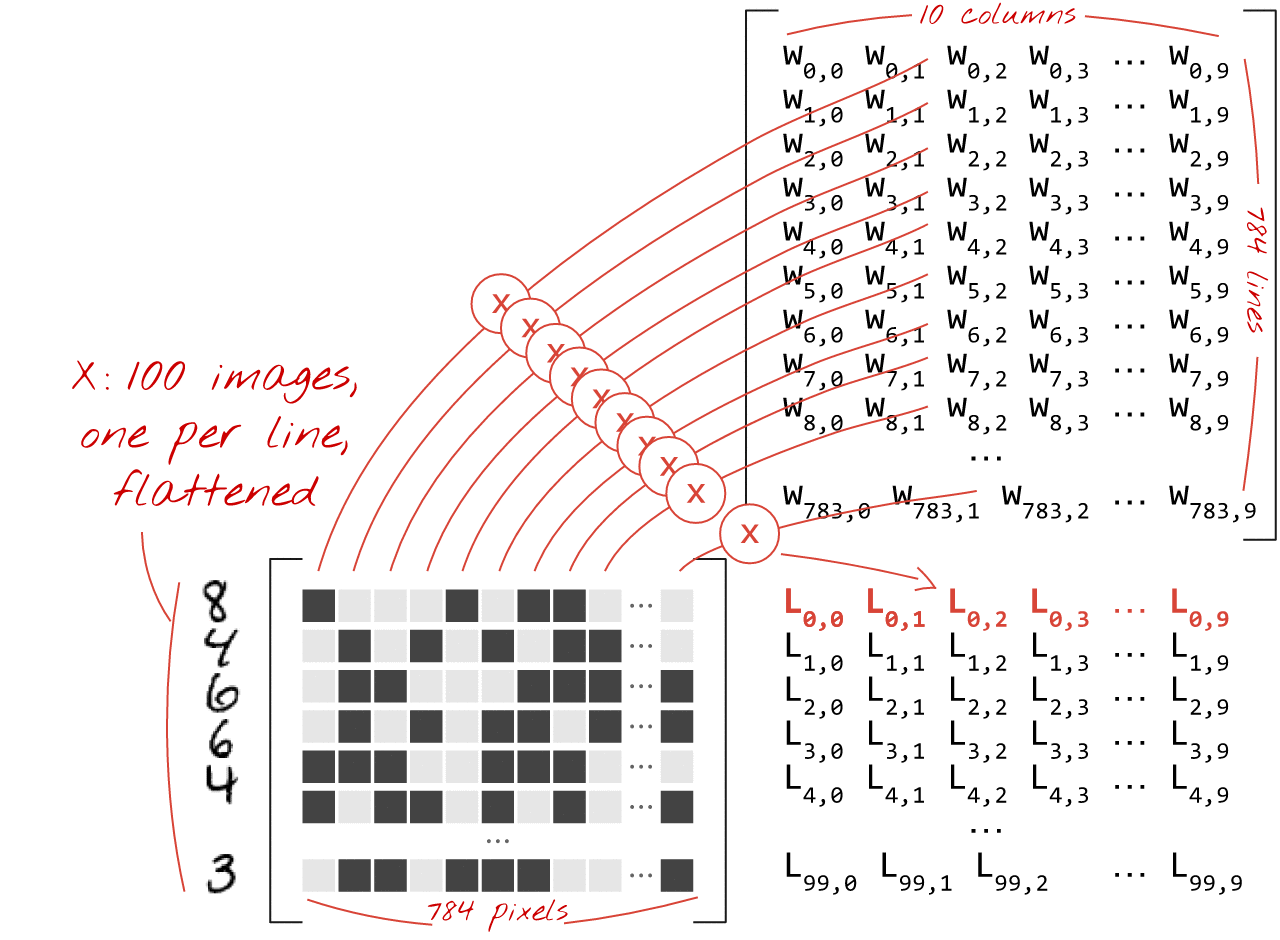
באמצעות העמודה הראשונה של המשקלים במטריצת המשקלים W, אנחנו מחשבים את הסכום המשוקלל של כל הפיקסלים בתמונה הראשונה. הסכום הזה תואם לנוירון הראשון. באמצעות העמודה השנייה של המשקלים, אנחנו עושים את אותו הדבר לנוירון השני וכן הלאה עד הנוירון העשירי. לאחר מכן נוכל לחזור על הפעולה לגבי 99 התמונות הנותרות. אם נסמן ב-X את המטריצה שמכילה את 100 התמונות שלנו, כל הסכומים המשוקללים של 10 הנוירונים שלנו, שמחושבים על 100 תמונות, הם פשוט X.W, כלומר כפל מטריצות.

עכשיו צריך להוסיף לכל נוירון את ההטיה שלו (קבוע). מכיוון שיש לנו 10 נוירונים, יש לנו 10 קבועי הטיה. נקרא לווקטור הזה של 10 ערכים b. צריך להוסיף אותו לכל שורה במטריצה שחושבה קודם. בעזרת קצת קסם שנקרא 'שידור', נכתוב את זה עם סימן פלוס פשוט.

‫Broadcasting הוא טריק סטנדרטי שמשמש ב-Python וב-numpy, ספריית החישובים המדעיים שלה. היא מרחיבה את האופן שבו פעולות רגילות פועלות על מטריצות עם מימדים לא תואמים. 'שידור של הוספה' פירושו: 'אם מוסיפים שתי מטריצות אבל אי אפשר כי המימדים שלהן לא תואמים, צריך לנסות לשכפל את המטריצה הקטנה כמה שצריך כדי שהפעולה תצליח'.

לבסוף, אנחנו מפעילים פונקציית הפעלה, למשל softmax (מוסבר בהמשך), ומקבלים את הנוסחה שמתארת רשת עצבית עם שכבה אחת, שמוחלת על 100 תמונות:

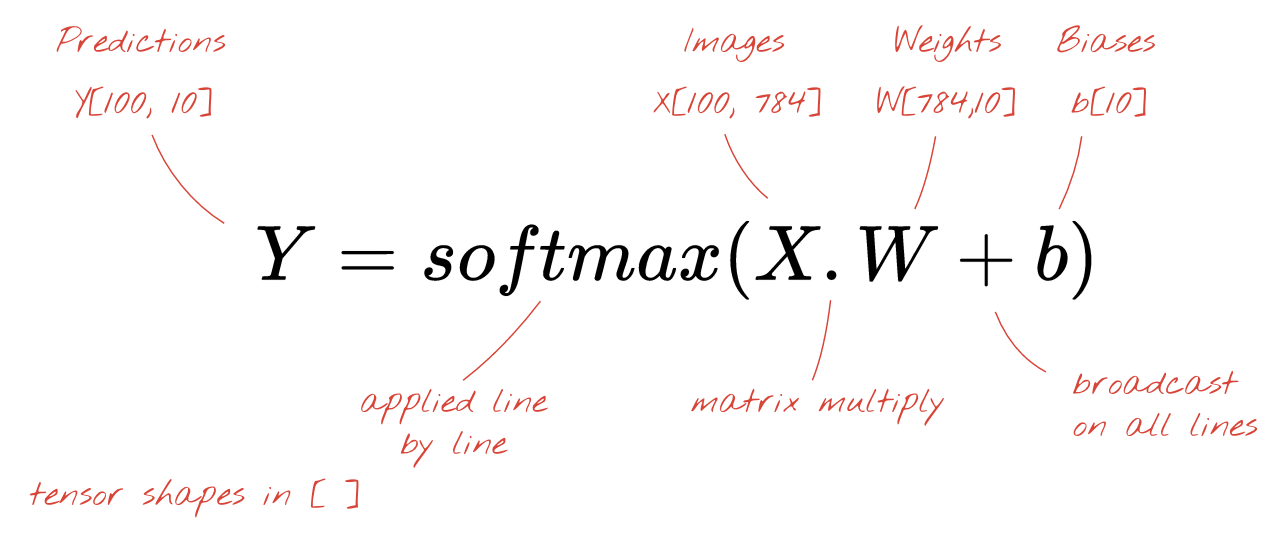
ב-Keras

אם משתמשים בספריות של רשתות עצביות ברמה גבוהה כמו Keras, לא צריך להטמיע את הנוסחה הזו. עם זאת, חשוב להבין ששכבת רשת עצבית היא בסך הכול אוסף של פעולות כפל וחיבור. ב-Keras, שכבה צפופה תיכתב כך:

tf.keras.layers.Dense(10, activation='softmax')

להעמיק

קל מאוד לשרשר שכבות של רשתות נוירונים. השכבה הראשונה מחשבת סכומים משוקללים של פיקסלים. שכבות עוקבות מחשבות סכומים משוקללים של הפלטים של השכבות הקודמות.

ההבדל היחיד, מלבד מספר הנוירונים, יהיה הבחירה של פונקציית ההפעלה.

פונקציות הפעלה: relu, ‏ softmax ו-sigmoid

בדרך כלל משתמשים בפונקציית ההפעלה relu בכל השכבות מלבד האחרונה. השכבה האחרונה, במסווג, תשתמש בהפעלה מסוג softmax.

שוב, 'נוירון' מחשב סכום משוקלל של כל הקלטים שלו, מוסיף ערך שנקרא 'הטיה' ומעביר את התוצאה דרך פונקציית ההפעלה.

פונקציית ההפעלה הכי פופולרית נקראת "RELU", קיצור של Rectified Linear Unit (יחידה ליניארית מתוקנת). זו פונקציה פשוטה מאוד, כפי שאפשר לראות בגרף שלמעלה.

פונקציית ההפעלה המסורתית ברשתות עצביות הייתה 'סיגמואיד', אבל הוכח שלפונקציה 'relu' יש מאפייני התכנסות טובים יותר כמעט בכל מקום, ולכן היא עדיפה כיום.

הפעלת Softmax לסיווג

השכבה האחרונה של הרשת העצבית שלנו כוללת 10 נוירונים, כי אנחנו רוצים לסווג ספרות בכתב יד ל-10 מחלקות (0 עד 9). הפלט צריך להיות 10 מספרים בין 0 ל-1 שמייצגים את ההסתברות לכך שהספרה הזו תהיה 0, 1, 2 וכן הלאה. לשם כך, בשכבה האחרונה נשתמש בפונקציית הפעלה שנקראת softmax.

כדי להחיל softmax על וקטור, מחשבים את האקספוננט של כל רכיב ואז מבצעים נורמליזציה של הווקטור, בדרך כלל על ידי חלוקה בנורמה L1 (כלומר, סכום הערכים המוחלטים) כדי שהערכים המנורמלים יסתכמו ל-1 ויהיה אפשר לפרש אותם כהסתברויות.

הפלט של השכבה האחרונה, לפני ההפעלה, נקרא לפעמים "לוגיטים". אם הווקטור הזה הוא L = [L0, L1, L2, L3, L4, L5, L6, L7, L8, L9], אז:

למה הפונקציה softmax נקראת כך? הפונקציה המעריכית היא פונקציה עולה בצורה חדה. היא תגדיל את ההבדלים בין התפוקות של הנוירונים. לאחר מכן, כשמנרמלים את הווקטור, הרכיב הגדול ביותר, שהוא הרכיב הדומיננטי בנורמה, ינורמל לערך שקרוב ל-1, וכל שאר הרכיבים יחולקו בערך גדול וינורמלו לערך שקרוב ל-0. הווקטור שמתקבל מראה בבירור איזו מחלקה היא המנצחת, כלומר המחלקה עם הערך המקסימלי, אבל הוא שומר על הסדר היחסי המקורי של הערכים, ולכן הוא נקרא 'רך'.

Cross-entropy loss

עכשיו, אחרי שרשת הנוירונים שלנו מייצרת תחזיות מתמונות קלט, אנחנו צריכים למדוד את רמת הדיוק שלהן, כלומר את המרחק בין מה שהרשת אומרת לנו לבין התשובות הנכונות, שלרוב נקראות 'תוויות'. חשוב לזכור שיש לנו תוויות נכונות לכל התמונות במערך הנתונים.

כל מרחק יתאים, אבל לבעיות סיווג, מה שנקרא 'מרחק אנטרופיה צולבת' הוא היעיל ביותר. נקרא לזה פונקציית השגיאה או 'ההפסד':

קידוד one-hot (חם-יחיד) אומר שאתם מייצגים את התווית 'זהו הספרה 3' באמצעות וקטור של 10 ערכים, כולם אפסים חוץ מהערך השלישי שהוא 1. הווקטור הזה מייצג הסתברות של 100% להיות 'הספרה 3'. רשת הנוירונים שלנו גם מוציאה את התחזיות שלה כווקטור של 10 ערכי הסתברות. קל להשוות ביניהם.

Gradient descent

'אימון' רשת הנוירונים בעצם אומר שימוש בתמונות ובתוויות אימון כדי להתאים את המשקלים וההטיות, כך שפונקציית אובדן האנטרופיה הצולבת תהיה מינימלית. כך זה עובד.

האנטרופיה הצולבת היא פונקציה של משקלים, הטיה, פיקסלים של תמונת האימון והסיווג הידוע שלה.

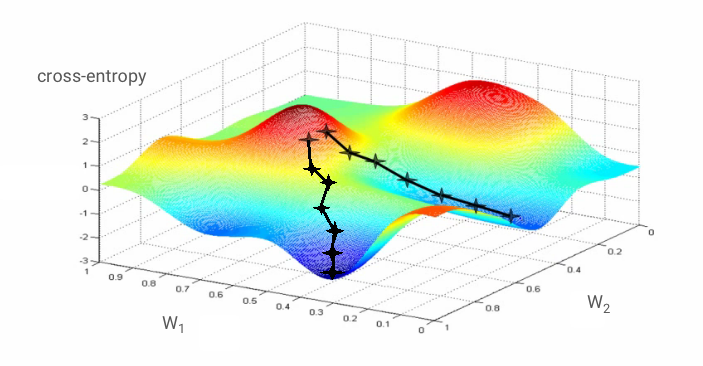
אם נחשב את הנגזרות החלקיות של האנטרופיה הצולבת ביחס לכל המשקלים ולכל ההטיות, נקבל 'גרדיאנט', שמחושב עבור תמונה, תווית וערך נוכחי של משקלים והטיות. חשוב לזכור שיכולים להיות מיליוני משקלים והטיות, ולכן חישוב הגרדיאנט נשמע כמו עבודה רבה. למזלנו, TensorFlow עושה את זה בשבילנו. המאפיין המתמטי של גרדיאנט הוא שהוא מצביע "למעלה". אנחנו רוצים להגיע למקום שבו האנטרופיה הצולבת נמוכה, ולכן נלך בכיוון ההפוך. אנחנו מעדכנים את המשקלים וההטיות בחלק קטן מהגרדיאנט. לאחר מכן אנחנו חוזרים על הפעולה שוב ושוב באמצעות קבוצות התמונות והתוויות הבאות לאימון, בלולאת אימון. התהליך הזה אמור להוביל למצב שבו האנטרופיה הצולבת היא מינימלית, אבל אין ערובה לכך שהמינימום הזה הוא ייחודי.

‫Learning rate (קצב למידה): אי אפשר לעדכן את המשקלים וההטיות לפי האורך המלא של הגרדיאנט בכל איטרציה. זה כמו לנסות להגיע לתחתית של עמק כשנועלים מגפיים של שבע ליגות. אתם קופצים מצד אחד של העמק לצד השני. כדי להגיע לתחתית, צריך לבצע צעדים קטנים יותר, כלומר להשתמש רק בחלק קטן מהשיפוע, בדרך כלל בטווח של 1/1000. השבר הזה נקרא 'קצב הלמידה'.

שימוש ב-mini-batching ובמומנטום

אפשר לחשב את הגרדיאנט רק על תמונה לדוגמה אחת ולעדכן את המשקלים וההטיות באופן מיידי, אבל אם עושים את זה על קבוצה של 128 תמונות לדוגמה, מקבלים גרדיאנט שמייצג טוב יותר את האילוצים שמוטלים על ידי תמונות לדוגמה שונות, ולכן סביר להניח שהפתרון יתקבל מהר יותר. גודל המיני-אצווה הוא פרמטר שניתן להתאמה.

לטכניקה הזו, שנקראת לפעמים "ירידה סטוכסטית של גרדיאנט", יש יתרון פרגמטי נוסף: עבודה עם אצוות פירושה גם עבודה עם מטריצות גדולות יותר, ובדרך כלל קל יותר לבצע אופטימיזציה שלהן במעבדי GPU וב-TPU.

עם זאת, יכול להיות שההתכנסות תהיה קצת כאוטית, ואפילו תיפסק אם וקטור הגרדיאנט יהיה אפס. האם זה אומר שמצאנו מינימום? לא תמיד. רכיב של מעבר צבע יכול להיות אפס במינימום או במקסימום. אם יש וקטור גרדיאנט עם מיליוני רכיבים, וכולם אפסים, ההסתברות שכל אפס מתאים לנקודת מינימום ואף אחד מהם לא מתאים לנקודת מקסימום היא די קטנה. במרחב עם הרבה ממדים, נקודות אוכף הן די נפוצות ואנחנו לא רוצים לעצור בהן.

איור: נקודת אוכף. השיפוע הוא 0, אבל זה לא מינימום בכל הכיוונים. (שיוך התמונה Wikimedia: By Nicoguaro - Own work, CC BY 3.0)

הפתרון הוא להוסיף לאלגוריתם האופטימיזציה תנופה מסוימת, כדי שהוא יוכל לעבור את נקודות האוכף בלי לעצור.

ספריית TensorFlow מספקת מגוון רחב של אופטימיזציות, החל מ-tf.train.GradientDescentOptimizer. אופטימיזטורים פופולריים מתקדמים יותר עם מומנטום מובנה הם tf.train.RMSPropOptimizer או tf.train.AdamOptimizer.

מילון מונחים

אצווה או אצווה קטנה: האימון מתבצע תמיד על אצוות של נתוני אימון ותוויות. הפעולה הזו עוזרת לאלגוריתם להגיע למצב של התכנסות. המאפיין 'batch' הוא בדרך כלל המאפיין הראשון של טנסורים של נתונים. לדוגמה, טנסור בצורה [100, 192, 192, 3] מכיל 100 תמונות בגודל 192x192 פיקסלים עם שלושה ערכים לכל פיקסל (RGB).

פונקציית אובדן של אנטרופיה צולבת: פונקציית אובדן מיוחדת שמשמשת לעיתים קרובות בסיווגים.

שכבה צפופה: שכבה של נוירונים שבה כל נוירון מחובר לכל הנוירונים בשכבה הקודמת.

תכונות: הקלטים של רשת נוירונים נקראים לפעמים 'תכונות'. האומנות של הבנת החלקים של מערך נתונים (או שילובים של חלקים) שצריך להזין לרשת נוירונים כדי לקבל תחזיות טובות נקראת 'הנדסת תכונות'.

תוויות: שם נוסף ל'סיווגים' או לתשובות נכונות בבעיית סיווג בפיקוח

קצב הלמידה: חלק מהשיפוע שלפיו המשקלים וההטיות מתעדכנים בכל איטרציה של לולאת האימון.

לוגיטים: הפלט של שכבת נוירונים לפני החלת פונקציית ההפעלה נקרא 'לוגיטים'. המונח הזה מגיע מהפונקציה הלוגיסטית, שנקראת גם פונקציית סיגמואיד, שהייתה פונקציית ההפעלה הכי פופולרית. השם 'Neuron outputs before logistic function' (פלט של נוירון לפני פונקציית לוגיסטיקה) קוצר ל-'logits'.

‫loss: פונקציית השגיאה שמשווה בין התפוקות של הרשת הנוירונית לבין התשובות הנכונות

נוירון: מחשב את הסכום המשוקלל של הקלט שלו, מוסיף הטיה ומעביר את התוצאה דרך פונקציית הפעלה.

קידוד "חם-יחיד": מחלקה 3 מתוך 5 מקודדת כווקטור של 5 אלמנטים, כולם אפסים חוץ מהאלמנט השלישי שהוא 1.

‫relu: יחידה לינארית מתוקנת. פונקציית הפעלה פופולרית לנוירונים.

‫sigmoid: פונקציית הפעלה נוספת שהייתה פופולרית בעבר ועדיין שימושית במקרים מיוחדים.

‫softmax: פונקציית הפעלה מיוחדת שפועלת על וקטור, מגדילה את ההפרש בין הרכיב הגדול ביותר לבין כל שאר הרכיבים, וגם מבצעת נורמליזציה של הווקטור כך שהסכום שלו יהיה 1, כדי שאפשר יהיה לפרש אותו כווקטור של הסתברויות. משמש כשלב האחרון בסיווגים.

‫tensor: טנזור הוא כמו מטריצה, אבל עם מספר שרירותי של ממדים. טנסור חד-ממדי הוא וקטור. טנסור דו-ממדי הוא מטריצה. אחר כך אפשר ליצור טנסורים עם 3, 4, 5 או יותר מימדים.

חוזרים למחברת המחקר, והפעם קוראים את הקוד.

keras_01_mnist.ipynb

תרגול מעשי:

בקטע הזה, המשימה שלכם היא לקרוא את הקוד ולהבין אותו כדי שתוכלו לשפר אותו בהמשך.

בואו נעבור על כל התאים ב-notebook הזה.

התא 'פרמטרים'

כאן מוגדרים גודל האצווה, מספר התקופות של זמן המערכת ומיקום קובצי הנתונים. קובצי הנתונים מתארחים בקטגוריה ב-Google Cloud Storage ‏ (GCS), ולכן הכתובת שלהם מתחילה ב-gs://

התא 'ייבוא'

כאן מיובאות כל ספריות Python הנדרשות, כולל TensorFlow וגם matplotlib להדמיות.

תא visualization utilities [RUN ME]

התא הזה מכיל קוד ויזואליזציה לא מעניין. הוא מכווץ כברירת מחדל, אבל אפשר לפתוח אותו ולעיין בקוד כשמתפנה זמן, באמצעות לחיצה כפולה עליו.

חובה להריץ את התא הזה (SHIFT-ENTER), אחרת הפונקציות שמוגדרות בתוכו לא ינותחו ותקבלו שגיאות בהמשך.

תא tf.data.Dataset: parse files and prepare training and validation datasets

התא הזה השתמש ב-tf.data.Dataset API כדי לטעון את מערך הנתונים MNIST מקובצי הנתונים. לא צריך להשקיע יותר מדי זמן בתא הזה. אם אתם רוצים ללמוד על tf.data.Dataset API, תוכלו לעיין במדריך הבא: צינורות להעברת נתונים במהירות TPU. בשלב הזה, העקרונות הבסיסיים הם:

התמונות והתוויות (תשובות נכונות) ממערך הנתונים MNIST מאוחסנות ברשומות באורך קבוע ב-4 קבצים. אפשר לטעון את הקבצים באמצעות הפונקציה הייעודית של רשומה קבועה:

imagedataset = tf.data.FixedLengthRecordDataset(image_filename, 28*28, header_bytes=16)

עכשיו יש לנו מערך נתונים של בייטים של תמונות. צריך לפענח אותם לתמונות. אנחנו מגדירים פונקציה כדי לעשות את זה. התמונה לא דחוסה, ולכן הפונקציה לא צריכה לפענח שום דבר (decode_raw לא עושה בעצם כלום). לאחר מכן התמונה מומרת לערכים של נקודה צפה בין 0 ל-1. אנחנו יכולים לשנות את הצורה של התמונה כאן לתמונה דו-ממדית, אבל אנחנו משאירים אותה כמערך שטוח של פיקסלים בגודל 28*28, כי זה מה שהשכבה הצפופה הראשונית שלנו מצפה לקבל.

def read_image(tf_bytestring):
    image = tf.decode_raw(tf_bytestring, tf.uint8)
    image = tf.cast(image, tf.float32)/256.0
    image = tf.reshape(image, [28*28])
    return image

אנחנו מפעילים את הפונקציה הזו על מערך הנתונים באמצעות .map ומקבלים מערך נתונים של תמונות:

imagedataset = imagedataset.map(read_image, num_parallel_calls=16)

אנחנו מבצעים את אותה פעולה של קריאה ופענוח גם לתוויות, ו.zip תמונות ותוויות יחד:

dataset = tf.data.Dataset.zip((imagedataset, labelsdataset))

עכשיו יש לנו מערך נתונים של זוגות (תמונה, תווית). זה מה שהמודל שלנו מצפה לקבל. אנחנו עדיין לא מוכנים להשתמש בו בפונקציית ההדרכה:

dataset = dataset.cache()
dataset = dataset.shuffle(5000, reshuffle_each_iteration=True)
dataset = dataset.repeat()
dataset = dataset.batch(batch_size)
dataset = dataset.prefetch(tf.data.experimental.AUTOTUNE)

ב-API ‏tf.data.Dataset יש את כל פונקציות השירות הדרושות להכנת מערכי נתונים:

‫.cache שומר במטמון את מערך הנתונים ב-RAM. זהו מערך נתונים קטן מאוד, ולכן הוא יעבוד. ‫.shuffle מערבב אותו עם מאגר של 5,000 רכיבים. חשוב שנתוני האימון יהיו מעורבבים היטב. ‫.repeat חוזר על מערך הנתונים. נאמן את המודל על הנתונים האלה מספר פעמים (מספר תקופות של זמן מערכת). ‫.batch מושך כמה תמונות ותוויות יחד לתוך מיני-נאצ' (mini-natch). לבסוף, .prefetch יכול להשתמש ב-CPU כדי להכין את האצווה הבאה בזמן שהאצווה הנוכחית עוברת אימון ב-GPU.

מכינים את מערך הנתונים validation באופן דומה. עכשיו אנחנו מוכנים להגדיר מודל ולהשתמש במערך הנתונים הזה כדי לאמן אותו.

התא Keras Model

כל המודלים שלנו יהיו רצפים ישרים של שכבות, כדי שנוכל להשתמש בסגנון tf.keras.Sequential כדי ליצור אותם. בשלב הראשון, זו שכבה צפופה אחת. יש לה 10 נוירונים כי אנחנו מסווגים ספרות בכתב יד ל-10 מחלקות. הוא משתמש בהפעלה מסוג softmax כי הוא השכבה האחרונה בסיווג.

מודל Keras צריך לדעת גם את הצורה של נתוני הקלט שלו. אפשר להשתמש ב-tf.keras.layers.Input כדי להגדיר אותו. כאן, וקטורי הקלט הם וקטורים שטוחים של ערכי פיקסלים באורך 28*28.

model = tf.keras.Sequential(
  [
    tf.keras.layers.Input(shape=(28*28,)),
    tf.keras.layers.Dense(10, activation='softmax')
  ])

model.compile(optimizer='sgd',
              loss='categorical_crossentropy',
              metrics=['accuracy'])

# print model layers
model.summary()

# utility callback that displays training curves
plot_training = PlotTraining(sample_rate=10, zoom=1)

הגדרת המודל מתבצעת ב-Keras באמצעות הפונקציה model.compile. כאן אנחנו משתמשים באופטימיזציה הבסיסית 'sgd' (Stochastic Gradient Descent). מודל סיווג דורש פונקציית אובדן של אנטרופיה צולבת, שנקראת 'categorical_crossentropy' ב-Keras. לבסוף, אנחנו מבקשים מהמודל לחשב את מדד 'accuracy', שהוא אחוז התמונות שסווגו בצורה נכונה.

‫Keras מציע את כלי השירות model.summary() שמאפשר להדפיס את פרטי המודל שיצרתם. המדריך הנחמד שלך הוסיף את כלי השירות PlotTraining (מוגדר בתא visualization utilities) שיציג עקומות אימון שונות במהלך האימון.

התא 'אימון ואימות של המודל'

כאן מתבצע האימון, על ידי קריאה ל-model.fit והעברה של מערכי הנתונים של האימון והאימות. כברירת מחדל, Keras מריץ סבב אימות בסוף כל תקופה.

model.fit(training_dataset, steps_per_epoch=steps_per_epoch, epochs=EPOCHS,
          validation_data=validation_dataset, validation_steps=1,
          callbacks=[plot_training])

ב-Keras, אפשר להוסיף התנהגויות מותאמות אישית במהלך האימון באמצעות פונקציות קריאה חוזרת (callback). כך הטמענו את תרשים האימון שמתעדכן באופן דינמי בסדנה הזו.

התא 'הצגת תחזיות'

אחרי שמסיימים לאמן את המודל, אפשר לקבל ממנו תחזיות על ידי קריאה ל-model.predict():

probabilities = model.predict(font_digits, steps=1)
predicted_labels = np.argmax(probabilities, axis=1)

כאן הכנו קבוצה של ספרות מודפסות שנוצרו מגופנים מקומיים, כבדיקה. חשוב לזכור שהרשת העצבית מחזירה וקטור של 10 הסתברויות מהפונקציה הסופית שלה 'softmax'. כדי לקבל את התווית, צריך לגלות איזו הסתברות היא הכי גבוהה. הפונקציה np.argmax מהספרייה numpy עושה את זה.

כדי להבין למה צריך את הפרמטר axis=1, חשוב לזכור שעיבדנו קבוצה של 128 תמונות, ולכן המודל מחזיר 128 וקטורים של הסתברויות. הצורה של טנסור הפלט היא [128, 10]. אנחנו מחשבים את argmax על פני 10 ההסתברויות שמוחזרות לכל תמונה, ולכן axis=1 (הציר הראשון הוא 0).

המודל הפשוט הזה כבר מזהה 90% מהספרות. לא רע, אבל עכשיו תשפר את זה משמעותית.

כדי לשפר את דיוק הזיהוי, נוסיף עוד שכבות לרשת העצבית.

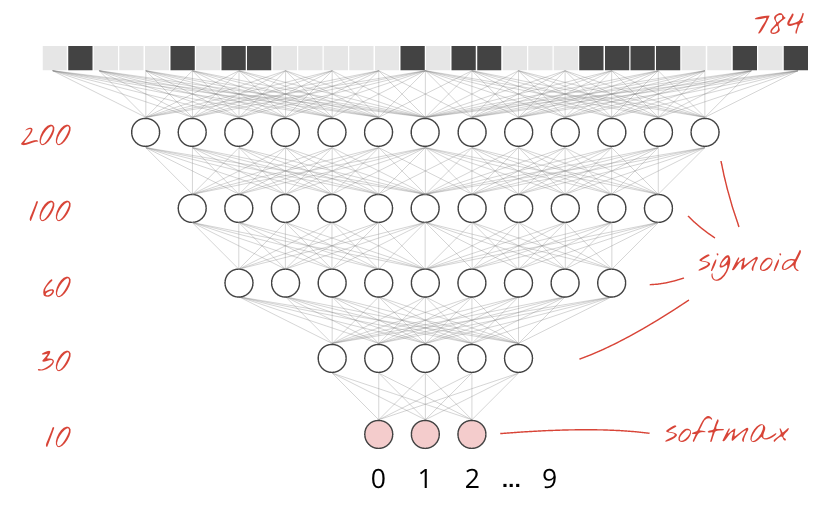
אנחנו משאירים את פונקציית ה-softmax כפונקציית ההפעלה בשכבה האחרונה, כי היא הכי מתאימה לסיווג. לעומת זאת, בשכבות ביניים נשתמש בפונקציית ההפעלה הקלאסית ביותר: הסיגמואיד:

תרגול מעשי:

צריך להוסיף כמה שכבות צפופות ביניים שהופעלו באמצעות sigmoid לפני שכבת ה-softmax. מספר הנוירונים יכול להיות כל מספר בין 784 (מספר פיקסלי הקלט) ל-10 (מספר נוירוני הפלט). ואז מאמנים מחדש את המודל.

אזהרה: כדי לאמן מחדש, צריך להריץ מחדש את התא 'מודל Keras' כדי להגדיר מודל חדש, ואז את תא האימון. פשוט מריצים מחדש את תא האימון כדי להמשיך את האימון של המודל הקודם.

לדוגמה, המודל יכול להיראות כך (אל תשכחו את הפסיקים, tf.keras.Sequential מקבל רשימה של שכבות שמופרדת בפסיקים):

model = tf.keras.Sequential(
  [
      tf.keras.layers.Input(shape=(28*28,)),
      tf.keras.layers.Dense(200, activation='sigmoid'),
      tf.keras.layers.Dense(60, activation='sigmoid'),
      tf.keras.layers.Dense(10, activation='softmax')
  ])

מעיינים ב'סיכום' של המודל. עכשיו יש בו לפחות פי 10 יותר פרמטרים. הוא צריך להיות טוב פי 10! אבל משום מה, הוא לא ...

נראה שההפסד גם עלה בצורה משמעותית. נראה שמשהו לא בסדר.

הרגע חוויתם רשתות נוירונים, כמו שאנשים נהגו לעצב אותן בשנות ה-80 וה-90. לא פלא שהם ויתרו על הרעיון, מה שהוביל למה שמכונה 'חורף הבינה המלאכותית'. למעשה, ככל שמוסיפים שכבות, לרשתות עצביות קשה יותר ויותר להתכנס.

מתברר שרשתות עצביות עמוקות עם הרבה שכבות (20, 50 ואפילו 100 כיום) יכולות לפעול בצורה טובה מאוד, בתנאי שמשתמשים בכמה טריקים מתמטיים כדי לגרום להן להתכנס. הגילוי של הטריקים הפשוטים האלה הוא אחת הסיבות לתחייה של למידה עמוקה בעשור השני של המאה ה-21.

הפעלת RELU

פונקציית ההפעלה הסיגמואידית היא בעייתית למדי ברשתות עמוקות. היא דוחסת את כל הערכים בין 0 ל-1, וכשעושים את זה שוב ושוב, התפוקות של הנוירונים והשיפועים שלהם יכולים להיעלם לגמרי. הוא מוזכר מסיבות היסטוריות, אבל ברשתות מודרניות נעשה שימוש ב-RELU (יחידה לינארית מתוקנת) שנראית כך:

תרגול מעשי:

מחליפים את כל המופעים של activation='sigmoid' ב-activation='relu' בשכבות ומבצעים אימון מחדש.

למה פונקציית הסיגמואיד בעייתית? תראו איך הוא מתנהג בצדדים: הוא משתטח.

כלומר הנגזרת שלה שם קרובה לאפס. כדי להבין איך האימון מתקדם, צריך לעקוב אחרי הגרדיאנט, שהוא וקטור של נגזרות. בשימוש בהפעלה סיגמואידית, במיוחד אם יש הרבה שכבות, הגרדיאנט יכול להיות קטן מאוד והאימון הופך לאיטי יותר ויותר.

לעומת זאת, ל-ReLU יש נגזרת של 1, לפחות בצד ימין שלה. עם הפעלת RELU, גם אם הגרדיאנטים שמגיעים מחלק מהנוירונים יכולים להיות אפס, תמיד יהיו אחרים שיספקו גרדיאנט ברור שאינו אפס, והאימון יכול להימשך בקצב טוב.

כלי אופטימיזציה משופר

במרחבים רב-ממדיים כמו כאן – יש לנו בסביבות 10,000 משקלים והטיות – 'נקודות אוכף' הן תופעה שכיחה. אלה נקודות שלא מייצגות מינימום מקומי, אבל הגרדיאנט בהן הוא אפס, והאופטימיזציה של ירידת הגרדיאנט נתקעת שם. ל-TensorFlow יש מגוון רחב של אופטימיזציות זמינות, כולל כאלה שפועלות עם כמות אינרציה ויעברו בבטחה נקודות אוכף.

תרגול מעשי:

מחליפים את האופטימיזציה 'sgd' באופטימיזציה טובה יותר, למשל 'adam', ומאמנים מחדש.

הפעלות אקראיות

אומנות ההגדרה של משקלים והטיות לפני אימון היא תחום מחקר בפני עצמו, ויש הרבה מאמרים שפורסמו בנושא. כאן אפשר לראות את כל הפונקציות לאתחול שזמינות ב-Keras. למזלנו, Keras עושה את הדבר הנכון כברירת מחדל ומשתמש ב-'glorot_uniform' initializer, שהוא הכי טוב כמעט בכל המקרים.

אתם לא צריכים לעשות כלום, כי Keras כבר עושה את מה שצריך.

NaN ???

הנוסחה של האנטרופיה הצולבת כוללת לוגריתם, והלוגריתם של 0 הוא לא מספר (NaN, קריסה מספרית אם תרצו). האם הקלט של האנטרופיה הצולבת יכול להיות 0? הקלט מגיע מ-softmax, שהוא למעשה פונקציה אקספוננציאלית, ופונקציה אקספוננציאלית אף פעם לא שווה לאפס. אז אנחנו בטוחים!

באמת? בעולם היפה של המתמטיקה, היינו בטוחים, אבל בעולם המחשבים, exp(-150), שמיוצג בפורמט float32, הוא אפס לכל דבר, והאנטרופיה הצולבת קורסת.

למזלנו, גם כאן אין צורך לעשות דבר, כי Keras מטפלת בזה ומחשבת את softmax ואחריו את האנטרופיה הצולבת בצורה זהירה במיוחד כדי להבטיח יציבות מספרית ולמנוע את ה-NaN המפחידים.

הצלחה?

עכשיו רמת הדיוק צריכה להיות 97%. המטרה בסדנה הזו היא להגיע לשיעור גבוה משמעותית מ-99%, אז בואו נמשיך.

אם נתקעתם, הנה הפתרון בשלב הזה:

keras_02_mnist_dense.ipynb

אולי אפשר לנסות לאמן מהר יותר? שיעור הלמידה שמוגדר כברירת מחדל באופטימיזציה של Adam הוא 0.001. אנסה להגדיל את עוצמת הקול.

תרגול מעשי:

הגדילו את קצב הלמידה מערך ברירת המחדל שלו, 0.001, ל-0.01. לשם כך, תצטרכו להחליף את האופטימיזציה המוגדרת מראש במופע בפועל של אופטימיזציית Adam, כדי שתהיה לכם גישה לפרמטרים של ההגדרה שלה:'adam'

optimizer=tf.keras.optimizers.Adam(lr=0.01)

בנוסף, צריך להגדיל את מקדם הזום ל-5 ב-PlotTraining. ההגדרה הזו מאפשרת לכם להגדיל את אזור האפס בערכי ההפסד ואת אזור ה-1 בערכי הדיוק, כדי שתוכלו לראות מה קורה: PlotTraining(sample_rate=10, zoom=5)

הגברת המהירות לא עוזרת במיוחד, ומה זה כל הרעש הזה?

עקומות האימון מאוד רועשות, וגם עקומות האימות קופצות למעלה ולמטה. המשמעות היא שאנחנו מתקדמים מהר מדי. אפשר לחזור למהירות הקודמת, אבל יש דרך טובה יותר.

הפתרון הטוב הוא להתחיל מהר ולהקטין את קצב הלמידה באופן אקספוננציאלי. ב-Keras, אפשר לעשות את זה באמצעות הקריאה החוזרת tf.keras.callbacks.LearningRateScheduler.

תרגול מעשי:

הטמעה של תזמון קצב למידה שבו קצב הלמידה יורד באופן אקספוננציאלי. בהמשך מפורטים קטעי קוד שימושיים.

קוד שימושי להעתקה והדבקה:

# lr decay function
def lr_decay(epoch):
  return 0.01 * math.pow(0.6, epoch)

# lr schedule callback
lr_decay_callback = tf.keras.callbacks.LearningRateScheduler(lr_decay, verbose=True)

# important to see what you are doing
plot_learning_rate(lr_decay, EPOCHS)

אל תשכחו להשתמש בlr_decay_callback שיצרתם. מוסיפים אותו לרשימת ההתקשרויות החוזרות ב-model.fit:

model.fit(...,  callbacks=[plot_training, lr_decay_callback])

ההשפעה של השינוי הקטן הזה היא מדהימה. אפשר לראות שרוב הרעשים נעלמו ודיוק הבדיקה עכשיו מעל 98% באופן קבוע.

נראה שהמודל מתכנס עכשיו בצורה טובה. ננסה להיכנס לעומק יותר.

תרגול מעשי:

אם עדיין לא עשיתם את זה, צריך להגדיל את העומק של המודל ל-4 שכבות צפופות לפחות ולאמן אותו מחדש. אפשר להשתמש במספר הנוירונים הבא בשכבות: 200, ‏ 100, ‏ 60, ‏ 10.

בנוסף, צריך להגדיל את מקדם הזום ל-10 ב-PlotTraining. ההגדרה הזו מאפשרת לכם להגדיל את אזור האפס בערכי ההפסד ואת אזור ה-1 בערכי הדיוק, כדי שתוכלו לראות מה קורה: PlotTraining(sample_rate=10, zoom=10)

האם זה עוזר?

לא ממש, רמת הדיוק עדיין תקועה על 98% ותסתכל על אובדן האימות. הוא עולה! אלגוריתם הלמידה פועל רק על נתוני אימון ומבצע אופטימיזציה של הפסד האימון בהתאם. הוא אף פעם לא רואה נתוני אימות, ולכן לא מפתיע שאחרי זמן מה העבודה שלו כבר לא משפיעה על הפסד האימות, שמפסיק לרדת ולפעמים אפילו עולה בחזרה.

הפעולה הזו לא משפיעה באופן מיידי על יכולות הזיהוי של המודל בעולם האמיתי, אבל היא תמנע מכם להריץ הרבה איטרציות, ובדרך כלל היא מעידה על כך שהאימון כבר לא משפיע באופן חיובי.

הניתוק הזה נקרא בדרך כלל "התאמת יתר", וכשרואים אותו, אפשר לנסות להחיל טכניקת רגולריזציה שנקראת "נשירה". טכניקת ה-dropout משביתה נוירונים אקראיים בכל איטרציה של אימון.

‫Dropout היא אחת מטכניקות הרגולריזציה הוותיקות ביותר בתחום הלמידה העמוקה. בכל איטרציה של אימון, המערכת משמיטה נוירונים אקראיים מהרשת בהסתברות p (בדרך כלל 25% עד 50%). בפועל, הפלט של הנוירון מוגדר ל-0. התוצאה הסופית היא שהנוירונים האלה לא ישתתפו בחישוב ההפסד הפעם, והמשקלים שלהם לא יעודכנו. בכל איטרציה של אימון, נוירונים שונים יושמטו.

כשבודקים את הביצועים של הרשת, כמובן שצריך להחזיר את כל הנוירונים (שיעור ההשמטה=0). ‫Keras עושה את זה באופן אוטומטי, כך שכל מה שצריך לעשות הוא להוסיף שכבת tf.keras.layers.Dropout. ההתנהגות הנכונה תתבצע באופן אוטומטי בזמן האימון וההערכה.

למה זה עובד? התיאוריה היא שלרשתות עצביות יש חופש פעולה רב בין השכבות הרבות שלהן, ולכן יכול להיות ששכבה מסוימת תפתח התנהגות לא תקינה והשכבה הבאה תפצה על כך. זה לא שימוש אידיאלי בנוירונים. בשיטת ה-dropout, יש סיכוי גבוה שהנוירון ש "מתקן" את הבעיה לא יהיה קיים בסבב אימון מסוים. ההתנהגות הלא תקינה של השכבה הבעייתית הופכת ברורה, והמשקלים מתפתחים לכיוון התנהגות טובה יותר.

תרגול מעשי:

אפשר להוסיף dropout אחרי כל שכבה צפופה ביניים ברשת. אל תוסיפו שכבת dropout אחרי שכבת softmax. ההסתברויות החזויות יימחקו. כדי להוסיף שיעור נטישה של 25%, משתמשים בפקודה: tf.keras.layers.Dropout(0.25)

זה עבד?

הרעש מופיע מחדש (לא מפתיע בהתחשב באופן הפעולה של ניתוקים). נראה שההפסד באימות לא עולה יותר, אבל הוא גבוה יותר באופן כללי מאשר בלי נשירה. ורמת הדיוק של האימות ירדה קצת. זו תוצאה די מאכזבת.

נראה שהפסקת השימוש לא הייתה הפתרון הנכון, או שאולי 'התאמת יתר' היא מושג מורכב יותר וחלק מהגורמים שלה לא ניתנים לתיקון באמצעות הפסקת השימוש.

מה זה "התאמת יתר"? התאמת יתר מתרחשת כשאימון רשת נוירונים לא מתבצע בצורה טובה, כלומר הרשת פועלת טוב בדוגמאות האימון אבל לא כל כך טוב בנתונים מהעולם האמיתי. יש טכניקות רגולריזציה כמו dropout שיכולות לחייב את המודל ללמוד בצורה טובה יותר, אבל לבעיית ההתאמה העודפת יש גם שורשים עמוקים יותר.

התאמת יתר בסיסית מתרחשת כשרשת נוירונים כוללת יותר מדי דרגות חופש לבעיה שבה היא עוסקת. תארו לעצמכם שיש לנו כל כך הרבה נוירונים שהרשת יכולה לאחסן בהם את כל תמונות האימון שלנו ואז לזהות אותן באמצעות התאמת תבניות. הוא ייכשל לחלוטין בנתונים מהעולם האמיתי. צריך להגביל במידה מסוימת את רשת הנוירונים כדי שהיא תיאלץ להכליל את מה שהיא לומדת במהלך האימון.

אם יש לכם מעט מאוד נתונים לאימון, גם רשת קטנה יכולה ללמוד אותם בעל פה ותראו "התאמת יתר". באופן כללי, תמיד צריך הרבה נתונים כדי לאמן רשתות נוירונים.

לבסוף, אם עשיתם הכול לפי הספר, ניסיתם גדלים שונים של רשת כדי לוודא שדרגות החופש שלה מוגבלות, הפעלתם dropout והכשרתם את המודל על הרבה נתונים, יכול להיות שעדיין תיתקעו ברמת ביצועים שלא נראה שאפשר לשפר אותה. המשמעות היא שהרשת העצבית שלכם, בצורה הנוכחית שלה, לא מסוגלת לחלץ יותר מידע מהנתונים שלכם, כמו במקרה שלנו כאן.

זוכרים איך אנחנו משתמשים בתמונות שלנו, אחרי שהן משוטחות לווקטור יחיד? זה היה רעיון ממש גרוע. ספרות בכתב יד מורכבות מצורות, והשמטנו את פרטי הצורה כששיטחנו את הפיקסלים. עם זאת, יש סוג של רשת נוירונים שיכולה לנצל את המידע על הצורה: רשתות קונבולוציה. בוא ננסה אותם.

אם נתקעתם, הנה הפתרון בשלב הזה:

keras_03_mnist_dense_lrdecay_dropout.ipynb

בקצרה

אם אתם כבר מכירים את כל המונחים מודגשים בפסקה הבאה, אתם יכולים לעבור לתרגיל הבא. אם אתם רק מתחילים להשתמש ברשתות נוירונים קונבולוציוניות, כדאי שתמשיכו לקרוא.

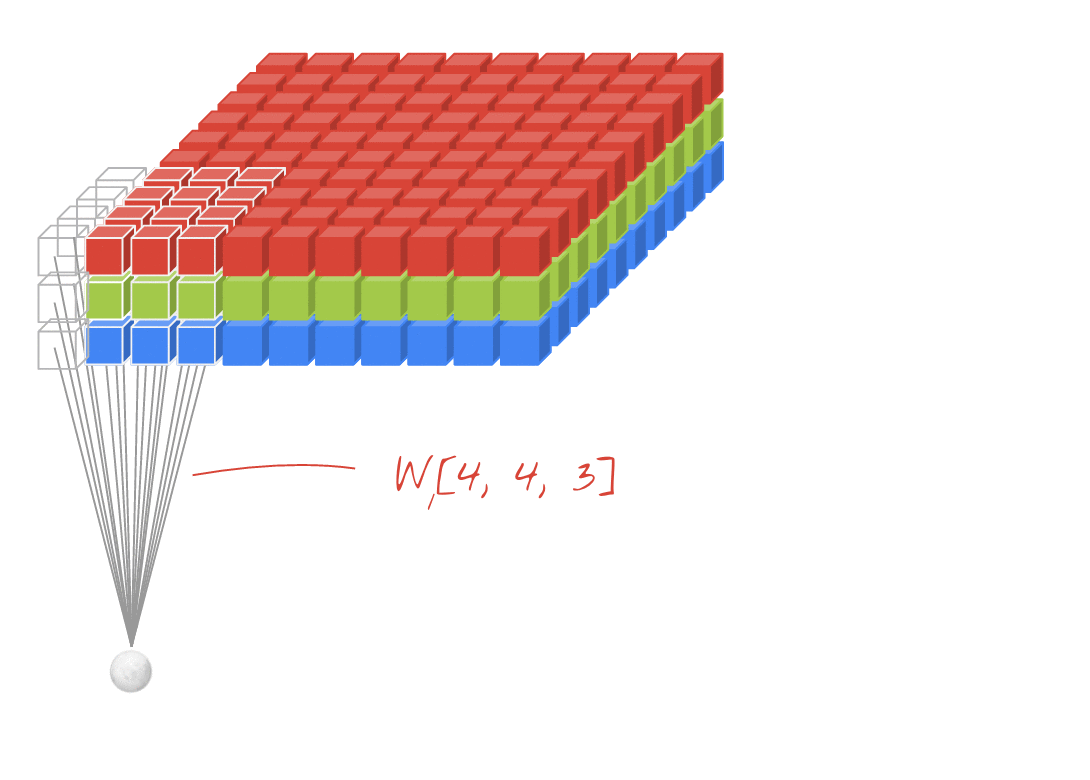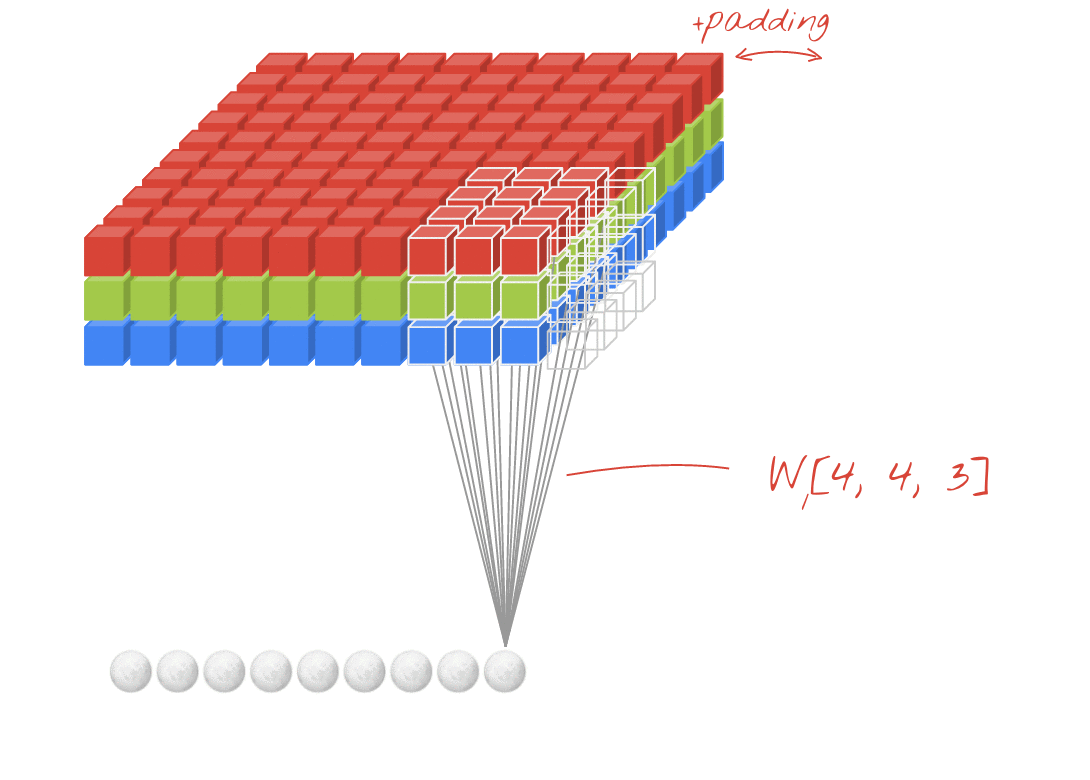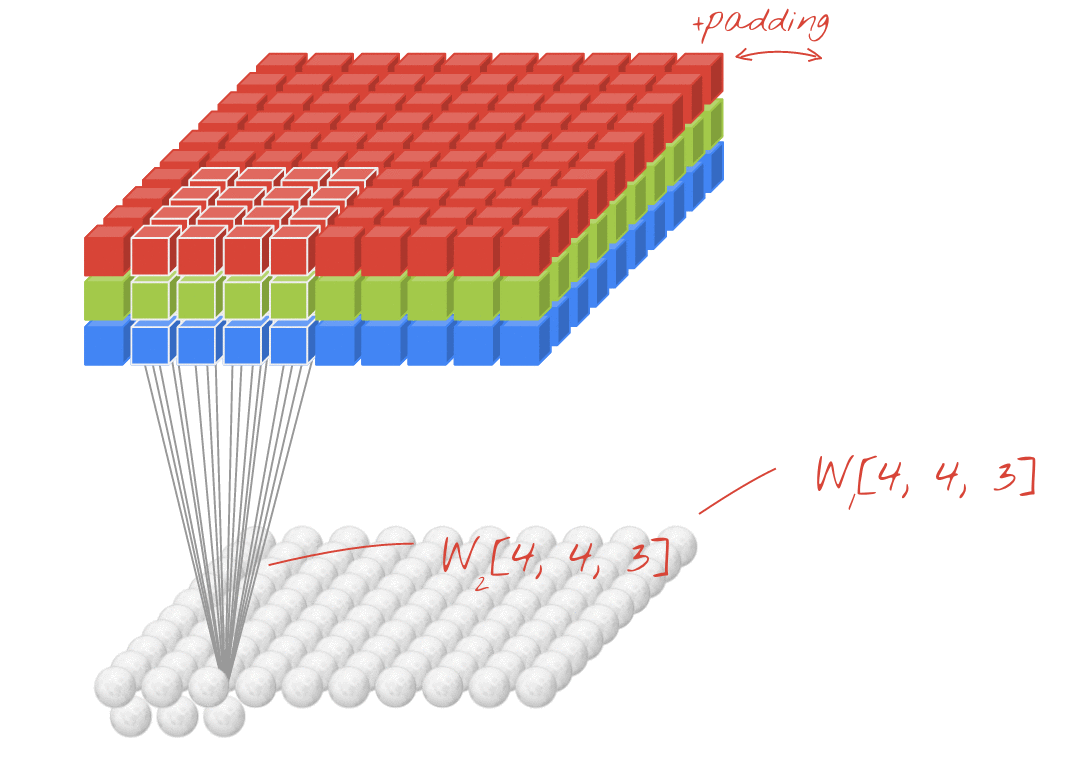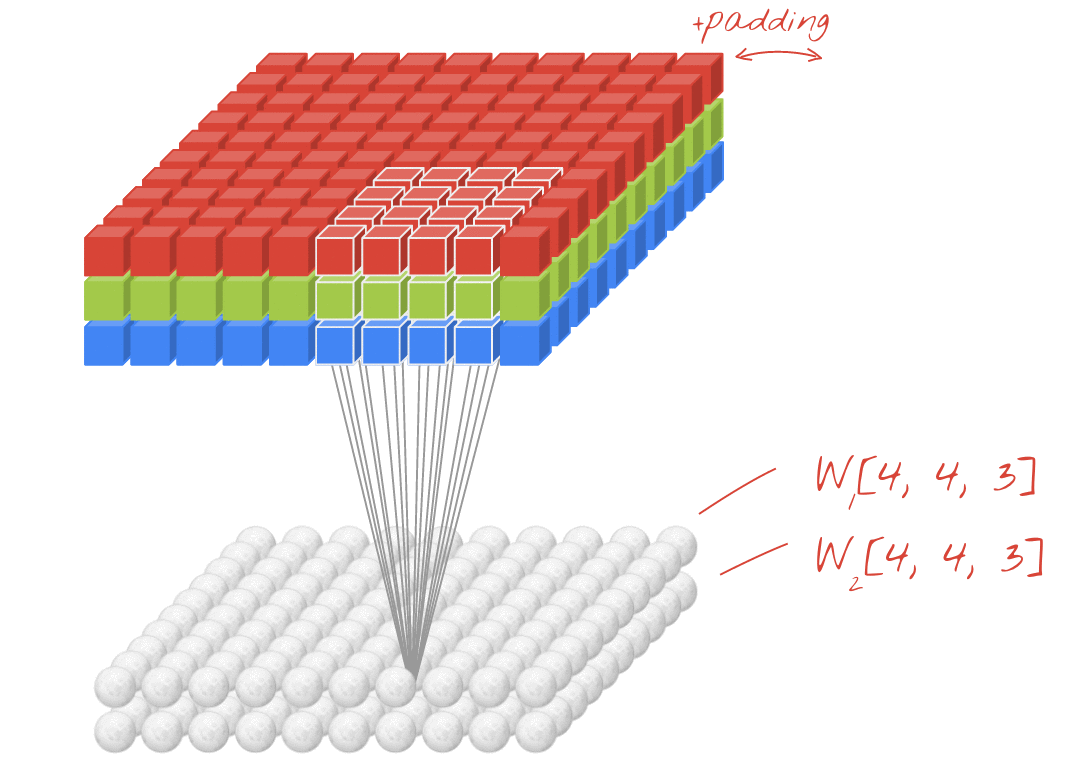
איור: סינון תמונה באמצעות שני מסננים עוקבים, כל אחד עם 48 משקלים שניתנים ללמידה (4x4x3=48).

רשתות נוירונים מתקפלות (CNN) מפעילות סדרה של מסננים שניתנים ללמידה על תמונת הקלט. שכבת קונבולוציה מוגדרת על ידי גודל המסנן (או הגרעין), מספר המסננים שמופעלים והצעד. לקלט ולפלט של שכבת קונבולוציה יש שלושה ממדים (רוחב, גובה, מספר הערוצים), החל מתמונת הקלט (רוחב, גובה, ערוצי RGB). כשמניחים שכבות קונבולוציה אחת על השנייה, אפשר לשנות את הרוחב והגובה של הפלט באמצעות צעד >1 או באמצעות פעולת max-pooling. כדי לשנות את עומק הפלט (מספר הערוצים), משתמשים ביותר או בפחות מסננים.

כך נראית רשת נוירונים מלאכותית פשוטה ב-Keras:

model = tf.keras.Sequential([
    tf.keras.layers.Reshape(input_shape=(28*28,), target_shape=(28, 28, 1)),
    tf.keras.layers.Conv2D(kernel_size=3, filters=12, activation='relu'),
    tf.keras.layers.Conv2D(kernel_size=6, filters=24, strides=2, activation='relu'),
    tf.keras.layers.Conv2D(kernel_size=6, filters=32, strides=2, activation='relu'),
    tf.keras.layers.Flatten(),
    tf.keras.layers.Dense(10, activation='softmax')
])

בשכבה של רשת קונבולוציונית, 'נוירון' אחד מבצע סכום משוקלל של הפיקסלים שמעליו, רק באזור קטן של התמונה. הוא מוסיף הטיה ומזין את הסכום דרך פונקציית הפעלה, בדיוק כמו נוירון בשכבה צפופה רגילה. הפעולה הזו חוזרת על עצמה בכל התמונה באמצעות אותם משקלים. חשוב לזכור ששכבות צפופות הן שכבות שבהן לכל נוירון יש משקלים משלו. כאן, 'תיקון' יחיד של משקלים מחליק על פני התמונה בשני הכיוונים (פעולת 'קונבולוציה'). בפלט יש מספר ערכים ששווה למספר הפיקסלים בתמונה (אבל צריך להוסיף קצת ריפוד בשוליים). זו פעולת סינון. באיור שלמעלה, נעשה שימוש במסנן של 4x4x3=48 משקלים.

עם זאת, 48 משקלים לא יספיקו. כדי להוסיף עוד דרגות חופש, חוזרים על אותה פעולה עם קבוצה חדשה של משקלים. כך נוצרת קבוצה חדשה של פלט מסנן. נקרא לזה 'ערוץ' של פלטים,בהשוואה לערוצי ה-R,‏ G ו-B בתמונת הקלט.

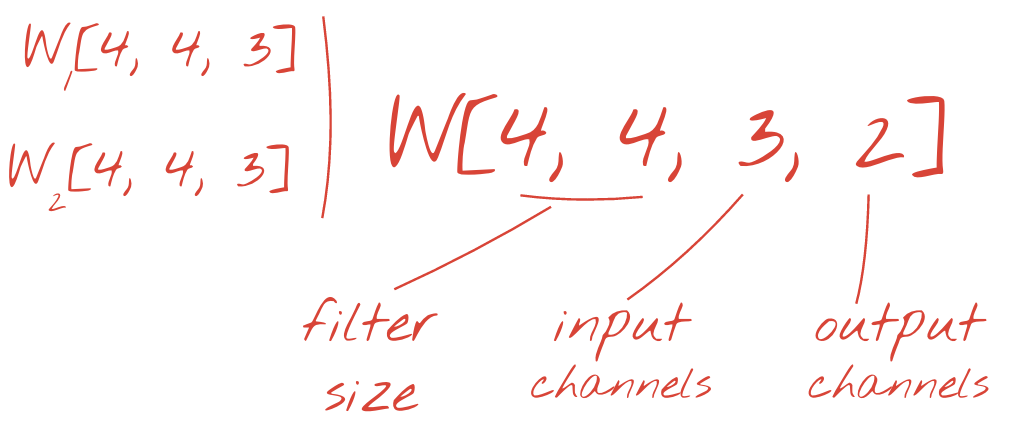
אפשר לסכם את שני (או יותר) מערכי המשקלים לטנזור אחד על ידי הוספת מימד חדש. כך מקבלים את הצורה הכללית של טנסור המשקלים לשכבת קונבולוציה. מכיוון שמספר ערוצי הקלט והפלט הם פרמטרים, אפשר להתחיל להוסיף שכבות קונבולוציה אחת על השנייה.

איור: רשת נוירונים מלאכותית (CNN) מבצעת טרנספורמציה של 'קוביות' נתונים ל'קוביות' נתונים אחרות.

קיפולים (קונבולציות) עם צעדים, יצירת מאגרים מקסימליים

אם מבצעים את הקונבולוציות עם צעד של 2 או 3, אפשר גם להקטין את קוביית הנתונים שמתקבלת בממדים האופקיים שלה. יש שתי דרכים נפוצות לעשות את זה:

• קונבולוציה עם צעדים: מסנן הזזה כמו למעלה, אבל עם צעד >1
• איגום מקסימלי: חלון הזזה שמחיל את פעולת ה-MAX (בדרך כלל על תיקוני 2x2, שחוזרים על עצמם כל 2 פיקסלים)

איור: הזזה של חלון החישוב ב-3 פיקסלים מובילה לפחות ערכי פלט. הפעלת קונבולוציה עם דילוג או איגום מקסימלי (max על חלון 2x2 עם דילוג של 2) היא דרך לצמצם את קוביית הנתונים בממדים האופקיים.

המושג Max-pooling יכול לעזור לנו להבין באופן אינטואיטיבי איך רשתות קונבולוציה פועלות: אם מניחים שבמהלך האימון, טלאי המשקלים מתפתחים למסננים שמזהים צורות בסיסיות (קווים אופקיים ואנכיים, עקומות וכו'), אז דרך אחת לצמצם את המידע השימושי היא לשמור בשכבות את הפלטים שבהם זוהתה צורה בעוצמה המקסימלית. בפועל, בשכבת איגום מקסימלי, הפלט של הנוירונים מעובד בקבוצות של 2x2, ורק הערך המקסימלי נשמר.

השכבה האחרונה

אחרי שכבת הקונבולוציה האחרונה, הנתונים הם בצורה של 'קוביה'. יש שתי דרכים להעביר אותו דרך השכבה הדחוסה הסופית.

האפשרות הראשונה היא לשטח את קוביית הנתונים לווקטור ואז להזין אותו לשכבת softmax. לפעמים אפשר אפילו להוסיף שכבה צפופה לפני שכבת ה-softmax. השיטה הזו בדרך כלל יקרה מבחינת מספר המשקלים. שכבה צפופה בסוף רשת קונבולוציה יכולה להכיל יותר ממחצית המשקלים של כל הרשת הנוירונית.

במקום להשתמש בשכבה צפופה ויקרה, אפשר גם לפצל את הנתונים הנכנסים לכל כך הרבה חלקים כמו שיש לנו מחלקות, לחשב את הממוצע של הערכים שלהם ולהזין אותם דרך פונקציית הפעלה מסוג softmax. השיטה הזו לבניית ראש הסיווג לא כרוכה בעלויות משקל. ב-Keras יש שכבה לזה: tf.keras.layers.GlobalAveragePooling2D().

רשתות נוירונים מלאכותיות (CNN) מזהות את המיקום של דברים. כשמסנן מגיב בעוצמה לתכונה מסוימת, הוא עושה זאת במיקום ספציפי (x, y). בהתאם לפעולה שרוצים לבצע, אפשר לאמן רשת נוירונים להשתמש בנתוני המיקום האלה או להתעלם מהם. השימוש ב-global average pooling גורם להשמטה מפורשת של כל נתוני המיקום. זה יכול להיות בסדר בשביל מסווג פרחים, אבל יכול להיות שלא יעבוד טוב למשימות אחרות, כמו ספירת פרחים בתמונה. צריך להשתמש באפשרות הזו בזהירות.

בקטע הבא נבנה רשת קונבולוציונית לבעיה הנוכחית.

בואו ניצור רשת קונבולוציה לזיהוי ספרות בכתב יד. נשתמש בשלוש שכבות קונבולוציה בחלק העליון, בשכבת הקריאה המסורתית של softmax בחלק התחתון, ונחבר אותן עם שכבה אחת שמחוברת באופן מלא:

שימו לב שהשכבות השנייה והשלישית של הקונבולוציה הן בעלות פסיעה של שתיים, ולכן הן מצמצמות את מספר ערכי הפלט מ-28x28 ל-14x14 ואז ל-7x7.

עכשיו נכתוב את הקוד של Keras.

נדרשת תשומת לב מיוחדת לפני שכבת הקונבולוציה הראשונה. למעשה, הוא מצפה ל'קוביה' תלת-ממדית של נתונים, אבל מערך הנתונים שלנו הוגדר עד עכשיו לשכבות צפופות וכל הפיקסלים של התמונות משוטחים לווקטור. אנחנו צריכים לשנות את הצורה שלהן בחזרה לתמונות בגודל ‎28x28x1 (ערוץ אחד לתמונות בגווני אפור):

tf.keras.layers.Reshape(input_shape=(28*28,), target_shape=(28, 28, 1))

אפשר להשתמש בשורה הזו במקום בשכבת tf.keras.layers.Input שהייתה לכם עד עכשיו.

ב-Keras, התחביר של שכבת קונבולוציה עם הפעלה מסוג relu הוא:

tf.keras.layers.Conv2D(kernel_size=3, filters=12, padding='same', activation='relu')

לפרמטר הריפוד בשכבות קונבולוציה יכולים להיות שני ערכים:

• ‫'same': הוספת אפסים כדי ליצור פלט עם אותו רוחב/גובה כמו הקלט
• ‫'valid': ללא ריווח פנימי, שימוש רק בפיקסלים אמיתיים

אנחנו משתמשים כאן במרווח פנימי, לכן צריך להגדיר את המרווח הפנימי כ-'same'.

כדי להגדיר קונבולוציה עם דילוג, כותבים:

tf.keras.layers.Conv2D(kernel_size=6, filters=24, padding='same', activation='relu', strides=2)

כדי לשטח קובייה של נתונים לווקטור שאפשר להשתמש בו בשכבה צפופה:

tf.keras.layers.Flatten()

ובשביל שכבה צפופה, התחביר לא השתנה:

tf.keras.layers.Dense(200, activation='relu')

תרגול מעשי:

משנים את המודל כדי להפוך אותו למודל קונבולוציוני. אפשר להשתמש בערכים מהשרטוט שלמעלה כדי לשנות את הגודל. אפשר להשאיר את קצב הדעיכה של קצב הלמידה כמו שהוא, אבל צריך להסיר את הנשירה בשלב הזה.

בנוסף, צריך להגדיל את מקדם הזום ל-16 ב-PlotTraining. ההגדרה הזו מאפשרת לכם להגדיל את אזור האפס בערכי ההפסד ואת אזור ה-1 בערכי הדיוק, כדי שתוכלו לראות מה קורה: PlotTraining(sample_rate=10, zoom=16)

האם המודל שלכם הצליח לעבור את רף הדיוק של 99%? די קרוב… אבל כדאי להסתכל על עקומת הירידה בערכי האימות. האם זה נשמע לך מוכר?

כדאי גם לעיין בתחזיות. בפעם הראשונה, אמורות להיות לכם תוצאות שבהן רוב 10,000 הספרות שבדקתם מזוהות בצורה נכונה. נותרו רק כ-4 שורות וחצי של זיהויים שגויים (כ-110 ספרות מתוך 10,000)

אם נתקעתם, הנה הפתרון בשלב הזה:

keras_04_mnist_convolutional.ipynb

האימון הקודם מראה סימנים ברורים של התאמת יתר (overfitting) (ועדיין לא מגיע לדיוק של 99%). רוצה לנסות שוב להפסיק את הלימודים?

תרגול מעשי:

מוסיפים שכבת dropout בין שתי השכבות הצפופות ברשת. שימוש בשיעור נטישה של 40% (=0.4):

tf.keras.layers.Dropout(0.4)

אפשר להחיל dropout על שכבות קונבולוציה, אבל זה עובד קצת אחרת ובדרך כלל לא יעיל כמו בשכבות רגילות, כי יש הרבה פחות משקלים בשכבות הקונבולוציה ולכן פחות סיכויים להתאמה משותפת לא טובה. לא נבדוק את האפשרות הזו.

איך היה הפעם?

נראה שהפעם ההשמטה עבדה. ההפסד של האימות לא עולה יותר, והדיוק הסופי צריך להיות גבוה בהרבה מ-99%. מעולה!

בפעם הראשונה שניסינו להשתמש בשיטת ה-dropout, חשבנו שיש לנו בעיה של התאמת יתר, אבל למעשה הבעיה הייתה בארכיטקטורה של הרשת העצבית. לא יכולנו להמשיך בלי שכבות קונבולוציה, ואין שום דבר ששיטת ה-dropout יכולה לעשות בנוגע לכך.

במקרה הזה, נראה שהתאמת יתר הייתה הגורם לבעיה, והשימוש ב-dropout עזר. חשוב לזכור שיש הרבה דברים שיכולים לגרום לניתוק בין עקומות ההפסד של האימון והאימות, כשההפסד של האימות עולה בהדרגה. התאמת יתר (יותר מדי דרגות חופש, שימוש לא נכון ברשת) היא רק אחת מהן. אם מערך הנתונים קטן מדי או שהארכיטקטורה של הרשת העצבית לא מתאימה, יכול להיות שתראו התנהגות דומה בעקומות ההפסד, אבל dropout לא יעזור.

לבסוף, ננסה להוסיף נורמליזציה של קבוצות.

מהי נורמליזציה של קבוצות?

בקיצור, נורמליזציה של קבוצות מנסה לפתור את הבעיה של אופן ההתפלגות של התפוקות של נוירונים ביחס לפונקציית ההפעלה של הנוירון. במיני-אצווה של נתוני אימון, הפלט של נוירון, לפני ההפעלה, יכול להיות עם ההתפלגויות הבאות:

אם המיקום רחוק מדי משמאל, אחרי הפעלת הסיגמואיד, הנוירון הזה כמעט תמיד יפיק פלט של 0.

הטווח צר מדי, הנוירון הזה אף פעם לא מוציא פלט של 0 או 1 ברורים.

זה לא כל כך נורא. לנוירון יהיה מגוון התנהגויות הוגן בקבוצת הנתונים הקטנה הזו.

כדי לפתור את הבעיה הזו, נורמליזציה של קבוצת נתונים (batch norm) מנרמלת את התפוקות של הנוירונים בקבוצת נתונים לאימון, כלומר היא מחסרת את הממוצע ומחלקת בסטיית התקן. אבל אם היינו עושים רק את זה, זה היה קשה מדי. אם ההתפלגות הייתה רחבה ונורמלית בכל מקום, ומרכזה היה בדיוק באמצע, לכל הנוירונים היה אותו התנהגות. הטריק הוא להוסיף שני פרמטרים נוספים שניתנים ללמידה לכל נוירון, 𝛼 ו-𝛽, ולחשב:

‫𝛼 . normalized_out + 𝛽

לאחר מכן, מחילים את פונקציית ההפעלה (סיגמואיד, relu וכו'). כך, הרשת מחליטה, באמצעות למידת מכונה, כמה מרכוז ושינוי קנה מידה להחיל על כל נוירון. הקוראים מוזמנים לבדוק אם יש ערכים של 𝛼 ו-𝛽 שיכולים להסיר את הנורמליזציה לחלוטין, אם זה הדבר הנכון לעשות.

בפועל, לא תמיד צריך את שני הערכים 𝛼 ו-𝛽. ב-Keras, הן נקראות scale ו-center, ואפשר להשתמש רק באחת מהן, למשל:

tf.keras.layers.BatchNormalization(scale=False, center=True)

הבעיה בנורמליזציה של קבוצות היא שבזמן החיזוי, אין לכם קבוצות אימון שתוכלו לחשב את הנתונים הסטטיסטיים של הפלט של הנוירון. אבל עדיין צריך את הערכים האלה. החלק הזה קצת מסובך. במהלך האימון, המערכת מחשבת את הממוצע ואת סטיית התקן של הפלט של נוירון 'טיפוסי' על פני מספר 'מספיק' של אצוות. בפועל, המערכת משתמשת בממוצע אקספוננציאלי מתמשך. הנתונים הסטטיסטיים האלה משמשים בזמן ההסקה.

החדשות הטובות הן שב-Keras אפשר להשתמש בשכבת tf.keras.layers.BatchNormalization, וכל החישובים האלה יתבצעו באופן אוטומטי.

זו התיאוריה, אבל בפועל, צריך לזכור רק כמה כללים:

נורמליזציה של קבוצות (Batch norm) 'לפי הספר':

1. נורמליזציה של קבוצות מתבצעת בין הפלט של שכבה לבין פונקציית ההפעלה שלה.
2. אם משתמשים ב-center=True בנורמליזציה של קבוצות, לא צריך להשתמש בהטיות בשכבה. ההיסט של הנרמול באצ' ממלא את התפקיד של הטיה.
3. אם משתמשים בפונקציית הפעלה שאינה משתנה ביחס לגודל (כלומר, הצורה שלה לא משתנה כשמבצעים זום), אפשר להגדיר את scale=False. פונקציית Relu היא בלתי תלויה בסקאלה. פונקציית הסיגמואיד לא.

זו התיאוריה, אבל הדרך היחידה לגלות אם הפרת הכללים האלה היא דבר רע היא לנסות.

נפעל לפי הספר בשלב הזה ונוסיף שכבת נורמליזציה של קבוצות לכל שכבת רשת עצבית, למעט האחרונה. לא מוסיפים אותו לשכבת ה-softmax האחרונה. היא לא תהיה שימושית שם.

# Modify each layer: remove the activation from the layer itself.
# Set use_bias=False since batch norm will play the role of biases.
tf.keras.layers.Conv2D(..., use_bias=False),
# Batch norm goes between the layer and its activation.
# The scale factor can be turned off for Relu activation.
tf.keras.layers.BatchNormalization(scale=False, center=True),
# Finish with the activation.
tf.keras.layers.Activation('relu'),

מה רמת הדיוק עכשיו?

עם שינויים קלים (BATCH_SIZE=64, פרמטר של ירידה בשיעור הלמידה 0.666, שיעור הנשירה בשכבה הצפופה 0.3) ומעט מזל, אפשר להגיע ל-99.5%. ההתאמות של קצב הלמידה וההשמטה בוצעו בהתאם לשיטות המומלצות לשימוש בנורמליזציה של קבוצות:

• נורמליזציה של קבוצות עוזרת לרשתות נוירונים להתכנס ומאפשרת בדרך כלל אימון מהיר יותר.
• נורמליזציה של קבוצות היא רגולריזציה. בדרך כלל אפשר להקטין את כמות ה-dropout שמשתמשים בה, או אפילו לא להשתמש ב-dropout בכלל.

מחברת הפתרון כוללת הרצת אימון של 99.5%:

keras_05_mnist_batch_norm.ipynb

גרסה של הקוד שמוכנה לשימוש בענן נמצאת בתיקייה mlengine ב-GitHub, יחד עם הוראות להרצת הקוד ב-Google Cloud AI Platform. כדי להריץ את החלק הזה, צריך ליצור חשבון Google Cloud ולהפעיל את החיוב. המשאבים שנדרשים להשלמת המעבדה צריכים לעלות פחות מכמה דולרים (בהנחה של שעת אימון אחת ב-GPU אחד). כדי להכין את החשבון:

1. יוצרים פרויקט ב-Google Cloud Platform‏ (http://cloud.google.com/console).
2. מפעילים את החיוב.
3. מתקינים את כלי שורת הפקודה של GCP (GCP SDK כאן).
4. יוצרים קטגוריה של Google Cloud Storage (במיקום us-central1). הקטגוריה תשמש להכנת קוד האימון ולאחסון המודל שאומן.
5. מפעילים את ממשקי ה-API הנדרשים ומבקשים את המכסות הנדרשות (מריצים את פקודת ההדרכה פעם אחת, ואמורות להופיע הודעות שגיאה שמציינות מה צריך להפעיל).

בנית רשת נוירונים ראשונה ואימנת אותה עד לרמת דיוק של 99%. הטכניקות שנלמדו לאורך הדרך לא ספציפיות למערך הנתונים של MNIST, למעשה הן נמצאות בשימוש נרחב כשעובדים עם רשתות נוירונים. כמתנת פרידה, הנה כרטיס 'הערות' ל-Lab, בגרסת קריקטורה. אתם יכולים להשתמש בו כדי לזכור מה למדתם:

השלבים הבאים

• אחרי רשתות קונבולוציה ורשתות עם חיבור מלא, כדאי לעיין ברשתות נוירונים חוזרות.
• כדי להריץ את האימון או את ההסקות בענן בתשתית מבוזרת, אפשר להשתמש ב-AI Platform של Google Cloud.
  
• בסופו של דבר, נשמח לקבל משוב. אם נתקלתם בבעיה ב-Google Lab הזה או שיש לכם הצעות לשיפור, נשמח לשמוע מכם. אנחנו מטפלים במשוב באמצעות בעיות ב-GitHub [קישור למשוב].

המחבר: מרטין גרנר טוויטר: @martin_gorner

כל התמונות המצוירות ב-Lab הזה מוגנות בזכויות יוצרים: alexpokusay / 123RF stock photos