Esta seção aborda as principais métricas do Meridian: resultado incremental, retorno do investimento (ROI), ROI marginal (mROI) e curvas de resposta.
Aprendizados rápidos
O resultado incremental, o retorno do investimento (ROI), o ROI marginal (mROI) e as curvas de resposta são as ferramentas que transformam as descobertas do seu modelo em uma estratégias de negócios práticas. Elas ajudam a responder às perguntas mais importantes do marketing: "Qual foi o desempenho dos meus canais?" e "Onde devo gastar em seguida?"
Ao entender essas métricas, você pode identificar seus canais mais eficientes, saber os níveis atuais de saturação e otimizar seu orçamento para maximizar os resultados dos negócios. Em especial, as curvas de resposta oferecem uma visualização eficiente de como o resultado incremental responde a mais gastos, que é a base da alocação de orçamento baseada em dados.
Exemplo de marketing
Imagine que você tem uma loja de calçados on-line e gasta R$ 10.000 em um canal de mídia de vídeo. Depois de executar o modelo do Meridian, você descobre que o canal gerou R$ 25.000 em vendas incrementais.
- O resultado incremental é o valor agregado pelo marketing. Por exemplo, suas vendas totais foram de R$ 150.000, mas o Meridian estima que, sem a campanha, elas teriam sido de R$ 125.000. O resultado incremental é a diferença: R$ 25.000.
- Seu ROI é de R$ 2,50 (R$ 25.000 em vendas / R$ 10.000 em custo), ou seja, você ganhou R$ 2,50 para cada real gasto. Consulte mais detalhes sobre os cálculos em Considerações para interpretar o ROI e as curvas de resposta.
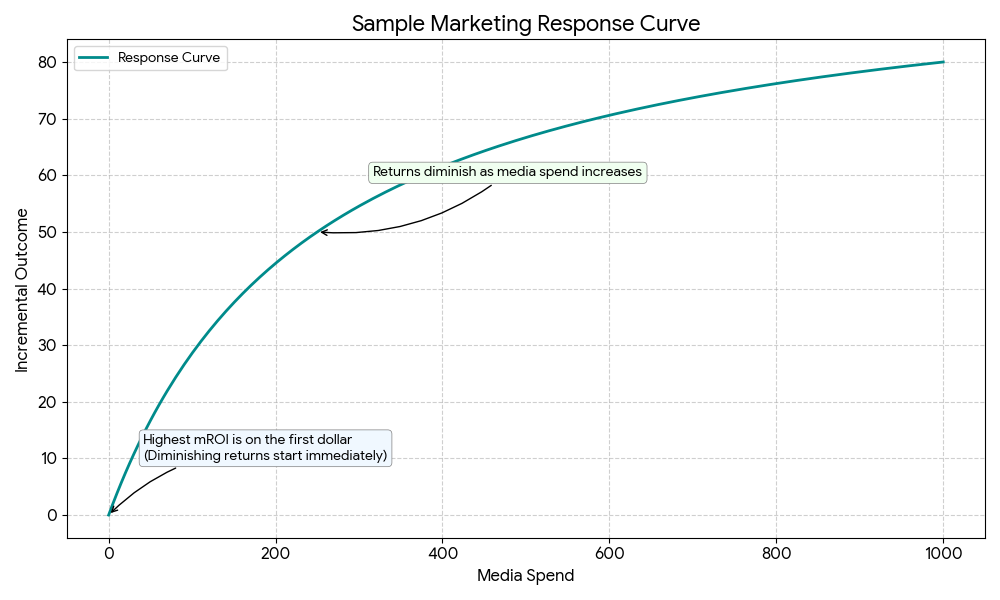
- A curva de resposta simula como suas vendas mudariam com diferentes níveis de gasto. Ela mostra que gastar ainda mais dinheiro gera retornos progressivamente menores.
- O mROI é o retorno que você receberia com um pequeno aumento no gasto (por exemplo, mais um real). Se o canal estiver perto da saturação, o mROI poderá ser de apenas R$ 0,80, indicando que é hora de investir em outro lugar.
Recomendação de regra prática
- Use o ROI para avaliar a performance histórica: ele oferece uma avaliação geral clara da eficácia dos seus gastos anteriores em um determinado canal.
- Use as curvas de resposta para otimizar orçamentos futuros: elas mostram o ponto de retornos decrescentes, ajudando você a entender quanto pode investir em um canal antes que ele se torne ineficiente.
- Use o mROI para avaliar o nível de saturação: se o mROI for muito menor em comparação com o ROI, o canal estará começando a saturar no nível de gasto histórico. Os canais com o maior mROI são os melhores para investir mais recursos.
Tabela de comparação
| Métrica | Ideal para | Definição |
|---|---|---|
| ROI | Avaliar a performance anterior. | Uma média histórica em todo o canal. |
| Curvas de resposta | Otimizar os gastos futuros e visualizar os retornos decrescentes. | Resultado incremental como uma função dos gastos. |
| mROI | Entender o nível de saturação atual. | O retorno do próximo real gasto. |
Exemplos de código
Para conhecer exemplos de códigos funcionais, consulte Exemplo: ROI, mROI e curvas de resposta no Meridian.
Explicação detalhada
Esta seção explica em mais detalhes as definições e metodologias por trás do ROI, do mROI e das curvas de resposta.
Explicação do resultado incremental
A base do ROI, do mROI e das curvas de resposta é o resultado incremental. É a parte do seu resultado, como vendas ou conversões, que foi gerada por uma atividade de marketing específica. Para calcular isso, o Meridian compara o resultado real com um cenário contrafactual em que a atividade de marketing nunca aconteceu. Para mídia paga, o resultado incremental pode ser contextualizado ainda mais pelos gastos das seguintes maneiras:
- A curva de resposta estima o resultado incremental em qualquer nível de gasto.
- O ROI é o resultado incremental no seu nível de gasto histórico dividido pelo gasto.
- O mROI é o resultado incremental do próximo real gasto acima do nível de orçamento histórico.
Como as curvas de resposta são geradas
Uma curva de resposta mostra a relação entre o gasto e o resultado incremental de um único canal, supondo que os gastos de todos os outros canais permaneçam iguais.
O Meridian gera essa curva em diferentes níveis de gastos para um canal. Ele aumenta ou diminui o gasto histórico do canal por um fator (por exemplo, de 1,2 vezes o gasto histórico) e estima o resultado incremental em cada nível. A distribuição histórica dos gastos ao longo do tempo e da geografia (o padrão do período de veiculação) é preservada durante esse ajuste. Esse processo revela o ponto em que um canal fica saturado e mais investimentos vão gerar retornos cada vez menores.
Considerações para interpretar o ROI e as curvas de resposta
- Efeitos de defasagem: a definição do ROI usa o custo total de um canal em um período específico como denominador. O numerador é o resultado incremental acumulado durante esse mesmo período. Esse numerador inclui efeitos de defasagem de anúncios veiculados antes do período, mas exclui efeitos futuros de anúncios veiculados durante o período. Em um período longo (por exemplo, um ano), isso tem um efeito pequeno na estimativa de ROI. No entanto, para períodos mais curtos, o efeito poderá ser mais significativo.
- Risco de extrapolação: para calcular o resultado incremental, o modelo precisa estimar o que teria acontecido se o gasto fosse zero. Se você sempre gastou de forma consistente em um canal, o modelo terá poucos dados para esse cenário de gasto zero e precisará extrapolar com base nas premissas aprendidas. O risco de extrapolação também afeta a estimativa de resultado incremental para pontos na curva de resposta que são maiores do que o gasto histórico, e o risco aumenta quanto mais longe você vai.
Apêndice matemático
Nesta seção, descrevemos como o Meridian define as principais estimações de interesse, incluindo resultado incremental, ROI, ROI marginal e curvas de resposta. Essas quantidades são definidas usando resultados potenciais e contrafactuais, que são a linguagem da inferência causal.
Com definições de estimação claras, você pode analisar as premissas exigidas para que a MMM forneça uma inferência válida. Essas premissas ajudam a garantir que o modelo seja capaz de estimar as quantidades. A estimativas serão fortemente tendenciosas se as premissas não forem atendidas.
Recomendamos que você defina com clareza as estimações causais e as premissas necessárias para qualquer metodologia de MMM. Caso contrário, a interpretação dos resultados do modelo provavelmente será incorreta. Além disso, ignorar as premissas necessárias pode gerar um grande viés que torna a análise praticamente sem sentido.
As definições na seção a seguir não dependem de nenhum aspecto da especificação do modelo do Meridian, elas valem para qualquer MMM. É essencial definir a estimação causal em qualquer análise de MMM para que os resultados sejam interpretáveis e para determinar se um modelo específico é adequado à análise e usando quais premissas.
Resultado incremental
Começamos com o resultado incremental, já que ele serve como base para o ROI, o mROI e as curvas de resposta.
Estrutura de inferência causal por trás do resultado incremental
O Meridian mede o efeito causal das variáveis de tratamento no resultado.
O resultado normalmente é a receita, mas, quando o KPI não é a receita e os dados de revenue_per_kpi não estão disponíveis, o Meridian define o resultado como o próprio KPI.
Definimos o resultado incremental usando a estrutura de inferência causal. Na inferência causal, é comum encontrar notações como \(Y^{(1)}\) e\(Y^{(0)}\) , que representam possíveis resultados nos cenários contrafactuais de tratamento e controle. O Meridian é semelhante, mas um pouco mais complexo, porque os cenários contrafactuais de tratamento e controle são matrizes tridimensionais em regiões geográficas $g$, tempo $t$ e variáveis de tratamento $i$. Denotamos os cenários contrafactuais de tratamento e controle como\(\left\{x^{(1)}_{g,t,i}\right\}\) e \(\left\{x^{(0)}_{g,t,i}\right\}\), respectivamente. Além disso, os resultados possíveis são uma matriz bidimensional em regiões geográficas e tempo. Denotamos os resultados potenciais nos cenários contrafactuais de tratamento e controle como\(\overset\sim Y_{g,t}^{\left(\left\{ x_{g,t,i}^{(1)} \right\}\right)}\)e \(\overset\sim Y_{g,t}^{\left(\left\{ x_{g,t,i}^{(0)} \right\}\right)}\), respectivamente.
O seguinte seria fundamental para decidir entre cenários contrafactuais:
No entanto, essa quantidade não é observável porque não é possível observar o resultado potencial nos dois cenários contrafactuais. No máximo, conseguimos ver apenas um cenário contrafactual. Para dois cenários contrafactuais de tratamento, \(\{x^{(1)}_{g,t,i} \}\) e\(\{ x^{(0)}_{g,t,i} \}\), defina o resultado incremental como:
em que \(\{z_{g,t,i}\}\) denota os valores observados para um conjunto de variáveis de controle. Essa notação abreviada é usada para indicar que a expectativa tem como condição que as variáveis de controle aleatórias assumam esses valores. Essa expectativa condicional pode ser estimada usando um modelo de regressão de MMM e um conjunto cuidadosamente selecionado de variáveis de controle. Consulte Estimar o resultado incremental usando regressão para mais informações.
Normalmente, a soma é feita com \(g=1,\dots G\) e \(t=1,\dots T\), mas você também pode definir um resultado incremental para qualquer subconjunto desses valores.
Cenários contrafactuais usados no Meridian
Embora o incremental_outcome ofereça flexibilidade suficiente para considerar qualquer cenário contrafactual, o Meridian usa por padrão um par específico de cenários de tratamento contrafactual. Como o ROI, o mROI e as curvas de resposta são criados com base nas configurações padrão de incremental_outcome, esse par específico é importante.
O Meridian permite que \(\left\{x^{(1)}_{g,t,i}\right\}\) sejam valores históricos reais e \(\left\{x^{(0)}_{g,t,i}\right\}\) sejam iguais aos valores históricos reais, exceto quando todos os valores de uma variável de tratamento específica são definidos como o valor de referência. Para mídia paga e orgânica, os valores de referência são zero. Para variáveis de tratamento não relacionadas à mídia, o valor de referência pode ser definido como o valor mínimo observado da variável (padrão), o máximo ou um ponto flutuante fornecido pelo usuário.
Para uma determinada variável de tratamento \(q\), o resultado incremental é definido como:
\[\text{IncrementalOutcome}_q = \text{IncrementalOutcome} \left(\Bigl\{ x_{g,t,i} \Bigr\}, \Bigl\{ x_{g,t,i}^{(0,q)} \Bigr\} \right)\]
Em que:
- \(\left\{ x_{g,t,i}\right\}\) são os valores de tratamento observados.
- \(\left\{ x_{g,t,i}^{(0,q)} \right\}\) denota os valores observados para todos os tratamentos, exceto \(q\), que é sempre definido como o valor de referência \(b_q\) . Mais especificamente:
- \(x_{g,t,q}^{(0,q)}=b_q\ \forall\ g,t\)
- \(x_{g,t,i}^{(0,q)}=x_{g,t,i}\ \forall\ g,t,i \neq q\)
O cenário de mídia contrafactual (\(\left\{ x_{g,t,i}^{(0,q)} \right\}\)) talvez não seja representado nos dados. Quando isso acontece, é necessário extrapolar as premissas do modelo para inferir o contrafactual.
ROI
O ROI de um canal de mídia paga \(q\) é definido como:
\[\text{ROI}_q = \dfrac{\text{IncrementalOutcome}_q}{\text{Cost}_q}\]
Em que \(\text{Cost}_q\) é o custo do canal de mídia paga \(q\) somado de todas as regiões e períodos.
A definição de ROI usa o custo total de um canal em um período específico como denominador. O numerador é o resultado incremental acumulado durante esse mesmo período. Esse numerador inclui efeitos de defasagem de anúncios veiculados antes do período, mas exclui efeitos futuros de anúncios veiculados durante o período. Em um período longo (por exemplo, um ano), isso tem um efeito pequeno na estimativa de ROI. No entanto, para períodos mais curtos, o efeito poderá ser mais significativo.
Curvas de resposta
Generalizando a definição de resultado incremental, a curva de resposta do canal de mídia paga \(q\) é uma função que retorna o resultado incremental como uma função do gasto no canal \(q\):
\[\text{IncrementalOutcome}_q (\omega \cdot \text{Cost}_q) = \text{IncrementalOutcome} \left(\left\{ x^{(\omega,q)}_{g,t,i} \right\}, \left\{ x^{(0,q)}_{g,t,i} \right\}\right)\]
Em que \(\left\{ x^{(\omega,q)}_{g,t,i} \right\}\) indica os valores de mídia observados para todos os canais, exceto \(q\), que é sempre multiplicado por um fator de \(\omega\) . Mais especificamente:
- \(x^{(\omega,q)}_{g,t,q}=\omega \cdot x_{g,t,q}\ \forall\ g,t\)
- \(x^{(\omega,q)}_{g,t,i}=x_{g,t,i} \forall\ g,t,i \neq q\)
ROI marginal (mROI)
O ROI marginal (mROI) do canal de mídia paga \(q\) é definido como:
Em que \(\delta\) é uma quantidade pequena, como \(0.01\).
As definições de curva de resposta e ROI marginal pressupõem implicitamente um custo constante por unidade de mídia que é igual à média histórica do custo por unidade de mídia.
