在营销组合建模分析中，一个常见的挑战是确保模型的结果反映您业务的复杂现实情况，强大的贝叶斯功能先验可帮助应对这一挑战。本页简要介绍了什么是先验，为什么它是 Meridian 方法的基石，以及使用先验时有哪些关键注意事项。
什么是先验？
“先验”是指您在模型分析数据之前向其提供的信息。您可以将先验理解为根据您的业务知识、行业基准或过往实验结果，为模型提供一个良好的开端或一些专家建议。这种关系是贝叶斯统计理论的核心，可以总结为：
\[ \underset{\text{(the model)}}{\text{Posterior}} \propto \underset{\text{(the data)}}{\text{Likelihood}} \cdot \underset{\text{(your belief)}}{\text{Prior}} \]
模型的后验分布（系统会根据它得出估计值）会同时考虑您的初始信念（先验）和数据本身所表明的情况（似然）。先验可使模型保持稳定，同时确保模型基于实际业务背景。
Meridian 的一个关键功能是能够直接使用您所关注的业务指标。Meridian 并不要求提供有关抽象回归系数的先验信息，而是旨在纳入有关可衡量的具体指标（例如投资回报率 [ROI]、边际投资回报率 [mROI] 和贡献百分比）的先验信息。
先验可以来自多种来源：
- 过往增量实验（例如提升效果测试或地理位置实验）的结果。
- 行业基准。
- 之前的 MMM 结果。
- 您团队自身的专业领域知识。
如果您没有这些，也不必担心。Meridian 具有内置的默认先验，可为您提供一个起点。
从分布的角度了解先验
为了让您直观地了解先验，我们提供了一些可视化示例，说明如何将业务直觉转换为 MMM 的先验。
先验分布的形态
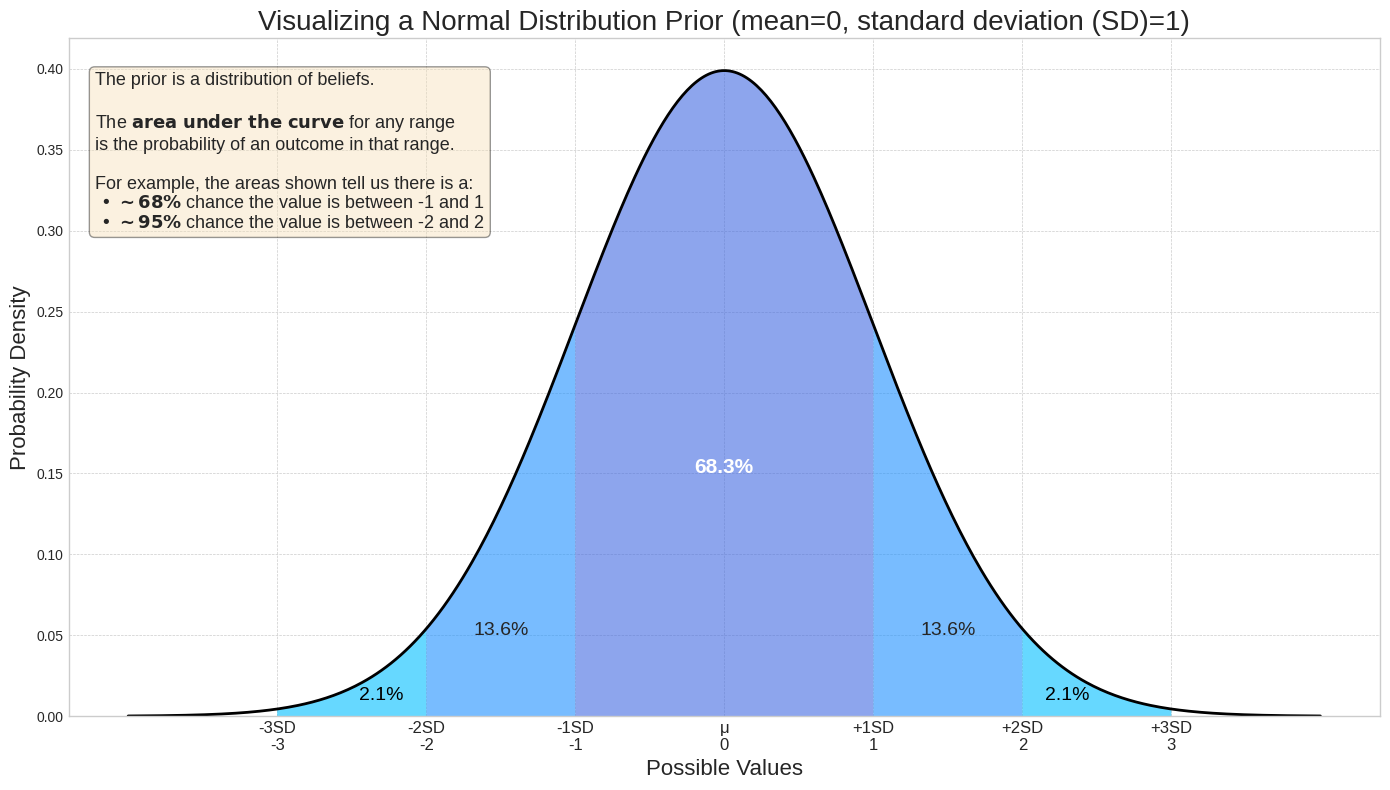
先验以概率分布的形式表示。分布会为形参（例如 ROI）的每个可能值分配一个密度（相对似然）。x 轴上任意两点之间的曲线下方面积表示真实值落入该范围内的概率。例如，以下分布图显示，值在 -1 和 1 之间的概率远高于在该范围之外的概率。对于均值为 0、标准差为 1 的正态分布，真实值介于 -1 和 1 之间的概率为 68.3%。
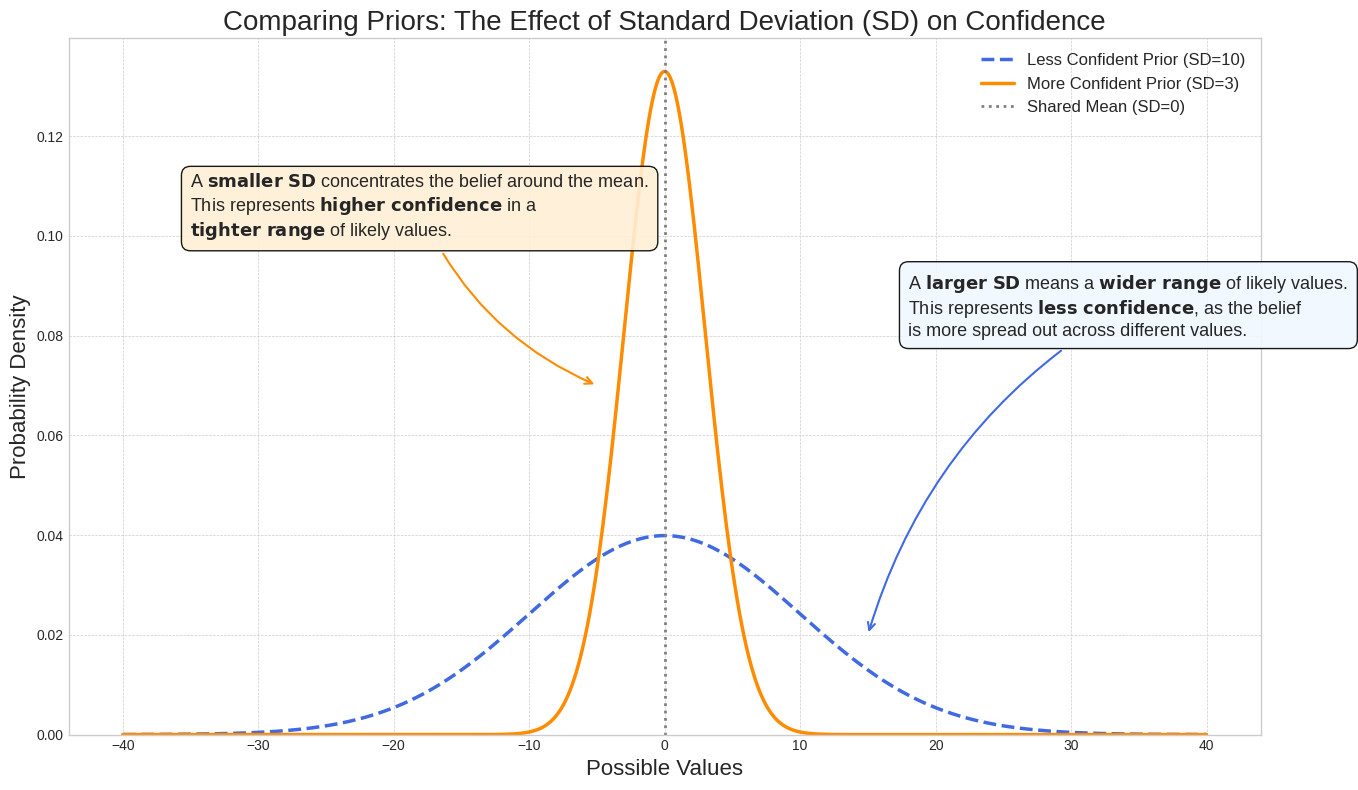
标准差对置信度的影响
标准差用于控制分布的宽度，可反映您对形参值的置信度。标准差越小，概率越集中在形参值附近，表明置信度越高；标准差越大，概率越分散，表明不确定性越大。
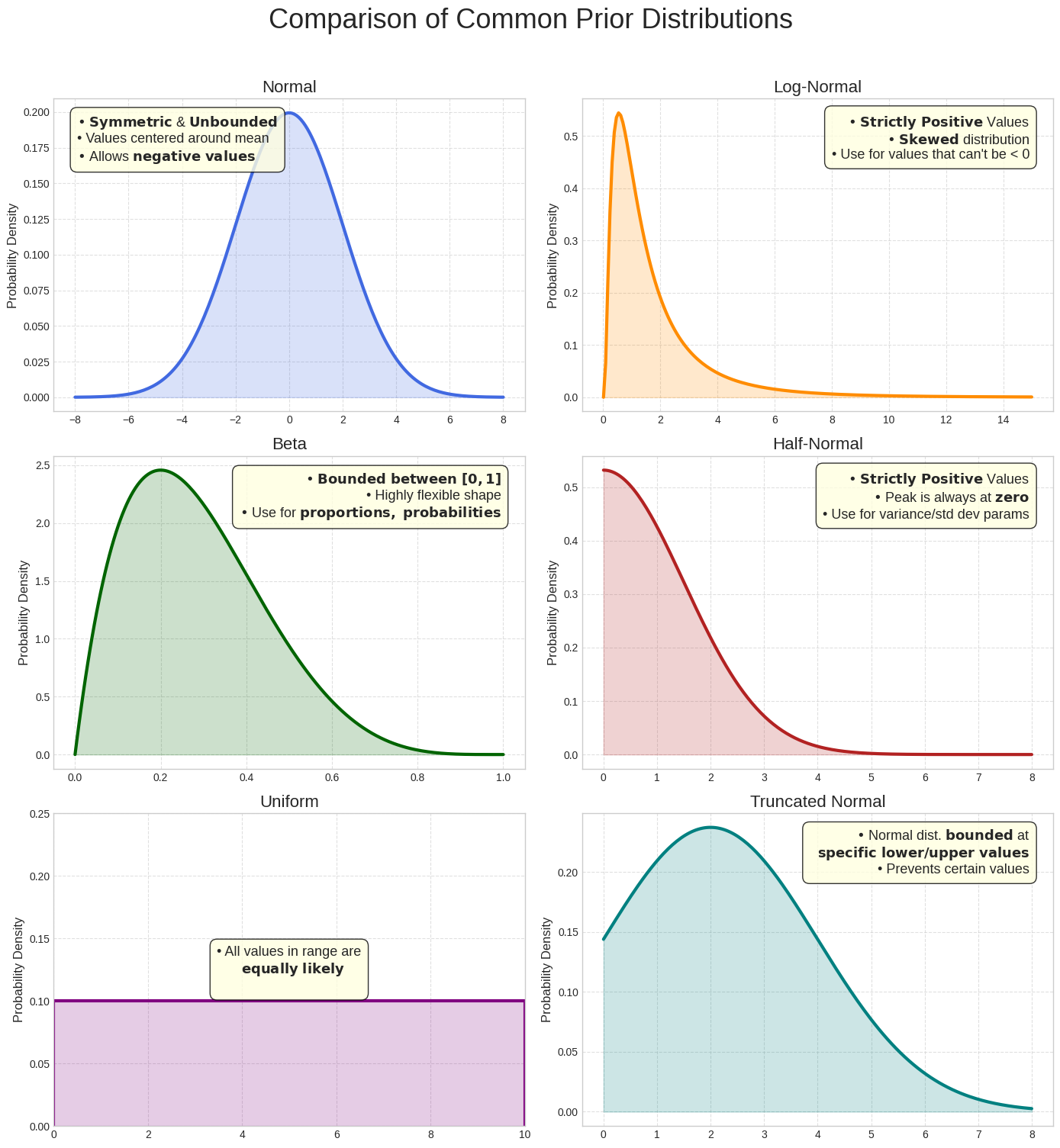
常见先验分布对比
虽然正态分布是一个很有用的示例，但根据纳入模型的形参，其他分布往往更为适合。例如，由于 ROI 应为正值，因此与允许有负值的正态分布相比，仅为正值分配概率的分布（例如对数正态分布或半正态分布）通常是更理想的选择。Meridian 使用多种常见分布，您可以选择最能反映您纳入模型的形参性质的分布。
代码示例：置信度与不确定性
以下示例展示了如何在代码中表达对三个不同付费媒体渠道的 ROI 的不同置信度。
from meridian.model import prior_distribution
# --- Channel 1: High Confidence ---
# You have strong experiment results showing ROI is consistently around 1.2.
# You use a small standard deviation (0.2) to reflect your high confidence.
strong_prior_channel_1 = prior_distribution.lognormal_dist_from_mean_std(
mean=1.2,
std=0.2
)
# --- Channel 2: Low Confidence ---
# You have weaker experiment results showing ROI is around 1.0.
# You use a small sigma (0.9) to reflect your weaker confidence in the
# experiment result than for Channel 1.
weak_prior_channel_2 = prior_distribution.lognormal_dist_from_mean_std(
mean=1.0,
std=0.9
)
# --- Channel 3: Confidence in a range ---
# You believe there's a 95% chance the ROI is between 2.0 and 6.0.
range_prior_channel_3 = prior_distribution.lognormal_dist_from_range(
low=2.0,
high=6.0
mass_percent=0.95
)
# You would then assign these distributions to their respective channels
# when you configure your model.
prior_config = prior_distribution.PriorDistribution(
roi_m=[strong_prior_channel_1, weaker_prior_channel_2, range_prior_channel_3]
)
直观呈现先验
绘制先验图非常简单，有助于确保先验与您的直觉相符。
from matplotlib import pyplot as plt
from meridian.model import prior_distribution
import numpy as np
# Define the LogNormal distribution
lognormal_dist = prior_distribution.lognormal_dist_from_mean_std(2.0, 0.5)
# Plot a histogram of samples from the LogNormal distribution
plt.hist(lognormal_dist.sample(1000))
为什么先验至关重要
使用先验不仅仅是一项技术功能，对于获得可信且可据以采取行动的因果估计也至关重要。
- 使用更少的数据获得更合理稳定的结果：汇总的营销数据可能稀疏或包含噪声。先验具有稳定效应，能引导模型给出合理的结果，并防止模型基于有限的数据得出错误的结论。
- 让结果基于业务实际情况：通过纳入提升效果研究等可信来源的知识，先验的稳定效应可引导模型与这些知识保持一致，从而提高利益相关者的信心。
- 融入业务直觉：您对自己的业务几乎总是有着某种直觉。例如，在您的行业中，ROI 可能很少会超过 6.0。即使您没有来自实验的确凿数据，也可以将这种直觉融入您的先验，以引导模型得出更贴近实际的结果。
- 进行直观的模型控制：设置先验就像与模型进行直观的对话。您无需调整抽象的形参，而是以自己理解的语言提供指导，例如“我有强有力的证据表明，我的渠道的 ROI 约为 1.5。”