Un enfoque científico para mejorar el rendimiento del modelo

Para los fines de este documento, se aplican las siguientes definiciones:

El objetivo final del desarrollo del aprendizaje automático es maximizar la utilidad del modelo implementado.

Por lo general, puedes usar los mismos pasos y principios básicos de esta sección en cualquier problema de AA.

En esta sección, se hacen las siguientes suposiciones:

• Ya tienes una canalización de entrenamiento en ejecución junto con una configuración que obtiene un resultado razonable.
• Tienes suficientes recursos de procesamiento para realizar experimentos de ajuste significativos y ejecutar al menos varios trabajos de entrenamiento en paralelo.

La estrategia de ajuste incremental

Recomendación: Comienza con una configuración simple. Luego, realiza mejoras de forma incremental mientras obtienes información sobre el problema. Asegúrate de que cualquier mejora se base en evidencia sólida.

Suponemos que tu objetivo es encontrar una configuración que maximice el rendimiento de tu modelo. A veces, tu objetivo es maximizar la mejora del modelo antes de una fecha límite fija. En otros casos, puedes seguir mejorando el modelo de forma indefinida, por ejemplo, mejorando continuamente un modelo que se usa en producción.

En principio, podrías maximizar el rendimiento con un algoritmo para buscar automáticamente todo el espacio de configuraciones posibles, pero esta no es una opción práctica. El espacio de configuraciones posibles es extremadamente grande y aún no existen algoritmos lo suficientemente sofisticados como para buscar de manera eficiente en este espacio sin orientación humana. La mayoría de los algoritmos de búsqueda automatizados se basan en un espacio de búsqueda diseñado manualmente que define el conjunto de configuraciones en el que se realizará la búsqueda, y estos espacios de búsqueda pueden ser muy importantes.

La forma más eficaz de maximizar el rendimiento es comenzar con una configuración simple y agregar funciones y realizar mejoras de forma incremental a medida que se adquiere información sobre el problema.

Te recomendamos que uses algoritmos de búsqueda automatizados en cada ronda de ajuste y que actualices continuamente los espacios de búsqueda a medida que aumente tu comprensión. A medida que explores, encontrarás de forma natural configuraciones cada vez mejores y, por lo tanto, tu "mejor" modelo mejorará continuamente.

El término "lanzamiento" hace referencia a una actualización de nuestra mejor configuración (que puede corresponder o no al lanzamiento real de un modelo de producción). Para cada "lanzamiento", debes asegurarte de que el cambio se base en evidencia sólida, no solo en una casualidad basada en una configuración afortunada, para no agregar complejidad innecesaria a la canalización de entrenamiento.

En términos generales, nuestra estrategia de ajuste incremental implica repetir los siguientes cuatro pasos:

1. Elige un objetivo para la próxima ronda de experimentos. Asegúrate de que el objetivo tenga el alcance adecuado.
2. Diseña la próxima ronda de experimentos. Diseñar y ejecutar un conjunto de experimentos que avancen hacia este objetivo
3. Aprende de los resultados experimentales. Evalúa el experimento en función de una lista de tareas.
4. Determina si se debe adoptar el cambio candidato.

En el resto de esta sección, se detalla esta estrategia.

Elige un objetivo para la próxima ronda de experimentos

Si intentas agregar varias funciones o responder varias preguntas a la vez, es posible que no puedas separar los efectos individuales en los resultados. Estos son algunos ejemplos de objetivos:

• Probar una posible mejora en la canalización (por ejemplo, un nuevo regularizador, una opción de preprocesamiento, etcétera)
• Comprender el impacto de un hiperparámetro del modelo en particular (por ejemplo, la función de activación)
• Minimiza el error de validación.

Prioriza el progreso a largo plazo por sobre las mejoras en los errores de validación a corto plazo

Resumen: La mayoría de las veces, tu objetivo principal es obtener información sobre el problema de ajuste.

Te recomendamos que dediques la mayor parte de tu tiempo a comprender el problema y relativamente poco tiempo a enfocarte en maximizar el rendimiento en el conjunto de validación. En otras palabras, dedica la mayor parte de tu tiempo a la "exploración" y solo una pequeña parte a la "explotación". Comprender el problema es fundamental para maximizar el rendimiento final. Priorizar las estadísticas por sobre las ganancias a corto plazo ayuda a hacer lo siguiente:

• Evita lanzar cambios innecesarios que se hayan producido en ejecuciones con buen rendimiento solo por accidente histórico.
• Identificar a qué hiperparámetros es más sensible el error de validación, qué hiperparámetros interactúan más y, por lo tanto, deben reajustarse juntos, y qué hiperparámetros son relativamente insensibles a otros cambios y, por lo tanto, se pueden fijar en experimentos futuros
• Sugerir posibles funciones nuevas para probar, como nuevos regularizadores cuando el sobreajuste es un problema
• Identificar las funciones que no ayudan y, por lo tanto, se pueden quitar, lo que reduce la complejidad de los experimentos futuros
• Reconocer cuándo es probable que las mejoras del ajuste de hiperparámetros se hayan saturado
• Reducimos nuestros espacios de búsqueda en torno al valor óptimo para mejorar la eficiencia del ajuste.

Con el tiempo, comprenderás el problema. Luego, puedes enfocarte únicamente en el error de validación, incluso si los experimentos no son lo más informativos posible sobre la estructura del problema de ajuste.

Diseña la próxima ronda de experimentos

Resumen: Identifica qué hiperparámetros son científicos, cuáles son molestos y cuáles son fijos para el objetivo experimental. Crea una secuencia de estudios para comparar diferentes valores de los hiperparámetros científicos mientras optimizas los hiperparámetros molestos. Elige el espacio de búsqueda de los hiperparámetros molestos para equilibrar los costos de los recursos con el valor científico.

Identifica los hiperparámetros científicos, de molestia y fijos

Para un objetivo determinado, todos los hiperparámetros se incluyen en una de las siguientes categorías:

• Los hiperparámetros científicos son aquellos cuyo efecto en el rendimiento del modelo es lo que intentas medir.
• Los hiperparámetros molestos son aquellos que se deben optimizar para comparar de manera justa diferentes valores de los hiperparámetros científicos. Los hiperparámetros molestos son similares a los parámetros molestos en las estadísticas.
• Los hiperparámetros fijos tienen valores constantes en la ronda actual de experimentos. Los valores de los hiperparámetros fijos no deben cambiar cuando comparas diferentes valores de los hiperparámetros científicos. Si fijas ciertos hiperparámetros para un conjunto de experimentos, debes aceptar que las conclusiones derivadas de los experimentos podrían no ser válidas para otros parámetros de configuración de los hiperparámetros fijos. En otras palabras, los hiperparámetros fijos generan advertencias para cualquier conclusión que extraigas de los experimentos.

Por ejemplo, supongamos que tu objetivo es el siguiente:

Determina si un modelo con más capas ocultas tiene un error de validación menor.

En este caso, ocurre lo siguiente:

• La tasa de aprendizaje es un hiperparámetro molesto porque solo puedes comparar de manera justa modelos con diferentes cantidades de capas ocultas si la tasa de aprendizaje se ajusta por separado para cada cantidad de capas ocultas. (En general, la tasa de aprendizaje óptima depende de la arquitectura del modelo).
• La función de activación podría ser un hiperparámetro fijo si determinaste en experimentos anteriores que la mejor función de activación no es sensible a la profundidad del modelo. O bien, puedes limitar tus conclusiones sobre la cantidad de capas ocultas para abarcar esta función de activación. Como alternativa, podría ser un hiperparámetro de molestia si estás preparado para ajustarlo por separado para cada cantidad de capas ocultas.

Un hiperparámetro en particular puede ser científico, de molestia o fijo. Su designación cambia según el objetivo experimental. Por ejemplo, la función de activación podría ser cualquiera de las siguientes:

• Hiperparámetro científico: ¿ReLU o tanh son una mejor opción para nuestro problema?
• Hiperparámetro de molestia: ¿El mejor modelo de cinco capas es mejor que el mejor modelo de seis capas cuando permites varias funciones de activación posibles diferentes?
• Hiperparámetro fijo: Para las redes ReLU, ¿ayuda agregar la normalización por lotes en una posición en particular?

Al diseñar una nueva ronda de experimentos, ten en cuenta lo siguiente:

1. Identifica los hiperparámetros científicos para el objetivo experimental. (En esta etapa, puedes considerar que todos los demás hiperparámetros son hiperparámetros molestos).
2. Convierte algunos hiperparámetros molestos en hiperparámetros fijos.

Con recursos ilimitados, dejarías todos los hiperparámetros no científicos como hiperparámetros molestos para que las conclusiones que extraigas de tus experimentos no tengan advertencias sobre los valores fijos de los hiperparámetros. Sin embargo, cuantos más hiperparámetros molestos intentes ajustar, mayor será el riesgo de que no los ajustes lo suficientemente bien para cada configuración de los hiperparámetros científicos y termines llegando a conclusiones incorrectas a partir de tus experimentos. Como se describe en una sección posterior, podrías contrarrestar este riesgo aumentando el presupuesto de procesamiento. Sin embargo, tu presupuesto máximo de recursos suele ser inferior al que se necesitaría para ajustar todos los hiperparámetros no científicos.

Recomendamos convertir un hiperparámetro de molestia en un hiperparámetro fijo cuando las advertencias que se introducen al fijarlo son menos onerosas que el costo de incluirlo como un hiperparámetro de molestia. Cuanto más interactúa un hiperparámetro de molestia con los hiperparámetros científicos, más perjudicial es fijar su valor. Por ejemplo, el mejor valor de la intensidad de la disminución del peso suele depender del tamaño del modelo, por lo que comparar diferentes tamaños de modelos suponiendo un solo valor específico de la disminución del peso no sería muy útil.

Algunos parámetros del optimizador

Como regla general, algunos hiperparámetros del optimizador (p.ej., la tasa de aprendizaje, el momentum, los parámetros del programa de la tasa de aprendizaje, los betas de Adam, etc.) son hiperparámetros molestos porque tienden a interactuar más con otros cambios. Estos hiperparámetros del optimizador rara vez son científicos, ya que un objetivo como "¿cuál es la mejor tasa de aprendizaje para la canalización actual?" no proporciona mucha información. Después de todo, el mejor parámetro de configuración podría cambiar con la próxima modificación de la canalización.

Es posible que, en ocasiones, fijes algunos hiperparámetros del optimizador debido a limitaciones de recursos o a evidencia particularmente sólida de que no interactúan con los parámetros científicos. Sin embargo, en general, debes suponer que debes ajustar los hiperparámetros del optimizador por separado para realizar comparaciones justas entre los diferentes parámetros de configuración de los hiperparámetros científicos y, por lo tanto, no deben fijarse. Además, no hay ninguna razón a priori para preferir un valor de hiperparámetro del optimizador sobre otro. Por ejemplo, los valores de hiperparámetro del optimizador no suelen afectar el costo computacional de los pases hacia adelante o los gradientes de ninguna manera.

La elección del optimizador

Por lo general, la elección del optimizador es una de las siguientes:

• un hiperparámetro científico
• un hiperparámetro fijo

Un optimizador es un hiperparámetro científico si tu objetivo experimental implica realizar comparaciones justas entre dos o más optimizadores diferentes. Por ejemplo:

Determina qué optimizador produce el error de validación más bajo en una cantidad determinada de pasos.

También puedes hacer que el optimizador sea un hiperparámetro fijo por varios motivos, incluidos los siguientes:

• Los experimentos anteriores sugieren que el mejor optimizador para tu problema de ajuste no es sensible a los hiperparámetros científicos actuales.
• Prefieres comparar los valores de los hiperparámetros científicos con este optimizador porque sus curvas de entrenamiento son más fáciles de analizar.
• Prefieres usar este optimizador porque consume menos memoria que las alternativas.

Hiperparámetros de regularización

Los hiperparámetros que se introducen con una técnica de regularización suelen ser hiperparámetros molestos. Sin embargo, la elección de incluir o no la técnica de regularización es un hiperparámetro científico o fijo.

Por ejemplo, la regularización de abandono agrega complejidad al código. Por lo tanto, cuando decidas si incluir la regularización por abandono, puedes hacer que "sin abandono" vs. "abandono" sea un hiperparámetro científico, pero la tasa de abandono sea un hiperparámetro de molestia. Si decides agregar regularización por abandono a la canalización en función de este experimento, la tasa de abandono sería un hiperparámetro molesto en experimentos futuros.

Hiperparámetros de arquitectura

Los hiperparámetros arquitectónicos suelen ser científicos o fijos, ya que los cambios en la arquitectura pueden afectar los costos de entrega y entrenamiento, la latencia y los requisitos de memoria. Por ejemplo, la cantidad de capas suele ser un hiperparámetro científico o fijo, ya que tiende a tener consecuencias drásticas en la velocidad de entrenamiento y el uso de memoria.

Dependencias de los hiperparámetros científicos

En algunos casos, los conjuntos de hiperparámetros fijos y de molestia dependen de los valores de los hiperparámetros científicos. Por ejemplo, supongamos que intentas determinar qué optimizador entre el momentum de Nesterov y Adam produce el error de validación más bajo. En este caso, ocurre lo siguiente:

• El hiperparámetro científico es el optimizador, que toma los valores {"Nesterov_momentum", "Adam"}
• El valor optimizer="Nesterov_momentum" introduce los hiperparámetros {learning_rate, momentum}, que pueden ser hiperparámetros molestos o fijos.
• El valor optimizer="Adam" introduce los hiperparámetros {learning_rate, beta1, beta2, epsilon}, que pueden ser hiperparámetros molestos o fijos.

Los hiperparámetros que solo están presentes para ciertos valores de los hiperparámetros científicos se denominan hiperparámetros condicionales. No supongas que dos hiperparámetros condicionales son iguales solo porque tienen el mismo nombre. En el ejemplo anterior, el hiperparámetro condicional llamado learning_rate es un hiperparámetro diferente para optimizer="Nesterov_momentum" que para optimizer="Adam". Su función es similar (aunque no idéntica) en los dos algoritmos, pero el rango de valores que funcionan bien en cada uno de los optimizadores suele ser diferente en varios órdenes de magnitud.

Crea un conjunto de estudios

Después de identificar los hiperparámetros científicos y los molestos, debes diseñar un estudio o una secuencia de estudios para avanzar hacia el objetivo experimental. Un estudio especifica un conjunto de configuraciones de hiperparámetros que se ejecutarán para el análisis posterior. Cada configuración se denomina prueba. Por lo general, la creación de un estudio implica elegir lo siguiente:

• Son los hiperparámetros que varían entre las pruebas.
• Los valores que pueden tomar esos hiperparámetros (el espacio de búsqueda).
• Es la cantidad de pruebas.
• Un algoritmo de búsqueda automatizado para tomar muestras de esa cantidad de pruebas del espacio de búsqueda.

Como alternativa, puedes crear un estudio especificando el conjunto de configuraciones de hiperparámetros de forma manual.

El objetivo de los estudios es hacer lo siguiente de forma simultánea:

• Ejecuta la canalización con diferentes valores de los hiperparámetros científicos.
• "Optimizar" los hiperparámetros molestos para que las comparaciones entre diferentes valores de los hiperparámetros científicos sean lo más justas posible

En el caso más simple, realizarías un estudio independiente para cada configuración de los parámetros científicos, en el que cada estudio ajusta los hiperparámetros molestos. Por ejemplo, si tu objetivo es seleccionar el mejor optimizador entre el momento de Nesterov y Adam, puedes crear dos estudios:

• Un estudio en el que optimizer="Nesterov_momentum" y los hiperparámetros molestos son {learning_rate, momentum}
• Otro estudio en el que optimizer="Adam" y los hiperparámetros molestos son {learning_rate, beta1, beta2, epsilon}.

Para comparar los dos optimizadores, selecciona la prueba con el mejor rendimiento de cada estudio.

Puedes usar cualquier algoritmo de optimización sin gradiente, incluidos métodos como la optimización bayesiana o los algoritmos evolutivos, para optimizar los hiperparámetros molestos. Sin embargo, preferimos usar la búsqueda cuasialeatoria en la fase de exploración del ajuste debido a las diversas ventajas que tiene en este contexto. Una vez que finaliza la exploración, recomendamos usar software de optimización bayesiana de vanguardia (si está disponible).

Considera un caso más complicado en el que deseas comparar una gran cantidad de valores de los hiperparámetros científicos, pero no es práctico realizar tantos estudios independientes. En este caso, puedes hacer lo siguiente:

• Incluye los parámetros científicos en el mismo espacio de búsqueda que los hiperparámetros molestos.
• Usar un algoritmo de búsqueda para muestrear valores de los hiperparámetros científicos y de molestia en un solo estudio

Cuando se adopta este enfoque, los hiperparámetros condicionales pueden causar problemas. Después de todo, es difícil especificar un espacio de búsqueda, a menos que el conjunto de hiperparámetros molestos sea el mismo para todos los valores de los hiperparámetros científicos. En este caso, nuestra preferencia por usar la búsqueda cuasi aleatoria en lugar de herramientas de optimización de caja negra más sofisticadas es aún mayor, ya que garantiza que se muestrearán de manera uniforme diferentes valores de los hiperparámetros científicos. Independientemente del algoritmo de búsqueda, asegúrate de que busque los parámetros científicos de manera uniforme.

Logra un equilibrio entre experimentos informativos y asequibles

Cuando diseñes un estudio o una secuencia de estudios, asigna un presupuesto limitado para alcanzar adecuadamente los siguientes tres objetivos:

• Comparar suficientes valores diferentes de los hiperparámetros científicos
• Ajustar los hiperparámetros molestos en un espacio de búsqueda lo suficientemente grande
• Muestrear el espacio de búsqueda de hiperparámetros molestos con la suficiente densidad

Cuanto mejor logres estos tres objetivos, más estadísticas podrás extraer del experimento. Comparar la mayor cantidad posible de valores de los hiperparámetros científicos amplía el alcance de las estadísticas que obtienes del experimento.

Incluir la mayor cantidad posible de hiperparámetros molestos y permitir que cada uno de ellos varíe en un rango lo más amplio posible aumenta la confianza en que existe un valor "bueno" de los hiperparámetros molestos en el espacio de búsqueda para cada configuración de los hiperparámetros científicos. De lo contrario, es posible que realices comparaciones injustas entre los valores de los hiperparámetros científicos al no buscar regiones posibles del espacio de hiperparámetros molestos en las que podrían encontrarse mejores valores para algunos valores de los parámetros científicos.

Muestrea el espacio de búsqueda de hiperparámetros molestos con la mayor densidad posible. De esta manera, aumenta la confianza en que el procedimiento de búsqueda encontrará cualquier configuración adecuada para los hiperparámetros molestos que existan en tu espacio de búsqueda. De lo contrario, es posible que realices comparaciones injustas entre los valores de los parámetros científicos, ya que algunos valores tienen más suerte con el muestreo de los hiperparámetros molestos.

Lamentablemente, las mejoras en cualquiera de estas tres dimensiones requieren una de las siguientes opciones:

• Aumentar la cantidad de pruebas y, por lo tanto, aumentar el costo de los recursos
• Encontrar una forma de ahorrar recursos en una de las otras dimensiones

Cada problema tiene sus propias peculiaridades y limitaciones computacionales, por lo que asignar recursos a estos tres objetivos requiere cierto nivel de conocimiento del dominio. Después de ejecutar un estudio, siempre intenta determinar si los hiperparámetros molestos se ajustaron lo suficiente. Es decir, el estudio buscó en un espacio lo suficientemente grande y de forma lo suficientemente exhaustiva como para comparar de manera justa los hiperparámetros científicos (como se describe con más detalle en la siguiente sección).

Aprende de los resultados experimentales

Recomendación: Además de intentar alcanzar el objetivo científico original de cada grupo de experimentos, revisa una lista de preguntas adicionales. Si detectas problemas, revisa y vuelve a ejecutar los experimentos.

En última instancia, cada grupo de experimentos tiene un objetivo específico. Debes evaluar la evidencia que proporcionan los experimentos en relación con ese objetivo. Sin embargo, si haces las preguntas correctas, a menudo puedes encontrar problemas que corregir antes de que un conjunto determinado de experimentos pueda avanzar hacia su objetivo original. Si no haces estas preguntas, es posible que saques conclusiones incorrectas.

Dado que ejecutar experimentos puede ser costoso, también debes extraer otras estadísticas útiles de cada grupo de experimentos, incluso si estas estadísticas no son relevantes de inmediato para el objetivo actual.

Antes de analizar un conjunto determinado de experimentos para avanzar hacia su objetivo original, hazte las siguientes preguntas adicionales:

• ¿El espacio de búsqueda es lo suficientemente grande? Si el punto óptimo de un estudio está cerca del límite del espacio de búsqueda en una o más dimensiones, es probable que la búsqueda no sea lo suficientemente amplia. En este caso, ejecuta otro estudio con un espacio de búsqueda más amplio.
• ¿Tomaste suficientes muestras del espacio de búsqueda? De lo contrario, ejecuta más puntos o sé menos ambicioso con los objetivos de ajuste.
• ¿Qué fracción de las pruebas de cada estudio son inviables? Es decir, ¿qué pruebas divergen, obtienen valores de pérdida muy malos o no se ejecutan en absoluto porque incumplen alguna restricción implícita? Cuando una fracción muy grande de puntos en un estudio no son factibles, ajusta el espacio de búsqueda para evitar muestrear esos puntos, lo que a veces requiere volver a parametrizar el espacio de búsqueda. En algunos casos, una gran cantidad de puntos no factibles puede indicar un error en el código de entrenamiento.
• ¿El modelo presenta problemas de optimización?
• ¿Qué puedes aprender de las curvas de entrenamiento de los mejores experimentos? Por ejemplo, ¿los mejores experimentos tienen curvas de entrenamiento coherentes con un sobreajuste problemático?

Si es necesario, según las respuestas a las preguntas anteriores, refina el estudio o el grupo de estudios más recientes para mejorar el espacio de búsqueda o tomar más muestras de pruebas, o bien toma alguna otra medida correctiva.

Una vez que hayas respondido las preguntas anteriores, podrás evaluar la evidencia que proporcionan los experimentos en relación con tu objetivo original; por ejemplo, evaluar si un cambio es útil.

Identifica los límites incorrectos del espacio de búsqueda

Un espacio de búsqueda es sospechoso si el mejor punto muestreado a partir de él está cerca de su límite. Es posible que encuentres un punto aún mejor si expandes el rango de búsqueda en esa dirección.

Para verificar los límites del espacio de búsqueda, te recomendamos que traces las pruebas completadas en lo que llamamos gráficos básicos del eje de hiperparámetros. En estos, graficamos el valor del objetivo de validación en comparación con uno de los hiperparámetros (por ejemplo, la tasa de aprendizaje). Cada punto del gráfico corresponde a una sola prueba.

Por lo general, el valor objetivo de validación para cada prueba debería ser el mejor valor que se logró durante el entrenamiento.

Figura 1: Ejemplos de límites inadecuados y adecuados del espacio de búsqueda.

Los diagramas de la figura 1 muestran la tasa de error (cuanto más baja, mejor) en función de la tasa de aprendizaje inicial. Si los mejores puntos se agrupan cerca del borde de un espacio de búsqueda (en alguna dimensión), es posible que debas expandir los límites del espacio de búsqueda hasta que el mejor punto observado ya no esté cerca del límite.

A menudo, un estudio incluye pruebas "inviables" que divergen o arrojan resultados muy malos (marcados con cruces rojas en la Figura 1). Si todas las pruebas son inviables para las tasas de aprendizaje superiores a un determinado valor de umbral y si las pruebas con mejor rendimiento tienen tasas de aprendizaje en el límite de esa región, es posible que el modelo tenga problemas de estabilidad que le impidan acceder a tasas de aprendizaje más altas.

No se toman muestras suficientes de puntos en el espacio de búsqueda.

En general, puede ser muy difícil saber si el espacio de búsqueda se muestreó con la suficiente densidad. 🤖 Ejecutar más pruebas es mejor que ejecutar menos, pero más pruebas generan un costo adicional obvio.

Dado que es muy difícil saber cuándo se tomó una muestra suficiente, te recomendamos lo siguiente:

• Prueba lo que puedes pagar.
• Calibrar tu confianza intuitiva observando repetidamente varios diagramas de ejes de hiperparámetros y tratando de comprender cuántos puntos hay en la región "buena" del espacio de búsqueda

Examina las curvas de entrenamiento

Resumen: Examinar las curvas de pérdida es una forma sencilla de identificar los modos de falla comunes y puede ayudarte a priorizar las posibles próximas acciones.

En muchos casos, el objetivo principal de tus experimentos solo requiere que se considere el error de validación de cada prueba. Sin embargo, ten cuidado cuando reduzcas cada prueba a un solo número, ya que ese enfoque puede ocultar detalles importantes sobre lo que sucede bajo la superficie. Para cada estudio, te recomendamos que observes las curvas de pérdida de, al menos, las mejores pruebas. Incluso si esto no es necesario para abordar el objetivo experimental principal, examinar las curvas de pérdida (incluidas la pérdida del entrenamiento y la pérdida de la validación) es una buena manera de identificar los modos de falla comunes y puede ayudarte a priorizar las próximas acciones que debes realizar.

Cuando examines las curvas de pérdida, enfócate en las siguientes preguntas:

• ¿Alguno de los experimentos muestra un sobreajuste problemático? El sobreajuste problemático ocurre cuando el error de validación comienza a aumentar durante el entrenamiento. En la configuración experimental en la que optimizas los hiperparámetros molestos seleccionando la "mejor" prueba para cada configuración de los hiperparámetros científicos, verifica si hay un sobreajuste problemático en, al menos, cada una de las mejores pruebas correspondientes a la configuración de los hiperparámetros científicos que comparas. Si alguna de las mejores pruebas muestra un sobreajuste problemático, haz una o ambas de las siguientes acciones:

  • Vuelve a ejecutar el experimento con técnicas de regularización adicionales
  • Vuelve a ajustar los parámetros de regularización existentes antes de comparar los valores de los hiperparámetros científicos. Esto podría no aplicarse si los hiperparámetros científicos incluyen parámetros de regularización, ya que, en ese caso, no sería sorprendente que los parámetros de configuración de baja intensidad de esos parámetros de regularización generaran un sobreajuste problemático.

  Reducir el sobreajuste suele ser sencillo con técnicas de regularización comunes que agregan una complejidad de código mínima o un procesamiento adicional (por ejemplo, la regularización de retirados, el suavizado de etiquetas y la disminución del peso). Por lo tanto, suele ser trivial agregar uno o más de estos a la siguiente ronda de experimentos. Por ejemplo, si el hiperparámetro científico es "cantidad de capas ocultas" y la mejor prueba que usa la mayor cantidad de capas ocultas presenta un sobreajuste problemático, te recomendamos que vuelvas a intentarlo con una regularización adicional en lugar de seleccionar de inmediato la menor cantidad de capas ocultas.

  Incluso si ninguna de las "mejores" pruebas exhibe un sobreajuste problemático, podría haber un problema si se produce en alguna de las pruebas. Seleccionar la mejor prueba suprime las configuraciones que muestran un sobreajuste problemático y favorece las que no lo hacen. En otras palabras, seleccionar la mejor prueba favorece las configuraciones con más regularización. Sin embargo, cualquier factor que empeore el entrenamiento puede actuar como regularizador, incluso si no se pretendía que fuera así. Por ejemplo, elegir una tasa de aprendizaje más pequeña puede regularizar el entrenamiento al dificultar el proceso de optimización, pero, por lo general, no queremos elegir la tasa de aprendizaje de esta manera. Ten en cuenta que la prueba "mejor" para cada configuración de los hiperparámetros científicos se puede seleccionar de tal manera que favorezca los valores "incorrectos" de algunos de los hiperparámetros científicos o de molestia.

• ¿Existe una alta varianza paso a paso en el error de entrenamiento o validación en la última etapa del entrenamiento? Si es así, podría interferir en lo siguiente:

  • Tu capacidad para comparar diferentes valores de los hiperparámetros científicos Esto se debe a que cada prueba finaliza de forma aleatoria en un paso "afortunado" o "desafortunado".
  • Tu capacidad para reproducir el resultado de la mejor prueba en producción Esto se debe a que el modelo de producción podría no terminar en el mismo paso "afortunado" que en el estudio.

  Las causas más probables de la variación entre pasos son las siguientes:

  • Varianza del lote debido al muestreo aleatorio de ejemplos del conjunto de entrenamiento para cada lote.
  • Conjuntos de validación pequeños
  • Usar una tasa de aprendizaje demasiado alta en la última etapa del entrenamiento

  Entre las soluciones posibles, se incluyen las siguientes:

  • Aumentar el tamaño del lote
  • Obtener más datos de validación
  • Se usa la disminución de la tasa de aprendizaje.
  • Usa el promedio de Polyak.

• ¿Las pruebas siguen mejorando al final del entrenamiento? Si es así, te encuentras en el régimen de "límite de procesamiento" y te puede resultar beneficioso aumentar la cantidad de pasos de entrenamiento o cambiar el programa de la tasa de aprendizaje.

• ¿El rendimiento en los conjuntos de entrenamiento y validación se saturó mucho antes del paso de entrenamiento final? Si es así, esto indica que estás en el régimen de "no vinculado a la capacidad de procesamiento" y que es posible que puedas disminuir la cantidad de pasos de entrenamiento.

Además de esta lista, se pueden observar muchos comportamientos adicionales si se examinan las curvas de pérdida. Por ejemplo, si la pérdida de entrenamiento aumenta durante el entrenamiento, suele indicar un error en la canalización de entrenamiento.

Cómo detectar si un cambio es útil con gráficos de aislamiento

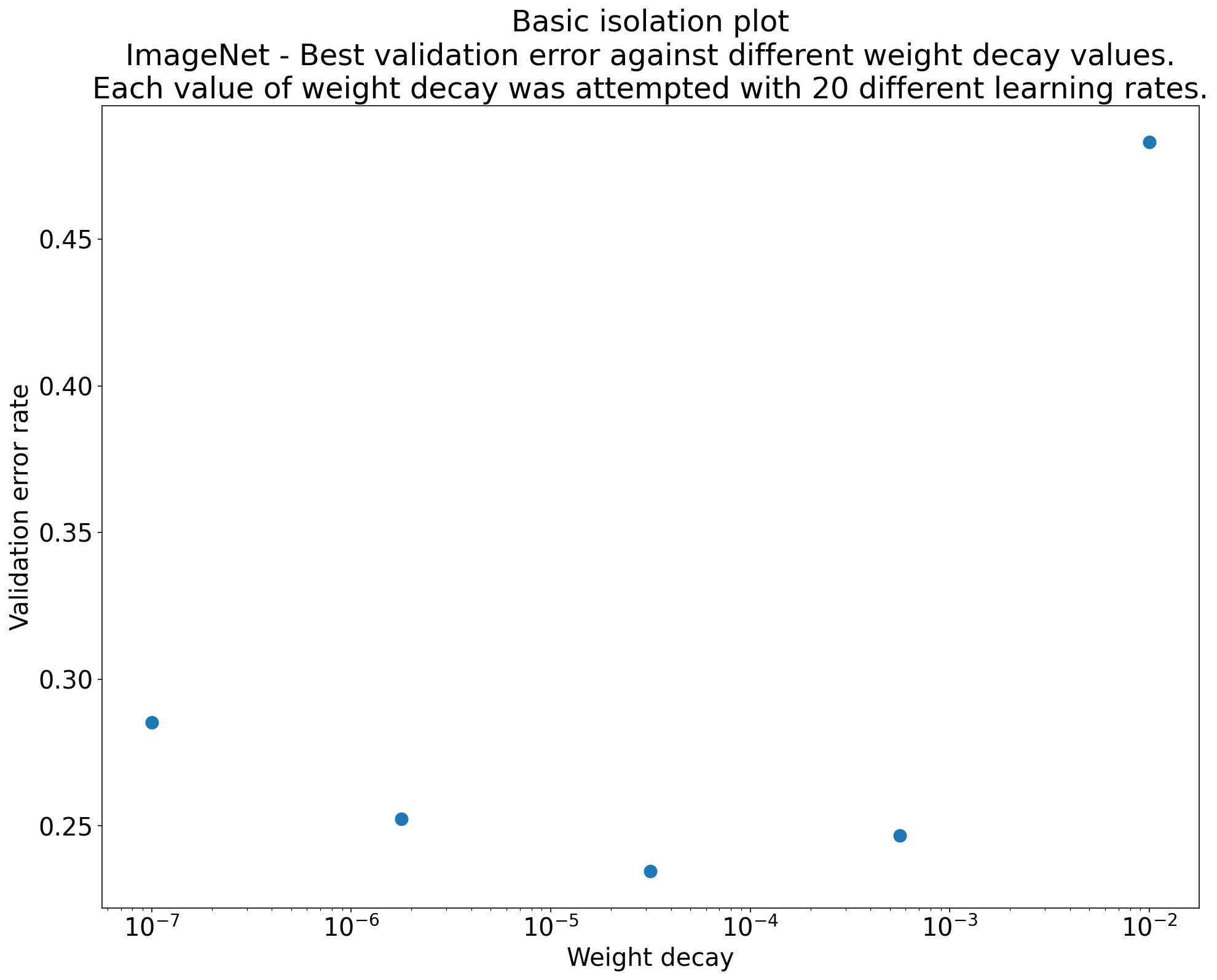
Figura 2: Gráfico de aislamiento que investiga el mejor valor de decaimiento del peso para ResNet-50 entrenado en ImageNet.

 

A menudo, el objetivo de un conjunto de experimentos es comparar diferentes valores de un hiperparámetro científico. Por ejemplo, supongamos que deseas determinar el valor de la disminución del peso que genera el mejor error de validación. Un gráfico de aislamiento es un caso especial del gráfico básico del eje de hiperparámetros. Cada punto de un gráfico de aislamiento corresponde al rendimiento de la mejor prueba en algunos (o todos) los hiperparámetros molestos. En otras palabras, grafica el rendimiento del modelo después de "optimizar" los hiperparámetros molestos.

Un gráfico de aislamiento simplifica la comparación directa entre diferentes valores del hiperparámetro científico. Por ejemplo, el gráfico de aislamiento de la figura 2 revela el valor de la disminución del peso que produce el mejor rendimiento de validación para una configuración particular de ResNet-50 entrenada en ImageNet.

Si el objetivo es determinar si se debe incluir la disminución del peso, compara el mejor punto de este gráfico con el valor de referencia sin disminución del peso. Para una comparación justa, el modelo de referencia también debe tener su tasa de aprendizaje ajustada de manera similar.

Cuando tienes datos generados por una búsqueda (casi) aleatoria y consideras un hiperparámetro continuo para un gráfico de aislamiento, puedes aproximar el gráfico de aislamiento agrupando los valores del eje X del gráfico básico del eje de hiperparámetros y tomando la mejor prueba en cada segmento vertical definido por los discretizaciones.

Automatiza gráficos genéricos útiles

Cuanto más esfuerzo requiera generar gráficos, menos probable será que los consultes tanto como deberías. Por lo tanto, te recomendamos que configures tu infraestructura para que genere automáticamente la mayor cantidad posible de gráficos. Como mínimo, te recomendamos que generes automáticamente gráficos básicos del eje de hiperparámetros para todos los hiperparámetros que varíes en un experimento.

Además, recomendamos que se generen automáticamente curvas de pérdida para todas las pruebas. Además, recomendamos que sea lo más fácil posible encontrar las mejores pruebas de cada estudio y examinar sus curvas de pérdida.

Puedes agregar muchos otros gráficos y visualizaciones útiles. Para parafrasear a Geoffrey Hinton:

Cada vez que creas un gráfico nuevo, aprendes algo nuevo.

Determina si se debe adoptar el cambio candidato

Resumen: Cuando decidas si realizar un cambio en nuestro modelo o procedimiento de entrenamiento, o bien adoptar una nueva configuración de hiperparámetros, ten en cuenta las diferentes fuentes de variación en tus resultados.

Cuando se intenta mejorar un modelo, un cambio candidato en particular puede lograr inicialmente un mejor error de validación en comparación con una configuración titular. Sin embargo, repetir el experimento podría demostrar que no hay una ventaja constante. De manera informal, las fuentes más importantes de resultados incoherentes se pueden agrupar en las siguientes categorías generales:

• Varianza del procedimiento de entrenamiento, varianza del reentrenamiento o varianza de la prueba: Es la variación entre las ejecuciones de entrenamiento que usan los mismos hiperparámetros, pero diferentes inicializaciones aleatorias. Por ejemplo, las diferentes inicializaciones aleatorias, las mezclas de datos de entrenamiento, las máscaras de abandono, los patrones de operaciones de aumento de datos y los ordenamientos de operaciones aritméticas paralelas son todas fuentes potenciales de varianza de la prueba.
• Varianza de la búsqueda de hiperparámetros o varianza del estudio: Es la variación en los resultados causada por nuestro procedimiento para seleccionar los hiperparámetros. Por ejemplo, puedes ejecutar el mismo experimento con un espacio de búsqueda determinado, pero con dos valores iniciales diferentes para la búsqueda cuasi aleatoria y terminar seleccionando valores de hiperparámetros diferentes.
• Varianza de muestreo y recopilación de datos: Es la varianza de cualquier tipo de división aleatoria en datos de entrenamiento, validación y prueba, o bien la varianza debida al proceso de generación de datos de entrenamiento de manera más general.

Es cierto que puedes comparar las tasas de error de validación estimadas en un conjunto de validación finito con pruebas estadísticas meticulosas. Sin embargo, a menudo, la varianza de la prueba por sí sola puede producir diferencias estadísticamente significativas entre dos modelos entrenados diferentes que usan la misma configuración de hiperparámetros.

La varianza del estudio es lo que más nos preocupa cuando intentamos sacar conclusiones que van más allá del nivel de un punto individual en el espacio de hiperparámetros. La varianza del estudio depende de la cantidad de pruebas y del espacio de búsqueda. Hemos visto casos en los que la varianza del estudio es mayor que la de la prueba y casos en los que es mucho menor. Por lo tanto, antes de adoptar un cambio candidato, considera ejecutar la mejor prueba N veces para caracterizar la varianza de la prueba de ejecución a ejecución. Por lo general, puedes salirte con la tuya solo con volver a caracterizar la varianza de la prueba después de cambios importantes en la canalización, pero es posible que necesites estimaciones más recientes en algunos casos. En otras aplicaciones, caracterizar la varianza de la prueba es demasiado costoso como para que valga la pena.

Si bien solo deseas adoptar los cambios (incluidas las nuevas configuraciones de hiperparámetros) que producen mejoras reales, exigir una certeza completa de que un cambio determinado ayuda tampoco es la respuesta correcta. Por lo tanto, si un nuevo punto de hiperparámetro (o cualquier otro cambio) obtiene un mejor resultado que el valor de referencia (teniendo en cuenta la varianza del reentrenamiento tanto del nuevo punto como del valor de referencia de la mejor manera posible), probablemente deberías adoptarlo como el nuevo valor de referencia para comparaciones futuras. Sin embargo, te recomendamos que solo adoptes los cambios que produzcan mejoras que superen cualquier complejidad que agreguen.

Después de que finalice la exploración

Resumen: Las herramientas de optimización bayesiana son una opción atractiva una vez que terminaste de buscar buenos espacios de búsqueda y decidiste qué hiperparámetros vale la pena ajustar.

Con el tiempo, tus prioridades cambiarán de aprender más sobre el problema de ajuste a producir una sola configuración óptima para lanzar o usar de otro modo. En ese punto, debería haber un espacio de búsqueda refinado que contenga cómodamente la región local alrededor de la mejor prueba observada y que se haya muestreado de forma adecuada. Tu trabajo de exploración debería haber revelado los hiperparámetros más importantes que se deben ajustar y sus rangos razonables que puedes usar para construir un espacio de búsqueda para un estudio de ajuste automático final con el mayor presupuesto de ajuste posible.

Dado que ya no te interesa maximizar la información sobre el problema de ajuste, muchas de las ventajas de la búsqueda cuasialeatoria ya no se aplican. Por lo tanto, debes usar herramientas de optimización bayesiana para encontrar automáticamente la mejor configuración de hiperparámetros. Vizier de código abierto implementa una variedad de algoritmos sofisticados para ajustar modelos de AA, incluidos los algoritmos de optimización bayesiana.

Supongamos que el espacio de búsqueda contiene un volumen no trivial de puntos divergentes, es decir, puntos que obtienen una pérdida de entrenamiento de NaN o incluso una pérdida de entrenamiento muchas desviaciones estándar peor que la media. En este caso, recomendamos usar herramientas de optimización de caja negra que controlen correctamente los intentos que divergen. (Consulta Bayesian Optimization with Unknown Constraints para conocer una excelente forma de abordar este problema). Vizier de código abierto admite el marcado de puntos divergentes marcando las pruebas como no factibles, aunque es posible que no use nuestro enfoque preferido de Gelbart et al., según cómo esté configurado.

Una vez que finalice la exploración, considera verificar el rendimiento en el conjunto de prueba. En principio, incluso podrías incluir el conjunto de validación en el conjunto de entrenamiento y volver a entrenar la mejor configuración encontrada con la optimización bayesiana. Sin embargo, esto solo es adecuado si no habrá lanzamientos futuros con esta carga de trabajo específica (por ejemplo, una competencia única de Kaggle).