এই পৃষ্ঠায় ডিসিশন ফরেস্টের শব্দকোষ রয়েছে। সকল শব্দকোষের জন্য এখানে ক্লিক করুন ।
ক
বৈশিষ্ট্য নমুনা
একটি সিদ্ধান্ত বন প্রশিক্ষণের জন্য একটি কৌশল যেখানে প্রতিটি সিদ্ধান্ত গাছ শর্ত শেখার সময় সম্ভাব্য বৈশিষ্ট্যগুলির একটি এলোমেলো উপসেট বিবেচনা করে। সাধারণত, প্রতিটি নোডের জন্য বৈশিষ্ট্যগুলির একটি ভিন্ন উপসেট নমুনা করা হয়। বিপরীতে, অ্যাট্রিবিউট স্যাম্পলিং ছাড়াই একটি সিদ্ধান্ত গাছকে প্রশিক্ষণ দেওয়ার সময়, প্রতিটি নোডের জন্য সমস্ত সম্ভাব্য বৈশিষ্ট্য বিবেচনা করা হয়।
অক্ষ-সারিবদ্ধ অবস্থা
একটি সিদ্ধান্ত গাছে , একটি শর্ত যা শুধুমাত্র একটি একক বৈশিষ্ট্য জড়িত। উদাহরণস্বরূপ, যদি area একটি বৈশিষ্ট্য হয়, তাহলে নিম্নলিখিতটি একটি অক্ষ-সারিবদ্ধ শর্ত:
area > 200
তির্যক অবস্থার সাথে বৈসাদৃশ্য।
খ
ব্যাগিং
একটি দলকে প্রশিক্ষণ দেওয়ার একটি পদ্ধতি যেখানে প্রতিটি উপাদান মডেল প্রতিস্থাপন সহ নমুনাযুক্ত প্রশিক্ষণ উদাহরণগুলির একটি এলোমেলো উপসেটে প্রশিক্ষণ দেয়। উদাহরণস্বরূপ, একটি এলোমেলো বন হল ব্যাগিংয়ের সাথে প্রশিক্ষিত সিদ্ধান্ত গাছের একটি সংগ্রহ।
ব্যাগিং শব্দটি b ootstrap agg regat ing এর জন্য সংক্ষিপ্ত।
আরও তথ্যের জন্য ডিসিশন ফরেস্ট কোর্সে এলোমেলো বন দেখুন।
বাইনারি অবস্থা
একটি সিদ্ধান্ত গাছে , এমন একটি শর্ত যার শুধুমাত্র দুটি সম্ভাব্য ফলাফল রয়েছে, সাধারণত হ্যাঁ বা না । উদাহরণস্বরূপ, নিম্নলিখিত একটি বাইনারি শর্ত:
temperature >= 100
অ-বাইনারি অবস্থার সাথে বৈসাদৃশ্য।
আরও তথ্যের জন্য ডিসিশন ফরেস্ট কোর্সে শর্তের প্রকার দেখুন।
গ
অবস্থা
একটি সিদ্ধান্ত গাছে , যে কোনো নোড একটি পরীক্ষা করে। উদাহরণস্বরূপ, নিম্নলিখিত সিদ্ধান্ত গাছে দুটি শর্ত রয়েছে: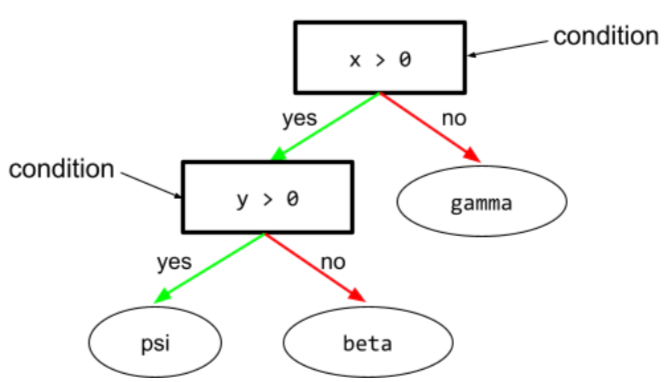
একটি শর্তকে বিভক্ত বা পরীক্ষাও বলা হয়।
পাতার সাথে বৈপরীত্য অবস্থা।
আরও দেখুন:
আরও তথ্যের জন্য ডিসিশন ফরেস্ট কোর্সে শর্তের প্রকার দেখুন।
ডি
সিদ্ধান্ত বন
একাধিক সিদ্ধান্ত গাছ থেকে তৈরি একটি মডেল। একটি সিদ্ধান্ত বন তার সিদ্ধান্ত গাছের পূর্বাভাস একত্রিত করে একটি ভবিষ্যদ্বাণী করে। জনপ্রিয় ধরনের সিদ্ধান্ত বনের মধ্যে রয়েছে এলোমেলো বন এবং গ্রেডিয়েন্ট বুস্টেড গাছ ।
আরও তথ্যের জন্য ডিসিশন ফরেস্ট কোর্সের সিদ্ধান্ত বন বিভাগটি দেখুন।
সিদ্ধান্ত গাছ
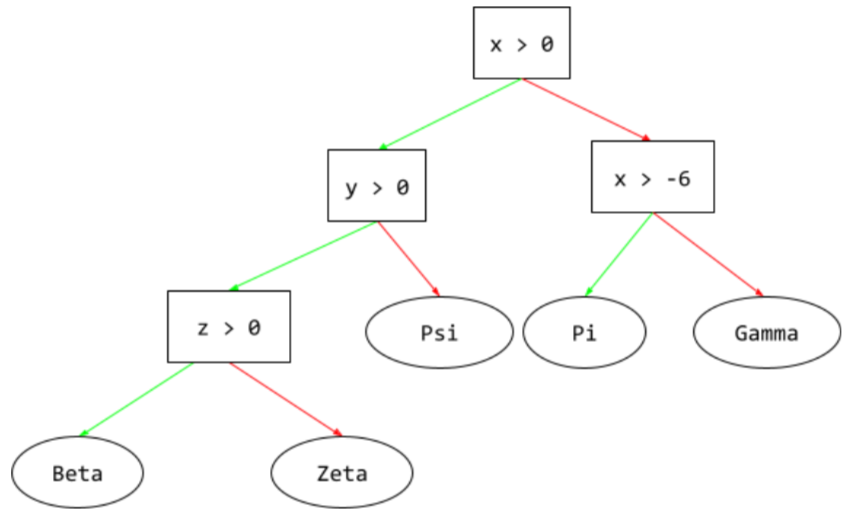
ক্রমানুসারে সংগঠিত শর্ত এবং পাতার একটি সেটের সমন্বয়ে একটি তত্ত্বাবধানে শিক্ষার মডেল। উদাহরণস্বরূপ, নিম্নলিখিত একটি সিদ্ধান্ত গাছ:
ই
এনট্রপি
তথ্য তত্ত্বে , সম্ভাব্যতা বন্টন কতটা অপ্রত্যাশিত তার বর্ণনা। বিকল্পভাবে, প্রতিটি উদাহরণে কতটা তথ্য রয়েছে তা হিসাবে এনট্রপিকেও সংজ্ঞায়িত করা হয়। একটি ডিস্ট্রিবিউশনের সর্বোচ্চ সম্ভাব্য এনট্রপি থাকে যখন একটি র্যান্ডম ভেরিয়েবলের সমস্ত মান সমানভাবে সম্ভব হয়।
দুটি সম্ভাব্য মান "0" এবং "1" সহ একটি সেটের এনট্রপি (উদাহরণস্বরূপ, একটি বাইনারি শ্রেণিবিন্যাস সমস্যায় লেবেল) নিম্নলিখিত সূত্র রয়েছে:
H = -p লগ p - q লগ q = -p লগ p - (1-p) * লগ (1-p)
কোথায়:
- H হল এনট্রপি।
- p হল "1" উদাহরণের ভগ্নাংশ।
- q হল "0" উদাহরণের ভগ্নাংশ। উল্লেখ্য যে q = (1 - p)
- লগ সাধারণত লগ 2 হয়। এই ক্ষেত্রে, এনট্রপি ইউনিট একটি বিট।
উদাহরণস্বরূপ, নিম্নলিখিত অনুমান করুন:
- 100টি উদাহরণে "1" মান রয়েছে
- 300টি উদাহরণে "0" মান রয়েছে
অতএব, এনট্রপি মান হল:
- p = 0.25
- q = 0.75
- H = (-0.25) লগ 2 (0.25) - (0.75) লগ 2 (0.75) = 0.81 বিট প্রতি উদাহরণ
একটি সেট যা পুরোপুরি ভারসাম্যপূর্ণ (উদাহরণস্বরূপ, 200 "0" s এবং 200 "1"s) প্রতি উদাহরণে 1.0 বিট এনট্রপি থাকবে। একটি সেট আরও ভারসাম্যহীন হওয়ার সাথে সাথে এর এনট্রপি 0.0 এর দিকে চলে যায়।
ডিসিশন ট্রিতে , এনট্রপি শ্রেণীবিভাগের সিদ্ধান্ত গাছের বৃদ্ধির সময় বিভাজনকারীকে শর্ত নির্বাচন করতে সাহায্য করার জন্য তথ্য অর্জন করতে সাহায্য করে।
এনট্রপির সাথে তুলনা করুন:
- জিনি অপবিত্রতা
- ক্রস-এনট্রপি ক্ষতি ফাংশন
এনট্রপিকে প্রায়শই শ্যাননের এনট্রপি বলা হয়।
আরও তথ্যের জন্য ডিসিশন ফরেস্ট কোর্সে সংখ্যাসূচক বৈশিষ্ট্য সহ বাইনারি শ্রেণীবিভাগের জন্য সঠিক স্প্লিটার দেখুন।
চ
বৈশিষ্ট্যের গুরুত্ব
পরিবর্তনশীল গুরুত্বের প্রতিশব্দ।
জি
জিনি অপবিত্রতা
এনট্রপির অনুরূপ একটি মেট্রিক। স্প্লিটাররা শ্রেণীবিভাগের সিদ্ধান্ত গাছের শর্ত রচনা করতে জিনি অশুদ্ধতা বা এনট্রপি থেকে প্রাপ্ত মান ব্যবহার করে। তথ্য লাভ এনট্রপি থেকে উদ্ভূত হয়। জিনি অপবিত্রতা থেকে প্রাপ্ত মেট্রিকের জন্য কোন সার্বজনীনভাবে গৃহীত সমতুল্য শব্দ বিদ্যমান নেই; যাইহোক, এই নামহীন মেট্রিক তথ্য লাভের মতোই গুরুত্বপূর্ণ।
জিনি অপবিত্রতাকে জিনি ইনডেক্স বা সহজভাবে জিনিও বলা হয়।
গ্রেডিয়েন্ট বুস্টেড (সিদ্ধান্ত) গাছ (GBT)
এক ধরনের সিদ্ধান্ত বন যেখানে:
- প্রশিক্ষণ গ্রেডিয়েন্ট বুস্টিং এর উপর নির্ভর করে।
- দুর্বল মডেল একটি সিদ্ধান্ত গাছ .
আরও তথ্যের জন্য ডিসিশন ফরেস্ট কোর্সে গ্রেডিয়েন্ট বুস্টেড ডিসিশন ট্রি দেখুন।
গ্রেডিয়েন্ট বুস্টিং
একটি প্রশিক্ষণ অ্যালগরিদম যেখানে দুর্বল মডেলগুলিকে একটি শক্তিশালী মডেলের গুণমান (ক্ষতি কমাতে) পুনরাবৃত্তিমূলকভাবে উন্নত করতে প্রশিক্ষণ দেওয়া হয়। উদাহরণস্বরূপ, একটি দুর্বল মডেল একটি রৈখিক বা ছোট সিদ্ধান্ত গাছ মডেল হতে পারে। শক্তিশালী মডেলটি পূর্বে প্রশিক্ষিত সমস্ত দুর্বল মডেলের সমষ্টি হয়ে যায়।
গ্রেডিয়েন্ট বুস্টিংয়ের সহজতম ফর্মে, প্রতিটি পুনরাবৃত্তিতে, একটি দুর্বল মডেলকে শক্তিশালী মডেলের ক্ষতি গ্রেডিয়েন্টের পূর্বাভাস দেওয়ার জন্য প্রশিক্ষণ দেওয়া হয়। তারপর, গ্রেডিয়েন্ট ডিসেন্টের অনুরূপ ভবিষ্যদ্বাণীকৃত গ্রেডিয়েন্ট বিয়োগ করে শক্তিশালী মডেলের আউটপুট আপডেট করা হয়।
কোথায়:
- $F_{0}$ হল শুরুর শক্তিশালী মডেল।
- $F_{i+1}$ হল পরবর্তী শক্তিশালী মডেল৷
- $F_{i}$ হল বর্তমান শক্তিশালী মডেল।
- $\xi$ হল 0.0 এবং 1.0 এর মধ্যে একটি মান যাকে সংকোচন বলা হয়, যা গ্রেডিয়েন্ট ডিসেন্টে শেখার হারের সাথে সাদৃশ্যপূর্ণ।
- $f_{i}$ হল দুর্বল মডেল যা $F_{i}$ এর ক্ষতি গ্রেডিয়েন্টের পূর্বাভাস দিতে প্রশিক্ষিত।
গ্রেডিয়েন্ট বুস্টিংয়ের আধুনিক বৈচিত্রগুলি তাদের গণনায় ক্ষতির দ্বিতীয় ডেরিভেটিভ (হেসিয়ান) অন্তর্ভুক্ত করে।
ডিসিশন ট্রি সাধারণত গ্রেডিয়েন্ট বুস্টিংয়ে দুর্বল মডেল হিসেবে ব্যবহৃত হয়। গ্রেডিয়েন্ট বুস্টেড (সিদ্ধান্ত) গাছ দেখুন।
আমি
অনুমান পথ
একটি সিদ্ধান্ত গাছে , অনুমান করার সময়, একটি নির্দিষ্ট উদাহরণ মূল থেকে অন্য অবস্থার দিকে নিয়ে যায়, একটি পাতা দিয়ে শেষ হয়। উদাহরণস্বরূপ, নিম্নলিখিত সিদ্ধান্ত গাছে, ঘন তীরগুলি নিম্নলিখিত বৈশিষ্ট্য মানগুলির সাথে একটি উদাহরণের জন্য অনুমান পথ দেখায়:
- x = 7
- y = 12
- z = -3
নীচের চিত্রের অনুমান পথটি পাতায় পৌঁছানোর আগে তিনটি অবস্থার মধ্য দিয়ে ভ্রমণ করে ( Zeta )।
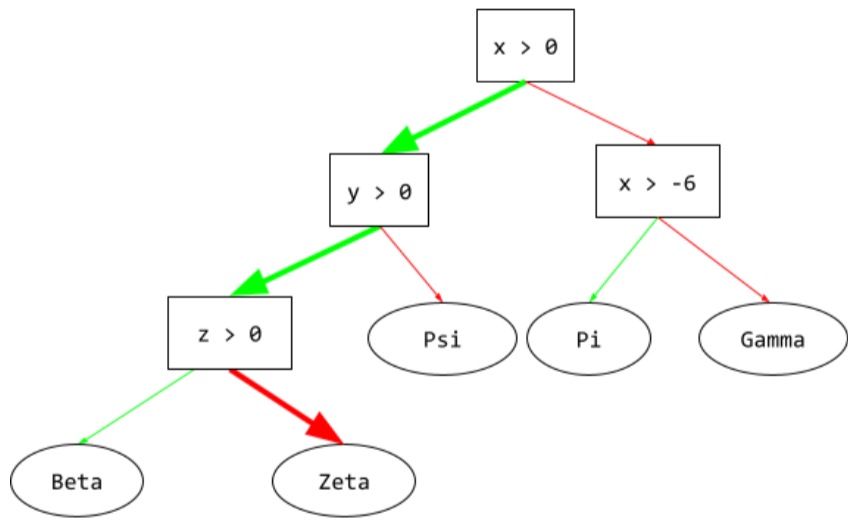
তিনটি পুরু তীর অনুমান পথ দেখায়।
আরও তথ্যের জন্য ডিসিশন ফরেস্ট কোর্সে সিদ্ধান্ত গাছ দেখুন।
তথ্য লাভ
সিদ্ধান্ত বনে , একটি নোডের এনট্রপি এবং ওজনযুক্ত (উদাহরণগুলির সংখ্যা অনুসারে) এর সন্তান নোডগুলির এনট্রপির যোগফলের মধ্যে পার্থক্য। একটি নোডের এনট্রপি হল সেই নোডের উদাহরণগুলির এনট্রপি।
উদাহরণস্বরূপ, নিম্নলিখিত এনট্রপি মান বিবেচনা করুন:
- প্যারেন্ট নোডের এনট্রপি = 0.6
- 16টি প্রাসঙ্গিক উদাহরণ সহ একটি চাইল্ড নোডের এনট্রপি = 0.2
- 24টি প্রাসঙ্গিক উদাহরণ সহ অন্য চাইল্ড নোডের এনট্রপি = 0.1
সুতরাং 40% উদাহরণ একটি চাইল্ড নোডে এবং 60% অন্য চাইল্ড নোডে রয়েছে। অতএব:
- চাইল্ড নোডের ওজনযুক্ত এনট্রপি যোগফল = (0.4 * 0.2) + (0.6 * 0.1) = 0.14
সুতরাং, তথ্য লাভ হল:
- তথ্য লাভ = প্যারেন্ট নোডের এনট্রপি - চাইল্ড নোডের ওজনযুক্ত এনট্রপি যোগফল
- তথ্য লাভ = 0.6 - 0.14 = 0.46
বেশিরভাগ বিভাজনকারী এমন পরিস্থিতি তৈরি করতে চায় যা সর্বাধিক তথ্য লাভ করে।
ইন-সেট অবস্থা
একটি সিদ্ধান্ত গাছে , একটি শর্ত যা আইটেমগুলির একটি সেটে একটি আইটেমের উপস্থিতির জন্য পরীক্ষা করে। উদাহরণস্বরূপ, নিম্নলিখিত একটি ইন-সেট শর্ত:
house-style in [tudor, colonial, cape]
অনুমানের সময়, যদি ঘর-শৈলী বৈশিষ্ট্যের মান tudor বা colonial বা cape হয়, তাহলে এই শর্তটি হ্যাঁ মূল্যায়ন করে। যদি ঘর-শৈলী বৈশিষ্ট্যের মান অন্য কিছু হয় (উদাহরণস্বরূপ, ranch ), তাহলে এই শর্তটি নং-এ মূল্যায়ন করে।
ইন-সেট শর্তগুলি সাধারণত এক-হট এনকোডেড বৈশিষ্ট্যগুলি পরীক্ষা করে এমন অবস্থার তুলনায় আরও দক্ষ সিদ্ধান্তের গাছের দিকে নিয়ে যায়।
এল
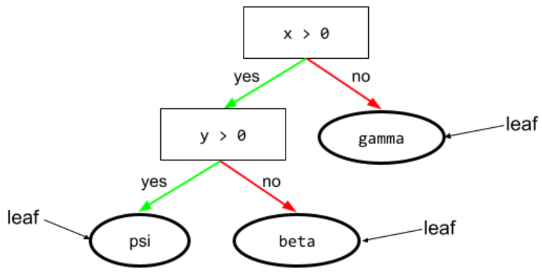
পাতা
একটি সিদ্ধান্ত গাছের কোন শেষ বিন্দু. একটি শর্তের বিপরীতে, একটি পাতা একটি পরীক্ষা সঞ্চালন করে না। বরং, একটি পাতা একটি সম্ভাব্য ভবিষ্যদ্বাণী। একটি পাতাও একটি অনুমান পথের টার্মিনাল নোড ।
উদাহরণস্বরূপ, নিম্নলিখিত সিদ্ধান্ত গাছে তিনটি পাতা রয়েছে:
আরও তথ্যের জন্য ডিসিশন ফরেস্ট কোর্সে সিদ্ধান্ত গাছ দেখুন।
এন
নোড (সিদ্ধান্ত গাছ)
একটি সিদ্ধান্ত গাছ , কোন অবস্থা বা পাতা .
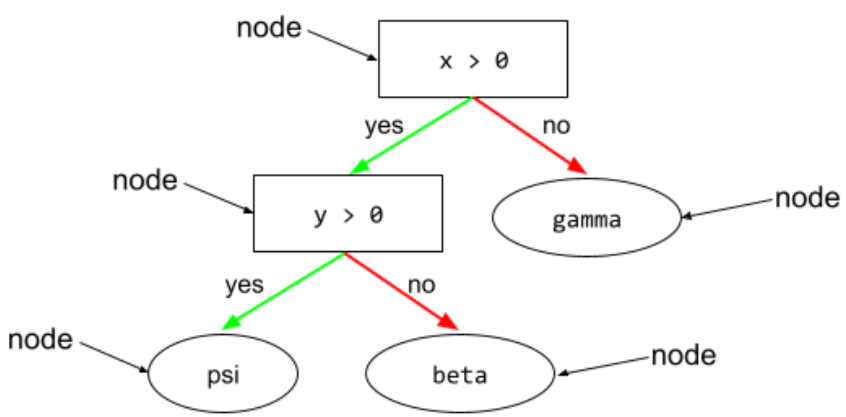
আরও তথ্যের জন্য ডিসিশন ফরেস্ট কোর্সে সিদ্ধান্ত গাছ দেখুন।
নন-বাইনারী অবস্থা
দুটি সম্ভাব্য ফলাফল সমন্বিত একটি শর্ত । উদাহরণস্বরূপ, নিম্নলিখিত নন-বাইনারী শর্তে তিনটি সম্ভাব্য ফলাফল রয়েছে:
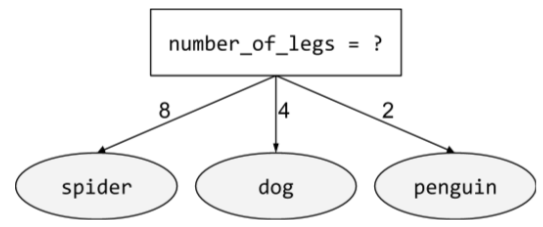
আরও তথ্যের জন্য ডিসিশন ফরেস্ট কোর্সে শর্তের প্রকার দেখুন।
ও
তির্যক অবস্থা
একটি সিদ্ধান্ত গাছে , একটি শর্ত যাতে একাধিক বৈশিষ্ট্য জড়িত থাকে। উদাহরণস্বরূপ, যদি উচ্চতা এবং প্রস্থ উভয়ই বৈশিষ্ট্য হয়, তাহলে নিম্নোক্ত একটি তির্যক অবস্থা:
height > width
অক্ষ-সারিবদ্ধ অবস্থার সাথে বৈসাদৃশ্য।
আরও তথ্যের জন্য ডিসিশন ফরেস্ট কোর্সে শর্তের প্রকার দেখুন।
ব্যাগের বাইরে মূল্যায়ন (OOB মূল্যায়ন)
সিদ্ধান্ত গাছের প্রশিক্ষণের সময় যে উদাহরণগুলি ব্যবহার করা হয়নি তার বিরুদ্ধে প্রতিটি সিদ্ধান্ত গাছ পরীক্ষা করে একটি সিদ্ধান্ত বনের গুণমান মূল্যায়নের একটি প্রক্রিয়া। উদাহরণস্বরূপ, নিম্নলিখিত চিত্রে, লক্ষ্য করুন যে সিস্টেমটি প্রতিটি সিদ্ধান্ত গাছকে প্রায় দুই-তৃতীয়াংশ উদাহরণের উপর প্রশিক্ষণ দেয় এবং তারপরে উদাহরণগুলির অবশিষ্ট এক-তৃতীয়াংশের বিপরীতে মূল্যায়ন করে।
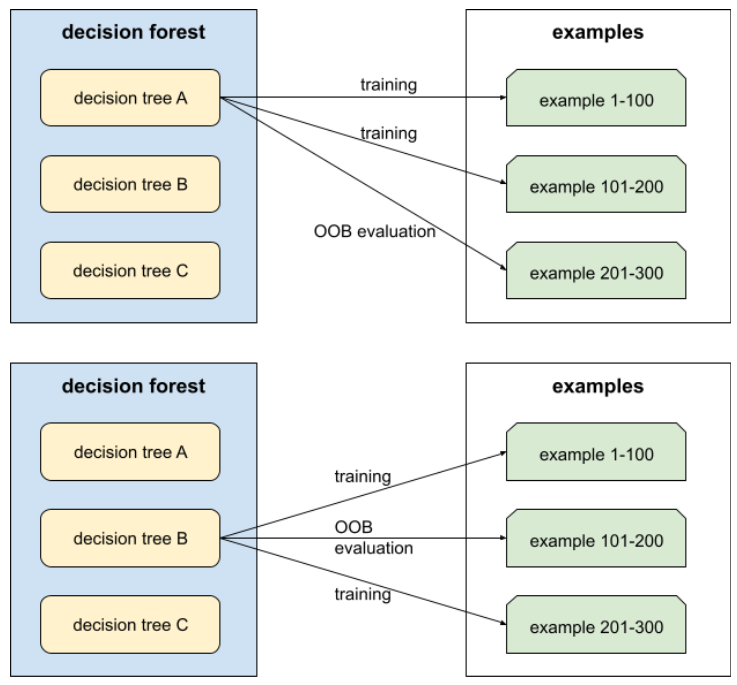
আউট-অফ-ব্যাগ মূল্যায়ন হল ক্রস-ভ্যালিডেশন মেকানিজমের একটি গণনাগতভাবে দক্ষ এবং রক্ষণশীল অনুমান। ক্রস-ভ্যালিডেশনে, প্রতিটি ক্রস-ভ্যালিডেশন রাউন্ডের জন্য একটি মডেল প্রশিক্ষিত হয় (উদাহরণস্বরূপ, 10টি মডেলকে 10-গুণ ক্রস-ভ্যালিডেশনে প্রশিক্ষণ দেওয়া হয়)। OOB মূল্যায়নের সাথে, একটি একক মডেল প্রশিক্ষিত হয়। যেহেতু ব্যাগিং প্রশিক্ষণের সময় প্রতিটি গাছ থেকে কিছু ডেটা আটকে রাখে, OOB মূল্যায়ন আনুমানিক ক্রস-বৈধকরণের জন্য সেই ডেটা ব্যবহার করতে পারে।
আরও তথ্যের জন্য ডিসিশন ফরেস্ট কোর্সে ব্যাগের বাইরে মূল্যায়ন দেখুন।
পৃ
পরিবর্তনশীল গুরুত্ব
পরিবর্তনশীল গুরুত্বের একটি প্রকার যা বৈশিষ্ট্যের মানগুলিকে অনুমতি দেওয়ার পরে একটি মডেলের ভবিষ্যদ্বাণী ত্রুটির বৃদ্ধিকে মূল্যায়ন করে৷ পারমুটেশন পরিবর্তনশীল গুরুত্ব একটি মডেল-স্বাধীন মেট্রিক।
আর
এলোমেলো বন
সিদ্ধান্ত গাছের একটি দল যেখানে প্রতিটি সিদ্ধান্ত গাছকে একটি নির্দিষ্ট এলোমেলো শব্দের সাথে প্রশিক্ষণ দেওয়া হয়, যেমন ব্যাগিং ।
এলোমেলো বন এক ধরনের সিদ্ধান্ত বন ।
আরও তথ্যের জন্য ডিসিশন ফরেস্ট কোর্সে র্যান্ডম ফরেস্ট দেখুন।
মূল
একটি সিদ্ধান্ত গাছে শুরু নোড (প্রথম শর্ত )। নিয়ম অনুসারে, ডায়াগ্রামগুলি সিদ্ধান্ত গাছের শীর্ষে মূল স্থাপন করে। যেমন:
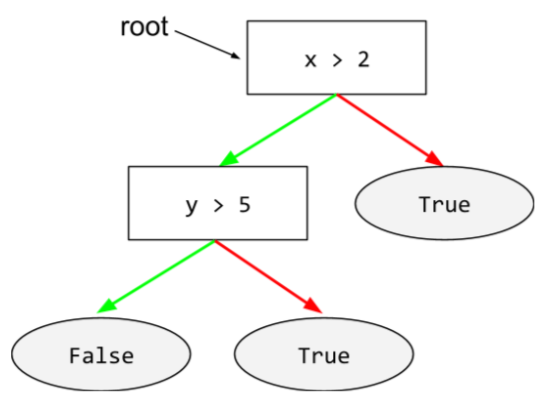
এস
প্রতিস্থাপন সহ নমুনা
প্রার্থী আইটেমগুলির একটি সেট থেকে আইটেম বাছাই করার একটি পদ্ধতি যেখানে একই আইটেম একাধিকবার বাছাই করা যেতে পারে। "প্রতিস্থাপন সহ" বাক্যাংশটির অর্থ হল প্রতিটি নির্বাচনের পরে, নির্বাচিত আইটেমটি প্রার্থীর আইটেমগুলির পুলে ফিরিয়ে দেওয়া হয়। বিপরীত পদ্ধতি, প্রতিস্থাপন ছাড়াই নমুনা নেওয়ার মানে হল যে একজন প্রার্থী আইটেম শুধুমাত্র একবার বাছাই করা যেতে পারে।
উদাহরণস্বরূপ, নিম্নলিখিত ফলের সেট বিবেচনা করুন:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango} ধরুন যে সিস্টেমটি এলোমেলোভাবে fig প্রথম আইটেম হিসাবে বেছে নিয়েছে। যদি প্রতিস্থাপনের সাথে স্যাম্পলিং ব্যবহার করা হয়, তাহলে সিস্টেম নিম্নলিখিত সেট থেকে দ্বিতীয় আইটেমটি বেছে নেয়:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango} হ্যাঁ, এটি আগের মতো একই সেট, তাই সিস্টেমটি সম্ভাব্যভাবে আবার fig বাছাই করতে পারে।
প্রতিস্থাপন ছাড়া নমুনা ব্যবহার করলে, একবার বাছাই করা হলে, একটি নমুনা আবার বাছাই করা যাবে না। উদাহরণস্বরূপ, যদি সিস্টেম এলোমেলোভাবে প্রথম নমুনা হিসাবে fig বাছাই করে, তাহলে fig আবার বাছাই করা যাবে না। অতএব, সিস্টেম নিম্নলিখিত (হ্রাস) সেট থেকে দ্বিতীয় নমুনা বাছাই করে:
fruit = {kiwi, apple, pear, cherry, lime, mango}সংকোচন
গ্রেডিয়েন্ট বুস্টিংয়ের একটি হাইপারপ্যারামিটার যা ওভারফিটিং নিয়ন্ত্রণ করে। গ্রেডিয়েন্ট বুস্টিংয়ে সংকোচন গ্রেডিয়েন্ট ডিসেন্টে শেখার হারের সাথে সাদৃশ্যপূর্ণ। সংকোচন হল 0.0 এবং 1.0 এর মধ্যে একটি দশমিক মান। একটি কম সংকোচন মান একটি বৃহত্তর সংকোচন মানের চেয়ে ওভারফিটিং কমিয়ে দেয়।
বিভক্ত
একটি সিদ্ধান্ত গাছে , একটি শর্তের অন্য নাম।
স্প্লিটার
একটি সিদ্ধান্ত গাছ প্রশিক্ষণের সময়, প্রতিটি নোডে সর্বোত্তম অবস্থা খোঁজার জন্য দায়ী রুটিন (এবং অ্যালগরিদম)।
টি
পরীক্ষা
একটি সিদ্ধান্ত গাছে , একটি শর্তের অন্য নাম।
থ্রেশহোল্ড (সিদ্ধান্ত গাছের জন্য)
একটি অক্ষ-সারিবদ্ধ অবস্থায় , একটি বৈশিষ্ট্যের সাথে যে মান তুলনা করা হচ্ছে। উদাহরণস্বরূপ, 75 হল নিম্নোক্ত অবস্থায় থ্রেশহোল্ড মান:
grade >= 75
আরও তথ্যের জন্য ডিসিশন ফরেস্ট কোর্সে সংখ্যাসূচক বৈশিষ্ট্য সহ বাইনারি শ্রেণীবিভাগের জন্য সঠিক স্প্লিটার দেখুন।
ভি
পরিবর্তনশীল গুরুত্ব
স্কোরের একটি সেট যা মডেলের প্রতিটি বৈশিষ্ট্যের আপেক্ষিক গুরুত্ব নির্দেশ করে।
উদাহরণস্বরূপ, একটি সিদ্ধান্ত গাছ বিবেচনা করুন যা বাড়ির দাম অনুমান করে। ধরুন এই সিদ্ধান্ত গাছ তিনটি বৈশিষ্ট্য ব্যবহার করে: আকার, বয়স এবং শৈলী। যদি তিনটি বৈশিষ্ট্যের জন্য পরিবর্তনশীল গুরুত্বের একটি সেট গণনা করা হয় {size=5.8, age=2.5, style=4.7}, তাহলে বয়স বা শৈলীর চেয়ে আকার সিদ্ধান্ত গাছের জন্য বেশি গুরুত্বপূর্ণ।
বিভিন্ন পরিবর্তনশীল গুরুত্বের মেট্রিক্স বিদ্যমান, যা মডেলের বিভিন্ন দিক সম্পর্কে এমএল বিশেষজ্ঞদের অবহিত করতে পারে।
ডব্লিউ
ভিড়ের জ্ঞান
ধারণা যে মানুষের একটি বৃহৎ গোষ্ঠীর মতামত বা অনুমানের গড় প্রায়ই আশ্চর্যজনকভাবে ভাল ফলাফল দেয়। উদাহরণস্বরূপ, এমন একটি খেলা বিবেচনা করুন যেখানে লোকেরা একটি বড় জারে প্যাক করা জেলি বিনের সংখ্যা অনুমান করে। যদিও বেশিরভাগ ব্যক্তিগত অনুমান ভুল হবে, তবে সমস্ত অনুমানের গড় পরীক্ষামূলকভাবে জারে জেলি বিনের প্রকৃত সংখ্যার আশ্চর্যজনকভাবে কাছাকাছি দেখানো হয়েছে।
Ensembles হল ভিড়ের জ্ঞানের একটি সফটওয়্যার এনালগ। এমনকি যদি পৃথক মডেলগুলি অত্যন্ত ভুল ভবিষ্যদ্বাণী করে, তবে অনেক মডেলের ভবিষ্যদ্বাণীগুলির গড় প্রায়ই আশ্চর্যজনকভাবে ভাল ভবিষ্যদ্বাণী তৈরি করে৷ উদাহরণস্বরূপ, যদিও একটি পৃথক সিদ্ধান্ত গাছ খারাপ ভবিষ্যদ্বাণী করতে পারে, একটি সিদ্ধান্ত বন প্রায়ই খুব ভাল ভবিষ্যদ্বাণী করে।
