統計的手法と可視化手法でデータを調べた後、モデルのトレーニングをより効果的に行うために、データを変換する必要があります。正規化の目的は、特徴を同様のスケールに変換することです。たとえば、次の 2 つの特徴について考えてみましょう。
- 特徴
Xの範囲は 154 ~ 24,917,482 です。 - 特徴量
Yの範囲は 5 ~ 22 です。
これら 2 つの特徴は、大きく異なる範囲にまたがっています。正規化では、X と Y が同様の範囲(0 ~ 1 など)になるように操作します。
正規化には次の利点があります。
- トレーニング中にモデルの収束を高速化します。特徴量の範囲が異なると、勾配降下法が「跳ね返り」、収束が遅くなることがあります。ただし、Adagrad や Adam などのより高度なオプティマイザーは、有効な学習率を時間とともに変化させることで、この問題を防ぎます。
- モデルがより優れた予測を推論できるようにします。特徴量の範囲が異なる場合、モデルの予測の有用性が低下する可能性があります。
- 特徴量の値が非常に高い場合に 「NaN トラップ」を回避するのに役立ちます。NaN は、not a number(数値ではない)の略です。モデルの値が浮動小数点精度の制限を超えると、システムは値を数値ではなく
NaNに設定します。モデル内の 1 つの数値が NaN になると、モデル内の他の数値も最終的に NaN になります。 - モデルが各特徴の適切な重みを学習するのに役立ちます。特徴スケーリングを行わないと、モデルは範囲の広い特徴に過度に注目し、範囲の狭い特徴には十分に注目しません。
範囲が大きく異なる数値特徴(年齢や収入など)を正規化することをおすすめします。また、city population. など、広範囲をカバーする単一の数値特徴を正規化することをおすすめします。
次の 2 つの機能について考えてみましょう。
- 特徴
Aの最小値は -0.5、最大値は +0.5 です。 - 特徴
Bの最小値は -5.0、最大値は +5.0 です。
特徴 A と特徴 B のスパンは比較的狭くなっています。ただし、Feature B のスパンは Feature A のスパンの 10 倍です。そのため、次のようになります。
- トレーニングの開始時に、モデルは特徴
Bが特徴Aよりも 10 倍「重要」であると想定します。 - トレーニングに通常よりも時間がかかる。
- 結果として得られるモデルは最適でない可能性があります。
正規化しないことによる全体的な影響は比較的小さいですが、特徴 A と特徴 B を同じスケール(-1.0 ~+1.0 など)に正規化することをおすすめします。
次に、範囲の差が大きい 2 つの特徴を考えてみましょう。
- 特徴量
Cの最小値は -1、最大値は +1 です。 - 特徴
Dの最小値は +5,000、最大値は +1,000,000,000 です。
特徴 C と特徴 D を正規化しないと、モデルが最適にならない可能性があります。さらに、トレーニングの収束に時間がかかったり、完全に収束しないこともあります。
このセクションでは、一般的な 3 つの正規化手法について説明します。
- 線形スケーリング
- Z スコア スケーリング
- 対数目盛
このセクションでは、クリッピングについても説明します。クリッピングは真の正規化手法ではありませんが、モデルの精度を高める範囲に数値特徴量を収めることができます。
均等目盛
線形スケーリング(通常は単にスケーリングと短縮されます)とは、浮動小数点値を自然な範囲から標準範囲(通常は 0 ~ 1 または -1 ~+1)に変換することを意味します。
線形スケーリングは、次のすべての条件が満たされている場合に適しています。
- データの下限と上限が時間とともに大きく変化しない。
- 外れ値がほとんどないか、まったくない。また、外れ値が極端ではない。
- 特徴は範囲全体にほぼ均一に分布しています。つまり、ヒストグラムではほとんどの値でほぼ均等なバーが表示されます。
人間の age が特徴量であるとします。線形スケーリングは、age に適した正規化手法です。理由は次のとおりです。
- おおよその下限と上限は 0 ~ 100 です。
ageには、外れ値が比較的少ない割合で含まれています。100 歳以上の人口はわずか 0.3% ほどです。- 特定の年齢層が他の年齢層よりも多く含まれている場合もありますが、大規模なデータセットにはすべての年齢層の十分な例が含まれている必要があります。
演習: 理解度を確認する
モデルに、さまざまな人の純資産を保持するnet_worth という名前の特徴があるとします。net_worth に線形スケーリングを正規化手法として使用するのは適切ですか?その理由もお聞かせください。
Z スコア スケーリング
Z スコアは、値が平均からどの程度離れているかを示す標準偏差の数です。たとえば、平均値より 2 標準偏差大きい値の Z スコアは +2.0 になります。平均値より 1.5 標準偏差小さい値の Z スコアは -1.5 です。
Z スコア スケーリングで特徴を表すことは、その特徴の Z スコアを特徴ベクトルに保存することを意味します。たとえば、次の図は 2 つのヒストグラムを示しています。
- 左は標準正規分布です。
- 右側は、Z スコア スケーリングで正規化された同じ分布です。
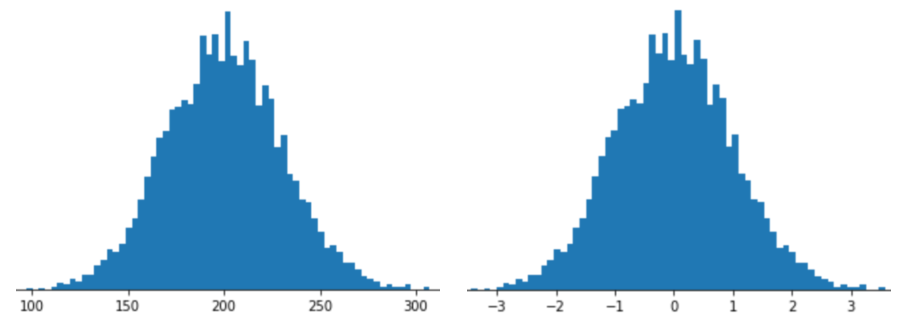
Z スコア スケーリングは、次の図に示すように、正規分布が曖昧なデータにも適しています。

データが正規分布または正規分布に似た分布に従っている場合は、Z スコアが適しています。
分布の大部分が正常範囲内であっても、極端な外れ値が含まれている場合があります。たとえば、net_worth 特徴量のほぼすべてのポイントが 3 標準偏差内に収まる場合でも、この特徴量のいくつかの例は平均から数百標準偏差離れている可能性があります。このような場合は、Z スコア スケーリングを別の形式の正規化(通常はクリッピング)と組み合わせて、この状況を処理できます。
演習: 理解度を確認する
モデルが、1,000 万人の女性の成人時の身長を保持するheight という名前の特徴でトレーニングされるとします。height の正規化手法として Z スコア スケーリングは適切ですか?その理由もお聞かせください。
対数目盛
ログ スケーリングは、未加工の値の対数を計算します。理論的には、対数の底は任意の値にできますが、実際には、対数スケーリングでは通常、自然対数(ln)が計算されます。
ログ スケーリングは、データがべき乗則分布に従う場合に役立ちます。簡単に言うと、べき乗則分布は次のようになります。
Xの値が小さいほど、Yの値は大きくなります。Xの値が増加すると、Yの値は急速に減少します。したがって、Xの値が高いほど、Yの値は非常に低くなります。
映画の評価は、べき乗則分布の好例です。次の図では、次の点に注意してください。
- 一部の映画には多くのユーザー評価があります。(
Xの値が小さいほど、Yの値は大きくなります)。 - ほとんどの映画にはユーザー評価がほとんどありません。(
Xの値が大きいほど、Yの値は小さくなります)。
対数スケーリングによって分布が変化し、より正確な予測を行うモデルのトレーニングに役立ちます。

2 つ目の例として、書籍の販売は次のような理由でべき乗則分布に従います。
- 出版された書籍のほとんどは、販売部数が 100 部か 200 部程度です。
- 中程度の販売部数(数千部)の書籍もあります。
- 100 万部以上売れるベストセラーはごくわずかです。
たとえば、本の表紙と本の売上の関係を調べるために線形モデルをトレーニングするとします。生の値で線形モデルをトレーニングする場合、100 万部売れた書籍の表紙と 100 部しか売れなかった書籍の表紙の間に 10,000 倍の差があることをモデルが学習する必要があります。ただし、すべての販売数値を対数スケールに変換すると、タスクの実現可能性が大幅に高まります。たとえば、100 の対数は次のようになります。
~4.6 = ln(100)
1,000,000 の対数は次のようになります。
~13.8 = ln(1,000,000)
したがって、1,000,000 の対数は 100 の対数の約 3 倍にすぎません。ベストセラーの書籍の表紙は、売れ行きの悪い書籍の表紙よりも(何らかの形で)3 倍ほど強力であると想像できるでしょう。
クリッピング
クリッピングは、極端な外れ値の影響を最小限に抑える手法です。簡単に言うと、クリッピングは通常、外れ値の値を特定の最大値に制限(削減)します。クリッピングは奇妙なアイデアですが、非常に効果的な場合があります。
たとえば、さまざまな住宅の部屋数(総部屋数を居住者数で割った値)を表す roomsPerPerson という特徴を含むデータセットがあるとします。次のプロットは、特徴量の値の 99% 以上が正規分布(平均 1.8、標準偏差 0.7)に適合していることを示しています。ただし、この特徴にはいくつかの外れ値が含まれており、そのうちのいくつかは極端な値です。

このような極端な外れ値の影響を最小限に抑えるにはどうすればよいですか?ヒストグラムは、均等分布、正規分布、べき乗則分布ではありません。roomsPerPerson の最大値を 4.0 などの任意の値で上限を設定またはクリップするとどうなるでしょうか?

特徴値を 4.0 でクリッピングしても、モデルが 4.0 より大きい値をすべて無視するわけではありません。4.0 より大きい値はすべて 4.0 になります。4.0 の奇妙な山は、このためです。この山を越えると、スケーリングされた特徴セットは元のデータよりも有用になります。
ちょっと待って!すべての外れ値を任意のしきい値に減らすことは本当に可能でしょうか?モデルのトレーニング時。
他の形式の正規化を適用した後に値をクリップすることもできます。たとえば、Z スコア スケーリングを使用しているが、いくつかの外れ値の絶対値が 3 をはるかに超えているとします。この場合は、次のことを行うことができます。
- クリップの Z スコアが 3 より大きい場合は、3 にクリップします。
- クリップの Z スコアが -3 未満の場合は、-3 になります。
クリッピングにより、モデルが重要でないデータに過剰にインデックス登録されるのを防ぐことができます。ただし、外れ値の中には重要なものもあるため、値を慎重にクリップしてください。
正規化手法の概要
| 正規化手法 | 数式 | 使用場面 |
|---|---|---|
| 均等目盛 | $$ x' = \frac{x - x_{min}}{x_{max} - x_{min}} $$ | 特徴が範囲全体にほぼ均一に分布している場合。平らな形状 |
| Z スコア スケーリング | $$ x' = \frac{x - μ}{σ}$$ | 特徴が正規分布している場合(ピークが平均に近い場合)。Bell-shaped |
| 対数目盛 | $$ x' = log(x)$$ | 特徴分布が裾の少なくとも一方に大きく偏っている場合。Heavy Tail-shaped |
| クリッピング | $x > max$ の場合、$x' = max$に設定します。 $x < min$ の場合、$x' = min$ に設定します。 |
特徴量に極端な外れ値が含まれている場合。 |
演習: 理解度テスト

データセンター内で測定された温度に基づいてデータセンターの生産性を予測するモデルを開発しているとします。データセット内の temperature 値のほとんどは 15 ~ 30(摂氏)の範囲に収まっていますが、次の例外があります。
- 年に 1 ~ 2 回、非常に暑い日に、31 ~ 45 の値が
temperatureに記録されます。 temperatureの 1,000 番目のポイントごとに、実際の温度ではなく 1,000 が設定されます。
temperature に適した正規化手法はどれですか?
1,000 という値は誤りであるため、クリップするのではなく削除する必要があります。
31 ~ 45 の値は正当なデータポイントです。データセットにこの温度範囲のサンプルが十分にないため、モデルをトレーニングして適切な予測を行うことができない場合は、これらの値をクリッピングすることをおすすめします。ただし、推論時には、クリップされたモデルは 45 度の気温と 35 度の気温に対して同じ予測を行うことに注意してください。