Un conjunto de datos de clasificación con proporciones de clase sesgadas se denomina desequilibrado. Las clases que conforman una gran proporción del conjunto de datos se denominan clases de mayoría. Aquellas que conforman una proporción más pequeña son clases minoritarias.
¿Qué se considera desequilibrado? La respuesta puede variar de moderada a extrema, como se muestra en la siguiente tabla.
| Grado de desequilibrio | Proporción de clases minoritarias |
|---|---|
| Leves | 20% a 40% del conjunto de datos |
| Moderada | 1 a 20% del conjunto de datos |
| Extremo | <1% del conjunto de datos |
¿Por qué debe prestar atención a los datos desequilibrados? Es posible que debas aplicar una técnica de muestreo en particular si tienes una tarea de clasificación con un conjunto de datos desequilibrado.
Considera el siguiente ejemplo de un modelo que detecta fraudes. Las instancias de fraude suceden una vez por cada 200 transacciones en este conjunto de datos, por lo que en la distribución verdadera, alrededor del 0.5% de los datos es positivo.
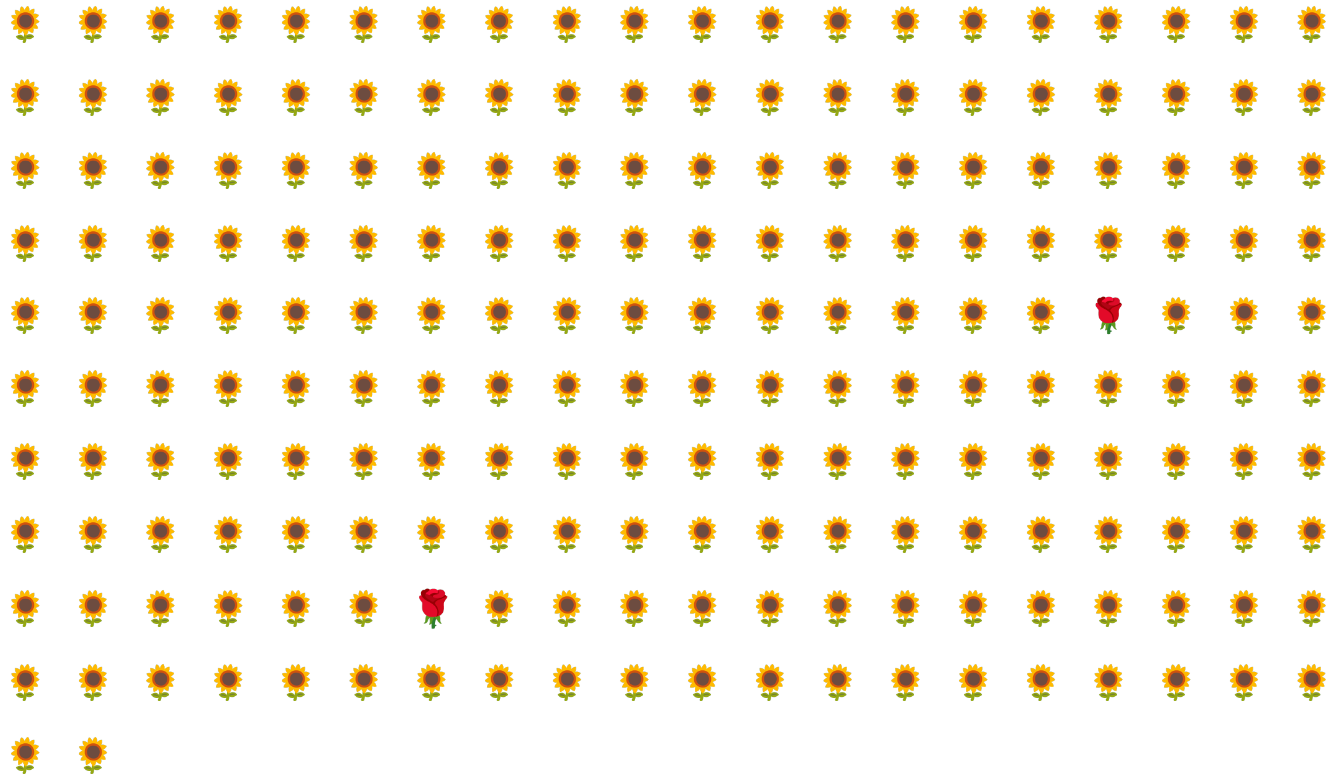
¿Por qué esto sería problemático? Con tan pocos positivos en relación con los negativos, el modelo de entrenamiento pasará la mayor parte de su tiempo en ejemplos negativos y no aprenderá lo suficiente de los positivos. Por ejemplo, si el tamaño del lote es de 128, muchos lotes no tendrán ejemplos positivos, por lo que los gradientes serán menos informativos.
Si tienes un conjunto de datos desequilibrados, primero trata de entrenar en la verdadera distribución. Si el modelo funciona y se generaliza, eso es todo. De lo contrario, prueba la siguiente técnica de reducción de muestreo y aumento de peso.
Submuestreo y aumento de peso
Una forma eficaz de manejar los datos desequilibrados es realizar una reducción de la muestra y aumentar la ponderación de la clase principal. Comencemos por definir estos dos términos nuevos:
- La reducción de muestreo (en este contexto) se refiere al entrenamiento en un subconjunto desproporcionadamente bajo de los ejemplos de clases principales.
- Ponderación significa agregar un peso de ejemplo a la clase con reducción de muestreo igual al factor por el que se realizó la reducción.
Paso 1: Reduce el muestreo de la clase mayoritaria. Volvamos a nuestro ejemplo del conjunto de datos de fraude, con 1 positivo a 200 negativos. La reducción de muestreo en un factor de 20 mejora el equilibrio de 1 positivo a 10 negativos (10%). Aunque el conjunto de entrenamiento resultante aún está desequilibrado de forma moderada, la proporción de positivos a negativos es mucho mejor que la proporción extremadamente desequilibrada original (0.5%).
Paso 2: Aumenta el peso de la clase con reducción de muestreo: el último paso es agregar ejemplos de ponderaciones a la clase con reducción de muestreo. Como se realizó una reducción de muestreo mediante un factor de 20, el peso de ejemplo debería ser 20.
Es posible que se utilice para escuchar el término peso cuando se refiere a parámetros del modelo, como conexiones en una red neuronal. Hablamos de pesos de ejemplo, lo que significa contar un ejemplo individual de forma más importante durante el entrenamiento. Un peso de ejemplo de 10 significa que el modelo lo trata como 10 veces más importante (cuando se pierde pérdida) como lo haría con un ejemplo de peso 1.
El peso debe ser igual al factor que usaste para la reducción de muestreo:
\[\text{ \{example weight\} = \{original example weight\} × \{downsampling factor\} }\]
¿Por qué utilizar la reducción de muestreo y el aumento de peso?
Puede parecer extraño agregar ponderaciones de ejemplo después del submuestreo. Intentamos mejorar nuestro modelo para la clase minoritaria. ¿Por qué aumentaríamos el peso de la mayoría? Estos son los cambios resultantes:
- Convergencia más rápida: Durante el entrenamiento, vemos la clase minoritaria con más frecuencia, lo que ayudará a que el modelo converja más rápido.
- Espacio en disco: Cuando se consolida la clase mayoritaria en menos ejemplos con pesos más grandes, gastamos menos espacio en disco al almacenarlos. Esto ahorra más espacio en el disco para la clase minoritaria, por lo que podemos recopilar una mayor cantidad y una mayor variedad de ejemplos de esa clase.
- Calibración: La ponderación asegura que nuestro modelo aún esté calibrado; los resultados aún se pueden interpretar como probabilidades.