ग्रेडिएंट डिसेंट एक गणितीय तकनीक है. यह बार-बार उन वेट और बायस का पता लगाती है जिनकी वजह से मॉडल में सबसे कम नुकसान होता है. ग्रेडिएंट डिसेंट, सबसे सही वेट और बायस का पता लगाता है. इसके लिए, वह उपयोगकर्ता के तय किए गए कई इटरेशन के लिए, यहां दी गई प्रोसेस को दोहराता है.
मॉडल, रैंडमाइज़ किए गए वेट और बायस के साथ ट्रेनिंग शुरू करता है. ये वैल्यू शून्य के आस-पास होती हैं. इसके बाद, मॉडल इन चरणों को दोहराता है:
मौजूदा वेट और बायस के हिसाब से नुकसान का हिसाब लगाएं.
वज़न और बायस को उस दिशा में ले जाना जिससे नुकसान कम हो.
वज़न और पक्षपात की वैल्यू को उस दिशा में थोड़ा बदलें जिससे नुकसान कम हो.
पहले चरण पर वापस जाएं और इस प्रोसेस को तब तक दोहराएं, जब तक मॉडल में और सुधार न हो सके.
नीचे दिए गए डायग्राम में, ग्रेडिएंट डिसेंट के उन चरणों के बारे में बताया गया है जिन्हें दोहराकर, सबसे कम नुकसान वाला मॉडल तैयार किया जाता है.
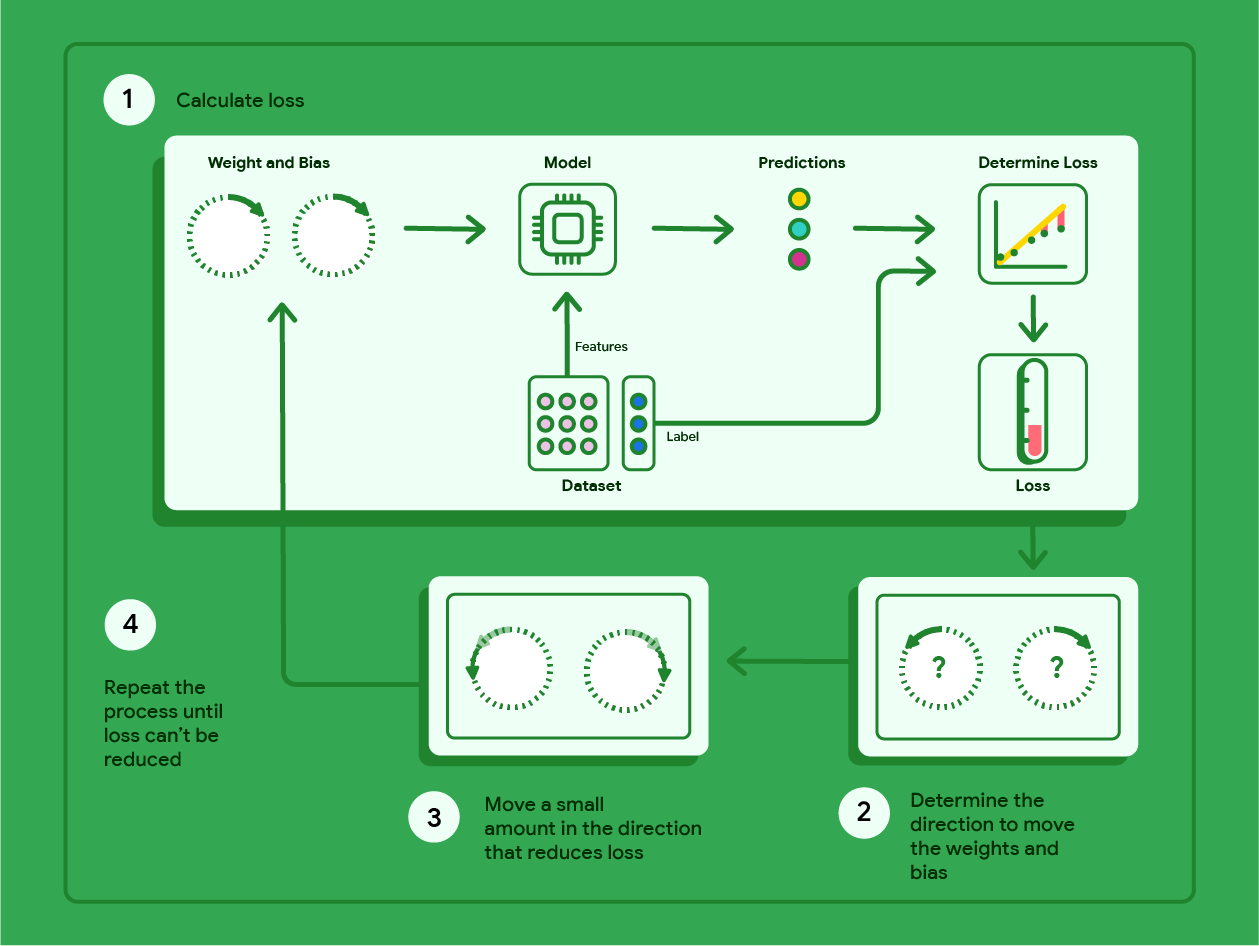
ग्यारहवीं इमेज. ग्रेडिएंट डिसेंट एक ऐसी प्रोसेस है जिसमें बार-बार काम किया जाता है. इससे ऐसे वेट और बायस का पता चलता है जिनसे मॉडल को सबसे कम नुकसान होता है.
ग्रेडिएंट डिसेंट के पीछे के गणित के बारे में ज़्यादा जानने के लिए, प्लस आइकॉन पर क्लिक करें.
हम यहां एक छोटे डेटासेट का इस्तेमाल करके, ग्रेडिएंट डिसेंट के चरणों के बारे में बता सकते हैं. इस डेटासेट में, कार के वज़न और उसके माइलेज के सात उदाहरण दिए गए हैं:
| हज़ारों पाउंड में (फ़ीचर) | माइल प्रति गैलन (लेबल) |
|---|---|
| 3.5 | 18 |
| 3.69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| 4.34 | 15 |
| 4.42 | 14 |
| 2.37 | 24 |
- मॉडल, वज़न और बायस को शून्य पर सेट करके ट्रेनिंग शुरू करता है:
- मौजूदा मॉडल पैरामीटर के साथ MSE लॉस का हिसाब लगाएं:
- हर वज़न और बायस पर, लॉस फ़ंक्शन के स्पर्शरेखा की ढलान का हिसाब लगाएं:
- अगले वज़न और बायस को पाने के लिए, नेगेटिव स्लोप की दिशा में थोड़ी दूरी तय करें. फ़िलहाल, हम "छोटी रकम" को 0.01 के तौर पर तय करेंगे:
स्लोप की गणना करने के बारे में जानने के लिए, प्लस आइकॉन पर क्लिक करें.
वज़न और बायस के लिए स्पर्शरेखाओं का स्लोप पाने के लिए, हम वज़न और बायस के हिसाब से लॉस फ़ंक्शन का डेरीवेटिव लेते हैं. इसके बाद, हम समीकरणों को हल करते हैं.
हम अनुमान लगाने के लिए समीकरण को इस तरह से लिखेंगे:
$ f_{w,b}(x) = (w*x)+b $.
हम असली वैल्यू को इस तरह लिखेंगे: $ y $.
हम MSE का हिसाब लगाने के लिए, इस फ़ॉर्मूले का इस्तेमाल करेंगे:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
यहां $i$ का मतलब $ith$ ट्रेनिंग उदाहरण से है और $M$ का मतलब उदाहरणों की संख्या से है.
वज़न के हिसाब से लॉस फ़ंक्शन के डेरिवेटिव को इस तरह लिखा जाता है:
$ \frac{\partial }{\partial w} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
और इसकी वैल्यू यह होती है:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2x_{(i)} $
सबसे पहले, हम अनुमानित वैल्यू में से असल वैल्यू को घटाते हैं. इसके बाद, हम इसे सुविधा की वैल्यू से दो बार गुणा करते हैं. इसके बाद, हम कुल संख्या को उदाहरणों की संख्या से भाग देते हैं. नतीजा, वेट की वैल्यू के टेंजेंट लाइन का स्लोप होता है.
अगर हम इस इक्वेशन को वज़न और बायस के साथ हल करते हैं, तो हमें लाइन के स्लोप के लिए -119.7 मिलता है.
भेदभाव से जुड़ा डेरिवेटिव
बायस के हिसाब से लॉस फ़ंक्शन के डेरिवेटिव को इस तरह लिखा जाता है:
$ \frac{\partial }{\partial b} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
और इसकी वैल्यू यह होती है:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2 $
सबसे पहले, हम हर अनुमानित वैल्यू में से असल वैल्यू घटाते हैं. इसके बाद, हम इसमें दो से गुणा करते हैं. इसके बाद, हम योग को उदाहरणों की संख्या से भाग देते हैं. नतीजा, लाइन का स्लोप होता है. यह स्लोप, बायस की वैल्यू के टेंजेंट होता है.
अगर हम इस समीकरण को वज़न और बायस के साथ हल करते हैं, तो हमें लाइन के स्लोप के लिए -34.3 मिलता है.
नए वेट और बायस का इस्तेमाल करके, नुकसान का हिसाब लगाएं और उसे दोहराएं. इस प्रोसेस को छह बार दोहराने पर, हमें ये वज़न, बायस, और लॉस मिलेंगे:
| इटरेशन | वज़न | पक्षपात | लॉस (एमएसई) |
|---|---|---|---|
| 1 | 0 | 0 | 303.71 |
| 2 | 1.20 | 0.34 | 170.84 |
| 3 | 2.05 | 0.59 | 103.17 |
| 4 | 2.66 | 0.78 | 68.70 |
| 5 | 3.09 | 0.91 | 51.13 |
| 6 | 3.40 | 1.01 | 42.17 |
अपडेट किए गए हर वज़न और पक्षपात के साथ, नुकसान कम होता जाता है. इस उदाहरण में, हमने छह बार दोहराने के बाद रोक दिया है. असल में, मॉडल तब तक ट्रेन होता है, जब तक कि वह कन्वर्ज नहीं हो जाता. जब मॉडल कन्वर्ज हो जाता है, तो अतिरिक्त इटरेशन से नुकसान कम नहीं होता. ऐसा इसलिए होता है, क्योंकि ग्रेडिएंट डिसेंट को ऐसे वेट और बायस मिल गए हैं जो नुकसान को कम करते हैं.
अगर मॉडल, कन्वर्जेंस के बाद भी ट्रेनिंग जारी रखता है, तो नुकसान में थोड़ा-बहुत उतार-चढ़ाव होने लगता है. ऐसा इसलिए होता है, क्योंकि मॉडल लगातार पैरामीटर को उनकी सबसे कम वैल्यू के आस-पास अपडेट करता रहता है. इससे यह पुष्टि करना मुश्किल हो सकता है कि मॉडल वाकई में कन्वर्ज हो गया है. मॉडल के कन्वर्ज होने की पुष्टि करने के लिए, आपको ट्रेनिंग तब तक जारी रखनी होगी, जब तक लॉस स्थिर न हो जाए.
मॉडल कन्वर्जेंस और लॉस कर्व
मॉडल को ट्रेन करते समय, अक्सर लॉस कर्व को देखा जाता है. इससे यह पता चलता है कि मॉडल कन्वर्ज हुआ है या नहीं. लॉस कर्व से पता चलता है कि मॉडल को ट्रेन करते समय, लॉस में कैसे बदलाव होता है. यहां एक सामान्य लॉस कर्व दिखाया गया है. y-ऐक्सिस पर लॉस और x-ऐक्सिस पर इटरेशन दिखाए गए हैं:
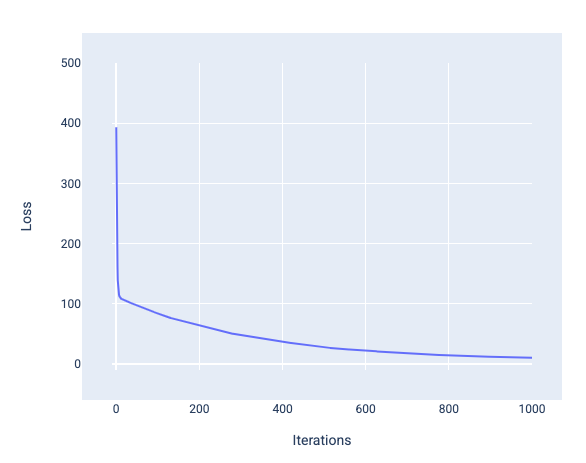
इमेज 12. लॉस कर्व में दिखाया गया है कि मॉडल, 1,000वें-इटरेशन मार्क के आस-पास कन्वर्ज हो रहा है.
इस ग्राफ़ में देखा जा सकता है कि पहले कुछ इटरेशन के दौरान, लॉस में काफ़ी कमी आई है. इसके बाद, यह धीरे-धीरे कम होता है. 1,000वें इटरेशन के आस-पास, यह स्थिर हो जाता है. 1,000 बार दोहराने के बाद, हम काफ़ी हद तक यह पक्का कर सकते हैं कि मॉडल कन्वर्ज हो गया है.
नीचे दिए गए आंकड़ों में, हमने ट्रेनिंग की प्रोसेस के दौरान मॉडल को तीन पॉइंट पर दिखाया है: शुरुआत, बीच, और आखिर. ट्रेनिंग प्रोसेस के दौरान, स्नैपशॉट में मॉडल की स्थिति को विज़ुअलाइज़ करने से, वज़न और पक्षपात को अपडेट करने, नुकसान को कम करने, और मॉडल कन्वर्जेंस के बीच का लिंक मज़बूत होता है.
आंकड़ों में, हम मॉडल को दिखाने के लिए किसी खास इटरेशन पर, निकाले गए वेट और बायस का इस्तेमाल करते हैं. डेटा पॉइंट और मॉडल स्नैपशॉट वाले ग्राफ़ में, मॉडल से डेटा पॉइंट तक नीली लॉस लाइनें, लॉस की मात्रा दिखाती हैं. लाइनें जितनी लंबी होंगी, उतना ही ज़्यादा नुकसान होगा.
नीचे दिए गए फ़िगर में, हम देख सकते हैं कि दूसरे इटरेशन के आस-पास मॉडल, अनुमान लगाने में अच्छा नहीं होगा. ऐसा इसलिए होगा, क्योंकि इसमें काफ़ी नुकसान हुआ है.
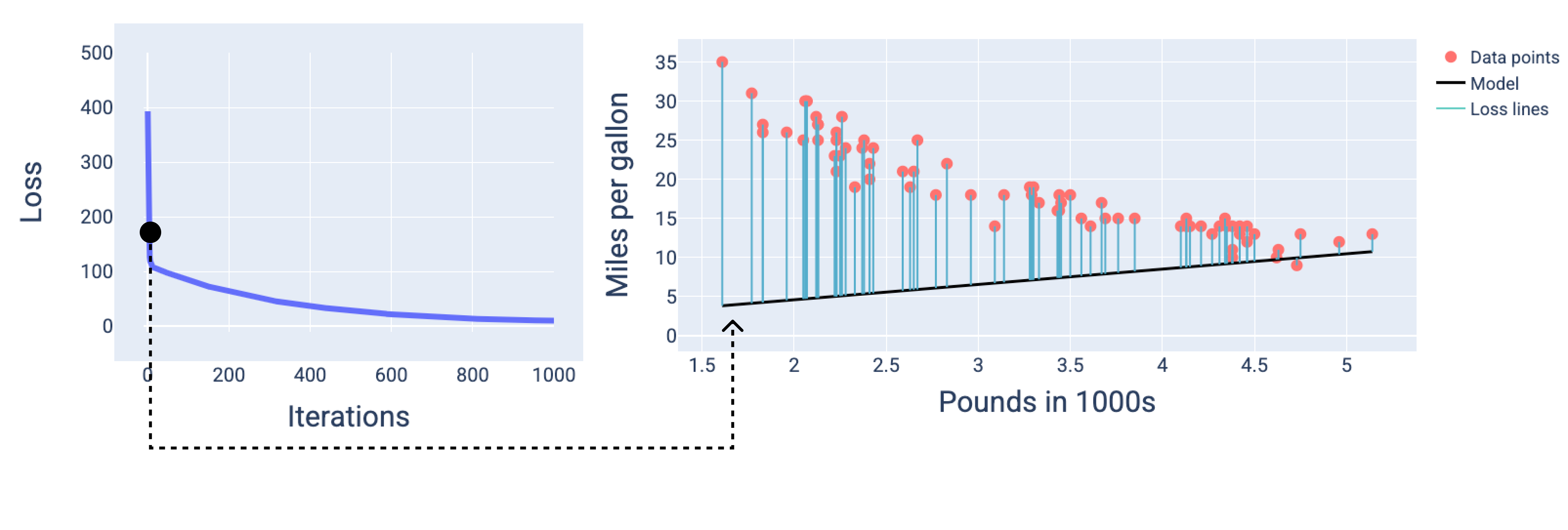
13वीं इमेज. ट्रेनिंग प्रोसेस की शुरुआत में मॉडल का लॉस कर्व और स्नैपशॉट.
लगभग 400वें इटरेशन पर, हम देख सकते हैं कि ग्रेडिएंट डिसेंट को ऐसा वेट और बायस मिला है जिससे बेहतर मॉडल तैयार होता है.
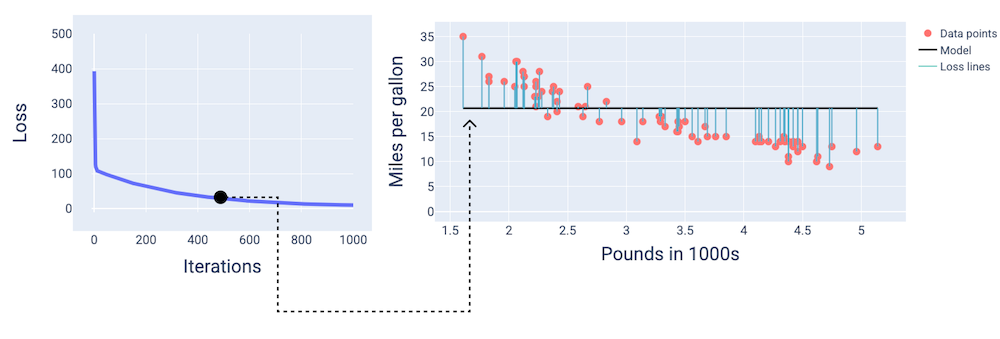
चौथी इमेज. ट्रेनिंग के बीच में मॉडल का लॉस कर्व और स्नैपशॉट.
इसके बाद, हम देख सकते हैं कि मॉडल 1,000वें इटरेशन के आस-पास कन्वर्ज हो गया है. इससे हमें सबसे कम नुकसान वाला मॉडल मिला है.
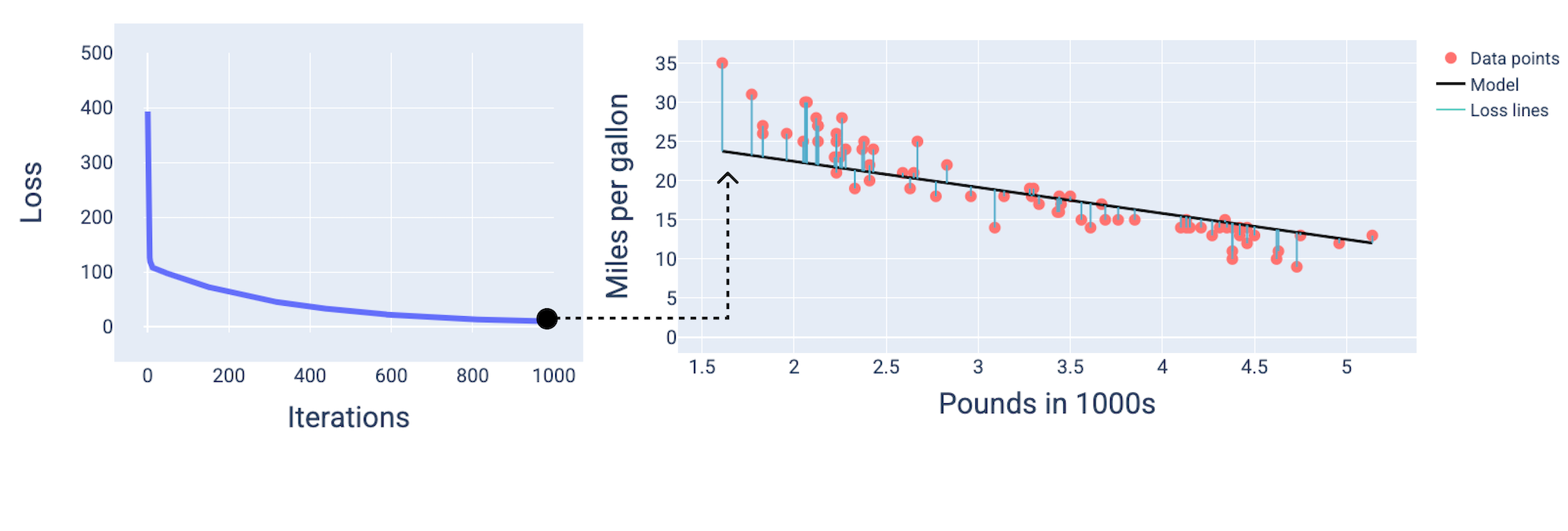
15वीं इमेज. ट्रेनिंग प्रोसेस के आखिर में, मॉडल का लॉस कर्व और स्नैपशॉट.
एक्सरसाइज़: देखें कि आपको कितना समझ आया
कन्वर्जेंस और कॉन्वेक्स फ़ंक्शन
लीनियर मॉडल के लिए लॉस फ़ंक्शन हमेशा कॉन्वेक्स सर्फ़ेस बनाते हैं. इस प्रॉपर्टी की वजह से, जब लीनियर रिग्रेशन मॉडल कन्वर्ज होता है, तो हमें पता चलता है कि मॉडल को ऐसे वेट और बायस मिल गए हैं जिनसे सबसे कम नुकसान होता है.
अगर हम एक सुविधा वाले मॉडल के लिए लॉस सर्फ़ेस का ग्राफ़ बनाते हैं, तो हमें इसका कॉन्वेक्स आकार दिखता है. यहां एक काल्पनिक डेटासेट के लिए लॉस सर्फ़ेस दिखाया गया है. वज़न x-ऐक्सिस पर, पूर्वाग्रह y-ऐक्सिस पर, और नुकसान z-ऐक्सिस पर है:
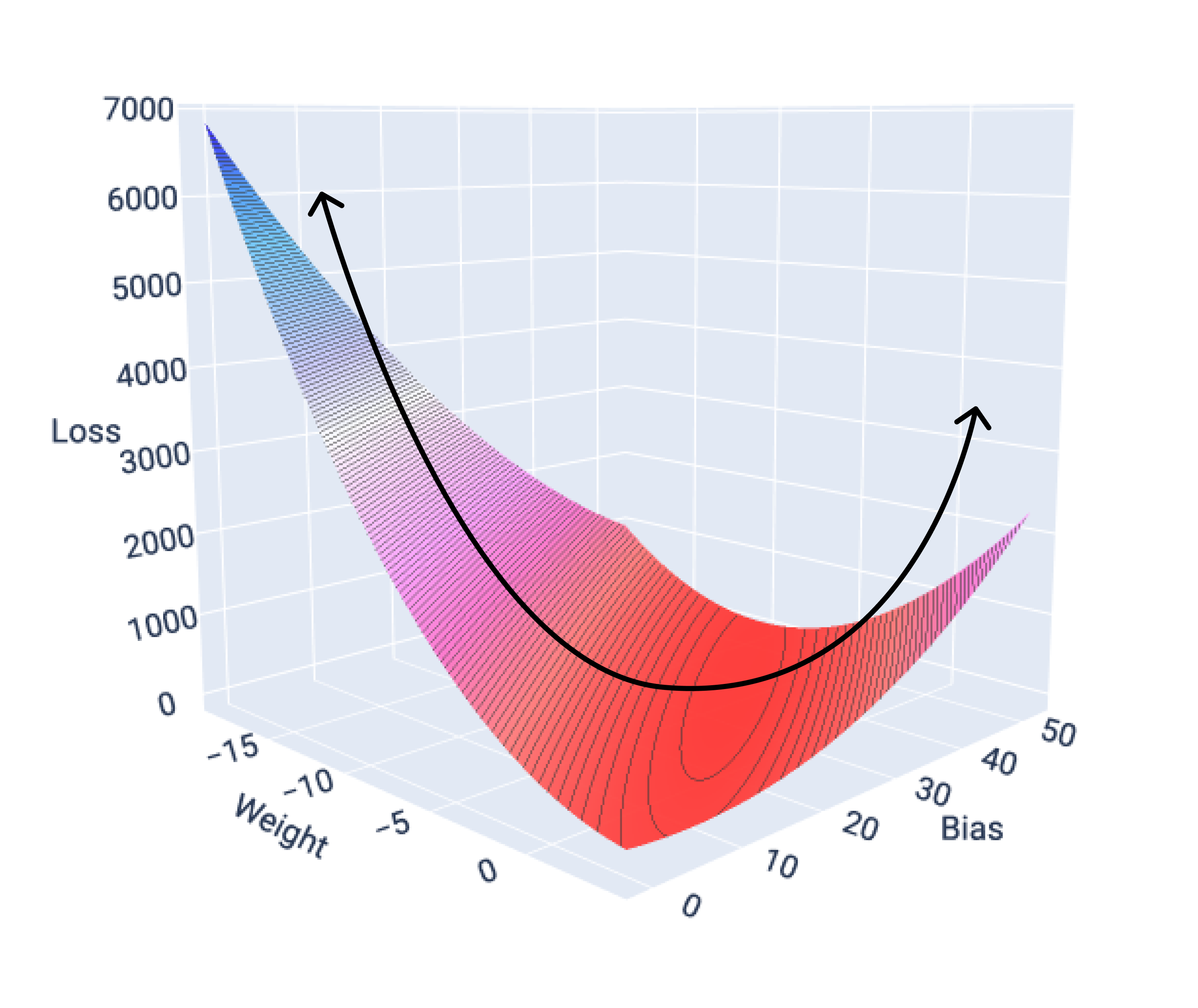
16वीं इमेज. लॉस सर्फ़ेस, जिसमें कॉन्वेक्स शेप दिख रहा है.
इस उदाहरण में, -5.44 के वेट और 35.94 के बायस से, 5.54 पर सबसे कम नुकसान होता है:
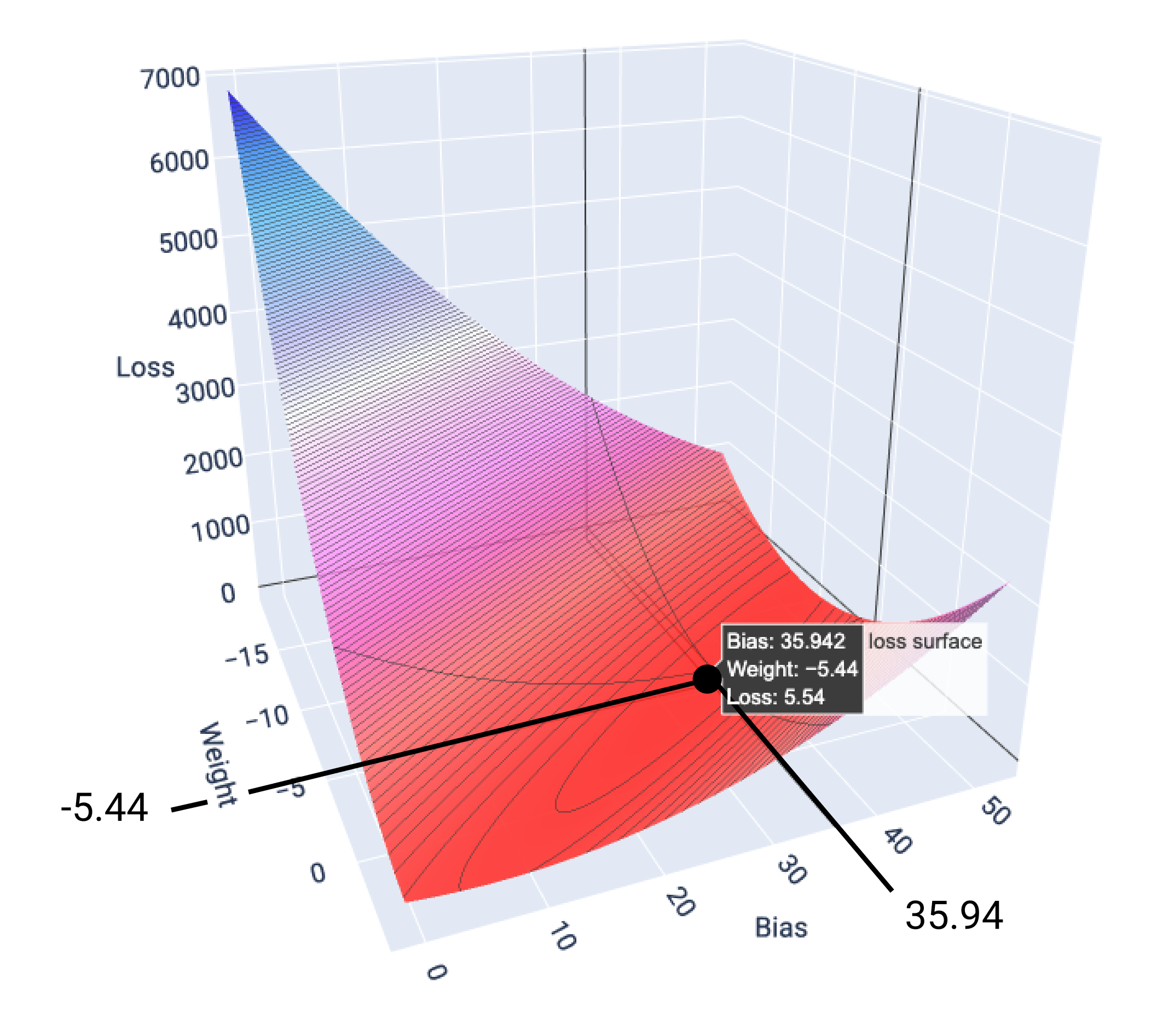
17वीं इमेज. वज़न और बायस की ऐसी वैल्यू दिखाने वाला लॉस सर्फ़ेस जिससे सबसे कम नुकसान होता है.
जब लीनियर मॉडल को कम से कम नुकसान होता है, तब वह कन्वर्ज होता है. इसलिए, अतिरिक्त इटरेशन से, ग्रेडिएंट डिसेंट सिर्फ़ वज़न और बायस वैल्यू को कम से कम वैल्यू के आस-पास बहुत कम मात्रा में ले जाता है. अगर हम ग्रेडिएंट डिसेंट के दौरान, वेट और बायस पॉइंट को ग्राफ़ पर दिखाएं, तो पॉइंट ऐसे दिखेंगे जैसे कोई गेंद पहाड़ी से नीचे लुढ़क रही हो. आखिर में, गेंद उस पॉइंट पर रुक जाएगी जहां ढलान खत्म हो जाता है.
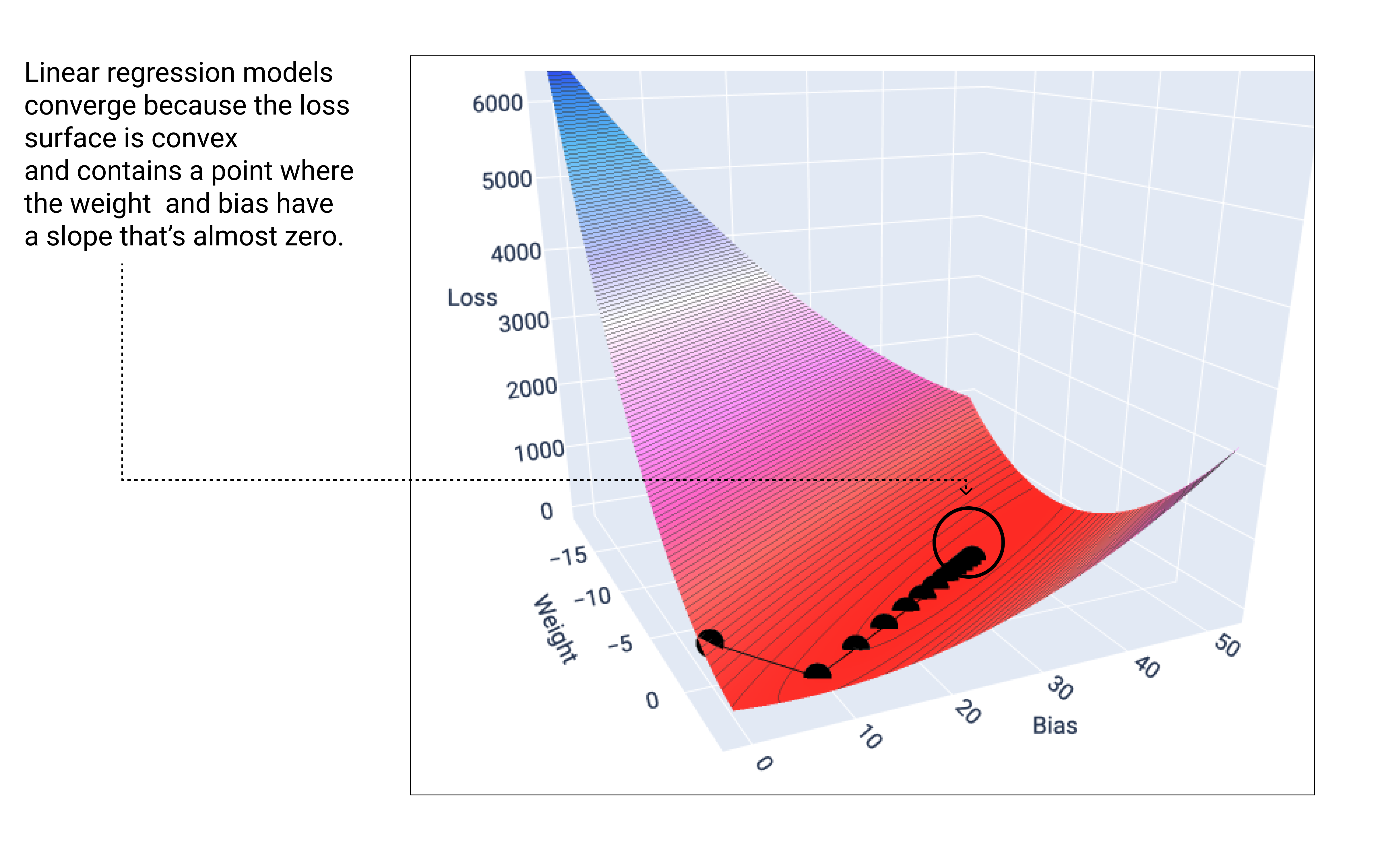
18वीं इमेज. इस इमेज में लॉस ग्राफ़ दिखाया गया है. इसमें ग्रेडिएंट डिसेंट पॉइंट, ग्राफ़ के सबसे निचले पॉइंट पर रुकते हुए दिख रहे हैं.
ध्यान दें कि काले रंग के लॉस पॉइंट, लॉस कर्व का सटीक आकार बनाते हैं: लॉस सरफेस पर सबसे निचले पॉइंट तक पहुंचने से पहले, इनमें तेज़ी से गिरावट आती है. इसके बाद, धीरे-धीरे गिरावट आती है.
यह ध्यान रखना ज़रूरी है कि मॉडल, हर वेट और बायस के लिए सटीक न्यूनतम वैल्यू का पता नहीं लगाता. इसके बजाय, यह ऐसी वैल्यू का पता लगाता है जो इसके बहुत करीब होती है. यह ध्यान रखना भी ज़रूरी है कि वज़न और बायस के लिए कम से कम वैल्यू, शून्य नुकसान के बराबर नहीं होती. यह सिर्फ़ वह वैल्यू होती है जो उस पैरामीटर के लिए सबसे कम नुकसान पहुंचाती है.
वज़न और पूर्वाग्रह की उन वैल्यू का इस्तेमाल करके, जिनसे सबसे कम नुकसान होता है—इस मामले में, वज़न -5.44 और पूर्वाग्रह 35.94 है—हम मॉडल को ग्राफ़ कर सकते हैं. इससे यह देखा जा सकता है कि मॉडल, डेटा के साथ कितना सही तरीके से फ़िट होता है:
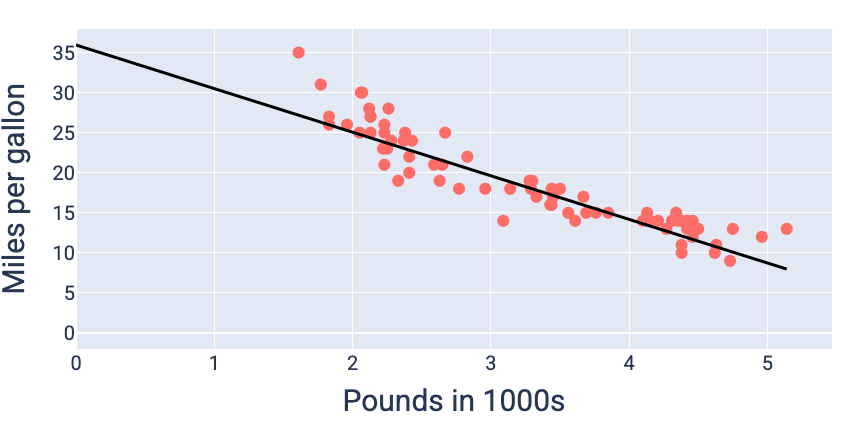
19वीं इमेज. वज़न और बायस की उन वैल्यू का इस्तेमाल करके मॉडल को ग्राफ़ किया गया है जिनसे सबसे कम नुकसान होता है.
यह इस डेटासेट के लिए सबसे अच्छा मॉडल होगा, क्योंकि वज़न और बायस की कोई अन्य वैल्यू, कम नुकसान वाला मॉडल नहीं बनाती है.
