Page Summary
-
This document explores multi-class classification models, which predict from multiple possibilities instead of just two, like binary classification models.
-
Multi-class classification can be achieved through two main approaches: one-vs.-all and one-vs.-one (softmax).
-
One-vs.-all uses multiple binary classifiers, one for each possible outcome, to determine the probability of each class independently.
-
One-vs.-one (softmax) predicts probabilities of each class relative to all other classes, ensuring all probabilities sum to 1 using the softmax function.
-
Softmax is efficient for fewer classes but can become computationally expensive with many classes; candidate sampling offers an alternative for increased efficiency.
Earlier, you encountered binary classification models that could pick between one of two possible choices, such as whether:
- A given email is spam or not spam.
- A given tumor is malignant or benign.
In this section, we'll investigate multi-class classification models, which can pick from multiple possibilities. For example:
- Is this dog a beagle, a basset hound, or a bloodhound?
- Is this flower a Siberian Iris, Dutch Iris, Blue Flag Iris, or Dwarf Bearded Iris?
- Is that plane a Boeing 747, Airbus 320, Boeing 777, or Embraer 190?
- Is this an image of an apple, bear, candy, dog, or egg?
Some real-world multi-class problems entail choosing from millions of separate classes. For example, consider a multi-class classification model that can identify the image of just about anything.
This section details the two main variants of multi-class classification:
- one-vs.-all
- one-vs.-one, which is usually known as softmax
One versus all
One-vs.-all provides a way to use binary classification for a series of yes or no predictions across multiple possible labels.
Given a classification problem with N possible solutions, a one-vs.-all solution consists of N separate binary classifiers—one binary classifier for each possible outcome. During training, the model runs through a sequence of binary classifiers, training each to answer a separate classification question.
For example, given a picture of a piece of fruit, four different recognizers might be trained, each answering a different yes/no question:
- Is this image an apple?
- Is this image an orange?
- Is this image a banana?
- Is this image a grape?
The following image illustrates how this works in practice.

This approach is fairly reasonable when the total number of classes is small, but becomes increasingly inefficient as the number of classes rises.
We can create a significantly more efficient one-vs.-all model with a deep neural network in which each output node represents a different class. The following image illustrates this approach.
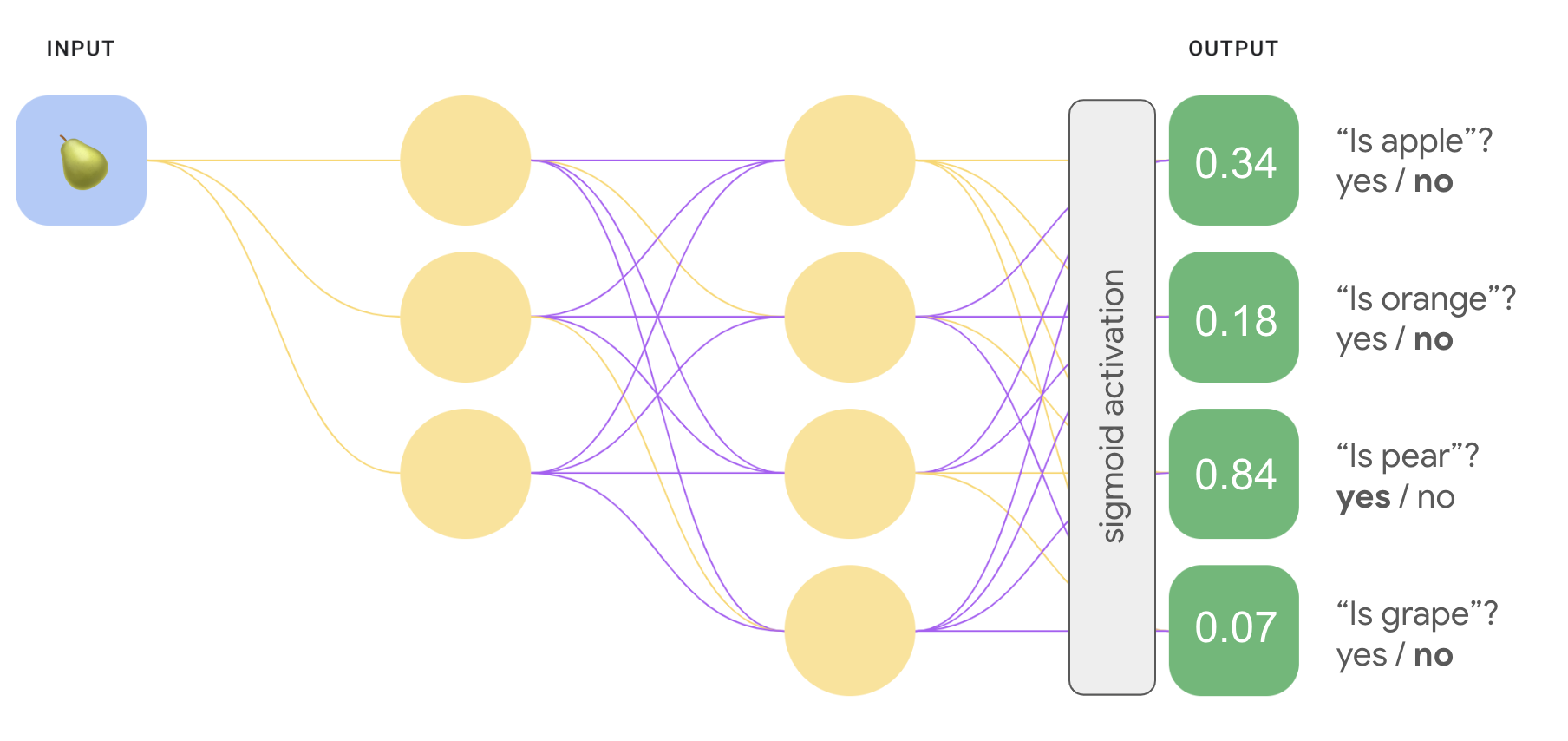
One versus one (softmax)
You may have noticed that the probability values in the output layer of Figure 8 don't sum to 1.0 (or 100%). (In fact, they sum to 1.43.) In a one-vs.-all approach, the probability of each binary set of outcomes is determined independently of all the other sets. That is, we're determining the probability of "apple" versus "not apple" without considering the likelihood of our other fruit options: "orange", "pear", or "grape."
But what if we want to predict the probabilities of each fruit relative to each other? In this case, instead of predicting "apple" versus "not apple", we want to predict "apple" versus "orange" versus "pear" versus "grape". This type of multi-class classification is called one-vs.-one classification.
We can implement a one-vs.-one classification using the same type of neural network architecture used for one-vs.-all classification, with one key change. We need to apply a different transform to the output layer.
For one-vs.-all, we applied the sigmoid activation function to each output node independently, which resulted in an output value between 0 and 1 for each node, but did not guarantee that these values summed to exactly 1.
For one-vs.-one, we can instead apply a function called softmax, which assigns decimal probabilities to each class in a multi-class problem such that all probabilities add up to 1.0. This additional constraint helps training converge more quickly than it otherwise would.
The following image re-implements our one-vs.-all multi-class classification task as a one-vs.-one task. Note that in order to perform softmax, the hidden layer directly preceding the output layer (called the softmax layer) must have the same number of nodes as the output layer.

Softmax options
Consider the following variants of softmax:
Full softmax is the softmax we've been discussing; that is, softmax calculates a probability for every possible class.
Candidate sampling means that softmax calculates a probability for all the positive labels but only for a random sample of negative labels. For example, if we are interested in determining whether an input image is a beagle or a bloodhound, we don't have to provide probabilities for every non-doggy example.
Full softmax is fairly cheap when the number of classes is small but becomes prohibitively expensive when the number of classes climbs. Candidate sampling can improve efficiency in problems having a large number of classes.
One label versus many labels
Softmax assumes that each example is a member of exactly one class. Some examples, however, can simultaneously be a member of multiple classes. For such examples:
- You may not use softmax.
- You must rely on multiple logistic regressions.
For example, the one-vs.-one model in Figure 9 above assumes that each input image will depict exactly one type of fruit: an apple, an orange, a pear, or a grape. However, if an input image might contain multiple types of fruit—a bowl of both apples and oranges—you'll have to use multiple logistic regressions instead.