Нейронні мережі: функції активації

У попередній вправі ви бачили, що простого додавання прихованих шарів до нашої мережі було недостатньо для представлення нелінійностей. Лінійні операції, що виконуються над лінійними операціями, все ще є лінійними.

Як можна налаштувати нейронну мережу для вивчення нелінійних зв'язків між значеннями? Нам потрібен спосіб вставляти нелінійні математичні операції в модель.

Якщо це здається вам дещо знайомим, це тому, що ми вже застосовували нелінійні математичні операції до виводу лінійної моделі раніше в курсі. У модулі логістичної регресії ми адаптували модель лінійної регресії для виведення неперервного значення від 0 до 1 (що представляє ймовірність), пропускаючи вивід моделі через сигмоподібну функцію .

Ми можемо застосувати той самий принцип до нашої нейронної мережі. Давайте повернемося до нашої моделі з вправи 2 раніше, але цього разу, перш ніж виводити значення кожного вузла, ми спочатку застосуємо сигмоподібну функцію:

Спробуйте покроково виконати обчислення кожного вузла, натиснувши кнопку >| (праворуч від кнопки відтворення). Перегляньте математичні операції, виконані для обчислення значення кожного вузла, на панелі «Обчислення» під графіком. Зверніть увагу, що вихід кожного вузла тепер є сигмоїдним перетворенням лінійної комбінації вузлів попереднього шару, а вихідні значення зведені між 0 та 1.

Тут сигмоподібна крива служить функцією активації для нейронної мережі, нелінійним перетворенням вихідного значення нейрона, перш ніж це значення передається на вхід для обчислень наступного шару нейронної мережі.

Тепер, коли ми додали функцію активації, додавання шарів має більший вплив. Накладання нелінійностей на нелінійності дозволяє нам моделювати дуже складні зв'язки між вхідними даними та прогнозованими виходами. Коротше кажучи, кожен шар фактично навчається складнішій функції вищого рівня на основі необроблених вхідних даних. Якщо ви хочете розвинути глибше розуміння того, як це працює, перегляньте чудову публікацію в блозі Кріса Олаха .

Загальні функції активації

Три математичні функції, які зазвичай використовуються як функції активації, це сигмоподібна, тангенціальна та ReLU.

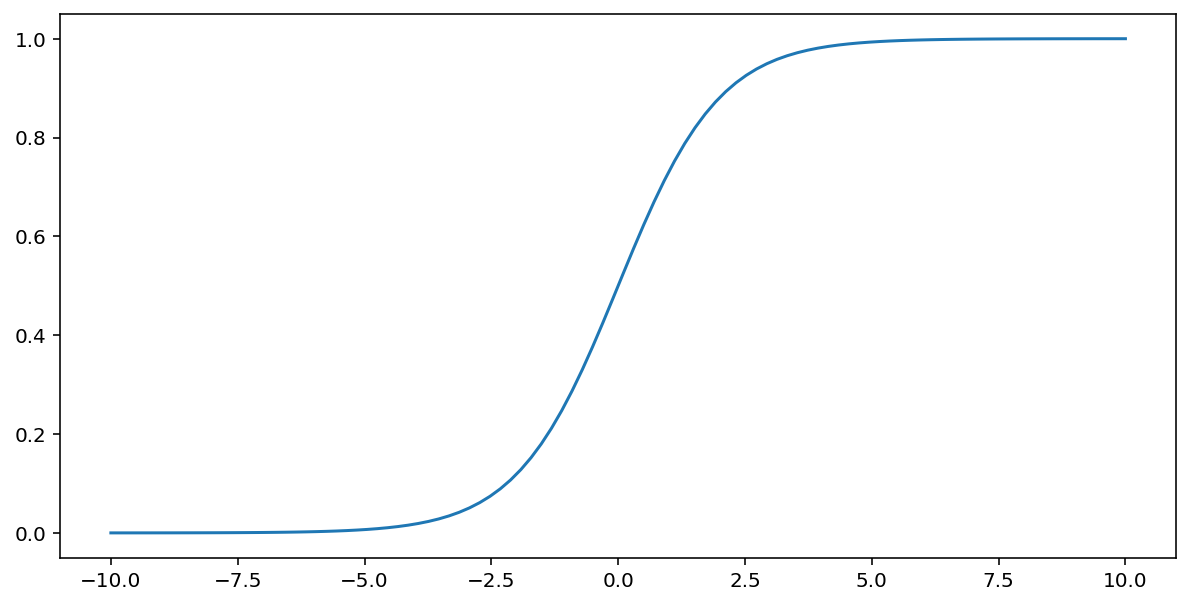
Сигмоїдна функція (обговорена вище) виконує наступне перетворення вхідного значення $x$, створюючи вихідне значення між 0 та 1:

\[F(x)=\frac{1} {1+e^{-x}}\]

Термін «сигмоподібна» часто використовується в більш загальному значенні для позначення будь-якої S-подібної функції. Більш технічно точний термін для конкретної функції $F(x)=\frac{1} {1+e^{-x}}$ — це логістична функція .

Ось графік цієї функції:

Рисунок 4. Графік сигмоподібної функції.

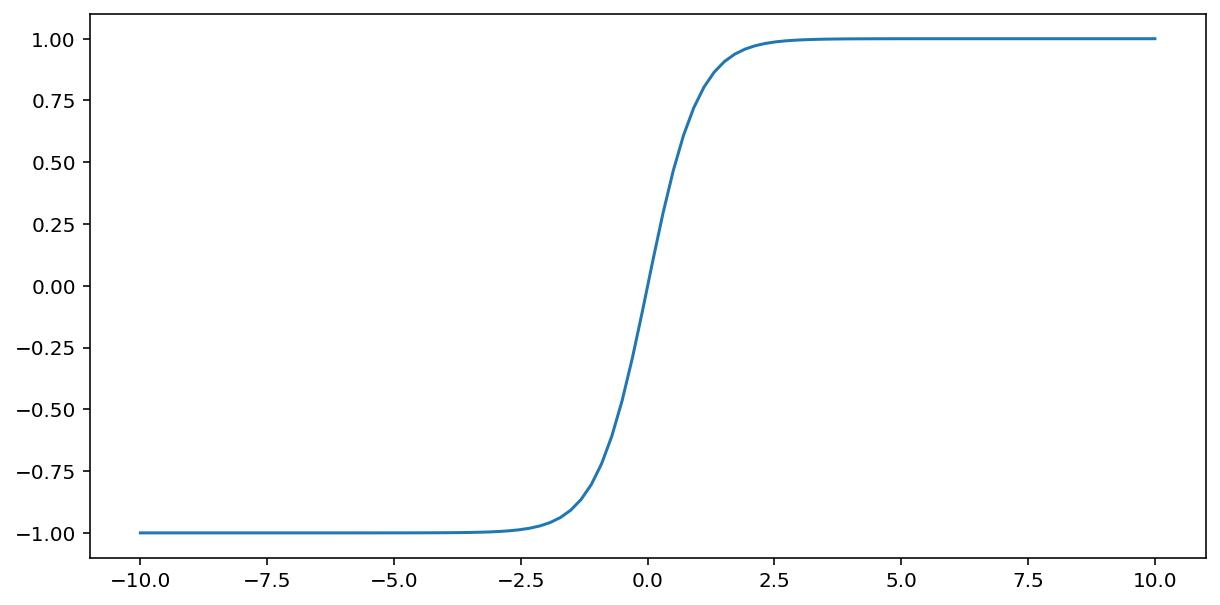
Функція tanh (скорочення від «гіперболічний тангенс») перетворює вхідне значення $x$ для отримання вихідного значення від –1 до 1:

\[F(x)=tanh(x)\]

Ось графік цієї функції:

Рисунок 5. Графік функції тангенса.

Зверніть увагу, що діапазон сигмоїдної функції становить від 0 до 1, а діапазон функції танга — від –1 до 1.

Випрямлена лінійна одинична активаційна функція (або скорочено ReLU ) перетворює вихідний сигнал за допомогою наступного алгоритму:

• Якщо вхідне значення $x$ менше за 0, повернути 0.
• Якщо вхідне значення $x$ більше або дорівнює 0, повернути вхідне значення.

ReLU можна представити математично за допомогою функції max():

$$F(x)=max(0,x)$$

Ось графік цієї функції:

Рисунок 6. Графік функції ReLU.

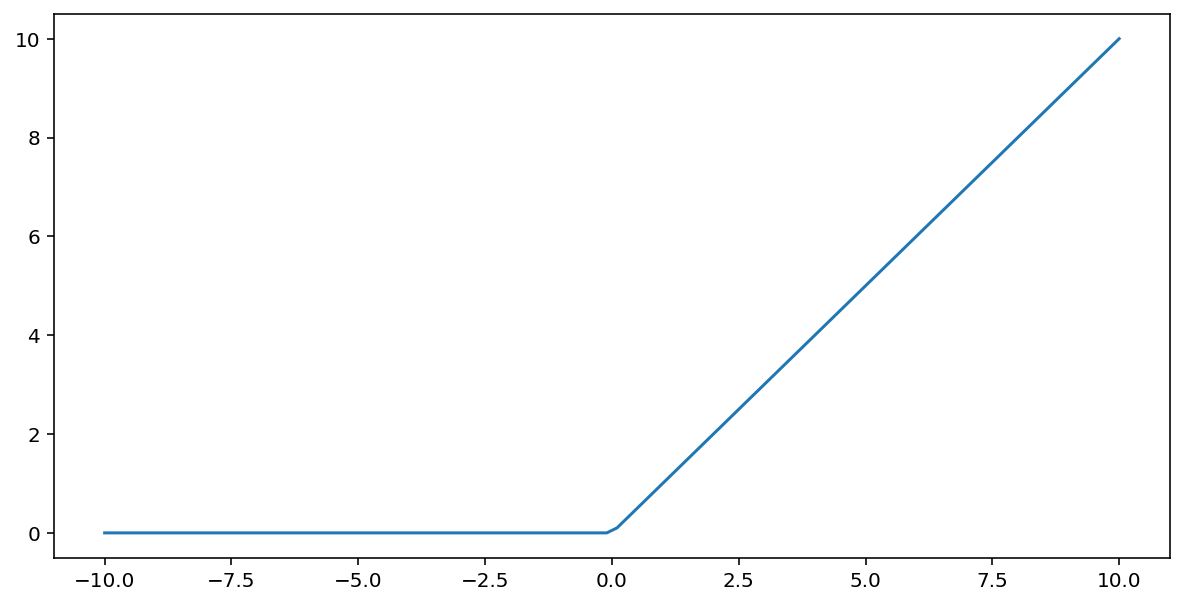
ReLU часто працює трохи краще як функція активації, ніж гладка функція, така як сигмоподібна або тангенціальна, оскільки вона менш чутлива до проблеми градієнта зникнення під час навчання нейронної мережі . ReLU також значно легше обчислювати, ніж ці функції.

Інші функції активації

На практиці, будь-яка математична функція може служити функцією активації. Припустимо, що \(\sigma\) представляє нашу функцію активації. Значення вузла в мережі визначається наступною формулою:

$$\sigma(\boldsymbol w \cdot \boldsymbol x+b)$$

Keras забезпечує готову підтримку багатьох функцій активації . Проте, ми все ж рекомендуємо почати з ReLU.

Короткий зміст

У наступному відео ви підсумуєте все, що ви дізналися про те, як побудовані нейронні мережі:

Тепер наша модель має всі стандартні компоненти того, що люди зазвичай мають на увазі, коли говорять про нейронну мережу:

• Набір вузлів, аналогічних нейронам, організованих у шари.
• Набір вивчених вагових коефіцієнтів та зміщень, що представляють зв'язки між кожним шаром нейронної мережі та шаром під ним. Шар під ним може бути іншим шаром нейронної мережі або якимось іншим типом шару.
• Функція активації, яка перетворює вихід кожного вузла в шарі. Різні шари можуть мати різні функції активації.

Застереження: нейронні мережі не завжди кращі за схрещування ознак, але нейронні мережі пропонують гнучку альтернативу, яка добре працює в багатьох випадках.

Ключові терміни:

• Функція активації
• Сигмоїдна функція
• Проблема зниклого градієнта

Довідковий центр