ใน แบบฝึกหัดก่อนหน้านี้ คุณได้เห็นแล้วว่าการเพิ่มเลเยอร์ที่ซ่อนอยู่ลงในเครือข่ายของเราเพียงอย่างเดียวไม่เพียงพอที่จะแสดงถึงความไม่เป็นเชิงเส้น การดำเนินการเชิงเส้นที่กระทำกับการดำเนินการเชิงเส้นก็ยังคงเป็นการดำเนินการเชิงเส้นอยู่ดี
เราจะกำหนดค่าโครงข่ายประสาทเทียมให้เรียนรู้ความสัมพันธ์ที่ไม่เป็นเชิงเส้นระหว่างค่าต่างๆ ได้อย่างไร? เราจำเป็นต้องมีวิธีการบางอย่างในการแทรกการดำเนินการทางคณิตศาสตร์ที่ไม่เป็นเชิงเส้นเข้าไปในแบบจำลอง
หากสิ่งนี้ดูคุ้นเคยบ้าง นั่นเป็นเพราะเราได้นำการดำเนินการทางคณิตศาสตร์แบบไม่เชิงเส้นมาใช้กับผลลัพธ์ของแบบจำลองเชิงเส้นไปแล้วในตอนต้นของหลักสูตร ในโมดูล การถดถอยโลจิสติก เราได้ปรับแบบจำลองการถดถอยเชิงเส้นให้ได้ค่าต่อเนื่องจาก 0 ถึง 1 (ซึ่งแสดงถึงความน่าจะเป็น) โดยการส่งผลลัพธ์ของแบบจำลองผ่าน ฟังก์ชันซิกมอยด์
เราสามารถนำหลักการเดียวกันนี้มาใช้กับโครงข่ายประสาทเทียมของเราได้ ลองกลับไปดูแบบจำลองของเราจาก แบบฝึกหัดที่ 2 ก่อนหน้านี้ แต่คราวนี้ ก่อนที่จะแสดงค่าของแต่ละโหนด เราจะใช้ฟังก์ชันซิกมอยด์ก่อน:
ลองดูขั้นตอนการคำนวณของแต่ละโหนดโดยคลิกปุ่ม >| (ทางด้านขวาของปุ่มเล่น) ตรวจสอบการดำเนินการทางคณิตศาสตร์ที่ใช้ในการคำนวณค่าของแต่ละโหนดในแผง การคำนวณ ด้านล่างกราฟ สังเกตว่าเอาต์พุตของแต่ละโหนดในขณะนี้คือการแปลงซิกมอยด์ของการรวมเชิงเส้นของโหนดในเลเยอร์ก่อนหน้า และค่าเอาต์พุตทั้งหมดจะถูกบีบให้อยู่ระหว่าง 0 ถึง 1
ในที่นี้ ฟังก์ชันซิกมอยด์ทำหน้าที่เป็น ฟังก์ชันกระตุ้น สำหรับโครงข่ายประสาทเทียม ซึ่งเป็นการแปลงค่าเอาต์พุตของนิวรอนแบบไม่เชิงเส้น ก่อนที่จะส่งค่าดังกล่าวเป็นอินพุตไปยังการคำนวณของเลเยอร์ถัดไปของโครงข่ายประสาทเทียม
เมื่อเราเพิ่มฟังก์ชันการกระตุ้นแล้ว การเพิ่มเลเยอร์จะมีผลกระทบมากขึ้น การซ้อนความไม่เป็นเชิงเส้นเข้าด้วยกันทำให้เราสามารถจำลองความสัมพันธ์ที่ซับซ้อนมากระหว่างอินพุตและเอาต์พุตที่คาดการณ์ได้ กล่าวโดยสรุป แต่ละเลเยอร์จะเรียนรู้ฟังก์ชันที่ซับซ้อนและระดับสูงขึ้นจากอินพุตดิบ หากคุณต้องการทำความเข้าใจวิธีการทำงานนี้ให้มากขึ้น โปรดดู บทความบล็อกที่ยอดเยี่ยมของ Chris Olah
ฟังก์ชันการเปิดใช้งานทั่วไป
ฟังก์ชันทางคณิตศาสตร์สามฟังก์ชันที่นิยมใช้เป็นฟังก์ชันกระตุ้น ได้แก่ ซิกมอยด์ (sigmoid), แทนห์ม (tanh) และ รีลู (ReLU)
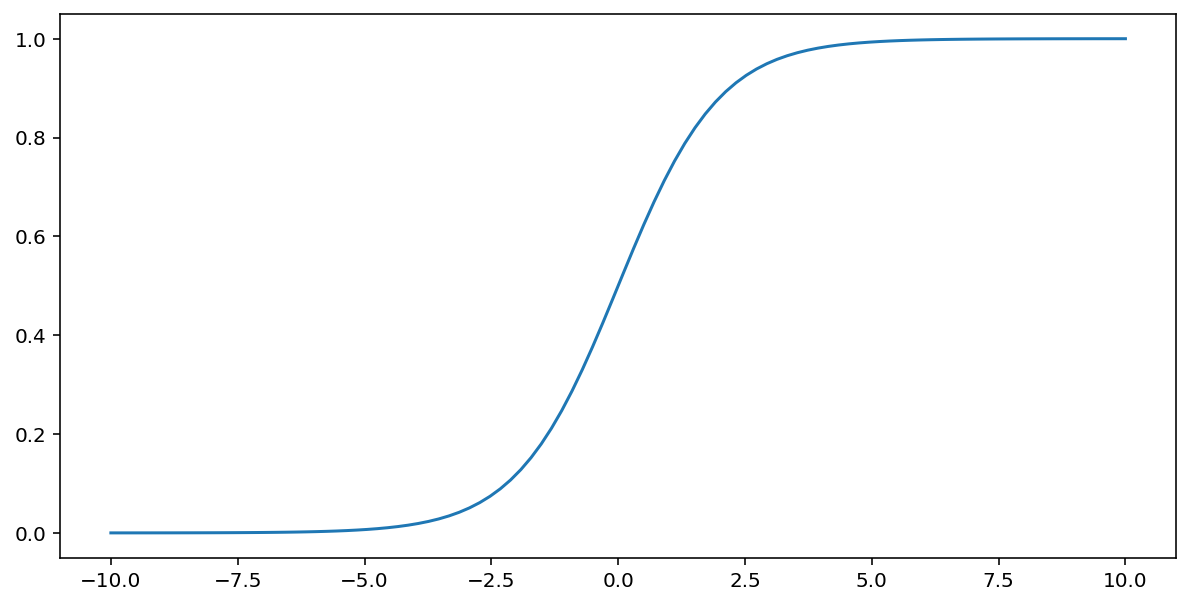
ฟังก์ชันซิกมอยด์ (ที่กล่าวถึงข้างต้น) จะทำการแปลงค่าอินพุต $x$ ดังต่อไปนี้ โดยให้ค่าเอาต์พุตอยู่ระหว่าง 0 ถึง 1:
\[F(x)=\frac{1} {1+e^{-x}}\]
นี่คือกราฟแสดงฟังก์ชันนี้:
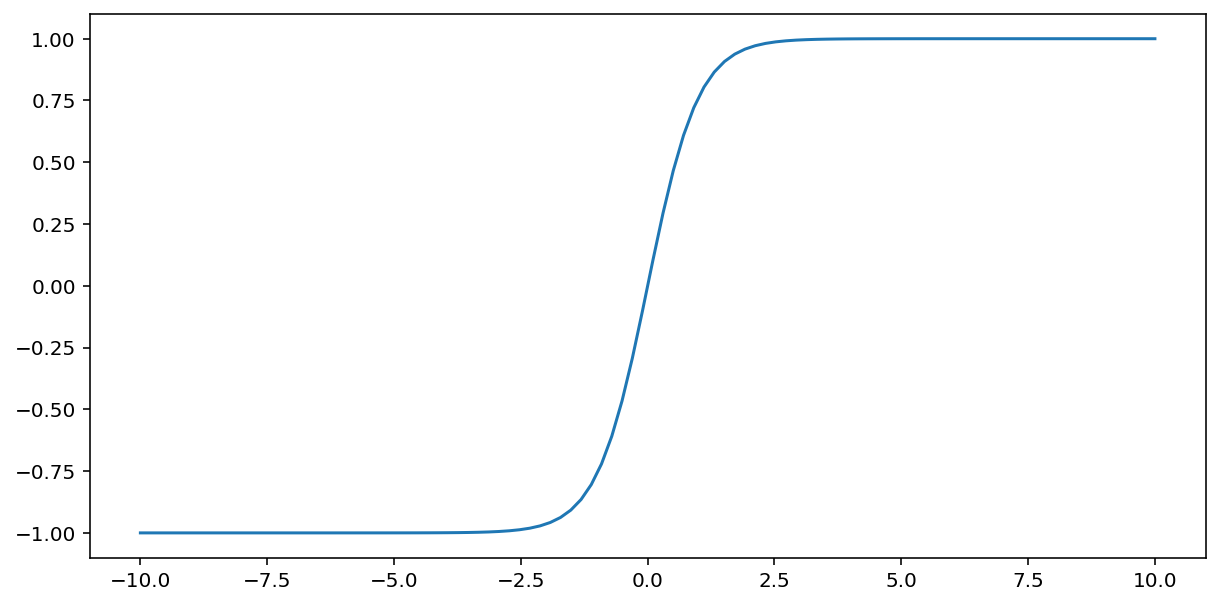
ฟังก์ชัน tanh (ย่อมาจาก "hyperbolic tangent") แปลงค่าอินพุต $x$ ให้ได้ค่าเอาต์พุตอยู่ระหว่าง –1 ถึง 1:
\[F(x)=tanh(x)\]
นี่คือกราฟแสดงฟังก์ชันนี้:
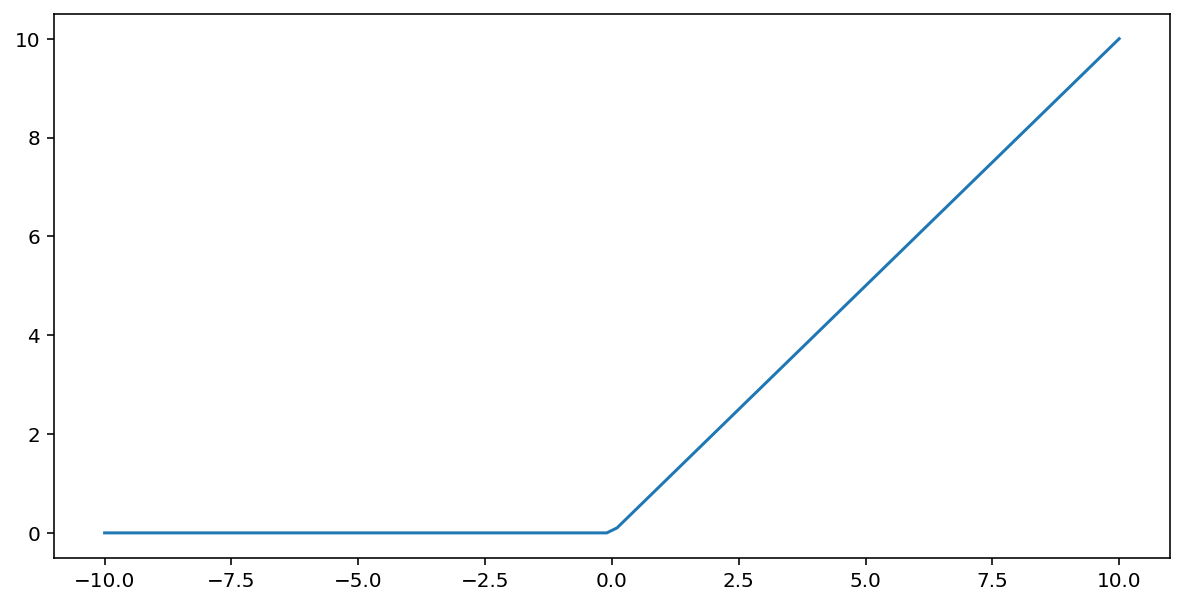
ฟังก์ชันการกระตุ้น แบบหน่วยเชิงเส้นปรับแก้ (หรือ ReLU ) จะแปลงเอาต์พุตโดยใช้อัลกอริทึมต่อไปนี้:
- ถ้าค่าที่ป้อนเข้ามา $x$ น้อยกว่า 0 ให้ส่งค่า 0 กลับมา
- ถ้าค่าที่ป้อนเข้ามา $x$ มากกว่าหรือเท่ากับ 0 ให้ส่งค่าที่ป้อนเข้ามานั้นกลับ
ReLU สามารถแสดงทางคณิตศาสตร์ได้โดยใช้ฟังก์ชัน max():
นี่คือกราฟแสดงฟังก์ชันนี้:
โดยทั่วไปแล้ว ReLU มักทำงานได้ดีกว่าในฐานะฟังก์ชันกระตุ้นเมื่อเทียบกับฟังก์ชันเรียบๆ เช่น sigmoid หรือ tanh เนื่องจาก ReLU มีโอกาสเกิด ปัญหาการลดลงของเกรเดียนต์ (vanishing gradient problem) น้อยกว่าในระหว่าง การฝึกโครงข่ายประสาทเทียม นอกจากนี้ ReLU ยังคำนวณได้ง่ายกว่าฟังก์ชันเหล่านั้นอย่างมาก
ฟังก์ชันการเปิดใช้งานอื่นๆ
ในทางปฏิบัติ ฟังก์ชันทางคณิตศาสตร์ใดๆ ก็สามารถใช้เป็นฟังก์ชันกระตุ้นได้ สมมติว่า \(\sigma\) แสดงถึงฟังก์ชันการกระตุ้นของเรา ค่าของโหนดในเครือข่ายกำหนดโดยสูตรต่อไปนี้:
Keras มี ฟังก์ชันการเปิดใช้งานหลายอย่างให้ใช้งานได้ ทันที อย่างไรก็ตาม เรายังคงแนะนำให้เริ่มต้นด้วย ReLU
สรุป
วิดีโอต่อไปนี้เป็นการสรุปสิ่งที่คุณได้เรียนรู้มาแล้วทั้งหมดเกี่ยวกับวิธีการสร้างโครงข่ายประสาทเทียม:
ตอนนี้โมเดลของเรามีส่วนประกอบมาตรฐานทั้งหมดที่คนทั่วไปมักหมายถึงเมื่อพูดถึงโครงข่ายประสาทเทียม:
- กลุ่มของโหนด ซึ่งเปรียบเสมือนเซลล์ประสาท จัดเรียงเป็นชั้นๆ
- ชุดของค่าน้ำหนักและค่าไบแอสที่เรียนรู้มา ซึ่งแสดงถึงการเชื่อมต่อระหว่างแต่ละชั้นของโครงข่ายประสาทเทียมกับชั้นที่อยู่ด้านล่าง ชั้นที่อยู่ด้านล่างอาจเป็นชั้นโครงข่ายประสาทเทียมอีกชั้นหนึ่ง หรืออาจเป็นชั้นประเภทอื่นก็ได้
- ฟังก์ชันการกระตุ้นที่แปลงเอาต์พุตของแต่ละโหนดในเลเยอร์ เลเยอร์ต่างๆ อาจมีฟังก์ชันการกระตุ้นที่แตกต่างกัน
ข้อควรระวัง: โครงข่ายประสาทเทียมไม่ได้ดีกว่าการไขว้คุณลักษณะเสมอไป แต่โครงข่ายประสาทเทียมก็เป็นทางเลือกที่ยืดหยุ่นและใช้งานได้ดีในหลายกรณี
