La pérdida es una métrica numérica que describe qué tan incorrectas son las predicciones de un modelo. La pérdida mide la distancia entre las predicciones del modelo y las etiquetas reales. El objetivo de entrenar un modelo es minimizar la pérdida y reducirla a su valor más bajo posible.
En la siguiente imagen, puedes visualizar la pérdida como flechas dibujadas desde los puntos de datos hacia el modelo. Las flechas muestran qué tan lejos están las predicciones del modelo de los valores reales.

Figura 8. La pérdida se mide desde el valor real hasta el valor predicho.
Distancia de pérdida
En estadística y aprendizaje automático, la pérdida mide la diferencia entre los valores predichos y los reales. La pérdida se enfoca en la distancia entre los valores, no en la dirección. Por ejemplo, si un modelo predice 2, pero el valor real es 5, no nos importa que la pérdida sea negativa (2 – 5= –3). En cambio, nos interesa que la distancia entre los valores sea de 3. Por lo tanto, todos los métodos para calcular la pérdida quitan el signo.
Estos son los dos métodos más comunes para quitar el signo:
- Toma el valor absoluto de la diferencia entre el valor real y la predicción.
- Eleva al cuadrado la diferencia entre el valor real y la predicción.
Tipos de pérdidas
En la regresión lineal, hay cinco tipos principales de pérdida, que se describen en la siguiente tabla.
| Tipo de pérdida | Definición | Ecuación |
|---|---|---|
| Pérdida de L1 | Es la suma de los valores absolutos de la diferencia entre los valores predichos y los valores reales. | $ ∑ | valor\ real - valor\ predicho | $ |
| Error absoluto medio (MAE) | Es el promedio de las pérdidas de L1 en un conjunto de N ejemplos. | $ \frac{1}{N} ∑ | valor\ real - valor\ predicho | $ |
| Pérdida de L2 | Es la suma de la diferencia al cuadrado entre los valores predichos y los valores reales. | $ ∑(valor\ real - valor\ predicho)^2 $ |
| Error cuadrático medio (ECM) | Es el promedio de las pérdidas de L2 en un conjunto de N ejemplos. | $ \frac{1}{N} ∑ (valor\ real - valor\ predicho)^2 $ |
| Raíz cuadrada del error cuadrático medio (RECM) | Es la raíz cuadrada del error cuadrático medio (ECM). | $ \sqrt{\frac{1}{N} ∑ (valor\ real - valor\ predicho)^2} $ |
La diferencia funcional entre la pérdida L1 y la pérdida L2 (o entre el MAE/RECM y el ECM) es la elevación al cuadrado. Cuando la diferencia entre la predicción y la etiqueta es grande, elevar al cuadrado hace que la pérdida sea aún mayor. Cuando la diferencia es pequeña (menor que 1), elevar al cuadrado hace que la pérdida sea aún menor.
Las métricas de pérdida, como el MAE y el RECM, pueden ser preferibles a la pérdida L2 o el ECM en algunos casos de uso porque tienden a ser más fáciles de interpretar para los humanos, ya que miden el error con la misma escala que el valor predicho del modelo.
Cuando proceses varios ejemplos a la vez, te recomendamos que calcules el promedio de las pérdidas en todos los ejemplos, ya sea que uses MAE, ECM o RECM.
Ejemplo de cálculo de pérdida
En la sección anterior, creamos el siguiente modelo para predecir la eficiencia del combustible según el peso del automóvil:
- Modelo: $ y' = 34 + (-4.6)(x_1) $
- Peso: USD –4.6
- Sesgo: USD 34
Si el modelo predice que un automóvil de 1,075 kg rinde 9.8 km/l, pero en realidad rinde 10.2 km/l, calcularíamos la pérdida de L2 de la siguiente manera:
| Valor | Ecuación | Resultado |
|---|---|---|
| Predicción | $\small{bias + (peso * valor\ del\ atributo)}$ $\small{34 + (-4.6*2.37)}$ |
$\small{23.1}$ |
| Valor real | $ \small{ label } $ | $ \small{ 24 } $ |
| Pérdida L2 | $ \small{ (valor\ real - valor\ predicho)^2 } $ $\small{ (24 - 23.1)^2 }$ |
$\small{0.81}$ |
En este ejemplo, la pérdida L2 para ese único dato es 0.81.
Cómo elegir una función de pérdida
Decidir si usar el MAE o el ECM puede depender del conjunto de datos y de la forma en que deseas controlar ciertas predicciones. La mayoría de los valores de atributos de un conjunto de datos suelen encontrarse dentro de un rango distinto. Por ejemplo, los automóviles suelen pesar entre 900 y 2,200 kg, y rinden entre 3 y 20 km por litro. Un automóvil de 3,600 kg o uno que recorre 160 km por galón se encuentran fuera del rango típico y se considerarían valores atípicos.
Un valor atípico también puede referirse a qué tan alejadas están las predicciones de un modelo de los valores reales. Por ejemplo, 1,360 kg se encuentra dentro del rango de peso típico de un automóvil, y 64 km por litro se encuentra dentro del rango de eficiencia de combustible típico. Sin embargo, un automóvil de 1,360 kg que rinde 64 km por galón sería un valor atípico en términos de la predicción del modelo, ya que este predeciría que un automóvil de 1,360 kg rendiría alrededor de 32 km por galón.
Cuando elijas la mejor función de pérdida, ten en cuenta cómo quieres que el modelo trate los valores atípicos. Por ejemplo, el ECM desplaza el modelo más hacia los valores atípicos, mientras que el MAE no lo hace. La pérdida L2 genera una penalización mucho mayor para un valor atípico que la pérdida L1. Por ejemplo, las siguientes imágenes muestran un modelo entrenado con MAE y un modelo entrenado con ECM. La línea roja representa un modelo completamente entrenado que se usará para hacer predicciones. Los valores atípicos están más cerca del modelo entrenado con ECM que del modelo entrenado con MAE.

Figura 9. La pérdida del ECM acerca el modelo a los valores atípicos.
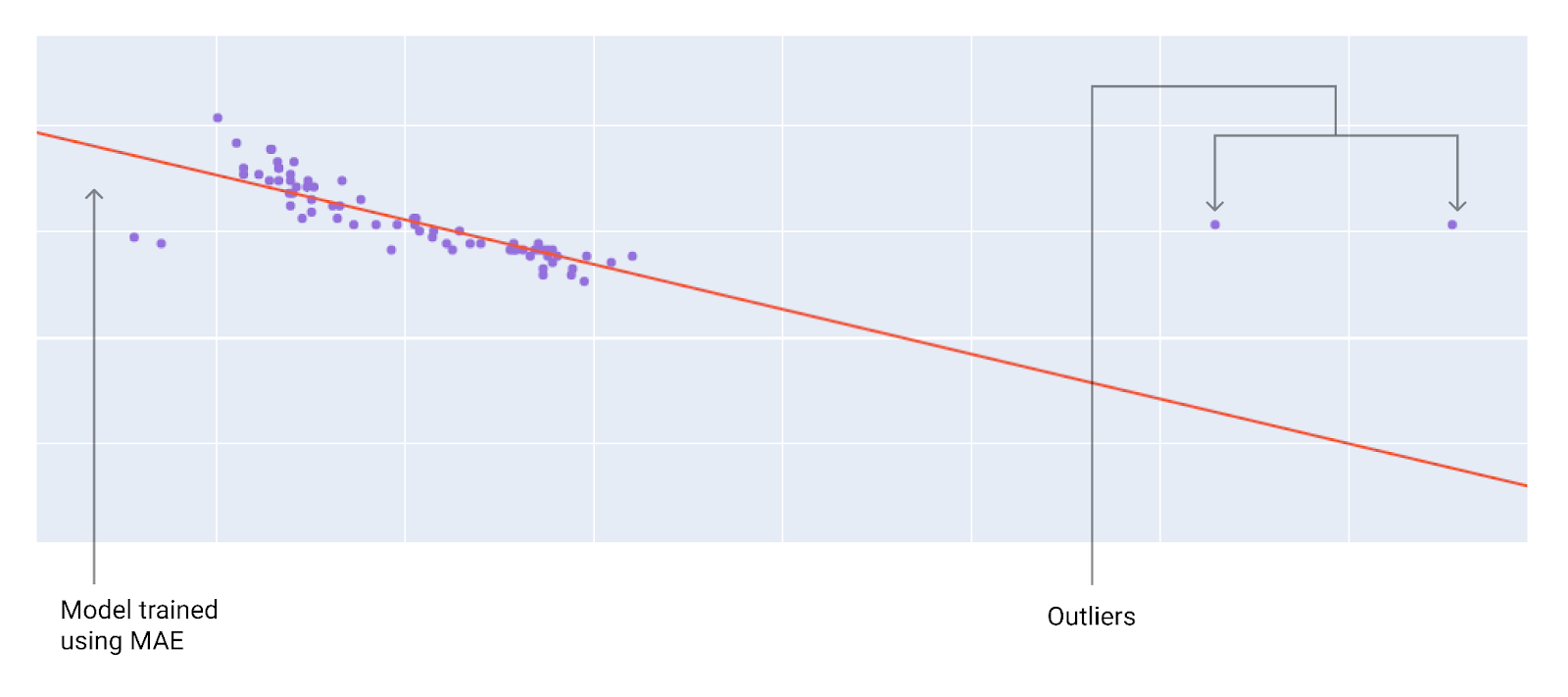
Figura 10: La pérdida del MAE mantiene el modelo más alejado de los valores atípicos.
Ten en cuenta la relación entre el modelo y los datos:
ECM. El modelo está más cerca de los valores atípicos, pero más lejos de la mayoría de los otros puntos de datos.
MAE. El modelo está más lejos de los valores atípicos, pero más cerca de la mayoría de los otros puntos de datos.
Comprueba tus conocimientos
Considera los siguientes dos diagramas de un ajuste de modelo lineal a un conjunto de datos:

|

|