エンベディングとは、データをエンベディング空間におけるベクトルで表現したものです。一般に、モデルは、初期データベクトルの高次元空間を下位次元空間に投影することで、潜在的なエンベディングを見つけ出します。 高次元データと低次元データに関する議論については、カテゴリデータ モジュールをご覧ください。
エンベディングを使うと、前のセクションで取り上げた食事のアイテムのようなスパース ベクトルで表現される大規模な特徴ベクトルに対して、ML をより簡単に行えるようになります。エンベディング空間でのアイテム同士の相対位置がセマンティックな関係を持つこともありますが、下位次元空間を見つけ出すプロセスや空間内での相対位置は人間には解釈できない場合が多く、得られたエンベディングも直感的に理解するのは困難です。
とはいえ、エンベディング ベクトルが情報をどのように表現しているかを人間が理解できるようにするため、次のような一次元の例で考えてみましょう。ホットドッグ、ピザ、サラダ、シャワルマ、ボルシチの各料理を、「最もサンドイッチに似ていない」から「最もサンドイッチに似ている」のスケールで並べます。ここでは「サンドイッチらしさ」という想像上の尺度を唯一の次元とします。

アップル シュトルーデルはこの軸のどこに当てはまるでしょうか。おそらく、hot dog と shawarma の間あたりでしょう。しかし、アップル シュトルーデルには、「甘さ」や「デザートらしさ」といった別の次元もあり、他の料理とは大きく異なるようにも見えます。
次の図では、その違いを「デザートらしさ」という次元を加えることで可視化しています。
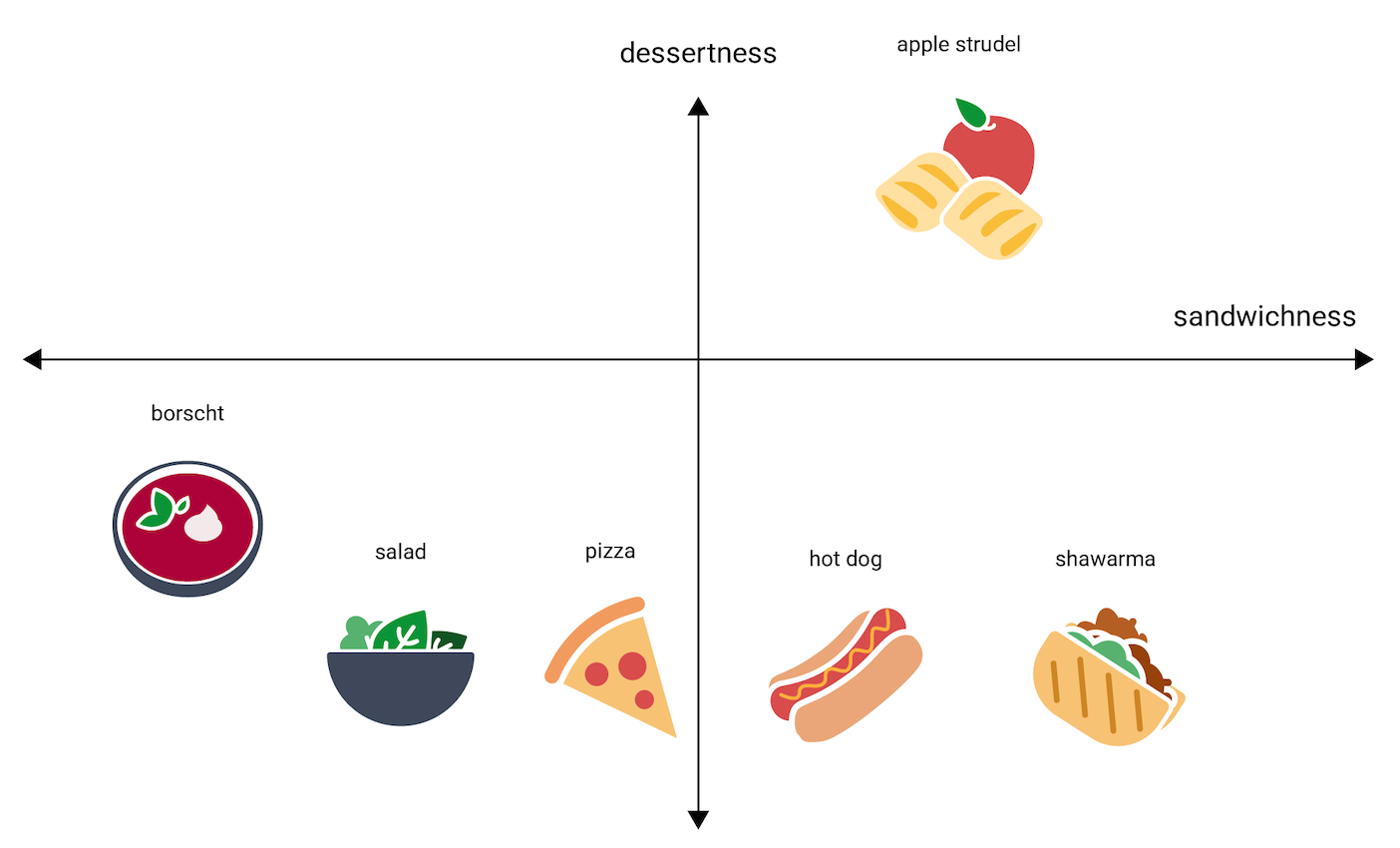
エンベディングは、n 次元空間にある各アイテムを n 個の浮動小数点数で表します(通常は -1~1 または 0~1 の範囲)。 図 3 のエンベディングは、1 次元空間にある各料理を 1 つの座標で表しており、図 4 のエンベディングは、2 次元空間にある各料理を 2 つの座標で表しています。図 4 で「アップル シュトルーデル」はグラフの右上の象限にあり、点(0.5, 0.3)を割り当てられます。一方、「ホットドッグ」は右下の象限にあり、点(0.2, –0.5)を割り当てられます。
エンベディングでは、任意の 2 つのアイテム間の距離を数学的に計算でき、その距離を、それら 2 つのアイテムの相対的な類似性の尺度として解釈できます。たとえば、図 4 の shawarma と hot dog は互いに近いため、互いに遠い apple strudel と borscht よりも、モデルの中ではより関連性の高いデータとして表現されていると言えます。
また、図 4 の 2 次元空間では、1 次元空間の場合よりも apple strudel と shawarma や hot dog との距離がかなり遠くなることにも注目してください。これは直感と一致します。apple strudel は、ホットドッグとシャワルマ間の類似度と比べると、ホットドッグやシャワルマとそれほど似ていません。
ここで、ボルシチについて考えます。ボルシチは他のアイテムよりも液体っぽいという特徴があります。この点を踏まえると、「液体らしさ」、つまりその料理がどの程度液体であるか、という 3 つ目の次元が浮かび上がります。 この次元を追加すると、各アイテムを以下のように 3 次元で可視化できます。

この 3 次元空間内で、湯円はどこに当てはまるでしょうか。湯円は、ボルシチのようにスープっぽく、アップル シュトルーデルのように甘いデザートで、間違いなくサンドイッチではありません。たとえば、以下のような配置が考えられます。

これら 3 つの次元で表現される情報量に注目してください。 4 次元、5 次元、それ以上の次元空間は可視化が難しいですが、料理の肉の量や焼き加減といった別の次元を追加することもできます。
実世界のエンベディング空間
実世界のエンベディング空間は d 次元(d は 3 よりはるかに大きいが、元のデータの次元よりは小さい)であり、データポイント間の関係は、上記の例のように直感的でわかりやすいとは限りません(ワード エンベディングでは、d は通常 256、512、1,024 のいずれかです1)。
実務では通常、ML 担当者が特定のタスクとエンベディングの次元数を設定し、そのエンベディング空間内でトレーニング サンプルどうしが近くなるように、モデルが配置を調整します。または、d が固定されていない場合は、モデルが次元数を調整します。個々の次元が、「デザートらしさ」や「液体らしさ」のようにわかりやすい意味を持つことは稀です。「意味」を推測できる場合もありますが、常にそうとは限りません。
エンベディングは通常、タスクに固有のものであり、タスクが異なればエンベディングも異なります。たとえば、ベジタリアン向けであるかないかの分類モデルで生成されたエンベディングは、時間帯や季節に基づいて料理を提案するモデルで生成されたエンベディングとは異なるものになります。仮に「シリアル」と「朝食用ソーセージ」なら、時間帯モデルのエンベディング空間では近い位置にあっても、ベジタリアン向けであるかないかのモデルのエンベディング空間では遠く離れた位置になるでしょう。
静的エンベディング
エンベディングはタスクごとに異なりますが、単語のコンテキストを推測するタスクには、一般的な適用性があります。単語のコンテキストを推測するようトレーニングされたモデルでは、似たようなコンテキストに出現する単語どうしは意味的に関連していると想定します。たとえば、トレーニング データに「彼らはロバに乗ってグランド キャニオンに降りていった」という文章と「彼らは馬に乗って峡谷に降りていった」という文章がある場合、このデータは「馬」が「ロバ」と類似したコンテキストで出現することを示唆しています。意味的類似性に基づいたエンベディングは、多くの一般的な言語タスクでうまく機能することがわかっています。
例としては古く、大部分が他のモデルに置き換えられているものの、現在でも説明の際に役立つのが word2vec モデルです。word2vec はドキュメントのコーパスでトレーニングを行い、単語ごとに単一のグローバル エンベディングを取得します。それぞれの単語やデータポイントに単一のエンベディング ベクトルがある場合、これを静的エンベディングと呼びます。以下の動画では、word2vec トレーニングを簡単に示した図について解説しています。
調査によると、これらの静的なエンベディングは、一度トレーニングされると、ある程度のセマンティック情報、特に単語間の関係性をエンコードすることがわかっています。 つまり、類似のコンテキストで使われる単語は、エンベディング空間で互いに近くなります。生成されるエンベディング ベクトルは、トレーニングに使用されるコーパスによって異なります。 詳しくは、T. Mikolov 他(2013)「Efficient Estimation of Word Representations in Vector Space」をご覧ください。
-
François Chollet、Deep Learning with Python (Shelter Island、NY: Manning、2017)、6.1.2. ↩