Neste tutorial, vamos apresentar a metodologia de modelagem de distribuição de espécies usando o Google Earth Engine. Vamos apresentar uma breve visão geral da modelagem de distribuição de espécies, seguida pelo processo de previsão e análise do habitat de uma espécie de ave ameaçada de extinção conhecida como pita-fada (nome científico: Pitta nympha).
Me execute primeiro
Execute a célula a seguir para inicializar a API. A saída vai conter instruções sobre como conceder acesso do notebook ao Earth Engine usando sua conta.
import ee
# Trigger the authentication flow.
ee.Authenticate()
# Initialize the library.
ee.Initialize(project='my-project')
Uma breve visão geral da modelagem de distribuição de espécies
Vamos explorar o que são modelos de distribuição de espécies, as vantagens de usar o Google Earth Engine para o processamento deles, os dados necessários para os modelos e como o fluxo de trabalho é estruturado.
O que é a estimativa de distribuição de espécies?
A modelagem de distribuição de espécies (SDM, na sigla em inglês) é a metodologia mais comum usada para estimar a distribuição geográfica real ou potencial de uma espécie. Isso envolve caracterizar as condições ambientais adequadas para uma espécie específica e identificar onde essas condições adequadas estão distribuídas geograficamente.
A SDM surgiu como um componente crucial do planejamento de conservação nos últimos anos, e várias técnicas de modelagem foram desenvolvidas para essa finalidade. A implementação de SDM no Google Earth Engine (GEE abaixo) oferece fácil acesso a dados ambientais em grande escala, além de recursos de computação avançados e suporte a algoritmos de machine learning, permitindo uma modelagem rápida.
Dados obrigatórios para o SDM
Normalmente, a SDM usa a relação entre registros de ocorrência de espécies conhecidas e variáveis ambientais para identificar as condições em que uma população pode sobreviver. Em outras palavras, são necessários dois tipos de dados de entrada do modelo:
- Registros de ocorrência de espécies conhecidas
- Várias variáveis ambientais
Esses dados são inseridos em algoritmos para identificar condições ambientais associadas à presença de espécies.
Fluxo de trabalho do SDM usando o GEE
O fluxo de trabalho para SDM usando o GEE é o seguinte:
- Coleta e pré-processamento de dados de ocorrência de espécies
- Definição da área de interesse
- Adição de variáveis de ambiente do GEE
- Geração de dados de pseudoausência
- Ajuste e previsão de modelos
- Importância da variável e avaliação de acurácia
Previsão e análise de habitat usando o GEE
A pitta-fada (Pitta nympha) será usada como um estudo de caso para demonstrar a aplicação do SDM baseado no GEE. Embora essa espécie específica tenha sido selecionada para um exemplo, os pesquisadores podem aplicar a metodologia a qualquer espécie de interesse com pequenas modificações no código-fonte fornecido.
A pita-fada é uma migrante de verão e de passagem rara na Coreia do Sul, cuja área de distribuição está se expandindo devido ao aquecimento climático recente na península coreana. Ela é classificada como uma espécie rara, vida selvagem ameaçada de extinção da classe II, Monumento Natural nº 204, avaliada como Regionalmente Extinta (RE) na Lista Vermelha Nacional e Vulnerável (VU) de acordo com as categorias da IUCN.
A realização de SDM para o planejamento de conservação da pitta-fada parece ser muito valiosa. Agora, vamos fazer a previsão e a análise de habitat usando o GEE.
Primeiro, as bibliotecas Python são importadas.A instrução import traz todo o conteúdo de um módulo, enquanto a instrução from import permite a importação de objetos específicos de um módulo.
# Import libraries
import geemap
import geemap.colormaps as cm
import pandas as pd, geopandas as gpd
import numpy as np, matplotlib.pyplot as plt
import os, requests, math, random
from ipyleaflet import TileLayer
from statsmodels.stats.outliers_influence import variance_inflation_factor
Coleta e pré-processamento de dados de ocorrência de espécies
Agora, vamos coletar dados de ocorrência para a pita-fada. Mesmo que você não tenha acesso a dados de ocorrência para a espécie de interesse, é possível obter dados de observação sobre espécies específicas usando a API do GBIF. A API do GBIF (link em inglês) é uma interface que permite o acesso aos dados de distribuição de espécies fornecidos pelo GBIF. Com ela, os usuários podem pesquisar, filtrar e baixar dados, além de adquirir várias informações relacionadas a espécies.
No código abaixo, a variável species_name recebe o nome científico da espécie (por exemplo, Pitta nympha para pita-fada), e a variável country_code recebe o código do país (por exemplo, KR para Coreia do Sul). A variável base_url armazena o endereço da API do GBIF. params é um dicionário que contém parâmetros a serem usados na solicitação de API:
scientificName: define o nome científico da espécie a ser pesquisada.country: limita a pesquisa a um país específico.hasCoordinate: garante que apenas dados com coordenadas (verdadeiro) sejam pesquisados.basisOfRecord: escolhe apenas registros de observação humana (HUMAN_OBSERVATION).limit: define o número máximo de resultados retornados como 10.000.
def get_gbif_species_data(species_name, country_code):
"""
Retrieves observational data for a specific species using the GBIF API and returns it as a pandas DataFrame.
Parameters:
species_name (str): The scientific name of the species to query.
country_code (str): The country code of the where the observation data will be queried.
Returns:
pd.DataFrame: A pandas DataFrame containing the observational data.
"""
base_url = "https://api.gbif.org/v1/occurrence/search"
params = {
"scientificName": species_name,
"country": country_code,
"hasCoordinate": "true",
"basisOfRecord": "HUMAN_OBSERVATION",
"limit": 10000,
}
try:
response = requests.get(base_url, params=params)
response.raise_for_status() # Raises an exception for a response error.
data = response.json()
occurrences = data.get("results", [])
if occurrences: # If data is present
df = pd.json_normalize(occurrences)
return df
else:
print("No data found for the given species and country code.")
return pd.DataFrame() # Returns an empty DataFrame
except requests.RequestException as e:
print(f"Request failed: {e}")
return pd.DataFrame() # Returns an empty DataFrame in case of an exception
Usando os parâmetros definidos anteriormente, consultamos a API do GBIF para registros de observação da pita-fada (Pitta nympha) e carregamos os resultados em um DataFrame para verificar a primeira linha. Um DataFrame é uma estrutura de dados para processar dados formatados em tabelas, consistindo em linhas e colunas. Se necessário, o DataFrame pode ser salvo como um arquivo CSV e lido novamente.
# Retrieve Fairy Pitta data
df = get_gbif_species_data("Pitta nympha", "KR")
"""
# Save DataFrame to CSV and read back in.
df.to_csv("pitta_nympha_data.csv", index=False)
df = pd.read_csv("pitta_nympha_data.csv")
"""
df.head(1) # Display the first row of the DataFrame
Em seguida, convertemos o DataFrame em um GeoDataFrame que inclui uma coluna para informações geográficas (geometry) e verificamos a primeira linha. Um GeoDataFrame pode ser salvo como um arquivo GeoPackage (*.gpkg) e lido novamente.
# Convert DataFrame to GeoDataFrame
gdf = gpd.GeoDataFrame(
df,
geometry=gpd.points_from_xy(df.decimalLongitude,
df.decimalLatitude),
crs="EPSG:4326"
)[["species", "year", "month", "geometry"]]
"""
# Convert GeoDataFrame to GeoPackage (requires pycrs module)
%pip install -U -q pycrs
gdf.to_file("pitta_nympha_data.gpkg", driver="GPKG")
gdf = gpd.read_file("pitta_nympha_data.gpkg")
"""
gdf.head(1) # Display the first row of the GeoDataFrame
Desta vez, criamos uma função para visualizar a distribuição de dados por ano e mês do GeoDataFrame e mostrar como um gráfico, que pode ser salvo como um arquivo de imagem. O uso de um mapa de calor permite entender rapidamente a frequência de ocorrência de espécies por ano e mês, fornecendo uma visualização intuitiva das mudanças e padrões temporais nos dados. Isso permite identificar padrões temporais e variações sazonais nos dados de ocorrência de espécies, além de detectar rapidamente outliers ou problemas de qualidade nos dados.
# Yearly and monthly data distribution heatmap
def plot_heatmap(gdf, h_size=8):
statistics = gdf.groupby(["month", "year"]).size().unstack(fill_value=0)
# Heatmap
plt.figure(figsize=(h_size, h_size - 6))
heatmap = plt.imshow(
statistics.values, cmap="YlOrBr", origin="upper", aspect="auto"
)
# Display values above each pixel
for i in range(len(statistics.index)):
for j in range(len(statistics.columns)):
plt.text(
j, i, statistics.values[i, j], ha="center", va="center", color="black"
)
plt.colorbar(heatmap, label="Count")
plt.title("Monthly Species Count by Year")
plt.xlabel("Year")
plt.ylabel("Month")
plt.xticks(range(len(statistics.columns)), statistics.columns)
plt.yticks(range(len(statistics.index)), statistics.index)
plt.tight_layout()
plt.savefig("heatmap_plot.png")
plt.show()
plot_heatmap(gdf)
Os dados de 1995 são muito esparsos, com lacunas significativas em comparação com outros anos. Além disso, os meses de agosto e setembro têm amostras limitadas e características sazonais diferentes em comparação com outros períodos. Excluir esses dados pode contribuir para melhorar a estabilidade e a capacidade preditiva do modelo.
No entanto, é importante observar que a exclusão de dados pode melhorar a capacidade de generalização do modelo, mas também pode levar à perda de informações valiosas relevantes para os objetivos da pesquisa. Portanto, essas decisões precisam ser tomadas com cuidado.
# Filtering data by year and month
filtered_gdf = gdf[
(~gdf['year'].eq(1995)) &
(~gdf['month'].between(8, 9))
]
Agora, o GeoDataFrame filtrado é convertido em um objeto do Google Earth Engine.
# Convert GeoDataFrame to Earth Engine object
data_raw = geemap.geopandas_to_ee(filtered_gdf)
Em seguida, vamos definir o tamanho do pixel raster dos resultados do SDM como resolução de 1 km.
# Spatial resolution setting (meters)
grain_size = 1000
Quando vários pontos de ocorrência estão presentes no mesmo pixel raster de resolução de 1 km, é muito provável que eles compartilhem as mesmas condições ambientais no mesmo local geográfico. Usar esses dados diretamente na análise pode introduzir viés nos resultados.
Em outras palavras, precisamos limitar o possível impacto do viés de amostragem geográfica. Para isso, vamos manter apenas um local em cada pixel de 1 km e remover todos os outros, permitindo que o modelo reflita de maneira mais objetiva as condições ambientais.
def remove_duplicates(data, grain_size):
# Select one occurrence record per pixel at the chosen spatial resolution
random_raster = ee.Image.random().reproject("EPSG:4326", None, grain_size)
rand_point_vals = random_raster.sampleRegions(
collection=ee.FeatureCollection(data), geometries=True
)
return rand_point_vals.distinct("random")
data = remove_duplicates(data_raw, grain_size)
# Before selection and after selection
print("Original data size:", data_raw.size().getInfo())
print("Final data size:", data.size().getInfo())
A visualização que compara o viés de amostragem geográfica antes (em azul) e depois (em vermelho) do pré-processamento é mostrada abaixo. Para facilitar a comparação, o mapa foi centralizado na área com uma alta concentração de coordenadas de ocorrência de pita-fada no Parque Nacional Hallasan.
# Visualization of geographic sampling bias before (blue) and after (red) preprocessing
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
# Add the random raster layer
random_raster = ee.Image.random().reproject("EPSG:4326", None, grain_size)
Map.addLayer(
random_raster,
{"min": 0, "max": 1, "palette": ["black", "white"], "opacity": 0.5},
"Random Raster",
)
# Add the original data layer in blue
Map.addLayer(data_raw, {"color": "blue"}, "Original data")
# Add the final data layer in red
Map.addLayer(data, {"color": "red"}, "Final data")
# Set the center of the map to the coordinates
Map.setCenter(126.712, 33.516, 14)
Map
Definição da área de interesse
Definir a área de interesse (AOI, na sigla em inglês, abaixo) se refere ao termo usado por pesquisadores para indicar a área geográfica que eles querem analisar. Ele tem um significado semelhante ao termo "Área de estudo".
Nesse contexto, extraímos a caixa delimitadora da geometria da camada de pontos de ocorrência e criamos um buffer de 50 quilômetros ao redor dela (com uma tolerância máxima de 1.000 metros) para definir a AOI.
# Define the AOI
aoi = data.geometry().bounds().buffer(distance=50000, maxError=1000)
# Add the AOI to the map
outline = ee.Image().byte().paint(
featureCollection=aoi, color=1, width=3)
Map.remove_layer("Random Raster")
Map.addLayer(outline, {'palette': 'FF0000'}, "AOI")
Map.centerObject(aoi, 6)
Map
Adição de variáveis de ambiente do GEE
Agora, vamos adicionar variáveis ambientais à análise. O GEE oferece uma ampla variedade de conjuntos de dados para variáveis ambientais, como temperatura, precipitação, elevação, cobertura do solo e terreno. Esses conjuntos de dados nos permitem analisar de forma abrangente vários fatores que podem influenciar as preferências de habitat da pitta-fada.
A seleção de variáveis ambientais do GEE na SDM precisa refletir as características de preferência de habitat da espécie. Para isso, é necessário fazer uma pesquisa e uma revisão da literatura sobre as preferências de habitat da pitta-fada. Este tutorial se concentra principalmente no fluxo de trabalho do SDM usando o GEE. Por isso, alguns detalhes mais complexos foram omitidos.
WorldClim V1 Bioclim: esse conjunto de dados fornece 19 variáveis bioclimáticas derivadas de dados mensais de temperatura e precipitação. Ele abrange o período de 1960 a 1991 e tem uma resolução de 927,67 metros.
# WorldClim V1 Bioclim
bio = ee.Image("WORLDCLIM/V1/BIO")
Elevação digital da NASA SRTM 30m: contém dados de elevação digital da Missão Topográfica por Radar do Ônibus Espacial (SRTM, na sigla em inglês). Os dados foram coletados principalmente por volta do ano 2000 e são fornecidos com uma resolução de aproximadamente 30 metros (1 arco-segundo). O código a seguir calcula as camadas de elevação, inclinação, aspecto e relevo dos dados do SRTM.
# NASA SRTM Digital Elevation 30m
terrain = ee.Algorithms.Terrain(ee.Image("USGS/SRTMGL1_003"))
Cobertura florestal global: cobertura de árvores global plurianual de 30 m: o conjunto de dados de campos contínuos de vegetação (VCF, na sigla em inglês) do Landsat estima a proporção de cobertura vegetal projetada verticalmente quando a altura da vegetação é superior a 5 metros. Esse conjunto de dados é fornecido para quatro períodos centrados nos anos 2000, 2005, 2010 e 2015, com uma resolução de 30 metros. Aqui, são usados os valores medianos desses quatro períodos.
# Global Forest Cover Change (GFCC) Tree Cover Multi-Year Global 30m
tcc = ee.ImageCollection("NASA/MEASURES/GFCC/TC/v3")
median_tcc = (
tcc.filterDate("2000-01-01", "2015-12-31")
.select(["tree_canopy_cover"], ["TCC"])
.median()
)
bio (variáveis bioclimáticas), terrain (topografia) e median_tcc (cobertura da copa das árvores) são combinadas em uma única imagem multibanda. A faixa elevation é selecionada em terrain, e um watermask é criado para locais em que elevation é maior que 0. Isso mascara regiões abaixo do nível do mar (por exemplo, o oceano) e prepara o pesquisador para analisar vários fatores ambientais da área de interesse de forma abrangente.
# Combine bands into a multi-band image
predictors = bio.addBands(terrain).addBands(median_tcc)
# Create a water mask
watermask = terrain.select('elevation').gt(0)
# Mask out ocean pixels and clip to the area of interest
predictors = predictors.updateMask(watermask).clip(aoi)
Quando variáveis preditoras altamente correlacionadas são incluídas juntas em um modelo, podem surgir problemas de multicolinearidade. A multicolinearidade é um fenômeno que ocorre quando há relações lineares fortes entre variáveis independentes em um modelo, o que leva à instabilidade na estimação dos coeficientes (pesos) do modelo. Essa instabilidade pode reduzir a confiabilidade do modelo e dificultar previsões ou interpretações para novos dados. Portanto, vamos considerar a multicolinearidade e continuar com o processo de seleção de variáveis preditoras.
Primeiro, vamos gerar 5.000 pontos aleatórios e extrair os valores da variável preditora da única imagem multibanda nesses pontos.
# Generate 5,000 random points
data_cor = predictors.sample(scale=grain_size, numPixels=5000, geometries=True)
# Extract predictor variable values
pvals = predictors.sampleRegions(collection=data_cor, scale=grain_size)
Vamos converter os valores de previsão extraídos para cada ponto em um DataFrame e verificar a primeira linha.
# Converting predictor values from Earth Engine to a DataFrame
pvals_df = geemap.ee_to_df(pvals)
pvals_df.head(1)
# Displaying the columns
columns = pvals_df.columns
print(columns)
Calcular os coeficientes de correlação de Spearman entre as variáveis preditoras e visualizar em um mapa de calor.
def plot_correlation_heatmap(dataframe, h_size=10, show_labels=False):
# Calculate Spearman correlation coefficients
correlation_matrix = dataframe.corr(method="spearman")
# Create a heatmap
plt.figure(figsize=(h_size, h_size-2))
plt.imshow(correlation_matrix, cmap='coolwarm', interpolation='nearest')
# Optionally display values on the heatmap
if show_labels:
for i in range(correlation_matrix.shape[0]):
for j in range(correlation_matrix.shape[1]):
plt.text(j, i, f"{correlation_matrix.iloc[i, j]:.2f}",
ha='center', va='center', color='white', fontsize=8)
columns = dataframe.columns.tolist()
plt.xticks(range(len(columns)), columns, rotation=90)
plt.yticks(range(len(columns)), columns)
plt.title("Variables Correlation Matrix")
plt.colorbar(label="Spearman Correlation")
plt.savefig('correlation_heatmap_plot.png')
plt.show()
# Plot the correlation heatmap of variables
plot_correlation_heatmap(pvals_df)
O coeficiente de correlação de Spearman é útil para entender as associações gerais entre variáveis preditoras, mas não avalia diretamente como várias variáveis interagem, especificamente detectando multicolinearidade.
O fator de inflação de variância (VIF, abaixo) é uma métrica estatística usada para avaliar a multicolinearidade e orientar a seleção de variáveis. Ele indica o grau de relação linear de cada variável independente com as outras variáveis independentes, e valores altos de VIF podem ser evidências de multicolinearidade.
Normalmente, quando os valores de VIF excedem 5 ou 10, isso sugere que a variável tem uma forte correlação com outras variáveis, o que pode comprometer a estabilidade e a capacidade de interpretação do modelo. Neste tutorial, um critério de valores de VIF menores que 10 foi usado para a seleção de variáveis. As seis variáveis a seguir foram selecionadas com base no VIF.
# Filter variables based on Variance Inflation Factor (VIF)
def filter_variables_by_vif(dataframe, threshold=10):
original_columns = dataframe.columns.tolist()
remaining_columns = original_columns[:]
while True:
vif_data = dataframe[remaining_columns]
vif_values = [
variance_inflation_factor(vif_data.values, i)
for i in range(vif_data.shape[1])
]
max_vif_index = vif_values.index(max(vif_values))
max_vif = max(vif_values)
if max_vif < threshold:
break
print(f"Removing '{remaining_columns[max_vif_index]}' with VIF {max_vif:.2f}")
del remaining_columns[max_vif_index]
filtered_data = dataframe[remaining_columns]
bands = filtered_data.columns.tolist()
print("Bands:", bands)
return filtered_data, bands
filtered_pvals_df, bands = filter_variables_by_vif(pvals_df)
# Variable Selection Based on VIF
predictors = predictors.select(bands)
# Plot the correlation heatmap of variables
plot_correlation_heatmap(filtered_pvals_df, h_size=6, show_labels=True)
Agora, vamos visualizar as seis variáveis preditoras selecionadas no mapa.
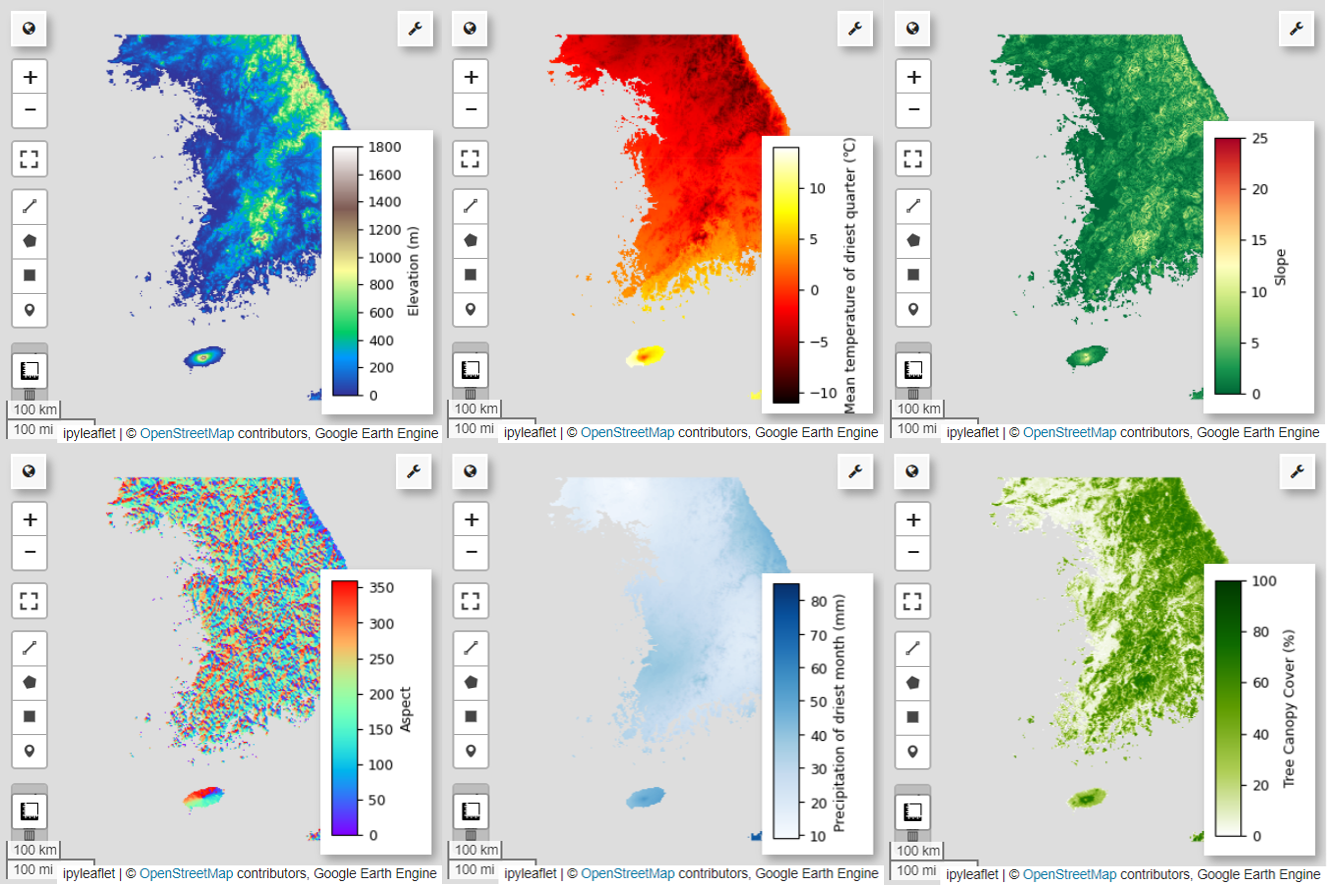
Use o código a seguir para conferir as paletas disponíveis para visualização de mapas. Por exemplo, a paleta terrain tem esta aparência.
cm.plot_colormaps(width=8.0, height=0.2)
cm.plot_colormap('terrain', width=8.0, height=0.2, orientation='horizontal')
# Elevation layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['elevation'], 'min': 0, 'max': 1800, 'palette': cm.palettes.terrain}
Map.addLayer(predictors, vis_params, 'elevation')
Map.add_colorbar(vis_params, label="Elevation (m)", orientation="vertical", layer_name="elevation")
Map.centerObject(aoi, 6)
Map
# Calculate the minimum and maximum values for bio09
min_max_val = (
predictors.select("bio09")
.multiply(0.1)
.reduceRegion(reducer=ee.Reducer.minMax(), scale=1000)
.getInfo()
)
# bio09 (Mean temperature of driest quarter) layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"min": math.floor(min_max_val["bio09_min"]),
"max": math.ceil(min_max_val["bio09_max"]),
"palette": cm.palettes.hot,
}
Map.addLayer(predictors.select("bio09").multiply(0.1), vis_params, "bio09")
Map.add_colorbar(
vis_params,
label="Mean temperature of driest quarter (℃)",
orientation="vertical",
layer_name="bio09",
)
Map.centerObject(aoi, 6)
Map
# Slope layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['slope'], 'min': 0, 'max': 25, 'palette': cm.palettes.RdYlGn_r}
Map.addLayer(predictors, vis_params, 'slope')
Map.add_colorbar(vis_params, label="Slope", orientation="vertical", layer_name="slope")
Map.centerObject(aoi, 6)
Map
# Aspect layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['aspect'], 'min': 0, 'max': 360, 'palette': cm.palettes.rainbow}
Map.addLayer(predictors, vis_params, 'aspect')
Map.add_colorbar(vis_params, label="Aspect", orientation="vertical", layer_name="aspect")
Map.centerObject(aoi, 6)
Map
# Calculate the minimum and maximum values for bio14
min_max_val = (
predictors.select("bio14")
.reduceRegion(reducer=ee.Reducer.minMax(), scale=1000)
.getInfo()
)
# bio14 (Precipitation of driest month) layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"bands": ["bio14"],
"min": math.floor(min_max_val["bio14_min"]),
"max": math.ceil(min_max_val["bio14_max"]),
"palette": cm.palettes.Blues,
}
Map.addLayer(predictors, vis_params, "bio14")
Map.add_colorbar(
vis_params,
label="Precipitation of driest month (mm)",
orientation="vertical",
layer_name="bio14",
)
Map.centerObject(aoi, 6)
Map
# TCC layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"bands": ["TCC"],
"min": 0,
"max": 100,
"palette": ["ffffff", "afce56", "5f9c00", "0e6a00", "003800"],
}
Map.addLayer(predictors, vis_params, "TCC")
Map.add_colorbar(
vis_params, label="Tree Canopy Cover (%)", orientation="vertical", layer_name="TCC"
)
Map.centerObject(aoi, 6)
Map
Geração de dados de pseudoausência
No processo de SDM, a seleção de dados de entrada para uma espécie é abordada principalmente usando dois métodos:
Método de presença-plano de fundo: compara os locais em que uma espécie específica foi observada (presença) com outros locais em que ela não foi observada (plano de fundo). Nesse caso, os dados de segundo plano não significam necessariamente áreas onde a espécie não existe, mas sim são configurados para refletir as condições ambientais gerais da área de estudo. Ele é usado para distinguir ambientes adequados em que a espécie pode existir de ambientes menos adequados.
Método de presença-ausência: compara locais onde a espécie foi observada (presença) com locais onde ela definitivamente não foi observada (ausência). Aqui, os dados de ausência representam locais específicos em que se sabe que a espécie não existe. Ela não reflete as condições ambientais gerais da área de estudo, mas sim indica locais onde se estima que a espécie não exista.
Na prática, é difícil coletar dados de ausência verdadeiros. Por isso, dados de pseudoausência gerados artificialmente são usados com frequência. No entanto, é importante reconhecer as limitações e os possíveis erros desse método, já que os pontos de pseudoausência gerados artificialmente podem não refletir com precisão as áreas de ausência real.
A escolha entre esses dois métodos depende da disponibilidade de dados, dos objetivos da pesquisa, da acurácia e da confiabilidade do modelo, além de tempo e recursos. Aqui, vamos usar dados de ocorrência coletados do GBIF e dados de pseudoausência gerados artificialmente para modelar usando o método "Presença-Ausência".
A geração de dados de pseudoausência será feita usando a "abordagem de criação de perfil ambiental", e as etapas específicas são as seguintes:
Classificação ambiental usando clustering k-means: o algoritmo de clustering k-means, com base na distância euclidiana, será usado para dividir os pixels na área de estudo em dois clusters. Um cluster vai representar áreas com características ambientais semelhantes a 100 locais de presença selecionados aleatoriamente, enquanto o outro vai representar áreas com características diferentes.
Geração de dados de pseudoausência em clusters diferentes: no segundo cluster identificado na primeira etapa (que tem características ambientais diferentes dos dados de presença), serão criados pontos de pseudoausência gerados aleatoriamente. Esses pontos de pseudoausência representam locais onde não se espera que a espécie exista.
# Randomly select 100 locations for occurrence
pvals = predictors.sampleRegions(
collection=data.randomColumn().sort('random').limit(100),
properties=[],
scale=grain_size
)
# Perform k-means clustering
clusterer = ee.Clusterer.wekaKMeans(
nClusters=2,
distanceFunction="Euclidean"
).train(pvals)
cl_result = predictors.cluster(clusterer)
# Get cluster ID for locations similar to occurrence
cl_id = cl_result.sampleRegions(
collection=data.randomColumn().sort('random').limit(200),
properties=[],
scale=grain_size
)
# Define non-occurrence areas in dissimilar clusters
cl_id = ee.FeatureCollection(cl_id).reduceColumns(ee.Reducer.mode(),['cluster'])
cl_id = ee.Number(cl_id.get('mode')).subtract(1).abs()
cl_mask = cl_result.select(['cluster']).eq(cl_id)
# Presence location mask
presence_mask = data.reduceToImage(properties=['random'],
reducer=ee.Reducer.first()
).reproject('EPSG:4326', None,
grain_size).mask().neq(1).selfMask()
# Masking presence locations in non-occurrence areas and clipping to AOI
area_for_pa = presence_mask.updateMask(cl_mask).clip(aoi)
# Area for Pseudo-absence
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
Map.addLayer(area_for_pa, {'palette': 'black'}, 'AreaForPA')
Map.centerObject(aoi, 6)
Map
Ajuste e previsão de modelos
Agora vamos dividir os dados em dados de treinamento e dados de teste. Os dados de treinamento serão usados para encontrar os parâmetros ideais treinando o modelo, enquanto os dados de teste serão usados para avaliar o modelo treinado anteriormente. Um conceito importante a ser considerado nesse contexto é a autocorrelação espacial.
A autocorrelação espacial é um elemento essencial na SDM, associado à lei de Tobler. Ele incorpora o conceito de que "tudo está relacionado a tudo, mas coisas próximas estão mais relacionadas do que coisas distantes". A autocorrelação espacial representa a relação significativa entre a localização das espécies e as variáveis ambientais. No entanto, se houver autocorrelação espacial entre os dados de treinamento e teste, a independência entre os dois conjuntos de dados poderá ser comprometida. Isso afeta significativamente a avaliação da capacidade de generalização do modelo.
Um método para resolver esse problema é a técnica de validação cruzada de bloco espacial, que envolve dividir os dados em conjuntos de dados de treinamento e teste. Essa técnica envolve dividir os dados em vários blocos, usando cada um deles de forma independente como conjuntos de dados de treinamento e teste para reduzir o impacto da autocorrelação espacial. Isso aumenta a independência entre os conjuntos de dados, permitindo uma avaliação mais precisa da capacidade de generalização do modelo.
O procedimento específico é o seguinte:
- Criação de blocos espaciais: divida todo o conjunto de dados em blocos espaciais de tamanho igual (por exemplo, 50x50 km).
- Atribuição de conjuntos de treinamento e teste: cada bloco espacial é atribuído aleatoriamente ao conjunto de treinamento (70%) ou ao conjunto de teste (30%). Isso evita que o modelo faça um overfitting dos dados de áreas específicas e busca resultados mais generalizados.
- Validação cruzada iterativa: todo o processo é repetido n vezes (por exemplo, 10 vezes). Em cada iteração, os blocos são divididos aleatoriamente em conjuntos de treinamento e teste novamente, o que tem como objetivo melhorar a estabilidade e a confiabilidade do modelo.
- Geração de dados de pseudoausência: em cada iteração, os dados de pseudoausência são gerados aleatoriamente para avaliar a performance do modelo.
Scale = 50000
grid = watermask.reduceRegions(
collection=aoi.coveringGrid(scale=Scale, proj='EPSG:4326'),
reducer=ee.Reducer.mean()).filter(ee.Filter.neq('mean', None))
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
Map.addLayer(grid, {}, "Grid for spatial block cross validation")
Map.addLayer(outline, {'palette': 'FF0000'}, "Study Area")
Map.centerObject(aoi, 6)
Map
Agora podemos ajustar o modelo. Ajustar um modelo envolve entender os padrões nos dados e ajustar os parâmetros do modelo (pesos e vieses) de acordo. Esse processo permite que o modelo faça previsões mais precisas quando recebe novos dados. Para isso, definimos uma função chamada SDM() para ajustar o modelo.
Vamos usar o algoritmo Random Forest.
def sdm(x):
seed = ee.Number(x)
# Random block division for training and validation
rand_blk = ee.FeatureCollection(grid).randomColumn(seed=seed).sort("random")
training_grid = rand_blk.filter(ee.Filter.lt("random", split)) # Grid for training
testing_grid = rand_blk.filter(ee.Filter.gte("random", split)) # Grid for testing
# Presence points
presence_points = ee.FeatureCollection(data)
presence_points = presence_points.map(lambda feature: feature.set("PresAbs", 1))
tr_presence_points = presence_points.filter(
ee.Filter.bounds(training_grid)
) # Presence points for training
te_presence_points = presence_points.filter(
ee.Filter.bounds(testing_grid)
) # Presence points for testing
# Pseudo-absence points for training
tr_pseudo_abs_points = area_for_pa.sample(
region=training_grid,
scale=grain_size,
numPixels=tr_presence_points.size().add(300),
seed=seed,
geometries=True,
)
# Same number of pseudo-absence points as presence points for training
tr_pseudo_abs_points = (
tr_pseudo_abs_points.randomColumn()
.sort("random")
.limit(ee.Number(tr_presence_points.size()))
)
tr_pseudo_abs_points = tr_pseudo_abs_points.map(lambda feature: feature.set("PresAbs", 0))
te_pseudo_abs_points = area_for_pa.sample(
region=testing_grid,
scale=grain_size,
numPixels=te_presence_points.size().add(100),
seed=seed,
geometries=True,
)
# Same number of pseudo-absence points as presence points for testing
te_pseudo_abs_points = (
te_pseudo_abs_points.randomColumn()
.sort("random")
.limit(ee.Number(te_presence_points.size()))
)
te_pseudo_abs_points = te_pseudo_abs_points.map(lambda feature: feature.set("PresAbs", 0))
# Merge training and pseudo-absence points
training_partition = tr_presence_points.merge(tr_pseudo_abs_points)
testing_partition = te_presence_points.merge(te_pseudo_abs_points)
# Extract predictor variable values at training points
train_pvals = predictors.sampleRegions(
collection=training_partition,
properties=["PresAbs"],
scale=grain_size,
geometries=True,
)
# Random Forest classifier
classifier = ee.Classifier.smileRandomForest(
numberOfTrees=500,
variablesPerSplit=None,
minLeafPopulation=10,
bagFraction=0.5,
maxNodes=None,
seed=seed,
)
# Presence probability: Habitat suitability map
classifier_pr = classifier.setOutputMode("PROBABILITY").train(
train_pvals, "PresAbs", bands
)
classified_img_pr = predictors.select(bands).classify(classifier_pr)
# Binary presence/absence map: Potential distribution map
classifier_bin = classifier.setOutputMode("CLASSIFICATION").train(
train_pvals, "PresAbs", bands
)
classified_img_bin = predictors.select(bands).classify(classifier_bin)
return [
classified_img_pr,
classified_img_bin,
training_partition,
testing_partition,
], classifier_pr
Os blocos espaciais são divididos em 70% para treinamento e 30% para teste do modelo, respectivamente. Os dados de pseudoausência são gerados aleatoriamente em cada conjunto de treinamento e teste em todas as iterações. Como resultado, cada execução gera diferentes conjuntos de dados de presença e pseudoausência para treinamento e teste do modelo.
split = 0.7
numiter = 10
# Random Seed
runif = lambda length: [random.randint(1, 1000) for _ in range(length)]
items = runif(numiter)
# Fixed seed
# items = [287, 288, 553, 226, 151, 255, 902, 267, 419, 538]
results_list = [] # Initialize SDM results list
importances_list = [] # Initialize variable importance list
for item in items:
result, trained = sdm(item)
# Accumulate SDM results into the list
results_list.extend(result)
# Accumulate variable importance into the list
importance = ee.Dictionary(trained.explain()).get('importance')
importances_list.extend(importance.getInfo().items())
# Flatten the SDM results list
results = ee.List(results_list).flatten()
Agora podemos visualizar o mapa de adequação de habitat e o mapa de distribuição potencial para a pita-fada. Nesse caso, o mapa de adequação de habitat é criado usando a função mean() para calcular a média de cada local de pixel em todas as imagens, e o mapa de distribuição potencial é gerado usando a função mode() para determinar o valor mais frequente em cada local de pixel em todas as imagens.
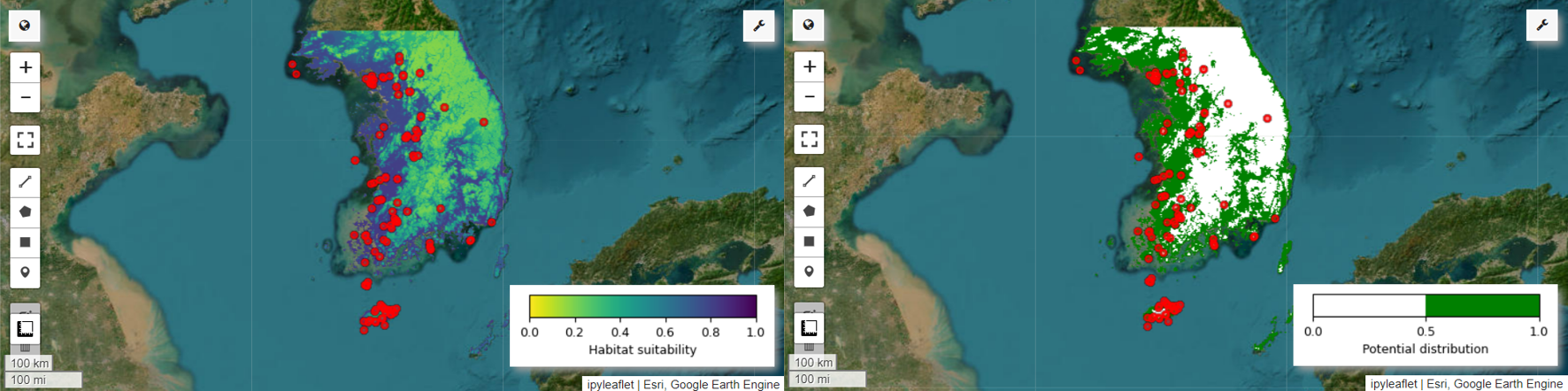
# Habitat suitability map
images = ee.List.sequence(
0, ee.Number(numiter).multiply(4).subtract(1), 4).map(
lambda x: results.get(x))
model_average = ee.ImageCollection.fromImages(images).mean()
Map = geemap.Map(layout={'height':'400px', 'width':'800px'}, basemap='Esri.WorldImagery')
vis_params = {
'min': 0,
'max': 1,
'palette': cm.palettes.viridis_r}
Map.addLayer(model_average, vis_params, 'Habitat suitability')
Map.add_colorbar(vis_params, label="Habitat suitability",
orientation="horizontal",
layer_name="Habitat suitability")
Map.addLayer(data, {'color':'red'}, 'Presence')
Map.centerObject(aoi, 6)
Map
# Potential distribution map
images2 = ee.List.sequence(1, ee.Number(numiter).multiply(4).subtract(1), 4).map(
lambda x: results.get(x)
)
distribution_map = ee.ImageCollection.fromImages(images2).mode()
Map = geemap.Map(
layout={"height": "400px", "width": "800px"}, basemap="Esri.WorldImagery"
)
vis_params = {"min": 0, "max": 1, "palette": ["white", "green"]}
Map.addLayer(distribution_map, vis_params, "Potential distribution")
Map.addLayer(data, {"color": "red"}, "Presence")
Map.add_colorbar(
vis_params,
label="Potential distribution",
discrete=True,
orientation="horizontal",
layer_name="Potential distribution",
)
Map.centerObject(data.geometry(), 6)
Map
Importância da variável e avaliação de acurácia
A floresta aleatória (ee.Classifier.smileRandomForest) é um dos métodos de aprendizado de ensemble, que opera construindo várias árvores de decisão para fazer previsões. Cada árvore de decisão aprende de forma independente com diferentes subconjuntos de dados, e os resultados são agregados para permitir previsões mais precisas e estáveis.
A importância da variável é uma medida que avalia o impacto de cada variável nas previsões do modelo de floresta aleatória. Vamos usar o importances_list definido anteriormente para calcular e imprimir a importância média da variável.
def plot_variable_importance(importances_list):
# Extract each variable importance value into a list
variables = [item[0] for item in importances_list]
importances = [item[1] for item in importances_list]
# Calculate the average importance for each variable
average_importances = {}
for variable in set(variables):
indices = [i for i, var in enumerate(variables) if var == variable]
average_importance = np.mean([importances[i] for i in indices])
average_importances[variable] = average_importance
# Sort the importances in descending order of importance
sorted_importances = sorted(average_importances.items(),
key=lambda x: x[1], reverse=False)
variables = [item[0] for item in sorted_importances]
avg_importances = [item[1] for item in sorted_importances]
# Adjust the graph size
plt.figure(figsize=(8, 4))
# Plot the average importance as a horizontal bar chart
plt.barh(variables, avg_importances)
plt.xlabel('Importance')
plt.ylabel('Variables')
plt.title('Average Variable Importance')
# Display values above the bars
for i, v in enumerate(avg_importances):
plt.text(v + 0.02, i, f"{v:.2f}", va='center')
# Adjust the x-axis range
plt.xlim(0, max(avg_importances) + 5) # Adjust to the desired range
plt.tight_layout()
plt.savefig('variable_importance.png')
plt.show()
plot_variable_importance(importances_list)
Usando os conjuntos de dados de teste, calculamos a AUC-ROC e a AUC-PR para cada execução. Em seguida, calculamos a AUC-ROC e a AUC-PR médias em n iterações.
AUC-ROC representa a área sob a curva do gráfico "Sensibilidade (recall) x 1-especificidade", ilustrando a relação entre sensibilidade e especificidade à medida que o limite muda. A especificidade é baseada em todas as não ocorrências observadas. Portanto, a AUC-ROC abrange todos os quadrantes da matriz de confusão.
AUC-PR representa a área sob a curva do gráfico "Precisão x recall (sensibilidade)", mostrando a relação entre precisão e recall à medida que o limite varia. A precisão é baseada em todas as ocorrências previstas. Portanto, a AUC-PR não inclui os verdadeiros negativos (TN).
def print_pres_abs_sizes(TestingDatasets, numiter):
# Check and print the sizes of presence and pseudo-absence coordinates
def get_pres_abs_size(x):
fc = ee.FeatureCollection(TestingDatasets.get(x))
presence_size = fc.filter(ee.Filter.eq("PresAbs", 1)).size()
pseudo_absence_size = fc.filter(ee.Filter.eq("PresAbs", 0)).size()
return ee.List([presence_size, pseudo_absence_size])
sizes_info = (
ee.List.sequence(0, ee.Number(numiter).subtract(1), 1)
.map(get_pres_abs_size)
.getInfo()
)
for i, sizes in enumerate(sizes_info):
presence_size = sizes[0]
pseudo_absence_size = sizes[1]
print(
f"Iteration {i + 1}: Presence Size = {presence_size}, Pseudo-absence Size = {pseudo_absence_size}"
)
# Extracting the Testing Datasets
testing_datasets = ee.List.sequence(
3, ee.Number(numiter).multiply(4).subtract(1), 4
).map(lambda x: results.get(x))
print_pres_abs_sizes(testing_datasets, numiter)
def get_acc(hsm, t_data, grain_size):
pr_prob_vals = hsm.sampleRegions(
collection=t_data, properties=["PresAbs"], scale=grain_size
)
seq = ee.List.sequence(start=0, end=1, count=25) # Divide 0 to 1 into 25 intervals
def calculate_metrics(cutoff):
# Each element of the seq list is passed as cutoff(threshold value)
# Observed present = TP + FN
pres = pr_prob_vals.filterMetadata("PresAbs", "equals", 1)
# TP (True Positive)
tp = ee.Number(
pres.filterMetadata("classification", "greater_than", cutoff).size()
)
# TPR (True Positive Rate) = Recall = Sensitivity = TP / (TP + FN) = TP / Observed present
tpr = tp.divide(pres.size())
# Observed absent = FP + TN
abs = pr_prob_vals.filterMetadata("PresAbs", "equals", 0)
# FN (False Negative)
fn = ee.Number(
pres.filterMetadata("classification", "less_than", cutoff).size()
)
# TNR (True Negative Rate) = Specificity = TN / (FP + TN) = TN / Observed absent
tn = ee.Number(abs.filterMetadata("classification", "less_than", cutoff).size())
tnr = tn.divide(abs.size())
# FP (False Positive)
fp = ee.Number(
abs.filterMetadata("classification", "greater_than", cutoff).size()
)
# FPR (False Positive Rate) = FP / (FP + TN) = FP / Observed absent
fpr = fp.divide(abs.size())
# Precision = TP / (TP + FP) = TP / Predicted present
precision = tp.divide(tp.add(fp))
# SUMSS = SUM of Sensitivity and Specificity
sumss = tpr.add(tnr)
return ee.Feature(
None,
{
"cutoff": cutoff,
"TP": tp,
"TN": tn,
"FP": fp,
"FN": fn,
"TPR": tpr,
"TNR": tnr,
"FPR": fpr,
"Precision": precision,
"SUMSS": sumss,
},
)
return ee.FeatureCollection(seq.map(calculate_metrics))
def calculate_and_print_auc_metrics(images, testing_datasets, grain_size, numiter):
# Calculate AUC-ROC and AUC-PR
def calculate_auc_metrics(x):
hsm = ee.Image(images.get(x))
t_data = ee.FeatureCollection(testing_datasets.get(x))
acc = get_acc(hsm, t_data, grain_size)
# Calculate AUC-ROC
x = ee.Array(acc.aggregate_array("FPR"))
y = ee.Array(acc.aggregate_array("TPR"))
x1 = x.slice(0, 1).subtract(x.slice(0, 0, -1))
y1 = y.slice(0, 1).add(y.slice(0, 0, -1))
auc_roc = x1.multiply(y1).multiply(0.5).reduce("sum", [0]).abs().toList().get(0)
# Calculate AUC-PR
x = ee.Array(acc.aggregate_array("TPR"))
y = ee.Array(acc.aggregate_array("Precision"))
x1 = x.slice(0, 1).subtract(x.slice(0, 0, -1))
y1 = y.slice(0, 1).add(y.slice(0, 0, -1))
auc_pr = x1.multiply(y1).multiply(0.5).reduce("sum", [0]).abs().toList().get(0)
return (auc_roc, auc_pr)
auc_metrics = (
ee.List.sequence(0, ee.Number(numiter).subtract(1), 1)
.map(calculate_auc_metrics)
.getInfo()
)
# Print AUC-ROC and AUC-PR for each iteration
df = pd.DataFrame(auc_metrics, columns=["AUC-ROC", "AUC-PR"])
df.index = [f"Iteration {i + 1}" for i in range(len(df))]
df.to_csv("auc_metrics.csv", index_label="Iteration")
print(df)
# Calculate mean and standard deviation of AUC-ROC and AUC-PR
mean_auc_roc, std_auc_roc = df["AUC-ROC"].mean(), df["AUC-ROC"].std()
mean_auc_pr, std_auc_pr = df["AUC-PR"].mean(), df["AUC-PR"].std()
print(f"Mean AUC-ROC = {mean_auc_roc:.4f} ± {std_auc_roc:.4f}")
print(f"Mean AUC-PR = {mean_auc_pr:.4f} ± {std_auc_pr:.4f}")
%%time
# Calculate AUC-ROC and AUC-PR
calculate_and_print_auc_metrics(images, testing_datasets, grain_size, numiter)
Este tutorial apresentou um exemplo prático de uso do Google Earth Engine (GEE) para modelagem de distribuição de espécies (SDM, na sigla em inglês). Uma conclusão importante é a versatilidade e a flexibilidade do GEE no campo da SDM. Aproveitar os recursos avançados de processamento de dados geoespaciais do Earth Engine abre inúmeras possibilidades para pesquisadores e ambientalistas entenderem e preservarem a biodiversidade no nosso planeta. Ao aplicar o conhecimento e as habilidades adquiridas neste tutorial, as pessoas podem explorar e contribuir para esse campo fascinante da pesquisa ecológica.
 Executar no Google Colab
Executar no Google Colab
 Ver código-fonte no GitHub
Ver código-fonte no GitHub