Na modelagem do mix de marketing (MMM), um desafio comum é garantir que os resultados do modelo reflitam a realidade complexa da sua empresa. Para isso, o Meridian usa um recurso bayesiano avançado: as distribuições a priori. Nesta página, você encontra uma introdução geral sobre o que são as distribuições a priori, por que elas são a base da metodologia do Meridian e as principais considerações para seu uso.
O que são distribuições a priori?
Uma distribuição a priori é uma informação que você fornece ao modelo antes da análise dos dados. É como dar ao modelo um impulso inicial ou alguns conselhos de especialista com base nos seus conhecimentos sobre o negócio, comparações de mercado ou resultados de experimentos anteriores. Essa relação é a base da estatística bayesiana e pode ser resumida da seguinte forma:
\[ \underset{\text{(the model)}}{\text{Posterior}} \propto \underset{\text{(the data)}}{\text{Likelihood}} \cdot \underset{\text{(your belief)}}{\text{Prior}} \]
A distribuição a posteriori do modelo, de onde derivam as estimativas, considera suas convicções iniciais (a distribuição a priori) e o que os dados sugerem (a verossimilhança). A distribuição a priori estabiliza o modelo e o mantém fundamentado no contexto de negócios real.
Um dos principais recursos do Meridian é a capacidade de trabalhar diretamente com as métricas de negócios que você considera importantes. Em vez de exigir informações a priori sobre coeficientes de regressão abstratos, o Meridian é estruturado para incorporar informações a priori sobre métricas tangíveis e mensuráveis, como retorno do investimento (ROI, na sigla em inglês), retorno marginal do investimento (mROI, na sigla em inglês) e porcentagem de contribuição.
Uma distribuição a priori pode vir de várias fontes:
- Resultados de experimentos de incrementalidade anteriores (por exemplo, testes de Lift ou experimentos geográficos).
- Comparações de mercado.
- Resultados anteriores da MMM.
- A experiência da sua equipe em um assunto específico.
Se você não tiver nenhuma experiência, não se preocupe, o Meridian tem padrões integrados que podem ser um ponto de partida.
Entenda as distribuições a priori
Para ajudar você a entender as distribuições a priori de forma intuitiva, apresentamos alguns exemplos visuais de como traduzir sua intuição nos negócios em distribuições a priori para sua MMM.
Como é uma distribuição a priori
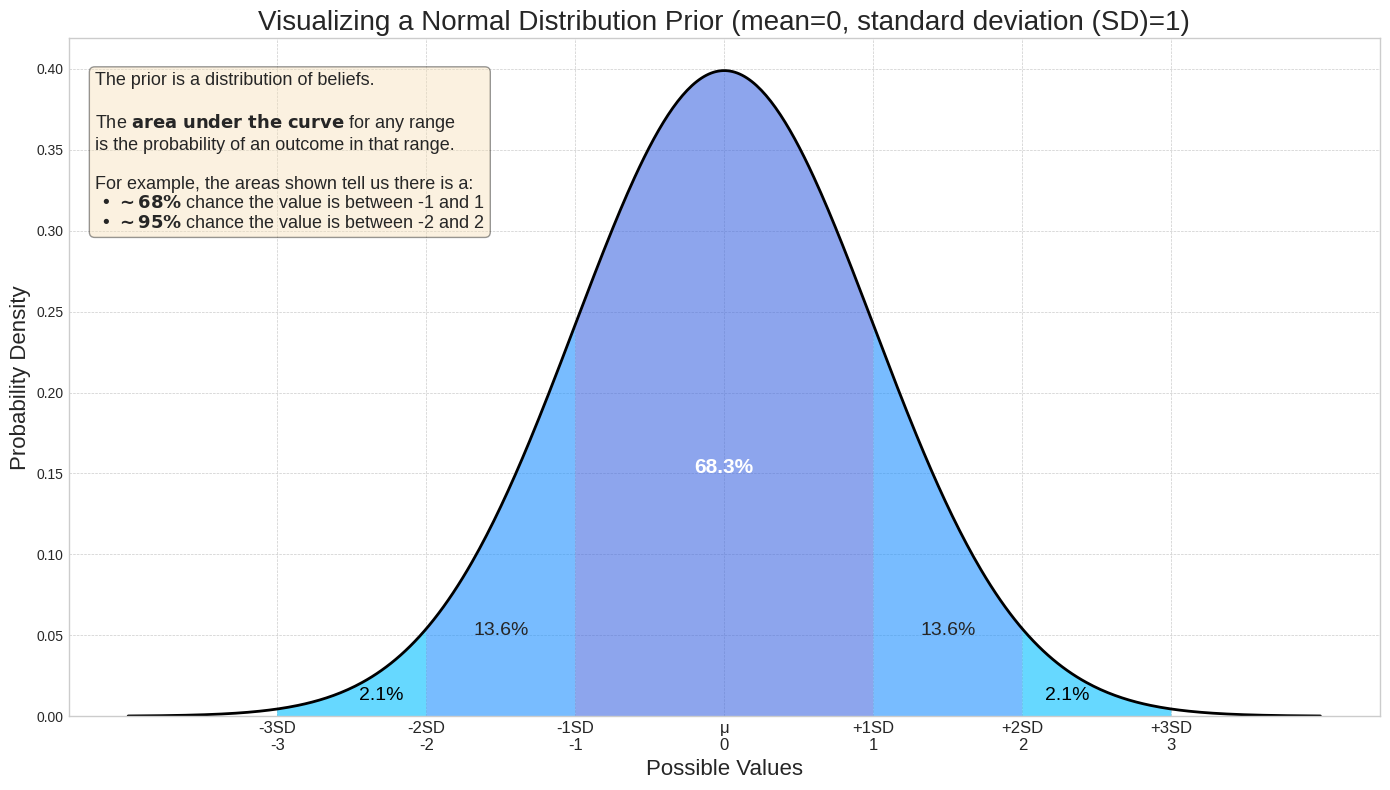
As distribuições a priori são expressas como distribuições de probabilidade. Uma distribuição atribui uma densidade (verossimilhança relativa) a todos os valores possíveis de um parâmetro, como o ROI. A área abaixo da curva entre dois pontos no eixo x representa a probabilidade de que o valor verdadeiro esteja dentro desse intervalo. Por exemplo, o gráfico de distribuição a seguir mostra que valores entre -1 e 1 são muito mais prováveis do que um valor fora desse intervalo. Para uma distribuição normal com média = 0 e desvio padrão = 1, há uma probabilidade de 68,3% de que o valor real esteja entre -1 e 1.
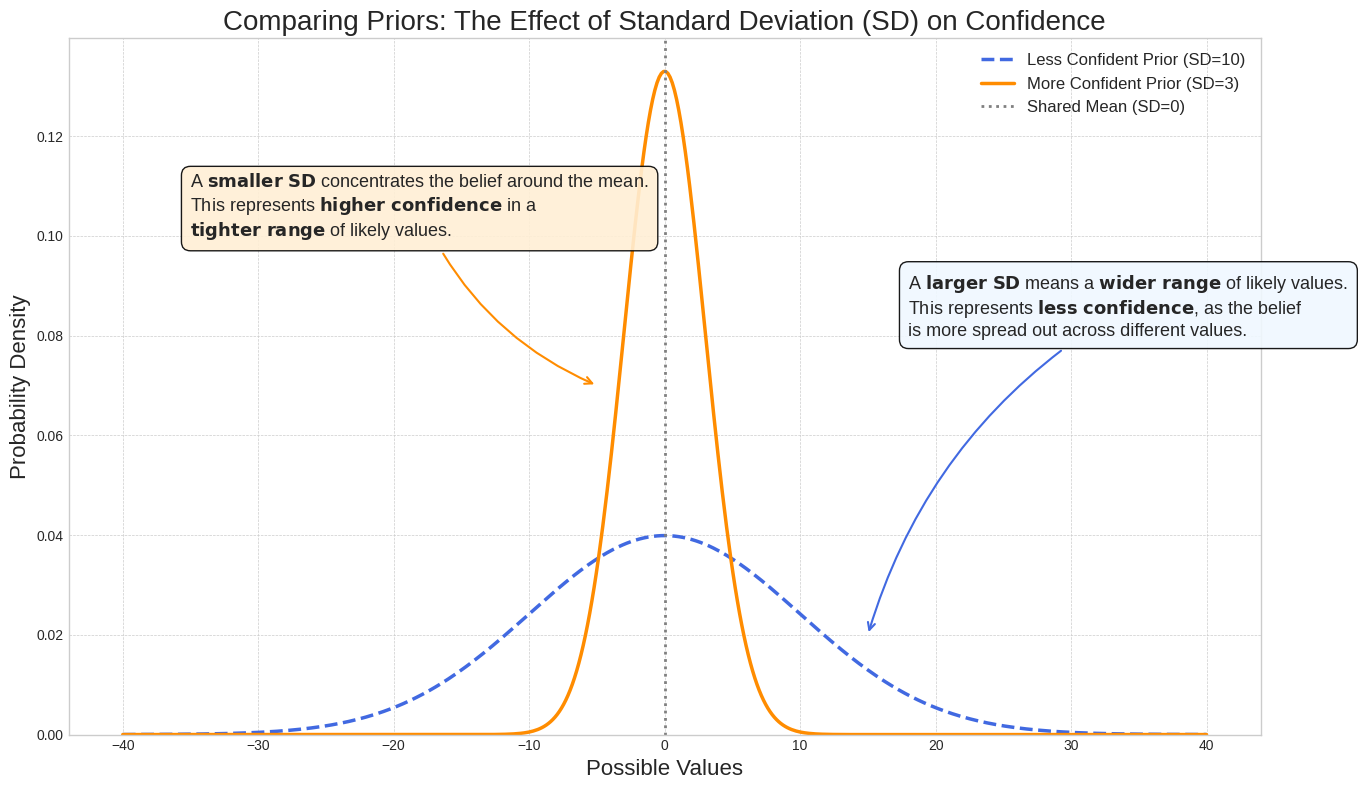
O efeito do desvio padrão na confiança
O desvio padrão controla a largura da distribuição e reflete sua confiança no valor de parâmetro. Um desvio padrão menor concentra a probabilidade em torno do valor do parâmetro, indicando maior confiança, enquanto um desvio padrão maior espalha a probabilidade, indicando mais incerteza.
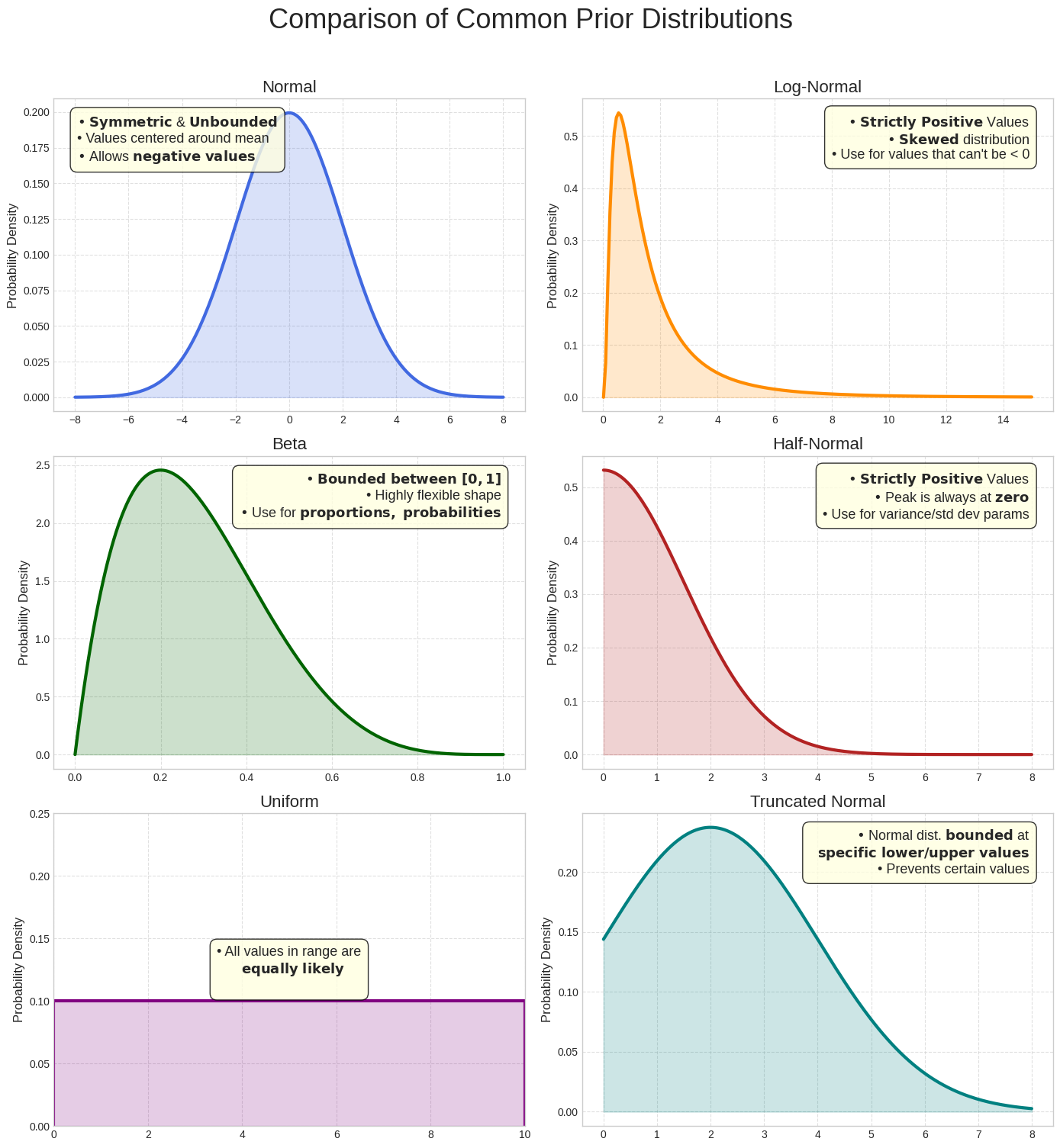
Comparação de distribuições a priori comuns
Embora a distribuição normal seja uma ilustração útil, outras distribuições costumam ser mais adequadas, dependendo do parâmetro modelado. Por exemplo, como o ROI precisa ser positivo, uma distribuição que só atribui probabilidade a valores positivos (como a lognormal ou a seminormal) costuma ser uma escolha melhor do que uma distribuição normal, que permite valores negativos. O Meridian usa várias distribuições comuns, permitindo que você selecione aquela que melhor reflete a natureza do parâmetro de modelagem.
Um exemplo em código: confiança x incerteza
Confira como você pode expressar diferentes níveis de crença sobre o ROI de três canais de mídia paga no seu código.
from meridian.model import prior_distribution
# --- Channel 1: High Confidence ---
# You have strong experiment results showing ROI is consistently around 1.2.
# You use a small standard deviation (0.2) to reflect your high confidence.
strong_prior_channel_1 = prior_distribution.lognormal_dist_from_mean_std(
mean=1.2,
std=0.2
)
# --- Channel 2: Low Confidence ---
# You have weaker experiment results showing ROI is around 1.0.
# You use a larger standard deviation (0.9) to reflect your weaker confidence in
# the experiment result than for Channel 1.
weak_prior_channel_2 = prior_distribution.lognormal_dist_from_mean_std(
mean=1.0,
std=0.9
)
# --- Channel 3: Confidence in a range ---
# You believe there's a 95% chance the ROI is between 2.0 and 6.0.
range_prior_channel_3 = prior_distribution.lognormal_dist_from_range(
low=2.0,
high=6.0,
mass_percent=0.95
)
# You would then assign these distributions to their respective channels
# when you configure your model.
prior_config = prior_distribution.PriorDistribution(
roi_m=[strong_prior_channel_1, weaker_prior_channel_2, range_prior_channel_3]
)
Visualizar suas distribuições a priori
É fácil criar gráficos das distribuições a priori, o que ajuda a garantir que elas correspondam à sua intuição.
from matplotlib import pyplot as plt
from meridian.model import prior_distribution
import numpy as np
# Define the LogNormal distribution
lognormal_dist = prior_distribution.lognormal_dist_from_mean_std(2.0, 0.5)
# Plot a histogram of samples from the LogNormal distribution
plt.hist(lognormal_dist.sample(1000))
Por que as distribuições a priori são importantes
O uso de distribuições a priori é mais do que apenas um recurso técnico. Ele é fundamental para conseguir estimativas causais confiáveis e úteis.
- Resultados mais plausíveis e estáveis com menos dados: os dados de marketing agregados podem ser esparsos ou ruidosos. As distribuições a priori oferecem um efeito estabilizador, orientando o modelo para resultados plausíveis e evitando que ele chegue a conclusões incorretas com base em dados limitados.
Resultados embasados na realidade empresarial: ao incorporar conhecimento de fontes confiáveis, como estudos de Lift, o efeito estabilizador da distribuição a priori orienta o modelo para o alinhamento com esse conhecimento, aumentando a confiança das partes interessadas. Quase sempre temos alguma intuição sobre nossos negócios. Por exemplo, talvez seja raro conseguir um ROI maior que 6,0 no seu setor. Você pode codificar essa intuição na distribuição a priori e orientar o modelo para resultados mais realistas, mesmo que não tenha dados concretos de um experimento.
Controles intuitivos de modelo: o Meridian oferece maneiras intuitivas de definir uma distribuição a priori. É como ter uma conversa com seu modelo. Em vez de ajustar parâmetros abstratos, você fornece orientação em uma linguagem que entende. Você pode dizer ao modelo: "Tenho evidências sólidas de que o ROI do meu canal é de cerca de 1,5".
