Dans la modélisation du mix marketing, il est souvent difficile de s'assurer que les résultats du modèle reflètent la réalité complexe de votre entreprise. C'est là qu'intervient une puissante fonctionnalité bayésienne : les a priori. Cette page présente de manière générale les a priori, explique pourquoi ils sont un élément clé de la méthodologie de Meridian et décrit les points importants à prendre en compte pour les utiliser.
Que sont les a priori ?
Un "a priori" est une information que vous fournissez au modèle avant qu'il analyse vos données. Il vous permet de lui donner une piste ou de partager avec lui votre expertise en vous appuyant sur votre connaissance de votre activité, les benchmarks du secteur ou les résultats de tests précédents. Cette relation est au cœur des statistiques bayésiennes et peut être résumée de la façon suivante :
\[ \underset{\text{(the model)}}{\text{Posterior}} \propto \underset{\text{(the data)}}{\text{Likelihood}} \cdot \underset{\text{(your belief)}}{\text{Prior}} \]
La distribution a posteriori du modèle, à partir de laquelle les estimations sont dérivées, prend en compte à la fois vos convictions initiales (l'a priori) et ce que suggèrent les données elles-mêmes (la probabilité). L'a priori stabilise votre modèle tout en le gardant ancré dans votre contexte commercial réel.
L'une des principales caractéristiques de Meridian est qu'il peut fonctionner directement avec les métriques commerciales qui vous intéressent. Au lieu d'exiger des informations a priori sur les coefficients de régression abstraits, Meridian est structuré pour intégrer des informations a priori sur des métriques tangibles et mesurables telles que le retour sur investissement (ROI), le retour sur investissement marginal (ROIm) et le pourcentage de contribution.
Un a priori peut provenir de nombreuses sources :
- Résultats des tests d'incrémentalité précédents (par exemple, tests d'impact ou tests géographiques)
- Benchmarks du secteur
- Résultats MMM précédents
- L'expertise de votre équipe dans le domaine concerné
Si vous n'avez pas d'a priori, ne vous inquiétez pas. Meridian intègre des valeurs par défaut qui peuvent vous servir de point de départ.
Comprendre les a priori en termes de distributions
Afin de vous aider à mieux comprendre les a priori, voici quelques exemples visuels qui vous montrent comment traduire votre intuition commerciale en a priori pour votre MMM.
À quoi ressemble une distribution a priori ?
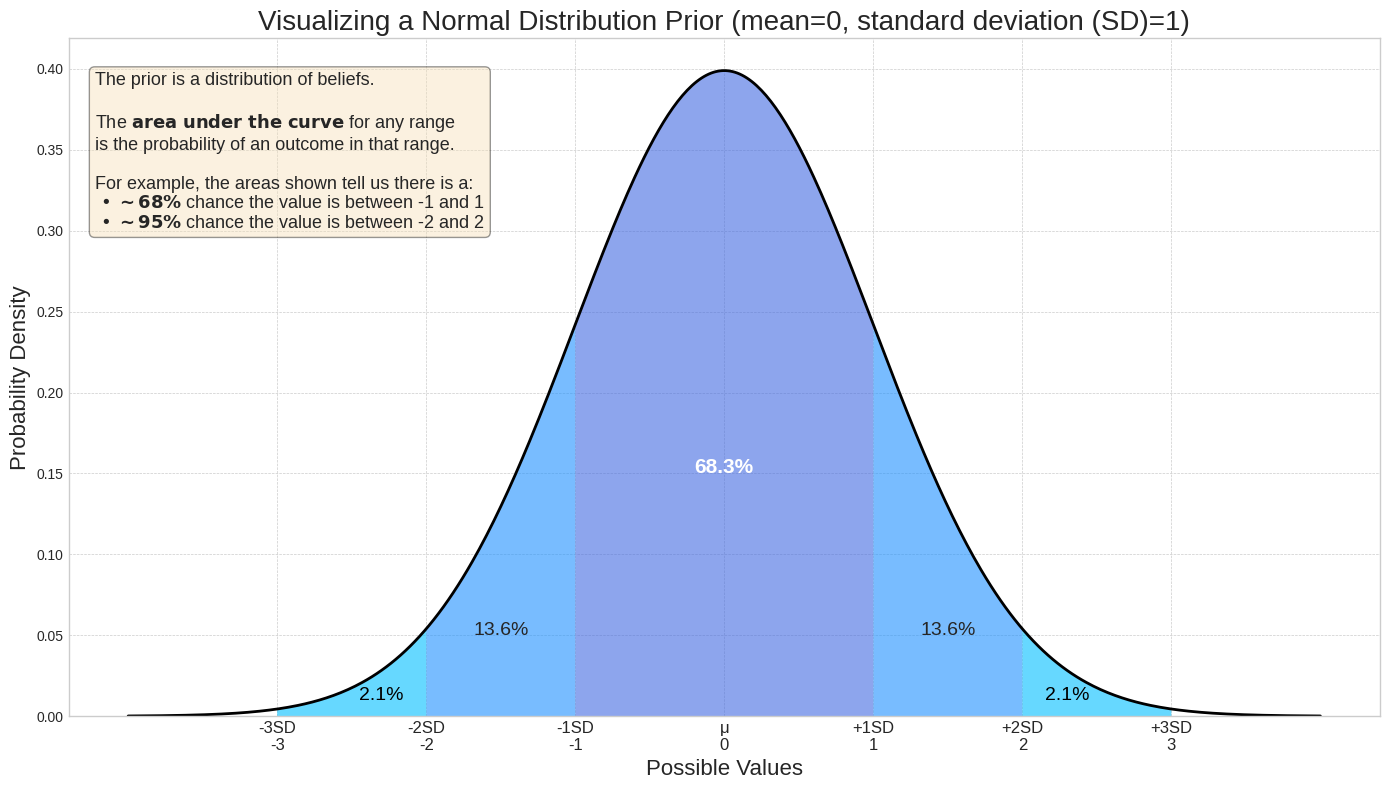
Les a priori sont exprimés sous forme de distributions de probabilité. Une distribution attribue une densité (probabilité relative) à chaque valeur possible d'un paramètre, comme le ROI. L'aire sous la courbe entre deux points de l'axe X représente la probabilité que la valeur réelle se situe dans cette plage. Par exemple, le graphique de distribution suivant montre que les valeurs comprises entre -1 et 1 sont beaucoup plus probables que celles en dehors de cette plage. Pour une distribution normale avec une moyenne de 0 et un écart-type de 1, la probabilité que la valeur réelle se situe entre -1 et 1 est de 68,3 %.
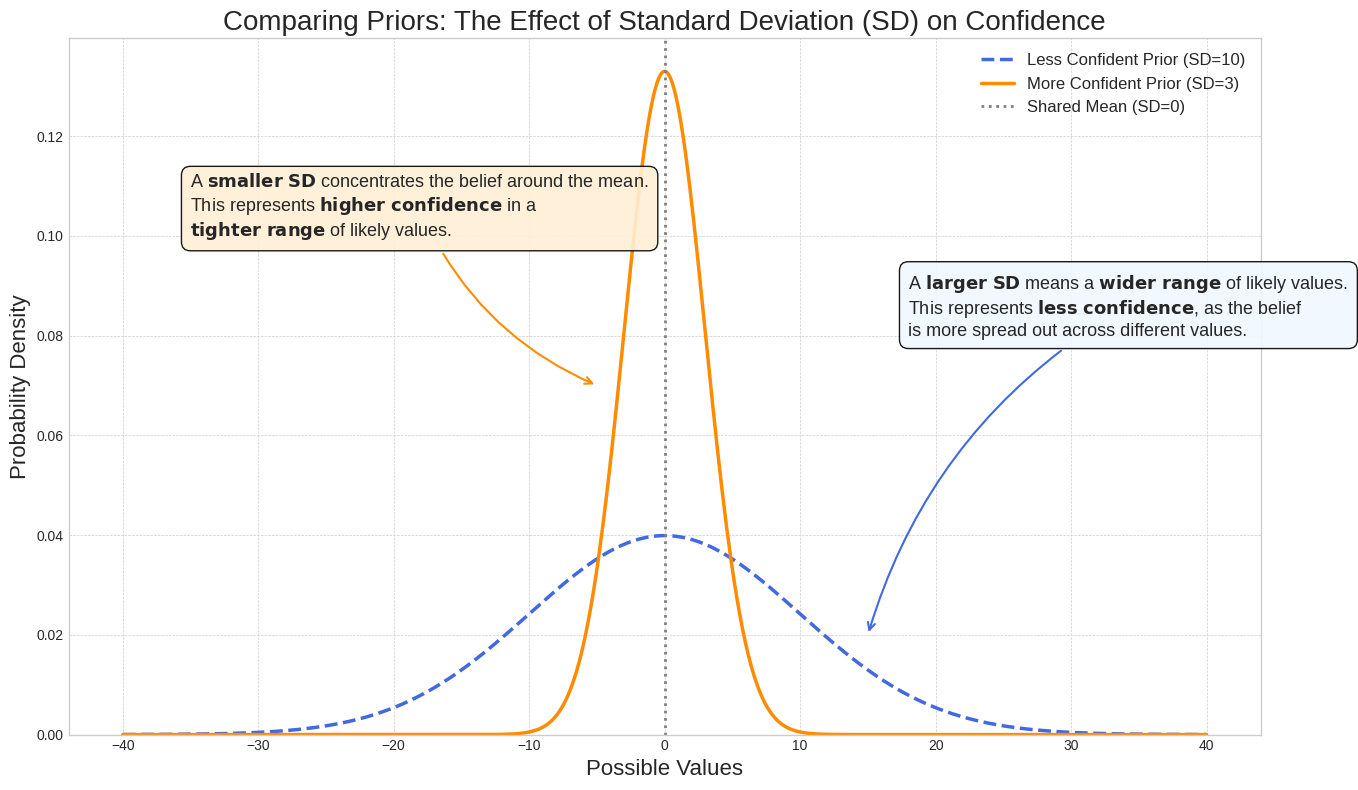
Effet de l'écart-type sur la confiance
L'écart-type contrôle la largeur de la distribution et reflète votre confiance dans la valeur du paramètre. Un écart-type plus faible concentre la probabilité autour de la valeur du paramètre, ce qui indique une plus grande confiance, tandis qu'un écart-type plus élevé répartit la probabilité, ce qui traduit une plus grande incertitude.
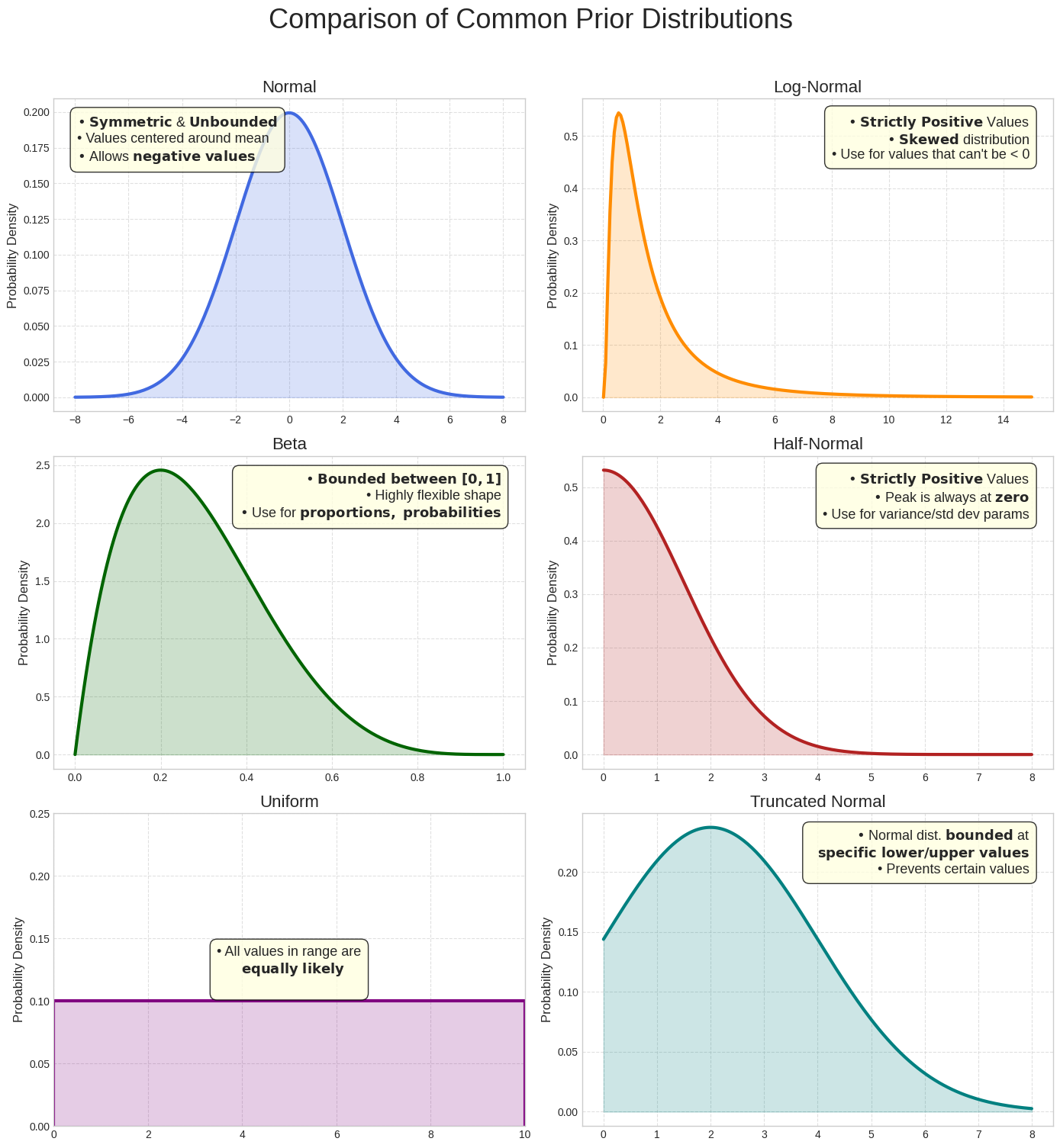
Comparaison des distributions a priori courantes
Bien que la distribution normale soit une illustration utile, d'autres distributions sont souvent plus appropriées en fonction du paramètre modélisé. Par exemple, comme le ROI doit être positif, une distribution qui n'attribue de probabilité qu'aux valeurs positives (comme la distribution log-normale ou semi-normale) est souvent un meilleur choix qu'une distribution normale, qui autorise les valeurs négatives. Meridian utilise plusieurs distributions courantes, ce qui vous permet de sélectionner celle qui reflète le mieux la nature du paramètre que vous modélisez.
Exemple de code : confiance vs incertitude
Voici comment vous pouvez exprimer différents niveaux de conviction concernant le ROI pour trois canaux média payants différents dans votre code.
from meridian.model import prior_distribution
# --- Channel 1: High Confidence ---
# You have strong experiment results showing ROI is consistently around 1.2.
# You use a small standard deviation (0.2) to reflect your high confidence.
strong_prior_channel_1 = prior_distribution.lognormal_dist_from_mean_std(
mean=1.2,
std=0.2
)
# --- Channel 2: Low Confidence ---
# You have weaker experiment results showing ROI is around 1.0.
# You use a small sigma (0.9) to reflect your weaker confidence in the
# experiment result than for Channel 1.
weak_prior_channel_2 = prior_distribution.lognormal_dist_from_mean_std(
mean=1.0,
std=0.9
)
# --- Channel 3: Confidence in a range ---
# You believe there's a 95% chance the ROI is between 2.0 and 6.0.
range_prior_channel_3 = prior_distribution.lognormal_dist_from_range(
low=2.0,
high=6.0
mass_percent=0.95
)
# You would then assign these distributions to their respective channels
# when you configure your model.
prior_config = prior_distribution.PriorDistribution(
roi_m=[strong_prior_channel_1, weaker_prior_channel_2, range_prior_channel_3]
)
Visualiser vos a priori
Il est facile de représenter vos a priori sous forme graphique, ce qui peut vous aider à vous assurer qu'ils correspondent à votre intuition.
from matplotlib import pyplot as plt
from meridian.model import prior_distribution
import numpy as np
# Define the LogNormal distribution
lognormal_dist = prior_distribution.lognormal_dist_from_mean_std(2.0, 0.5)
# Plot a histogram of samples from the LogNormal distribution
plt.hist(lognormal_dist.sample(1000))
Pourquoi les a priori sont-ils importants ?
L'utilisation d'a priori n'est pas qu'une fonctionnalité technique. Elle est essentielle pour obtenir des estimations causales fiables et exploitables.
- Des résultats plus plausibles et plus stables avec moins de données : les données marketing agrégées peuvent être rares ou bruitées. Les a priori ont un effet stabilisateur en guidant le modèle vers des résultats plausibles et en l'empêchant de tirer des conclusions incorrectes à partir de données limitées.
- Résultats ancrés dans la réalité commerciale : en intégrant des connaissances provenant de sources fiables telles que les études d'impact, l'effet stabilisateur de l'a priori guide le modèle pour qu'il s'aligne sur ces connaissances, ce qui renforce la confiance des personnes impliquées.
- Intégrer votre intuition commerciale : vous avez presque toujours une certaine intuition concernant votre entreprise. Par exemple, il peut être rare d'obtenir un ROI supérieur à 6,0 dans votre secteur. Vous pouvez intégrer cette intuition dans votre a priori pour orienter le modèle vers des résultats plus réalistes, même si vous ne disposez pas de données concrètes issues d'un test.
- Paramètres intuitifs pour le modèle : définir un a priori revient à avoir une conversation intuitive avec votre modèle. Au lieu de modifier des paramètres abstraits, vous fournissez des indications dans une langue que vous comprenez (par exemple, "J'ai des preuves solides que le ROI de mon canal est d'environ 1,5.").