Eine häufige Herausforderung beim Marketing Mix Modeling (MMM) besteht darin, dafür zu sorgen, dass die Ergebnisse des Modells die komplexe Realität Ihres Unternehmens widerspiegeln. Hier kommt ein leistungsstarkes bayessches Konzept ins Spiel: Priors. Auf dieser Seite finden Sie eine allgemeine Einführung in Priors. Sie erfahren, warum sie ein Eckpfeiler der Meridian-Methodik sind und welche wichtigen Aspekte bei ihrer Verwendung zu beachten sind.
Was sind Priors?
Ein „Prior“ ist eine Information, die dem Modell zur Verfügung gestellt wird, bevor es die Daten analysiert. Damit geben Sie dem Modell sozusagen einen Vorsprung oder fachlichen Hinweis – basierend auf Ihrem Geschäftswissen, Branchenbenchmarks oder den Ergebnissen früherer Tests. Diese Beziehung steht im Zentrum der bayesschen Statistik und lässt sich so zusammenfassen:
\[ \underset{\text{(the model)}}{\text{Posterior}} \propto \underset{\text{(the data)}}{\text{Likelihood}} \cdot \underset{\text{(your belief)}}{\text{Prior}} \]
Die Posterior-Verteilung des Modells, aus der Schätzungen abgeleitet werden, berücksichtigt sowohl Ihre ursprünglichen Annahmen (den Prior) als auch das, was die Daten selbst nahelegen (die Wahrscheinlichkeit). Der Prior stabilisiert Ihr Modell und verankert es zugleich im realen geschäftlichen Kontext.
Ein zentrales Merkmal von Meridian ist seine Fähigkeit, direkt mit den für Ihr Unternehmen relevanten Messwerten zu arbeiten. Anstatt Prior-Informationen zu abstrakten Regressionskoeffizienten zu benötigen, ist Meridian so aufgebaut, dass Prior-Informationen zu greifbaren und messbaren Größen wie Return on Investment (ROI), Grenz-ROI und Prozentwert für den Beitrag einbezogen werden.
Ein Prior kann aus vielen Quellen stammen:
- Ergebnisse früherer Tests zur Steigerung, z. B. Tests zum Suchanstieg und zur Conversion-Steigerung oder Geo-Tests.
- Branchenbenchmarks
- Frühere MMM-Ergebnisse
- Das Fachwissen Ihres Teams
Falls Sie keine haben, ist das kein Problem. Meridian bietet integrierte Standardeinstellungen, die als Ausgangspunkt dienen können.
Priors in Bezug auf Verteilungen
Damit Sie ein Gefühl dafür bekommen, was Priors sind, zeigen wir einige Beispiele, die veranschaulichen, wie Sie Ihre geschäftliche Intuition in Priors für Ihr MMM umsetzen können.
So sieht eine Prior-Verteilung aus
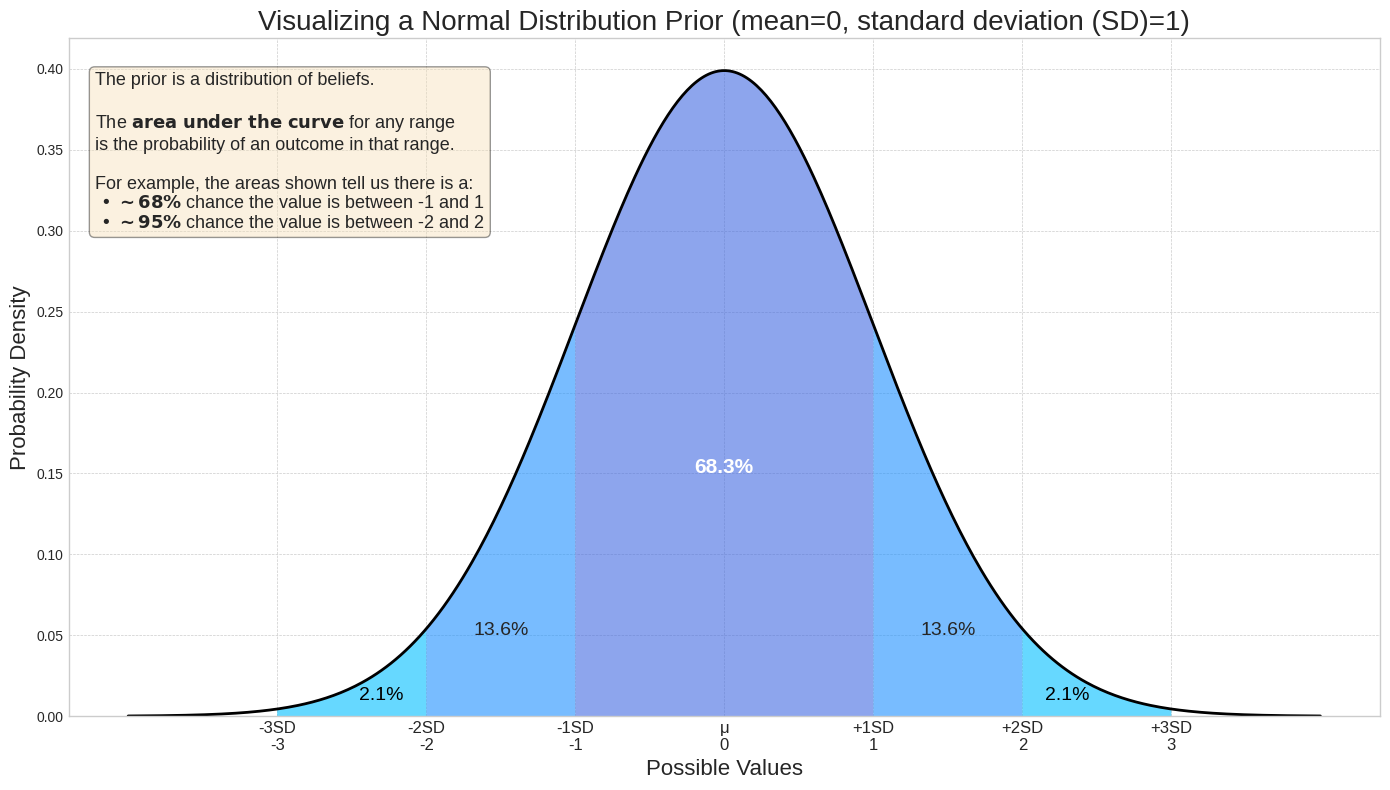
Priors werden als Wahrscheinlichkeitsverteilungen dargestellt. Eine Verteilung weist jedem möglichen Wert eines Parameters, etwa des ROI, eine Dichte (relative Wahrscheinlichkeit) zu. Die Fläche unter der Kurve zwischen zwei Punkten auf der x-Achse entspricht der Wahrscheinlichkeit, dass der tatsächliche Wert in diesem Bereich liegt. Das folgende Verteilungsdiagramm zeigt beispielsweise, dass Werte zwischen −1 und 1 viel wahrscheinlicher sind als Werte außerhalb dieses Bereichs. Bei einer Normalverteilung mit einem Mittelwert von 0 und einer Standardabweichung von 1 liegt der tatsächliche Wert mit einer Wahrscheinlichkeit von 68,3 % zwischen −1 und 1.
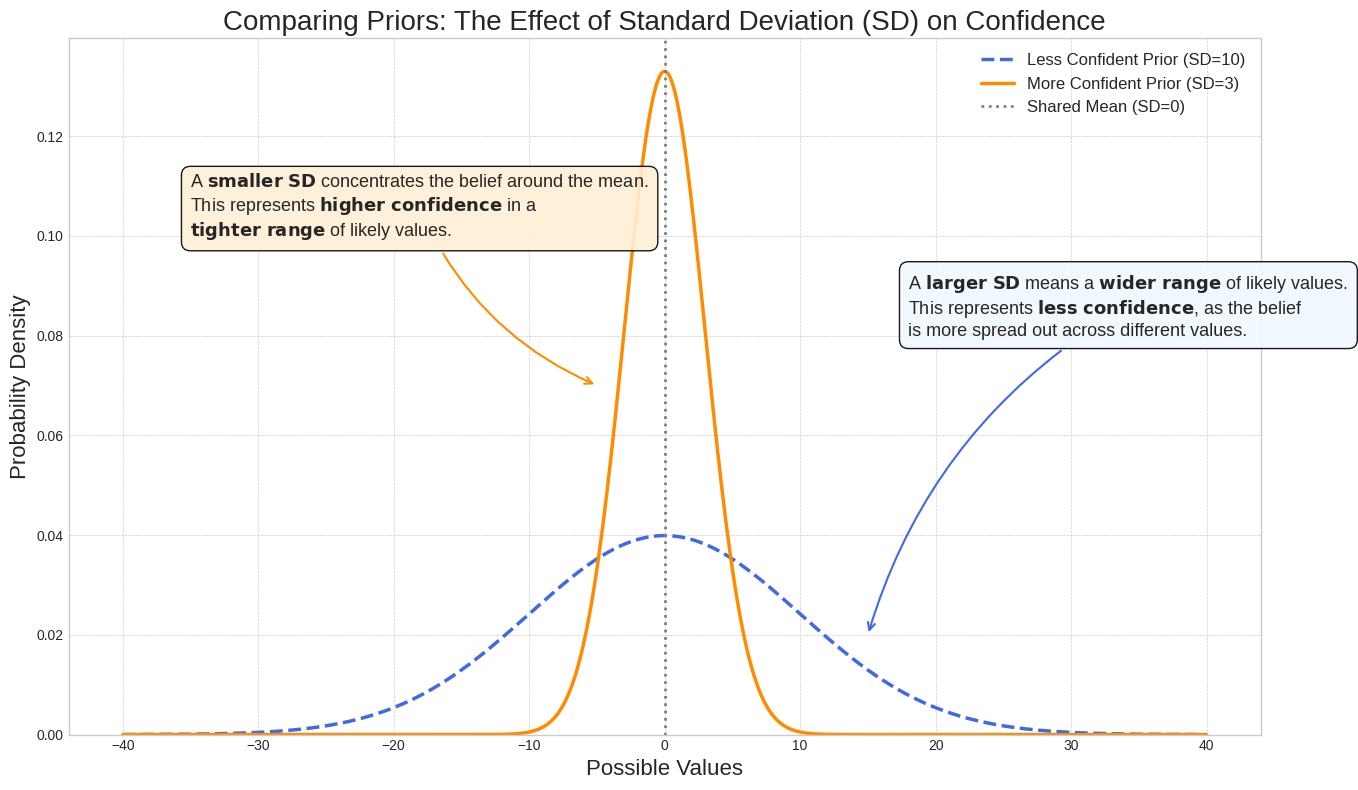
Auswirkungen der Standardabweichung auf das Konfidenzniveau
Die Standardabweichung beeinflusst, wie breit eine Verteilung ist, und zeigt damit, wie sicher Sie sich in Bezug auf einen bestimmten Parameterwert sind. Ist die Standardabweichung klein, konzentriert sich die Wahrscheinlichkeit eng um den Wert. Das bedeutet ein hohes Maß an Vertrauen. Ist sie groß, verteilt sich die Wahrscheinlichkeit weiter. Das weist auf mehr Unsicherheit hin.
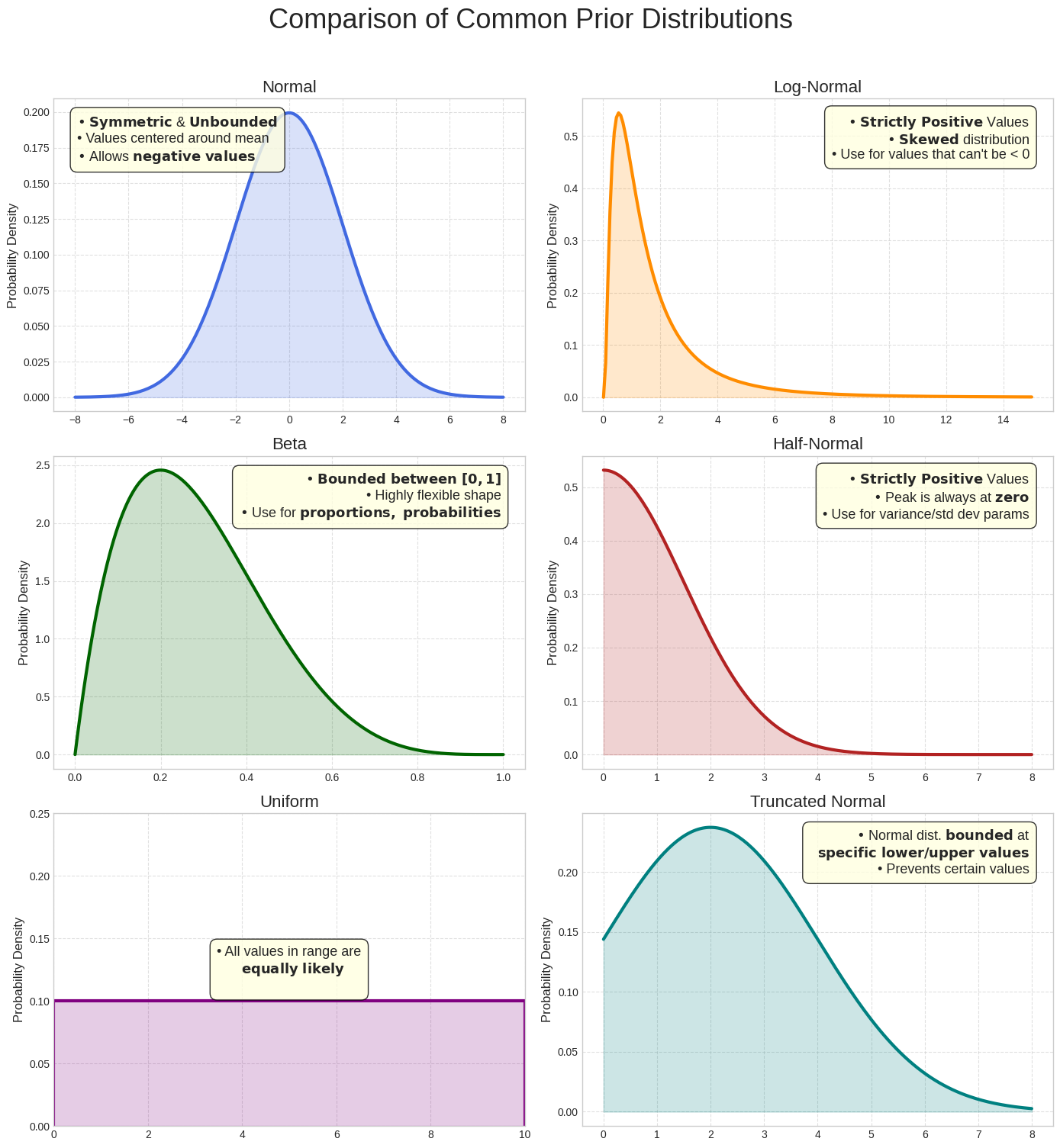
Vergleich gängiger Prior-Verteilungen
Die Normalverteilung ist zwar eine nützliche Veranschaulichung, aber je nach dem zu modellierenden Parameter sind oft andere Verteilungen besser geeignet. Da der ROI beispielsweise positiv sein sollte, ist eine Verteilung, die nur positiven Werten eine Wahrscheinlichkeit zuweist, z. B. die Log-Normal- oder die Halbnormalverteilung, oft eine bessere Wahl als eine Normalverteilung, die auch negative Werte zulässt. In Meridian werden mehrere gängige Verteilungen verwendet. Sie können die auswählen, die am besten zu dem Parameter passt, der modelliert werden soll.
Codebeispiel: Konfidenz im Vergleich zur Unsicherheit
So können Sie verschiedene Überzeugungsgrade in Bezug auf den ROI für drei verschiedene kostenpflichtige Media-Channels in Ihrem Code ausdrücken.
from meridian.model import prior_distribution
# --- Channel 1: High Confidence ---
# You have strong experiment results showing ROI is consistently around 1.2.
# You use a small standard deviation (0.2) to reflect your high confidence.
strong_prior_channel_1 = prior_distribution.lognormal_dist_from_mean_std(
mean=1.2,
std=0.2
)
# --- Channel 2: Low Confidence ---
# You have weaker experiment results showing ROI is around 1.0.
# You use a small sigma (0.9) to reflect your weaker confidence in the
# experiment result than for Channel 1.
weak_prior_channel_2 = prior_distribution.lognormal_dist_from_mean_std(
mean=1.0,
std=0.9
)
# --- Channel 3: Confidence in a range ---
# You believe there's a 95% chance the ROI is between 2.0 and 6.0.
range_prior_channel_3 = prior_distribution.lognormal_dist_from_range(
low=2.0,
high=6.0
mass_percent=0.95
)
# You would then assign these distributions to their respective channels
# when you configure your model.
prior_config = prior_distribution.PriorDistribution(
roi_m=[strong_prior_channel_1, weaker_prior_channel_2, range_prior_channel_3]
)
Priors visualisieren
Das Visualisieren von Priors ist einfach und kann Ihnen helfen, sicherzustellen, dass Ihre Priors Ihren Erwartungen entsprechen.
from matplotlib import pyplot as plt
from meridian.model import prior_distribution
import numpy as np
# Define the LogNormal distribution
lognormal_dist = prior_distribution.lognormal_dist_from_mean_std(2.0, 0.5)
# Plot a histogram of samples from the LogNormal distribution
plt.hist(lognormal_dist.sample(1000))
Warum Priors wichtig sind
Die Verwendung von Priors ist mehr als nur eine technische Funktion. Sie ist eine wesentliche Voraussetzung, um verlässliche kausale Schätzungen zu erhalten, die als Grundlage für Entscheidungen dienen können.
- Plausiblere und stabilere Ergebnisse mit weniger Daten: Aggregierte Marketingdaten können Lücken enthalten oder verrauscht sein. Priors haben eine stabilisierende Wirkung. Sie lenken das Modell in Richtung plausibler Ergebnisse und verhindern, dass es auf Grundlage begrenzter Daten zu falschen Schlussfolgerungen kommt.
- Ergebnisse mit Bezug zur geschäftlichen Realität: Wird Wissen aus vertrauenswürdigen Quellen einbezogen, etwa aus Lift-Studien, kann das Modell dank der stabilisierenden Wirkung des Priors entsprechend angepasst werden, was das Vertrauen der Stakeholder stärkt.
- Geschäftliche Intuition einbeziehen: In der Regel haben Sie ein gewisses Gespür für Ihr Geschäft. So kann es in Ihrer Branche beispielsweise ungewöhnlich sein, einen ROI von mehr als 6,0 zu erzielen. Dieses Wissen können Sie in Ihren Prior einbeziehen, um das Modell auf realistischere Ergebnisse auszurichten, auch wenn keine belastbaren Testdaten vorliegen.
- Intuitive Modellsteuerung: Einen Prior festzulegen ist, als würden Sie ein intuitives Gespräch mit Ihrem Modell führen. Anstatt abstrakte Parameter anzupassen, geben Sie dem Modell eine Anleitung in einer Sprache, die Sie verstehen, z. B. „Ich habe klare Anhaltspunkte dafür, dass der ROI für meinen Channel bei etwa 1,5 liegt.“