En el Marketing Mix Modeling, un desafío común es garantizar que los resultados del modelo reflejen la compleja realidad de tu empresa con una potente función de análisis bayesiano: las distribuciones a priori. Esta página brinda una introducción general a las distribuciones a priori, explica por qué son una de las bases de la metodología de Meridian y presenta las consideraciones clave para usarlas.
¿Qué son las distribuciones a priori?
Una "distribución a priori" representa la información que proporcionas al modelo antes de que analice tus datos. Piensa que es como darle al modelo una ventaja inicial o un consejo especializado a partir de tus conocimientos comerciales, las comparativas de sectores o los resultados de experimentos anteriores. Esta relación constituye el fundamento de la estadística bayesiana y se puede resumir de la siguiente manera:
\[ \underset{\text{(the model)}}{\text{Posterior}} \propto \underset{\text{(the data)}}{\text{Likelihood}} \cdot \underset{\text{(your belief)}}{\text{Prior}} \]
La distribución a posteriori del modelo, a partir de la que se derivan las estimaciones, tiene en cuenta tanto tus conjeturas iniciales (la distribución a priori) como lo que sugieren los datos en sí (la verosimilitud). La distribución a priori estabiliza tu modelo y, al mismo tiempo, lo mantiene arraigado en el contexto empresarial del mundo real.
Una función clave de Meridian es que puede utilizar directamente las métricas comerciales que te interesan. La estructura de Meridian permite incorporar información de distribución a priori sobre métricas tangibles y mensurables, como el retorno de la inversión (ROI), el retorno de la inversión marginal (mROI) y el porcentaje de contribución, en vez de exigir que esa información se base en coeficientes de regresión abstractos.
Una distribución a priori puede provenir de diversas fuentes:
- Resultados de experimentos de incrementalidad anteriores (por ejemplo, pruebas de efectividad o experimentos de ubicación geográfica)
- Comparativas de sectores
- Resultados anteriores del MMM
- Conocimientos técnicos de tu equipo
No te preocupes si no tienes este tipo de información. Meridian incorpora parámetros de configuración predeterminada que pueden servirte como punto de partida.
Interpreta las distribuciones a priori en términos de distribuciones de probabilidad
Para que adquieras un conocimiento instintivo de las distribuciones a priori, te mostramos algunos ejemplos visuales sobre cómo puedes traducir tu intuición comercial en distribuciones a priori para el MMM.
Estructura de una distribución a priori
Las distribuciones a priori se expresan como distribuciones de probabilidad. Una distribución asigna una densidad (probabilidad relativa) a cada valor posible de un parámetro, como el ROI. El área bajo la curva entre dos puntos dados del eje X representa la probabilidad de que el valor real se encuentre dentro de ese rango. Por ejemplo, el siguiente gráfico de distribución muestra que los valores entre -1 y 1 son mucho más probables que los valores fuera de ese rango. Para una distribución normal con una media = 0 y una desviación estándar = 1 , la probabilidad de que el valor real se encuentre entre -1 y 1 es de un 68.3%.
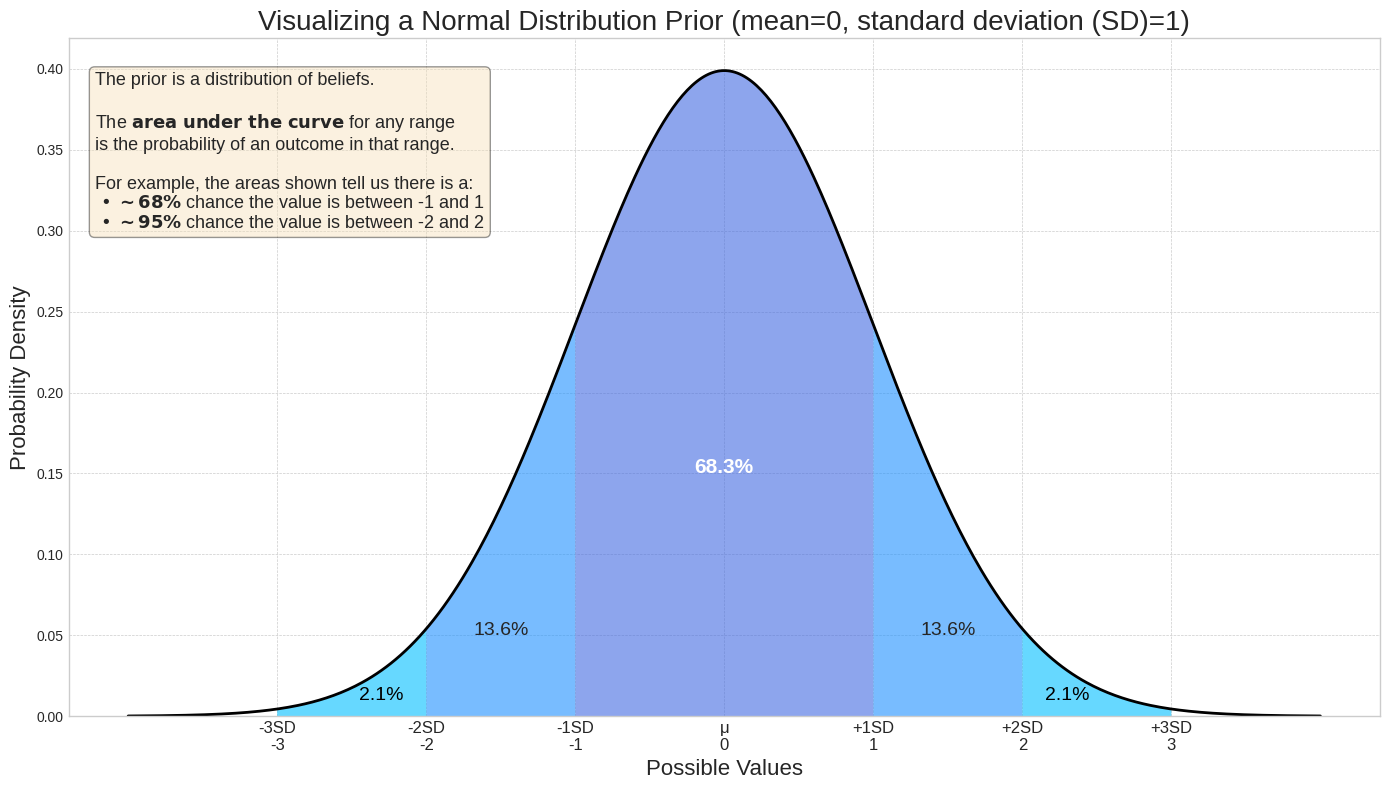
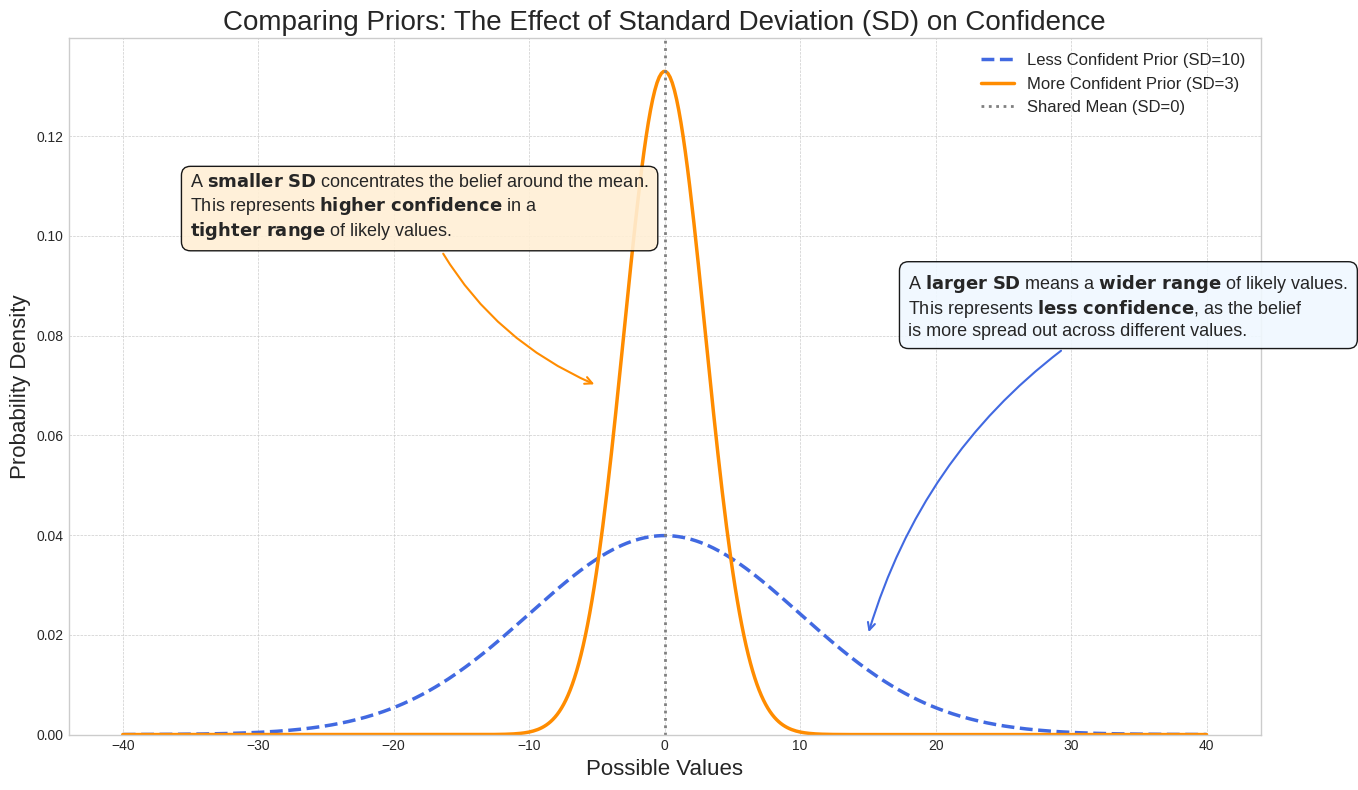
Efecto de la desviación estándar en el nivel de confianza
La desviación estándar controla el ancho de la distribución y refleja tu nivel de confianza en el valor del parámetro. Una desviación estándar más pequeña concentra la probabilidad alrededor del valor del parámetro, lo que indica una mayor confianza, mientras que una desviación estándar más grande extiende la probabilidad, lo que indica una mayor incertidumbre.
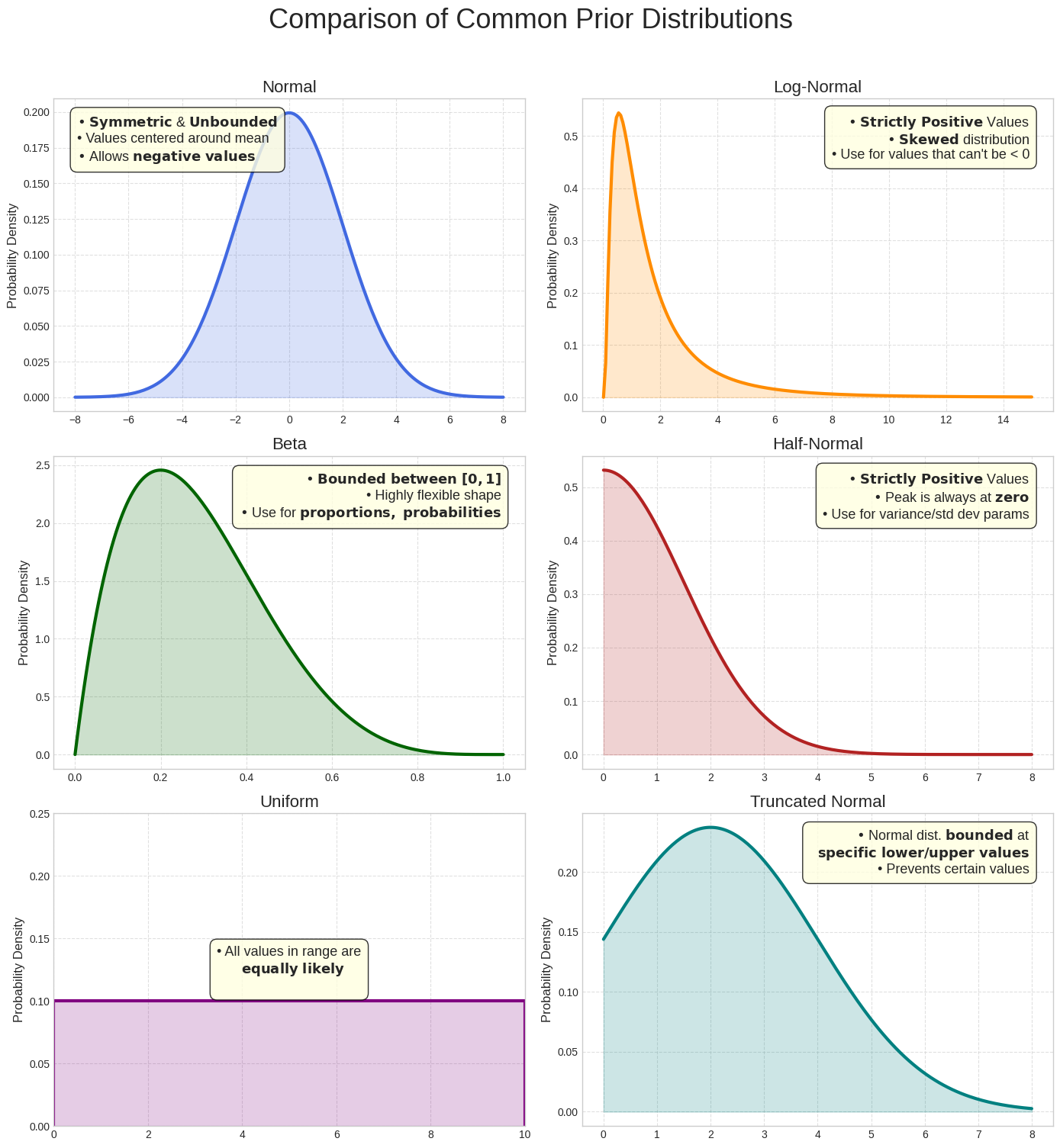
Comparación de distribuciones a priori comunes
Si bien la distribución normal es una ilustración útil, otras distribuciones suelen ser más adecuadas según el parámetro modelado. Por ejemplo, dado que el ROI debería ser positivo, una distribución que solo asigna la probabilidad a valores positivos (como la distribución normal logarítmica o la distribución seminormal) suele ser una mejor opción que una distribución normal, que permite valores negativos. Meridian utiliza varias distribuciones comunes, lo que te permite seleccionar la que mejor refleje la naturaleza del parámetro que quieres modelar.
Ejemplo de código: la confianza frente a la incertidumbre
Consulta a continuación cómo podrías expresar en tu código diferentes niveles de certeza sobre el ROI de tres canales de medios pagados diferentes.
from meridian.model import prior_distribution
# --- Channel 1: High Confidence ---
# You have strong experiment results showing ROI is consistently around 1.2.
# You use a small standard deviation (0.2) to reflect your high confidence.
strong_prior_channel_1 = prior_distribution.lognormal_dist_from_mean_std(
mean=1.2,
std=0.2
)
# --- Channel 2: Low Confidence ---
# You have weaker experiment results showing ROI is around 1.0.
# You use a small sigma (0.9) to reflect your weaker confidence in the
# experiment result than for Channel 1.
weak_prior_channel_2 = prior_distribution.lognormal_dist_from_mean_std(
mean=1.0,
std=0.9
)
# --- Channel 3: Confidence in a range ---
# You believe there's a 95% chance the ROI is between 2.0 and 6.0.
range_prior_channel_3 = prior_distribution.lognormal_dist_from_range(
low=2.0,
high=6.0
mass_percent=0.95
)
# You would then assign these distributions to their respective channels
# when you configure your model.
prior_config = prior_distribution.PriorDistribution(
roi_m=[strong_prior_channel_1, weaker_prior_channel_2, range_prior_channel_3]
)
Visualización de tus distribuciones a priori
La manera de trazar tus distribuciones a priori es sencilla y puede ayudarte a garantizar que coincidan con tu intuición.
from matplotlib import pyplot as plt
from meridian.model import prior_distribution
import numpy as np
# Define the LogNormal distribution
lognormal_dist = prior_distribution.lognormal_dist_from_mean_std(2.0, 0.5)
# Plot a histogram of samples from the LogNormal distribution
plt.hist(lognormal_dist.sample(1000))
Importancia de las distribuciones a priori
El uso de distribuciones a priori no es tan solo una función técnica: es fundamental para obtener estimaciones causales en las que puedas confiar y que te permitan tomar medidas adecuadas.
- Resultados más plausibles y estables con menos datos: Los datos de marketing agregados pueden ser dispersos o ruidosos. Las distribuciones a priori brindan un efecto estabilizador, ya que guían el modelo hacia resultados plausibles y evitan que llegue a conclusiones incorrectas basadas en datos limitados.
- Resultados basados en la realidad empresarial: Al incorporar conocimientos de fuentes confiables, como los estudios de efectividad, el efecto estabilizador de la distribución a priori guía el modelo para que se corresponda con esos conocimientos, lo que aumenta la confianza de las partes interesadas.
- Codificación de la intuición comercial: Casi siempre tienes una cierta intuición sobre tu empresa. Por ejemplo, tal vez en tu industria sea poco común obtener un ROI superior a 6.0, así que puedes codificar esa intuición en tu distribución a priori para guiar el modelo hacia resultados más realistas, incluso si no dispones de datos concretos de ningún experimento.
- Controles intuitivos del modelo: Establecer una distribución a priori es como tener una conversación intuitiva con tu modelo. En lugar de ajustar parámetros abstractos, proporcionas orientación en un lenguaje que comprendes; por ejemplo, "Tengo pruebas sólidas de que el ROI de mi canal es de alrededor de 1.5".