En esta sección, se describen las distribuciones a priori predeterminadas del modelo de Meridian. Todas las distribuciones a priori se especifican con el argumento prior_distribution, que admite un objeto PriorDistribution. Cada parámetro tiene su propio argumento en el constructor PriorDistribution, y la distribución a priori conjunta supone que todas las distribuciones a priori son independientes.
Las distribuciones se pueden especificar como un vector (p. ej., tfp.distributions.Normal([1, 2, 3], [1, 1, 2])) o como un escalar (p. ej., tfp.distributions.Normal(1, 2)). Se emplea un proceso de broadcasting en todas las distribuciones escalares según la longitud del vector del parámetro que representan.
knot_values
Parámetro: \(b_k\)
Distribución a priori predeterminada: Normal(0, 5)
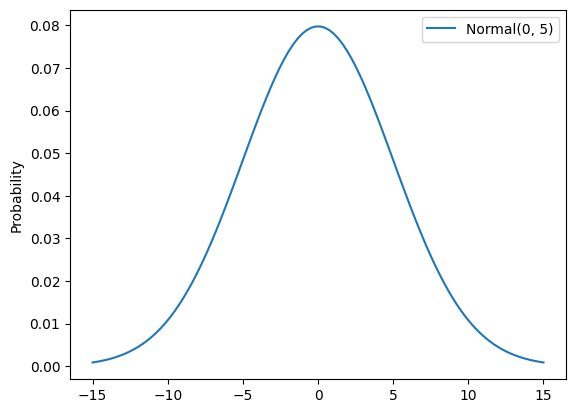
Fundamentos:
- Es una distribución a priori no informativa que indica el período durante el que puede producirse un efecto.
- Es no informativa porque necesitas flexibilidad para disponer de un período en el que pueda producirse un efecto significativo.
- Se puede obtener de los datos que proporcionan varias ubicaciones geográficas por período y también varios períodos por nudo cuando la cantidad de nudos es baja.
tau_g_excl_baseline
Parámetro: \(\tau_g\)
Distribución a priori predeterminada: Normal(0, 5)

Fundamentos:
- Es una distribución a priori no informativa que indica las diferencias geográficas.
- Es no informativa porque necesitas flexibilidad para disponer de una ubicación geográfica en la que pueda producirse un efecto significativo.
- Se puede obtener de los datos que proporcionan varios períodos por ubicación geográfica.
roi_m y roi_rf
Parámetro: \(\text{ROI}_i^{[M]},\text{ROI}_{i}^{[RF]}\)
Distribución a priori predeterminada: LogNormal(0.2, 0.9)
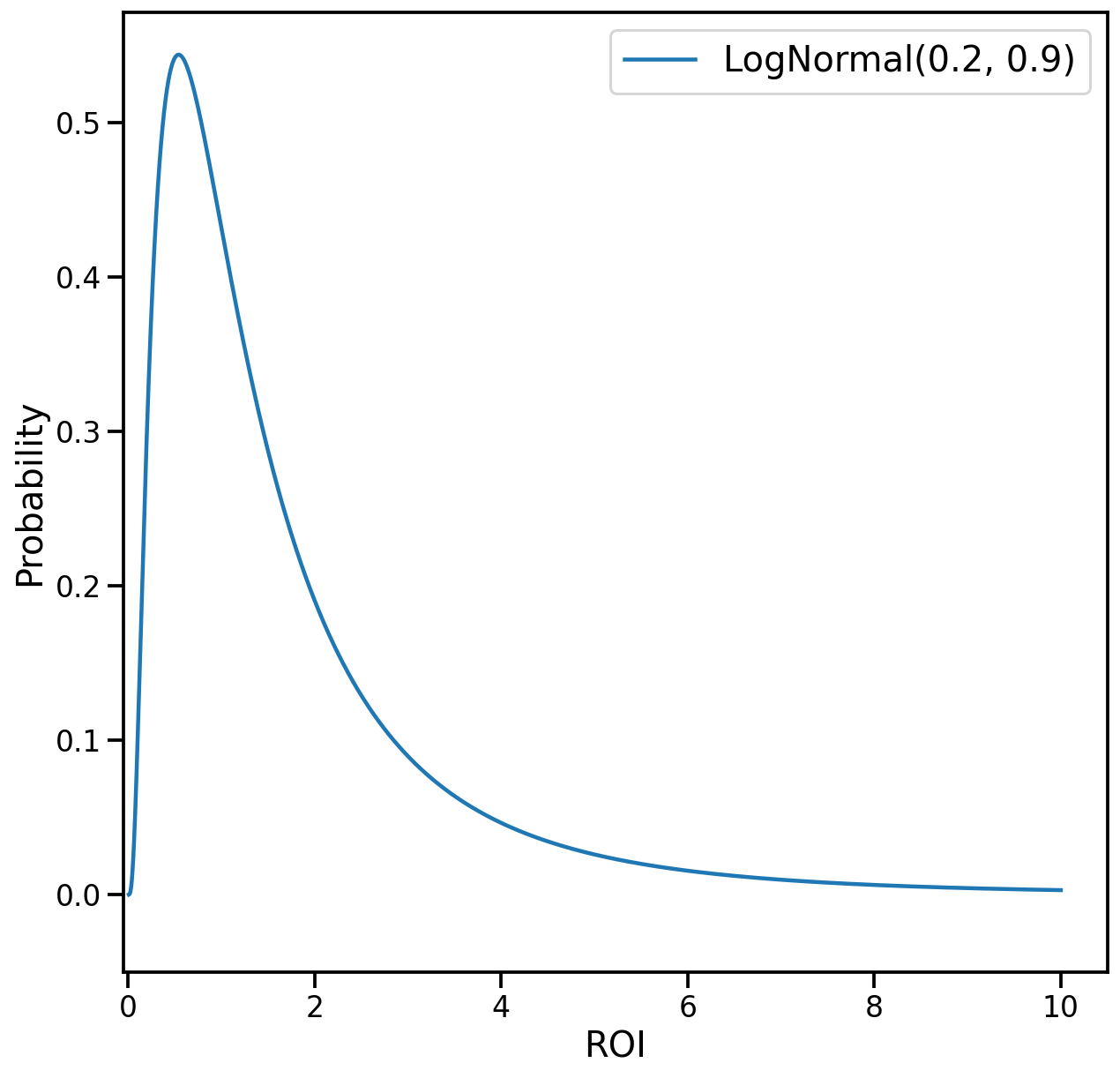
Fundamentos:
- Esta distribución a priori indica lo siguiente: el ROI medio a priori de cada canal es de 1.83, el 50% de los ROI es superior a 1.22, el 80% es de 0.5 a 6.0, el 95% es de 0.25 a 9.0, y el 99% es inferior a 10.0.
- Si el KPI no corresponde a los ingresos y no hay disponibles datos sobre los ingresos por KPI, se aplica una distribución a priori del ROI común a todos los canales, de modo que la proporción incremental del KPI generada por todos los canales de medios de comunicación pagos tenga una distribución a priori media del 40% y una desviación estándar del 20% (denominada "distribución a priori de la contribución total de medios de comunicación pagos"). Para obtener más información sobre esta configuración predeterminada, consulta Distribución a priori predeterminada de la contribución total de medios de comunicación pagos.
- La distribución predeterminada es estrictamente positiva, lo cual es necesario cuando los efectos aleatorios del coeficiente de medios son normales a nivel logarítmico (
media_effects_dist='log_normal'). Se podría usar una distribución a priori que permita los valores negativos cuando los efectos aleatorios seanmedia_effects_dist='normal', pero, por lo general, esto no se recomienda, ya que puede aumentar la varianza posterior y causar problemas de convergencia del muestreo de MCMC.
mroi_m y mroi_rf
Parámetro: \(\text{mROI}_i^{[M]},\text{mROI}_{i}^{[RF]}\)
Distribución a priori predeterminada LogNormal(0.0, 0.5)
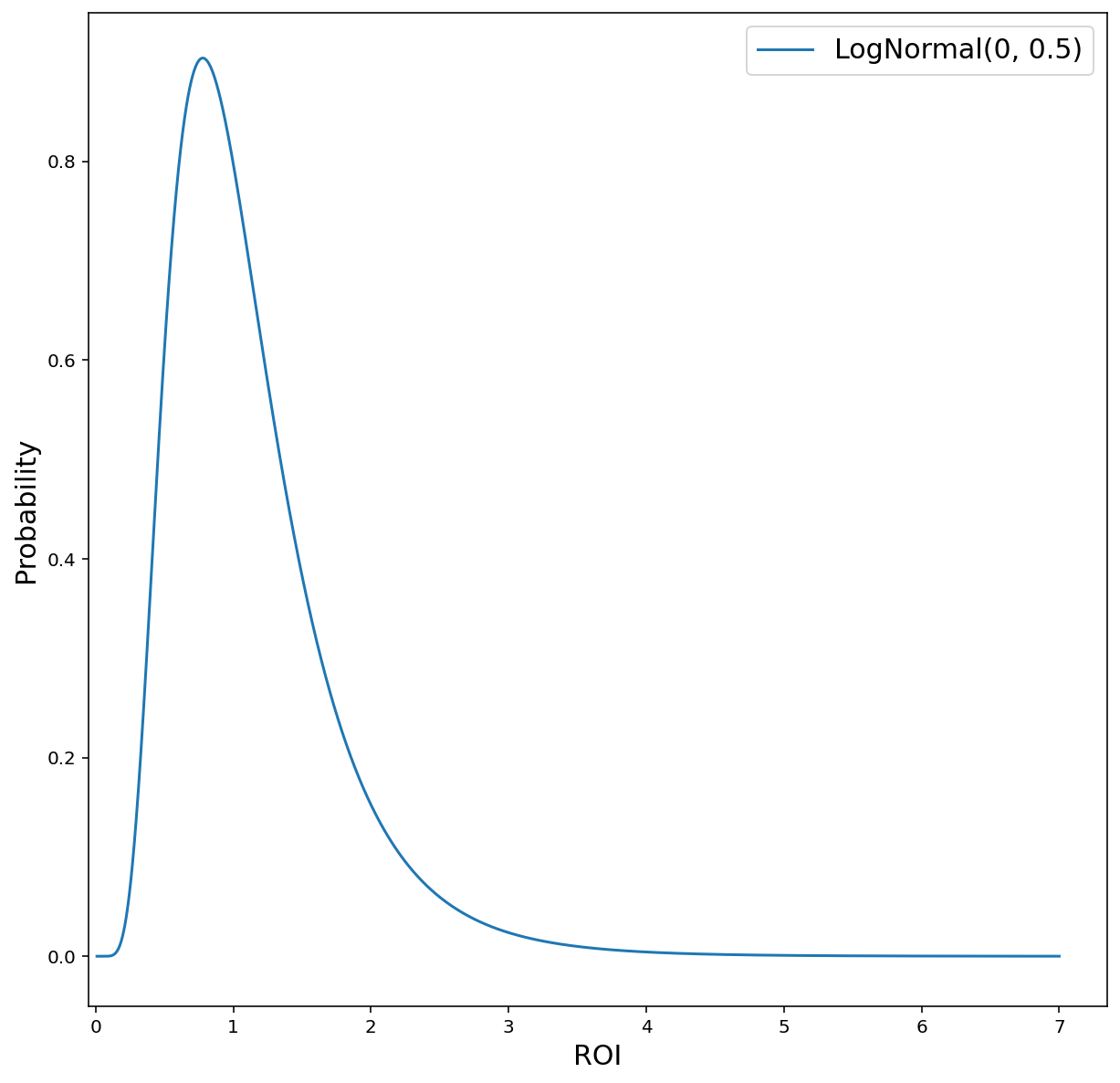
Fundamentos:
- Esta distribución a priori indica que el mROI medio de cada canal es de 1.13 a priori; un 50% de los mROI es superior a 1.0; un 80% se encuentra entre 0.53 y 1.90; un 95%, entre 0.33 y 2.66, y un 99% es inferior a 3.20.
- De forma predeterminada, a cada canal se le asigna la misma distribución a priori del mROI.
- Si el KPI no se basa en los ingresos y los datos de los ingresos por KPI no están disponibles, todavía se pueden utilizar las distribuciones a priori del mROI, pero se debe especificar una distribución personalizada para
roi_myroi_rf. En este caso, el mROI se interpreta como unidades de KPI incrementales por unidad de inversión (atribuidas a un pequeño aumento de la inversión).
contribution_m, contribution_rf, contribution_om y contribution_orf
Parámetro: \(\text{Contribution}_i^{[M]},\text{Contribution}_{i}^{[RF]}\), \(\text{Contribution}_i^{[OM]},\text{Contribution}_{i}^{[ORF]}\)
Distribución a priori predeterminada: Beta(1.0, 99.0)

Fundamentos:
- La distribución a priori predeterminada indica que, a priori, la contribución promedio de cada canal es del 1%, el 50% de los valores de contribución son superiores al 0.7%, el 80% están entre el 0.1% y el 2.3%, el 95% están entre el 0.03% y el 3.7%, y el 99% son inferiores al 4.5%.
- La distribución predeterminada no permite que la contribución de ningún canal individual supere 1.0 (100% de los resultados observados). Sin embargo, esto no necesariamente impide que la contribución combinada de varios canales supere el 100%.
- La distribución predeterminada es estrictamente positiva, lo cual es necesario cuando los efectos aleatorios del coeficiente de medios son normales a nivel logarítmico (
media_effects_dist='log_normal'). Se podría usar una distribución a priori que permita los valores negativos cuando los efectos aleatorios seanmedia_effects_dist='normal', pero, por lo general, esto no se recomienda, ya que puede aumentar la varianza posterior y causar problemas de convergencia del muestreo de MCMC. - La distribución predeterminada se regulariza hasta cierto punto para mitigar la convergencia de MCMC y los problemas de modelos de referencia negativos. Considera establecer una distribución a priori personalizada que sea efectiva para tu caso de uso.
contribution_n
Parámetro: \(\text{Contribution}_i^{[N]}\)
Distribución a priori predeterminada: TruncatedNormal(0.0, 0.1, -1.0, 1.0)

Fundamentos:
- El valor a priori predeterminado indica que, a priori, las contribuciones media y mediana de cada canal son del 0% del resultado total observado, el 80% se encuentran entre un -12.8% y un +12.8%, el 95% se encuentran entre un -19.6% y un +19.6%, y el 99% se encuentran entre un -25.8% y un +25.8%.
- La distribución a priori predeterminada permite los valores negativos porque los tratamientos que no son de medios pueden tener una contribución negativa o positiva según el tipo de tratamiento y el valor del tratamiento del modelo de referencia correspondiente. Si tienes conocimiento previo de que la contribución de una variable en particular es estrictamente positiva o negativa, esto se debe incorporar en la distribución a priori.
beta_m, beta_rf, beta_om y beta_orf
Parámetro: \(\beta_i^{[M]},\beta_{i}^{[RF]},\beta_{i}^{[OM]}, \beta_{i}^{[ORF]}\)
Distribución a priori predeterminada: HalfNormal(5)

Fundamentos:
- Es una distribución a priori no informativa sobre el parámetro relacionado con la distribución jerárquica de los efectos de los medios a nivel de la ubicación geográfica para los canales de medios orgánicos de impresión y para los canales de medios de comunicación pagos de alcance y frecuencia, respectivamente (
beta_gom; beta_gorf). Cuandomedia_effects_distse establece en'normal', representa la media jerárquica. Cuandomedia_effects_distse establece en'log_normal', es el parámetro jerárquico para la media de la distribución subyacenteNormaltransformada en logaritmos. - Es una distribución a priori no informativa sobre el parámetro relacionado con la distribución jerárquica de los efectos de los medios a nivel de la ubicación geográfica para los canales de medios de comunicación pagos de impresión y para los canales de medios de comunicación pagos de alcance y frecuencia, respectivamente (
beta_gm; beta_grf). Cuandomedia_effects_distse establece en'normal', representa la media jerárquica. Cuandomedia_effects_distse establece en'log_normal', es el parámetro jerárquico para la media de la distribución subyacenteNormaltransformada en logaritmos. - Es no informativa porque la interpretación de
beta_m,beta_rf,beta_omybeta_orfpuede variar en gran medida según las transformaciones, el ajuste de la escala y el tipo de ejecución de medios. - De forma predeterminada, Meridian usa las distribuciones a priori del ROI (
roi_myroi_rf) para los canales de medios pagados. Si deseas utilizar las distribuciones a prioribeta_mybeta_rfpara los medios de comunicación pagos, establecemedia_prior_type='coefficient'yrf_prior_type='coefficient'. De forma predeterminada, Meridian utiliza distribuciones a priori de contribución para los canales de medios orgánicos (
contribution_omycontribution_orf). Para usar las distribuciones a priori debeta_omybeta_orfpara los medios orgánicos, estableceorganic_media_prior_type='coefficient'yorganic_rf_prior_type='coefficient'.[M]denota un canal de medios de comunicación pagos con impresiones.[RF]denota un canal de medios de comunicación pagos con alcance y frecuencia.[OM]denota un canal de medios orgánicos con impresiones.[ORF]denota un canal de medios orgánicos con alcance y frecuencia.
eta_m, eta_rf, eta_om y eta_orf
Parámetro: \(\eta_i^{[M]},\eta_{i}^{[RF]},\eta_{i}^{[OM]}, \eta_{i}^{[ORF]}\)
Distribución a priori predeterminada: HalfNormal(1)
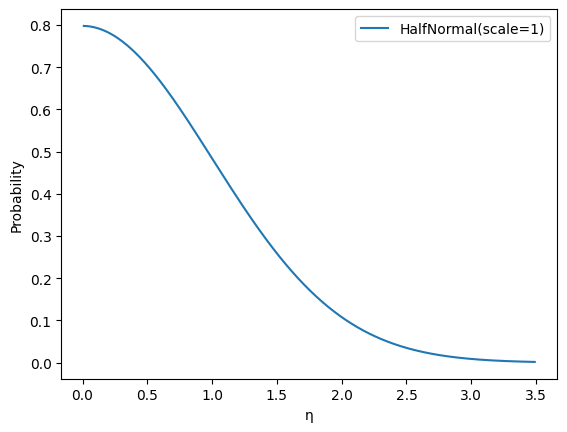
Fundamentos:
La regularización moderada fomenta la reducción de las diferentes ubicaciones geográficas. Esto genera estimaciones de varianza más baja a costa de un sesgo más alto y permite que el modelo use los datos de manera más eficiente.
gamma_c y gamma_n
Parámetro: \(\gamma_i^{[C]},\gamma_i^{[N]}\)
Distribución a priori predeterminada: Normal(0, 5)

Fundamentos:
- Es no informativa debido a la amplia cantidad de variables de control o de tratamiento no relacionadas con los medios que puedes observar.
- De forma predeterminada, Meridian usa las distribuciones a priori de la contribución (
contribution_n) para los canales de tratamiento que no son de medios. Si deseas utilizar las distribuciones a priori degamma_npara las variables de tratamiento no relacionadas con medios, establecenon_media_treatments_prior_type='coefficient'.
xi_c y xi_n
Parámetro: \(\xi_i^{[C]},\xi_i^{[N]}\)
Distribución a priori predeterminada: HalfNormal(5)

Fundamentos:
- Es no informativa para permitir un amplio rango de variación geográfica en los efectos de las variables de control y de tratamiento no relacionadas con los medios.
- De forma predeterminada, la reducción es más débil para los efectos de las variables de control y las de tratamiento no relacionadas con los medios que para los efectos de los medios, ya que los primeros son lineales simples (sin la complejidad de las transformaciones de Hill y Adstock).
alpha_m, alpha_rf, alpha_om y alpha_orf
Parámetro: \(\alpha_i^{[M]},\alpha_{i}^{[RF]},\alpha_{i}^{[OM]}, \alpha_{i}^{[ORF]}\)
Distribución a priori predeterminada: Uniform(0, 1)
Fundamentos:
Es no informativa para permitir que los datos influyan en la tasa de decaimiento.
Si tienes una intuición sobre la tasa de decaimiento, considera establecer una distribución a priori personalizada que tenga sentido para tu caso de uso. Consulta La distribución a priori alfa para obtener orientación sobre cómo establecer una distribución a priori personalizada.
ec_m y ec_om
Parámetro: \(ec_i^{[M]}, ec_{i}^{[OM]}\)
Distribución a priori predeterminada: TruncatedNormal(0.8, 0.8, 0.1, 10); es la distribución condicional \(X|0.1 < X < 10\), donde \(X \sim N(0.8,0.8)\).

Fundamentos:
- Los datos se ajustan de modo que, cuando \(ec=1\), la mitad de la saturación ocurre al valor de la mediana de las unidades de medios per cápita distintas de cero en las distintas ubicaciones geográficas y períodos. En cambio,\(ec=X\) significa que la mitad de la saturación ocurre a un valor de \(X\) veces el valor de la mediana de las unidades de medios per cápita distintas de cero en las distintas ubicaciones geográficas y períodos.
- Esta distribución a priori tiene una media cercana a uno, lo que constituye un supuesto a priori razonable acerca del punto en el que se da la mitad de la saturación.
- El truncamiento se realiza para mantener el parámetro dentro de un rango razonable que permita su identificación.
- Si un canal está, en gran medida, infrasaturado (\(ec > 10\)) o sobresaturado (\(ec < 0.1\)), los datos no incluyen información sobre el punto en el que se da la saturación media. En esos casos, el parámetro
ec_mdetermina la forma de la curva de respuesta, pero no debería interpretarse como una estimación exacta de la saturación media.
ec_rf y ec_orf
Parámetro: \(ec_{i}^{[RF]},ec_{i}^{[ORF]}\)
Distribución a priori predeterminada: LogNormal(0.7, 0.4) + 1

# Tensorflow Probability Syntax
tfp.distributions.TransformedDistribution(
tfp.distributions.LogNormal(0.7, 0.4),
tfp.bijectors.Shift(0.1)
)
Fundamentos:
- Es moderadamente informativa para evitar una falta de identificación con
slope_rf. - Se establece junto con la distribución a priori de
slope_rf, de forma tal que la distribución a priori de la frecuencia óptima tenga una media de 2.1 y un IC de un 90% de[1.0, 4.4]. Esto se considera un rango razonable de frecuencia óptima.
slope_m y slope_om
Parámetro: \(\text{slope}_i^{[M]},\text{slope}_{i}^{[OM]}\)
Distribución a priori predeterminada: Deterministic(1)
Fundamentos:
- Es difícil de obtener por motivos de identificación.
Deterministic(1)significa que se limita a curvas de Hill cóncavas.- El algoritmo de optimización del presupuesto devuelve un valor óptimo global cuando las curvas de Hill son cóncavas. Cambiar esta distribución a priori puede generar curvas de Hill no cóncavas, con lo que la optimización del presupuesto ya no podría devolver un valor óptimo global.
slope_rf y slope_orf
Parámetro: \(\text{slope}_{i}^{[RF]},\text{slope}_{i}^{[ORF]}\)
Distribución a priori predeterminada: LogNormal(0.7, 0.4)

Fundamentos:
- Es moderadamente informativa para evitar una falta de identificación con
ec_rf. Se establece junto con la distribución a priori de
ec_rf, de modo que la distribución a priori de la frecuencia óptima tenga una media de 2.1 y un IC del 90% de[1, 4.4], es decir, un rango razonable de frecuencia óptima.[M]denota un canal de medios de comunicación pagos con impresiones.[RF]denota un canal de medios de comunicación pagos con alcance y frecuencia.[OM]denota un canal de medios orgánicos con impresiones.[ORF]denota un canal de medios orgánicos con alcance y frecuencia.
sigma
Parámetro: \(\sigma_g\)
Distribución a priori predeterminada: HalfNormal(5)

Fundamentos:
Es no informativa porque la varianza residual cambia mucho de un anunciante a otro.
