নিউরাল নেটওয়ার্ক: অ্যাক্টিভেশন ফাংশন

আপনি আগের অনুশীলনে দেখেছেন যে আমাদের নেটওয়ার্কে কেবল লুকানো স্তর যুক্ত করাই অরৈখিকতা উপস্থাপনের জন্য যথেষ্ট নয়। রৈখিক ক্রিয়াকলাপগুলিতে সম্পাদিত রৈখিক ক্রিয়াকলাপগুলি এখনও রৈখিক।

মানগুলির মধ্যে অরৈখিক সম্পর্ক শেখার জন্য আপনি কীভাবে একটি নিউরাল নেটওয়ার্ক কনফিগার করতে পারেন? একটি মডেলে অরৈখিক গাণিতিক ক্রিয়াকলাপ সন্নিবেশ করার জন্য আমাদের কিছু উপায় প্রয়োজন।

যদি এটি কিছুটা পরিচিত মনে হয়, তবে এর কারণ হল আমরা কোর্সের শুরুতে একটি রৈখিক মডেলের আউটপুটে অরৈখিক গাণিতিক ক্রিয়াকলাপ প্রয়োগ করেছি। লজিস্টিক রিগ্রেশন মডিউলে, আমরা একটি রৈখিক রিগ্রেশন মডেলকে অভিযোজিত করেছি যাতে 0 থেকে 1 পর্যন্ত একটি অবিচ্ছিন্ন মান আউটপুট করা যায় (একটি সম্ভাব্যতা প্রতিনিধিত্ব করে) একটি সিগময়েড ফাংশনের মাধ্যমে মডেলের আউটপুট পাস করে।

আমরা আমাদের নিউরাল নেটওয়ার্কের ক্ষেত্রেও একই নীতি প্রয়োগ করতে পারি। আসুন আমরা আগে অনুশীলনী ২ থেকে আমাদের মডেলটি আবার দেখি, কিন্তু এবার, প্রতিটি নোডের মান আউটপুট করার আগে, আমরা প্রথমে সিগময়েড ফাংশনটি প্রয়োগ করব:

>| বোতামে ক্লিক করে প্রতিটি নোডের গণনার মধ্য দিয়ে যাওয়ার চেষ্টা করুন (প্লে বোতামের ডানদিকে)। গ্রাফের নীচের গণনা প্যানেলে প্রতিটি নোডের মান গণনা করার জন্য সম্পাদিত গাণিতিক ক্রিয়াকলাপগুলি পর্যালোচনা করুন। মনে রাখবেন যে প্রতিটি নোডের আউটপুট এখন পূর্ববর্তী স্তরের নোডগুলির রৈখিক সংমিশ্রণের একটি সিগময়েড রূপান্তর, এবং আউটপুট মানগুলি 0 এবং 1 এর মধ্যে স্কুইশ করা হয়েছে।

এখানে, সিগময়েড নিউরাল নেটওয়ার্কের জন্য একটি অ্যাক্টিভেশন ফাংশন হিসেবে কাজ করে, যা নিউরাল নেটওয়ার্কের পরবর্তী স্তরের গণনায় ইনপুট হিসেবে মানটি পাস করার আগে একটি নিউরনের আউটপুট মানের একটি অরৈখিক রূপান্তর।

এখন যেহেতু আমরা একটি অ্যাক্টিভেশন ফাংশন যোগ করেছি, লেয়ার যোগ করলে আরও বেশি প্রভাব পড়বে। নন-লিনিয়ারিটির উপর নন-লিনিয়ারিটি স্ট্যাক করার মাধ্যমে আমরা ইনপুট এবং পূর্বাভাসিত আউটপুটের মধ্যে খুব জটিল সম্পর্ক মডেল করতে পারি। সংক্ষেপে, প্রতিটি লেয়ার কার্যকরভাবে কাঁচা ইনপুটগুলির উপর আরও জটিল, উচ্চ-স্তরের ফাংশন শিখছে। এটি কীভাবে কাজ করে সে সম্পর্কে আপনি যদি আরও অন্তর্দৃষ্টি বিকাশ করতে চান, তাহলে ক্রিস ওলাহর চমৎকার ব্লগ পোস্টটি দেখুন।

সাধারণ অ্যাক্টিভেশন ফাংশন

অ্যাক্টিভেশন ফাংশন হিসেবে সাধারণত ব্যবহৃত তিনটি গাণিতিক ফাংশন হল সিগময়েড, ট্যানহ এবং রিলু।

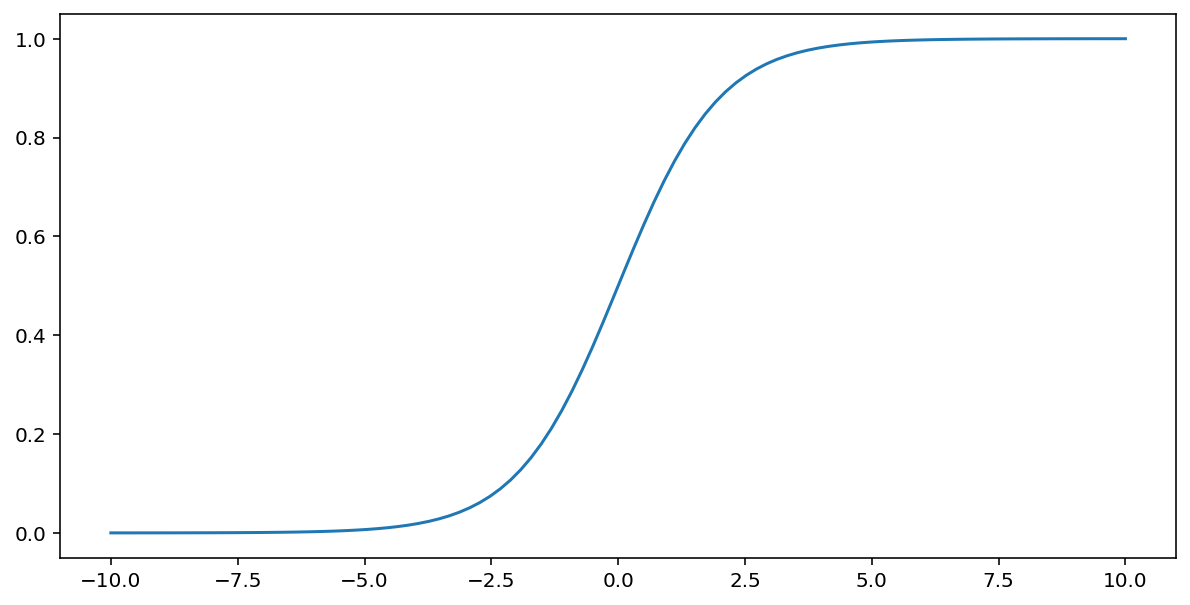
সিগময়েড ফাংশন (উপরে আলোচনা করা হয়েছে) $x$ ইনপুটে নিম্নলিখিত রূপান্তর সম্পাদন করে, 0 এবং 1 এর মধ্যে একটি আউটপুট মান তৈরি করে:

\[F(x)=\frac{1} {1+e^{-x}}\]

এই ফাংশনের একটি প্লট এখানে দেওয়া হল:

চিত্র ৪. সিগময়েড ফাংশনের প্লট: একটি s-আকৃতির বক্ররেখা যা x ঋণাত্মকের কাছে পৌঁছানোর সাথে সাথে লক্ষণহীনভাবে x-অক্ষের কাছে আসে অসীম এবং x অসীমের কাছে পৌঁছানোর সাথে সাথে 1।
চিত্র ৪। সিগময়েড ফাংশনের প্লট।

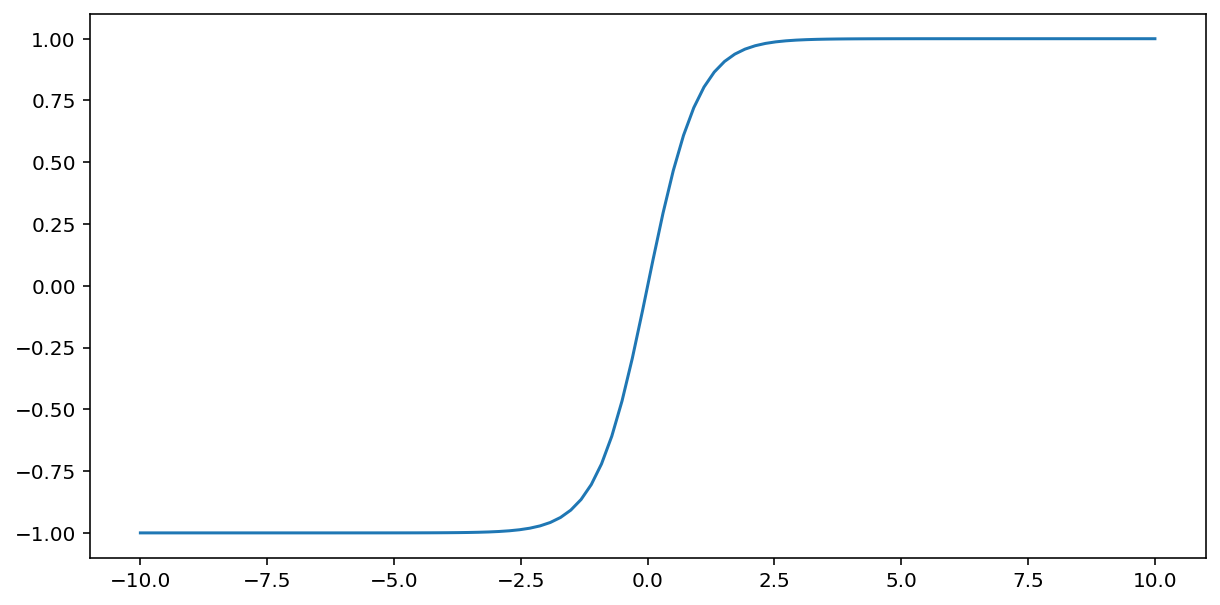
tanh ("হাইপারবোলিক ট্যানজেন্ট" এর সংক্ষিপ্ত রূপ) ফাংশন ইনপুট $x$ কে রূপান্তর করে -1 এবং 1 এর মধ্যে একটি আউটপুট মান তৈরি করে:

\[F(x)=tanh(x)\]

এই ফাংশনের একটি প্লট এখানে দেওয়া হল:

চিত্র ৫. tanh ফাংশনের প্লট: সিগময়েড ফাংশনের তুলনায় সামান্য খাড়া s-আকৃতির বক্ররেখা, যা লক্ষণহীনভাবে x ঋণাত্মক অসীমের কাছে পৌঁছালে –1 এবং x অসীমের কাছে পৌঁছালে 1 এর কাছাকাছি চলে আসে।
চিত্র ৫। tanh ফাংশনের প্লট।

সংশোধিত রৈখিক ইউনিট অ্যাক্টিভেশন ফাংশন (অথবা সংক্ষেপে ReLU ) নিম্নলিখিত অ্যালগরিদম ব্যবহার করে আউটপুট রূপান্তর করে:

  • যদি ইনপুট মান $x$ 0 এর কম হয়, তাহলে 0 প্রদান করুন।
  • যদি ইনপুট মান $x$ 0 এর চেয়ে বড় বা সমান হয়, তাহলে ইনপুট মানটি ফেরত দিন।

Max() ফাংশন ব্যবহার করে ReLU কে গাণিতিকভাবে উপস্থাপন করা যেতে পারে:

$$F(x)=max(0,x)$$

এই ফাংশনের একটি প্লট এখানে দেওয়া হল:

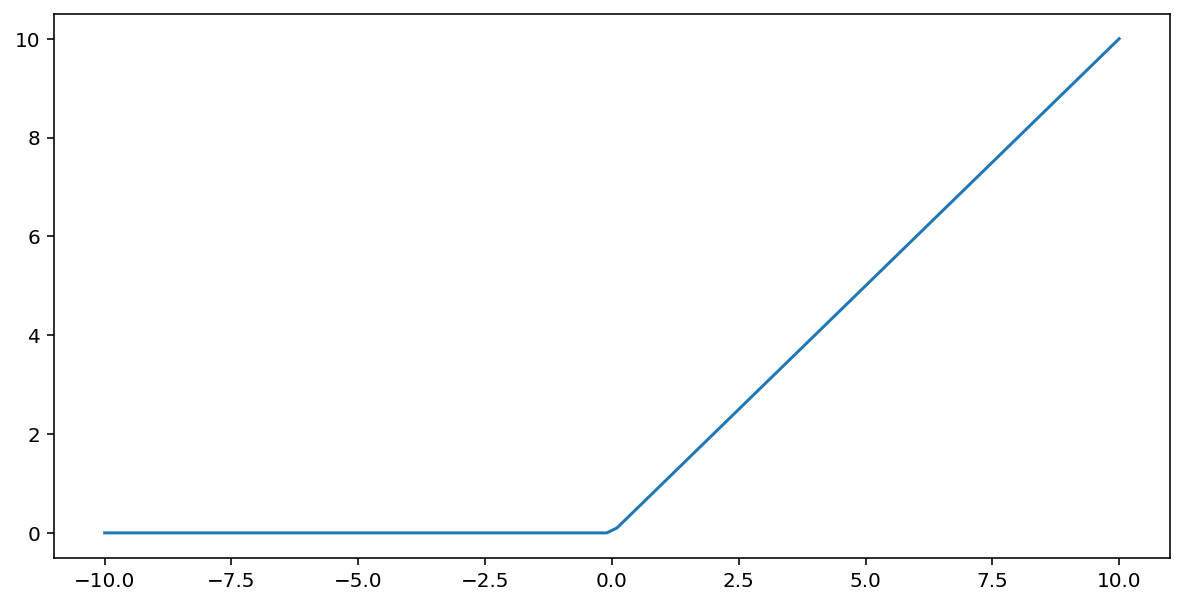
চিত্র ৬. ReLU ফাংশনের প্লট: একটি অনুভূমিক রেখা ঋণাত্মক অসীম থেকে 0 পর্যন্ত x-অক্ষ বরাবর, যা একটি তির্যক রেখায় পরিণত হয় 0 থেকে অসীম পর্যন্ত ঢাল 1 (y=x) সহ উপরে এবং ডানদিকে যায়।
চিত্র ৬। ReLU ফাংশনের প্লট।

সিগময়েড বা ট্যানের মতো মসৃণ ফাংশনের তুলনায় রিলু অ্যাক্টিভেশন ফাংশন হিসেবে কিছুটা ভালো কাজ করে, কারণ নিউরাল নেটওয়ার্ক প্রশিক্ষণের সময় এটি ভ্যানিশিং গ্রেডিয়েন্ট সমস্যার প্রতি কম সংবেদনশীল। এই ফাংশনগুলির তুলনায় রিলু গণনা করাও উল্লেখযোগ্যভাবে সহজ।

অন্যান্য সক্রিয়করণ ফাংশন

বাস্তবে, যেকোনো গাণিতিক ফাংশন একটি সক্রিয়করণ ফাংশন হিসেবে কাজ করতে পারে। ধরুন যে \(\sigma\) আমাদের অ্যাক্টিভেশন ফাংশন প্রতিনিধিত্ব করে। নেটওয়ার্কে একটি নোডের মান নিম্নলিখিত সূত্র দ্বারা দেওয়া হয়:

$$\sigma(\boldsymbol w \cdot \boldsymbol x+b)$$

Keras অনেক অ্যাক্টিভেশন ফাংশনের জন্য আউট-অফ-দ্য-বক্স সাপোর্ট প্রদান করে। তবুও, আমরা এখনও ReLU দিয়ে শুরু করার পরামর্শ দিচ্ছি।

সারাংশ

নিউরাল নেটওয়ার্ক কীভাবে তৈরি হয় সে সম্পর্কে আপনি এখন পর্যন্ত যা কিছু শিখেছেন তার সংক্ষিপ্তসার নিম্নলিখিত ভিডিওটিতে দেওয়া হয়েছে:

এখন আমাদের মডেলে নিউরাল নেটওয়ার্ক বলতে মানুষ সাধারণত যা বোঝায় তার সমস্ত স্ট্যান্ডার্ড উপাদান রয়েছে:

  • স্তরে স্তরে সংগঠিত নিউরনের অনুরূপ নোডের একটি সেট।
  • প্রতিটি নিউরাল নেটওয়ার্ক স্তর এবং তার নীচের স্তরের মধ্যে সংযোগ প্রতিনিধিত্বকারী শেখা ওজন এবং পক্ষপাতের একটি সেট। নীচের স্তরটি অন্য একটি নিউরাল নেটওয়ার্ক স্তর, অথবা অন্য কোনও ধরণের স্তর হতে পারে।
  • একটি অ্যাক্টিভেশন ফাংশন যা একটি লেয়ারের প্রতিটি নোডের আউটপুটকে রূপান্তরিত করে। বিভিন্ন লেয়ারের বিভিন্ন অ্যাক্টিভেশন ফাংশন থাকতে পারে।

একটি সতর্কতা: নিউরাল নেটওয়ার্কগুলি সর্বদা ফিচার ক্রসের চেয়ে ভাল হয় না, তবে নিউরাল নেটওয়ার্কগুলি একটি নমনীয় বিকল্প প্রদান করে যা অনেক ক্ষেত্রেই ভাল কাজ করে।

পূর্ববর্তী
নোড এবং লুকানো স্তর (15 মিনিট)
পরবর্তী
ব্যাকপ্রপাগেশন ব্যবহার করে প্রশিক্ষণ (10 মিনিট)