Como você viu no exercício anterior , adicionar camadas ocultas à nossa rede não foi suficiente para representar as não linearidades. Operações lineares realizadas sobre operações lineares continuam sendo lineares.
Como configurar uma rede neural para aprender relações não lineares entre valores? Precisamos de alguma forma de inserir operações matemáticas não lineares em um modelo.
Se isso lhe parece um pouco familiar, é porque já aplicamos operações matemáticas não lineares à saída de um modelo linear anteriormente no curso. No módulo de Regressão Logística , adaptamos um modelo de regressão linear para gerar um valor contínuo de 0 a 1 (representando uma probabilidade) passando a saída do modelo por uma função sigmoide .
Podemos aplicar o mesmo princípio à nossa rede neural. Vamos revisitar o modelo do Exercício 2 , mas desta vez, antes de exibir o valor de cada nó, aplicaremos a função sigmoide:
Experimente percorrer os cálculos de cada nó clicando no botão >| (à direita do botão de reprodução). Analise as operações matemáticas realizadas para calcular o valor de cada nó no painel Cálculos, abaixo do gráfico. Observe que a saída de cada nó agora é uma transformação sigmoide da combinação linear dos nós na camada anterior, e os valores de saída estão todos comprimidos entre 0 e 1.
Nesse caso, a função sigmoide serve como função de ativação para a rede neural, uma transformação não linear do valor de saída de um neurônio antes que esse valor seja passado como entrada para os cálculos da próxima camada da rede neural.
Agora que adicionamos uma função de ativação, adicionar camadas tem um impacto maior. Empilhar não linearidades sobre não linearidades nos permite modelar relações muito complexas entre as entradas e as saídas previstas. Em resumo, cada camada está efetivamente aprendendo uma função mais complexa e de nível superior sobre as entradas brutas. Se você quiser desenvolver uma intuição maior sobre como isso funciona, veja a excelente postagem de Chris Olah no blog .
Funções de ativação comuns
Três funções matemáticas comumente usadas como funções de ativação são a sigmoide, a tangente hiperbólica (tanh) e a ReLU.
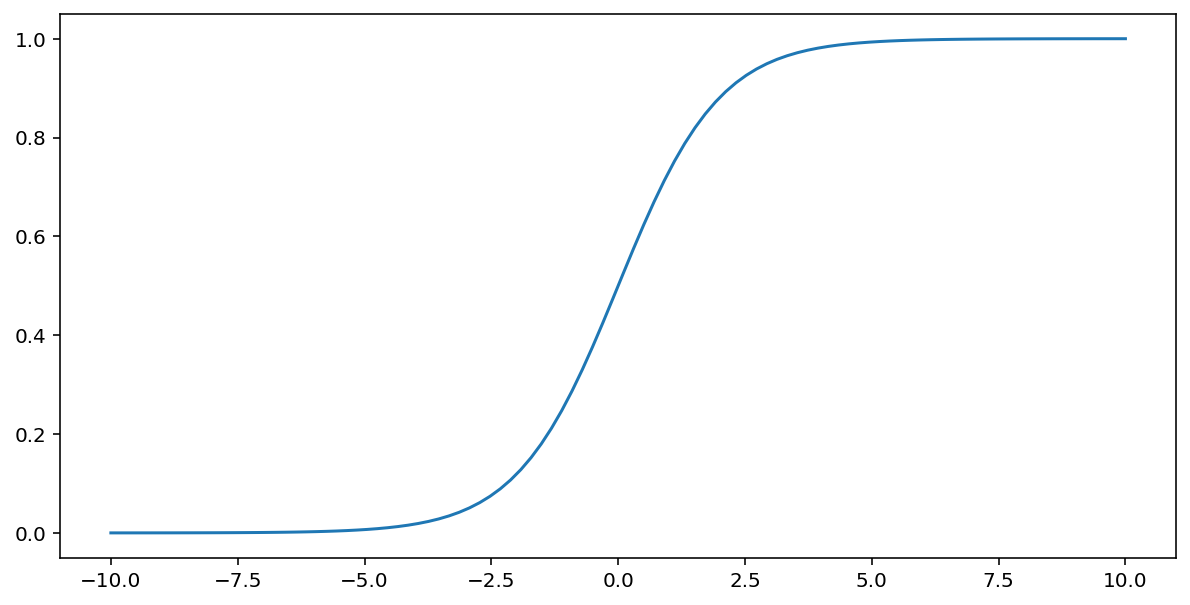
A função sigmoide (discutida acima) realiza a seguinte transformação na entrada $x$, produzindo um valor de saída entre 0 e 1:
\[F(x)=\frac{1} {1+e^{-x}}\]
Aqui está um gráfico dessa função:
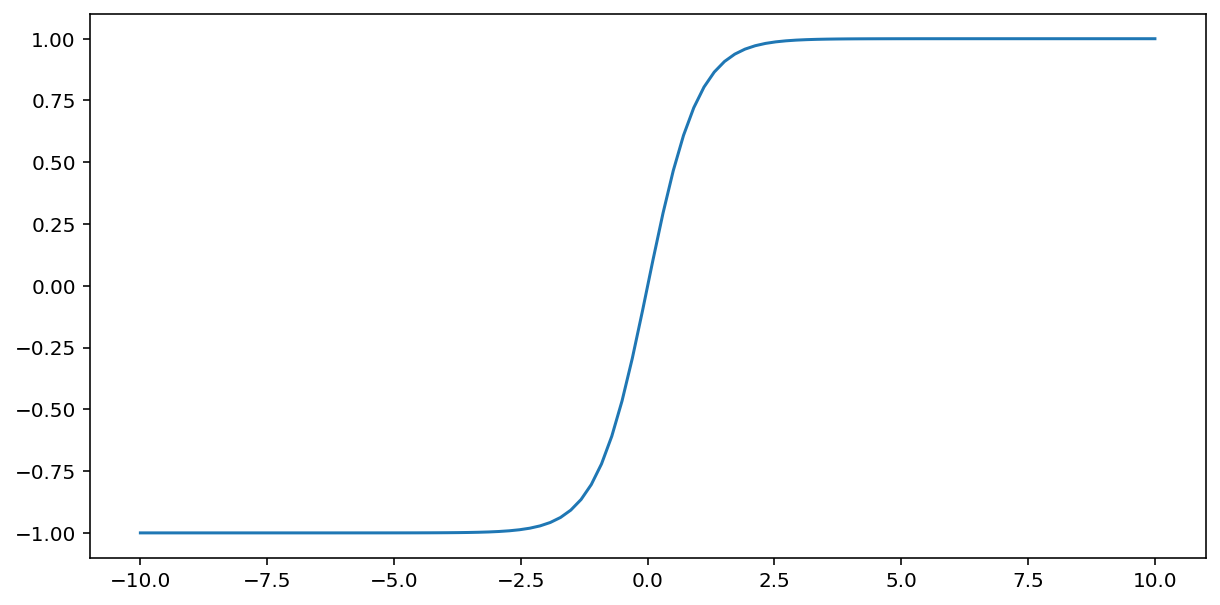
A função tanh (abreviação de "tangente hiperbólica") transforma a entrada $x$ para produzir um valor de saída entre -1 e 1:
\[F(x)=tanh(x)\]
Aqui está um gráfico dessa função:
A função de ativação da unidade linear retificada (ou ReLU , para abreviar) transforma a saída usando o seguinte algoritmo:
- Se o valor de entrada $x$ for menor que 0, retorne 0.
- Se o valor de entrada $x$ for maior ou igual a 0, retorne o valor de entrada.
A ReLU pode ser representada matematicamente usando a função max():
Aqui está um gráfico dessa função:
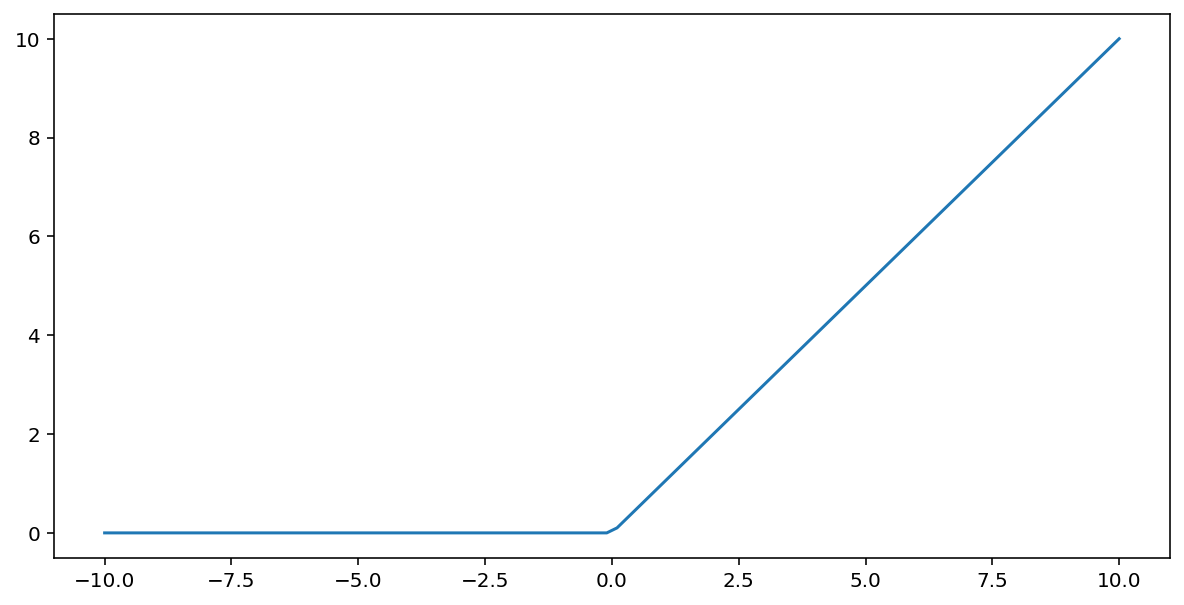
A função ReLU costuma funcionar um pouco melhor como função de ativação do que funções suaves como a sigmoide ou a tangente hiperbólica (tanh), pois é menos suscetível ao problema do desaparecimento do gradiente durante o treinamento de redes neurais . Além disso, a ReLU é significativamente mais fácil de calcular do que essas funções.
Outras funções de ativação
Na prática, qualquer função matemática pode servir como função de ativação. Suponha que \(\sigma\) representa nossa função de ativação. O valor de um nó na rede é dado pela seguinte fórmula:
O Keras oferece suporte imediato a muitas funções de ativação . Dito isso, ainda recomendamos começar com a ReLU.
Resumo
O vídeo a seguir recapitula tudo o que você aprendeu até agora sobre como as redes neurais são construídas:
Agora, nosso modelo possui todos os componentes padrão que as pessoas geralmente entendem por rede neural:
- Um conjunto de nós, análogos a neurônios, organizados em camadas.
- Um conjunto de pesos e vieses aprendidos que representam as conexões entre cada camada da rede neural e a camada abaixo dela. A camada abaixo pode ser outra camada da rede neural ou algum outro tipo de camada.
- Uma função de ativação que transforma a saída de cada nó em uma camada. Camadas diferentes podem ter funções de ativação diferentes.
Uma ressalva: as redes neurais nem sempre são melhores do que o cruzamento de características, mas oferecem uma alternativa flexível que funciona bem em muitos casos.
